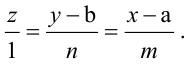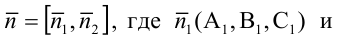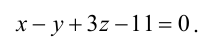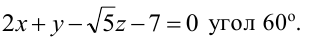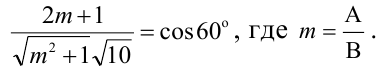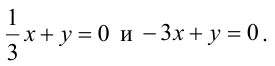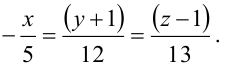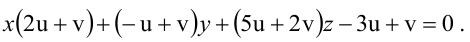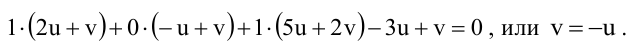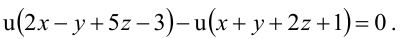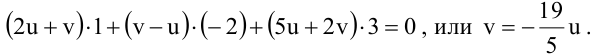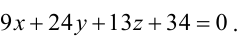1. Общее уравнение прямой.
Прямая в пространстве
может быть задана как пересечение двух
плоскостей:

(1)
О1.
Геометрическое место точек пространства,
удовлетворяющих системе уравнений (1),
называется
прямой
в пространстве,
а
система уравнений (1) называется общим
уравнением прямой.
З1. Для того чтобы
система уравнений (1) определяла прямую
в пространстве необходимо и достаточно,
чтобы нормальные вектора плоскостей,
определяющих
прямую,
и
были неколлинеарными, т.е. выполняется
одно из неравенств:или
.
Пусть прямая
проходит через точку
параллельно вектору
,
который называется направляющим
вектором прямой
(см. Лекцию
№ 7),
тогда ее уравнение называется каноническим
и имеет вид:
.
(2)
З2. Если в уравнении
(2) одна из проекций направляющего вектора
равна 0, то это означает, что прямая
перпендикулярна соответствующей
координатной оси.
Пример 1.
Как расположена прямая
относительно координатных осей.
Согласно замечанию
2 эта прямая будет перпендикулярна осям
абсцисс и ординат (параллельна оси
аппликат) и будет проходить через точку
.
Приравняв каждую
дробь уравнения (2) параметру
,
получимпараметрическое
уравнение прямой:
Пример 2.
Записать уравнение прямой
в параметрическом виде.
Приравняем каждую
дробь к параметру
:
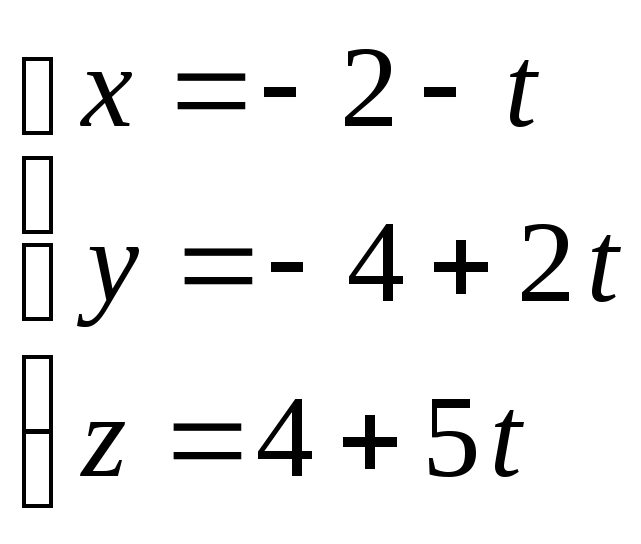
Если пря-
мая проходит через
две известные точки
и
,
то ее уравнение имеет вид (см.Лекцию
№ 7):
и назы-ваетсяуравнением
прямой,
проходящей
через две заданные точки.
2. Основные задачи.
а) Переход
от общего уравнения прямой к каноническому.
Пусть прямая задана общим уравнением

Для того, чтобы перейти от этого уравнения
прямой к каноническому, поступают
следующим образом:
– находят
координаты любой точки, удовлетворяющие
приведенной системе, для чего одну из
переменных величин, например
,
полагают равной нулю и решают систему
линейных алгебраических уравнений
относительно оставшихся переменных
величин;
– направляющий
вектор
прямой находят как векторное произведение
нормальных векторов
и
:
;
– зная
точку, через которую проходит прямая,
и направляющий вектор прямой записывают
каноническое уравнение прямой.
Пример 3.
Записать уравнение прямой

Положив
,
получим СЛАУ
.
Подставив это значение переменнойво второе уравнение системы, по-лучим
.
Таким образом, прямая проходит через
точку
.
Найдем направляющий вектор прямой как
векторное произведение нормальных
векторов заданных плоскостей:
б)
Угол
между пересекающимися прямыми.
Угол
между двумя пересека-ющимися прямыми
определяется как угол между их
направляющими векторами.
Если прямые
и
имеют направляющие вектора
и
,
соответственно,
то угол между прямыми определяется по
формуле:
.
Сл1.
Если
прямые перпендикулярны (),
тоусловием
перпен-дикулярности
прямых является
равенство:
.
Сл2.
Если прямые параллельны, то направляющие
вектора коллинеарны, следовательно,
условие
параллельности прямых:
.
в)
Координаты
точки пересечения прямой и плоскости.
Пусть прямая
задана общим уравнением
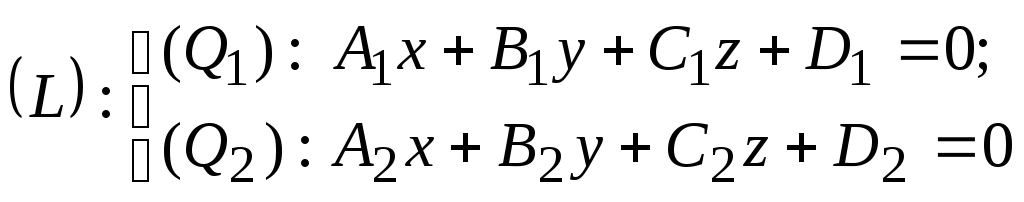
а плоскостьуравнением
.Так
как точка пересечения прямой и плоскости
принадлежит одновременно обоим этим
объектам, то ее координаты находят из
решения системы уравнений:

Если прямая
задана
каноническим уравнением,
а плоскость
уравнением
,
то поступают по следующей
схеме:
– переходят
от канонического уравнения прямой к
параметрическому, т.е. записывают
уравнение прямой в виде

– полученные
выражения подставляют в уравнение
заданной плоскости
и
находят параметр
:
.
Рассмотрим возможные
случаи:
1) если
выполняются условия

то прямая не пересекает плоскость
(прямая параллельна плоскости);
2) при
условиях

3) если
,
прямая пересекает плоскость в одной
точке.
– вычисляют
координаты точки пересечения, подставив
найденное значение
в параметрическое уравнение прямой

г)
Угол
между прямой и плоскостью.
Пусть дана плоскость
с нормальным вектором
и пересекающая ее прямая
с направляющим вектором
(Рис.
53).
Рис.
53.
Угол между
прямой
и
плоскостью.
Угол
является углом между прямой
и плоскостью
.
Угол между нормальным вектором плоскости
и прямой обозначим через.
Из рисунка видно, что.
Следовательно,
.
Сл1.
Если прямая
перпендикулярна плоскости (),
тоусловие
перпендикулярности прямой и плоскости
имеет вид:
.
Сл2.
Если прямая
параллельна плоскости (),
то направляющий вектор прямой и нормальный
вектор плоскости перпендикулярны (),
следовательно,условие
параллельности прямой и плоскости:
.
21
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Прямая в пространстве – это линия, которая проходит от одной точки к другой, а также за пределы этих точек в бесконечность. Есть несколько видов уравнения прямой в пространстве: каноническое, параметрическое, угол между двумя прямыми в пространстве и т. д. Про это расскажем в данной статье и для наглядности предоставим несколько примеров.
Параметрическое и каноническое уравнение прямой в пространстве
Параметрическое и каноническое уравнение прямой рассматривается практически так, как и для прямой на плоскости. Значит, нужно составить уравнение прямой , которая проходит через данную точку
параллельно направляющему вектору
.
Пусть, – произвольная точка прямой, тогда векторы
и
коллинеарные, а это значит, что координаты их пропорциональны, поэтому получаем:
(1)
это и есть канонические уравнения прямой.
Приравнивая каждую из дробей (1) к параметру , запишем параметрические уравнения прямой:
(2)
Уравнение прямой в пространстве, которая проходит через две заданные точки
Уравнение прямой в пространстве – тема очень лёгкая, так как здесь самое важное – знать нужную формулу. Тогда легко можно решить любую задачу.
Итак, через две точки и
можно не только геометрично провести линию, но и сложить её уравнения.
За направляющий вектор возьмём , тогда по формуле (1) у нас получается:
(3)
уравнение прямой в пространстве, которые проходят через две заданные точки.
Нужна помощь в написании работы?

Написание учебной работы за 1 день от 100 рублей. Посмотрите отзывы наших клиентов и узнайте стоимость вашей работы.
Подробнее
Общее уравнение прямой – переход к каноническому уравнению
Объяснение про общее уравнение прямой начнём с прямой, которая задана двумя плоскостями, что пересекаются по этой прямой.
Пусть известны их уравнения:
(4)
Тогда система (4) называется общим уравнением прямой.
Чтобы перейти к каноническим уравнениям вида (1), необходимо найти вектор и точку
этой прямой.
Точку находим, как один из решений системы (4). Например, положив в (4)
находим
, тогда и точку
. Направляющий вектор
, который параллелен к каждой из плоскостей
и
и перпендикулярен к их нормальным векторам
и
, то есть
,
. (см. рис. 1). Поэтому вектор
можно найти при помощи векторного произведения
и
=
x
=
Найдены координаты и
подставим в каноническое уравнение (1).
Например, от общих уравнений прямой:
Перейдём к каноническим, положив в системе (при нём относительно больше коэффициенты). найдём
. Нормальные векторы
и
. Тогда направляющий вектор
Рис. 1
x
=
,
и канонические уравнения станут:
Угол между двумя прямыми в пространстве. Условия параллельности и перпендикулярности прямых
Угол между двумя прямыми :
и
равен углу между их направляющими векторами и
, поэтому
=
(5)
Условия параллельности и перпендикулярности прямых соответственно запишутся:
и
.
(6)
Примеры решения задач
Давайте рассмотрим первый пример, где можно двумя способами построить прямую:
Задача
При точке и направляющем векторе
необходимо:
- составить каноническое уравнение прямой;
- построить эту прямую.
Решение
1) По формуле (1) запишем каноническое уравнение прямой :
=
.
2) Рассмотрим два способа построения прямой .
Первый способ
В системе координат строим вектор
и точку
и проводим через точку
прямую параллельную вектору
.
Второй способ
По формуле (2) запишем каноническое уравнение прямой в параметрическом виде:
На рисунке видно, что при произвольных значениях из системы находим координаты соответствующих точек, которые принадлежат прямой
. Так при
находим координаты
. Через две точки
и
проводим прямую
.
Очевидно, что найти острый угол между прямыми совершенно не сложно при знании темы и определённых формул. Давайте разберём такой пример:
Задача
Найти острый угол между прямыми:
,
(7)
Решение
По формуле (7) получаем:
=
=
=
Так как , тогда угол
тупой,
, а острый угол
.
Ответ
.
Рассмотрим последний пример, где нужно составить уравнение. Здесь, как и в каждой задаче, важно знать и понимать, какой формулой нужно воспользоваться.
Задача
Составить уравнение прямой , которая проходит через точку
и параллельна прямой
.
Решение
От параметрического уравнения переходим к каноническому При условии параллельности прямых
то есть направляющим вектором новой прямой может служить известный вектор
и по формуле (1) у нас получается:
.
Ответ
.
Уравнения прямых в пространстве
Уравнение прямой как линии пересечения двух плоскостей
Пусть в координатном пространстве (в прямоугольной системе координат) две плоскости заданы общими уравнениями
в которых коэффициенты при неизвестных непропорциональны, т.е. . Это условие означает, что плоскости
и
пересекаются (см. условие (4.25)), поскольку их нормали
и
неколлинеарны (рис.4.25). Тогда линия пересечения плоскостей описывается системой уравнений
(4.31)
Система (4.31) называется общим уравнением прямой в пространстве.
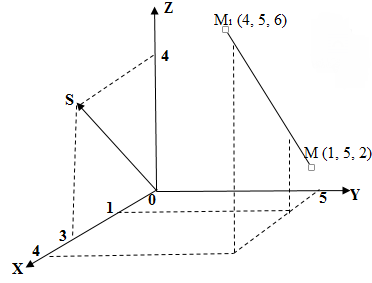
Пример 4.13. В координатном пространстве (в прямоугольной системе координат) заданы вершины
треугольника (рис.4.26). Требуется составить уравнение прямой, содержащей высоту
треугольника.
Решение. Прямая является линией пересечения двух плоскостей: плоскости
, треугольника
и плоскости
, проходящей через точку
перпендикулярно вектору
(рис.4.26). По формуле (4.21) составим уравнение плоскости
проходящей через три точки
По формуле (4.14) составим уравнение плоскости , проходящей через точку
перпендикулярно вектору
Следовательно, общее уравнение (4.31) прямой имеет вид
Параметрическое уравнение прямой в пространстве
Напомним, что направляющий вектором прямой называется ненулевой вектор, коллинеарный этой прямой, т.е. принадлежащий или параллельный ей.
Пусть в координатном пространстве заданы точка
и ненулевой вектор
(рис.4.27). Требуется составить уравнение прямой, коллинеарной вектору
и проходящей через точку
.
Выберем на прямой произвольную точку . Обозначим
— радиус-векторы точек
и
(рис.4.28).
Точка принадлежит заданной прямой тогда и только тогда, когда векторы
и
коллинеарны. Запишем условие коллинеарности:
, где
— некоторое действительное число (параметр). Учитывая, что
, получим векторное параметрическое уравнение прямой в пространстве:
(4.32)
где — направляющий вектор прямой, а
— радиус-вектор заданной точки
принадлежащей прямой.
Координатная форма записи уравнения (4.32) называется параметрическим уравнением прямой в пространстве
(4.33)
где — координаты направляющего вектора
прямой. Параметр
в уравнениях (4.32),(4.33) имеет следующий геометрический смысл: величина
пропорциональна расстоянию от заданной точки
до точки
. Физический смысл параметра
в параметрических уравнениях (4.32),(4.33) — это время при равномерном и Прямолинейном движении точки
по прямой. При
точка
совпадает с заданной точкой
. При возрастании параметра
движение происходит в направлении направляющего вектора.
Каноническое уравнение прямой в пространстве
Выразим параметр из каждого уравнения системы (4.33):
, а затем исключим этот параметр:
(4.34)
Уравнение (4.34) называется каноническим уравнением прямой в пространстве. В этом уравнении коэффициенты не равны нулю одновременно, так как это координаты направляющего вектора прямой.
Замечания 4.6.
1. Если один или два из трех знаменателей дробей в (4.34) равны нулю, то считается, что соответствующий числитель дроби равен нулю. Например:
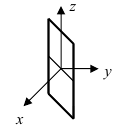
а) каноническое уравнение — это уравнение
прямой, параллельной оси аппликат (рис.4.29,а);
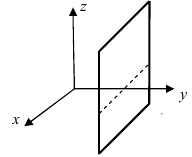
б) каноническое уравнение — это уравнение
прямой, параллельной координатной плоскости
(рис.4.29,б).
2. Направляющий вектор прямой определяется неоднозначно. Например, любой ненулевой вектор
, где
, также является направляющим вектором для той же прямой.
Переход от общего уравнение к каноническому
3. Для перехода от общего уравнения прямой (4.31) к каноническому (4.34) нужно выполнить следующие действия:
1) найти любое решение системы
определяя тем самым координаты точки
, принадлежащей прямой;
2) найти направляющий вектор прямой как векторное произведение нормалей
заданных плоскостей:
3) записать каноническое уравнение (4.34) с учетом пунктов 1 и 2.
4. Чтобы перейти от канонического уравнения к общему, достаточно двойное равенство (4.34) записать в виде системы
и привести подобные члены.
5. Чтобы перейти от канонического уравнения к параметрическому, следует приравнять каждую дробь в уравнении (4.34) параметру t и записать полученные равенства в виде системы (4.33):
6. Если в каноническом уравнении (4.34) прямой фиксировать координаты точки
, а коэффициентам
придавать произвольные значения (не равные нулю одновременно), то получим уравнение связки прямых с центром в точке
, т.е. совокупность всех прямых, проходящих через точку
.
7. Параметрическое (4.33) и каноническое (4.34) уравнения прямой, полученные в прямоугольной системе координат, имеют тот же вид в любой другой аффинной системе координат. Геометрический смысл коэффициентов в уравнениях остается прежним.
Пример 4.14. В координатном пространстве (в прямоугольной системе координат) заданы вершины
треугольника (рис. 4.30). Требуется:
а) составить каноническое уравнение прямой, содержащей высоту треугольника;
б) составить общее уравнение прямой, содержащей биссектрису треугольника.
Решение. а) Общее уравнение прямой получено в примере 4.13:
Перейдем от общего уравнения к каноническому.
1) Найдем любое решение системы, например,
(это координаты точки
).
2) Найдем направляющий вектор прямой как векторное произведение нормалей
заданных плоскостей
3) Запишем каноническое уравнение (4.34): .
б) Сначала составим каноническое уравнение прямой . Для этого нужно найти направляющий вектор
этой прямой. Учитывая, что диагональ ромба является биссектрисой,
, где
и
— единичные векторы, одинаково направленные с векторами
и
соответственно. Находим
Составляем каноническое уравнение прямой .
Записывая двойное равенство в виде системы, получаем общее уравнение прямой
Расстояние от точки до прямой в пространстве
Найдем расстояние от точки
до прямой
, заданной каноническим уравнением (рис.4.31)):
Искомое расстояние равно высоте параллелограмма, построенного на векторах
и
, то есть.
(4.35)
Уравнение прямой, проходящей через две заданные точки
Пусть в координатном пространстве заданы две точки
и
. Требуется составить уравнение прямой, проходящей через заданные точки.
Как показано в разд., точка принадлежит прямой
тогда и только тогда, когда ее радиус-вектор
удовлетворяет условию (рис.4.32):
, где
— некоторое действительное число (параметр). Это уравнение, а также его координатную форму
(4.36)
будем называть аффинным уравнением прямой, проходящей через две точки и
.
Выражая параметр из каждого уравнения системы (4.36), получаем:
. Исключая параметр
, приходим к уравнению прямой, проходящей через две точки
и
:
(4.37)
Уравнение (4.37) можно получить из канонического уравнения (4.34), выбирая в качестве направляющего вектора вектор
т.е. подставляя
Пример 4.15. В координатном пространстве (в прямоугольной системе координат) заданы вершины
треугольника (рис.4.33). Требуется:
а) составить уравнение прямой ;
б) составить уравнение прямой, содержащей медиану треугольника;
в) найти высоту треугольника, опущенную на сторону
.
Решение. а) Записываем уравнение (4.37) прямой, проходящей через точки
б) Находим координаты середины стороны
. Составляем уравнение (4.37) прямой
в) Искомую высоту находим по формуле (4.35), полагая
и
Математический форум (помощь с решением задач, обсуждение вопросов по математике).
Если заметили ошибку, опечатку или есть предложения, напишите в комментариях.
Содержание:
Плоскость в пространстве
Общее уравнение плоскости
Определение: Уравнение вида
Определение: Порядок поверхности определяется по высшему показателю степени переменных х, у и z или по сумме показателей степени в произведении этих величин.
Определение: Уравнение вида Ax+By+Cz+D=O называется общим уравнением плоскости.
Рассмотрим частные случаи приведенного уравнения:
1. D = 0; Ах + By + Сz = 0. Из этого уравнения видно, что точка О(0; 0; 0) удов- летворяет этому уравнению, следовательно, это уравнение описывает плоскость, проходящую через начало координат (Рис. 36).
Рис. 36. Плоскость, проходящая через начало координат.
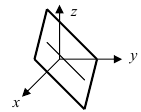
2. С = 0; Ах + Ву + D = 0. Этому уравнению удовлетворяет любое значение переменной z, поэтому данное уравнение описывает плоскость, которая параллельна оси аппликат (Oz) (Рис. 37).
Рис. 37. Плоскость, проходящая параллельно оси аппликат.
Замечание: При отсутствии в уравнении плоскости одной из переменных величин говорит о том, что плоскость параллельна соответствующей координатной оси.
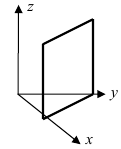
3. С=0; D=0; Ах+ By=0 — плоскость проходит через начало отсчета параллельно оси аппликат (Рис. 38).
Рис. 38. Плоскость, проходящая через начало координат параллельно оси аппликат.
4. 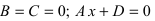
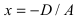
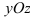
Рис. 39. Плоскость, проходящая параллельно координатной плоскости
5. В = С = D = 0; Ах = 0=>х = 0 — уравнение описывает плоскость 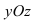
Рис. 40. Координатная плоскость 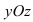
Другие уравнения плоскости
1. Уравнение плоскости в отрезках. Пусть в уравнении 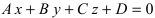
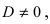
Введем следующие обозначения 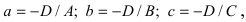
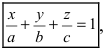
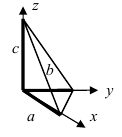
Откладывая на координатных осях точки М, N и Р, соединяя их прямыми лучим изображение данной плоскости (для определенности принято, что параметры а, b, с положительные) (Рис. 41):
Рис. 41. Отрезки, отсекаемые плоскостью на координатных осях.
Из рисунка видно, что числа а, b, с показывают отрезки, отсекаемые плоскостью на координатных осях, считая от начала координат.
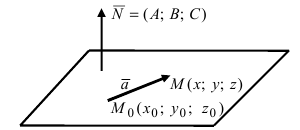
2. Уравнение плоскости, проходящей через заданную точку перпендикулярно к заданному вектору. Пусть задана точка 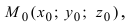
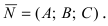
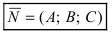
Возьмем на плоскости произвольную точку 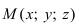
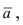
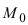
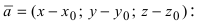
Рис. 42. Плоскость, проходящая через заданную точку перпендикулярно к нормальному вектору.
В силу того, вектор 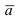
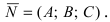
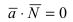
Пример:
Составить уравнение плоскости, проходящей через т. 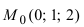
Решение:
Так как искомая плоскость параллельна плоскости (Q), то нормальный вектор этой плоскости 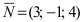
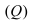
Пример:
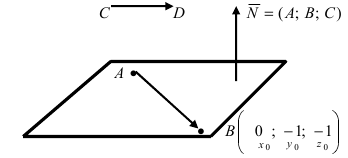
Составить уравнение плоскости, проходящей через точки А(—1; 1 ;2) и В(0; —1; —1) параллельно вектору 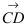
Решение:
Построим на искомой плоскости вектор 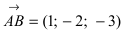
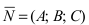
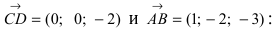
Уравнение плоскости, проходящей через заданную точку 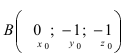
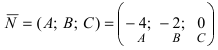
Отметим, что при выборе точки, через которую проходит искомая плоскость из точек 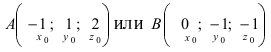
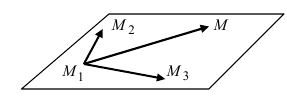
3. Уравнение плоскости, проходящей через три заданные точки. Пусть плоскость проходит через 3 известные точки 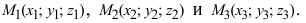
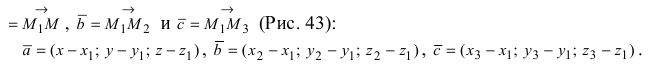
Рис. 43. Плоскость, проходящая через три заданные точки.
Вектора 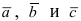
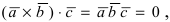
Замечание: Полученный определитель третьего порядка раскрывается по элементам первой строки.
Пример:
Составить уравнение плоскости, проходящей через три заданные точки
Решение:
Составим определитель третьего порядка 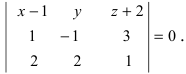
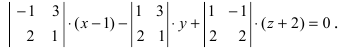
Основные задачи о плоскости в пространстве
1. Угол между пересекающимися плоскостями. Пусть даны две пересекающиеся плоскости 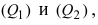
Пусть линия пересечения плоскостей определяется прямой (l). Из одной точки этой прямой проведем два перпендикулярных к прямой вектора 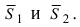
Рис.44. Угол между плоскостями.
В силу того, что 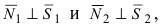
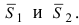
Следствие: Если плоскости перпендикулярны (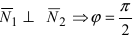
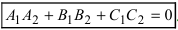
Следствие: Если плоскости параллельны, то нормальные вектора коллинеарны, следовательно, условие параллельности плоскостей:
2. Расстояние от данной точки до заданной плоскости. Расстояние от данной точки 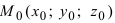
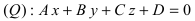
Пример:
На каком расстоянии от плоскости 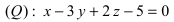
Решение:
Воспользуемся приведенной формулой:
Прямая в пространстве
Общее уравнение прямой
Прямая в пространстве может быть задана как пересечение двух плоскостей:
Определение: Геометрическое место точек пространства, удовлетворяющих системе уравнений (1), называется прямой в пространстве, а система уравнений (1) называется общим уравнением прямой.
Замечание: Для того чтобы система уравнений (1) определяла прямую в пространстве необходимо и достаточно, чтобы нормальные вектора плоскостей, определяющих прямую, 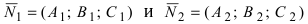
Пусть прямая проходит через точку 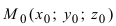
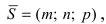
Замечание: Если в уравнении (2) одна из проекций направляющего вектора равна 0, то это означает, что прямая перпендикулярна соответствующей координатной оси.
Пример:
Как расположена прямая 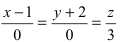
Решение:
Согласно замечанию эта прямая будет перпендикулярна осям абсцисс и ординат (параллельна оси аппликат) и будет проходить через точку 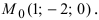
Пример:
Записать уравнение прямой 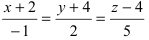
Решение:
Приравняем каждую дробь к параметру t: 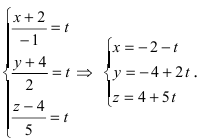
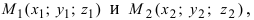
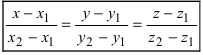
Пример:
Составить канонические и параметрические уравнения прямых, проходящих через точки А (— 1; 1; 2 ), В (0; -1; -1) И С (1; 0; -1), D (l; 0; 1 ).
Решение:
Составим каноническое уравнение прямой линии, проходящей через точки
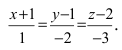
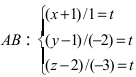
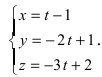
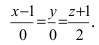
Основные задачи о прямой в пространстве
1. Переход от общего уравнения прямой к каноническому. Пусть прямая задана общим уравнением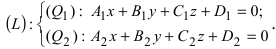
Пример:
Записать уравнение прямой 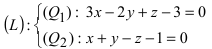
Решение:
Положив х = 0, получим СЛАУ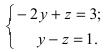
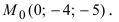
Запишем каноническое 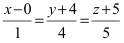
Угол между пересекающимися прямыми
Угол между двумя пересекающимися прямыми определяется как угол между их направляющими векторами. Если прямые 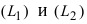
соответственно, то угол между прямыми определяется по формуле:
Следствие: Если прямые перпендикулярны (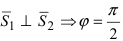
Следствие: Если прямые параллельны, то направляющие вектора коллинеарны, следовательно, условие параллельности прямых:
Координаты точки пересечения прямой и плоскости
Пусть прямая (L) задана общим уравнением 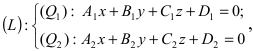
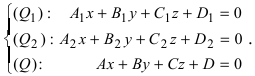
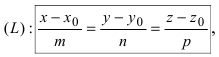
Рассмотрим возможные случаи:
- если выполняются условия
, то прямая не пересекает плоскость (прямая параллельна плоскости);
- при условиях
прямая лежит на плоскости;
- если
, прямая пересекает плоскость в одной точке.
Пример:
Найти координаты точки пересечения прямой (L), заданной уравнением 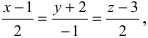
Решение:
Перепишем уравнение прямой (L) в параметрическом виде 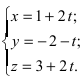
Найденное значение параметра 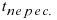
- Заказать решение задач по высшей математике
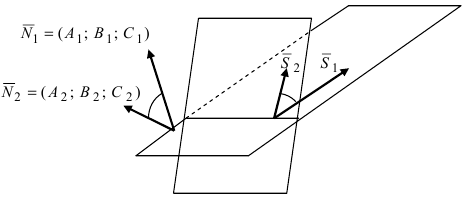
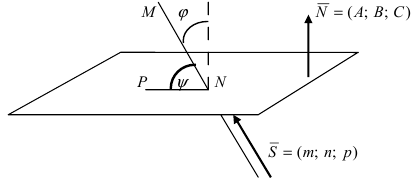
Угол между прямой и плоскостью
Пусть дана плоскость (Q) с нормальным вектором 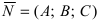
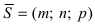
Рис. 45. Угол между прямой и плоскостью.
Угол 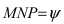
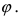
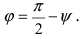
Следствие: Если прямая перпендикулярна плоскости (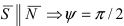
Следствие: Если прямая параллельна плоскости (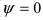
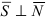
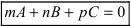
Плоскость и прямая в пространстве
Всякое уравнение первой степени относительно координат 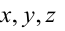

Вектор 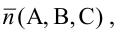
Особые случаи уравнения (3.1):
- D = 0, Ах + By + Cz = 0 — плоскость проходит через начало координат.
- С = 0, Ах + By + D = 0 — плоскость параллельна оси Oz.
- С = D = 0, Ах + By = 0 — плоскость проходит через ось Oz.
- С = В = 0, Ах + D = 0 — плоскость параллельна плоскости Oyz.
Уравнения координатных плоскостей:
Прямая в пространстве может быть задана:
- как линия пересечения двух плоскостей, т.е. системой уравнений:
- двумя своими точками
тогда прямая, через них проходящая, задается уравнениями:
- точкой
ей принадлежащей, и вектором
ей коллинеарным.
Тогда прямая определяется уравнениями:
Уравнения (3.4) называются каноническими уравнениями прямой.
Вектор 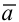
Параметрические уравнения прямой получим, приравняв каждое из отношений (3.4) параметру t: 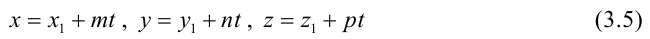
От уравнений (3.6) можно перейти к каноническим уравнениям, находя z из каждого уравнения и приравнивая полученные значения:
От общих уравнений (3.2) можно переходить к каноническим и другим способом, если найти какую-либо точку этой прямой и ее направляющий вектор 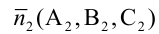
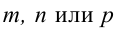
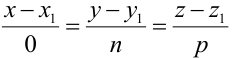
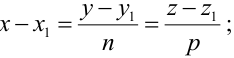
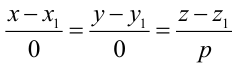
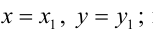
Пример:
Составьте уравнение плоскости, зная, что точка А(1,-1,3) служит основанием перпендикуляра, проведенного из начала координат к этой плоскости.
Решение:
По условию задачи вектор 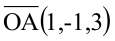
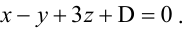
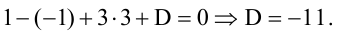
Пример:
Составьте уравнение плоскости, проходящей через ось Oz и образующей с плоскостью
Решение:
Плоскость, проходящая через ось Oz, задается уравнением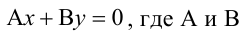
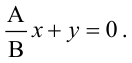
Решая квадратное уравнение 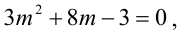
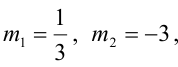
Пример:
Составьте канонические уравнения прямой: 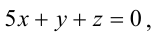
Решение:
Канонические уравнения прямой имеют вид:
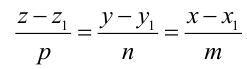
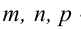
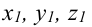
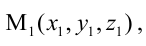
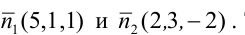
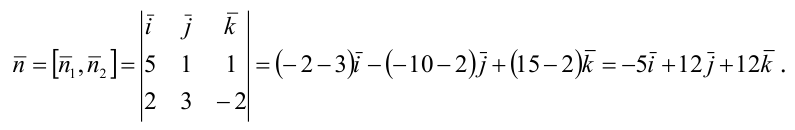
Пример:
В пучке, определяемом плоскостями 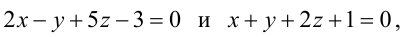
Решение:
Уравнение пучка, определяемого данными плоскостями, имеет вид 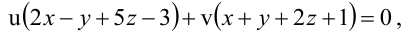
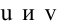
Для того, чтобы из пучка выделить плоскость, проходящую через точку М, подставим координаты точки М в уравнение пучка. Получим:
Тогда уравнение плоскости, содержащей М, найдем, подставив 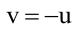
Т.к. и 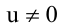
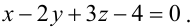
Значит, уравнение второй плоскости имеет вид: 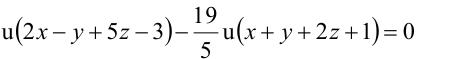
- Определитель матрицы
- Критерий совместности Кронекера-Капелли
- Формулы Крамера
- Матричный метод
- Производная сложной функции
- Пределы в математике
- Функции многих переменных
- Уравнения прямых и кривых на плоскости
Получить уравнение прямой, проходящей через две точки помогут созданные нами калькуляторы. Предлагаем найти каноническое и параметрическое уравнение прямой, а также уравнение прямой с угловым коэффициентом как на плоскости, так и в пространстве.
Прямая — это бесконечная линия, по которой проходит кратчайший путь между любыми двумя её точками.
Уравнения прямой, проходящей через две точки могут быть следующих видов:
- каноническое уравнение,
- параметрическое уравнение,
- общее уравнение прямой,
- уравнение прямой с угловым коэффициентом,
- уравнение прямой в полярных координатах и другие.
Для получения уравнений введите координаты двух точек прямой. Онлайн-калькулятор найдет уравнения и выдаст результат с подробным решением.
Каноническое уравнение прямой на плоскости
{dfrac{x-x_a}{x_b-x_a} = dfrac{y-y_a}{y_b-y_a}}
xa и ya — координаты первой точки A,
xb и yb — координаты второй точки B
Параметрическое уравнение прямой на плоскости
{begin{cases} x=l cdot t + x_a \ y=m cdot t + y_a end{cases}}
xa, ya — координаты точки, лежащей на прямой,
{l;m} — координаты направляющего вектора прямой,
t — произвольный параметр, аналогичный параметру в векторно-параметрическом уравнении.
Каноническое уравнение прямой в пространстве
{dfrac{x-x_a}{x_b-x_a} = dfrac{y-y_a}{y_b-y_a} = dfrac{z-z_a}{z_b-z_a}}
xa, ya и za — координаты первой точки A,
xb, yb и zb — координаты второй точки B
Параметрическое уравнение прямой в пространстве
{ begin{cases} x=l cdot t + x_a \ y=m cdot t + y_a \ z=n cdot t + z_a end{cases} }
xa, ya и za — координаты точки, лежащей на прямой,
{l;m;n} — координаты направляющего вектора прямой,
t — произвольный параметр, аналогичный параметру в векторно-параметрическом уравнении.
Пример нахождения уравнения прямой, проходящей через две точки
Найдем уравнения прямой, проходящей через точки A(1,2) и B(3,8).
Каноническое уравнение прямой
Каноническое уравнение прямой, проходящей через две точки имеет вид {dfrac{x-x_a}{x_b-x_a} = dfrac{y-y_a}{y_b-y_a}}
Подставим в формулу координаты точек A и B: {dfrac{x-1}{3-1} = dfrac{y-2}{8-2}}
Получаем каноническое уравнение прямой: {dfrac{x-1}{2} = dfrac{y-2}{4}}
Уравнение прямой с угловым коэффициентом
Из канонического уравнения получаем уравнение прямой с угловым коэффициентом: {y=3x-1}
Параметрическое уравнение прямой
Параметрическое уравнение прямой имеет вид:
{ begin{cases} x=l cdot t + x_a \ y=m cdot t + y_a end{cases} }
где {x_a, y_b} — координаты точки, лежащей на прямой, {{l;m}} — координаты направляющего вектора прямой, t — произвольный параметр, аналогичный параметру в векторно-параметрическом уравнении. В качестве координат используем координаты точки {A(x_a, y_b)}.
Найдем координаты направляющего вектора:
overline{AB} = {x_b — x_a; y_b — y_a} = {3-1; 8-2} = {2; 6}
Получаем параметрическое уравнение:
begin{cases} x=2 t + 1 \ y=6 t + 2 end{cases}
Используем калькулятор для проверки полученного ответа.


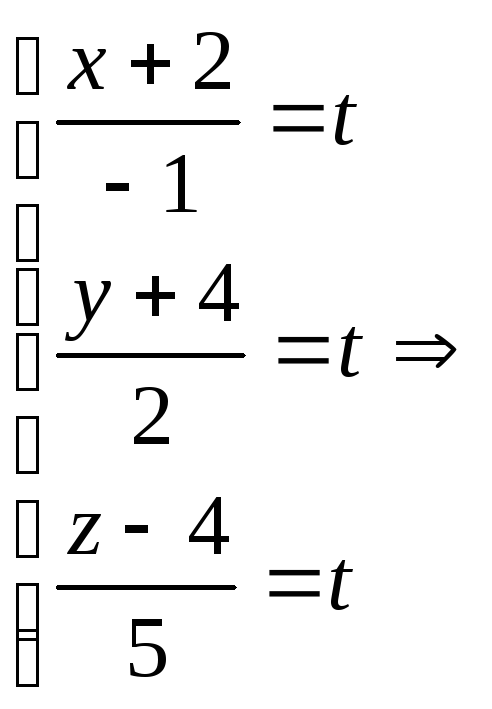

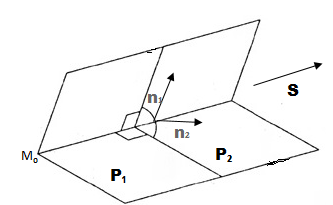
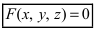
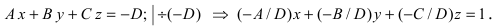
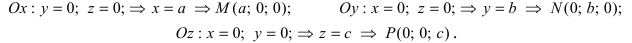
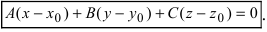
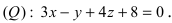
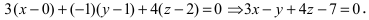
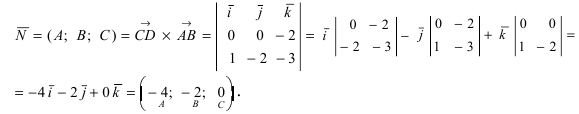
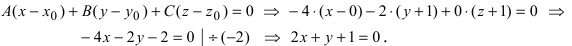

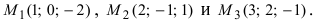
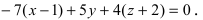
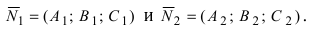
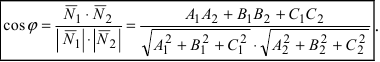
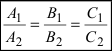
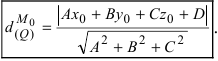
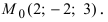
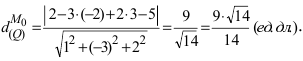
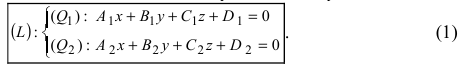
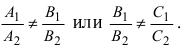

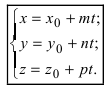
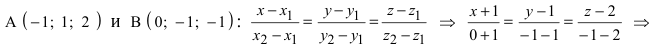
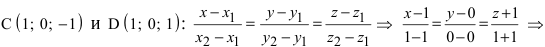
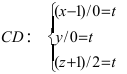
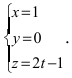
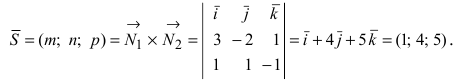
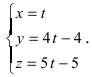
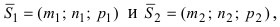

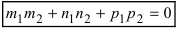
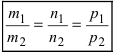
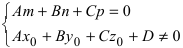 , то прямая не пересекает плоскость (прямая параллельна плоскости);
, то прямая не пересекает плоскость (прямая параллельна плоскости);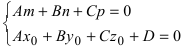 прямая лежит на плоскости;
прямая лежит на плоскости;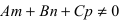 , прямая пересекает плоскость в одной точке.
, прямая пересекает плоскость в одной точке.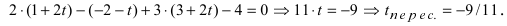
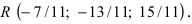
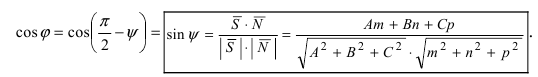
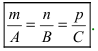
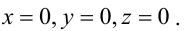
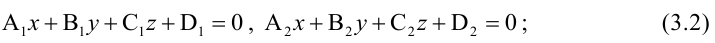
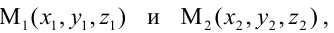 тогда прямая, через них проходящая, задается уравнениями:
тогда прямая, через них проходящая, задается уравнениями: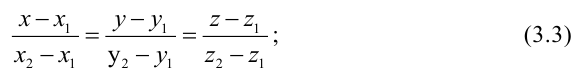
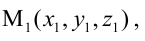 ей принадлежащей, и вектором
ей принадлежащей, и вектором 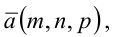 ей коллинеарным.
ей коллинеарным.