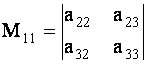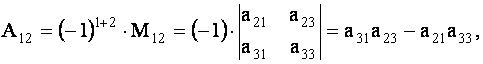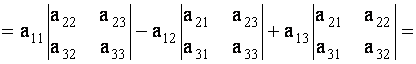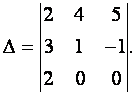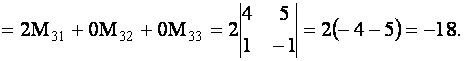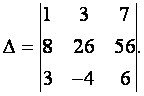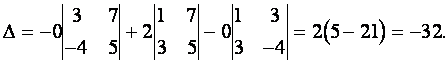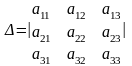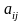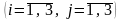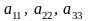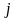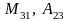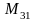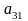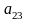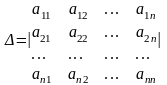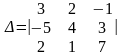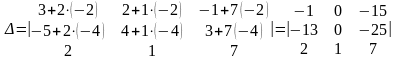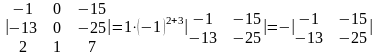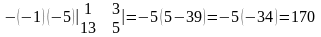Мы уже знакомы с понятием определителя матрицы. Также мы рассмотрели правила вычисления детерминантов (определителей) первого и второго порядка. Познакомимся с различными вариантами нахождения определителей третьего порядка.
Вычисление определителей по правилу треугольника
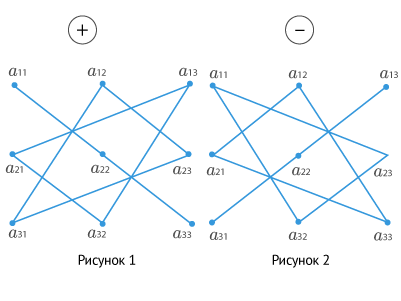
Схематически раскрытие определителя по этому правилу выглядит так:
Согласно рисункам №1 и №2 мы перемножаем элементы, соединенные прямыми. Произведения элементов будут иметь определенные знаки: для рисунка 1 — «+», для рисунка 2 — «-».
| Произведения, которые берутся со знаком «+» | Произведения, которые берутся со знаком «-» |
|---|---|
| a11⋅a22⋅a33a_{11} cdot a_{22} cdot a_{33} | a13⋅a22⋅a31a_{13}cdot a_{22}cdot a_{31} |
| a12⋅a23⋅a31a_{12} cdot a_{23} cdot a_{31} | a12⋅a33⋅a21a_{12}cdot a_{33}cdot a_{21} |
| a13⋅a32⋅a21a_{13} cdot a_{32} cdot a_{21} | a11⋅a23⋅a32a_{11}cdot a_{23}cdot a_{32} |
На рисунке 1 мы видим равнобедренные треугольники с основаниями, параллельными главной диагонали; на рисунке 2 — равнобедренные треугольники с основаниями, параллельными второй (побочной) диагонали. Поэтому данное правило имеет такое название.
Определитель может быть вычислен по формуле:
∣a11a12a13a21a22a23a31a32a33∣=begin{vmatrix}a_{11}&a_{12}&a_{13}\a_{21}&a_{22}&a_{23}\a_{31}&a_{32}&a_{33}end{vmatrix}=
=a11⋅a22⋅a33+a12⋅a23⋅a31+a13⋅a32⋅a21−a13⋅a22⋅a31−a12⋅a33⋅a21−a11⋅a23⋅a32=a_{11}cdot a_{22}cdot a_{33}+a_{12}cdot a_{23}cdot a_{31}+a_{13}cdot a_{32}cdot a_{21}-a_{13}cdot a_{22}cdot a_{31}-a_{12}cdot a_{33}cdot a_{21}-a_{11}cdot a_{23}cdot a_{32}.
Примеры
Рассмотрим примеры нахождения определителя по правилу треугольника.
Найти определитель ∣925148637∣begin{vmatrix}9&2&5\1&4&8\6&3&7end{vmatrix} по правилу треугольника.
По правилу треугольника определитель третьего порядка равен:
∣925148637∣=9⋅4⋅7+2⋅8⋅6+5⋅3⋅1−5⋅4⋅6−2⋅7⋅1−9⋅8⋅3=begin{vmatrix}9&2&5\1&4&8\6&3&7end{vmatrix}=9cdot4cdot7+2cdot8cdot6+5cdot3cdot1-5cdot4cdot6-2cdot7cdot1-9cdot8cdot3=
=252+96+15−120−14−216=13=252+96+15-120-14-216=13.
Найти определитель ∣21−46−3510−1∣begin{vmatrix}2&1&-4\6&-3&5\1&0&-1end{vmatrix} по правилу треугольника.
Искомый определитель третьего порядка равен:
∣21−46−3510−1∣=begin{vmatrix}2&1&-4\6&-3&5\1&0&-1end{vmatrix}=
=2⋅(−3)⋅(−1)+1⋅5⋅1+(−4)⋅0⋅6−(−4)⋅(−3)⋅1−1⋅(−1)⋅6−2⋅5⋅0=6+5−12+6=5=2cdot(-3)cdot(-1)+1cdot5cdot1+(-4)cdot0cdot6-(-4)cdot(-3)cdot1-1cdot(-1)cdot6-2cdot5cdot0=6+5-12+6=5.
При вычислении определителей таким способом можно легко совершить ошибку из-за невнимательности. Чтобы избежать таких ошибок существует второй способ, называемый правилом Саррюса, или способом «параллельных полосок».
Вычисление определителей по правилу Саррюса
Правило Саррюса также именуют способом присоединения двух строк/столбцов или правилом параллельных полосок.
Основная идея этого правила состоит в приписывании первого и второго столбца справа от определителя.
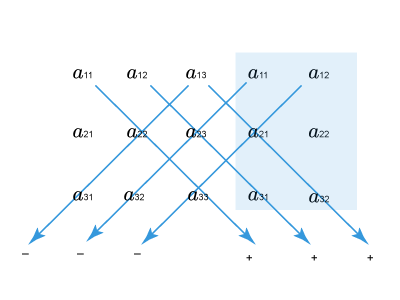
Вычисления будем производить по следующей схеме:
Перемножаем элементы, соединенные прямыми. Данные произведения берем со знаком «+», если диагональ, на которой они стоят, является главной или параллельной ей; со знаком «-», если она является второй (побочной) или параллельной ей.
| Произведения, которые берутся со знаком «+» | Произведения, которые берутся со знаком «-» |
|---|---|
| a11⋅a22⋅a33a_{11} cdot a_{22} cdot a_{33} | a13⋅a22⋅a31a_{13}cdot a_{22}cdot a_{31} |
| a12⋅a23⋅a31a_{12} cdot a_{23} cdot a_{31} | a11⋅a23⋅a32a_{11}cdot a_{23}cdot a_{32} |
| a13⋅a21⋅a32a_{13} cdot a_{21} cdot a_{32} | a12⋅a21⋅a33a_{12}cdot a_{21}cdot a_{33} |
В общем виде вычисление по правилу Саррюса можно записать следующим образом:
∣a11a12a13a21a22a23a31a32a33∣=∣a11a12a13a21a22a23a31a32a33∣a11a12a21a22a31a32=begin{vmatrix}a_{11}&a_{12}&a_{13}\a_{21}&a_{22}&a_{23}\a_{31}&a_{32}&a_{33}end{vmatrix}=begin{vmatrix}a_{11}&a_{12}&a_{13}\a_{21}&a_{22}&a_{23}\a_{31}&a_{32}&a_{33}end{vmatrix}begin{matrix}a_{11}&a_{12}\a_{21}&a_{22}\a_{31}&a_{32}end{matrix}=
=a11⋅a22⋅a33+a12⋅a23⋅a31+a13⋅a21⋅a32−a13⋅a22⋅a31−a11⋅a23⋅a32−a12⋅a21⋅a33=a_{11}cdot a_{22}cdot a_{33}+a_{12}cdot a_{23}cdot a_{31}+a_{13}cdot a_{21}cdot a_{32}-a_{13}cdot a_{22}cdot a_{31}-a_{11}cdot a_{23}cdot a_{32}-a_{12}cdot a_{21}cdot a_{33}.
Сравнивая эти два способа вычисления определителей, видим одинаковые множители, которые во втором случае немного переставлены местами.
Возможность допустить ошибку, вычисляя определитель по правилу Саррюса, намного меньше.
Примеры
Найти определитель ∣925148637∣begin{vmatrix}9&2&5\1&4&8\6&3&7end{vmatrix} по правилу Саррюса.
Приписываем два первых столбца справа от определителя и вычисляем его:
∣925148637∣921463=begin{vmatrix}9&2&5\1&4&8\6&3&7end{vmatrix}begin{matrix}9&2\1&4\6&3end{matrix}=
=9⋅4⋅7+2⋅8⋅6+5⋅1⋅3−5⋅4⋅6−9⋅8⋅3−2⋅1⋅7=252+96+15−120−216−14=13=9cdot4cdot7+2cdot8cdot6+5cdot1cdot3-5cdot4cdot6-9cdot8cdot3-2cdot1cdot7=252+96+15-120-216-14=13.
Найти определитель ∣21−46−3510−1∣begin{vmatrix}2&1&-4\6&-3&5\1&0&-1end{vmatrix} по правилу Саррюса.
Приписываем два первых столбца справа от определителя и вычисляем его:
∣21−46−3510−1∣216−310=begin{vmatrix}2&1&-4\6&-3&5\1&0&-1end{vmatrix}begin{matrix}2&1\6&-3\1&0end{matrix}=
=2⋅(−3)⋅(−1)+1⋅5⋅1+(−4)⋅6⋅0−(−4)⋅(−3)⋅1−2⋅5⋅0−1⋅6⋅(−1)=6+5−12+6=5=2cdot(-3)cdot(-1)+1cdot5cdot1+(-4)cdot6cdot0-(-4)cdot(-3)cdot1-2cdot5cdot0-1cdot6cdot(-1)=6+5-12+6=5.
Существует еще одна вариация правила Саррюса. Она состоит в приписывании первой и второй строки снизу от определителя. Вычисления производятся аналогично.
Минор и алгебраическое дополнение
Прежде чем перейти к рассмотрению еще одного способа вычисления определителей 3-го порядка разберем 2 понятия: минор, алгебраическое дополнение.
Минор
Минором MijM_{ij} к элементу aija_{ij} определителя n-го порядка называется определитель (n−1)(n-1)-го порядка, который получается из исходного определителя вычеркиванием ii-той строки и jj-того столбца.
Таким образом, минор — это определитель, который остается после вычеркивания определенной строки и определенного столбца. Например, M11M_{11} получается вычеркиванием 1-й строки и 1-го столбца, M23M_{23} — вычеркиванием 2-й строки и 3-го столбца.
Алгоритм нахождения миноров:
- вычеркиваем ii-ю строку;
- вычеркиваем jj-й столбец;
- записываем определитель, который получили в результате действий 1 и 2.
Примеры
Найти миноры матрицы F=(925148637)F=begin{pmatrix}9&2&5\1&4&8\6&3&7end{pmatrix}.
Те строки и столбцы, которые будем вычеркивать, обозначим зеленым цветом.
M11=∣925148637∣=∣4837∣=4⋅7−3⋅8=28−24=4M_{11}=begin{vmatrix}color{green}9&color{green}2&color{green}5\color{green}1&4&8\color{green}6&3&7end{vmatrix}=begin{vmatrix}4&8\3&7end{vmatrix}=4cdot7-3cdot8=28-24=4,
M12=∣925148637∣=∣1867∣=1⋅7−6⋅8=7−48=−41M_{12}=begin{vmatrix}color{green}9&color{green}2&color{green}5\1&color{green}4&8\6&color{green}3&7end{vmatrix}=begin{vmatrix}1&8\6&7end{vmatrix}=1cdot7-6cdot8=7-48=-41,
M13=∣925148637∣=∣1463∣=1⋅3−6⋅4=3−24=−21M_{13}=begin{vmatrix}color{green}9&color{green}2&color{green}5\1&4&color{green}8\6&3&color{green}7end{vmatrix}=begin{vmatrix}1&4\6&3end{vmatrix}=1cdot3-6cdot4=3-24=-21,
M21=∣925148637∣=∣2537∣=2⋅7−3⋅5=14−15=−1M_{21}=begin{vmatrix}color{green}9&2&5\color{green}1&color{green}4&color{green}8\color{green}6&3&7end{vmatrix}=begin{vmatrix}2&5\3&7end{vmatrix}=2cdot7-3cdot5=14-15=-1,
M22=∣925148637∣=∣9567∣=9⋅7−6⋅5=63−30=33M_{22}=begin{vmatrix}9&color{green}2&5\color{green}1&color{green}4&color{green}8\6&color{green}3&7end{vmatrix}=begin{vmatrix}9&5\6&7end{vmatrix}=9cdot7-6cdot5=63-30=33,
M23=∣925148637∣=∣9263∣=9⋅3−6⋅2=27−12=15M_{23}=begin{vmatrix}9&2&color{green}5\color{green}1&color{green}4&color{green}8\6&3&color{green}7end{vmatrix}=begin{vmatrix}9&2\6&3end{vmatrix}=9cdot3-6cdot2=27-12=15,
M31=∣925148637∣=∣2548∣=2⋅8−4⋅5=16−20=−4M_{31}=begin{vmatrix}color{green}9&2&5\color{green}1&4&8\color{green}6&color{green}3&color{green}7end{vmatrix}=begin{vmatrix}2&5\4&8end{vmatrix}=2cdot8-4cdot5=16-20=-4,
M32=∣925148637∣=∣9518∣=9⋅8−1⋅5=72−5=67M_{32}=begin{vmatrix}9&color{green}2&5\1&color{green}4&8\color{green}6&color{green}3&color{green}7end{vmatrix}=begin{vmatrix}9&5\1&8end{vmatrix}=9cdot8-1cdot5=72-5=67,
M33=∣925148637∣=∣9214∣=9⋅4−1⋅2=36−2=34M_{33}=begin{vmatrix}9&2&color{green}5\1&4&color{green}8\color{green}6&color{green}3&color{green}7end{vmatrix}=begin{vmatrix}9&2\1&4end{vmatrix}=9cdot4-1cdot2=36-2=34.
Найти миноры матрицы G=(21−46−3510−1)G=begin{pmatrix}2&1&-4\6&-3&5\1&0&-1end{pmatrix}.
Те строки и столбцы, которые будем вычеркивать, обозначим зеленым цветом.
M11=∣21−46−3510−1∣=∣−350−1∣=(−3)⋅(−1)−0⋅5=3−0=3M_{11}=begin{vmatrix}color{green}2&color{green}1&color{green}-4\color{green}6&-3&5\color{green}1&0&-1end{vmatrix}=begin{vmatrix}-3&5\0&-1end{vmatrix}=(-3)cdot(-1)-0cdot5=3-0=3,
M12=∣21−46−3510−1∣=∣651−1∣=6⋅(−1)−1⋅5=−6−5=−11M_{12}=begin{vmatrix}color{green}2&color{green}1&color{green}-4\6&color{green}-3&5\1&color{green}0&-1end{vmatrix}=begin{vmatrix}6&5\1&-1end{vmatrix}=6cdot(-1)-1cdot5=-6-5=-11,
M13=∣21−46−3510−1∣=∣6−310∣=6⋅0−1⋅(−3)=0+3=3M_{13}=begin{vmatrix}color{green}2&color{green}1&color{green}-4\6&-3&color{green}5\1&0&color{green}-1end{vmatrix}=begin{vmatrix}6&-3\1&0end{vmatrix}=6cdot0-1cdot(-3)=0+3=3,
M21=∣21−46−3510−1∣=∣1−40−1∣=1⋅(−1)−0⋅(−4)=−1−0=−1M_{21}=begin{vmatrix}color{green}2&1&-4\color{green}6&color{green}-3&color{green}5\color{green}1&0&-1end{vmatrix}=begin{vmatrix}1&-4\0&-1end{vmatrix}=1cdot(-1)-0cdot(-4)=-1-0=-1,
M22=∣21−46−3510−1∣=∣2−41−1∣=2⋅(−1)−1⋅(−4)=−2+4=2M_{22}=begin{vmatrix}2&color{green}1&-4\color{green}6&color{green}-3&color{green}5\1&color{green}0&-1end{vmatrix}=begin{vmatrix}2&-4\1&-1end{vmatrix}=2cdot(-1)-1cdot(-4)=-2+4=2,
M23=∣21−46−3510−1∣=∣2110∣=2⋅0−1⋅1=0−1=−1M_{23}=begin{vmatrix}2&1&color{green}-4\color{green}6&color{green}-3&color{green}5\1&0&color{green}-1end{vmatrix}=begin{vmatrix}2&1\1&0end{vmatrix}=2cdot0-1cdot1=0-1=-1,
M31=∣21−46−3510−1∣=∣1−4−35∣=1⋅5−(−3)⋅(−4)=5−12=−7M_{31}=begin{vmatrix}color{green}2&1&-4\color{green}6&-3&5\color{green}1&color{green}0&color{green}-1end{vmatrix}=begin{vmatrix}
1&-4\-3&5end{vmatrix}=1cdot5-(-3)cdot(-4)=5-12=-7,
M32=∣21−46−3510−1∣=∣2−465∣=2⋅5−6⋅(−4)=10+24=34M_{32}=begin{vmatrix}2&color{green}1&-4\6&color{green}-3&5\color{green}1&color{green}0&color{green}-1end{vmatrix}=begin{vmatrix}2&-4\6&5end{vmatrix}=2cdot5-6cdot(-4)=10+24=34,
M33=∣21−46−3510−1∣=∣216−3∣=2⋅(−3)−6⋅1=−6−6=−12M_{33}=begin{vmatrix}2&1&color{green}-4\6&-3&color{green}5\color{green}1&color{green}0&color{green}-1end{vmatrix}=begin{vmatrix}2&1\6&-3end{vmatrix}=2cdot(-3)-6cdot1=-6-6=-12.
Алгебраическое дополнение
Алгебраическим дополнением AijA_{ij} к элементу aija_{ij} определителя nn-го порядка называется число Aij=(−1)i+j⋅MijA_{ij}=(-1)^{i+j}cdot M_{ij},
где ii, jj — соответствующие строка и столбец,
MijM_{ij} — минор к элементу aija_{ij}.
Алгоритм нахождения алгебраических дополнений:
- найти сумму номеров строки (i)(i) и столбца (j)(j);
- найти минор MijM_{ij} по алгоритму нахождения миноров, который представлен выше;
- подставить значения, полученные на шагах 1 и 2, в формулу Aij=(−1)i+j⋅MijA_{ij}=(-1)^{i+j}cdot M_{ij}.
Примеры
Найти алгебраические дополнения матрицы F=(925148637)F=begin{pmatrix}9&2&5\1&4&8\6&3&7end{pmatrix}.
A11=(−1)1+1⋅M11=(−1)2⋅∣4837∣=4A_{11}=(-1)^{1+1}cdot M_{11}= (-1)^{2}cdotbegin{vmatrix}4&8\3&7end{vmatrix}=4,
A12=(−1)1+2⋅M12=(−1)3⋅∣1867∣=41A_{12}=(-1)^{1+2}cdot M_{12}= (-1)^{3}cdotbegin{vmatrix}1&8\6&7end{vmatrix}=41,
A13=(−1)1+3⋅M13=(−1)4⋅∣1463∣=−21A_{13}=(-1)^{1+3}cdot M_{13}= (-1)^{4}cdotbegin{vmatrix}1&4\6&3end{vmatrix}=-21,
A21=(−1)2+1⋅M21=(−1)3⋅∣2537∣=1A_{21}=(-1)^{2+1}cdot M_{21}= (-1)^{3}cdotbegin{vmatrix}2&5\3&7end{vmatrix}=1,
A22=(−1)2+2⋅M22=(−1)4⋅∣9567∣=33A_{22}=(-1)^{2+2}cdot M_{22}= (-1)^{4}cdotbegin{vmatrix}9&5\6&7end{vmatrix}=33,
A23=(−1)2+3⋅M23=(−1)5⋅∣9263∣=−15A_{23}=(-1)^{2+3}cdot M_{23}= (-1)^{5}cdotbegin{vmatrix}9&2\6&3end{vmatrix}=-15,
A31=(−1)3+1⋅M31=(−1)4⋅∣2548∣=−4A_{31}=(-1)^{3+1}cdot M_{31}=(-1)^{4}cdotbegin{vmatrix}2&5\4&8end{vmatrix}=-4,
A32=(−1)3+2⋅M32=(−1)5⋅∣9518∣=−67A_{32}=(-1)^{3+2}cdot M_{32}=(-1)^{5}cdotbegin{vmatrix}9&5\1&8end{vmatrix}=-67,
A33=(−1)3+3⋅M33=(−1)6⋅∣9214∣=34A_{33}=(-1)^{3+3}cdot M_{33}=(-1)^{6}cdotbegin{vmatrix}9&2\1&4end{vmatrix}=34.
Найти алгебраические дополнения матрицы G=(21−46−3510−1)G=begin{pmatrix}2&1&-4\6&-3&5\1&0&-1end{pmatrix}.
A11=(−1)1+1⋅M11=(−1)2⋅∣−350−1∣=3A_{11}=(-1)^{1+1}cdot M_{11}=(-1)^{2}cdotbegin{vmatrix}-3&5\0&-1end{vmatrix}=3,
A12=(−1)1+2⋅M12=(−1)3⋅∣651−1∣=11A_{12}=(-1)^{1+2}cdot M_{12}=(-1)^{3}cdotbegin{vmatrix}6&5\1&-1end{vmatrix}=11,
A13=(−1)1+3⋅M13=(−1)4⋅∣6−310∣=3A_{13}=(-1)^{1+3}cdot M_{13}=(-1)^{4}cdotbegin{vmatrix}6&-3\1&0end{vmatrix}=3,
A21=(−1)2+1⋅M21=(−1)3⋅∣1−40−1∣=1A_{21}=(-1)^{2+1}cdot M_{21}=(-1)^{3}cdotbegin{vmatrix}1&-4\0&-1end{vmatrix}=1,
A22=(−1)2+2⋅M22=(−1)4⋅∣2−41−1∣=2A_{22}=(-1)^{2+2}cdot M_{22}=(-1)^{4}cdotbegin{vmatrix}2&-4\1&-1end{vmatrix}=2,
A23=(−1)2+3⋅M23=(−1)5⋅∣2110∣=1A_{23}=(-1)^{2+3}cdot M_{23}=(-1)^{5}cdotbegin{vmatrix}2&1\1&0end{vmatrix}=1,
A31=(−1)3+1⋅M31=(−1)4⋅∣1−4−35∣=−7A_{31}=(-1)^{3+1}cdot M_{31}=(-1)^{4}cdotbegin{vmatrix}1&-4\-3&5end{vmatrix}=-7,
A32=(−1)3+2⋅M32=(−1)5⋅∣2−465∣=−34A_{32}=(-1)^{3+2}cdot M_{32}=(-1)^{5}cdotbegin{vmatrix}2&-4\6&5end{vmatrix}=-34,
A33=(−1)3+3⋅M33=(−1)6⋅∣216−3∣=−12A_{33}=(-1)^{3+3}cdot M_{33}=(-1)^{6}cdotbegin{vmatrix}2&1\6&-3end{vmatrix}=-12.
Зная, что такое миноры и алгебраические дополнения, рассмотрим вычисление определителя по строке и столбцу.
Вычисление определителя по строке или столбцу
Определитель матрицы равен сумме произведений элементов строки (столбца) на их алгебраические дополнения.
Алгоритм вычисления определителя по строке или столбцу:
- находим алгебраические дополнения элементов строки или столбца;
- находим произведения элементов на их алгебраические дополнения;
- находим сумму, полученных на шаге 2, произведений.
Примеры
Найти определитель ∣925148637∣begin{vmatrix}9&2&5\1&4&8\6&3&7end{vmatrix} по 2 столбцу.
∣925148637∣=2⋅A12+4⋅A22+3⋅begin{vmatrix}9&2&5\1&4&8\6&3&7end{vmatrix}=2cdot A_{12}+4cdot A_{22}+3cdot
A32=2(−1)3M12+4(−1)4M22+3(−1)5M32=2(−1)3∣1867∣+4(−1)4∣9567∣+3(−1)5∣9518∣=A_{32}=2(-1)^{3}M_{12}+4(-1)^{4}M_{22}+3(-1)^{5}M_{32}=2(-1)^{3}begin{vmatrix}1&8\6&7end{vmatrix}+4(-1)^{4}begin{vmatrix}9&5\6&7end{vmatrix}+3(-1)^{5}begin{vmatrix}9&5\1&8end{vmatrix}=
=−2⋅(−41)+4⋅33−3⋅67=82+132−201=13=-2cdot(-41)+4cdot33-3cdot67=82+132-201=13.
Найти определитель ∣21−46−3510−1∣begin{vmatrix}2&1&-4\6&-3&5\1&0&-1end{vmatrix} по 3 строке.
∣21−46−3510−1∣=1⋅A31+0⋅A32−1⋅A33=1(−1)4M31+0(−1)5M32−1(−1)6M33=begin{vmatrix}2&1&-4\6&-3&5\1&0&-1end{vmatrix}=1cdot A_{31}+0cdot A_{32}-1cdot A_{33}=1(-1)^{4}M_{31}+0(-1)^{5}M_{32}-1(-1)^{6}M_{33}=
=1(−1)4∣1−4−35∣+0(−1)5∣2−465∣−1(−1)6∣216−3∣=−7+0+12=5=1(-1)^{4}begin{vmatrix}1&-4\-3&5end{vmatrix}+0(-1)^{5}begin{vmatrix}2&-4\6&5end{vmatrix}-1(-1)^{6}begin{vmatrix}2&1\6&-3end{vmatrix}=-7+0+12=5.
Любой из рассмотренных способов можно применять при нахождении определителей третьего порядка. В следующий раз мы разберем вычисление определителей матриц высших порядков.
Оформите решение задачи на заказ онлайн, если возникают трудности с выполнением!
Тест по теме «Как вычислить определитель матрицы третьего порядка»
Пусть дана квадратная матрица третьего порядка
ОПРЕДЕЛЕНИЕ 1.8
Определителем третьего порядка, соответствующим данной квадратной матрице А, называется число
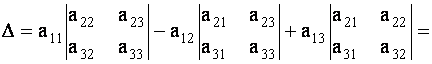 |
(1.7) |
Определитель третьего порядка обозначается символом
 |
(1.8) |
где числа называются его элементами.
Индексы у элемента
показывают номера строки и столбца, на пересечении которых записан этот элемент.
Например, элемент расположен на пересечении второй строки
и третьего столбца
.
Элементы образуют главную диагональ определителя, а элементы
побочную диагональ.
Определение имеет сложный по форме вид, поэтому для нахождения определителя третьего порядка предложены более простые правила. Так, согласно правилу треугольников необходимо:
- вычислить с собственными знаками произведения элементов , лежащих на главной диагонали и в вершинах двух равнобедренных треугольников, основания которых параллельны этой диагонали ;
- найти произведения элементов, лежащих на побочной диагонали и в вершинах двух равнобедренных треугольников, основания которых параллельны побочной диагонали, и взять их с противоположными знаками ;
- найти общую сумму всех произведений.
ПРИМЕР 1.1.7
Все свойства определителей второго порядка справедливы и для определителей третьего порядка. Доказательства этих свойств основаны на вычислении определителя третьего порядка по формуле (1.7).
Например, покажем, что определитель, у которого элементы двух его строк пропорциональны, равен нулю. Действительно,
Аналогично проверяется справедливость и других свойств.
Пусть дан определитель (1.8) третьего порядка.
ОПРЕДЕЛЕНИЕ 1.9: Минором элемента
, где
определителя третьего порядка, называется определитель второго порядка, полученный из данного вычеркиванием
й строки и
го столбца. Так, например, минор
элемента
есть определитель
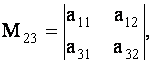
есть
С помощью миноров определитель (7) можно записать в виде
| (1.9) |
ОПРЕДЕЛЕНИЕ 1.10: Алгебраическим дополнением элемента
, где
, называется минор
этого элемента, взятый со знаком
. По определению 4.3 имеем
Например,
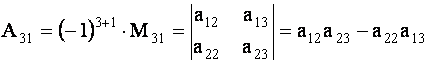
ТЕОРЕМА 1.1 Разложение определителя по элементам строки или столбца
Определитель третьего порядка равен сумме произведений элементов любой его строки (столбца) на их алгебраические дополнения. Иными словами, имеют место шесть равенств:
| (1.11) |
Проверим, например, справедливость равенства
Согласно определениям минора и алгебраического дополнения получим
ТЕОРЕМА 1.2 Сумма произведений элементов какой- либо строки (столбца) определителя на алгебраические дополнения элементов любой другой его строки (столбца) равна нулю.
Для определенности выберем элементы первой строки и алгебраические дополнения
элементов второй строки определителя. Составим сумму произведений
и покажем, что эта сумма равна нулю.
Действительно,
Аналогично проверяется равенство нулю и всех других подобных сумм.
В заключение рассмотрим схему использования свойств определителя и теоремы разложения при вычислении определителя.
ПРИМЕР 1.1.8
Вычислить определитель
Решение. Разложим определитель по элементам третьей строки.
ПРИМЕР 1.1.9
Вычислить определитель
Решение. Прибавляя ко второй строке первую, умноженную на — 8,
получим 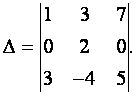
- Определители n-го порядка с примерами
- Курс математики
Сохранить или поделиться с друзьями
Вы находитесь тут:
На нашем сайте Вы можете получить решение задач и онлайн помощь
Подробнее
Определитель третьего порядка
Определитель
третьего порядка:
,
– элементы определителя
.
Следует
запомнить, что элементы
образуют
главную диагональ определителя, элементы
составляют его побочную диагональ.
Вычисление определителя третьего порядка.
-
Вычисление
определителя третьего порядка по
правилу треугольников

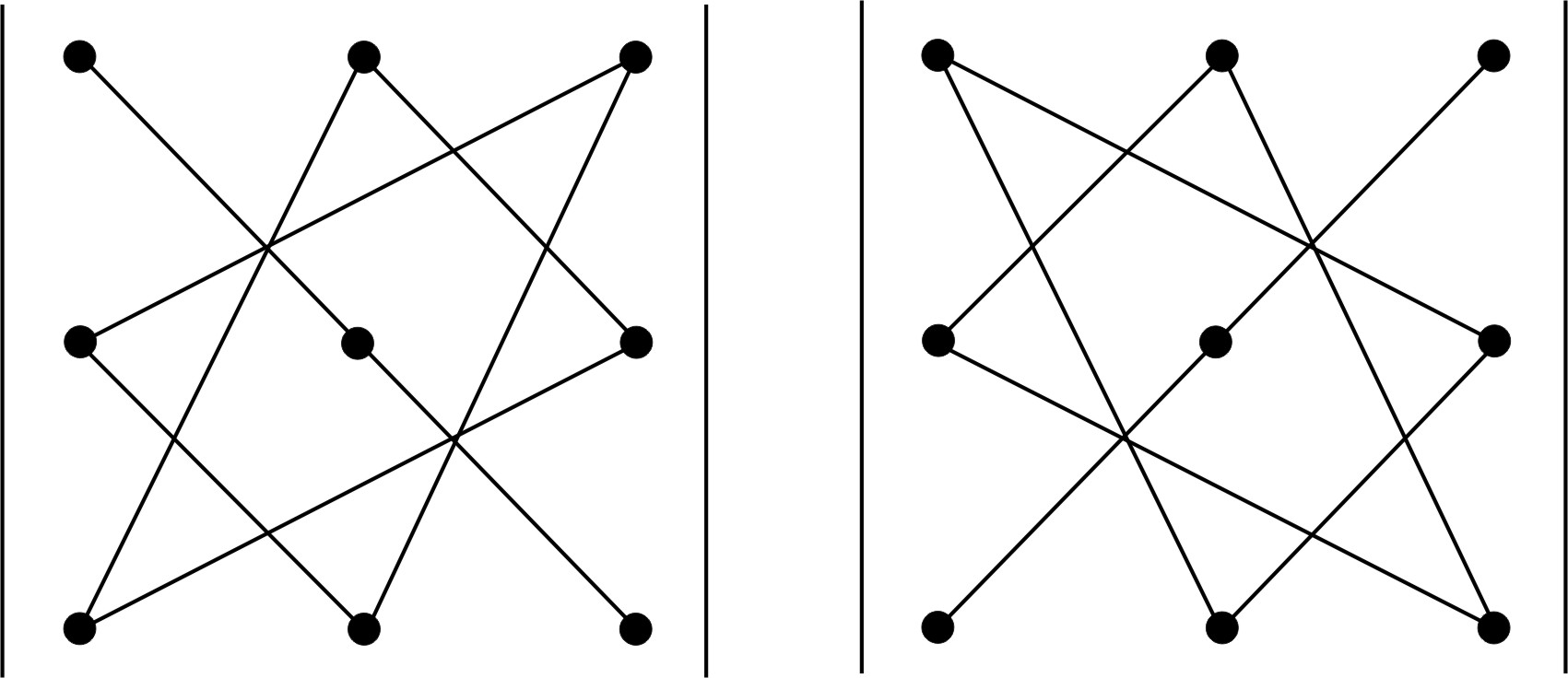
Рис.
1 Рис. 2
Данное правило
заключается в том, что первые три
слагаемые в правой части равенства
вычисляются так, как это показано на
Рис. 1, они представляют собой произведения
элементов, стоящих на главной диагонали
и вершинах двух треугольников, у которых
одна из сторон параллельна главной
диагонали. Остальные три слагаемых
правой части равенства вычисляются
аналогично (Рис. 2), только за основу
взята побочная диагональ. Причем эти
слагаемые берутся с обратным знаком.
Определение:
Минором данного элемента
определителя третьего порядка называется
определитель второго порядка, полученный
из данного определителя вычеркиванием
строки и столбца, на пересечении которых
стоит данный элемент.
— минор данного
элемента определителя третьего порядка.
Определение:
Алгебраическое дополнение
данного элемента – это минор, взятый
со знаком «плюс», если сумма
— четное число, и со знаком «минус», если
эта сумма нечетная.
— алгебраическое дополнение данного
элемента определителя третьего порядка.
.
Замечание.
Здесь
означает номер строки, а
— номер столбца, на пересечении которых
находится данный элемент.
Пример
2. Дана матрица
.
Найти
.
Решение
Минор
,
соответствующий элементу
,
есть определитель
.
Он получается, если вычеркнуть из данного
определителя третьего порядка третью
строку и первый столбец.

По
формуле (14) находим алгебраическое
дополнение для элемента
.
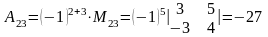
-
Разложение
определителя по элементам строки (или
столбца).
— разложение
определителя по элементам первой строки.

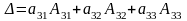
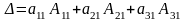
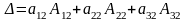
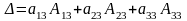
Определитель равен
сумме произведений элементов какой –
либо строки (или столбца) на их
алгебраические дополнения.
Замечание.
Все свойства
определителей второго порядка остаются
справедливыми для определителей третьего
и более высокого порядка.
Определители высших порядков
Определитель
n – го порядка.
.
— разложение
определителя n – го порядка по
элементам первой строки.
Замечание.
Для определителей
любых порядков остаются в силе определения
минора и алгебраического дополнения
данного элемента.
Пример
3. Вычислить определитель третьего
порядка
.
-
по
правилу треугольников -
используя
разложение по элементам строки (или
столбца) -
используя
разложение по элементам строки (или
столбца), с предварительным образованием
нулей.
Решение
-
Вычисляем
определитель по правилу треугольников,
используя формулу (2).

-
Разложим
определитель по элементам первой
строки, используя формулу (3)
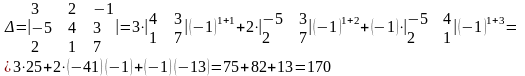
-
Используя
свойство (8), можно значительно упростить
вычисление определителя, получая нули
в некотором столбце или строке.
Умножая третью
строку на (- 4) и складывая ее со второй,
а умножая третью строку на (- 2) и складывая
ее с первой, получим
.
Вычислим этот определитель, разлагая
его по элементам второго столбца (т. к.
из трех элементов – два нуля):
.
Согласно свойству (3) , из первого столбца
выносим (-1), а из второго (-5), получаем
.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Содержание:
- Вычисления определителей второго порядка
- Методы вычисления определителей третьего порядка
- Приведение определителя к треугольному виду
- Правило треугольника
- Правило Саррюса
- Разложение определителя по строке или столбцу
- Разложение определителя по элементам строки или столбца
- Теорема Лапласа
В общем случае правило вычисления определителей
$n$-го порядка
является довольно громоздким. Для определителей второго и третьего порядка существуют рациональные способы их вычислений.
Вычисления определителей второго порядка
Чтобы вычислить определитель матрицы 
элементов главной диагонали отнять произведение
элементов побочной диагонали:
$$left| begin{array}{ll}{a_{11}} & {a_{12}} \ {a_{21}} & {a_{22}}end{array}right|=a_{11} cdot a_{22}-a_{12} cdot a_{21}$$
Пример
Задание. Вычислить определитель второго порядка
$left| begin{array}{rr}{11} & {-2} \ {7} & {5}end{array}right|$
Решение. $left| begin{array}{rr}{11} & {-2} \ {7} & {5}end{array}right|=11 cdot 5-(-2) cdot 7=55+14=69$
Ответ. $left| begin{array}{rr}{11} & {-2} \ {7} & {5}end{array}right|=69$
Методы вычисления определителей третьего порядка
Для вычисления определителей третьего порядка существует такие правила.
Правило треугольника
Схематически это правило можно изобразить следующим образом:
Произведение элементов в первом определителе, которые соединены прямыми,
берется со знаком «плюс»; аналогично, для второго определителя — соответствующие произведения берутся со знаком «минус», т.е.
$$left| begin{array}{ccc}{a_{11}} & {a_{12}} & {a_{13}} \ {a_{21}} & {a_{22}} & {a_{23}} \ {a_{31}} & {a_{32}} & {a_{33}}end{array}right|=a_{11} a_{22} a_{33}+a_{12} a_{23} a_{31}+a_{13} a_{21} a_{32}-$$
$$-a_{11} a_{23} a_{32}-a_{12} a_{21} a_{33}-a_{13} a_{22} a_{31}$$

236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 430 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!
Пример
Задание. Вычислить определитель $left| begin{array}{rrr}{3} & {3} & {-1} \ {4} & {1} & {3} \ {1} & {-2} & {-2}end{array}right|$ методом треугольников.
Решение. $left| begin{array}{rrr}{3} & {3} & {-1} \ {4} & {1} & {3} \ {1} & {-2} & {-2}end{array}right|=3 cdot 1 cdot(-2)+4 cdot(-2) cdot(-1)+$
$$+3 cdot 3 cdot 1-(-1) cdot 1 cdot 1-3 cdot(-2) cdot 3-4 cdot 3 cdot(-2)=54$$
Ответ. $left| begin{array}{rrr}{3} & {3} & {-1} \ {4} & {1} & {3} \ {1} & {-2} & {-2}end{array}right|=54$
Правило Саррюса
Справа от определителя дописывают первых два столбца и произведения элементов на главной диагонали и на диагоналях, ей
параллельных, берут со знаком «плюс»; а произведения элементов побочной диагонали и диагоналей, ей параллельных,
со знаком «минус»:
$$-a_{13} a_{22} a_{31}-a_{11} a_{23} a_{32}-a_{12} a_{21} a_{33}$$
Пример
Задание. Вычислить определитель $left| begin{array}{rrr}{3} & {3} & {-1} \ {4} & {1} & {3} \ {1} & {-2} & {-2}end{array}right|$ с помощью правила Саррюса.
Решение.
$$+(-1) cdot 4 cdot(-2)-(-1) cdot 1 cdot 1-3 cdot 3 cdot(-2)-3 cdot 4 cdot(-2)=54$$
Ответ. $left| begin{array}{rrr}{3} & {3} & {-1} \ {4} & {1} & {3} \ {1} & {-2} & {-2}end{array}right|=54$
Разложение определителя по строке или столбцу
Определитель равен сумме произведений элементов строки определителя на их
алгебраические дополнения. Обычно выбирают
ту строку/столбец, в которой/ом есть нули. Строку или столбец, по которой/ому ведется разложение, будет обозначать стрелкой.
Пример
Задание. Разложив по первой строке, вычислить определитель $left| begin{array}{lll}{1} & {2} & {3} \ {4} & {5} & {6} \ {7} & {8} & {9}end{array}right|$
Решение. $left| begin{array}{lll}{1} & {2} & {3} \ {4} & {5} & {6} \ {7} & {8} & {9}end{array}right| leftarrow=a_{11} cdot A_{11}+a_{12} cdot A_{12}+a_{13} cdot A_{13}=$
$1 cdot(-1)^{1+1} cdot left| begin{array}{cc}{5} & {6} \ {8} & {9}end{array}right|+2 cdot(-1)^{1+2} cdot left| begin{array}{cc}{4} & {6} \ {7} & {9}end{array}right|+3 cdot(-1)^{1+3} cdot left| begin{array}{cc}{4} & {5} \ {7} & {8}end{array}right|=-3+12-9=0$
Ответ. $left| begin{array}{lll}{1} & {2} & {3} \ {4} & {5} & {6} \ {7} & {8} & {9}end{array}right|=0$
Этот метод позволяет вычисление определителя свести к вычислению определителя более низкого порядка.
Пример
Задание. Вычислить определитель $left| begin{array}{lll}{1} & {2} & {3} \ {4} & {5} & {6} \ {7} & {8} & {9}end{array}right|$
Решение. Выполним следующие
преобразования над строками определителя: из второй строки отнимем четыре
первых, а из третьей первую строку, умноженную на семь, в результате, согласно свойствам определителя, получим определитель,
равный данному.
$$left| begin{array}{ccc}{1} & {2} & {3} \ {4} & {5} & {6} \ {7} & {8} & {9}end{array}right|=left| begin{array}{ccc}{1} & {2} & {3} \ {4-4 cdot 1} & {5-4 cdot 2} & {6-4 cdot 3} \ {7-7 cdot 1} & {8-7 cdot 2} & {9-7 cdot 3}end{array}right|=$$
$$=left| begin{array}{rrr}{1} & {2} & {3} \ {0} & {-3} & {-6} \ {0} & {-6} & {-12}end{array}right|=left| begin{array}{ccc}{1} & {2} & {3} \ {0} & {-3} & {-6} \ {0} & {2 cdot(-3)} & {2 cdot(-6)}end{array}right|=0$$
Определитель равен нулю, так как вторая и третья строки являются пропорциональными.
Ответ. $left| begin{array}{lll}{1} & {2} & {3} \ {4} & {5} & {6} \ {7} & {8} & {9}end{array}right|=0$
Для вычисления определителей четвертого порядка и выше применяется либо разложение по строке/столбцу, либо приведение
к треугольному виду, либо с помощью теоремы Лапласа.
Разложение определителя по элементам строки или столбца
Пример
Задание. Вычислить определитель
$left| begin{array}{llll}{9} & {8} & {7} & {6} \ {5} & {4} & {3} & {2} \ {1} & {0} & {1} & {2} \ {3} & {4} & {5} & {6}end{array}right|$ , разложив его по элементам какой-то строки или какого-то столбца.
Решение. Предварительно выполним
элементарные преобразования над строками определителя, сделав
как можно больше нулей либо в строке, либо в столбце. Для этого вначале от первой строки отнимем девять третьих,
от второй — пять третьих и от четвертой — три третьих строки, получаем:
$$left| begin{array}{cccc}{9} & {8} & {7} & {6} \ {5} & {4} & {3} & {2} \ {1} & {0} & {1} & {2} \ {3} & {4} & {5} & {6}end{array}right|=left| begin{array}{cccc}{9-1} & {8-0} & {7-9} & {6-18} \ {5-5} & {4-0} & {3-5} & {2-10} \ {1} & {0} & {1} & {2} \ {0} & {4} & {2} & {0}end{array}right|=left| begin{array}{rrrr}{0} & {8} & {-2} & {-12} \ {0} & {4} & {-2} & {-8} \ {1} & {0} & {1} & {2} \ {0} & {4} & {2} & {0}end{array}right|$$
Полученный определитель разложим по элементам первого столбца:
$$left| begin{array}{rrrr}{0} & {8} & {-2} & {-12} \ {0} & {4} & {-2} & {-8} \ {1} & {0} & {1} & {2} \ {0} & {4} & {2} & {0}end{array}right|=0+0+1 cdot(-1)^{3+1} cdot left| begin{array}{rrr}{8} & {-2} & {-12} \ {4} & {-2} & {-8} \ {4} & {2} & {0}end{array}right|+0$$
Полученный определитель третьего порядка также разложим по элементам строки и столбца, предварительно получив нули,
например, в первом столбце. Для этого от первой строки отнимаем две вторые строки, а от третьей — вторую:
$$left| begin{array}{rrr}{8} & {-2} & {-12} \ {4} & {-2} & {-8} \ {4} & {2} & {0}end{array}right|=left| begin{array}{rrr}{0} & {2} & {4} \ {4} & {-2} & {-8} \ {0} & {4} & {8}end{array}right|=4 cdot(-1)^{2+2} cdot left| begin{array}{ll}{2} & {4} \ {4} & {8}end{array}right|=$$
$$=4 cdot(2 cdot 8-4 cdot 4)=0$$
Ответ. $left| begin{array}{cccc}{9} & {8} & {7} & {6} \ {5} & {4} & {3} & {2} \ {1} & {0} & {1} & {2} \ {3} & {4} & {5} & {6}end{array}right|=0$
Замечание
Последний и предпоследний определители можно было бы и не вычислять,
а сразу сделать вывод о том, что они равны нулю, так как содержат пропорциональные строки.
Приведение определителя к треугольному виду
С помощью элементарных преобразований над строками или столбцами определитель приводится к треугольному виду и тогда его
значение, согласно свойствам определителя, равно произведению
элементов стоящих на главной диагонали.
Пример
Задание. Вычислить определитель
$Delta=left| begin{array}{rrrr}{-2} & {1} & {3} & {2} \ {3} & {0} & {-1} & {2} \ {-5} & {2} & {3} & {0} \ {4} & {-1} & {2} & {-3}end{array}right|$ приведением его к треугольному виду.
Решение. Сначала делаем нули в первом столбце под главной диагональю. Все преобразования
будет выполнять проще, если элемент $a_{11}$ будет
равен 1. Для этого мы поменяем местами первый и второй столбцы определителя, что, согласно свойствам определителя,
приведет к тому, что он сменит знак на противоположный:
$$Delta=left| begin{array}{rrrr}{-2} & {1} & {3} & {2} \ {3} & {0} & {-1} & {2} \ {-5} & {2} & {3} & {0} \ {4} & {-1} & {2} & {-3}end{array}right|=-left| begin{array}{rrrr}{1} & {-2} & {3} & {2} \ {0} & {3} & {-1} & {2} \ {2} & {-5} & {3} & {0} \ {-1} & {4} & {2} & {-3}end{array}right|$$
Далее получим нули в первом столбце, кроме элемента $a_{11}$ ,
для этого из третьей строки вычтем две первых, а к четвертой строке прибавим первую, будем иметь:
$$Delta=-left| begin{array}{rrrr}{1} & {-2} & {3} & {2} \ {0} & {3} & {-1} & {2} \ {0} & {-1} & {-3} & {-4} \ {0} & {2} & {5} & {-1}end{array}right|$$
Далее получаем нули во втором столбце на месте элементов, стоящих под главной диагональю. И снова, если
диагональный элемент будет равен $pm 1$ , то
вычисления будут более простыми. Для этого меняем местами вторую и третью строки (и при этом меняется на
противоположный знак определителя):
$$Delta=left| begin{array}{rrrr}{1} & {-2} & {3} & {2} \ {0} & {-1} & {-3} & {-4} \ {0} & {3} & {-1} & {2} \ {0} & {2} & {5} & {-1}end{array}right|$$
Далее делаем нули во втором столбце под главной диагональю, для этого поступаем следующим образом:
к третьей строке прибавляем три вторых, а к четвертой — две вторых строки, получаем:
$$Delta=left| begin{array}{rrrr}{1} & {-2} & {3} & {2} \ {0} & {-1} & {-3} & {-4} \ {0} & {0} & {-10} & {-10} \ {0} & {0} & {-1} & {-9}end{array}right|$$
Далее из третьей строки выносим (-10) за определитель и делаем нули в третьем столбце под
главной диагональю, а для этого к последней строке прибавляем третью:
$$Delta=-10 left| begin{array}{rrrr}{1} & {-2} & {3} & {2} \ {0} & {-1} & {-3} & {-4} \ {0} & {0} & {1} & {1} \ {0} & {0} & {-1} & {-9}end{array}right|=$$
$$=-10 cdot left| begin{array}{cccc}{1} & {-2} & {3} & {2} \ {0} & {-1} & {-3} & {-4} \ {0} & {0} & {1} & {1} \ {0} & {0} & {0} & {-8}end{array}right|=(-10) cdot 1 cdot(-1) cdot 1 cdot(-8)=-80$$
Ответ. $Delta=-80$
Теорема Лапласа
Теорема
Пусть $Delta$ — определитель
$n$-го порядка. Выберем в нем произвольные
$k$ строк (или столбцов), причем
$k leq n-1$ . Тогда сумма произведений всех
миноров
$k$-го порядка, которые содержатся в выбранных
$k$ строках (столбцах), на их
алгебраические дополнения равна определителю.
Пример
Задание. Используя теорему Лапласа, вычислить определитель
$left| begin{array}{rrrrr}{2} & {3} & {0} & {4} & {5} \ {0} & {1} & {0} & {-1} & {2} \ {3} & {2} & {1} & {0} & {1} \ {0} & {4} & {0} & {-5} & {0} \ {1} & {1} & {2} & {-2} & {1}end{array}right|$
Решение. Выберем в данном определителе пятого порядка две строки —
вторую и третью, тогда получаем (слагаемые, которые равны нулю, опускаем):
$$left| begin{array}{rrrrr}{2} & {3} & {0} & {4} & {5} \ {0} & {1} & {0} & {-1} & {2} \ {3} & {2} & {1} & {0} & {1} \ {0} & {4} & {0} & {-5} & {0} \ {1} & {1} & {2} & {-2} & {1}end{array}right|=left| begin{array}{cc}{1} & {-1} \ {4} & {-5}end{array}right| cdot(-1)^{2+4+2+4} cdot left| begin{array}{ccc}{2} & {0} & {5} \ {3} & {1} & {1} \ {1} & {2} & {1}end{array}right|+$$
$$+left| begin{array}{ll}{1} & {2} \ {4} & {0}end{array}right| cdot(-1)^{2+4+2+5} cdot left| begin{array}{rrr}{2} & {0} & {4} \ {3} & {1} & {0} \ {1} & {2} & {-2}end{array}right|+left| begin{array}{cc}{-1} & {2} \ {-5} & {0}end{array}right| cdot(-1)^{2+4+5} cdot left| begin{array}{ccc}{2} & {3} & {0} \ {3} & {2} & {1} \ {1} & {1} & {2}end{array}right|=$$
$$=-23+128+90=195$$
Ответ. $left| begin{array}{rrrrr}{2} & {3} & {0} & {4} & {5} \ {0} & {1} & {0} & {-1} & {2} \ {3} & {2} & {1} & {0} & {1} \ {0} & {4} & {0} & {-5} & {0} \ {1} & {1} & {2} & {-2} & {1}end{array}right|=195$
Читать дальше: обратная матрица.
Щебетун Виктор
Эксперт по предмету «Математика»
Задать вопрос автору статьи
Существует несколько способов нахождения определителей матриц третьего порядка. Рассмотрим их подробнее.
Перечислим основные способы, используемые для этого:
- Правило Саррюса;
- Правило треугольников;
- Использование специальной формулы для вычисления;
- Использование метода Гаусса или иначе метода перестановок.
Правило Саррюса
Правило Саррюса для вычисления матриц 3-ьего порядка применяется просто: достаточно соответственно рисунку переписать 2 первых столбика справа рядом с матричной таблицей, а затем записать произведения, стоящие по диагоналям со знаками.
Замечание 1
Если диагональ идёт сверху слева вниз направо — то произведение записывается со знаком «+», а если диагональ идёт из правого верхнего угла в нижний левый — то со знаком «-».
Рисунок 1. Формула третьего порядка. Автор24 — интернет-биржа студенческих работ
Пример 1
Дана матричная таблица $A$. Вычислите детерминант с помощью правила Саррюса.
$A = begin{pmatrix} 0 & 3 & -1 \ 1 & 4 & 2 \ 2 & 5 & 3 \ end{pmatrix}$
Решение:
Рисунок 2. Вычисление определителя 3 порядка. Автор24 — интернет-биржа студенческих работ
$Δ = 0 cdot 4 cdot 3 + 3 cdot 2 cdot 2 – 1 cdot 1 cdot 5 – 3 cdot 1 cdot 3 – 0 cdot 2 cdot 5 + 1 cdot 4 cdot 2 = 0 + 12 – 5 — 9 – 0 + 8 = 6$
Правило треугольников
Это правило немного похоже на предыдущее. Суть его в том, что произведения элементов с главной диагонали и двух треугольников, задействующих все остальные элементы как показано на рисунке, записываются со знаком плюс, а произведения элементов с побочной диагонали и двух синих треугольников — с противоположным.
«Найти определитель матрицы третьего порядка» 👇
Рисунок 3. Треугольники. Автор24 — интернет-биржа студенческих работ
Пример 2
Найдите определитель из прошлого задания, используя метод треугольников.
Решение:
Рисунок 4. Наглядный пример как пользоваться. Автор24 — интернет-биржа студенческих работ
$Δ= 0 cdot 4 3 + 3 cdot 2 cdot 2 – 1 cdot 5 cdot 1 + 1 cdot 4 cdot 2 – 1 cdot 3 cdot 3 – 2 cdot 5 cdot 0 = 0 + 12 – 5 + 8 – 9 – 0 = 6$
Использование формулы разложения по строчке
$A = begin{pmatrix} a_{11} & a_{12} & a_{13} \ a_{21} & a_{22} & a_{23} \ a_{31} & a_{32} & a_{33} \ end{pmatrix}$
Для матрицы 3 на 3, приведённой выше, определитель можно сосчитать по формуле:
$Δ =begin{array}{|ccc|} a_{11} & a_{12} & a_{13} \ a_{21} & a_{22} & a_{23} \ a_{31} & a_{32} & a_{33} \ end{array}=a_{11} cdot begin{array}{|cc|} a_{22} & a_{23} \ a_{32} & a_{33} \ end{array} – a_{12} cdot begin{array}{|cc|} a_{11} & a_{13} \ a_{21} & a_{23} \ a_{31} & a_{33} \ end{array} + a_{13} cdot begin{array}{|cc|} a_{11} & a_{12} \ a_{21} & a_{22} \ a_{31} & a_{32} \ end{array}= a_{11} cdot a_{22} cdot a_{33} – a_{12} cdot a_{23} cdot a_{31} + a_{13} cdot a_{21} cdot a_{32} — a_{13} cdot a_{22} cdot a_{31}$.
Пример 3
Разложите определитель матрицы из предыдущих примеров по 1-ой строчке и найдите его.
Решение:
$Δ = 0 cdot begin{array}{|cc|} 4 & 2 \ 5 & 3 \ end{array} – 3 cdot begin{array} {|cc|} 1 & 2 \ 2 & 3 \ end{array} + (-1) cdot begin{array}{|cc|} 1 & 4 \ 2 & 5 \ end{array} = 0 – 3 cdot (1 cdot 3 – 2 cdot 2) + (-1) cdot (5 – 
Метод Гаусса
Чтобы вычислить детерминант этим методом, нужно используя разрешённые преобразования получить треугольную матрицу.
Разрешёнными преобразованиями являются сложение и вычитание строчек и столбцов, в то время как при перестановке строчек и столбцов между собой необходимо помнить о смене знака определителя в конце.
После этого нужно перемножить элементы, стоящие на главной диагонали, их произведение и будет определителем.
Пример 4
Примените метод Гаусса для получения детерминанта матрицы из предыдущих примеров.
Решение:
$A = begin{pmatrix} 0 & 3 & -1 \ 1 & 4 & 2 \ 2 & 5 & 3 \ end{pmatrix}$
Переставим первую строчку со второй, при этом запомним, что знак детерминанта в конце поменяется:
$begin{pmatrix} 1 & 4 & 2 \ 0 & 3 & -1 \ 2 & 5 & 3 \ end{pmatrix}$;
Вычтем из третьей строчки 1-ую, умноженную на 2:
$begin{pmatrix} 1 & 4 & 2 \ 0 & 3 & -1 \ 0 & -3 & -1 \ end{pmatrix}$;
Сложим между собой третью строчку со второй:
$begin{pmatrix} 1 & 4 & 2 \ 0 & 3 & -1 \ 0 & 0 & -2 \ end{pmatrix}$;
Получили искомый вид матрицы. Теперь можно сосчитать определитель, минус появляется из-за перемены строчек местами:
$Δ=-begin{pmatrix} 1 & 4 & 2 \ 0 & 3 & -1 \ 0 & 0 & -2 \ end{pmatrix}= -(1 cdot 3 cdot ( — 2) ) = 6 $
Находи статьи и создавай свой список литературы по ГОСТу
Поиск по теме