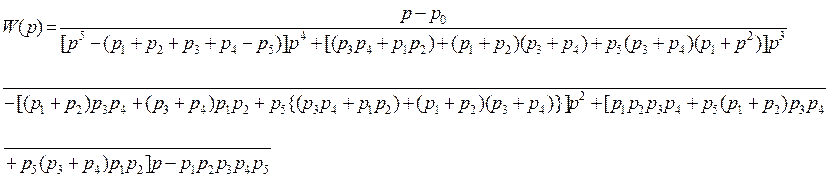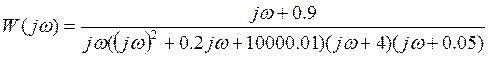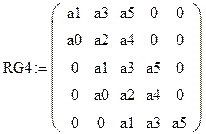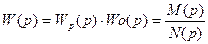Как составить передаточную функцию замкнутой системы

Время на прочтение
7 мин

Количество просмотров 14K

Продолжаем публикацию лекций по курсу «Управление в Технических Системах» автор — Олег Степанович Козлов на кафедре Э7 МГТУ им. Н.Э. Баумана.

Данные лекции готовятся к публикации в виде книги, а поскольку здесь есть специалисты по ТАУ, студенты и просто интересующиеся предметом, то любая критика приветствуется. В предыдущих сериях:

1. Введение в теорию автоматического управления.
2. Математическое описание систем автоматического управления 2.1 — 2.3, 2.3 — 2.8, 2.9 — 2.13.
3. ЧАСТОТНЫЕ ХАРАКТЕРИСТИКИ ЗВЕНЬЕВ И СИСТЕМ АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ РЕГУЛИРОВАНИЯ.
3.1. Амплитудно-фазовая частотная характеристика: годограф, АФЧХ, ЛАХ, ФЧХ. 3.2. Типовые звенья систем автоматического управления регулирования. Классификация типовых звеньев. Простейшие типовые звенья. 3.3. Апериодическое звено 1–го порядка инерционное звено. На примере входной камеры ядерного реактора. 3.4. Апериодическое звено 2-го порядка. 3.5. Колебательное звено. 3.6. Инерционно-дифференцирующее звено. 3.7. Форсирующее звено.  3.8. Инерционно-интегрирующее звено (интегрирующее звено с замедлением). 3.9. Изодромное звено (изодром). 3.10 Минимально-фазовые и не минимально-фазовые звенья. 3.11 Математическая модель кинетики нейтронов в «точечном» реакторе «нулевой» мощности. 4 Структурные преобразования систем автоматического регулирования.

Будет как всегда позновательной увлекательно и жестко

5.1. Главная передаточная функция. Передаточные функции по возмущающему воздействию и для ошибки (рассогласования)

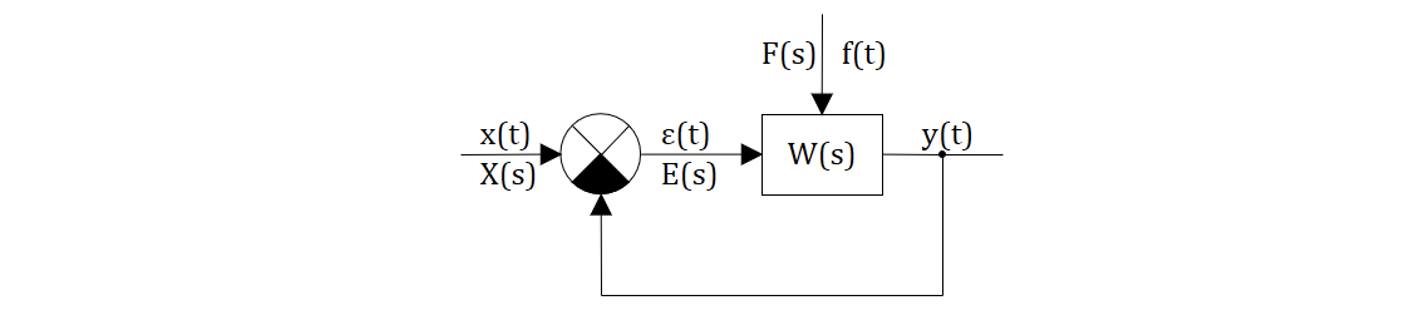
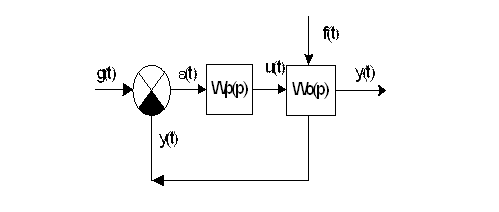
Используя структурные преобразования (см. раздел 4), структурную схему практически любой линейной или линеаризованной САР (САУ) можно привести к виду: 

Где функции по времени:

— управляющее  воздействие;

– регулируемая  величина (выходное  воздействие);

– возмущающее  воздействие;

Или в изображениях: 

Определение: Если единичная обратная связь охватывает все элементы (звенья) САР – она  называется главной.

Определение: Если главная обратная связь отсутствует — САР считается разомкнутой.

Передаточная функция может быть любой сложности (т.е. содержать местные обратные связи, параллельные и последовательные цепи и т.д.).

Возмущающих воздействий может быть несколько и приложены они могут быть в любом  месте структурной схемы. 

Передаточную функцию которую  в Теории Управления называют  передаточной  функцией  разомкнутой  САР, будем представлять в  следующем  виде (для единообразия):  

где – общий коэффициент усиления;  – полиномы по степеням переменной , причем свободные члены в них равны 1 (единице). 

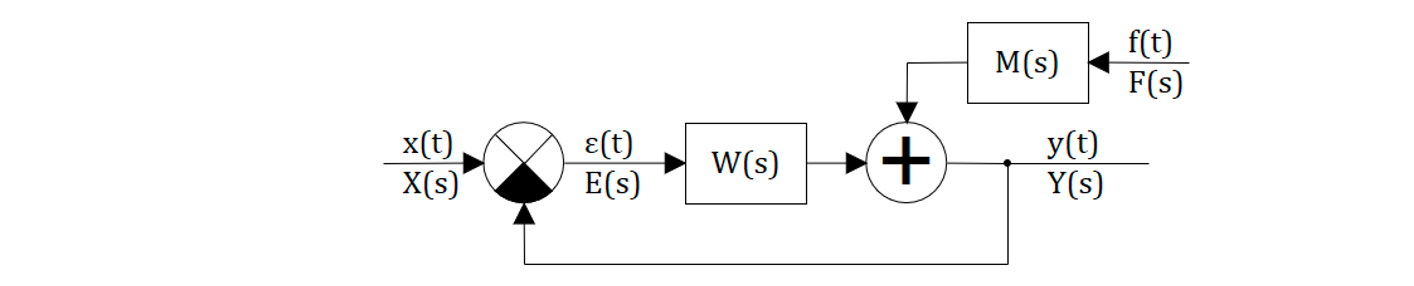
Учитывая, что САР линейна или линеаризована, разделим на структурной схеме каналы прохождения управляющего и возмущающего воздействий.  Выделим в отдельное звено (может быть и очень сложное) ту часть системы, через которую проходит возмущающее воздействие обозначим ее через  Структурная схема САР принимает вид:  

где:

В Теории Управления используют 3 основных передаточных функций замкнутой САР: 

•  главная передаточная функция ;

• передаточная функция  по возмущающему воздействию ;

• передаточная функция для ошибки (рассогласования)  

Рассмотрим более подробно вышеупомянутые передаточные функции. 

Главная передаточная функция

Главная передаточная функция -передаточная функция по управляющему воздействию  математическое определение этой передаточной функции:  

выведем формулу при условии если возмущеющие воздействие равно . «Обойдем» структурную схемв по контуру:

Примечание.  Формула (5.3) совпадает с формулой для передаточной функции цепи с местной единичной обратной связью (см. раздел 4 – «Структурные преобразования»).

Подставляя  вместо  ее выражение через полиномы   и    

где:

Анализ выражения (5.4) показывает, что свойства главной передаточной функции замкнутой САР однозначно определяются свойствами разомкнутой САР, т.е. через полиномы и .

Передаточная функция замкнутой САР по внешнему возмущающему воздействию

Дадим математическое определение рассматриваемой передаточной функции если управляющие воздействи , а возмущеющие воздействие отличное от нуля . В этом случае (см. рисунок 5.1.2) получается:

Перрейдем к изображением и «обойдем» схему (см. рис. 5.1.2) по контуру

Подставляя  вместо  ее выражение через полиномы   и    получаем:

где: — вид данного полинома зависит от места приложения возмущающего воздействия;

Формулы 5.4 и 5.6 имеют общий занаменатель

Передаточная функция замкнутой САР для ошибки (рассогласования)

Дадим математическое определение рассматриваемой передаточной функции если управляющие воздействиt отлично от 0 , а возмущеющие воздействие равно 0 . В этом случае для передаточной функции получается (см. рис. 5.1.2):

Сделаем вывод соответствующих формул, выполнив «обход» по контуру схемы (см. рис. 5.1.2)

Учитывая формулу для главной передаточной функции можно записать выражения для передаточной функции рассоглаосвания:

Подставляя  вместо  ее выражение через полиномы   и    получаем:

где:

Опять замечаем, что знаменатель передаточной функции  равен полиному следовательно, характерным признаком передаточных функций замкнутой САР является  общность знаменателей ! ! !

В Теории Управления выражение  имеет «собственное» название:  характеристический полином  замкнутой  САР.

5.2 Уравнения динамики замкнутой САР

Как указывалось в подразделе 5.1, любую замкнутую САР можно привести к виду представленному на рисунке 5.2.1:

Выведены соотношения для 3-х основных передаточных функций замкнутой САР  позволяют записать выражения для регулируемой величины в изображениях:

Подставляя значения  и через полиномы  и  разомкнутой САР  получаем:

подставим значения для характеристического полинома получим выражение для динамического уравнения замкнутой САР в изображениях:

Переходя к оригиналам получаем символическую форму записи обыкновенного дифференциального уравнения замкнутой САР:

Решение диференциального уравнения состоит из двух частей:

где: —  собственная часть, решение однородного дифференциального уравнения ;

— вынужденная часть решения (частное решение), определяемая правой частью уравнения ( 5.2.3 ).

Решения однородного уравнения замкнутой САР:

записываем соответствующее характеристическое уравнение:

находим корни степенного уравнения если все корни уравнения разные:

Если есть совпадающие корни характеристического уравнения, то формула для  изменится (см. Математическое описание систем автоматического управления). 

Обычно находят по виду правой части уравнения (5.2.3) или, используя другие методы (например, метод вариаций постоянных). 

Необходимо отметить, что порядок дифференциального уравнения (5.2.3) равен «n», т.е. такой же, как и у разомкнутой САР

если нет возмущающего воздействия, т.к. порядок дифференциального оператора L(p) обычно значительно выше, чем N(p).

По аналогии с выводом уравнения (5.2.3) можно получить уравнение динамики для  рассогласования : 

подставляя значения и (см. 5.6 и 5.9) получаем:

Уравнение (5.2.5)- уравнение динамики замкнутой САР в ихображениях для рассогласования (ошибки) при наличии  управляющего и возмущающего воздействий. 

Особенностью данного уравнения (5.2.5) является то, что левая часть его практически  совпадает с левой частью (5.2.2), в то время, как порядок правой части заметно выше , т.к. порядок многочленов D (s) и L (s)  — одинаков, а порядок N(s) меньше L(s).

Это означает, что внешние воздействия  и влияют на более сильным  образом.

Дифференциальное уравнение замкнутой САР для ошибки:

Способы решения уравнения ( 5.2.6 ) такие же, как и для уравнения ( 5.2.3 ) .                    

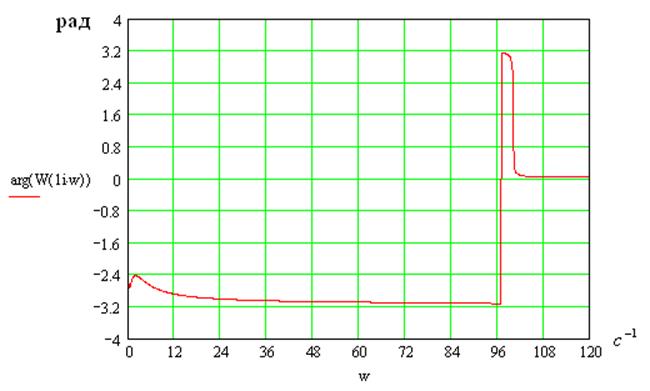
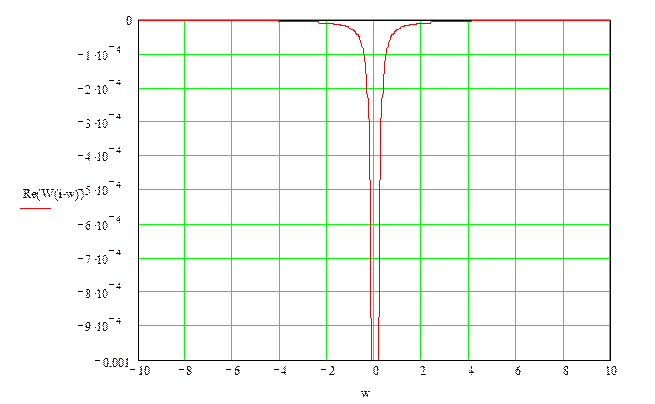
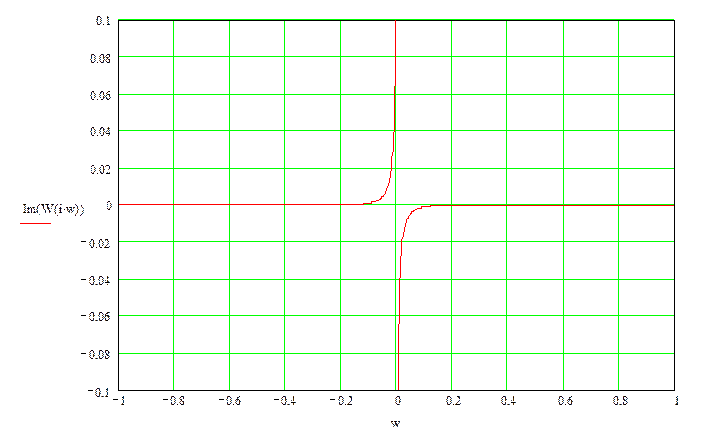
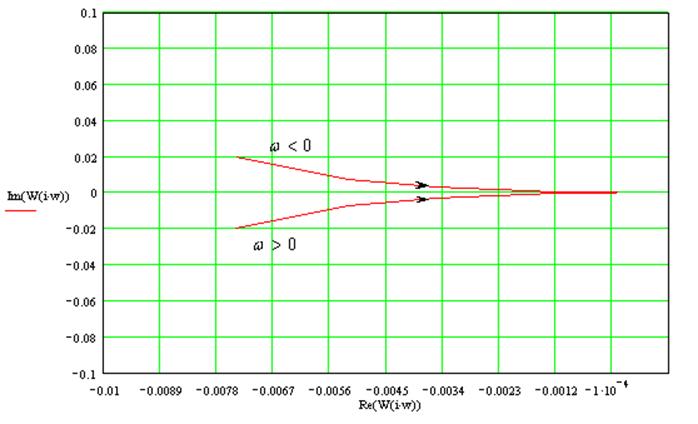
5.3. Частотные характеристики замкнутой  САР. 

Наибольший интерес при анализе замкнутых САР имеет АФЧХ замкнутой САР по управляющему воздействию:

где передаточная функция:

Учитывая, что —  комплексное число, по аналогии имеем:

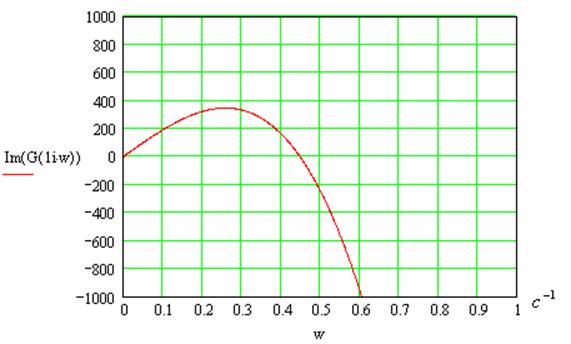
Где — вещественная часть функции, — мнимая часть функиции.

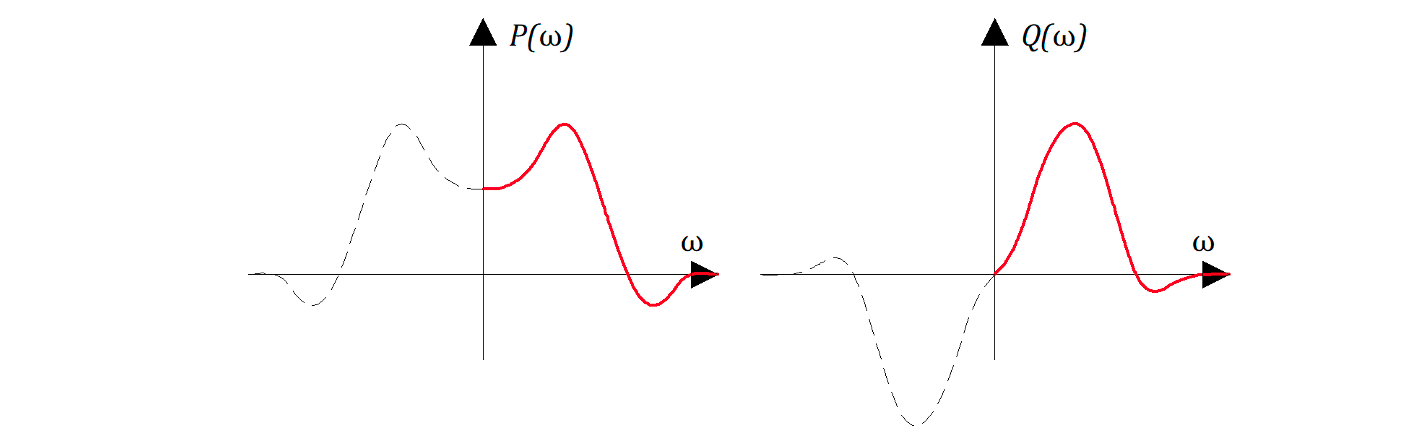
На этих рисунках представлен «примерный» вид зависимостей P (w)и Q(w) для «какой-то»  замкнутой САР   причем  P(w) —  четная функция, т.е. P(w) = P(-w);  Q(w) —  нечетная функция, т.е. Q(w) = — Q(-w).

Если известны частотные свойства разомкнутой САР, то можно определить частотные свойства замкнутой САР. Воспользуемся показательной формой для АФЧХ

Где — амплитуда (модуль), — сдвиг фазы (фаза).  Подставляя это в (5.3.1), имеем получаем:

Учитывая, что

Приравнивая чисто вещественные и чисто мнимые части, имеем  

Для нахождения амплитуды и сдвига фазы замкнутой передаточной функции как функции от амплитуды и сдвига фазы разомкнутой системы. Разделив (2) на (1)  получим:

Сдвиг фазы замкнутой системы через характеристики разомкнутой системы:

Для получения амплитуды замкнутоей системы возведем оба уравнения системы  (5.3.5) в квадрат:  

складываем эти два уравнения:

Аналогичным образом можно выразить, например, P(w) и Q(w)  —  характеристики замкнутой САР через u(w) и u(w)  —  характеристики разомкнутой САР.

Пример

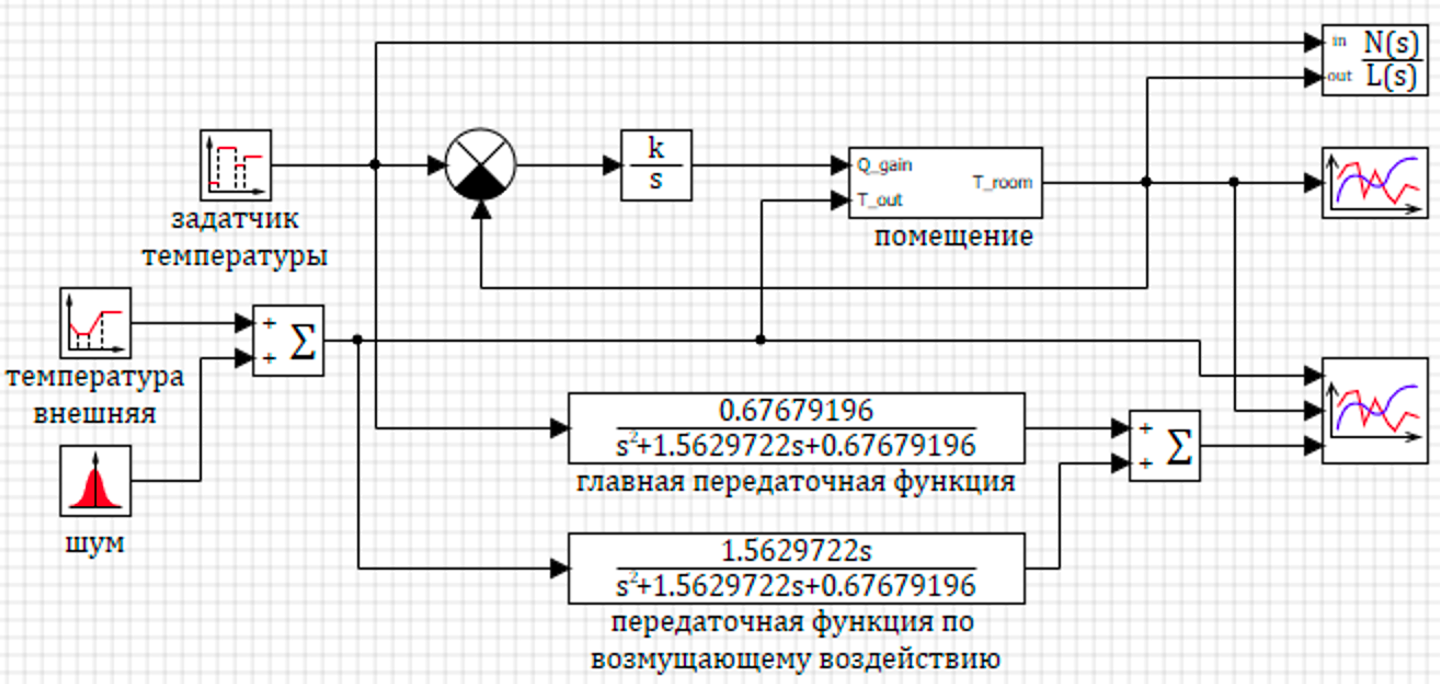
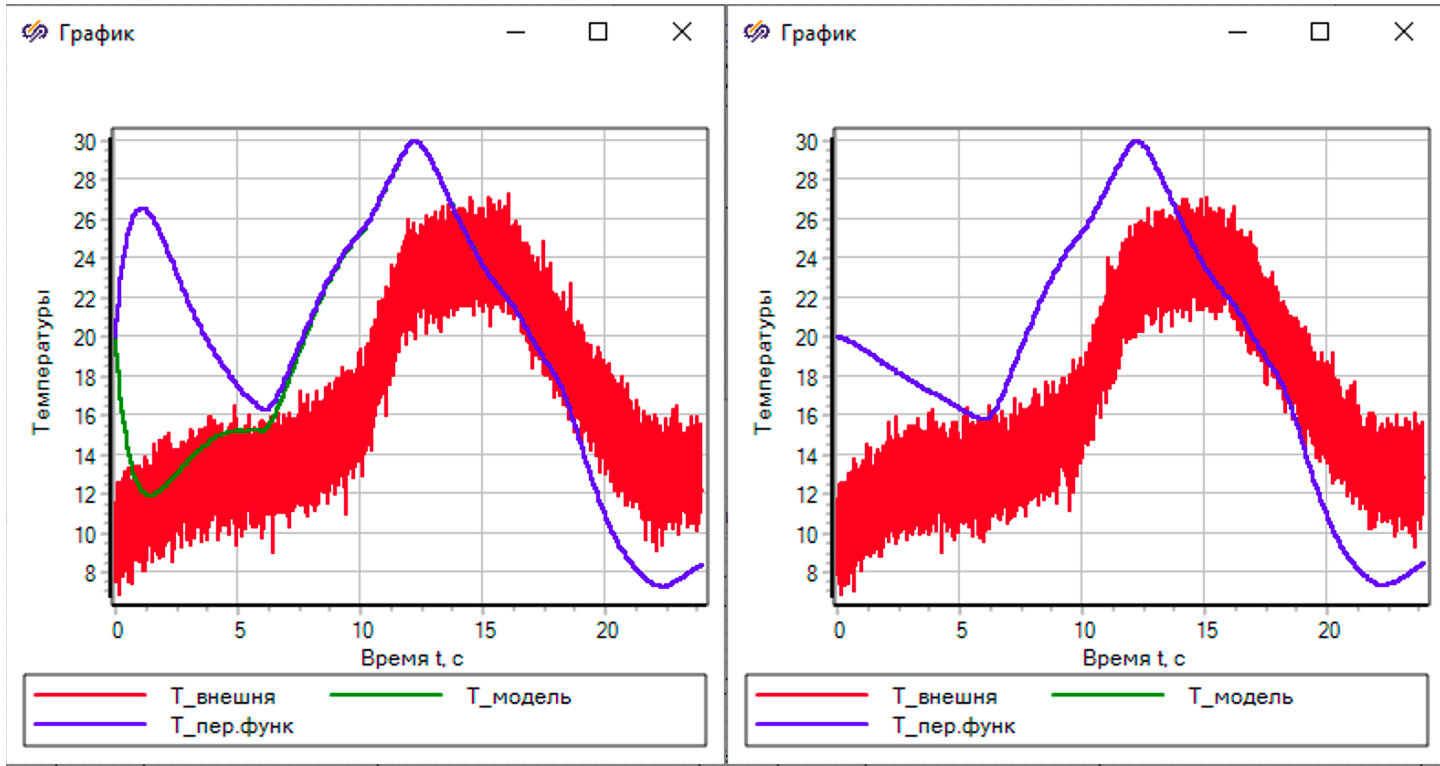
В качестве примера на рисунке 5.4.1 приведена модель помещения, в котором с помощью интегрирующего звена обеспечивается подвод тепла для поддержания температуры. Температура задается в виде ступенчатой функции. В качестве внешнего воздействия используется внешняя температура.

Передаточные функции построены средтвами автоматического анализа. Видно, что знаменатель главной передаточной функции и знаменатель передаточной функции по возмущающиму воздействию одинаковы.

График справа показывает расхождение результаты модели (зеленая линия) и передаточных функций (синит линя) в начале расчета, но потом функции сходятся. Расхождение объясняются разными начальными условиями по производным. Слева тот же самый график, но в это случае начальное состояние определено с помощю загрузки стационарного состояния, полученного предварительным моделированием. В этом случае совпадение модели и передаточных функций полное.

Ссылку на модель примера можено взять здесь…

1. Передаточные функции разомкнутых и замкнутых сау

При анализе САУ в результате структурных
преобразований, чаще всего стремятся
получить одноконтурную САУ, так как
методы анализа и синтеза подобных систем
разработаны наиболее полно. Рассмотрим
простейшую одноконтурную САР (рисунок
4.6, а). Она представляет собой систему с
главной отрицательной обратной связью.
Произведем размыкание системы в точке
«А».

Передаточной функцией разомкнутой
системы W_p(p)называется
отношение изображения по Лапласу сигнала
обратной связи к изображению по Лапласу
сигнала ошибки при нулевых начальных
условиях, т.е.

(4.14)

Следует иметь в виду, что для разомкнутой
системы X(t)=X(t)и все возмущающие воздействия считаются
равными нулю.

Таким образом, передаточная функция
разомкнутой системы равна произведению
передаточных функций отдельных звеньев
разомкнутого контура, включая передаточную
функцию элемента обратной связи.

Рисунок 4.6
Преобразования одноконтурной САУ

При анализе САУ, особенно следящих,
возникает необходимость анализа
поведения ошибки управления. Для этого
составляют передаточную функцию
относительно ошибки управления.

Передаточной функцией замкнутой системы
по ошибке регулирования называется
отношение изображения по Лапласу ошибки
регулирования к изображению по Лапласу
управляющего воздействия. Ошибка
регулирования в САР выявляется после
узла сравнения. Если выходной величиной
САР считать ошибку регулирования X(t),
а входной — управляющее воздействиеX(t), то структурная схема примет вид,
показанный на рисунке 4.6, б.

Пользуясь правилами преобразования,
получим передаточную функцию для ошибки
воспроизведения управляющего воздействия.

, (4.15)

Аналогично можно написать передаточную
функцию и для любой координаты САР,
например Y₂(t).

Из структурной схемы (рисунок 4.6, в),
считая Y₂(t)выходной
величиной, получим

, (4.16)

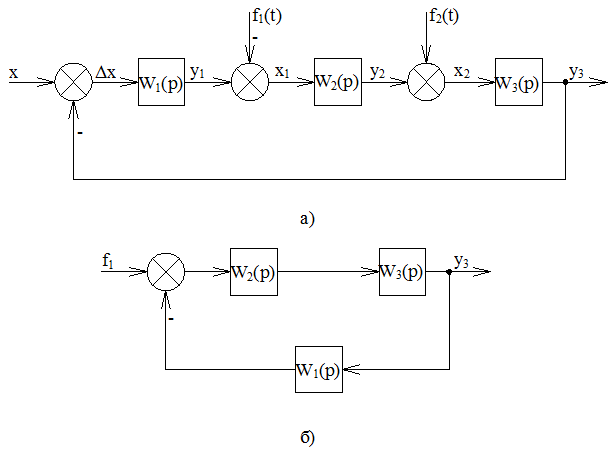
Рассмотрим случай, когда к САУ приложено
несколько возмущающих воздействий
(рисунок 4.7, а). Как было показано ранее,
каждому возмущающему воздействию
соответствует передаточная функция,
причем все остальные возмущения и
управляющие воздействия полагаются
равными нулю. Составим передаточную
функцию относительно возмущения f₁(t)(рисунок 4.7, б). Из структурной схемы
следует

, (4.17)

Из выражения (4.17) следует, что передаточная
функция замкнутой САУ по данному
возмущению равна дроби, в числителе
которой передаточная функция прямого
канала от точки приложения возмущения
до выходной величины, а в знаменателе
— единица плюс передаточная функция
разомкнутой системы.

Согласно принципу суперпозиции, реакция
выходной величины определяется как
сумма реакций от каждого из воздействий,
т.е.

Рисунок
4.7 Одноконтурная САУ при приложении
нескольких воздействий

,
(4.18)

где

;

;

W₁(p),W₂(p),W₃(p)— передаточные функции прямых цепей
элементов, заключенных между точками
приложения воздействий и выходной
величиной.

Известно, что при исследовании свободного
движения САУ оперируют характеристическим
уравнением системы. Найдем характеристические
полиномы разомкнутой и замкнутой САУ.

Для разомкнутой системы можно записать
уравнение:

, (4.19)

где D_p(p)— характеристичекий
полином разомкнутой системы.

Для замкнутой системы получим:

, (4.20)

Пусть
,
тогда характеристическое уравнение
замкнутой системы

, (4.21)

или

, (4.22)

Таким образом, характеристическое
уравнение замкнутой САУ при отрицательной
обратной связи равно сумме характеристических
полиномов левой и правой части уравнения
разомкнутой системы.

Рассмотрим пример преобразований САУ
к виду, удобному для анализа.

Система управления имеет два внутренних
контура и один внешний. Внешний контур
регулирования содержит обратную связь
по скорости двигателя. Эта связь
называется главной обратной связью, и
поэтому система называется системой
автоматического регулирования скорости.
Соответственно, устройство, обеспечивающее
поддержание заданного алгоритма
функционирования, называется регулятором
скорости.

Внутренние контуры регулирования
являются вспомогательными и предназначены
для улучшения характеристики объекта
управления и поддержания промежуточных
координат САР в заданных пределах с
целью компенсации вредного влияния
внутренних возмущений и инерционностей
системы.

В данном случае имеем два внутренних
контура — контур напряжения и контур
тока. Подробно принципы построения
таких систем будут рассмотрены в курсе
«Автоматическое управления
электроприводами», поэтому мы остановимся
лишь на вопросах, связанных с преобразованием
таких структурных схем. Рассмотрим
каждый контур в отдельности.

Контур напряжения включает в себя:
регулятор напряжения (РН), тиристорный
возбудитель, генератор с передаточными
функциями:

; (4.23)

; (4.24)

. (4.25)

При анализе такие системы, как правило,
приводят к единичной обратной связи
так, как это показано на рисунке 4.8, а.

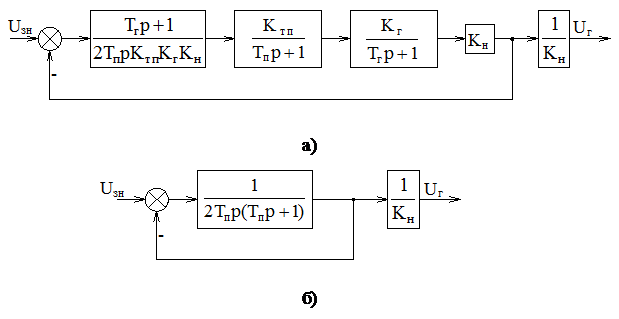
Рисунок 4.8 Структурные
схемы контура напряжения

Учитывая (4.23) и правило последовательного
соединения звеньев, структурная схема
(рисунок 4.8, б) может быть представлена
одним эквивалентным звеном с передаточной
функцией

, (4.26)

Управляющим воздействием для контура
тока является сигнал задания тока
двигателя U_зт,
а выходной величиной ток двигателя.
Регулятор тока имеет передаточную
функцию

, (4.27)

С учетом (4.26), (4.27) структурная схема
контура тока приведенного к единичной
обратной связи представлена на (рисунке
4.9, а).

Такая структурная схема получена при
условии, что Т_м>>Т_э.
В этом случае пренебрегают обратной
связью по ЭДС двигателя т.е. полагают,
чтоE=K_E=0.
В результатеW_к(p)=1.
После преобразования структурная схема
замкнутого контура тока примет вид,
показанный на (рисунок 4.9, б).

Этой структурной схеме может быть
поставлена в соответствие передаточная
функция замкнутого контура тока

, (4.28)

Учитывая, что замкнутый контур тока
является внутренним по отношению к
контуру скорости, и приводя к единичной
обратной связи, получим структурную
схему, изображенную на (рисунок 4.9, в). В
данном случае считаем, что передаточная
функция регулятора известна и имеет
вид

, (4.29)

Из структурной схемы видно, что к системе
прикладывается два воздействия —
управляющее U_вх(t)и
возмущающееI_с(t).
ПолагаяU_вх(t)=0,I_с(t)=0и размыкая обратную связь, получим
передаточную функцию разомкнутой
системы (рисунок 4.9, г)

, (4.30)

Передаточная функция по управляющему
воздействию

, (4.31)

Принимая за входную величину возмущающее
воздействие, получим структурную схему,
представленную на (рисунке 4.9, в).

Этой структурной схеме соответствует
передаточная функция по возмущающему
воздействию

,
(4.32)

Таким образом, мы получим структурные
схемы и передаточные функции (4.31), (4.32),
составленные относительно управляющего
и возмущающего воздействий.

Используя принцип суперпозиции, мы
можем записать выражение для определения
реакции системы при одновременном
приложении возмущающего и управляющего
воздействий.

, (4.33)

Рисунок
4.9 Структурные преобразования САУ

Таким образом:

1. Применение аппарата структурных
   преобразований позволяет значительно
   упростить методики исследования САУ.
   При этом необходимо иметь в виду, что
   упрощение структурных схем ведет к
   повышению порядка дифференциального
   уравнения, описывающего поведение
   координат САУ;

2. Применение принципа суперпозиций
   позволяет определить реакцию системы
   при одновременном приложении нескольких
   возмущающих и управляющих воздействий.
   Исследования САУ могут проводиться
   отдельно для любого из воздействий. В
   этом случае принимают, что остальные
   воздействия равны нулю;

3. При исследовании многоконтурных САУ,
   имеющих внутренние автономные контуры,
   каждый контур исследуется отдельно,
   начиная с внутреннего;

4. В большинстве случаев при исследовании
   САУ последние приводятся к простейшим
   одноконтурным системам с единичной
   обратной связью.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

Методические указания к практическим занятиям
Оглавление.

1. 
Задание на расчет……………………………………………………..3

2. 
Передаточная
функция разомкнутой системы………………………4

3. 
Передаточная
функция замкнутой системы…………………………4

4. 
Дифференциальное
уравнение системы…………………………….4

5. 
Структурная схема
замкнутой системы…………………………….5

6. 
АЧХ системы…………………………………………………………5

7. 
ФЧХ системы…………………………………………………………6

8. 
АФХ
системы…………………………………………………………7

9. 
Переходная
характеристика…………………………………………9

10. Весовая функция ……………………………………………………10

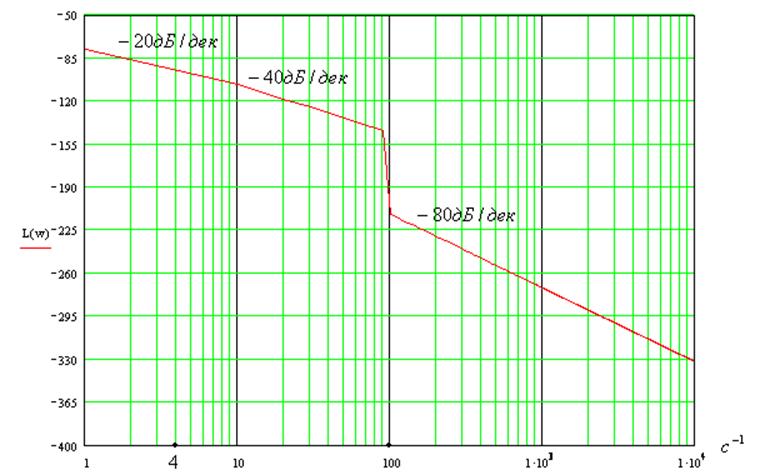
11. Асимптотическую ЛАЧХ и ЛФЧХ………………………………..11

12. Анализ устойчивости системы методом
Рауса – Гурвица……….13

13. Анализ устойчивости системы методом
Михайлова…………….14

14. Анализ устойчивости системы методом
Найквиста……………..16

15. Анализ устойчивости системы при
помощи ЛАЧХ и ЛФЧХ……17

16. Запас устойчивости…………………………………………………20

Задание на расчет:

По заданным нулю и пяти полюсам передаточной функции
разомкнутой системы автоматического регулирования выполнить следующие задания:

·  Записать функцию разомкнутой системы

·  Записать функцию замкнутой системы

·  Записать дифференциальное уравнение
системы

·  Начертить структурную схему замкнутой
системы

·  Определить АЧХ системы

·  Определить ФЧХ системы

·  Построить АФХ

·  Определить переходную характеристику

·  Определить весовую функцию

·  Построить асимптотическую ЛАЧХ и ЛФЧХ

·  Проанализировать устойчивость системы
методом Рауса – Гурвица

·  Проанализировать устойчивость системы
методом Михайлова

·  Проанализировать устойчивость системы
методом Найквиста

·  Проанализировать устойчивость системы
при помощи ЛАЧХ и ЛФЧХ

·  Определить запас устойчивости

2. Запишем передаточную функцию разомкнутой системы:

,

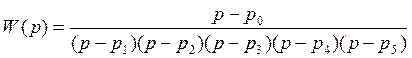
Подставив значения корней и полюсов, получим:

, раскрывая скобки:

.

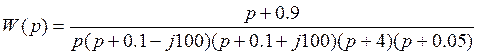
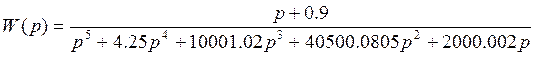
3. Запишем передаточную функцию для замкнутой системы:

Переход от разомкнутой системы к замкнутой осуществим по
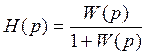
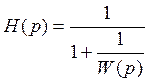
формуле:  или ,
подставляя передаточную функцию разомкнутой системы, получим:

, или

.

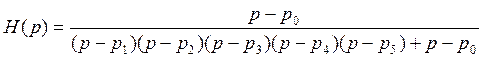
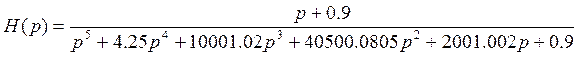
4. Запишем дифференциальное уравнение для замкнутой системы:

Передаточную функцию можно представить как отклик  на воздействие , при
этом оператор 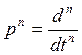, учитывая вышесказанное, запишем
дифференциальное уравнение:

.

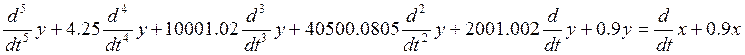
5. Нарисуем структурную схему замкнутой системы:

Структурная схема замкнутой системы представляет собой
разомкнутую систему, охваченную отрицательной обратной связью. Разомкнутая
система представляет собой каскадное соединение различных звеньев. Учитывая
вышесказанное, нарисуем структурную схему замкнутой системы:

.

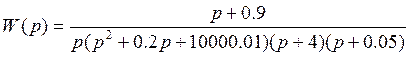
Структурная схема:

Где  — форсирующее звено;

 и  —
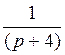
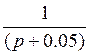
апериодические звенья 1-го порядка;

 — колебательное звено 2-го
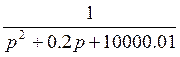
порядка;

 — идеальное интегрирующее звено.

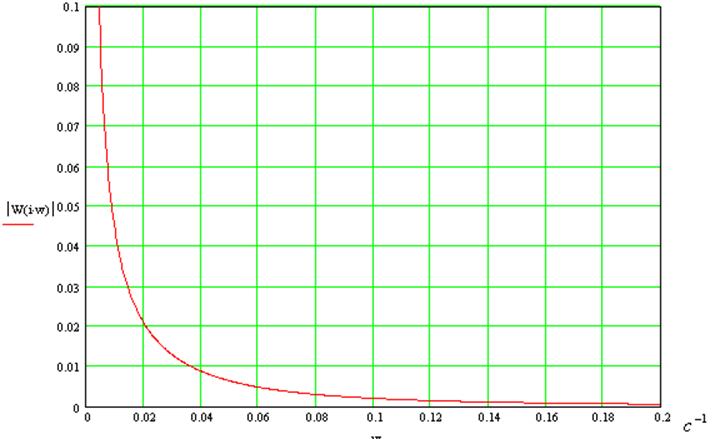
6. Амплитудно-частотная характеристика системы:

Передаточная функция системы в частотной области может быть
получена заменой  на :

Тогда

В области резонанса:

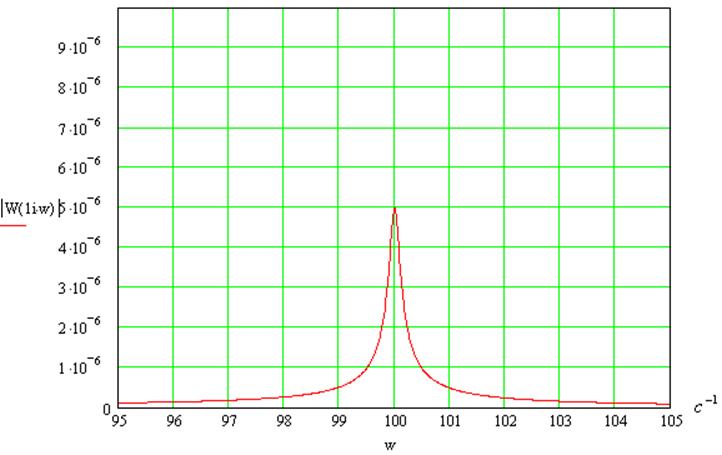
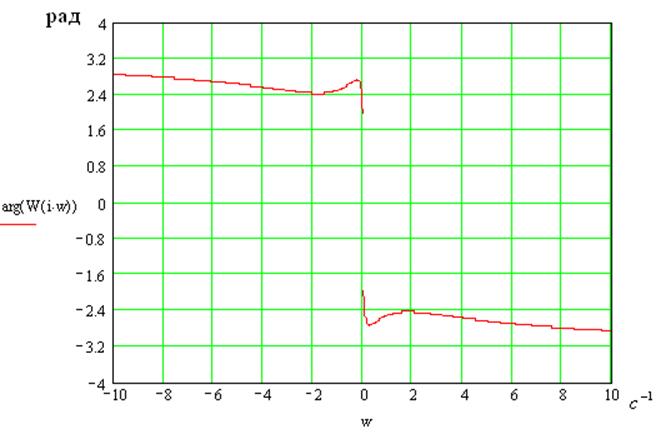
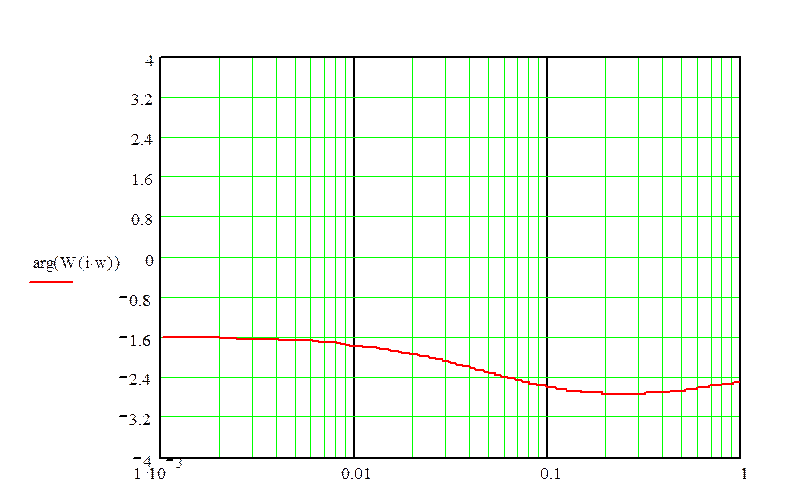
7. Фазо-частотная характеристика системы

 [рад]

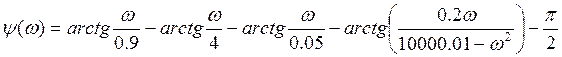
В области резонанса:

8. Амплитудно-фазовая характеристика системы:

Найдем реальную и мнимую части передаточной функции. Домножим
числитель и знаменатель на комплексно сопряженное выражение

, получим:

:

:

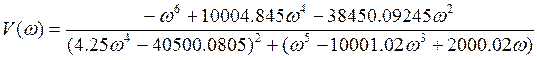
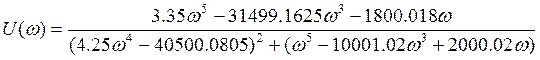
АФХ:

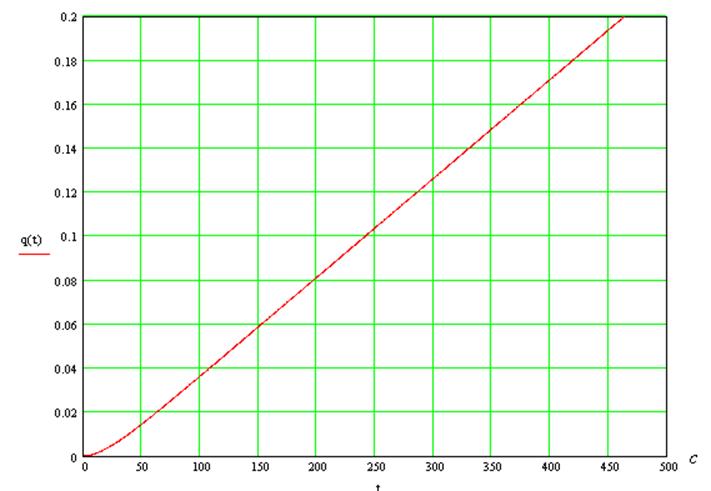
9. Определим переходную характеристику системы:

Переходная характеристика может быть выражена через
передаточную функцию системы следующим образом:

, найдя оригинал от , получим:

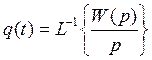
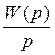
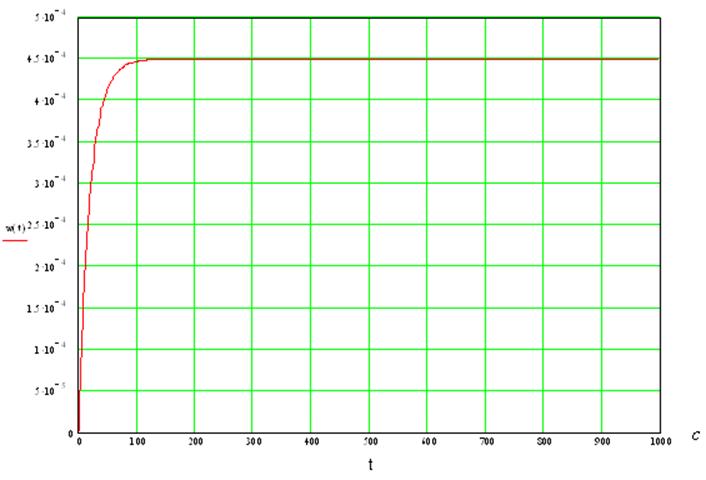
10. Определим весовую функцию, которая может быть выражена
через передаточную функцию следующим образом:

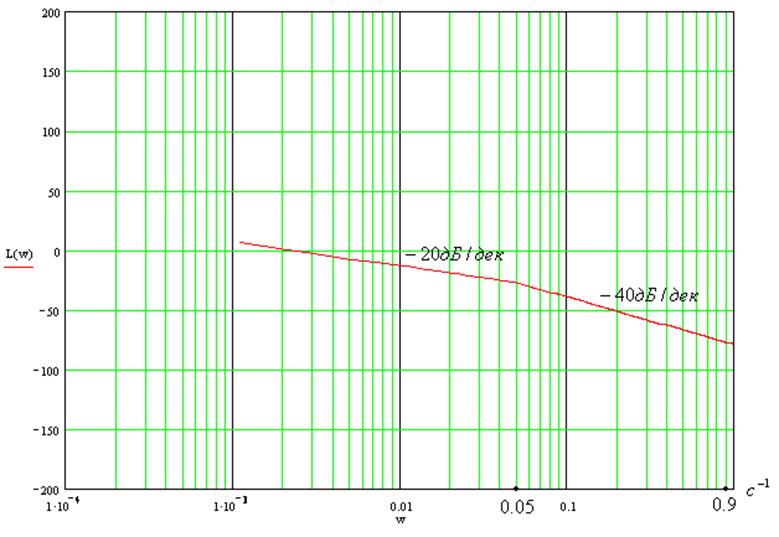
11. Найти и построить асимптотическую ЛАЧХ и ЛФЧХ:

ЛАЧХ:

, запишем в другом виде:

 — колебательное звено 2-го
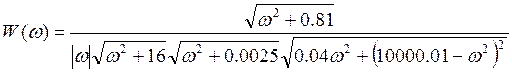
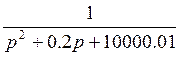
порядка.

;

;

;

.

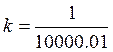
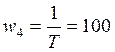
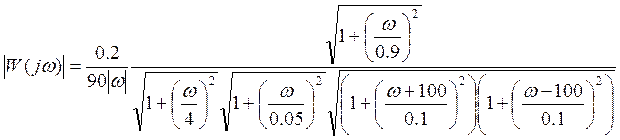
Сопрягающие частоты:

, , , ;

Тогда асимптотическую ЛАЧХ можно разбить на следующие
интервалы:

При :

;

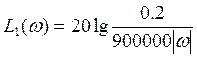
При :

;

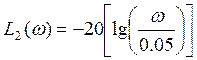
При :

;

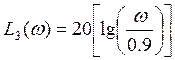
При:

;

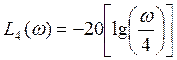
При :

;

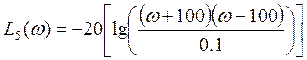
График асимптотической ЛАЧХ:

График ЛФЧХ:

12.
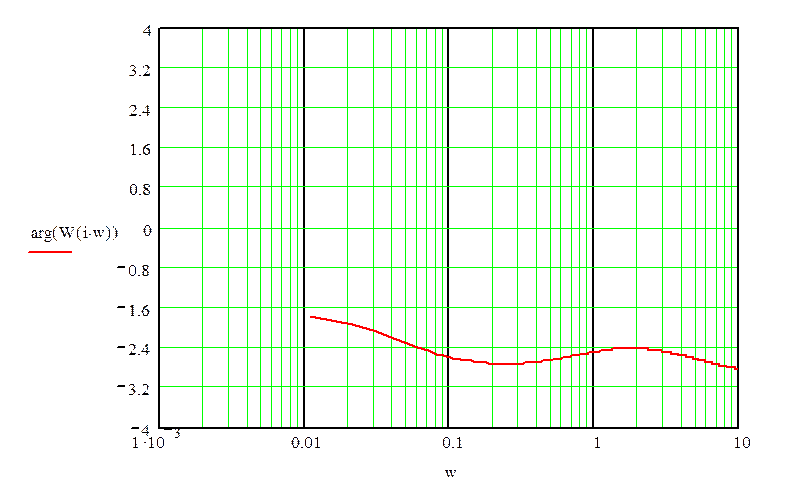
Проанализируем устойчивость системы методом Рауса — Гурвица:

Для того чтобы система автоматического управления была
устойчива, необходимо и достаточно, чтобы все определители Гурвица имели знаки,
одинаковые со знаком первого коэффициента характеристического уравнения а₀,
т. е. при а₀> 0 были положительными.

Рассчитаем определители, если характеристическое уравнение
системы

, тогда:

;

;

;

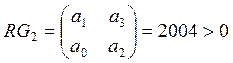
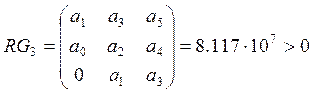
Так как все определители положительны, система устойчива.

13. Проанализируем устойчивость системы методом Михайлова:

Для того чтобы система автоматического управления была
устойчива, необходимо и достаточно, чтобы кривая (годограф) Михайлова при
изменении частоты  от 0 до ,
начинаясь при  на вещественной положительной
полуоси, обходила только против часовой стрелки последовательно п квадрантов
координатной плоскости, где п — порядок характеристического уравнения.

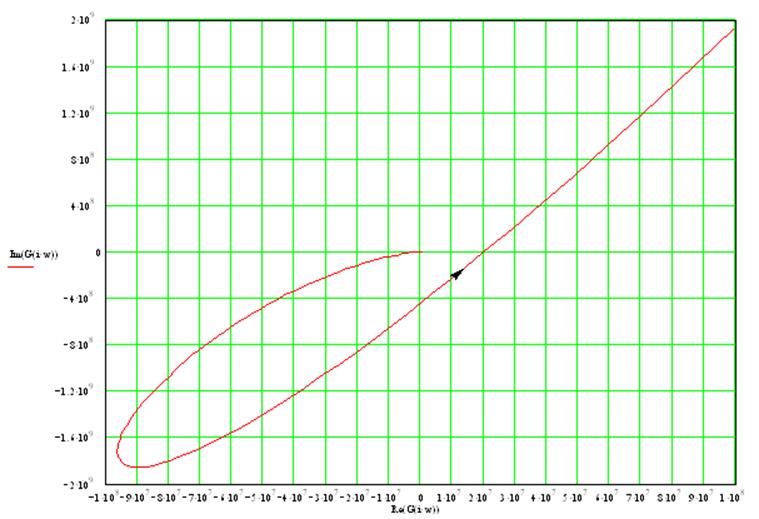
Годограф Михайлова:

Вектор совершает поворот на  5 квадрантов, следовательно, система
устойчива.

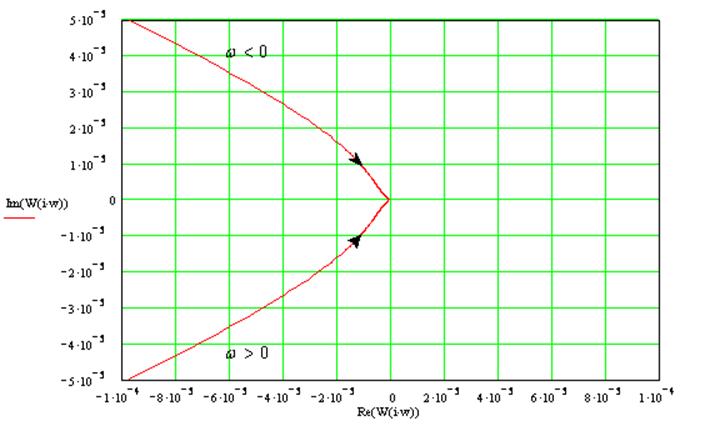
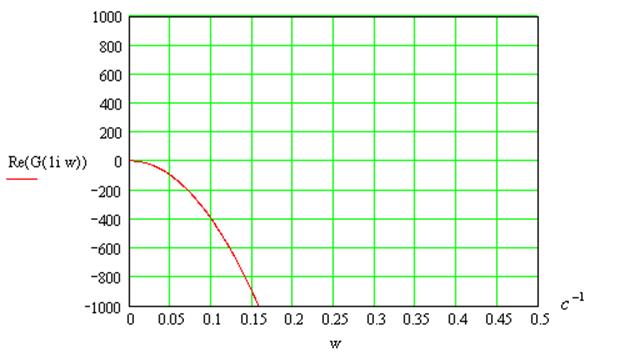
14. Проанализируем устойчивость системы методом Найквиста:

Для устойчивости астатической системы 1-го порядка необходимо
и достаточно, чтобы годограф разомкнутой системы не охватывал точку -1+j0.

;

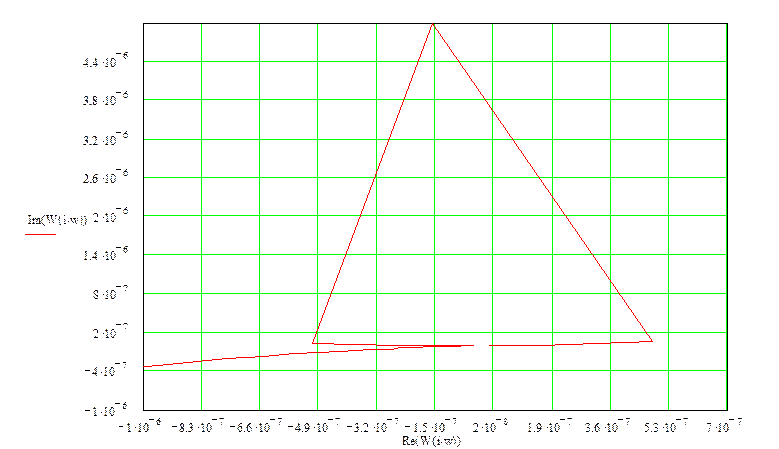
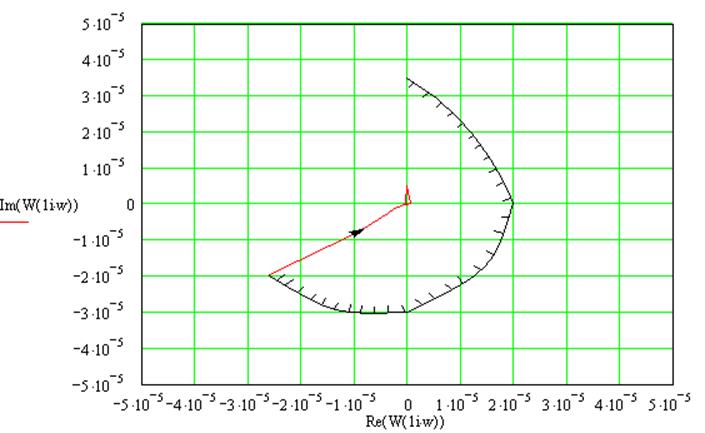
Годограф разомкнутой системы:

Годограф не охватывает точку -1+j0, следовательно, замкнутая система будет устойчива.

15. Анализ устойчивости по ЛАЧХ и ЛФЧХ:

Для устойчивости системы необходимо, чтобы число переходов
ЛФЧХ через  при изменении  от 0 до
было четным, при условии, что ЛФЧХ

Передаточные функции разомкнутой и замкнутой системы

1) Замкнутые системы – это САР с обратной связью, в которых регулируемый параметр непрерывно измеряется и сравнивается с задающим воздействием (рис.3.6.1).

Рис. 3.6.1 Структурная схема замкнутой САР

Если разорвать главную обратную связь (рис.3.6.1), то получим разомкнутую систему, состоящую из последовательного соединения объекта с передаточной функцией Wo(p) и регулятора с передаточной функцией Wp(p).

g(t) u(t) y(t)

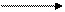
Рис. 3.6.2 Структурная схема разомкнутой САР

Передаточная функция разомкнутой системы по задающему воздействию находится путём перемножения передаточных функций всех звеньев прямой цепи регулирования.

Так для рис.3.5.2 передаточная функция разомкнутой системы имеет вид:

Передаточная функция замкнутой системы (рис.3.6.1) находится из выражения:

,

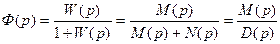
где W(p)- передаточная функция разомкнутой системы,

M(p),N(p),D(p)- полиномы от комплексной переменной р.

Характеристическим уравнением разомкнутой (замкнутой) системы называется полином знаменателя передаточной функции разомкнутой (замкнутой) системы, приравненный нулю (N(p)=0, D(p)=0).

Передаточная функция разомкнутой системы. Передаточная функция замкнутой системы. Дифференциальное уравнение системы

Страницы работы

Фрагмент текста работы

Методические указания к практическим занятиям
Оглавление.

2. Передаточная функция разомкнутой системы……………………. 4

3. Передаточная функция замкнутой системы………………………. 4

4. Дифференциальное уравнение системы…………………………….4

5. Структурная схема замкнутой системы…………………………….5

9. Переходная характеристика…………………………………………9

11. Асимптотическую ЛАЧХ и ЛФЧХ………………………………..11

12. Анализ устойчивости системы методом Рауса – Гурвица……….13

13. Анализ устойчивости системы методом Михайлова…………….14

14. Анализ устойчивости системы методом Найквиста……………..16

15. Анализ устойчивости системы при помощи ЛАЧХ и ЛФЧХ…. 17

16. Запас устойчивости……………………………………………. …20

По заданным нулю и пяти полюсам передаточной функции разомкнутой системы автоматического регулирования выполнить следующие задания:

· Записать функцию разомкнутой системы

· Записать функцию замкнутой системы

· Записать дифференциальное уравнение системы

· Начертить структурную схему замкнутой системы

· Определить АЧХ системы

· Определить ФЧХ системы

· Определить переходную характеристику

· Определить весовую функцию

· Построить асимптотическую ЛАЧХ и ЛФЧХ

· Проанализировать устойчивость системы методом Рауса – Гурвица

· Проанализировать устойчивость системы методом Михайлова

· Проанализировать устойчивость системы методом Найквиста

· Проанализировать устойчивость системы при помощи ЛАЧХ и ЛФЧХ

· Определить запас устойчивости

2. Запишем передаточную функцию разомкнутой системы:

,

Подставив значения корней и полюсов, получим:

, раскрывая скобки:

.

3. Запишем передаточную функцию для замкнутой системы:

Переход от разомкнутой системы к замкнутой осуществим по формуле: или , подставляя передаточную функцию разомкнутой системы, получим:

, или

.

4. Запишем дифференциальное уравнение для замкнутой системы:

Передаточную функцию можно представить как отклик на воздействие , при этом оператор , учитывая вышесказанное, запишем дифференциальное уравнение:

.

5. Нарисуем структурную схему замкнутой системы:

Структурная схема замкнутой системы представляет собой разомкнутую систему, охваченную отрицательной обратной связью. Разомкнутая система представляет собой каскадное соединение различных звеньев. Учитывая вышесказанное, нарисуем структурную схему замкнутой системы:

.

Где — форсирующее звено;

и — апериодические звенья 1-го порядка;

— колебательное звено 2-го порядка;

— идеальное интегрирующее звено.

6. Амплитудно-частотная характеристика системы:

Передаточная функция системы в частотной области может быть получена заменой на :

В области резонанса:

7. Фазо-частотная характеристика системы

[рад]

В области резонанса:

8. Амплитудно-фазовая характеристика системы:

Найдем реальную и мнимую части передаточной функции. Домножим числитель и знаменатель на комплексно сопряженное выражение

, получим:

:

:

9. Определим переходную характеристику системы:

Переходная характеристика может быть выражена через передаточную функцию системы следующим образом:

, найдя оригинал от , получим:

10. Определим весовую функцию, которая может быть выражена через передаточную функцию следующим образом:

11. Найти и построить асимптотическую ЛАЧХ и ЛФЧХ:

, запишем в другом виде:

— колебательное звено 2-го порядка.

;

;

;

.

, , , ;

Тогда асимптотическую ЛАЧХ можно разбить на следующие интервалы:

При :

;

При :

;

При :

;

При:

;

При :

;

График асимптотической ЛАЧХ:

12. Проанализируем устойчивость системы методом Рауса — Гурвица:

Для того чтобы система автоматического управления была устойчива, необходимо и достаточно, чтобы все определители Гурвица имели знаки, одинаковые со знаком первого коэффициента характеристического уравнения а₀, т. е. при а₀> 0 были положительными.

Рассчитаем определители, если характеристическое уравнение системы

, тогда:

;

;

;

Так как все определители положительны, система устойчива.

13. Проанализируем устойчивость системы методом Михайлова:

Для того чтобы система автоматического управления была устойчива, необходимо и достаточно, чтобы кривая (годограф) Михайлова при изменении частоты от 0 до , начинаясь при на вещественной положительной полуоси, обходила только против часовой стрелки последовательно п квадрантов координатной плоскости, где п — порядок характеристического уравнения.

Вектор совершает поворот на 5 квадрантов, следовательно, система устойчива.

14. Проанализируем устойчивость системы методом Найквиста:

Для устойчивости астатической системы 1-го порядка необходимо и достаточно, чтобы годограф разомкнутой системы не охватывал точку -1+j0.

;

Годограф разомкнутой системы:

Годограф не охватывает точку -1+j0, следовательно, замкнутая система будет устойчива.

15. Анализ устойчивости по ЛАЧХ и ЛФЧХ:

Для устойчивости системы необходимо, чтобы число переходов ЛФЧХ через при изменении от 0 до было четным, при условии, что ЛФЧХ

Передаточная функция замкнутой системы относительно управляемой величины по возмущающему воздействию

Введение

Теория автоматического управления (ТАУ), — научная дисциплина, предметом изучения которой являются информационные процессы, протекающие в системах управления техническими и технологическими объектами. ТАУ выявляет общие закономерности функционирования, присущие автоматическим системам различной физической природы, и на основе этих закономерностей разрабатывает принципы построения высококачественных систем управления.

ТАУ при изучении процессов управления абстрагируется от физи- ческих и конструктивных особенностей систем и вместо реальных систем рассматривает их адекватные математические модели. Основными методами исследования в ТАУ являются математическое моделирование, теория обыкновенных дифференциальных уравнений, операционное исчисление и гармонический анализ

Передаточные функции систем автоматического управления по задающему и возмущающему воздействиям

САУ характеризуется несколькими передаточными функциями. При одной выходной координате их количество равно числу входных (для всей системы) воздействий (рис. 1).

Рис. 1. Структурная схема замкнутой САУ

Если система автоматического управления имеет несколько входных воздействий (задающих и возмущающих), то при определении передаточной функции относительно какого-либо одного из этих воздействий остальные воздействия полагают равными нулю (согласно принципу суперпозиции).

Вводится понятие передаточной функции разомкнутой системы — отношение изображения X_ос(s) — сигнала главной отрицательной обратной связи x_ос(t) к изображению G(s) — задающего воздействия g(t).

При этом контур управления предполагают разомкнутым около главного сравнивающего устройства, при равенстве нулю всех внешних воздействий, кроме задающего. Для САУ, структурная схема которой представлена на рис. 1, передаточная функция разомкнутой системы:

Вводится также понятие передаточной функции прямого участка цепи САУ от точки приложения входного воздействия до выходной ко- ординаты при равенстве нулю остальных воздействий и разрыве глав- ной отрицательной обратной связи:

Передаточная функция замкнутой САУ относительно управляемой величины по задающему воздействию

Передаточная функция замкнутой системы относительно управля- емой величины x(t) по задающему воздействию g(t) — W_xg(s) может быть определена на основании правил преобразования схем. При f(t) = 0 структурная схема САУ (рис. 1) принимает вид (рис. 2):

Рис. 2. Структурные схемы замкнутой САУ по задающему воздействию: а – исходная; б – эквивалентная

Тогда, согласно правилам преобразования структурных схем, пе- редаточная функция замкнутой системы относительно управляемой ве- личины x(t) по задающему воздействию g(t) равна:

Передаточная функция замкнутой системы относительно управляемой величины по возмущающему воздействию

При g(t) = 0 структурная схема САУ (рис. 1) принимает вид, представленный на рис. 3.

Рис. 3. Структурные схемы замкнутой САУ по возмущающему воздей- ствию: а – исходная; б – эквивалентная

Как следует из структурной схемы (рис. 3), передаточная функция замкнутой САУ относительно управляемой величины x(t) по воз- мущающему воздействию f(t) равна:

В результате исходная структурная схема САУ (рис. 1) преобра- зуется к виду (рис. 4).

Рис. 4. Эквивалентная структурная схема замкнутой САУ

В итоге изображение управляемой величины будет равно:

Таким образом, передаточная функция замкнутой системы относительно рассматриваемого воздействия – есть отношение передаточной функции прямого участка цепи от точки приложения воздействия до выходной координаты (при разомкнутой ГООС и

равенстве нулю остальных входных воздействий) W gx (s) либо W fx (s) к

(1+ Wраз(s)) :