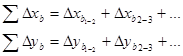Как составить план теодолитного хода

Одна из главных задач геодезии состоит в отображении земной поверхности на горизонтальной плоскости. Большие территории обычно изображают на карте, а на планы наносят небольшие участки в крупном масштабе. Рассмотрим далее порядок его построения и особенности.

Назначение плана теодолитного хода и этапы его составления

Поскольку на небольших территориях искажения измеренных углов и длин будут не столь значительными, их пренебрежение не приведет к значительной потере точности.

Как уже было сказано выше, первостепенная задача этого чертежа – отображение земной поверхности и объектов, которые на ней расположены. Обычно создаются в масштабах 1:500, 1:1000, 1:2000, 1:5000 и 1:10 000.

Принято также различать следующие виды планов:

1. Топографические. Все объекты на местности, включая здания, сооружения, а также растительность и элементы гидрографии должны быть отображены.
2. Ситуационные. Нанесение только наиболее важных и крупных дискретных объектов, расположенных на земной поверхности.
3. Специализированные. Отображение местоположения в пространстве только конкретных элементов. В основном создается для проектирования и последующего строительства сложных инженерных сооружений. Может выполняться в особо крупном масштабе 1:200 и 1:100.

Для составления всех этих графических материалов в основном проводится теодолитная съемка. Сам процесс изготовления плана проводится в такой последовательности:

– создание координатной сетки;

– нанесение точек хода на чертеж;

– отображение ситуации местности.

– оформление.

Подготовка чертежа: построение сетки координат

Перед тем, как нанести на план все его составляющие необходимо должным образом подготовить его. На плотном листе бумаги чертится координатная сетка со сторонами квадратов равными 10 сантиметрам. В работе используют различные инструменты, вроде штангенциркуля, координатографа, линейки Дробышева или обычной масштабной.

Чтобы определить, какое количество квадратов нужно построить для X и Y, используют выражение:

(N_{X}=(X_{max}-X_{min})/d )

(N_{Y}=(Y_{max}-Y_{min})/d )

Переменные (X_{max}) и (Y_{max}) – максимальное значение координат с округлением их в большую сторону до кратных длине сетки, а (X_{min}) ,(Y_{min}) – в меньшую сторону.

(d )– длина стороны квадрата на местности (в метрах). Для масштаба 1:1000 это будет 100 метров, а 1:2000 – 200 метров и т.д.

Рисунок 1. Числовая ось сетки координат

Создавайте будущее вместе с нами

Присоединяйтесь к нашей команде: мы создаем финтех-сервисы для 28 млн клиентов и опережаем рынок на 5 лет. Работаем на результат и делаем больше, чем от нас ждут.

Максимальные и минимальные значения координат также принято изображать в конце сетки.

Нанесение точек теодолитного хода

Когда сетка координат построена, по ней отсчитывают значения для каждой точки и наносят на чертеж с учетом заданного масштаба. Желательно использовать для этих целей хорошо заостренный твердый карандаш. Данные берутся из ведомости координат.

Рисунок 2. Схема теодолитного хода на плане

Лучше для начала определить положение одной или двух точек и проверить правильность их нанесения. Это можно сделать по направлению дирекционного угла, которое должно соответствовать направлению линии на чертеже.

Также необходимо проверить, сходятся ли расстояние между ними с горизонтальным проложением. Допустимая разница не должна превышать 0,2 мм. В случае выявления расхождений необходимо проверить качество координатной сетки и правильность откладывания отрезков.

Поскольку построение осуществляется в прямоугольной системе, направление оси абсцисс (Х) будет направлено на север, а ординат (Y) – на восток.

Нанесение ситуации и оформление

Для дальнейших работ применяются абрисы, которые были составлены во время полевой съемки. Чтобы как можно точнее отобразить на плане ситуацию нужно использовать транспортир, прямоугольный треугольник и миллиметровую линейку хорошего качества.

Абрис содержит в себе детальную информацию о местоположении характерных точек жестких контуров местности относительно вершин хода. Выполняется в произвольном масштабе непосредственно во время полевых измерений. Всего различают такие способы съемки ситуации:

1. Перпендикуляров. Местоположение точек определяют длинами перпендикуляров и расстояниями до заданного пункта.
2. Полярных координат. Сторона хода берется за начало координатной оси, а вершина за полюс. Положение точек контуров определяют посредство измерения угла между заданным направлением и расстоянием до них.
3. Биполярных координат (линейная засечка). Измеряются углы между двумя сторонами хода и направлением на заданную точку. Их пересечение и позволит получить ее на чертеже.
4. Створов (промеров). Если ситуация находится на пересечении хода или его сторон проводят линейные промеры. Активно используют для съемки застроенных участков.
5. Обходный способ. Создается дополнительный ход с привязкой к основному.

Рисунок 3. Абрис сторон теодолитного хода

При последовательном нанесении контурных точек из абриса на план они будут накладываться друг на друга, формируя местность. Очень важно регулярно проверять их точность, чтобы избежать ошибок.

Когда все объекты нанесены карандашом, их вычерчивают тушью, соблюдая правила оформления чертежей. Потом выполняют зарамочное оформление с обязательным указанием названия плана, его масштаба и другой информации.

Рисунок 4. Готовый чертеж плана теодолитного хода

Чтобы графически обозначить различные объекты и особенности местности на чертеже используют специальную систему обозначений – условные знаки. После выполнение всех вышеперечисленных процедур процедуру составления плана теодолитного хода можно считать законченной.

Графические
работы состоят в построении плана
теодолитной съемки на основе координат
вершин теодолитного хода и абрисов
съемки ситуации. Составление плана
выполняется в следующей последовательности:
1) построение
координатной сетки; 2) накладка
теодолитного хода на план; 3) нанесение
ситуации; 4) оформление плана.

Построение
координатной сетки.
Для
планов масштабов 1: 10000 и крупнее стороны
квадратов координатной сетки принимают
равными 10 см. Построение сетки может
быть выполнено при помощи циркуля-измерителя
(или штангенциркуля) и масштабной
линейки, линейки Дробышева, а также
координатографом.

Построение
координатной сетки начинается с расчета
необходимого числа квадратов по осям
х
и
у.
Пусть
требуется составить план в масштабе
1:2000, при котором длина стороны квадрата
сетки (10см) соответствует 200 м
горизонтального проложения местности.
Исходя из значений координат хода,
определяют величины

;

,

где
x_max,
y_max
—
максимальные значения координат точек,
округленные в большую сторону до
величин, кратных длине квадрата сетки
в данном масштабе;

x_min,
y_min
—
минимальные
значения координат, округленные в
меньшую сторону до величин, кратных
длине квадрата сетки в данном масштабе.

; ;

; ; ;

; .

Вычерчивание
координатной сетки с небольшим числом
квадратов выполняется при помощи
циркуля и масштабной линейки (рисунок
41, а). На листе бумаги проводят диагонали
АВ
и
CD.
Из
точки пересечения диагоналей (точки
О)
делают циркулем засечки одинакового
размера. Полученные точки а,
в,
с
и d
соединяют
прямыми линиями. Стороны прямоугольника
aвсd
делят
пополам и через точки деления проводят
прямые 1
— 2
и
3—4,
которые
должны пройти через точку О
пересечения диагоналей. Если число
квадратов четное, то от точек 1,
2,
3
и
4
откладывают
отрезки по 10 см. При нечетном числе
квадратов (как в рассматриваемом
примере) от этих точек вначале в обе
стороны откладывают отрезки по 5 см, а
затем — по 10 см. Соединив линиями
соответствующие точки на противоположных
сторонах прямоугольника, получают
сетку квадратов циркулем-измерителем
проверяют правильность построения
координатной сетки путем измерения
диагоналей ее квадратов; длины диагоналей
должны быть равны 14,14 см или отличаться
от этой величины не более чем на 0,2 мм.

Координатные
сетки 50X50 см удобно строить при помощи
линейки Ф. В. Дробытева
ЛД-1
(рисунок 41, б).
ЛД-1
представляет собой металлическую
линейку со скошенными ребрами дли
прочерчивания линий. По длине линейки
через 10 см друг от друга расположены
шесть прямоугольных вырезов (окон).
Скошенный край первого выреза сделан
по прямой, а края остальных вырезов и
скошенный торец имеют форму дуг
окружностей радиусов 10, 20, 30, 40, 40 и 70,711
см, центр которых находится в точке
пересечения штриха со скошенным ребром
крайнего окна О.
Построение прямого угла линейкой
Дробышева основано на построении
прямоугольного треугольника с катетами
по 50 см и гипотенузой 70,711 см; порядок
построения показан на рисунке 41, в.

В
положении I
отмечают
по вырезам шесть черточек. В положении
II
совмещают штрих, нанесенный на середине
скошенного края первого выреза, с концом
линии, полученной в положении I,
и по вырезам отмечают пять дуг. В
положении III
совмещают середину скошенного края
первого выреза с одной из точек первой
черточки, полученной в положении I,
и концом линейки засекают последнюю
дугу, полученную в положении II;
таким образом, получают первый
прямоугольный треугольник. Построив
второй прямоугольный треугольник, как
показано на рисунке 41, в (положения IV
и
V),
соединив точки, расположенные на
противоположных сторонах построенного
таким образом прямоугольника, получают
сетку квадратов (положение VI).

Рисунок
41 —
Схема
построения координат

При
правильном построении сетки 5X5 квадратов
вершины малых квадратов должны лёжать
на диагоналях большого квадрата или
на линиях, параллельных им. Расхождения
между диагоналями малых квадратов не
должны превышать 0,2 мм. При несоблюдении
указанных условий сетку квадратов
строят заново.

При
больших объемах работ для построения
координатных сеток используют
координатографы.
Координатографы
бывают полевые, с помощью которых строят
координатные сетки в полевых условиях,
и стационарные, устанавливаемые в цехах
геодезических и картографических
предприятий. При помощи координатографов
одновременно с построением координатной
сетки можно по координатам наносить
точки на план с точностью до 0,05 мм.

Координатную
сетку подписывают в соответствии с
координатами точек теодолитного хода
(рисунок 41, г). Для этого берут минимальное
и максимальное значения х
и
у,
которые
использовались для нахождения числа
квадратов сетки по осям х
и
у.
У
нижней горизонтальной линии сетки
слева от крайней вертикальной линии
подписывают минимальное значение
абсцисс (х=
6000 м), а у верхней крайней линии —
максимальное значение (х
=
6600 м). Промежуточные горизонтальные
линии сетки имеют абсциссы, кратные
длине стороны квадрата сетки. Аналогично
подписывают вертикальные линии
(ординаты) сетки, При оцифровке сетки
следует помнить, что значения абсцисс
возрастают снизу вверх, а ординат —
слева направо.

Нанесение
на план точек теодолитного хода и
ситуации.
Оформление
плана.
Нанесение
на план точек теодолитного хода
производится по их вычисленным
координатам. Правильность нанесения
на план двух соседних точек проверяют
по длинам сторон хода. Расхождение не
должно превышать 0,2
мм
на плане, т. е. графической точности
масштаба. Кроме того, правильность
нанесения теодолитного хода на план
можно проконтролировать, измерив
транспортиром горизонтальные углы и
дирекционные углы сторон и сравнив их
с соответствующими значениями,
приведенными в ведомости.

Нанесение
на план ситуации
производится от сторон и вершин
теодолитного хода согласно абрисам
съемки. При этом местные предметы и
характерные точки контуров наносятся
на план в соответствии с результатами
и способами съемки. Сначала на план
наносят контуры, снятые способом
створов, затем — способами перпендикуляров,
полярных и биполярных координат и
способом обхода. При накладке ситуации
на план расстояния откладываются при
помощи циркуля-измерителя и масштабной
линейки, а углы — транспортиром. При
нанесении точек, снятых способом
перпендикуляров, перпендикуляры к
сторонам хода восставляют прямоугольным
треугольником.

Для
накладки на план точек, снятых способом
створов, от соответствующих вершин
теодолитного хода с помощью
циркуля-измерителя откладывают в
масштабе плана расстояния до точек,
указанные в абрисе.

Для
нанесения точек, снятых полярным
способом, центр транспортира совмещают
с вершиной хода, принятой за полюс, а
нуль транспортира — с направлением
стороны хода. По дуге транспортира
откладывают углы, измеренные теодолитом
при визировании на точки местности, и
прочерчивают направления, для которых
откладывают расстояния до точек,
указанные в абрисе.

При
нанесении точек способом угловых
засечек транспортиром в вершинах
опорных сторон откладывают углы и
прочерчивают направления, пересечения
которых определяют положения искомых
точек. Нанесение точек способом линейных
засечек выполняется при помощи
циркуля-измерителя и сводится к
построению треугольника по трем
сторонам, длины которых измерены на
местности.

По
мере накладки точек на план по ним в
соответствии с абрисами вычерчивают
предметы местности и контуры и заполняют
их установленными условными знаками.
Затем выполняют зарамочное оформление
и вычерчивают план тушью с соблюдением
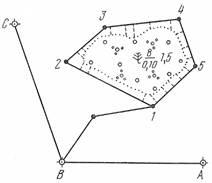
правил топографического черчения. На
рисунке 42 представлен ситуационный
план участка местности, составленный
на основе абриса теодолитной съемки.

Рисунок
42 – Ситуационный план участка местности

ЛЕКЦИЯ
14

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

Практическая работа №26. Построение плана теодолитной съемки.

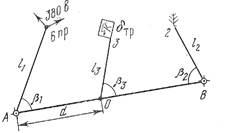
Теодолитная съемка выполняется на основе съемочного обоснования, создаваемого в виде теодолитных ходов.

Теодолитный ход – это система ломаных линий, для которых измерены расстояния между точками и горизонтальные углы между сторонами. Бывают замкнутые и разомкнутые ходы, свободные и несвободные.

Свободный ход – ход, в котором имеются только необходимые исходные данные, а несвободный ход имеет избыточные данные.

Порядок работ при теодолитной съемке:

1.                   Рекогносцировка – осмотр местности с выбором и закреплением будущих точек съемочного обоснования.

2.                   Привязка пунктов съемочного обоснования к пунктам ГГC. Для этого на местности выполняют измерения примычных углов и расстояний.

3.                   Измерение горизонтальных углов и длин сторон теодолитного хода. Горизонтальные углы измеряются способом приемов, расстояние при помощи стальной мерной ленты или рулетки в прямом и обратном направлениях, с относительной погрешностью не более 1:2000. Для определения горизонтального проложения также измеряют углы наклона местности теодолитом.

4.                   Съемка контуров местности (ситуации). Заключается в привязке этих контуров к пунктам съемочного обоснования.

Съемка контуров местности выполняется следующими способами:

1.        Способ перпендикуляров (способ прямоугольных координат)

2.        Способ полярных координат

3.        Способ угловых засечек

4.        Способ  линейных засечек

5.        Способ створов – применяется в тех случаях когда смешанный контур пересекает сторону теодолитного хода или ее продолжение.

По результатам съемки составляют абрис.

Абрис – это схематичный чертеж на котором изображены стороны теодолитного хода, снимаемые контуры и результаты угловых и линейных промеров (β и l)

Абрис может быть составлен для всего хода или отдельно для каждой стороны.

Камеральная обработка результатов измерения теодолитного хода

1.      Вычисление координат точек теодолитного хода.

Перед началом вычисления проверяют все журналы (значения вычисленных горизонтальных и вертикальных углов, горизонтальных проложений). Уравнивают горизонтальные углы, для этого вычисляют сумму измеренных горизонтальных углов:

Σβ_ф=β₁+β₂+…+β_n

Вычисляют теоретическую сумму углов

Σβ_т=180º(n–2) – для замкнутого хода

Σβ_т=α_нач– α_кон±180º∙n – для разомкнутого хода

n – число измеренных углов

Вычисляют угловую невязку: f_β= Σβ_ф– Σβ_т сравнивая ее с допустимой: f_{β доп} =1.5t

 где t–точность отсчетного приспособления теодолита.

Невязка f_β по абсолютной величине не должна превышать допустимого значения f_{β доп}, в противном случае углы измеряют заново. Если условие вычисляют поправку в каждый угол и записывают в ведомость над значениями измеренных углов: δ_β=– f_β/n.

Контролем правильности распределения невязки служит равенство: Σδ_β=– f_β

Исправленные углы вычисляют по формуле: β_{i испр}= β_{i изм} + δ_{β i}

Для контроля подсчитывают сумму исправленных углов, которая должна быть равна теоретической сумме углов: Σβ_испр= Σβ_т

Примычный угол β_прим не исправляют.

2.  Вычисление дирекционных углов и румбов.

По исходному дирекционному углу α_пт–I и исправленным значениям   углов определяют дирекционные углы сторон теодолитного хода:

α_n=α_n–1±180º–β_n – для правых углов

α_n=α_n–1±180º+β_n – для левых углов

Контролем правильности вычислений дирекционных углов является совпадение значения дирекционного угла начальной стороны α_I–II:

α_I–II= α_пт–1±180º–β_пр=α_V–I±180º–β₁

Вычисляют румбы

№ четв.	Дирекционный угол	Назв. румба	Формулы	Знаки приращения
∆x	∆y
I	0º–90º	СВ	r=α	+	+
II	90º–180º	ЮВ	r=180º–α	–	+
III	180º–270º	ЮЗ	r=α–180º	–	–
IV	270º–360º	СЗ	r=360º–α	+	–

3. Вычисление приращений координат

По значениям дирекционных углов и горизонтальными проложениям сторон теодолитного хода вычисляют приращения координат с точностью до 0.01м:

∆х=d·cos r

∆у=d·sin r

Знаки приращения координат определяют в зависимости от названия румба.

4. Вычисление линейных невязок по осям координат

Находят суммы вычисленных приращений

И теоретические суммы приращений

ΣΔх_т=х_кон–х_нач

ΣΔу_т=у_кон–у_нач

Линейные невязки по осям координат

f_x= Σ∆х_ф– Σ∆х_т

f_у= Σ∆у_ф–Σ∆у_т

Вычисление абсолютной и относительной невязок теодолитного хода

f_абс =

Определяют относительную линейную невязку f_отн теодолитного хода: f_отн=

где Р – периметр хода.

Допустимое значение относительной невязки не должно превышать погрешности линейных измерений . Если это условие нарушено, то длины линий перемеряют, а если выполняется, то вычисляют поправки в вычисления координат:

Поправки округляют до 0.01 мм и выписывают их со своими знаками над соответствующими приращениям ∆х и ∆у.

Сумма поправок должна равняться невязке с обратным знаком:

Σδ_Δx=–f_x

Σδ_Δy=–f_y

Вычисляют исправленные приращения координат и записывают результаты в ведомость:

∆х_испр= ∆х_{выч  +} δ_Δх

∆у_испр= ∆у_{выч  +} δ_Δу

Для контроля определяют суммы исправленных приращений координат, которые должны быть равны теоретическим суммам приращений:

∆х_испр= Σх_т

∆у_испр= Σу_т

5. Вычисление координат точек теодолитного хода

x_n=x_n–1+∆x_{n испр}

y_n=y_n–1+∆y_{n испр}

Контролем вычислений служит получение координат известных точек х₁ и у₁:

x₁=x_пт+∆x_пт–1= x_V+∆x_V–I

y₁=y_пт+∆y_пт–1= y_V+∆y_V–I

Вычисленные значения координат вершин теодолитного хода записывают в ведомость.

6.  Построение плана теодолитной съемки.

Построение координатной сетки: на листе бумаги проводят две пересекающиеся линии и от точки их пересечения откладывают произвольные равные отрезки при помощи циркуля. Получают точки АВСД, где ОА=ОВ=ОС=ОД. Соединив эти точки получают правильный прямоугольник. Вспомогательные линии стирают, на сторонах прямоугольника откладывают по 10 см и строят квадраты – сетку. Правильность построения сетки квадратов проверяют по равенству длин сторон и длин диагоналей – циркулем–измерителем.

Точки пересечения всех координатных линий по диагонали должны лежать на одной прямой.

Оцифровка координатной сети.

Производиться в соответствии с масштабом чертежа таким образом, чтобы значение координатных линий были кратны 10 см в заданном масштабе и все точки съемочного обоснования поместились на чертеже и расположились по возможности в средней его части.

Нанесение точек съемочного обоснования.

Контролем правильности будет служить равенство дирекционных углов сторон на плане и в ведомости и равенства длин сторон на плане и ведомости.

Нанесение ситуации на план.

Ситуация наносить по абрису и изображается условными знаками, при этом вспомогательные линии на план не переносят.

Оформление надписи на плане.

Вдоль северной рамки подписывают название чертежа, вдоль южной – масштаб, внизу справа – год съемки и исполнитель.