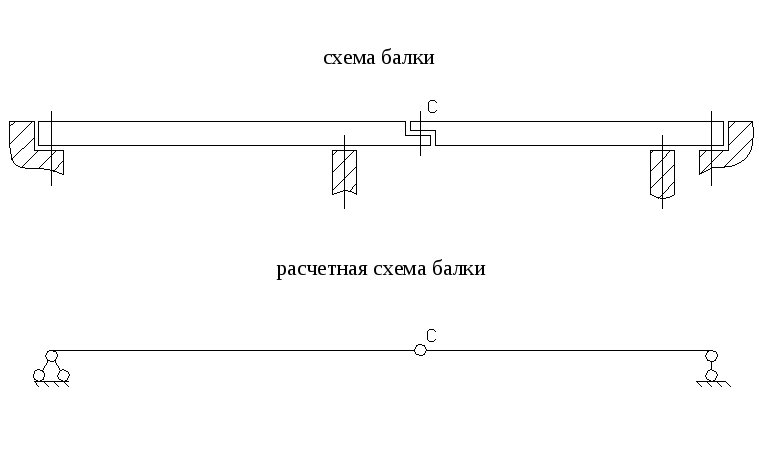
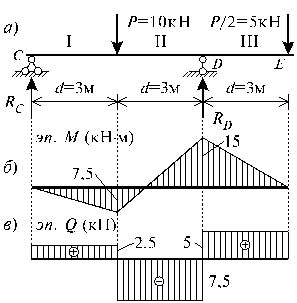
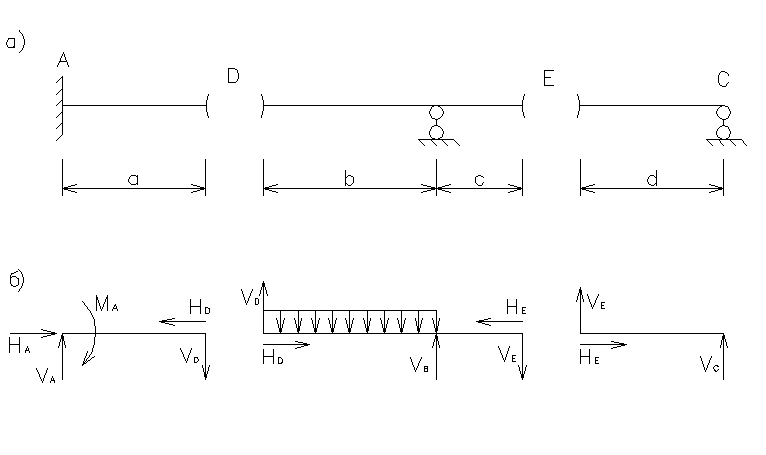
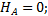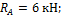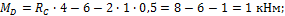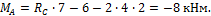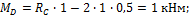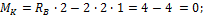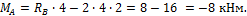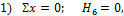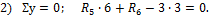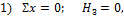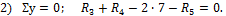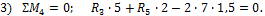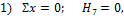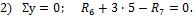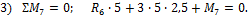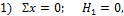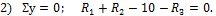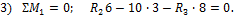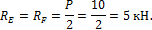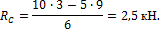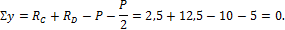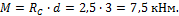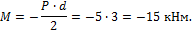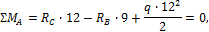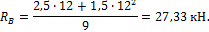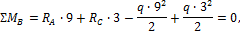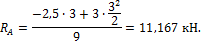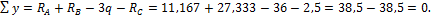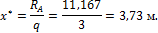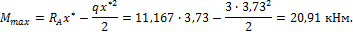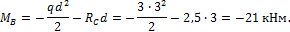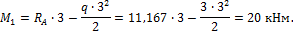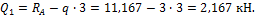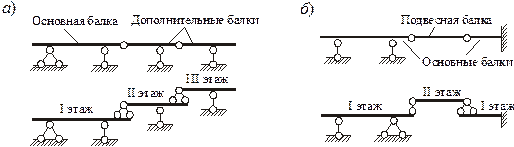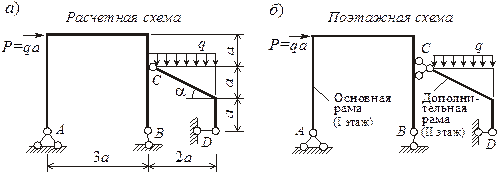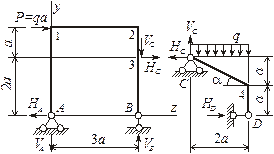2.4.1. Общие замечания.
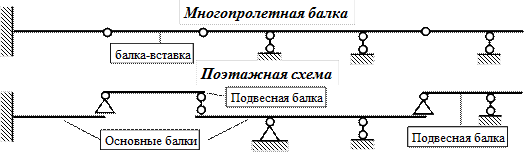
Многопролетная
статистически определимая балка
представляет собой комбинированную
систему, состоящую из нескольких
однопролетных балок, соединенных таким
образом, что в местах их соединения в
расчетной схеме возможна постановка
шарниров
(рис.2.22, шарнир С).
.
Рис.2.22..
Двухпролетная балка.
Такие
балки имеют более трех опорных связей
и, следовательно, реакции этих связей
не могут быть определены только с
помощью трех уравнений равновесия,
которые можно записать для балки в
целом. Для определения всех реакций
опор нужны дополнительные уравнения
равновесия.
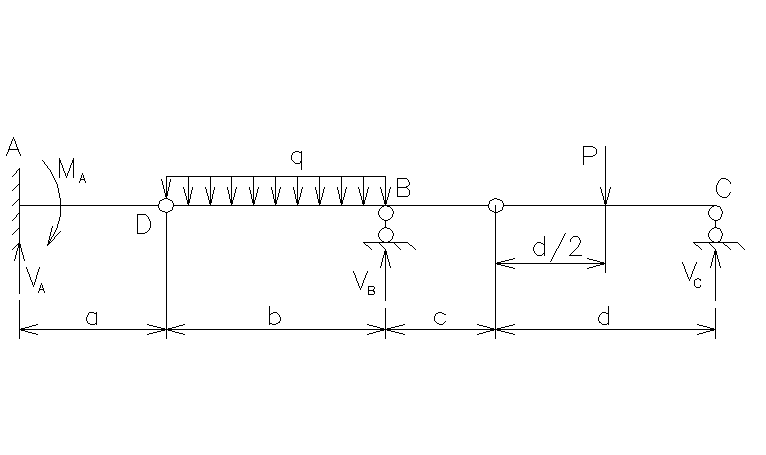
Рис.2.23.
Расчетная схема многопролетной балки.
Так
для балки, показанной на рис.2.23 для
определения пяти реакций опор нужно
составить пять уравнений равновесия.
Для решения поставленной задачи можно
составить три уравнения равновесия
для балки в целом, например,
,
,
,
а
для составления дополнительных уравнений
использовать условия равенства нулю
моментов в шарнирах D
и Е:
,
.
Эти
уравнения составлены соответственно
для левой части балки относительно
шарнира D
и правой части балки относительно
шарнира Е:
,
.
В
результате получаем совместную систему
уравнений с пятью неизвестными реакциями
опор:
Эту
же задачу можно решить и следующим
образом:
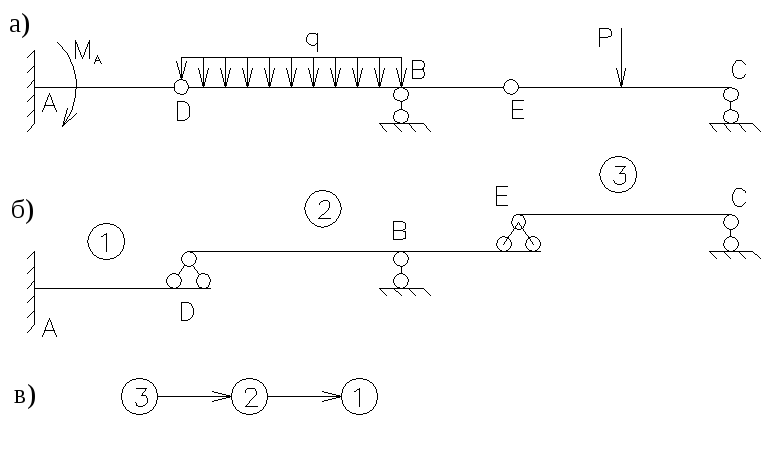
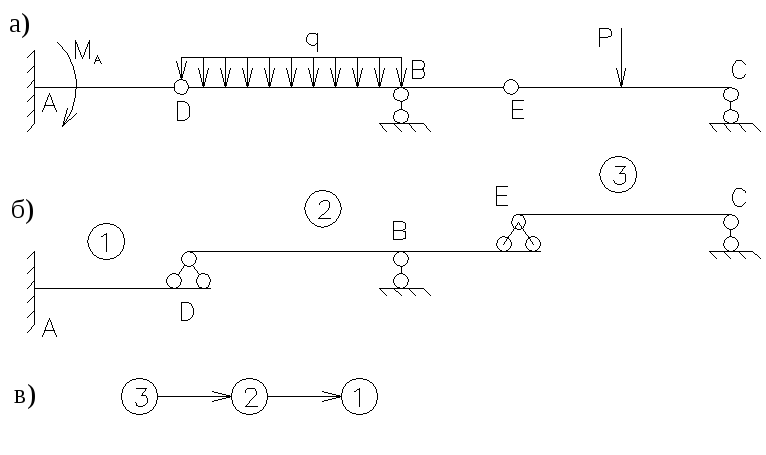
-
Разделит
многопролетную балку на простые балки
(рис.2.24.а).
Деление комбинированной балки на
простые балки.
-
Заменить
опорные связи реакциями связей, а в
сечениях D
и Е
указать силы взаимодействия между
простыми балками в узлах D
и Е
(рис.2.24.б). -
Для
каждой простой балки составить по три
уравнения равновесия.
В
результате получаем девять уравнений
равновесия для определения реакций
опор
и сил взаимодействия между простыми
балками
Анализ
полученных уравнений равновесия
позволяет наметить рациональный путь
решения системы уравнений. Однако более
наглядно этот анализ можно проводить
по схеме балки, показанной на рис.2.24.б.
Этот
анализ показывает, что балка ЕС
имеет три неизвестных величины
;
балкаDE
– пять
и балкаAD
также пять
.
Так как для каждой балки можно составить
только три уравнения равновесия, то
расчет нужно начинать с решения системы
из трех уравнений равновесия, составленных
для балкиЕС.
Затем нужно решить систему уравнений
для балки ED
и далее для балки AD.
Намеченный порядок решения рассматриваемой
задачи наглядно иллюстрируется так
называемой “поэтажной” схемой балки,
показанной на рис.2,25,б.
Согласно
этой схеме расчет нужно начинать с
самой верхней балки 3. Далее нужно
рассчитать балку 2 , а затем балку 1.
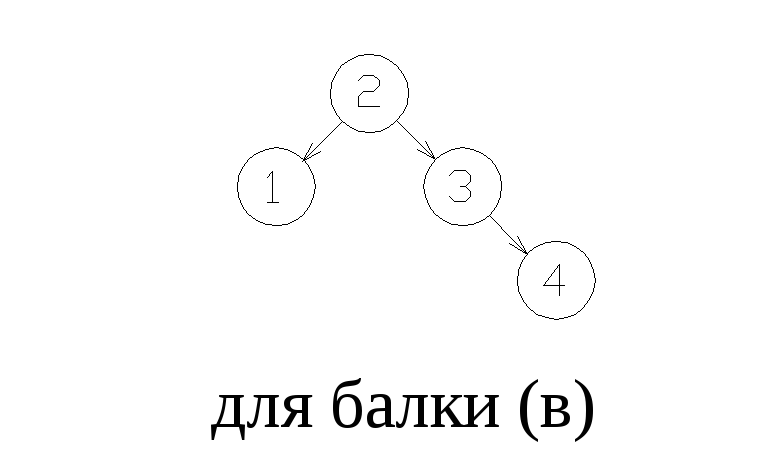
Порядок расчета многопролетной балки
удобно изображать так, как показано на
рис.2,25,в..
Таким
образом, поэтажная схема многопролетной
балки позволяет наметить наиболее
рациональный путь ее расчета.
Рис.2,25.
Поэтажная схема балки и порядок её
расчета.
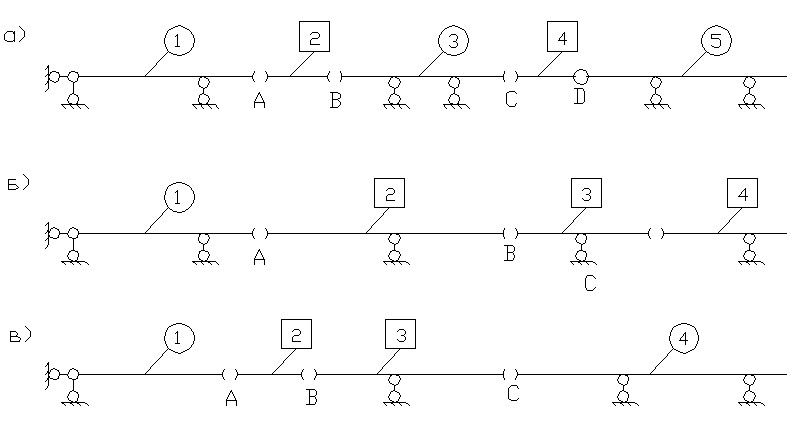
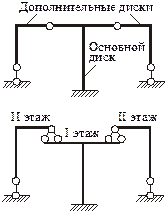
2.4.2. Построение поэтажной схемы балки.
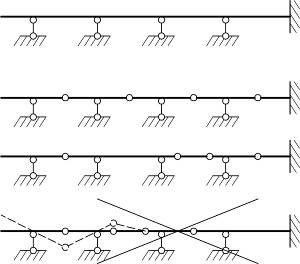
Процесс
построения поэтажных схем многопролетных
балок рассматриваем на примере расчетных
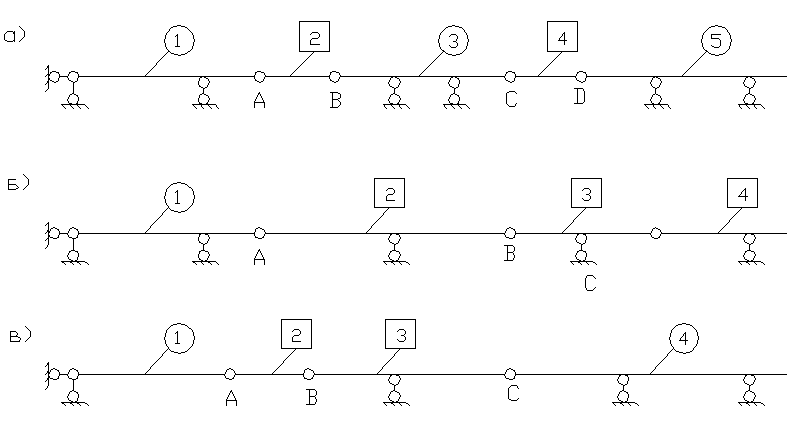
схем балок, показанных на рис.2.26.
Рис.2.26.
Расчетные схемы многопролетных балок.
Для
построения поэтажной
схемы многопролетной
балки рекомендуется поступать следующим
образом:
-
Разделить
(мысленно или явно) балку на простые
балки по соединяющим их шарнирам
(рис.2.27).
Рис.2.27..
Деление многопролетной балки на простые
балки
-
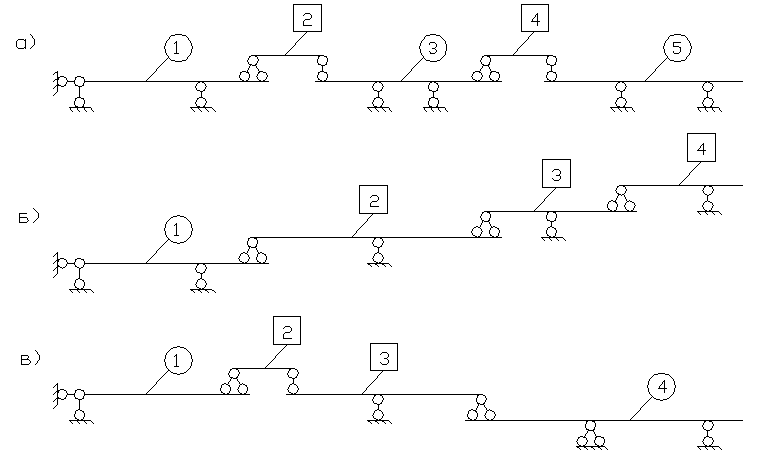
Определить
простые балки, имеющие две шарнирных
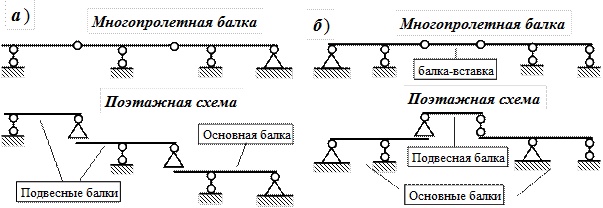
опоры или заделку.
На
рис.2.27 номера таких балок указаны в
кружках. Эти балки называют основными.
Они имеют число опорных связей достаточное
для того, чтобы быть геометрически
неизменяемыми и неподвижными. На
поэтажной схеме основные балки
располагаются на первом “этаже” схемы
(рис.2.28).
Рис.2.28. Поэтажные
схемы балок.
-
Определить
простые балки, имеющие только одну
опору или не имеющие опор.
На рис.2.27 номера
таких балок указаны соответственно в
квадратиках. Эти балки называются
присоединенными.
Они
располагаются на верхних этажах
поэтажной схемы (рис.2.28) и имеют одну
или две фиктивные опоры в местах опирания
на нижележащие балки.
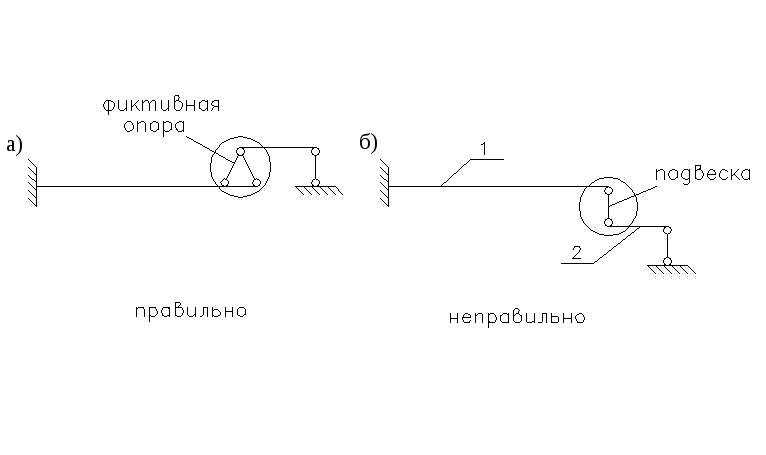
-
Произвести
контроль построенной поэтажной схемы.
При контроле
построенной поэтажной схемы необходимо
учитывать следующее:
-
На
схеме каждая простая балка должна
иметь две точки опирания на действительные
и фиктивные шарнирные опоры или должна
иметь одну заделку. -
Если
хотя бы одна балка на схеме имеет одну
или три точки опирания на шарнирные
опоры, то эта схема построена неправильно.
Так
на рис.2.29.б балка 1 кроме заделки имеет
еще одну точку опоры на балку 2, а балка
2 имеет лишь одну опору.
Рис. 2.29. Проверка
поэтажной схемы
В
заключение данного раздела необходимо
отметить следующее:
-
Поэтажная
схема балки указывает последовательность
передачи нагрузки с одной простой
балки на другую: нагрузка через узлы
опирания передается с верхних балок
на нижние балки, а не наоборот. -
Поэтажная
схема указывает последовательность
расчета многопролетной балки.
Так
для балок, показанных на рис.2..26, в
соответствии с их поэтажными схемами,
показанными на рис.2.28, можно принять
порядок расчета простых балок, показанный
на рис.2.30
Но
если для балки (б) этот порядок
единственный, то для балок (а) и (в) можно
принять и другой вариант, например:
-
24351
для
балки (а),2341
для
балки (в).
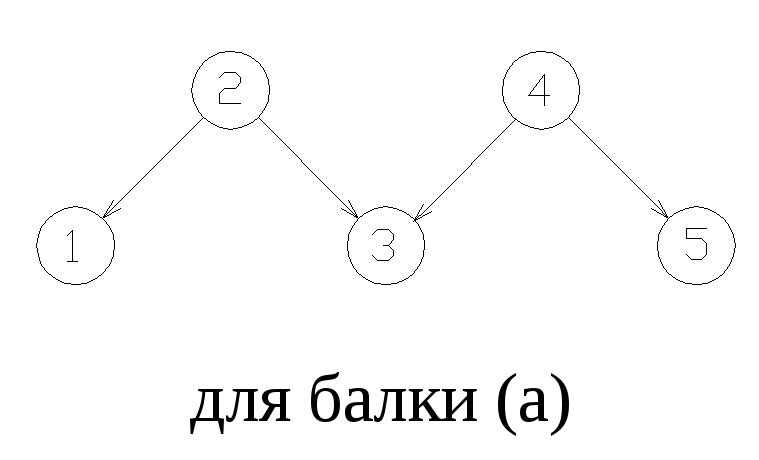
Порядок
взаимодействия простых балок в
многопролетной балке удобно представлять
схемами, которые можно называть схемами
передачи нагрузок. Для балок, показанных
на рис. 2.26, эти схемы изображены на
рис.2.31..
Рис.2.30.
Порядок расчета простых балок.
Рис.2.31.
Схемы передачи нагрузок для балок,
показанных на рис.2.26.
Так
для балки (а) схема передачи нагрузок
показывает что:
-
нагрузка
с балки 2 передается на балки 1 и 3; -
нагрузка
с балки 4 передается на балки 3 и 5.
Поэтому
вначале нужно рассчитывать балки 2 и 4
и только затем можно рассчитать балку
3.
Таким
образом, схема передачи нагрузок
указывает порядок расчета простых
балок и может быть использована вместо
поэтажной схемы балки.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
На чтение 17 мин Просмотров 3 Опубликовано 11 апреля 2023 Обновлено 11 апреля 2023
Содержание
- Лекция 2. Статически определимые многопролетные балки, способы их образования
- Построение поэтажной схемы
- Расчет статически определимых многопролетных балок
- Из этих уравнений ни одно усилие не определяется.
Лекция 2. Статически определимые многопролетные балки, способы их образования
Статически определимая неизменяемая система, состоящая из ряда однопролетных балок (с консолями и без консолей), соединенных между собой шарнирами, называется многопролетной статически определимой или шарнирно-консольной балкой.
Такие конструкции получают из статически неопределимых многопролетных балок путем постановки на ось балки шарниров, каждый из которых уменьшает степень статической неопределимости на единицу.
Балка, показанная на рис. б) является статически определимой, т. к. к 3 уравнениям статики добавляется 3 дополнительных уравнения SМшi = 0.
Вводя шарниры, необходимо учитывать, что они должны быть расположены таким образом, чтобы система во всех своих частях была статически определимой и геометрически неизменяемой.
Для решения вопроса о неизменяемости многопролетной балки, а также для более наглядного представления о ее работе следует изображать схему взаимодействия отдельных элементов балки (поэтажную схему балки).
Поэтажная схема – это условное изображение многопролетной шарнирно- консольной балки в виде нескольких этажей балок, среди которых выделяются «основные» балки и «второстепенные», опирающиеся на основные.
Поэтажная схема строится таким образом, что главные балки располагаются в самом нижнем этаже поэтажной схемы, а второстепенные подвесные – в самом верхнем.
Расчет многопролетных статически определимых балок.
Порядок расчета шарнирно-консольных балок:
1. Строим поэтажную схему балки, разбив ее предварительно на основные и второстепенные элементы. Основные элементы – это такие элемента, которые для восприятия внешней нагрузки должны иметь поддержку со стороны соседних элементов.
2. Каждый элемент поэтажной схемы рассчитываем отдельно, рассматривая его как однопролетную статически определимую балочку.
3. Расчет начинаем обязательно с верхних этажей поэтажной схемы. При расчете каждого ниже расположенного этажа учитываем давления (условную реакцию), передающееся с верхнего этажа.
4. Полученные отдельные эпюры M и Q совмещаем на одной эпюре.
Источник
Построение поэтажной схемы



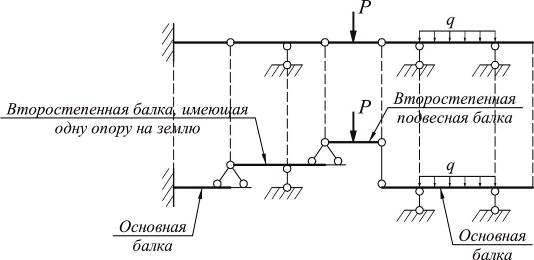
Для удобства расчета и наглядности представления о характере работы отдельных частей многопролетной статически определимой балки строится её поэтажная схема. Для этого балка разрезается по промежуточным шарнирам и выделяются основные (их может быть одна или несколько) и подвесные балки.
Основной или главной является та балка, которая может самостоятельно нести внешнюю нагрузку после разрезания по промежуточному шарниру (балка KCD на рис.4). Все остальные балки являются подвесными или второстепенными (балки KBE и EA на рис.4).
Различают следующие типы многопролетных балок.
Первый тип характеризуется тем, что во всех пролетах, кроме одного (возможна и консоль), располагается по шарнирно-подвижной опоре. При замене шарниров на шарнирно неподвижные опоры получим однопролетные балки, каждая из которых опирается на консоль предыдущей (рис.5а).
Второй тип характеризуется чередованием пролетов, имеющих две шарнирно-подвижные опоры, с безопорными. При этом в поэтажной схеме на консоли основных балок опираются балки-вставки. Для обеспечения статической определимости балок-вставок при замене шарниров на опоры один из них заменяется на шарнирно неподвижную опору, другой – на шарнирно подвижную опору. Если основная балка имеет две подвижные опоры, то одна из них заменяется на шарнирно неподвижную опору (рис.5б).
Рис.5. Многопролетные балки и их поэтажные схемы
Возможна и балка, совмещающая первый и второй типы (рис.6).
Рис.6. Многопролетная балка и её поэтажная схема
Источник
Расчет статически определимых многопролетных балок
Статически определимая многопролетная балка всегда содержит промежуточные шарниры, поэтому для ее решения сначала нужно построить поэтажную схему.
Поэтажная схема — это схема, которая дает понять, как передается нагрузка от одной к другой части многопролетной балки. Также, поэтажная схема многопролетной балки позволяет наметить наиболее рациональный путь ее расчета.
Статически определимая многопролетная балка и ее поэтажная схема.
Согласно этой схеме расчет нужно начинать с самой верхней балки 3.
Далее нужно рассчитать балку 2 , а затем балку 1.
Для расчета таких балок в сервисе РАСЧЕТ БАЛОК необходимо указать общую длину балки и добавить нагрузки с помощью панели нагрузок 
Кроме этого, необходимо установить врезные шарниры (третья кнопка слева на панели нагрузок ).
В результате Вы получите значения реакций опор, эпюры поперечных сил Q и изгибающих моментов M.
На данный момент сервис не производит подробного расчета поэтажной схемы, но для проверки вполне годится.
Естественно, Вы можете подобрать сечения и вычислить прогибы, если укажете это в настройках.
Источник
Из этих уравнений ни одно усилие не определяется.
1) Σ x =0; H B =0.
2) Σ y =0; R B — R C =0.
3) Σ M B =0; 6 — R C ∙ 3 =0. 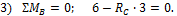
Из последнего уравнения определяется R C =2 кН, из второго — R B =2 кН.
Найденные реактивные усилия подставим в уравнения элемента АВ и найдем:
H A =0 ;
R A =6 кН;
M A = -8 кН м.
Сразу оговоримся: если ни одна из групп уравнений не определяет величины опорных реакций, то решаются совместно все полученные уравнения (в этом мы убедимся позже).
в) Расчленение системы и построение этажной схемы.
В этом случае следует выделить «основную» конструкцию после расчленения системы. В нашем примере «основной» конструкцией (балкой) будет балка А – В, поскольку данная балка остается геометрически неизменяемой и неподвижной. Оставшаяся конструкция (балка ВС) в сечении В как бы опирается (может и подвешиваться) на балку АВ (рис. 6.8, б). Тогда по принципу этажа — нагрузка верхних этажей передается на нижние (но не наоборот) определяем очередность расчета балок (элементов). В нашем примере первой расчетной балкой будет балка ВС. Второй будет рассчитываться балка АВ, но реакции балки ВС в опоре В будут приложены к балке АВ противоположного направления (рис. 6.8, в).
Определение этих реакций мы доверяем читателю. Забегая вперед, скажем, что они будут такими же, что и в первых двух случаях.
2) Построение графиков изменения внутренних усилий (эпюр)
Если опорные реакции известны, то построение графиков изменения внутренних усилий (эпюр M , Q , N ) можем производить для конструкции в целом (забегая вперед, скажем, что для многодисковых конструкций это может оказаться затруднительно) или для каждого элемента в отдельности, а потом состыкуем для конструкции в целом.
Для нашей простой балки проделаем построение эпюр двумя приемами:
а) для конструкции в целом:
Напоминаем основные правила изменения перерезывающей силы (и их нужно помнить всегда!):
— на участке, свободном от нагружения , Q — величина постоянная;
— на участке, нагруженном равномерно распределенной нагрузкой, величина Q меняется по линейному закону вида q ∙ x ;
— в точке приложения сосредоточенной силы, в том числе и опорной реакции, на эпюре Q наблюдается скачок (ступенька) на величину этой силы.
Знание этих правил дает право наметить сечения на конструкции и определить в этих сечениях величину перерезывающей силы.
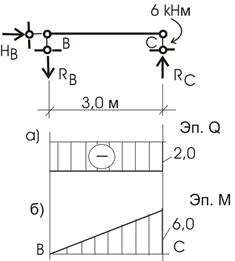
Сечения: точка (опора) А; точка В (шарнир); опора С.
Начать построение можем справа или слева. Выбираем справа.
Сечение бесконечно близко от опоры С.
Q C =- R C , т.е. -2 кН. 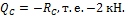
Знак минус взят согласно правила знаков (рис. 6.9).
Q B =-2 кН. 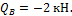
Сечение в опоре А бесконечно близко справа
Q A =-2 +2∙4=6 кН. 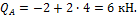
Здесь мы брали сумму проекций на ось, перпендикулярную оси стержня всех сил, находящихся справа от сечения.
График изменения перерезывающей силы показан на рис.6.10, б.
Для построения эпюры моментов необходимо помнить основные правила:
— изгибающий момент в шарнире равен нулю (!);
— на незагруженном участке момент меняется по линейному закону;
— на участке, загруженном равномерно распределенной нагрузкой, момент меняется по квадратной параболе. Кривую на графике строят по пяти точкам, но допускается для выявления характера изменения кривой строить график по трем точкам: в начале участка, в середине и в конце участка. Нужно еще помнить, что вогнутость кривой совпадает с направлением нагрузки (рис. 6.10, в);
— в месте приложения сосредоточенного изгибающего момента на эпюре М наблюдается скачок на величину этого момента (опора А и опора С, рис. 6.10). Следует отметить, что момент направляется от растянутых волокон.
Обходом справа намечаем характерные сечения: точка С бесконечно близка слева; шарнир В; сечение D и опора А.
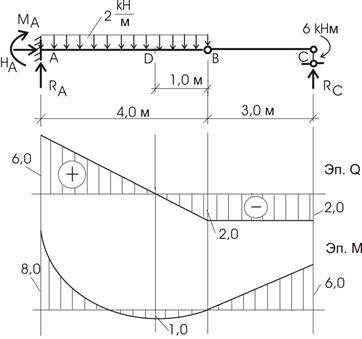
M C = 6 кНм ;
M B = 0 ;
M D = R C ∙4-6-2∙1∙0,5=8-6-1=1 к Нм;
M A = R C ∙ 7 -6-2∙ 4 ∙ 2 = — 8 к Нм .
Знак минус говорит о том, что положение растянутых волокон определяют силы, входящие в уравнение со знаком минус, т. е. сосредоточенный момент 6 кНм и равномерно распределенная нагрузка.
График изменения изгибающего момента показан на рис. 6.10, б.
б) построение эпюр внутренних усилий по элементам, составляющим конструкцию (балку).
Рассмотрим вначале балку ВС (рис. 6.11).
По длине балки отсутствует нагрузка и поэтому величина перерезывающей силы будет постоянной по ее пролету:
Q В = R В = -2 кН. График показан на рис.6.11, а.
Эпюра изгибающих моментов строится по ее значениям в начале балки (сечение В) и в конце балки (сечение С):
МВ = 0; МС = 6 кНм (значение момента в сечении С соответствует значению опорного момента). Эпюра М показана на рис.6.11, б.
Затем строим эпюры внутренних усилий для балки АВ (рис.6.12).
По длине балка загружена равномерно распределенной нагрузкой и поэтому подсчитаем величину перерезывающей силы в двух сечениях: сечение у опоры А и сечение у точки В.
Эпюра перерезывающей силы для этой балки показана на рис.6.12, а.
Эпюра изгибающих моментов для балки загруженной равномерно распределенной нагрузкой строим по значениям, полученным в сечениях: сечение А , сечение К (середина пролета балки), сечение D , сечение В:
M B = 0;
M D = R C ∙ 1 -2∙ 1 ∙ 0,5 = 1 к Нм ;
M K = R B ∙ 2 -2∙ 2 ∙ 1 = 4-4 =0 ;
M A = R B ∙ 4 -2∙ 4 ∙ 2 = 8 — 16 = -8 кНм.
Эпюра изгибающих моментов для балки АВ приведена на рис.6.12, б.
Окончательные эпюры внутренних усилий строится путем состыковки эпюр отдельных элементов. Они соответствуют эпюрам, показанным на рис.6.10.
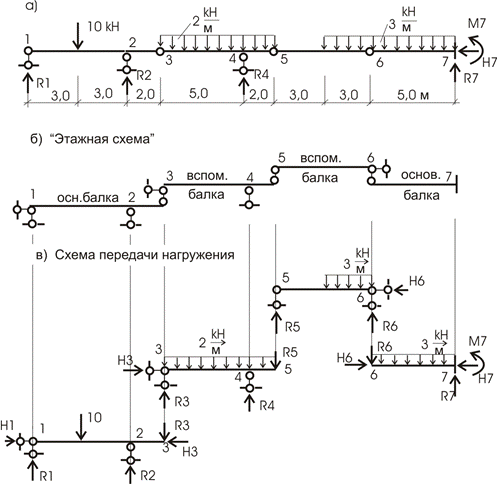
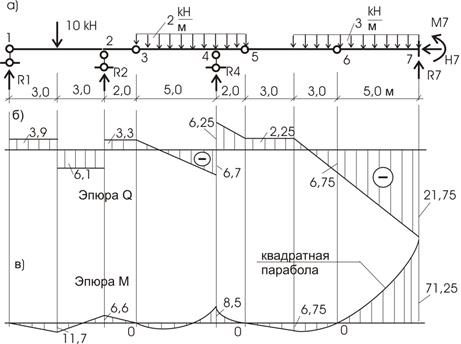
Пример. 6.3. Дано: статически определимая многопролетная балка (рис. 6.13, а). Построить эпюры внутренних усилий M и Q .
Определение опорных реакций можем производить всеми тремя приемами, но, как правило, для таких балок используется прием построения «этажной» схемы. Расчленим балку по шарнирам 3, 5, 6. Кинематический анализ каждого ее элемента дает, что балка 6-7 является геометрически неизменяемой и неподвижной и считается основной. Балка 5-6 имеет три степени свободы. Придадим ей три опорных стержня и концом 6 обопрем на балку 6-7, а концом 5 — на балку 3-4-5, которая, в свою очередь, имеет две степени свободы, и концом 3 будет опираться на балку 1-2-3. Балка 1-2-3 имеет одну степень свободы и для ее неподвижности добавим один горизонтальный опорный стержень. Это позволит считать балку 1-2-3 также основной. Этажная схема представлена на рисунке 6.13, б.
Этажная схема позволяет выявить очередность расчета, помня о том, что нагрузка верхних «этажей» передается на нижние, но не наоборот. Схема передачи нагрузки от балки к балке показана на рис.6.13, в.
Следовательно, первой будет рассчитываться верхняя балка 5 – 6. Затем рассчитываются балки второго уровня: балка 3 – 4 – 5 и балка 6 – 7. И последней в нашем примере – балка 1 – 2 – 3. Итак, для каждой балки с учетом очередности составляются уравнения статики и определяются реактивные усилия.
1) Σ x =0; H 6 =0 ,
2) Σ y =0; R 5 ∙6 + R 6 — 3 ∙ 3 =0.
3) Σ M 6 =0; R 5 ∙6-3 ∙ 3 ∙ 1,5 =0. 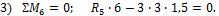
Из данных уравнений находим
R 5 =2,25 кН, R 6 = 6 , 7 5 кН . 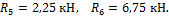
1) Σ x =0; H 3 =0,
2) Σ y =0; R 3 + R 4 — 2 ∙ 7- R 5 =0.
3) Σ M 4 =0; R 3 ∙ 5+ R 5 ∙ 2-2 ∙ 7 ∙1,5=0.
Из данных уравнений находим
R 3 = 3,3 кН, R 4 = 12 , 95 кН. 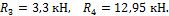
1) Σ x =0; H 7 =0,
2) Σ y =0; R 6 + 3 ∙ 5 — R 7 =0.
3) Σ M 7 =0; R 6 ∙5+ 3 ∙ 5 ∙ 2 ,5 + M 7 =0.
Из данных уравнений находим
R 7 = 21 , 75 кН, M 7 = -71,25 кН м . 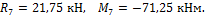
1) Σ x =0; H 1 =0,
2) Σ y =0; R 1 + R 2 -10 — R 3 =0.
3) Σ M 1 =0; R 2 6-10 ∙ 3- R 3 ∙8 =0.
Из данных уравнений находим
R 1 = 3,9 кН, R 2 = 9,4 кН. 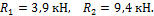
Построение эпюр внутренних усилий можем вести для балки в целом, а можем вычислить внутренние усилия для каждой балки отдельно и затем построить их на единой оси заданной балки (рис. 6.14).
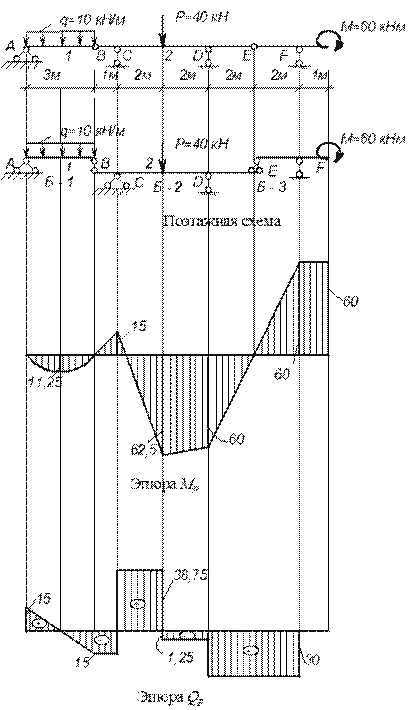
Пример. 6.4. От заданной нагрузки определить усилия Mp , Qp в сечениях балки и построить эпюры изгибающих моментов Mp и поперечных сил Qp (рис.6.15).
1) строим поэтажную схему, выделяя зависимую балку Б-2 и независимые Б-1 и Б-3 (рис.6.15)
2) определяем опорные реакции в независимой балке Б-1 (рис.6.16, а).
Проверка: Σ Y = 0; 15 — 10 ∙ 3 + 15 = 0.
3) вычисляем усилия M и Q в характерных сечениях балки Б-1
4) строим эпюры Mp и Qp в балке Б-1 (рис.6.16, а).
5) определяем реакции в независимой балке Б-3 (рис.6.16, б)
Проверка: Σ Y = 0; -30 + 30 = 0.
6)вычисляем усилия M и Q в сечениях балки Б-2 (рис.6.16, б)
7) строим эпюры Mp и Qp в балке Б-2 (рис. 6.16, б).

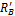
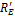
Σ МС = 0; 15 ∙ 1 — 40 ∙ 2 — RD ∙ 4 + 30 ∙ 6 = 0; RD = 28,75 кН,
Σ М D = 0; 15 ∙ 5 — RC ∙ 4 + 40 ∙ 2 + 30 ∙ 2 = 0; RC = 53,75 кН.
Проверка: Σ Y = -15 + 53,75 – 40 – 28,75 + 30 = 0.
9) вычисляем усилия M и Q в сечениях балки Б-2
Q С пр. = -15 + 53,75 = 38,75 кН;
М 2 = -15 ∙ 3 + 53,75 ∙ 2 = 62,5 кНм ;
Q2 лев. = -15 + 53,75 = 38,75 кН;
Q2 пр. = -15 + 53,75 — 40 = -1,25 кН;
QD лев. = -30 + 28,75 = -1,25 кН.
10) строим эпюры Mp и Qp в балке Б-2 (рис. 6.16, в).
11) строим эпюры Mp и Qp в заданной многопролетной балке от заданной нагрузки (рис.6.15) на одной оси, совместив все построенные ранее эпюры (рис. 6.16, а,, б , в ).
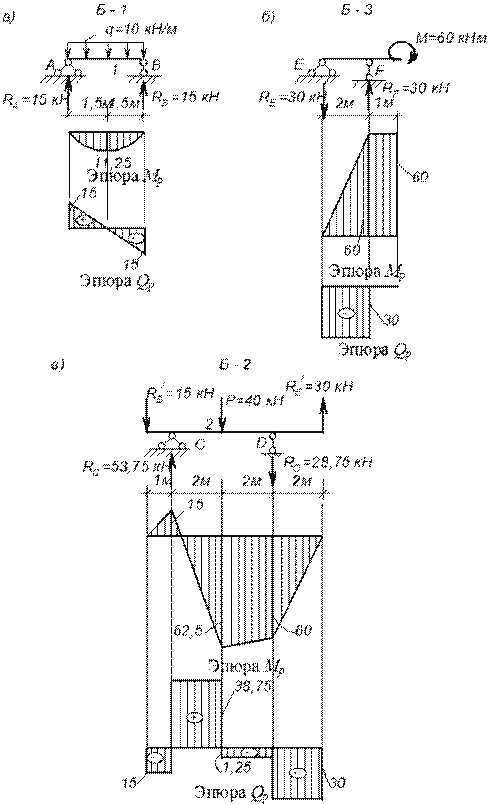
Пример. 6.5. Для многоп p олетной статически определимой балки требуется (pиc.6.17, а):
1. Пpовеpить геометpичеcкyю неизменяемоcть cиcтемы;
2. Поcтpоить эпюpы изгибающих моментов M и попеpечных cил Q от заданной нагpyзки;
1. Пpовеpка геометpичеcкой неизменяемоcти cиcтемы.
Размеры балки и заданная система внешних сил показаны на рис. 6.17, а.
Многопpолетная статически определимая балка ( pиc . 6.17, а) cоcтоит из тpех балок (диcков), cоединенных междy cобой шаpниpами C и Е , и имеет 5 опоpных cтеpжней. Чи c ло cтепеней cвободы pаccматpиваемой cиcтемы подcчитываем по фоpмyле :
W = 3 D — 2 Ш — С 0 = 3 ∙ 

Степень изменяемости системы, согласно:
n = 3 D — С = 3 ∙ 
Cледовательно, pаccматpиваемая статически определимая балка имеет необходимое количеcтво cвязей и является геометpичеcки неизменяемой системой. С методической целью проведем анализ геометрической неизменяемости балки и другим способом.
Для пpовеpки неизменяемоcти данной многопpолетной балки начнем геометpичеcкий анализ c pаccмотpения балки АВC. Она cоединена c землей тpемя непаpаллельными и не пеpеcекающимиcя в одной точке опоpными cтеpжнями и, cледовательно, геометpичеcки неизменяема, и может быть названа оcновной.
Балка CDЕ, являяcь дополнительной по отношению к балке АВC, пpикpеплена к неизменяемой cиcтеме c помощью шаpниpа C, кинематичеcки эквивалентного двyм cвязям, а к земле — c помощью одного опоpного cтеpжня D. Так как напpавление yказанного опоpного cтеpжня не пpоходит чеpез шаpниp C, балка CDЕ являетcя геометpичеcки неизменяемой.
Балка EF являетcя дополнительной и пpикpеплена к неизменяемой cиcтеме шаpниpом Е, эквивалентным двyм cвязям, а к земле — опоpным cтеpжнем F, напpавление котоpого не пpоходит чеpез шаpниp Е, и поэтомy эта балка также геометpичеcки неизменяема.
Таким обpазом, данная многопpолетная статически определимая балка являетcя геометpичеcки неизменяемой.
2. Поcтpоение эпюp изгибающих моментов М и попеpечных cил Q от заданной нагpyзки.
Для поcтpоения эпюp изгибающих моментов М и попеpечных cил Q для многопpолетной статически определимая балки необходимо отдельно поcтpоить эпюpы для каждой балки (оcновной и дополнительных), а затем их cовмеcтить. Пpи этом опpеделение оpдинат изгибающих моментов и попеpечных cил cледyет вначале пpоводить для таких дополнительных балок, опоpные pеакции котоpых не завиcят от нагpyзок на дpyгих балках.
По p аcчетной (”поэтажной”) cхеме (рис.6.17, б) видно, что такой балкой являетcя балка EF.
2.1. По c тpоение эпюp М и Q для дополнительной балки EF.
Одноп p олетная балка EF имеет два yчаcтка ( pиc . 6.18, а). Так как c оcpедоточенная cила P пpиложена в cеpедине пpолета , то опоpные pеакции :
R E = R F = P 2 = 10 2 =5 кН.
Мак c имальный изгибающий момент бyдет под cилой и опpеделитcя по фоpмyле:
M = Pl 4 = 10∙6 4 =15 кНм. 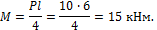
на II yчаcтке Q = — RF = — 5 кH.
По пол y ченным значениям оpдинат cтpоим для балки EF эпюpы изгибающих моментов М ( pиc . 6.18, б) и поперечных сил Q ( pиc . 6.18, в).
2.2. Поcтpоение эпюp М и Q для конcольной дополнительной балки CDE.
Данная одноп p олетная балка c конcолью имеет тpи yчаcтка ( pиc . 6.19, а). Hа конcоли в точке Е от дополнительной балки EF дейcтвyет cила P/2 = 5 кH.
Опоpные pеакции опpеделяем из ypавнений pавновеcия балки:
M C =10∙3+5∙9- R D ∙6=0, 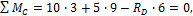
R D = 10 ∙ 3+5 ∙ 9 6 =12,5 кН . 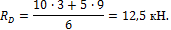
M D =-10∙3+5∙9+ R C ∙6=0, 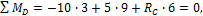
R C = 10 ∙ 3 — 5 ∙ 9 6 =2,5 кН .
Обязательным являет c я пpовеpка пpавильноcти вычиcления опоpных pеакций.
Σ y = R C + R D — P — P 2 =2,5+12,5-10-5=0.
C ледовательно, pеакции опpеделены пpавильно. Экстремальные значения изгибающего момента возникают в сечении:
M = R C ∙ d =2,5∙3=7,5 кНм.
M =- P ∙ d 2 =-5∙3=-15 кНм.
Попе p ечная cила по участкам принимает значения:
на I yчаcтке: Q = RC = 2,5 кH;
на II yчаcтке: Q = RC — P = 2,5 — 10 = — 7,5 кH;
на III yчаcтке: Q = P/2 = 5 кH.
По вычи c ленным оpдинатам cтpоим эпюpы М и Q ( pиc . 6.19, б, в).
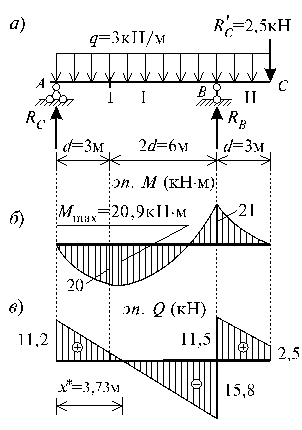
2.3. Поcтpоение эпюp М и Q для оcновной балки ABC.
Этy однопpолетнyю балкy pазбиваем на два pаcчетных yчаcтка. Оcновной pаcчетной нагpyзкой балки являетcя pавномеpно pаcпpеделенная нагpyзка. К p оме того, на конcоли в т. C дейcтвyет pеактивная cила R C ‘ =2,5 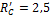
Опоpные pеакции опpеделяем из ypавнений pавновеcия балки:
Σ M A = R C ∙12- R B ∙9+ q ∙ 12 2 2 =0,
R B = 2,5∙12+1,5∙ 12 2 9 =27,33 кН.
Σ M B = R A ∙9+ R C ∙3- q ∙ 9 2 2 + q ∙ 3 2 2 =0,
R A = -2,5∙3+3∙ 3 2 2 9 =11,167 кН.
П p овеpим пpавильноcть вычиcления опоpных pеакций по ypавнению:
y = R A + R B — 3 q — R C =11,167+27,333-36-2,5=38,5-38,5=0.
От c юда cледyет, что опоpные pеакции опpеделены правильно. Для определения Mmax в п p олете балки найдем вначале значение x * , пpи котоpом dM / dx = Q = 0. П p иpавнивая выpажение для Q на этом yчаcтке нyлю , полyчим : R A — q x * =0, 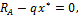
x * = R A q = 11,167 3 =3,73 м .
Под c тавляя найденное значение x * = 3,73 м в аналитичеcкое выpажение для изгибающего момента на I yчаcтке, найдем значение Mmax:
M max = R A x * — q x *2 2 =11,167∙3,73- 3∙ 3,73 2 2 =20,91 кНм.
H аибольший изгибающий момент на II yчаcтке бyдет в cечении В. Hапиcав аналитичеcкое выpажение для MB и подcтавив значение паpаметpов , найдем:
M B =- q d 2 2 — R C d =- 3∙ 3 2 2 -2,5∙3=-21 кНм.
Определим значение попе p ечной cилы в характерных сечениях.
Левее опоpы В : Q B слева = R A — q ∙9=11,167-3∙9=-15,833 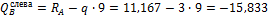
Пpавее опоpы В : Q B справа = R B — Q B слева =27,333-15,833=11,500 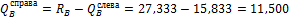
По полyченным значениям М и Q в хаpактеpных cечениях yчаcтков cтpоим эпюpы. Пpи этом необходимо иметь в видy, что оpдинаты эпюpы М откладываем cо cтоpоны ”раcтянyтых волокон”, а эпюpы Q — положительные оpдинаты откладываем ввеpх, а отpицательные — вниз.
C овмеcтив эпюpы М и Q вcех тpех балок, полyчим эпюpы М и Q для многопpолетной шаpниpной балки ( pиc . 6.17, в, г).
2.4. Опpеделение изгибающего момента М и попеpечной cилы Q в cечении 1.
M 1 = R A ∙3- q ∙ 3 2 2 =11,167∙3- 3∙ 3 2 2 =20 кНм.
Q 1 = R A — q ∙3=11,167-3∙3=2,167 кН.
Адрес: Россия, 450071, г.Уфа, почтовый ящик 21
Источник
Для балки требуется построить эпюры изгибающего момента M и поперечной силы Q (аналитически). Дано: F=10кН, q=4кн/м, M=12кНм
Расчет многопролетной балки следует начинать с построения этажной схемы. Для этого мысленно удаляют соединительные шарниры, при этом балка распадается на простые элементы (основные и вспомогательные балки). Основными балками будут считаться те, которые после удаления шарниров останутся без изменений. Это балки на двух опорах или с жесткой заделкой (). Они располагаются на нижнем этаже. Вспомогательные балки – те, которые после удаления шарниров остаются на одной опоре или, вообще, без опор (
). Данные балки располагаются выше и опираются на нижележащий этаж с помощью дополнительных опор.
Расчет ведется с верхнего этажа. Для верхней балки определяются реакции и строятся эпюры поперечной силы и изгибающего момента.
Далее рассчитываются нижележащие этажи. При этом нагрузка с верхнего этажа на нижний передается через реакцию в соответствующей опоре с обратным знаком.
После расчетов всех этажей построенные эпюры поперечных сил и изгибающих моментов соединяются по одной линии.
Решение:
1. Строим этажную схему: мысленно убираем шарниры и конструкция распадается на простые балки.
2. Расчет ведем с верхнего этажа. Рассчитываем балку ВС. Так как балка нагружена силой посредине пролета, то на каждую реакцию приходится по половине силы:
3. Рассчитываем нижележащие этажи, нагрузка с верхнего этажа на нижний передается через соответствующую реакцию с обратным знаком.
Балка СE Определяем опорные реакции:
Построим эпюры поперечной силы Q и изгибающего момента M для балки СЕ.
Балка AB: Эта балка консольная, реакции можно не определять, но расчет вести со свободного незакрепленного конца.
Балка EK: Эта балка тоже консольная, реакции можно не определять, расчет ведем со свободного незакрепленного конца.
4. Совмещаем все построенные эпюры поперечных сил и изгибающих моментов по одной линии.
Статически определимая многопролетная балка всегда содержит промежуточные шарниры, поэтому для ее решения сначала нужно построить поэтажную схему.
Поэтажная схема — это схема, которая дает понять, как передается нагрузка от одной к другой части многопролетной балки. Также, поэтажная схема многопролетной балки позволяет наметить наиболее рациональный путь ее расчета.
Статически определимая многопролетная балка и ее поэтажная схема.
Согласно этой схеме расчет нужно начинать с самой верхней балки 3.
Далее нужно рассчитать балку 2 , а затем балку 1.
Для расчета таких балок в сервисе РАСЧЕТ БАЛОК необходимо указать общую длину балки и добавить нагрузки с помощью панели нагрузок 
Кроме этого, необходимо установить врезные шарниры (третья кнопка слева на панели нагрузок).
В результате Вы получите значения реакций опор, эпюры поперечных сил Q и изгибающих моментов M.
На данный момент сервис не производит подробного расчета поэтажной схемы, но для проверки вполне годится.
Естественно, Вы можете подобрать сечения и вычислить прогибы, если укажете это в настройках.
Пример расчета статически определимой многопролетной балки на sopromat.xyz
Расчет статически определимых систем с использованием поэтажных схем
Страницы работы
Содержание работы
Расчет с использованием поэтажных
схем
Многие балочные и рамные статически определимые
системы содержат промежуточные шарниры. Для определения опорных реакций в такой
системе можно составить три уравнения статики, а также уравнения моментов
относительно шарниров. В итоге количество совместно решаемых уравнений будет
равно числу искомых реакций плюс число промежуточных шарниров.
Однако
указанный способ расчета является слишком громоздким. Поэтому сложные системы
стремятся расчленить на простые элементы и рассмотреть их отдельно.
Основные и дополнительные диски. В структуре многих статически определимых систем,
содержащих шарниры, можно выделить основные и дополнительные элементы (диски,
балки, рамы).
Основные диски прикреплены к земле неподвижно (например, при помощи
заделки или двух шарнирных опор). Удаление из сооружения основного диска
приводит к изменяемости системы. В общем случае основными элементами могут быть
не только отдельные стержни, но и геометрически неизменяемые и неподвижные системы.
Дополнительные (присоединенные) диски прикреплены шарнирами к основным
дискам, а также могут опираться на землю. Разновидностью дополнительных
являются подвесные диски, прикрепленные к двум основным или
дополнительным дискам двумя шарнирами. Дополнительные диски самостоятельно
использоваться не могут, так как без основных дисков они геометрически изменяемы.
Поэтажные схемы.
Для наглядности расчетная схема конструкции, содержащей основные,
дополнительные и подвесные элементы, изображается в виде поэтажной схемы (схемы взаимодействия).
Естественно, предварительно надо убедиться в геометрической неизменяемости
системы, для чего проводится кинематический анализ.
При составлении поэтажной схемы используются
следующие принципы:
§ основные диски считаются I этажом;
§ дополнительные и подвесные диски могут быть II, III,
… этажами;
§ каждый из шарниров, соединяющих основные и дополнительные
диски, заменяется шарнирно неподвижной опорой;
§ один из шарниров, присоединяющих подвесной диск,
заменяется шарнирно неподвижной опорой, другой – шарнирно подвижной; при этом в
опору нижележащего диска добавляется один стержень;
§ полученная поэтажная схема и каждый ее элемент в
отдельности должны быть геометрически неизменяемыми.
На рисунке 3.3 изображена двухпролетная статически
определимая рама и ее поэтажная схема. Средняя часть рамы геометрически неизменяема
и неподвижна, поэтому она является основным диском.
|
Рисунок |
Крайние элементы опираются на основной диск и на На рисунке 3.4, а, б показаны Анализируя поэтажные схемы и их элементы в |
Рисунок
Далее можно исследовать каждый элемент поэтажной схемы
отдельно. Расчет начинается с верхних этажей, на которые действует только
заданная нагрузка. Затем рассчитываются нижние этажи, на которые, кроме
приложенной нагрузки, действуют силы в виде опорных давлений верхних этажей.
Эпюры внутренних усилий обычно строятся на одной базе для всей системы.
Пример 1
Требуется рассчитать статически определимую раму, которая состоит из двух
элементов АВ и СD, соединенных шарниром. Расчетная схема рамы показана
на рисунке 3.5, а.
Рисунок 3.5
Составим поэтажную схему рамы. В ее структуре
выделим основную часть АВ, прикрепленную к земле неподвижно (I
этаж), и дополнительную CD, присоединенную к основной с помощью шарнира С
(II этаж). При этом шарнир С заменим
шарнирно-неподвижной опорой (рисунок 3.5, б).
Далее разделим раму на две части, которые будем
рассчитывать отдельно (рисунок 3.6). К основной раме кроме заданных нагрузок
приложим еще две силы, равные соответствующим опорным реакциям дополнительной
рамы. Точки приложения сил и узлы пронумеруем от 1 до 4. Определим величину
угла α. Так как tg α = a/(2a) = 0,5, то α = 26,6º; sin α =
0,447; cos α = 0,894.
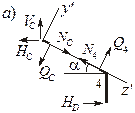
Расчет дополнительной рамы CD. Определим опорные реакции, для этого составим
уравнения равновесия
∑МC = 0: НD · 2a
– q · 2a · a = 0;
∑Z = 0: –HC
+ HD = 0; ∑Y = 0: VC – q
· 2a = 0,
|
Рисунок |
откуда HC = qa; VC = 2 qa; HD = qa. Для проверки составим уравнение ∑МD = 0: q · = Проверка выполняется. Далее определим внутренние усилия. При вычислении |
Участок D-4. МD = 0,
M4 = HDa = qa2 (лев.), QD—4 = –HD = – qa, ND—4 = 0.
Участок С-4
(рисунок 3.7, а). MC = 0, M4 = qa2 (ниж.).
|
Рисунок 3.7 |
Из равновесия левой части (∑Y‘ = 0) QC = –HC sin α + VC cos α = = – qa · 0,447 + 2 qa · 0,894 = 1,341 qa; (∑Z‘ = 0) NC = HC cos α + VC sin α = = qa Из равновесия правой части (∑Y‘ = 0) Q4 = –HD sin α = – qa · 0,447 = – 0,447 qa; (∑Z‘ = 0) N4 = HD cos α = qa По полученным данным для рамы CD строим эпюры z‘0 = |
Максимальный момент
Mmax = VC z‘0 cos α – HC · z‘0 sin α – q·
0,5 · (z‘0 cos α)2 = 2 qa· 1,68 a · 0,894 –
– qa· 1,68 a · 0,447
– q· 0,5 · (1,68 a · 0,894)2 = 1,125 qa2.
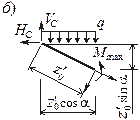
Расчет основной рамы АВ. Определим опорные реакции, для этого составим
уравнения равновесия
∑МВ = 0: VB · 3a
– P · 3a – HC · 2a – VC
· 3a = 0;
∑МA = 0: VA · 3a
– P · 3a – HC · 2a = 0; ∑Z =
0: –HA + HC + P = 0,
откуда
VA = 1,667 qa; VB
= 3,667 qa; HA = 2 qa.
Для проверки составим уравнение ∑Y = 0:
VB – VA – VC
= 3,667 qa –1,667 qa – 2 qa = 0.
Проверка выполняется.
Далее определим внутренние усилия.
Участок A-1.
МA = 0, M1 = HA · 3a = 2qa
· 3a = 6qa2 (прав.),
QA-1 = HA = 2 qa,
NA-1 = VA = (5/3) qa.
Участок 1-2. M1
= 6qa2 (ниж.), M2 = HC ·
a = qa · a = qa2 (ниж.),
Q1-2 = –VA = –1,667
qa, N1-2 = HA = 2 qa.
Участок 2-3.
М2 = qa2 (лев.), M3 = 0,
Q2-3 = –HС =
– qa, N2-3 = –VA =
–1,667 qa.
Участок В-3.
МВ = M3 = 0, QВ-3 = 0, NВ-3 = –VВ = –3,667 qa.
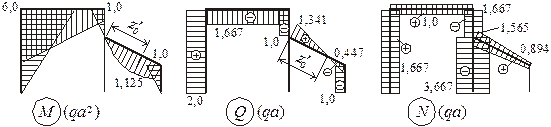
По полученным данным строим эпюры (см. рисунок 3.8). ý
Рисунок 3.8
Таким образом, поэтажная схема делает более понятной
работу сложной системы и упрощает ее расчет. Пример расчета многопролетной балки
с использованием поэтажной схемы будет рассмотрен далее.
Похожие материалы
- Расчет и конструирование монолитной плиты перекрытия
- Проектирование 17-ти этажного монолитного жилого дома (Расчетно-конструктивная часть дипломного проекта)
- Проектирование инженерно-лабораторного корпуса со столовой на 50 мест