Как составить последовательность простых чисел

Последовательность, почти всегда возвращающая простые числа

Возможно, самым интересным в теории чисел является раздел, посвященный простым числам. При этом он один из самых малоизученных. Из простейшего определения понятия простого числа — это число, которое делится на себя и единицу, — вытекает множество загадок, многие из которых удалось разгадать сравнительно недавно, а некоторые еще ждут своего разрешения. Разгадав некоторые из них, человечество продвинется далеко вперед, а возможно, спровоцирует мировой кризис.

О важности простых чисел в математике говорит основная теорема арифметики: любое число можно представить в виде произведения простых множителей. Вся математика опирается на простые числа, но закономерности появления их в натуральном ряду так никто еще и не объяснил.

Математики всего мира не раз пытались найти ту формулу, при вычислениях по которой всегда получались бы простые числа. Если в этой фразе отбросить слово «всегда», то таких формул удастся привести довольно много, например: f(n)=n2 + n + 17; f(n) = n2 – n + 41; f(n) = 2n2 + 29.

Последовательно подставляя, например, в первую формулу вместо n натуральные числа, получим числа 19, 23, 29, 37. Все они являются простыми, но торжествовать рано — уже f(16) = 289 = 172, то есть получилось составное число.

Эти формулы порождают много простых чисел, но это «много» еще не означает «всегда»! Более того, можно доказать, что никакой многочлен с целыми коэффициентами не может для всякого натурального значения n равняться простому числу.

На самом деле для простых чисел не существует никакой формулы, никакой комбинации алгебраических операций над n, выполняя которые можно было бы получить очередное n­ное простое число. Многие люди впадали в заблуждение на этот счет, достигнув некоторых первоначальных успехов.

Полотно Улама

Так чем же объясняются закономерности в распределении простых чисел? Пока ответа на этот вопрос нет, но все же есть множество визуальных наблюдений. Одну из таких закономерностей случайно открыл Станислав Улам, американский математик, поляк по происхождению. Сидя как­то на скучной лекции, он, ни о чем не думая, начал рисовать решетку из горизонтальных и вертикальных линий. В одной из полученных таким образом клеток он поставил 1 и стал нумеровать остальные клетки по спирали, расходящейся от первой клетки:

5 4 3

6 1 2

7 8 9

Когда спираль совершила несколько оборотов, Улам начал обводить кружками простые числа, не преследуя никакой определенной цели. Однако вскоре заметил, как на его глазах возникает довольно любопытная закономерность. Откуда ни возьмись, стали появляться прямые линии. Улам, конечно, сразу понял, что такие линии говорят о закономерности, которую можно облечь в формулу для простых чисел.

Составление формулы простого числа

Чтобы увидеть всё своими глазами, а не полагаться только на слова, составим простую компьютерную программу, которая бы рисовала точку в центре, а вокруг нее по спирали располагала бы все числа натурального ряда. Программа будет отмечать черным цветом точки, соответствующие простым числам, а серыми — составные. Вот что мы получим:

У самого центра диаграммы одна такая закономерность пролегает сверху вниз и слева направо. Она состоит из последовательности чисел: 7, 23, 47, 79… Оказывается, эту последовательность можно описать квадратичной функцией р = 4х2 + 4х – 1.

С помощью этого графика можно задать формулой любую последовательность простых чисел. Рассмотрим, например, последовательность, берущую свое начало из точки 5 и идущую справа налево сверху вниз. Следующее число в этой последовательности 19, затем идут 41, 71… Попробуем описать ее рекуррентной формулой. Для этого сначала рассмотрим каждый квадрат, состоящий из точек. У любого такого квадрата на восемь точек больше, чем у вложенного в него, — это очень легко доказать. Значит, разность между любыми двумя точками, лежащими в соседних квадратах по одному правилу, будет увеличиваться на восемь по сравнению с предыдущими. Для определенности за отношение «лежать по одному правилу» примем точки, лежащие в соседних квадратах, причем из точки, лежащей в меньшем квадрате,  можно перейти к точке из большего квадрата, если перейти в другой квадрат по кратчайшему расстоянию и затем сместиться на число t, где t целое, причем t — постоянное число для данного правила. В нашем случае t = 1.

Если разность между точками, лежащими в 1­м и 2­м квадратах от центра, равна 14, то разность между точками 2­го и 3­го квадратов возрастет на 8 и будет равна 22. Теперь можно составить формулу: следующий член последовательности будет отличаться от предыдущего на 14 + 8·n, где n — номер члена последовательности, то есть номер квадрата от центра. Если считать 5 нулевым членом и каждый член больше предыдущего на 8·(n – 1), где n — номер квадрата, то получим:

x_n = x_{n – 1} + 14 + 8(n – 1)

x_n = x_{n – 1} + 8n + 6

Это и есть формула данной последовательности.

И таким образом можно составить сколько угодно формул последовательностей простых чисел, но всегда на каком­то номере окажется, что число вовсе не простое. Примечательно, что если в качестве начальной точки взять число не 1, а 41, то мы увидим последовательность, состоящую из 41 простого числа!

Никакая целая рациональная функция от х с целыми коэффициентами не может для любого натурального значения х равняться простому числу (теорема Гольбаха).

САПР и графика 1`2010

Алгоритм нахождения простых чисел

Оптимизация алгоритма нахождения простых чисел

2 3 5 7 11 13 17 19 23 29 31… $250.000…

Дело было давно, в университете, когда мы начали изучать язык программирования Pascal и домашним заданием стало создание алгоритма нахождения простых чисел.

Алгоритм был придуман и тутже реализован на изучаемом языке. Программа запрашивала у пользователя число N и искала все простые числа до N включительно. После первого успешного теста сразу же возникло непреодолимое желание ввести N = «много». Программа работала, но не так быстро как хотелось бы. Естественно, дело было в многочисленных проверках (порядка N*N/2), поэтому пришлось избавиться от лишних. В итоге получилось 5 похожих алгоритмов каждый из которых работал быстре предыдущего. Недавно захотелось их вспомнить и реализовать, но на этот раз на Python.

Итак, поехали. Первый алгоритм, ударивший в студенческую голову, продемонстрирован в Листинге 1.

# Листинг 1
# вводим N
n = input("n=")
# создаем пустой список для хранения простых чисел
lst = []
# в k будем хранить количество делителей
k = 0
# пробегаем все числа от 2 до N
for i in xrange(2, n+1):
    # пробегаем все числа от 2 до текущего
    for j in xrange(2, i):
        # ищем количество делителей
        if i % j == 0:
            k = k + 1
    # если делителей нет, добавляем число в список
    if k == 0:
        lst.append(i)
    else:
        k = 0
# выводим на экран список
print lst

Очень быстро понимаешь, что в подсчете делителей каждого числа нет никакой надобности и поэтому переменную k можно освободить от своих обязанностей. Действительно, если хотябы один делитель имеется, то число уже не простое. Смотрим Листинг 2.

# Листинг 2
n = input("n=")
lst = []
for i in xrange(2, n+1):
    for j in xrange(2, i):
        if i % j == 0:
            # если делитель найден, число не простое.
            break
    else:
        lst.append(i)
print lst

Конструкция break позволяет нам завершить выполнение внутреннего цикла и перейти к следующей итерации внешнего.
Далее возникает вопрос: «а зачем делить на 4, если на 2 число не делится?». Приходим к выводу, что искать делители нужно только среди простых чисел не превышающих делимое. Наш алгоритм превращается в… см. Листинг 3.

# Листинг 3
n = input("n=")
lst=[]
for i in xrange(2, n+1):
    # пробегаем по списку (lst) простых чисел
    for j in lst:
        if i % j == 0:
            break
    else:
        lst.append(i)
print lst

А потом вспоминаем теорию чисел и понимаем, что переберать надо только числа, не превосходящие корня из искомого. К примеру, если число M имеет делитель pi, то имеется делитель qi, такой, что pi * qi = M. То есть, чтобы найти пару, достаточно найти меньшее. Среди всех пар, предполагаемая пара с максимальным наименьшим — это пара с равными pi и qi, то есть pi * pi = M => pi = sqrt(M). Смотрим Листинг 4.

# Листинг 4 
from math import sqrt
n = input("n=")
lst=[]
for i in xrange(2, n+1):
    for j in lst:
        if j > int((sqrt(i)) + 1):
            lst.append(i)
            break
        if (i % j == 0):
            break
    else:
        lst.append(i)
print lst

Код из Листинга 4 при N=10000 выполняется примерно в 1000 раз быстрее, чем самый первый вариант. Есть еще один «ускоритель», проверять только те числа, которые заканчиваются на 1, 3, 7 или 9 (так как остальные очевидно делятся на 2 или 5). Наблюдаем Листинг 5.

# Листинг 5
from math import sqrt
n = input("n=")
lst=[]
for i in xrange(2, n+1):
    if (i > 10):
        if (i%2==0) or (i%10==5):
            continue
    for j in lst:
        if j > int((sqrt(i)) + 1):
            lst.append(i)
            break
        if (i % j == 0):
            break
    else:
        lst.append(i)
print lst

В следствии незначительного изменения Листинга 5 получаем небольшую прибавку в скорости:

# Листинг 6
from math import sqrt
n = input("n=")
lst=[2]
for i in xrange(3, n+1, 2):
    if (i > 10) and (i%10==5):
        continue
    for j in lst:
        if j > int((sqrt(i)) + 1):
            lst.append(i)
            break
        if (i % j == 0):
            break
    else:
        lst.append(i)
print lst

Итого: Программа из последнего листинга выполняется, примерно, в 1300 раз быстрее первоначального варианта.
Я не ставил перед собой задачи написать программу максимально быстро решающую данную задачу, это скорее демонстрация начинающим программистам того, что правильно составленный алгоритм играет далеко не последнюю роль в оптимизации Ваших программ.

P.S.
Благодаря замечаниям получаем Листинг 7:

# Листинг 7
n = input("n=")
lst=[2]
for i in xrange(3, n+1, 2):
	if (i > 10) and (i%10==5):
		continue
	for j in lst:
		if j*j-1 > i:
			lst.append(i)
			break
		if (i % j == 0):
			break
	else:
		lst.append(i)
print lst

при N=10000, поучаем время:
time 1 = 26.24
time 2 = 3.113
time 3 = 0.413
time 4 = 0.096
time 5 = 0.087
time 6 = 0.083
time 7 = 0.053

Решето Эратосфена:

# Листинг 8
n = input("n=")
a = range(n+1)
a[1] = 0
lst = []

i = 2
while i <= n:
    if a[i] != 0:
        lst.append(a[i])
        for j in xrange(i, n+1, i):
            a[j] = 0
    i += 1
print lst

Результаты при n = 1 000 000:
time 7 = 7.088
time 8 = 1.143

Знаете ответ?

In number theory, a formula for primes is a formula generating the prime numbers, exactly and without exception. No such formula which is efficiently computable is known.^{[clarification needed]} A number of constraints are known, showing what such a «formula» can and cannot be.

Formulas based on Wilson’s theorem[edit]

A simple formula is

for positive integer , where is the floor function, which rounds down to the nearest integer.
By Wilson’s theorem, is prime if and only if . Thus, when is prime, the first factor in the product becomes one, and the formula produces the prime number . But when is not prime, the first factor becomes zero and the formula produces the prime number 2.^[1]
This formula is not an efficient way to generate prime numbers because evaluating requires about multiplications and reductions modulo .

In 1964, Willans gave the formula

for the th prime number .^[2]
This formula reduces to^[3][4] ; that is, it tautologically defines as the smallest integer m for which the prime-counting function is at least n. This formula is also not efficient. In addition to the appearance of , it computes by adding up copies of ; for example, .

The articles What is an Answer? by Herbert Wilf (1982)^[5] and Formulas for Primes by Underwood Dudley (1983)^[6] have further discussion about the worthlessness of such formulas.

Formula based on a system of Diophantine equations[edit]

Because the set of primes is a computably enumerable set, by Matiyasevich’s theorem, it can be obtained from a system of Diophantine equations. Jones et al. (1976) found an explicit set of 14 Diophantine equations in 26 variables, such that a given number k + 2 is prime if and only if that system has a solution in nonnegative integers:^[7]

The 14 equations α₀, …, α₁₃ can be used to produce a prime-generating polynomial inequality in 26 variables:

That is,

is a polynomial inequality in 26 variables, and the set of prime numbers is identical to the set of positive values taken on by the left-hand side as the variables a, b, …, z range over the nonnegative integers.

A general theorem of Matiyasevich says that if a set is defined by a system of Diophantine equations, it can also be defined by a system of Diophantine equations in only 9 variables.^[8] Hence, there is a prime-generating polynomial as above with only 10 variables. However, its degree is large (in the order of 10⁴⁵). On the other hand, there also exists such a set of equations of degree only 4, but in 58 variables.^[9]

Mills’ formula[edit]

The first such formula known was established by W. H. Mills (1947), who proved that there exists a real number A such that, if

then

is a prime number for all positive integers n.^[10] If the Riemann hypothesis is true, then the smallest such A has a value of around 1.3063778838630806904686144926… (sequence A051021 in the OEIS) and is known as Mills’ constant.^[11] This value gives rise to the primes , , , … (sequence A051254 in the OEIS). Very little is known about the constant A (not even whether it is rational). This formula has no practical value, because there is no known way of calculating the constant without finding primes in the first place.

Note that there is nothing special about the floor function in the formula. Tóth proved that there also exists a constant such that

is also prime-representing for .^[12]

In the case , the value of the constant begins with 1.24055470525201424067… The first few primes generated are:

Without assuming the Riemann hypothesis, Elsholtz developed several prime-representing functions similar to those of Mills. For example, if , then is prime for all positive integers . Similarly, if , then is prime for all positive integers .^[13]

Wright’s formula[edit]

Another prime-generating formula similar to Mills’ comes from a theorem of E. M. Wright. He proved that there exists a real number α such that, if

and

for ,

then

is prime for all .^[14]
Wright gives the first seven decimal places of such a constant: . This value gives rise to the primes , , and . is even, and so is not prime. However, with , , , and are unchanged, while is a prime with 4932 digits.^[15] This sequence of primes cannot be extended beyond without knowing more digits of . Like Mills’ formula, and for the same reasons, Wright’s formula cannot be used to find primes.

A function that represents all primes[edit]

Given the constant (sequence A249270 in the OEIS), for , define the sequence

(1)

where is the floor function.
Then for , equals the th prime:
,
,
, etc.
^[16]
The initial constant given in the article is precise enough for equation (1) to generate the primes through 37, the th prime.

The exact value of that generates all primes is given by the rapidly-converging series

where is the th prime, and is the product of all primes less than . The more digits of that we know, the more primes equation (1) will generate. For example, we can use 25 terms in the series, using the 25 primes less than 100, to calculate the following more precise approximation:

This has enough digits for equation (1) to yield again the 25 primes less than 100.

As with Mills’ formula and Wright’s formula above, in order to generate a longer list of primes, we need to start by knowing more digits of the initial constant, , which in this case requires a longer list of primes in its calculation.

Plouffe’s formulas[edit]

In 2018 Simon Plouffe conjectured a set of formulas for primes. Similarly to the formula of Mills, they are of the form

where is the function rounding to the nearest integer. For example, with and , this gives 113, 367, 1607, 10177, 102217… Using and with a certain number between 0 and one half, Plouffe found that he could generate a sequence of 50 probable primes (with high probability of being prime). Presumably there exists an ε such that this formula will give an infinite sequence of actual prime numbers. The number of digits starts at 501 and increases by about 1% each time.^[17][18]

Prime formulas and polynomial functions[edit]

It is known that no non-constant polynomial function P(n) with integer coefficients exists that evaluates to a prime number for all integers n. The proof is as follows: suppose that such a polynomial existed. Then P(1) would evaluate to a prime p, so . But for any integer k, also, so cannot also be prime (as it would be divisible by p) unless it were p itself. But the only way for all k is if the polynomial function is constant.
The same reasoning shows an even stronger result: no non-constant polynomial function P(n) exists that evaluates to a prime number for almost all integers n.

Euler first noticed (in 1772) that the quadratic polynomial

is prime for the 40 integers n = 0, 1, 2, …, 39, with corresponding primes 41, 43, 47, 53, 61, 71, …, 1601. The differences between the terms are 2, 4, 6, 8, 10… For n = 40, it produces a square number, 1681, which is equal to 41 × 41, the smallest composite number for this formula for n ≥ 0. If 41 divides n, it divides P(n) too. Furthermore, since P(n) can be written as n(n + 1) + 41, if 41 divides n + 1 instead, it also divides P(n). The phenomenon is related to the Ulam spiral, which is also implicitly quadratic, and the class number; this polynomial is related to the Heegner number . There are analogous polynomials for (the lucky numbers of Euler), corresponding to other Heegner numbers.

Given a positive integer S, there may be infinitely many c such that the expression n² + n + c is always coprime to S. The integer c may be negative, in which case there is a delay before primes are produced.

It is known, based on Dirichlet’s theorem on arithmetic progressions, that linear polynomial functions produce infinitely many primes as long as a and b are relatively prime (though no such function will assume prime values for all values of n). Moreover, the Green–Tao theorem says that for any k there exists a pair of a and b, with the property that is prime for any n from 0 through k − 1. However, as of 2020, the best known result of such type is for k = 27:

is prime for all n from 0 through 26.^[19] It is not even known whether there exists a univariate polynomial of degree at least 2, that assumes an infinite number of values that are prime; see Bunyakovsky conjecture.

Possible formula using a recurrence relation[edit]

Another prime generator is defined by the recurrence relation

where gcd(x, y) denotes the greatest common divisor of x and y. The sequence of differences a_n+1 − a_n starts with 1, 1, 1, 5, 3, 1, 1, 1, 1, 11, 3, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 23, 3, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 47, 3, 1, 5, 3, … (sequence A132199 in the OEIS). Rowland (2008) proved that this sequence contains only ones and prime numbers. However, it does not contain all the prime numbers, since the terms gcd(n + 1, a_n) are always odd and so never equal to 2. 587 is the smallest prime (other than 2) not appearing in the first 10,000 outcomes that are different from 1. Nevertheless, in the same paper it was conjectured to contain all odd primes, even though it is rather inefficient.^[20]

Note that there is a trivial program that enumerates all and only the prime numbers, as well as more efficient ones, so such recurrence relations are more a matter of curiosity than of any practical use.

See also[edit]

• Prime number theorem

References[edit]

Further reading[edit]

• Regimbal, Stephen (1975), «An explicit Formula for the k-th prime number», Mathematics Magazine, Mathematical Association of America, 48 (4): 230–232, doi:10.2307/2690354, JSTOR 2690354.
• A Venugopalan. Formula for primes, twinprimes, number of primes and number of twinprimes. Proceedings of the Indian Academy of Sciences—Mathematical Sciences, Vol. 92, No 1, September 1983, pp. 49–52 errata

External links[edit]

• Eric W. Weisstein, Prime Formulas (Prime-Generating Polynomial) at MathWorld.

Простые числа – это натуральные числа, их можно разделить только на два значения: единицу и себя. К натуральным относят те, которые используются во время счета, поэтому должно выполняться требование, чтобы они были положительными и целыми. Делители также не должны быть отрицательными и дробными.

Они широко применяются в криптографии, когда необходимо закодировать важную информацию от посторонних глаз. Шифрование касается каждого человека, так как используется в создании электронной почты, банковских карт. Даже мобильная связь защищается кодами. 

Кроме того, используются на системах, защищающих транспортные средства от угонщиков, создают преграду для атак вирусов и взломов компьютерных сайтов. При попытке продолжить разложение простых чисел или определить закономерность появления, возникают новые способы математических расчетов.

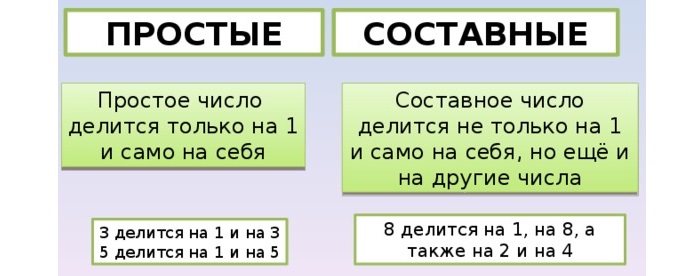
Простые и составные числа — что это такое

Математика предлагает начинать знакомиться с данными понятиями в средней школе, в 5 или в 6 классе. 

Проверка на принадлежность к определенному множеству достаточно простая:

1. Простые числа можно делить только на 1 и на такое же число. Например 3 и 7 — простые числа, 3 делится на 1 и на 3, 7 делится на 1 и на 7.

2. Составные числа можно делить не только на себя и единицу. При этом не должно получаться остатка. Они делятся на одно или несколько значений. Например, 8 и 6 относят к составным. Восьмерка делится на 1, 2, 4, 8; шестерка – на 1, 2, 3 и 6.

Определение простых чисел позволяет исключить из их ряда единицу. Она характеризуется наличием только одного делителя, не являющегося отрицательным значением. Получить ее можно, используя только один способ, умножив саму на себя.

Простые двузначные числа определяются по внешнему виду:

1. Если оканчиваются четной цифрой, то точно являются составными. То же касается и значений, имеющих больше двух знаков.

2. Если на конце находится цифра 5, то она входит в число делителей.

Такие простые способы помогают легко классифицировать многозначные показатели.

Некоторые двузначные вводят в заблуждение с первого взгляда, если оканчиваются на единицу. Кажется, что разложить на множители их невозможно. Но есть исключения, например: 21, 81. Чем дальше, тем больше отклонений от этой закономерности.

Последовательность простых чисел

Есть целые алгоритмы, помогающие получать новое, ранее неизвестное значение. 

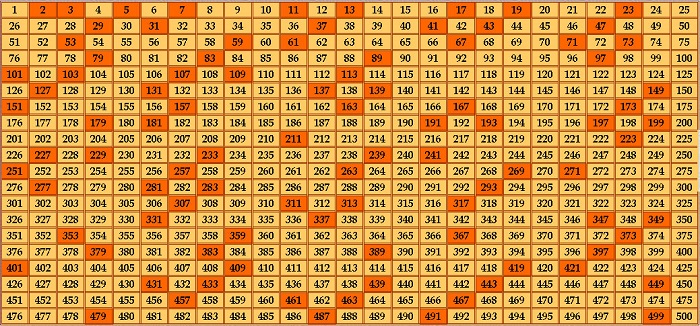
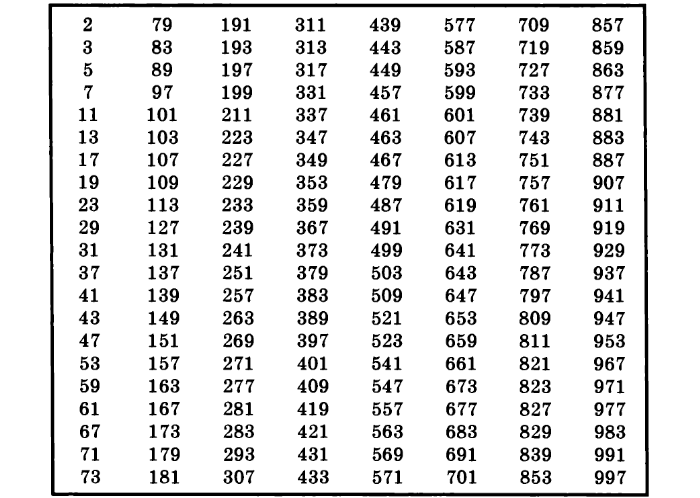
Существуют таблицы, в которых собраны найденные числа, имеющие не больше двух делителей, например, до 200, 1000 или больше. 

Последовательность можно продолжать бесконечно, начинается она так: 2, 3, 5, 7, 11, 13, 17, 19 и т. д.

Наименьшее и наибольшее простое число

Самым меньшим значением, делящимся на себя и 1, является 2. Это единственное простое значение, являющееся четным. Остальные всегда делятся на два, то есть получают третий делитель. 

Простых чисел много и их количество стремится к бесконечности, потому узнать самое большое невозможно.

Нескончаемость ряда была доказана еще до нашей эры Евклидом. Он предложил перемножить все известные исследуемые значения и прибавить к ним единицу. 

При его делении в любом случае будет оставаться остаток, то есть отнести к составным невозможно. Что противоречит тому факту, что были использованы все известные простые числа, в том числе и самое большое. Значит, предположение о конечности ряда является неверным.

В настоящее время известно значение, имеющее около 25 миллионов знаков. Оно относится к наибольшему из открытых наукой, это 2^{82 589 933}

Множество простых чисел

Множествами называются совокупности элементов, объединенных в одно целое общими свойствами. 

Для изучаемых объектов к ним относятся:

• принадлежность к натуральным;

• наличие максимум двух делителей.

Простые числа можно определить, используя решето Эратосфена. Нужно выписать в ряд все значения, с которыми предстоит работать. Выбрать самое маленькое и вычеркнуть его, затем продолжать действие, убирая кратные ему. 

Например, в ряду от 1 до 100 первым таким объектом будет 2. Поэтому и вычеркивать нужно значения, кратные двойке, то есть те, которые делятся на нее. 

По окончании из оставшихся выбрать новое простое, искать кратные ему и также убирать. Повторять, пока это представляется возможным. 

В итоге, все составные окажутся зачеркнутыми.

Эратосфен использовал свое открытие следующим образом. Он брал папирус, записывал на нем необходимые значения, при отборе прокалывал неподходящие острым предметом (отсюда название «решето Эратосфена»). Поэтому они как будто просеивались через сито, и в списке оставались видимыми только необходимые.

Некоторые свойства простых чисел

Выделяют свойства, объединенные в теоремы, постулаты. Многие являются основой математических правил, используемых в настоящее время. 

Изучением занимается теория чисел, при использовании формул простые числа обозначаются буквой n.

Известны следующие правила:

1. Если рассматривать два простых числа (n), одно из которых делится на другое, то можно утверждать, что они равны.

2. Все являются нечетными, за исключением двойки.

3. Можно выделить пары, разница между которым равна 2. При их сложении получается значение, кратное трем. Их так и называют парными или близнецами. Исключение составляют две первые цифры в ряду, 3 и 5, так как сумму, полученную при их сложении, нельзя разделить на 3.

4. Для каждого натурального значения (N), большего единицы, существует n, превышающее его. При этом удвоенное натуральное будет больше n.

5. Если одно из двух N делится на n, то их произведение также будет делиться на него.

6. Любое N, за исключением единицы, можно отнести к n или представить в виде их произведения.

7. Если взять составное число и разложить его на множители n, то среди них окажется один, квадрат которого будет меньше первоначального составного.

8. Некоторые n имеют пары, которые можно найти, перевернув n наоборот. Например, 13 и 31, 37 и 73. То же самое касается трехзначных n: 107 и 701, 709 и 907.

9. Если N возвести в степень, представленную n, а затем вычесть N, то полученное значение будет делиться на используемое n. Это правило представляет собой малую теорему Ферма.

Действия с простыми числами

Можно использовать разные арифметические действия, складывать, умножать, вычитать, делить. Простые числа могут являться основанием и показателем степени. 

Извлечь корень из них невозможно.

Таблица простых чисел до 1000

Таблица простых числе до 10000

Еще статьи по математике:

• Дружественные числа