Как составить практическую задачу - Исправление недочетов и поиск решений вместе с Examum.ru

Авторы
Резюме
Файлы
Ключевые слова
Литература

Воистинова Г.Х.

1

Солощенко М.Ю.

1 Стерлитамакский филиал ФГБОУ ВПО «Башкирский государственный университет»

В данной статье проведен краткий анализ литературы, посвященной актуальной проблеме составления и решения задач, в частности, практических задач. При конструировании задач перед педагогом возникает два важных вопроса: зачем учить составлять задачи и как составлять такие задачи? В ходе проведенного исследования было выявлено, что наибольшую трудность при решении практических задач вызывают задачи, математическими моделями которых являются задачи на построение в силу специфики их решения: использование чертежных инструментов, выделение четырех этапов (анализ, построение, доказательство, исследование) и т.п. Авторами предложен механизм составления геометрических задач на построение с практическим содержанием, раскрытый на конкретных примерах с подробным решением. В статье продемонстрирована замена практической задачи на математическую и обратно – математической задачи на практическую.

решение задачи

составление задачи

задача на построение

практическая задача

1. Воистинова Г.Х. Обучение решению задач на построение с практическим содержанием: Учебное пособие по курсу теории и методики обучения математике для студентов 4-5 кур-сов / Г.Х. Воистинова, М.Ю. Солощенко. – Уфа: РИЦ БашГУ, 2007 – 80 с.

2. Воистинова Г.Х. Решение задач на построение с практическим содержанием: Моногра-фия / Г.Х. Воистинова М.Ю. Солощенко. – Стерлитамак: Стерлитамакский филиал БашГУ, 2013 – 148 с.

3. Из материалов рукописных работ Р.Г. Хазанкина // Математика в школе. – 1987. – № 4. – С. 16.

4. Канин Е.С. Развитие темы задачи // Математика в школе. – 1991. – № 3. – С. 8-12.

5. Солощенко М.Ю. Задачи межпредметного характера в школьном курсе математики: учебное пособие для студ. пед. вузов 3-5-х курсов. – Уфа: РИЦ БашГУ, 2009. – 171 с.

Введение

Важнейшим средством формирования научного мировоззрения студентов, на наш взгляд, является решение и самостоятельное составление задач. По мнению Р.Г. Хазанкина [3], при решении каждой задачи необходимо: обобщать, анализировать, рассматривать варианты, строить контрпримеры, составлять свои задачи – не только аналогичные разработанным, но и вытекающие из правил, формул, теорем и т.д.

При анализе решения полезно устанавливать возможность обобщения данной задачи, выявлять ее особенности, сопоставлять решение данной задачи с ранее решенными, составлять и решать некоторые другие (в том числе и практические) задачи, «порожденные» разобранной, или, иначе, задачи, развивающие тему данной задачи. Е.С. Канин, в статье «Развитие темы задачи» [4], к ним относит задачи, которые получаются из исходной: заменой части данных в исходной задаче другими данными без замены заключения задачи; при обобщении данных и искомых; путем специализации данных и искомых; добавлением новых заключений при сохранении данных; заменой части данных исходной задачи ее искомыми, то есть путем обобщения задачи; составлением сложных задач из более простых; заменой одних объектов другими без изменения искомых (переформулировка задачи).

В методическом отношении развитие темы, включающее и составление задач, особенно ценно тем, что приучает решающих к конструированию задач, что является одним из основных приемов поиска решения.

Развитие темы задачи в качестве заключительного этапа работы над ней особенно ценно при творческом подходе преподавателя к обучению решению задач.

Приведем примеры аналогичных задач.

Задача 1. (математическая). Провести окружность, касающуюся трех данных несовпадающих прямых BC, CA, AB.

Задача 1′. (практическая). На карте города изображены три пересекающиеся дороги BC, CA, AB. Постройте кольцевую дорогу, касающуюся трех данных дорог.

Задача 2. (математическая). К данной окружности построить касательную, проходящую через данную точку вне окружности.

Задача 2′. (практическая). Пруд, находящийся неподалеку от деревни, имеет округлую форму. Дорожникам надо построить прямую дорогу к пруду от деревни так, чтобы дорога прилегала к пруду.

Задача 3. (математическая). Даны прямая a и точка M, не лежащая на ней. Постройте прямую, проходящую через точку M и перпендикулярную к прямой a.

Задача 3′. (практическая). Через данное село и шоссе, не проходящее через село, построить проселочную дорогу так, чтобы расстояние от населенного пункта до шоссе были минимальными.

Простое применение аналогии дает задачу, подобную, однопорядковую с исходной. При составлении задач по аналогии может случиться, что формально вычисленный ответ не будет иметь смысла. Поэтому студенты (учащиеся) должны проверять ответы, найденные при решении составленных ими задач. По мнению Е.С. Канина [4], составление таких задач помогает учащимся лучше понять структуру математических задач, т.е. существенно углубляет и расширяет математические представления и знания учащихся.

При замене практической задачи на математическую (и обратно – математической на практическую), решаются важные методические задачи: решающие лучше усваивают структуру задачи; взаимосвязь данных; данных и искомых; усваивают способ решения задачи.

Составление и решение задач, порожденных данной, – это творческая деятельность. Место этой деятельности чаще всего на стадии завершающего, обобщающего обучения. Важно время от времени обращаться к составлению задач, родственных данной математической задаче.

При самостоятельном составлении задачи решающий должен осознанно применять соответствующие математические термины, правила и законы. Ему приходится самому анализировать пройденный материал, т.к. при выполнении упражнения на составление задачи необходимо оперировать фактами и понятиями, которые были изложены в этом материале.

Прежде чем говорить непосредственно о методических рекомендациях по составлению задач практического характера мы остановимся на проблеме составления задач вообще. В рамках этой проблемы перед нами встает ряд вопросов:

Зачем учить составлять задачи?
Как составлять задачи?

Попытаемся ответить на эти вопросы.

Все рассуждения, приведенные выше, по поводу составления задач, можно отнести к ответу на первый вопрос. Так же самостоятельно составленная задача запоминается полнее и прочнее, чем просто решенная; составленную самим задачу решить легче, нежели готовую, чужую задачу.

Человек только тогда разберется в проблеме, когда он сам научится ее ставить. Дело в том, что составление задач часто требует проведения рассуждений, которые при решении заданных задач не выполняются. Составление задач служит развитию творческого и логического мышления, повышает интерес к учебе.

Перейдем к самому главному вопросу нашего исследования: как составлять задачи?

Составлению задач посвятили свои труды такие ученые, как Д. Пойа, Ю.М. Колягин, П.М. Эрдниев и другие. Однако и у них нет конкретных рекомендаций по составлению задач, даются лишь общие рассуждения, демонстрируемые на частных примерах. Одним из авторов [5] данной монографии разработаны методические рекомендации по составлению задач межпредметного характера на основе графиков и тестов. Таким образом, можно сделать вывод, что проблема составления практических задач на построение не достаточно разработана в научно-методической литературе.

Опираясь на психолого–педагогическую и методическую литературу, и передовой опыт учителей, нами [1, 2], сделана попытка разработать методические рекомендации по составлению задач практического характера, соответствующих задачам на построение.

Механизм составления таких задач может быть описан с помощью следующей последовательности действий:

Выделите геометрические фигуры, о которых идет речь в условии задачи на построение.
Какую фигуру требуется построить в заключении задачи на построение?
Определите, как связаны между собой фигуры (отношение, принадлежность и т.п.).
Поставьте разумные вопросы, связанные с окружающей нас действительностью, в ответах на которые будут использованы данные геометрические фигуры.
Сформулируйте условие практической задачи.

Сказанное поясним на примерах.

Возвращаясь к предложенным выше задачам 1–3, рассмотрим, какие геометрические фигуры используются в них, и установим отношения между этими фигурами. В задаче 1 следующие геометрические фигуры: три данные несовпадающие прямые BC, CA, AB и искомая окружность; зависимость – окружность, касающаяся данных прямых. В задаче 2 геометрические фигуры: окружность, точка вне окружности и искомая касательная; зависимость – касательная к окружности, проходящая через данную точку. В задаче 3 геометрические фигуры: прямая а, точка M, не лежащая на ней, и искомая прямая b; зависимость – прямая b, проходящая через точку M перпендикулярно к прямой a.

Например, разумными вопросами к данным задачам могут быть следующие:

Образами каких реальных объектов могут служить следующие геометрические фигуры: точки, прямые, окружности?
Какие зависимости между реальными объектами можно заменить отношениями принадлежности, равноудаленности, касания и т.п.?

Следует отметить, что предложенные вопросы позволяют к одной и той же математической задаче сформулировать несколько практических задач. Например, к задаче 1 можно, кроме предложенной задачи 1′, сформулировать еще одну:

Задача 1». (практическая). Построить пляж приблизительно круглой формы, прилегающий (касающийся) трех пересекающихся рек.

Но прежде чем, переходить к составлению и решению задач практического характера, нужно хорошо усвоить тему «Геометрические построения» и научиться решать планиметрические задачи на построение циркулем и линейкой.

Далее приведем задачи практического характера, составленные авторами статьи.

Задача 4. (математическая). Постройте квадрат, две противоположные вершины которого лежат на прямой p, а две другие – на двух окружностях e и f.

По условию задачи даны две окружности e, f и прямая p (рис. 1, а).

Анализ: Предположим, что задача решена, искомый квадрат построен (рис. 1, б).

По условию две его вершины А и С лежат на прямой р, а две другие вершины B и D соответственно на окружностях e и f. Так как диагонали квадрата являются его осями симметрии, то вершины B и D симметричны относительно прямой р. Поэтому если найти одну из них, например D, то легко построить точку B.

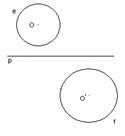
рис. 1, а. Данные окружности

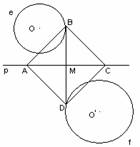
рис. 1, б. Искомый квадрат

Так как точка B лежит на окружности e, то точка D, симметричная точке B, лежит на окружности e1, симметричной окружности e. Кроме того, точка D по условию лежит на окружности f. Таким образом, точка D – есть точка пересечения двух окружностей e1 и f. Построив D, можно построить симметричную ей точку В, лежащую на окружности е. Отложив МА=МС=МD (где М – точка пересечения отрезка DВ с прямой р), получим искомый квадрат.

Построение:1) Строим окружность, симметричную относительно р (рис. 1, в).

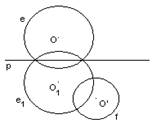
рис. 1, в. Построение симметричной окружности

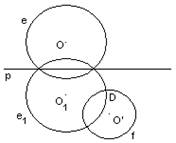
рис. 1, г. Построение точки пересечения

2) Находим точку D пересечения окружностей e1 и f (рис. 1, г).

3) Проведем DM перпендикулярно р. B – точка пересечения DM с окружностью е (рис. 1, д).

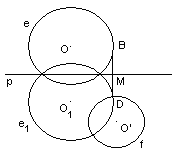
рис. 1, д. Построение перпендикуляра

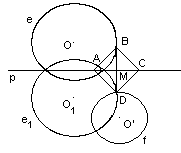
рис. 1, е. Построение искомого квадрата

4) Отложим МА=МС=МD. ABCD – искомый квадрат (рис. 1, е).

5) Взяв вторую точку D1 пересечения окружностей e1 и f, аналогично построим второй квадрат A1B1C1D1, удовлетворяющий условию задачи (рис. 1, ж).

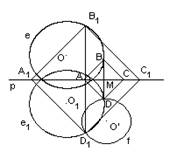
рис. 1, ж. Построение второго квадрата

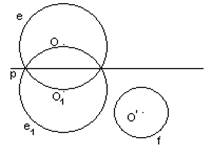
рис. 1, з. Исследование: нет решений

Доказательство: Диагонали четырехугольника ABCD в точке пересечения делятся пополам. Следовательно, ABCD – параллелограмм. Т.к. АС перпендикулярно BD, то ABCD – ромб. Поскольку АС= BD, то ABCD – прямоугольник. Поэтому ABCD – квадрат. Вершины его удовлетворяют условию задачи. Аналогично A1B1C1D1 – искомый квадрат.

Исследование: а) Окружности e1 и f общих точек не имеют – решений нет (рис.1, з);

б) Окружности e1 и f касаются – единственное решение (рис. 1, и).

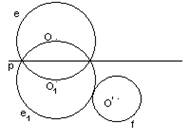
рис. 1, и. Исследование: единственное решение

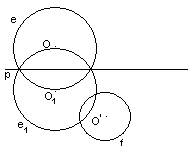
рис. 1, к. Исследование: два решения

в) Окружности e1 и f пересекаются – два решения (рис. 1, к).

г) Окружности e1 и f совпадают (это возможно тогда, когда окружности e и f симметричны относительно р) – искомых квадратов бесконечно много (рис. 1, л).

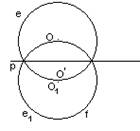
рис. 1, л. Исследование: бесконечное множество решений

К предложенной задаче можно сформулировать аналогичную ей практическую задачу:

Задача 4′. (практическая). Официанту поручили засервировать стол в ресторане. Между двумя тарелками он положил салфетку ABCD, так что две ее противоположные вершины лежат на прямой, не пересекающей эти тарелки, а две другие – на краях тарелок. Причем точки касания двух вершин салфетки и тарелки известны. Определить местоположение салфетки.

Задача 5. (математическая). Построить прямую, равноудаленную от трех данных точек.

В условии задачи даны три точки A, B, C (рис. 2, а). Требуется построить прямую, равноудаленную от данных точек.

рис. 2, а. Данные точки

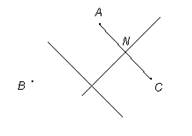
рис. 2, б. Искомая прямая

Анализ: Пусть искомая прямая построена. Прямая, равноудаленная от точек A и C, является либо серединным перпендикуляром к AC, либо параллельна прямой АС (рис. 2, б).

Аналогично для точек А, В и В, С. Прямая равноудаленная от всех точек А, В, С или проходит через Р и N – это будет прямая РN, или проходит через Р и параллельна АС – это будет прямая РM, или проходит через N и параллельна АВ – это будет прямая NM (рис. 2, в).

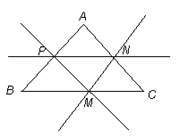
рис. 2, в. Прямые, равноудаленные от данных точек

То есть искомые прямые есть средние линии треугольника АВС. Отсюда ясно построение и доказательство.

Исследование: 1) если точки А, В, С не лежат на одной прямой, задача имеет три решения; 2) если точки А, В, С лежат на одной прямой, то решением будут все прямые, параллельные прямой, содержащей A, B, C, т.е. задача имеет бесконечное множество решений.

К предложенной задаче можно сформулировать аналогичную ей практическую задачу:

Задача 5′. (практическая). Построить автомобильную трассу так, чтобы путь от трех данных деревень до нее был одинаковым.

Данного рода работа может идти и в обратном направлении: к предложенной практической задаче сформулировать задачу на построение.

Приведем для примера ряд таких задач без рассмотрения их решения.

Задача 6′. (практическая). Кукурузное поле имеет квадратную форму. Нужно увеличить посевную площадь в 2 раза под эту культуру, не меняя формы поля.

Задача 6. (математическая). Построить квадрат, площадь которого вдвое больше площади данного квадрата.

Задача 7′. (практическая). Нужно построить каркас крыши дома треугольной формы, если известны середины его сторон.

Задача 7. (математическая). Построить треугольник, если даны середины его сторон.

Задача 8′. (практическая). Две автострады пересекаются под данным углом. На дороге, которая равноудалена от двух шоссе, расположена АЗС. Дорожникам нужно проложить асфальтную дорожку, соединяющую автостраду и проходящую через АЗС, если в плане заранее установлена её длина.

Задача 8. (математическая). Дан угол и точка на его биссектрисе. Требуется через данную точку провести прямую так, чтобы точки ее пересечения со сторонами данного угла определили отрезок данной длины.

В заключении отметим, что предложенный механизм составления геометрических задач на построение с практическим содержанием, способствует лучшему усвоению процесса поиска решения задач в целом и на построение, в частности.

Рецензенты:

Гусев В.А., д.п.н., профессор, заведующий кафедрой теории и методики обучения математике Московского педагогического государственного университета, г. Москва.

Михайлов П.Н., д.ф.-м.н., профессор, ученый секретарь ГАНУ «Институт прикладных исследований республики Башкортостан», г. Стерлитамак.

Библиографическая ссылка

Воистинова Г.Х., Солощенко М.Ю. СОСТАВЛЕНИЕ И РЕШЕНИЕ ПРАКТИЧЕСКИХ ЗАДАЧ НА ПОСТРОЕНИЕ // Современные проблемы науки и образования. – 2013. – № 6.
;

URL: https://science-education.ru/ru/article/view?id=10748 (дата обращения: 26.05.2023).

Предлагаем вашему вниманию журналы, издающиеся в издательстве «Академия Естествознания»

(Высокий импакт-фактор РИНЦ, тематика журналов охватывает все научные направления)

Источник

Прикладная направленность обучения математике
предполагает ориентацию его содержания и
методов на тесную связь с жизнью, основами других
наук, на подготовку школьников к использованию
математических знаний в предстоящей
профессиональной деятельности, на широкое
применение в процессе обучения
электронно-вычислительной технике. Практическая
направленность обучения математике
предусматривает ориентацию его содержания и
методов на изучение математической теории в
процессе решения задач, на формирование у
школьников прочих навыков самостоятельной
деятельности. Прикладная и практическая
направленность неразрывно переплетаются в
учебно-воспитательном процессе.

Проблемой прикладной направленности обучения
математике в курсе средней школы занимались и
математики и методисты: Г.Д. Глейзер, В.А. Гусев,
Г.В. Дорофеев, Н.Я. Виленкин и др. Пути реализации
прикладной и практической направленности
обучения математике чрезвычайно широкая
методическая проблема. Одним из основных
средств, применение которого создает хорошие
условия для достижения данной цели, являются
задачи с практико-ориентированным содержанием.
Содержание и структура экзаменационных работ
ЕГЭ и ГИА по математике содержат задания, которые
дают возможность полно применять умения по
использованию приобретенных знаний в
практической деятельности и повседневной жизни.
Поэтому прикладная направленность в обучении
математике имеет практическую ценность для
учащихся в развитии математической
компетентности.

В федеральном компоненте государственного
стандарта основного и среднего (полного) общего
образования сформулированы требования к уровню
подготовки выпускников, которыми принято
руководствоваться при характеристике уровня
математической компетентности: “Использовать
приобретённые знания и умения в практической
жизни для:

— практических расчётов по формулам, включая
формулы, содержащие степени, радикалы, логарифмы
и тригонометрические функции;

— построения и исследования простейших
математических моделей;

— описания и исследования с помощью функций
реальных зависимостей, представления их
графически; интерпретации графиков реальных
процессов;

— решения геометрических, физических,
экономических, юридических и других прикладных
задач, в том числе задач на нахождение
наибольшего и наименьшего значений с
применением аппарата математического анализа;

— анализа реальных числовых данных,
представленных в виде диаграмм, графиков,
анализа информации статистического характера;

— моделирования несложных практических
ситуаций на основе изученных формул и свойств
фигур; вычисления длин, площадей и объёмов
реальных объектов при решении практических
задач, используя при необходимости справочники и
вычислительные устройства”[1]. Для формирования
и проверки сформированности компетентностей
необходимо разрабатывать специальные (отличные
от традиционных) задания и задачи. Анализ
литературы показал, что сейчас активно ведется
работа в этом направлении, хотя разные авторы
по-разному называют задачи: компетентностные,
контекстные, ситуационные, сюжетные,
практико-направленные,
компетентностно-ориентированные,
учебно-практические позволяющие проверять
уровень сформированности различных компетенций.
Мы используем термин “практико-ориентированные
задачи”, учитывая их целевое назначение в
процессе обучения.

Под практико-ориентированными задачами
понимают задачи из окружающей действительности,
связанные с формированием практических навыков,
необходимых в повседневной жизни, в том числе с
использованием материалов краеведения,
элементов производственных процессов.

Цель этих задач – формирование умений
действовать в социально-значимой ситуации. Они
базируются на знаниях и умениях, но требуют
умения применять накопленные знания в
практической деятельности. Назначение
практико-ориентированных задач – “окунуть” в
решение “жизненной” задачи. Важными
отличительными особенностями
практико-ориентированных задач от стандартных
математических (предметных, межпредметных,
прикладных) являются:

— значимость (познавательная, профессиональная,
общекультурная, социальная) получаемого
результата, что обеспечивает познавательную
мотивацию учащегося;

— условие задачи сформулировано как сюжет,
ситуация или проблема, для разрешения которой
необходимо использовать знания из разных
разделов основного предмета – математики, из
другого предмета или из жизни, на которые нет
явного указания в тексте задачи;

— информация и данные в задаче могут быть
представлены в различной форме (рисунок, таблица,
схема, диаграмма, график и т.д.), что потребует
распознавания объектов;

— указание (явное или неявное) области
применения результата, полученного при решении
задачи.

Кроме выделенных четырех обязательных
характеристических особенностей,
практико-ориентированные задачи имеют
следующие:

по структуре эти задачи – нестандартные, т.е. в
структуре задачи неопределенны некоторые из ее
компонентов;
наличие избыточных, недостающих или
противоречивых данных в условии задачи, что
приводит к объемной формулировке условия;
наличие нескольких способов решения (различная
степень рациональности), причем данные способы
могут быть неизвестны учащимся, и их потребуется
сконструировать.

Мы выделили три уровня сложности
практико-ориентированных задач и их связь с
уровнем математической компетентности (см.
таблица 3).

Таблица 3

Уровни сложности
практико-ориентированных задач

Уровень	Практико-ориентированная задача	Соответствие уровню компетентности
1 уровень	Для решения требуется один теоретический факт при разрешении практической ситуации.	1 уровень – уровень воспроизведения
2 уровень	Для решения требуется комбинация нескольких математических идей при разрешении практической ситуации, применяются знания из разных разделов математики, личные наблюдения.	2 уровень – уровень связи
3 уровень	Для решения требуется исследовательский подход при построении математической модели ситуации, изучении нового материала, поиска нескольких способов решения одной задачи.	3 уровень – уровень размышления

Анализ ситуаций, возникающих в повседневной
жизни, для разрешения которых требуются знания и
умения, формируемые при обучении математике,
показывают, что перечень необходимых для этого
предметных умений невелик:

умение проводить вычисления, включая
округление и оценку результатов действий,
использовать для подсчётов известные формулы;
умение извлечь и проинтерпретировать
информацию, представленную в различной форме
(таблиц, диаграмм, графиков, схем и др.);
умение применять знание элементов статистики и
вероятности для характеристики несложных
реальных явлений и процессов;
умение вычислять длины, площади и объёмы
реальных объектов при решении практических
задач.

Указанные выше результаты обучения
формируются в основном в 5-9 классах, а овладение
более сложными математическими методами
происходит в старшей школе.

Определим структуру практико-ориентированной
задачи. За основу возьмём структуру задач
предлагаемых в тестах PISA.

1) Стимул погружает в контекст задания и
мотивирует на его выполнение. Стимул должен быть
настолько кратким, насколько это возможно. Он
должен содержать только ту информацию, которая
помогает заинтересовать обучающегося в
выполнении задания или облегчает понимание
задачной формулировки, следующей за стимулом.
Если описание ситуации содержательно важно для
выполнения учащихся задания, оно играет в
структуре практико-ориентированного задания
роль одного из источников информации и
размещается после задачной формулировки.

2) Задачная формулировка точно указывает на
деятельность учащегося, необходимую для
выполнения задания. Задачная формулировка не
может допускать различных толкований.

3) Источник информации содержит информацию,
необходимую для успешной деятельности учащегося
по выполнению задания. Другими словами, он
является ресурсом для деятельности учащегося.
Поэтому главное требование, предъявляемое к
источнику, чтобы он был необходимым и
достаточным для выполнения заданной
деятельности. Чтобы практико-ориентированное
задание было надежным, преподаватель должен быть
уверен, что успешность обучающегося не зависит
от того, располагает ли он тем или иным знанием. В
отдельных случаях преподаватель может
предлагать задание, которое основывается не
только на внешних информационных ресурсах, но и
на внутренних – программном содержании, которое
было усвоено обучающимися. Предлагая такое
задание, преподаватель должен, во-первых,
предварительно убедиться (например, с помощью
теста), что знания учащимися усвоены, во-вторых,
перечислить, на какие предметные знания
обучающийся должен опираться при выполнении
задания.

4) Инструмент проверки:

— модельный ответ – перечень вероятных верных и
частично верных ответов для задания открытого
типа с заданной структурой ответа;

— ключ – эталон результата выполнения учащимся
задания закрытого типа;

— наблюдения – способ детализации критериев
оценки процесса деятельности учащегося по
выполнению задания.

Каждая составляющая практико-ориентированного
задания подчинена тому, что это задание должно
организовать деятельность учащегося, а не
воспроизведение им информации или отдельных
действий.

Анализ задачников по элементарной математике и
другой литературы показал, что
практико-ориентированных задач недостаточно,
поэтому нами были разработаны пути получения и
способы конструирования таких задач. (Схема 1)

Схема 1

В качестве источника практико-ориентированных
задач можно использовать задания, предлагаемые в
тестах PISA, исследованиях TIMSS и в
контрольно-измерительных материалах для
итоговой аттестации выпускников основной и
средней школы. В современных учебниках немного
практико-ориентированных задач (в основном это
задачи первого уровня), но на базе имеющихся
заданий можно разработать свои задания, т. е.
“преобразовать” математическую задачу [2].
Возможны два варианта этой работы: под имеющуюся
ситуацию выделить математические факты или под
конкретную задачу подобрать ситуацию из жизни.
Например, при изучении темы “Единицы измерения
площадей” в 5 классе предложить учащимся
определить, сколько краски понадобится для
покраски пола кабинета математики,
предварительно решив задачу №762 из учебника [3].
Задача следующая: “Пол покрасили масляной
краской два раза. В первый раз на каждый
квадратный метр пошло 125 г краски, а во второй – 75
г. Сколько понадобится краски, если длина комнаты
6 м, а ширина 5 м?”. Данные задачи используются как
источник информации.

“Преобразовать” задачу можно, дополнив её
вопросами и заданиями. Например, рассмотрим
задачу №733 из учебника 6 класса [4]: “В классе 40
учащихся, из них 8 учащихся учатся по математике
на “5”. Сколько процентов учащихся класса
составляют отличники?” Можно добавить следующее
задание: “В этом классе учится 16 мальчиков. Из
них по математике четверо имеют оценку “5”.
Ответьте на вопросы:

Сколько процентов мальчиков учится на “5”?
Сколько процентов девочек учится на “5”?
Результаты занесите в таблицу.

	Всего	Учится на “5” (количество)	Учится на 5 (в процентах)
Мальчики
Девочки

4) Постройте круговую диаграмму, изображающую
отношение “отличников” к общему числу учащихся.

Гораздо сложнее составить новую задачу.
Сконструированная новая задача должна
соответствовать определению
практико-ориентированной задачи и содержать в
себе несколько отличительных особенностей,
которые отличают ее от стандартных
математических задач. Определим алгоритм
составления таких задач.

Определить цель задачи, её место на уроке, в
теме, в курсе.
Определить уровень сложности задачи.
Выбрать форму предоставления информации
(текстовая, презентация, график, диаграмма,
таблица и т.д.).
Сформулировать стимул и задачу.
Определить степень самостоятельности учащихся
в получении и обработке информации.
Определить форму ответа на вопрос задачи
(однозначный, многовариантный, нестандартный,
отсутствие ответа, ответ в виде графика, рисунка,
таблицы.).

Выделим ещё два типа требований к
практико-ориентированным задачам: требования к
тексту задачи (стилистические) и требования к
организации её решения (организационные).

Проанализируем, прежде всего, стилистические
требования к таким задачам. Текст задачи должен
описывать реально существующую, житейскую
ситуацию. Следовательно, как и описание любой
жизненной ситуации, задачный текст должен быть
“зашумлен”, избыточен, то есть иметь ряд
подробностей, не относящихся к основному
требованию задачи. Кроме того, текст задачи не
должен указывать на способы и средства ее
решения. Проблема или ситуация должны быть
адаптированы к возрастным и психологическим
особенностям школьника, мотивировать его
познавательный интерес.

Не менее важно соблюдать и организационные
требования. Задача должна содержать открытую
цепочку последовательных заданий. Каждое
отдельное задание общей задачи должно содержать
требование и набор необходимых (и избыточных)
данных. Часть данных может располагаться в
преамбуле задачи. Предложенные задания должны
быть связанны между собой (не обязательно,
линейно – последующее с предыдущим).

Рассмотрим конструирование задачи на примере.
Составим задачу для 5 класса к теме “Умножение и
деление на разрядную единицу”.

Цель: отработать умножение и деление на
разрядную единицу, повторить понятия единиц
измерения объёма. Используется на уроках
обобщения темы, для самостоятельной работы
учащихся.

Уровень сложности: второй.

За основу берём занимательный материал из
природоведения. Информацию представляем в виде
текста и рисунка для образного представления.

“Женщины индианских племен, живущие возле реки
Амазонки, во время сбора семян водных растений
часто берут с собой маленьких детей. Для
безопасности малышей они усаживают их на листья
амазонского Лотоса. Каждый листок в поперечнике
достигает 2 м, а его края высоко загнуты вверх.
Поэтому детям есть место для игры и они из листка
не выпадают. Один исследователь для определения
грузоподъемности листка насыпал на него 10
десятилитровых ведра песка. Только тогда листок
утонул”

Составляем вопросы. Нужную информацию
представляем в виде таблицы.

Чему равен объём одного ведра? Выразите объём в
кубических дециметрах. (Учащиеся знают из
учебника, что 1 литр равен 1 кубическому
дециметру)
Сколько кубических дециметров содержится в
кубическом метре?
Определите по таблице, сколько килограммов
весит 1 кубический метр песка.

Таблица плотностей некоторых веществ (вес в
килограммах 1 кубического метра)

Гравий	1600	Песок	1500
Картофель	670	Уголь	840

Чему равен вес одного ведра песка?
Какой вес может выдержать один такой листок?
Сколько детей может удержаться на этом листке,
если считать средний вес ребёнка 10 кг?

Продумываем запись ответов к задаче, приложив
бланк. Ответы однозначные.

Бланк ответов

1	Объём одного ведра равен ______
2	1м³ = ____дм³
3	1 м³ песка весит ________кг
4	1 ведро песка весит _____кг
5	1 лист лотоса выдержит до _________кг
6	На листе может удержаться _____ малышей

Решение практико-ориентированных задач на
уроке означает использования дополнительных
возможностей изучаемого материала, адекватных
способов организации изучения традиционного
программного материала.

Для применения на уроке
практико-ориентированных задач учителем могут
быть использованы следующие дополнительные
возможности изучаемого материала:

— прикладной характер содержания темы;

— содержание, включающее в себя оценку явлений и
событий; различные концепции; различные
толкования причин и следствий, другие
противоречивые сведения или позиции,
допускающие различное толкование;

— материал, имеющий существенное значение для
местного сообщества, связанный с широко
обсуждаемыми в обществе вопросами (например,
проблемы экологии, вопросы межэтнических
отношений и т.п.);

— содержание программы, связанное с событиями,
явлениями, объектами, доступными
непосредственному восприятию школьника (в том
числе в учебных ситуациях);

— материал, работа с которым допускает выход за
пределы школы, его изучение на базе предприятий,
высших учебных заведений, учреждений культуры;

— содержание учебной программы, связанное с
формированием учебных умений и навыков;

— содержание учебного материала, которое может
найти применение в воспитательной, досуговой,
организационной и т.п. деятельности.

Развитие у школьников умений решать
практико-ориентированные задачи в процессе
обучения математике следует рассматривать как
один из способов формирования у них
математической компетентности. Такой подход к
обучению позволяет в дальнейшем выпускнику
школы решать проблемы, возникающие в жизни и в
профессиональной деятельности.

Литература

Сборник нормативных документов. Математика /
сост. Э.Д. Днепров, А.Г.Аркадьев. М.: Дрофа, 2007. 128 с.
Курганов С.Ю. Ключевые учебные ситуации и
тестирование // Школьные технологии. 2006. №4. С.97-102
Виленкин Н.Я. и др. Математика: учебник для 5
класса общеобразовательных учреждений 19-е изд.
М.: Мнемозина, 2006. 280 с.
Виленкин Н.Я. и др. Математика: учебник для 6
класса общеобразовательных учреждений 15-е изд.
М.: Мнемозина, 2005. 288 с.

Приложение

Источник

Дисциплина: математика

ТЕМА ЗАНЯТИЯ: Решение задач практического содержания

КОЛИЧЕСТВО ЧАСОВ :2

РАЗРАБОТЧИК: Антонюк Е.В.

Цели занятия:

рассмотреть практическую значимости учебного материала, перспективы его использования
показать роль и место задач с практическим содержанием в процессе обучения математике
привитие интереса к предмету
повышение мотивации к изучению математики

www.themegallery.com

Задачи:

Показать приложение математики в окружающей действительности, смежных дисциплинах и профессии, технологии и экономике современного производства, сфере обслуживания, быту, при выполнении трудовых операций
Раскрыть понятие задачи с практическим содержанием.
Описать методику решения задач с практическим содержанием.

www.themegallery.com

Понятие задачи с

практическим

содержанием

Под практической задачей следует понимать задачу, в которой отражаются реальные ситуации из жизни, в ходе решения которой можно научаться применять математические знания на практике.

Типы практических

задач

Геометри

ческие

задачи

Житейские задачи

Старинные

задачи

Задачи на

проценты

Задачи

на движение

Задачи

на смеси

и сплавы

Экономические

задачи

Задачи на

производитель

ность

Этапы решения

практической задачи:

анализ условия;

2) поиск пути решения — выдвижение гипотез — составление плана решения;

3) реализация полученного плана;

4) исследование полученного решения — «взгляд назад» …

На деле эти этапы резко друг от друга не отделены».

Задачи на движение

Житель Екатеринбурга купил американский автомобиль, на спидометре которого скорость измеряется в милях в час. Американская миля равна 1609 м. Какова скорость автомобиля в километрах в час, если спидометр показывает 42 мили в час? Ответ округлите до целого числа.

Решение:

1) 42 ∙ 1609 = 67578 (м)

2) 1 км = 1000 м

3) 67578 м : 1000= 67,578 (км)

4) 67,578 км, т.е. 68 км

Ответ: 68

Задачи на производительность

Первый и второй закройщик могут выполнить заказ за 5 дней. Второй и третий закройщик могут выполнить тот же заказ за 6 дней, а третий и первый – за 20 дней. За сколько закройщики выполнят заказ, работая втроем?

Решение:

за 1 день первый и второй закройщик выполняют часть заказа.

за 1 день второй и третий закройщик выполняют часть заказа, а третий и закройщики часть заказа.

тогда за 1 день первый и второй, второй и третий, третий и первый вместе выполняют: +=заказа

В последнем выражении вклад каждого рабочего был учтён дважды, значит, за день первый, второй и третий рабочие выполняют заказа .

Им понадобится 1: = 4,8 дней.

Ответ: 4,8

Экономические задачи

Клиент взял в банке кредит 48000 рублей на год под 14% годовых. Он должен погашать кредит, внося в банк ежемесячно одинаковую сумму денег, с тем, чтобы через год выплатить всю сумму, взятую в кредит, вместе с процентами. Сколько рублей он должен вносить в банк ежемесячно?

Решение:

48000 (руб.) – 100%

х (руб.) – 14%

2) х = 48000 ∗14100 = 6720(руб.) -это

14% от 48000

3) 48000 + 6720 = 54720(руб.) должен выплатить за 1 год

4) 54720 : 12 = 4560 (руб.) в месяц

Ответ: 4560

Житейские задачи

1 киловатт-час энергии стоит 1 руб. 60 коп. 1 ноября счетчик электроэнергии показывал 32544 киловатт-часа, а 1 декабря – 32726 киловатт-часов. Сколько рублей нужно заплатить хозяину квартиры за электроэнергию за ноябрь?

Решение:

1) 32726 – 32544 = 182 (киловатт-часа) разница

2) 1 руб. 60 коп. = 1,6 руб

3) 182 ∙ 1,6 = 291,2 (руб.) за ноябрь

Ответ: 291,2

Задачи на проценты

Налог на доходы составляет 13 % от заработной платы. После удержания налога на доходы Мария Сергеевна получила 13920рублей. Сколько рублей составляет заработная плата Марии Сергеевны?

Решение:

1) 100 – 13 = 87 (%)

после вычета налога

2) Было: х (руб.) – 100 %

Стало: 13920 (руб.) – 87 %

3) х = 13920 ·10087= 16000 (руб.)

заработная плата без налога

Ответ: 16000 рублей

Геометрические

задачи

В детском оздоровительном центре делают бассейн цилиндрической формы. Длина окружности его основания равна 36 м, высота – 1,2 м. Стены бассейна выкладывают плиткой. Сколько кг клея нужно приобрести, если на 1 м 2 расходуется 2 кг клея?

Решение.

1)Развертка боковой поверхности цилиндра представляет прямоугольник со сторонами 36 м и 1,2 м.

2) 36 · 1,2 = 43,2 (м 2 ) – площадь боковой поверхности бассейна

3) 43,2 · 2 = 46,4 (кг) – масса клея

Ответ: 46,4 кг

www.themegallery.com

Задачи на смеси и

сплавы

Студент смешал раствор, содержащий 20% кислоты и раствор, содержащий 40% той же кислоты. В итоге у него получился раствор, содержащий 32,5% кислоты, причём объём полученного раствора 4 литра. Сколько литров раствора, содержащего 20%, использовал Сергей при смешивании?

Решение:

Пусть х литров раствора, содержащего 20% кислоты использовал студент при смешивании

Тогда 4-х литров раствора, содержащего 40% кислоты использовал студент при смешивании, объём кислоты в растворе, содержащем 20% кислоты,

объём кислоты в растворе, содержащем 40% кислоты.

Так как в итоге кислоты оказалось литра, то: +=1,3. Откуда находим х=1,5.

Ответ: 1,5

Задачи ЕГЭ

Задачи B1 – одни из самых простых в ЕГЭ. Для их решения нужно применить жизненные знания и произвести несколько элементарных арифметических действий

Шоколадка стоит 28 рублей. Какое наибольшее количество шоколадок можно купить на 160 рублей.

В1

Решение.

Всего 160 рублей. На 28 рублей можно купить 1 шоколадку.

На 160 рублей – 160:28=5,714 шоколадки.

А теперь подумаем, можно ли купить 5,7145,714 шоколадки? Конечно же нет! Можно купить или 5 или 6 шоколадок. Очевидно, что 6 шоколадок будут стоить — 6⋅28=168. А у нас есть только 160.

Ответ: 5

Спасибо за внимание!

www.themegallery.com

Источник

Решение практических задач на уроках
математики.

«В учении, чтобы не формально усвоить материал,

нужно не «отбыть» его, а прожить его нужно, чтобы

обучение вошло в жизнь, чтобы оно
имело

жизненный смысл для учащихся». (А. Герцен)

Одной
из главных задач школы является не только сообщение определённой суммы знаний
учащимся, но и развитие у них познавательных интересов, творческого отношения к
делу, стремления к самостоятельному «добыванию» и обогащению знаний и
умений, применяя их в своей практической деятельности.

По-прежнему
актуален вопрос: как развить у учеников стремление к знаниям? И конкретный
ответ – им должно быть интересно. Надо позаботиться о том, чтобы на уроках
каждый ученик работал активно и увлеченно, и использовать это как отправную
точку для возникновения и развития любознательности, глубоко познавательного
интереса. Это особенно важно в подростковом возрасте, когда еще формируются, а
иногда только определяются постоянные интересы и склонности к тому или иному
предмету. Именно в этот период нужно стремиться раскрыть притягательные стороны
математики

Увеличение
умственной нагрузки на уроках математики заставляет задуматься над тем, как
поддержать интерес ученика к изучаемому материалу и его активность на
протяжении всего урока. В связи с этим ведутся поиски новых эффективных методов
обучения и таких методических приемов, которые активизировали бы мысль
школьников, стимулировали бы их к самостоятельному приобретению знаний.

На
уроках математики сегодня не достаточно, чтобы ученик овладел полученной
информацией. Важен не только уровень достигнутых знаний, умений и навыков, но и
сформированность самостоятельной умственной деятельности.

Активизация – эта
такая организация познавательной деятельности учащихся, при которой учебный
материал становится предметом активных мыслительных и практических действий
каждого ученика. Она должна обеспечить не только простое запоминание материала
и формирование устойчивого внимания, но и дать учащимся некоторые навыки и умения
самостоятельно добывать знания. Главным условием формирования познавательной
активности школьников являются содержание и организация урока. Отбирая материал
и продумывая приемы, которые будут использованы на уроке, учителю надо
оценивать их с точки зрения возможности возбудить и поддерживать интерес к
предмету.

Каким
же образом можно заинтересовать учащихся?

Одним
из способов активизации познавательного интереса является решение задачи с
практическим содержанием.

Что же такое «задача с практическим
содержанием»? «Под математической задачей с практическим содержанием мы
понимаем задачу, фабула которой раскрывает приложения математики в смежных
учебных дисциплинах, знакомит с ее использованием в организации, технологии и
экономике современного производства, в сфере обслуживания, в быту, при
выполнении бытовых операций»

В курсе математики 5-6
классов встречаются задачи с практическим содержанием (задачи на части,
проценты). Далее в курсе алгебры таких задач все меньше, да и времени на
решение прикладных задач, которые показывают связь теории и ее практического
применения в жизни, в будущей профессии, недостаточно в силу перенасыщенности
программы теоретическими сведениями. Между тем практика показывает, что эти
задачи вызывают затруднения у выпускников, так как они не имеют прочных навыков
решения этих задач.

Другими словами, решение
подобных задач дает ответ на вопрос учащихся: «А зачем нам это нужно?»

Задачи с практическим содержанием целесообразно
использовать в процессе обучения для раскрытия многообразия применения
математики в жизни, своеобразия отражения ею реального мира и достижения
дидактических целей таких, как:

·
Мотивация введения новых математических
понятий и методов.

·
Иллюстрация учебного
материала.

·
Закрепление и углубление
знаний по предмету.

·
Формирование практических
умений и навыков.

Наблюдения показывают, что на тех уроках, где
выполняются практические задания, активность обучающихся намного выше, чем на
других уроках, а в результате и качество запоминания и воспроизведения изучаемого
материала лучше. Причина в том, что при такой работе ученики не только
воспринимают материал из уст учителя, но и сами активно участвуют в его
создании и усвоении путем сочетания мыслительных операций с практическими
действиями.

Чтобы как можно более полно
раскрыть непосредственную связь математики с современной жизнью, межпредметные связи приходится
составлять задачи с практическим содержанием, включаю в эту работу ребят. Решения задач с практическим содержанием были
представлены в виде творческих проектов : «Ремонт в моей комнате», «Праздничное
оформление зала», «Покупка техники в кредит», «Социологический опрос».

Примеры задач, составленных учениками 6 клаcса на тему
«Математика в профессии моих родителей».

	Профессия	Задачи
1.	Домохозяйка	Для приготовления летнего салата для семьи нужно 500г помидор по цене 25 руб. за 1 кг, 300 г огурцов по цене 40 руб. , 30 г зеленого лука по цене 6 руб., 50 г сметаны по цене 50 руб. за баночку массой 200 г. Какова будет стоимость салата?
2	Продавец	В школьный буфет привезли пирожки. Ученики старших классов скупили 120 пирожков, что составило 28% всего количества. Сколько всего привезли пирожков? Сколько пирожков купили ученики младших классов, если 10 пирожков остались не проданными?
3	Таксист	Таксист за месяц проехал 10000 км. Стоимость 1 л. бензина 30,5 руб. Средний расход бензина на 100 км составляет 7 литров. Сколько рублей потратил таксист на заправку автомобиля?

Содержательная часть задач
основывается на настоящих и будущих экономических и социальных ролях учащихся
(я – личность и гражданин, я – собственник, я – участник финансового рынка, я –
потребитель, я – производитель и др.). Эти элементы должны помочь учащимся
применять знания, умения, навыки по математике на практике. Они помогают знакомить
учащихся с такими сферами жизни как профессиональная деятельность, совершение
и оплата покупок, совершать разнообразные денежные расчеты; дает
возможности для коррекции познавательной деятельности учащихся. При решении
задач дети могут обучиться элементарным расчетам.

Например, учащимся предлагается выполнить расчёт платежей за
коммунальные услуги: воду, отопление, канализацию.
Каждый вид услуги требует объяснения, учащиеся должны знать, какие услуги нами
оплачивается и где, а так же что мы как пользователи и плательщики можем
требовать от жилищно-коммунальных хозяйств. В целях подготовки учащихся к жизни
это имеет большое значение, они должны знать и уметь защищать свои права.

Например: « В
семье 4 человека. Сколько стоит оплата в месяц за холодную воду, если не
установлен счётчик холодной воды? Как изменится плата за воду. Если поставить
счетчик? (Тариф -25р.40к.)» или «Сколько платит семья из пяти человек за вывоз
ТБО (твёрдых бытовых отходов) в месяц? Изменится ли плата, если будет
проживать меньше жильцов? (Тариф 16р.00 к.)».

Среди практических задач следует
выделить задачи на проценты. К текстовым задачам на проценты относятся
задачи, в которых речь идет о вкладах в банк под тем или иным процентом, о
прибыли, о выполнении плана, об изменении цены на товар. Задачи этого
типа очень часто входят составной частью в решение других типовых задач. Задачи
на проценты актуальны, так как сфера практического приложения процентных
расчетов расширяется. Это повышение цен; объявления коммерческих банков,
привлекающих деньги населения на различных условиях; сведения о повышении
процента банковского кредита; сведения о доходах по акциям различных
предприятий и фондов и т.д. Примеры таких задач;

Задача 1.Кочегару по итогам месяца выплатили премию в
размере 25% оклада. Сколько денег получит кочегар, если его оклад составляет
4 800р.?

Задача 2. В магазине «Эксперт» беспроцентный кредит на
бытовую технику на 4 месяца. Первый взнос 40% от стоимости покупки. Рассчитайте
оплату при покупке и по кредиту на каждый месяц, если телевизор стоит
12 860р.?

Большое воспитательное значение имеют задачи об
экономии и бережливости. Решение
таких задач обогащает социально-нравственный опыт учащихся, способствует
развитию качеств личности, необходимых в условиях рыночной экономики, формирует
гражданскую позицию и психологическую настроенность на рациональное и экономное
использование природных ресурсов.

Задача 1. Расход
семьи Ивановых за электричество составлял 650 рублей в месяц. После
замены ламп накаливания на энергосберегающие лампы они сэкономили 20% денег
потраченных ранее. Сколько рублей в месяц стали платить Ивановы за использованное
электричество?

Задача 2. Дверь
подъезда многоэтажного дома вследствие ребячьих шалостей пришла в негодность.
Родителям этих детей пришлось купить новую дверь, за которую они заплатили 8
700 рублей и за установку – ещё 2 300 рублей. Сколько всего
заплатили родители, и сколько денег внесла каждая семья, если в установке
участвовало 5 семей?

Для укрепления межпредметных связей математики
и других предметов, использую на своих уроках знания учащихся, которые
они получают на уроках естествознания, истории, географии, технологии, и, даже,
их небольшой жизненный опыт.

Задача 1.Одна
личинка колорадского жука за свою жизнь съедает 6,2 г листьев картофеля, а
взрослый жук в 4 раза больше. Сколько картофельной ботвы съедает 25 взрослых
жуков за день, месяц, лето? (Биология)

Задача 2 .Тесто
для вареников содержит 16 частей творога, 2 части муки, 1 часть масла, 3 части
сметаны, 3 части сахара. Определите массу каждого продукта в отдельности для
приготовления 1 кг теста. (Технология)

Для создания собственной базы практических задач для подготовки
учащихся к итоговой аттестации в 9-х и 11-х классах использую современные
интернет – ресурсы. Это сайты:открытый банк задач ЕГЭ по математике, открытый
банк задач ГИА по математике, Решу ЕГЭ, сайт Ларина Александра Александровича,
Досье математика и др.

Решение задач – одно из основных средств
математического развития школьников. Каждая математическая задача служит
конкретным целям обучения, но основная цель любой задачи — развитие
творческого и математического мышления школьников, повышение их интереса к
математике. Этому способствуют, прежде всего, прикладные задачи или задачи
практического содержания. Математика имеет существенное преимущество перед
другими школьными дисциплинами в том, что она с помощью задач на каждом уроке
касаться самых разнообразных явлений природы и окружающей жизни, что позволяет
расширять интересы учащихся.

Жизнь ставит перед учителем математики новые требования. И решение
задач практического характера, межпредметных задач, изучение основ теории
вероятности и элементов статистики на уроках математики полностью отвечают
содержанию современного школьного образования

Дальнейшее использование задач с
практическим содержанием предполагает и дальнейшее совершенствование путей их
реализации: использование межпредметных методических объединений, расширение
практики интегрированных уроков по математике, а также организация внеурочной
деятельности (кружки, факультативы). Все это будет способствовать усиления и
укреплению связей математики с другими науками и с жизнью.

Закончить хочу словами Лобачевского: «Математике должны учить в школе
еще с той целью, чтобы познания, здесь приобретаемые, были достаточными для
обыкновенных потребностей в жизни» .

Источник

Мастер класс «Задачи с практическим содержанием в процессе обучения математике»

В повседневной жизни люди постоянно сталкиваются с решением тех или иных ситуаций. Зачастую школьникам приходится прилагать много усилий для разрешения возникших трудностей реальной жизни: они не знают с чего начать, как действовать, какое решение лучше предпринять. Для того, чтобы в реальной жизни ученики могли не бояться встретившихся на их пути проблем, необходимо разбирать такие задачи, которые будут отражать реальную действительность и которые можно с легкостью решить математическими методами.

Актуальность данной проблемы обосновывает выбор темы мастер класса «Задачи с практическим содержанием в процессе обучения математике».

Цель данной работы — описать роль и место, которые выполняют и занимают задачи с практическим содержанием в процессе обучения математике.

Задачи:

Раскрыть понятие задачи с практическим содержанием.
Описать методику решения задач с практическим содержанием.
Охарактеризовать какую роль выполняют и какое место занимают задачи с практическим содержанием в процессе обучения математике.
Описать применение практических задач в мотивации обучения математике.

Под практической задачей следует понимать задачу, в которой отражаются реальные ситуации из жизни и после решения которой ученики научаться применять математические знания на практике.

Необходимо рассмотреть разновидность задач с практическим содержанием. Задачи на движение: движение лодки, катера по реке; движение автомобиля, пешехода по дороге; движение навстречу друг другу, в противоположные стороны либо в одном направлении.

Пример «два велосипедиста одновременно выехали из пункта А в одном и том же направлении. Скорость первого на 2 км/ч больше скорость второго. Через 12 мин первый велосипедист остановился на 6 мин, чтобы устранить неисправность, и, возобновив движение, догнал второго велосипедиста на расстоянии 14 км от места своей остановки. Определите скорость велосипедистов»

Задачи на производительность: изготовление деталей или изделий токарем либо бригадой, уборка урожая комбайном, вспашка поля трактором и так далее.

Пример «двое рабочих выполняют некоторую работу. После 45 мин совместного труда первый рабочий был переведен на другую работу, а второй закончил оставшуюся часть работы за 2 ч 15 мин. За какое время мог бы выполнить всю работу каждый рабочий в отдельности, если известно, что второму на это понадобиться на 1 ч больше, чем первому?»

Задачи на смеси и сплавы, которые у большинства обучающихся вызывают затруднения, потому что для получения ответа, кроме математических вычислений, требуется применение знаний на проценты.

Пример «в сплав меди и цинка, содержащий 5 кг цинка, добавили 15 кг цинка, после чего содержание цинка в сплаве повысилось на 30%. Какова первоначальная масса сплава, если известно, что в нём меди было больше, чем цинка?»

Задачи на проценты. К ним относятся задачи о вкладах в банк, о кредитах, о прибыли либо об изменении цены на товар. Такие задачи крайне актуальны и очень полезны для обучающихся, потому что, благодаря им, ученики не только учатся работать с процентами, но и могут применить данные знания на практике самостоятельно.

Пример «первый банк даёт 5% годовых, а второй — 10%. Вкладчик часть своих денег положил в первый банк, а остальные — во второй. Через 2 года суммарное число вложенных денег увеличилось на 18,85%. Какую долю своих денег положил вкладчик в первый банк?»

Житейские задачи, в которых требуется найти, сколько понадобиться краски для забора, рулонов обоев для комнаты, досок для строительства, килограммов ягод для варенья, кирпичей для камина и так далее.

Пример: «сколько рулонов обоев необходимо приобрести для того, чтобы оклеить стены квадратной комнаты, высота которой равна 3 м, площадь пола — 9 м2, окна — 1,5 м2, двери — 1,8 м2, если одним рулоном можно оклеить 7,2 м2?»

Экономические задачи. К ним обычно относятся задачи, требующие рассчитать расходы семьи за услуги ЖКХ, рассчитать экономическую выгоду от установления счётчика на воду, рассчитать выгоду от использования энергосберегающих приборов и так далее. К сожалению, экономических задач с практическим содержанием очень мало предлагается для решения ученикам, но данный вид формирует у обучающихся, не только математические навыки, но и подготавливает их к реальной жизни, учит экономии и бережливости.

Пример «в квартире Ивана Петровича установлен двухтарифный счётчик, который позволяет учитывать расход электроэнергии по разным тарифам в дневное и ночное время. В январе расход электроэнергии в дневное время составил 200 киловатт (кВт), а в ночное — 20 кВт. По квитанции Иван Петрович заплатил 640 р. В июле расход электроэнергии в дневное время составил 20 кВт, а в ночное — 10 кВт. По квитанции Иван Петрович заплатил 380 р. Вычислите дневной и ночной тариф расходы электроэнергии (Тариф — это цена 1 киловатта электроэнергии)»

Исторические или старинные задачи. Рассмотрение таких задач на уроке повышает мотивацию учеников к обучению математике, расширяет их познавательную сферу.

Пример: «говорят, что на вопрос о том, сколько у него учеников, древнегреческий математик Пифагор ответил так: «половина моих учеников изучает математику, четверть изучает природу, седьмая часть проводит время в молчаливом размышлении, остальную часть составляют три девы». Сколько учеников было у Пифагора?»

Геометрические задачи, которые непосредственно связаны с реальной жизнью и практической деятельностью учеников.

Пример: «стаканчик для мороженого конической формы имеет глубину 12 см и диаметр верхней части 5 см. На него сверху положили две ложки мороженого в виде полушарий диаметром 5 см. Переполнит ли мороженое стаканчик, если оно растает?»

Способность самостоятельно решить задачу — главное умение для всех обучающихся. В реальной жизни люди ежедневно ставят и решают задачи, конечно, они отличаются от задач, предлагаемых школьными учебниками математики, поэтому важным является умение решать именно задачу практического содержания, которая в наименьшей степени будет отличаться от задач повседневной жизни. Умение организовать и самостоятельно решить практическую задачу присуще активным, самостоятельным, высокоинтеллектуальным ученикам.

Чтобы научиться решать задачу с практическим содержанием, необходимо уметь анализировать условие данной задачи; уметь применять полученные ранее знания на практике, т.е. понимать, когда и какие знания нужно использовать; также следует уметь абстрагироваться и находить общее решение, которое можно будет использовать при решении другой задачи; и, конечно, нужно контролировать и проверять каждое своё действие, т.е. проводить самоконтроль. Именно из этих действий складывается умение решать практическую задачу.

На уроках учитель обязательно должен объяснить школьникам, для чего они учатся решать практические задачи. Во-первых, главная цель решения таких задач — сформировать умение решать задачи, которые могут встретиться каждому в реальной жизни. Во-вторых, немаловажная цель решения практических задач состоит в том, чтобы показать ученикам важность и практическую нужность изучения математики. В-третьих, решение задач практического содержания в короткой перспективе пригодится для сдачи ГИА, а в долгой перспективе пригодится в любой профессии либо увлечении, потому что решать и ставить задачи людями приходится постоянно, чем бы они не занимались.

Особенность процесса решения задач с практическим содержанием состоит в том, что необходимо более детально анализировать текст задачи, проверить задачу на избыток и недостаток условий, выявить взаимную связь с другими разделами математики и с различными сферами деятельности, правильно составить математическую модель для решения, не упустив важных условий задачи, и, наконец, необходимо верно интерпретировать полученный результат.

Решение любой задачи как с практическим содержанием, так и нет, можно осуществить по четырём этапам. Л.В. Виноградова выделяет следующие этапы решения задачи: «1) анализ условия; 2) поиск пути решения — выдвижение гипотез — составление плана решения; 3) реализация полученного плана; 4) исследование полученного решения — «взгляд назад» … На деле эти этапы резко друг от друга не отделены».

Для рассмотрения каждого этапа решения задачи более подробно, необходимо разобрать конкретный пример. Задача: «в жилом доме всего 215 квартир. Сколько из них однокомнатных, если известно, что трёхкомнатных квартир на 10 меньше, чем двухкомнатных, и на 5 больше, чем однокомнатных?» На первом этапе проводится анализ условия задачи, где должны быть осознанны все данные, необходимо четко понимать, что дано, какие условия и что нужно найти. Для этого с учениками проводится работа по составлению списка вопросов и ответов к ним

Список вопросов и ответов к тексту задачи

Вопросы	Ответы
О чём задача?	О жилом доме, в котором есть одно-, двух- и трёхкомнатные квартиры
Что требуется найти?	Количество однокомнатных квартир
Известно, сколько всего квартир?	Да, 215 квартир
Известно, сколько двухкомнатных квартир?	Нет
Известно, сколько трёхкомнатных квартир?	Нет
Что известно про трёхкомнатные квартиры?	Их на 10 меньше, чем двухкомнатных, и на 5 больше, чем однокомнатных

По возможности все данные сводятся в единую схему, таблицу, чертеж, рисунок или краткую запить. К данной задаче можно составить краткую запись:

Однокомнатная — ?

Двухкомнатная — ?

Трёхкомнатная — ? на 10 меньше, чем 2к, на 5 больше, чем 1к

Второй этап выполняется через введения взаимных связей между тем, что дано, и тем, что надо найти. Если напрямую этого сделать не получается, то следует переформулировать данные задачи и заново попытаться связать условия и требования. Поиск пути решения может осуществляться как от условия к заключению, так и наоборот, либо двигаться сразу с двух сторон. Применительно к данной задаче ученики, скорее всего, предложат её решить через введение новой переменной. Данный способ распространен и несложен. Для упрощения, лучше всего за x обозначить количество однокомнатных квартир, чтобы сразу получить нужный ответ. Тогда представленная таблица по тексту задачи (табл. 2) будет выглядеть следующим образом (табл. 3):

Запись условия по тексту задачи после введения переменной:

Однокомнатная — х

Двухкомнатная – х+5+10

Трёхкомнатная – х+5

Далее необходимо сложить количество однокомнатных, двухкомнатных и трёхкомнатных квартир, полученное введением переменной x, и приравнять к общему количеству квартир в доме, т.е. к 215. Поиск пути решения завершен.

На третьем этапе важно грамотно и достаточно развернуто записать решение, каждое действие должно быть обосновано и доказано. Применительно к данной задаче решение оформляется с помощью уравнения:

x + (x+5+10) + (x+5) = 215

3x = 195

x = 65

Ответ: 65 однокомнатных квартир в жилом доме.

На четвёртом этапе проверку полученного ответа можно осуществить, подставив его в краткую запись. Можно допустить, что полученный ответ равен не 65, а, например, 30. Подставив его в таблицу 3, можно заметить, что однокомнатных квартир 30, двухкомнатных — 45, трёхкомнатных — 35, а всего 30 + 45 + 35 = 110. Дети заметят, что задача решена неверно, а, подставив полученный ранее ответ, всё получается правильно. Кроме того, на данном этапе можно предложить ученикам решить туже задачу, только за x взять количество не однокомнатных квартир, а двухкомнатных или трёхкомнатных, и сравнить получившиеся результаты.

Как было сказано ранее, результативным обучение в области математики станет тогда, когда предложенные задания будут активизировать мыслительную деятельность обучающихся, помогать овладению математическими знаниями, побуждать у учеников желание и интерес к математике, развивать способность каждого школьника и, конечно, прививать умения самостоятельно использовать приобретенные математические знания в реальной жизни. Для достижения этих целей лучше всего использовать решение задач практического содержания, а одно из главных условий достижения их — мотивация. Желаемый процесс обучения математике будет способствовать достижению наиболее лучших результатов в учёбе. Чтобы добиться такого обучения, изначально необходимо мотивировать учеников тем, что полученные новые знания будут необходимы и полезны для них в дальнейшем; показать, как математика применяется на практике и где она используется в других областях знаний.

Можно рассмотреть некоторые способы мотивации учеников с помощью практических задач.

Во-первых, если изначально рассмотреть какие-либо физические явления или технические проблемы и на основе этого сформулировать для решения практическую задачу, то обучающиеся воспримут её намного лучше и будут решать её с большим желанием, потому что они наглядно рассмотрели, из чего и как именно она возникла.

Во-вторых, для мотивации обучения математике можно использовать исторические или старинные задачи, которые создадут эмоциональный настрой в классе, вызовут интерес к новой теме, несмотря на то, что изначально она им может показаться совершенно неинтересной. Для большей стимуляции детей к обучению можно использовать задачи с необычной формулировкой, ссылаясь на древний источник.

В-третьих, перед изучением новой темы можно предложить практическую задачу, которая изначально покажется ученикам простой и ответ на которую они дадут незамедлительно.

Но полученные ответы окажутся разными, из-за чего возникнет спор. Активные дискуссии во время спора увлекут учащихся, им захочется узнать верное решение и ответ, который они смогут получить, только изучив новую тему.

В-четвертых, в начале урока учитель может предложить ученикам практическую задачу, ответом на которую будет некруглое число. Школьники подумают, что допустили где-то ошибку и получили неверный ответ, проверив все вычисления, дети придут в недоумение, которое учитель должен развить, изучив новую тему урока.

В-пятых, для мотивации обучения можно использовать практические задачи из банка заданий по ГИА, мотивировав учеников тем, что полученные навыки и умения пригодятся им для сдачи экзамена. В-шестых, для мотивации можно использовать практические задачи, которые будут проиллюстрированы с помощью компьютерной техники, способствующей творческому умению решать задачи, устойчивой мотивации получения нового знания. В дополнение, задачи с практическим содержанием можно использовать на уроке для того, чтобы показать дальнейшую перспективу применения полученных знаний в повседневной жизни.

Задание1.

Предлагаю решить практические задачи 5-6 класса, разбившись на группы.

Задача 1. Известно, что площадь г. Луганска равна 269,61 км кв, а площадь г. Кировска равна 34,94 км кв . Во сколько раз площадь Луганска больше площади г. Кировска? Ответ округлите до десятых.

Задача 2. Длина ямы равна 2 м, ширина 5м, а её высота равна 3 м. Сколько нужно кирпича, чтобы выложить эту яму, если в одном метре квадратном 40 кирпичей?

Задача 3. Расстояние на карте ЛНР между г. Луганск и г. Кировск равно 2 см. Найти расстояние на местности, если масштаб карты 1 : 5000000.

Задача 4. Один килограмм мяса стоит 320 рублей. Мама купила 1,5 килограмма мяса и отдала 1 тысячу рублей. Сколько рублей сдачи мама должна получить?

Задача 5. Магазин открывается в 10 часов утра, а закрывается в 10 часов вечера. Обеденный перерыв длится с 15 до 16 часов. Сколько часов в день открыт магазин?

Задача 6. Сколько штук обрезной доски нужно для 2 кубов досок, если одна обрезная доска имеет размеры 15 см *4 см *6,5 м? Ответ округлите до целых

Более сложные задания

Задача 7: В комиссионном магазине цена товара, выставленного на продажу, уменьшается на одно и то же число % от прежней цены. Определите, на сколько % каждый месяц уменьшалась цена магнитофона, если выставленный на продажу за 4 тыс. рублей после двух снижений он был продан за 2250 рублей?

Задача 8. Семья из трех человек едет из Томмота в Якутск. Можно ехать поездом, а можно — на своей машине. Билет на поезд стоит 780 рублей на одного человека. Автомобиль расходует 9 литров бензина на 100 километров пути, расстояние по шоссе равно 700 км, а цена бензина равна 18 руб. за литр. Сколько рублей придется заплатить за наиболее дешевую поездку на троих?

Задача 9. Магазин детских товаров закупает погремушку по оптовой цене 260 рублей за одну штуку и продаёт с 40-процентной наценкой. Сколько будут стоить 3 такие погремушки, купленные в этом магазине?

В качестве домашнего задания можно предложить задачу, которую школьники могут решать вместе с родителями. Примером такой задачи может служить задача «Ремонт». Обычно это бывает мини- проект.

Задача 10 «Ремонт». Семья Ивановах решила отремонтировать полы в своей квартире, было также решено, что их расходы на ремонт пола не должны превышать 50000 руб. Используя предложенные источники, произведите необходимые расчеты, сделайте вывод и дайте практические рекомендации семье Ивановых, подкрепленные математическими расчетами и содержащие объяснения, почему следует воспользоваться данной рекомендацией.

Стоимость материала

Материал	Количество	Расцветка	Цена
Обои	1 рулон		250 руб.
Краска	1 банка (3 кг)	белая	280 руб.
Краска	1 банка (3 кг)	голубая	250 руб.
Краска	1 банка (3 кг на покраску 10 м²пола)	коричневая	240 руб.
Потолочноепокрытие	1 м²		55 руб.
Потолочное покрытие	1 м²		75 руб.
Кафельная плитка	1 м²		225 руб.
Бордюр	1 рулон		220 руб.
Плинтус	1 м		85 руб.
Паркет	1 м²		750 руб.
Линолеум	1 м²		390 руб.
Клей обойный	1 упаковка		75 руб.
Клей для потолочных покрытий	1 банка		65 руб.
Замазка	1 банка		75 руб.

Джордж Пойа говорил: «Математический опыт учащегося нельзя считать полным, если он не имел случая решать задачу, изобретенную им самим».

Задание 2. Предлагаю составить самим практическую задачу.

Источник