Как найти присоединенную матрицу
Найти присоединенную матрицу можно только для квадратной исходной матрицы, поскольку метод расчета подразумевает предварительное транспонирование. Это одна из операций в матричной алгебре, итогом которой является замена столбцов соответствующими строками. Кроме того, необходимо определить алгебраические дополнения.

Инструкция
Основой матричной алгебры являются операции над матрицами и поиск их основных характеристик. Чтобы найти присоединенную матрицу необходимо выполнить транспонирование и сформировать на основе ее результата новую матрицу из соответствующих алгебраических дополнений.
Транспонирование квадратной матрицы – это запись ее элементов в другом порядке. Первый столбец меняется на первую строку, второй – на вторую и т.д. в общем виде это выглядит так (см. рисунок).
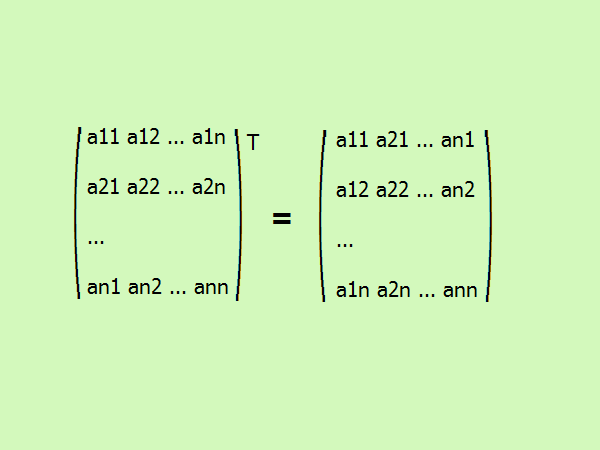
Второй этап нахождения присоединенной матрицы – поиск алгебраических дополнений. Эти числовые характеристики матричных элементов получаются путем вычисления миноров. Те, в свою очередь, являются определителями исходной матрицы порядка, меньшего на 1, и получаются вычеркиванием соответствующих строк и столбцов. Например, M11 = (a22•a33 – a23•a32). Алгебраическое дополнение отличается от минора коэффициентом, равным (-1) в степени суммы номеров элемента: A11 = (-1)^(1+1)• (a22•a33 – a23•a32).
Рассмотрите пример: найдите присоединенную матрицу к данной. Для удобства возьмем третий порядок. Это позволит быстрее понять алгоритм, не прибегая к тяжелым вычислениям, ведь для расчета определителей матрицы третьего порядка достаточно всего четырех элементов.
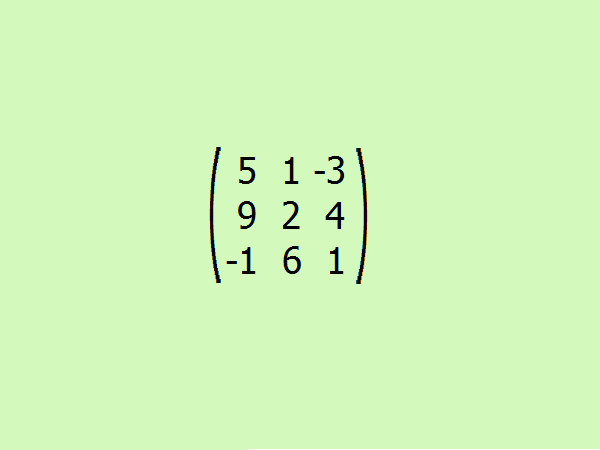
Проведите транспонирование заданной матрицы. Здесь требуется поменять местами первую строку на первый столбец, вторую – на второй и третью – на третий.
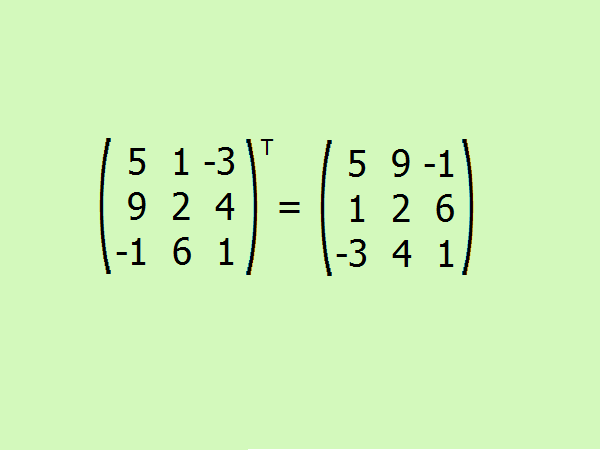
Запишите выражения для поиска алгебраических дополнений, всего их будет 9 по количеству элементов матрицы. Будьте внимательны со знаком, лучше воздержаться от расчетов в уме и расписать все подробно.
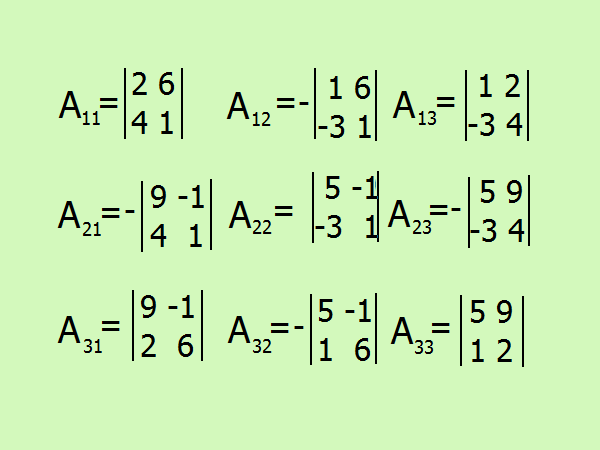
A11 = (-1)²•(2 -24) = -22;
A12 = (-1)³•(1+ 18) = -19;
A13 = (-1)^4•(4 + 6) = 10;
A21 = (-1)³•(9 + 4) = -13;
A22 = (-1)^4•(5 — 3) = 2;
A23 = (-1)^5•(20 + 27);
A31 = (-1)^4•(54 + 2) = 56;
A32 = (-1)^5•(30 + 1) = -31;
A33 = (-1)^6•(10 — 9) = 1.
Составьте итоговую присоединенную матрицу из получившихся алгебраических дополнений.
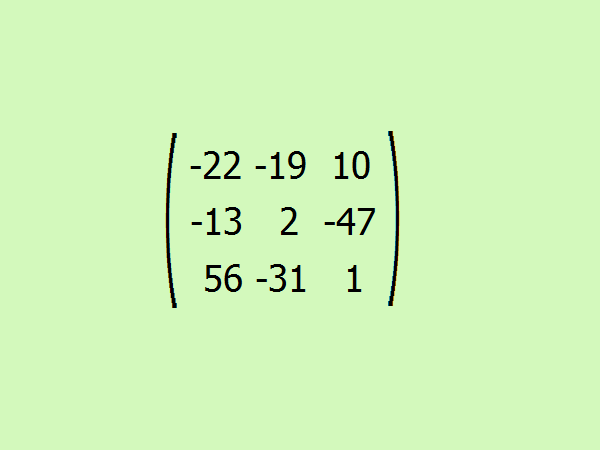
Войти на сайт
или
Забыли пароль?
Еще не зарегистрированы?
This site is protected by reCAPTCHA and the Google Privacy Policy and Terms of Service apply.
Алгоритм вычисления обратной матрицы с помощью алгебраических дополнений: метод присоединённой (союзной) матрицы.
Матрица $A^{-1}$ называется обратной по отношению к квадратной матрице $A$, если выполнено условие $A^{-1}cdot A=Acdot A^{-1}=E$, где $E$ – единичная матрица, порядок которой равен порядку матрицы $A$.
Невырожденная матрица – матрица, определитель которой не равен нулю. Соответственно, вырожденная матрица – та, у которой равен нулю определитель.
Обратная матрица $A^{-1}$ существует тогда и только тогда, когда матрица $A$ – невырожденная. Если обратная матрица $A^{-1}$ существует, то она единственная.
Есть несколько способов нахождения обратной матрицы, и мы рассмотрим два из них. На этой странице будет рассмотрен метод присоединённой матрицы, который полагается стандартным в большинстве курсов высшей математики. Второй способ нахождения обратной матрицы (метод элементарных преобразований), который предполагает использование метода Гаусса или метода Гаусса-Жордана, рассмотрен во второй части.
Метод присоединённой (союзной) матрицы
Пусть задана матрица $A_{ntimes n}$. Для того, чтобы найти обратную матрицу $A^{-1}$, требуется осуществить три шага:
- Найти определитель матрицы $A$ и убедиться, что $Delta Aneq 0$, т.е. что матрица А – невырожденная.
- Составить алгебраические дополнения $A_{ij}$ каждого элемента матрицы $A$ и записать матрицу $A_{ntimes n}^{*}=left(A_{ij} right)$ из найденных алгебраических дополнений.
- Записать обратную матрицу с учетом формулы $A^{-1}=frac{1}{Delta A}cdot {A^{*}}^T$.
Матрицу ${A^{*}}^T$ часто именуют присоединённой (взаимной, союзной) к матрице $A$.
Если решение происходит вручную, то первый способ хорош лишь для матриц сравнительно небольших порядков: второго (пример №2), третьего (пример №3), четвертого (пример №4). Чтобы найти обратную матрицу для матрицы высшего порядка, используются иные методы. Например, метод Гаусса, который рассмотрен во второй части.
Пример №1
Найти матрицу, обратную к матрице $A=left( begin{array} {cccc} 5 & -4 &1 & 0 \ 12 &-11 &4 & 0 \ -5 & 58 &4 & 0 \ 3 & -1 & -9 & 0 end{array} right)$.
Решение
Так как все элементы четвёртого столбца равны нулю, то $Delta A=0$ (т.е. матрица $A$ является вырожденной). Так как $Delta A=0$, то обратной матрицы к матрице $A$ не существует.
Ответ: матрицы $A^{-1}$ не существует.
Пример №2
Найти матрицу, обратную к матрице $A=left(begin{array} {cc} -5 & 7 \ 9 & 8 end{array}right)$. Выполнить проверку.
Решение
Используем метод присоединённой матрицы. Сначала найдем определитель заданной матрицы $A$:
$$
Delta A=left| begin{array} {cc} -5 & 7\ 9 & 8 end{array}right|=-5cdot 8-7cdot 9=-103.
$$
Так как $Delta A neq 0$, то обратная матрица существует, посему продолжим решение. Находим алгебраические дополнения каждого элемента заданной матрицы:
begin{aligned}
& A_{11}=(-1)^2cdot 8=8; ; A_{12}=(-1)^3cdot 9=-9;\
& A_{21}=(-1)^3cdot 7=-7; ; A_{22}=(-1)^4cdot (-5)=-5.\
end{aligned}
Составляем матрицу из алгебраических дополнений: $A^{*}=left( begin{array} {cc} 8 & -9\ -7 & -5 end{array}right)$.
Транспонируем полученную матрицу: ${A^{*}}^T=left( begin{array} {cc} 8 & -7\ -9 & -5 end{array}right)$ (полученная матрица часто именуется присоединённой или союзной матрицей к матрице $A$).
Используя формулу $A^{-1}=frac{1}{Delta A}cdot {A^{*}}^T$, имеем:
$$
A^{-1}=frac{1}{-103}cdot left( begin{array} {cc} 8 & -7\ -9 & -5 end{array}right)
=left( begin{array} {cc} -8/103 & 7/103\ 9/103 & 5/103 end{array}right)
$$
Итак, обратная матрица найдена:
$$A^{-1}=left( begin{array} {cc} -8/103 & 7/103\ 9/103 & 5/103 end{array}right).$$
Чтобы проверить истинность результата, достаточно проверить истинность одного из равенств: $A^{-1}cdot A=E$ или $Acdot A^{-1}=E$. Проверим выполнение равенства $A^{-1}cdot A=E$. Дабы поменьше работать с дробями, будем подставлять матрицу $A^{-1}$ не в форме $left( begin{array} {cc} -8/103 & 7/103\ 9/103 & 5/103 end{array}right)$, а в виде $-frac{1}{103}cdot left( begin{array} {cc} 8 & -7\ -9 & -5 end{array}right)$:
$$
A^{-1}cdot{A}
=-frac{1}{103}cdot left( begin{array} {cc} 8 & -7\ -9 & -5 end{array}right)cdotleft(begin{array} {cc} -5 & 7 \ 9 & 8 end{array}right)
=-frac{1}{103}cdotleft(begin{array} {cc} -103 & 0 \ 0 & -103 end{array}right)
=left(begin{array} {cc} 1 & 0 \ 0 & 1 end{array}right)
=E
$$
Проверка пройдена успешно, обратная матрица $A^{-1}$ найдена верно.
Ответ: $A^{-1}=left( begin{array} {cc} -8/103 & 7/103\ 9/103 & 5/103 end{array}right)$.
Пример №3
Найти обратную матрицу для матрицы $A=left( begin{array} {ccc} 1 & 7 & 3 \ -4 & 9 & 4 \ 0 & 3 & 2end{array} right)$. Выполнить проверку.
Решение
Начнём с вычисления определителя матрицы $A$. Итак, определитель матрицы $A$ таков:
$$
Delta A=left| begin{array} {ccc} 1 & 7 & 3 \ -4 & 9 & 4 \ 0 & 3 & 2end{array} right| = 18-36+56-12=26.
$$
Так как $Delta Aneq 0$, то обратная матрица существует, посему продолжим решение. Находим алгебраические дополнения каждого элемента заданной матрицы:
$$
begin{aligned}
& A_{11}=(-1)^{2}cdotleft|begin{array}{cc} 9 & 4\ 3 & 2end{array}right|=6;;
A_{12}=(-1)^{3}cdotleft|begin{array}{cc} -4 &4 \ 0 & 2end{array}right|=8;;
A_{13}=(-1)^{4}cdotleft|begin{array}{cc} -4 & 9\ 0 & 3end{array}right|=-12;\
& A_{21}=(-1)^{3}cdotleft|begin{array}{cc} 7 & 3\ 3 & 2end{array}right|=-5;;
A_{22}=(-1)^{4}cdotleft|begin{array}{cc} 1 & 3\ 0 & 2end{array}right|=2;;
A_{23}=(-1)^{5}cdotleft|begin{array}{cc} 1 & 7\ 0 & 3end{array}right|=-3;\
& A_{31}=(-1)^{4}cdotleft|begin{array}{cc} 7 & 3\ 9 & 4end{array}right|=1;;
A_{32}=(-1)^{5}cdotleft|begin{array}{cc} 1 & 3\ -4 & 4end{array}right|=-16;;
A_{33}=(-1)^{6}cdotleft|begin{array}{cc} 1 & 7\ -4 & 9end{array}right|=37.
end{aligned}
$$
Составляем матрицу из алгебраических дополнений и транспонируем её:
$$
A^*=left( begin{array} {ccc} 6 & 8 & -12 \ -5 & 2 & -3 \ 1 & -16 & 37end{array} right); ;
{A^*}^T=left( begin{array} {ccc} 6 & -5 & 1 \ 8 & 2 & -16 \ -12 & -3 & 37end{array} right).
$$
Используя формулу $A^{-1}=frac{1}{Delta A}cdot {A^{*}}^T$, получим:
$$
A^{-1}=frac{1}{26}cdot left( begin{array} {ccc} 6 & -5 & 1 \ 8 & 2 & -16 \ -12 & -3 & 37end{array} right)=
left( begin{array} {ccc} 3/13 & -5/26 & 1/26 \ 4/13 & 1/13 & -8/13 \ -6/13 & -3/26 & 37/26 end{array} right)
$$
Чтобы проверить истинность результата, достаточно проверить истинность одного из равенств: $A^{-1}cdot A=E$ или $Acdot A^{-1}=E$. Проверим выполнение равенства $Acdot A^{-1}=E$. Дабы поменьше работать с дробями, будем подставлять матрицу $A^{-1}$ не в форме $left( begin{array} {ccc} 3/13 & -5/26 & 1/26 \ 4/13 & 1/13 & -8/13 \ -6/13 & -3/26 & 37/26 end{array} right)$, а в виде $frac{1}{26}cdot left( begin{array} {ccc} 6 & -5 & 1 \ 8 & 2 & -16 \ -12 & -3 & 37end{array} right)$:
$$
Acdot{A^{-1}}
=left( begin{array}{ccc}
1 & 7 & 3 \
-4 & 9 & 4\
0 & 3 & 2end{array} right)cdot
frac{1}{26}cdot left( begin{array} {ccc} 6 & -5 & 1 \ 8 & 2 & -16 \ -12 & -3 & 37end{array} right)
=frac{1}{26}cdotleft( begin{array} {ccc} 26 & 0 & 0 \ 0 & 26 & 0 \ 0 & 0 & 26end{array} right)
=left( begin{array} {ccc} 1 & 0 & 0 \ 0 & 1 & 0 \ 0 & 0 & 1end{array} right)
=E
$$
Проверка пройдена успешно, обратная матрица $A^{-1}$ найдена верно.
Ответ: $A^{-1}=left( begin{array} {ccc} 3/13 & -5/26 & 1/26 \ 4/13 & 1/13 & -8/13 \ -6/13 & -3/26 & 37/26 end{array} right)$.
Пример №4
Найти матрицу, обратную матрице $A=left( begin{array} {cccc} 6 & -5 & 8 & 4\ 9 & 7 & 5 & 2 \ 7 & 5 & 3 & 7\ -4 & 8 & -8 & -3 end{array} right)$.
Решение
Для матрицы четвёртого порядка нахождение обратной матрицы с помощью алгебраических дополнений несколько затруднительно. Однако такие примеры в контрольных работах встречаются.
Чтобы найти обратную матрицу, для начала нужно вычислить определитель матрицы $A$. Лучше всего в данной ситуации это сделать с помощью разложения определителя по строке (столбцу). Выбираем любую строку или столбец и находим алгебраические дополнения каждого элемента избранной строки или столбца.
Например, для первой строки получим:
$$
A_{11}=left|begin{array}{ccc} 7 & 5 & 2\ 5 & 3 & 7\ 8 & -8 & -3 end{array}right|=556;;
A_{12}=-left|begin{array}{ccc} 9 & 5 & 2\ 7 & 3 & 7 \ -4 & -8 & -3 end{array}right|=-300;
$$
$$
A_{13}=left|begin{array}{ccc} 9 & 7 & 2\ 7 & 5 & 7\ -4 & 8 & -3 end{array}right|=-536;;
A_{14}=-left|begin{array}{ccc} 9 & 7 & 5\ 7 & 5 & 3\ -4 & 8 & -8 end{array}right|=-112.
$$
Определитель матрицы $A$ вычислим по следующей формуле:
$$
Delta{A}=a_{11}cdot A_{11}+a_{12}cdot A_{12}+a_{13}cdot A_{13}+a_{14}cdot A_{14}=6cdot 556+(-5)cdot(-300)+8cdot(-536)+4cdot(-112)=100.
$$
А далее продолжаем находить алгебраические дополнения:
$$
begin{aligned}
& A_{21}=-77;;A_{22}=50;;A_{23}=87;;A_{24}=4;\
& A_{31}=-93;;A_{32}=50;;A_{33}=83;;A_{34}=36;\
& A_{41}=473;;A_{42}=-250;;A_{43}=-463;;A_{44}=-96.
end{aligned}
$$
Матрица из алгебраических дополнений:
$$A^*=left(begin{array}{cccc} 556 & -300 & -536 & -112\ -77 & 50 & 87 & 4 \ -93 & 50 & 83 & 36\ 473 & -250 & -463 & -96end{array}right)$$
Присоединённая матрица:
$${A^*}^T=left(begin{array} {cccc} 556 & -77 & -93 & 473\ -300 & 50 & 50 & -250 \ -536 & 87 & 83 & -463\ -112 & 4 & 36 & -96end{array}right)$$
Обратная матрица:
$$
A^{-1}=frac{1}{100}cdot left( begin{array} {cccc} 556 & -77 & -93 & 473\ -300 & 50 & 50 & -250 \ -536 & 87 & 83 & -463\ -112 & 4 & 36 & -96 end{array} right)=
left( begin{array} {cccc} 139/25 & -77/100 & -93/100 & 473/100 \ -3 & 1/2 & 1/2 & -5/2 \ -134/25 & 87/100 & 83/100 & -463/100 \ -28/25 & 1/25 & 9/25 & -24/25 end{array} right)
$$
Проверка, при желании, может быть произведена так же, как и в предыдущих примерах.
Ответ: $A^{-1}=left( begin{array} {cccc} 139/25 & -77/100 & -93/100 & 473/100 \ -3 & 1/2 & 1/2 & -5/2 \ -134/25 & 87/100 & 83/100 & -463/100 \ -28/25 & 1/25 & 9/25 & -24/25 end{array} right)$.
Во второй части будет рассмотрен иной способ нахождения обратной матрицы, который предполагает использование преобразований метода Гаусса или метода Гаусса-Жордана.
Алгоритм вычисления обратной матрицы. (Метод присоединенной матрицы).
-
Находим
.
Если=0,
то матрица вырожденная и А-1
не существует. Если
,
то А невырожденная и А-1
существует. -
Находим
АТ. -
Находим
алгебраические дополнения элементов
транспонированной матрицы
,
(i=1,2,…,n; j=1,2,…,n) и составляем из них
присоединенную матрицу:
(i=1,2,…,n; j=1,2,…,n).
-
Вычисляем
обратную матрицу по формуле (10). -
Проверяем
правильность вычисления А-1
по определению:А-1А=Е.
Пример.
А=

АТ=
А11=-4 А12=3 А13=-5
А21=-8 А22=6 А23=-5
А31=-5 А32=5 А33=-5
А-1=
Для
невырожденных матриц выполняются
следующие свойства:
1.


(А-1)Т=(АТ)-1.
2.
(А-1)-1=А; 4.
(АВ)-1=В-1А-1;
Элементарные преобразования над матрицами.
-
Отбрасывание
нулевой строки (столбца). -
Умножение
всех элементов строки (столбца) на
число, отличное от нуля. -
Перемена
местами двух строк (столбцов) местами. -
Прибавление
к элементам одной строки (столбца)
соответствующих элементов другой
строки (столбца), умноженных на любое
число. -
Транспонирование
матрицы.
Матрица
В, полученная из матрицы А с помощью
элементарных преобразований, называется
эквивалентной матрице А (В~А).
При
помощи элементарных преобразований
можно найти обратную матрицу к
невырожденной матрице А.
Метод
элементарных преобразований (метод
Гаусса).
Приписывая
справа к квадратной матрице А порядка
n единичную матрицу такого же порядка.
Получим прямоугольную матрицу В=(А|Е)
размера nx2n. С помощью элементарных
преобразований над строками матрицы В
приведем ее к виду (Е|А-1).
Пример.
А=
Составим матрицу В.

Матричные
ур-я. АХ=В, Х=А-1В
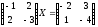
Х=
Ранг матрицы. Рассмотрим произвольную, необязательно квадратную, матрицу а размера mxn. Линейная зависимость строк.
Понятие
ранга матрицы связано с понятием линейной
зависимости (независимости) строк
(столбцов) матрицы. Рассмотрим это
понятие для строк. Для столбцов –
аналогично.
Обозначим
стоки матрицы А:
е1=(а11,а12,…,а1n); е2=(а21,а22,…,а2n);…,
еm=(аm1,аm2,…,аmn)
ek=es
если akj=asj,
j=1,2,…,n
Арифметические
операции над строками матрицы (сложение,
умножение на число) вводятся как операции,
проводимые поэлементно: λеk=(λаk1,λаk2,…,λаkn);
ek+еs=[(аk1+as1),(ak2+as2),…,(аkn+asn)].
Строка
е называется линейной
комбинацией
строк е1,
е2,…,еk,
если она равна сумме произведений этих
строк на произвольные действительные
числа:
е=λ1е1+λ2е2+…+λkеk
Строки
е1,
е2,…,еm
называются линейно
зависимыми,
если существуют действительные числа
λ1,λ2,…,λm,
не все равные нулю, что линейная комбинация
этих строк равна нулевой строке:
λ1е1+λ2е2+…+λmеm=0,
где
0=(0,0,…,0) (1)
Если
линейная комбинация равна нулю тогда
и только тогда, когда все коэффициенты
λi
равны нулю (λ1=λ2=…=λm=0),
то строки е1,
е2,…,еm
называются линейно
независимыми.
Теорема
1.
Для
того, чтобы строки е1,е2,…,еm
были линейно зависимы, необходимо
и достаточно,
чтобы одна из этих строк была линейной
комбинацией
остальных строк.
Доказательство.
Необходимость.
Пусть строки е1,
е2,…,еm
линейно зависимы. Пусть, для определенности
в (1) λm≠0,
тогда
или
Т.о.
строка еm
является линейной комбинацией остальных
строк. Ч.т.д.
Достаточность.
Пусть одна из строк, например еm,
является линейной комбинацией остальных
строк. Тогда найдутся числа


которое можно переписать в виде
где
хотя бы 1 из коэффициентов, (-1), не равен
нулю. Т.е. строки линейно зависимы.
Ч.т.д.
Определение.
Минором k-го порядка
матрицы А размера mxn называется
определитель k-го порядка с элементами,
лежащими на пересечении любых k строк
и любых k столбцов матрицы А. (k≤min(m,n)).

Пример.

миноры 1-го порядка:

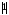

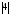
миноры
2-го порядка:

3-го порядка
У
матрицы 3-го порядка 9 миноров 1-го порядка,
9 миноров 2-го порядка и 1 минор 3-го порядка
(определитель этой матрицы).
Определение.
Рангом матрицы А
называется наивысший порядок отличных
от нуля миноров этой матрицы. Обозначение
— rg A или r(A).
Свойства
ранга матрицы.
-
ранг
матрицы Anxm
не превосходит меньшего из ее размеров,
т.е.
r(A)≤min(m,n).
-
r(A)=0
когда
все элементы матрицы равны 0, т.е. А=0. -
Для
квадратной матрицы А n –го порядка
r(A)=n
,
когда А невырожденная.
(Ранг
диагональной
матрицы равен количеству
ее
ненулевых
диагональных
элементов).
4)
Если ранг матрицы равен r,
то матрица имеет хотя бы один минор
порядка r,
не равный нулю, а все миноры больших
порядков равны нулю.
Для
рангов матрицы справедливы следующие
соотношения:
-
r(AT)=r(A)
-
r(A+B)≤r(A)+r(B); 3)
r(AB)≤min{r(A),r(B)}; -
r(A+B)≥│r(A)-r(B)│; 4)
r(ATA)=r(A);
-
r(AB)=r(A),
если В — квадратная невырожденная
матрица. -
r(AB)≥r(A)+r(B)-n,
где n-число столбцов матрицы А или строк
матрицы В.
Определение.
Ненулевой минор порядка r(A) называется
базисным
минором. (У
матрицы А может быть несколько базисных
миноров). Строки и столбцы, на пересечении
которых стоит базисный минор, называются
соответственно базисными
строками и
базисными
столбцами.
Теорема
2 (о базисном миноре). Базисные
строки (столбцы) линейно независимы.
Любая строка (любой столбец) матрица А
является линейной комбинацией базисных
строк (столбцов).
Доказательство.
(Для строк). Если бы базисные строки были
линейно зависимы, то по теореме (1) одна
из этих строк была бы линейной комбинацией
других базисных строк, тогда, не изменяя
величины базисного минора, можно вычесть
из этой строки указанную линейную
комбинацию и получить нулевую строку,
а это противоречит тому, что базисный
минор отличен от нуля. Т.о. базисные
строки линейно независимы.
Докажем,
что любая строка матрицы А является
линейной комбинацией базисных строк.
Т.к. при произвольных переменах строк
(столбцов) определитель сохраняет
свойство равенства нулю, то, не ограничивая
общности, можно считать, что базисный
минор находится в верхнем левом углу
матрицы
А=
на первых r
строках и первых r
столбцах. Пусть 1jn,
1im.
Покажем, что определитель (r+1)-го
порядка

0.
Если
jr
или ir,
то этот определитель равен нулю, т.к. у
него будет два одинаковых столбца или
две одинаковых строки.
Если
же j>r
и i>r,
то этот определитель является минором
(r+1)-го
порядка матрицы А. Т.к. ранг матрицы
равен r, значит любой минор большего
порядка равен 0.
Раскладывая
его по элементам последнего (добавленного)
столбца, получаем
a1jA1j+a2jA2j+…+arjArj+aijAij=0,
где последнее алгебраическое дополнение
Aij
совпадает с базисным минором Мr
и поэтому Aij=
Мr≠0.
Разделив
последнее равенство на Aij,
можем выразить элемент aij,
как линейную комбинацию:

где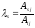
Зафиксируем
значение i (i>r) и получаем, что для любого
j (j=1,2,…,n) элементы i-й строки ei
линейно выражаются через элементы строк
е1,
е2,…,еr,
т.е. i-я строка является линейной
комбинацией базисных строк:

Ч.т.д.
Теорема
3. (необходимое и достаточное условие
равенства нулю определителя). Для
того, чтобы определитель n-го
порядка
был равен нулю, необходимо и достаточно,
чтобы его строки (столбцы) были линейно
зависимы.
Доказательство
(с.40).
Необходимость.
Если определитель n-го
порядка
равен нулю, то базисный минор его матрицы
имеет порядок r<n.
Тогда хотя бы одна из его строк является
не базисной. По теореме 2 эта строка
является линейной комбинацией базисных
строк. В эту линейную комбинацию можно
включить и все оставшиеся строки с
коэффициентами 0.
Т.о.,
одна строка является линейной комбинацией
других остальных. Тогда по теореме 1
строки определителя линейно зависимы.
Достаточность.
Если строки
линейно зависимы, то по теореме 1 одна
строка Аi
является линейной комбинацией остальных
строк. Вычитая из строки Аi
указанную линейную комбинацию, не
изменив величины ,
получим нулевую строку. Следовательно,
по свойствам определителей, =0. ч.т.д.
Т.о.
можно считать, что ранг
матрицы равен максимальному числу ее
линейно независимых строк или столбцов.
Теорема
4. При
элементарных преобразованиях ранг
матрицы не меняется.
Доказательство.
Как было показано при рассмотрении
свойств определителей,
при преобразованиях
квадратных
матриц их определители
либо не изменяются, либо умножаются на
ненулевое число, либо меняют знак. При
этом наивысший порядок отличных от нуля
миноров исходной матрицы сохраняется,
т.е. ранг матрицы не изменяется. Ч.т.д.
Если
r(A)=r(B),
то А и В –эквивалентные:
А~В.
Теорема
5. При помощи
элементарных преобразований можно
привести матрицу к ступенчатому
виду. Матрица
называется
ступенчатой, если она имеет вид:
А=
где aii≠0,
i=1,2,…,r; r≤k.
Условия
r≤k всегда можно достигнуть транспонированием.
Теорема
6. Ранг
ступенчатой матрицы равен количеству
ее ненулевых строк.
Т.е.
Ранг ступенчатой матрицы равен r, т.к.
есть отличный от нуля минор порядка r:
| Определение: |
| Обратная матрица — такая матрица , при умножении на которую, исходная матрица даёт в результате единичную матрицу
|
Содержание
- 1 Обратимость в алгебре
- 2 Критерий обратимости матрицы
- 3 Свойства обратной матрицы
- 4 Методы нахождения обратной матрицы
- 4.1 Метод Гаусса для нахождения обратной матрицы
- 4.1.1 Пример
- 4.2 Метод присоединенной матрицы
- 4.2.1 Алгоритм получения обратной матрицы
- 4.1 Метод Гаусса для нахождения обратной матрицы
- 5 Ссылки
- 6 Источники
Обратимость в алгебре
| Определение: |
| Пусть — алгебра над . называется единицей , если , причем единственна |
| Определение: |
| Пусть в алгебре , тогда называется левым обратным по отношению к , а — правым обратным по отношению к |
| Определение: |
| Пусть . Левый обратный элементу , являющийся одновременно и правым обратным к нему, называется обратным и обозначается . При этом сам элемент называется обратимым. |
| Лемма: |
|
Пусть алгебре — левый обратный — правый обратный. Тогда обратим, при этом и |
| Доказательство: |
|
Факт 1. , но , тогда по определению . Факт 2. Пусть , но |
Критерий обратимости матрицы
| Теорема: |
|
Квадратная матрица обратима (имеет обратную матрицу) тогда и только тогда, когда она невырожденная, то есть . |
| Доказательство: |
|
Шаг 1. Если матрица обратима, то для некоторой матрицы . Тогда, если квадратные матрицы одного и того же порядка, то : , следовательно, . Шаг 2. Докажем обратное утверждение. Пусть . 1) Докажем существование правой обратной матрицы . Предположим , где , фиксируем , тогда: , тогда получим, что — матрица системы уравнений, так как , то по Крамеру В итоге для всех получим матрицу , что и требовалось. 2) Докажем существование левой обратной матрицы . Предположим Фиксируем , тогда ,получаем заполнение по строчкам, аналогично первому пункту показываем . 3) Тогда по лемме , теорема доказана. |
Свойства обратной матрицы
Методы нахождения обратной матрицы
Метод Гаусса для нахождения обратной матрицы
Возьмём две матрицы: саму и . Приведём матрицу к единичной матрице методом Гаусса. После применения каждой операции к первой матрице применим ту же операцию ко второй. Когда приведение первой матрицы к единичному виду будет завершено, вторая матрица окажется равной .
Пример
Найдем обратную матрицу для матрицы
- 1) Для начала убедимся, что ее определитель не равен нулю(она невырожденная).
- 2) Справа от исходной матрицы припишем единичную.
- 3) Методом Гаусса приведем левую матрицу к единичной, применяя все операции одновременно и к левой, и к правой матрицам.
- 4)
Метод присоединенной матрицы
, где — присоединенная матрица;
| Определение: |
| Присоединенная(союзная, взаимная) матрица — матрица, составленная из алгебраических дополнений для соответствующих элементов исходной матрицы. |
Исходная матрица:
Где:
- — присоединённая(союзная, взаимная) матрица;
- — алгебраические дополнения исходной матрицы;
- — элементы исходной матрицы.
Алгебраическим дополнением элемента матрицы называется число
,
где — дополнительный минор, определитель матрицы, получающейся из исходной матрицы путем вычёркивания i -й строки и j -го столбца.
Алгоритм получения обратной матрицы
-
- заменить каждый элемент исходной матрицы на его алгебраическое дополнение — в результате будет получена присоединенная матрица
- разделить каждый элемент транспонированной присоединенной матрицы на определитель исходной матрицы.
Ссылки
- Обратный оператор
Источники
- Википедия — Обратная матрица
- Википедия — Союзная матрица
- Википедия — Алгебраическое дополнение
- Wikipedia — Invertible matrix
- Анин конспект
Обратная матрица и её свойства
15 февраля 2018
- Домашняя работа
- Ответы
Эта тема является одной из самых ненавистных среди студентов. Хуже, наверное, только определители.
Фишка в том, что само понятие обратного элемента (и я сейчас не только о матрицах) отсылает нас к операции умножения. Даже в школьной программе умножение считается сложной операцией, а уж умножение матриц — вообще отдельная тема, которой у меня посвящён целый параграф и видеоурок.
Сегодня мы не будем вдаваться в подробности матричных вычислений. Просто вспомним: как обозначаются матрицы, как они умножаются и что из этого следует.
Повторение: умножение матриц
Прежде всего договоримся об обозначениях. Матрицей $A$ размера $left[ mtimes n right]$ называется просто таблица из чисел, в которой ровно $m$ строк и $n$ столбцов:
[A=left[ mtimes n right]=underbrace{left[ begin{matrix} {{a}_{11}} & {{a}_{12}} & … & {{a}_{1n}} \ {{a}_{21}} & {{a}_{22}} & … & {{a}_{2n}} \ … & … & … & … \ {{a}_{m1}} & {{a}_{m2}} & … & {{a}_{mn}} \end{matrix} right]}_{n}]
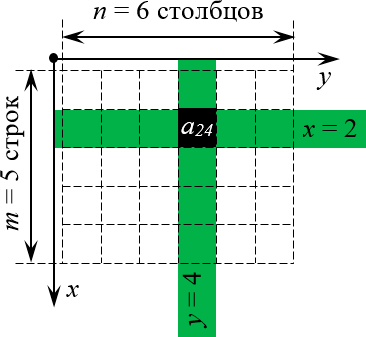
Чтобы случайно не перепутать строки и столбцы местами (поверьте, на экзамене можно и единицу с двойкой перепутать — что уж говорить про какие-то там строки), просто взгляните на картинку:
Что происходит? Если разместить стандартную систему координат $OXY$ в левом верхнем углу и направить оси так, чтобы они охватывали всю матрицу, то каждой клетке этой матрицы можно однозначно сопоставить координаты $left( x;y right)$ — это и будет номер строки и номер столбца.
Почему система координат размещена именно в левом верхнем углу? Да потому что именно оттуда мы начинаем читать любые тексты. Это очень просто запомнить.
А почему ось $x$ направлена именно вниз, а не вправо? Опять всё просто: возьмите стандартную систему координат (ось $x$ идёт вправо, ось $y$ — вверх) и поверните её так, чтобы она охватывала матрицу. Это поворот на 90 градусов по часовой стрелке — его результат мы и видим на картинке.
В общем, как определять индексы у элементов матрицы, мы разобрались. Теперь давайте разберёмся с умножением.
Определение. Матрицы $A=left[ mtimes n right]$ и $B=left[ ntimes k right]$, когда количество столбцов в первой совпадает с количеством строк во второй, называются согласованными.
Именно в таком порядке. Можно сумничать и сказать, мол, матрицы $A$ и $B$ образуют упорядоченную пару $left( A;B right)$: если они согласованы в таком порядке, то совершенно необязательно, что $B$ и $A$, т.е. пара $left( B;A right)$ — тоже согласована.
Умножать можно только согласованные матрицы.
Определение. Произведение согласованных матриц $A=left[ mtimes n right]$ и $B=left[ ntimes k right]$ — это новая матрица $C=left[ mtimes k right]$, элементы которой ${{c}_{ij}}$ считаются по формуле:
[{{c}_{ij}}=sumlimits_{k=1}^{n}{{{a}_{ik}}}cdot {{b}_{kj}}]
Другими словами: чтобы получить элемент ${{c}_{ij}}$ матрицы $C=Acdot B$, нужно взять $i$-строку первой матрицы, $j$-й столбец второй матрицы, а затем попарно перемножить элементы из этой строки и столбца. Результаты сложить.
Да, вот такое суровое определение. Из него сразу следует несколько фактов:
- Умножение матриц, вообще говоря, некоммутативно: $Acdot Bne Bcdot A$;
- Однако умножение ассоциативно: $left( Acdot B right)cdot C=Acdot left( Bcdot C right)$;
- И даже дистрибутивно: $left( A+B right)cdot C=Acdot C+Bcdot C$;
- И ещё раз дистрибутивно: $Acdot left( B+C right)=Acdot B+Acdot C$.
Дистрибутивность умножения пришлось отдельно описывать для левого и правого множителя-суммы как раз из-за некоммутативности операции умножения.
Если всё же получается так, что $Acdot B=Bcdot A$, такие матрицы называются перестановочными.
Среди всех матриц, которые там на что-то умножаются, есть особые — те, которые при умножении на любую матрицу $A$ снова дают $A$:
Определение. Матрица $E$ называется единичной, если $Acdot E=A$ или $Ecdot A=A$. В случае с квадратной матрицей $A$ можем записать:
[Acdot E=Ecdot A=A]
Единичная матрица — частый гость при решении матричных уравнений. И вообще частый гость в мире матриц.:)
А ещё из-за этой $E$ кое-кто придумал всю ту дичь, которая будет написана дальше.
Что такое обратная матрица
Поскольку умножение матриц — весьма трудоёмкая операция (приходится перемножать кучу строчек и столбцов), то понятие обратной матрицы тоже оказывается не самым тривиальным. И требующим некоторых пояснений.
Ключевое определение
Что ж, пора познать истину.
Определение. Матрица $B$ называется обратной к матрице $A$, если
[Acdot B=Bcdot A=E]
Обратная матрица обозначается через ${{A}^{-1}}$ (не путать со степенью!), поэтому определение можно переписать так:
[Acdot {{A}^{-1}}={{A}^{-1}}cdot A=E]
Казалось бы, всё предельно просто и ясно. Но при анализе такого определения сразу возникает несколько вопросов:
- Всегда ли существует обратная матрица? И если не всегда, то как определить: когда она существует, а когда — нет?
- А кто сказал, что такая матрица ровно одна? Вдруг для некоторой исходной матрицы $A$ найдётся целая толпа обратных?
- Как выглядят все эти «обратные»? И как, собственно, их считать?
Насчёт алгоритмов вычисления — об этом мы поговорим чуть позже. Но на остальные вопросы ответим прямо сейчас. Оформим их в виде отдельных утверждений-лемм.
Основные свойства
Начнём с того, как в принципе должна выглядеть матрица $A$, чтобы для неё существовала ${{A}^{-1}}$. Сейчас мы убедимся в том, что обе эти матрицы должны быть квадратными, причём одного размера: $left[ ntimes n right]$.
Лемма 1. Дана матрица $A$ и обратная ей ${{A}^{-1}}$. Тогда обе эти матрицы — квадратные, причём одинакового порядка $n$.
Доказательство. Всё просто. Пусть матрица $A=left[ mtimes n right]$, ${{A}^{-1}}=left[ atimes b right]$. Поскольку произведение $Acdot {{A}^{-1}}=E$ по определению существует, матрицы $A$ и ${{A}^{-1}}$ согласованы в указанном порядке:
[begin{align} & left[ mtimes n right]cdot left[ atimes b right]=left[ mtimes b right] \ & n=a end{align}]
Это прямое следствие из алгоритма перемножения матриц: коэффициенты $n$ и $a$ являются «транзитными» и должны быть равны.
Вместе с тем определено и обратное умножение: ${{A}^{-1}}cdot A=E$, поэтому матрицы ${{A}^{-1}}$ и $A$ тоже согласованы в указанном порядке:
[begin{align} & left[ atimes b right]cdot left[ mtimes n right]=left[ atimes n right] \ & b=m end{align}]
Таким образом, без ограничения общности можем считать, что $A=left[ mtimes n right]$, ${{A}^{-1}}=left[ ntimes m right]$. Однако согласно определению $Acdot {{A}^{-1}}={{A}^{-1}}cdot A$, поэтому размеры матриц строго совпадают:
[begin{align} & left[ mtimes n right]=left[ ntimes m right] \ & m=n end{align}]
Вот и получается, что все три матрицы — $A$, ${{A}^{-1}}$ и $E$ — являются квадратными размером $left[ ntimes n right]$. Лемма доказана.
Что ж, уже неплохо. Мы видим, что обратимыми бывают лишь квадратные матрицы. Теперь давайте убедимся, что обратная матрица всегда одна.
Лемма 2. Дана матрица $A$ и обратная ей ${{A}^{-1}}$. Тогда эта обратная матрица — единственная.
Доказательство. Пойдём от противного: пусть у матрицы $A$ есть хотя бы два экземпляра обратных —$B$ и $C$. Тогда, согласно определению, верны следующие равенства:
[begin{align} & Acdot B=Bcdot A=E; \ & Acdot C=Ccdot A=E. \ end{align}]
Из леммы 1 мы заключаем, что все четыре матрицы — $A$, $B$, $C$ и $E$ — являются квадратными одинакового порядка: $left[ ntimes n right]$. Следовательно, определено произведение:
[Bcdot Acdot C]
Поскольку умножение матриц ассоциативно (но не коммутативно!), мы можем записать:
[begin{align} & Bcdot Acdot C=left( Bcdot A right)cdot C=Ecdot C=C; \ & Bcdot Acdot C=Bcdot left( Acdot C right)=Bcdot E=B; \ & Bcdot Acdot C=C=BRightarrow B=C. \ end{align}]
Получили единственно возможный вариант: два экземпляра обратной матрицы равны. Лемма доказана.
Приведённые рассуждения почти дословно повторяют доказательство единственность обратного элемента для всех действительных чисел $bne 0$. Единственное существенное дополнение — учёт размерности матриц.
Впрочем, мы до сих пор ничего не знаем о том, всякая ли квадратная матрица является обратимой. Тут нам на помощь приходит определитель — это ключевая характеристика для всех квадратных матриц.
Лемма 3. Дана матрица $A$. Если обратная к ней матрица ${{A}^{-1}}$ существует, то определитель исходной матрицы отличен от нуля:
[left| A right|ne 0]
Доказательство. Мы уже знаем, что $A$ и ${{A}^{-1}}$ — квадратные матрицы размера $left[ ntimes n right]$. Следовательно, для каждой из них можно вычислить определитель: $left| A right|$ и $left| {{A}^{-1}} right|$. Однако определитель произведения равен произведению определителей:
[left| Acdot B right|=left| A right|cdot left| B right|Rightarrow left| Acdot {{A}^{-1}} right|=left| A right|cdot left| {{A}^{-1}} right|]
Но согласно определению $Acdot {{A}^{-1}}=E$, а определитель $E$ всегда равен 1, поэтому
[begin{align} & Acdot {{A}^{-1}}=E; \ & left| Acdot {{A}^{-1}} right|=left| E right|; \ & left| A right|cdot left| {{A}^{-1}} right|=1. \ end{align}]
Произведение двух чисел равно единице только в том случае, когда каждое из этих чисел отлично от нуля:
[left| A right|ne 0;quad left| {{A}^{-1}} right|ne 0.]
Вот и получается, что $left| A right|ne 0$. Лемма доказана.
На самом деле это требование вполне логично. Сейчас мы разберём алгоритм нахождения обратной матрицы — и станет совершенно ясно, почему при нулевом определителе никакой обратной матрицы в принципе не может существовать.
Но для начала сформулируем «вспомогательное» определение:
Определение. Вырожденная матрица — это квадратная матрица размера $left[ ntimes n right]$, чей определитель равен нулю.
Таким образом, мы можем утверждать, что всякая обратимая матрица является невырожденной.
Как найти обратную матрицу
Сейчас мы рассмотрим универсальный алгоритм нахождения обратных матриц. Вообще, существует два общепринятых алгоритма, и второй мы тоже сегодня рассмотрим.
Тот, который будет рассмотрен сейчас, очень эффективен для матриц размера $left[ 2times 2 right]$ и — частично — размера $left[ 3times 3 right]$. А вот начиная с размера $left[ 4times 4 right]$ его лучше не применять. Почему — сейчас сами всё поймёте.
Алгебраические дополнения
Готовьтесь. Сейчас будет боль. Нет, не переживайте: к вам не идёт красивая медсестра в юбке, чулках с кружевами и не сделает укол в ягодицу. Всё куда прозаичнее: к вам идут алгебраические дополнения и Её Величество «Союзная Матрица».
Начнём с главного. Пусть имеется квадратная матрица размера $A=left[ ntimes n right]$, элементы которой именуются ${{a}_{ij}}$. Тогда для каждого такого элемента можно определить алгебраическое дополнение:
Определение. Алгебраическое дополнение ${{A}_{ij}}$ к элементу ${{a}_{ij}}$, стоящего в $i$-й строке и $j$-м столбце матрицы $A=left[ ntimes n right]$ — это конструкция вида
[{{A}_{ij}}={{left( -1 right)}^{i+j}}cdot M_{ij}^{*}]
Где $M_{ij}^{*}$ — определитель матрицы, полученной из исходной $A$ вычёркиванием той самой $i$-й строки и $j$-го столбца.
Ещё раз. Алгебраическое дополнение к элементу матрицы с координатами $left( i;j right)$ обозначается как ${{A}_{ij}}$ и считается по схеме:
- Сначала вычёркиваем из исходной матрицы $i$-строчку и $j$-й столбец. Получим новую квадратную матрицу, и её определитель мы обозначаем как $M_{ij}^{*}$.
- Затем умножаем этот определитель на ${{left( -1 right)}^{i+j}}$ — поначалу это выражение может показаться мозговыносящим, но по сути мы просто выясняем знак перед $M_{ij}^{*}$.
- Считаем — получаем конкретное число. Т.е. алгебраическое дополнение — это именно число, а не какая-то новая матрица и т.д.
Саму матрицу $M_{ij}^{*}$ называют дополнительным минором к элементу ${{a}_{ij}}$. И в этом смысле приведённое выше определение алгебраического дополнения является частным случаем более сложного определения — того, что мы рассматривали в уроке про определитель.
Важное замечание. Вообще-то во «взрослой» математике алгебраические дополнения определяются так:
- Берём в квадратной матрице $k$ строчек и $k$ столбцов. На их пересечении получится матрица размера $left[ ktimes k right]$ — её определитель называется минором порядка $k$ и обозначается ${{M}_{k}}$.
- Затем вычёркиваем эти «избранные» $k$ строчек и $k$ столбцов. Снова получится квадратная матрица — её определитель называется дополнительным минором и обозначается $M_{k}^{*}$.
- Умножаем $M_{k}^{*}$ на ${{left( -1 right)}^{t}}$, где $t$ — это (вот сейчас внимание!) сумма номеров всех выбранных строчек и столбцов. Это и будет алгебраическое дополнение.
Взгляните на третий шаг: там вообще-то сумма $2k$ слагаемых! Другое дело, что для $k=1$ мы получим лишь 2 слагаемых — это и будут те самые $i+j$ — «координаты» элемента ${{a}_{ij}}$, для которого мы ищем алгебраическое дополнение.
Таким образом сегодня мы используем слегка упрощённое определение. Но как мы увидим в дальнейшем, его окажется более чем достаточно. Куда важнее следующая штука:
Определение. Союзная матрица $S$ к квадратной матрице $A=left[ ntimes n right]$ — это новая матрица размера $left[ ntimes n right]$, которая получается из $A$ заменой ${{a}_{ij}}$ алгебраическими дополнениями ${{A}_{ij}}$:
[A=left[ begin{matrix} {{a}_{11}} & {{a}_{12}} & … & {{a}_{1n}} \ {{a}_{21}} & {{a}_{22}} & … & {{a}_{2n}} \ … & … & … & … \ {{a}_{n1}} & {{a}_{n2}} & … & {{a}_{nn}} \end{matrix} right]Rightarrow S=left[ begin{matrix} {{A}_{11}} & {{A}_{12}} & … & {{A}_{1n}} \ {{A}_{21}} & {{A}_{22}} & … & {{A}_{2n}} \ … & … & … & … \ {{A}_{n1}} & {{A}_{n2}} & … & {{A}_{nn}} \end{matrix} right]]
Первая мысль, возникающая в момент осознания этого определения — «это сколько же придётся всего считать!» Расслабьтесь: считать придётся, но не так уж и много.:)
Что ж, всё это очень мило, но зачем это нужно? А вот зачем.
Основная теорема
Вернёмся немного назад. Помните, в Лемме 3 утверждалось, что обратимая матрица $A$ всегда не вырождена (т.е. её определитель отличен от нуля: $left| A right|ne 0$).
Так вот, верно и обратное: если матрица $A$ не вырождена, то она всегда обратима. И даже существует схема поиска ${{A}^{-1}}$. Зацените:
Теорема об обратной матрице. Пусть дана квадратная матрица $A=left[ ntimes n right]$, причём её определитель отличен от нуля: $left| A right|ne 0$. Тогда обратная матрица ${{A}^{-1}}$ существует и считается по формуле:
[{{A}^{-1}}=frac{1}{left| A right|}cdot {{S}^{T}}]
А теперь — всё то же самое, но разборчивым почерком. Чтобы найти обратную матрицу, нужно:
- Посчитать определитель $left| A right|$ и убедиться, что он отличен от нуля.
- Составить союзную матрицу $S$, т.е. посчитать 100500 алгебраических дополнений ${{A}_{ij}}$ и расставить их на месте ${{a}_{ij}}$.
- Транспонировать эту матрицу $S$, а затем умножить её на некое число $q={1}/{left| A right|};$.
И всё! Обратная матрица ${{A}^{-1}}$ найдена. Давайте посмотрим на примеры:
Задача. Найдите обратную матрицу:
[left[ begin{matrix} 3 & 1 \ 5 & 2 \end{matrix} right]]
Решение. Проверим обратимость. Посчитаем определитель:
[left| A right|=left| begin{matrix} 3 & 1 \ 5 & 2 \end{matrix} right|=3cdot 2-1cdot 5=6-5=1]
Определитель отличен от нуля. Значит, матрица обратима. Составим союзную матрицу:
[S=left[ begin{matrix} {{A}_{11}} & {{A}_{12}} \ {{A}_{21}} & {{A}_{22}} \end{matrix} right]]
Посчитаем алгебраические дополнения:
[begin{align} & {{A}_{11}}={{left( -1 right)}^{1+1}}cdot left| 2 right|=2; \ & {{A}_{12}}={{left( -1 right)}^{1+2}}cdot left| 5 right|=-5; \ & {{A}_{21}}={{left( -1 right)}^{2+1}}cdot left| 1 right|=-1; \ & {{A}_{22}}={{left( -1 right)}^{2+2}}cdot left| 3 right|=3. \ end{align}]
Обратите внимание: определители |2|, |5|, |1| и |3| — это именно определители матриц размера $left[ 1times 1 right]$, а не модули. Т.е. если в определителях стояли отрицательные числа, убирать «минус» не надо.
Итого наша союзная матрица выглядит так:
[S=left[ begin{array}{*{35}{r}}2 & -5 \ -1 & 3 \end{array} right]]
Осталось посчитать обратную:
[{{A}^{-1}}=frac{1}{left| A right|}cdot {{S}^{T}}=frac{1}{1}cdot {{left[ begin{array}{*{35}{r}} 2 & -5 \ -1 & 3 \end{array} right]}^{T}}=left[ begin{array}{*{35}{r}} 2 & -1 \ -5 & 3 \end{array} right]]
Ну вот и всё. Задача решена.
Ответ. $left[ begin{array}{*{35}{r}} 2 & -1 \ -5 & 3 \end{array} right]$
Задача. Найдите обратную матрицу:
[left[ begin{array}{*{35}{r}} 1 & -1 & 2 \ 0 & 2 & -1 \ 1 & 0 & 1 \end{array} right]]
Решение. Опять считаем определитель:
[begin{align} & left| begin{array}{*{35}{r}} 1 & -1 & 2 \ 0 & 2 & -1 \ 1 & 0 & 1 \end{array} right|=begin{matrix} left( 1cdot 2cdot 1+left( -1 right)cdot left( -1 right)cdot 1+2cdot 0cdot 0 right)- \ -left( 2cdot 2cdot 1+left( -1 right)cdot 0cdot 1+1cdot left( -1 right)cdot 0 right) \end{matrix}= \ & =left( 2+1+0 right)-left( 4+0+0 right)=-1ne 0. \ end{align}]
Определитель отличен от нуля — матрица обратима. А вот сейчас будет самая жесть: надо посчитать аж 9 (девять, мать их!) алгебраических дополнений. И каждое из них будет содержать определитель $left[ 2times 2 right]$. Полетели:
[begin{matrix} {{A}_{11}}={{left( -1 right)}^{1+1}}cdot left| begin{matrix} 2 & -1 \ 0 & 1 \end{matrix} right|=2; \ {{A}_{12}}={{left( -1 right)}^{1+2}}cdot left| begin{matrix} 0 & -1 \ 1 & 1 \end{matrix} right|=-1; \ {{A}_{13}}={{left( -1 right)}^{1+3}}cdot left| begin{matrix} 0 & 2 \ 1 & 0 \end{matrix} right|=-2; \ … \ {{A}_{33}}={{left( -1 right)}^{3+3}}cdot left| begin{matrix} 1 & -1 \ 0 & 2 \end{matrix} right|=2; \ end{matrix}]
Короче, союзная матрица будет выглядеть так:
[S=left[ begin{matrix} 2 & -1 & -2 \ 1 & -1 & -1 \ -3 & 1 & 2 \end{matrix} right]]
Следовательно, обратная матрица будет такой:
[{{A}^{-1}}=frac{1}{-1}cdot left[ begin{matrix} 2 & -1 & -2 \ 1 & -1 & -1 \ -3 & 1 & 2 \end{matrix} right]=left[ begin{array}{*{35}{r}}-2 & -1 & 3 \ 1 & 1 & -1 \ 2 & 1 & -2 \end{array} right]]
Ну и всё. Вот и ответ.
Ответ. $left[ begin{array}{*{35}{r}} -2 & -1 & 3 \ 1 & 1 & -1 \ 2 & 1 & -2 \end{array} right]$
Как видите, в конце каждого примера мы выполняли проверку. В связи с этим важное замечание:
Не ленитесь выполнять проверку. Умножьте исходную матрицу на найденную обратную — должна получиться $E$.
Выполнить эту проверку намного проще и быстрее, чем искать ошибку в дальнейших вычислениях, когда, например, вы решаете матричное уравнение.
Альтернативный способ
Как я и говорил, теорема об обратной матрице прекрасно работает для размеров $left[ 2times 2 right]$ и $left[ 3times 3 right]$ (в последнем случае — уже не так уж и «прекрасно»), а вот для матриц больших размеров начинается прям печаль.
Но не переживайте: есть альтернативный алгоритм, с помощью которого можно невозмутимо найти обратную хоть для матрицы $left[ 10times 10 right]$. Но, как это часто бывает, для рассмотрения этого алгоритма нам потребуется небольшая теоретическая вводная.
Элементарные преобразования
Среди всевозможных преобразований матрицы есть несколько особых — их называют элементарными. Таких преобразований ровно три:
- Умножение. Можно взять $i$-ю строку (столбец) и умножить её на любое число $kne 0$;
- Сложение. Прибавить к $i$-й строке (столбцу) любую другую $j$-ю строку (столбец), умноженную на любое число $kne 0$ (можно, конечно, и $k=0$, но какой в этом смысл? Ничего не изменится же).
- Перестановка. Взять $i$-ю и $j$-ю строки (столбцы) и поменять местами.
Почему эти преобразования называются элементарными (для больших матриц они выглядят не такими уж элементарными) и почему их только три — эти вопросы выходят за рамки сегодняшнего урока. Поэтому не будем вдаваться в подробности.
Важно другое: все эти извращения нам предстоит выполнять над присоединённой матрицей. Да, да: вы не ослышались. Сейчас будет ещё одно определение — последнее в сегодняшнем уроке.
Присоединённая матрица
Наверняка в школе вы решали системы уравнений методом сложения. Ну, там, вычесть из одной строки другую, умножить какую-то строку на число — вот это вот всё.
Так вот: сейчас будет всё то же, но уже «по-взрослому». Готовы?
Определение. Пусть дана матрица $A=left[ ntimes n right]$ и единичная матрица $E$ такого же размера $n$. Тогда присоединённая матрица $left[ Aleft| E right. right]$ — это новая матрица размера $left[ ntimes 2n right]$, которая выглядит так:
[left[ Aleft| E right. right]=left[ begin{array}{rrrr|rrrr}{{a}_{11}} & {{a}_{12}} & … & {{a}_{1n}} & 1 & 0 & … & 0 \{{a}_{21}} & {{a}_{22}} & … & {{a}_{2n}} & 0 & 1 & … & 0 \… & … & … & … & … & … & … & … \{{a}_{n1}} & {{a}_{n2}} & … & {{a}_{nn}} & 0 & 0 & … & 1 \end{array} right]]
Короче говоря, берём матрицу $A$, справа приписываем к ней единичную матрицу $E$ нужного размера, разделяем их вертикальной чертой для красоты — вот вам и присоединённая.:)
В чём прикол? А вот в чём:
Теорема. Пусть матрица $A$ обратима. Рассмотрим присоединённую матрицу $left[ Aleft| E right. right]$. Если с помощью элементарных преобразований строк привести её к виду $left[ Eleft| B right. right]$, т.е. путём умножения, вычитания и перестановки строк получить из $A$ матрицу $E$ справа, то полученная слева матрица $B$ — это обратная к $A$:
[left[ Aleft| E right. right]to left[ Eleft| B right. right]Rightarrow B={{A}^{-1}}]
Вот так всё просто! Короче говоря, алгоритм нахождения обратной матрицы выглядит так:
- Записать присоединённую матрицу $left[ Aleft| E right. right]$;
- Выполнять элементарные преобразования строк до тех пор, пока права вместо $A$ не появится $E$;
- Разумеется, слева тоже что-то появится — некая матрица $B$. Это и будет обратная;
- PROFIT!:)
Конечно, сказать намного проще, чем сделать. Поэтому давайте рассмотрим парочку примеров: для размеров $left[ 3times 3 right]$ и $left[ 4times 4 right]$.
Задача. Найдите обратную матрицу:
[left[ begin{array}{*{35}{r}} 1 & 5 & 1 \ 3 & 2 & 1 \ 6 & -2 & 1 \end{array} right]]
Решение. Составляем присоединённую матрицу:
[left[ begin{array}{rrr|rrr} 1 & 5 & 1 & 1 & 0 & 0 \ 3 & 2 & 1 & 0 & 1 & 0 \ 6 & -2 & 1 & 0 & 0 & 1 \end{array} right]]
Поскольку последний столбец исходной матрицы заполнен единицами, вычтем первую строку из остальных:
[begin{align} & left[ begin{array}{rrr|rrr} 1 & 5 & 1 & 1 & 0 & 0 \ 3 & 2 & 1 & 0 & 1 & 0 \ 6 & -2 & 1 & 0 & 0 & 1 \end{array} right]begin{matrix} downarrow \ -1 \ -1 \end{matrix}to \ & to left[ begin{array}{rrr|rrr} 1 & 5 & 1 & 1 & 0 & 0 \ 2 & -3 & 0 & -1 & 1 & 0 \ 5 & -7 & 0 & -1 & 0 & 1 \end{array} right] \ end{align}]
Больше единиц нет, кроме первой строки. Но её мы не трогаем, иначе в третьем столбце начнут «размножаться» только что убранные единицы.
Зато можем вычесть вторую строку дважды из последней — получим единицу в левом нижнем углу:
[begin{align} & left[ begin{array}{rrr|rrr} 1 & 5 & 1 & 1 & 0 & 0 \ 2 & -3 & 0 & -1 & 1 & 0 \ 5 & -7 & 0 & -1 & 0 & 1 \end{array} right]begin{matrix} \ downarrow \ -2 \end{matrix}to \ & left[ begin{array}{rrr|rrr} 1 & 5 & 1 & 1 & 0 & 0 \ 2 & -3 & 0 & -1 & 1 & 0 \ 1 & -1 & 0 & 1 & -2 & 1 \end{array} right] \ end{align}]
Теперь можно вычесть последнюю строку из первой и дважды из второй — таким образом мы «занулим» первый столбец:
[begin{align} & left[ begin{array}{rrr|rrr} 1 & 5 & 1 & 1 & 0 & 0 \ 2 & -3 & 0 & -1 & 1 & 0 \ 1 & -1 & 0 & 1 & -2 & 1 \end{array} right]begin{matrix} -1 \ -2 \ uparrow \end{matrix}to \ & to left[ begin{array}{rrr|rrr} 0 & 6 & 1 & 0 & 2 & -1 \ 0 & -1 & 0 & -3 & 5 & -2 \ 1 & -1 & 0 & 1 & -2 & 1 \end{array} right] \ end{align}]
Умножим вторую строку на −1, а затем вычтем её 6 раз из первой и прибавим 1 раз к последней:
[begin{align} & left[ begin{array}{rrr|rrr} 0 & 6 & 1 & 0 & 2 & -1 \ 0 & -1 & 0 & -3 & 5 & -2 \ 1 & -1 & 0 & 1 & -2 & 1 \end{array} right]begin{matrix} \ left| cdot left( -1 right) right. \ \end{matrix}to \ & to left[ begin{array}{rrr|rrr} 0 & 6 & 1 & 0 & 2 & -1 \ 0 & 1 & 0 & 3 & -5 & 2 \ 1 & -1 & 0 & 1 & -2 & 1 \end{array} right]begin{matrix} -6 \ updownarrow \ +1 \end{matrix}to \ & to left[ begin{array}{rrr|rrr} 0 & 0 & 1 & -18 & 32 & -13 \ 0 & 1 & 0 & 3 & -5 & 2 \ 1 & 0 & 0 & 4 & -7 & 3 \end{array} right] \ end{align}]
Осталось лишь поменять местами строки 1 и 3:
[left[ begin{array}{rrr|rrr} 1 & 0 & 0 & 4 & -7 & 3 \ 0 & 1 & 0 & 3 & -5 & 2 \ 0 & 0 & 1 & -18 & 32 & -13 \end{array} right]]
Готово! Справа — искомая обратная матрица.
Ответ. $left[ begin{array}{*{35}{r}}4 & -7 & 3 \ 3 & -5 & 2 \ -18 & 32 & -13 \end{array} right]$
Задача. Найдите обратную матрицу:
[left[ begin{matrix} 1 & 4 & 2 & 3 \ 1 & -2 & 1 & -2 \ 1 & -1 & 1 & 1 \ 0 & -10 & -2 & -5 \end{matrix} right]]
Решение. Снова составляем присоединённую:
[left[ begin{array}{rrrr|rrrr} 1 & 4 & 2 & 3 & 1 & 0 & 0 & 0 \ 1 & -2 & 1 & -2 & 0 & 1 & 0 & 0 \ 1 & -1 & 1 & 1 & 0 & 0 & 1 & 0 \ 0 & -10 & -2 & -5 & 0 & 0 & 0 & 1 \end{array} right]]
Немного позалимаем, попечалимся от того, сколько сейчас придётся считать… и начнём считать. Для начала «обнулим» первый столбец, вычитая строку 1 из строк 2 и 3:
[begin{align} & left[ begin{array}{rrrr|rrrr} 1 & 4 & 2 & 3 & 1 & 0 & 0 & 0 \ 1 & -2 & 1 & -2 & 0 & 1 & 0 & 0 \ 1 & -1 & 1 & 1 & 0 & 0 & 1 & 0 \ 0 & -10 & -2 & -5 & 0 & 0 & 0 & 1 \end{array} right]begin{matrix} downarrow \ -1 \ -1 \ \end{matrix}to \ & to left[ begin{array}{rrrr|rrrr} 1 & 4 & 2 & 3 & 1 & 0 & 0 & 0 \ 0 & -6 & -1 & -5 & -1 & 1 & 0 & 0 \ 0 & -5 & -1 & -2 & -1 & 0 & 1 & 0 \ 0 & -10 & -2 & -5 & 0 & 0 & 0 & 1 \end{array} right] \ end{align}]
Наблюдаем слишком много «минусов» в строках 2—4. Умножим все три строки на −1, а затем «выжжем» третий столбец, вычитая строку 3 из остальных:
[begin{align} & left[ begin{array}{rrrr|rrrr} 1 & 4 & 2 & 3 & 1 & 0 & 0 & 0 \ 0 & -6 & -1 & -5 & -1 & 1 & 0 & 0 \ 0 & -5 & -1 & -2 & -1 & 0 & 1 & 0 \ 0 & -10 & -2 & -5 & 0 & 0 & 0 & 1 \end{array} right]begin{matrix} \ left| cdot left( -1 right) right. \ left| cdot left( -1 right) right. \ left| cdot left( -1 right) right. \end{matrix}to \ & to left[ begin{array}{rrrr|rrrr} 1 & 4 & 2 & 3 & 1 & 0 & 0 & 0 \ 0 & 6 & 1 & 5 & 1 & -1 & 0 & 0 \ 0 & 5 & 1 & 2 & 1 & 0 & -1 & 0 \ 0 & 10 & 2 & 5 & 0 & 0 & 0 & -1 \end{array} right]begin{matrix} -2 \ -1 \ updownarrow \ -2 \end{matrix}to \ & to left[ begin{array}{rrrr|rrrr} 1 & -6 & 0 & -1 & -1 & 0 & 2 & 0 \ 0 & 1 & 0 & 3 & 0 & -1 & 1 & 0 \ 0 & 5 & 1 & 2 & 1 & 0 & -1 & 0 \ 0 & 0 & 0 & 1 & -2 & 0 & 2 & -1 \end{array} right] \ end{align}]
Теперь самое время «поджарить» последний столбец исходной матрицы: вычитаем строку 4 из остальных:
[begin{align} & left[ begin{array}{rrrr|rrrr} 1 & -6 & 0 & -1 & -1 & 0 & 2 & 0 \ 0 & 1 & 0 & 3 & 0 & -1 & 1 & 0 \ 0 & 5 & 1 & 2 & 1 & 0 & -1 & 0 \ 0 & 0 & 0 & 1 & -2 & 0 & 2 & -1 \end{array} right]begin{matrix} +1 \ -3 \ -2 \ uparrow \end{matrix}to \ & to left[ begin{array}{rrrr|rrrr} 1 & -6 & 0 & 0 & -3 & 0 & 4 & -1 \ 0 & 1 & 0 & 0 & 6 & -1 & -5 & 3 \ 0 & 5 & 1 & 0 & 5 & 0 & -5 & 2 \ 0 & 0 & 0 & 1 & -2 & 0 & 2 & -1 \end{array} right] \ end{align}]
Финальный бросок: «выжигаем» второй столбец, вычитая строку 2 из строки 1 и 3:
[begin{align} & left[ begin{array}{rrrr|rrrr} 1 & -6 & 0 & 0 & -3 & 0 & 4 & -1 \ 0 & 1 & 0 & 0 & 6 & -1 & -5 & 3 \ 0 & 5 & 1 & 0 & 5 & 0 & -5 & 2 \ 0 & 0 & 0 & 1 & -2 & 0 & 2 & -1 \end{array} right]begin{matrix} 6 \ updownarrow \ -5 \ \end{matrix}to \ & to left[ begin{array}{rrrr|rrrr} 1 & 0 & 0 & 0 & 33 & -6 & -26 & -17 \ 0 & 1 & 0 & 0 & 6 & -1 & -5 & 3 \ 0 & 0 & 1 & 0 & -25 & 5 & 20 & -13 \ 0 & 0 & 0 & 1 & -2 & 0 & 2 & -1 \end{array} right] \ end{align}]
И снова слева единичная матрица, значит справа — обратная.:)
Ответ. $left[ begin{matrix} 33 & -6 & -26 & 17 \ 6 & -1 & -5 & 3 \ -25 & 5 & 20 & -13 \ -2 & 0 & 2 & -1 \end{matrix} right]$
Ну вот и всё. Проверку сделайте сами — мне в лом.:)
Смотрите также:
- Определитель
- Дополнительные соображения
- Тест к уроку «Площади многоугольников на координатной сетке» (легкий)
- Четырехугольная пирамида в задаче C2
- Задача B5: площадь кольца
- Случай четырехугольной пирамиды

 .
. =0,
=0, ,
,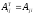 ,
,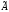 :
: (i=1,2,…,n; j=1,2,…,n).
(i=1,2,…,n; j=1,2,…,n).








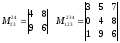
 когда
когда ,
,