Двоичное число: прямой, обратный и дополнительный коды
Прямой код двоичного числа
Обратный код двоичного числа
Дополнительный код двоичного числа
Прямой, обратный и дополнительный коды двоичного числа — способы представления двоичных чисел с фиксированной запятой в компьютерной (микроконтроллерной) арифметике, предназначенные для записи отрицательных и неотрицательных чисел
Мы знаем, что десятичное число можно представить в двоичном виде. К примеру, десятичное число 100 в двоичном виде будет равно 1100100, или в восьмибитном представлении 0110 0100. А как представить отрицательное десятичное число в двоичном виде и произвести с ним арифметические операции? Для этого и предназначены разные способы представления чисел в двоичном коде.
Сразу отмечу, что положительные числа в двоичном коде вне зависимости от способа представления (прямой, обратный или дополнительный коды) имеют одинаковый вид.
Прямой код
Прямой код — способ представления двоичных чисел с фиксированной запятой. Главным образом используется для записи неотрицательных чисел
Прямой код используется в двух вариантах.
В первом (основной) — для записи только неотрицательных чисел:
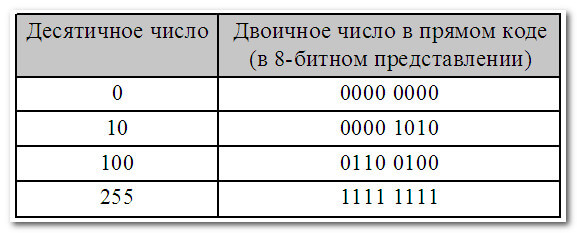
Второй вариант — для записи как положительных, так и отрицательных чисел.
В этом случае старший бит (в нашем случае — восьмой) объявляется знаковым разрядом (знаковым битом).
При этом, если:
— знаковый разряд равен 0, то число положительное
— знаковый разряд равен 1, то число отрицательное
В этом случае диапазон десятичных чисел, которые можно записать в прямом коде составляет от — 127 до +127:
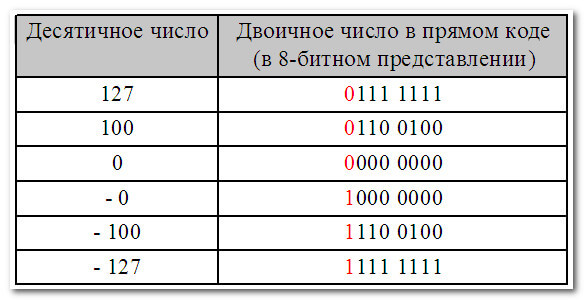
Прямой код используется главным образом для представления неотрицательных чисел.
Использование прямого кода для представления отрицательных чисел является неэффективным — очень сложно реализовать арифметические операции и, кроме того, в прямом коде два представления нуля — положительный ноль и отрицательный ноль (чего не бывает):
Обратный код
Обратный код — метод вычислительной математики, позволяющий вычесть одно число из другого, используя только операцию сложения.
Обратный двоичный код положительного числа состоит из одноразрядного кода знака (битового знака) — двоичной цифры 0, за которым следует значение числа.
Обратный двоичный код отрицательного числа состоит из одноразрядного кода знака (битового знака) — двоичной цифры 1, за которым следует инвертированное значение положительного числа.
Для неотрицательных чисел обратный код двоичного числа имеет тот же вид, что и запись неотрицательного числа в прямом коде.
Для отрицательных чисел обратный код получается из неотрицательного числа в прямом коде, путем инвертирования всех битов (1 меняем на 0, а 0 меняем на 1).
Для преобразования отрицательного числа записанное в обратном коде в положительное достаточного его проинвертировать.
При 8-битном двоичном числе — знаковый бит (как и в прямом коде) старший (8-й)
Диапазон десятичных чисел, который можно записать в обратном коде от -127 до + 127
Арифметические операции с отрицательными числами в обратном коде:
(Арифметические операции с двоичными числами)
1-й пример (для положительного результата)
Дано два числа:
100 = 0110 0100
-25 = — 0001 1001
Необходимо их сложить:
100 + (-25) = 100 — 25 = 75
1-й этап
Переводим число -25 в двоичное число в обратном коде:
25 = 0001 1001
-25= 1110 0110
и складываем два числа:
0110 0100 (100) + 1110 0110 (-25) = 1 0100 1010, отбрасываем старшую 1 (у нас получился лишний 9-й разряд — переполнение), = 0100 1010
2-й этап
Отброшенную в результате старшую единицу прибавляем к результату:
0100 1010 + 1 = 0100 1011 (знаковый бит =0, значит число положительное), что равно 75 в десятичной системе
2-й пример (для отрицательного результата)
Дано два числа:
5 = 0000 0101
-10 = — 0000 1010
Необходимо их сложить:
5 + (-10) = 5 — 10 = -5
1-й этап
Переводим число -10 в двоичное число в обратном коде:
10 = 0000 1010
-10= 1111 0101
и складываем два числа:
0000 0101 (5) + 1111 0101 (-10) = 1111 1010 (знаковый бит =1, значит число отрицательное)
2-й этап
Раз результат получился отрицательный, значит число представлено в обратном коде.
Переводим результат в прямой код (путем инвертирования значения, знаковый бит не трогаем):
1111 1010 —-> 1000 0101
Проверяем:
1000 0101 = — 0000 0101 = -5
Обратный код решает проблему сложения и вычитания чисел с различными знаками, но и имеет свои недостатки:
— арифметические операции проводятся в два этапа
— как и в прямом коде два представления нуля — положительный и отрицательный
Дополнительный код
Дополнительный код — наиболее распространенный способ представления отрицательных чисел. Он позволяет заменить операцию вычитания на операцию сложения и сделать операции сложения и вычитания одинаковыми для знаковых и беззнаковых чисел.
В дополнительном коде (как и в прямом и обратном) старший разряд отводится для представления знака числа (знаковый бит).
Диапазон десятичных чисел которые можно записать в дополнительном коде от -128 до +127. Запись положительных двоичных чисел в дополнительном коде та-же, что и в прямом и обратном кодах.
Дополнительный код отрицательного числа можно получить двумя способами
1-й способ:
— инвертируем значение отрицательного числа, записанного в прямом коде (знаковый бит не трогаем)
— к полученной инверсии прибавляем 1
Пример:
Дано десятичное число -10
Переводим в прямой код:
10 = 0000 1010 —-> -10 = 1000 1010
Инвертируем значение (получаем обратный код):
1000 1010 —-> 1111 0101
К полученной инверсии прибавляем 1:
1111 0101 + 1 = 1111 0110 — десятичное число -10 в дополнительном коде
2-й способ:
Вычитание числа из нуля
Дано десятичное число 10, необходимо получить отрицательное число (-10) в дополнительном двоичном коде
Переводим 10 в двоичное число:
10 = 0000 1010
Вычитаем из нуля:
0 — 0000 1010 = 1111 0110 — десятичное число -10 в дополнительном коде
Арифметические операции с отрицательными числами в дополнительном коде
Дано: необходимо сложить два числа -10 и 5
-10 + 5 = -5
Решение:
5 = 0000 0101
-10 = 1111 0110 (в дополнительном коде)
Складываем:
1111 0110 + 0000 0101 = 1111 1011, что соответствует числу -5 в дополнительном коде
Как мы видим на этом примере — дополнительный код отрицательного двоичного числа наиболее подходит для выполнения арифметических операций сложения и вычитания отрицательных чисел.
Вывод:
1. Для арифметических операций сложения и вычитания положительных двоичных чисел наиболее подходит применение прямого кода
2. Для арифметических операций сложения и вычитания отрицательных двоичных чисел наиболее подходит применение дополнительного кода
Предыдущие статьи:
1. Микроконтроллеры — первый шаг
2. Системы счисления: десятичная, двоичная и шестнадцатиричная
3. Логические операции, логические выражения, логические элементы
4. Битовые операции

Загрузка…
Люба Снежкова
Эксперт по предмету «Информатика»
Задать вопрос автору статьи
Определение 1
Прямой, обратный и дополнительный коды — это методы отображения двоичных чисел, имеющих фиксированную запятую, в компьютерных вычислительных операциях, которые предназначены для представления отрицательных и положительных чисел.
Введение
Прямой, обратный и дополнительный коды двоичных чисел являются способами отображения двоичных чисел, имеющих фиксированную запятую, в компьютерных вычислительных операциях, которые предназначены для представления отрицательных и положительных чисел. Известно, что любые десятичные числа можно представить в двоичном коде. Например, десятичное число 101 в двоичном формате равняется 1100101, или в восьми битном формате это выглядит как 0110 0101. А чтобы представить отрицательные десятичные числа в двоичном виде и обеспечить возможность выполнения с ними арифметических операций, как раз и предназначены различные методы отображения чисел в двоичном коде.
Сдай на права пока
учишься в ВУЗе
Вся теория в удобном приложении. Выбери инструктора и начни заниматься!
Получить скидку 3 000 ₽
Прямой, обратный и дополнительный коды
Следует подчеркнуть, что положительные числа в двоичном коде не зависимо от метода их представления, то есть в прямом, обратном или дополнительном кодах, обладают одинаковым видом.
Прямой код является методом отображения двоичных чисел с фиксированной запятой, который в основном применяется для записи неотрицательных чисел. Прямой код может применяться в следующих вариантах:
- В основном варианте он служит для записи только неотрицательных чисел. В этом случае для восьми битного двоичного числа может быть записано максимальное число 255 (всего чисел 256, то есть, от нуля до 255).
- Во втором варианте он служит для записи как положительных, так и отрицательных чисел.
Во втором случае старший бит принято считать знаковым разрядом (знаковым битом). Причём, если:
- Знаковый разряд равняется нулю, то число является положительным.
- Знаковый разряд равняется единице, то число является отрицательным.
В таком варианте диапазон десятичных чисел, которые могут быть записаны в прямом коде, составляет от — 127 до +127.
«Прямой, обратный и дополнительный коды» 👇
Таким образом, на основании изложенного выше можно сделать вывод, что прямой код может применяться в основном для представления неотрицательных чисел. Применение прямого кода для представления отрицательных чисел считается малоэффективным, поскольку при этом достаточно сложно реализовать арифметические операции и, помимо этого, в прямом коде существует два представления нуля, а именно, положительный нуль и отрицательный нуль (чего не бывает).
Обратный код является способом вычислительной математики, который позволяет осуществить вычитание одного числа из другого, применяя лишь операцию суммирования. Обратный двоичный код положительного числа представляет собой одноразрядный код знака, то есть, двоичного числа нуль, за которым должно следовать числовое значение.
Обратные двоичные коды отрицательных чисел представляет собой одноразрядный код знака, а именно, двоичную цифру единица, за которой должны следовать инвертированные значения положительных чисел. Для положительных чисел обратный код двоичных чисел обладает таким же видом, что и представление неотрицательных чисел в прямом коде.
Для отрицательных чисел обратный код может быть получен из неотрицательного числа в прямом коде, путем инвертирования всех битов, то есть, единицы заменяются нулями, а нули должны быть заменены на единицы. Для преобразования отрицательного числа, которое записано в обратном коде, в положительное необходимо просто выполнить его инвертирование. Для восьми битного двоичного числа знаковым битом, как и в прямом коде, является старший, то есть, восьмой бит. Диапазон десятичных чисел, которые могут быть записаны в обратном коде, простирается от -127 до + 127. Ниже приведены примеры записи чисел в обратном коде.
Рисунок 1. Примеры записи чисел в обратном коде. Автор24 — интернет-биржа студенческих работ
Далее рассмотрим выполнение арифметических операций с отрицательными числами в обратном коде (арифметические операции с двоичными числами).
Имеем следующие два числа:
100 = 0110 0100
–25 = – 0001 1001
Необходимо выполнить их сложение, которое в десятичном формате имеет общеизвестный вид:
100 + (–25) = 100 — 25 = 75
Для реализации этой операции в двоичных кодах, необходимо сначала выполнить перевод числа -25 в двоичное число в обратном коде:
25 = 0001 1001
–25= 1110 0110
Затем необходимо осуществить собственно операцию сложения двух чисел:
0110 0100 (100) + 1110 0110 (–25) = 1 0100 1010.
Старший единичный разряд необходимо отбросить, так как получился лишний девятый разряд, как результат переполнения:
= 0100 1010
Далее отброшенную в результате старшую единицу следует прибавить к результату:
0100 1010 + 1 = 0100 1011.
При этом знаковый бит равняется нулю и это означает, что число является положительным и равным 75 в десятичной системе.
Обратный код способен решить проблему сложения и вычитания чисел с разными знаками, но также и обладает определёнными недостатками:
- Для выполнения арифметических операций необходимо осуществить два этапа.
- Как и для прямого кода существует два представления нуля, а именно, положительный и отрицательный.
Дополнительный код является самым распространенным способом представления отрицательных чисел. Он предоставляет возможность замены операции вычитания операцией сложения, а также позволяет сделать операции сложения и вычитания одинаковыми для знаковых и без знаковых чисел.
Дополнительный код, аналогично прямому и обратному кодам, использует старший разряд для обозначения знака числа, то есть, этот разряд является знаковым битом. Диапазон десятичных чисел, которые могут быть записаны в дополнительном коде, простирается от -128 до +127. Запись положительных двоичных чисел в дополнительном коде выполняется так же, как и в прямом и обратном кодах.
Дополнительный код отрицательного числа может быть получен следующими способами:
- Необходимо выполнить инвертирование значения отрицательного числа, которое записано в прямом коде (знаковый бит сюда не входит), а к полученной инверсии следует прибавить единицу.
- Необходимо выполнить вычитание преобразуемого числа из нуля.
Находи статьи и создавай свой список литературы по ГОСТу
Поиск по теме
Машинные коды[править]
Все операции в ЭВМ выполняются над числами, представленными специальными машинными кодами. Их использование позволяет обрабатывать знаковые разряды чисел так же, как и значащие разряды, а также заменять операцию вычитания операцией сложения.
Различают следующие коды двоичных чисел:
- прямой код (П),
- обратный код (ОК),
- дополнительный код (ДК).
Прямой код[править]
Прямой код двоичного числа образуется из абсолютного значения этого числа и кода знака (0 или 1) перед его старшим числовым разрядом.
Пример.
А10 = +10; А2 = +1010; [А2]п = 0|1010
В10 = –15; В2 = –1111; [В2]п = 1|1111
Обратный код[править]
Обратный код двоичного числа образуется по следующему правилу. Обратный код положительных чисел совпадает с их прямым кодом. Обратный код отрицательного числа содержит единицу в знаковом разряде числа, а значащие разряды числа заменяются на инверсные, т.е. нули заменяются единицами, а единицы нулями.
Пример.
А10 = +10; А2 = +1010; [А2]ок = [А2]п = 0|1010
В10 = –15; В2 = –1111; [В2]ок = 1|0000
Свое название обратный код получил потому, что коды цифр отрицательного числа заменены на инверсные. Наиболее важные свойства обратного кода чисел:
- сложение положительного числа С с его отрицательным значением в обратном коде дает т.н. машинную единицу МЕок=1|11…11, состоящую из единиц в знаковом и в значащих разрядах числа;
- нуль в обратном коде имеет двоякое значение. Он может быть как положительным числом – 0|00…00, так и отрицательным 1|11…11. Значение отрицательного числа совпадает с МЕок. Двойственное представление 0 явилось причиной того, что в современных ЭВМ все числа представляются не обратным, а дополнительным кодом.
Дополнительный код[править]
Дополнительный код положительных чисел совпадает с их прямым кодом. Дополнительный код отрицательного числа представляет собой результат суммирования обратного кода числа с единицей младшего разряда (20 – для целых чисел, 2-л – для дробных)
Пример.
А10 = +10; А2 = +1010; [А2]дк = [А2]ок = [А2]п = 0|1010
В10 = –15; В2 = –1111; [В2]дк = [В2]ок + 20 = 1|0000+1 = 1|0001
Основные свойства дополнительного кода:
• сложение дополнительных кодов положительного числа С с его отрицательным значением дает т.н. машинную единицу дополнительного кода:
МЕдк=МЕок + 20 = 10|00…00,
т.е. число 10 (два) в знаковых разрядах числа;
• дополнительный код называется так потому, что представление отрицательных чисел является дополнением прямого кода чисел до машинной единицы
МЕдк.
Модифицированные обратные и дополнительные коды[править]
Модифицированные обратные и дополнительные коды двоичных чисел отличаются соответственно от обратных и дополнительных кодов удвоением значений знаковых разрядов. Знак «+» в этих кодах кодируется двумя нулевыми знаковыми разрядами, а знак «–» – двумя единичными разрядами.
Пример.
А10 = +10; А2 = +1010; [А2]дк = [А2]ок = [А2]п = 0|1010
[А2]мок = [А2]мдк = 00|1010
В10 = –15; В2 = –1111; [В2]дк= [В2]ок+20 = 1|0000+1 = 1|0001
[В2]мок= [В2]мдк= 11|0001
Целью введения модифицированных кодов являются фиксация и обнаружение случаев получения неправильного результата, когда значение результата превышает максимально возможный результат в отведенной разрядной сетке машины. В этом случае перенос из значащего разряда может исказить значение младшего знакового разряда. Значение знаковых разрядов «01» свидетельствует о положительном переполнении разрядной сетки, а «10» — об отрицательном переполнении. В настоящее время практически во всех компьютерах роль сдвоенных разрядов для фиксации переполнения разрядной сетки играют переносы, идущие в знаковый и из знакового разряда.
Арифметические действия в машинных кодах.[править]
Сложение (вычитание). Операция вычитания приводится к операции сложения путем преобразования чисел в обратный или дополнительный код согласно таблице.
| Требуемая операция | Необходимое преобразование |
|---|---|
| А+В | А+В |
| А-В | А+(-В) |
| -А+В | (-А)+В |
| -А-В | (-А)+(-В) |
Здесь А и В неотрицательные числа.
Скобки в представленных выражениях указывают на замену операции вычитания операцией сложения с обратным или дополнительным кодом соответствующего числа. Сложение двоичных чисел осуществляется последовательно, поразрядно в соответствии с таблицей. При выполнении сложения цифр необходимо соблюдать следующие правила:
- Слагаемые должны иметь одинаковое число разрядов. Для выравнивания разрядной сетки слагаемых можно дописывать незначащие нули слева к целой части числа и незначащие нули справа к дробной части числа.
- Знаковые разряды участвуют в сложении так же, как и значащие.
- Необходимые преобразования кодов производятся с изменением знаков чисел. Приписанные незначащие нули изменяют свое значение при преобразованиях по общему правилу.
- При преобразовании единицы переноса из старшего знакового разряда, в случае использования ОК, эта единица складывается с младшим числовым разрядом. При использовании ДК единица переноса теряется. Знак результата формируется автоматически, результат представляется в том коде, в котором представлены исходные слагаемые.
Пример 1. Сложить два числа: А10 = 7, В10 = 16.
А2 = +111 = +0111; В2 = +10000.
Исходные числа имеют различную разрядность, необходимо провести выравнивание разрядной сетки:
[A2]п = [A2]ок = [A2]дк = 0|00111; [В2]п = [В2]ок = [В2]дк = 0|10000.
Сложение в обратном или дополнительном коде дает один и тот же результат:
0|00111
+0|10000
———-
С2 = 0|10111
С10 = +23
Пример 2. Сложить два числа: А10 = +16, В10 = -7 в ОК и ДК.
По таблице необходимо преобразование А+(-В), в которой второй член преобразуется с учетом знака
[A2]п = [A2]ок = [A2]дк = 0|10000;
[В2]п = 1|111 = 1|00111; [В2]ок = 1|11000; [В2]дк = 1|11001
При сложении чисел в ОК и ДК были получены переносы в знаковый разряд и из знакового разряда. В случае ОК перенос из знакового разряда требует дополнительного прибавления единицы младшего разряда (п.4 правил). В случае ДК этот перенос игнорируется.
Практическая часть.[править]
Задание:
- Взять две пары десятичных двузначных целых числа: А, В, С, D. (Варианты по списку)
- Вычислить (А-В)ок, (В-А)дк, (С-D)ок, (D-C)дк.
Варианты
- Вариант — 78, 56, 11, 35;
- Вариант — 67, 36, 45, 22;
- Вариант — 21, 87, 38, 44;
- Вариант — 99, 26, -73, 26,
- Вариант — 28, 33, 42, 54;
- Вариант — 61, 43, 65, 41;
- Вариант — 11, 84, 49, 53;
- Вариант — 85,- 47, 43, 66;
- Вариант — 48, 52, 65, 88;
- Вариант — 26, 58, 63, 77;
- Вариант — 91, 22, 46, -14;
- Вариант — 57, 14, 69, 55;
- Вариант — 77, 98, 25, -88;
- Вариант — 46, 66, 35, 36;
- Вариант — 44, 37, 92, 28;
- Вариант — 63, 46, 83, 71;
- Вариант — 35, -51, 63, 24;
- Вариант — 25, 95, -38, 33;
- Вариант — 32, 29, 86, 27;
- Вариант — 49, 55, -73, 22
- Вариант — 33, -77, 53, 71;
- Вариант — 48, 86, 62, 42;
- Вариант — 69, -48, 11, 20;
- Вариант — 10; 82, 80, 45;
- Вариант — 70, 93, -27, 30;
- Вариант — 88, -40, 16, 83;
- Вариант — 64, 80, -17, 77;
- Вариант — 40, 46, -73, 19;
- Вариант — 14, -60, 11, 27;
- Вариант — 90, 73, -10, 20.
Очень часто в вычислениях должны использоваться не только положительные, но и отрицательные числа.
Число со знаком в вычислительной технике представляется путем представления старшего разряда числа в качестве знакового. Принято считать, что 0 в знаковом разряде означает знак «плюс» для данного числа, а 1 – знак «минус».
Выполнение арифметических операций над числами с разными знаками представляется для аппаратной части довольно сложной процедурой. В этом случае нужно определить большее по модулю число, произвести вычитание и присвоить разности знак большего по модулю числа.
Применение дополнительного кода позволяет выполнить операцию алгебраического суммирования и вычитания на обычном сумматоре. При этом не требуется определения модуля и знака числа.
Прямой код представляет собой одинаковое представление значимой части числа для положительных и отрицательных чисел и отличается только знаковым битом. В прямом коде число 0 имеет два представления «+0» и «–0».
Обратный код для положительных чисел имеет тот же вид, что и прямой код, а для отрицательных чисел образуется из прямого кода положительного числа путем инвертирования всех значащих разрядов прямого кода. В обратном коде число 0 также имеет два представления «+0» и «–0».
Дополнительный код для положительных чисел имеет тот же вид, что и прямой код, а для отрицательных чисел образуется путем прибавления 1 к обратному коду. Добавление 1 к обратному коду числа 0 дает единое представление числа 0 в дополнительном коде. Однако это приводит к асимметрии диапазонов представления чисел относительно нуля. Так, в восьмиразрядном представлении диапазон изменения чисел с учетом знака.
-128 <= x <= 127.
Таблица прямого, обратного и дополнительного кода 4-битных чисел.
| Число | Прямой код | Обратный код | Дополнительный код |
| -8 | — | — | 1000 |
| -7 | 1111 | 1000 | 1001 |
| -6 | 1110 | 1001 | 1010 |
| -5 | 1101 | 1010 | 1011 |
| -4 | 1100 | 1011 | 1100 |
| -3 | 1011 | 1100 | 1101 |
| -2 | 1010 | 1101 | 1110 |
| -1 | 1001 | 1110 | 1111 |
| 00 | 10000000 | 11110000 | 0000 |
| 1 | 0001 | 0001 | 0001 |
| 2 | 0010 | 0010 | 0010 |
| 3 | 0011 | 0011 | 0011 |
| 4 | 0100 | 0100 | 0100 |
| 5 | 0101 | 0101 | 0101 |
| 6 | 0110 | 0110 | 0110 |
| 7 | 0111 | 0111 | 0111 |
Сложение и вычитание чисел со знаком в дополнительном коде
Если оба числа имеют n–разрядное представление, то алгебраическая сумма будет получена по правилам двоичного сложения (включая знаковый разряд), если отбросить возможный перенос из старшего разряда. Если числа принадлежат диапазону представимых данных и имеют разные знаки, то сумма всегда будет лежать в этом диапазоне. Переполнение может иметь место, если оба cлагаемых имеют одинаковые знаки.
Пример 1: 6 – 4 = ?
6 – положительное число с кодом 0110
–4 – отрицательное число с дополнительным кодом 1100
(перенос игнорируется): 6 – 4 = 2.
Пример 2: –5 + 2 = ?
2 – положительное число с кодом 0010
–5 – отрицательное число с дополнительным кодом 1011
Число с кодом 1101 является отрицательным, модуль этого числа имеет код 00112 = 310.
Назад: Представление данных и архитектура ЭВМ
В большинстве компьютеров с целью
упрощения конструкции АЛУ операция
вычитания не используется. Она заменяется
операцией сложения путем замены знака
вычитаемого на противоположный и
прибавления его к уменьшаемому:
В связи с этим для машинного изображения
отрицательных чисел используют прямой,
дополнительный и обратный коды.
Положительные числа в прямом, обратном
и дополнительном кодах изображаются
одинаково – двоичными кодами с цифрой
0 в знаковом разряде (см., например, рис.
2.8в).
Отрицательные числа в прямом, обратном
и дополнительном кодах имеют разное
изображение. Рассмотрим эти коды и их
применение на примере отрицательных
чисел, представленных в форме с
фиксированной запятой.
-
Прямой
код числа получается, если в знаковый
разряд поместить цифру 1, а в разряды
числовой части числа — двоичный код
его абсолютной величины. -
Обратный
код получается инвертированием (заменой
на обратные значения) всех цифр двоичного
кода абсолютной величины числа, включая
разряд знака: нули заменяются единицами,
а единицы – нулями.
Пример. Число: -1
Код модуля числа (в однобайтовом формате)
0,0000001
Обратный код 1,1111110
Представление числа в разрядной сетке
показано на рис. 2.10
|
1 |
1 |
1 |
1 |
1 |
1 |
1 |
0 |
Рис. 2.10.
Пример. Число –127
Код модуля числа 0,1111111
Обратный код числа 1,0000000. Представление
числа в обратном коде показано на рис.
2.11
|
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
Рис. 2.11
-
Дополнительный
код получается образованием обратного
кода с последующим прибавлением единицы
к его младшему разряду.
Пример. Представление числа –1 в
дополнительном коде показано на рис.
2.12
|
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
Рис.
2.12
Представление числа –127 в дополнительном
коде показано на рис. 2.13
|
1 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
Рис.
2.13
Обычно отрицательные десятичные числа
при вводе в машину автоматически
преобразуются в обратный или дополнительный
двоичный код и в таком виде хранятся и
участвуют в операциях. При выводе таких
чисел из машины происходит обратное
преобразование в отрицательные десятичные
числа.
Использование различных способов
изображения отрицательных чисел в ЦВМ
обуславливает целый ряд особенностей
выполнения операции алгебраического
сложения двоичных чисел.
При сложении обратных кодов чисел Х1и Х2имеют место четыре основных
и два особых случая.
-
Х1>0
иX2>0. При суммировании
складываются все разряды, включая
разряд знака.
Пример
Десятичная запись Двоичные коды
|
0 |
0000101 |
|
+ |
|
|
0 |
0001001 |
|
0 |
0001110 |
(5)
+
(9)
(14)
-
Х1>0,X2<0 и |X2|>X1
Пример
Десятичная запись Двоичные коды
|
0 |
0000011 |
|
+ |
|
|
1 |
1110101 |
|
1 |
1111000 |
3
+
Обратный код
числа -1010
-10
Обратный код
суммы
-7
При переводе обратного кода (обр) в
прямой (пр) получим:
-
1111000обр=1 0000111пр=
-710
-
Х1>0,X2<0 и |X2|<X1
Пример
Десятичная запись Двоичные коды
|
0 |
0001010 |
|
+ |
|
|
1 |
1111100 |
|
0 |
0000110 |
|
+1 |
|
|
0 |
0000111 |
10
+
Обратный код
числа -310
-3
7
Полученный непосредственно сразу
неверный результат (число 6) исправляется
путем переноса единицы из знакового
разряда в младший разряд суммы. При этом
получается правильный результат –
число 710
-
Х1<0
иX2<0
Пример.
Десятичная запись Двоичные коды
|
1 |
1111100 |
|
+ |
|
|
1 |
1111000 |
|
1 |
1110100 |
|
+1 |
|
|
1 |
1110101 |
Обратный код
числа -310
-3
+
Обратный код
числа -710
-7
-10
Обратный код
числа -1010
Полученный непосредственно сразу
неверный результат (обратный код числа
–1110) исправляется путем переноса
единицы из знакового разряда в младший
разряд суммы.
При выполнении операции может появиться
число, старшие разряды которого не
помещаются в отведенной для него области
памяти – возникает переполнение
разрядной сетки формата числа. Рассмотрим
два возможных случая переполнения.
-
Х1>0
, X2>0
и S=X1+X22n-1,
гдеn– количество
разрядов формата числа (для однобайтового
форматаn=8, 2n-1=27=128)
Пример
Десятичная запись Двоичные коды
|
0 |
1000001 |
|
+ |
|
|
0 |
1100001 |
|
1 |
0100010 |
65
+
97
Переполнение
162
Здесь имеет место переполнение разрядной
сетки: семи разрядов цифровой части
недостаточно для размещения восьмиразрядной
суммы (16210=101000102), поэтому
старший разряд суммы оказывается в
знаковом разряде и знак суммы оказывается
несовпадающим со знаком слагаемых, что
является признаком переполнения
разрядной сетки.
-
Х1<0,X2<0 иS=|X1|+|X2|
2n-1
Пример
Десятичная запись Двоичные коды
|
1 |
1000000 |
|
+ |
|
|
1 |
0100000 |
|
0 |
1100000 |
|
+1 |
Обратный код
числа -6310
-63
+
Обратный код
числа -9510
-95
-158
Переполнение
Здесь также знак суммы не совпадает со
знаками слагаемых, что является признаком
переполнения разрядной сетки.
При сложении дополнительных кодов чисел
Х1и Х2имеют место те же
четыре основных и два особых случая.
1. Х1>0 иX2>0.
Аналогично случаю 1 для обратных кодов.
2. Х1>0,X2<0
и |X2|>X1.
Пример.
Десятичная запись Двоичные коды
|
0 |
0000011 |
|
+ |
|
|
1 |
1110110 |
|
1 |
1111001 |
3
—
Дополнительный
код числа -1010
10
Дополнительный
код числа -710
-7
При переводе дополнительного (доп) кода
в прямой (пр) получим:
3. Х1>0,X2<0
и |X2|<Х1
Пример
Десятичная запись Двоичные коды
|
0 |
0001010 |
|
+ |
|
|
1 |
1111101 |
|
0 |
0000111 |
10
—
Дополнительный
код числа -310
3
перенос
отбрасывается
7
Единица переноса из знакового разряда
отбрасывается.
-
Х1<0,X2<0
Пример
Дополнительный
код числа -310
Десятичная запись Двоичные коды
|
1 |
1111101 |
|
+ |
|
|
1 |
1111001 |
|
1 |
1110110 |
-3
+
Дополнительный
код числа -710
-7
Дополнительный
код числа -1010
-10
перенос
отбрасывается
Случаи переполнения разрядной сетки
аналогичны случаям переполнения для
обратных кодов.
Сравнение использования обратного и
дополнительного кодов показывает, что
преобразование отрицательного числа
в обратный код занимает меньше времени,
однако время выполнения сложения в
дополнительных кодах меньше, чем в
обратных, так как в этом случае отсутствует
необходимость переноса единицы из
знакового разряда в младший разряд
результата.
Соседние файлы в папке Информатика
- #
- #
- #
- #
- #
- #
- #
- #
- #














