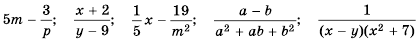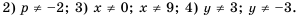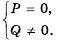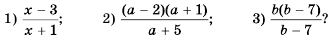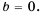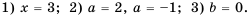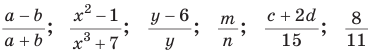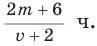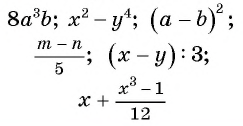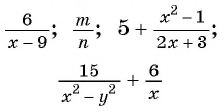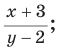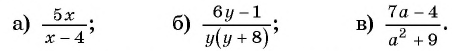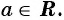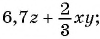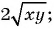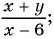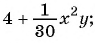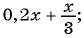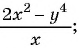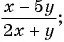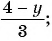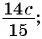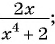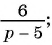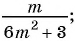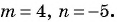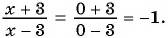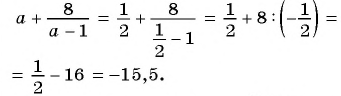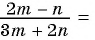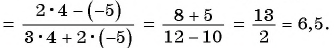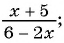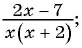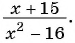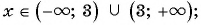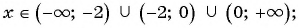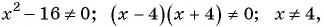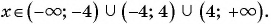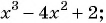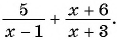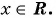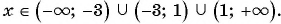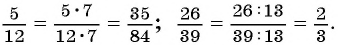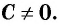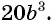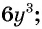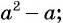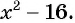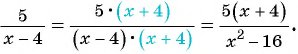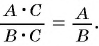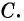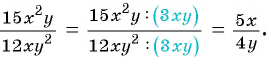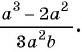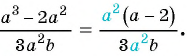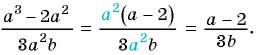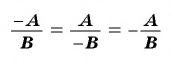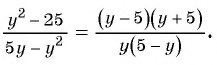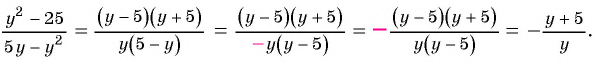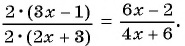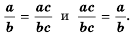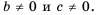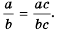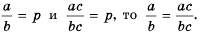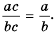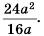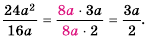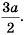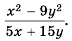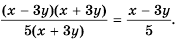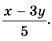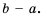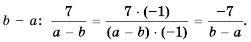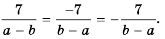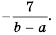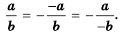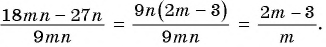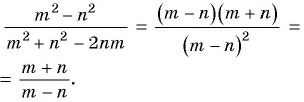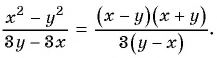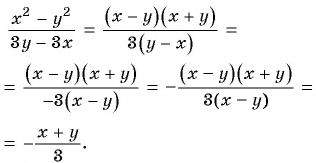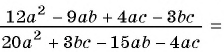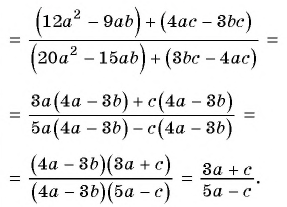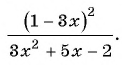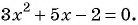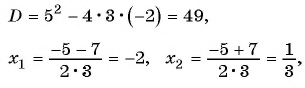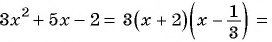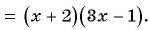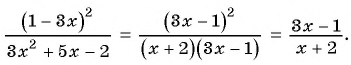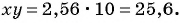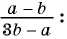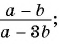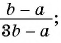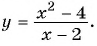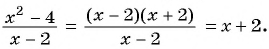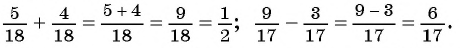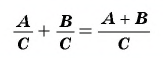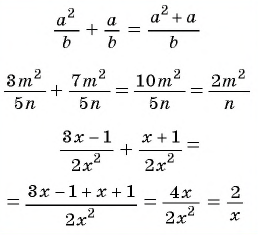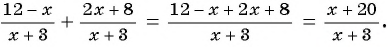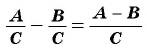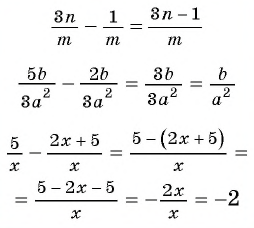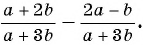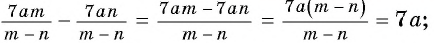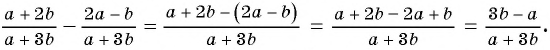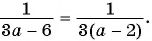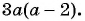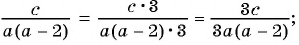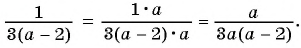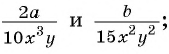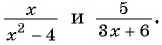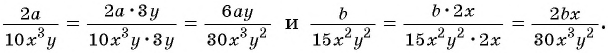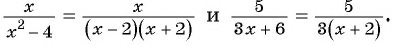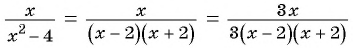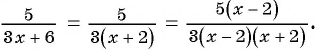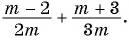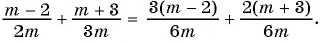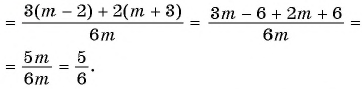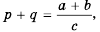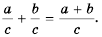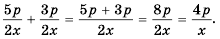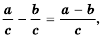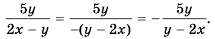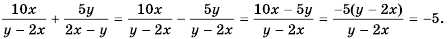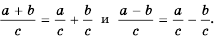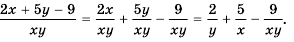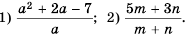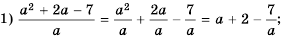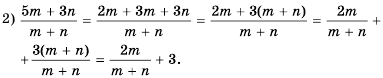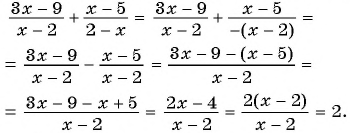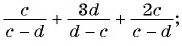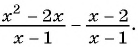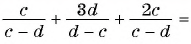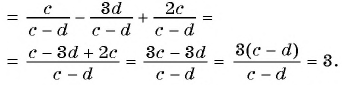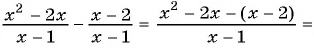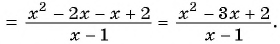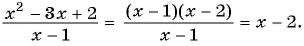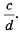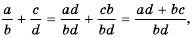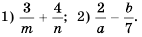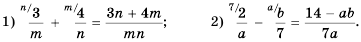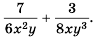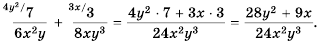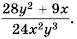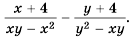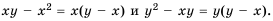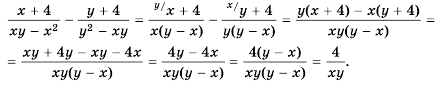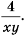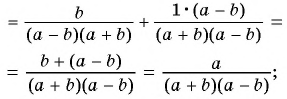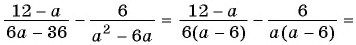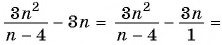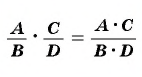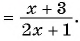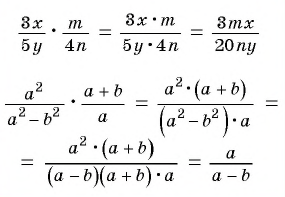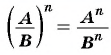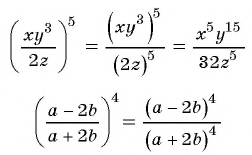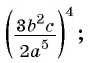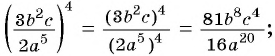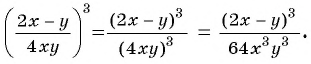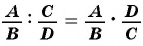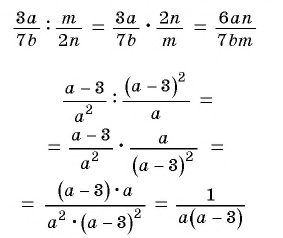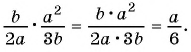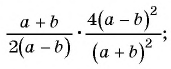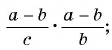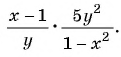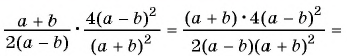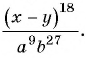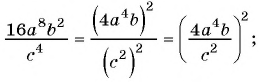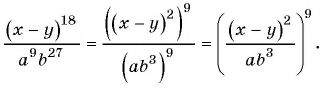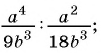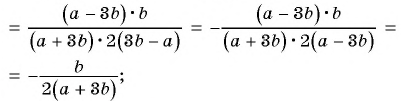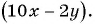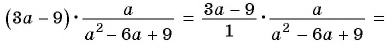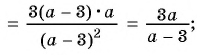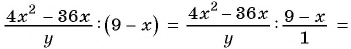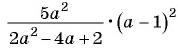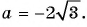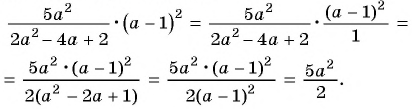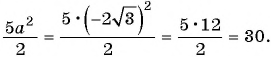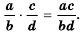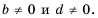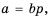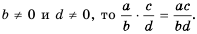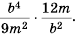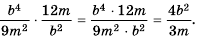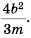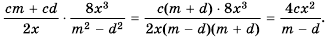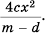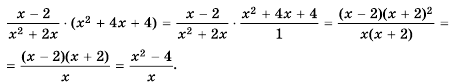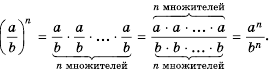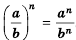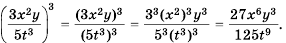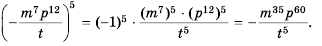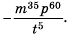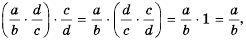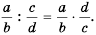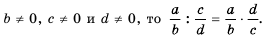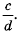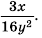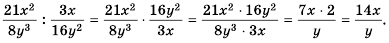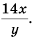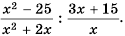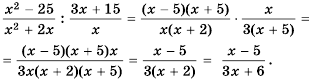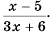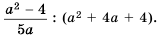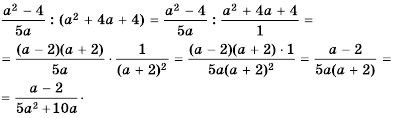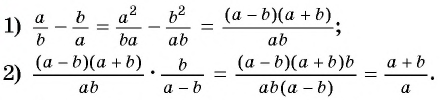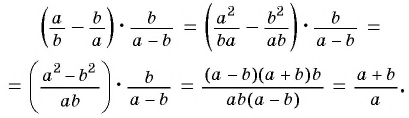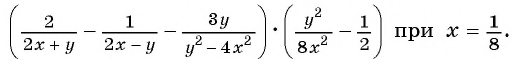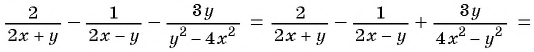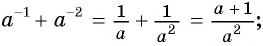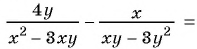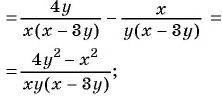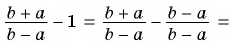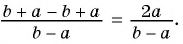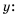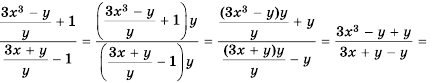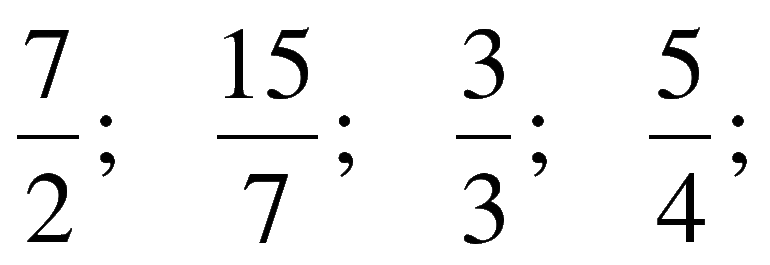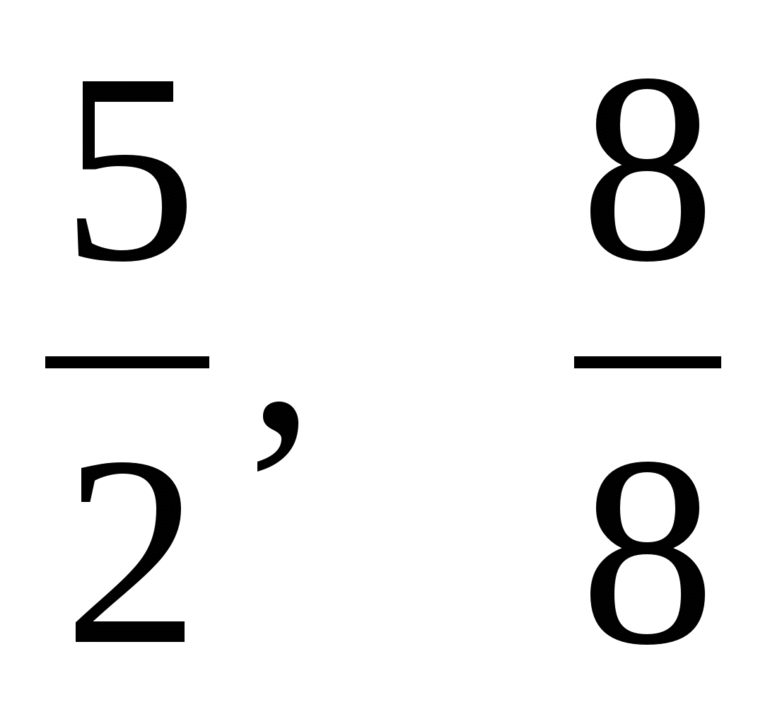Содержание:
Вы уже знакомы с целыми рациональными выражениями, то есть с выражениями, которые не содержат деления на выражение с переменной, например:
Любое целое выражение можно представить в виде многочлена стандартного вида, например:
В отличие от целых выражений, выражения
содержат деление на выражение с переменной. Такие выражения называют дробными рациональными выражениями. Целые рациональные и дробные рациональные выражения называют рациональными выражениями.
Рациональные выражения — это математические выражения, содержащие действии сложения, вычитания, умножения, деления и возведения в степень с целым показателем.
Определение рациональной дроби
Рациональное выражение вида 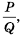
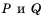
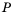
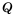
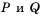
Целое рациональное выражение имеет смысл при любых значениях входящих в него переменных, так как при нахождении его значения выполняют действия сложения, вычитания, умножения и деления на число, отличное от нуля, что всегда выполнимо.
Рассмотрим дробное рациональное выражение — 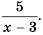
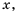
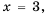
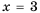
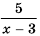
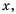
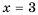
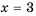
Значения переменных, при которых выражение имеет смысл, называют допустимыми значениями переменных в выражении.
Эти значения образуют область определения выражения, или область допустимых значений переменных в выражении.
Пример:
Найдите допустимые значения переменной в выражении:
Решение:
1) Выражение имеет смысл при любых значениях переменной 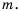
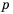
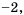
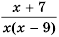
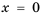
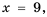
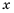
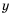
Кратко ответы можно записать следующим образом: 1) 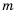
Рассмотрим условие равенства дроби нулю. Так как 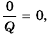
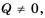
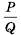
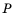
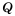
Пример:
При каких значениях переменной равно нулю значение дроби:
Решение:
1) Числитель дроби равен нулю при 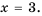
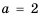

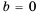
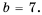
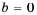
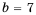
Ответ.
А еще раньше
Древнегреческий математик Диофант (прибл. 
записанных символикой того времени.
Выдающийся английский ученый Исаак Ньютон (1643-1727) в своей монографии «Универсальная арифметика» (1707 г.) определяет дробь следующим образом: «Запись одной из двух величин под другой, ниже которой между ними проведена черта, означает часть или же величину, возникающую при делении верхней величины на нижнюю». В этой работе Ньютон рассматривает не топько обычные дроби, но и рациональные.
Определение: Дробь, числитель и знаменатель которой — многочлены, называется рациональной дробью.
Например, выражения
являются рациональными дробями.
Рациональная дробь является рациональным выражением. Выражения, составленные из чисел, переменных с помощью действий сложения, вычитания, умножения, деления, возведения в натуральную степень, называют рациональными выражениями.
Если рациональное выражение не содержит деления на выражение с переменными, то оно называется целым рациональным выражением.
Рассмотрим задачу: Туристы в первый день проплыли на лодке по течению реки 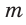
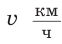
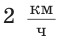
Решение:
Так как за два дня туристы преодолели 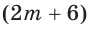
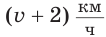
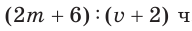
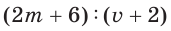
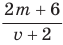
Ответ:
При решении этой задачи получили дробь, в числителе и знаменателе которой записаны многочлены. Такая дробь называется рациональной.
Целые рациональные выражения
Например, выражения 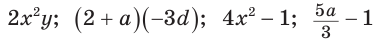
Рациональное выражение, содержащее деление на выражение с переменными, называют дробным рациональным выражением.
Дробные рациональные выражения
Например, выражения 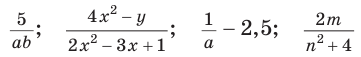
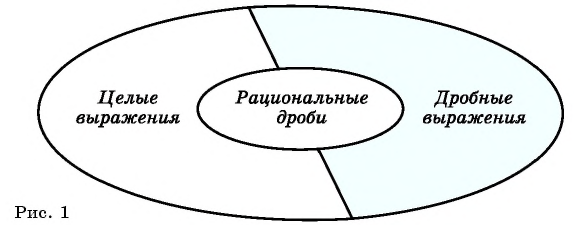
Связь между понятиями «рациональная дробь», «целое рациональное выражение» и «дробное рациональное выражение» иллюстрирует рисунок 1.
Целые рациональные выражения имеют смысл при любых значениях входящих в них переменных.
Например, областью определения выражения 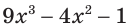
Рациональные выражения:
Дробные рациональные выражения имеют смысл при всех значениях переменных, кроме тех, которые обращают знаменатели дробей в нуль.
Например, выражение 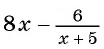
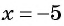
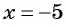
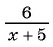
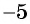
Рациональная дробь 
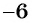
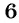
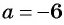
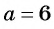
Областью определения рациональной дроби является множество всех значений входящих в нее переменных, кроме тех, которые обращают ее знаменатель в нуль.
Пример №1
Найдите область определения рациональной дроби:
Решение:
а) Областью определения рациональной дроби 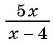
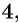
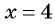
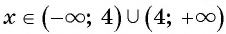
б) Найдем, при каких значениях переменной знаменатель дроби 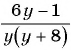
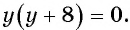
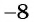
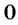
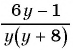
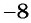
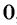
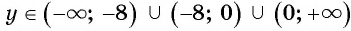
в) Поскольку выражение 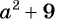
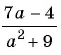
Рациональные выражения:
Пример №2
Какие из следующих выражений:
а)
б)
в)
г)
д) 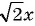
Решение:
Выражения а), в), г) и д) являются рациональными, так как составлены из чисел, переменных и содержат действия сложения, вычитания, умножения и деления. Выражение б) не является рациональным, так как содержит действие извлечения корня из выражения с переменными.
Пример №3
Какие из следующих выражений:
а)
б)
в)
г)
д) 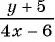
Решение:
Выражения б), в), д) являются дробными рациональными, так как составлены из чисел, переменных, натуральных степеней переменных с помощью действий сложения, вычитания, умножения и содержат действие деления на рациональное выражение с переменными.
Пример №4
Какие из следующих выражений:
а)
б)
в)
г)
д) 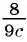
Решение:
Выражения а) — д) являются рациональными дробями, так как каждое из них представляет собой дробь, числитель и знаменатель которой являются многочленами.
Пример №5
Найдите значение выражения:
а) 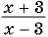
б) 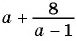
в) 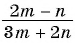
Решение:
а) Подставим 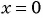
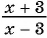
б) При 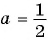
в) Если 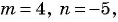
Область определения рациональной дроби
Пример №6
Найдите область определения рациональной дроби:
а)
б)
в)
Решение:
а) Найдем, при каком значении переменной знаменатель дроби обращается в нуль. Для этого решим уравнение 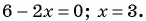
б) 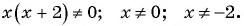
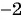
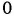
в) 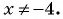
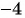
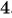
Пример №7
Найдите область определения рационального выражения:
а)
б)
Решение:
а) Выражение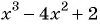
б) Знаменатель первой дроби обращается в нуль при 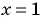
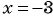
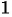
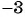
Основное свойство рациональной дроби
Действия с рациональными дробями выполняются по тем же правилам, что с обыкновенными дробями. Так, согласно основному свойству обыкновенных дробей, если числитель и знаменатель дроби умножить или разделить на одно и то же число, не равное нулю, то получится дробь, равная данной.
Например,
Аналогичное свойство можно сформулировать для рациональных дробей.
Если числитель и знаменатель дроби умножить или разделить на одно и то же выражение, не равное нулю, то получится дробь, тождественно равная данной.
Это свойство называют основным свойством дроби.
Для любой рациональной дроби 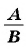
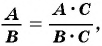
Умножим числитель и знаменатель дроби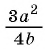
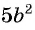
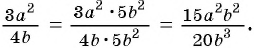
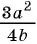
Пример №8
Приведите дробь:
а) 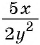
б) 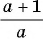
в) 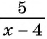
Решение:
а)
б)
в)
Если основное свойство дроби записать справа налево, то получится равенство
Это равенство позволяет дробь 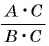
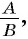
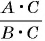
Например, разделим числитель и знаменатель дроби 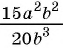
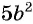
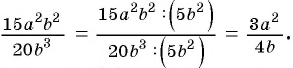
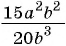
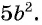
Сократить рациональную дробь — это значит числитель и знаменатель дроби разделить на их общий множитель.
Например, сократим дробь 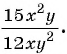
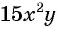
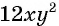
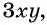
Чтобы сократить рациональную дробь, нужно:
- Разложить (если возможно) числитель и знаменатель дроби на множители.
- Определить общий множитель числителя и знаменателя дроби.
- Разделить числитель и знаменатель данной дроби на общий множитель.
Сократите дробь
(1)
(2) 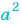
(3)
Пример №9
Сократите дробь:
а)
б)
Решение:
а)
б)
Из основного свойства дроби следует, что 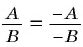
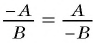
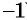
Пример №10
Приведите дробь 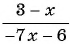
Решение:
Воспользуемся равенством 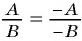
Пример №11
Сократите дробь:
а)
б)
Решение:
а) Разложим знаменатель дроби на множители и получим:
Выражения 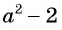
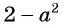
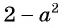
Полученный ответ можно записать в виде 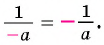
б) Разложим числитель и знаменатель дроби на множители и получим:
Поменяем знаки одного из множителей 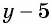
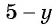
Пример №12
Приведите дробь 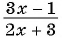
а)
б)
Решение:
а) Умножим числитель и знаменатель дроби на 2 и получим:
б) Умножим числитель и знаменатель дроби на 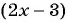
Разберём лекцию подробно:
Вспомним основное свойство обыкновенной дроби: если числитель и знаменатель дроби умножить или разделить на одно и то же натуральное число, то получим дробь, равную данной. Иначе говоря, для любых натуральных чисел 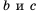
Докажем, что эти равенства являются верными не только для натуральных значений 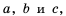
Докажем сначала, что
Пусть 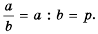
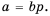
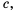
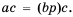
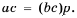
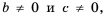
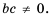
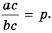
Это равенство является тождеством, следовательно, можем поменять в нем левую и правую части местами:
Это тождество дает возможность заменить дробь 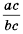
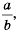
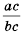
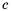
Свойство дроби, выраженное равенствами 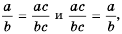
Если числитель и знаменатель дроби умножить или разделить на одно и то же отличное от нуля выражение, то получим дробь, равную данной.
Рассмотрим примеры применения этого свойства для дробей на их области допустимых значений переменной.
Пример №13
Сократите дробь
Решение:
Представим числитель и знаменатель этой дроби в виде произведений, содержащих одинаковый (общий) множитель 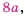
Ответ:
Пример №14
Сократите дробь
Решение:
Разложим на множители числитель и знаменатель дроби: 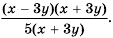
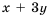
Ответ:
Таким образом, чтобы сократить дробь, нужно:
- разложить на множители числитель и знаменатель дроби, если это необходимо;
- выполнить деление числителя и знаменателя на их общий множитель и записать ответ.
Тождество 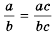
Пример №15
Приведите дробь 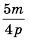
Решение:
Поскольку 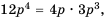
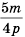
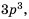
Множитель 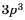
Ответ:
Пример №16
Приведите дробь 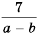
Решение:
Поскольку 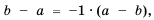
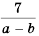
Дробь 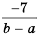
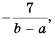
Поэтому
Ответ.
Аналогично, например, 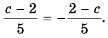
- если изменить знак в числителе (или знаменателе) дроби одновременно со знаком перед дробью, то получим дробь, тождественно равную данной.
Это правило можно записать с помощью тождества:
Пример №17
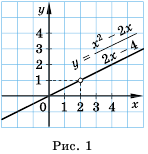
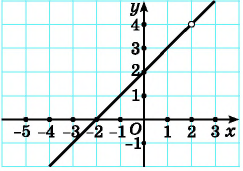
Найдите область определения функции 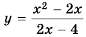
Решение:
Область определения функции — все числа, кроме тех, которые обращают знаменатель 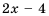
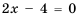
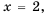
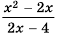
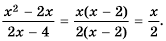
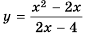
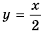
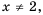
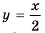
График функции 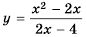
Сокращение рациональных дробей
Пример №18
Сократите дробь
Решение:
Дробь можно сократить на 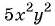
Пример №19
Сократите дробь:
а)
б)
в)
г)
Решение:
а) Разложим на множители числитель дроби и сократим дробь:
б) С помощью формул сокращенного умножения разложим на множители числитель и знаменатель дроби и получим:
в) Разложим на множители числитель и знаменатель дроби:
Множители 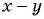
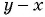
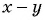
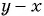
г) После разложения на множители числителя дроби имеем:
Воспользуемся тем, что 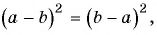
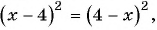
Пример №20
Сократите дробь:
а)
б)
Решение:
а) С помощью способа группировки разложим числитель и знаменатель дроби на множители и сократим дробь:
б)
Пример №21
Сократите дробь:
Решение:
Для разложения на множители знаменателя дроби воспользуемся формулой разложения квадратного трехчлена на множители: 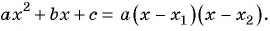
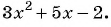
тогда
Сократим дробь:
Пример №22
Упростите выражение 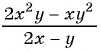
Решение:
Упростим выражение, сократив дробь:
Подставим 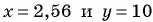
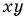
Пример №23
Из данных рациональных дробей выберите дробь, тождественно равную дроби
а)
б)
в)
Решение:
Выполним преобразования:
Дроби 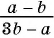
Пример №24
Приведите дробь:
а) 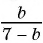
б) 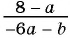
Решение:
Умножим числитель и знаменатель дроби на 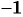
а)
б)
Пример №25
Постройте график функции
Решение:
Областью определения данной функции является множество всех действительных чисел, кроме числа 2.
Сократим дробь 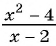
Необходимо построить график функции 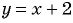
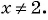
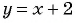
Сложение и вычитание рациональных дробей
Вспомним, как складывают и вычитают обыкновенные дроби. Например:
Сложение и вычитание рациональных дробей выполняются по таким же правилам, что сложение и вычитание обыкновенных дробей.
Чтобы сложить дроби с одинаковыми знаменателями, нужно сложить их числители, а знаменатель оставить тем же.
Затем, если возможно, следует сократить полученную дробь.
Пример №26
Найдите сумму рациональных дробей:
а)
б)
Решение:
а)
б)
Чтобы вычесть дроби с одинаковыми знаменателями, нужно из числителя уменьшаемого вычесть числитель вычитаемого, а знаменатель оставить тем же. Затем, если возможно, следует сократить полученную дробь.
Пример №27
Найдите разность рациональных дробей:
а)
б)
Решение:
а)
б)
При сложении и вычитании обыкновенных дробей с разными знаменателями их приводят к общему знаменателю (например, 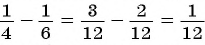
Для того чтобы выполнить сложение или вычитание рациональных дробей с разными знаменателями, их также нужно привести к общему знаменателю.
Чтобы привести рациональные дроби к общему знаменателю, нужно:
- Разложить знаменатель каждой дроби на множители (если это необходимо) и определить общий знаменатель дробей.
- Умножить числитель и знаменатель каждой дроби на недостающие множители из общего знаменателя дробей.
Приведите к общему знаменателю рациональные дроби 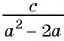
(1) 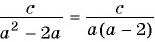
Общий знаменатель
(2)
Пример №28
Приведите к общему знаменателю дроби: а)
б)
Решение:
а) Общим знаменателем данных дробей является одночлен 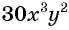
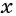
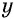
Умножим числитель и знаменатель первой дроби на 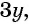
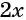
б) Разложим на множители знаменатель каждой дроби и получим:
Умножим числитель и знаменатель первой дроби на 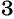
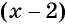
и
Чтобы выполнить сложение (вычитание) рациональных дробей с разными знаменателями, нужно:
- Привести дроби к общему знаменателю.
- Применить правила сложения (вычитания) дробей с одинаковыми знаменателями.
Найдите сумму рациональных дробей
(1)
(2)
Пример №29
Найдите разность рациональных дробей
Решение:
Сложение и вычитание дробей с одинаковыми знаменателями
Вспомним, как сложить дроби с одинаковыми знаменателями. Нужно сложить их числители, а знаменатель оставить тот же. Например:
Запишем это правило в виде формулы:
Это равенство справедливо для любых дробей. Докажем его (при условии
Пусть 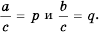
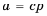
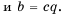
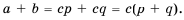
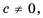
следовательно,
Сформулируем правило сложения дробей с одинаковыми знаменателями:
чтобы сложить дроби с одинаковыми знаменателями, нужно сложить их числители, а знаменатель оставить тот же.
Пример №30
Аналогично можно доказать тождество
при помощи которого записывают правило вычитания дробей с одинаковыми знаменателями.
Сформулируем правило вычитания дробей с одинаковыми знаменателями:
чтобы вычесть дроби с одинаковыми знаменателями, нужно от числителя уменьшаемого отнять числитель вычитаемого, а знаменатель оставить тот же.
Пример №31
Рассмотрим еще несколько примеров.
Пример №32
Найдите сумму и разность дробей
Решение:
Ответ.
Пример №33
Упростите выражение
Решение:
Ответ:
Пример №34
Найдите сумму
Решение:
Так как 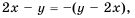
Тогда
Ответ:
Если в тождествах 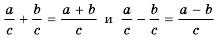
С помощью этих тождеств дробь, числитель которой является суммой или разностью нескольких выражений, можно записать в виде суммы или разности нескольких дробей.
Пример №35
Пример №36
Запишите дробь в виде суммы или разности целого выражения и дроби:
Решение:
Ответ.
Пример №37
Выполните сложение рациональных дробей:
а)
б)
Решение:
а)
б)
Пример №38
Найдите разность рациональных дробей:
а)
б)
в)
Решение:
а)
б)
в)
Пример №39
Выполните действия:
а)
б)
Решение:
а) Знаменатели дробей отличаются только знаком. Поменяем знак в знаменателе второй дроби и перед этой дробью и получим:
б)
Пример №40
Выполните действия:
а)
б)
Решение:
а)
б)
Разложим на множители квадратный трехчлен в числителе дроби и сократим дробь:
Сложение и вычитание дробей с разными знаменателями
Если дроби имеют разные знаменатели, то их, как и обычные дроби, сначала приводят к общему знаменателю, а потом складывают или вычитают по правилу сложения или вычитания дробей с одинаковыми знаменателями.
Рассмотрим, как прибавить дроби 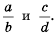
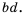
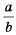
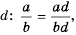
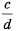
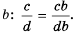
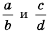
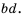
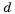
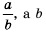
Описанную последовательность действий для сложения дробей с разными знаменателями можно записать так:
или сокращенно:
Аналогично выполняют и вычитание дробей с разными знаменателями:
Пример №41
Выполните действие:
Решение:
Общим знаменателем двух или более дробей может быть не только произведение их знаменателей. Вообще у дробей есть бесконечно много общих знаменателей. Часто при сложении и вычитании дробей с разными знаменателями удается найти более простой общий знаменатель, чем произведение знаменателей этих дробей. В таком случае говорят о простейшем общем знаменателе (аналогично наименьшему общему знаменателю числовых дробей).
Рассмотрим пример, где знаменатели дробей — одночлены.
Пример №42
Выполните сложение
Решение. Общим знаменателем данных дробей можно считать одночлен 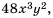
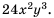
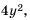
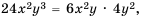
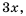
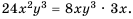
Ответ:
Обратите внимание, что в примере 2 при приведении дробей к общему знаменателю дополнительные множители 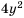
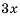
Рассмотрим пример, в котором знаменателями дробей являются многочлены.
Пример №43
Выполните вычитание
Решение:
Чтобы найти общий знаменатель, разложим знаменатели на множители:
Простейшим общим знаменателем дробей будет выражение 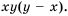
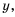
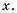
Ответ.
Таким образом, чтобы выполнить сложение или вычитание дробей с разными знаменателями, нужно:
- разложить на множители знаменатели дробей, если это необходимо;
- найти общий знаменатель, лучше простейший;
- записать дополнительные множители;
- найти дробь, которая является суммой или разницей данных дробей;
- упростить эту дробь и получить ответ.
Аналогично выполняют сложение и вычитание целого выражения и дроби.
Пример №44
Упростите выражение
Решение:
Запишем выражение 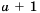
Ответ:
Пример №45
Выполните сложение рациональных дробей:
а)
б)
в)
г)
Решение:
а)
б)
в)
г)
Пример №46
Выполните вычитание:
а)
б)
в)
г)
д)
Решение:
а)
б)
в)
г)
д) Разложим на множители квадратный трехчлен в знаменателе первой дроби и получим:
Пример №47
Представьте в виде дроби выражение
Решение:
Умножение и деление рациональных дробей
Вспомним, как умножают и делят обыкновенные дроби.
Правила умножения и деления рациональных дробей аналогичны правилам умножения и деления обыкновенных дробей.
Произведение рациональных дробей равно дроби, числитель которой равен произведению числителей данных дробей, а знаменатель равен произведению знаменателей данных дробей.
Чтобы найти произведение рациональных дробей, нужно:
- Произведение числителей данных дробей записать в числителе новой дроби, а произведение знаменателей данных дробей записать в знаменателе новой дроби.
- Сократить полученную дробь, если это возможно.
Найдите произведение рациональных дробей
(1)
(2)
Пример №48
Найдите произведение рациональных дробей:
а)
б)
Решение:
а)
б)
Правило умножения рациональных дробей можно использовать при возведении рациональной дроби в степень. Например:
Обобщим этот прием и получим правило:
Чтобы возвести рациональную дробь в степень, нужно возвести в эту степень числитель дроби и полученный результат записать в числителе новой дроби, возвести в эту степень знаменатель дроби и полученный результат записать в знаменателе новой дроби.
Пример №49
Возведите в степень дробь:
а)
б)
Решение:
а)
б)
Чтобы разделить одну рациональную дробь на другую, нужно делимое умножить на дробь, обратную делителю.
Пример №50
Найдите частное:
а)
б)
Решение:
а)
б)
Пример №51
Представьте в виде дроби рациональное выражение:
а)
б)
Решение:
а) Представим множитель 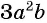
Выполним умножение дробей:
б) Представим выражение 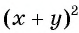
Пример №52
Выполните умножение рациональных дробей:
а)
б)
Решение:
а)
б)
Пример №53
Представьте в виде рациональной дроби произведение:
а)
б)
в)
Решение:
а)
б)
в)
Пример №54
Представьте в виде рациональной дроби выражение:
а)
б)
в)
Решение:
а)
б)
в)
Пример №55
Представьте в виде степени рациональную дробь:
а)
б)
Решение:
а)
б)
Пример №56
Выполните деление рациональных дробей:
а)
б)
в)
г)
д)
Решение:
а)
б)
в)
г)
д) Воспользуемся формулой разложения квадратного трехчлена на множители и получим:
Тогда
Пример №57
Выполните действия:
а)
б)
в)
Решение:
а)
б)
в) Разложим на множители многочлен, применив способ группировки:
Тогда
Пример №58
Найдите значение выражения
при
Решение:
Выполним деление:
При 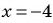
Пример №59
Найдите значение выражения
при
Решение:
Выполним умножение:
При 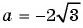
Умножение дробей
Напомним, что произведением двух обыкновенных дробей является дробь, числитель которой равен произведению числителей, а знаменатель — произведению знаменателей данных дробей:
Докажем, что это равенство является тождеством для любых значений 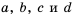
Пусть 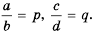
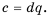
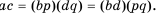
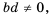
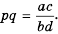
Сформулируем правило умножения дробей.
Чтобы умножить дробь на дробь, нужно перемножить отдельно числители и отдельно знаменатели сомножителей и записать первый результат в числителе, а второй — в знаменателе произведения дробей.
Пример №60
Выполните умножение
Решение:
Ответ:
Пример №61
Найдите произведение
Решение.
Используем правило умножения дробей и разложим на множители числитель первой дроби и знаменатель второй:
Ответ.
Обратите внимание, что в примерах 1 и 2 при умножении дробей мы не находили сразу же результат умножения числителей и знаменателей. Сначала мы записали произведения в числителе и в знаменателе по правилу умножения дробей, потом сократили полученную дробь, так как она оказалась сократимой, а уже затем выполнили умножение в числителе и в знаменателе и записали ответ. Целесообразно это учитывать и в дальнейшем.
Пример №62
Умножить дробь 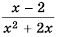
Решение:
учитывая, что 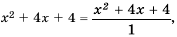
Ответ.
Правило умножения дробей можно распространить на произведение трех и более множителей.
Пример №63
Возведение дроби в степень
Рассмотрим возведение дроби 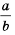
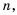
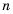
По определению степени и правилу умножения дробей имеем:
Следовательно:
Сформулируем правило возведения дроби в степень.
Чтобы возвести дробь в степень, нужно возвести в эту степень числитель и знаменатель и первый результат записать в числитель, а второй — в знаменатель дроби.
Пример №64
Пример №65
Представьте выражение 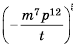
Решение:
Ответ:
Деление дробей
Напомним, чтобы найти частное двух обыкновенных дробей, нужно делимое умножить на дробь, обратную делителю:
Формулой это можно записать так:
Докажем, что это равенство является тождеством для любых значений 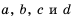
Так как:
то по определению частного имеем:
Следовательно, если
Дробь 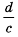
Сформулируем правило деления дробей.
Чтобы разделить одну дробь на другую, нужно первую дробь у множить на дробь, обратную второй.
Пример №66
Разделите дробь 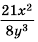
Решение:
Ответ.
Пример №67
Выполните деление
Решение:
Ответ:
Пример №68
Упростите выражение:
Решение:
Так как 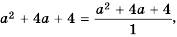
Ответ:
Преобразования рациональных выражений
При решении многих задач требуется упрощать рациональные выражения, приводя их к рациональным дробям. Для этого выполняют преобразования рациональных выражений.
Чтобы преобразовать рациональное выражение, нужно:
- Установить порядок действий в выражении.
- Выполнить действия по порядку, используя правила сложения, вычитания, умножения и деления рациональных дробей.
Упростите выражение:
(1)
(2)
Пример №69
Представьте выражение 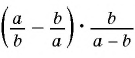
Решение:
(1) Сначала необходимо выполнить вычитание выражений, стоящих в скобках, а затем выполнить умножение.
(2)
Преобразование рационального выражения можно выполнить не по действиям, а «цепочкой». В данном случае получим:
Пример №70
Найдите значение выражения
Решение:
Упростим выражение, выполнив действия по порядку:
1)
2)
3)
При 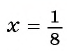
Преобразования рациональных выражений можно выполнять наряду с другими, ранее изученными преобразованиями.
Пример №71
Упростите выражение 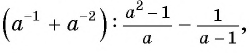
Решение:
1)
2)
3)
Правила преобразования рациональных выражений можно использовать и для преобразования выражений, содержащих корни.
Пример №72
Сократите дробь:
а)
б)
в)
Решение:
а)
б)
в)
Пример №73
Упростите выражение
Решение:
1)
2)
3)
Пример №74
Представьте выражение 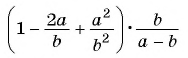
Решение:
1)
2)
Пример №75
Найдите значение выражения 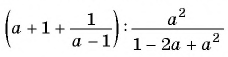
Решение:
Преобразуем данное выражение «цепочкой»:
При 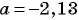
Пример №76
Упростите выражение
Решение:
1) Корнями квадратного трехчлена 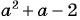
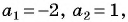
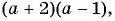
2)
Пример №77
Докажите, что значение выражения
не зависит от значений переменных.
Решение:
Значение выражения при различных значениях переменных из области его определения можно найти, предварительно упростить его:
1)
2)
Получили, что результат упрощения равен числу 1, значит при любых значениях переменных из области определения значение данного выражения равно 1, т. е. не зависит от значений переменных.
Пример №78
Упростите выражение
Решение:
Запишем дробь в виде частного и получим:
Пример №79
Упростите выражение
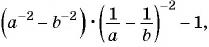
Решение:
1)
2)
3)
4)
Пример №80
Примените к выражению алгоритм сокращения рациональной дроби:
а)
б)
Решение:
а)
б)
Пример №81
Упростите выражение
Решение:
1)
2)
Пример №82
Найдите значение выражения 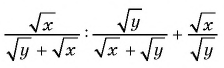
Решение:
Упростим данное выражение:
При 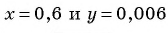
- Заказать решение задач по высшей математике
Тождественные преобразования рациональных выражений
Рассмотрим примеры преобразований рациональных выражений.
Пример №83
Докажите тождество
Решение:
Упростим левую часть равенства:
С помощью тождественных преобразований мы привели левую часть равенства к правой. Следовательно, равенство является тождеством.
Пример №84
Упростите выражение
Решение:
Сначала выполним действие в каждой из скобок, а потом — действие деления:
Ответ:
Решение можно было записать и в виде «цепочки»:
Каждое выражение, содержащее сумму, разность, произведение и частное рациональных дробей, можно представить в виде рациональной дроби.
Пример №85
Докажите, что при всех допустимых значениях переменных значение дроби 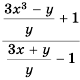
Решение:
Можно представить эту дробь в виде частного 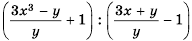
А можно, используя основное свойство дроби, умножить числитель и знаменатель данной дроби на их общий знаменатель, то есть на
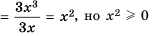
- Функция в математике
- Наибольшее и наименьшее значения функции
- Раскрытие неопределенностей
- Дробно-рациональные уравнения
- Система показательных уравнений
- Непрерывные функции и их свойства
- Правило Лопиталя
- Вычисления в Mathematica с примерами
Рациональная дробь и ее основное свойство
Целые выражения в алгебре представляют собой такие выражения, которые состоят из чисел и переменных, полученных путем арифметических действия сложения, вычитания, умножения и деления на число, не равное нулю. Для дробных выражений характерно также использование деления на выражение, содержащее переменные. Данные выражения, целые и дробные, объединены общим понятием рациональных выражений.
Рациональная дробь является дробью, в которой числитель и знаменатель представляют собой многочлены.
Рациональная дробь (рациональная функция) является отношением пары многочленов (P_{m} (x)) и (Q_{n} (x)) со степенями m и n соответственно:
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
(R(x)=frac{P_{m} (x)}{Q_{n} (x)} =frac{a_{0} x^{m} +a_{1} x^{m-1} +…+a_{m-1} x+a_{m} }{b_{0} x^{n} +b_{1} x^{n-1} +…+b_{n-1} x+b_{n} } ,, , a_{0} ne 0,b_{0} ne 0)
Объяснение основного свойства дроби: когда числитель и знаменатель какой-либо рациональной дроби умножают на одинаковый многочлен, который не равен тождественно нулю, получается дробь, равная начальной.
Ключевое свойство рациональной дроби можно выразить формулой:
(frac{P}{Q} = frac{PR}{QR})
Данное тождество является справедливым равенством, если (R neq 0) и (Q neq 0), а R является целым рациональным выражением.
Допустимо умножать и делить на одинаковое число, которое не равно нулю, одночлен или многочлен, числитель и знаменатель рациональной дроби. В качестве примера можно преобразовать следующее выражение подобного типа:
(frac{frac{1}{3} x^{3}- frac{1}{2} x^{2}+1}{frac{1}{4} x^{2}- frac{1}{6} x+frac{1}{2}} = frac{12(frac{1}{3} x^{3}- frac{1}{2} x^{2}+1)}{12(frac{1}{4} x^{2}- frac{1}{6} x+frac{1}{2})} = frac{4 x^{3}- 6x^{2}+12}{3 x^{2}- 2x+6})
Используя свойство дроби, можно упростить работу и изменять знаки у элементов дроби. Когда числитель и знаменатель дроби (frac{P}{Q}) умножают на -1, в результате получается (frac{P}{Q} = frac{-P}{-Q}.) Значение дроби в итоге останется прежним при смене знаков одновременно и в числителе, и в знаменателе.
Когда меняют знак лишь у числителя, либо только у знаменателя, дробь меняет свой знак:
(frac{-P}{Q} =- frac{P}{Q})
(frac{P}{-Q} = -frac{P}{Q})
Можно сделать вывод, что:
(frac{P}{Q} = -frac{-P}{Q}=-frac{P}{-Q})
В качестве самостоятельного примера приведем выражение:
(frac{3x — 2}{3x + 4} = -frac-{3x — 2}{3x + 4} = -frac{2-3x}{3x + 4})
Область определения рациональной дроби
Допустимыми значениями переменных называют такие значения переменных, при которых выражение приобретает смысл.
Область определения рациональной дроби представляет собой все значения для переменных, которые не обращают знаменатель в нуль.
Пример 1
(15x^{2} — 11x + 3x^{2} – 4)
В данном случае областью определения являются все действительные числа, за исключением таких чисел, при которых (x^{2} – 4 = 0), то есть кроме 2 и -2.
Рациональные дроби и операции над ними
Тождеством называют равенство, которое является верным при любых допустимых значениях переменных, входящих в состав этого равенства. Арифметические действия с рациональными дробями характеризуются следующими свойствами:
- когда а, b, с являются многочленами, при этом с обладает не нулевым значением, то:
(frac{a}{c}+frac{b}{c} = frac{a+b}{c})
(frac{a}{c}-frac{b}{c} = frac{a-b}{c})
- когда a, b, c, d являются многочленами при b и d, которые тождественно не равны нулю, то:
(frac{a}{b}timesfrac{c}{d} = frac{ac}{bd})
((frac{a}{b})^{n} = frac{a^{n} }{b^{n}})
- в том случае, когда a, b, с, d являются многочленами, при этом b, с и d тождественно не равны нулю, то:
(frac{a}{b}div frac{c}{d} = frac{ad}{bc})
Сокращение рациональных дробей
При сокращении дробей требуется разделить числитель и знаменатель дроби на единый множитель. Такая возможность доступна благодаря ключевому свойству дроби.
В том случае, когда нужно выполнить сокращение рациональной дроби, следует разложить на множители и числитель, и знаменатель. При наличии у числителя и знаменателя общих множителей представляется возможным сократить такую дробь. При отсутствии единых множителей подобное преобразование невозможно.
Приведение рациональных дробей к общему знаменателю
Общий знаменатель для нескольких дробей, являющихся рациональными, представляет собой такое целое рациональное выражение, которое можно разделить на знаменатель каждой из дробей.
Пример 2
Определим общий знаменатель дробей:
(frac{x}{x+2} ) и (frac{3x-1}{x-2})
Таким знаменателем является многочлен: ((х+2)(х-2).) Это объясняется возможностью разделить данный многочлен на ((х + 2)) и на ((х – 2)).
В качестве общего знаменателя также можно выбрать следующие выражения:
(3(x+2)^{2} times (x-2))
(5x^{2} (x+2) times (x-2) ^{3})
Следует выбрать такой общий знаменатель, на который можно поделить любой другой общий знаменатель. Наиболее простой знаменатель является наименьшим общим знаменателем.
Таким образом, для рассмотренного выражения наименьшим общим знаменателем является ((х+2)(х-2)):
(frac{x}{x+2} = frac{x(x-2)}{(x+2)(x-2)})
( frac{3x-1}{x-2} = frac{(3x-1)(x+2)}{(x+2)(x-2)})
Рассмотренные в примере дроби были приведены к общему знаменателю с помощью умножения числителя и знаменателя первой дроби на ((х-2)). Одновременно с этим числитель и знаменатель второй дроби умножили на (х+2). Многочлены ((х-2) ) и ((х+2)) являются дополнительными множителями.
Дополнительный множитель для заданной дроби равен частному от деления общего знаменателя на знаменатель данной дроби.
Алгоритм действий для приведения нескольких рациональных дробей к единому знаменателю:
- Разложить знаменатель каждой из дробей на множители.
- Определить общий знаменатель путем добавления в произведение всех множителей, которые были получены ранее. Когда какой-либо множитель представлен в нескольких разложениях, то следует взять его с показателем степени, соответствующим максимальному значению из тех, которые имеются.
- Вычислить множители, являющиеся дополнительными для каждой из представленных дробей с помощью деления единого знаменателя на знаменатель дроби.
- Умножить числитель и знаменатель дробей на определенный дополнительный множитель с последующим приведением дробей к общему знаменателю.
Сложение и вычитание рациональных дробей
Сумма пары или большего количества рациональных дробей, которые имеют одинаковые знаменатели, тождественно равна дроби с аналогичным знаменателем и с числителем, соответствующим сумме числителей дробей, участвующих в сложении:
(frac{P1}{Q}+frac{P2}{Q} = frac{P1+P2}{Q})
Данное правило распространяется и на действия с вычитанием дробей, имеющих одинаковые знаменатели:
(frac{P1}{Q}-frac{P2}{Q} = frac{P1-P2}{Q})
Умножение и деление рациональных дробей
Произведение пары или большего количества рациональных дробей тождественно равно дроби с числителем, равным произведению числителей, и знаменателем, который соответствует произведению знаменателей перемножаемых дробей:
(frac{P1}{Q1}times frac{P2}{Q2} = frac{P1times P2}times {Q1times Q2})
Частное от деления пары рациональных дробей тождественно равно дроби с числителем, равным произведению числителя первой дроби и знаменателя второй дроби, и знаменателем, который является произведением знаменателя первой дроби и числителя второй дроби:
(frac{P1}{Q1}div frac{P2}{Q2} = frac{P1times Q2}div {Q1times P2})
В том случае, когда требуется умножить или разделить рациональную дробь на многочлен, можно использовать данные правила. Перед вычислениями потребуется перевести заданный многочлен в дробь, знаменатель которой равен единице.
С учетом опции сокращения рациональной дроби, полученной по итогам умножения или деления рациональных дробей, обычно при решении задач в первую очередь раскладывают числители и знаменатели начальных дробей на множители, а затем переходят к выполнению умножения или деления.
Возведение рациональной дроби в целую степень
При возведении рациональной дроби ( frac{P}{Q}) в натуральную степень n требуется возвести в указанную степень по отдельности числитель и знаменатель дроби. Первое выражение является числителем, а второе выражение соответствует знаменателю результирующей дроби:
((frac{P}{Q})^{n}=frac{P^{n}}{Q^{n}})
В том случае, когда необходимо возвести дробь в целую отрицательную степень, потребуется применить тождество:
((frac{P}{Q})^{-n}=frac{Q^{n}}{P^{n}})
Данное тождество является справедливым равенством для всех переменных, при которых (P neq 0), (Qneq 0).
Преобразование рациональных выражений
В процессе преобразования какого-либо рационального выражения складывают, вычитают, умножают и делят рациональные дроби, а также возводят в натуральную степень. Любое рациональное выражение преобразуется в дробь с числителем и знаменателем в виде целых выражений. Это является целью тождественных преобразований рациональных выражений.
Пояснения на примерах
Задача 1
Требуется выполнить сокращение дроби:
(frac{ x^{2} -3xy }{9y^{2} — x^{2}})
Решение
Выполним преобразования:
(x^{2} -3xy = x(x -3y))
(9y^{2} — x^{2} = -( x^{2} — 9y^{2}) = -(x- 3y)(x+3y))
Таким образом:
(frac{ x^{2} -3xy }{9y^{2} — x^{2}} = frac{ x(x -3y)}{ -(x- 3y)(x+3y)} =- frac{ x}{ x+3y})
При (x-3y neq 0 ) сокращение дроби выполнено.
Задача 2
Имеются дроби, которые требуется привести к общему знаменателю:
(frac{a}{12a^{2} – 12b^{2}})
(frac{b}{18a^{3} + 18a^{2}b})
(frac{a+b}{24a^{2} — 24ab})
Решение
В первую очередь следует разложить знаменатели дробей на множители:
(12a^{2} – 12b^{2} = 12(a – b) (a + b))
(18a^{3} + 18a^{2}b = 18a^{2}(a+b))
(24a^{2} — 24ab = 24a(a – b))
В единый знаменатель следует записать множители:
((a-b)), ((a+b)), (a^{2})
Кроме того, в общий знаменатель нужно включить минимальное общее кратное чисел 12, 18, 24, то есть:
(К (12, 18, 24) = 72)
В результате единый знаменатель равен:
(72a^{2}times (a-b)(a+b))
Дополнительным множителем в случае первой дроби является (6a^{2}).
Дополнительный множитель для второй дроби имеет вид (4(a-b)).
В случае третьей дроби дополнительный множитель равен (3a(a+b)).
Таким образом:
(frac{6a^{3}}{72a^{2}(a-b)(a+b)})
(frac{4b(a-b)} {72a^{2}(a-b)(a+b)})
(frac{3a(a+b)^{2}}{72a^{2}(a-b)(a+b)})
В результате дроби приведены к общему знаменателю.
Задача 3
Требуется упростить выражение:
(frac{x^{3}}{x+y} +frac{y^{3}}{x+y})
Решение
В этом случае требуется выполнить сложение рациональных дробей, у которых отличаются знаменатели. Используя алгоритм сложения, приведем дроби к общему знаменателю. Далее выполним арифметические действия с дробями, имеющими одинаковые знаменатели:
(frac{x^{3}}{x+y} +frac{y^{3}}{x+y} = frac{x^{3}+ y^{3}}{x+y} = frac {(x+y)(x^{2}-xy+y^{2}}{x+y} = x^{2} – xy + y^{2})
Ответ: (x^{2} – xy + y^{2})
Задача 4
Требуется упростить выражение:
(frac{3}{2x^{2}+2x} +frac{2x-1}{x^{2}-1} -frac{2}{x})
Решение
Выполним преобразования:
(2x^{2}+2x = 2x (x+1))
(x^{2} – 1 = (x-1)(x+1))
Таким образом:
(frac{3}{2x^{2}+2x} +frac{2x-1}{x^{2}-1} -frac{2}{x} = frac{3(x-1) + 2x(2x-1)-4(x-1)(x+1)}{2x(x-1)(x+1)} = frac{x+1}{2x(x-1)(x+1)} = frac{1}{2x(x-1)})
Ответ: (frac{1}{2x(x-1)})
Задача 5
Необходимо перемножить две рациональные дроби:
(frac{x^{2} + 2x +1}{18x^{3}} times frac{9x^{4} }{x^{2}-1})
Решение
Выполним преобразования:
(frac{x^{2} + 2x +1}{18x^{3}} = frac{(x+1)^{2}}{18x^{3}})
(frac{9x^{4} }{x^{2}-1} = frac{9x^{4} }{(x-1)(x+1)})
С помощью правила умножения дробей вычислим:
(frac{(x+1)^{2}}{18x^{3}}times frac{9x^{4} }{(x-1)(x+1)} = frac{(x+1)x^{2}times 9x^{4}}{18x^{3}(x-1)(x+1)} = frac{x(x+1)}{2(x-1)})
Ответ: (frac{x(x+1)}{2(x-1)})
Задача 6
Нужно найти частное дробей:
(frac{a^{3} – 2a^{2}}{ 3a+3}div frac{a^{2} – 4}{ 3a^{2} +6a+3})
Решение
Выполним преобразования:
(frac{a^{3} – 2a^{2}}{ 3a+3} = frac{a^{2}(a-2)}{ 3(a+1)})
(frac{a^{2} – 4}{ 3a^{2} +6a+3} = frac{(a-2)(a+2)}{ 3(a+1)^{2}})
С помощью правила деления дробей выполним вычисления:
(frac{a^{3} – 2a^{2}}{ 3a+3}div frac{a^{2} – 4}{ 3a^{2} +6a+3} = frac{a^{2}(a-2)}{ 3(a+1)} div frac{(a-2)(a+2)}{ 3(a+1)^{2}} = frac{a^{2}(a-2)times 3(a+1)^{2}}{ 3(a+1)(a-2)(a+2)} = frac{a^{2}(a+1)}{ a+2})
Ответ: (frac{a^{2}(a+1)}{ a+2})
Задача 7
Дана дробь, которую требуется возвести в степень:
((frac{2x^{2}y^{3}}{3z^{5}})^{3})
Решение
Используя правила возведения в степень для дроби и одночлена, получим:
((frac{2x^{2}y^{3}}{3z^{5}})^{3} = frac{(2x^{2}y^{3})^{3}}{(3z^{5})^{3}} = frac{8x^{6}y^{9}}{27z^{15}})
Ответ: (frac{8x^{6}y^{9}}{27z^{15}})
Задача 8
Имеется некое выражение, которое нужно преобразовать в дробь:
((frac{(a+b)^{2}(a-b) ^{3}}{(a+2b)^{4}})^{-5})
Решение
((frac{(a+b)^{2}(a-b) ^{3}}{(a+2b)^{4}})^{-5} = (frac{(a+2b)^{4}}{(a+b)^{2}(a-b) ^{3} })^{5} = frac{(a+2b)^{20}}{(a+b)^{10}(a-b) ^{15} })
Ответ: (frac{(a+2b)^{20}}{(a+b)^{10}(a-b) ^{15}})
Общие сведения
Математика — наука о числах и действиях над ними. Значение, которое можно записать в виде обыкновенной дроби, называют рациональным. Оно состоит из целого числа в числителе и натурального в знаменателе. Простое выражение можно представить как бесконечную десятичную дробь. Множество рациональных чисел обозначают латинской буквой Q. Если действительное значение не рациональное, оно иррациональное.
Рациональные дроби — это конструкции над многочленами. Это следует из того, что делимое и делитель представляют собой сумму нескольких одночленов. Если в выражении стоит знак минус, на него не стоит обращать внимание, ведь он относится к числовому коэффициенту одночлена, поэтому многочлен всё равно является суммой. Например, -4/d2 * (b — c), (f + 2,67 * f + 2 3/8 — f2 * y* t)/(f2 + d2 +42).
Выражения могут быть представлены в нестандартном виде, поэтому приходится выполнять дополнительные преобразования. Это возможно, так как делимое и делитель являются самодостаточными. Упрощения выполняются путём разложения на множители. При этом по возможности следует выполнять действия как для числителя, так и знаменателя. Операции преобразования включают в себя:
- сокращение;
- приведение к общему знаменателю и нахождению дополнительных членов;
- вынесение общего множителя за скобку.
Наиболее часто вызывает сложность подбор общего знаменателя. Это приведение основывается на основном свойстве дроби. Согласно ему, умножение на ненулевой многочлен одновременно делимого и делителя не приводит к изменению результата. Отсюда следует, что числитель и знаменатель можно возводить в квадрат, извлекать корень.
Для успешного выполнения действий важно знать формулы сокращённого умножения. Это базисные знания, без которых решать рациональные дроби в 8 классе будет невозможно.
Всего используется 7 теорем: разность кубов и квадратов, произведение разности и суммы, куб суммы и разности, умножение на неполный квадрат. Используя знания, полученные в седьмом классе, многие операции можно выполнять в уме и приводить многочлен к стандартному виду без предварительного раскрытия скобок.
Свойства дроби
Пусть имеется множество, каждому члену которого поставлено в соответствие число игрек. Про такое положение говорят, что множеству задана числовая функция: y = f (x), где x Є D. Описывается область определением функции и обозначается как D (f (x)). Множество можно представить как отношение двух многочленов. Когда в числителе стоит многочлен энной степени, а в знаменателе эмной, то f (x) называют рациональным отношением или дробью.
Такие выражения обладают рядом свойств. Основное из них выражают формулой: P (x)/Q (x) = P (x) * R (x) / Q (x) * R (x). Справедливо оно лишь для случая, при котором множества Q (x) и R (x) неравны нулю, при этом R (x) является многочленом. Формулировка свойства звучит следующим образом: делимое и делитель можно помножить на одинаковое выражение. Например, им может быть число, одночлен или другой многочлен.
К другим свойствам относят:
- ассоциативность;
- коммутативность;
- дистрибутивность;
- транзитивность.
Если равенство f/g =y/x справедливо, при этом y/x = n/m, верным будет и выражение: f/g = n/m. Отсюда следует, что рациональную дробь можно превратить в обыкновенную, если её делитель и делимое можно умножить или разделить на одинаковый многочлен. Единственное условие — он должен быть отличным от нуля.
Рациональную дробь можно представить в виде суммы. Выполняют это действие, основываясь на правиле сложения или вычитания выражений с одинаковыми знаменателями. Например, k * m — k / k+1 = 1/k + (k2 * m — k2 — k — 1) / (k2 + k).
Из свойств рациональных отношений следует, что для вычитания их друг из друга нужно привести члены к общему знаменателю и найти разность числителей. Аналогично поступают и для операции сложения, только вычитание в числителе заменяют складыванием. Произведение же находится простым перемножением делимых и делителей. А вот деление выполняют по-другому. Чтобы найти частное, нужно первое выражение умножить на обратную вторую дробь. Чтобы возвести дробь в степень, нужно отдельно в неё возвести числитель и знаменатель. По тому же принципу извлекают и корень.
Понимая, как правильно использовать приведённые свойства, решать задания на контрольной работе в школе будет несложно. Но перед сдачей теста необходимо попрактиковаться в самостоятельном решении.
Изменение знака
При решении заданий основное свойство дроби используют и для изменения знаков. Действительно, если числитель и знаменатель помножить на минус единицу, ответ не изменится. Полученное выражение будет полностью тождественным исходному. Записать это правило можно равенством: a/b = (-1 * a) / (-1 * b) = -a/-b. Например, (-23x — 34) / (x — y) = (23x + 34) / (y — x).
Из теоремы существует следствие. Согласно ему, a / b = — (-a) / b = — (a) / (-b). Доказать это утверждение просто если взять за основу правило умножения чисел. Дробь — (-a) / b = -((-a): b) = (-1) * (((-1) * a): b) = (-1) * (-1) * a: b = a: b = a / b. Аналогичные действия можно выполнить и для равенства: a / b = — (a) / (-b).
Правило изменения знаков очень важно, поэтому обычно ему уделяют целый урок при изучении рациональных дробей и их свойств в 8 классе. Понять, насколько полезно это свойство можно, рассмотрев пример. Найти сумму рациональных чисел: ((3 — 14x) / (3x * y — z)) + ((14 — 56x) / (z -3x * y)). Чтобы сложить два члена, нужно найти общий знаменатель. Применяя стандартные методы, вычислить его довольно сложно. Решение получится громоздким и неудобным. Если же присмотреться к выражениям, можно увидеть похожесть знаменателей, отличие их будет только в знаках.
Используя правило изменения, можно умножить второй член на минус единицу, то есть помножить на -1 делитель и делимое: -1 * (14 — 56x) / -1* (z -3x * y). В результате получится дробь тождественная исходной: (-14 + 56x) / (-z + 3x * y) = (56x — 14) / (3x * y — z). Теперь полученный результат можно подставить в пример и выполнить сложение: ((3 — 14x) / (3x * y — z)) + (56x — 14) / (3x * y — z) = ((3 — 14x) + (56x — 14)) / (3x * y — z) = ((3 — 14) + (56x — 14x)) / (3x * y — z) = (44x -11) / (3x * y — z).
Следует отметить, что приём по изменению знака часто используют при разложении рациональных отношений на простейшие дроби. Например, (2×3 — 3) / (- x3 — x). Так как степень числа в числителе меньше чем в знаменателе, нужно использовать разложение. Причём в другом случае пришлось бы применять деление для нахождения целой части. Для удобства действия выражение нужно умножить на минус единицу. В результате несложно будет определить верность равенства: 2×3 + 3 / (x3 + x) = 2 + (-2x + 3) / (x3 + x).
Решение примеров
Самостоятельное решение рациональных дробей в алгебре в 8 классе строится на цепочке преобразований. Первое, что нужно сделать — оценить возможность разложения отношения на множители. Для этого лучше использовать формулы сокращённого умножения или дискриминант. Алгоритм преобразований можно представить в следующем виде:
- подобрать формулу сокращённого умножения, то есть перевести выражение в максимально возможную степень;
- вынести общую степень за скобку;
- при существовании коэффициентов найти их по формуле квадратного разложения.
Вот 3 типовые задачи, которые обычно предлагают решить студентам при сдаче зачёта:
- Используя свойства дробных отношений, выполнить преобразование до стандартного вида: (3 *a — a*b — 2*b*(5/6)*b + 2 3/7*a*b) / (a3*b2 — 5*a2*b + 3*a**b -15). Оценивая пример, можно увидеть, что к числителю возможно применить свойство степени из-за одинаковых оснований: 3*a — a*b — 2*b*(5/6)*b + 2 3/7*a*b = 3*a — a*b — (5/3)*b2 + 2 3/7*a*b. В полученном выражении подобный член можно убрать за скобки: 3*a + (-a*b + 2 3/7*a*b) — 5/3*b2 = 3*a + 1 3/7 *a*b — 5/3*b2. Теперь можно перейти к разложению знаменателя. В нём общий множитель вынести за скобки. В результате должно получиться выражение: a*b*(a2*b + 3) — 5*(a2*b + 3) = (a2*b + 13)*(a*b -5). Осталось только записать полученные результаты в числитель и знаменатель.
- Сократить дробь: (45z*x2*y3) / (45z*x*y7). Сразу видно, что числитель и знаменатель содержит одинаковый множитель, на который можно сократить. Затем, применив свойство степени, выражение можно представить в следующем виде: x2*y3 / x*y7 = (x*x)*y3 / x*(y3*y4) = x/y4.
- Определить, при каких значениях n рациональная дробь (n4 — 2 * n3 + 4 * n — 5) / (n-2) будет равняться целому числу. Для решения задачи нужно выполнить деление. Для этого удобно воспользоваться методом столбика. После преобразования дробь должна принять вид: n3 + 4 + 3/(n-2). Так как n3 + 4 при любом значении неизвестной будет целым, анализировать нужно дробь: 3/(n-2). Она будет целой, только если знаменатель будет равняться: 1, −1, 3, -3. Соответственно искомые значения равняются: 3;1;5;1.
При упрощении рациональных отношений сложность связана с тем, что не всегда просто найти общий множитель для числителя и знаменателя. Причём он и не всегда существует, поэтому и нужно пробовать разложение на множители. Если такого члена нет, дробь упростить нельзя.
Целые выражения — это выражения, составленные из чисел и переменных с использованием действий сложения, вычитания, умножения и деления на число, отличное от нуля.
Дробные выражения допускают также деление на выражение с переменными.
Целые и дробные выражения называют рациональными выражениями.
Допустимые значения переменных — это те значения переменных, при которых выражение имеет смысл.
Рациональная дробь — это дробь, числителем и знаменателем которой являются многочлены.
Основное свойство дроби: если числитель и знаменатель некоторой рациональной дроби умножить на один и тот же многочлен, не равный тождественно нулю, то получится дробь, равная исходной.
Тождество — это равенство, которое верно при всех допустимых значениях переменных, входящих в это равенство.
Свойства действий с рациональными дробями:
Если а, b, с — многочлены, причем многочлен c не равен нулю тождественно, то верно:
-
$frac{a}{c}+frac{b}{c} = frac{a+b}{c}$
-
$frac{a}{c}-frac{b}{c} = frac{a-b}{c}$
Если a, b,c,d- многочлены, причем многочлены b и d тождественно не равны нулю, то верно:
-
$frac{a}{b}cdot frac{c}{d} = frac{ac}{bd}$
-
$(frac{a}{b})^n = frac{a^n}{b^n}$
Если a, b, с, d — многочлены, причем многочлены b, с и d тождественно не равны нулю, то верно:
-
$frac{a}{b} : frac{c}{d} = frac{ad}{bc}$
Пример 1. Сократите дробь $frac{x^2-2xy+y^2-1}{x-y+1}$
Решение:
$frac{x^2-2xy+y^2-1}{x-y+1} = frac{(x-y)^2-1}{x-y+1} = frac{(x-y-1)(x-y+1)}{x-y+1} = x-y-1 $
Ответ: х-у-1.
Пример 2. Упростите выражение $frac{2x^2-5}{(x-5)^3} — frac{45}{(x-5)^3}$
Решение:
$frac{2x^2-5}{(x-5)^3} — frac{45}{(x-5)^3} = frac{2x^2-5-45}{(x-5)^3} = frac{2(x^2-25)}{(x-5)^3} = frac{2(x^2-5^2)}{(x-5)^3} = $
$= frac{2(x-5)(x+5)}{(x-5)(x^2+5x+25)} = frac{2(x+5)}{x^2+5x+25} = frac{2x+10}{x^2+5x+25}$
Ответ: $frac{2x+10}{x^2+5x+25}$
Пример 3. Упростите выражение $(frac{3a^2}{a-b} — frac{3b^2}{a+b}) cdot frac{a^2-b^2}{4(a+b)^2}$
Решение:
$(frac{3a^2}{a-b} — frac{3b^2}{a+b}) cdot frac{a^2-b^2}{4(a+b)^2} = frac{3a^2(a+b) — 3b^2(a-b)}{a^2-b^2}cdot frac{a^2-b^2}{4(a+b)^2} =$
$= frac{3a^3+3a^2b-3ab^2-3b^3}{4(a+b)^2} = frac{3(a^3-b^3)+3ab(a-b)}{4(a+b)^2} = frac{3(a-b)(a^2+ab+b^2)+3ab(a-b)}{4(a+b)^2} =$
$= frac{3(a-b)(a^2+2ab+b^2)}{4(a+b)^2} = frac{3}{4}a — frac{3}{4}b = 0,75(a-b)$
Ответ: 0,75(a-b)
Пример 4. Выполните деление: $frac{x^2-3x}{2y^2} : frac{x-3}{4y}$
Решение:
$frac{x^2-3x}{2y^2} : frac{x-3}{4y} = frac{x(x-3)cdot 4y}{2y^2(x-3)} = frac{2x}{y}$
Ответ: $frac{2x}{y}$
Разложение рациональных дробей на элементарные (простейшие) дроби. Первая часть.
Начнём с некоторых определений. Многочленом n-й степени (или n-го порядка) будем именовать выражение вида
$$P_n(x)=sumlimits_{i=0}^{n}a_{i}x^{n-i}=a_{0}x^{n}+a_{1}x^{n-1}+a_{2}x^{n-2}+ldots+a_{n-1}x+a_n$$
Например, выражение $4x^{14}+87x^2+4x-11$ есть многочлен, степень которого равна $14$. Его можно обозначить так: $P_{14}(x)=4x^{14}+87x^2+4x-11$.
Отношение двух многочленов $frac{P_n(x)}{Q_m(x)}$ называется рациональной функцией или рациональной дробью. Если более точно, то это рациональная функция одной переменной (т.е. переменной $x$).
Рациональная дробь называется правильной, если $n < m$, т.е. если степень многочлена, стоящего в числителе, меньше степени многочлена, стоящего в знаменателе. В противном случае (если $n ≥ m$) дробь называется неправильной.
Пример №1
Указать, какие из приведённых ниже дробей являются рациональными. Если дробь является рациональной, то выяснить, правильная она или нет.
Решение
1) Данная дробь не является рациональной, поскольку содержит $sin x$. Рациональная дробь этого не допускает.
2) Мы имеем отношение двух многочленов: $5x^2+3x-8$ и $11x^9+25x^2-4$. Следовательно, согласно определению, выражение $frac{5x^2+3x-8}{11x^9+25x^2-4}$ есть рациональная дробь. Так как степень многочлена в числителе равна $2$, а степень многочлена в знаменателе равна $9$, то данная дробь является правильной (ибо $2 < 9$).
3) И в числителе, и в знаменателе данной дроби расположены многочлены (разложенные на множители). Нам совершенно неважно, в какой форме представлены многочлены числителя и знаменателя: разложены они на множители или нет. Так как мы имеем отношение двух многочленов, то согласно определению выражение
$$frac{(2x^3+8x+4)(8x^4+5x^3+x+145)^9(5x^7+x^6+9x^5+3)}{(5x+4)(3x^2+9)^{15}(15x^{10}+9x-1)}$$
есть рациональная дробь.
Дабы ответить на вопрос о том, является ли данная дробь правильной, следует определить степени многочленов в числителе и знаменателе. Начнём с числителя, т.е. с выражения
$$(2x^3+8x+4)(8x^4+5x^3+x+145)^9(5x^7+x^6+9x^5+3)$$
Для определения степени этого многочлена можно, конечно, раскрыть скобки. Однако разумно поступить гораздо проще, ибо нас интересует лишь наибольшая степень переменной $x$. Выберем из каждой скобки переменную $x$ в наибольшей степени. Из скобки $(2x^3+8x+4)$ возьмём $x^3$, из скобки $(8x^4+5x^3+x+9)^9$ возьмём $(x^4)^9=x^{4cdot9}=x^{36}$, а из скобки $(5x^7+x^6+9x^5+3)$ выберем $x^7$. Тогда после раскрытия скобок наибольшая степень переменной $x$ будет такой:
$$
x^3cdot x^{36}cdot x^7=x^{3+36+7}=x^{46}.
$$
Степень многочлена, расположенного в числителе, равна $46$. Теперь обратимся к знаменателю, т.е. к выражению $(5x+4)(3x^2+9)^{15}(15x^{10}+9x-1)$. Степень этого многочлена определяется так же, как и для числителя, т.е.
$$
xcdot (x^2)^{15}cdot x^{10}=x^{1+30+10}=x^{41}.
$$
В знаменателе расположен многочлен 41-й степени. Так как степень многочлена в числителе (т.е. 46) не меньше степени многочлена в знаменателе (т.е. 41), то рациональная дробь
$$frac{(2x^3+8x+4)(8x^4+5x^3+x+145)^9(5x^7+x^6+9x^5+3)}{(5x+4)(3x^2+9)^{15}(15x^{10}+9x-1)}$$
является неправильной.
4) В числителе дроби $frac{3}{(5x^6+4x+19)^4}$ стоит число $3$, т.е. многочлен нулевой степени. Формально числитель можно записать так: $3x^0=3cdot1=3$. В знаменателе имеем многочлен, степень которого равна $6cdot 4=24$. Отношение двух многочленов есть рациональная дробь. Так как $0 < 24$, то данная дробь является правильной.
Ответ: 1) дробь не является рациональной; 2) рациональная дробь (правильная); 3) рациональная дробь (неправильная); 4) рациональная дробь (правильная).
Теперь перейдём к понятию элементарных дробей (их ещё именуют простейшими рациональными дробями). Существуют четыре типа элементарных рациональных дробей:
- $frac{A}{x-a}$;
- $frac{A}{(x-a)^n}$ ($n=2,3,4,ldots$);
- $frac{Mx+N}{x^2+px+q}$ ($p^2-4q < 0$);
- $frac{Mx+N}{(x^2+px+q)^n}$ ($p^2-4q < 0$; $n=2,3,4,ldots$).
Примечание (желательное для более полного понимания текста): показатьскрыть
Задача состоит в следующем: заданную правильную рациональную дробь представить в виде суммы элементарных рациональных дробей. Решению этой задачи и посвящён материал, изложенный на данной странице. Для начала нужно убедиться, что выполнено следующее условие: многочлен в знаменателе правильной рациональной дроби разложен на множители таким образом, что оное разложение содержит лишь скобки вида $(x-a)^n$ или $(x^2+px+q)^n$ ($p^2-4q < 0$).Грубо говоря, это требование означает необходимость максимального разложения многочлена в знаменателе, т.е. чтобы дальнейшее разложение было невозможно. Только если это условие выполнено, то можно применять такую схему:
Если же дробь неправильная, то перед применением вышеизложенной схемы следует разбить её на сумму целой части (многочлен) и правильной рациональной дроби. Как именно это делается, разберём далее (см. пример №2 пункт 3). Пару слов насчёт буквенных обозначений в числителях (т.е. $A$, $A_1$, $C_2$ и тому подобные). Буквы можно использовать любые – на свой вкус. Важно лишь, чтобы эти буквы были различными во всех элементарных дробях. Чтобы найти значения этих параметров применяют метод неопределённых коэффициентов или метод подстановки частных значений (см. примеры №3, №4 и №5).
Пример №2
Разложить заданные рациональные дроби на элементарные (без нахождения параметров):
Решение
1) Имеем рациональную дробь. В числителе этой дроби расположен многочлен 4-й степени, а в знаменателе многочлен, степень которого равна $17$ (как определить эту степень детально пояснено в пункте №3 примера №1). Так как степень многочлена в числителе меньше степени многочлена в знаменателе, то данная дробь является правильной. Обратимся к наменателю этой дроби. Начнём со скобок $(x-5)$ и $(x+2)^4$, которые полностью подпадают под вид $(x-a)^n$. Кроме того, имеются ещё и скобки $(x^2+3x+10)$ и $(x^2+11)^5$. Выражение $(x^2+3x+10)$ имеет вид $(x^2+px+q)^n$, где $p=3$; $q=10$, $n=1$. Так как $p^2-4q=9-40=-31 < 0$, то данную скобку больше нельзя разложить на множители. Обратимся ко второй скобке, т.е. $(x^2+11)^5$. Это тоже скобка вида $(x^2+px+q)^n$, но на сей раз $p=0$, $q=11$, $n=5$. Так как $p^2-4q=0-121=-121 < 0$, то данную скобку больше нельзя разложить на множители. Итак, мы имеем следующий вывод: многочлен в знаменателе разложен на множители таким образом, что оное разложение содержит лишь скобки вида $(x-a)^n$ или $(x^2+px+q)^n$ ($p^2-4q < 0$). Теперь можно переходить и к элементарным дробям. Мы будем применять правила (1)-(4), изложенные выше. Согласно правилу (1) скобке $(x-5)$ будет соответствовать дробь $frac{A}{x-5}$. Это можно записать так:
$$
frac{5x^4-10x^3+x^2-9}{(x-5)(x+2)^4 (x^2+3x+10)(x^2+11)^5}=frac{A}{x-5}+ldots
$$
Согласно правилу (2) скобке $(x+2)^4$ будет соответствовать сумма четырёх дробей $frac{A_1}{x+2}+frac{A_2}{(x+2)^2}+frac{A_3}{(x+2)^3}+frac{A_4}{(x+2)^4}$. Допишем эту сумму к уже имеющемуся разложению:
$$
frac{5x^4-10x^3+x^2-9}{(x-5)(x+2)^4 (x^2+3x+10)(x^2+11)^5}=frac{A}{x-5}+frac{A_1}{x+2}+frac{A_2}{(x+2)^2}+frac{A_3}{(x+2)^3}+frac{A_4}{(x+2)^4}+ldots
$$
Согласно правилу (3) скобке $(x^2+3x+10)$ будет соответствовать дробь $frac{Cx+D}{x^2+3x+10}$. Допишем эту дробь к разложению:
$$
frac{5x^4-10x^3+x^2-9}{(x-5)(x+2)^4 (x^2+3x+10)(x^2+11)^5}=frac{A}{x-5}+frac{A_1}{x+2}+frac{A_2}{(x+2)^2}+frac{A_3}{(x+2)^3}+frac{A_4}{(x+2)^4}+\
+frac{Cx+D}{x^2+3x+10}+ldots
$$
И, наконец, согласно правилу (4) скобке $(x^2+11)^5$ будет соответствовать сумма пяти дробей
$$frac{C_1x+D_1}{x^2+11}+frac{C_2x+D_2}{(x^2+11)^2}+frac{C_3x+D_3}{(x^2+11)^3}+frac{C_4x+D_4}{(x^2+11)^4}+frac{C_5x+D_5}{(x^2+11)^5}$$
Допишем эту сумму к уже имеющемуся разложению и задача будет решена, ибо все скобки знаменателя исчерпаны:
$$
frac{5x^4-10x^3+x^2-9}{(x-5)(x+2)^4 (x^2+3x+10)(x^2+11)^5}=frac{A}{x-5}+frac{A_1}{x+2}+frac{A_2}{(x+2)^2}+frac{A_3}{(x+2)^3}+frac{A_4}{(x+2)^4}+\
+frac{Cx+D}{x^2+3x+10}+frac{C_1x+D_1}{x^2+11}+frac{C_2x+D_2}{(x^2+11)^2}+frac{C_3x+D_3}{(x^2+11)^3}+frac{C_4x+D_4}{(x^2+11)^4}+frac{C_5x+D_5}{(x^2+11)^5}.
$$
2) Имеем рациональную дробь. Степень многочлена в числителе (т.е. 2) меньше степени многочлена в знаменателе (т.е. 9), поэтому данная дробь – правильная. Обратимся к знаменателю. Скобка $(x-2)^3$ подпадает под вид $(x-a)^n$, посему пойдём далее. Скобка $(x^3-8)$ не подпадает ни под вид $(x-a)^n$ ни под вид $(x^2+px+q)^n$. Это говорит о том, что скобку $(x^3-8)$ необходимо разложить на множители. Сие легко сделать, если вспомнить формулу разности кубов:
$$
x^3-8=x^3-2^3=(x-2)(x^2+2x+4).
$$
Скобка $(x-2)$ подпадает под вид $(x-a)^n$. Скобка $(x^2+2x+4)$ имеет вид $(x^2+px+q)^n$, где $p=2$, $q=4$, $n=1$. При этом $p^2-4q=4-16=-12 < 0$, посему дальнейшее разложение невозможно. Итак, $x^3-8=(x-2)(x^2+2x+4)$, поэтому знаменатель станет таким:
$$
(x-2)^3(x^3-8)(3x+5)(3x^2-x-10)=\
=(x-2)^3(x-2)(x^2+2x+4)(3x+5)(3x^2-x-10)=(x-2)^4(x^2+2x+4)(3x+5)(3x^2-x-10)
$$
Пойдём далее. Следующая скобка на очереди – это $(3x+5)$. Эта скобка подпадала бы под форму $(x-a)^n$, если бы не коэффициент $3$ перед $x$. Вынесем эту тройку за скобку: $(3x+5)=3cdotleft(x+frac{5}{3}right)$. Знаменатель теперь преобразится таким образом:
$$
(x-2)^4(x^2+2x+4)(3x+5)(3x^2-x-10)=3cdot (x-2)^4(x^2+2x+4)left(x+frac{5}{3}right)(3x^2-x-10)
$$
Теперь настало время для скобки $(3x^2-x-10)$. Она подпадала бы под форму $(x^2+px+q)^n$, если бы не «лишний» коэффициент $3$ перед $x^2$. Кроме того, скобка $(3x^2-x-10)$ разложима на множители, в чём несложно убедиться, решив соответствующее квадратное уравнение:
$$
3x^2-x-10=0;\
D=(-1)^2-4cdot3cdot(-10)=1+120=121;\
x_1=frac{-(-1)-sqrt{121}}{2cdot3}=frac{1-11}{6}=-frac{10}{6}=-frac{5}{3};\
x_2=frac{-(-1)+sqrt{121}}{2cdot3}=frac{1+11}{6}=2.\
3x^2-x-10=3cdot left(x-left(-frac{5}{3}right)right)(x-2)=3cdot left(x+frac{5}{3}right)(x-2).
$$
Так как $3x^2-x-10=3cdot left(x+frac{5}{3}right)(x-2)$, то знаменатель станет таким:
$$
3cdot (x-2)^4(x^2+2x+4)left(x+frac{5}{3}right)(3x^2-x-10)=\
=9cdot (x-2)^4(x^2+2x+4)left(x+frac{5}{3}right)left(x+frac{5}{3}right)(x-2)=
9cdot (x-2)^5(x^2+2x+4)left(x+frac{5}{3}right)^2
$$
И сама исходная дробь ныне станет такой:
$$
frac{x^2+10}{(x-2)^3(x^3-8)(3x+5)(3x^2-x-10)}
=frac{x^2+10}{9cdot (x-2)^5(x^2+2x+4)left(x+frac{5}{3}right)^2}=\
=frac{frac{1}{9}x^2+frac{10}{9}}{(x-2)^5(x^2+2x+4)left(x+frac{5}{3}right)^2}
$$
Теперь можно перейти непосредственно к элементарным дробям. Действуя точно так же, как и в пункте №1 этого примера, будем иметь:
$$
frac{frac{1}{9}x^2+frac{10}{9}}{(x-2)^5(x^2+2x+4)left(x+frac{5}{3}right)^2}=\
=frac{A_1}{x-2}+frac{A_2}{(x-2)^2}+frac{A_3}{(x-2)^3}+frac{A_4}{(x-2)^4}+frac{A_5}{(x-2)^5}+
frac{Cx+D}{x^2+2x+4}+frac{B_1}{x+frac{5}{3}}+frac{B_2}{left(x+frac{5}{3}right)^2}
$$
3) Имеем рациональную дробь. Степень могочлена в числителе (т.е. 5) не меньше степени многочлена в знменателе (т.е. 3), посему данная дробь является неправильной. Следовательно, перед тем, как раскладывать данную рациональную дробь на элементарные, придётся выделить целую часть (многочлен). Для этого разделим многочлен, расположенный в числителе, на многочлен в знаменателе. Используем способ деления «уголком»:
Полученный результат можно записать так:
$$
3x^5-5x^4+10x^3-16x^2-7x+22=(x^3-2x^2+4x-8)(3x^2+x)+4x^2+x+22.
$$
Тогда дробь $frac{3x^5-5x^4+10x^3-16x^2-7x+22}{x^3-2x^2+4x-8}$ представима в иной форме:
$$
frac{3x^5-5x^4+10x^3-16x^2-7x+22}{x^3-2x^2+4x-8}=frac{(x^3-2x^2+4x-8)(3x^2+x)+4x^2+x+22}{x^3-2x^2+4x-8}=\
=frac{(x^3-2x^2+4x-8)(3x^2+x)}{x^3-2x^2+4x-8}+frac{4x^2+x+22}{x^3-2x^2+4x-8}=\
=3x^2+x+frac{4x^2+x+22}{x^3-2x^2+4x-8}.
$$
Дробь $frac{4x^2+x+22}{x^3-2x^2+4x-8}$ является правильной рациональной дробью, ибо степень многочлена в числителе (т.е. 2) меньше степени многочлена в знаменателе (т.е. 3). Теперь обратимся к знаменателю данной дроби. В знаменателе расположен многочлен, который нужно разложить на множители. Иногда для разложения на множители полезна схема Горнера, но в нашем случае проще обойтись стандартным «школьным» методом группировки слагаемых:
$$
x^3-2x^2+4x-8=x^2cdot(x-2)+4cdot(x-2)=(x-2)cdot(x^2+4);\
3x^2+x+frac{4x^2+x+22}{x^3-2x^2+4x-8}=3x^2+x+frac{4x^2+x+22}{(x-2)cdot(x^2+4)}
$$
Применяя те же методы, что и в предыдущих пунктах, получим:
$$
frac{4x^2+x+22}{(x-2)cdot(x^2+4)}=frac{A}{x-2}+frac{Cx+D}{x^2+4}
$$
Итак, окончательно имеем:
$$
frac{3x^5-5x^4+10x^3-16x^2-7x+22}{x^3-2x^2+4x-8}=3x^2+x+frac{A}{x-2}+frac{Cx+D}{x^2+4}
$$
Продолжение этой темы будет рассмотрено во второй части.