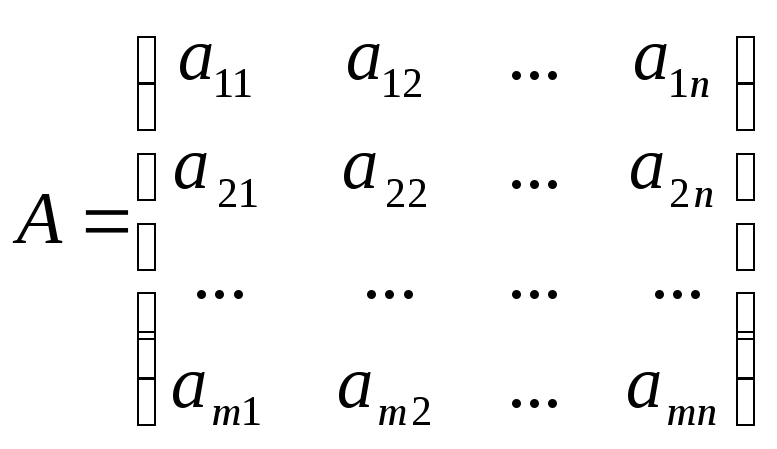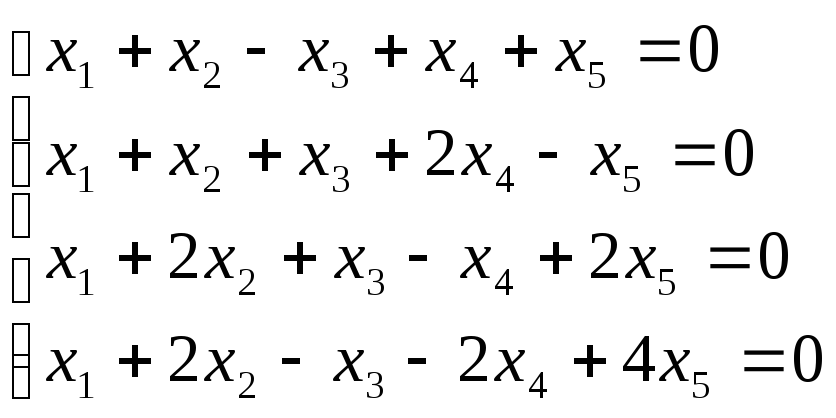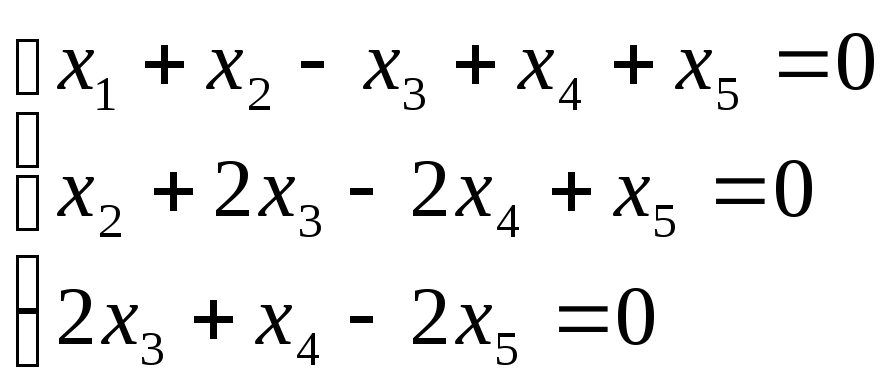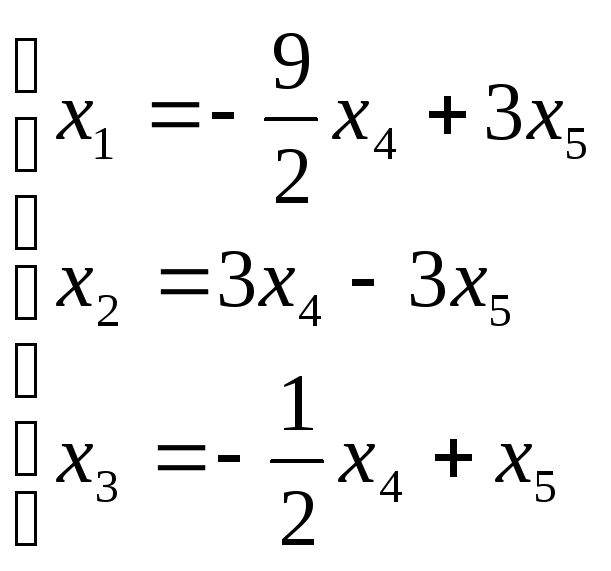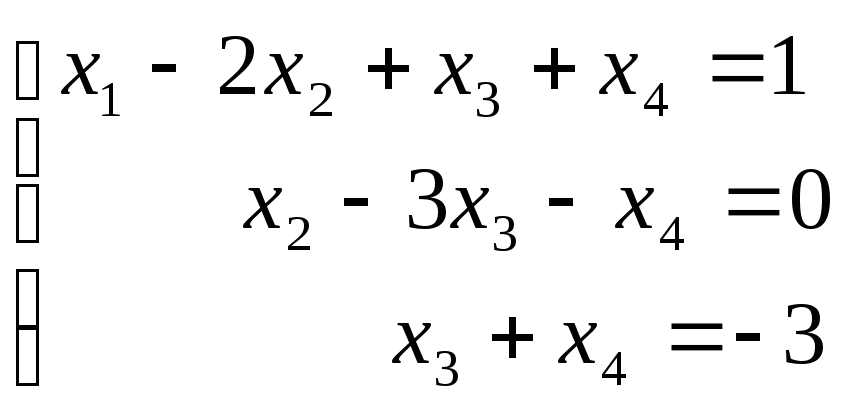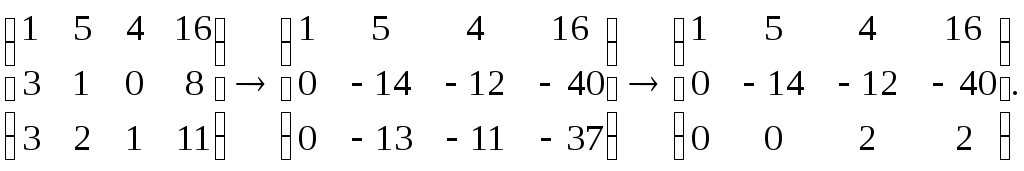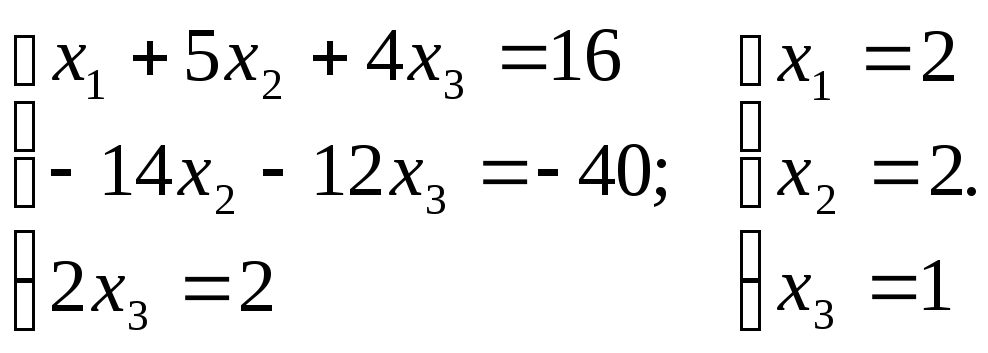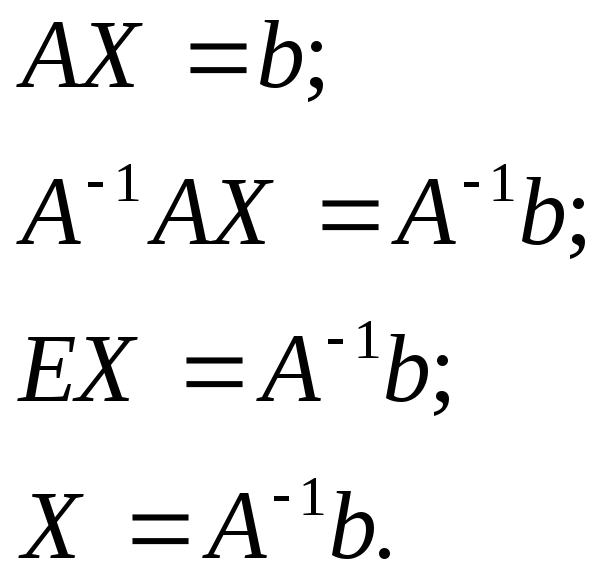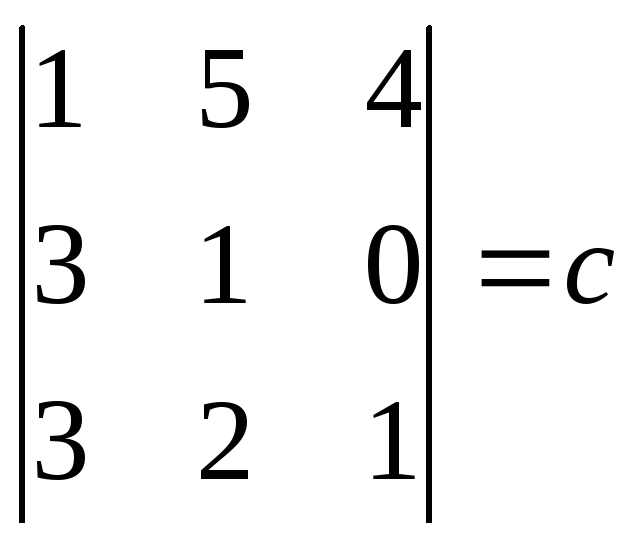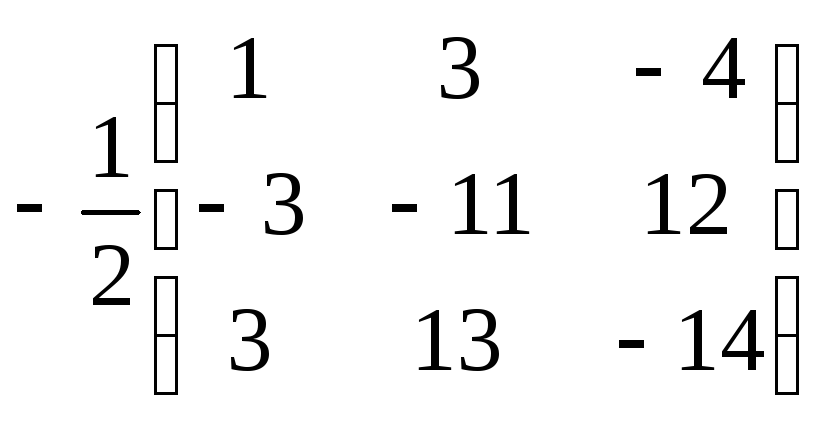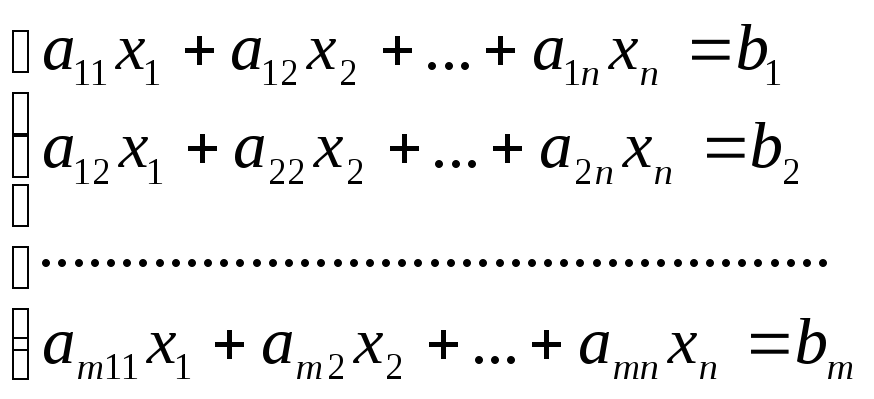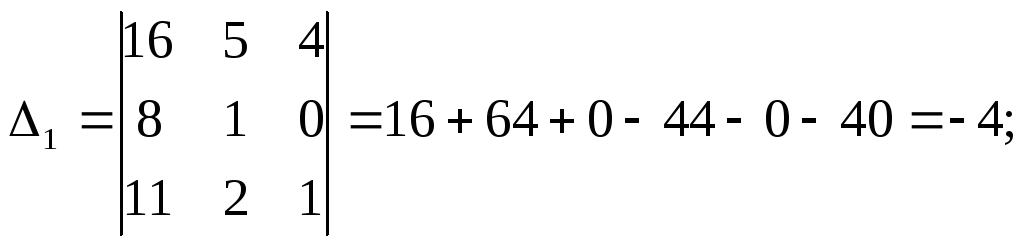Как составить расширенную матрицу системы

Система линейных алгебраических уравнений

В данной публикации мы рассмотрим определение системы линейных алгебраических уравнений (СЛАУ), как она выглядит, какие виды бывают, а также как ее представить в матричной форме, в том числе расширенной.

Определение системы линейных уравнений

Система линейных алгебраических уравнений (или сокращенно “СЛАУ”) – это система, которая в общем виде выглядит так:

Индексы коэффициентов ( a_ij ) формируются следующим образом:

• i – номер линейного уравнения;
• j – номер переменной, к которой относится коэффициент.

Решение СЛАУ – такие числа c₁, c₂,…, c_n , при постановке которых вместо x₁, x₂,…, x_n , все уравнения системы превратятся в тождества.

Виды СЛАУ

1. Однородная – все свободные члены системы равны нулю ( b₁ = b₂ = … = b_m = 0 ).
   

В зависимости от количества решений, СЛАУ может быть:

1. Совместная – имеет хотя бы одно решение. При этом если оно единственное, система называется определенной, если решений несколько – неопределенной.
   
   СЛАУ выше является совместной, т.к. есть хотя бы одно решение: , y = 3 .
2. Несовместная – система не имеет решений.
   
   Правые части уравнений одинаковые, а левые – нет. Таким образом, решений нет.

Матричная форма записи системы

СЛАУ можно представить в матричной форме:

Пример
Представим систему уравнений ниже в матричном виде:

Пользуясь формами выше, составляем основную матрицу с коэффициентами, столбцы с неизвестными и свободными членами.

Полная запись заданной системы уравнений в матричном виде:

Расширенная матрица СЛАУ

Если к матрице системы A добавить справа столбец свободных членов B , разделив данные вертикальной чертой, то получится расширенная матрица СЛАУ.

Для примера выше получается так:

– обозначение расширенной матрицы.

Расширенная матрица

Расширенная матрица представляет собой краткое обозначение системы линейных алгебраических уравнений (SLAE).

Пусть множество SLAU

Матрица А, составленная из коэффициентов для неизвестных ,называется главной матрицей системы или матрицы системы:

Матрица , полученная из основной матрицы, путем добавления столбца свободных членов вправо, называется расширенной матрицей SLAE:

Примеры решения задач с расширенными матрицами

Выписать основные и расширенные матрицы следующей системы линейных уравнений

Мы составляем основную матрицу коэффициентов с неизвестными

Добавив столбец свободных членов справа от основной матрицы, получим расширенную матрицу:

Методы решения систем линейных алгебраических уравнений (СЛАУ) с примерами

Содержание:

Методы решения систем линейных алгебраических уравнений (СЛАУ)

Метод Крамера

Определение: Системой линейных алгебраических уравнений (СЛАУ) называется выражение

Определение: Определитель, составленный из коэффициентов при неизвестных, называется главным определителем системы

Крамер предложил следующий метод решения СЛАУ: умножим главный определитель на для этого умножим все элементы первого столбца на эту неизвестную:

Второй столбец умножим на третий столбец — на -ый столбец — на и все эти произведения прибавим к первому столбцу, при этом произведение не изменится:

Согласно записи СЛАУ первый столбец получившегося определителя представляет собой столбец свободных коэффициентов, т.е.

Определение: Определитель называется первым вспомогательным определителем СЛАУ.

Поступая аналогично тому, как описано выше, найдем все вспомогательные определители СЛАУ:

31. Для того чтобы найти вспомогательный определитель i, надо в главном определителе СЛАУ заменить столбец i на столбец свободных коэффициентов.

Определение: Полученные выше соотношения называются формулами Крамера. Используя формулы Крамера, находят неизвестные величины Проанализируем полученные формулы:

Пример:

Решить СЛАУ методом Крамера

Решение:

Прежде всего, обращаем внимание на то, что в последнем уравнении переменные записаны в неправильном порядке, в этом случае говорят, что СЛАУ записана в ненормализованном виде. Нормализуем СЛАУ, для чего запишем неизвестные в последнем уравнении системы в правильном порядке, чтобы одноименные неизвестные были записаны друг под другом

Найдем главный определитель СЛАУ (раскрываем по первой строке)

Так как главный определитель системы отличен от нуля, то СЛАУ имеет единственное решение. Найдем три вспомогательных определителя

Воспользуемся формулами Крамера

Замечание: После нахождения решения СЛАУ надо обязательно провести проверку, для чего найденные числовые значения неизвестных подставляется в нормализованную систему линейных алгебраических уравнений.

Выполним проверку Отсюда видно, что СЛАУ решена верно.

Матричный способ решения СЛАУ

Для решения СЛАУ матричным способом введем в рассмотрение матрицу, составленную из коэффициентов при неизвестных матpицы-столбцы неизвестных и свободных коэффициентов

Тогда СЛАУ можно записать в матричном виде Матричный способ решения СЛАУ состоит в следующем: умножим слева матричное уравнение на обратную матрицу к матрице А, получим в силу того, что произведение найдем Таким образом, для нахождения неизвестных матричным способом, надо найти обратную к А матрицу после чего надо умножить эту матрицу на матрицу-столбец свободных коэффициентов.

Пример:

Решить СЛАУ матричным способом

Решение:

Введем в рассмотрение следующие матрицы

Найдем матрицу (см. Лекцию № 2): найдем детерминант матрицы А.

Пример:

Решение:

Найдем алгебраические дополнения всех элементов Запишем обратную матрицу (в правильности нахождения обратной матрицы убедиться самостоятельно). Подействуем пай денной матрицей на матрицу-столбец свободных коэффициентов В:

Отсюда находим, что х = 1; y = l; z = l.

Метод Гаусса

Метод Гаусса или метод исключения неизвестных состоит в том, чтобы за счет элементарных преобразований привести СЛАУ к треугольному виду. Покажем использование расширенной матрицы, составленной из коэффициентов при неизвестных и расширенной за счет столбца свободных коэффициентов, для приведения СЛАУ к треугольному виду на примере системы, рассматриваемой в этой лекции. Расширенная матрица для СЛАУ имеет вид:

Замечание: В методе Гаусса желательно, чтобы первая строка расширенной матрицы начиналась с единицы.

Обменяем в расширенной матрице первую и вторую строки местами, получим Приведем матрицу к треугольному виду, выполнив следующие преобразования: умножим элементы первой строки на (-2) и прибавим к соответствующим элементам второй строки Разделим все элементы второй строки на (-5), получим эквивалентную матрицу

Умножим элементы первой строки на (—1) и прибавим к соответствующим элементам третьей строки Разделим все элементы третьей строки на (-3), получим Таким образом, эквивалентная СЛАУ имеет вид (напомним, что первый столбец это коэффициенты при неизвестной х, второй — при неизвестной у, третий — при неизвестной z, а за вертикальной чертой находится столбец свободных коэффициентов):

Из первого уравнения находим, что х = 1.

Вывод: Из вышеизложенного материала следует, что вне зависимости от

способа решения СЛАУ всегда должен получаться один и тот же ответ.

Замечание: После нахождения решения СЛАУ надо обязательно выполнить проверку, то есть подставить полученные значения неизвестных в заданную СЛАУ и убедиться в тождественности левой части всех равенств системы соответствующим правым частям. Отметим, что задание СЛАУ всегда верно, то есть, если проверка показывает нарушение оговоренной тождественности, то надо искать ошибку в проведенных вычислениях.

Ранг матрицы. Теорема Кронекера-Капелли

Определение: Рангом матрицы называется наивысший порядок отличного от нуля минора этой матрицы.

Если то среди всевозможных миноров этой матрицы есть хотя бы один минор порядка r, который отличен от нулю, а все миноры порядков больших, чем r, равны нулю.

При вычислении ранга необходимо начинать вычислять миноры 2 порядка, затем миноры 3 порядка и так далее, пока не будут найдены миноры, обращающиеся в нуль. Если все миноры порядка p равны нулю, то и все миноры, порядок которых больше p, равны нулю.

Пример:

Найти ранг матрицы

Решение:

Очевидно, что среди миноров второго порядка есть миноры отличные от нуля, например, среди миноров третьего порядка также есть миноры, которые не равны нулю, например, Очевидно, что определитель четвертого порядка равен нулю, так как он будет содержать строку, состоящую из одних нулей (см. свойство для определителей). Следовательно, ранг матрицы А равен 3.

Теорема Кронекера-Капелли (критерий совместности СЛАУ). Для совместности системы линейных алгебраических уравнений (СЛАУ) необходимо и достаточно, чтобы ранг расширенной матрицы совпадал с рангом основной матрицы, составленной из коэффициентов при неизвестных величинах.

Следствия из теоремы Кронекера — Капелли

Следствие: Если ранг матрицы совместной системы равен числу неизвестных, то система имеет единственное решение (то есть она определенная).

Следствие: Если ранг матрицы совместной системы меньше числа неизвестных, то система имеет бесчисленное множество решений (т.е. она неопределенная).

В случае неопределенной системы решения ищут следующим образом: выбираются главные неизвестные, число которых равно рангу, а остальные неизвестные считаются свободными; далее главные неизвестные выражаются через свободные и получают множество решений, зависящих от свободных неизвестных. Это множество решений называется общим решением системы. Придавая свободным неизвестным различные произвольные значения, получим бесчисленное множество решений, каждое из которых называется частным решением системы.

Рекомендую подробно изучить предметы:

Математика Алгебра Линейная алгебра Векторная алгебра Высшая математика Дискретная математика Математический анализ Математическая логика

Ещё лекции с примерами решения и объяснением:

• Скалярное произведение и его свойства
• Векторное и смешанное произведения векторов
• Преобразования декартовой системы координат
• Бесконечно малые и бесконечно большие функции
• Критерий совместности Кронекера-Капелли
• Формулы Крамера
• Матричный метод
• Экстремум функции

При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org

Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи

Сайт пишется, поддерживается и управляется коллективом преподавателей

Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.

Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.

Как найти расширенную матрицу

Матрицей называют таблицу, состоящую из определенных значений и имеющую размерность в n столбцов и m строк. Система линейных алгебраических уравнений (СЛАУ) большого порядка может решаться с помощью связанных с ней матриц — матрицы системы и расширенной матрицы. Первая представляет собой массив А коэффициентов системы, стоящих при неизвестных переменных. При добавлении к данному массиву столбца-матрицы В свободных членов СЛАУ получается расширенная матрица (А|В). Построение расширенной матрицы является одним из этапов в решении произвольной системы уравнений.

Инструкция

В общем виде систему линейных алгебраических уравнений можно решить методом подстановки, но для СЛАУ большой размерности такое вычисление весьма трудоемко. И чаще в этом случае используют связанные матрицы, в том числе и расширенную.

Запишите заданную систему линейных уравнений. Проведите ее преобразование, упорядочив множители в уравнениях таким образом, чтобы одинаковые неизвестные переменные располагались в системе строго друг под другом. Свободные коэффициенты без неизвестных перенесите в другую часть уравнений. При перестановке слагаемых и переносе учитывайте их знак.

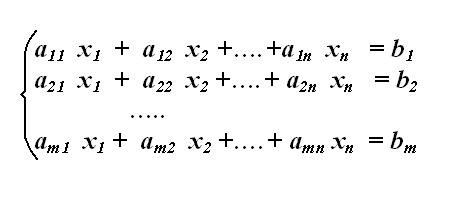
Определите матрицу системы. Для этого отдельно выпишите коэффициенты, стоящие при искомых переменных СЛАУ. Выписывать нужно в том порядке, как они расположены в системе, т.е. из первого уравнения первый коэффициент поставьте на пересечении первой строки и первого столбца матрицы. Порядок строк новой матрицы соответствует порядку уравнений системы. Если одна из неизвестных системы в данном уравнении отсутствует, значит, ее коэффициент здесь равен нулю – внесите ноль в матрицу на соответствующую позицию строки. Получаемая матрица системы должна быть квадратной (m=n).

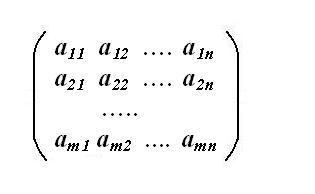
Найдите расширенную матрицу системы. Свободные коэффициенты в уравнениях системы за знаком равенства выпишите в отдельный столбец, сохраняя тот же порядок строк. В квадратной матрице системы справа от всех коэффициентов поставьте вертикальную черту. За чертой допишите полученный столбец свободных членов. Это и будет расширенная матрица исходной СЛАУ размерностью (m, n+1), где m – число строк, n – число столбцов.

Обратите внимание

Именно по расширенной матрице согласно методу Гаусса вычисляются корни системы линейных алгебраических уравнений. Метод Гаусса является одним из наиболее активно используемых способов решения СЛАУ большого порядка.

Источники:

• расширенная матрица системы

Войти на сайт

или

Забыли пароль?
Еще не зарегистрированы?

Рассмотрим систему
m
уравнений с n
неизвестными

(1)

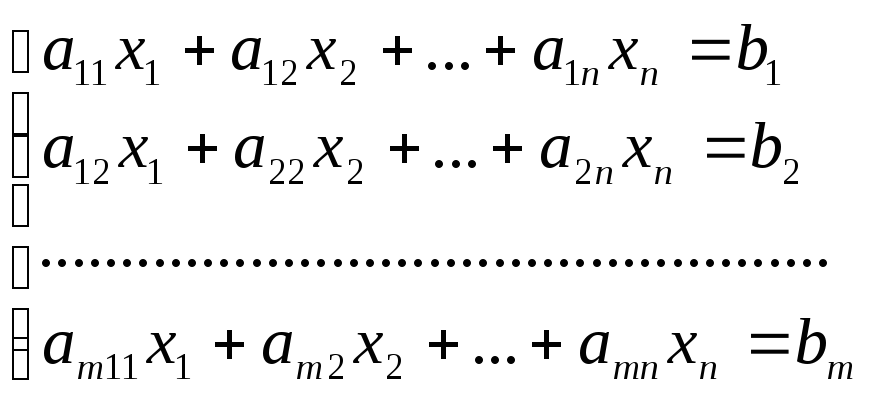
Матрица А,
составленная из коэффициентов при
неизвестных системы, называется матрицей
системы уравнений (1):

Матрица
называется расширенной матрицей.

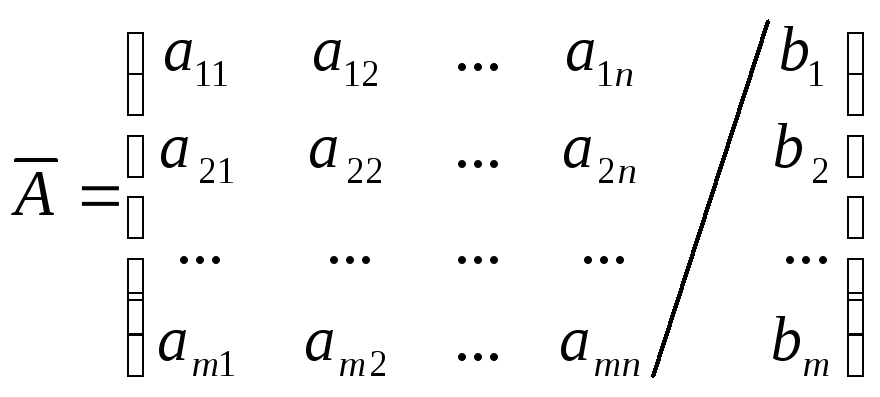
Вектор
называется вектором неизвестных, векторназывается вектором свободных членов.

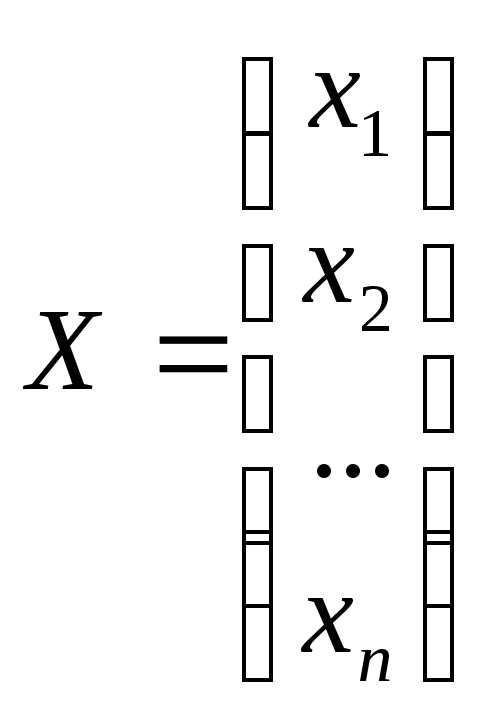
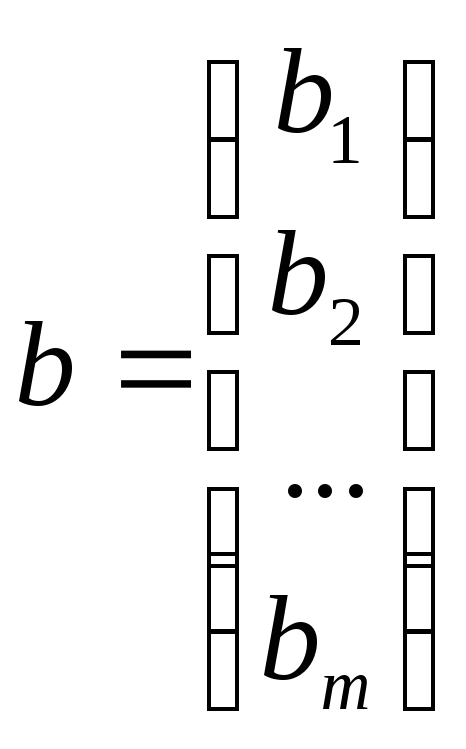
Матричная запись
системы (1) имеет вид:

Если вектор b=0,
то система называется однородной, если
b≠0
(хотя бы один из элементов отличен от
нуля), то система называется неоднородной.

Решением системы
(1) называется такой вектор X=,
что при подстановке чиселв систему (1) получаются верные равенства
(тождества).

Система, имеющая
хотя бы одно решение, называется
совместной, в противном случае –
несовместной.

Две системы
называются эквивалентными, если множества
их решений совпадают. Заметим, что
операции над системой уравнений сводятся
к элементарным преобразованиям над
расширенной матрицей

Однородные
системы

Рассмотрим
однородную систему
.

Заметим, что
однородная система всегда совместна,
поскольку нуль-вектор Х=ее решение.

Для решения
однородной системы уравнений применяется
метод Гаусса. Метод Гаусса для решения
систем уравнений состоит из прямого и
обратного хода. Прямым ходом заданную
систему приводят к эквивалентной
ступенчатой системе.

Проиллюстрируем
алгоритм метода на примере:

Прямой ход метода
Гаусса. Приведем матрицы системы к
ступенчатому виду:

.

Матрица приведена
к ступенчатому виду, ее ранг равен 3.

Выпишем соответствующую
систему уравнений:

Переменные
,
не связанные с угловыми элементами,
называются свободными, переменные—
зависимые переменные (несвободные,
базисные). Зависимыми переменными всегда
объявляются переменные, коэффициентами
которых являются угловые элементы.
Заметим, что при другом способе приведения
матрицы к ступенчатому виду свободными
переменными могут оказаться переменные
с другими индексами. Однако число
свободных переменных всегда равноn—r
(r
– ранг матрицы).

Обратный ход метода
Гаусса заключается в том, что зависимые
переменные выражаются через свободные
из ступенчатой системы, начиная с
последнего уравнения и «поднимаясь»
вверх к первому. В результате получим

Полученное выражение
называют общим решением системы в
координатной форме.

Полученные выражения
дают описание всего множества решений
однородной системы. Давая свободным
переменным произвольные значения, и
вычисляя значения зависимых переменных,
получаем некоторое частное решение
системы.

Запишем общее
решение в векторной форме. Придадим
свободным переменным значения
,
получими;
затем,
получими.
Векторылинейно независимы и образуют
фундаментальную систему решений (ФСР).

Общее решение
системы, записанное в векторной форме,
имеет вид:

Неоднородные
системы

Пусть задана
неоднородная система уравнений

Теорема
Кронекера-Капелли (критерий совместности
неоднородной системы). Система совместна
тогда и только тогда, когда ранг основной
матрицы А равен рангу расширенной
матрицы
:.

Методы решения
систем линейных уравнений

1. Метод Гаусса

Рассмотрим на
примере системы

Прямой ход метода
Гаусса. Приведем расширенную матрицу
системы к ступенчатому виду:

Здесь
,
система совместна.

Запишем эквивалентную
ступенчатую систему:

Переменные
являются
зависимыми, а—
свободной переменной.

Обратный ход метода
Гаусса. Выразим зависимые переменные
через свободные, получим:

.

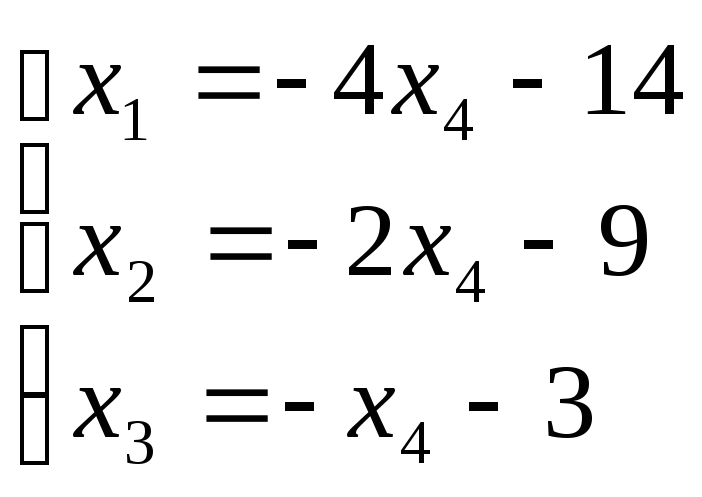
Пример 2. Решить
систему уравнений методом Гаусса

.

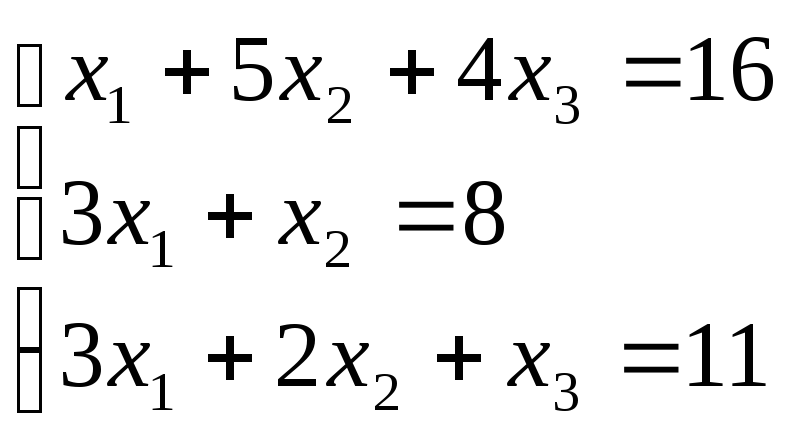
Составим расширенную
матрицу и приведем ее к ступенчатому
виду:

Запишем эквивалентную
ступенчатую систему:

Таким образом,
решением данной системы уравнений
является вектор
.

2. Метод решения
системы уравнений с помощью обратной
матрицы.

Найдем решение
системы уравнений из примера 2 с помощью
обратной матрицы. Прежде всего, определим
обратную матрицу А^-1
с помощью алгебраических дополнений.

det A=

Для каждого элемента
определим алгебраические дополнения:

,
,,,,,,,.

Тогда, А^-1
=.

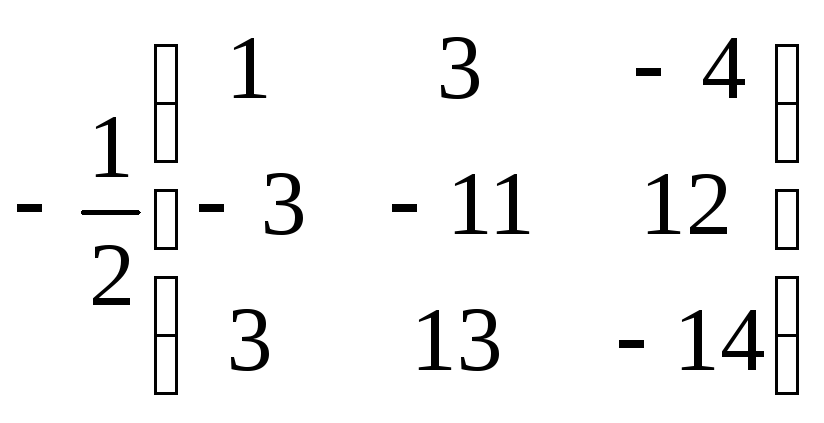
Решение системы
уравнений имеет вид:

Х=.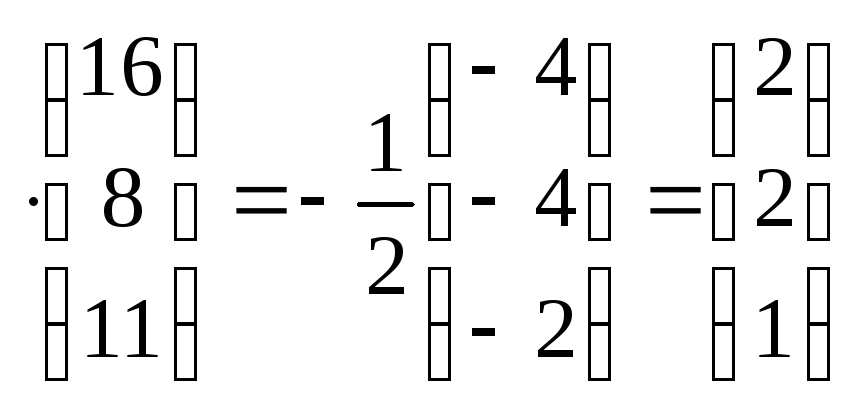

Таким образом,
решением данной системы уравнений
является вектор
.

3. Метод Крамера
решения системы уравнений.

Рассмотрим
неоднородную систему уравнений
с невырожденной матрицей А (det
A≠0):

Теорема Крамера.
Система
,
гдеdet
A≠0,
имеет единственное решение, которое
вычисляется по формулам:

,

где Δ= det
A,
— получается из определителя Δ заменойi-го
столбца на столбец свободных членов.

Пример. Найти
решение системы уравнений методом
Крамера

.

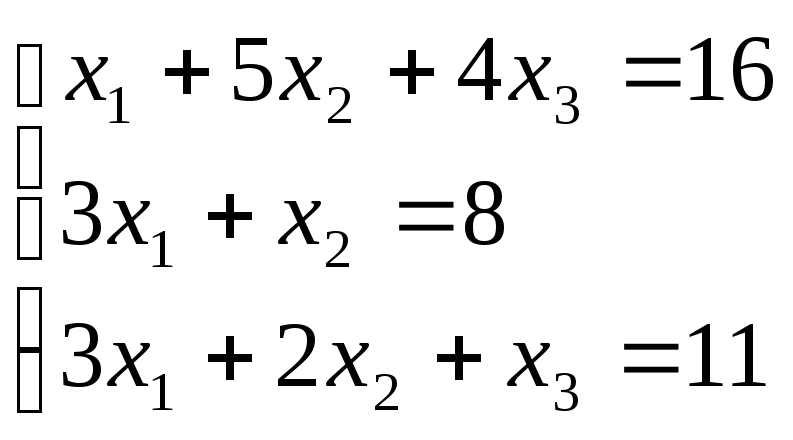
Решение.

Итак,

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #