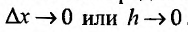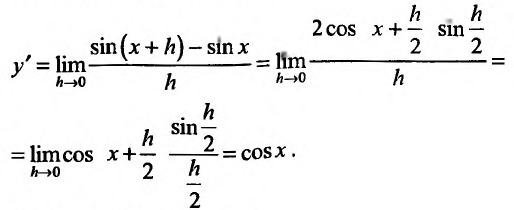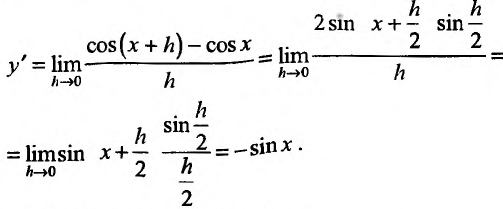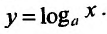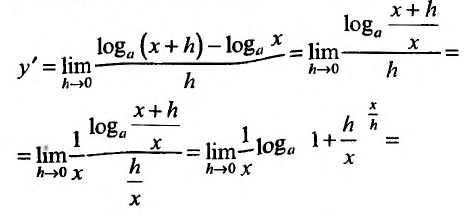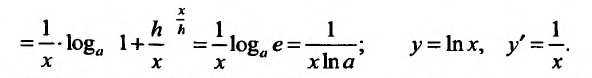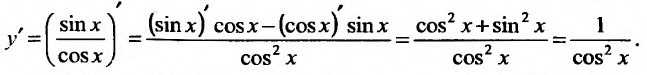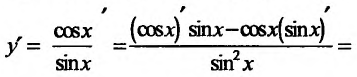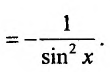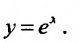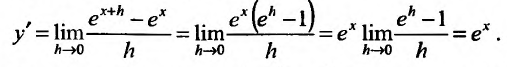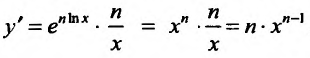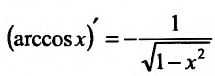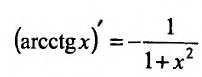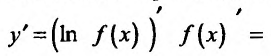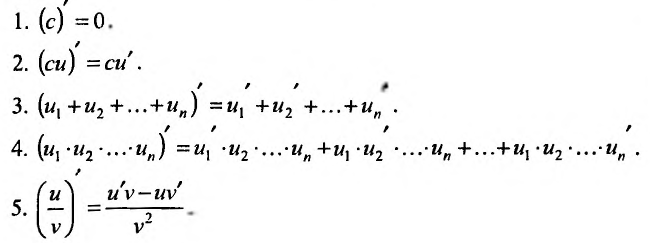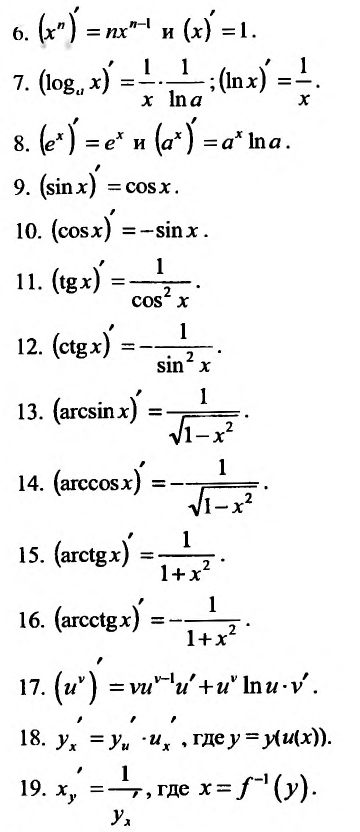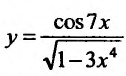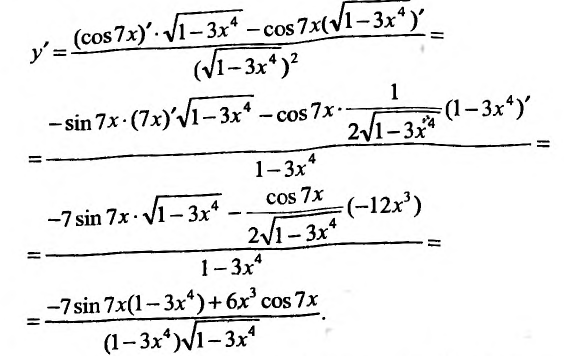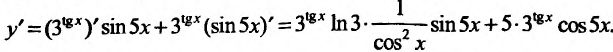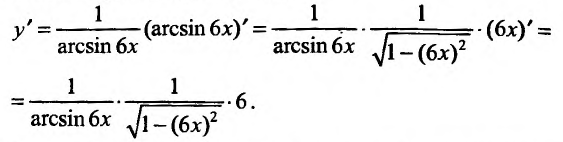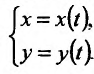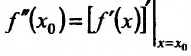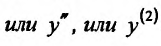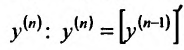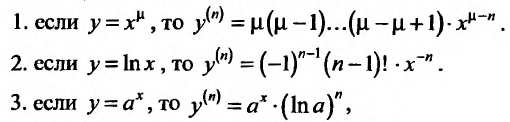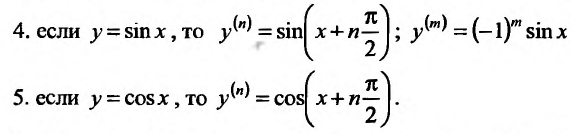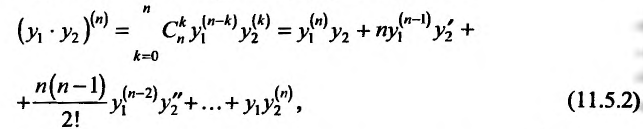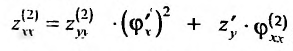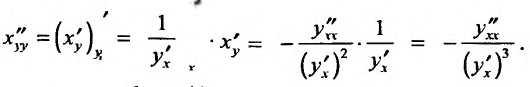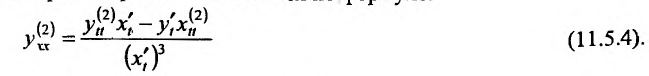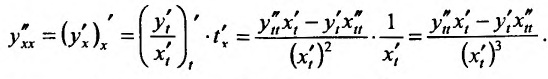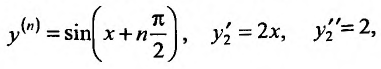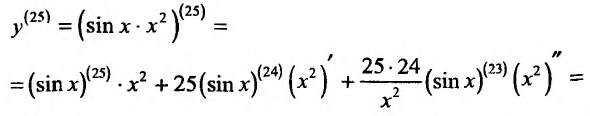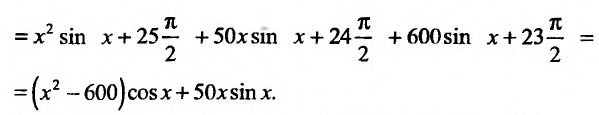Содержание:
Определение производной, её геометрический смысл:
Рассмотрим функцию
называется разностным отношением (в данной точке). Разностное отношение — это функция, которая определена для всех значений аргумента, кроме 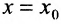
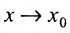
Определение 11.1.1. Пусть функция y=f(x) определена в некоторой окрестности точки 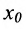
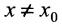
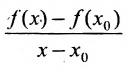
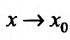
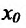
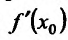
Если ввести обозначения 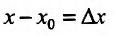
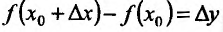
Если для некоторого значения 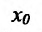
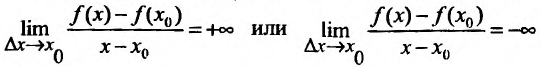
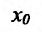
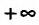
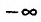
В дальнейшем под выражением «функция имеет производную» мы будем понимать, что функция имеет конечную производную, которую будем обозначать
Определение 11.1.2, Если функция f определена в правосторонней (левосторонней) окрестности точки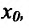
то он называется конечной или бесконечной производной справа (слева) функции f в точке х и обозначается f+(xq) (или f’.(x0)).
Из теоремы 10.2.1 об односторонних пределах следует, что функция f, определенная в некоторой окрестности точки 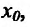
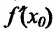
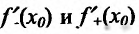
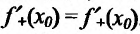
Заметим, что если у функции 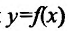
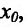
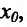
не имеет производной в точке 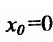
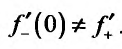
а левая производная равна:
Понятие производной в данной точке связано с понятием касательной к графику функции в этой точке. Чтобы выяснить эту связь, определим, прежде всего, касательную.
Пусть функция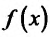
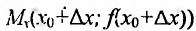
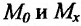
или
или
где
Если существует предельное положение секущей 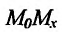
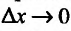
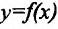
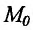
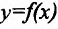
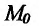
причем указанный предел 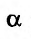
Предположим, что функция 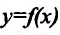
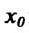
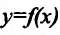
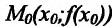
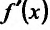
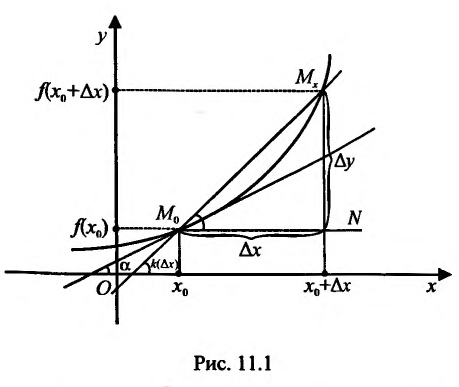
Рассмотрим рис. 11.1. Из треугольника 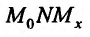
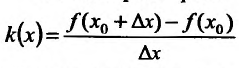
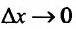
Поскольку в точке 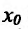
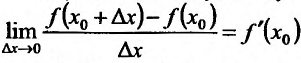
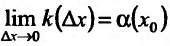
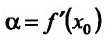
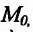
Правила вычисления производных, связанные с арифметическими действиями над функциями
Предположим, что все функции, рассматриваемые ниже, определены в некоторой окрестности точки
Теорема 11.2.1. Если функция f имеет производную в некоторой точке 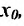
Доказательство. Рассмотрим разность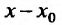
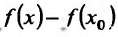
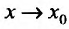
т.е. бесконечно малому приращению независимой переменной соответствует бесконечно малое приращение функции, значит, / непрерывна в точке
Заметим, что обратная теорема не верна, т.е. функция может быть непрерывной в точке 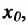
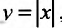
Теорема 11.2.2. Если функции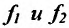
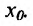
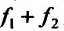
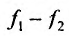
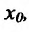
Доказательство. Пусть функции 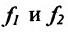
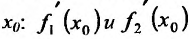
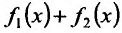
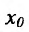
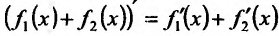
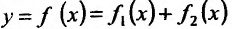
Составим разностное отношение
, если 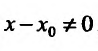
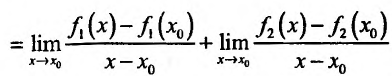
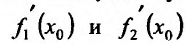
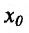
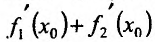
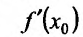
Теорема 11.2.3. Пусть функции 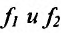
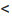
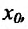
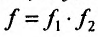
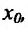
а если 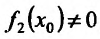
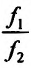
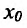
Доказательство. Пусть 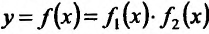
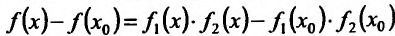
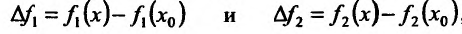
Подставим эти выражения в формулу приращения функции f, получим:
Составим разностное отношение
Рассматривая предел разностного отношения при 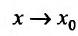
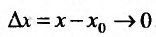
или
так как 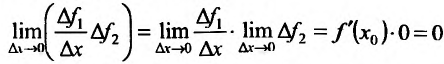
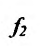
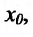
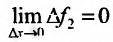
Пуста 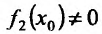
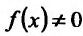
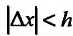
Поэтому 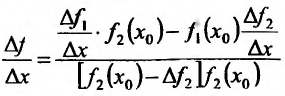
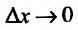
Следствие 11.2.1. Пусть функция f имеет производную в точке 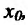
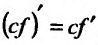
Следствие 11.2.2. Пусть функции 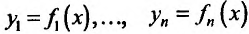
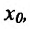
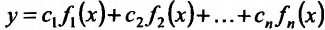
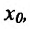
Производные сложной и обратной функций
Определим правила, позволяющие вычислять производные обратных и сложных функций.
Теорема 11.3.1. Пусть функция f определена, непрерывна и строго монотонна в некоторой окрестности точки 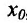
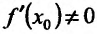
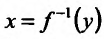
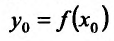
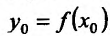
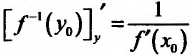
Доказательство. Зафиксируем некоторую окрестность точки 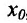
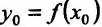
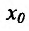
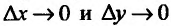
Зададим аргументу у функции 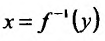
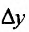
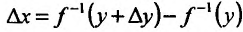
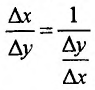
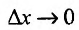
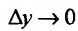
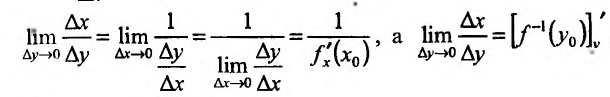
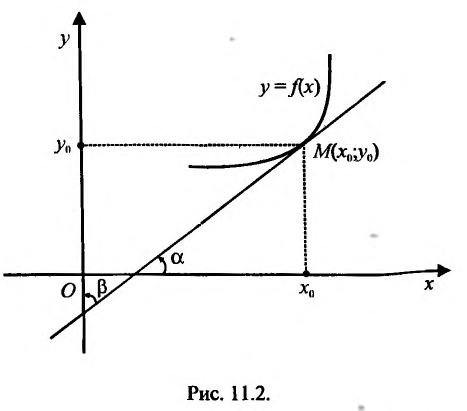
Эта теорема допускает наглядную геометрическую интерпретацию (рис. 11.2).
Известно, что производная функции в точке 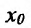
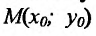
Поскольку у функции 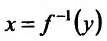
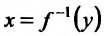
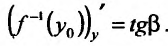
Поскольку 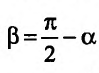
Пример №1
Найти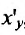
Решение:
Имеем 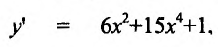
Теорема 11.3.2. Пусть 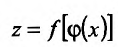
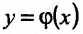
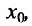
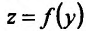
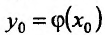
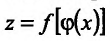
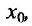
Доказательство. Придадим приращение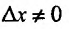
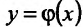
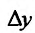
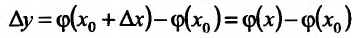
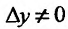
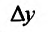
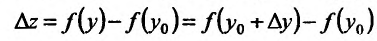
Составим разностное отношение 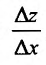
поскольку 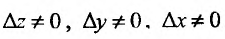
функции 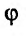
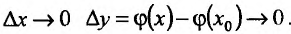
Заметим, что, используя правило вычисления производной сложной функции, можно находить производные функций, заданных неявно
Действительно, пусть функция 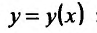
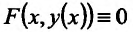
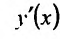
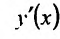
Пример №2
Найти 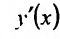
Решение:
Дифференцируем данное уравнение по х, считая у функцией от х:
Таблица производных
Для непосредственного вычисления производной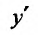
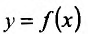
- выбирают приращение аргумента
, находят соответствующее приращение функции
и составляют разностное отношение
;
- преобразуют разностное отношение;
- вычисляют предел преобразованного разностного отношения, при
Если предел существует, то и производная существует и она равна пределу разностного отношения.
Применим это правило для определения производных простейших функций.
Свойство 11.4.1. у = с (const).
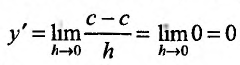
Свойство 11.4.2. у = sin x .
Свойство 11.4.3. у = cos x.
Свойство 11.4.4.
Свойство 11.4.5. у = tg x. Применим правило для производной частного двух функций:
Свойство 11.4.6. у = ctgx Применяя правило дифференцирования частного, будем иметь:
Свойство 11.4.7.
Свойство 14.4.8. 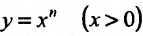
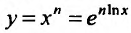
Свойство 11.4.9. у = arcsinх. Если 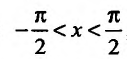
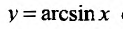
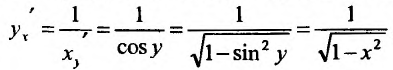
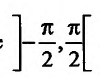
Свойство 11.4.10. у = arctgx. Если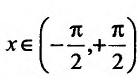
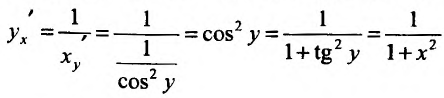
Свойство 11.4.11. 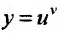
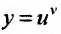
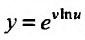
Свойство 11.4.12. 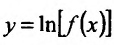
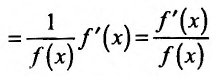
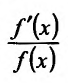
Приведём таблицу производных простейших элементарных функций:
Пример №3
Вычислить производную функции
Решение:
Воспользовавшись формулой вычисления производной частного, получим:
- Заказать решение задач по высшей математике
Пример №4
Вычислить производную функции 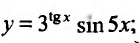
Решение:
Воспользовавшись формулой вычисления производной произведения, получим:
Пример:
Вычислить производную функции у = In arcsin/6х;
Решение:
Воспользовавшись формулой вычисления производной сложной функции, получим:
Выведем ещё формулу для вычисления производной параметрически заданных функций, т.е. функций, заданных формулами вида
Если функции x = x(t) И y = y(t) имеют в точке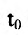
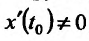
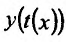
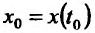
В самом деле, по правилу вычисления производной сложной функции имеем 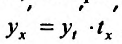
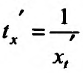
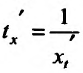
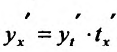
Производные высших порядков
Производная 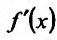
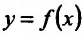
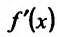
Определение 11.5.1. Пусть функция f определённая на интервале (а.b), в каждой точке 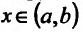
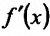
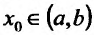
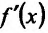
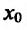
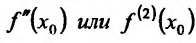
т.е.
После того, как введено определение второй производной, можно последовательно ввести определение третьей производной, затем четвертой производной, и т.д. Если предположить, что уже введено определение (n-1)-ой производной и что (n-1)-ая производная имеет производную в некоторой точке 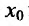
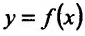
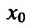
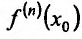
Кроме того считают, что 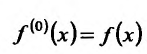
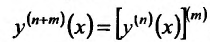
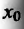
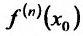
Определение 11.5.2. Функция f называется n раз непрерывной дифференцируемой на некотором промежутке, если на этом промежутке существует непрерывная производная n-ого порядка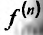
По индукции можно доказать, что:
в частности , если
Кроме того, по индукции можно доказать, что сумма функций,, слагаемые которой имеют производные n-го порядка, также имеет производную n-го порядка, вычисляемую по формуле:’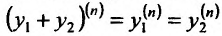
где 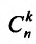
Рассмотрим некоторые производные 2-го порядка:
— для сложной функции 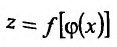
— для обратной функции 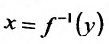
так как
для функции 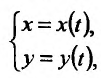
Действительно, так как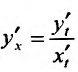
Пример №5
Найти 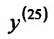
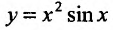
Решение:
Полагая в формуле Лейбница (11.5.2) 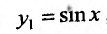
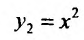
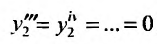
Подчеркнем, что формула Лейбница особенно эффективна в том случае, когда одна из перемножаемых функций имеет лишь конечное число отличных от нуля производных и не представляет затруднения вычисление всех производных другой из перемножаемых функций.
- Приложения производной функции одной переменной
- Исследование поведения функций
- Предел и непрерывность функции двух переменны
- Дифференцируемость функции нескольких переменных
- Метод Гаусса — определение и вычисление
- Прямая линия на плоскости и в пространстве
- Плоскость в трехмерном пространстве
- Функция одной переменной
plyengsat609
Вопрос по алгебре:
Составить разностное отношение,если:
1) f(x) = 4x
2)f(x)=x-1
3)f(x)=4x^2
4)f(x)=x^2+2
5)f(x)=x^3-x^2
6)f(x)-2x^3+x
Трудности с пониманием предмета? Готовишься к экзаменам, ОГЭ или ЕГЭ?
Воспользуйся формой подбора репетитора и занимайся онлайн. Пробный урок — бесплатно!
Ответы и объяснения 1
bated
F(x)=4x
f(x+h)=4(x+h)
lim=4x+4h-4x снизу делим это всё на h (дробь)=4
Знаете ответ? Поделитесь им!
Гость ?
Как написать хороший ответ?
Как написать хороший ответ?
Чтобы добавить хороший ответ необходимо:
- Отвечать достоверно на те вопросы, на которые знаете
правильный ответ; - Писать подробно, чтобы ответ был исчерпывающий и не
побуждал на дополнительные вопросы к нему; - Писать без грамматических, орфографических и
пунктуационных ошибок.
Этого делать не стоит:
- Копировать ответы со сторонних ресурсов. Хорошо ценятся
уникальные и личные объяснения; - Отвечать не по сути: «Подумай сам(а)», «Легкотня», «Не
знаю» и так далее; - Использовать мат — это неуважительно по отношению к
пользователям; - Писать в ВЕРХНЕМ РЕГИСТРЕ.
Есть сомнения?
Не нашли подходящего ответа на вопрос или ответ отсутствует?
Воспользуйтесь поиском по сайту, чтобы найти все ответы на похожие
вопросы в разделе Алгебра.
Трудности с домашними заданиями? Не стесняйтесь попросить о помощи —
смело задавайте вопросы!
Алгебра — раздел математики, который можно нестрого охарактеризовать как обобщение и расширение арифметики.
Найди верный ответ на вопрос ✅ «Составить разностное отношение, если: 1) f (x) = 4x 2) f (x) = x-1 3) f (x) = 4x^2 4) f (x) = x^2+2 5) f (x) = x^3-x^2 6) f (x) — 2x^3+x …» по предмету 📙 Алгебра, а если ответа нет или никто не дал верного ответа, то воспользуйся поиском и попробуй найти ответ среди похожих вопросов.
Искать другие ответы
Главная » Алгебра » Составить разностное отношение, если: 1) f (x) = 4x 2) f (x) = x-1 3) f (x) = 4x^2 4) f (x) = x^2+2 5) f (x) = x^3-x^2 6) f (x) — 2x^3+x
6.1. Производная функции, ее геометрический и физический смысл
Если x0 – точка числовой оси, то любой интервал (a,b) , ее содержащий, называется окрестностью точки x0. Пусть y = f (x) – функция, определенная в
|
некоторой окрестности (a,b) фиксированной точки x0 и |
x (a,b) – |
|||||
|
произвольная точка. |
||||||
|
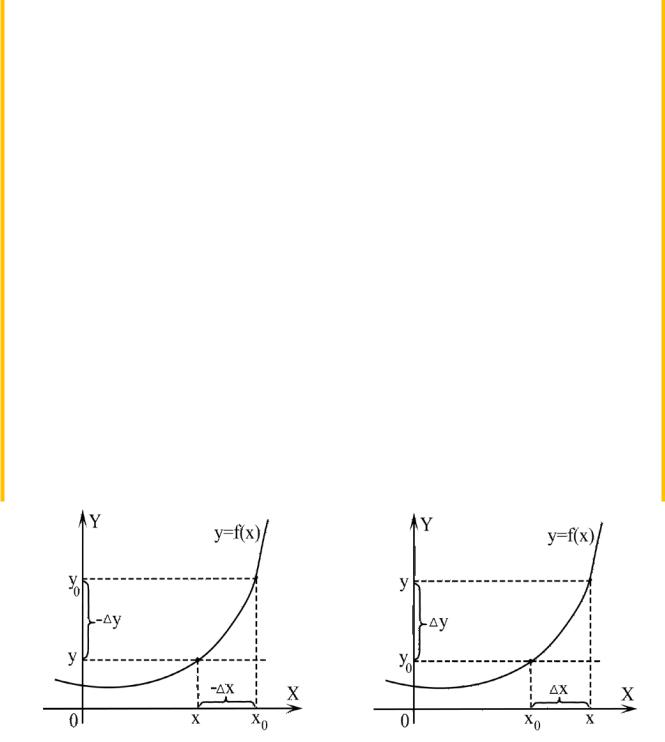
Приращением аргумента называют разность x − x0 и обозначают ее ∆x . |
||||||
|
Приращением функции f (x) в точке x0, |
соответствующим приращению |
|||||
|
аргумента ∆x , называется разность (рис. 6.1) ∆y = f (x) − f (x0 ) |
или иначе |
|||||
|
∆y = f (x0 + ∆x) − f (x0 ) . |
||||||
|
Так как x0 – фиксированная точка, а x |
– переменная, то разность ∆y |
|||||
|
является функцией аргумента ∆x . |
||||||
|
Разностное отношение – это отношение приращения ∆y |
функции к |
|||||
|
соответствующему приращению ∆x аргумента: |
||||||
|
∆y = |
f (x) − f (x0 ) |
= |
f (x0 + ∆x) − f (x0 ) |
. |
||
|
∆x |
x − x |
∆x |
||||
|
0 |
Разностное отношение также является функцией аргумента ∆x, определенной при всех ∆x ≠ 0.
Рис. 6.1
184

|
Определение производной. Пусть функция |
y = f (x) определена |
в |
||||||||
|
некоторой окрестности точки x0. |
||||||||||
|
Предел |
разностного отношения при |
∆x →0 |
(если он существует) |
|||||||
|
называют производной функции f в точкех0 и обозначают f ′(x0 ) : |
||||||||||
|
f ′(x0 ) = lim |
f (x0 + ∆x) − f (x0 ) |
= |
lim |
∆y |
||||||
|
∆x |
||||||||||
|
∆x→0 |
∆x |
∆x→0 |
||||||||
|
или так как x = x0 + ∆ x , то при ∆ x → 0 будет x → x0 |
и |
|||||||||
|
′ |
f (x) − f (x0 ) |
|||||||||
|
f (x |
) = lim |
x − x |
. |
|||||||
|
0 |
x→x0 |
|||||||||
|
0 |
||||||||||
|
Если этот предел существует и конечен, то говорят, что функция f имеет в |
||||||||||
|
точке х0 |
конечную производную, а также называют функцию f |
|||||||||
|
дифференцируемой в точке х0. |
||||||||||
|
Если предел разностного отношения существует и равен +∞ или −∞, |
то |
|||||||||
|
говорят, что функция имеет бесконечнуюпроизводную в точке х0. |
Если предел не существует, то говорят, что функция f не имеет производной в точке х0 , т.е. не дифференцируема в этой точке.
Операция нахождения производной называется дифференцированием. Если функция имеет конечную производную в каждой точке х интервала (a, b ,
то ее называют дифференцируемой на интервале (a, b . Эта производная будет представлять собой некоторую функцию аргумента х, определенную на интервале (a, b .
Производную функцию обычно обозначают так:
|
f ′(x), |
fx′(x) , y ‘(x), y ‘, |
df (x) |
, |
df dy(x) |
, |
dy |
, |
||||||||||
|
dx |
dx |
dx |
dx |
||||||||||||||
|
а значение производной функции в точке х0: |
|||||||||||||||||
|
f ′(x0 ) , fx′(x0 ) , f ′(x) |
x=x |
, df (x0 ) , |
df (x) |
x=x , |
y ‘(x0 ), dy(x) |
x=x |
, |
dy(x0 ) . |
|||||||||
|
0 |
dx |
dx |
0 |
dx |
0 |
dx |
185

Чтобы найти производную функции y = f (x) в заданной точке x0 непосредственно по определению, следует выполнить следующие действия
I. Придаем аргументу x0 произвольное приращение ∆x ≠0 и находим выражение для соответствующего приращения у функции y = f (x) в этой точке x0: ∆y = f (x0 + ∆x) − f (x0 )
II. Делим приращение функции у на приращение аргумента x, т.е. составляем разностное отношение ∆y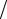
III. Ищем предел этого отношения при искомое значение f ′(x0 ) производной функции
∆x →0 . Этот предел и дает y = f (x) в точке x0 .
Пример 6.1. Найдите по определению производные следующих
|
элементарных функций: |
|||||||||||||
|
1) y = C (C – постоянная); |
2) y = x ; |
3) y = sin x. |
|||||||||||
|
Решение. 1) поскольку ∆y = f (x + ∆x) − f (x ) =C −C = 0, то |
lim ∆y = 0. |
||||||||||||
|
0 |
0 |
∆x→0 ∆x |
|||||||||||
|
Поэтому C′ = 0 – производная постоянной равна нулю; |
|||||||||||||
|
2) так как ∆y = f (x + ∆x) − f (x) = x + ∆x − x = ∆x, то lim |
∆y |
= lim |
∆x =1. |
||||||||||
|
Поэтому y (x) = x =1; |
∆x→0 ∆x |
∆x→0 |
∆x |
||||||||||
|
′ |
′ |
||||||||||||
|
3) поскольку ∆y = sin(x + ∆x) −sin x = 2sin ∆x cos(x + ∆x), |
то |
||||||||||||
|
2 |
2 |
||||||||||||
|
lim |
∆y |
= lim |
2sin(∆x 2)cos(x + ∆x 2) |
= |
|||||||||
|
∆x |
|||||||||||||
|
∆x→0 |
∆x→0 |
∆x |
|||||||||||
|
= lim |
sin(∆x 2) |
lim cos(x + ∆x |
2)= cos x . |
||||||||||
|
∆x→0 |
∆x 2 |
∆x→0 |
|||||||||||
|
Значит, |
(sin x) |
= cos x. |
|||||||||||
|
′ |
|||||||||||||
|
Пример 6.2. Пользуясь определением производной, вычислите |
f (−2) , |
||||||||||||
|
′ |
|||||||||||||
|
если f (x) = |
. |
||||||||||||
|
x +3 |
|||||||||||||
|
Решение. |
Имеем: x0 = −2, |
f (x0 ) = |
=1, |
x0 + ∆x = −2 + ∆x, |
|||||||||
|
−2 +3 |
f (x0 + ∆x) = 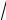
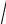
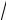
186
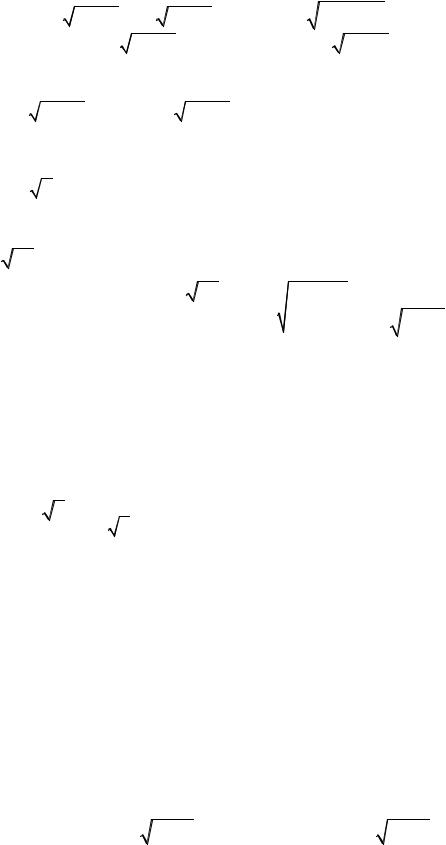
|
−12 ) |
|||||||||||||||||||||
|
( |
−1)( |
+1) |
( (1 |
+ ∆x)2 |
|||||||||||||||||
|
′ |
= lim |
1+ ∆x |
1 |
+ ∆x |
= |
lim |
= |
||||||||||||||
|
f (−2) |
∆x( 1+ ∆x |
+1) |
∆x( 1 |
+ ∆x +1) |
|||||||||||||||||
|
∆x→0 |
∆x→0 |
||||||||||||||||||||
|
= lim |
1+ ∆x −1 |
= |
lim |
1 |
= 1 . |
||||||||||||||||
|
∆x→0 |
∆x( 1+ ∆x |
+1) |
∆x→0 |
1+ ∆x +1 |
2 |
Пример 6.3. Пользуясь определением производной, вычислите f ′(0) для функции f (x) = 3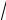
|
Решение. |
Имеем: |
x0 = 0, |
f (x0 ) = f (0) = 0 , |
x0 + ∆x = ∆x, |
|||||||||||||||||||||||||||||||||||||||||||||
|
f (x + ∆x) = 3 |
. Согласно определению производной находим |
||||||||||||||||||||||||||||||||||||||||||||||||
|
∆x |
|||||||||||||||||||||||||||||||||||||||||||||||||
|
0 |
|||||||||||||||||||||||||||||||||||||||||||||||||
|
∆f (0) |
3 |
1 |
|||||||||||||||||||||||||||||||||||||||||||||||
|
′ |
∆x |
= lim |
∆x |
||||||||||||||||||||||||||||||||||||||||||||||
|
= |
lim |
3 |
= |
lim |
= +∞. |
||||||||||||||||||||||||||||||||||||||||||||
|
f |
(0) = lim |
∆x |
∆x |
(∆x)3 |
|||||||||||||||||||||||||||||||||||||||||||||
|
∆x→0 |
∆x→0 |
∆x→0 |
∆x→0 3 (∆x)2 |
||||||||||||||||||||||||||||||||||||||||||||||
|
Таким образом, имеем бесконечную производную в точке |
x0 = 0 . |
||||||||||||||||||||||||||||||||||||||||||||||||
|
Производные основных элементарных функций |
|||||||||||||||||||||||||||||||||||||||||||||||||
|
1) |
С′ = 0; |
2) |
(x |
m |
′ |
m-1 |
; |
||||||||||||||||||||||||||||||||||||||||||
|
) = mx |
|||||||||||||||||||||||||||||||||||||||||||||||||
|
3) ( |
)′ = |
1 |
4) 1 |
′ |
1 |
||||||||||||||||||||||||||||||||||||||||||||
|
; |
= − |
; |
|||||||||||||||||||||||||||||||||||||||||||||||
|
x |
|||||||||||||||||||||||||||||||||||||||||||||||||
|
2 |
x |
2 |
|||||||||||||||||||||||||||||||||||||||||||||||
|
x |
x |
||||||||||||||||||||||||||||||||||||||||||||||||
|
5) (ex )′ = ex ; |
6) (ax )′ = ax ln a ; |
||||||||||||||||||||||||||||||||||||||||||||||||
|
7) |
(ln x)′ = |
1 ; |
|
(loga x)′ |
= |
1 |
; |
||||||||||||||||||||||||||||||||||||||||||
|
xln a |
|||||||||||||||||||||||||||||||||||||||||||||||||
|
x |
|||||||||||||||||||||||||||||||||||||||||||||||||
|
9) |
(sin x)′ |
= cos x ; |
10) |
(cos x)′ |
= −sin x ; |
||||||||||||||||||||||||||||||||||||||||||||
|
′ |
1 |
′ |
1 |
||||||||||||||||||||||||||||||||||||||||||||||
|
11) |
(tg x) |
= |
; |
12) |
(ctg x) = − |
; |
|||||||||||||||||||||||||||||||||||||||||||
|
cos2 x |
sin2 x |
||||||||||||||||||||||||||||||||||||||||||||||||
|
13) |
(arcsin x)′ = |
1 |
; |
14) |
(arccos x)′ = − |
1 |
; |
||||||||||||||||||||||||||||||||||||||||||
|
1− x2 |
1− x2 |
||||||||||||||||||||||||||||||||||||||||||||||||
|
15) |
(arctg x)′ = |
1 |
; |
16) |
(arcctg x)′ = − |
1 |
. |
||||||||||||||||||||||||||||||||||||||||||
|
1+ x2 |
1+ x2 |
187

Односторонние производные. Правой производной функции y = f (x) в
точке х=х0 называется правый предел отношения ∆∆yx , если он существует:
|
f+′(x0 ) = f ′(x0 |
+ 0) |
= lim ∆y |
= |
lim |
f (x0 + ∆x) − f (x0 ) |
. |
|
∆x→0+ ∆x |
x→x0 +0 |
∆x |
Левой производной функции y = f (x) в точке х=х0 называется левый предел отношения ∆∆yx , если он существует:
|
f−′(x0 ) = f ′(x0 −0) = |
lim ∆y |
= |
lim |
f (x0 + ∆x) − f (x0 ) |
. |
|
∆x→0− ∆x |
x→x0 −0 |
∆x |
Производные слева и справа называются односторонними производными. Односторонние производные могут быть конечными, бесконечными или вовсе не существовать.
Из свойств пределов функций следует, что производная функции f (x) в
точке х0 существует тогда и только тогда, когда в этой точке существуют обе односторонние производные f−′(x0 ) , f+′(x0 ), и они совпадают междусобой. При этом f ′(x0 ) = f−′(x0 ) = f+′(x0 )
Если у функции f (x) существуют правая и левая производные в точке х0, но эти производные не равны друг другу, то у этой функции не существует производной в точке х0
|
( f ′(x0 −0) = A, f ′(x0 + 0) = B, A ≠ B) ( f ′(x0 ) |
не существует). |
|
Например, функция f (x) =| x | имеет в точке х=0 |
левую производную |
f−′(0) = −1, правую производную f+′(0) =1, непрерывна в этой точке, но не имеет в ней производной, так как f−′(0) ≠ f+′(0).
Под производной функции в граничной точке промежутка понимают соответствующую одностороннюю производную. Так, если функция f (x) рассматривается на отрезке [a,b], то под производной в точке а понимается правая производная, а под производной в точке b – левая производная.
Вычисление односторонней производной непосредственно по определению отличается от вычисления обычной производной лишь тем, что ∆x <0 – при нахождении левой и ∆x >0 – при нахождении правой производной.
188
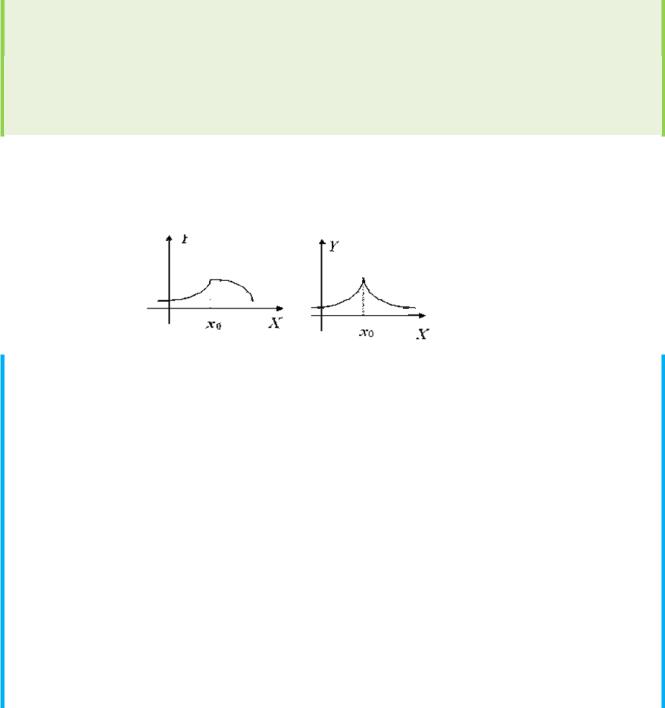
Непрерывность и дифференцируемость. Если функция y = f (x)
дифференцируема в данной точке x, то она и непрерывна в этой точке (т.е. бесконечно малым приращениям аргумента соответствуют бесконечно малые приращения функции). Непрерывность функции есть необходимое (но не достаточное) условие существования производной.
Функция, непрерывная в некоторой точке х, может не иметь в этой точке производной. Такую точку называют угловой точкой графика функции или
точкой его излома (рис. 6.2).
|
Рис. 6.2 |
||||||||
|
Физический |
смысл |
производной. |
Разностное |
отношение |
∆y |
|||
|
∆x |
||||||||
|
представляет |
собой |
среднюю скорость |
изменения |
функции на |
отрезке |
|||
|
[x0, x0 + ∆x]. |
Существование |
производной |
в точке |
x0 |
означает, |
что |
при |
стремлении ∆x к нулю разностное отношение (средняя скорость изменения) стабилизируется возле своего предельного значения, называемого мгновенной скоростью в точке x0.
Производная в точке x0 – это предельная (мгновенная) скорость изменения функции y = f (x) в точке x0 (иными словами, скорость изменения зависимой переменной у по отношению к изменению независимой переменной х в точке x0). В частности, если х – время, а y = f (x) – координата точки, движущейся по прямой, в момент х, то f ′(x0 ) – это мгновенная скорость точки в момент времени x0.
Пример 6.4. Дано уравнение прямолинейного движения точки s = 2t2 +3. Определите среднюю скорость движения: а) за первые 5 секунд; б) за промежуток времени от конца 2 -й до конца 5 -й секунды; в) мгновенную скорость в момент t = 5.
Решение. Придадим аргументу t приращение ∆t и найдем приращение координаты s
∆s = s(t0 + ∆t) − s(t0 ) = 2(t02 + 2t0 ∆t+ ∆t2 ) +3 −(2t02 +3) = 4t0 ∆t+ 2 ∆t2 .
Составим разностное отношение ∆s = 4t0 ∆t+ 2 ∆t2 = 4t0 + 2 ∆t :
∆t ∆t
189
|
а) здесь t0 = 0, |
∆t = 5. |
Тогда vср = (4t0 |
+ 2 ∆t) |
t0 |
=0 = 4 0 + 2 5 =10; |
|||||||||
|
б) здесь t0 = 2, |
∆t = 3. |
Тогда vср = (4t0 |
+ 2 ∆t) |
∆t=5 |
= 4 2 + 2 3 =14; |
|||||||||
|
t0=2 |
||||||||||||||
|
( |
t0 =5 ) |
∆t=3 |
||||||||||||
|
в) v(5) = lim v |
= lim |
(4t |
+ 2 ∆t) |
= lim (4 5 + 2 ∆t)= 20. |
||||||||||
|
∆t→0 ср |
∆t→0 |
0 |
∆t→0 |
|||||||||||
|
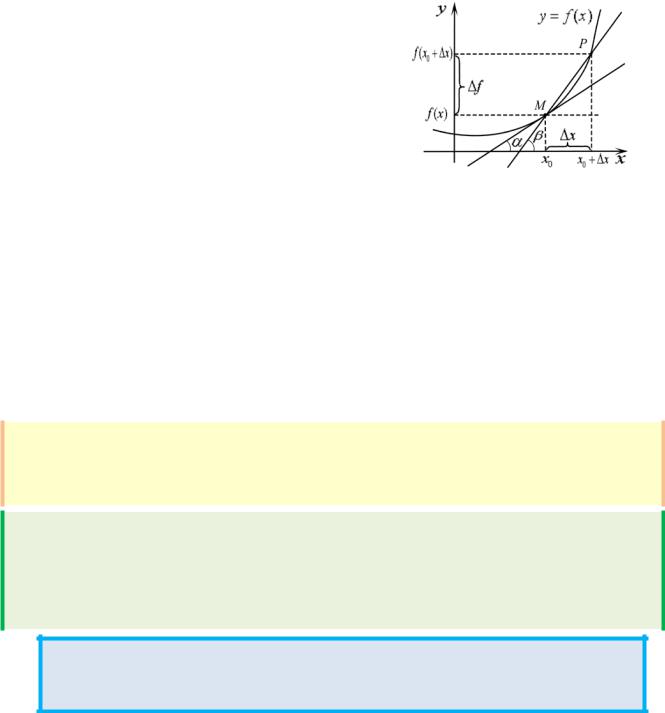
Геометрический смысл производной. |
Пусть f (x) |
определена на некотором |
||||||||||||
|
промежутке (a, b . Прямую, |
проходящую через две точки графика M (x0, f (x0 )) и |
|||||||||||||
|
P(x0 + ∆x, f (x0 + ∆x)) ,называютсекущей. |
||||||||||||||
|
Угол β наклона секущей MP (рис. 6.3) к оси |
||||||||||||||
|
Ox функционально зависит от приращения |
||||||||||||||
|
∆x . Величина этого угла в радианах |
||||||||||||||
|
заключена в пределах от 0 до π , а тангенс |
||||||||||||||
|
равен разностному отношению: |
||||||||||||||
|
tg β = ∆f , |
β (0, π ). |
|||||||||||||
|
∆x |
Рис. 6.3
При стремлении ∆x к нулю точка P приближается к точке M. Секущая MP при этом поворачивается вокруг точки M и стремится к своему предельному положению, которое однозначно определяется предельным значением α угла наклона β . При этом тангенс угла α равен по величине пределу разностного отношения, т.е. производной функции в точке x0:
|
tgα = lim tg β = lim |
∆f |
= f ′(x0 ) |
|
|
P→M |
∆x→0 |
∆x |
Касательная к графику функции в точке M (x0, f (x0 )) – это прямая, определяемая как предельное положение секущей MP при стремлении ∆x к нулю.
Если у функции y = f (x) в данной фиксированной точке х0 есть производная, то в точке (x0, f (x0 )) существует касательная к графику функции y = f (x), причем угловой коэффициент k этой касательной (т.е. тангенс угла наклона ее к оси Ох) равен производной f ′(x0 ) .
Касательная к кривой y = f (x) в точке (x0, f (x0 )) задается уравнением y − y0 = f ′(x0 ) (x − x0 )
190

Нормаль к кривой y = f (x) в точке (x0, f (x0 )) – это перпендикуляр к касательной, проходящий через эту точку.
|
Нормаль к кривой y = f (x) в точке (x0, f (x0 )) задается уравнением |
||||||||
|
y − y = − |
1 |
(x − x ) . |
||||||
|
0 |
f ′(x0 ) |
0 |
||||||
|
Если f ′(x0 ) = +∞ (или −∞), |
то в |
этом |
случае |
угол |
α равен π 2, а |
|||
|
касательная к графику функции y = f ( x) |
в точке x0 перпендикулярна к оси Ох и |
|||||||
|
задается уравнением x = x0 . Если |
f ′(x0 ) = 0, |
то в точке (x0, f (x0 )) графика |
||||||
|
функции касается горизонтальная прямая |
y = f (x0 ) . |
|||||||
|
Пусть две кривые пересекаются в точке |
(x0, y0 ), |
т.е. |
y0 = f (x0 ) = g(x0 ). |
Угол ϕ между кривыми y = f (x) и y = g(x) в точке их пересечения может быть
|
определен как угол между касательными или, |
что то же самое, угол между |
||||||||||||||||||||
|
нормалями, проведенными к кривым в этой точке: |
|||||||||||||||||||||
|
tgϕ |
= |
k2 − k1 |
= |
g ‘(x0 ) − f ′(x0 ) |
. |
||||||||||||||||
|
1+ k1k2 |
1+ f ′(x0 )g ‘(x0 ) |
||||||||||||||||||||
|
Пример 6.5. Составьте уравнения касательной и нормали к кривой y = x3 |
|||||||||||||||||||||
|
в точке M0 (2 ; |
|||||||||||||||||||||
|
Решение. Имеем |
f |
(x) = x |
3 |
, f |
′ |
3 |
′ |
2 |
; |
f (x0 ) = f (2) =8; |
|||||||||||
|
(x) = (x |
) = 3x |
||||||||||||||||||||
|
f ′(x0 ) = f ′(2) = 3 22 =12. |
Используя |
уравнение |
y − y0 = f ′(x0 )(x − x0 ) , |
||||||||||||||||||
|
получаем уравнение касательной y =12(x − 2) +8, |
или |
y =12x −16 . Используя |
|||||||||||||||||||
|
уравнение y − y = − |
1 |
(x − x ) , получаем уравнение нормали: |
|||||||||||||||||||
|
0 |
f ′(x0 ) |
0 |
|||||||||||||||||||
|
y =8 − |
1 |
(x − 2) или 12y = 96 − x + 2 , |
т.е. |
x +12y −98 = 0. |
|||||||||||||||||
|
12 |
|||||||||||||||||||||
|
Пример 6.6.. По оси Ох движутся две материальные точки, законы |
|||||||||||||||||||||
|
движения которых x |
= t3 |
− 4 |
и x = 7 t2 |
−12t +3 (x – в метрах, t — в секундах). |
|||||||||||||||||
|
1 |
3 |
2 |
3 |
||||||||||||||||||
Найдите моменты времени, в которые их скорости окажутся равными. Решение. Находим скорости обеих точек: x1′ = t2 , x2′ = 7t −12. Так как
x1′ = x2′ , то t2 = 7t −12 , t2 −7t +12 = 0 , t1 = 3с, t2 = 4 с.
191
Задачи для самостоятельного решения
|
6.1. Составить выражение для |
∆y = f (x0 + ∆x) − f (x0 ) |
и найти область |
||
|
определения функции ∆y , если: |
а) |
f (x)= arcsin x, |
x0 =1 2 ; |
|
|
б) f (x)= ln x, x0 = 2 ; |
в) |
f (x) |
= sin x, x0 = 2π . |
6.2.Дана функция y = x2 . Найти приближенные значения производной в точке x = 3 , полагая последовательно ∆x равным:
|
а) 0,5; |
б) 0,1; |
в) 0,01; |
г) 0,001. |
6.3. Пользуясь определением производной, найти производную функции:
|
а) |
y =10x в точке x |
= 0 ; |
б) y = ln x в точке |
x = 2 ; |
||||
|
0 |
0 |
|||||||
|
в) |
y = |
в точке x0 = 4 . |
||||||
|
x |
||||||||
|
6.4. Исходя из определения производной, найти f ′(0): |
||||||||
|
а) f (x)= x3 +5x2 ; |
б) f (x)= 3x2 +5x −3; |
в) f (x)= |
. |
|||||
|
4x +1 |
6.5. Найти угловой коэффициент касательной, проведенной к параболе y = x2 :
|
а) в начале координат; |
б) в точке (3; 9); |
в) в точке пересечения ее с |
|
прямой y = 3x − 2 . |
6.6. Под каким углом пересекается парабола y = x2 с прямой 3x − y − 2 = 0?
6.7.Под каким углом пересекаются параболы y = x2 и y2 = x ?
6.8.Составить уравнение касательной и нормали, проведенных к кривой y = x3
вточке с абсциссой 2.
6.9. 1. Пользуясь определением производной, найти производную функции в точке с абсциссой x0 .
2. Составить уравнение нормали к данной кривой в точке с абсциссой x0 :
|
а) y = −x2 4, x = 2; |
б) y = 2x2 +3x −1, x = − 2 |
|||||||||||||||||
|
0 |
0 |
|||||||||||||||||
|
в) |
y = x − x3, |
x = − 1 |
г) |
y =8 |
−32, |
x |
= 4; |
|||||||||||
|
x |
||||||||||||||||||
|
0 |
0 |
|||||||||||||||||
|
y = 3 |
− 20, |
|||||||||||||||||
|
д) |
y = x + |
x3 |
, |
x |
= 1 |
е) |
x2 |
x |
= −8; |
|||||||||
|
0 |
0 |
|||||||||||||||||
|
y = |
1+ |
, |
||||||||||||||||
|
ж) |
x |
x |
= 4; |
з) |
y =84 |
−70, |
x |
=16; |
||||||||||
|
x |
||||||||||||||||||
|
1− |
x |
0 |
0 |
|||||||||||||||
|
и) y = 2x2 −3x +1, x = 1 |
к) y = x2 −3x + 6, x = 3; |
|||||||||||||||||
|
0 |
0 |
192
6.10.1 . Пользуясь определением производной, найти производную функции в точке с абсциссой x0 .
2. Составитьуравнениекасательнойкданнойкривойвточкесабсциссой x0 :
|
а) y = 2x |
2 +3, x = − 1; |
б) y = x29 + 6, x = 1 |
|||||
|
0 |
0 |
||||||
|
в) y = 2x + 1 , x = 1 |
г) y = x4 +1, x = 1; |
||||||
|
x |
0 |
0 |
|||||
|
д) y = |
x5 +1 |
, x = 1 |
е) y = |
x16 +9 |
, x = 1 |
||
|
x4 |
+1 |
0 |
1−5x2 |
0 |
|||
6.11.Дано уравнение прямолинейного движения точки: s = 5t + 6. Определить среднюю скорость движения: а) за первые 6 секунд; б) за промежуток времени от конца 3-й до конца 6-й секунды.
6.12. Дано уравнение прямолинейного движения: s(t) = t3 +3 / t . Найти среднюю скорость движения за промежуток времени от t = 4 до t1 = 4+Δt,
полагая t =2; 1; 0,1; 0,03.
6.13.Закон движения точки по прямой задан формулой s = t3 – 3t2 + 3t + 5 (s – в метрах, t – в секундах). В какие моменты времени t скорость точки равна нулю?
|
6.14. Две точки движутся по прямой по законам s = t3 |
−5t2 |
+17t − 4 и |
|
|
1 |
|||
|
s = t3 |
−3t . В какой момент времени их скорости равны? |
||
|
2 |
6.15. Тело, брошенное вверх, движется по закону s = −4,905t2 +981t +950 (s – в метрах, t – в секундах). Найдите скорость тела в любой момент времени и его начальную скорость. В какой момент времени скорость тела станет равной нулю и какой наивысшей высоты в этот момент времени достигнет тело.
6.16. Переменные величины у и х связаны соотношением y2 =12x.. Аргумент х возрастает равномерно со скоростью 2 единицы в секунду. С какой скоростью возрастает упри x = 3 ?
6.17. Ордината точки, описывающей окружность y2 + x2 = 25, убывает со скоростью 1,5 см/с. С какой скоростью изменяется абсцисса точки, когда ордината становится равной 4 см?
6.18.В какой точке эллипса 9y2 +16x2 = 400 ордината убывает с такой же скоростью, с какой абсцисса возрастает?
193
6.19.Сторона квадрата увеличивается со скоростью v. Какова скорость изменения периметраиплощадиквадратавтотмомент,когдасторонаегоравнаa?
6.20.Радиускругаизменяетсясоскоростьюv.Каковаскоростьизменениядлины окружностииплощадикругавтотмомент,когдаегорадиусравен r?
6.21.Радиус шара изменяется со скоростью v. С какой скоростью изменяются объем и поверхность шара?
6.22.Предполагая, что объем ствола дерева пропорционален кубу его диаметра и что последний равномерно увеличивается из года в год, показать, что скорость роста объема, когда диаметр равен 90 см, в 25 раз больше скорости, когда диаметр равен 18 см.
6.23. В какой точке кривой y2 = 4x3 касательная перпендикулярна к прямой
x+3y −1 = 0 ?
6.24.Выяснить, в каких точках кривой y = sin 2x касательная составляет с осью Ох угол x =π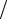
6.25.Выяснить, в какой точке кривой y = 2x3 −1 касательная составляет с осью Ох угол α =π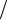
|
x3 |
9x |
2 |
|||||||||||
|
6.26. |
Найти точки на кривой y = |
− |
+ 20x −7 , в которых касательные |
||||||||||
|
3 |
2 |
||||||||||||
|
параллельны оси Ох. |
|||||||||||||
|
6.27. |
Найти |
точку |
на |
кривой |
y = 3x2 −5x −11, |
касательная |
в |
которой |
|||||
|
параллельна прямой x − y +10 = 0 . |
|||||||||||||
|
6.28. Найти |
точку |
на |
кривой |
y = 3x2 − 4x + 6 , касательная в которой |
|||||||||
|
параллельна прямой 8x − y −5 = 0 . |
|||||||||||||
|
6.29. |
Найти |
точку |
на |
кривой |
y = −3x2 + 4x −7 , |
касательная |
в |
которой |
|||||
|
перпендикулярна к прямой x − 20y +5 = 0 . |
|||||||||||||
|
6.30. |
Найти |
точку |
на |
кривой |
y = 5x2 − 4x +1, |
касательная |
в |
которой |
|||||
|
перпендикулярна к прямой x + 6y +15 = 0 . |
6.31.Траектория движения тела – кубическая парабола 12y = x3 В каких ее точках скорости возрастания абсциссы и ординаты одинаковы?
6.32.По оси Ох движутся две материальные точки, законы движения которых x = 4t2 −7 и x = 3t2 − 4t +38 . С какой скоростью эти точки удаляются друг от друга в момент встречи?
194
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Составить разностное отношение, если : 1) f(x) = 4x
2)f(x) = x — 1
3)f(x) = 4x ^ 2
4)f(x) = x ^ 2 + 2
5)f(x) = x ^ 3 — x ^ 2
6)f(x) — 2x ^ 3 + x.
Вы находитесь на странице вопроса Составить разностное отношение, если : 1) f(x) = 4×2)f(x) = x — 13)f(x) = 4x ^ 24)f(x) = x ^ 2 + 25)f(x) = x ^ 3 — x ^ 26)f(x) — 2x ^ 3 + x? из категории Алгебра.
Уровень сложности вопроса рассчитан на учащихся 10 — 11 классов. На странице
можно узнать правильный ответ, сверить его со своим вариантом и обсудить
возможные версии с другими пользователями сайта посредством обратной связи.
Если ответ вызывает сомнения или покажется вам неполным, для проверки
найдите ответы на аналогичные вопросы по теме в этой же категории, или создайте
новый вопрос, используя ключевые слова: введите вопрос в поисковую строку,
нажав кнопку в верхней части страницы.

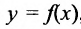


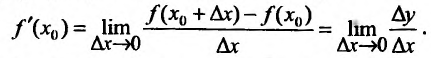
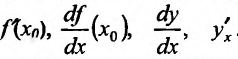
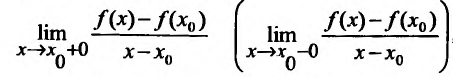
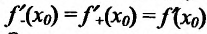
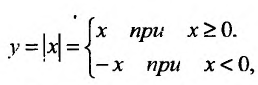
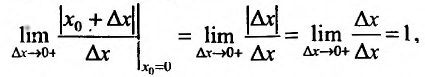
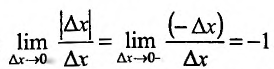
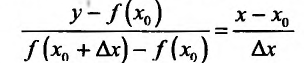
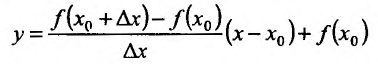
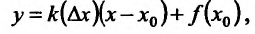
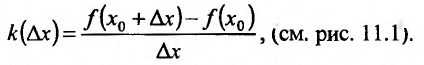
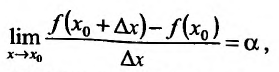
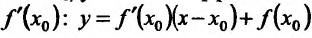
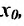
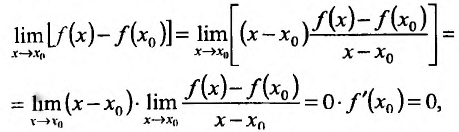
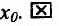
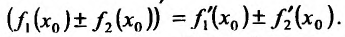
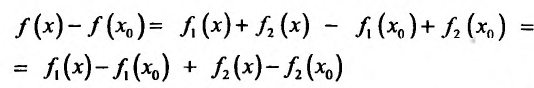
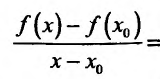
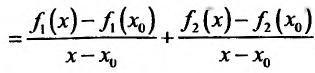
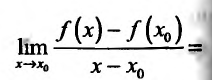
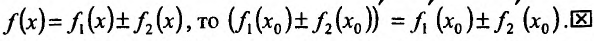
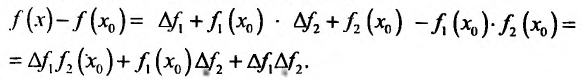
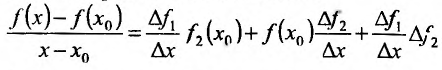
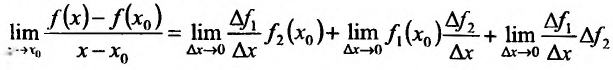
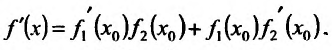
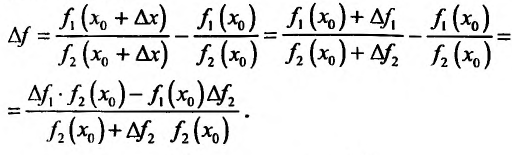
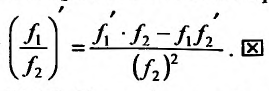
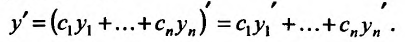
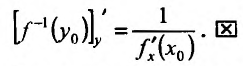
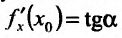
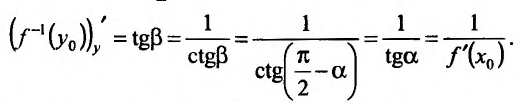
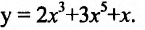
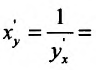
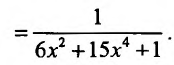
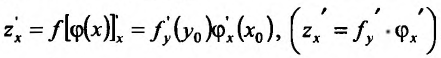
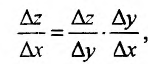
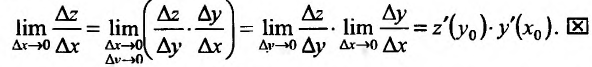
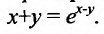
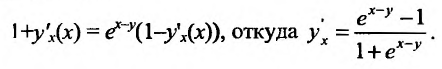
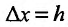 , находят соответствующее приращение функции
, находят соответствующее приращение функции 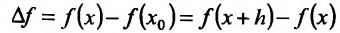 и составляют разностное отношение
и составляют разностное отношение 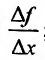 ;
;