Решения разностных уравнений
Разностные уравнения для чайников
На этой странице мы рассмотрим примеры решения типовых задач, встречающихся в курсе дифференциальных и разностных уравнений, а именно нахождение общего или частного решения линейного разностного уравнения с постоянными коэффициентами. Чаще всего в контрольных встречаются уравнения второго или третьего порядка:
$$
a_0 y(x) + a_1 y(x+1) + a_2 y(x+2)=f(x), \ a_0 y(x) + a_1 y(x+1) + a_2 y(x+2)+ a_3 y(x+3)=f(x).
$$
Здесь $a_i$ — постоянные коэффициенты, $f(x)$ — правая часть (неоднородность уравнения), $y(x)$ — искомая неизвестная функция.
Решение разностных уравнений практически полностью аналогично решению линейных дифференциальных уравнений с постоянными коэффициентами (см. тут примеры): ищется решение однородного уравнения через составление характеристического уравнения, и частное решение неоднородного уравнения по виду правой части.
Спасибо за ваши закладки и рекомендации
Примеры решений разностных уравнений
Задача 1. Решить разностное уравнение: $y(x+2)-4y(x+1)+4y(x)=2^x$
Задача 2. Найти общее решение линейного разностного неоднородного уравнения второго порядка с постоянными коэффициентами.
$$ y(i+2)-4y(i+1)-12y(i)=6cdot 6^i.$$
Задача 3. Решить разностное уравнение третьего порядка
$$ y(x+3)-16y(x+2)+83y(x+1)-140y(x)=0, quad y(0)=3, y(1)=18, y(2)=120. $$
Задача 4. Найти частное решение однородного разностного уравнения:
$$ y(x+3)-6y(x+2)+11y(x+1)-6y(x)=0, quad y(0)=0, y(1)=2, y(2)=8. $$
Помощь с разностными уравнениями
Если вам нужна помощь с решением задач и контрольных по дифференциальным и разностным уравнениям (и другим разделам математического анализа), обращайтесь в МатБюро. Стоимость подробной консультации от 100 рублей, оформление производится в Word, срок от 1 дня.
Поможем с решением задач и уравнений
Дополнительная информация
- Задачи по дифференциальным уравнениям с решениями
- Онлайн-помощь на контрольной
- Почему МатБюро?
Содержание:
- Разностные уравнения
- Разностные уравнения первого порядка с постоянными коэффициентами
- Разностные уравнения второго порядка с постоянными коэффициентами
Разностные уравнения
Понятие разницы и разностного уравнения
Если для значений переменной x1, x2, x3, … функция f (x) принимает значения f (x1), f (x2), f (x3) … , то приращения функции составляют f (x2) – f (x1), f (x3) – f (x2), …
Приращение функции при переходе от значения xi к значению xi+1 будем обозначать: 
Введем обозначения ΔΔf (x) = Δ2 f (x), тогда Δ2 f (x) = f (x + 2) — 2 f (x + 1) + f (x) и называется разностью второго порядка.
Аналогично можно найти разности третьего, четвертого и т. д. порядков.
Определим разности некоторых важнейших функций.
1) Если f (x) = С, где С — постоянная величина, то
Δf (x) = f (x + 1) – f (x) = С – С = 0.
Понятно, что и все разности следующих порядков будут также равняться нулю.
2) Если f (x) = ax + b, то
Δf = Δf (x + 1) — f (x) = a (x + 1) + b — ax — b = a.
Разница первого порядка линейной функции равна постоянной, а все остальные будут равны нулю.
3) Если f (x) = ax2 + bx + c, то
Поскольку разница первого порядка является линейной функцией, то разница второго порядка — постоянная, а все последующие разности равны нулю.
4) Если f (x) = ax, то
В экономических исследованиях часто встречаются задачи, в которых время t является независимой переменной, а зависимая переменная определяется для времени t, t + 1, t + 2 и т. д.
Обозначим yt — значение функции y в момент времени t; yt+1 — значение функции в момент, сдвинутый на одну единицу, например, на следующий час, на следующую неделю и т. д., yt+2 — значение функции y в момент, сдвинутый на две единицы и т. д.
Очевидно, что
Откуда:
За разность второго порядка, имеем 
поэтому
Аналогично можно доказать, что
Итак, любую функцию
можно представить в виде: 
и наоборот.
Определение. Уравнение

называется разностным уравнением n-го порядка.
Решить разностное уравнение n-го порядка — это значит найти такую функцию yt, которая превращает уравнение (7.50) или (7.51) в тождество.
Решение, в котором есть произвольная постоянная, называется общим; решение, в котором постоянная отсутствует, называется частным.
Определение. Уравнение

где a0, a1, …, an — постоянные числа, называется неоднородным разностным
уравнением n-го порядка с постоянными коэффициентами.
Если в уравнении (7.52) f (t) = 0, то уравнение называется однородным разностным уравнением n-го порядка с постоянными коэффициентами:

Уравнение 

ТЕОРЕМА 1. Если решениями однородного разностного уравнения (7.53) является y1 (t) и y2 (t), то его решением будет также функция y1 (t) + y2 (t).
ТЕОРЕМА 2. Если y (t) является решением однородного разностного уравнения (7.53), то его решением будет также функция Ay (t), где А — произвольная постоянная.
ТЕОРЕМА 3. Если y (t) — частное решение неоднородного уравнения (7.52) и y (t, A1, A2, …, An) — общее решение однородного уравнения (7.53), то общим решением неоднородного разностного уравнения будет функция: y (t) + y (t, A1, A2, …, An).
Эти теоремы схожи с теоремами для дифференциальных уравнений, которые были приведены нами в предыдущем разделе.
Разностные уравнения первого порядка с постоянными коэффициентами
Рассмотрим неоднородное разностное уравнение

Соответствующее ему однородное уравнение будет:

Возьмем функцию 


Итак, 
По теореме (2) общее решение однородного разностного уравнения (7.55) является функция 
Пусть 
Частное решение найти нетрудно, если f (t) = α, где α — некоторая постоянная. На самом деле, если 
Итак, общее решение уравнения (7.54) запишем в виде: 
Разностные уравнения второго порядка с постоянными коэффициентами
Пусть задано неоднородное разностное уравнение второго порядка с постоянными коэффициентами:

и соответствующее ему однородное уравнение

Убедимся, что функция 


Это уравнение называется характеристическим уравнением для уравнения (7.57).
Здесь могут иметь место следующие три случая:
1. D = a2 – 4b > 0, тогда уравнение (7.58) будет иметь два действительных различных корня.
Общее решение уравнения (7.57) запишется в виде:
а общее решение неоднородного уравнения (7.56) запишется так:
2. D = a2 – 4b = 0, тогда 

В этом случае однородное уравнение (7.57) примет вид:

Тогда
Легко убедиться, что решением уравнения (7.59) является также функция


3. D = a2 – 4b < 0, тогда характеристическое уравнение (7.58) имеет два комплексных сопряженных корня:
Обозначим 

Пример 1. Решить разностное уравнение:
Решение. Запишем соответствующее ему однородное уравнение:
Характеристическое уравнение λ2 – 5λ + 6 = 0 будет иметь действительные разные корни (D = 25 – 24 = 1 > 0), λ1 =2, λ2 = 3.
Общим решением однородного уравнения является функция
Далее положим, что yt = y — частное решение неоднородного уравнения, тогда
Таким образом, общим решением неоднородного уравнения является функция 
Решим эту систему уравнений относительно A1 и A2:
Откуда
Итак, 
Примеры применения разностных уравнений в экономических задачах
Пример 1. Пусть некоторая сумма средств выдается под сложный процент p, то к концу t-го года ее размер будет составлять:


Если положить y0 = F , то A = F, откуда
Это известная формула величины фонда F, который выдается под сложный процент.
Пример 2. Пусть величина предложения сельскохозяйственной продукции в t-м году есть функция цены прошлого года 

Цена равновесия для данной продукции определяется равенством:

Положим, что функция спроса определяется формулой 
Цена равновесия запишется: 


Тогда p0 = A и решением уравнения является функция
Если начальная цена p0 = 0, то pt = 0 для всех значений t.
Следовательно, цена не подлежит изменению.
Вообще говоря, функция предложения — возрастающая, а потому b > 0; а функция спроса — убывающая, и поэтому a < 0. Откуда 

Здесь имеют место три случая:
1) Если 

Тогда говорят, что колебания цены сдерживается.
2) Если 
В этом случае говорят, что колебания цены периодические.
3) Если 

Говорят, что колебания цены растет.
Лекции:
- Случайная вероятность
- Эквивалентные бесконечно малые функции. Сравнение бесконечно больших функций
- Решение определённых интегралов
- Параллельные прямые
- Кривизна и кручение пространственной кривой. Формулы Френе
- Пределы в математике
- Дифференциал функции
- Объемы подобных фигур
- Алгебра логики
- Эластичность функции
В
общем случае линейное разностное
уравнение порядка M
с постоянными коэффициентами имеет вид
,
(8.16)
где
описывают конкретную систему, причем
.
8.2.3.1. Решение разностных уравнений методом прямой подстановки
Уравнение
(8.16) записано в виде, удобном для решения
методом прямой
подстановки.
Имея набор начальных условий (например,
дляi=-1,
-2, …, —M)
и входную последовательность
по формуле (8.16)т можно непосредственно
вычислить выходную последовательностьдля
.
Пример.
Дана
последовательность
Разностное
уравнение имеет вид
(8.17)
с
начальными условиями.
Данное
уравнение можно решить подстановкой,
что дает:
8.2.3.2. Решение разностных уравнений в
явном виде
Хотя
решение разностного уравнения
подстановкой
и целесообразно
в некоторых случаях, значительно полезнее
получить решения в явном
виде.
Основная
идея сводится к получению двух решений
разностного уравнения: однородного
и частного.
Однородное
уравнение получается путем подстановки
нулей вместо всех членов, содержащих
элементы входной последовательности
и определение отклика при нулевой
входной последовательности.
Частное
решение
получается из подбора вида последовательности
навыходе
при заданной входной
последовательности
.
Для определения произвольных постоянных
однородного решения используются
начальные условия.
Пример.
Решить
уравнение (8.17) этим методом.
Однородное
уравнение имеет вид
(8.18)
Известно,
что характеристическими
решениями однородных уравнений,
соответствующих линейным разностным
уравнениям с постоянными коэффициентами,
является решение вида
.
Поэтому, подставляя вместов (8.18),
получим
Отсюда
однородное решение имеет вид
.
(8.19)
Частное
решение, соответствующее входной
последовательности
,
попробуем найти в виде
.
(8.20)
Из
уравнения (8.16) получаем
.
Поскольку
коэффициенты при равных степенях
в левой и правой частях уравнения должны
совпадать, то из получаемой системы
(трех уравнений) находим три искомых
коэффициента:.
Таким
образом, общее решение имеет вид:
,
(8.21)
В этом выражении
коэффициент
находится из начального условия
.
Тогда
из (8.21) получим
(8.22)
Проверка
решения (8.22) при
показывает полное совпадение с приведенным
выше прямым решением.
Преимущество
решения (8.22) заключается в том, что оно
позволяет весьма просто определить
для любого конкретного
.
8.2.3.3. Схемы реализации цифровых систем
Важное
значение разностных уравнений состоит
в том, что они непосредственно определяют
способ
построения цифровой системы.
Так,
разностное уравнение первого
порядка
самого общего вида
(8.23)
м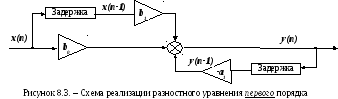
реализовать с помощью схемы
Блок
“задержки” осуществляет задержку
сигнала на один отсчет.
Разностное
уравнение второго
порядка самого общего вида
(8.24)
м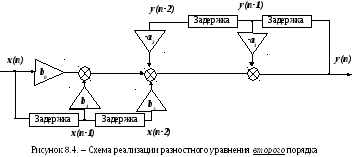
быть реализовано при помощи схемы,
приведенной на рисунке 8.4.
Системы
первого и второго порядка могут быть
использованы при реализации систем
более высокого поряджка, т.к. последние
могут быть представлены в виде
последовательного или параллельного
соединения систем первого и второго
порядка.
8.2.4. Z – преобразование
Одним
из методов представления последовательностей
является Z-преобразование.
Для
последовательности
,
заданной при всех,Z-преобразование
определяется следующим степенным
рядом
.
(8.25)
где
— комплексная переменная.
8.2.4. 1. Последовательности конечной
длины
Если
отлична от нуля только в интервале
,
где—конечны, то
сходится в
— плоскости везде, за исключением, может
быть, точкиили
.
Линейную
систему с постоянными параметрами,
импульсная характеристика которой
является последовательностью конечной
длины, называют системой с конечной
импульсной характеристикой, или, что
то же самое, КИХ-фильтром.
Т
импульсная характеристикаконечной длины изображена на рисунке
8.5.
Системой
(фильтром) с бесконечной импульсной
характеристикой (БИХ) называется
система (фильтр), длина импульсной
характеристики которой не ограничена
слева
или справа
или с обеих сторон.
8.2.4. 2. Примеры Z-преобразования.
-
Найти
Z-преобразование
единичного импульса.
Решение.
Так
как
при любых
,
кроме,
при котором,
то согласно (8.25) имеем
.
(8.26)
-
Найти
Z-преобразование
единичного
скачка.
Так
как
везде, кроме
,
где,
то из (8.25) получим
.
(8.27)
Бесконечный
ряд сходится при
,
т.к.имеет единственную особую точку
.
(Примечание.
Результат (8.27) вытекает из формулы суммы
геометрической прогрессии
).
-
Найти
Z-преобразование
комплексной
экспоненты.
.
(8.28)
сходится при
,
т.к. единственной особой точкой является.
-
Найти
Z-преобразование
простой экспоненциальной
последовательности.
В
этом случае
при
и
при
.
Тогда
согласно (8.25) получаем
.
(8.29)
сходится при
,
т.к. единственной особой точкой является.
8.2.4. 3. Свойства Z
– преобразования
Линейность.
Z
– преобразование линейно.
Пусть
— z
– преобразования
последовательностей
.
Тогда
справедливо
.
(8.30)
Задержка.
Если
,
то
. (8.31)
Это
свойство полезно при переходе от
представления линейной системы с
постоянными переменными к представлению
ее z
– преобразованием
и наоборот.
Пример.
Пусть
имеется разностное уравнение
.
Представим
его в виде z
– преобразования
или
,
где
Свертка
последовательностей
Пусть
входные и выходные последовательности
дискретной линейной системы с постоянными
параметрами,— импульсная характеристика системы,
— их соответствующиеz
– преобразования.
Тогда
имеет место
,
(8.32)
или
Как
следует из рассмотрения (8.32), операция
свертки последовательностей сводится
к перемножению их z
– преобразований.
8.2.4.4. Решение разностных уравнений
с применением одностороннего z
– преобразования
Разностные
уравнения обычно определены при
и имеют набор начальных условий.
Разностное
уравнение первого
порядка
,
(8.33)
начальное
условие
.
Пусть
на вход поступает последовательность
.
Чтобы
найти одностороннее z
– преобразование, умножим обе части
равенства (8.33) на
и просуммируем от
до
.
Из
свойства задержки
.
Отсюда
.
Поскольку
,
то
.
Разложив
второе слагаемое на простые дроби,
получим

Обратное
z
– преобразование дает последовательность
– решение разностного уравнения
Соседние файлы в папке НОВИКОВ_2013-14
- #
- #
- #
- #
- #
- #
- Категория: Цифровая обработка сигналов
Разностные уравнения – это алгоритм функционирования дискретной цепи. Разностное уравнение записывается непосредственно по схеме.
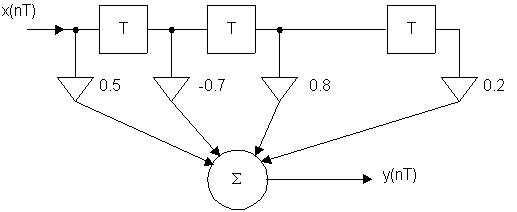
Пример: Составить разностное уравнение.
y(nT) = 0.5·x(nT) + (-0.7) ·x(nT-T) + 0.8·x(nT-2T) + 0.2·x(nT-3T)
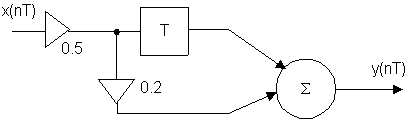
Пример: Определить y(nT) если x(nT)={1;0.5} для цепи:
y(nT) = 0.1·x(nT) + 0.5·x(nT-T)
Воспользуемся численным методом.
n=0; y(0T) = 0.1·x(0T) + 0.5·x(-T) = 0.1 + 0.5·0 = 0.1
n=1; y(1T) = 0.1·x(1T) + 0.5·x(0T) = 0.1·0.5 + 0.5·1 = 0.55
n=2; y(2T) = 0.1·x(2T) + 0.5·x(1T) = 0.1·0 + 0.5·0.5 = 0.25
n=3; y(3T) = 0.1·x(3T) + 0.5·x(2T) = 0.1·0 + 0.5·0 = 0
y(nT) = {0.1; 0.55; 0.25}
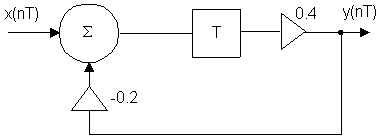
Пример: Определить сигнал на выходе, если x(nT) = {1; 1}
Цепь с обратной связью.
Составим разностное уравнение из двух слагаемых:
y(nT) = 0.4·x(nT-T) – 0.2·0.4·y(nT-T)
вх.сигнал вых.сигнал
n=0; y(0T) = 0.4·x(-T) – 0.08·y(-T) = 0, где: x(-T) = y(-T) = 0
n=1; y(1T) = 0.4·x(0T) – 0.08·y(0T) = 0.4·x(T-T) – 0.08·y(T-T) = 0.4·1-0.08·0 = = 0.4
n=2; y(2T) = 0.4·x(1T) – 0.08·y(1T) = 0.4·1 – 0.08·0.4 = 0.4 – 0.032 = 0.368
n=3; y(3T) = 0.4·x(2T) – 0.08·y(2T) = 0.4·0 – 0.08·0.368 = –0.02944
n=…
y(nT) = {0; 0.4; 0.368; –0.2944; …}
Цепь дискретная, содержащая обратную связь, называется рекурсивной, а цепь, не содержащая обратной связи, называется не рекурсивной.
1.3. Составление и решение разностных уравнений
Разности решетчатых функций аналогичны производным непрерывных функций [68]. Первая разность, или разность 1-го порядка, определяется как разность между предыдущей и последующей ординатами решетчатой функции
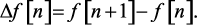
Разность 2-го порядка определяется следующим выражением:
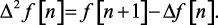
Согласно (1.26), имеем 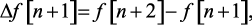
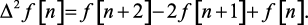
Выражение разности 3-го порядка имеет следующий вид
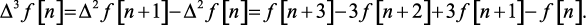
Разность k-го порядка определяется по алгоритму, представленному математическим выражением
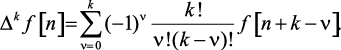
Пример 1.1. Решетчатая функция характеризуется выражением f[n] = an2. Определить разность этой функции.
Решение. Первая разность
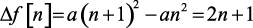
и вторая разность
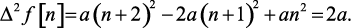
Уравнение, связывающее решетчатую функцию и ее разности с аргументом n, называется разностным уравнением, или уравнением в конечных разностях.
В общем виде неоднородное линейное разностное уравнение с постоянными коэффициентами m-го порядка можно записать в виде:
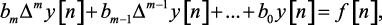
где y[n] – искомая функция (реакция); f[n] – заданная функция (возмущение). При f[n] = 0 уравнение (1.31) будет однородным.
Если в разностном уравнении (1.31) разности заменить решетчатыми функциями по формуле (1.30), то получим другой вид разностного уравнения:
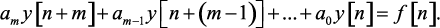
Нетрудно установить связь между коэффициентами ak и bk. Например, если дано уравнение
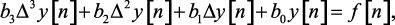
то, подставляя в него значение 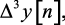
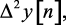
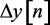
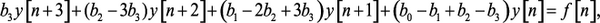
отсюда 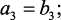
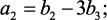
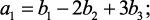
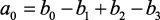
Разностное уравнение, записанное в формуле (1.32), можно рассматривать как рекуррентную формулу, позволяющую последовательно вычислять значения y[m], y[m + 1], y[m + 2], … , если известны y[0], y[1], y[2], …, y[m – 1]. В этом заключается одно из отличий разностных уравнений от дифференциальных. Другое отличие состоит в том, что порядок разностного уравнения может не совпадать с наивысшим порядком разности.
Для разностного уравнения m-го порядка задаются начальные значения решетчатой функции: либо y[0] и Δky[0] (при k = 1, 2,…, m – 1), если уравнение имеет вид (1.31), либо y[0], y[1], y[2], …, y[m – 1], если уравнение имеет вид (1.32).
Пример 1.2. Дано разностное уравнение
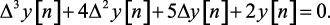
Определить другой вид (1.32) разностного уравнения.
Решение. Заменим разности соответствующими значениями решетчатой функции. В результате выполненной операции получим
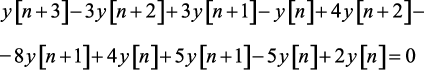
или y[n + 3] + y[n + 2] = 0. После замены n1 = n + 2 это уравнение принимает вид y[n1 + 1] + y[n1] = 0, то есть переходит в однородное разностное уравнение 1-го порядка.
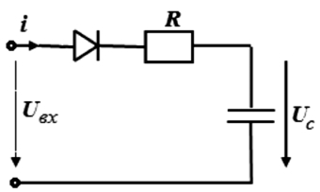
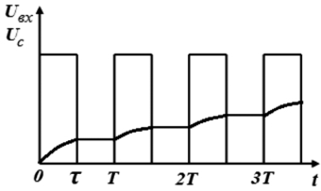
Пример 1.3. Составим временное разностное уравнение для конденсаторного счетчика импульсов (рис. 1.9, а) при uc(0) = 0. На рис. 1.9, б изображена времяимпульсная диаграмма, поясняющая работу счетчика импульсов. Входным напряжением счетчика является импульсный сигнал, представляющий собой последовательность прямоугольных импульсов с амплитудой Um, длительностью τ и периодом следования T. В интервале времени, когда на вход счетчика поступает импульс, происходит заряд конденсатора до некоторого напряжения, которое после окончания действия этого импульса сохраняется до прихода
следующего импульса.
а б
Рис. 1.9. Конденсаторный счетчик импульсов
и его времяимпульсная диаграмма
Решение. В качестве решетчатой функции рассмотрим значения напряжения на конденсаторе в конце периода, которые соответствуют напряжениям при срезах импульсов сигнала uвх(t). Предположим, что в начале n-го интервала напряжение на конденсаторе было равно uc(n). Для удобства анализа введем переменную интервала t, которая изменяется в пределах от нуля до T, а в данном примере она фактически не превышает величины τ.
В интервале действия импульса напряжение на конденсаторе определяется выражением [1]
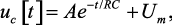
где A – коэффициент свободной составляющей uc[t], который определяется из начальных условий; Um – принужденная составляющая uc[t], которая равна амплитуде импульса.
Напряжение на конденсаторе в конце n-го интервала равно
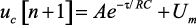
или
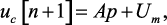
где 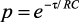
Определим из начальных условий коэффициент свободной составляющей A, подставив в уравнение (1.34) значения t = 0 и uc[n + 1] = uc[n]:
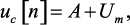
откуда
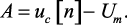
Затем подставив выражение (1.37) в уравнение (1.35), получим рекуррентную формулу для вычисления напряжения на конденсаторе
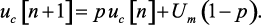
Отсюда при начальном условии uc[0] = 0, получим
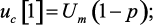
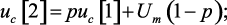
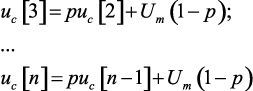
или
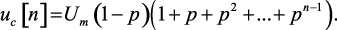
Последнее выражение (1.39) представляет собой сумму членов геометрической прогрессии. Следовательно,
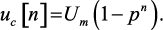
Подставляя сюда значение p, получим выражение для напряжения на конденсаторе в начале n-го интервала
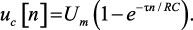
Необходимо обратить внимание на то, что в решении (1.41) отсутствует величина периода T, что связано с принципом действия счетчика импульсов, так как в нем происходит только заряд конденсатора в течение времени τ.