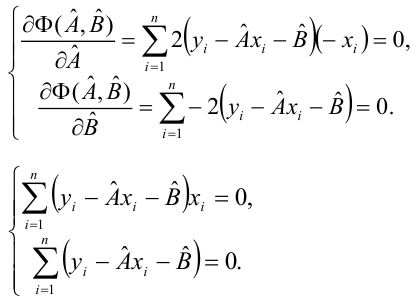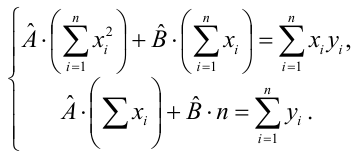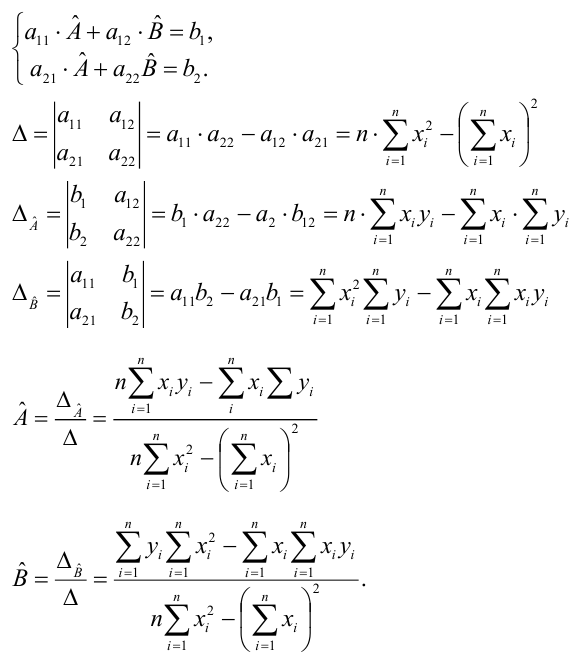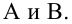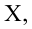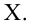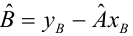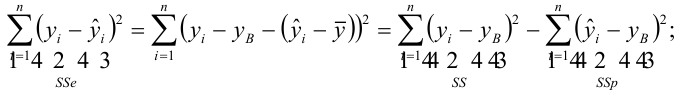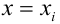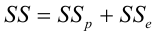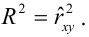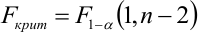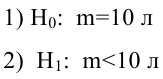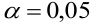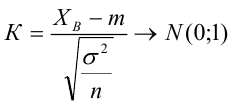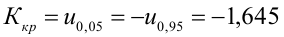Решаем уравнение простой линейной регрессии
Время на прочтение
23 мин
Количество просмотров 25K
В статье рассматривается несколько способов определения математического уравнения линии простой (парной) регрессии.
Все рассматриваемые здесь способы решения уравнения основаны на методе наименьших квадратов. Обозначим способы следующим образом:
- Аналитическое решение
- Градиентный спуск
- Стохастический градиентный спуск
Для каждого из способов решения уравнения прямой, в статье приведены различные функции, которые в основном делятся на те, которые написаны без использования библиотеки NumPy и те, которые для проведения расчетов применяют NumPy. Считается, что умелое использование NumPy позволит сократить затраты на вычисления.
Весь код, приведенный в статье, написан на языке python 2.7 с использованием Jupyter Notebook. Исходный код и файл с данными выборки выложен на гитхабе
Статья в большей степени ориентирована как на начинающих, так и на тех, кто уже понемногу начал осваивать изучение весьма обширного раздела в искусственном интеллекте — машинного обучения.
Для иллюстрации материала используем очень простой пример.
Условия примера
У нас есть пять значений, которые характеризуют зависимость Y от X (Таблица №1):
Таблица №1 «Условия примера»
Будем считать, что значения
— это месяц года, а
— выручка в этом месяце. Другими словами, выручка зависит от месяца года, а
— единственный признак, от которого зависит выручка.
Пример так себе, как с точки зрения условной зависимости выручки от месяца года, так и с точки зрения количества значений — их очень мало. Однако такое упрощение позволит, что называется на пальцах, объяснить, не всегда с легкостью, усваиваемый новичками материал. А также простота чисел позволит без весомых трудозатрат, желающим, порешать пример на «бумаге».
Предположим, что приведенная в примере зависимость, может быть достаточно хорошо аппроксимирована математическим уравнением линии простой (парной) регрессии вида:
где
— это месяц, в котором была получена выручка,
— выручка, соответствующая месяцу,
и
— коэффициенты регрессии оцененной линии.
Отметим, что коэффициент
часто называют угловым коэффициентом или градиентом оцененной линии; представляет собой величину, на которую изменится
при изменении
.
Очевидно, что наша задача в примере — подобрать в уравнении такие коэффициенты
и
, при которых отклонения наших расчетных значений выручки по месяцам от истинных ответов, т.е. значений, представленных в выборке, будут минимальны.
Метод наименьших квадратов
В соответствии с методом наименьших квадратов, отклонение стоит рассчитывать, возводя его в квадрат. Подобный прием позволяет избежать взаимного погашения отклонений, в том случае, если они имеют противоположные знаки. Например, если в одном случае, отклонение составляет +5 (плюс пять), а в другом -5 (минус пять), то сумма отклонений взаимно погасится и составит 0 (ноль). Можно и не возводить отклонение в квадрат, а воспользоваться свойством модуля и тогда у нас все отклонения будут положительными и будут накапливаться. Мы не будем останавливаться на этом моменте подробно, а просто обозначим, что для удобства расчетов, принято возводить отклонение в квадрат.
Вот так выглядит формула, с помощью которой мы определим наименьшую сумму квадратов отклонений (ошибки):
где
— это функция аппроксимации истинных ответов (то есть посчитанная нами выручка),
— это истинные ответы (предоставленная в выборке выручка),
— это индекс выборки (номер месяца, в котором происходит определение отклонения)
Продифференцируем функцию, определим уравнения частных производных и будем готовы перейти к аналитическому решению. Но для начала проведем небольшой экскурс о том, что такое дифференцирование и вспомним геометрический смысл производной.
Дифференцирование
Дифференцированием называется операция по нахождению производной функции.
Для чего нужна производная? Производная функции характеризует скорость изменения функции и указывает нам ее направление. Если производная в заданной точке положительна, то функция возрастает, в обратном случае — функция убывает. И чем больше значение производной по модулю, тем выше скорость изменения значений функции, а также круче угол наклона графика функции.
Например, в условиях декартовой системы координат, значение производной в точке M(0,0) равное +25 означает, что в заданной точке, при смещении значения
вправо на условную единицу, значение
возрастает на 25 условных единиц. На графике это выглядит, как достаточно крутой угол подъема значений
с заданной точки.
Другой пример. Значение производной равное -0,1 означает, что при смещении
на одну условную единицу, значение
убывает всего лишь на 0,1 условную единицу. При этом, на графике функции, мы можем наблюдать едва заметный наклон вниз. Проводя аналогию с горой, то мы как будто очень медленно спускаемся по пологому склону с горы, в отличие от предыдущего примера, где нам приходилось брать очень крутые вершины:)
Таким образом, проведя дифференцирование функции
по коэффициентам
и
, определим уравнения частных производных 1-го порядка. После определения уравнений, мы получим систему из двух уравнений, решив которую мы сможем подобрать такие значения коэффициентов
и
, при которых значения соответствующих производных в заданных точках изменяются на очень и очень малую величину, а в случае с аналитическим решением не изменяются вовсе. Другими словами, функция ошибки при найденных коэффициентах достигнет минимума, так как значения частных производных в этих точках будут равны нулю.
Итак, по правилам дифференцирования уравнение частной производной 1-го порядка по коэффициенту
примет вид:
уравнение частной производной 1-го порядка по
примет вид:
В итоге мы получили систему уравнений, которая имеет достаточно простое аналитическое решение:
begin{equation*}
begin{cases}
na + bsumlimits_{i=1}^nx_i — sumlimits_{i=1}^ny_i = 0
\
sumlimits_{i=1}^nx_i(a +bsumlimits_{i=1}^nx_i — sumlimits_{i=1}^ny_i) = 0
end{cases}
end{equation*}
Прежде чем решать уравнение, предварительно загрузим, проверим правильность загрузки и отформатируем данные.
Загрузка и форматирование данных
Необходимо отметить, что в связи с тем, что для аналитического решения, а в дальнейшем для градиентного и стохастического градиентного спуска, мы будем применять код в двух вариациях: с использованием библиотеки NumPy и без её использования, то нам потребуется соответствующее форматирование данных (см. код).
Код загрузки и обработки данных
# импортируем все нужные нам библиотеки
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import math
import pylab as pl
import random
# графики отобразим в Jupyter
%matplotlib inline
# укажем размер графиков
from pylab import rcParams
rcParams['figure.figsize'] = 12, 6
# отключим предупреждения Anaconda
import warnings
warnings.simplefilter('ignore')
# загрузим значения
table_zero = pd.read_csv('data_example.txt', header=0, sep='t')
# посмотрим информацию о таблице и на саму таблицу
print table_zero.info()
print '********************************************'
print table_zero
print '********************************************'
# подготовим данные без использования NumPy
x_us = []
[x_us.append(float(i)) for i in table_zero['x']]
print x_us
print type(x_us)
print '********************************************'
y_us = []
[y_us.append(float(i)) for i in table_zero['y']]
print y_us
print type(y_us)
print '********************************************'
# подготовим данные с использованием NumPy
x_np = table_zero[['x']].values
print x_np
print type(x_np)
print x_np.shape
print '********************************************'
y_np = table_zero[['y']].values
print y_np
print type(y_np)
print y_np.shape
print '********************************************'
Визуализация
Теперь, после того, как мы, во-первых, загрузили данные, во-вторых, проверили правильность загрузки и наконец отформатировали данные, проведем первую визуализацию. Часто для этого используют метод pairplot библиотеки Seaborn. В нашем примере, ввиду ограниченности цифр нет смысла применять библиотеку Seaborn. Мы воспользуемся обычной библиотекой Matplotlib и посмотрим только на диаграмму рассеяния.
Код диаграммы рассеяния
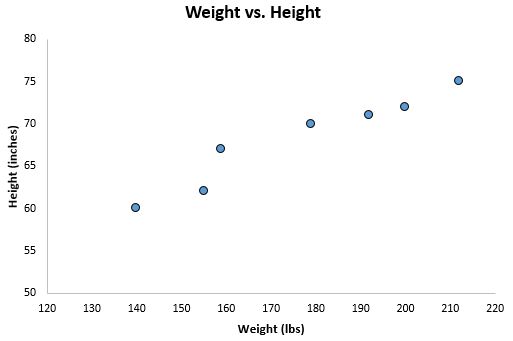
print 'График №1 "Зависимость выручки от месяца года"'
plt.plot(x_us,y_us,'o',color='green',markersize=16)
plt.xlabel('$Months$', size=16)
plt.ylabel('$Sales$', size=16)
plt.show()
График №1 «Зависимость выручки от месяца года»
Аналитическое решение
Воспользуемся самыми обычными инструментами в python и решим систему уравнений:
begin{equation*}
begin{cases}
na + bsumlimits_{i=1}^nx_i — sumlimits_{i=1}^ny_i = 0
\
sumlimits_{i=1}^nx_i(a +bsumlimits_{i=1}^nx_i — sumlimits_{i=1}^ny_i) = 0
end{cases}
end{equation*}
По правилу Крамера найдем общий определитель, а также определители по
и по
, после чего, разделив определитель по
на общий определитель — найдем коэффициент
, аналогично найдем коэффициент
.
Код аналитического решения
# определим функцию для расчета коэффициентов a и b по правилу Крамера
def Kramer_method (x,y):
# сумма значений (все месяца)
sx = sum(x)
# сумма истинных ответов (выручка за весь период)
sy = sum(y)
# сумма произведения значений на истинные ответы
list_xy = []
[list_xy.append(x[i]*y[i]) for i in range(len(x))]
sxy = sum(list_xy)
# сумма квадратов значений
list_x_sq = []
[list_x_sq.append(x[i]**2) for i in range(len(x))]
sx_sq = sum(list_x_sq)
# количество значений
n = len(x)
# общий определитель
det = sx_sq*n - sx*sx
# определитель по a
det_a = sx_sq*sy - sx*sxy
# искомый параметр a
a = (det_a / det)
# определитель по b
det_b = sxy*n - sy*sx
# искомый параметр b
b = (det_b / det)
# контрольные значения (прооверка)
check1 = (n*b + a*sx - sy)
check2 = (b*sx + a*sx_sq - sxy)
return [round(a,4), round(b,4)]
# запустим функцию и запишем правильные ответы
ab_us = Kramer_method(x_us,y_us)
a_us = ab_us[0]
b_us = ab_us[1]
print '33[1m' + '33[4m' + "Оптимальные значения коэффициентов a и b:" + '33[0m'
print 'a =', a_us
print 'b =', b_us
print
# определим функцию для подсчета суммы квадратов ошибок
def errors_sq_Kramer_method(answers,x,y):
list_errors_sq = []
for i in range(len(x)):
err = (answers[0] + answers[1]*x[i] - y[i])**2
list_errors_sq.append(err)
return sum(list_errors_sq)
# запустим функцию и запишем значение ошибки
error_sq = errors_sq_Kramer_method(ab_us,x_us,y_us)
print '33[1m' + '33[4m' + "Сумма квадратов отклонений" + '33[0m'
print error_sq
print
# замерим время расчета
# print '33[1m' + '33[4m' + "Время выполнения расчета суммы квадратов отклонений:" + '33[0m'
# % timeit error_sq = errors_sq_Kramer_method(ab,x_us,y_us)
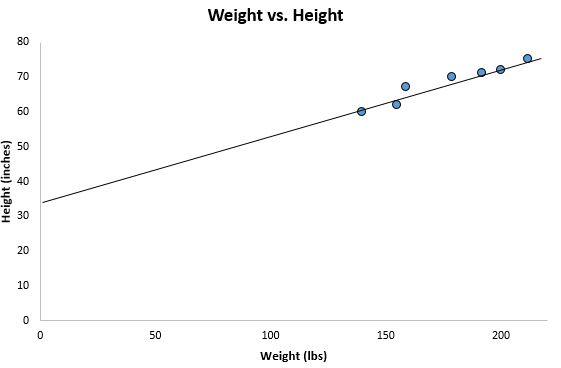
Вот, что у нас получилось:
Итак, значения коэффициентов найдены, сумма квадратов отклонений установлена. Нарисуем на гистограмме рассеяния прямую линию в соответствии с найденными коэффициентами.
Код линии регрессии
# определим функцию для формирования массива рассчетных значений выручки
def sales_count(ab,x,y):
line_answers = []
[line_answers.append(ab[0]+ab[1]*x[i]) for i in range(len(x))]
return line_answers
# построим графики
print 'Грфик№2 "Правильные и расчетные ответы"'
plt.plot(x_us,y_us,'o',color='green',markersize=16, label = '$True$ $answers$')
plt.plot(x_us, sales_count(ab_us,x_us,y_us), color='red',lw=4,
label='$Function: a + bx,$ $where$ $a='+str(round(ab_us[0],2))+',$ $b='+str(round(ab_us[1],2))+'$')
plt.xlabel('$Months$', size=16)
plt.ylabel('$Sales$', size=16)
plt.legend(loc=1, prop={'size': 16})
plt.show()
График №2 «Правильные и расчетные ответы»
Можно посмотреть на график отклонений за каждый месяц. В нашем случае, какой-либо значимой практической ценности мы из него не вынесем, но удовлетворим любопытство в том, насколько хорошо, уравнение простой линейной регрессии характеризует зависимость выручки от месяца года.
Код графика отклонений
# определим функцию для формирования массива отклонений в процентах
def error_per_month(ab,x,y):
sales_c = sales_count(ab,x,y)
errors_percent = []
for i in range(len(x)):
errors_percent.append(100*(sales_c[i]-y[i])/y[i])
return errors_percent
# построим график
print 'График№3 "Отклонения по-месячно, %"'
plt.gca().bar(x_us, error_per_month(ab_us,x_us,y_us), color='brown')
plt.xlabel('Months', size=16)
plt.ylabel('Calculation error, %', size=16)
plt.show()
График №3 «Отклонения, %»
Не идеально, но нашу задачу мы выполнили.
Напишем функцию, которая для определения коэффициентов
и
использует библиотеку NumPy, точнее — напишем две функции: одну с использованием псевдообратной матрицы (не рекомендуется на практике, так как процесс вычислительно сложный и нестабильный), другую с использованием матричного уравнения.
Код аналитического решения (NumPy)
# для начала добавим столбец с не изменяющимся значением в 1.
# Данный столбец нужен для того, чтобы не обрабатывать отдельно коэффицент a
vector_1 = np.ones((x_np.shape[0],1))
x_np = table_zero[['x']].values # на всякий случай приведем в первичный формат вектор x_np
x_np = np.hstack((vector_1,x_np))
# проверим то, что все сделали правильно
print vector_1[0:3]
print x_np[0:3]
print '***************************************'
print
# напишем функцию, которая определяет значения коэффициентов a и b с использованием псевдообратной матрицы
def pseudoinverse_matrix(X, y):
# задаем явный формат матрицы признаков
X = np.matrix(X)
# определяем транспонированную матрицу
XT = X.T
# определяем квадратную матрицу
XTX = XT*X
# определяем псевдообратную матрицу
inv = np.linalg.pinv(XTX)
# задаем явный формат матрицы ответов
y = np.matrix(y)
# находим вектор весов
return (inv*XT)*y
# запустим функцию
ab_np = pseudoinverse_matrix(x_np, y_np)
print ab_np
print '***************************************'
print
# напишем функцию, которая использует для решения матричное уравнение
def matrix_equation(X,y):
a = np.dot(X.T, X)
b = np.dot(X.T, y)
return np.linalg.solve(a, b)
# запустим функцию
ab_np = matrix_equation(x_np,y_np)
print ab_np
Сравним время, которое было затрачено на определение коэффициентов
и
, в соответствии с 3-мя представленными способами.
Код для вычисления времени расчетов
print '33[1m' + '33[4m' + "Время выполнения расчета коэффициентов без использования библиотеки NumPy:" + '33[0m'
% timeit ab_us = Kramer_method(x_us,y_us)
print '***************************************'
print
print '33[1m' + '33[4m' + "Время выполнения расчета коэффициентов с использованием псевдообратной матрицы:" + '33[0m'
%timeit ab_np = pseudoinverse_matrix(x_np, y_np)
print '***************************************'
print
print '33[1m' + '33[4m' + "Время выполнения расчета коэффициентов с использованием матричного уравнения:" + '33[0m'
%timeit ab_np = matrix_equation(x_np, y_np)
На небольшом количестве данных, вперед выходит «самописная» функция, которая находит коэффициенты методом Крамера.
Теперь можно перейти к другим способам нахождения коэффициентов
и
.
Градиентный спуск
Для начала определим, что такое градиент. По-простому, градиент — это отрезок, который указывает направление максимального роста функции. По аналогии с подъемом в гору, то куда смотрит градиент, там и есть самый крутой подъем к вершине горы. Развивая пример с горой, вспоминаем, что на самом деле нам нужен самый крутой спуск, чтобы как можно быстрее достичь низины, то есть минимума — места где функция не возрастает и не убывает. В этом месте производная будет равна нулю. Следовательно, нам нужен не градиент, а антиградиент. Для нахождения антиградиента нужно всего лишь умножить градиент на -1 (минус один).
Обратим внимание на то, что функция может иметь несколько минимумов, и опустившись в один из них по предложенному далее алгоритму, мы не сможем найти другой минимум, который возможно находится ниже найденного. Расслабимся, нам это не грозит! В нашем случае мы имеем дело с единственным минимумом, так как наша функция
на графике представляет собой обычную параболу. А как мы все должны прекрасно знать из школьного курса математики — у параболы существует только один минимум.
После того, как мы выяснили для чего нам потребовался градиент, а также то, что градиент — это отрезок, то есть вектор с заданными координатами, которые как раз являются теми самыми коэффициентами
и
мы можем реализовать градиентный спуск.
Перед запуском, предлагаю прочитать буквально несколько предложений об алгоритме спуска:
- Определяем псевдослучайным образом координаты коэффициентов
и
. В нашем примере, мы будем определять коэффициенты вблизи нуля. Это является распространённой практикой, однако для каждого случая может быть предусмотрена своя практика.
- От координаты
вычитаем значение частной производной 1-го порядка в точке
. Так, если производная будет положительная, то функция возрастает. Следовательно, отнимая значение производной, мы будем двигаться в обратную сторону роста, то есть в сторону спуска. Если производная отрицательна, значит функция в этой точке убывает и отнимая значение производной мы двигаемся в сторону спуска.
- Проводим аналогичную операцию с координатой
: вычитаем значение частной производной в точке
.
- Для того, чтобы не перескочить минимум и не улететь в далекий космос, необходимо установить размер шага в сторону спуска. В общем и целом, можно написать целую статью о том, как правильнее установить шаг и как его менять в процессе спуска, чтобы снизить затраты на вычисления. Но сейчас перед нами несколько иная задача, и мы научным методом «тыка» или как говорят в простонародье, эмпирическим путем, установим размер шага.
- После того, как мы из заданных координат
и
вычли значения производных, получаем новые координаты
и
. Делаем следующий шаг (вычитание), уже из рассчитанных координат. И так цикл запускается вновь и вновь, до тех пор, пока не будет достигнута требуемая сходимость.
Все! Теперь мы готовы отправиться на поиски самого глубокого ущелья Марианской впадины. Приступаем.
Код для градиентного спуска
# напишем функцию градиентного спуска без использования библиотеки NumPy.
# Функция на вход принимает диапазоны значений x,y, длину шага (по умолчанию=0,1), допустимую погрешность(tolerance)
def gradient_descent_usual(x_us,y_us,l=0.1,tolerance=0.000000000001):
# сумма значений (все месяца)
sx = sum(x_us)
# сумма истинных ответов (выручка за весь период)
sy = sum(y_us)
# сумма произведения значений на истинные ответы
list_xy = []
[list_xy.append(x_us[i]*y_us[i]) for i in range(len(x_us))]
sxy = sum(list_xy)
# сумма квадратов значений
list_x_sq = []
[list_x_sq.append(x_us[i]**2) for i in range(len(x_us))]
sx_sq = sum(list_x_sq)
# количество значений
num = len(x_us)
# начальные значения коэффициентов, определенные псевдослучайным образом
a = float(random.uniform(-0.5, 0.5))
b = float(random.uniform(-0.5, 0.5))
# создаем массив с ошибками, для старта используем значения 1 и 0
# после завершения спуска стартовые значения удалим
errors = [1,0]
# запускаем цикл спуска
# цикл работает до тех пор, пока отклонение последней ошибки суммы квадратов от предыдущей, не будет меньше tolerance
while abs(errors[-1]-errors[-2]) > tolerance:
a_step = a - l*(num*a + b*sx - sy)/num
b_step = b - l*(a*sx + b*sx_sq - sxy)/num
a = a_step
b = b_step
ab = [a,b]
errors.append(errors_sq_Kramer_method(ab,x_us,y_us))
return (ab),(errors[2:])
# запишем массив значений
list_parametres_gradient_descence = gradient_descent_usual(x_us,y_us,l=0.1,tolerance=0.000000000001)
print '33[1m' + '33[4m' + "Значения коэффициентов a и b:" + '33[0m'
print 'a =', round(list_parametres_gradient_descence[0][0],3)
print 'b =', round(list_parametres_gradient_descence[0][1],3)
print
print '33[1m' + '33[4m' + "Сумма квадратов отклонений:" + '33[0m'
print round(list_parametres_gradient_descence[1][-1],3)
print
print '33[1m' + '33[4m' + "Количество итераций в градиентном спуске:" + '33[0m'
print len(list_parametres_gradient_descence[1])
print
Мы погрузились на самое дно Марианской впадины и там обнаружили все те же значения коэффициентов
и
, что собственно и следовало ожидать.
Совершим еще одно погружение, только на этот раз, начинкой нашего глубоководного аппарата будут иные технологии, а именно библиотека NumPy.
Код для градиентного спуска (NumPy)
# перед тем определить функцию для градиентного спуска с использованием библиотеки NumPy,
# напишем функцию определения суммы квадратов отклонений также с использованием NumPy
def error_square_numpy(ab,x_np,y_np):
y_pred = np.dot(x_np,ab)
error = y_pred - y_np
return sum((error)**2)
# напишем функцию градиентного спуска с использованием библиотеки NumPy.
# Функция на вход принимает диапазоны значений x,y, длину шага (по умолчанию=0,1), допустимую погрешность(tolerance)
def gradient_descent_numpy(x_np,y_np,l=0.1,tolerance=0.000000000001):
# сумма значений (все месяца)
sx = float(sum(x_np[:,1]))
# сумма истинных ответов (выручка за весь период)
sy = float(sum(y_np))
# сумма произведения значений на истинные ответы
sxy = x_np*y_np
sxy = float(sum(sxy[:,1]))
# сумма квадратов значений
sx_sq = float(sum(x_np[:,1]**2))
# количество значений
num = float(x_np.shape[0])
# начальные значения коэффициентов, определенные псевдослучайным образом
a = float(random.uniform(-0.5, 0.5))
b = float(random.uniform(-0.5, 0.5))
# создаем массив с ошибками, для старта используем значения 1 и 0
# после завершения спуска стартовые значения удалим
errors = [1,0]
# запускаем цикл спуска
# цикл работает до тех пор, пока отклонение последней ошибки суммы квадратов от предыдущей, не будет меньше tolerance
while abs(errors[-1]-errors[-2]) > tolerance:
a_step = a - l*(num*a + b*sx - sy)/num
b_step = b - l*(a*sx + b*sx_sq - sxy)/num
a = a_step
b = b_step
ab = np.array([[a],[b]])
errors.append(error_square_numpy(ab,x_np,y_np))
return (ab),(errors[2:])
# запишем массив значений
list_parametres_gradient_descence = gradient_descent_numpy(x_np,y_np,l=0.1,tolerance=0.000000000001)
print '33[1m' + '33[4m' + "Значения коэффициентов a и b:" + '33[0m'
print 'a =', round(list_parametres_gradient_descence[0][0],3)
print 'b =', round(list_parametres_gradient_descence[0][1],3)
print
print '33[1m' + '33[4m' + "Сумма квадратов отклонений:" + '33[0m'
print round(list_parametres_gradient_descence[1][-1],3)
print
print '33[1m' + '33[4m' + "Количество итераций в градиентном спуске:" + '33[0m'
print len(list_parametres_gradient_descence[1])
print
Значения коэффициентов
и
неизменны.
Посмотрим на то, как изменялась ошибка при градиентном спуске, то есть как изменялась сумма квадратов отклонений с каждым шагом.
Код для графика сумм квадратов отклонений
print 'График№4 "Сумма квадратов отклонений по-шагово"'
plt.plot(range(len(list_parametres_gradient_descence[1])), list_parametres_gradient_descence[1], color='red', lw=3)
plt.xlabel('Steps (Iteration)', size=16)
plt.ylabel('Sum of squared deviations', size=16)
plt.show()
График №4 «Сумма квадратов отклонений при градиентном спуске»
На графике мы видим, что с каждым шагом ошибка уменьшается, а спустя какое-то количество итераций наблюдаем практически горизонтальную линию.
Напоследок оценим разницу во времени исполнения кода:
Код для определения времени вычисления градиентного спуска
print '33[1m' + '33[4m' + "Время выполнения градиентного спуска без использования библиотеки NumPy:" + '33[0m'
%timeit list_parametres_gradient_descence = gradient_descent_usual(x_us,y_us,l=0.1,tolerance=0.000000000001)
print '***************************************'
print
print '33[1m' + '33[4m' + "Время выполнения градиентного спуска с использованием библиотеки NumPy:" + '33[0m'
%timeit list_parametres_gradient_descence = gradient_descent_numpy(x_np,y_np,l=0.1,tolerance=0.000000000001)
Возможно мы делаем что-то не то, но опять простая «самописная» функция, которая не использует библиотеку NumPy опережает по времени выполнения расчетов функцию, использующую библиотеку NumPy.
Но мы не стоим на месте, а двигаемся в сторону изучения еще одного увлекательного способа решения уравнения простой линейной регрессии. Встречайте!
Стохастический градиентный спуск
Для того, чтобы быстрее понять принцип работы стохастического градиентного спуска, лучше определить его отличия от обычного градиентного спуска. Мы, в случае с градиентным спуском, в уравнениях производных от
и
использовали суммы значений всех признаков и истинных ответов, имеющихся в выборке (то есть суммы всех
и
). В стохастическом градиентном спуске мы не будем использовать все значения, имеющиеся в выборке, а вместо этого, псевдослучайным образом выберем так называемый индекс выборки и используем его значения.
Например, если индекс определился за номером 3 (три), то мы берем значения
и
, далее подставляем значения в уравнения производных и определяем новые координаты. Затем, определив координаты, мы опять псевдослучайным образом определяем индекс выборки, подставляем значения, соответствующие индексу в уравнения частных производных, по новому определяем координаты
и
и т.д. до
позеленения
сходимости. На первый взгляд, может показаться, как это вообще может работать, однако работает. Правда стоит отметить, что не с каждым шагом уменьшается ошибка, но тенденция безусловно имеется.
Каковы преимущества стохастического градиентного спуска перед обычным? В случае, если у нас размер выборки очень велик и измеряется десятками тысяч значений, то значительно проще обработать, допустим случайную тысячу из них, нежели всю выборку. Вот в этом случае и запускается стохастический градиентный спуск. В нашем случае мы конечно же большой разницы не заметим.
Смотрим код.
Код для стохастического градиентного спуска
# определим функцию стох.град.шага
def stoch_grad_step_usual(vector_init, x_us, ind, y_us, l):
# выбираем значение икс, которое соответствует случайному значению параметра ind
# (см.ф-цию stoch_grad_descent_usual)
x = x_us[ind]
# рассчитывыаем значение y (выручку), которая соответствует выбранному значению x
y_pred = vector_init[0] + vector_init[1]*x_us[ind]
# вычисляем ошибку расчетной выручки относительно представленной в выборке
error = y_pred - y_us[ind]
# определяем первую координату градиента ab
grad_a = error
# определяем вторую координату ab
grad_b = x_us[ind]*error
# вычисляем новый вектор коэффициентов
vector_new = [vector_init[0]-l*grad_a, vector_init[1]-l*grad_b]
return vector_new
# определим функцию стох.град.спуска
def stoch_grad_descent_usual(x_us, y_us, l=0.1, steps = 800):
# для самого начала работы функции зададим начальные значения коэффициентов
vector_init = [float(random.uniform(-0.5, 0.5)), float(random.uniform(-0.5, 0.5))]
errors = []
# запустим цикл спуска
# цикл расчитан на определенное количество шагов (steps)
for i in range(steps):
ind = random.choice(range(len(x_us)))
new_vector = stoch_grad_step_usual(vector_init, x_us, ind, y_us, l)
vector_init = new_vector
errors.append(errors_sq_Kramer_method(vector_init,x_us,y_us))
return (vector_init),(errors)
# запишем массив значений
list_parametres_stoch_gradient_descence = stoch_grad_descent_usual(x_us, y_us, l=0.1, steps = 800)
print '33[1m' + '33[4m' + "Значения коэффициентов a и b:" + '33[0m'
print 'a =', round(list_parametres_stoch_gradient_descence[0][0],3)
print 'b =', round(list_parametres_stoch_gradient_descence[0][1],3)
print
print '33[1m' + '33[4m' + "Сумма квадратов отклонений:" + '33[0m'
print round(list_parametres_stoch_gradient_descence[1][-1],3)
print
print '33[1m' + '33[4m' + "Количество итераций в стохастическом градиентном спуске:" + '33[0m'
print len(list_parametres_stoch_gradient_descence[1])
Смотрим внимательно на коэффициенты и ловим себя на вопросе «Как же так?». У нас получились другие значения коэффициентов
и
. Может быть стохастический градиентный спуск нашел более оптимальные параметры уравнения? Увы, нет. Достаточно посмотреть на сумму квадратов отклонений и увидеть, что при новых значениях коэффициентов, ошибка больше. Не спешим отчаиваться. Построим график изменения ошибки.
Код для графика суммы квадратов отклонений при стохастическом градиентном спуске
print 'График №5 "Сумма квадратов отклонений по-шагово"'
plt.plot(range(len(list_parametres_stoch_gradient_descence[1])), list_parametres_stoch_gradient_descence[1], color='red', lw=2)
plt.xlabel('Steps (Iteration)', size=16)
plt.ylabel('Sum of squared deviations', size=16)
plt.show()
График №5 «Сумма квадратов отклонений при стохастическом градиентном спуске»
Посмотрев на график, все становится на свои места и сейчас мы все исправим.
Итак, что же произошло? Произошло следующее. Когда мы выбираем случайным образом месяц, то именно для выбранного месяца наш алгоритм стремится уменьшить ошибку в расчете выручки. Затем выбираем другой месяц и повторяем расчет, но ошибку уменьшаем уже для второго выбранного месяца. А теперь вспомним, что у нас первые два месяца существенно отклоняются от линии уравнения простой линейной регрессии. Это значит, что когда выбирается любой из этих двух месяцев, то уменьшая ошибку каждого из них, наш алгоритм серьезно увеличивает ошибку по всей выборке. Так что же делать? Ответ простой: надо уменьшить шаг спуска. Ведь уменьшив шаг спуска, ошибка так же перестанет «скакать» то вверх, то вниз. Вернее, ошибка «скакать» не перестанет, но будет это делать не так прытко:) Проверим.
Код для запуска SGD с меньшим шагом
# запустим функцию, уменьшив шаг в 100 раз и увеличив количество шагов соответсвующе
list_parametres_stoch_gradient_descence = stoch_grad_descent_usual(x_us, y_us, l=0.001, steps = 80000)
print '33[1m' + '33[4m' + "Значения коэффициентов a и b:" + '33[0m'
print 'a =', round(list_parametres_stoch_gradient_descence[0][0],3)
print 'b =', round(list_parametres_stoch_gradient_descence[0][1],3)
print
print '33[1m' + '33[4m' + "Сумма квадратов отклонений:" + '33[0m'
print round(list_parametres_stoch_gradient_descence[1][-1],3)
print
print '33[1m' + '33[4m' + "Количество итераций в стохастическом градиентном спуске:" + '33[0m'
print len(list_parametres_stoch_gradient_descence[1])
print 'График №6 "Сумма квадратов отклонений по-шагово"'
plt.plot(range(len(list_parametres_stoch_gradient_descence[1])), list_parametres_stoch_gradient_descence[1], color='red', lw=2)
plt.xlabel('Steps (Iteration)', size=16)
plt.ylabel('Sum of squared deviations', size=16)
plt.show()
График №6 «Сумма квадратов отклонений при стохастическом градиентном спуске (80 тыс. шагов)»
Значения коэффициентов улучшились, но все равно не идеальны. Гипотетически это можно поправить таким образом. Выбираем, например, на последних 1000 итерациях значения коэффициентов, с которыми была допущена минимальная ошибка. Правда нам для этого придется записывать еще и сами значения коэффициентов. Мы не будем этого делать, а лучше обратим внимание на график. Он выглядит гладким, и ошибка как будто уменьшается равномерно. На самом деле это не так. Посмотрим на первые 1000 итераций и сравним их с последними.
Код для графика SGD (первые 1000 шагов)
print 'График №7 "Сумма квадратов отклонений по-шагово. Первые 1000 итераций"'
plt.plot(range(len(list_parametres_stoch_gradient_descence[1][:1000])),
list_parametres_stoch_gradient_descence[1][:1000], color='red', lw=2)
plt.xlabel('Steps (Iteration)', size=16)
plt.ylabel('Sum of squared deviations', size=16)
plt.show()
print 'График №7 "Сумма квадратов отклонений по-шагово. Последние 1000 итераций"'
plt.plot(range(len(list_parametres_stoch_gradient_descence[1][-1000:])),
list_parametres_stoch_gradient_descence[1][-1000:], color='red', lw=2)
plt.xlabel('Steps (Iteration)', size=16)
plt.ylabel('Sum of squared deviations', size=16)
plt.show()
График №7 «Сумма квадратов отклонений SGD (первые 1000 шагов)»
График №8 «Сумма квадратов отклонений SGD (последние 1000 шагов)»
В самом начале спуска мы наблюдаем достаточно равномерное и крутое уменьшение ошибки. На последних итерациях мы видим, что ошибка ходит вокруг да около значения в 1,475 и в некоторые моменты даже равняется этому оптимальному значению, но потом все равно уходит ввысь… Повторюсь, можно записывать значения коэффициентов
и
, а потом выбрать те, при которых ошибка минимальна. Однако у нас возникла проблема посерьезнее: нам пришлось сделать 80 тыс. шагов (см. код), чтобы получить значения, близкие к оптимальным. А это, уже противоречит идее об экономии времени вычислений при стохастическом градиентном спуске относительно градиентного. Что можно поправить и улучшить? Не трудно заметить, что на первых итерациях мы уверенно идем вниз и, следовательно, нам стоит оставить большой шаг на первых итерациях и по мере продвижения вперед шаг уменьшать. Мы не будем этого делать в этой статье — она и так уже затянулась. Желающие могут и сами подумать, как это сделать, это не сложно

Теперь выполним стохастический градиентный спуск, используя библиотеку NumPy (и не будем спотыкаться о камни, которые мы выявили раннее)
Код для стохастического градиентного спуска (NumPy)
# для начала напишем функцию градиентного шага
def stoch_grad_step_numpy(vector_init, X, ind, y, l):
x = X[ind]
y_pred = np.dot(x,vector_init)
err = y_pred - y[ind]
grad_a = err
grad_b = x[1]*err
return vector_init - l*np.array([grad_a, grad_b])
# определим функцию стохастического градиентного спуска
def stoch_grad_descent_numpy(X, y, l=0.1, steps = 800):
vector_init = np.array([[np.random.randint(X.shape[0])], [np.random.randint(X.shape[0])]])
errors = []
for i in range(steps):
ind = np.random.randint(X.shape[0])
new_vector = stoch_grad_step_numpy(vector_init, X, ind, y, l)
vector_init = new_vector
errors.append(error_square_numpy(vector_init,X,y))
return (vector_init), (errors)
# запишем массив значений
list_parametres_stoch_gradient_descence = stoch_grad_descent_numpy(x_np, y_np, l=0.001, steps = 80000)
print '33[1m' + '33[4m' + "Значения коэффициентов a и b:" + '33[0m'
print 'a =', round(list_parametres_stoch_gradient_descence[0][0],3)
print 'b =', round(list_parametres_stoch_gradient_descence[0][1],3)
print
print '33[1m' + '33[4m' + "Сумма квадратов отклонений:" + '33[0m'
print round(list_parametres_stoch_gradient_descence[1][-1],3)
print
print '33[1m' + '33[4m' + "Количество итераций в стохастическом градиентном спуске:" + '33[0m'
print len(list_parametres_stoch_gradient_descence[1])
print
Значения получились почти такими же, как и при спуске без использования NumPy. Впрочем, это логично.
Узнаем сколько же времени занимали у нас стохастические градиентные спуски.
Код для определения времени вычисления SGD (80 тыс. шагов)
print '33[1m' + '33[4m' +
"Время выполнения стохастического градиентного спуска без использования библиотеки NumPy:"
+ '33[0m'
%timeit list_parametres_stoch_gradient_descence = stoch_grad_descent_usual(x_us, y_us, l=0.001, steps = 80000)
print '***************************************'
print
print '33[1m' + '33[4m' +
"Время выполнения стохастического градиентного спуска с использованием библиотеки NumPy:"
+ '33[0m'
%timeit list_parametres_stoch_gradient_descence = stoch_grad_descent_numpy(x_np, y_np, l=0.001, steps = 80000)
Чем дальше в лес, тем темнее тучи: опять «самописная» формула показывает лучший результат. Все это наводит на мысли о том, что должны существовать еще более тонкие способы использования библиотеки NumPy, которые действительно ускоряют операции вычислений. В этой статье мы о них уже не узнаем. Будет о чем подумать на досуге:)
Резюмируем
Перед тем как резюмировать, хотелось бы ответить на вопрос, который скорее всего, возник у нашего дорогого читателя. Для чего, собственно, такие «мучения» со спусками, зачем нам ходить по горе вверх и вниз (преимущественно вниз), чтобы найти заветную низину, если в наших руках такой мощный и простой прибор, в виде аналитического решения, который мгновенно телепортирует нас в нужное место?
Ответ на этот вопрос лежит на поверхности. Сейчас мы разбирали очень простой пример, в котором истинный ответ
зависит от одного признака
. В жизни такое встретишь не часто, поэтому представим, что у нас признаков 2, 30, 50 или более. Добавим к этому тысячи, а то и десятки тысяч значений для каждого признака. В этом случае аналитическое решение может не выдержать испытания и дать сбой. В свою очередь градиентный спуск и его вариации будут медленно, но верно приближать нас к цели — минимуму функции. А на счет скорости не волнуйтесь — мы наверняка еще разберем способы, которые позволят нам задавать и регулировать длину шага (то есть скорость).
А теперь собственно краткое резюме.
Во-первых, надеюсь, что изложенный в статье материал, поможет начинающим «дата сайнтистам» в понимании того, как решать уравнения простой (и не только) линейной регрессии.
Во-вторых, мы рассмотрели несколько способов решения уравнения. Теперь, в зависимости от ситуации, мы можем выбрать тот, который лучше всего подходит для решения поставленной задачи.
В-третьих, мы увидели силу дополнительных настроек, а именно длины шага градиентного спуска. Этим параметром нельзя пренебрегать. Как было подмечено выше, с целью сокращения затрат на проведение вычислений, длину шага стоит изменять по ходу спуска.
В-четвертых, в нашем случае, «самописные» функции показали лучший временной результат вычислений. Вероятно, это связано с не самым профессиональным применением возможностей библиотеки NumPy. Но как бы то ни было, вывод напрашивается следующий. С одной стороны, иногда стоит подвергать сомнению устоявшиеся мнения, а с другой — не всегда стоит все усложнять — наоборот иногда эффективнее оказывается более простой способ решения задачи. А так как цель у нас была разобрать три подхода в решении уравнения простой линейной регрессии, то использование «самописных» функций нам вполне хватило.
Предыдущая работа автора — «Исследуем утверждение центральной предельной теоремы с помощью экспоненциального распределения»
Следующая работа автора — «Приводим уравнение линейной регрессии в матричный вид»
Литература (или что-то вроде того)
1. Линейная регрессия
http://statistica.ru/theory/osnovy-lineynoy-regressii/
2. Метод наименьших квадратов
mathprofi.ru/metod_naimenshih_kvadratov.html
3. Производная
www.mathprofi.ru/chastnye_proizvodnye_primery.html
4. Градиент
mathprofi.ru/proizvodnaja_po_napravleniju_i_gradient.html
5. Градиентный спуск
habr.com/ru/post/471458
habr.com/ru/post/307312
artemarakcheev.com//2017-12-31/linear_regression
6. Библиотека NumPy
docs.scipy.org/doc/numpy-1.10.1/reference/generated/numpy.linalg.solve.html
docs.scipy.org/doc/numpy-1.10.0/reference/generated/numpy.linalg.pinv.html
pythonworld.ru/numpy/2.html
“Теоретическая
кривая никогда не проходит в точности
через все точки, полученные в результате
измерений…” В. Фукс [1975].
Рассчитать уравнение регрессии не
представляет особой сложности, особенно
при наличии компьютера с установленным
табличным процессором Microsoft Excel, или
любого другого пакета статистических
программ. Основные методологические
трудности возникают в ходе проверки
выполнения априорных предпосылок
регрессионного анализа и последующей
оценки адекватности полученного
уравнения.
Парная
(однофакторная) регрессия является
частным случаем множественной регрессии.
Схематически модель множественной
регрессии записывается в виде:
,
где y
– результативный экономический
показатель, x1,
x2,
…,xn
– входные
факторы.
Множественная регрессия широко
используется в решении проблем спроса,
доходности акций, при изучении функций
издержек производства, в макроэкономических
расчетах и при решении других вопросов
в различных экономических сферах. В
настоящее время множественная регрессия
– один из наиболее распространенных
методов в эконометрике.
Основная
цель множественной регрессии –
построение модели с большим числом
факторов и определение влияния каждого
из них в отдельности, а также совокупное
их воздействие на моделируемый показатель
y.
Построение уравнения множественной
регрессии начинается с решения вопроса
о спецификации модели (выбор факторов,
вида уравнения и др.)
Отбор факторов регрессионной модели.
Факторы, включаемые в модель
множественной регрессии, должны отвечать
следующим требованиям:
-
должны быть
количественно измеримы; -
не
должны быть интеркоррелированы1
или находится в функциональной
зависимости; -
в
одну модель нельзя включать совокупный
фактор и образующие его частные факторы,
что может привести к неоправданному
увеличенному их влияние на зависимый
показатель, к искажению реальной
действительности; -
количество
включаемых в модель факторов не должно
превышать одной трети числа наблюдений
в выборке.
Отбор
факторов для регрессионной модели
обычно осуществляется в две стадии: на
первой подбираются факторы, исходя из
сущности проблемы; на второй – на основе
матрицы показателей корреляции определяют
t
— статистики для параметров регрессии.
Коэффициенты
интеркорреляции позволяют исключать
из модели дублирующие факторы. Считается,
что две переменные явно коллинеарны,
т.е. находятся между собой в линейной
зависимости, если коэффициент
интеркорреляции
.
Из двух явно коллинеарных факторов, из
уравнения регрессии рекомендуется
исключить один. Предпочтение при этом
отдается тому фактору, который при
достаточно тесной связи с результатом
имеет наименьшую тесноту связи с другими
факторами.
Пример.
для
зависимости
в таблице 12 задана матрица парных
коэффициентов корреляции.
Т а б л и ц а 12
-
y
x1
x2
x3
y
1
x1
0,8
1
x2
0,7
0,8
1
x3
0,6
0,5
0,2
1
Из
таблицы очевидно, что факторы x1
и
x2
коррелированны
друг с другом. В уравнение регрессии
целесообразно включить фактор x2,
а не x1,
так как корреляция x2
с y
– слабее, чем корреляция фактора x1
с y
,
но зато
.
Поэтому в уравнение множественной
регрессии включаются факторы x2
и x3.
Этапы
построения регрессионной модели.
Двумя наиболее
важными этапами построения многофакторных
моделей являются:
-
выбор
формы связи (уравнения регрессии); -
отбор факторных
признаков.
На
первом этапе
построения РМ производится выбор вида
(структуры) уравнения регрессии. Наиболее
приемлемым способом
выбора формы связи, то есть вида исходного
уравнения, является метод перебора
различных уравнений. При этом значительное
число различных уравнений регрессии
реализуется на ЭВМ с помощью специально
разработанного алгоритма перебора с
последующей статистической проверкой
(обычно на основе t-критерия Стьюдента).
Уравнения как парной так и множественной
регрессии могут быть линейными и
нелинейными.
Наиболее часто используются линейная
и степенная функции:
– линейная,
– степенная.
широко
применяются и следующие уравнения
множественной регрессии:
– экспоненциального
вида,
– гиперболического
вида.
В
качестве уравнений множественной
регрессии могут быть использованы и
другие виды математических функций.
После выбора формы связи определяются
неизвестные коэффициенты модели, для
чего чаще всего используется широко
известный метод наименьших квадратов
(МНК).
При нелинейной форме связи для определения
коэффициентов могут быть использованы
два подхода:
-
когда
нелинейная форма связи представляется
в виде линеаризованной функции; при
котором исследователь сначала выбирает
форму нелинейной РМ, а затем ее
линеаризует, преобразуя члены уравнения
регрессии;
2) когда используется итерационный
нелинейный метод наименьших квадратов.
На
втором этапе
построения уравнения множественной
регрессии можно выделить три стадии
отбора факторов, включаемых в модель.
-
На
первой стадии осуществляется априорный
анализ и на факторы, включаемые в
предварительный состав модели, не
накладывается каких-либо особых
ограничений. -
На
второй (наиболее важной) стадии
производится сравнительная оценка и
отсев части факторов. Это достигается
анализом парных коэффициентов и оценкой
их значимости. -
На
третьей стадии
производят
окончательный отбор факторов путем
анализа значимости оценок параметров
различных вариантов уравнений с
использованием критерия Стьюдента.
9.4.
Полный факторный эксперимент и уравнение
регрессии
Перечисленные
два этапа построения многофакторных
моделей на практике часто решаются с
помощью методики ПФЭ типа 2k.
Применение этой методики позволяет
достаточно просто и эффективно
количественно оценить все линейные
эффекты факторов и их взаимодействия
(«перекрестные связи»). взаимодействие
возникает в том случае, если эффект
одного фактора зависит от уровня, на
котором находится другой фактор. Вначале
рассмотрим методику получения линейной
РМ.
Линейная
регрессионная модель.
Уравнение регрессии – это формула
статистической связи между зависимыми
и независимыми переменными. Если это
уравнение линейное, то речь идет о
линейной регрессии. Формула статистической
связи двух переменных называется парной
регрессией, зависимость от нескольких
переменных – множественной регрессией.
Например, Кейнсом была предложена
линейная формула зависимости частного
потребления С
от располагаемого
дохода
:
где
– величина автономного потребления,
– предельная склонность к потреблению.
Установление
формы связи (9.2.1) начинают, как правило,
с рассмотрения линейной регрессии вида
.
(9.4.1)
Целью
исследователя является определение
неизвестных коэффициентов
линейной модели (9.4.1) по результатам
эксперимента (по матрице ПФЭ). Эксперимент,
содержащий конечное число опытов N,
позволяет получить только выборочные
оценки для коэффициентов уравнения
(9.4.1). Их точность и надежность зависит
от свойств выборки и нуждается в
статистической проверке. Как проводится
такая проверка, рассмотрим далее, а пока
займемся вычислением неизвестных
коэффициентов
Используя для этого метод наименьших
квадратов (МНК) для линейной РМ получим
простую формулу
(9.4.2)
где
индекс
относится к фиктивному фактору
который во всех опытах принимает значение
+1, т.е.
и вводится для удобства пользования
формулой (9.4.2).
Пример.
подсчитаем
коэффициенты для линейной двухфакторной
РМ
.
Для этого воспользуемся значениями
из таблицы 10 для ПФЭ типа 22. По
формуле (9.4.2) получим:
Коэффициент
есть среднее арифметическое значение
параметра оптимизации, а коэффициенты
указывают на силу влияния факторов xj.
Нелинейная
регрессионная модель. Если
при проверке гипотезы о линейности РМ
устанавливается, что статистический
материал (или результат ПФЭ) не может
быть описан линейным уравнением, то
переходят к поиску нелинейной модели.
Как уже указывалось, структура нелинейной
РМ может быть совершенно различной.
Пользуясь результатами ПФЭ можно
достаточно просто построить нелинейную
модель, включающую эффекты взаимодействия
(«перекрестные связи») факторов: парные
(),
тройные ()
и т.д. К сожалению, для других видов
нелинейностей простой способ построения
РМ на основе матрицы ПФЭ типа
2k
не проходит
и следует использовать другие более
сложные методы, основанные на использовании
нелинейного регрессионного анализа.
Максимальное
число всех возможных эффектов (всех
членов уравнения регрессии, включая
),
линейные эффекты и взаимодействия всех
порядков, можно определить по формуле
числа сочетаний
(9.4.3)
где
k
– число факторов, m
– число элементов во взаимодействии,
N
– количество опытов в эксперименте
(число строк в матрице планирования
ПФЭ).
Пример.
для
ПФЭ 24
число возможных парных взаимодействий
равно шести:
Для определения коэффициентов в модели
при парных взаимодействиях надо,
пользуясь правилом перемножения
столбцов, получить столбец произведения
двух факторов. Для вычисления коэффициента
при соответствующем эффекте взаимодействия,
с новым вектор-столбцом можно обращаться
так же, как с вектор-столбцом любого
фактора.
В табл.13 представлена матрица планирования
ПФЭ типа 2 2 с учетом перекрестных
связей между факторами.
Т а б л и ц а 13
|
Номер опыта |
|
|
|
|
y |
|
1 2 3 4 |
+1 +1 +1 +1 |
+1 –1 +1 –1 |
+1 +1 –1 –1 |
+1 –1 –1 +1 |
y1 y2 y3 y4 |
Полная нелинейная РМ в данном случае
имеет следующий вид:
(9.4.4)
Коэффициент
вычисляется по прежнему алгоритму
(9.4.2):
(9.4.5)
Для
определения коэффициентов в модели при
тройных взаимодействиях и взаимодействиях
более высокого порядка поступают
аналогично. В табл.14 приведены условия
проведения ПФЭ типа 23
и дополнительные столбцы для расчета
коэффициентов в перекрестных связях.
Полная нелинейная РМ с учетом всех
возможных взаимодействий в этом случае
имеет вид:
(9.4.6)
Коэффициент
вычисляется
с помощью таблицы 14:
(9.4.7)
Т а б л и ц а 14
|
Номер опыта |
|
|
|
|
|
|
|
|
y |
|
1 2 3 4 5 6 7 8 |
+1 +1 +1 +1 +1 +1 +1 +1 |
+1 –1 +1 –1 +1 –1 +1 –1 |
+1 +1 –1 –1 +1 +1 –1 –1 |
+1 +1 +1 +1 –1 –1 –1 –1 |
+1 –1 –1 +1 +1 –1 –1 +1 |
+1 –1 +1 –1 –1 +1 –1 +1 |
+1 +1 –1 –1 –1 –1 +1 +1 |
+1 –1 –1 +1 –1 +1 +1 –1 |
y1 y2 y3 y4 y5 y6 y7 y8 |
Метод
наименьших квадратов. Метод
наименьших квадратов
(МНК), или Least
Squares
Method
(LS),
это наиболее распространенный метод
вычисления коэффициентов регрессионной
модели. Как уже отмечалось, вычисление
коэффициентов РМ с использованием
матрицы планирования ПФЭ накладывает
существенные ограничения на структуру
РМ и является частным случаем МНК.
МНК минимизирует сумму квадратов
отклонений наблюдений зависимой
переменной от искомого уравнения
регрессии (РМ). Рассмотрим суть метода
на примере определения коэффициентов
однофакторной линейной регрессионной
модели
.
(9.4.8)
Для вычисления неизвестных коэффициентов
проведем серию опытов в точках
и получим экспериментальные значения
.
Подставив значения
и
в формулу (9.4.8), получим систему уравнений
(9.4.9)
где
разности (ошибки, невязки) между
экспериментальными
и вычисленными по уравнению регрессии
значениями параметра оптимизации у
в i—ой
экспериментальной точке (рис.42).
y
x
Рис.42
Требуется найти такие коэффициенты
регрессии (9.4.8), при которых невязки
будут минимальными.
В МНК коэффициенты находят из условия
минимума функции V
(9.4.10)
Подставив (9.4.9) в (9.4.10), получим:
(9.4.11)
Минимум функции, если он существует,
достигается при одновременном равенстве
нулю частных производных по всем
неизвестным, т.е.
(9.4.12)
Из выражений (9.4.11) и (9.4.12) получим систему
уравнений для определения искомых
коэффициентов РМ (9.4.8):
(9.4.13)
Решение системы (9.4.13) значительно
упрощается, если использовать рассмотренные
ранее свойства ПФЭ (9.2.6) – (9.2.8). В этом
случае
(9.4.14)
Обобщая результат для любого количества
факторов, можно записать общую формулу
расчета коэффициентов множественной
линейной регрессии для ПФЭ типа
в виде (9.4.2)
Эту формулу мы уже использовали для
определения коэффициентов РМ с помощью
матрицы планирования ПФЭ.
Чтобы формально можно было решить
поставленную задачу, то есть найти
некоторый наилучший вектор параметров
РМ, должно выполняться неравенство
.
Положительная разность
называется числом степеней свободы.
Если число степеней свободы мало, то
статистическая надежность оцениваемой
формулы невысока. Обычно при оценке
множественной регрессии требуется,
чтобы число наблюдений (опытов) по
крайней мере в три раза превосходило
число оцениваемых параметров модели.
Можно показать, что система нормальных
уравнений (9.4.12) МНК в матричном виде
записывается следующим образом:
(9.4.15)
где
обозначает матрицу, транспонированную
по отношению к матрице
Из (9.4.15) получаем уравнение для определения
коэффициентов в векторно-матричной
форме:
(9.4.16)
где
имеет размерность k+1,
а Y – размерность N
.
Проверка
адекватности модели. После выбора
структуры и вычисления коэффициентов
регрессионной модели (РМ) встает вопрос
о степени ее адекватности, т.е. о степени
ее соответствия исследуемой системе.
При проверке с помощью методов
регрессионного анализа гипотезы об
адекватности модели или о значимости
входящих в РМ коэффициентов, приходится
учитывать законы распределения случайных
параметров.
регрессионный
анализ применим при следующих
предположениях.
-
Параметр
оптимизации у
есть случайная величина с
нормальным законом распределения. -
Дисперсия
не зависит от абсолютной величины
у. Выполнение
этого предположения проверяется с
помощью критерия однородности дисперсий
в разных точках факторного пространства. -
Значения
факторов xj
суть
неслучайные величины.
Если в рассматриваемой задаче выполняются
все предположения, то можно проверять
статистические гипотезы.
Для проверки гипотезы об адекватности
модели можно использовать критерий
Фишера (этот критерий мы уже использовали
для проверки однородности дисперсий):
(9.4.17)
Здесь
– дисперсия воспроизводимости со своим
числом степеней свободы, которая
вычисляется по формулам (9.2.12) или
(9.2.13);
– дисперсия адекватности, определяемая
по формуле
(9.4.18)
где
– остаточная сумма квадратов невязок;
– число степеней свободы, K
– число коэффициентов в РМ.
Если рассчитанное значение критерия
не превышает табличного (),
то с соответствующей доверительной
вероятностью модель можно считать
адекватной. При превышении табличного
значения эту принятую гипотезу приходится
отвергать.
В случае если опыты в матрице планирования
дублируются, то дисперсия адекватности
рассчитывается по формуле
(9.4.19)
где
ni
– число параллельных опытов в i
—ой строке матрицы планирования;
–
среднее арифметическое из ni
параллельных опытов;
–
предсказанное по уравнению РМ значение
в этом опыте.
Для определения коэффициентов
нельзя записать универсальную расчетную
формулу. Всякий раз их приходится
рассчитывать разными методами, самым
популярным из которых является МНК.
Проиллюстрируем решение задачи получения
РМ на простом примере.
Пример. В табл.15 приведена матрица
планирования ПФЭ типа 22 с двумя
параллельными опытами в каждой строке.
Во втором опыте один из параллельных
опытов пришлось отбросить как грубый.
При двух параллельных опытах со значениями
и
дисперсия в каждой строке матрицы
табл.15 вычисляется с использованием
формулы (9.2.10)
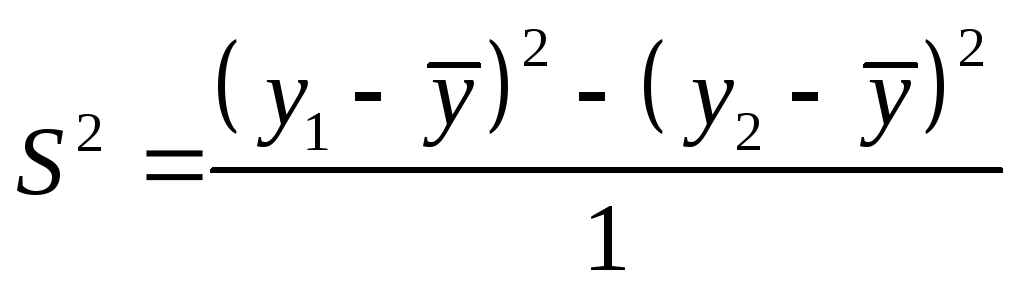
|
№ |
|
|
|
|
|
|
|
|
|
|
|
|
|
1 2 3 4 |
+1 +1 +1 +1 |
–1 +1 –1 +1 |
–1 –1 +1 +1 |
4,5 3,0 2,0 0,5 |
5,5 — 2,0 1,5 |
5,0 3,0 2,0 1,0 |
4,75 3,25 2,25 0,75 |
0,25 -0,25 -0,25 0,25 |
0,0625 0,0625 0,0625 0,0625 |
0,125 0,0625 0,125 0,125 |
0,5 — 0 0,5 |
1 0 1 1 |
Т а б л и ц а 15
Зададимся начальной структурой
регрессионной модели (РМ) в линейной
форме
По результатам ПФЭ требуется определить
коэффициенты РМ и доказать, что принятая
модель адекватна.
Используя свойства и методику определения
коэффициентов РМ с помощью матрицы
планирования, по формуле (9.4.2) подсчитаем
значения коэффициентов РМ.
Итак, мы получили линейную РМ:
Проверим адекватность этой модели.
Вспомогательные расчеты представлены
в последних шести столбцах табл.15.
Рассчитываем дисперсию воспроизводимости
по формуле (9.2.13) с тремя степенями
свободы:
Рассчитываем дисперсию адекватности
по формуле (9.4.18) с одной степенью свободы:
Экспериментальное значение критерия
Фишера рассчитаем по формуле (9.4.17):
Табличное значение критерия
Условие
выполняется, следовательно, с вероятностью
0,95 принятую
РМ можно считать адекватной.
Методы упрощения уравнения регрессии.
При построении
РМ для целевой функции у
на
начальном этапе обычно стараются учесть
как можно большее число факторов,
влияющих на изменение у.
В этом случае часто получаются неоправданно
сложные модели, особенно при использовании
нелинейных форм. эти
модели можно значительно упростить,
если выявить те факторы, которые
незначительно влияют на функцию отклика,
и исключить эти факторы из уравнения
регрессии.
При отборе влияющих
факторов используются статистические
методы отбора. Так, существенного
сокращения числа влияющих факторов
можно достичь с помощью пошаговых
процедур отбора переменных. Ни одна их
этих процедур не гарантирует получения
оптимального набора переменных. Однако
при практическом применении они позволяют
получить достаточно хорошие наборы
существенно влияющих факторов.
Для анализа РМ с целью упрощения
используются несколько методов. Коротко
рассмотрим некоторые из них.
1. Метод всех регрессий. В
этом методе функцию отклика представляют
в виде комбинаций зависимостей, в которых
меняют число факторов. Так для уравнения
регрессии
можно
записать функцию отклика в различных
комбинациях:
Для каждого уравнения
вычисляются коэффициенты регрессии и
определяется дисперсия адекватности
,
по наименьшему значению которой и
выбирается лучшая РМ. Однако, применение
этого метода связано с трудоемкими
вычислениями.
2. Метод
исключения переменных.
Метод
исключения предполагает построение
РМ, включающей всю совокупность
переменных, с последующим последовательным
(пошаговым) сокращением числа переменных
в модели до тех пор, пока не выполнится
некоторое, наперед заданное, условие.
После построения
РМ с целью сокращения членов в уравнении
РМ и ее упрощения зачастую различными
способами проводят оценку значимости
коэффициентов модели. оценку
значимости можно осуществить с помощью
t-критерия
Стьюдента.
При проверке
значимости коэффициентов
по t-критерию
используется формула
(9.4.20)
где
–среднеквадратическое
отклонение коэффициента
Вычисленное значение
сравнивается с табличным
при заданном уровне значимости α
и соответствующем числе степеней свободы
f
и делается
вывод о значимости коэффициента. Если
,
то с доверительной вероятностью
можно считать рассматриваемый
коэффициент незначимым и приравнять
его нулю.
3. Метод
включения переменных.
Суть
метода включения состоит в последовательном
включении переменных в модель до тех
пор, пока регрессионная модель не будет
отвечать заранее установленному критерию
качества. Последовательность включения
определяется с помощью частных
коэффициентов корреляции: переменные,
имеющие относительно исследуемого
показателя большие значения частного
коэффициента корреляции, первыми
включаются в регрессионное уравнение.
4. Метод анализа невязок
состоит в том, что анализируется разница
между значениями функции
и значением
,
предсказанном по уравнению регрессии
(см. рис.42). Определяя невязки
проверяют
их среднее значение, которое должно
быть близким к нулю:
Если это условие не выполняется, то в
уравнение модели вносят дополнительные
члены или принимают другую структуру
РМ.
В
30-е гг. ХХ века повсеместное увлечение
множественной регрессией сменилось
разочарованием. Строя уравнение
множественной регрессии и, стремясь
включить как можно больше объясняющих
переменных, исследователи все чаще
сталкивались с бессмысленными
результатами. Причина заключалась в
том, что изолированно взятое уравнение
регрессии есть не что иное, как модель
«черного ящика», поскольку в ней не
раскрыт механизм зависимости выходной
переменной Y от входных переменных Хi
, а лишь констатируется факт наличия
такой зависимости.
Для
проведения правильного анализа нужно
знать всю совокупность связей между
переменными. Одним из первых подходов
к решению этой задачи является конфлюэнтный
анализ, разработанный в 1934 г. Р.Фришем.
Он предложил изучать иерархию регрессий
между всеми сочетаниями переменных.
Значительный
интерес представляет аналитический
метод выбора типа уравнения регрессии,
который основан на изучении материальной
природы связи исследуемых признаков.
Соседние файлы в папке Уч.пособие
- #
- #
- #
- #
- #
- #
Имеются следующие данные разных стран об индексе розничных цен на продукты питания (х) и об индексе промышленного производства (у).
| Индекс розничных цен на продукты питания (х) | Индекс промышленного производства (у) | |
|---|---|---|
| 1 | 100 | 70 |
| 2 | 105 | 79 |
| 3 | 108 | 85 |
| 4 | 113 | 84 |
| 5 | 118 | 85 |
| 6 | 118 | 85 |
| 7 | 110 | 96 |
| 8 | 115 | 99 |
| 9 | 119 | 100 |
| 10 | 118 | 98 |
| 11 | 120 | 99 |
| 12 | 124 | 102 |
| 13 | 129 | 105 |
| 14 | 132 | 112 |
Требуется:
1. Для характеристики зависимости у от х рассчитать параметры следующих функций:
А) линейной;
Б) степенной;
В) равносторонней гиперболы.
2. Для каждой модели рассчитать показатели: тесноты связи и среднюю ошибку аппроксимации.
3. Оценить статистическую значимость параметров регрессии и корреляции.
4. Выполнить прогноз значения индекса промышленного производства у при прогнозном значении индекса розничных цен на продукты питания х=138.
Решение:
1. Для расчёта параметров линейной регрессии
Решаем систему нормальных уравнений относительно a и b:
Построим таблицу расчётных данных, как показано в таблице 1.
Таблица 1 Расчетные данные для оценки линейной регрессии
| № п/п | х | у | ху | x2 | y2 |  |
 |
|---|---|---|---|---|---|---|---|
| 1 | 100 | 70 | 7000 | 10000 | 4900 | 74,26340 | 0,060906 |
| 2 | 105 | 79 | 8295 | 11025 | 6241 | 79,92527 | 0,011712 |
| 3 | 108 | 85 | 9180 | 11664 | 7225 | 83,32238 | 0,019737 |
| 4 | 113 | 84 | 9492 | 12769 | 7056 | 88,98425 | 0,059336 |
| 5 | 118 | 85 | 10030 | 13924 | 7225 | 94,64611 | 0,113484 |
| 6 | 118 | 85 | 10030 | 13924 | 7225 | 94,64611 | 0,113484 |
| 7 | 110 | 96 | 10560 | 12100 | 9216 | 85,58713 | 0,108467 |
| 8 | 115 | 99 | 11385 | 13225 | 9801 | 91,24900 | 0,078293 |
| 9 | 119 | 100 | 11900 | 14161 | 10000 | 95,77849 | 0,042215 |
| 10 | 118 | 98 | 11564 | 13924 | 9604 | 94,64611 | 0,034223 |
| 11 | 120 | 99 | 11880 | 14400 | 9801 | 96,91086 | 0,021102 |
| 12 | 124 | 102 | 12648 | 15376 | 10404 | 101,4404 | 0,005487 |
| 13 | 129 | 105 | 13545 | 16641 | 11025 | 107,1022 | 0,020021 |
| 14 | 132 | 112 | 14784 | 17424 | 12544 | 110,4993 | 0,013399 |
| Итого: | 1629 | 1299 | 152293 | 190557 | 122267 | 1299,001 | 0,701866 |
| Среднее значение: | 116,3571 | 92,78571 | 10878,07 | 13611,21 | 8733,357 | х | х |
 |
8,4988 | 11,1431 | х | х | х | х | х |
 |
72,23 | 124,17 | х | х | х | х | х |
Среднее значение определим по формуле:
Cреднее квадратическое отклонение рассчитаем по формуле:
и занесём полученный результат в таблицу 1.
Возведя в квадрат полученное значение получим дисперсию:
Параметры уравнения можно определить также и по формулам:
Таким образом, уравнение регрессии:
Следовательно, с увеличением индекса розничных цен на продукты питания на 1, индекс промышленного производства увеличивается в среднем на 1,13.
Рассчитаем линейный коэффициент парной корреляции:
Связь прямая, достаточно тесная.
Определим коэффициент детерминации:
Вариация результата на 74,59% объясняется вариацией фактора х.
Подставляя в уравнение регрессии фактические значения х, определим теоретические (расчётные) значения 
Так как
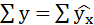
следовательно, параметры уравнения определены правильно.
Рассчитаем среднюю ошибку аппроксимации – среднее отклонение расчётных значений от фактических:
В среднем расчётные значения отклоняются от фактических на 5,01%.
Оценку качества уравнения регрессии проведём с помощью F-теста.
F-тест состоит в проверке гипотезы Н0 о статистической незначимости уравнения регрессии и показателя тесноты связи. Для этого выполняется сравнение фактического Fфакт и критического (табличного) Fтабл значений F-критерия Фишера.
Fфакт определяется по формуле:
где n – число единиц совокупности;
m – число параметров при переменных х.
Таким образом, Н0 – гипотеза о случайной природе оцениваемых характеристик отклоняется и признаётся их статистическая значимость и надёжность.
Полученные оценки уравнения регрессии позволяют использовать его для прогноза.
Если прогнозное значение индекса розничных цен на продукты питания х = 138, тогда прогнозное значение индекса промышленного производства составит:
2. Степенная регрессия имеет вид:
Для определения параметров производят логарифмирование степенной функции:
Для определения параметров логарифмической функции строят систему нормальных уравнений по способу наименьших квадратов:
Построим таблицу расчётных данных, как показано в таблице 2.
Таблица 2 Расчетные данные для оценки степенной регрессии
| №п/п | х | у | lg x | lg y | lg x*lg y | (lg x)2 | (lg y)2 |
|---|---|---|---|---|---|---|---|
| 1 | 100 | 70 | 2,000000 | 1,845098 | 3,690196 | 4,000000 | 3,404387 |
| 2 | 105 | 79 | 2,021189 | 1,897627 | 3,835464 | 4,085206 | 3,600989 |
| 3 | 108 | 85 | 2,033424 | 1,929419 | 3,923326 | 4,134812 | 3,722657 |
| 4 | 113 | 84 | 2,053078 | 1,924279 | 3,950696 | 4,215131 | 3,702851 |
| 5 | 118 | 85 | 2,071882 | 1,929419 | 3,997528 | 4,292695 | 3,722657 |
| 6 | 118 | 85 | 2,071882 | 1,929419 | 3,997528 | 4,292695 | 3,722657 |
| 7 | 110 | 96 | 2,041393 | 1,982271 | 4,046594 | 4,167284 | 3,929399 |
| 8 | 115 | 99 | 2,060698 | 1,995635 | 4,112401 | 4,246476 | 3,982560 |
| 9 | 119 | 100 | 2,075547 | 2,000000 | 4,151094 | 4,307895 | 4,000000 |
| 10 | 118 | 98 | 2,071882 | 1,991226 | 4,125585 | 4,292695 | 3,964981 |
| 11 | 120 | 99 | 2,079181 | 1,995635 | 4,149287 | 4,322995 | 3,982560 |
| 12 | 124 | 102 | 2,093422 | 2,008600 | 4,204847 | 4,382414 | 4,034475 |
| 13 | 129 | 105 | 2,110590 | 2,021189 | 4,265901 | 4,454589 | 4,085206 |
| 14 | 132 | 112 | 2,120574 | 2,049218 | 4,345518 | 4,496834 | 4,199295 |
| Итого | 1629 | 1299 | 28,90474 | 27,49904 | 56,79597 | 59,69172 | 54,05467 |
| Среднее значение | 116,3571 | 92,78571 | 2,064624 | 1,964217 | 4,056855 | 4,263694 | 3,861048 |
 |
8,4988 | 11,1431 | 0,031945 | 0,053853 | х | х | х |
 |
72,23 | 124,17 | 0,001021 | 0,0029 | х | х | х |
Продолжение таблицы 2 Расчетные данные для оценки степенной регрессии
| №п/п | х | у |  |
 |
 |
 |
|---|---|---|---|---|---|---|
| 1 | 100 | 70 | 74,16448 | 17,34292 | 0,059493 | 519,1886 |
| 2 | 105 | 79 | 79,62057 | 0,385112 | 0,007855 | 190,0458 |
| 3 | 108 | 85 | 82,95180 | 4,195133 | 0,024096 | 60,61728 |
| 4 | 113 | 84 | 88,59768 | 21,13866 | 0,054734 | 77,1887 |
| 5 | 118 | 85 | 94,35840 | 87,57961 | 0,110099 | 60,61728 |
| 6 | 118 | 85 | 94,35840 | 87,57961 | 0,110099 | 60,61728 |
| 7 | 110 | 96 | 85,19619 | 116,7223 | 0,11254 | 10,33166 |
| 8 | 115 | 99 | 90,88834 | 65,79901 | 0,081936 | 38,6174 |
| 9 | 119 | 100 | 95,52408 | 20,03384 | 0,044759 | 52,04598 |
| 10 | 118 | 98 | 94,35840 | 13,26127 | 0,037159 | 27,18882 |
| 11 | 120 | 99 | 96,69423 | 5,316563 | 0,023291 | 38,6174 |
| 12 | 124 | 102 | 101,4191 | 0,337467 | 0,005695 | 84,90314 |
| 13 | 129 | 105 | 107,4232 | 5,872099 | 0,023078 | 149,1889 |
| 14 | 132 | 112 | 111,0772 | 0,85163 | 0,00824 | 369,1889 |
| Итого | 1629 | 1299 | 1296,632 | 446,4152 | 0,703074 | 1738,357 |
| Среднее значение | 116,3571 | 92,78571 | х | х | х | х |
 |
8,4988 | 11,1431 | х | х | х | х |
 |
72,23 | 124,17 | х | х | х | х |
Решая систему нормальных уравнений, определяем параметры логарифмической функции.
Получим линейное уравнение:
Выполнив его потенцирование, получим:
Подставляя в данное уравнение фактические значения х, получаем теоретические значения результата 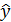
Связь достаточно тесная.
В среднем расчётные значения отклоняются от фактических на 5,02%.
Таким образом, Н0 – гипотеза о случайной природе оцениваемых характеристик отклоняется и признаётся их статистическая значимость и надёжность.
Полученные оценки уравнения регрессии позволяют использовать его для прогноза. Если прогнозное значение индекса розничных цен на продукты питания х = 138, тогда прогнозное значение индекса промышленного производства составит:
3. Уравнение равносторонней гиперболы
Для определения параметров этого уравнения используется система нормальных уравнений:
Произведем замену переменных
и получим следующую систему нормальных уравнений:
Решая систему нормальных уравнений, определяем параметры гиперболы.
Составим таблицу расчётных данных, как показано в таблице 3.
Таблица 3 Расчетные данные для оценки гиперболической зависимости
| №п/п | х | у | z | yz | 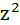 |
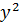 |
|---|---|---|---|---|---|---|
| 1 | 100 | 70 | 0,010000000 | 0,700000 | 0,0001000 | 4900 |
| 2 | 105 | 79 | 0,009523810 | 0,752381 | 0,0000907 | 6241 |
| 3 | 108 | 85 | 0,009259259 | 0,787037 | 0,0000857 | 7225 |
| 4 | 113 | 84 | 0,008849558 | 0,743363 | 0,0000783 | 7056 |
| 5 | 118 | 85 | 0,008474576 | 0,720339 | 0,0000718 | 7225 |
| 6 | 118 | 85 | 0,008474576 | 0,720339 | 0,0000718 | 7225 |
| 7 | 110 | 96 | 0,009090909 | 0,872727 | 0,0000826 | 9216 |
| 8 | 115 | 99 | 0,008695652 | 0,860870 | 0,0000756 | 9801 |
| 9 | 119 | 100 | 0,008403361 | 0,840336 | 0,0000706 | 10000 |
| 10 | 118 | 98 | 0,008474576 | 0,830508 | 0,0000718 | 9604 |
| 11 | 120 | 99 | 0,008333333 | 0,825000 | 0,0000694 | 9801 |
| 12 | 124 | 102 | 0,008064516 | 0,822581 | 0,0000650 | 10404 |
| 13 | 129 | 105 | 0,007751938 | 0,813953 | 0,0000601 | 11025 |
| 14 | 132 | 112 | 0,007575758 | 0,848485 | 0,0000574 | 12544 |
| Итого: | 1629 | 1299 | 0,120971823 | 11,13792 | 0,0010510 | 122267 |
| Среднее значение: | 116,3571 | 92,78571 | 0,008640844 | 0,795566 | 0,0000751 | 8733,357 |
 |
8,4988 | 11,1431 | 0,000640820 | х | х | х |
 |
72,23 | 124,17 | 0,000000411 | х | х | х |
Продолжение таблицы 3 Расчетные данные для оценки гиперболической зависимости
| №п/п | х | у |  |
 |
 |
 |
|---|---|---|---|---|---|---|
| 1 | 100 | 70 | 72,3262 | 0,033231 | 5,411206 | 519,1886 |
| 2 | 105 | 79 | 79,49405 | 0,006254 | 0,244083 | 190,0458 |
| 3 | 108 | 85 | 83,47619 | 0,017927 | 2,322012 | 60,61728 |
| 4 | 113 | 84 | 89,64321 | 0,067181 | 31,84585 | 77,1887 |
| 5 | 118 | 85 | 95,28761 | 0,121031 | 105,8349 | 60,61728 |
| 6 | 118 | 85 | 95,28761 | 0,121031 | 105,8349 | 60,61728 |
| 7 | 110 | 96 | 86,01027 | 0,10406 | 99,79465 | 10,33166 |
| 8 | 115 | 99 | 91,95987 | 0,071112 | 49,56344 | 38,6174 |
| 9 | 119 | 100 | 96,35957 | 0,036404 | 13,25272 | 52,04598 |
| 10 | 118 | 98 | 95,28761 | 0,027677 | 7,357059 | 27,18882 |
| 11 | 120 | 99 | 97,41367 | 0,016024 | 2,516453 | 38,6174 |
| 12 | 124 | 102 | 101,46 | 0,005294 | 0,291565 | 84,90314 |
| 13 | 129 | 105 | 106,1651 | 0,011096 | 1,357478 | 149,1889 |
| 14 | 132 | 112 | 108,8171 | 0,028419 | 10,1311 | 369,1889 |
| Итого: | 1629 | 1299 | 1298,988 | 0,666742 | 435,7575 | 1738,357 |
| Среднее значение: | 116,3571 | 92,78571 | х | х | х | х |
 |
8,4988 | 11,1431 | х | х | х | х |
 |
72,23 | 124,17 | х | х | х | х |
Значения параметров регрессии a и b составили:
Получено уравнение:
Индекс корреляции:
Связь достаточно тесная.
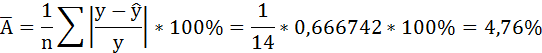
В среднем расчётные значения отклоняются от фактических на 4,76%.
Таким образом, Н0 – гипотеза о случайной природе оцениваемых характеристик отклоняется и признаётся их статистическая значимость и надёжность.
Полученные оценки уравнения регрессии позволяют использовать его для прогноза. Если прогнозное значение индекса розничных цен на продукты питания х = 138, тогда прогнозное значение индекса промышленного производства составит:
По уравнению равносторонней гиперболы получена наибольшая оценка тесноты связи по сравнению с линейной и степенной регрессиями. Средняя ошибка аппроксимации остаётся на допустимом уровне.
Содержание:
Регрессионный анализ:
Регрессионным анализом называется раздел математической статистики, объединяющий практические методы исследования корреляционной зависимости между случайными величинами по результатам наблюдений над ними. Сюда включаются методы выбора модели изучаемой зависимости и оценки ее параметров, методы проверки статистических гипотез о зависимости.
Пусть между случайными величинами X и Y существует линейная корреляционная зависимость. Это означает, что математическое ожидание Y линейно зависит от значений случайной величины X. График этой зависимости (линия регрессии Y на X) имеет уравнение
Линейная модель пригодна в качестве первого приближения и в случае нелинейной корреляции, если рассматривать небольшие интервалы возможных значений случайных величин.
Пусть параметры линии регрессии 
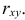
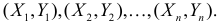
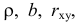
Неизвестная нам линия регрессии 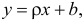

Такие значения 
Решения этой системы уравнений дают оценки называемые оценками по методу наименьших квадратов.
и
Известно, что оценки по методу наименьших квадратов являются несмещенными и, более того, среди всех несмещенных оценок обладают наименьшей дисперсией. Для оценки коэффициента корреляции можно воспользоваться тем, что 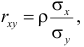
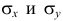
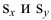
По методу наименьших квадратов можно находить оценки параметров линии регрессии и при нелинейной корреляции. Например, для линии регрессии вида 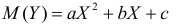
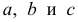
Пример:
По данным наблюдений двух случайных величин найти коэффициент корреляции и уравнение линии регрессии Y на X
Решение. Вычислим величины, необходимые для использования формул (3.7.1)–(3.7.3):
По формулам (3.7.1) и (3.7.2) получим
Итак, оценка линии регрессии имеет вид 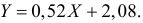
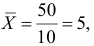
Аналогично, 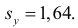
Ответ.
Пример:
Получена выборка значений величин X и Y
Для представления зависимости между величинами предполагается использовать модель 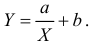
Решение. Рассмотрим сначала задачу оценки параметров этой модели в общем виде. Линия 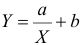
Необходимые условия экстремума приводят к системе из двух уравнений:
Откуда
Решения системы уравнений (3.7.4) и (3.7.5) и будут оценками по методу наименьших квадратов для параметров
На основе опытных данных вычисляем:
В итоге получаем систему уравнений (?????) и (?????) в виде
Эта система имеет решения
Ответ.
Если наблюдений много, то результаты их обычно группируют и представляют в виде корреляционной таблицы.
В этой таблице 
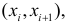
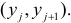
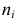
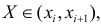
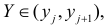
Если величины дискретны, то вместо интервалов указывают отдельные значения этих величин. Для непрерывных случайных величин представителем каждого интервала считают его середину и полагают, что 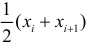
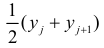
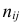
При больших значениях X и Y можно для упрощения вычислений перенести начало координат и изменить масштаб по каждой из осей, а после завершения вычислений вернуться к старому масштабу.
Пример:
Проделано 80 наблюдений случайных величин X и Y. Результаты наблюдений представлены в виде таблицы. Найти линию регрессии Y на X. Оценить коэффициент корреляции.
Решение. Представителем каждого интервала будем считать его середину. Перенесем начало координат и изменим масштаб по каждой оси так, чтобы значения X и Y были удобны для вычислений. Для этого перейдем к новым переменным 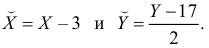
Чтобы иметь представление о виде линии регрессии, вычислим средние значения 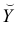
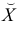
Нанесем эти значения на координатную плоскость, соединив для наглядности их отрезками прямой (рис. 3.7.1).
По виду полученной ломанной линии можно предположить, что линия регрессии Y на X является прямой. Оценим ее параметры. Для этого сначала вычислим с учетом группировки данных в таблице все величины, необходимые для использования формул (3.31–3.33):
Тогда
В новом масштабе оценка линии регрессии имеет вид 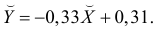
Для оценки 
Подобным же образом можно оценить 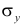
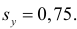
Вернемся к старому масштабу:
Коэффициент корреляции пересчитывать не нужно, так как это величина безразмерная и от масштаба не зависит.
Ответ.
Пусть некоторые физические величины X и Y связаны неизвестной нам функциональной зависимостью 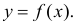
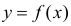
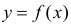
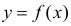
Регрессионный анализ
Основные положения регрессионного анализа:
Основная задача регрессионного анализа — изучение зависимости между результативным признаком Y и наблюдавшимся признаком X, оценка функции регрессий.
Предпосылки регрессионного анализа:
- Y — независимые случайные величины, имеющие постоянную дисперсию;
- X— величины наблюдаемого признака (величины не случайные);
- условное математическое ожидание
можно представить в виде
Выражение (2.1), как уже упоминалось в п. 1.2, называется функцией регрессии (или модельным уравнением регрессии) Y на X. Оценке в этом выражении подлежат параметры 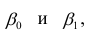
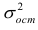
Остаточной дисперсией называется та часть рассеивания результативного признака, которую нельзя объяснить действием наблюдаемого признака; Остаточная дисперсия может служить для оценки точности подбора вида функции регрессии (модельного уравнения регрессии), полноты набора признаков, включенных в анализ. Оценки параметров функции регрессии находят, используя метод наименьших квадратов.
В данном вопросе рассмотрен линейный регрессионный анализ. Линейным он называется потому, что изучаем лишь те виды зависимостей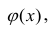
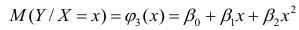
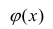
Важное место в линейном регрессионном анализе занимает так называемая «нормальная регрессия». Она имеет место, если сделать предположения относительно закона распределения случайной величины Y. Предпосылки «нормальной регрессии»:
- Y — независимые случайные величины, имеющие постоянную дисперсию и распределенные по нормальному закону;
- X— величины наблюдаемого признака (величины не случайные);
- условное математическое ожидание
можно представить в виде (2.1).
В этом случае оценки коэффициентов регрессии — несмещённые с минимальной дисперсией и нормальным законом распределения. Из этого положения следует что при «нормальной регрессии» имеется возможность оценить значимость оценок коэффициентов регрессии, а также построить доверительный интервал для коэффициентов регрессии и условного математического ожидания M(YX=x).
Линейная регрессия
Рассмотрим простейший случай регрессионного анализа — модель вида (2.1), когда зависимость 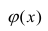
по переменным. Оценки параметров модели (2.1) 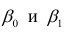
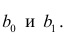
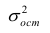
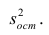
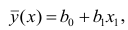
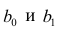
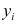
Составим систему нормальных уравнений: первое уравнение
откуда
второе уравнение
откуда
Итак,
Оценки, полученные по способу наименьших квадратов, обладают минимальной дисперсией в классе линейных оценок. Решая систему (2.2) относительно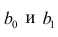
Остаётся получить оценку параметра 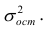
где т — количество наблюдений.
Еслит велико, то для упрощения расчётов наблюдавшиеся данные принята группировать, т.е. строить корреляционную таблицу. Пример построения такой таблицы приведен в п. 1.5. Формулы для нахождения коэффициентов регрессии по сгруппированным данным те же, что и для расчёта по несгруппированным данным, но суммы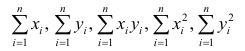
где 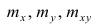
Нелинейная регрессия
Рассмотрим случай, когда зависимость нелинейна по переменным х, например модель вида
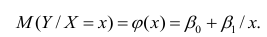
На рис. 2.1 изображено поле корреляции. Очевидно, что зависимость между Y и X нелинейная и её графическим изображением является не прямая, а кривая. Оценкой выражения (2.6) является уравнение регрессии
где 
Принцип нахождения коэффициентов тот же — метод наименьших квадратов, т.е.
или
Дифференцируя последнее равенство по 
В общем случае нелинейной зависимости между переменными Y и X связь может выражаться многочленом k-й степени от x:
Коэффициенты регрессии определяют по принципу наименьших квадратов. Система нормальных уравнений имеет вид
Вычислив коэффициенты системы, её можно решить любым известным способом.
Оценка значимости коэффициентов регрессии. Интервальная оценка коэффициентов регрессии
Проверить значимость оценок коэффициентов регрессии — значит установить, достаточна ли величина оценки для статистически обоснованного вывода о том, что коэффициент регрессии отличен от нуля. Для этого проверяют гипотезу о равенстве нулю коэффициента регрессии, соблюдая предпосылки «нормальной регрессии». В этом случае вычисляемая для проверки нулевой гипотезы 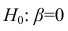
имеет распределение Стьюдента с к= n-2 степенями свободы (b — оценка коэффициента регрессии, 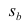
коэффициента регрессии, иначе стандартная ошибка оценки). По уровню значимости а и числу степеней свободы к находят по таблицам распределения Стьюдента (см. табл. 1 приложений) критическое значение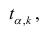
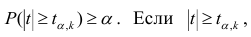
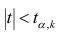
Оценки среднеквадратического отклонения коэффициентов регрессии вычисляют по следующим формулам:
где 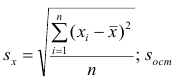
формуле (2.5).
Доверительный интервал для значимых параметров строят по обычной схеме. Из условия
где а — уровень значимости, находим
Интервальная оценка для условного математического ожидания
Линия регрессии характеризует изменение условного математического ожидания результативного признака от вариации остальных признаков.
Точечной оценкой условного математического ожидания 
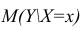
построить доверительный интервал в точке
Известно, что 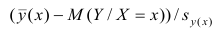
Стьюдента с k=n—2 степенями свободы. Найдя оценку среднеквадратического отклонения для условного среднего, можно построить доверительный интервал для условного математического ожидания
Оценку дисперсии условного среднего вычисляют по формуле
или для интервального ряда
Доверительный интервал находят из условия
где а — уровень значимости. Отсюда
Доверительный интервал для условного математического ожидания можно изобразить графически (рис, 2.2).
Из рис. 2.2 видно, что в точке 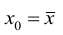
Проверка значимости уравнения регрессии
Оценить значимость уравнения регрессии — значит установить, соответствует ли математическая, модель, выражающая зависимость между Y и X, экспериментальным данным. Для оценки значимости в предпосылках «нормальной регрессии» проверяют гипотезу 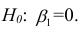
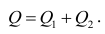
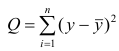
X) и 
Для проверки нулевой гипотезы вычисляют статистику 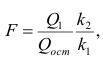
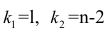
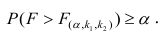
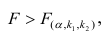
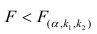
Многомерный регрессионный анализ
В случае, если изменения результативного признака определяются действием совокупности других признаков, имеет место многомерный регрессионный анализ. Пусть результативный признак У, а независимые признаки 
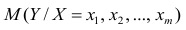
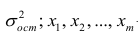
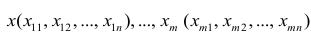
Оценке подлежат параметры 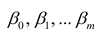
Заменив параметры их оценками, запишем уравнение регрессии
Коэффициенты в этом выражении находят методом наименьших квадратов.
Исходными данными для вычисления коэффициентов 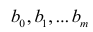

Как и в двумерном случае, составляют систему нормальных уравнений
которую можно решить любым способом, известным из линейной алгебры. Рассмотрим один из них — способ обратной матрицы. Предварительно преобразуем систему уравнений. Выразим из первого уравнения значение 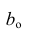
Подставим в остальные уравнения системы вместо 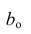
Пусть С — матрица коэффициентов при неизвестных параметрах 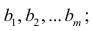
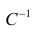
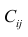
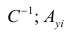
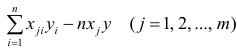
запишем окончательные выражения для параметров:
Оценкой остаточной дисперсии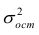
где 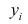
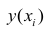
Если выборка получена из нормально распределенной генеральной совокупности, то, аналогично изложенному в п. 2.4, можно проверить значимость оценок коэффициентов регрессии, только в данном случае статистику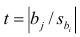
где 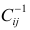
го столбца;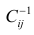
При заданном уровне значимости а и числе степеней свободы к=n— m—1 по табл. 1 приложений находят критическое значение 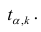
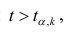
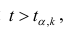
Для значимых коэффициентов регрессии целесообразно построить доверительные интервалы по формуле (2.10). Для оценки значимости уравнения регрессии следует проверить нулевую гипотезу о том, что все коэффициенты регрессии (кроме свободного члена) равны нулю: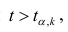
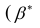
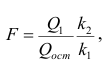
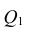
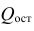
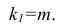
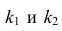
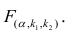
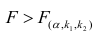
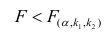
Факторный анализ
Основные положения. В последнее время всё более широкое распространение находит один из новых разделов многомерного статистического анализа — факторный анализ. Первоначально этот метод
разрабатывался для объяснения многообразия корреляций между исходными параметрами. Действительно, результатом корреляционного анализа является матрица коэффициентов корреляций. При малом числе параметров можно произвести визуальный анализ этой матрицы. С ростом числа параметра (10 и более) визуальный анализ не даёт положительных результатов. Оказалось, что всё многообразие корреляционных связей можно объяснить действием нескольких обобщённых факторов, являющихся функциями исследуемых параметров, причём сами обобщённые факторы при этом могут быть и неизвестны, однако их можно выразить через исследуемые параметры.
Один из основоположников факторного анализа Л. Терстоун приводит такой пример: несколько сотен мальчиков выполняют 20 разнообразных гимнастических упражнений. Каждое упражнение оценивают баллами. Можно рассчитать матрицу корреляций между 20 упражнениями. Это большая матрица размером 20><20. Изучая такую матрицу, трудно уловить закономерность связей между упражнениями. Нельзя ли объяснить скрытую в таблице закономерность действием каких-либо обобщённых факторов, которые в результате эксперимента непосредственно, не оценивались? Оказалось, что обо всех коэффициентах корреляции можно судить по трём обобщённым факторам, которые и определяют успех выполнения всех 20 гимнастических упражнений: чувство равновесия, усилие правого плеча, быстрота движения тела.
Дальнейшие разработки факторного анализа доказали, что этот метод может быть с успехом применён в задачах группировки и классификации объектов. Факторный анализ позволяет группировать объекты со сходными сочетаниями признаков и группировать признаки с общим характером изменения от объекта к объекту. Действительно, выделенные обобщённые факторы можно использовать как критерии при классификации мальчиков по способностям к отдельным группам гимнастических упражнений.
Методы факторного анализа находят применение в психологии и экономике, социологии и экономической географии. Факторы, выраженные через исходные параметры, как правило, легко интерпретировать как некоторые существенные внутренние характеристики объектов.
Факторный анализ может быть использован и как самостоятельный метод исследования, и вместе с другими методами многомерного анализа, например в сочетании с регрессионным анализом. В этом случае для набора зависимых переменных наводят обобщённые факторы, которые потом входят в регрессионный анализ в качестве переменных. Такой подход позволяет сократить число переменных в регрессионном анализе, устранить коррелированность переменных, уменьшить влияние ошибок и в случае ортогональности выделенных факторов значительно упростить оценку значимости переменных.
Представление, информации в факторном анализе
Для проведения факторного анализа информация должна быть представлена в виде двумерной таблицы чисел размерностью 
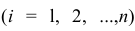
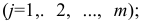
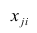
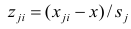
Основная модель факторного анализа. Основная модель факторного анализа имеет вид
где 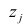
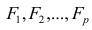
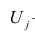
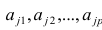
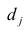
Модель предполагает, что каждый из j признаков, входящих в исследуемый набор и заданных в стандартной форме, может быть представлен в виде линейной комбинации небольшого числа общих факторов 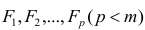
Термин «общий фактор» подчёркивает, что каждый такой фактор имеет существенное значение для анализа всех признаков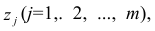
Термин «характерный фактор» показывает, что он относится только к данному j-му признаку. Это специфика признака, которая не может быть, выражена через факторы
Факторные нагрузки 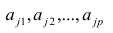
Для j-го признака и i-го объекта модель (2.19) можно записать в. виде
где 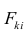
Дисперсию признака 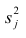
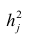
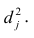
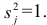
Если общие и характерные факторы не коррелируют между собой, то дисперсию j-го признака можно представить в виде
где 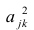
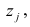
Полный вклад k-го фактора в суммарную дисперсию признаков
Вклад общих факторов в суммарную дисперсию
Факторное отображение
Используя модель (2.19), запишем выражения для каждого из параметров:
Коэффициенты системы (2,21) — факторные нагрузки — можно представить в виде матрицы, каждая строка которой соответствует параметру, а столбец — фактору.
Факторный анализ позволяет получить не только матрицу отображений, но и коэффициенты корреляции между параметрами и
факторами, что является важной характеристикой качества факторной модели. Таблица таких коэффициентов корреляции называется факторной структурой или просто структурой.
Коэффициенты отображения можно выразить через выборочные парные коэффициенты корреляции. На этом основаны методы вычисления факторного отображения.
Рассмотрим связь между элементами структуры и коэффициентами отображения. Для этого, учитывая выражение (2.19) и определение выборочного коэффициента корреляции, умножим уравнения системы (2.21) на соответствующие факторы, произведём суммирование по всем n наблюдениям и, разделив на n, получим следующую систему уравнений:
где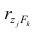
м фактором;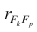
Если предположить, что общие факторы между собой, не коррелированы, то уравнения (2.22) можно записать в виде
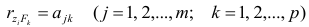
элементам структуры.
Введём понятие, остаточного коэффициента корреляции и остаточной корреляционной матрицы. Исходной информацией для построения факторной модели (2.19) служит матрица выборочных парных коэффициентов корреляции. Используя построенную факторную модель, можно снова вычислить коэффициенты корреляции между признаками и сравнись их с исходными Коэффициентами корреляции. Разница между ними и есть остаточный коэффициент корреляции.
В случае независимости факторов имеют место совсем простые выражения для вычисляемых коэффициентов корреляции между параметрами: для их вычисления достаточно взять сумму произведений коэффициентов отображения, соответствующих наблюдавшимся признакам:
где 
и к-м признаком. Остаточный коэффициент корреляции
Матрица остаточных коэффициентов корреляции называется остаточной матрицей или матрицей остатков
где 
Результаты факторного анализа удобно представить в виде табл. 2.10.
Здесь суммы квадратов нагрузок по строкам — общности параметров, а суммы квадратов нагрузок по столбцам — вклады факторов в суммарную дисперсию параметров. Имеет место соотношение
Определение факторных нагрузок
Матрицу факторных нагрузок можно получить различными способами. В настоящее время наибольшее распространение получил метод главных факторов. Этот метод основан на принципе последовательных приближений и позволяет достичь любой точности. Метод главных факторов предполагает использование ЭВМ. Существуют хорошие алгоритмы и программы, реализующие все вычислительные процедуры.
Введём понятие редуцированной корреляционной матрицы или просто редуцированной матрицы. Редуцированной называется матрица выборочных коэффициентов корреляции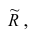
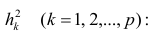
Редуцированная и полная матрицы связаны соотношением
где D — матрица характерностей.
Общности, как правило, неизвестны, и нахождение их в факторном анализе представляет серьезную проблему. Вначале определяют (хотя бы приближённо) число общих факторов, совокупность, которых может с достаточной точностью аппроксимировать все взаимосвязи выборочной корреляционной матрицы. Доказано, что число общих факторов (общностей) равно рангу редуцированной матрицы, а при известном ранге можно по выборочной корреляционной матрице найти оценки общностей. Числа общих факторов можно определить априори, исходя из физической природы эксперимента. Затем рассчитывают матрицу факторных нагрузок. Такая матрица, рассчитанная методом главных факторов, обладает одним интересным свойством: сумма произведений каждой пары её столбцов равна нулю, т.е. факторы попарно ортогональны.
Сама процедура нахождения факторных нагрузок, т.е. матрицы А, состоит из нескольких шагов и заключается в следующем: на первом шаге ищут коэффициенты факторных нагрузок при первом факторе так, чтобы сумма вкладов данного фактора в суммарную общность была максимальной:
Максимум 
где 
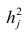
Затем рассчитывают матрицу коэффициентов корреляции с учётом только первого фактора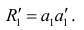
На втором шаге определяют коэффициенты нагрузок при втором факторе так, чтобы сумма вкладов второго фактора в остаточную общность (т.е. полную общность без учёта той части, которая приходится на долю первого фактора) была максимальной. Сумма квадратов нагрузок при втором факторе
Максимум 
где 
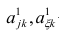
Факторный анализ учитывает суммарную общность. Исходная суммарная общность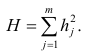
Адекватность факторной модели оценивается по матрице остатков (если величины её коэффициентов малы, то модель считают адекватной).
Такова последовательность шагов для нахождения факторных нагрузок. Для нахождения максимума функции (2.24) при условии (2.25) используют метод множителей Лагранжа, который приводит к системе т уравнений относительно m неизвестных
Метод главных компонент
Разновидностью метода главных факторов является метод главных компонент или компонентный анализ, который реализует модель вида
где m — количество параметров (признаков).
Каждый из наблюдаемых, параметров линейно зависит от m не коррелированных между собой новых компонент (факторов) 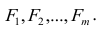
Если для дальнейшего анализа оставить все найденные т компонент, то тем самым будет использована вся информация, заложенная в корреляционной матрице. Однако это неудобно и нецелесообразно. На практике обычно оставляют небольшое число компонент, причём количество их определяется долей суммарной дисперсии, учитываемой этими компонентами. Существуют различные критерии для оценки числа оставляемых компонент; чаще всего используют следующий простой критерий: оставляют столько компонент, чтобы суммарная дисперсия, учитываемая ими, составляла заранее установленное число процентов. Первая из компонент должна учитывать максимум суммарной дисперсии параметров; вторая — не коррелировать с первой и учитывать максимум оставшейся дисперсии и так до тех пор, пока вся дисперсия не будет учтена. Сумма учтённых всеми компонентами дисперсий равна сумме дисперсий исходных параметров. Математический аппарат компонентного анализа полностью совпадает с аппаратом метода главных факторов. Отличие только в исходной матрице корреляций.
Компонента (или фактор) через исходные переменные выражается следующим образом:
где 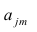
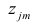
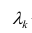
компонент.
Для иллюстрации возможностей факторного анализа покажем, как, используя метод главных компонент, можно сократить размерность пространства независимых переменных, перейдя от взаимно коррелированных параметров к независимым факторам, число которых р
Следует особо остановиться на интерпретации результатов, т.е. на смысловой стороне факторного анализа. Собственно факторный анализ состоит из двух важных этапов; аппроксимации корреляционной матрицы и интерпретации результатов. Аппроксимировать корреляционную матрицу, т.е. объяснить корреляцию между параметрами действием каких-либо общих для них факторов, и выделить сильно коррелирующие группы параметров достаточно просто: из корреляционной матрицы одним из методов
факторного анализа непосредственно получают матрицу нагрузок — факторное решение, которое называют прямым факторным решением. Однако часто это решение не удовлетворяет исследователей. Они хотят интерпретировать фактор как скрытый, но существенный параметр, поведение которого определяет поведение некоторой своей группы наблюдаемых параметров, в то время как, поведение других параметров определяется поведением других факторов. Для этого у каждого параметра должна быть наибольшая по модулю факторная нагрузка с одним общим фактором. Прямое решение следует преобразовать, что равносильно повороту осей общих факторов. Такие преобразования называют вращениями, в итоге получают косвенное факторное решение, которое и является результатом факторного анализа.
Приложения
Значение t — распределения Стьюдента
Понятие о регрессионном анализе. Линейная выборочная регрессия. Метод наименьших квадратов (МНК)
Основные задачи регрессионного анализа:
- Вычисление выборочных коэффициентов регрессии
- Проверка значимости коэффициентов регрессии
- Проверка адекватности модели
- Выбор лучшей регрессии
- Вычисление стандартных ошибок, анализ остатков
Построение простой регрессии по экспериментальным данным.
Предположим, что случайные величины 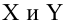
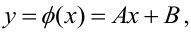
Диаграмма рассеяния (разброса, рассеивания)
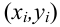
Выборочное уравнение прямой линии регрессии 
Задача: подобрать 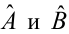
Для того, что бы провести прямую 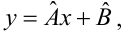
чтобы
Постулаты регрессионного анализа, которые должны выполняться при использовании МНК.
подчинены нормальному закону распределения.
- Дисперсия
постоянна и не зависит от номера измерения.
- Результаты наблюдений
в разных точках независимы.
- Входные переменные
независимы, неслучайны и измеряются без ошибок.
Введем функцию ошибок 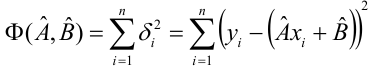
Решив систему, получим искомые значения
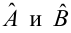
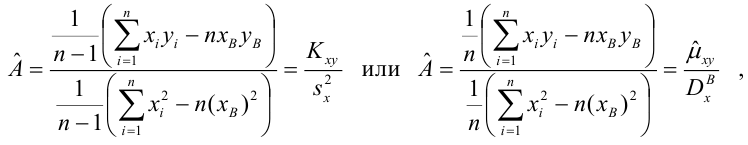
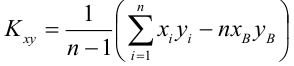
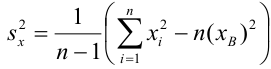
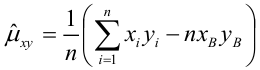
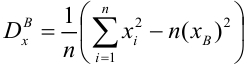
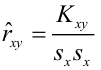
Коэффициент детерминации
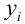
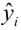
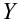
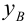
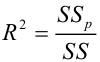
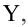
Коэффициент детерминации принимает значения от 0 до 1. Чем ближе значение коэффициента к 1, тем сильнее зависимость. При оценке регрессионных моделей это используется для доказательства адекватности модели (качества регрессии). Для приемлемых моделей предполагается, что коэффициент детерминации должен быть хотя бы не меньше 0,5 (в этом случае коэффициент множественной корреляции превышает по модулю 0,7). Модели с коэффициентом детерминации выше 0,8 можно признать достаточно хорошими (коэффициент корреляции превышает 0,9). Подтверждение адекватности модели проводится на основе дисперсионного анализа путем проверки гипотезы о значимости коэффициента детерминации.
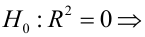
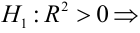
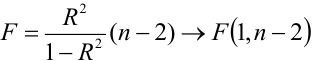
Критическая область — правосторонняя;
Если 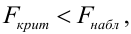
Мощность статистического критерия. Функция мощности
Определение. Мощностью критерия 
Задача: построить критическую область таким образом, чтобы мощность критерия была максимальной.
Определение. Наилучшей критической областью (НКО) называют критическую область, которая обеспечивает минимальную ошибку второго рода
Пример:
По паспортным данным автомобиля расход топлива на 100 километров составляет 10 литров. В результате измерения конструкции двигателя ожидается, что расход топлива уменьшится. Для проверки были проведены испытания 25 автомобилей с модернизированным двигателем; выборочная средняя расхода топлива по результатам испытаний составила 9,3 литра. Предполагая, что выборка получена из нормально распределенной генеральной совокупности с математическим ожиданием 
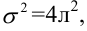
3) Уровень значимости
4) Статистический критерий
5) Критическая область — левосторонняя
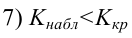
Пример:
В условиях примера 1 предположим, что наряду с 
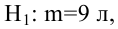
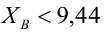
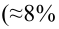
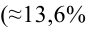
Определение. Пусть проверяется 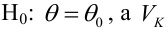
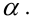
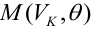
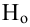
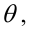
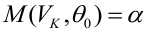
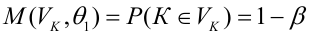
Пример:
Построить график функции мощности из примера 2 для

Пример:
Какой минимальный объем выборки следует взять в условии примера 2 для того, чтобы обеспечить
Лемма Неймана-Пирсона.
При проверке простой гипотезы 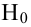
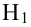
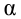
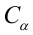
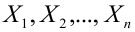
Пример:
Случайная величина 
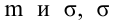
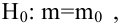
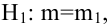
Решение:
Ошибка первого рода:
НКО:
Пример:
Для зависимости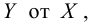
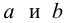
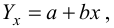
Решение. Воспользуемся предыдущими результатами
Согласно формуле (24), уравнение регрессии будет иметь вид 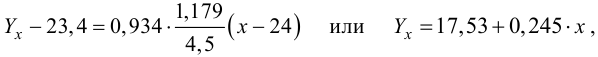
Для выяснения значимости уравнения регрессии вычислим суммы 
Из (27) и (28) по данным таблицы получим
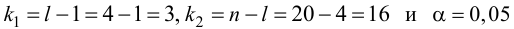
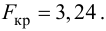
Вычислим статистику
Так как 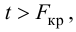
- Корреляционный анализ
- Статистические решающие функции
- Случайные процессы
- Выборочный метод
- Проверка гипотезы о равенстве вероятностей
- Доверительный интервал для математического ожидания
- Доверительный интервал для дисперсии
- Проверка статистических гипотез
Простая линейная регрессия — это статистический метод, который можно использовать для понимания связи между двумя переменными, x и y.
Одна переменная x известна как предикторная переменная .
Другая переменная, y , известна как переменная ответа .
Например, предположим, что у нас есть следующий набор данных с весом и ростом семи человек:
Пусть вес будет предикторной переменной, а рост — переменной отклика.
Если мы изобразим эти две переменные с помощью диаграммы рассеяния с весом по оси x и высотой по оси y, вот как это будет выглядеть:
Предположим, нам интересно понять взаимосвязь между весом и ростом. На диаграмме рассеяния мы ясно видим, что по мере увеличения веса рост также имеет тенденцию к увеличению, но для фактической количественной оценки этой взаимосвязи между весом и ростом нам нужно использовать линейную регрессию.
Используя линейную регрессию, мы можем найти линию, которая лучше всего «соответствует» нашим данным. Эта линия известна как линия регрессии наименьших квадратов, и ее можно использовать, чтобы помочь нам понять взаимосвязь между весом и ростом. Обычно вы должны использовать программное обеспечение, такое как Microsoft Excel, SPSS или графический калькулятор, чтобы найти уравнение для этой линии.
Формула линии наилучшего соответствия записывается так:
ŷ = б 0 + б 1 х
где ŷ — прогнозируемое значение переменной отклика, b 0 — точка пересечения с осью y, b 1 — коэффициент регрессии, а x — значение переменной-предиктора.
Связанный: 4 примера использования линейной регрессии в реальной жизни
Поиск «Линии наилучшего соответствия»
Для этого примера мы можем просто подключить наши данные к калькулятору линейной регрессии Statology и нажать « Рассчитать »:
Калькулятор автоматически находит линию регрессии методом наименьших квадратов :
ŷ = 32,7830 + 0,2001x
Если мы уменьшим масштаб нашей диаграммы рассеяния и добавим эту линию на диаграмму, вот как это будет выглядеть:
Обратите внимание, как наши точки данных близко разбросаны вокруг этой линии. Это потому, что эта линия регрессии методом наименьших квадратов лучше всего подходит для наших данных из всех возможных линий, которые мы могли бы нарисовать.
Как интерпретировать линию регрессии методом наименьших квадратов
Вот как интерпретировать эту линию регрессии наименьших квадратов: ŷ = 32,7830 + 0,2001x
б0 = 32,7830.Это означает, что когда предикторная переменная веса равна нулю фунтов, прогнозируемый рост составляет 32,7830 дюйма. Иногда может быть полезно знать значение b 0 , но в этом конкретном примере на самом деле нет смысла интерпретировать b 0 , поскольку человек не может весить ноль фунтов.
б 1 = 0,2001.Это означает, что увеличение x на одну единицу связано с увеличением y на 0,2001 единицы. В этом случае увеличение веса на один фунт связано с увеличением роста на 0,2001 дюйма.
Как использовать линию регрессии наименьших квадратов
Используя эту линию регрессии наименьших квадратов, мы можем ответить на такие вопросы, как:
Какого роста мы ожидаем от человека, который весит 170 фунтов?
Чтобы ответить на этот вопрос, мы можем просто подставить 170 в нашу линию регрессии для x и найти y:
ŷ = 32,7830 + 0,2001 (170) = 66,8 дюйма
Какого роста мы ожидаем от человека, который весит 150 фунтов?
Чтобы ответить на этот вопрос, мы можем подставить 150 в нашу линию регрессии для x и найти y:
ŷ = 32,7830 + 0,2001 (150) = 62,798 дюйма
Предупреждение. При использовании уравнения регрессии для ответа на подобные вопросы убедитесь, что вы используете только те значения переменной-предиктора, которые находятся в пределах диапазона переменной-предиктора в исходном наборе данных, который мы использовали для создания линии регрессии методом наименьших квадратов. Например, вес в нашем наборе данных варьировался от 140 до 212 фунтов, поэтому имеет смысл отвечать на вопросы о прогнозируемом росте только тогда, когда вес составляет от 140 до 212 фунтов.
Коэффициент детерминации
Одним из способов измерения того, насколько хорошо линия регрессии наименьших квадратов «соответствует» данным, является использование коэффициента детерминации , обозначаемого как R 2 .
Коэффициент детерминации — это доля дисперсии переменной отклика, которая может быть объяснена предикторной переменной.
Коэффициент детерминации может варьироваться от 0 до 1. Значение 0 указывает на то, что переменная отклика вообще не может быть объяснена предикторной переменной. Значение 1 указывает, что переменная отклика может быть полностью объяснена без ошибок с помощью переменной-предиктора.
R 2 между 0 и 1 указывает, насколько хорошо переменная отклика может быть объяснена переменной-предиктором. Например, R 2 , равный 0,2, указывает, что 20% дисперсии переменной отклика можно объяснить переменной-предиктором; R 2 , равное 0,77, указывает, что 77% дисперсии переменной отклика можно объяснить переменной-предиктором.
Обратите внимание, что в нашем предыдущем выводе мы получили значение R2, равное 0,9311 , что указывает на то, что 93,11% изменчивости роста можно объяснить предикторной переменной веса:
Это говорит нам о том, что вес является очень хорошим предиктором роста.
Предположения линейной регрессии
Чтобы результаты модели линейной регрессии были достоверными и надежными, нам необходимо проверить выполнение следующих четырех допущений:
1. Линейная зависимость. Существует линейная зависимость между независимой переменной x и зависимой переменной y.
2. Независимость: Остатки независимы. В частности, нет корреляции между последовательными остатками в данных временных рядов.
3. Гомоскедастичность: остатки имеют постоянную дисперсию на каждом уровне x.
4. Нормальность: остатки модели нормально распределены.
Если одно или несколько из этих предположений нарушаются, то результаты нашей линейной регрессии могут быть ненадежными или даже вводящими в заблуждение.
Обратитесь к этому сообщению для объяснения каждого предположения, как определить, выполняется ли предположение, и что делать, если предположение нарушается.


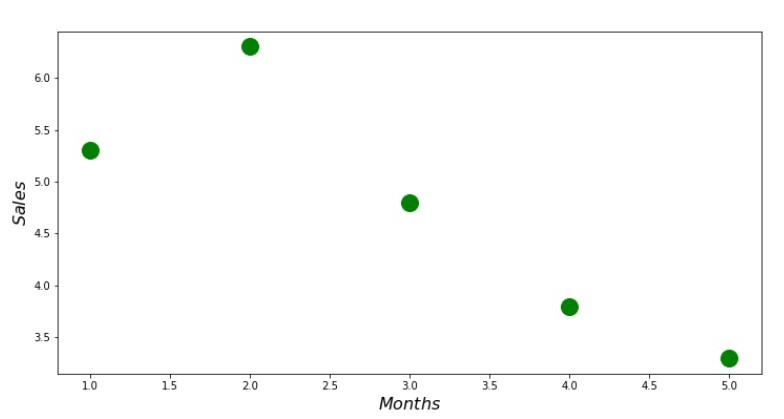

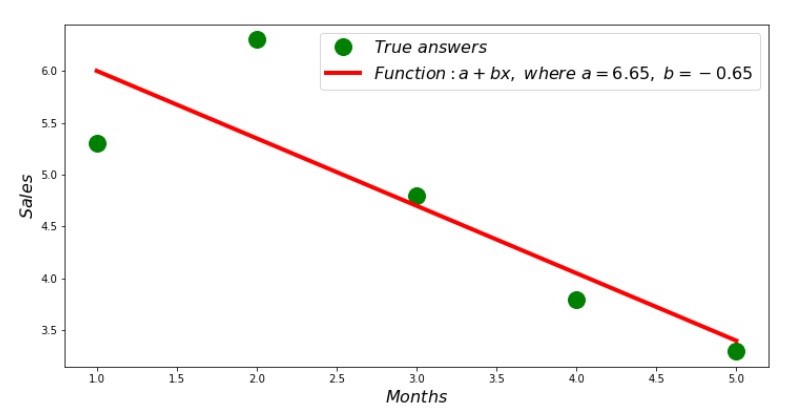
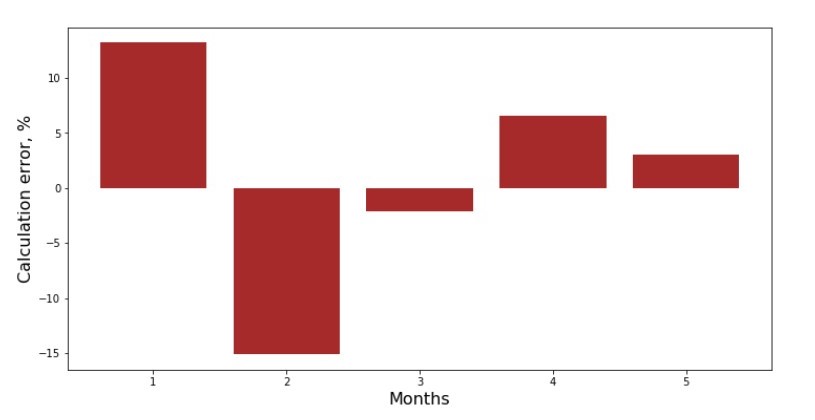



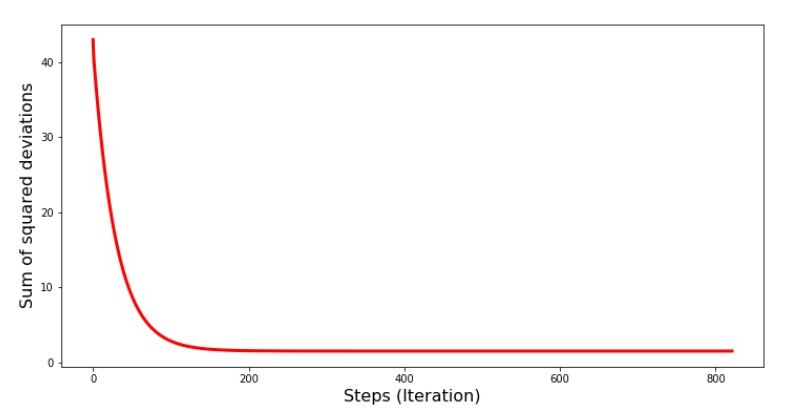


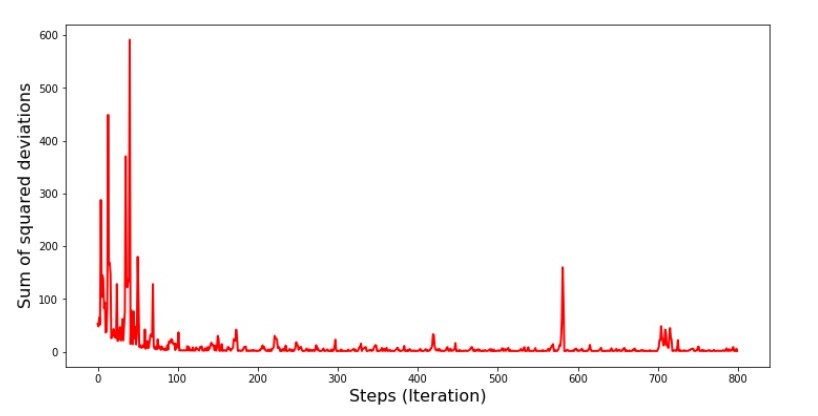

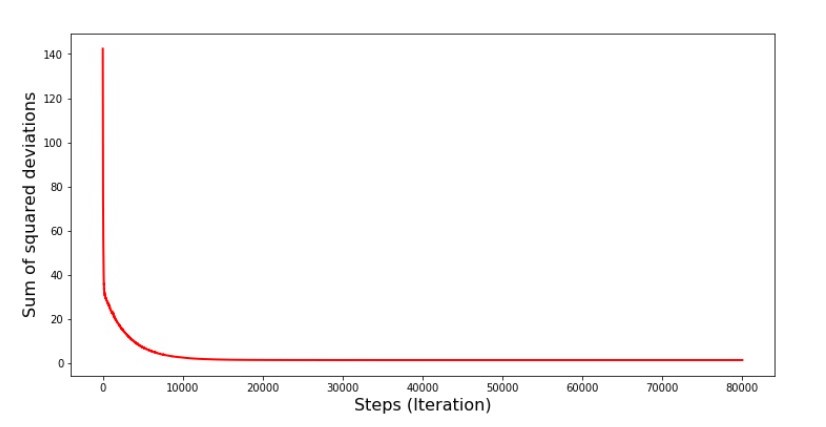
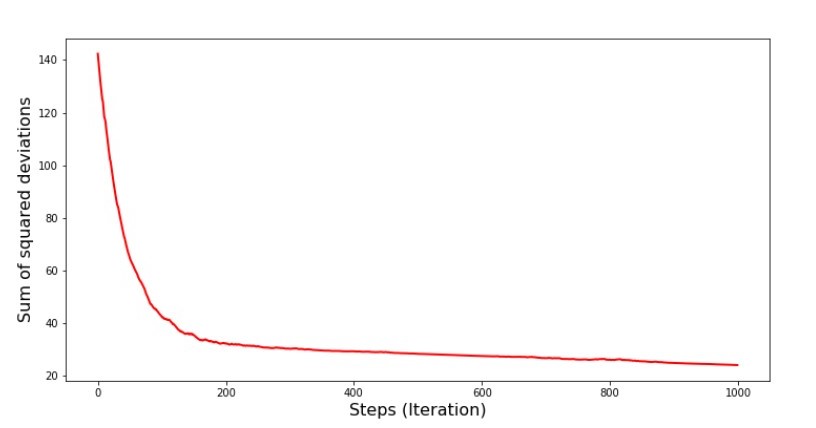
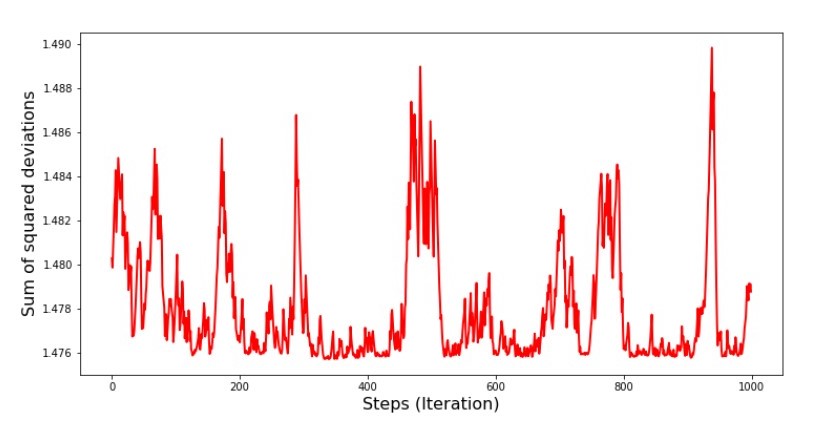




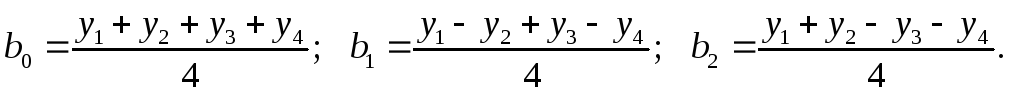
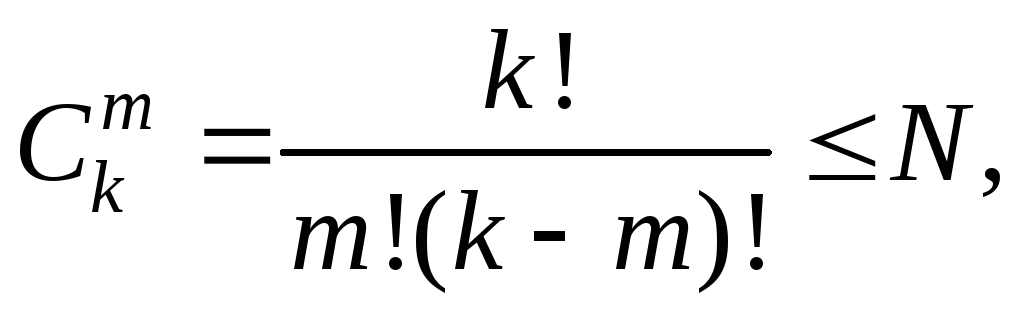

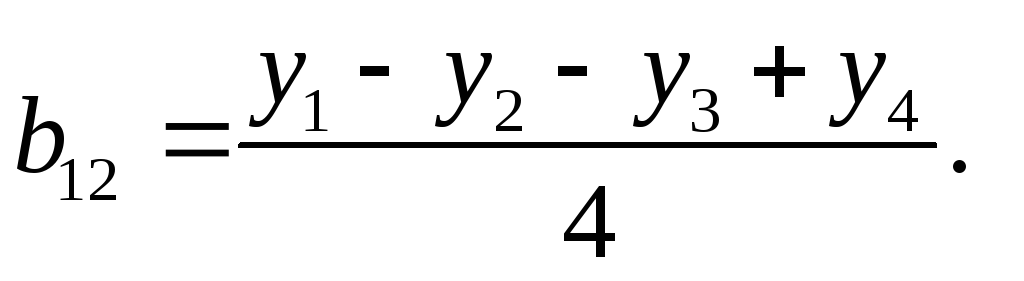



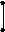















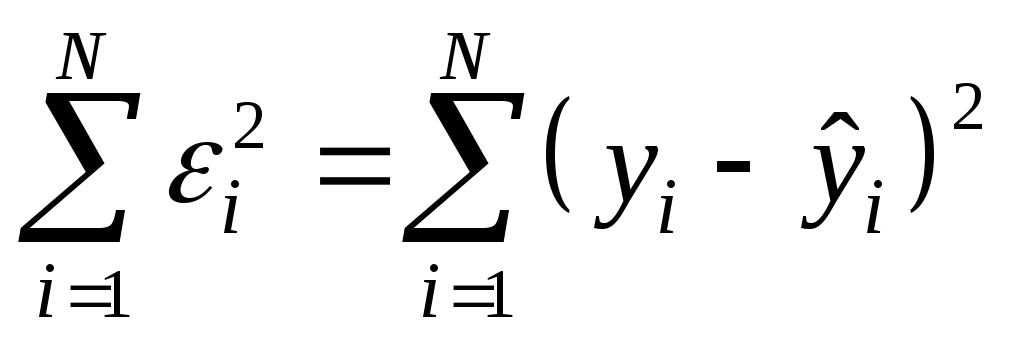






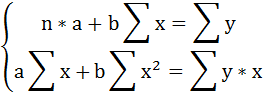
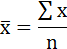
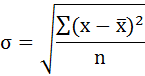
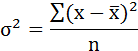
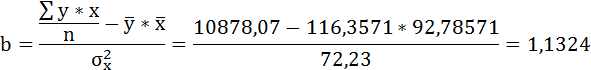
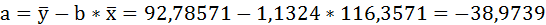
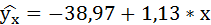
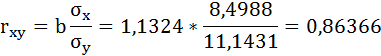
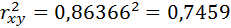
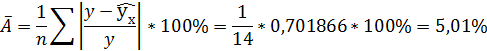
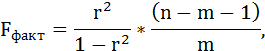
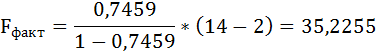
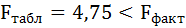
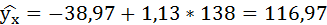
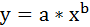
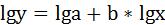
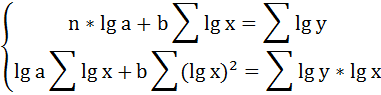
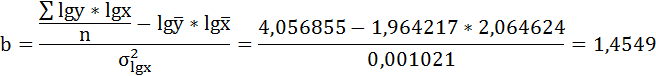
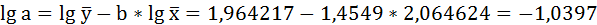
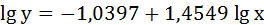
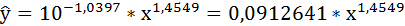
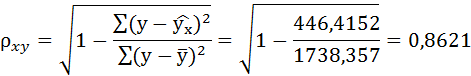
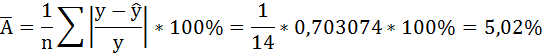
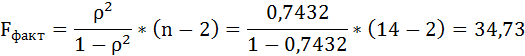
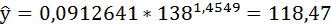
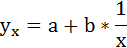
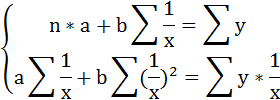
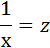
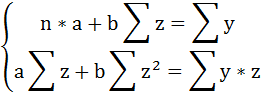
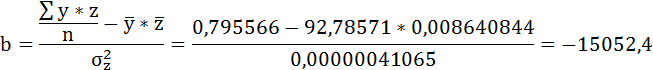
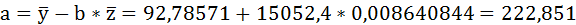
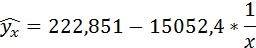
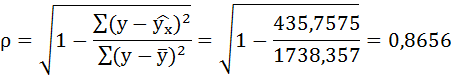
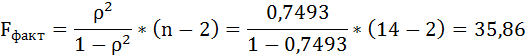
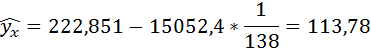
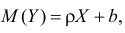
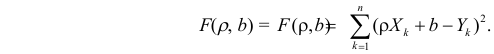
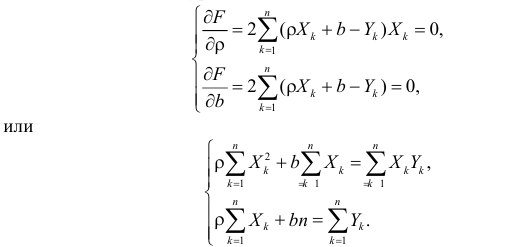
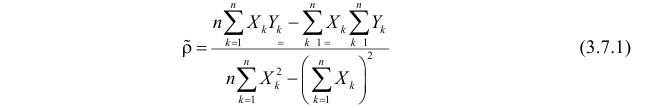
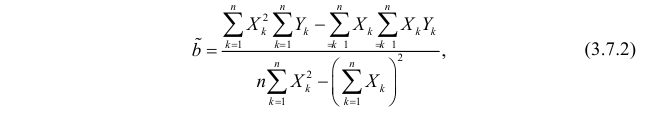
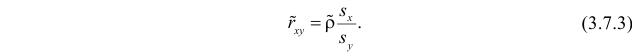
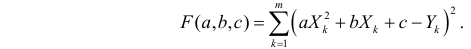

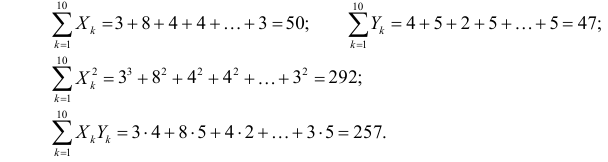
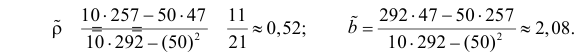
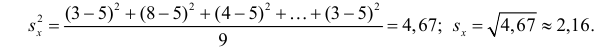
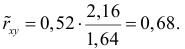
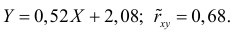

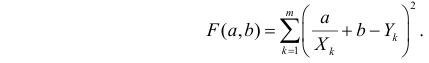
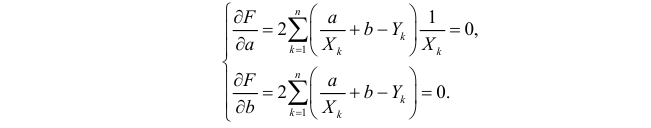
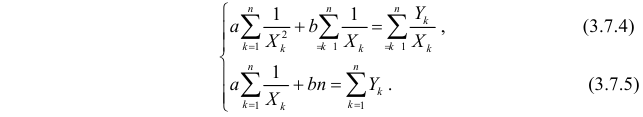
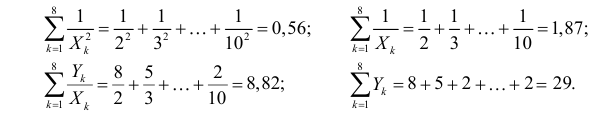
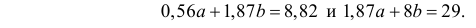
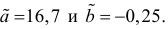
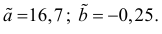

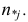



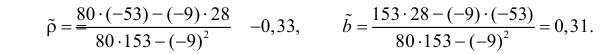
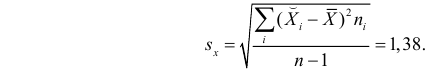
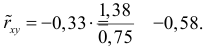
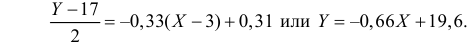
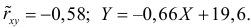
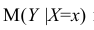 можно представить в виде
можно представить в виде 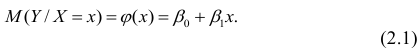
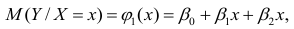
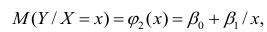
 можно представить в виде (2.1).
можно представить в виде (2.1).
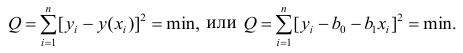
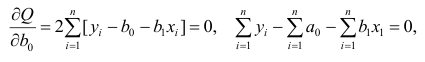
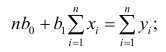
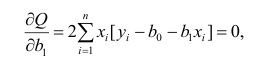
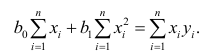
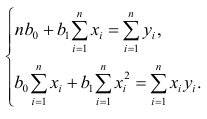
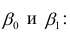
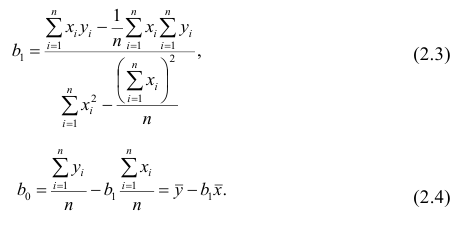
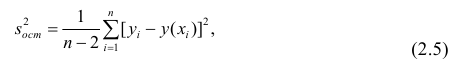
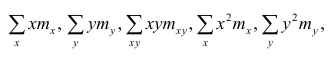
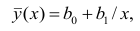
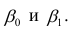
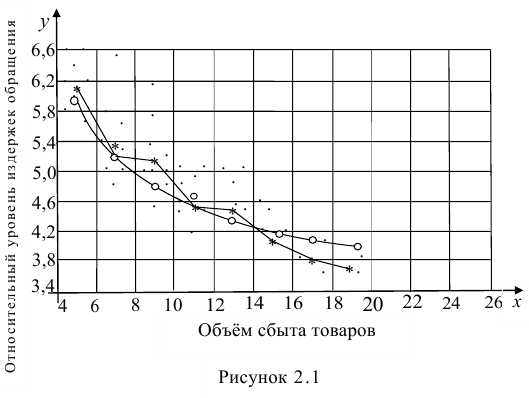
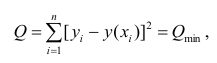
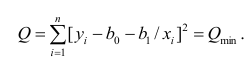
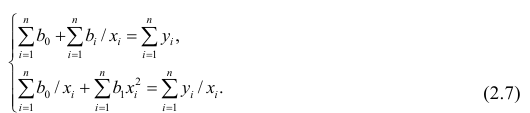
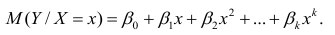
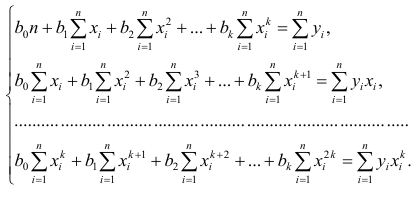

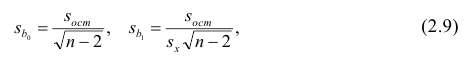
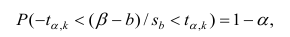

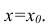
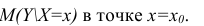
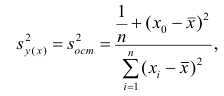
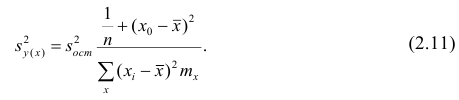
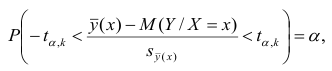
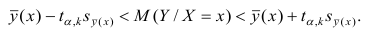
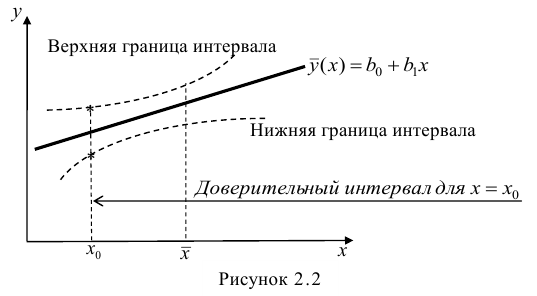
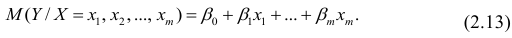
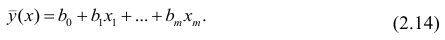
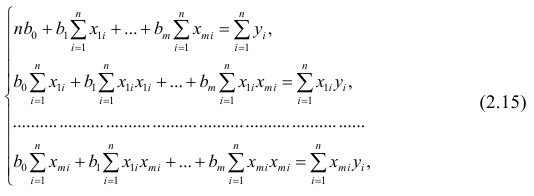
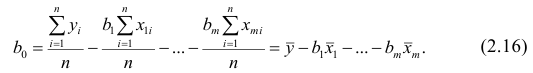
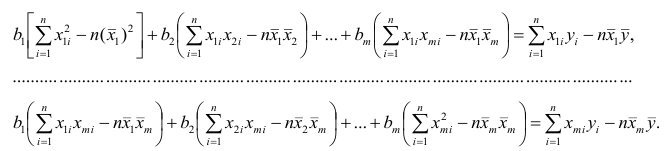
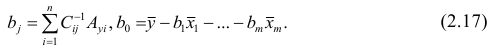
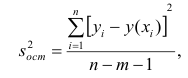
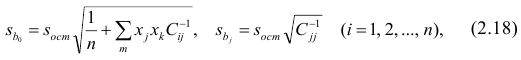
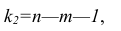
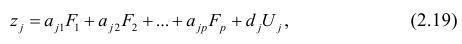
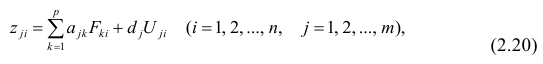
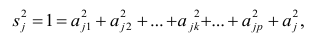
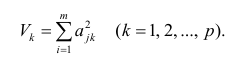
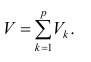
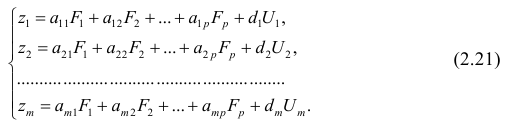
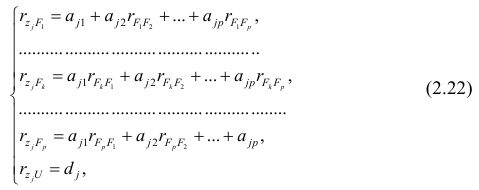
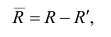

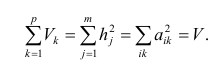
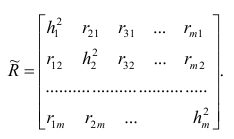


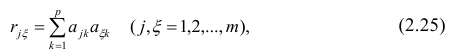

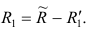

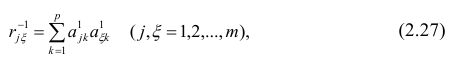
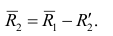
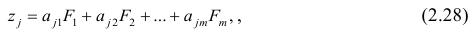
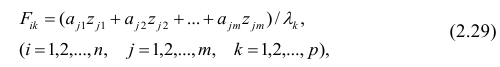
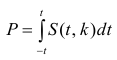
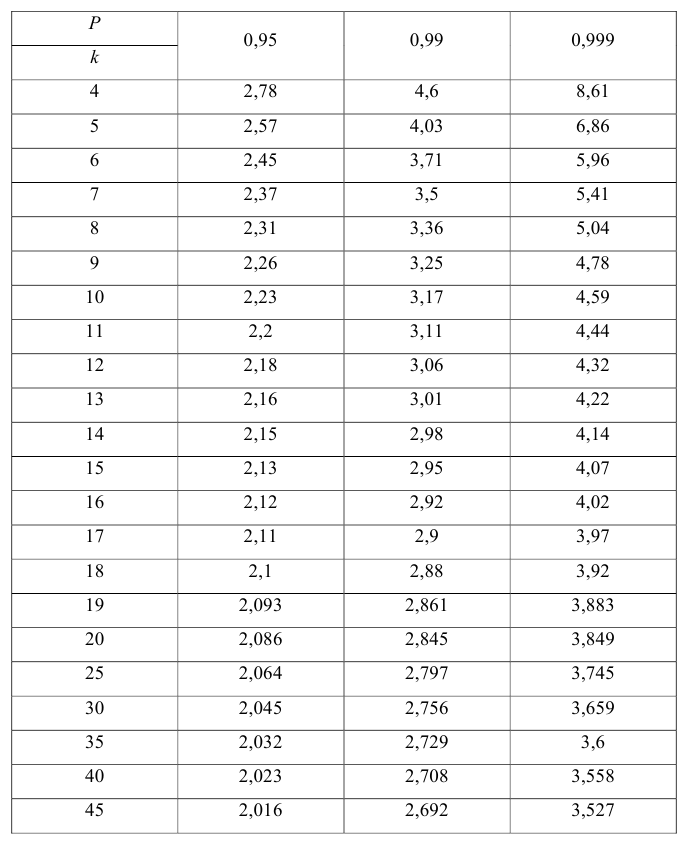
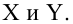
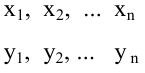
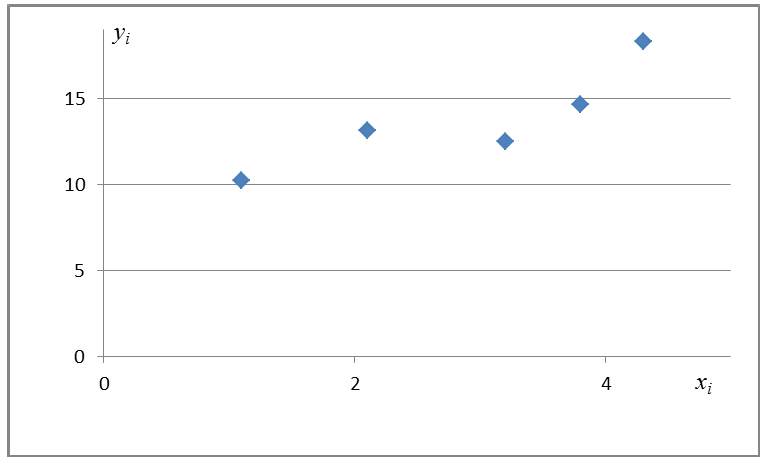
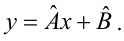
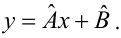
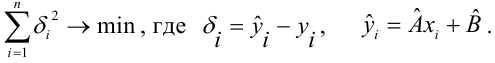
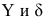 подчинены нормальному закону распределения.
подчинены нормальному закону распределения. постоянна и не зависит от номера измерения.
постоянна и не зависит от номера измерения.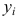 в разных точках независимы.
в разных точках независимы.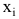 независимы, неслучайны и измеряются без ошибок.
независимы, неслучайны и измеряются без ошибок.