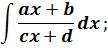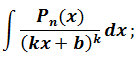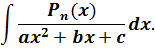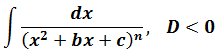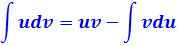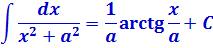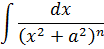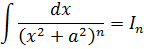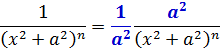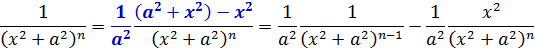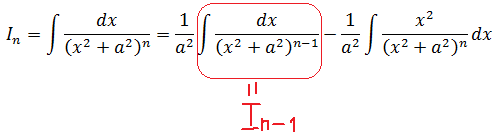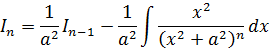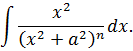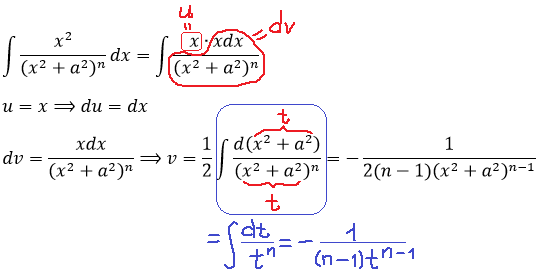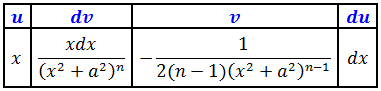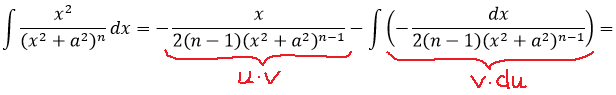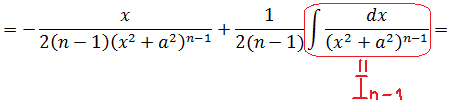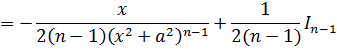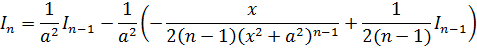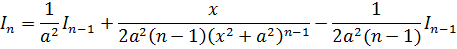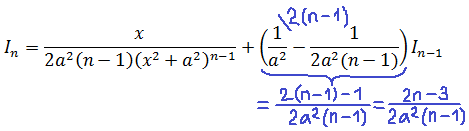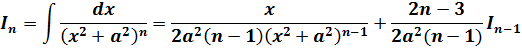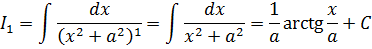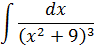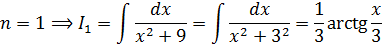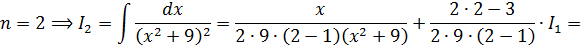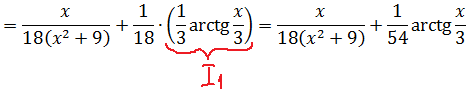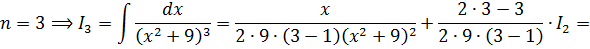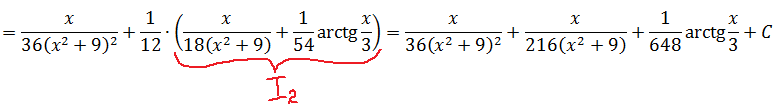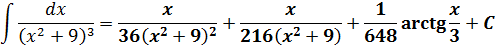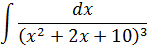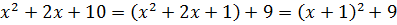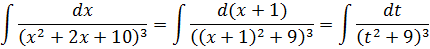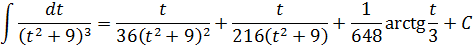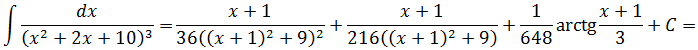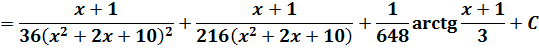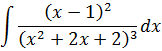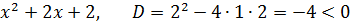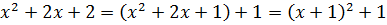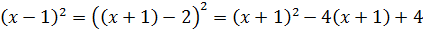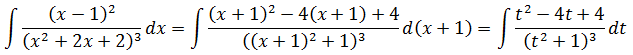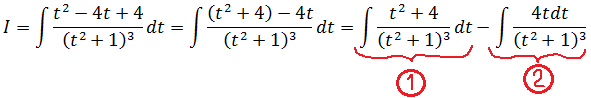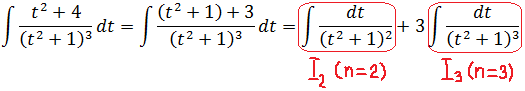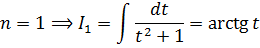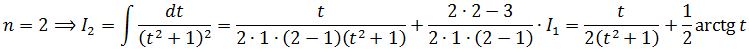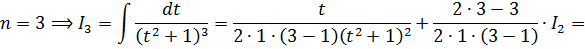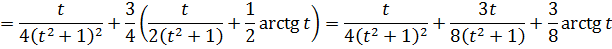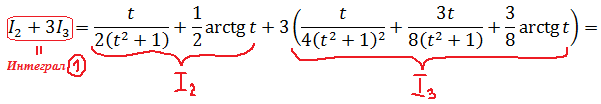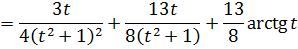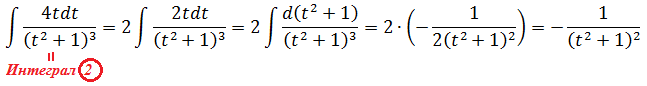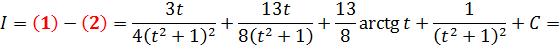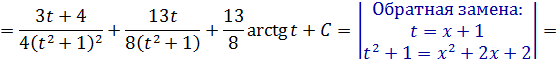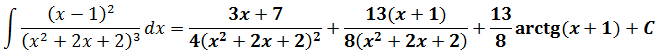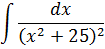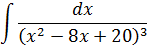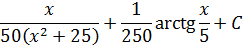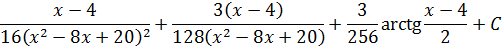Как составить рекуррентную формулу для интеграла - Исправление недочетов и поиск решений вместе с Examum.ru

Рекуррентные формулы

В этом пункте мы
рассмотрим несколько примеров, в которых
с помощью интегрирования по частям
получаются рекуррентные формулы для
определенных интегралов.

1.22.
Вычислим интеграл

,
где n –
натуральное число.

Решение.
Разложение подынтегральной функции по
формуле бинома Ньютона приводит к
громоздким выкладкам. Проще вывести
рекуррентную формулу. Представим
интеграл I_n
в виде

–

.

Последний интеграл
проинтегрируем по частям:

=
=

=

.

Таким образом,

I_n
=

.

Отсюда вытекает

I_n=

I_n_-1.

Очевидно, что I₀= a.
Отсюда получаем

I_n
=
I_n_–1=

I_n_–2=

I_n_–3=…

…=
a²ⁿ^+1

.

Принято
обозначать 135…(2n
+
1) = (2n
+ 1)!!, 2 4

…(2
n)
= (2
n)!!.
Тогда
интеграл равен

I_n= a²ⁿ⁺¹.

Замечание.
При выводе
формулы

I_n
=

I_n_-1

нигде не использовалось
то, что n –
натуральное число. В действительности
эта формула справедлива для любых
действительных n,
отличных от 0 и от

.

1.23.
Вычислить интеграл

,
где m
– натуральное
число.

Решение.
Сделаем подстановку

:

Здесь

– интеграл из предыдущей задачи 1.22. Но

Следовательно,

Если m –
нечетное число, то полученная рекуррентная
формула сводит

поэтому при

Если

–
четное число, то рекуррентная формула
сводит

поэтому

Замечание.
С помощью подстановки

легко убедиться, что

1.24.
Вычислить интеграл

где

;
n –
натуральное число.

Решение.
Отметим прежде всего, что хотя
подынтегральная функция

не имеет смысла при

,
тем не менее, положив

,
мы получаем функцию, непрерывную на

.
Действительно,

что
легко проверяется с помощью правила
Лопиталя. Применяем формулу интегрирования
по частям:

=
–
.

Таким образом,
получаем

Отсюда вытекает

=…=
.

Так как

то окончательно
получаем

1.25. Вычислить
интеграл

где

и

–
целые неотрицательные числа.

Решение.
Вычисляем интеграл по частям:

=
=

=
+
.

Отсюда получаем

Отметим, что
полученная формула справедлива не
только для целых

,
а для всех

и

.
Если

–
натуральное число, то, применяя формулу
несколько раз, запишем

=…=
,

но

Следовательно,

=
.

Если

–
тоже целое неотрицательное число, то
отсюда получаем

=
=
=
,

где

–
число сочетаний из m
+ n
+ 1 по n.

Задачи для самостоятельного решения

Вычислить
следующие интегралы.

1.26.

;
1.27.
;
1.28.
;

1.29.
;
1.30.
;
1.31.
.

1.32.
Выяснить (не вычисляя), какой из интегралов
больше:

а)

или

;
б)

или

;

в)

или

.

1.33.
Оценить интеграл

1.34.
Доказать неравенства

1
<

< e.

1.35.
Найти производную:

а)

;
б)
;
в)

.

1.36.
Найти пределы:

а)

;
б)

.

Вычислить
интегралы (1.37)–(1.43)

1.37.

.
1.38.

.
1.39.

.

1.40.
. 1.41.
.
1.42.

;

1.43.

.

Вычислить следующие
интегралы, используя пример 1.19:

1.44.

;
1.45.

;

1.46.
.

Вычислить
следующие интегралы:

1.47.

;
1.48.
;

1.49.

;
1.50.

.

1.51.
Пусть

,
n = 3,4…

Доказать рекуррентную
формулу

+

.

1.52.
Вычислить интеграл

где m,
n –
целые неотрицательные числа.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

Источник

Учимся интегрировать рациональные дроби. Вывод полезной рекуррентной формулы для интегрирования некоторых дробей.

Ну что, друзья, продолжаем наши игры с рациональными дробями! В прошлом уроке у нас было начальное знакомство с их интегрированием и тренировка на самых простейших примерах. В этом же уроке будет ~~хирургия без наркоза~~ ээээ… нет… всего лишь формула.) Одна единственная. Но зато какая! Рекуррентная! Прошу не пугаться этого страшного названия.) Для начала прочитаем ещё разок само это красивое слово, чтобы не косячить в простой орфографии. А то будем как безграмотные шеф-повара элитных ресторанов, путающих гаспаЧо (холодный испанский томатный суп) и карпаЧЧо (блюдо из тонко-тонко нарезанного мяса, рыбы или овощей).

Ну как, аппетит прорезался? Тогда начинаем знакомиться и аккуратно выводить нашу рекуррентную формулу.

Для начала немного об устройстве рекуррентных формул вообще.

Как это ни странно, рекуррентные формулы знакомы вам ещё со школы. Прогрессии помните? Например, арифметическую? Вспомнили? Гуд.)

Как мы обычно задаём арифметическую прогрессию? Чаще всего формулой n-го члена:

a_n = a₁ + d(n-1)

Это для вас привычно. Также прогрессию можно задать просто рядом чисел. Например, так:

1, 2, 3, 4, 5, …

А ещё можно задать общий член арифметической прогрессии через предыдущий член! Например, вот так:

a_n = a_n-1 + 2 (n = 2, 3, 4, …)

a₁ = 3

Такой не очень привычный способ задания арифметической прогрессии называется рекуррентным способом. Здесь a_n — n-й член прогрессии. Тот, который нас интересует. А вот a_n-1 — это и есть предыдущий (n-1)-й член нашей прогрессии. Под номером n-1. На единичку меньше, чем n. Скажем, если интересующий нас член a_n = a₁₀, то предыдущий член будет a_n-1 = a₉. Элементарно, Ватсон!

Ещё нам отдельно дан первый член a₁ = 3. Зачем? А затем, что у первого члена нет предыдущего! Именно поэтому перечисление значений n я начал с двойки, а не с единицы.

Теперь, зная первый член, можно запросто посчитать второй:

a₂ = a₁ + 2 = 3+2 = 5

Третий член можно посчитать через второй:

a₃= a₂ + 2 = 5+2 = 7

Четвёртый член можно посчитать через третий, пятый — через четвёртый, и так далее… Продолжая эту славную цепочку, можно добраться до любого интересующего нас члена. А как можно посчитать сразу, скажем, 30-й член? А никак! Пока 29-й член не узнаем, 30-й найти не сможем! В этом принципиальное отличие рекуррентной формулы от формулы n-го члена.

Страшное слово «рекуррентный» переводится на простой русский язык как «возвратный». Или, более понятно, через предыдущий (соседний). И всё.)

Возможно, кто-то скажет: «И зачем городить огород с какой-то рекуррентной формулой, когда можно сразу посчитать любой член по обычной формуле n-го члена? Чего в рекуррентной формуле хорошего? Возиться, считать последовательно все члены подряд…»

Согласен, хорошего мало. Однако, если количество рассчитываемых членов n не очень большое (скажем, три или пять), рекуррентные формулы вовсе не так уж и плохи. И именно этим фактом мы и воспользуемся в сегодняшнем уроке.

Ну вот, про рекуррентные формулы немножко поговорили. На простейшем примере принцип их работы прочувствовали. Однако основная тема нашего урока — интегрирование рациональных дробей, не так ли? Так что начнём ближе к делу. Итак!

Давайте, немножко вернёмся к прошлому уроку и вспомним, какие же дроби мы учились интегрировать в прошлый раз.

— дробно-линейные функции (числитель и знаменатель дроби — линейные конструкции)

— дроби, знаменатель которых — линейная функция (сама по себе, либо в степени), а числитель — любой многочлен

— дроби, в знаменателе которых стоит одиночный квадратный трёхчлен

И пока всё. Три вида дробей. Негусто, но уже кое что.) В первых двух типах интегралов мы тождественными преобразованиями выделяли из числителя знаменатель, раскладывали дробь в сумму более простых и последовательно интегрировали каждую из них. С квадратным трёхчленом мы расправлялись выделением полного квадрата. Вспомнили? Хорошо.)

В этом же уроке мы научимся интегрировать ещё один тип рациональных дробей с квадратным трёхчленом в знаменателе. Но у трёхчлена этого будет две важные особенности:

1. Квадратный трёхчлен дополнительно возводится в степень n;

2. Квадратный трёхчлен имеет отрицательный дискриминант. Или, что то же самое, неразложим на линейные множители.

Таким образом, постановка задачи этого урока — научиться брать интегралы вот такого типа:

В числителе dx, а в знаменателе — неразложимый квадратный трёхчлен в степени.

Что для этого сегодня нам потребуется.

1. Формула интегрирования по частям:

Кто до сих пор не в курсе, что это за закорючки такие, читайте урок: «Неопределённый интеграл. Метод интегрирования по частям». Пока не поздно. Там всё популярно изложено, нарисовано, подписано… Старался как мог.)

2. Табличный интеграл №8 из нашей сводной таблицы:

Вот, собственно, и весь инструментарий. Теперь ближе к делу.

Для большей простоты изложения материала я сейчас проведу некоторые упрощения в нашем квадратном трёхчлене x² + bx + c. А именно:

— обнулю коэффициент b (b = 0),

— свободный член c переобозначу как a².

Все эти превращения я проделал чисто с целью подчеркнуть неразложимость нашего квадратного трёхчлена и упростить дальнейшие выкладки.

А сейчас я начну брать вот такой интересный интеграл:

Для начала я обозначу искомый интеграл латинской буквой I, но c индексом n (n-й степени). Вот так:

А теперь начинаем наше интегрирование. Первым делом я выделю в подынтегральной функции 1/(x²+a²)ⁿзнаменатель из числителя. Вы спросите: «Как же из единички можно выделить выражение (x²+a²)ⁿ ?» А вот так (расписываю по шагам):

1. Умножаем и тут же делим всю нашу дробь на а²:

2. В числителе прибавляем и тут же вычитаем слагаемое x², а затем почленно делим числитель на знаменатель, раскладывая дробь на две. Это дело уже знакомо:

А теперь подставляем всё это добро в наш интеграл вместо исходной дроби. Константу 1/а² сразу везде выносим за знак интеграла. Получаем:

Первый интеграл (тот, что обведён красным) получен из исходного интеграла понижением показателя степени n на единичку: (n-1). Его, для краткости, можно переобозначить как I_n-1. Итого пока что имеем следующее:

И теперь наша задача — взять оставшийся второй интеграл:

А его мы будем брать по частям!)

Те, кто в танке, прочитали соответствующий материал про части? Ну, ладно, я предупредил! Поехали!

Для начала разбиваем наше подынтегральное выражение на произведение функции u и дифференциала dv. В качестве функции u я предлагаю взять просто множитель х. Ну, а в качестве dv берём оставшуюся часть подынтегрального выражения. Также до кучи ищем v и du.

Вот так:

Кто не понял, как именно получена функция v, тот, к сожалению, плохо освоил интегрирование подведением под знак дифференциала. Перечитайте соответствующий урок, пока не поздно!

Отлично. Великолепная четвёрка u—dv—v—du получена, заполняем теперь нашу стандартную анкету:

Несуразные выражения, конечно. А что делать… Теперь интегрируем по частям. Имеем в виду, что весь процесс интегрирования у нас проходит по переменной икс. Стало быть, буковка n — это такая же константа, как и слагаемое a². И поэтому множитель 2(n-1), сидящий в знаменателе функции v, можно целиком отправить за знак интеграла.

Вот как выглядит весь процесс интегрирования:

Отлично. Чем же хорош данный результат? А тем, что наш второй интеграл также оказался выраженным через интеграл степенью ниже I_n-1! Подставляем теперь этот результат в наше исходное равенство вместо второго интеграла, раскрываем все скобки и упрощаем:

Вот он, наш окончательный результат. Та самая рекуррентная формула понижения степени!

Почему данная формула носит название рекуррентной, да ещё и понижения степени? Разбираемся.

Для начала разберёмся с понижением степени. Ибо проще это. В чём суть: слева в формуле стоит интеграл степени n (I_n). А вот справа стоит тот же самый интеграл, но уже степени на единичку ниже (I_n-1). Под степенью здесь, конечно же, подразумевается не степень интеграла как такового, а всего лишь степень знаменателя подынтегральной дроби. Это и так понятно, я думаю.) Зачем же нам понижать степень интеграла (знаменателя)? Да потому, что с маленькой степенью работать всяко проще, чем с большой! И не только в интегралах. В тригонометрии, например. Там тоже есть свои формулы понижения степени. Например, для выражений типа sinⁿx, cosⁿx и тому подобных. Полистайте соответствующую литературу (или Гугл)).

Чем примечательна эта, казалось бы, громоздкая и малопонятная формула? А тем, что она позволяет свести исходный интеграл I_n к интегралу степенью ниже I_n_-1. Именно поэтому она и называется формулой понижения степени.

Например, если n=3, то интеграл I₃ можно сначала свести к интегралу I₂, а I₂, в свою очередь, уже свести к I₁. Одним словом, устроена эта формула по принципу матрёшки. Или домино. Вот и вся суть понижения степени.)

Однако, реально работать с этой формулой надо немного по-другому. И теперь мы плавненько переходим ко второй части названия данной формулы — почему же она именуется ещё и рекуррентной. А вот почему. Дело всё в том, что для получения исходного интеграла I_n нам надо знать предыдущий интеграл I_n-1.

Для поиска I_n-1 надо знать I_n-2.

Для I_n-2 надо знать I_n-3…

И так далее по снижающейся траектории приходим к выводу, что для поиска интеграла I₂ надо знать интеграл I₁.

Вопрос на засыпку: а что собой представляет интеграл 1-й степени I₁? Ну, берём, подставляем единичку вместо n в наш исходный интеграл и смотрим… Да! Табличный интеграл №8, с арктангенсом:

И именно от него мы и начинаем плясать. А дальше — одеваем нашу матрёшку: по интегралу I₁ считаем I₂, по найденному I₂ считаем I₃ — и так далее, пока не доберёмся до исходного интеграла I_n. Того, который дан в примере. Именно так и нужно работать с данной формулой.) И именно по этой причине формула и называется рекуррентной.

Вот мы и разобрались полностью с названием и сутью данной формулы.

Да, я не спорю, формула достаточно страшная и громоздкая. Ничего не поделать: мы тоже с вами всё-таки уже далеко не школьники, а вовсю изучаем высшую математику, правда ведь?

Ну что, посмотрим на рекуррентную формулу в действии?

Пример 1

Найти неопределённый интеграл:

Анализируем подынтегральную функцию:

n = 3,

a²= 9, т.е. а=3.

Исходная степень квадратного трёхчлена в знаменателе — тройка. Значит, наше интегрирование будет происходить в три шага.

Шаг 1

Для интегрирования этой нехорошей дроби плясать начинаем от интеграла 1-й степени (I₁, n=1). Он табличный:

Шаг 2

Вычисляем теперь интеграл 2-й степени (I₂, n=2), используя рекуррентную формулу и результат предыдущего шага I₁.

Выпишем нашу формулу, дабы иметь её перед глазами:

И теперь просто берём и аккуратно подставляем в формулу вместо n двойку, вместо a² — девятку, а вместо I_n-1 — наш интеграл 1-й степени I₁.

И считаем:

Есть.)

Шаг 3

Вот мы и добрались до последнего третьего шага. Считаем теперь интеграл 3-й степени I₃. Для этого подставляем в рекуррентную формулу теперь уже n=3 и результат второго шага I₂. И прибавляем (теперь уже) константу С. Вот так:

Всё. Интегрирование завершено. Вот наш окончательный ответ:

Продифференцируйте, проверьте!

Данная рекуррентная формула позволяет успешно интегрировать и более крутые дроби с квадратными трёхчленами в степенях. Например, такую:

Пример 2

В подобных примерах перед тем как что-то интегрировать, первым делом проверяем разложимость квадратного трёхчлена на множители. Считаем дискриминант:

D = 2²— 4∙1∙10 = 4–40 = -36 <0

Дискриминант отрицательный. Стало быть, наш трёхчлен действительных корней не имеет и неразложим на более простые множители. Ладно.)

Что делать, если трёхчлен (вдруг) окажется разложим на множители? Такие примеры будут разбираться дальше. В следующих уроках.)

Что делать дальше? А дальше — запоминаем:

Если под интегралом дана дробь, содержащая квадратный трёхчлен, то первым делом выделяем из трёхчлена полный квадрат! А дальше — видно будет…

Вот и выделяем. Здесь это совсем просто:

Теперь, кстати, отчётливо видно, почему дискриминант получился отрицательным: если к неотрицательному выражению (х+1)² прибавить ещё девятку, то получится всяко положительное число. Но не ноль!

А дальше дело за малым. Подводим скобку (х+1) под дифференциал и заменяем эту самую скобку новой буквой t:

Интеграл свёлся к виду I_n. Берущемуся по рекуррентной формуле (n=3, a²=9).

А дальше я предлагаю немного схитрить и нагло скоммуниздить уже готовый результат предыдущего примера:

Найдите, как говорится, 7 отличий:

Ну да, вместо икса везде буква t появилась. Ну и что? Мы же знаем, что любому интегралу (даже самому навороченному) по барабану, что там за буква стоит — икс или тэ. Лишь бы везде одна и та же стояла — в функции и под дифференциалом.)

Вспоминаем, что наше t — это скобка (х+1) и смело записываем окончательный ответ:

Вот такие дела.)

Разумеется, заучивать наизусть данную рекуррентную формулу не нужно, а вот знать, как её вывести (в случае чего) и, главное, уметь применять – очень полезно.

Что делать, если в числителе — не dx, а многочлен?

Пример 3

Ну, если попался такой монстр, то тут, как говорится, ваше дело — труба… Ибо интегралы от таких дробей (в знаменателе неразложимый трёхчлен в степени n + ещё и многочлен в числителе) — самые скверные, да. Либо вы — студент мехмата, ВМК или физтеха, либо же попали под горячую руку преподавателя. Так что разберу и такой пример. На всякий пожарный. Чтобы быть во всеоружии.)

Как ни странно, и тут тоже можно обойтись БЕЗ метода неопределённых коэффициентов! Но придётся порядком попотеть с этой самой рекуррентной формулой из-за куба в знаменателе. Так что ближе к делу.

Первым делом разберёмся с квадратным трёхчленом в знаменателе:

Трёхчлен неразложим на множители, да сам ещё и в кубе. Дело попахивает рекуррентной формулой… Неохота с ней возюкаться, но ничего не поделать, да.

Выделяем полный квадрат в знаменателе:

Так, в скобках образовалось х+1. Теперь надо эту же скобку выделить в числителе. Зачем? А затем, чтобы можно было подвести эту скобку под дифференциал, ввести новую переменную t и немного упростить пример.

Процедура уже знакома:

Есть. Числитель дроби разложен по степеням (х+1). Теперь подводим скобку (х+1) под дифференциал и вводим замену х+1 = t:

Дальше полученный интеграл я почленным делением разобью на два. И для краткости обозначу его буквой I. Вот так:

Или, в краткой записи: I = (1) — (2)

Почему именно такое разбиение я выбрал, станет ясно дальше. Разбираемся теперь поочерёдно с каждым из интегралов (1) и (2). Для начала с первым. Вот тут уже начинается хардкор, да… Для успешной расправы с ним первым делом выделим в числителе знаменатель t²+1 и опять разобьём интеграл на два:

Хардкор данного этапа решения заключается в том, что оба полученных интеграла… берутся по рекуррентной формуле, да!) Дело в том, что наша конструкция, если как следует присмотреться, имеет вид I₂+ 3I₃. В обозначениях рекуррентной формулы. В первом интеграле в знаменателе сидит квадрат, во втором — куб. Всё логично. Запускаем в дело нашу формулу. Шагов нам потребуется всего три. Поскольку максимальная степень знаменателя — третья. Вперёд! Уже без лишних комментариев:

Шаг 1

Шаг 2

Шаг 3

Готово! Самая сложная часть примера осталась позади.) Теперь составляем нужное нам выражение I₂ + 3I₃ и получаем результат интеграла под цифрой (1).

Естественно, раскрываем скобки, приводим подобные и упрощаем, где надо (складываем арктангенсы и дроби с одинаковыми знаменателями). А, чтобы народ не заблудился в громоздких выкладках, я подпишу всё то, что мы подставляем и получаем:

Ну вот. Первый (и самый трудоёмкий) интеграл благополучно взят. А взять оставшийся второй интеграл (2) — пара пустяков. Ибо он берётся безо всяких ухищрений обычным подведением знаменателя под дифференциал, сводясь к степенной функции.)

Что ж, оба промежуточных интеграла успешно взяты. Вот и финишная прямая! Вычитаем теперь интеграл (2) из интеграла (1), приводим подобные, обратно заменяем переменную t на x+1, прибавляем константу С и получаем окончательный ответ нашего жуткого примера:

Окончательно:

Вот так вот распутываются сложные примеры. Самое главное — аккуратность и предельное внимание, чтобы не запутаться в знаках, скобках и многочисленных коэффициентах и постоянно держать в уме, что именно вы вычисляете или подставляете.

Кстати, вы не поверите, но я взял черновик, продифференцировал этот длинный ответ, привёл ВСЁ к общему знаменателю, упростил и… Аллилуйя! Получилась исходная подынтегральная функция!)

Разумеется, разбор конкретного сложного примера — бестолковое дело, прямо скажем. Ибо не попадётся он. А вот разъяснить на конкретном примере, куда надо стремиться во всех подобных ситуациях — совсем другое дело, согласитесь! Кстати, открою приятный бонус: разобранные типы интегралов от дробей в этом уроке и в предыдущем — это вся необходимая база для нахождения интегралов от любых рациональных дробей. Да-да, любых! Дело в том, что интеграл от любой, даже очень навороченной, рациональной дроби будет сводиться к комбинации интегралов от уже рассмотренных типов дробей — с линейным многочленом или неразложимым квадратным трёхчленом в знаменателе. Все подробности — в следующих уроках по интегрированию рациональных дробей!

Ну что ж, ладно, отмучились на сегодня!

А теперь пара несложных примеров для самостоятельного решения.

Пользуясь рекуррентной формулой понижения степени, найти неопределённые интегралы от рациональных дробей:

Ответы:

Разумеется, надо не просто тупо сдуть готовые ответы, а получить эти ответы! Иначе весь этот урок впустую. Уважьте мой труд.) До скорых встреч!

Источник

Интегрирование по частям

Интегрирование по частям в неопределенном интеграле

Метод вычисления интегралов, называемый интегрированием по частям, основан на правиле дифференцирования произведения.

Пусть u=u(x),~v=v(x) — функции, дифференцируемые на некотором промежутке . Тогда, как известно, дифференциал произведения этих функций вычисляется по формуле

d(uv)=u,dv+v,du,.

Взяв неопределенный интеграл от обеих частей этого равенства, получим:

int d(uv)=intbigl(u,dv+v,dubigr). Так как int d(uv)=uv+C , а intbigl(u,dv+v,dubigr)= int u,dv+int v,du ,

то получаем: uv+C=int u,dv+int v,du , откуда int u,dv=uv+C-int v,du .

Поскольку textstyle{int v,du} уже содержит произвольную постоянную, в правой части полученного равенства можно опустить и записать равенство в виде

int u,dv=uv-int v,du,.

(1)

Полученная формула называется формулой интегрирования по частям.

При выводе формулы (1) мы предположили, что функции u(x) и v(x) дифференцируемы. Этой формулой обычно пользуются в тех случаях, когда подынтегральное выражение v,du проще, чем подынтегральное выражение u,dv .

Заметим, что одно и то же подынтегральное выражение можно различными способами записать в виде u,dv . Например,

$x^4sin{x},dx=x^4cdot d(-cos{x})=sin{x}cdot d!left(frac{x^5}{5}right)= x^2sin{x}cdot d!left(frac{x^3}{3}right)$

и т. д. Поэтому иногда приходится испытывать различные формы такой записи, прежде чем метод приведет к успеху. Обычно стараются подынтегральное выражение разбить на части {u} и так, чтобы вид {v} был не сложнее, чем вид {v'} , а вид {u'} проще, чем вид {u} . В частности, полезно иметь в виду, что для таких функций, как y=ln{x}, y=x^n, y=operatorname{arctg}x, y=operatorname{arcctg}x , производные имеют вид более простой, чем сами функции. Поэтому в большинстве случаев эти функции удобно принимать за функцию {u} .

Пример 1. Вычислим по частям неопределенный интеграл int xcos{x},dx .

Решение. Положим u=x,~dv=cos{x},dx . Тогда du=dx,~ v=sin{x} .

Используя формулу интегрирования по частям (1), получаем:

int xcos{x},dx=xsin{x}-intsin{x},dx=xsin{x}+cos{x}+C.

Замечание. При нахождении {v} не пишут промежуточную произвольную постоянную C_1 , так как она не оказывает влияния на окончательный результат.

Пример 2. Вычислим интеграл $int x^2sin{x},dx$ с помощью метода интегрирования по частям.

Решение. Положим $u=x^2,~dv=sin{x},dx$ . Тогда du=2x,dx,~v=-cos{x} .

Используя формулу (1), получим:

$int x^2sin{x},dx=-x^2cos{x}+2int xcos{x},dx.$

(2)

Чтобы вычислить полученный в правой части равенства (2) интеграл, приходится снова использовать метод интегрирования по частям. Получим (см. пример 1):

$int xcos{x},dx=xsin{x}+cos{x}+C_1.$

Возвращаясь к исходному интегралу и воспользовавшись промежуточным равенством (2), окончательно получаем:

$int x^2sin{x},dx=-x^2cos{x}+ 2(xsin{x}+cos{x}+C_1)= 2xsin{x}+(2-x^2)cos{x}+C~~(C=2C_1).$

Пример 3. Вычислим неопределённый интеграл $int x^3ln{x},dx$ .

Решение. В данном случае удобнее за и принять не степенную функцию, как в предыдущих примерах, а логарифмическую функцию.

Положим $u=ln{x},~~dv=x^3,dx$ . Тогда $du=frac{1}{x},dx,~~ v=int x^3,dx=frac{x^4}{4},.$ .

Используя формулу (1), будем иметь:

$begin{aligned}int x^3ln{x},dx&= frac{x^4}{4}ln{x}-intfrac{x^4}{4} cdotfrac{1}{x},dx= frac{x^4}{4}ln{x}-frac{1}{4}int x^3,dx=\ &=frac{x^4}{4} ln{x}-frac{1}{4}!left(frac{x^4}{4}+C_1right)= frac{x^4}{4}ln{x}-frac{x^4}{16}+C. end{aligned}$

Пример 4. Вычислим $int e^xsin{x},dx$ .

Решение. В данном случае под знаком интеграла содержится произведение двух функций e^x и sin{x} . Производная и первообразная каждой из этих функций не проще самой функции. Это значит, что в данном случае за и можно принять любую из функций $e^x,~sin{x}$ .

Положим $u=e^x,~~dv=sin{x},dx$ . Тогда $du=e^x,dx,~~ v=-cos{x},dx$ .

Преобразуем данный интеграл, воспользовавшись формулой (1):

$int e^xsin{x},dx= -e^xcos{x}+intcos{x}cdot e^x,dx.$

В правой части получили интеграл того же вида, что и данный. Для его вычисления применим метод интегрирования по частям, снова взяв за {u} показательную функцию:

$u=e^x,~~dv=cos{x},dx$ . Тогда $du=e^x,dx,~~v=sin{x}$ .

Таким образом,

$int e^xsin{x},dx= -e^xcos{x}+e^xsin{x}-int e^xsin{x},dx.$

(3)

В правой части равенства (3) содержится точно такой же интеграл, что и в левой части, но с другим знаком. Из равенства (3) получаем:

$2int e^xsin{x},dx=e^xsin{x}-e^xcos{x}+C_1$

и далее:

$int e^xsin{x},dx=frac{1}{2},e^x (sin{x}-cos{x})+C~,left(C= frac{C_1}{2}right)!.$

Замечание. После переноса интеграла в левую часть равенства (3) надо оставить в правой части произвольную постоянную C_1 , неявно содержащуюся в записи интеграла.

Интегрирование по частям в определенном интеграле

Для определенного интеграла формула интегрирования по частям принимает следующий вид:

$intlimits_{a}^{b}u,dv=Bigl.{uv}Bigr|_{a}^{b}-intlimits_{a}^{b}v,du.$

(4)

В самом деле, если

int u,dv=F(x)+C_1,qquad int v,du=Phi(x)+C2,

то по формуле интегрирования по частям для неопределенного интеграла имеем:

F(x)=u(x)v(x)-Phi(x)+C.

Поэтому

F(b)=u(b)v(b)-Phi(b)+C и F(a)=u(a)v(a)-Phi(a)+C .

Значит, F(b)-F(a)=bigl(u(b)v(b)-u(a)v(a)bigr)-bigl(Phi(b)-Phi(a)bigr) , а это и есть формула (4).

Пример 5. Вычислить по частям определённый интеграл $intlimits_{1}^{2}x,e^x,dx$ .

Решение. Положим u=x,~~dv=e^x,dx . Тогда du=dx,~~v=e^x .

Воспользовавшись формулой (4), получим:

$intlimits_{1}^{2}x,e^x,dx= Bigl.{x,e^x}Bigr|_{1}^{2}- intlimits_{1}^{2} e^x,dx= 2cdot e^2-1cdot e^1-Bigl.{e^x}Bigr|_{1}^{2}= 2e^2-e-(e^2-e)=e^2.$

Рекуррентные формулы: вывод интегрированием по частям

Метод интегрирования по частям применяется в ряде случаев для вывода рекуррентных (возвратных) формул. Рассмотрим примеры вывода рекуррентных формул как в случае неопределенного, так и в случае определенного интеграла,

Пример 6. Вычислим $intfrac{dx}{(a^2+x^2)^n}~ (n=1,2,3,ldots)$ .

Решение. Введем обозначение $I_k=intfrac{dx}{(a^2+x^2)^k}$ .

Положим $u=frac{1}{(a^2+x^2)^n},~dv=dx$ . Тогда $du=-n(a^2+x^2)^{-n-1} cdot2x,dx=-frac{2nx,dx}{(a^2+x^2)^{n+1}},~v=x$ .

Воспользовавшись формулой (1), получим:

$I_n=intfrac{dx}{(a^2+x^2)^n}= frac{x}{(a^2+x^2)^n}+ 2nintfrac{x^2,dx}{(a^2+x^2)^{n+1}},.$

(5)

Преобразуем интеграл, содержащийся в правой части равенства (5), следующим образом:

$intfrac{x^2,dx}{(a^2+x^2)^{n+1}}= intfrac{(a^2+x^2)-a^2}{(a^2+x^2)^{n+1}},dx= intfrac{dx}{(a^2+x^2)^n}- a^2intfrac{dx}{(a^2+x^2)^{n+1}}=I_n-a^2I_{n+1}.$

Подставим полученное выражение в формулу (5):

$I_n=frac{x}{(a^2+x^2)^n}+2n(I_n-a^2I_{n+1}).$

Из этого равенства находим:

$I_{n+1}=frac{2n-1}{2na^2},I_n+frac{1}{2na^2}cdotfrac{x}{(a^2+x^2)^n},.$

(6)

Полученная рекуррентная формула (6), как бы возвращая нас назад от n+1 к {n} позволяет свести вычисление интеграла с индексом n+1 к вычислению интеграла с меньшим индексом {n} .

Пусть, например, нужно вычислить интеграл $intfrac{dx}{(a^2+x^2)^2}$ . Воспользуемся рекуррентной формулой (б). В данном случае n+1=2 , следовательно, n=1 . Имеем:

$I_2=frac{1}{2a^2},I_1+frac{1}{2a^2}cdotfrac{x}{a^2+x^2},,$

то есть

$I_2=intfrac{dx}{(a^2+x^2)^2}= frac{1}{2a^2}intfrac{dx}{a^2+x^2}+ frac{1}{2a^2}cdotfrac{x}{a^2+x^2}= frac{1}{2a^2}!left(frac{1}{a}operatorname{arctg} frac{x}{a}+ frac{x}{a^2+x^2}right)+C.$

Для определенных интегралов рекуррентные формулы часто упрощаются за счет того, что при подстановке пределов интегрирования {a} и {b} произведение u(x)v(x) обращается в нуль.

Пример 7. Вычислить определённый интеграл от тригонометрической функции $intlimits_{0}^{pi/2}sin^nx,dx~(n=1,2,3,ldots)$ .

Решение. Введем обозначение $I_n=intlimits_{0}^{pi/2}sin^nx,dx$ и положим

$u=sin^{n-1}x,~~dv=sin{x},dx$ . Тогда $du=(n-1)sin^{n-2}xcos{x},dx,~~ v=-cos{x},.$

Воспользовавшись формулой (4), получим:

$begin{aligned}I_n&=intlimits_{0}^{pi/2}sin^nx,dx= intlimits_{0}^{pi/2} sin^{n-1}xsin{x},dx= Bigl.{-cos{x}sin^{n-1}x}Bigr|_{0}^{pi/2}+ (n-1)intlimits_{0}^{pi/2} sin^{n-2}xcos^2x,dx=\ &=-left(cosfrac{pi}{2}sin^{n-1}frac{pi}{2}-cos0sin^{n-1}0right)+ (n-1)intlimits_{0}^{pi/2} sin^{n-2}x(1-sin^2x),dx=\ &=0+(n-1)intlimits_{0}^{pi/2} sin^{n-2}x,dx- (n-1)intlimits_{0}^{pi/2} sin^{n}x,dx=(n-1)I_{n-2}-(n-1)I_n. end{aligned}$

Итак, $I_n=(n-1)I_{n-2}-(n-1)I_n$ . Это значит, что

$I_n=frac{n-1}{n},I_{n-2},$

(7)

то есть

$intlimits_{0}^{pi/2} sin^{n}x,dx= frac{n-1}{n}intlimits_{0}^{pi/2} sin^{n-2}x,dx,.$

Таким образом, рекуррентная формула (7) позволяет свести вычисление интеграла $intlimits_{0}^{pi/2}sin^{n}x,dx$ к вычислению интеграла, где sin{x} имеет более низкую степень. Например,

$I_3=intlimits_{0}^{pi/2}sin^{3}x,dx= frac{3-1}{3},I_1= frac{2}{3}intlimits_{0}^{pi/2}sin{x},dx= frac{2}{3}Bigl.{-cos{x}}Bigr|_{0}^{pi/2}= -frac{2}{3}!left(cosfrac{pi}{2}-cos0right)= frac{2}{3},.$

Математический форум (помощь с решением задач, обсуждение вопросов по математике).

Кнопка "Поделиться"

Если заметили ошибку, опечатку или есть предложения, напишите в комментариях.

Источник