Можно представить, что рекурсивная функция уже написана. При решении задачи использовать её как уже написанную. После этого убедиться, что существуют граничные условия, при которых рекурсия остановится.
Например, пусть у нас есть следующая задача: нужно найти число возможных способов размена 100 рублей монетами 10 рублей, 5 рублей, 2 рубля и 1 рубль.
То есть нам надо написать функцию f(сумма, набор_монет), которую мы сможем вызвать так: result = f(100, [10, 5, 2, 1]). Первый аргумент — сумма, которую нам надо разменять, а второй — список из уникальных монет, с помощью которых можно представить эту сумму.
Представим, что функция f уже написана. Как теперь мы можем ей воспользоваться? Ключевой момент: придумаем способ разделения возможных вариантов, желательно простой.
Например, заметим, что 100 рублей можно разменять как с использованием десятирублёвой монеты, так и без использования десятирублёвой монеты. Эта идея, можно сказать, и есть решение задачи.
Сумма этих вариантов будет равна искомому числу. Тогда реализацию функции f можно записать как сумму рекурсивных вызовов самой себя с «укороченными» аргументами: f(90, [1, 2, 5, 10]) + f(100, [1, 2, 5]).
f(90, [1, 2, 5, 10]) — мы как бы «забрали» десятирублёвую монету из 100, но не ограничиваем дальнейший выбор монет;
f(100, [1, 2, 5]) — мы ничего не забрали из суммы, но ограничили набор монет.
Оба слагаемых вызываются рекурсивно. При этом видно, что количество вариантов будет уменьшаться с каждым рекурсивным вызовом.
Остаётся добавить граничные условия, чтобы функция не вызывалась бесконечно. Для этого нужно определить, при каких аргументах возвращать 1, а при каких — 0.
Рекурсия — одно из самых распространенных алгоритмических понятий. Если говорить просто, то рекурсивным алгоритм становится, если вызывает сам себя.
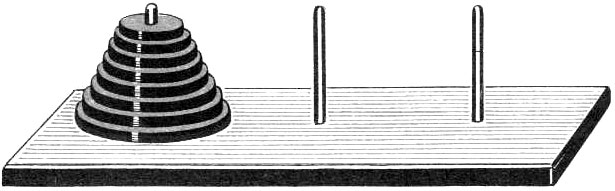
Головоломка Ханойские башни состоит из трёх стержней, пронумеруем их слева направо: 1, 2 и 3. Также в головоломке используется стопка дисков с отверстием посередине. Радиус дисков уменьшается снизу вверх. Изначально диски расположены на левом стержне (стержень 1), самый большой диск находится внизу. Диски в игре перемещаются по одному со стержня на стержень. Диск можно надеть на стержень, только если он пустой или верхний диск на нём большего размера, чем перемещаемый. Цель головоломки — перенести все диски со стержня 1 на стержень 3. Попробуйте нашу интерактивную версию Ханойских башен и узнайте, как переместить все диски с одного стержня на другой.
Ханойские башни: Вывод списка действий, необходимых для решения головоломки «Ханойские башни».
- Входные данные: Целое число $n$.
- Выходные данные: Последовательность ходов для решения головоломки «Ханойские башни» из $n$ дисков.
Решить головоломку с одним диском легко — просто переместите его на правый стержень. Головоломка на два диска ненамного сложнее. Сначала нужно переместить маленький диск на стержень посередине, а большой — на стержень справа. Затем переместить маленький диск на большой на правом стержне.
Версия на три диска чуть сложнее, но и ее можно решить с помощью следующих семи шагов:
- Переместить диск со стержня 1 на стержень 3
— Переместить диск со стержня 1 на стержень 2
— Переместить диск со стержня 3 на стержень 2
— Переместить диск со стержня 1 на стержень 3
— Переместить диск со стержня 2 на стержень 1
— Переместить диск со стержня 2 на стержень 3
— Переместить диск со стержня 1 на стержень 3
Теперь давайте посчитаем, сколько шагов потребуется для решения версии на четыре диска. Нам нужно обязательно переместить самый большой диск, но для этого придётся сперва поместить все остальные диски на пустой стержень. Если у нас не три диска, а четыре, то нужно переложить три верхних диска на пустой стержень (7 действий), а затем переместить самый большой диск (1 действие). Теперь нужно снова переместить три диска с «временного» стержня на самый большой диск (еще 7 действий). Весь процесс будет состоять из $7 + 1 + 7 = 15$ действий.
Обобщим. Чтобы переместить $n$ дисков с левого стержня на правый, сначала необходимо переместить $n — 1$ дисков на стержень посередине. Затем, когда диск под номером $n$, самый большой, оказывается на правом стержне, нужно переместить на него оставшиеся диски со стержня посередине. Чтобы переместить $n-1$ дисков со стержня посередине направо, нужно сначала переместить $n-2$ дисков на стержень слева, затем переместить $(n-1)$-й диск вправо, потом переместить $n-2$ дисков с левого стержня на правый и так далее.
На первый взгляд задача «Ханойские башни» может показаться сложной. Тем не менее данный рекурсивный алгоритм находит нужные перемещения дисков всего за 8 строк!
HanoiTowers(n,fromPeg,toPeg)
if n = 1:
output “Move disk from peg fromPeg to peg toPeg”
return
unusedPeg = 6 - fromPeg - toPeg
HanoiTowers(n−1,fromPeg,unusedPeg)
output “Move disk from peg fromPeg to peg toPeg”
HanoiTowers(n−1,unusedPeg,toPeg)
Переменные $fromPeg, toPeg$ и $unusedPeg$ указывают на три разных стержня. Таким образом, HanoiTowers(n, 1, 3) перемещает диски ($n$ шт.) с первого стержня на третий. Переменная $unusedPeg$ указывает, какой из трёх стержней можно использовать для временного хранения первых ($n-1$) дисков. Обратите внимание, что $fromPeg+toPeg+unusedPeg$ всегда равняется $1+2+3 = 6$. Таким образом, значение переменной $unusedPeg$ можно определить как $6 — fromPeg — toPeg$. Представленная таблица показывает результаты $6 — fromPeg — toPeg$ для всех возможных переменных $fromPeg$ и $toPeg$.
| fromPeg | toPeg | unusedPeg |
|---|---|---|
| 1 | 2 | 3 |
| 1 | 3 | 2 |
| 2 | 1 | 3 |
| 2 | 3 | 1 |
| 3 | 1 | 2 |
| 3 | 2 | 1 |
Определив $unusedPeg$ как $6 — fromPeg — toPeg$, операторы
HanoiTowers(n−1,fromPeg,unusedPeg)
output “Move disk from peg fromPeg to peg toPeg”
HanoiTowers(n−1,unusedPeg,toPeg)
выполняют более простую задачу: они сначала перемещают $n-1$ дисков на временный стержень, затем перекладывают большой диск, а потом складывают на него оставшиеся $n-1$ дисков. Обратите внимание, что нет необходимости указывать, какой диск игрок должен переложить с $fromPeg$ на $toPeg$: перемещается всегда тот диск, что является верхним на $fromPeg$.
💡 Остановитесь и подумайте:
Сколько нужно действий, чтобы переместить $6$ дисков?
Хотя решение Ханойских башен можно уложить в 9 строк псевдокода, его выполнение займет на удивление много времени. Решение головоломки на пять дисков состоит из 31 действия. А в решении башни из сотни дисков количество действий будет больше, чем атомов на Земле. Такое резкое увеличение числа действий для HanoiTowers неудивительно. Заметим, что каждый раз, когда вызывается HanoiTowers(n, 1, 3), алгоритм дважды вызывает сам себя для перемещения $n-1$ дисков, что запускает четыре вызова для перемещения $n-2$ дисков и так далее.
Это можно проиллюстрировать с помощью рекурсивного дерева, изображенного на рис.. Вызов HanoiTowers(4, 1, 3) приводит к вызовам HanoiTowers(3, 1, 2) и HanoiTowers(3, 2, 3); каждый из них вызывает HanoiTowers(2, 1, 3), HanoiTowers(2, 3, 2) и HanoiTowers(2, 2, 1), HanoiTowers(2, 1, 3) и так далее. Каждый вызов подпрограммы HanoiTowers занимает определенное время. Мы хотим узнать, сколько времени уйдёт на такой алгоритм.
Чтобы вычислить время выполнения HanoiTowers размера $n$, мы введём в рассмотрение функцию $T(n)$ — количество перемещений дисков, которые выполняет HanoiTowers(n). Получается следующее уравнение:
$$
T (n) = 2 cdot T (n — 1) + 1 , .
$$
Начиная с $T (1) = 1$, это рекуррентное соотношение задаёт последовательность:
$$
1, 3, 7, 15, 31, 63,
$$
и так далее. Мы можем вычислить $T (n)$, прибавив 1 с обеих сторон и обнаружив, что
$$
T (n) + 1 = 2 cdot T (n — 1) + 1 + 1 = 2cdot(T (n — 1) + 1) , .
$$
Если мы введём новое обозначение, $U(n) = T (n) + 1$, то $U(n) = 2 cdot U(n — 1)$. Таким образом, нужно решить следующее рекуррентное соотношение:
$$
U(n) = 2 cdot U(n — 1) , .
$$
Начиная с $U(1) = 2$, получаем последовательность
$$
2, 4, 8, 16, 32, 64, dotsc
$$
То есть, $U(n) = 2^n$ и $T(n) = U(n) — 1 =2^n — 1$. Следовательно, HanoiTowers(n) — экспоненциальный алгоритм.
Рекурсией называется ситуация, когда подпрограмма вызывает сама себя. Впервые сталкиваясь с такой алгоритмической конструкцией, большинство людей испытывает определенные трудности, однако немного практики и рекурсия станет понятным и очень полезным инструментом в вашем программистском арсенале.
Содержание
1. Сущность рекурсии
Процедура или функция может содержать вызов других процедур или функций. В том числе процедура может вызвать саму себя. Никакого парадокса здесь нет – компьютер лишь последовательно выполняет встретившиеся ему в программе команды и, если встречается вызов процедуры, просто начинает выполнять эту процедуру. Без разницы, какая процедура дала команду это делать.
Пример рекурсивной процедуры:
procedure Rec(a: integer);
begin
if a>0 then
Rec(a-1);
writeln(a);
end;
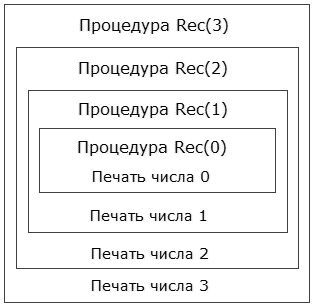
Рассмотрим, что произойдет, если в основной программе поставить вызов, например, вида Rec(3). Ниже представлена блок-схема, показывающая последовательность выполнения операторов.
Рис. 1. Блок схема работы рекурсивной процедуры.
Процедура Rec вызывается с параметром a = 3. В ней содержится вызов процедуры Rec с параметром a = 2. Предыдущий вызов еще не завершился, поэтому можете представить себе, что создается еще одна процедура и до окончания ее работы первая свою работу не заканчивает. Процесс вызова заканчивается, когда параметр a = 0. В этот момент одновременно выполняются 4 экземпляра процедуры. Количество одновременно выполняемых процедур называют глубиной рекурсии.
Четвертая вызванная процедура (Rec(0)) напечатает число 0 и закончит свою работу. После этого управление возвращается к процедуре, которая ее вызвала (Rec(1)) и печатается число 1. И так далее пока не завершатся все процедуры. Результатом исходного вызова будет печать четырех чисел: 0, 1, 2, 3.
Еще один визуальный образ происходящего представлен на рис. 2.
Рис. 2. Выполнение процедуры Rec с параметром 3 состоит из выполнения процедуры Rec с параметром 2 и печати числа 3. В свою очередь выполнение процедуры Rec с параметром 2 состоит из выполнения процедуры Rec с параметром 1 и печати числа 2. И т. д.
В качестве самостоятельного упражнения подумайте, что получится при вызове Rec(4). Также подумайте, что получится при вызове описанной ниже процедуры Rec2(4), где операторы поменялись местами.
procedure Rec2(a: integer);
begin
writeln(a);
if a>0 then
Rec2(a-1);
end;
Обратите внимание, что в приведенных примерах рекурсивный вызов стоит внутри условного оператора. Это необходимое условие для того, чтобы рекурсия когда-нибудь закончилась. Также обратите внимание, что сама себя процедура вызывает с другим параметром, не таким, с каким была вызвана она сама. Если в процедуре не используются глобальные переменные, то это также необходимо, чтобы рекурсия не продолжалась до бесконечности.
2. Сложная рекурсия
Возможна чуть более сложная схема: функция A вызывает функцию B, а та в свою очередь вызывает A. Это называется сложной рекурсией. При этом оказывается, что описываемая первой процедура должна вызывать еще не описанную. Чтобы это было возможно, требуется использовать опережающее описание.
Пример:
procedure A(n: integer); {Опережающее описание (заголовок) первой процедуры}
procedure B(n: integer); {Опережающее описание второй процедуры}
procedure A(n: integer); {Полное описание процедуры A}
begin
writeln(n);
B(n-1);
end;
procedure B(n: integer); {Полное описание процедуры B}
begin
writeln(n);
if n<10 then
A(n+2);
end;
Опережающее описание процедуры B позволяет вызывать ее из процедуры A. Опережающее описание процедуры A в данном примере не требуется и добавлено из эстетических соображений.
Если обычную рекурсию можно уподобить уроборосу (рис. 3), то образ сложной рекурсии можно почерпнуть из известного детского стихотворения, где «Волки с перепуга, скушали друг друга». Представьте себе двух съевших друг друга волков, и вы поймете сложную рекурсию.
Рис. 3. Уроборос – змей, пожирающий свой хвост. Рисунок из алхимического трактата «Synosius» Теодора Пелеканоса (1478г).
Рис. 4. Сложная рекурсия.
3. Имитация работы цикла с помощью рекурсии
Если процедура вызывает сама себя, то, по сути, это приводит к повторному выполнению содержащихся в ней инструкций, что аналогично работе цикла. Некоторые языки программирования не содержат циклических конструкций вовсе, предоставляя программистам организовывать повторения с помощью рекурсии (например, Пролог, где рекурсия — основной прием программирования).
Для примера сымитируем работу цикла for. Для этого нам потребуется переменная счетчик шагов, которую можно реализовать, например, как параметр процедуры.
Пример 1.
procedure LoopImitation(i, n: integer);
{Первый параметр – счетчик шагов, второй параметр – общее количество шагов}
begin
writeln('Hello N ', i); //Здесь любые инструкции, которые будут повторятся
if i<n then //Пока счетчик цикла не станет равным максимальному
LoopImitation(i+1, n); //значению n, повторяем инструкции путем вызова
//нового экземпляра процедуры
end;
Результатом вызова вида LoopImitation(1, 10) станет десятикратное выполнение инструкций с изменением счетчика от 1 до 10. В данном случае будет напечатано:
Hello N 1
Hello N 2
…
Hello N 10
Вообще, не трудно видеть, что параметры процедуры это пределы изменения значений счетчика.
Можно поменять местами рекурсивный вызов и подлежащие повторению инструкции, как в следующем примере.
Пример 2.
procedure LoopImitation2(i, n: integer);
begin
if i<n then
LoopImitation2(i+1, n);
writeln('Hello N ', i);
end;
В этом случае, прежде чем начнут выполняться инструкции, произойдет рекурсивный вызов процедуры. Новый экземпляр процедуры также, прежде всего, вызовет еще один экземпляр и так далее, пока не дойдем до максимального значения счетчика. Только после этого последняя из вызванных процедур выполнит свои инструкции, затем выполнит свои инструкции предпоследняя и т.д. Результатом вызова LoopImitation2(1, 10) будет печать приветствий в обратном порядке:
Hello N 10
…
Hello N 1
Если представить себе цепочку из рекурсивно вызванных процедур, то в примере 1 мы проходим ее от раньше вызванных процедур к более поздним. В примере 2 наоборот от более поздних к ранним.
Наконец, рекурсивный вызов можно расположить между двумя блоками инструкций. Например:
procedure LoopImitation3(i, n: integer);
begin
writeln('Hello N ', i); {Здесь может располагаться первый блок инструкций}
if i<n then
LoopImitation3(i+1, n);
writeln('Hello N ', i); {Здесь может располагаться второй блок инструкций}
end;
Здесь сначала последовательно выполнятся инструкции из первого блока затем в обратном порядке инструкции второго блока. При вызове LoopImitation3(1, 10) получим:
Hello N 1
…
Hello N 10
Hello N 10
…
Hello N 1
Потребуется сразу два цикла, чтобы сделать то же самое без рекурсии.
Тем, что выполнение частей одной и той же процедуры разнесено по времени можно воспользоваться. Например:
Пример 3: Перевод числа в двоичную систему.
Получение цифр двоичного числа, как известно, происходит с помощью деления с остатком на основание системы счисления 2. Если есть число , то его последняя цифра в его двоичном представлении равна
.
Взяв же целую часть от деления на 2:
,
получим число, имеющее то же двоичное представление, но без последней цифры. Таким образом, достаточно повторять приведенные две операции пока поле очередного деления не получим целую часть равную 0. Без рекурсии это будет выглядеть так:
while x>0 do begin c:=x mod 2; x:=x div 2; write(c); end;
Проблема здесь в том, что цифры двоичного представления вычисляются в обратном порядке (сначала последние). Чтобы напечатать число в нормальном виде придется запомнить все цифры в элементах массива и выводить в отдельном цикле.
С помощью рекурсии нетрудно добиться вывода в правильном порядке без массива и второго цикла. А именно:
procedure BinaryRepresentation(x: integer);
var
c, x: integer;
begin
{Первый блок. Выполняется в порядке вызова процедур}
c := x mod 2;
x := x div 2;
{Рекурсивный вызов}
if x>0 then
BinaryRepresentation(x);
{Второй блок. Выполняется в обратном порядке}
write(c);
end;
Вообще говоря, никакого выигрыша мы не получили. Цифры двоичного представления хранятся в локальных переменных, которые свои для каждого работающего экземпляра рекурсивной процедуры. То есть, память сэкономить не удалось. Даже наоборот, тратим лишнюю память на хранение многих локальных переменных x. Тем не менее, такое решение кажется мне красивым.
4. Рекуррентные соотношения. Рекурсия и итерация
Говорят, что последовательность векторов задана рекуррентным соотношением, если задан начальный вектор
и функциональная зависимость последующего вектора от предыдущего
Простым примером величины, вычисляемой с помощью рекуррентных соотношений, является факториал
Очередной факториал можно вычислить по предыдущему как:
Введя обозначение , получим соотношение:
Вектора из формулы (1) можно интерпретировать как наборы значений переменных. Тогда вычисление требуемого элемента последовательности будет состоять в повторяющемся обновлении их значений. В частности для факториала:
x := 1; for i := 2 to n do x := x * i; writeln(x);
Каждое такое обновление (x := x * i) называется итерацией, а процесс повторения итераций – итерированием.
Обратим, однако, внимание, что соотношение (1) является чисто рекурсивным определением последовательности и вычисление n-го элемента есть на самом деле многократное взятие функции f от самой себя:
В частности для факториала можно написать:
function Factorial(n: integer): integer;
begin
if n > 1 then
Factorial := n * Factorial(n-1)
else
Factorial := 1;
end;
Следует понимать, что вызов функций влечет за собой некоторые дополнительные накладные расходы, поэтому первый вариант вычисления факториала будет несколько более быстрым. Вообще итерационные решения работают быстрее рекурсивных.
Прежде чем переходить к ситуациям, когда рекурсия полезна, обратим внимание еще на один пример, где ее использовать не следует.
Рассмотрим частный случай рекуррентных соотношений, когда следующее значение в последовательности зависит не от одного, а сразу от нескольких предыдущих значений. Примером может служить известная последовательность Фибоначчи, в которой каждый следующий элемент есть сумма двух предыдущих:
При «лобовом» подходе можно написать:
function Fib(n: integer): integer;
begin
if n > 1 then
Fib := Fib(n-1) + Fib(n-2)
else
Fib := 1;
end;
Каждый вызов Fib создает сразу две копии себя, каждая из копий – еще две и т.д. Количество операций растет с номером n экспоненциально, хотя при итерационном решении достаточно линейного по n количества операций.
На самом деле, приведенный пример учит нас не КОГДА рекурсию не следует использовать, а тому КАК ее не следует использовать. В конце концов, если существует быстрое итерационное (на базе циклов) решение, то тот же цикл можно реализовать с помощью рекурсивной процедуры или функции. Например:
// x1, x2 – начальные условия (1, 1)
// n – номер требуемого числа Фибоначчи
function Fib(x1, x2, n: integer): integer;
var
x3: integer;
begin
if n > 1 then
begin
x3 := x2 + x1;
x1 := x2;
x2 := x3;
Fib := Fib(x1, x2, n-1);
end else
Fib := x2;
end;
И все же итерационные решения предпочтительны. Спрашивается, когда же в таком случае, следует пользоваться рекурсией?
Любые рекурсивные процедуры и функции, содержащие всего один рекурсивный вызов самих себя, легко заменяются итерационными циклами. Чтобы получить что-то, не имеющее простого нерекурсивного аналога, следует обратиться к процедурам и функциям, вызывающим себя два и более раз. В этом случае множество вызываемых процедур образует уже не цепочку, как на рис. 1, а целое дерево. Существуют широкие классы задач, когда вычислительный процесс должен быть организован именно таким образом. Как раз для них рекурсия будет наиболее простым и естественным способом решения.
5. Деревья
Теоретической базой для рекурсивных функций, вызывающих себя более одного раза, служит раздел дискретной математики, изучающий деревья.
5.1. Основные определения. Способы изображения деревьев
Определение: Деревом будем называть конечное множество T, состоящее из одного или более узлов, таких что:
а) Имеется один специальный узел, называемый корнем данного дерева.
б) Остальные узлы (исключая корень) содержатся в попарно непересекающихся подмножествах
, каждое из которых в свою очередь является деревом. Деревья
называются поддеревьями данного дерева.
Это определение является рекурсивным. Если коротко, то дерево это множество, состоящее из корня и присоединенных к нему поддеревьев, которые тоже являются деревьями. Дерево определяется через само себя. Однако данное определение осмысленно, так как рекурсия конечна. Каждое поддерево содержит меньше узлов, чем содержащее его дерево. В конце концов, мы приходим к поддеревьям, содержащим всего один узел, а это уже понятно, что такое.
Рис. 3. Дерево.
На рис. 3 показано дерево с семью узлами. Хотя обычные деревья растут снизу вверх, рисовать их принято наоборот. При рисовании схемы от руки такой способ, очевидно, удобнее. Из-за данной несогласованности иногда возникает путаница, когда говорят о том, что один из узлов находится над или под другим. По этой причине удобнее пользоваться терминологией, употребляемой при описании генеалогических деревьев, называя более близкие к корню узлы предками, а более далекие потомками.
Узлы, не содержащие поддеревьев, называются концевыми узлами или листьями. Множество не пересекающихся деревьев называется лесом. Например, лес образуют поддеревья, исходящие из одного узла.
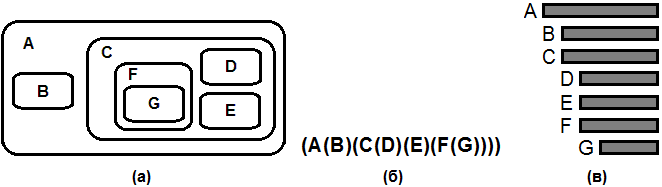
Графически дерево можно изобразить и некоторыми другими способами. Некоторые из них представлены на рис. 4. Согласно определению дерево представляет собой систему вложенных множеств, где эти множества или не пересекаются или полностью содержатся одно в другом. Такие множества можно изобразить как области на плоскости (рис. 4а). На рис. 4б вложенные множества располагаются не на плоскости, а вытянуты в одну линию. Рис. 4б также можно рассматривать как схему некоторой алгебраической формулы, содержащей вложенные скобки. Рис. 4в дает еще один популярный способ изображения древовидной структуры в виде уступчатого списка.
Рис. 4. Другие способы изображения древовидных структур: (а) вложенные множества; (б) вложенные скобки; (в) уступчатый список.
Уступчатый список имеет очевидное сходство со способом форматирования программного кода. Действительно, программа, написанная в рамках парадигмы структурного программирования, может быть представлена как дерево, состоящее из вложенных друг в друга конструкций.
Также можно провести аналогию между уступчатым списком и внешним видом оглавлений в книгах, где разделы содержат подразделы, те в свою очередь поподразделы и т.д. Традиционный способ нумерации таких разделов (раздел 1, подразделы 1.1 и 1.2, подподраздел 1.1.2 и т.п.) называется десятичной системой Дьюи. В применении к дереву на рис. 3 и 4 эта система даст:
1. A; 1.1 B; 1.2 C; 1.2.1 D; 1.2.2 E; 1.2.3 F; 1.2.3.1 G;
5.2. Прохождение деревьев
Во всех алгоритмах, связанных с древовидными структурами неизменно встречается одна и та же идея, а именно идея прохождения или обхода дерева. Это – такой способ посещения узлов дерева, при котором каждый узел проходится точно один раз. При этом получается линейная расстановка узлов дерева. В частности существует три способа: можно проходить узлы в прямом, обратном и концевом порядке.
Алгоритм обхода в прямом порядке:
- Попасть в корень,
- Пройти все поддеревья слева на право в прямом порядке.
Данный алгоритм рекурсивен, так как прохождение дерева содержит прохождение поддеревьев, а они в свою очередь проходятся по тому же алгоритму.
В частности для дерева на рис. 3 и 4 прямой обход дает последовательность узлов: A, B, C, D, E, F, G.
Получающаяся последовательность соответствует последовательному слева направо перечислению узлов при представлении дерева с помощью вложенных скобок и в десятичной системе Дьюи, а также проходу сверху вниз при представлении в виде уступчатого списка.
При реализации этого алгоритма на языке программирования попадание в корень соответствует выполнение процедурой или функцией некоторых действий, а прохождение поддеревьев – рекурсивным вызовам самой себя. В частности для бинарного дерева (где из каждого узла исходит не более двух поддеревьев) соответствующая процедура будет выглядеть так:
// Preorder Traversal – английское название для прямого порядка
procedure PreorderTraversal({Аргументы});
begin
//Прохождение корня
DoSomething({Аргументы});
//Прохождение левого поддерева
if {Существует левое поддерево} then
PreorderTransversal({Аргументы 2});
//Прохождение правого поддерева
if {Существует правое поддерево} then
PreorderTransversal({Аргументы 3});
end;
То есть сначала процедура производит все действия, а только затем происходят все рекурсивные вызовы.
Алгоритм обхода в обратном порядке:
- Пройти левое поддерево,
- Попасть в корень,
- Пройти следующее за левым поддерево.
- Попасть в корень,
- и т.д пока не будет пройдено крайнее правое поддерево.
То есть проходятся все поддеревья слева на право, а возвращение в корень располагается между этими прохождениями. Для дерева на рис. 3 и 4 это дает последовательность узлов: B, A, D, C, E, G, F.
В соответствующей рекурсивной процедуре действия будут располагаться в промежутках между рекурсивными вызовами. В частности для бинарного дерева:
// Inorder Traversal – английское название для обратного порядка
procedure InorderTraversal({Аргументы});
begin
//Прохождение левого поддерева
if {Существует левое поддерево} then
InorderTraversal({Аргументы 2});
//Прохождение корня
DoSomething({Аргументы});
//Прохождение правого поддерева
if {Существует правое поддерево} then
InorderTraversal({Аргументы 3});
end;
Алгоритм обхода в концевом порядке:
- Пройти все поддеревья слева на право,
- Попасть в корень.
Для дерева на рис. 3 и 4 это даст последовательность узлов: B, D, E, G, F, C, A.
В соответствующей рекурсивной процедуре действия будут располагаться после рекурсивных вызовов. В частности для бинарного дерева:
// Postorder Traversal – английское название для концевого порядка
procedure PostorderTraversal({Аргументы});
begin
//Прохождение левого поддерева
if {Существует левое поддерево} then
PostorderTraversal({Аргументы 2});
//Прохождение правого поддерева
if {Существует правое поддерево} then
PostorderTraversal({Аргументы 3});
//Прохождение корня
DoSomething({Аргументы});
end;
5.3. Представление дерева в памяти компьютера
Если некоторая информация располагается в узлах дерева, то для ее хранения можно использовать соответствующую динамическую структуру данных. На Паскале это делается с помощью переменной типа запись (record), содержащей указатели на поддеревья того же типа. Например, бинарное дерево, где в каждом узле содержится целое число можно сохранить с помощью переменной типа PTree, который описан ниже:
type
PTree = ^TTree;
TTree = record
Inf: integer;
LeftSubTree, RightSubTree: PTree;
end;
Каждый узел имеет тип PTree. Это указатель, то есть каждый узел необходимо создавать, вызывая для него процедуру New. Если узел является концевым, то его полям LeftSubTree и RightSubTree присваивается значение nil. В противном случае узлы LeftSubTree и RightSubTree также создаются процедурой New.
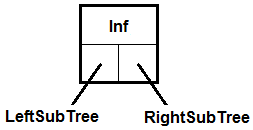
Схематично одна такая запись изображена на рис. 5.
Рис. 5. Схематичное изображение записи типа TTree. Запись имеет три поля: Inf – некоторое число, LeftSubTree и RightSubTree – указатели на записи того же типа TTree.
Пример дерева, составленного из таких записей, показан на рисунке 6.
Рис. 6. Дерево, составленное из записей типа TTree. Каждая запись хранит число и два указателя, которые могут содержать либо nil, либо адреса других записей того же типа.
Если вы ранее не работали со структурами состоящими из записей, содержащих ссылки на записи того же типа, то рекомендуем ознакомиться с материалом о рекурсивных структурах данных.
6. Примеры рекурсивных алгоритмов
6.1. Рисование дерева
Рассмотрим алгоритм рисования деревца, изображенного на рис. 6. Если каждую линию считать узлом, то данное изображение вполне удовлетворяет определению дерева, данному в предыдущем разделе.
Рис. 6. Деревце.
Рекурсивная процедура, очевидно должна рисовать одну линию (ствол до первого разветвления), а затем вызывать сама себя для рисования двух поддеревьев. Поддеревья отличаются от содержащего их дерева координатами начальной точки, углом поворота, длиной ствола и количеством содержащихся в них разветвлений (на одно меньше). Все эти отличия следует сделать параметрами рекурсивной процедуры.
Пример такой процедуры, написанный на Delphi, представлен ниже:
procedure Tree(
Canvas: TCanvas; //Canvas, на котором будет рисоваться дерево
x,y: extended; //Координаты корня
Angle: extended; //Угол, под которым растет дерево
TrunkLength: extended; //Длина ствола
n: integer //Количество разветвлений (сколько еще предстоит
//рекурсивных вызовов)
);
var
x2, y2: extended; //Конец ствола (точка разветвления)
begin
x2 := x + TrunkLength * cos(Angle);
y2 := y - TrunkLength * sin(Angle);
Canvas.MoveTo(round(x), round(y));
Canvas.LineTo(round(x2), round(y2));
if n > 1 then
begin
Tree(Canvas, x2, y2, Angle+Pi/4, 0.55*TrunkLength, n-1);
Tree(Canvas, x2, y2, Angle-Pi/4, 0.55*TrunkLength, n-1);
end;
end;
Для получения рис. 6 эта процедура была вызвана со следующими параметрами:
Tree(Image1.Canvas, 175, 325, Pi/2, 120, 15);
Заметим, что рисование осуществляется до рекурсивных вызовов, то есть дерево рисуется в прямом порядке.
6.2. Ханойские башни
Согласно легенде в Великом храме города Бенарас, под собором, отмечающим середину мира, находится бронзовый диск, на котором укреплены 3 алмазных стержня, высотой в один локоть и толщиной с пчелу. Давным-давно, в самом начале времен монахи этого монастыря провинились перед богом Брамой. Разгневанный, Брама воздвиг три высоких стержня и на один из них поместил 64 диска из чистого золота, причем так, что каждый меньший диск лежит на большем. Как только все 64 диска будут переложены со стержня, на который Бог Брама сложил их при создании мира, на другой стержень, башня вместе с храмом обратятся в пыль и под громовые раскаты погибнет мир.
В процессе требуется, чтобы больший диск ни разу не оказывался над меньшим. Монахи в затруднении, в какой же последовательности стоит делать перекладывания? Требуется снабдить их софтом для расчета этой последовательности.
Независимо от Брамы данную головоломку в конце 19 века предложил французский математик Эдуард Люка. В продаваемом варианте обычно использовалось 7-8 дисков (рис. 7).
Рис. 7. Головоломка «Ханойские башни».
Предположим, что существует решение для n-1 диска. Тогда для перекладывания n дисков надо действовать следующим образом:
1) Перекладываем n-1 диск.
2) Перекладываем n-й диск на оставшийся свободным штырь.
3) Перекладываем стопку из n-1 диска, полученную в пункте (1) поверх n-го диска.
Поскольку для случая n = 1 алгоритм перекладывания очевиден, то по индукции с помощью выполнения действий (1) – (3) можем переложить произвольное количество дисков.
Создадим рекурсивную процедуру, печатающую всю последовательность перекладываний для заданного количества дисков. Такая процедура при каждом своем вызове должна печатать информацию об одном перекладывании (из пункта 2 алгоритма). Для перекладываний из пунктов (1) и (3) процедура вызовет сама себя с уменьшенным на единицу количеством дисков.
//n – количество дисков
//a, b, c – номера штырьков. Перекладывание производится со штырька a,
//на штырек b при вспомогательном штырьке c.
procedure Hanoi(n, a, b, c: integer);
begin
if n > 1 then
begin
Hanoi(n-1, a, c, b);
writeln(a, ' -> ', b);
Hanoi(n-1, c, b, a);
end else
writeln(a, ' -> ', b);
end;
Заметим, что множество рекурсивно вызванных процедур в данном случае образует дерево, проходимое в обратном порядке.
6.3. Синтаксический анализ арифметических выражений
Задача синтаксического анализа заключается в том, чтобы по имеющейся строке, содержащей арифметическое выражение, и известным значениям, входящих в нее переменных, вычислить значение выражения.
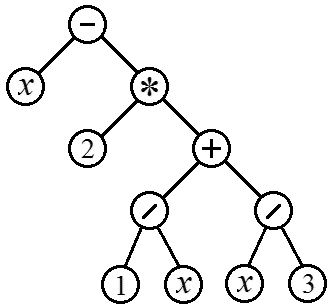
Процесс вычисления арифметических выражений можно представить в виде бинарного дерева. Действительно, каждый из арифметических операторов (+, –, *, /) требует двух операндов, которые также будут являться арифметическими выражениями и, соответственно могут рассматриваться как поддеревья. Рис. 8 показывает пример дерева, соответствующего выражению:
Рис. 8. Синтаксическое дерево, соответствующее арифметическому выражению (6).
В таком дереве концевыми узлами всегда будут переменные (здесь x) или числовые константы, а все внутренние узлы будут содержать арифметические операторы. Чтобы выполнить оператор, надо сначала вычислить его операнды. Таким образом, дерево на рисунке следует обходить в концевом порядке. Соответствующая последовательность узлов
называется обратной польской записью арифметического выражения.
При построении синтаксического дерева следует обратить внимание на следующую особенность. Если есть, например, выражение
и операции сложения и вычитания мы будем считывать слева на право, то правильное синтаксическое дерево будет содержать минус вместо плюса (рис. 9а). По сути, это дерево соответствует выражению Облегчить составление дерева можно, если анализировать выражение (8) наоборот, справа налево. В этом случае получается дерево с рис. 9б, эквивалентное дереву 8а, но не требующее замены знаков.
Аналогично справа налево нужно анализировать выражения, содержащие операторы умножения и деления.
Рис. 9. Синтаксические деревья для выражения a – b + c при чтении слева направо (а) и справа налево (б).
В файле SynAn.pas приведен пример функции, вычисляющей значения выражений, содержащих только одну переменную x. Дадим краткое описание реализованного там алгоритма:
- Вычисляющая выражение функция (CalcExpression) находит в строке все знаки «+» и «–», не заключенные в скобки. Эти знаки разбивают выражение на части, содержащие (вне скобок) только операции умножения и деления. Для вычисления значений этих частей вызывается функция CalcMultDiv.
- Функция CalcMultDiv находит в строке все знаки «*» и «/», не заключенные в скобки. Эти знаки разбивают выражение на части, содержащие числовые константы, переменную x или выражения в скобках. Для вычисления значений этих частей вызывается функция CalcValuesOrOpenParentheses.
- Функция CalcValuesOrOpenParentheses определяет тип попавшего ей на вход выражения. Если это числовая константа или переменная x, то она возвращает их значение. Если это выражение в скобках, то для его вычисления рекурсивно вызывается процедура CalcExpression.
Заметим, что в данном примере вычисления производятся одновременно с анализом строкового выражения. Это приводит к тому, что для некоторых выражений вычисления могут происходить в 100 – 1000 раз медленнее, чем, если бы эти выражения были скомпилированы как часть программы. Если одно и то же выражение требуется вычислить много раз при различных значения переменных, то следует разделить анализ строки и вычисления. Такой подход может позволить ускорить вычисления в сотни раз.
Результатом анализа строки должна быть последовательность узлов дерева в концевом порядке. Каждый узел должен хранить информацию о подузлах и о той операции, которая в нем совершается. Например, узлы можно реализовать в виде записей, одно из полей который имеет процедурный тип. Другой вариант – каждый узел это объект, где операция реализована как виртуальный метод.
6.4. Быстрые сортировки
Простые методы сортировки вроде метода выбора или метода пузырька сортируют массив из n элементов за O(n2) операций. Однако с помощью принципа «разделяй и властвуй» удается построить более быстрые, работающие за O(n log2 n) алгоритмы. Суть этого принципа в том, что решение получается путем рекурсивного разделения задачи на несколько простые подзадачи того же типа до тех пор, пока они не станут элементарными. Приведем в качестве примеров несколько быстрых алгоритмов такого рода.
Алгоритм 1: «Быстрая» сортировка (quicksort).
1. Выбирается опорный элемент (например, первый или случайный).
2. Реорганизуем массив так, чтобы сначала шли элементы меньшие опорного, потом равные ему, затем большие. Для этого достаточно помнить, сколько было найдено меньших (m1) и больших (m2), чем опорный и ставить очередной элемент на место с индексом m1, а очередной больший на место с индексом n-1-m2.
После выполнения такой операции опорный элемент и равные ему стоят на своем месте, их переставлять больше не придется. Между «меньшей» и «большей» часть массива перестановок также быть не может. То есть эти части можно сортировать независимо друг от друга.
3. Если «меньшая» или «большая» часть состоит из одного элемента, то она уже отсортирована и делать ничего не надо. Иначе сортируем эти части с помощью алгоритма быстрой сортировки (то есть, выполняем для нее шаги 1-3).
Как видите, быстрая сортировка состоит из выполнения шагов 1 и 2 и рекурсивного вызова алгоритма для получившихся частей массива.
Алгоритм 2: Сортировка слиянием (merge sort).
- Делим массив на две части примерно одинакового размера и, если получившаяся половина массива содержит больше одного элемента, то сортируем ее с помощью сортировки слиянием. Как видите, этот пункт содержит рекурсивное обращение ко всему алгоритму в целом.
- Соединяем две отсортированные половины так, чтобы получился один отсортированный массив. Для этого помещаем во вспомогательный массив элементы из первой половины, пока они не превосходят очередного элемента из второй половины. Затем начинаем помещать туда элементы второй половины, пока они не превосходят очередного элемента из первой половины. Затем снова берем элементы первой половины и т.д. Эта операция называется слиянием и требует столько шагов, сколько элементов в обоих соединяемых массивах.
Алгоритм 3: Сортировка деревом (tree sort).
Прежде чем переходить к объяснению сути алгоритма введем одно понятие. Двоичным деревом поиска называется бинарное дерево, в узлах которого располагаются числа таким образом, что в левом поддереве каждого узла находятся числа меньшие, чем в этом узле, а в правом поддереве больше или равные тому, что в этом узле. На рис. 10 показано два примера деревьев поиска, составленных из одних и тех же чисел.
Рис. 10. Двоичные деревья поиска, составленные из чисел 1, 3, 4, 6, 7, 8, 10, 13, 14.
Если для каждой вершины высота поддеревьев различается не более чем на единицу, то дерево называется сбалансированным. Сбалансированные деревья поиска также называются АВЛ-деревьями (по первым буквам фамилий изобретателей Г. М. Адельсона-Вельского и Е. М. Ландиса). Как видно на рис. 10а показано сбалансированное дерево, на рис. 10б несбалансированное.
Заметим, что расположение чисел по возрастанию получится, если обходить эти деревья в обратном прядке.
Сортировка деревом получится, если мы сначала последовательно будем добавлять числа из массива в двоичное дерево поиска, а затем обойдем его в обратном порядке.
Если дерево будет близко к сбалансированному, то сортировка потребует примерно n log2 n операций. Если не повезет и дерево окажется максимально несбалансированным, то сортировка займет n2 операций.
6.5. Произвольное количество вложенных циклов
Разместив рекурсивные вызовы внутри цикла, по сути, получим вложенные циклы, где уровень вложенности равен глубине рекурсии.
Для примера напишем процедуру, печатающую все возможные сочетания из k чисел от 1 до n (). Числа, входящие в каждое сочетание, будем печатать в порядке возрастания. Сочетания из двух чисел (k=2) печатаются так:
for i1 := 1 to n do
for i2 := i1 + 1 to n do
writeln(i1, ' ', i2);
Сочетания из трех чисел (k=3) так:
for i1 := 1 to n do
for i2 := i1 + 1 to n do
for i3 := i2 + 1 to n do
writeln(i1, ' ', i2, ' ', i3);
Однако, если количество чисел в сочетании задается переменной, то придется прибегнуть к рекурсии.
procedure Combinations(
n, k: integer;
//Массив, в котором будем формировать сочетания
var Indexes: array of integer;
//Счетчик глубины рекурсии
d: integer);
var
i, i_min: integer;
s: string;
begin
if d < k then
begin
if d = 0 then
i_min := 1
else
i_min := Indexes[d-1] + 1;
for i := i_min to n do
begin
Indexes[d] := i;
Combinations(n, k, Indexes, d+1);
end;
end
else
begin
for i := 0 to k-1 do
write(Indexes[i], ' ');
writeln;
end;
end;
6.6. Задачи на графах
Графом называют графическое изображение, состоящее из вершин (узлов) и соединяющих некоторые пары вершин ребер (рис. 11а).
Более строго: граф – совокупность множества вершин и множества ребер. Множество ребер – подмножество евклидова квадрата множества вершин (то есть ребро соединяет ровно две вершины).
Ребрам можно также присвоить направление. Граф в этом случае называется ориетированным (рис. 11б).
Рис. 11. (а) Граф. (б) Ориентированный граф.
Теория графов находит применения в самых разных областях. Несколько примеров:
- Логистика и транспортные системы. Вершинами будут склады с товарами или пункты назначения, а ребра – дороги, их соединяющие.
- Маршрутизация сетей. Вершины – компьютеры, соединенные в сеть, ребра – связи между ними. Решается задача о путях передачи данных с одного компьютера на другой.
- Компьютерная химия. Модели в виде графов используются для описания путей протекания сложных реакций. Вершины – участвующие в реакциях вещества, ребра – пути превращений веществ. Также графом является изображение структур молекул: вершины – атомы, ребра – химические связи.
- Электрические сети.
- Сайты в Интернете можно считать узлами ориентированного графа, ребрами которого будут гиперссылки.
- И т. д.
Современная теория графов представляет собой мощную формальную систему, имеющую необозримое множество применений.
Путем или цепью в графе называется последовательность вершин, в которой каждая вершина соединена ребром со следующей. Пути, в которых начальная и конечная вершина совпадают, называют циклами. Если для каждой пары вершин существует путь их соединяющих, то такой граф называют связным.
В программировании используются три способа хранения в памяти информации о стуктуре графов.
1) Матрицы смежности
Квадратная матрица M, где как строки, так и столбцы соответствуют вершинам графа. Если вершины с номерами i и j соединены ребром, то Mij = 1, иначе Mij = 0. Для неориентированного графа матрица, очевидно, симметрична. Ориентированный граф задается антисимметричной матрицей. Если ребро выходит из узла i и приходит в узел j, то Mij = 1, а симметричный элемент Mji = -1.
2) Матрица инцидентности
Столбцы матрицы соответствуют вершинам, а строки ребрам. Если ребро с номером i соединяет вершины с номерами j и k, то элементы матрицы Iij = Iik = 1. Остальные элементы i-й строки равны 0.
3) Список ребер
Просто набор пар номеров вершин, соединенных ребрами.
Рассмотренные выше деревья являются частным случаем графов. Деревом будет любой связный граф, не содержащий циклов.
Задачи, возникающие в теории графов многочисленны и разнообразны. Про них пишутся толстые книги, и нет никакой возможности сколько-нибудь полно их здесь обозреть. Поэтому мы ограничимся замечанием, что многие из этих задач требуют систематического перебора вершин. Если перебирать вершины, связанные ребрами и при этом посещать каждую вершину только один раз, то множество посещаемых алгоритмом вершин будет образовывать дерево, а сам алгоритм естественно сделать рекурсивным.
Например, классической задачей является поиск пути из одной вершины в другую. Алгоритм поиска должен будет построить дерево возможных путей из начальной вершины, концевыми узлами которого будут вершины, из которых нельзя попасть ни в какую вершину, не принадлежащую ранее построенной ветви (не помеченную как уже посещенную). Задача будет решена, когда один из концевых узлов совпадет с конечной вершиной, путь в которую требуется найти.
6.7. Фракталы
Фракталами называют геометрические фигуры, обладающие свойством самоподобия, то есть состоящие из частей, подобных всей фигуре.
Классическим примером является кривая Коха, построение которой показано на рис. 12. Изначально берется отрезок прямой (рис. 12а). Он делится на три части, средняя часть изымается и вместо нее строится угол (рис. 12б), стороны которого равны длине изъятого отрезка (то есть 1/3 от длины исходного отрезка). Такая операция повторяется с каждым из получившихся 4-х отрезков (рис. 12в). И так далее (рис. 12г). Кривая Коха получается после бесконечного числа таких итераций. На практике построение можно прекратить, когда размер деталей окажется меньше разрешения экрана (рис. 12д).
Рис. 12. Процесс построения кривой Коха.
Еще одним примером может служить деревце на рис. 6. Оно также содержит части, подобные всему дереву в целом, что делает его фракталом.
Фракталы, по сути, рекурсивные структуры и их построение естественно производить с помощью рекурсивных процедур.
7. Избавление от рекурсии
Любой рекурсивный алгоритм может быть переписан без использования рекурсии. Заметим, что быстродействие алгоритмов при избавлении от рекурсии, как правило, повышается. Еще одной причиной чтобы избавиться от рекурсии является ограничение на объем хранимых программой локальных переменных и значений параметров одновременно выполняющихся процедур. При очень глубокой рекурсии этот объем возрастает, и программа перестает работать, выдавая ошибку «Stack overflow» (переполнение стека).
Так почему же люди продолжают пользоваться рекурсивными алгоритмами? Очевидно, потому что это проще и естественнее, чем соответствующие нерекурсивные решения. Тем не менее, знание о способах обойтись без рекурсии необходимо.
Ниже представлено несколько вариантов того, как это можно сделать.
7.1. Явное использование стека
Стеком называется структура данных, в которой добавление и извлечение данных происходит с одного конца, называемого вершиной стека (рис. 13). Наглядным образом стека может служить стопка тарелок – добавлять или забрать тарелки можно только сверху. Каждая тарелка соответствует элементу данных.
Рис. 13. Наглядное представление стека. Push (проталкивание) – традиционное название для операции добавления данных в стек, Pop (выталкивание) – традиционное название для операции извлечения данных из стека.
Когда одна процедура или функция вызывает другую, то параметры первой процедуры, а также место, с которого ее выполнение должно продолжиться после того как отработает вызванная процедура (точка возврата), запоминаются в так называемом стеке вызовов. Если вызванная процедура в свою очередь чего-нибудь вызывает, то ее параметры и точка возврата также добавляются в стек.
При рекурсивных вызовах стек вызовов хранит цепочку из данных об одновременно работающих процедурах. Во всех продвинутых средах разработки эту цепочку вместе с запомненными параметрами процедур можно просмотреть во время отладки. Соответствующая команда обычно называется “Call Stack” (в Delphi ей соответствует сочетание клавиш Ctrl – Alt – S).
Универсальный способ избавиться от рекурсии – это самостоятельно запрограммировать те действия со стеком, которые фактически происходят, когда вы используете рекурсивные вызовы. Покажем, как это можно сделать, на примере дважды вызывающей себя рекурсивной процедуры.
Для начала реализуем в виде класса стек, хранящий параметры процедуры:
type
//Запись для хранения параметров процедур
Parameters = record
//Список параметров
end;
//Стек удобно реализовать с помощью связанных списков
//(http://www.tvd-home.ru/prog/16_4)
PList = ^List;
List = record
Data: Parameters;
Next: PList;
end;
//Описанный одновсязанный список соединим с методами
//добавления и удаления элементов и получим стек.
Stack = class
private
StackTop: PList;
public
//Добавление данных
procedure Push(NewData: Parameters);
//Извлечение данных
function Pop: Parameters;
//Проверка наличия данных
function Empty: boolean;
end;
implementation
//Добавление данных
procedure Stack.Push(NewData: Parameters);
var
NewElement: PList;
begin
New(NewElement);
NewElement^.Data := NewData;
NewElement^.Next := StackTop;
StackTop := NewElement;
end;
//Извлечение данных
function Stack.Pop: Parameters;
var
PopedElement: PList;
begin
PopedElement := StackTop;
StackTop := StackTop^.Next;
Pop := PopedElement^.Data;
Dispose(PopedElement);
end;
//Проверка наличия данных
function Stack.Empty: boolean;
begin
Empty := StackTop = nil;
end;
Рассмотрим обобщенную рекурсивную процедуру с двумя вызовами самой себя.
procedure Recurs(P1: Parameters);
begin
DoSomething(P1);
if <условие> then
begin
P2 := F(P1);
Recurs(P2);
P3 := G(P1);
Recurs(P3);
end;
end;
В данной процедуре некоторые действия (DoSomething) выполняются много раз при разных значениях параметров. Нерекурсивный аналог должен хранить эти параметры в стеке. Каждый рекурсивный вызов будет соответствовать добавлению очередных параметров в стек. Вместо рекурсии появляется цикл, который выполняется, пока в стеке есть необработанные параметры.
procedure NonRecurs(P1: Parameters);
var
S: Stack;
P: Parameters;
begin
S := Stack.Create;
S.Push(P1);
while not S.Empty do
begin
P1 := S.Pop;
DoSomething(P1);
if <условие> then
begin
P3 := G(P1);
S.Push(P3);
P2 := F(P1);
S.Push(P2);
end;
end;
end;
Обратите внимание, что рекурсивные вызовы шли сначала для параметров P2, потом для P3. В нерекурсивной процедуре в стек отправляются сначала параметры P3, а только потом P2. Это связано с тем, что при рекурсивных вызовах в стек, по сути, отправляется недовыполненная часть процедуры, которая в нашем случае содержит вызов Recurs(P3).
Упомянутой выше перестановки можно избежать, если вместо стека использовать очередь – структуру данных, где добавление и извлечение элементов происходит с разных концов. Это будет некоторым отступлением от точной имитации процессов при рекурсивных вызовах. Однако в данном примере это кажется более удобным: каждый рекурсивный вызов будет прямо заменяться добавлением параметров в очередь.
7.2. Запоминание последовательности рекурсивных вызовов
Как говорилось выше, рекурсивные вызовы образуют дерево, где каждый узел соответствует вызову одной процедуры. Последовательность выполнения этих процедур соответствует тому или иному алгоритму обхода узлов. Если требуется много раз обойти узлы одного и того же дерева, то можно один раз обойти их рекурсивно, запомнить количество и последовательность узлов, а затем, пользуясь этой информацией, обходить узлы уже нерекурсивно.
Например, в разделе 6.3 обсуждалась задача вычисления арифметических выражений, заданных строкой. Может возникнуть ситуация, когда одно и то же выражение потребуется вычислить много раз при различных значениях переменной x. Синтаксическое дерево, которое требуется обходить при таких вычислениях, не зависит от x. Можно обойти его один раз, построив при этом массив, где каждый элемент будет соответствовать узлу дерева, а их последовательность – порядку обхода. Повторные вычисления при новом x потребуют только нерекурсивного перебора элементов массива.
Еще один пример такого запоминания в задаче о вычислении значений многомерных полиномов смотрите тут: http://tvd-home.ru/numerical/polynom.
Такой подход не избавляет нас от рекурсии полностью. Однако он позволяет ограничиться только одним обращением к рекурсивной процедуре, что может быть достаточно, если мотивом является забота о максимальной производительности.
7.3. Определение узла дерева по его номеру
Идея данного подхода в том, чтобы заменить рекурсивные вызовы простым циклом, который выполнится столько раз, сколько узлов в дереве, образованном рекурсивными процедурами. Что именно будет делаться на каждом шаге, следует определить по номеру шага. Сопоставить номер шага и необходимые действия – задача не тривиальная и в каждом случае ее придется решать отдельно.
Например, пусть требуется выполнить k вложенных циклов по n шагов в каждом:
for i1 := 0 to n-1 do
for i2 := 0 to n-1 do
for i3 := 0 to n-1 do
…
Если k заранее неизвестно, то написать их явным образом, как показано выше невозможно. Используя прием, продемонстрированный в разделе 6.5 можно получить требуемое количество вложенных циклов с помощью рекурсивной процедуры:
procedure NestedCycles(Indexes: array of integer; n, k, depth: integer);
var
i: integer;
begin
if depth <= k then
for i:=0 to n-1 do
begin
Indexes[depth] := i;
NestedCycles(Indexes, n, k, depth + 1);
end
else
DoSomething(Indexes);
end;
Чтобы избавиться от рекурсии и свести все к одному циклу, обратим внимание, что если нумеровать шаги в системе счисления с основанием n, то каждый шаг имеет номер, состоящий из цифр i1, i2, i3, … или соответствующих значений из массива Indexes. То есть цифры соответствуют значениям счетчиков циклов. Номер шага в обычной десятичной системе счисления:
Всего шагов будет nk. Перебрав их номера в десятичной системе счисления и переведя каждый из них в систему с основанием n, получим значения индексов:
M := round(IntPower(n, k));
for i := 0 to M-1 do
begin
Number := i;
for p := 0 to k-1 do
begin
Indexes[k – p] := Number mod n;
Number := Number div n;
end;
DoSomething(Indexes);
end;
Еще раз отметим, что метод не универсален и под каждую задачу придется придумывать что-то свое.
Еще один замечательный пример — вычисление по номеру шага перекладываний в задаче о Ханойских башнях смотрите тут: http://algolist.manual.ru/maths/combinat/hanoi.php
Контрольные вопросы
1. Определите, что сделают приведенные ниже рекурсивные процедуры и функции.
(а) Что напечатает приведенная ниже процедура при вызове Rec(4)?
procedure Rec(a: integer);
begin
writeln(a);
if a>0 then
Rec(a-1);
writeln(a);
end;
(б) Чему будет равно значение функции Nod(78, 26)?
function Nod(a, b: integer): integer;
begin
if a > b then
Nod := Nod(a – b, b)
else
if b > a then
Nod := Nod(a, b – a)
else
Nod := a;
end;
(в) Что будет напечатано приведенными ниже процедурами при вызове A(1)?
procedure A(n: integer); procedure B(n: integer); procedure A(n: integer); begin writeln(n); B(n-1); end; procedure B(n: integer); begin writeln(n); if n < 5 then A(n+2); end;
(г) Что напечатает нижеприведенная процедура при вызове BT(0, 1, 3)?
procedure BT(x: real; D, MaxD: integer);
begin
if D = MaxD then
writeln(x)
else
begin
BT(x – 1, D + 1, MaxD);
BT(x + 1, D + 1, MaxD);
end;
end;
2. Уроборос – змей, пожирающий собственный хвост (рис. 14) в развернутом виде имеет длину L, диаметр около головы D, толщину брюшной стенки d. Определите, сколько хвоста он сможет в себя впихнуть и в сколько слоев после этого будет уложен хвост?
Рис. 14. Развернутый уроборос.
3. Для дерева на рис. 10а укажите последовательности посещения узлов при прямом, обратном и концевом порядке обхода.
4. Изобразите графически дерево, заданное с помощью вложенных скобок: (A(B(C, D), E), F, G).
5. Изобразите графически синтаксическое дерево для следующего арифметического выражения:
Запишите это выражение в обратной польской записи.
6. Для приведенного ниже графа (рис. 15) запишите матрицу смежности и матрицу инцидентности.
Рис. 15.
Задачи
1. Вычислив факториал достаточно большое количество раз (миллион или больше), сравните эффективность рекурсивного и итерационного алгоритмов. Во сколько раз будет отличаться время выполнения и как это отношение будет зависеть от числа, факториал которого рассчитывается?
2. Напишите рекурсивную функцию, проверяющую правильность расстановки скобок в строке. При правильной расстановке выполняются условия:
(а) количество открывающих и закрывающих скобок равно.
(б) внутри любой пары открывающая – соответствующая закрывающая скобка, скобки расставлены правильно.
Примеры неправильной расстановки: )(, ())(, ())(() и т.п.
3. В строке могут присутствовать скобки как круглые, так и квадратные скобки. Каждой открывающей скобке соответствует закрывающая того же типа (круглой – круглая, квадратной- квадратная). Напишите рекурсивную функцию, проверяющую правильность расстановки скобок в этом случае.
Пример неправильной расстановки: ( [ ) ].
4. Число правильных скобочных структур длины 6 равно 5: ()()(), (())(), ()(()), ((())), (()()).
Напишите рекурсивную программу генерации всех правильных скобочных структур длины 2n.
Указание: Правильная скобочная структура минимальной длины «()». Структуры большей длины получаются из структур меньшей длины, двумя способами:
(а) если меньшую структуру взять в скобки,
(б) если две меньших структуры записать последовательно.
5. Создайте процедуру, печатающую все возможные перестановки для целых чисел от 1 до N.
6. Создайте процедуру, печатающую все подмножества множества {1, 2, …, N}.
7. Создайте процедуру, печатающую все возможные представления натурального числа N в виде суммы других натуральных чисел.
8. Создайте функцию, подсчитывающую сумму элементов массива по следующему алгоритму: массив делится пополам, подсчитываются и складываются суммы элементов в каждой половине. Сумма элементов в половине массива подсчитывается по тому же алгоритму, то есть снова путем деления пополам. Деления происходят, пока в получившихся кусках массива не окажется по одному элементу и вычисление суммы, соответственно, не станет тривиальным.
Замечание: Данный алгоритм является альтернативой приему накопления суммы. В случае вещественнозначных массивов он, обычно, позволяет получать меньшие погрешности округления.
9. Запрограммируйте быстрые методы сортировки массивов, описанные в разделе 6.4.
10. Создайте процедуру, рисующую кривую Коха (рис. 12).
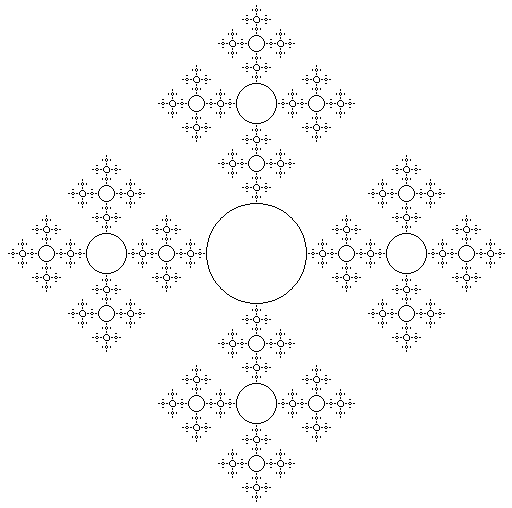
11. Воспроизведите рис. 16. На рисунке на каждой следующей итерации окружности в 2.5 раза меньше (этот коэффициент можно сделать параметром).
Рис. 16.
Литература
1. Д. Кнут. Искусство программирования на ЭВМ. т. 1. (раздел 2.3. «Деревья»).
2. Н. Вирт. Алгоритмы и структуры данных.
Другие материалы на этом сайте
Близкие разделы учебника по программированию:
Рекуррентные соотношения
Рекурсивные структуры данных
Вычисление полиномов от нескольких переменных — еще один пример рекурсивного алгоритма.

Здравствуйте, друзья!
Мы продолжаем разбирать максимально простым языком алгоритмы и структуры данных на JavaScript. Тема нашей сегодняшней статьи — рекурсия. Для многих разработчиков рекурсия кажется чем-то очень сложным и непонятным, но не переживайте, не так страшен черт, как его малюют.
И сегодня мы узнаем, как устроена рекурсия, а также разберем алгоритм сортировки массива под названием Quick Sort или, как еще его называют, быстрая сортировка Хоара. Как вы уже догадались, этот алгоритм рекурсивный.
Если вы еще не читали нашу первую статью (про алгоритмы поиска и Big O нотацию), то можете найти ее здесь.
Ссылку на вторую статью (про алгоритмы сортировки и оценку сложности алгоритмов по скорости и памяти) вы можете найти здесь.
А сейчас давайте перейдем к теме статьи.
Рекурсия
Рекурсия, если максимально упростить, это вызов функцией самой себя. Этот приём программирования можно использовать, когда есть возможность разбить задачу на несколько более простых подзадач. И, написав решение этой подзадачи в функции и вызывая такую функцию рекурсивно, мы можем все эти подзадачи итеративно решить.
Давайте взглянем на простой пример.
У нас есть простая функция обратного отсчёта:
function countDown(n) {
for (let i = n; i > 0; i--) {
console.log(i);
}
console.log('Финиш');
}Данная функция принимает аргументом число n и выводит на экран числовую последовательность от n до 1 включительно, а в конце, после завершения работы цикла, выводит на экран слово «Финиш».
Давайте вызовем эту функцию, передав в нее число 3. В консоли мы получим следующий результат: «3 2 1 Финиш».
countDown(3); // 3 2 1 ФинишТеперь перепишем эту функцию на рекурсивный манер:
function countDownRecursive(n) {
if (n <= 0) {
console.log('Финиш');
return;
}
console.log(n);
countDownRecursive(n - 1);
}Разберемся, как эта функция работает. Первым делом, чтобы не получить бесконечный цикл вызовов функции и как результат ошибку «stack overflow», которая говорит нам о превышении лимита вызовов для функции в стеке, нужно определить так называемый базовый случай.
Базовый случай — это условие, при котором наша функция должна перестать вызывать саму себя рекурсивно.
Так как наш цикл работал до тех пор, пока i > 0, то здесь условие для прерывания цикла должно быть следующим:
if (n <= 0) {
console.log('Финиш');
return;
}То есть, как только n будет меньше или равно нулю, мы перестаем рекурсивно вызывать функцию и выходим из нее. Перед выполнением оператора return необходимо будет вызвать наш console.log('Финиш'), потому что именно это действие и будет последним в работе функции.
По сути, базовый случай работает как оператор break в циклах, то есть прерывает вызов функцией самой себя, чтобы мы могли вернуть результат ее выполнения.
function countDownRecursive(n) {
if (n <= 0) {
console.log('Финиш');
return;
}
console.log(n); // Выводим в консоль n
countDownRecursive(n - 1);
}Дальше мы выводим в консоль текущее значение числа n. И, следующим шагом, снова вызываем нашу функцию countDownRecursive() и передаем в нее n - 1.
Как вы помните, в примере с циклом for, на каждой итерации цикла мы уменьшали число i на единицу (i--), поэтому здесь, по аналогии, передаем n - 1.
Запустим функцию и получим в консоли следующий результат:
countDownRecursive(3); // 3 2 1 ФинишРезультат, как вы видите, аналогичен результату работы простой функции countDown.
Давайте теперь чуть подробнее разберём, как работает рекурсивная функция.
Как работает рекурсивная функция
function countDownRecursive(n) {
if (n <= 0) {
console.log('Финиш');
return;
}
console.log(n);
countDownRecursive(n - 1);
}
countDownRecursive(3); // 3 2 1 ФинишИтак, сначала мы вызываем функцию countDownRecursive со значением 3.
countDownRecursive(3);Базовый случай не отрабатывает, потому что n > 0. Мы выводим число 3 в консоль и дальше снова вызываем функцию, передав в нее n - 1, то есть 3 — 1 или просто число 2.
countDownRecursive(3);
countDownRecursive(2);Повторяем эту процедуру, пока не дойдем до нуля:
countDownRecursive(3);
countDownRecursive(2);
countDownRecursive(1);
countDownRecursive(0); // Отрабатывает базовый случай!И вот здесь уже срабатывает базовый случай. Так как 0 === 0, выводим в консоль слово «Финиш» и дальше срабатывает оператор return.
countDownRecursive(3);
countDownRecursive(2);
countDownRecursive(1);
countDownRecursive(0); // Отрабатывает базовый случай!
return;
return;
return;
return;Дальше происходит завершение работы всех предыдущих функций (потому что неявно завершенная функция возвращает undefined, то есть как только выполнение нашей функции доходит до закрывающей фигурной скобки, происходит return undefined).
Здесь вы можете подумать, что это всё очень сложно, и почему бы не использовать такой понятный и простой цикл for?
Важно отметить, что, действительно, не везде нужно применять рекурсию. Но бывают задачи, где рекурсивное решение выглядет очень элегантно и занимает гораздо меньше строчек кода, чем с использованием традиционных циклов.
Давайте разберем один из таких примеров.
Числа Фибоначчи
Как вы знаете, ряд Фибоначчи — это числовая последовательность, первые два числа которой являются единицами, а каждое последующее за ними число является суммой двух предыдущих.
Автором данной числовой последовательности был Леонардо Пизанский (более известный под прозвищем Фибоначчи) из итальянского города Пизы — один из крупнейших математиков средневековой Европы.
Вот так ряд Фибоначчи выглядит на практике:
1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987, 1597, 2584,
4181 //...и так далее до бесконечности.Иногда перед первой единицей добавляют еще и ноль, но мы не будем рассматривать данный случай, а рассмотрим классический ряд Фибоначчи, как в средневековых книгах (но только без кроликов).
Наша задача — написать функцию, которой можно передать номер элемента ряда Фибоначчи, и на выходе из функции получить значение этого элемента.
Допустим, мы ищем 10-ый элемент в последовательности. Значением этого элемента будет 55. Для 12-го элемента значением будет 144 и так далее.
Вот так будет выглядеть эта функция, написанная с применением рекурсии:
const fibonachi = (n) => {
if (n < 2) {
return n;
}
return fibonachi(n - 1) + fibonachi(n - 2);
};
console.log(fibonachi(6)); // 8В результате работы функции в консоли мы получим число 8. Можете это проверить: если вы посмотрите на ряд Фибоначчи выше, то увидите, что значением 6-го элемента в ряду будет число 8.
Давайте разберём, как работает данная функция.
const fibonachi = (n) => {
// Реализация функции
};Объявляем стрелочную функцию fibonachi, которая принимает аргументом число искомого элемента в ряду — n.
const fibonachi = (n) => {
if (n < 2) {
return n;
}
};Далее определяем базовый случай, т.е. условие, при котором выходим из рекурсии.
Так как мы будем последовательно уменьшать число n (об этом ниже), то нет смысла делать это бесконечно.
Как только n оказывается меньше 2, то это значит, что мы достигли начала ряда Фибоначчи, а значит дальше нам двигаться не нужно и можно возвращать n обратно вызывающему коду.
const fibonachi = (n) => {
if (n < 2) {
return n;
}
return fibonachi(n - 1) + fibonachi(n - 2);
};
console.log(fibonachi(6)); // 8Если же базовый случай не отработал, то снова вызываем функцию, передав в ее аргументы n - 1 и n - 2 соответственно, и складываем результат этих функций между собой по следующей формуле: F(n) = F(n - 1) + F(n - 2). Эта формула позволяет нам найти число из ряда Фибоначчи. Так как каждое число равно сумме двух предыдущих чисел в цепочке, то именно эту формулу мы реализовали в нашей функции.
Если вам до конца не понятно объяснение данного алгоритма, то, во-первых, это абсолютно нормально, а во-вторых, можете посмотреть подробное видео, объясняющее работу данной функции здесь.
Быстрая сортировка Хоара
А теперь рассмотрим более сложный алгоритм. Он называется быстрая сортировка (Quick Sort) или сортировка Хоара.
Данный алгоритм был разработан английским информатиком Тони Хоаром во время работы в МГУ в 1960 году.
И вот здесь как раз будет применяться рекурсия.
Как вы помните, в предыдущей статье мы с вами разбирали широко известный в узких кругах алгоритм — пузырьковую сортировку. Ее единственный недостаток — это крайне низкая эффективность. Быстрая же сортировка является улучшенной версией подобных алгоритмов сортировки с помощью прямого обмена.
Итак, в чем суть. Имеется неотсортированный массив чисел arr.
const arr = [-5, 23, 7, 5, 3, -12, -29, 21, 54, 35, 0];Наша задача написать функцию, которая будет принимать в себя аргументом этот массив и возвращать его полностью отсортированным по возрастанию.
Быстрая сортировка относится к алгоритмам из серии «разделяй и властвуй».
Небольшое отступление. Алгоритмы типа «разделяй и властвуй» (англ. divide and conquer) — это парадигма разработки алгоритмов, заключающаяся в рекурсивном разбиении решаемой задачи на две или более подзадачи того же типа, но меньшего размера, и комбинировании их решений для получения ответа к исходной задаче. Разбиения выполняются до тех пор, пока все подзадачи не окажутся элементарными.
Наш алгоритм будет сводиться к следующим шагам:
1. Выбираем элемент из массива и считаем его опорным (в англоязычной литературе его называют pivot).
2. Сортируем элементы в массиве таким образом, чтобы элементы меньше опорного размещались в подмассиве перед ним, а большие или равные — в подмассиве после.
3. Рекурсивно применяем первые два шага к двум подмассивам слева и справа от опорного элемента. Т.е. дробим наш массив на подмассивы и сортируем их относительно опорного элемента, пока в этих подмассивах не останется по одному элементу или меньше. Рекурсия не применяется к массиву, в котором только один элемент или отсутствуют элементы. Это как раз и будет базовым условием, при котором мы прервем рекурсию.
Вот здесь вы можете увидеть визуализацию работы быстрой сортировки (а также многих других алгоритмов).
А вот так выглядит реализация сортировки Хоара на JavaScript:
const arr = [-5, 23, 7, 5, 3, -12, -29, 21, 54, 35, 0];
function quickSort(arr) {
if (arr.length <= 1) {
return arr;
}
let pivotIndex = Math.floor(arr.length / 2);
let pivot = arr[pivotIndex];
let less = [];
let greater = [];
for (let i = 0; i < arr.length; i++) {
if (i === pivotIndex) continue;
if (arr[i] < pivot) {
less.push(arr[i]);
} else {
greater.push(arr[i]);
}
}
return [...quickSort(less), pivot, ...quickSort(greater)];
}
console.log(quickSort(arr));Подробный разбор алгоритма сортировки Хоара
Давайте подробно разберём, как работает данная сортировка.
const arr = [-5, 23, 7, 5, 3, -12, -29, 21, 54, 35, 0];
function quickSort(arr) {
// Реализация алгоритма
}Создаем функцию quickSort() и передаем аргументом неотсортированный массив.
Дальше, как вы помните, необходимо определить базовый случай выхода из рекурсии.
const arr = [-5, 23, 7, 5, 3, -12, -29, 21, 54, 35, 0];
function quickSort(arr) {
// Базовый случай выхода из рекурсии
if (arr.length <= 1) {
return arr;
}
}Так как нам предстоит дробить основной массив на подмассивы и сортировать элементы в этих подмассивах относительно опорного элемента (об этом ниже), то как только такие подмассивы будут содержать по одному элементу или будут пустыми, нам нет смысла дальше продолжать разбивать их на более мелкие части, поэтому здесь мы выйдем из рекурсии.
const arr = [-5, 23, 7, 5, 3, -12, -29, 21, 54, 35, 0];
function quickSort(arr) {
if (arr.length <= 1) {
return arr;
}
// Индекс опорного элемента в массиве
let pivotIndex = Math.floor(arr.length / 2);
// Опорный элемент
let pivot = arr[pivotIndex];
}Теперь определим индекс в массиве так называемого опорного элемента. Для этого создадим переменную pivotIndex, передадим в функцию Math.floor длину массива, поделим результат на 2 и получившееся число присвоим переменной pivotIndex. Функция Math.floor, как вы знаете, округляет результат в меньшую сторону:
Math.floor(5.5); // 5Затем определим сам опорный элемент. Для этого кладем в переменную pivot значение массива по индексу pivotIndex. В массиве arr значением pivotIndex будет 5 (длина массива — 11. 11 делим на 2 и округляем в меньшую сторону, получаем 5). Значением pivot будет -12.
const arr = [-5, 23, 7, 5, 3, -12, -29, 21, 54, 35, 0];
function quickSort(arr) {
if (arr.length <= 1) {
return arr;
}
let pivotIndex = Math.floor(arr.length / 2);
let pivot = arr[pivotIndex];
// Сюда положим все элементы меньше опорного
let less = [];
// Сюда положим все элементы больше опорного
let greater = [];
}Дальше нужно объявить два пустых подмассива less и greater. В массив less будем сохранять все элементы, которые меньше опорного, а в greater все элементы, которые больше опорного.
Дальше в цикле for мы пробегаем по всем элементам массива и сравниваем каждый элемент с опорным.
const arr = [-5, 23, 7, 5, 3, -12, -29, 21, 54, 35, 0];
function quickSort(arr) {
if (arr.length <= 1) {
return arr;
}
let pivotIndex = Math.floor(arr.length / 2);
let pivot = arr[pivotIndex];
let less = [];
let greater = [];
for (let i = 0; i < arr.length; i++) {
// Пропускаем итерацию, если индекс текущей итерации совпадает
// с индексом опорного элемента
if (i === pivotIndex) continue;
// Если опорный элемент больше элемента в массиве, добавляем
// этот элемент в массив less
if (arr[i] < pivot) {
less.push(arr[i]);
// Иначе добавляем его в массив greater
} else {
greater.push(arr[i]);
}
}
}Затем у нас идут три условия. В первом условии мы сравниваем индекс текущей итерации цикла с индексом опорного элемента в массиве.
Если они совпадают, то текущую итерацию цикла мы завершаем с помощью ключевого слова continue, так как нам не нужно добавлять опорный элемент в один из наших подмассивов.
Далее во втором условии мы сравниваем элемент массива с опорным элементом. Если опорный элемент больше, то добавляем наш текущий элемент массива в массив less.
В противном же случае, добавляем текущий элемент массива в массив greater (третье условие).
В итоге, после завершения цикла for, у нас на выходе будет 2 массива: less с числами меньше опорного и greater с числами больше опорного или равными ему.
И дальше мы возвращаем массив, в который разворачиваем результат рекурсивного выполнения функции, принимающей в качестве аргумента массив less. Дальше вставляем наш опорный элемент pivot, а после снова разворачиваем результат выполнения функции для массива greater.
const arr = [-5, 23, 7, 5, 3, -12, -29, 21, 54, 35, 0];
function quickSort(arr) {
if (arr.length <= 1) {
return arr;
}
let pivotIndex = Math.floor(arr.length / 2);
let pivot = arr[pivotIndex];
let less = [];
let greater = [];
for (let i = 0; i < arr.length; i++) {
if (i === pivotIndex) continue;
if (arr[i] < pivot) {
less.push(arr[i]);
} else {
greater.push(arr[i]);
}
}
// Рекурсивно вызываем функцию quickSort, передаем туда наши
// массивы и разворачиваем результат в возвращаемый массив,
// не забывая вставлять посередине опорный элемент
return [...quickSort(less), pivot, ...quickSort(greater)];
}
// Выводим в логи результат работы функции
console.log(quickSort(arr));Когда функция доходит до базового случая, рекурсивный вызов функции заканчивается и все одиночные массивы соединяются в один большой отсортированный массив.
Выведем в консоль результат работы функции и убедимся в этом.
Быстрая сортировка в среднем и лучшем случае выполняется за Θ(n * log(n)) и Ω(n * log(n)) соответственно.
В худшем случае время выполнения алгоритма занимает О(n^2).
Более подробно про лучшее, среднее и худшее время выполнения алгоритма быстрой сортировки можно прочитать здесь.
На этом мы закончили третью статью из нашего цикла статей по алгоритмам. Спасибо за внимание и до новых встреч!

Ханойская башня — это знаменитая древняя головоломка. Она состоит из трех стержней, на один из которых надеты кольца разного размера.
Надо перенести все кольца на другой стержень, при этом кольца можно переносить только по одному. Главное правило: никогда нельзя класть кольцо большего размера на кольцо меньшего.
Попробуем спроектировать алгоритм, который решит эту головоломку. Для начала формализуем задачу:
-
Обозначим стержни числами 1, 2 и 3
-
Определимся, что нам нужен универсальный алгоритм, который решает головоломку при любой высоте башен
-
Назовем функцию
hanoiи зададим ей три параметра:-
Количество колец (высота башни, которую мы хотим перенести)
-
Номер стержня, откуда мы будем переносить башню
-
Номер стержня, куда мы будем переносить башню
-
Таким образом, вызов hanoi(10, 1, 3) будет означать: «Перенести башню из десяти колец с первого стержня на третий».
Функция должна печатать последовательность переносов: взять верхнее кольцо со стержня №1 и перенести его на стержень №2. Мы не можем взять второе сверху кольцо или пятое сверху — только самое верхнее. Поэтому нам достаточно просто выводить номера обоих стержней: откуда снимать кольцо и куда переносить.
Если оставить все как есть, мы столкнемся с такой проблемой: можно перенести первые два кольца, но третье кольцо переместить не получится, потому что оно больше обоих колец на соседних стержнях. Как быть?
Здесь на помощь приходит рекурсия. Попробуем упростить задачу и свести ее к самой себе:
-
Предположим, что мы уже умеем переносить башню из четырех колец
-
Дальше нам надо перенести башню из пяти с первого стержня на второй
-
Воспользуемся третьим стержнем и перенесем на него четыре верхних кольца
-
Теперь можем взять самое большое кольцо с первого стержня и перенести его на пустой второй
-
Осталось снять башню из четырех колец со вспомогательного третьего стержня и перенести ее на второй стержень, на котором уже лежит большое пятое кольцо второго стержня — это мы уже умеем
Можно ли будет класть какие-то кольца поверх самого большого пятого? Да, потому что правила запрещают только класть большие кольца на меньше, а наоборот — нет. Оказывается, что этих рассуждений достаточно, чтобы написать рекурсивную функцию.
Только мы знаем, что рекурсия должна где-то останавливаться. В нашем случае минимальная задача, которую мы можем решить — перенос башни из одного кольца. Она решается тривиально: одно кольцо мы можем перенести безо всяких условий, поэтому нам достаточно просто вывести номера стержней «откуда» и «куда»:
const hanoi = (height, from, to) => {
if (height === 1) {
console.log("с %d на %d", from, to);
return;
}
const temporary = 6 - from - to;
hanoi(height - 1, from, temporary);
console.log("с %d на %d", from, to);
hanoi(height - 1, temporary, to);
};
hanoi(4, 1, 2);
// => с 1 на 3
// => с 1 на 2
// => с 3 на 2
// => с 1 на 3
// => с 2 на 1
// => с 2 на 3
// => с 1 на 3
// => с 1 на 2
// => с 3 на 2
// => с 3 на 1
// => с 2 на 1
// => с 3 на 2
// => с 1 на 3
// => с 1 на 2
// => с 3 на 2Python
def hanoi(height, start, to):
if height == 1:
print(f'с {start} на {to}')
return
temporary = 6 - start - to
hanoi(height - 1, start, temporary)
print(f'с {start} на {to}')
hanoi(height - 1, temporary, to)
hanoi(4, 1, 2)
# => с 1 на 3
# => с 1 на 2
# => с 3 на 2
# => с 1 на 3
# => с 2 на 1
# => с 2 на 3
# => с 1 на 3
# => с 1 на 2
# => с 3 на 2
# => с 3 на 1
# => с 2 на 1
# => с 3 на 2
# => с 1 на 3
# => с 1 на 2
# => с 3 на 2PHP
<?php
function hanoi($height, $from, $to)
{
if ($height === 1) {
print_r("с {$from} на {$to}");
return;
}
$temporary = 6 - $from - $to;
hanoi($height - 1, $from, $temporary);
print_r("с {$from} на {$to}");
hanoi($height - 1, $temporary, $to);
}
hanoi(4, 1, 2);
// => с 1 на 3
// => с 1 на 2
// => с 3 на 2
// => с 1 на 3
// => с 2 на 1
// => с 2 на 3
// => с 1 на 3
// => с 1 на 2
// => с 3 на 2
// => с 3 на 1
// => с 2 на 1
// => с 3 на 2
// => с 1 на 3
// => с 1 на 2
// => с 3 на 2Java
class App {
public static void hanoi(int height, int from, int to) {
if (height == 1) {
System.out.println(String.format("с %d на %d", from, to));
return;
}
var temporary = 6 - from - to;
hanoi(height - 1, from, temporary);
System.out.println(String.format("с %d на %d", from, to));
hanoi(height - 1, temporary, to);
}
}
App.hanoi(4, 1, 2);
// => с 1 на 3
// => с 1 на 2
// => с 3 на 2
// => с 1 на 3
// => с 2 на 1
// => с 2 на 3
// => с 1 на 3
// => с 1 на 2
// => с 3 на 2
// => с 3 на 1
// => с 2 на 1
// => с 3 на 2
// => с 1 на 3
// => с 1 на 2
// => с 3 на 2Удивительно, что этот алгоритм казался сложным на словах, но в коде получился таким простым. Здесь мы применили один трюк, который помогает упростить код. Разберем его подробнее.
Во время работы алгоритма стержни постоянно меняются ролями. Например, если мы хотим перенести башню с первого стержня на третий, то второй стержень выступает как вспомогательный — туда мы перенесем все кольца, кроме нижнего. А если мы переносим маленькую башню с первого стержня на второй, то роль вспомогательного переходит третьему стержню.
Чтобы определить номер вспомогательного стержня, надо написать сложное условие:
if (from === 1 && to === 2 || from === 2 && to === 1) {
temporary = 3;
} else if (from === 2 && to === 3 || from === 3 && to === 2) {
temporary = 1;
} else if (from === 1 && to === 3 || from === 3 && to === 1) {
temporary = 2;
}Python
if (start == 1 and to == 2) or (start == 2 and to == 1):
temporary = 3
elif (start == 2 and to == 3) or (start == 3 and to == 2):
temporary = 1
elif (start == 1 and to == 3) or (start == 3 and to == 1):
temporary = 2PHP
<?php
if ($from === 1 && $to === 2 || $from === 2 && $to === 1) {
$temporary = 3;
} else if ($from === 2 && $to === 3 || $from === 3 && $to === 2) {
$temporary = 1;
} else if ($from === 1 && $to === 3 || $from === 3 && $to === 1) {
$temporary = 2;
}Java
if (from == 1 && to == 2 || from == 2 && to == 1) {
temporary = 3;
} else if (from == 2 && to == 3 || from == 3 && to == 2) {
temporary = 1;
} else if (from == 1 && to == 3 || from == 3 && to == 1) {
temporary = 2;
}Несмотря на то, что логика этого кода понятна, само условие выглядит громоздким. Разберем по шагам, как оно работает. В коде используют три константы:
-
from— номер стержня, с которого мы перемещаем кольца -
to— номер стержня, на который мы хотим переместить наши кольца -
temporary— номер стержня, который мы используем для временного хранения первых n-1 дисков
Еще в вызове указано количество колец — высота башни, которую мы хотим перенести. Таким образом, вызов hanoi(n, 1, 3) будет означать: «Перенести башню из n колец с первого стержня на третий».
Обратите внимание, что сумма from, to и temporary всегда равна 6. Можно взять число 6 и вычесть из него номера стержней from и to, и тогда мы узнаем номер вспомогательного стержня:
const temporary = 6 - from - to;Python
temporary = 6 - start - toPHP
<?php
$temporary = 6 - $start - $to;Java
var temporary = 6 - from - to;Этот код гораздо проще, но требует разъяснений. В начале каждой рекурсивной функции мы должны проверить граничное условие — оно помогает не войти в бесконечный вызов. В задаче о ханойской башне граничное условие — это башня из одного кольца.
Если встретилась такая башня, надо перенести кольцо и завершить работу:
if (height === 1) {
console.log("с %d на %d", from, to);
return;
}Python
if height == 1:
print(f'с {start} на {to}')
returnPHP
<?php
if ($height === 1) {
print_r("с {$from} на {$to}");
return;
}Java
if (height == 1) {
System.out.println(String.format("с %d на %d", from, to));
return;
}Если высота башни height больше единицы, мы упрощаем задачу и сводим ее к самой себе. В случае ханойской башни такая задача — перенести башни высотой height - 1 на вспомогательный стержень. После этого можно перенести самое большое кольцо на стержень «куда», а потом — переместить на него маленькую башню со вспомогательного стержня:
hanoi(height - 1, from, temporary);
console.log("с %d на %d", from, to);
hanoi(height - 1, temporary, to);Python
hanoi(height - 1, up, temporary)
print(f'с {start} на {to}');
hanoi(height - 1, temporary, to)PHP
<?php
hanoi($height - 1, $from, $temporary);
print_r("с {$from} на {$to}");
hanoi($height - 1, $temporary, $to);Java
hanoi(height - 1, from, temporary);
System.out.println(String.format("с %d на %d", from, to));
hanoi(height - 1, temporary, to);