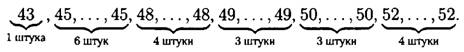Как составить ряд распределения числа - Исправление недочетов и поиск решений вместе с Examum.ru

Составление ряда распределений и вычисление числовых характеристик для подсчета вероятностей числа успехов. Независимые повторные испытания. Схема Бернулли.

Задача
9. Вероятность
того, что образец бетона выдержит
нормативную нагрузку, равна 0.9. Случайная
величина X
– число образцов, которые выдержат
испытания. Составить ряд распределения,
найти функцию распределения ДСВ X,
построить её график и найти все числовые
характеристики, если в нашем распоряжении
5 образцов.

Решение:

№ п/п	Алгоритмы	Конкретное соответствие задания заданному алгоритму
1.	Ввести обозначения для заданных величин	n — число испытаний m — число образцов, выдержавших испытания p — вероятность выдержать испытание p=0.9, q=1-p=0.1, n=7 Найти ; ; ; ; ;
2.	Сосчитать требуемую вероятность, выбрав соответствующую содержанию задачи формулу Бернулли.	Так как , нужно воспользоваться формулой Бернулли – пункт а) ;
3	Найти числовые характеристики ДСВ по формулам МX=np DX=npq	МX=np=5·0.9=0.45 DX=npq=5·0.9·0.1=0.045 .
4	Составить ряд распределений случайной величины X – числа возможных образцов
	x	0	1	2	3	4	5
P	0.00001	0.00045	0.0081	0.0729	0.328	0.59

5	Составить функцию распределения случайной величины X – числа возможных образцов

Алгоритм 10

Составление ряда распределений и вычисление числовых характеристик для вычисления вероятностей числа успехов в k-ом испытании

(геометрические
распределения)

Задача
№ 10. Вероятность
того, что образец бетона выдержит
нормативную нагрузку, равна 0.9. Случайная
величина X
– число возможных испытаний до появления
первого бракованного образца. Составить
ряд распределения, найти функцию
распределения ДСВ X,
построить её график и найти все числовые
характеристики (ограничиться тремя-пятью
испытаниями).

№ п/п	Алгоритмы	Конкретное соответствие задания заданному алгоритму
1.	Ввести обозначения для заданных величин	n – число испытаний p – вероятность выдержать испытание p=0.9, q=1-p=0.1, Найти , , , , ,
2.	Сосчитать требуемую вероятность, выбрав соответствующую содержанию задачи формулу	Т.к. случайная величина X-число возможных испытаний до появления первого бракованного образца, то воспользуемся геометрической вероятностью: и т.д.
3	Найти числовые характеристики ДСВ по формулам М(х)= D(x)=	М(х)= , D(x)= , .
4	Составить ряд распределений случайной величины X – числа возможных образцов
	x	1	2	3	4	5
P	0.1	0.09	0.0081	0.0729	0.0656

5	Составить функцию распределения случайной величины X – числа возможных образцов и построить график.

Алгоритм 11

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

Источник

Содержание

I. Определение случайной величины (СВ), дискретной случайной величины (ДСВ). Закон и многоугольник распределения ДСВ
Функция распределения
II. Операции над дискретными случайными величинами

I. Определение случайной величины (СВ), дискретной случайной величины (ДСВ). Закон и многоугольник распределения ДСВ

При бросании игральной кости могут появиться числа 1, 2, 3, 4, 5 и 6. Заранее определить возможные исходы невозможно, так как они зависят от многих случайных причин, которые не могут быть полностью учтены. В данном примере выпавшее число очков есть величина случайная, а числа 1, 2, 3, 4, 5 и 6 есть возможные значения этой величины.

Случайная величина — величина, которая в результате опыта со случайным исходом принимает то или иное числовое значение, причем заранее неизвестно, какое именно. Случайные величины (кратко: СВ) обозначают большими латинскими буквами , а принимаемые ими значения — малыми буквами

Из приведенного выше примера, видно, что случайная величина Х может принять одно из следующих возможных значений: 1, 2, 3, 4, 5, 6. Эти значения отделены одно от другого промежутками, в которых нет возможных значений Х. Таким образом, в этом примере СВ принимает отдельные, изолированные возможные значения.

Дискретной (прерывной) называют случайную величину, которая принимает отдельные, изолированные возможные значения с определенными вероятностями. Число возможных значений дискретной случайной величины может быть конечным или бесконечным.

Законом распределения дискретной случайной величины называют соответствие между возможными значениями и их вероятностями; его можно задать таблично, аналитически (в виде формулы) и графически.

Закон распределения ДСВ Х удобно задавать с помощью следующей таблицы

называемой рядом распределения. При этом возможные значения СВ Х в верхней строке этой таблицы располагаются в определенном порядке, а в нижней — соответствующие вероятности $p_i=P{X=x_i} quad (sum_i p_i=1)$ .

Графически ряд распределения изображают в виде многоугольника (или полигона) распределения.

1.1. В ящике 2 нестандартные и 4 стандартные детали. Из него последовательно вынимают детали до первого появления стандартной детали. Построить ряд и многоугольник распределения ДСВ — числа извлеченных деталей.

Решение.

Рассмотрим все возможные значения, которые может принимать случайна величина (СЛ) :

— первой вынули стандартную деталь;

— первая вынутая деталь нестандартная, вторая стандартная;

— первая деталь нестандартная, вторая деталь нестандартная, третья деталь стандартная.

Соответствующие им вероятности найдем воспользовавшись правилом умножения вероятностей (заметьте, что события зависимы):

$p_1=P{X=x_1=1}=frac{4}{6}=frac{2}{3}$

$p_2=P{X=x_2=2}=frac{2}{6}cdot frac{4}{5}=frac{4}{15}$

$p_3=P{X=x_3=3}=frac{2}{6}cdot frac{1}{5}cdot frac{4}{4}=frac{1}{15}$

Тогда закон распределения дискретной случайной величины Х примет вид:

Построим многоугольник распределения, отложив на оси абсцисс (ОХ) значения ДСВ Х, а на оси ординат (ОY) соответствующие им вероятности:

1.2. В партии, содержащей 20 изделий, имеется четыре изделия с дефектами. Наудачу отобрали три изделия для проверки их качества. Построить ряд распределения числа дефектных изделий, содержащихся в указанной выборке.

Решение.

— число дефектных изделий, содержащихся в выборке.

Рассмотрим все возможные значения, которые может принимать случайна величина (СЛ) :

— ни одно изделие выборки не является дефектным, т.е. все изделия удовлетворяют стандарту;

— выборка содержит одно изделие с дефектом и два стандартных изделия;

— выборка содержит два изделия с дефектом и одно стандартное изделие;

— выборка содержит три изделия с дефектом;

Найдем соответствующие им вероятности :

$[p_1=P(X=0)=frac{C_{16}^3cdot C_{4}^0}{C_{20}^3}]$

$[p_2=P(X=1)=frac{C_{16}^2cdot C_{4}^1}{C_{20}^3}]$

$[p_3=P(X=2)=frac{C_{16}^1cdot C_{4}^2}{C_{20}^3}]$

$[p_4=P(X=3)=frac{C_{16}^0cdot C_{4}^3}{C_{20}^3}]$

Тогда закон распределения дискретной случайной величины Х примет вид:

	0	1	2	3
	$frac{28}{57}$	$frac{8}{19}$	$frac{8}{95}$	$frac{1}{285}$

1.3. Три стрелка, ведущие огонь по цели, сделали по одному выстрелу. Вероятности их попадания в цель соответственно равны 0,5; 0,6; 0,8. Построить ряд и многоугольник распределения СВ X — числа попаданий в цель.

Решение.

Пусть вероятности попадания для 1-го, 2-го и 3-го стрелков соответственно равны , тогда вероятности их промахов равны . Из предыдущих занятий должны помнить как связаны противоположные события: .

Рассмотрим все значения, которые может принять ДСВ Х — числа попаданий в цель.

— ни один из стрелков не попал в цель;

— один из стрелков попал в цель;

— двое стрелков поразили цель;

— три стрелка поразили цель.

Найдем соответствующие им вероятности :

$p_0=P{X=0}=g_1 cdot g_2 cdot g_3 =0,5cdot 0,4 cdot 0,2=0,04;$

$p_1=P{X=1}=h_1 cdot g_2 cdot g_3+g_1 cdot h_2 cdot g_3 +g_1 cdot g_2 cdot h_3=\ =0,5cdot 0,4 cdot 0,2+0,5cdot 0,6 cdot 0,2+0,5cdot 0,4 cdot 0,8=0,04+0,06+0,16=0,26.$

Запись вида означает, что 1-й стрелок попал, два других промахнулись, аналогичные рассуждения применимы к другим слагаемым.

$p_2=P{X=2}=h_1 cdot h_2 cdot g_3+g_1 cdot h_2 cdot h_3 +h_1 cdot g_2 cdot h_3=\ =0,5cdot 0,6 cdot 0,2+0,5cdot 0,6 cdot 0,8+0,5cdot 0,4 cdot 0,8=0,06+0,24+0,16=0,46$ — (двое из трех поразили цель);

$p_3=P{X=3}=h_1 cdot h_2 cdot h_3=0,5cdot 0,6 cdot 0,8=0,24$ — (три стрелка поразили цель).

Контроль: $sum_{i=0}^3=0,04+0,26+0,46+0,24=1$

	0	1	2	3
	0,04	0,26	0,46	0,24

Многоугольник распределения:

Функция распределения

Функцией распределения называют функцию , определяющую вероятность того, что случайная величина в результате испытания примет значение, меньшее некоторого фиксированного значения

Свойства функции распределения:

— неубывающая функция, т.е. , если
непрерывна слева в любой точке , т.е.

Функция распределения ДСВ имеет вид

$[F(x)=sum_{x_i<x} p_i]$

где суммирование ведется по всем индексам , для которых

1.4. Задан закон распределения ДСВ Х:

	-2	-1	0	2	3
	0,1	0,2	0,3	0,3	0,1

Найти функцию распределения и построить ее график.

Решение.

По определению функции распределения находим:

если , то , так как значения меньше -2 ДСВ Х не принимает;

если , то

если , то , так как может принять значения -2 или -1

если , то

если , то $F(x)=P{X<x}=P{X=-2}+P{X=-1}+P{X=0}+\+P{X=2}+P{X=3}=0,1+0,2+0,3+0,3+0,1=1$

Таким образом, функция распределения имеет вид:

$begin{displaymath} F(x) = left{ begin{array}{ll} 0, qquad xle -2 , \ 0,1, qquad -2< x le -1,\ 0,3, qquad -1< x le 0,\ 0,6, qquad 0< x le 2,\ 0,9, qquad 2< x le 3, \ 1, qquad x>3. end{array} right. end{displaymath}$

II. Операции над дискретными случайными величинами

Суммой (соответственно, разностью или произведением) ДСВ Х, принимающей значения с вероятностями $p_i=P{X=x_i}, quad i=1,2, ... , n$ и ДСВ Y, принимающей значения с вероятностями $q_j=P{Y=y_j}, quad j=1,2, ... , m$ называется ДСВ, принимающая все значения вида (соответственно, или ) с вероятностями $p_{ij}=P{{X=x_i}cdot {Y=y_j}}=P{X=x_i,quad Y=y_j}.$

Обозначение: (соответственно, или ).

Произведением ДСВ Х на число называется ДСВ , принимающая значения с вероятностями $p_i=P{X=x_i}.$

Квадратом (соответственно, m-ой степенью) ДСВ Х называется ДСВ, принимающая значения (соответственно, ) с вероятностями $p_i=P{X=x_i}.$ Обозначение: (соответственно, ).

Дискретные СВ Х и Y называются независимыми, если независимы события ${X=x_i}$ и ${Y=y_j}$ при любых

2.1. Задано распределение ДСВ Х

	-2	-1	1	2	3
	0,2	0,25	0,3	0,15	0,1

Построить ряд распределения случайных величин:

а)

б)

Решение.

Возможные значения СВ Y таковы:

Вероятности значений СВ Y равны вероятностям соответствующих значений СВ Х (например, и т. д.), т.е. каждое значение СВ Х мы умножаем на 2, а вероятности оставляем прежними. Таким образом

	-4	-2	2	4	6
	0,2	0,25	0,3	0,15	0,1

б) Значения СВ Z таковы (возведем каждое значение СВ Х в квадрат):

$[z_1={(-2)}^2=4; z_2={(-1)}^2=1,]$

Составим вспомогательную таблицу для распределения СВ

	4	1	1	4	9
	0,2	0,25	0,3	0,15	0,1

При этом мы должны помнить, что при одинаковых значениях СВ Z, соответствующие им вероятности нужно сложить, т.е.

$[P{Z=1}=P{X^2=1}=P{X=-1}+P{X=1}=0,25+0,3=0,55;]$

$[P{Z=4}=P{X^2=4}=P{X=-2}+P{X=2}=0,20+0,15=0,35.]$

Поэтому ряд распределения СВ Z имеет вид

2.2. Дискретная случайная величина Х имеет ряд распределения:

		$frac{pi}{4}$	$frac{pi}{2}$	$frac{3pi}{4}$		$frac{5pi}{4}$	$frac{3pi}{2}$
	$frac{1}{16}$	$frac{1}{8}$	$frac{3}{16}$	$frac{1}{4}$	$frac{3}{16}$	$frac{1}{8}$	$frac{1}{16}$

Построить:

а) ряд распределения СВ $Y=sin(X-frac{pi}{4});$

б) График функции распределения СВ Y

Решение.

а) Вычисляем все значения СВ Y, подставляя соответствующие значения в формулу $Y=sin(X-frac{pi}{4})$ :

$y_1=sinleft(0-frac{pi}{4}right)=sin(-frac{pi}{4})=-frac{sqrt{2}}{2}$

$y_2=sin(frac{pi}{4}-frac{pi}{4})=sin(0)=0$

$y_3=sin(frac{pi}{2}-frac{pi}{4})=sin(frac{pi}{4})=frac{sqrt{2}}{2}$

$y_4=sin(frac{3pi}{4}-frac{pi}{4})=sin(frac{pi}{2})=1$

$y_5=sin(pi-frac{pi}{4})=sin(frac{pi}{4})=frac{sqrt{2}}{2}$

$y_6=sin(frac{5pi}{4}-frac{pi}{4})=sin(pi)=0$

$y_7=sin(frac{3pi}{2}-frac{pi}{4})=-cos(frac{pi}{4})=-frac{sqrt{2}}{2}$

Составим вспомогательную таблицу ряда распределения:

	$-frac{sqrt{2}}{2}$		$frac{sqrt{2}}{2}$		$frac{sqrt{2}}{2}$		$-frac{sqrt{2}}{2}$
	$frac{1}{16}$	$frac{1}{8}$	$frac{3}{16}$	$frac{1}{4}$	$frac{3}{16}$	$frac{1}{8}$	$frac{1}{16}$

Составим ряд распределения.

При этом

$P{Y=-frac{sqrt{2}}{2}}=P{X=0}+P{X=frac{3pi}{2}}=frac{1}{16}+frac{1}{16}=frac{1}{8}$

$P{Y=0}=P{X=frac{pi}{4}}+P{X=frac{5pi}{4}}=frac{1}{8}+frac{1}{8}=frac{1}{4}$

$P{Y=frac{sqrt{2}}{2}}=P{X=frac{pi}{2}}+P{X=pi}=frac{3}{16}+frac{3}{16}=frac{3}{8}$

Т. е. записываем значения ДСВ Y в таблицу в порядке возрастания. При одинаковых значениях ДСВ соответствующие вероятности складываем.

Итак, получаем

	$-frac{sqrt{2}}{2}$		$frac{sqrt{2}}{2}$
	$frac{1}{8}$	$frac{1}{4}$	$frac{3}{8}$	$frac{1}{4}$

б) Самостоятельно.

2.3. Заданы распределения двух независимых случайных величин X и Y:

Найти:

а) функцию распределения СВ Х;

б) ряд распределения случайных величин ;

в) ;

г) построить многоугольники распределения СВ Z ,W и V.

Решение.

а) Найдите функцию распределения СВ Х самостоятельно.

б) Найдем всевозможные значения $z_{ij}=x_{i}+y_{j}$ , т. е. просуммируем все значения, которые принимает ДСВ Х, со всеми значениями ДСВ Y.

Предлагаю сделать это так, первое значение ДСВ Х сложить последовательно с каждым значением ДСВ Y, потом то же самое проделать со вторым значением ДСВ Х и с третьим. Все операции показаны в таблице ниже.

0+2=2	1+2=3	2+2=4
0+3=3	1+3=4	2+3=5
0+4=4	1+4=5	2+4=6

Т. е. случайная величина принимает значения:

Найдем вероятности этих значений:

$[p_1=P{Z=2}=P{X=0,Y=2}]$

Запись вида означает вероятность наступления 2-х независимых событий {X=0} и {Y=2}, т. е.

$p_1=P{X=0,Y=2}=P{{X=0}cdot {Y=2}}=P{X=0}cdot P{Y=2}=0,2cdot 0,3=0,06$

Для нахождения вероятностей воспользуемся правилом сложения несовместных событий:

$p_2=P{Z=3}=P{X=0,Y=3}+P{X=1,Y=2}=0,2cdot 0,3+0,4cdot 0,3=0,06+0,12=0,18;$

$p_3=P{Z=4}=P{X=0,Y=4}+P{X=1,Y=3}+P{X=2,Y=2}=0,2cdot 0,4+ \ +0,4cdot 0,3+0,4cdot 0,3=0,08+0,12+0,12=0,32;$

$p_4=P{Z=5}=P{X=1,Y=4}+P{X=2,Y=3}=0,4cdot 0,4+0,4cdot 0,3=0,16+0,12=0,28;$

$p_5=P{Z=6}=P{X=2,Y=4}=0,4cdot 0,4=0,16$

Запишем ряд распределения ДСВ

	2	3	4	5	6
	0,06	0,18	0,32	0,28	0,16

Сделаем проверку:

$sum_{i=1}^{5} p_{i}=0,06+0,18+0,32+0,28+0,16=1.$

Многоугольник распределения СВ Z представлен ниже:

Далее рассмотрим ДСВ

Найдем всевозможные значения $w_{ij}=x_{i}-y_{j}$ .

Все вычисления сведены в таблицу ниже.

0-2=-2	1-2=-1	2-2=0
0-3=-3	1-3=-2	2-3=-1
0-4=-4	1-4=-3	2-4=-2

Таким образом случайная величина принимает значения:

Замечание. Как вы видите, я выписал для удобства все значения СДВ W в порядке возрастания, так как при составления ряда распределения их (значения случайной величины) нужно располагать по возрастанию.

Найдем вероятности этих значений:

$p_1=P{W=-4}=P{X=0,Y=4}=0,2cdot 0,4=0,08$

$p_2=P{W=-3}=P{X=0,Y=3}+P{X=1,Y=4}=0,2cdot 0,3+0,4cdot 0,4=0,06+0,16=0,22;$

$p_3=P{W=-2}=P{X=0,Y=2}+P{X=1,Y=3}+P{X=2,Y=4}=0,2cdot 0,3+ \ +0,4cdot 0,3+0,4cdot 0,4=0,06+0,12+0,16=0,34;$

$p_4=P{W=-1}=P{X=1,Y=2}+P{X=2,Y=3}=0,4cdot 0,3+0,4cdot 0,3=0,12+0,12=0,24;$

$p_5=P{W=0}=P{X=2,Y=4}=0,4cdot 0,3=0,12$

Запишем ряд распределения ДСВ

	-4	-3	-2	-1	0
	0,08	0,22	0,34	0,24	0,12

Сделаем проверку: $sum_{i=1}^{5} p_{i}=0,08+0,22+0,34+0,24+0,12=1$

Многоугольник распределения СВ W представлен ниже:

По аналогии с предыдущими пунктами найдем все значения ДСВ V : $v_{ij}=x_{i}cdot y_{j}$ . Все вычисления сведены в таблицу ниже.

0·2=0	1·2=2	2·2=4
0·3=0	1·3=3	2·3=6
0·4=0	1·4=4	2·4=8

Таким образом случайная величина принимает значения:

Найдем вероятности этих значений:

$p_1=P{V=0}=P{X=0,Y=2}+P{X=0,Y=3}+P{X=0,Y=4}=0,2cdot 0,3+0,2cdot 0,3+0,2cdot 0,4=0,06+0,06+0,08=0,2;$

$p_2=P{V=2}=P{X=1,Y=2}=0,4cdot 0,3=0,12$

$p_3=P{V=3}=P{X=1,Y=3}=0,4cdot 0,3=0,12$

$p_4=P{V=4}=P{X=1,Y=4}+P{X=2,Y=2}=0,4cdot 0,4+0,4cdot 0,3=0,16+0,12=0,28;$

$p_5=P{V=6}=P{X=2,Y=3}=0,4cdot 0,3=0,12$

$p_6=P{V=8}=P{X=2,Y=4}=0,4cdot 0,4=0,16$

Запишем ряд распределения ДСВ

	0	2	3	4	6	8
	0,2	0,12	0,12	0,28	0,12	0,16

Сделаем проверку: $sum_{i=1}^{5} p_{i}=0,2+0,12+0,12+0,28+0,12+0,16=1$

Многоугольник распределения СВ V представлен ниже:

в) Найдем . Пусть .

Построим ряд распределения ДСВ М, используя абсолютные величины значений ДСВ , иными словами возьмем по модулю все значения ДСВ W, например, .

Получим ряд

	0	1	2	3	4
	0,12	0,24	0,34	0,22	0,08

Найдем вероятности всех значений ДСВ М, которые меньше, либо равны 2

Список использованной литературы:

Лунгу, К. Н. Сборник задач по высшей математике, 2 курс [Текст]/ К.Н. Лунгу, В.П. Норин, Д.Т. Письменный, Ю.А. Шевченко, Е.Д. Куланин; под редакцией С.Н. Федина.7-е изд. — М.: Айрис-пресс, 2009. — 592с.
Гмурман, В.Е. Теория вероятностей и математическая статистика [Текст]/ В.Е. Гмурман, 12-е изд., перераб. — М.: Высшее образование, Юрайт-Издат, 2009. — 479с.

Источник

Дискретная случайная величина

На этой странице мы собрали краткую теорию и примеры решения учебных задач, в которых дискретная случайная величина уже задана своим рядом распределения (табличный вид) и требуется ее исследовать: найти числовые характеристики, построить графики и т.д. Примеры на известные виды распределения вы можете найти по ссылкам:

Биномиальный закон распределения
Гипергеометрический закон распределения
Геометрический закон распределения
Закон распределения Пуассона

Понравилось? Добавьте в закладки

Краткая теория о ДСВ

Дискретная случайная величина задается своим рядом распределения: перечнем значений $x_i$, которые она может принимать, и соответствующих вероятностей $p_i=P(X=x_i)$. Количество значений случайной величины может быть конечным или счетным. Для определенности будем рассматривать случай $i=overline{1,n}$. Тогда табличное представление дискретной случайной величины имеет вид:

$$
begin{array}{|c|c|}
hline
X_i & x_1 & x_2 & dots & x_n \
hline
p_i & p_1 & p_2 & dots & p_n \
hline
end{array}
$$

При этом выполняется условие нормировки: сумма всех вероятностей должна быть равна единице

$$sum_{i=1}^{n} p_i=1$$

Графически ряд распределения можно представить полигоном распределения (или многоугольником распределения). Для этого на плоскости откладываются точки с координатами $(x_i,p_i)$ и соединяются по порядку ломаной линией. Подробные примеры вы найдете ниже.

Числовые характеристики ДСВ

Математическое ожидание:

$$M(X) = sum_{i=1}^{n} x_i cdot p_i$$

Дисперсия:

$$ D(X)=M(X^2)-(M(X))^2 = sum_{i=1}^{n} x_i^2 cdot p_i — (M(X))^2$$

Среднее квадратическое отклонение:

$$sigma (X) = sqrt{D(X)}$$

Коэффициент вариации:

$$V(X) = frac{sigma(X)}{M(X)}$$.

Мода: значение $Mo=x_k$ с наибольшей вероятностью $p_k=max_i{p_i}$.

Вы можете использовать онлайн-калькуляторы для вычисления математического ожидания, дисперсии и среднего квадратического отклонения ДСВ.

Функция распределения ДСВ

По ряду распределения можно составить функцию распределения дискретной случайной величины $F(x)=P(Xlt x)$. Эта функция задает вероятность того, что случайная величина $X$ примет значение меньшее некоторого числа $x$. Примеры построения с подробными вычислениями и графиками вы найдете в примерах ниже.

Примеры решенных задач

Задача 1. Дискретная случайная величина задана рядом распределения:

1 2 3 4 5 6 7

0,05 0,15 0,3 0,2 0,1 0,04 0,16
Построить многоугольник распределения и функцию распределения $F(x)$. Вычислить: $M[X], D[X], sigma[X]$, а также коэффициент вариации, асимметрии, эксцесса, моду и медиану.

Задача 2. Дан закон распределения дискретной случайной величины Х. Требуется:
а) определить математическое ожидание М(х), дисперсию D(х) и среднее квадратическое отклонение (х) случайной величины Х;
б) построить график этого распределения.
хi 0 1 2 3 4 5 6
pi 0,02 0,38 0,30 0,16 0,08 0,04 0,02

Задача 3. Для случайной величины Х с данным рядом распределения
-1 0 1 8
0,2 0,1 $р_1$ $р_2$
А) найдите $р_1$ и $р_2$ так, чтобы $М(Х)=0,5$
Б) после этого вычислите математическое ожидание и дисперсию случайной величины $Х$ и постройте график ее функции распределения

Задача 4. Дискретная СВ $X$ может принимать только два значения: $x_1$ и $x_2$, причем $x_1 lt x_2$. Известны вероятность $P$ возможного значения, математическое ожидание $M(x)$ и дисперсия $D(x)$. Найти: 1) Закон распределения этой случайной величины; 2) Функцию распределения СВ $X$; 3) Построить график $F(x)$.
$P=0,3; M(x)=6,6; D(x)=13,44.$

Задача 5. Случайная величина Х принимает три значения: 2, 4 и 6. Найти вероятности этих значений, если $M(X)=4,2$, $D(X)=1,96$.

Задача 6. Дан ряд распределения дискретной с.в. $Х$. Найти числовые характеристики положения и рассеивания с.в. $Х$. Найти м.о. и дисперсию с.в. $Y=X/2-2$, не записывая ряда распределения с.в. $Y$, проверить результат с помощью производящей функции.
Построить функцию распределения с.в. $Х$.
¦ x¦ 8 ¦ 12 ¦ 18 ¦ 24 ¦ 30 ¦
¦ p¦ 0,3¦ 0,1¦ 0,3¦ 0,2¦ 0,1¦

Задача 7. Распределение дискретной случайной величины $Х$ задано следующей таблицей (рядом распределения):
-6 3 9 15

0,40 0,30 ? 0,10
Определить недостающее значение в таблице распределения. Вычислить основные числовые характеристики распределения: $M_x, D_x, sigma_x$. Найти и построить функцию распределения $F(x)$. Определить вероятность того, что случайная величина $Х$ примет значения:
А) больше чем 6,
Б) меньше чем 12,
В) не больше 9.

Задача 8. В задаче требуется найти: а) математическое ожидание; б) дисперсию; в) среднее квадратическое отклонение дискретной случайной величины X по заданному закону её распределения, заданному таблично (в первой строке таблицы указаны возможные значения, во второй строке – вероятности возможных значений).

Задача 9. Задан закон распределения дискретной случайной величины $X$ (в первой строке указаны возможные значения $x_i$, во второй строке – вероятности возможных значений $p_i$).
Найти:
А) математическое ожидание $M(X)$, дисперсию $D(X)$ и среднее квадратическое отклонение $sigma(X)$;
Б) составить функцию распределения случайной величины $F(x)$ и построить ее график;
В) вычислить вероятности попадания случайной величины $X$ в интервал $x_2 lt X lt x_4$, пользуясь составленной функцией распределения $F(x)$;
Г) составить закон распределения величины $Y=100-2X$;
Д) вычислить математическое ожидание и дисперсию составленной случайной величины $Y$ двумя способами, т.е. пользуясь
свойством математического ожидания и дисперсии, а также непосредственно по закону распределения случайной величины $Y$.
10 20 30 40 50

0,1 0,2 0,1 0,2 0,4

Задача 10. Дискретная случайная величина задана таблице. Вычислить ее начальные и центральные моменты до 4 порядка включительно. Найти вероятности событий $xi lt Mxi$, $xi ge M xi$, $xi lt 1/2 M xi$, $xi ge 1/2 M xi$.

X 0 0,3 0,6 0,9 1,2

P 0,2 0,4 0,2 0,1 0,1

Мы отлично умеем решать задачи по теории вероятностей

Решебник по терверу

Нужны еще решения? Более 11000 подробно решенных и оформленных задач. Найди в решебнике сейчас:

Источник

Рядом данных называют результаты измерения, перечисленные в порядке их получения. Каждый из результатов называется вариантой измерения.
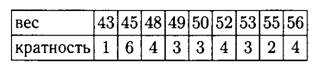
Например, результаты написания контрольной работы по математике для класса из 20 человек можно представить в виде следующего ряда данных: 3, 4, 4, 5, 3, 4, 3, 3, 3, 5, 5, 4, 5, 4, 5, 3, 3, 3, 4, 3. Эту же информацию можно представить в
виде таблицы:

Кратность варианты — количество её повторений в ряду данных. В нашем ряду оценка «3» появилась 9 раз, поэтому её кратность равна 9.
Понятно, что таблица распределения отображает данные более наглядно и компактно.
Числовые характеристики данных
Объём измерения — количество всех данных этого измерения. Одна из наиболее важных характеристик варианты — это её частота. Частота варианты показывает долю этой
варианты в ряду распределения. Она вычисляется по формуле:

частота =кратность варианты/объём измерения

В нашем примере частота варианты «4» равна $displaystyle frac{6}{20}=0,3$ .
Это означает, что оценка 4 составляет 0,3 всех полученных оценок.
Размах измерения — разность между максимальной и минимальной вариантами этого измерения. В нашем примере максимальная варианта равна 5, минимальная — 3, значит, размах равен 5-3=2 .
Мода измерения — варианта, которая в измерении встретилась чаще других. В приведённом выше примере чаще всех встретилась оценка 3, значит, она и будет модой этого распределения.
Медиана распределения — это центральное число в упорядоченном ряду данных, если в ряду нечётное количество чисел, или полусумма двух центральных, если в ряду чётное количество чисел.
Например, для ряда распределения 1, 2, 3, 6, 9, объём измерения которого равен 5, медианой распределения будет третье число этого ряда, то есть 3.
Для ряда распределения 7, 3, 2, 1 с объёмом измерения, равным 4, медианой будет полусумма двух центральных чисел данного ряда, то есть число, равное $displaystyle frac{2+3}{2}=2,5$ .
Для нахождения медианы распределения необходимо
1. Упорядочить ряд распределения по возрастанию или по убыванию: $a_{1},a_{2},...$ .
2. Если объём измерения нечётный, то есть 2n+1 , то получим следующую ситуацию:

В этом случае медианой является число $a_{n+1}$ .
3. Если объём измерения чётный, то есть , то имеем

В этом случае медианой является число — $displaystyle frac{a_{n}+a_{n+1}}{2}$ .
Среднее ряда (среднее арифметическое) — сумма всех чисел ряда, делённая на их количество. Если имеется таблица распределения, то можно
1) умножить каждую варианту на её кратность;
2) просуммировать полученные значения;
3) разделить результат на объём измерения. Например, для ряда распределения 2, 4, б, 8, у которого объём измерения равен 4, среднее значение равно $displaystyle frac{2+4+6+8}{4}=frac{20}{4}=5.$
Задача 1. Даны результаты измерения веса школьников 9 класса: 55, 53, 56, 48, 45, 56, 49, 52, 53, 49, 50, 56, 45, 52, 56, 45, 45, 48, 55, 52, 43, 48, 52, 49, 50, 45, 48, 45, 50, 53.
а) Постройте таблицу распределения данных.
б) Найдите объём измерения.
в) Найдите размах ряда.
г) Найдите частоту появления каждого веса в указанном ряду.
д) Найдите медиану, моду и среднее указанного ряда.
Решение.
а) Наименьшее число в ряду — 43, оно встречается в ряду один раз, значит, его кратность равна 1. Следующее по величине — число 45, оно встречается шесть раз, значит, его кратность равна 6. Далее 48, оно встречалось 4 раза, значит, его кратность равна 4.
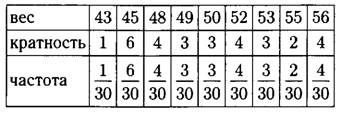
Продолжая аналогично, заполним таблицу:

б) Найти объём измерения можем несколькими способами.
1- й способ.
Посчитаем количество чисел в ряду, получим 30.
2- й способ.
Сложим кратности всех вариант: 1+6+4+3+3+4+3+2+4=30.
Ответ: 30.
в) Наибольшее значение в ряду 56, наименьшее — 43, значит, размах равен 56-43=13.
Ответ: 13.
г) Для каждой варианты делим её кратность на объём измерения (на 30), результаты пишем в таблицу.

д) В данном ряду 30 чисел, значит, медиана равна полусумме 15-го и 16-го чисел в упорядоченном ряду.

Как видно из такой записи чисел, от 43 до 49 — 14 чисел, значит, 15-ое и 16-ое числа равны 50, и значит, медиана равна $displaystyle frac{50+50}{2}=50.$
Мода — то значение, которое встречается чаще всех, то есть то, у которого больше кратность. Из таблицы распределения находим, что наибольшую кратность имеет число 45, значит, мода равна 45.
Для нахождения среднего необходимо найти сумму всех чисел ряда и разделить ее на количество этих чисел. Сумму можно найти просто складывая подряд все числа ряда. А можно поступить иначе: каждую варианту умножить на её кратность и сложить полученные результаты. Имеем:
3cdot 1+45cdot 6+48cdot 4+49cdot 3+50cdot 3+52cdot 4+53cdot 3+55cdot 2+56cdot 4=1503 .
Осталось разделить полученную сумму на количество всех чисел: $displaystyle frac{1503}{30}=50,1$ .
Ответ: медиана: 50; мода: 45; среднее: 50,1.
Задача 2. Пятерых учеников попросили подсчитать, сколько времени (в минутах) они тратят на дорогу от дома до школы. Получили следующие результаты: 5,15,10,15,20.
1) На сколько среднее значение этого ряда меньше его размаха?
2) На сколько мода этого ряда больше медианы?
3) Найдите процентную частоту значения 10.
Решение.
1) Среднее ряда: $displaystyle frac{5+15+10+15+20}{5}=13$ , размах: 20-5=15 . Искомое значение равно 15-13=2 .
Ответ: 2.
2) Найдём медиану. Расположим числа в порядке возрастания: 5, 10, 15, 15, 20. Медианой этого набора будет третье число в упорядоченном ряду, то есть 15.
В данном ряду число 15 встретилось 2 раза, остальные — по одному разу. Мода ряда равна 15. Мода и медиана этого ряда равны, значит, ответ 0.
Ответ: 0.
3) Кратность значения 10 равна 1, объём измерения равен 5 (всего 5 чисел). Частота значения 10 равна $displaystyle frac{1}{5}=0,2$ , процентная частота равна displaystyle 0,2cdot 100%=20% .
Ответ: 20.
Задача 3. Имеется 4 группы породистых котов. Для некоторого соревнования отбирают котов с длиной шерсти не менее 8 см.
Известно следующее:
1) в первой группе наибольшая длина шерсти равна 10 см;
2) во второй группе средняя длина шерсти равна 8 см;
3) в третьей группе мода длины шерсти равна 8 см;
4) в четвёртой группе медиана длины шерсти равна 9 см.
В какой из групп хотя бы половина котов гарантированно подходит по длине шерсти?
Решение.
1) Из того, что наибольшая длина шерсти равна 10 см, не следует никакой другой информации, то есть ничего не можем сказать про остальных котов этой группы.
2) Рассмотрим для примера группу котов с длиной шерсти 7 см, 7 см и 10 см. Среднее равно $displaystyle frac{7+7+10}{3}=8$ , но в этой группе нет половины котов, удовлетворяющих требованиям.
3) Рассмотрим для примера группу котов с шерстью длиной 8 см, 8 см, 7 см, б см, 5 см. Мода равна 8, но опять же нет половины котов, удовлетворяющих требованиям.
4) Если медиана равна 9 см, то есть половина котов с шерстью меньшей или равной длины и половина — с большей или равной длины. Значит, в этой группе найдётся половина котов с шерстью длиной не менее 8 см.
Ответ: 4.
Задача 4. По статистике автозавода из 1000 машин в среднем 20 бракованных. Сколько бракованных машин следует ожидать, если завод собирается выпустить 300 500 машин?
Решение.
Если из 1000 машин 20 бракованных, то частота появления бракованной машины равна $displaystyle frac{20}{1000}=0,02$ . То есть доля бракованных машин будет равна 0,02, тогда из 300 500 машин будет displaystyle 300500cdot 0,02=6010 бракованных.
Ответ: 6010.

Источник