На чтение 3 мин. Просмотров 205k.
Обновлено 12.08.2021
В этой ветке форума вы найдете основные типы задач для второго класса и схемы к ним. Теперь требования в начальной школе отличаются от тех требований, по которым учили нас в свое время. Раньше учили лишь записывать краткую запись, учителю важно было правильное решение и ответ. Теперь же обязательно требуется схема к задаче в виде одного или нескольких отрезков. На отрезках указываются данные и неизвестное.
Решение задачи у каждого ученика было по 3 ручки и 2 карандаша смотрите здесь
Содержание
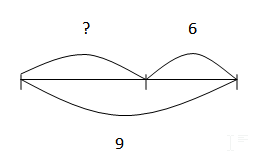
- Задачи на нахождение суммы
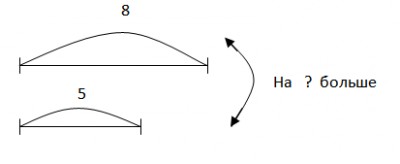
- Задачи на увеличение уменьшение числа на несколько единиц
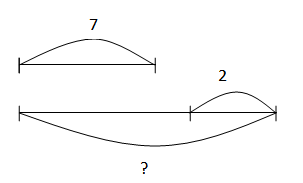
- Задачи на нахождение неизвестного слагаемого
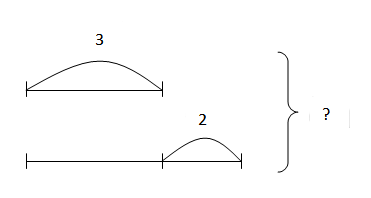
- Задачи на нахождение остатка
- Задачи на нахождение неизвестного вычитаемого и слагаемого
- Задачи на разностное сравнение
- Задачи с косвенными вопросами
- Составные задачи на нахождение суммы
- Составные задачи на нахождение остатка
- Составные задачи на нахождение слагаемого и вычитаемого
- Составные задачи на нахождение третьего слагаемого
- Составные задачи на нахождение суммы
- Составные задачи на нахождение уменьшаемого
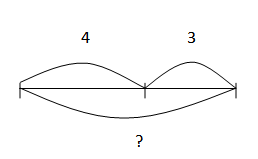
Задачи на нахождение суммы
У Сони было 4 синих карандаша и 3 коричневых. Сколько было всего карандашей у Сони?
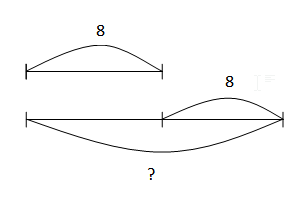
Задачи на увеличение уменьшение числа на несколько единиц
Ване 8 лет, а его сестре – на 8 лет больше. Сколько лет сестре?
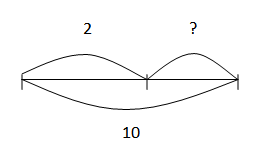
Задачи на нахождение неизвестного слагаемого
У кошки было 10 котят. 2 из них белого цвета, остальные — серого. Сколько серых котят было у кошки?
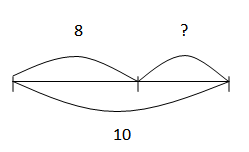
Задачи на нахождение остатка
.
У Вероники было 10 рублей. Она купила ручку за 8 рублей. Сколько денег осталось у Вероники?
Задачи на нахождение неизвестного вычитаемого и слагаемого
У Вики было 9 конфет. Когда несколько конфет Вика отдала друзьям, у нее осталось — 6. Сколько конфет подарила Вика?
Задачи на разностное сравнение
У Марины было 8 тетрадей, а у Маши — 5. На сколько больше тетрадей у Марины, чем у Маши?
Задачи с косвенными вопросами
Мама купила 7 кг вишни. что на 2 кг меньше, чем облепихи. Сколько кг облепихи купила мама?
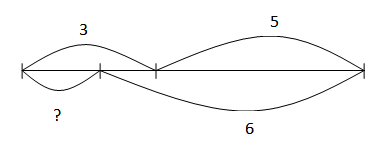
Составные задачи на нахождение суммы
Хозяйка купила 3 кг яблок, а груш на 2 кг больше. Сколько всего фруктов купила хозяйка?
Составные задачи на нахождение остатка
Пете задали читать на лето 3 книги зарубежной литературы и 5 книг отечественной. После прочтения 6 книг, Пете осталось читать еще несколько. Cколько книг осталось прочитать Пете?
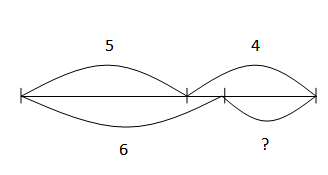
Составные задачи на нахождение слагаемого и вычитаемого
У кошки было 5 белых котят и 4 дымчатых. Когда несколько котят отдали, то их осталось 6. Сколько котят отдали?
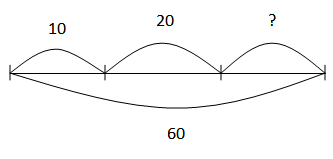
Составные задачи на нахождение третьего слагаемого
Три друга – Миша, Саша и Ваня — получили за четверть 60 пятерок. Миша получил 10 пятерок, Саша – 20. Сколько пятерок получил Ваня?
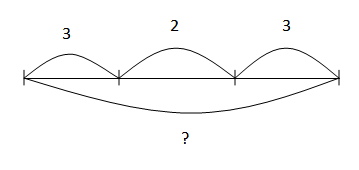
Составные задачи на нахождение суммы
У Василисы 6 карамелек, шоколадных конфет на 4 меньше, мятных подушечек на 2 больше, чем шоколадных конфет. Сколько мятных подушечек у Василисы?
Составные задачи на нахождение уменьшаемого
Из пенала Витя взял 3 карандаша и 2 ручки. Сколько школьных принадлежностей в пенале было сначала, если в ней осталось 3 фломастера?
спасибо за схемы. но есть еще правила к схемам, а как они пишутся?
adoksana69, правил для составления схем нигде не видел. Нужно знать как, к каждому типу задач составляется схема. Ребенок справляется с заданием с помощью выработка навыка.
В современной начальной школе требования к оформлению задачи несколько отличаются от привычных родителям. Стало обязательным использование схем в виде одного или нескольких отрезков, на которых отображаются данные и неизвестное. Иногда сложность у ребенка вызывает именно решение задачи с использованием схемы.
Суть схем в том, чтобы по условию задачи определить, что за тип схемы ей соответствует, и найти решение с использованием этой схемы. Такой подход помогает упростить решение текстовых задач в старших классах и составление системы уравнений.
В этой статье мы проиллюстрируем все схемы к математическим задачам, а потренироваться определять схему и подготовиться к решению задач вы сможете на тренажере.
Задачи на нахождение суммы
У Максима было 4 яблока и 3 груши. Сколько всего было фруктов у Максима?
Задачи на увеличение и уменьшение числа на несколько единиц
У Иры 8 карандашей, а у Коли – на 8 больше. Сколько карандашей у Коли?
Задачи на нахождение неизвестного слагаемого
У Васи было 10 рублей. Два рубля он потратил на леденец, а остальные – на жвачку. Сколько рублей Вася потратил на жвачку?
Задачи на нахождение остатка
У Юры было 10 конфет, 8 конфет Юра раздал друзьям . Сколько конфет осталось у Юры?
Задачи на нахождение неизвестного вычитаемого и слагаемого
У Петиной кошки родилось 9 котят. Когда Петя раздал несколько котят знакомым, у него осталось 6 котят. Сколько котят раздал Петя?
Задачи на разностное сравнение
У Маши было 8 комиксов, а у Наташи – 5. На сколько комиксов больше у Маши, чем у Наташи?
Задачи с косвенными вопросами
Бабушка сварила 7 банок малинового варенья, что на 2 банки меньше, чем абрикосового варенья. Сколько банок абрикосового варенья сварила бабушка?
Составные задачи на нахождение суммы
Папа купил 3 килограмма леденцовых конфет, а шоколадных конфет на 2 кг больше. Сколько всего килограмм конфет купил папа?
Составные задачи на нахождение остатка
Лене задали решить 3 задачи на сложение и 5 задач на вычитание. После решения 6 задач, Лене осталось сделать еще несколько. Cколько задач осталось решить Лене?
Составные задачи на нахождение слагаемого и вычитаемого
У Вити было 5 игрушечных гоночных машин и 4 обычных игрушечных машины. Несколько машин Витя подарил Толе, и у Вити осталось 6 машин. Сколько игрушечных машин Витя подарил Коле?
Составные задачи на нахождение третьего слагаемого
На трех грядках росли свекла, редис и морковь. С трех грядок хозяйка собрала 60 овощей. С двух грядок получилось 10 свекл и 20 редисок. Сколько морковок собрала хозяйка?
Составные задачи на нахождение уменьшаемого
Из мешка с подарками Дед Мороз достал 3 куклы и 2 набора Лего. Сколько всего подарков было у Деда Мороза в мешке, если в нем осталось 3 мягких игрушки?
Составные задачи на сложение и вычитание
В этом уроке познакомимся с логическим построением составных задач на сложение и вычитание, а также научимся записывать их решение по круговой схеме.
Рассмотрим три задачи.
Задача 1.
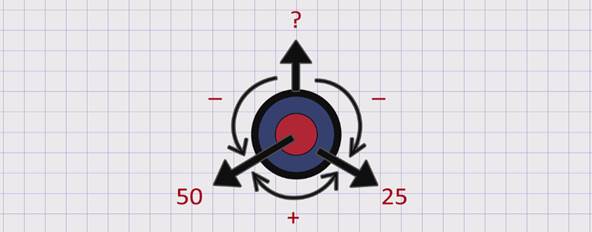
В библиотеке было 50 учебников математики. Закупили еще 25 учебников. Сколько учебников математики стало в библиотеке?
Составим схему, соответствующую этой задаче. Для этого выделим необходимые данные условия: учебников было 50, купили еще 25. Требование задачи: сколько стало учебников?
Данная задача простая, она решается одним действием – сложением:
50 + 25 = 75
Ответ: 75 учебников стало в библиотеке.
Задача 2.
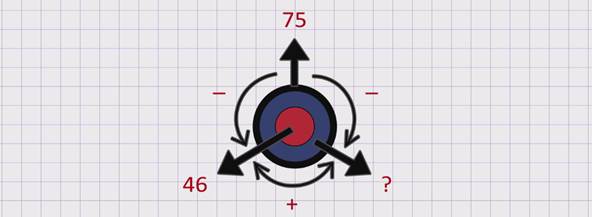
В библиотеке было 75 учебников математики. Ученикам выдали 46 учебников. Сколько учебников математики осталось в библиотеке?
Составим схему к этой задаче. Выделим данные условия: было 75 учебников, выдали 46 учебников. Требование задачи: сколько учебников осталось?
Вторая задача тоже простая и решается одним действием – вычитанием:
75 – 46 = 29
Ответ: 29 учебников осталось в библиотеке.
Задача 3.
В библиотеке было 50 учебников математики, закупили еще 25 таких же учебников, 46 учебников выдали. Сколько учебников математики осталось в библиотеке?
Для этой задачи составим дуговую схему: книг было 50, закупили 25, выдали 46, сколько книг осталось?
Данная задача не является простой, её нельзя решить в одно действие. Сформулируем промежуточное требование: сколько учебников стало после закупки 25 книг? Решение:
50 + 25 = 75 (уч.) – стало после закупки.
Сформулируем основное требование задачи: сколько учебников осталось в библиотеке? Второе действие:
75 – 46 = 29 (уч.) – осталось в библиотеке.
Сравним решение первых двух простых задач и третьей задачи. Решение первой задачи:
50 + 25 = 75
является первым действием третьей задачи. Решение второй задачи:
75 – 46 = 29
является вторым действием третьей задачи. Третья задача решается в два действия, такие задачи называются составными.
Составная задача – это задача, решение которой нельзя записать с помощью выражения, содержащего одно действие.
В решении составной задачи два или больше действий.
Составную задачу можно рассматривать как последовательность логически связанных простых задач. Так, в третьей задаче мы объединили условия первой и второй простых задач. Чтобы решить третью задачу, мы ответили на требование, которое задано сначала в первой задаче, потом во второй задаче.
Искомое предыдущей задачи играет роль данного следующей задачи. А именно, в первой задаче мы находили количество учебников, которое стало после того, как закупили учебники. Это искомое первой задачи стало данным второй задачи.
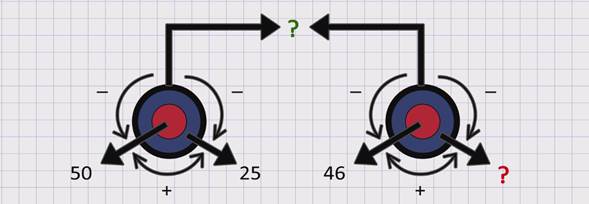
В третьей задаче мы объединили две предыдущие простые задачи и решили её в два действия. Число простых задач в логической структуре составной задачи определяет число действий в решении этой задачи. Используя две круговые схемы первых двух задач, можно составить схему для третьей задачи.
В схеме красный вопросительный знак обозначает искомое, а зеленый – промежуточное неизвестное. Левая часть схемы определяет первое действие решения задачи:
50 + 25 = 75
Правая часть схемы определяет второе действие решения задачи:
75 – 46 = 29
Рассмотрим
возможность использования схем при
знакомстве с составной задачей и обучении
решению составных задач на сложение и
вычитание в 1 и 2 классе.
Использование
схематического моделирования
рассмотренного вида позволяет построить
процесс знакомства с составной задачей
на основе частично-поискового метода:
при таком подходе достаточно после
решения простой задачи задать еще один
вопрос, и схема приобретает новый вид,
моделируя ситуацию составной задачи.
Рассмотрим
этот прием на задаче:
Саша
нашел 7 грибов, а Петя — на 2 гриба больше.
Сколько грибов у Пети?
После
составления схемы и записи решения
учитель спрашивает:
— А
если Саша и Петя на обратном пути сложили
все грибы в одну большую корзину, можно
узнать, сколько в ней оказалось грибов?
(Да,
можно, если узнать, сколько грибов
положил туда Петя и сколько Саша.)
— Давайте
обозначим эту корзину на схеме. Знаем
мы сразу сколько в ней грибов? (Нет.)
— Обозначим
ее символом (У)
— Покажите,
какие грибы положили в нее дети.
Ученик
у доски движением руки показывает, какие
грибы положены в корзину, и вслед за
движением руки рисует стрелки. Схема
приобретает вид:

Вторая
часть схемы определяет сложение, значит,
можно поставить знак: +.
Схематический
рисунок такого вида ученики легко
переводят в символическую запись
решения. При желании на схеме можно
проставить порядок действий:

В
таком виде схема играет роль плана
решения. После
того, как найден ответ на второй вопрос,
учитель обращает внимание детей на тот
факт, что до сих пор они таких задач еще
не решали. Вводится понятие составной
задачи как задачи, для решения которой
требуется выполнить больше одного
действия.
Использование
приема моделирования простой задачи с
помощью схемы снимает необходимость
готовить ученика к решению составных
задач как к чему-то новому. Обученный
прежде всего обращать внимание на данные
и искомое, на характер и структуру связей
между ними, ученик переносит это умение
на процесс решения составной задачи.
Разница для него только в том, что данных
стало больше и характер связей стал
более разнообразным.
Уже
на первых уроках знакомства с составной
задачей детям можно предлагать схемы
составных задач, помогая составить по
ним задачи и решить их.
Например:

Практика
показывает, что дети уже на первых уроках
знакомства со схемами составных задач
легко «читают» такие схемы, составляют
по ним задачи и решают их, записывая при
этом решения в виде выражения там, где
это соответствует структуре схемы
(схемы I и II).
Далее
при обучении решению составных задач
учитель ориентируется на те же этапы,
что и в работе с простой задачей. Умения,
сформированные у детей при решении
простых задач, получают дальнейшее
развитие, становятся более совершенными.
Приемы работы с моделью, используемые
на каждом этапе работы с задачей, носят
более разнообразный и сложный характер.
В
автобусе ехали 10 человек. На первой
остановке в автобус вошли 9 человек, на
второй вошел еще 1 человек. Сколько
человек стало в автобусе?
В
связи с тем, что при решении составной
задачи может быть использована новая
форма записи ее решения — в виде
выражения, при разборе этой задачи может
быть использован такой методический
прием.
После
чтения задачи и разбора ее текста учитель
предлагает детям рассмотреть готовые
схемы на доске и выбрать ту, которая
подходит к данной задаче.

При
анализе выбранных схем I и III учитель
обращает внимание учащихся на то, что
схема I отражает последовательность
событий: 9 человек вошли на первой
остановке, 1 человек — на второй остановке.
Но поскольку все они в конечном счете
едут в одном автобусе и в задаче
спрашивается «Сколько человек стало в
автобусе?», схема III также отражает
структуру этой ситуации.
При
выборе схем учитель показывает детям
две формы записи решения:
1)
10 + 9 — 19 (ч.) и 10 + 9 + 1 = 20 (ч.)
2)
19+1=20
(ч.)
и
предлагает определить, какая из форм
записи подходит к схеме III, а какая — к
схеме I. Схема III определяет форму записи
выражением, схема I — по действиям. Такие
упражнения на установление связей между
структурой схемы и формой записи решения
способствуют формированию аналитических
способностей: ученик в состоянии
проанализировать структуру схемы и
соотнести ее со структурой записи
решения. Здесь же можно обсудить вопрос
о том, какая из схем и, соответственно,
приемов записи решения задачи имеют
более экономную компактную форму.
После
работы над этой задачей полезно обратить
внимание учащихся на схему И:
— Почему
вы считаете, что эта схема не подходит
к данной задаче? (Стрелка
показывает, что 1 пассажир вышел, а не
вошел.)
— Составьте
задачу по этой схеме. (Дети
составляют задачу.)
— Чем
похожи эти задачи? (У
них одинаковые данные и одинаковые
вопросы.)
— Чем
они отличаются? (Характером
событий, а значит, и решения будут
разные.)
— Зная,
что в автобусе было 10 пассажиров и на
остановке вошли 9 пассажиров, что можно
узнать? (Сколько
пассажиров стало в автобусе после первой
остановки.)
— Какое
действие нужно использовать? (Сложение.)
Схему
дополняют знаком действия.
— Зная,
сколько всего пассажиров в автобусе и
что один пассажир вышел на следующей
остановке, что можно узнать? (Сколько
их осталось.)
— Какое
действие? (Вычитание.)
Схему
дополняют знаком действия, и в таком
виде она выполняет роль плана решения:

Решение
данной задачи целесообразно записать
и по действиям и выражениям, так как ее
схема не имеет ярко выраженного характера,
соответствующего той или иной форме
записи.
Приведем
примеры составных задач:
Девочка
купила блокнот за 8 рублей, карандаш за
3 рубля и линейку за б рублей. Сколько
денег она потратила?
Схема
к этой задаче может быть составлена по
типу схемы III (см. выше).
В
бидоне 24 л молока. Одному покупателю
отлили 3 л, другому 5 л. Сколько молока
осталось в бидоне?
Схема
к этой задаче может быть составлена
двух видов:

Схема
I соответствует записи решения выражением.
Схема II отражает последовательность
событий (сначала одному покупателю
отлили З л, потом другому — 5 л) и
соответствует записи решения по действиям
(количество строк записи решения
показывает и количество знаков вопроса
в схеме).
Решение
большинства составных задач в 1—2 классе
тесно связано со свойствами арифметических
действий (прибавление числа к сумме,
вычитание числа из суммы, прибавление
суммы к числу, вычитание суммы из числа).
Эти свойства позволяют решать составные
задачи различными способами.
Утром
ушли в море 20 маленьких и 8 больших лодок.
6 лодок вернулись. Сколько лодок должно
еще вернуться?
Для
того чтобы нахождение разных способов
решения данной задачи не превратилось
в формальное манипулирование числами
на основе свойств арифметических
действий, необходимо уделить основное
внимание анализу ситуации, которая дана
в задаче. При анализе текста главным
будет являться вопрос: «Знаем мы, какие
лодки возвращались — большие, маленькие
или те и другие?» (Нет.
Мы знаем только, что их вернулось 6.)
После
уточнения этого факта можно использовать
такой методический прием: учитель
открывает на доске три заготовленных
заранее схемы и предлагает детям выбрать
подходящую к данной задаче. Ученик,
выбирающий схему, должен рассказать
соответствующую этой схеме версию
событий задачи (вернулись только большие
лодки, только маленькие, те и другие).
Схемы к этой задаче имеют вид:

Этим
трем схемам соответствуют три разных
способа решения, которые дети составляют
после разбора каждой схемы:
I.
1) 20 + 8 = 28 (л.)
II. 1) 20 — 6 = 14 (л.)
III. 1)8-6
= 2 (л.)
2)
28 — 6 = 22 (л.)
2)
14 + 8 = 22 (л.) 2)20+ 2 = 22(л.)
Все
три решения имеют одинаковый ответ,
следовательно задача решена верно.
Можно
было использовать и такой методический
прием: предложить учащимся не только
три готовые схемы, но и сразу три варианта
решения. Это упражнение направлено на
формирование аналитических способностей:
ученики должны соотнести структуру
схемы со способом решения и выбрать к
каждой схеме соответствующую запись,
объясняя логику своего выбора.
Использование
приема моделирования при формировании
умения решать задачи предполагает в
основном синтетический подход к ее
разбору. Психологически это обусловлено
тем, что в возрасте 6—7 лет развитие
способности к синтезу опережает развитие
способности к анализу. На этом этапе
ребенку ближе и понятнее синтетический
подход к задаче («от данных»), который,
кроме того, значительно короче, а значит,
более доступен. Синтетическая схема, в
отличие от аналитической, является
прежде всего моделью ситуации, предлагаемой
в задаче. В связи с этим она как бы
направляет ход мысли. Синтетическая
схема обычно отражает ход событий в
задаче, приучая ребенка к внимательному
изучению ситуации, соблюдению хронологии,
помогает выстраивать цепочку рассуждений,
следуя за главными событиями, не
отвлекаясь на второстепенные детали.
Приведем
пример синтетического разбора задачи,
сопровождаемого составлением схемы.
Первоклассники
заготовили для птиц б кг рябины и 4 кг
семян арбуза. За зиму они скормили птицам
9 кг корма. Сколько кг корма осталось?
— Что
можно узнать, если известно, что дети
заготовили рябины 6 кг и арбузных семян
4 кг? (Можно
узнать, сколько корма заготовили всего.)
— Как
это сделать? С помощью какого действия?
(Надо
сложить 6 кг и 4 кг.)
— Что
можно узнать, если известно, сколько
корма было всего и сколько съели птицы?
(Можно
узнать, сколько его осталось.)
— Как
это узнать? (Надо
от всего корма отнять 9 кг.) Схема,
соответствующая этому разбору, выглядит
так:

Характерно,
что синтетический разбор обычно
сопровождается составлением плана
решения, так как при каждом следующем
«шаге» используется данное, найденное
на предыдущем «шаге».
Приведем
аналитический разбор («от вопроса») той
же задачи:
— Что
нужно знать, чтобы ответить на вопрос
задачи? Или: Что нужно знать, чтобы
определить, сколько килограммов корма
осталось? (Нужно
знать, сколько корма заготовили и сколько
скормили птицам.)
— Известно,
сколько скормили птицам? (Да,
9 кг.)
— Известно,
сколько корма заготовили? (Неизвестно.)
— Что
нужно знать, чтобы определить, сколько
корма заготовили? (Нужно
знать, сколько заготовили рябины и
арбузных семечек.)
— Известно,
сколько было рябины? (Да,
6 кг.)
— Известно,
сколько было арбузных семян? (Да,
4 кг.) Схема,
соответствующая такому разбору, выглядит
так:

Чтобы
составить план решения, надо вернуться
по этой схеме «обратно»:
— Как
узнать, сколько корма запасли? (Сложение.)
— Как
узнать, сколько корма осталось?
(Вычитание.)
Как
видно из приведенного примера, составление
аналитической схемы требует хорошо
развитого «обратного» хода мысли,
высокого уровня сформированное™
аналитических способностей.
При
постепенном переходе от использования
предметной наглядности к использованию
схемы (абстрактного изображения ситуации,
предложенной в задаче) создаются
предпосылки и фактически ведется работа
по формированию у ребенка умения
абстрагироваться: умения, являющегося
необходимым для развития математического
мышления.
Схема
состоит из элементов, смысл которых
легко понимается маленькими детьми:
кружков, квадратиков, стрелок. Таким
образом, схема, с одной стороны, легко
выполняется учеником, так как не требует
никаких специальных графических умений,
а с другой — не требует умения достаточно
хорошо писать опорные слова, что
необходимо для оформления краткой
записи. Такая модель задачи позволяет
сделать математические связи и зависимости
наглядными для учеников, причем это
относится не только к явным, но и скрытым
зависимостям между величинами. Схема
является абстрактным изображением той
ситуации, которая дана в задаче, она
позволяет абстрагироваться от
несущественных подробностей, приучает
ученика быстро находить главное в задаче
(данные, искомое) и тем самым помогает
осознать условие и выбрать действие.
Таким
образом, схема несет двоякую нагрузку:
с одной стороны, она является абстрактной
моделью, с другой стороны, схема достаточно
конкретна: зримо воспринимаемая,
воплощает фактически те мыслительные
действия, которые ученик проделывает,
моделируя задачу, т. е. является итоговым
результатом внутренних действий.
Возможность воплотить эти действия и
их результат во внешнюю опору для многих
учеников служит той самой необходимой
ступенькой, поднявшись на которую, они
могут двигаться дальше к адекватной
мысленной модели ситуации. Наличие
схемы на доске или индивидуальной
карточке поможет сориентироваться даже
слабым учащимся. Анализ проводится,
когда схема в первом приближении
составлена, что облегчает ученику эту
процедуру и резко сокращает затраты
времени. Кроме того, готовая схема
исключает этап поиска пути решения, так
как она сама является схемой способа
действия, способа решения. И, наконец,
схема является также и средством контроля
(самоконтроля), поскольку ребенок всегда
может сравнить выполняемые им действия
со способом действия, зафиксированным
в схеме. Если учесть при этом, что
использование приема моделирования
(со схемой в качестве модели) помогает
формированию таких приемов умственной
деятельности как абстрагирование,
анализ, синтез, а также способствует
формированию внутреннего плана действий
у ребенка, то можно с уверенностью
утверждать, что использование описанного
приема моделирования при обучении
решению задач в первом классе будет
способствовать развитию мышления,
развитию математических способностей.
В
настоящее время методисты стали много
внимания уделять приему моделирования
задачи с помощью различных схем (Н.Б.
Истомина, Л.Г. Петерсон и многие другие).
Однако во всех случаях идет речь об
обучении ребенка использованию сразу
графической модели в виде отрезков —
так называемой схемы
в отрезках, где
различные совокупности или величины,
заданные в задаче, изображаются с помощью
отрезков. Безусловно, эти схемы являются
очень действенными и, как будет показано
ниже, фактически универсальными при
обучении ребенка решению задач. Но сама
форма этой схемы является очень
абстрактной и слишком условной для
понимания многих шестилетних школьников.
У учителя обычно уходит много сил на
обучение детей этому способу моделирования
уже с 1 класса. Возможно, именно поэтому
новый вариант учебника математики Н.Б.
Истоминой для четырехлетней школы,
активно использующий схему в отрезках
для обучения решению задач, предполагает
знакомство с задачей только во 2 классе.
Схема в отрезках, даже предъявляемая
ребенку в учебнике готовой, не дает
ученику, если он заранее не обучен
специально вычерчиванию и чтению этой
модели, визуально сразу схватываемую
и понятную с первого взгляда картину
выбора действия.
Учителя
уже обращают внимание на то, что наличие
в учебниках большого количества готовых
схем в отрезках ко многим задачам значимо
не влияет на уровень сформированное™
умения решать задачи у школьников. Это
объясняется тем, само умение строить
графическую модель к задаче является
базовым для обучения ее решению.
Формировать это умение следует постепенно
повышая уровень абстрактности используемой
модели, переход от предметного
моделирования сразу к абстрактной схеме
в отрезках для многих детей слишком
сложен. Опыт показывает, что даже для
учителя составление схемы в отрезках
для задач чуть более повышенного уровня
сложности требует специального обучения.
Предлагаемый
нами для 1 класса вариант схемы является
намного более простым как в исполнении,
так и для понимания ребенка, и не требует
для начала даже обучения вычерчиванию
отрезков и пониманию процесса суммирования
отрезков, что необходимо для работы со
схемой в отрезках. Использование этого
варианта схемы позволяет знакомить
детей с задачей в соответствии с
программой традиционного учебника уже
в начале 1 класса.
Разбор составной задачи.
3 класс 2 часть «Школа России», с. 45
Задача.
В столовой 5 дней расходовали по 12 кг крупы, а 2 дня – по 9 кг. Сколько крупы израсходовали за все эти дни?
Анализ текста задачи.
— Прочитайте задачу и скажите, о чём говорится в задаче?
(Задача о расходе крупы в столовой по дням)
— Прочитайте вопрос. Что надо знать, чтобы ответить на главный вопрос задачи?
(Знать сколько крупы израсходовали за все эти дни?)
— Известно ли нам, сколько крупы израсходовали за день? (12 кг и 9 кг)
— Как это обозначить в схематической записи? (Внесем данные в столбец, расход в день)
— Что еще известно в задаче?
(количество дней 5 и 2 дня)
— Известен ли общий расход? (Не известен) Как это обозначить? (В таблице ставим?)
Составляем таблицу.
Схематическая запись условия (в виде таблицы).
|
Расход в день |
Количество дней |
Общий расход |
|
12 кг |
5 дней |
? |
|
9 кг |
2 дня |
Поиск решения задачи, составление плана решения.
— Можем ли мы сразу ответить на вопрос задачи? (Нет)
— А что нам для этого нужно знать? (Сколько расходовали крупы за 5 и 2 дня вместе)
— Знаем ли мы сколько крупы израсходовали за 5дней? (Не знаем)
— А сколько кг крупы израсходовали за 2 дня? (Не знаем)
— А можем ли мы это узнать? Какие данные для этого необходимы? (Из условия задачи можем узнать сколько расходовали крупы за 5 дней, за 2 дня)
— Выберите арифметическое действие для решения задачи.
Узнаем сколько расходовали крупы за 5 дней – умножением.
Каким действием узнаем сколько расходовали крупы за 2 дня?
(Умножением).
Каким действием узнаем сколько крупы израсходовали за все эти дни?
(Сложением).
Во сколько действий задача? (3 действия).
Решение собственно математической задачи, т.е. вычисление значения числового выражения.
1) 5*12=60 (кг) крупы израсходовали за 5 дней.
2) 2*9=18 (кг) крупы израсходовали за 2 дня.
3) 60+18=78 (кг)крупы израсходовали за все эти дни.
Ответ: 78 килограмм.
Проверка полученного ответа.
В столовой расходовали крупу 2 и 5 дней, всего 78 кг, 5 дней расходовали по 12 кг. По сколько кг крупы расходовали 2 дня?
1) 78-5*12=18 (кг) крупы израсходовали за 2 дня.
2) 18:2=9 (кг) по 9 кг крупы расходовали 2 дня.
Ответ: 9 килограмм.