Диана Загировна Филиппенкова
Эксперт по предмету «Информатика»
Задать вопрос автору статьи
Нормальная форма логической формулы не содержит знаков импликации, эквивалентности и отрицания неэлементарных формул.
Нормальная форма существует в двух видах:
-
конъюнктивная нормальная форма (КНФ) — конъюнкция нескольких дизъюнкций, например, $left(Avee overline{B}vee Cright)wedge left(Avee Cright)$;
-
дизъюнктивная нормальная форма (ДНФ) — дизъюнкция нескольких конъюнкций, например, $left(Awedge overline{B}wedge Cright)vee left(Bwedge Cright)$.
СКНФ
Совершенная конъюнктивная нормальная форма (СКНФ) — это КНФ, удовлетворяющая трем условиям:
-
не содержит одинаковых элементарных дизъюнкций;
-
ни одна из дизъюнкций не содержит одинаковых переменных;
-
каждая элементарная дизъюнкция содержит каждую переменную из входящих в данную КНФ.
Любая булева формула, которая не является тождественно истинной, может быть представлена в СКНФ.
Сдай на права пока
учишься в ВУЗе
Вся теория в удобном приложении. Выбери инструктора и начни заниматься!
Получить скидку 3 000 ₽
Правила построения СКНФ по таблице истинности
Для каждого набора переменных, при котором функция равна 0, записывается сумма, причем переменные, которые имеют значение 1, берутся с отрицанием.
СДНФ
Совершенная дизъюнктивная нормальная форма (СДНФ) — это ДНФ, удовлетворяющая трем условиям:
-
не содержит одинаковых элементарных конъюнкций;
-
ни одна из конъюнкций не содержит одинаковых переменных;
-
каждая элементарная конъюнкция содержит каждую переменную из входящих в данную ДНФ, к тому же в одинаковом порядке.
Любая булева формула, которая не является тождественно ложной, может быть представлена в СДНФ, к тому же единственным образом.
Правила построения СДНФ по таблице истинности
Для каждого набора переменных, при котором функция равна 1, записывается произведение, причем переменные, которые имеют значение 0 берут с отрицанием.
Примеры нахождения СКНФ и СДНФ
Пример 1
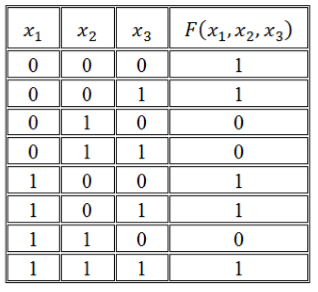
Записать логическую функцию по ее таблице истинности:
Рисунок 1.
Решение:
Воспользуемся правилом построения СДНФ:
Рисунок 2.
Получим СДНФ:
[Fleft(x_1, x_2, x_3right)=left(overline{x_1}wedge overline{x_2}wedge overline{x_3}right)vee left(overline{x_1}wedge overline{x_2}wedge x_3right)vee left(x_1wedge overline{x_2}wedge overline{x_3}right)vee left(x_1wedge overline{x_2}wedge x_3right)vee left(x_1wedge x_2wedge x_3right)]
Воспользуемся правилом построения СКНФ:
Рисунок 3.
Получим СКНФ:
[Fleft(x_1, x_2, x_3right)=left(x_1vee overline{x_2}vee x_3right)wedge left(x_1vee overline{x_2}vee overline{x_3}right)wedge left(overline{x_1}vee overline{x_2}vee x_3right)]
«Построение СКНФ и СДНФ по таблице истинности» 👇
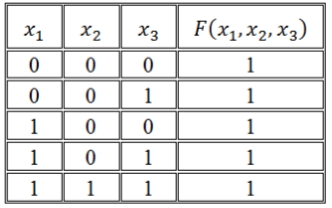
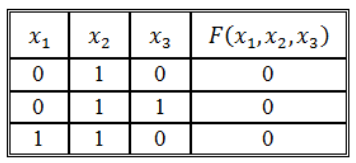
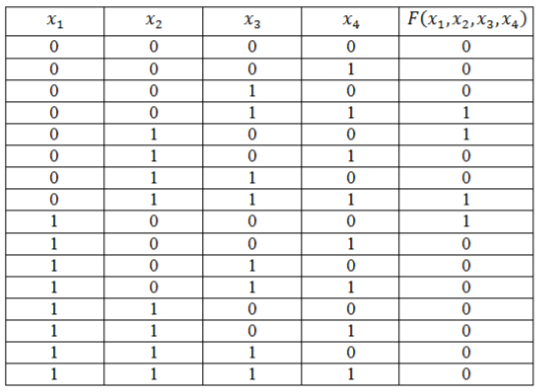
Пример 2
Функция задана таблицей истинности:
Рисунок 4.
Представить эту функцию в виде СДНФ и СКНФ.
Решение:
-
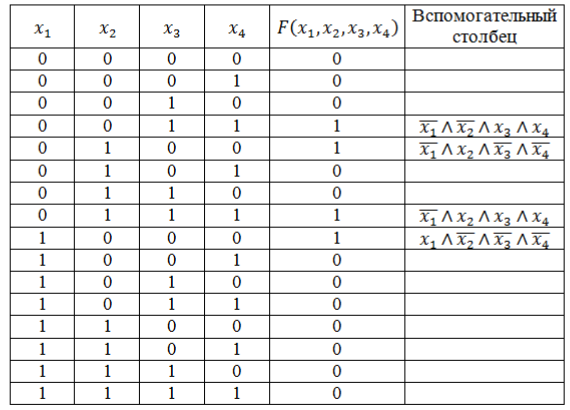
Запишем логическую функцию в СДНФ. Для удобства решения добавим к таблице вспомогательный столбец.
Используя правило составления СДНФ не забываем вводить знак отрицания для переменных со значением 0. Инвертировать нулевые значения переменных обязательно, т.к. иначе они превратят значения конъюнкций в нули основной функции.
Рисунок 5.
Полученные во вспомогательном столбце конъюнкции соединим знаком дизъюнкции и получим искомую логическую функцию в виде СДНФ:
[Fleft(x_1,x_2,x_3,x_4right)=left(overline{x}wedge overline{y}wedge zwedge fright)vee left(overline{x_1}wedge x_2wedge overline{x_3}wedge overline{x_4}right)vee left(overline{x_1}wedge x_2wedge x_3wedge x_4right)vee left(x_1wedge overline{x_2}wedge overline{x_3}wedge overline{x_4}right).]
-
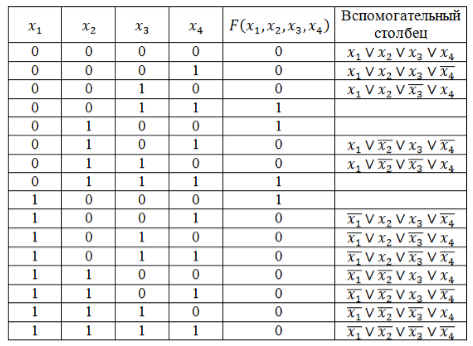
Запишем логическую функцию в СКНФ.
Используя правило составления СКНФ не забываем вводить знак отрицания для переменных со значением 1. Инвертировать единичные значения переменных обязательно, т.к. иначе они превратят значения дизъюнкций в единицы основной функции.
Рисунок 6.
Полученные во вспомогательном столбце дизъюнкции соединим знаком конъюнкции и получим искомую логическую функцию в виде СКНФ:
[Fleft(x_1,x_2,x_3,x_4right)=left(x_1vee x_2vee x_3vee x_4right)wedge left(x_1vee x_2vee x_3vee overline{x_4}right)wedge left(x_1vee x_2vee overline{x_3}vee x_4right)wedge left(x_1vee overline{x_2}vee x_3vee overline{x_4}right)wedge left(x_1vee overline{x_2}vee overline{x_3}vee x_4right)wedge left(overline{x_1}vee x_2vee x_3vee overline{x_4}right)wedge left(overline{x_1}vee x_2vee overline{x_3}vee x_4right)wedge left(overline{x_1}vee x_2vee overline{x_3}vee overline{x_4}right)wedge left(overline{x_1}vee overline{x_2}vee x_3vee x_4right)wedge left(overline{x_1}vee overline{x_2}vee x_3vee overline{x_4}right)wedge left(overline{x_1}vee overline{x_2}vee overline{x_3}vee x_4right)wedge left(overline{x_1}vee overline{x_2}vee overline{x_3}vee overline{x_4}right).]
Находи статьи и создавай свой список литературы по ГОСТу
Поиск по теме

1 Цель работы
Научиться синтезировать логические схемы по заданной таблице истинности.
2 Краткие теоретические сведения
Любая логическая схема без памяти полностью описывается таблицей истинности. Эта таблица является исходной информацией для синтеза схемы на основе логических элементов «И», «ИЛИ», «НЕ». Для разработки требуемого цифрового устройства сначала на основе таблицы истинности записывают его логическое выражение. Затем с целью упрощения цифрового устройства минимизируют его логическое выражение и далее разрабатывают схему, реализующую полученное логическое выражение. Логические выражения можно получить двумя способами:
- на основе совершенной дизъюнктивной нормальной формы (СДНФ);
- на основе совершенной конъюнктивной нормальной формы (СКНФ).
Совершенная дизъюнктивная нормальная форма (СДНФ)
Функция представляется суммой групп. Каждая группа состоит из произведения, в которую входят все переменные.
Например:
f(x1,x2,x3) = x1·x2·x3 + x1·x2·x3 + x1·x2·x3
Совершенная конъюнктивная нормальная форма (СКНФ)
Функция представляется произведением групп. Каждая группа состоит из суммы, в которую входят все переменные.
Например:
f(x1,x2,x3) = (x1+x2+x3)·(x1+x2+x3)·(x1+x2+x3)
Если схема имеет несколько выходов, то каждый выход описывается своей функцией. Такая система функций называется системой собственных функций. СДНФ составляется на основе таблицы истинности по следующему правилу: для каждого набора переменных, при котором функция равна 1, записывается произведение, в котором с отрицанием берутся переменные, имеющие значение «0».
Пример:
Таблица 2.1 – Заданная таблица истинности
| x1 | x2 | x3 | y |
| 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 1 |
| 0 | 1 | 0 | 0 |
| 0 | 1 | 1 | 1 |
| 1 | 0 | 0 | 0 |
| 1 | 0 | 1 | 0 |
| 1 | 1 | 0 | 1 |
| 1 | 1 | 1 | 1 |
СДНФ:
y = f(x1,x2,x3) = x1·x2·x3 + x1·x2·x3 + x1·x2·x3 + x1·x2·x3
СКНФ составляется на основе таблицы истинности по правилу: для каждого набора переменных, при котором функция равна 0, записывается сумма, в которой с отрицанием берутся переменные, имеющие значение 1.
Таблица 2.2 – Заданная таблица истинности
| x1 | x2 | x3 | y |
| 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 1 |
| 0 | 1 | 0 | 0 |
| 0 | 1 | 1 | 1 |
| 1 | 0 | 0 | 0 |
| 1 | 0 | 1 | 0 |
| 1 | 1 | 0 | 1 |
| 1 | 1 | 1 | 1 |
СКНФ:
y = f(x1,x2,x3) = (x1+x2+x3)·(x1+x2+x3)·(x1+x2+x3)·(x1+x2+x3)
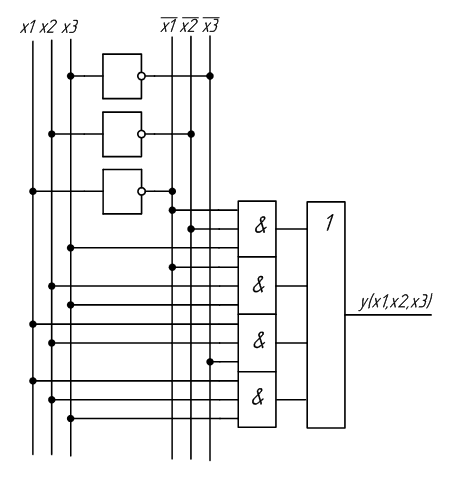
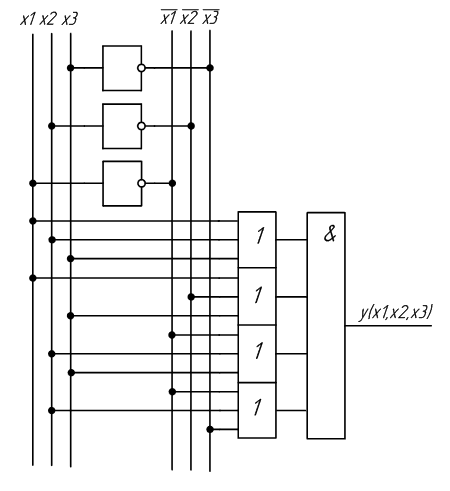
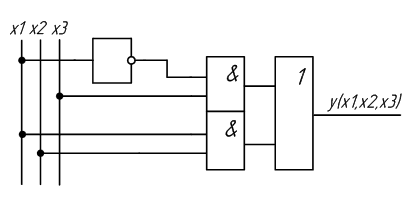
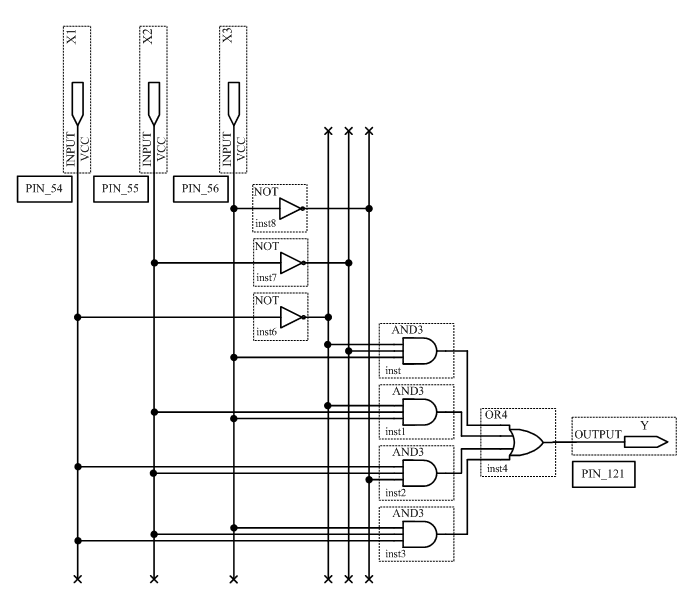
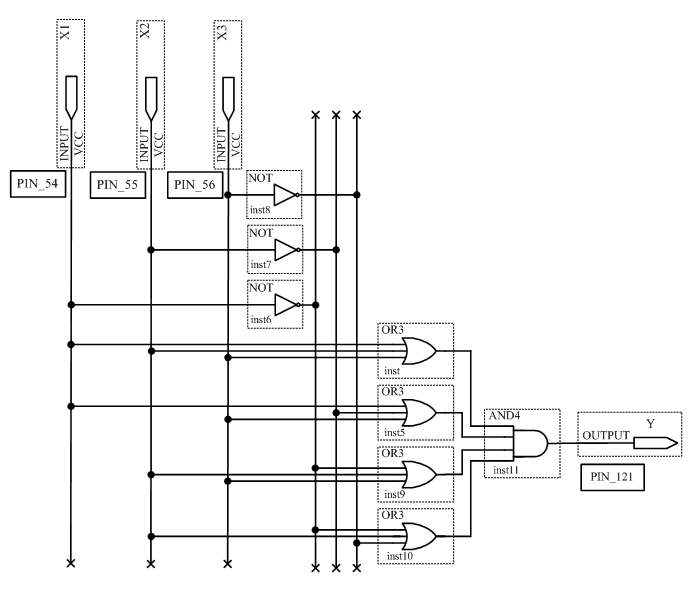
На основе полученных выражений можно составить схему устройства, реализующего заданную функцию. Схема устройства, полученная на основе СДНФ, изображена на рисунке 2.1, а на основе СКНФ на рисунке 2.2.
Рисунок 2.1 – Схема устройства, полученная на основе СДНФ
Рисунок 2.2 – Схема устройства, полученная на основе СКНФ
С целью упрощения цифрового устройства применяют минимизацию функций. Используя законы алгебры логики, можно упростить исходную функцию.
y(x1,x2,x3) = x1·x2·x3 + x1·x2·x3 + x1·x2·x3 + x1·x2·x3 =
= x1·x3·(x2+x2) + x1·x2·(x3+x3) = x1·x3 + x1·x2
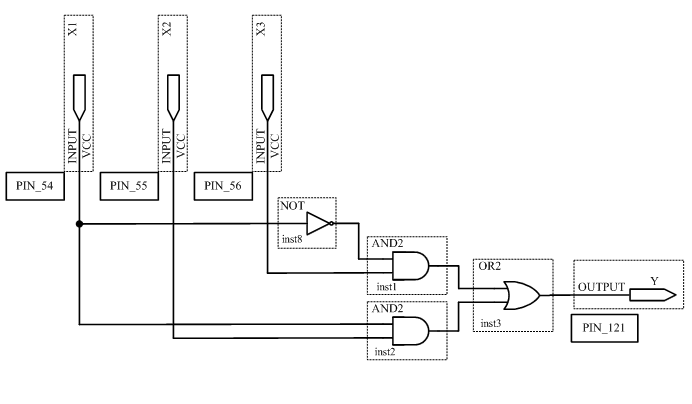
На основе полученного выражения составим новую схему устройства (рисунок 2.3).
Рисунок 2.3 – Схема устройства, полученная после минимизации логической функции
3 Задание к работе
3.1 Исследовать схему, полученную по таблице истинности (таблица 2.1) на основе СДНФ. Для этого сконфигурировать ПЛИС в соответствии со схемой рисунок 2.1. Подключить к входам схемы переключатели S7,S8,S9, а к выходу светодиод LED 8. Схема устройства в среде Quartus II будет выглядеть в соответствии с рисунком 3.1.
Рисунок 3.1 – Схема устройства в среде Quartus II, составленная на основе СДНФ
Устанавливая на входах схемы с помощью переключателей все возможные кодовые комбинации и наблюдая за светодиодом, заполнить таблицу истинности исследуемого устройства.
3.2 Исследовать схему, полученную по таблице истинности (таблица 2.2) на основе СКНФ.
Для этого сконфигурировать ПЛИС в соответствии со схемой рисунок 2.2. Подключить к входам схемы переключатели S7,S8,S9, а к выходу светодиод LED 8. Схема устройства в среде Quartus II будет выглядеть в соответствии с рисунком 3.2. Можно не создавать новый проект, а отредактировать проект, созданный в пункте 3.1. Устанавливая на входах схемы с помощью переключателей все возможные кодовые комбинации и наблюдая за светодиодом, заполнить таблицу истинности исследуемого устройства.
Рисунок 3.2 – Схема устройства в среде Quartus II, составленная на основе СКНФ
3.3 Исследовать минимизированную схему (рисунок 2.3.)
Для этого сконфигурировать ПЛИС в соответствии со схемой рисунок 2.3. Подключить к входам схемы переключатели S7,S8,S9, а к выходу светодиод LED 8. Схема устройства в среде Quartus II будет выглядеть в соответствии с рисунком 3.3. Устанавливая на входах схемы с помощью переключателей все возможные кодовые комбинации и наблюдая за светодиодом, заполнить таблицу истинности устройства.
Рисунок 3.3 – Схема устройства в среде QUARTUS II, составленная на основе СДНФ с последующей минимизацией.
4 Содержание отчета
- Цель работы.
- Заданная таблица истинности.
- Логическое выражение на основе СДНФ.
- Логическое выражение на основе СКНФ.
- Минимизированное логическое выражение.
- Схемы, синтезированные на основе СДНФ, СКНФ и в результате минимизации.
- Таблицы истинности, полученные в результате исследования схем.
- Выводы.
5 Контрольные вопросы
- Что такое СДНФ?
- Что такое СКНФ?
- Как записать СДНФ, используя таблицу истинности устройства?
- Как записать СКНФ, используя таблицу истинности устройства?
- Как разработать схему логического устройства, используя СДНФ?
- Как разработать схему логического устройства, используя СКНФ?
- Как лучше синтезировать логическое устройство (на основе СДНФ или СКНФ), если значение функции в таблице истинности имеет больше нулей, чем единиц?
- Как разработать логическое устройство, если оно имеет несколько выходов?
- Что такое минимизация логического выражения?
- Запишите основные законы алгебры логики.
- Расскажите, как определить таблицу истинности логического устройства экспериментально, используя лабораторный стенд.
Узнать больше об аппаратном синтезе логическ схем в ПЛИС можно из статьи
Архитектура ПЛИС. Часть 1. Логический элемент
Для любой логической формулы можно построить бесконечное количество равносильных ей формул. Для этого потребуется произвести некоторое количество тождественных преобразований. Одной из главных задач в алгебре логики является нахождение канонических форм формул. Проще говоря таких, которые построены по одному канону (правилу).
Форма представления какой-либо логической функции будет считаться нормальной, если она выражена через конъюнкцию, дизъюнкцию, а также отрицание переменных. Среди всех нормальных форм можно выделить совершенно нормальные. Это тот случай, когда функция может быть записана только одним единственным способом.
Классы СКНФ и СДНФ
В при решении задач в алгебре логики особая роль отводится классам конъюнктивных и дизъюнктивных совершенно нормальных форм. Они основаны на стандартных понятиях элементарной конъюнкции и дизъюнкции.
Определение 1 — 2
Элементарной конъюнкцией принято называть формулу в том случае, когда она представляет собой конъюнкцию любого количества переменных, которые берутся без отрицания либо с отрицанием. При этом одночленной элементарной конъюнкцией считается только одна единственная переменная либо ее отрицание.
Элементарной дизъюнкцией называют формулу при условии, что она будет являться дизъюнкцией некоторого любого количества переменных и отрицаний, при этом она может быть и одночленной.
СКНФ
Форма любой логической формулы нормального типа не может содержать знаки эквивалентности, импликации, а также отрицания неэлементарных формул. Она может существовать только в двух видах:
- КНФ – конъюнктивная нормальная форма, представляющая собой конъюнкцию нескольких дизъюнкций. К примеру, [(A vee bar{B} vee C) wedge(A vee C)];
- ДНФ – дизъюнктивная нормальная форма, которая является дизъюнкцией нескольких конъюнкций. К примеру, [(A wedge bar{B} wedge C) vee(A wedge C)].
Определение 3
Совершенной конъюнктивной нормальной формой (СКНФ) называют КНФ, удовлетворяющую нескольким условиям:
- В ней не содержится двух и более элементарных дизъюнкций;
- Во всех дизъюнкциях отсутствуют одинаковые переменные;
- Каждая ДНФ содержит в себе все переменные из входящих в нее КНФ.
Любую булеву формулу, не являющуюся тождественной истиной, можно представить в виде СКНФ.
Правила построения СКНФ
В алгебре логики для любого набора переменных, при котором конечное значение функции становится нулевым, можно записать сумму. При этом переменные, имеющие числовые значение больше единицы, должны браться с отрицательным знаком.
Построение должно осуществляться по следующему алгоритму:
- В таблице нужно отметить такие наборы переменных, при которых [f=1].
- Для каждого выбранного набора переменных записываем КНФ, при этом если значение какой-либо из них равно 1, то она включается в неизменном виде, иначе – ее отрицание.
- На последнем этапе все полученные конъюнкции следует связать операциями дизъюнкции.
СНДФ
Определение 4
Совершенной дизъюнктивной нормальной формой (СНДФ) называют удовлетворяющую нескольким условиям ДНФ. Всего должно выполняться три условия:
- В ДНФ не должно содержаться двух и более одинаковых СКНФ.
- Ни в одной из конъюнкций не должно содержаться одинаковых переменных.
- В каждой элементарной КНФ должны содержаться все переменные, входящих в нее ДНФ, при этом их порядок должен полностью совпадать.
Любую булеву формулу в алгебре логики, не являющуюся тождественно ложной, можно представить в виде СНДФ, но только в одном единственном виде.
Правила построения СДНФ
Если существует определённый набор переменных, при котором значение функции равно единице, то можно записать произведения, учитывая, что переменные, значение которых больше нуля, нужно брать с отрицанием.
Алгоритм построения будет следующим:
- В таблице отмечаются все те наборы переменных, при которых [f=0]
- Для каждого отмеченного набора всех переменных записывается ДНФ, при этом если значение какой-либо из них равно нулю, то включается сама переменная, в любом другом случае ее нужно инвертировать.
- В конце все полученные дизъюнкции связываются друг с другом операциями конъюнкции.
Нет времени решать самому?
Наши эксперты помогут!
Примеры нахождения СКНФ и СДНФ
Рассмотрим несколько примеров нахождения СКНФ и СДНФ с помощью данных таблицы истинности.
Примеры 1 — 2
Необходимо по таблице истинности записать логическую функцию.

Решение. Для того чтобы выполнить задачу будем использовать правило построения СДНФ.

Получим СДНФ, которая имеет следующий вид:
[Fleft(x_{1}, x_{2}, x_{3}right)=left(overline{x_{1}} wedge overline{x_{2}} wedge overline{x_{3}}right) veeleft(overline{x_{1}} wedge overline{x_{2}} wedge x_{3}right) veeleft(x_{1} wedge overline{x_{2}} wedge overline{x_{3}}right) veeleft(x_{1} wedgeright.left.overline{x_{2}} wedge x_{3}right) veeleft(x_{1} wedge x_{2} wedge x_{3}right)]
Далее будем действовать согласно правилу построения СКНФ:

В результате получим:
[Fleft(x_{1}, x_{2}, x_{3}right)=left(x_{1} wedge overline{x_{2}} wedge x_{3}right) wedgeleft(x_{1} wedge overline{x_{2}} wedge overline{x_{3}}right) wedgeleft(overline{x_{1}} wedge overline{x_{2}} wedge x_{3}right)]
Требуется представить функцию, которая задана в таблице в виде СДНФ и СКНФ.

Решение: Для начала запишем в СНДФ заданную логическую функцию. Чтобы было проще, добавим еще один вспомогательный столбец. Руководствуемся правилом составления СДНФ и учитываем, что требуется ввести знак отрицания, если значение переменной будет нулевым. Это нужно для того, чтобы они не превратили в нули основной функции значение конъюнкции.

Значения, которые получились во вспомогательном столбце соединяем знаком дизъюнкции, в результате чего получаем искомую логическую функцию, которая примет следующий вид:
[Fleft(x_{1}, x_{2}, x_{3}, x_{4}right)=(bar{x} wedge bar{y} wedge z wedge f) veeleft(overline{x_{1}} wedge overline{x_{2}} wedge overline{x_{3}} wedge overline{x_{4}}right) veeleft(overline{x_{1}} wedge x_{2} wedge x_{3} wedgeright.left.x_{4}right) veeleft(x_{1} wedge overline{x_{2}} wedge overline{x_{3}} wedge overline{x_{4}}right)]
После этого потребуется записать логическую функцию в СКНФ. Для этого используем правило ее составления и вводим знаки отрицания для тех переменных, значение которых равно 1. Если пренебречь инвертированием единичных значений, то они могут превратить ДНФ в единицы основных функций.

Все полученные нами значения во вспомогательном столбце соединяем знаком конъюнкции и в итоге получаем логическую функцию в следующем виде.
[Fleft(x_{1}, x_{2}, x_{3}, x_{4}right)=left(x_{1} vee x_{2} vee x_{3} vee x_{4}right) wedgeleft(x_{1} vee x_{2} vee x_{3} vee overline{x_{4}}right) wedgeleft(x_{1} vee x_{2} veeright.\left.overline{x_{3}} vee x_{4}right) wedgeleft(x_{1} vee overline{x_{2}} vee x_{3} vee overline{x_{4}}right) wedgeleft(x_{1} vee overline{x_{2}} vee overline{x_{3}} vee x_{4}right) wedgeleft(overline{x_{1}} vee x_{2} vee x_{3} veeright.\left.overline{x_{4}}right) wedgeleft(overline{x_{1}} vee x_{2} vee overline{x_{3}} vee x_{4}right) wedgeleft(overline{x_{1}} vee x_{2} vee overline{x_{3}} vee overline{x_{4}}right) wedgeleft(overline{x_{1}} vee overline{x_{2}} vee x_{3} vee x_{4}right) wedge\left(overline{x_{1}} vee overline{x_{2}} vee x_{3} vee overline{x_{4}}right) wedgeleft(overline{x_{1}} vee overline{x_{2}} vee overline{x_{3}} vee x_{4}right) wedgeleft(overline{x_{1}} wedge overline{x_{2}} wedge overline{x_{3}} wedge overline{x_{4}}right)]
После рассмотрения примеров построения СДНФ и СКНФ с использованием таблицы истинности, стал понятен принцип построения логических функций.
Комбинированные цифровые схемы. Построение цифровой схемы по произвольной таблице истинности (скнф)
СКНФ-
Совершенная конъюктивная нормальная
форма
Еще
одним способом реализации цифровых
комбинационных схем является запись
логического выражения в совершенной
конъюктивной нормальной форме (СКНФ).
Применение СКНФ оправдано при большом
количестве логических единиц в выходном
сигнале проектируемой цифровой схемы,
как это показано в качестве примера в
таблице истинности 2, или в
ЭСЛ-микросхемах.
Таблица 2 Пример
таблицы истинности 2
|
№ комбинации |
Входы |
Выходы |
||||
|
8 |
4 |
2 |
1 |
a |
b |
|
|
0 |
0 |
0 |
0 |
0 |
1 |
1 |
|
1 |
0 |
0 |
0 |
1 |
0 |
1 |
|
2 |
0 |
0 |
1 |
0 |
1 |
1 |
|
3 |
0 |
0 |
1 |
1 |
1 |
1 |
|
4 |
0 |
1 |
0 |
0 |
0 |
1 |
|
5 |
0 |
1 |
0 |
1 |
1 |
0 |
|
6 |
0 |
1 |
1 |
0 |
1 |
0 |
|
7 |
0 |
1 |
1 |
1 |
1 |
1 |
|
8 |
1 |
0 |
0 |
0 |
1 |
1 |
|
9 |
1 |
0 |
0 |
1 |
1 |
1 |
Для
реализации цифрового комбинационного
устройства по таблице истинности при
помощи логических элементов «ИЛИ»
(СКНФ) достаточно рассмотреть только
те строки таблицы истинности, которые
содержат логические «0» в выходном
сигнале. Строки, содержащие в выходном
сигнале логическую «1» в построении
логического выражения, а, следовательно,
и принципиальной схемы цифрового
устройства не участвуют. Каждая строка,
содержащая в выходном сигнале логический
«0», реализуется схемой логического
элемента «ИЛИ» с количеством входов,
совпадающим с количеством входных
сигналов в таблице истинности.
Для
построения схемы, реализующей сигнал
Out0, достаточно рассмотреть строки,
выделенные курсивом. В рассматриваемой
таблице истинности имеются всего две
строки, содержащие логический ноль в
выходном сигнале a, поэтому в формуле
СКНФ будет содержаться две суммы входных
сигналов:
Входные
сигналы, описанные в таблице истинности
логическим нулём, подаются на вход этой
схемы непосредственно, а входные сигналы,
описанные в таблице истинности логической
единицей, подаются на логического
элемента «ИЛИ» через инверторы.
Объединение сигналов с выходов схем
«ИЛИ», реализующих отдельные строки
таблицы истинности, производится при
помощи схемы логического элемента «И».
Количество входов в схеме «И»
определяется количеством строк в таблице
истинности, в которых в выходном сигнале
присутствует логическая единица.
Полученная
формула в схеме на рисунке 9 реализуются
микросхемой D2.
Для
построения схемы, реализующей сигнал
b, достаточно рассмотреть строки,
выделенные жирным шрифтом. Эти строки
в схеме на рисунке реализуются микросхемой
D3. Принцип построения этой схемы не
отличается от примера, рассмотренного
выше. В таблице истинности присутствуют
всего две строки, содержащие ноль в
выходном сигнале b, поэтому в формуле
СКНФ выхода b будет содержаться две
суммы входных сигналов:
Комбинированные цифровые схемы. Декодер. Десятичный дешифратор
Декодеры
(дешифраторы) позволяют преобразовывать
одни виды бинарных кодов в другие.
Например, преобразовывать позиционный
двоичный код в линейный восьмеричный
или шестнадцатеричный. Преобразование
производится по правилам, описанным в
таблицах истинности, поэтому построение
дешифраторов не представляет трудностей.
Рассмотрим
пример построения дешифратора (декодера)
из двоичного кода в десятичный. Десятичный
код обычно отображается одним битом на
одну десятичную цифру. Это классический
пример, иллюстрирующий, что нулями и
единицами описываются не только двоичные
коды. В десятичном коде десять цифр,
поэтому для отображения одного десятичного
разряда требуется десять выходов
дешифратора. Около каждого разряда
десятичного кода подписана десятичная
цифра, которую отображает логическая
единица в этом разряде. Сигнал с этих
выводов дешифратора можно подать на
десятичный индикатор. В простейшем
случае над светодиодом можно просто
подписать индицируемую цифру. На входе
дешифратора двоичный код записывается
в соответствии с правилами двоичной
системы счисления. Таблица истинности
десятичного декодера приведена в
таблице 1.
Таблица 1.
Таблица истинности десятичного декодера.
|
№ |
Входы |
Выходы |
||||||||||||
|
8 |
4 |
2 |
1 |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
|
|
0 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
1 |
0 |
0 |
0 |
1 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
2 |
0 |
0 |
1 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
3 |
0 |
0 |
1 |
1 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
|
4 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
|
5 |
0 |
1 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
|
6 |
0 |
1 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
|
7 |
0 |
1 |
1 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
|
8 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
|
9 |
1 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
В
соответствии с принципами построения
схемы по произвольной таблице истинности
получим схему декодера, реализующего
таблицу истинности, приведённую в
таблице 1. Эта схема приведена на
рисунке 1.
Рисунок 1.
Принципиальная схема двоично-десятичного
дешифратора (декодера)
Как
видно на этой схеме для реализации
каждой строки таблицы истинности
потребовалась схема «4И». Схема
«ИЛИ» не потребовалась, так как в
таблице истинности на каждом выходе
присутствует только одна единица.
Дешифраторы
выпускаются в виде отдельных микросхем
или используются в составе других
микросхем. В настоящее время десятичные
или восьмеричные дешифраторы используются
в основном как составная часть других
микросхем, таких как мультиплексоры,
демультиплексоры, ПЗУ
или ОЗУ.
Условно-графическое
обозначение микросхемы дешифратора на
принципиальных схемах приведено на
рисунке 2. На этом рисунке приведено
обозначение двоично-десятичного
дешифратора, полная внутренняя
принципиальная принципиальная схема
которого изображена на рисунке 1.
Рисунок 2.
Условно-графическое обозначение
двоично-десятичного дешифратора
Соседние файлы в предмете Информатика
- #
15.03.2015134.38 Кб31.pdf
- #
- #
- #
- #
- #
- #
- #
- #
Построение СКНФ и СДНФ по таблице истинности
- СКНФ
- СДНФ
Нормальной форме логической формулы не свойственна эквивалентность, отрицание формул неэлементарного типа и знаки импликации.
Выделяют такие виды формы нормального типа:
СКНФ
Совершенная КНФ является разновидностью конъюнктивной нормальной формы, удовлетворяющей такие условия:
- отсутствие одинаковых элементарных дизъюнкций;
- дизъюнкции не содержат одинаковые переменные;
- все дизъюнкции содержат каждую переменную из входящих в конъюнктивную НФ такого типа.
Так и не нашли ответ на вопрос?
Просто напишите,с чем нужна помощь
Мне нужна помощь
Построение СКНФ согласно таблице истинности
Если функция равна нулю, то в случае каждого набора записывают сумму, причем с отрицанием берутся те переменные, которые равны единице.
СДНФ
Совершенная ДНФ является разновидностью дизъюнктивной нормальной формы, удовлетворяющей следующие условия:
- отсутствие одинаковых элементарных конъюнкций;
- конъюнкции не свойственно обладать одинаковыми переменными;
в случае любой конъюнкции элементарного типа имеет место быть переменная, входящая в такую нормальную дизъюнктивную форму. При этом в одинаковом порядке.
Все формулы булевого типа, которые не относятся к тождественно ложным, могут быть представлены в совершенной разновидности ДНФ, при этом в единственном возможном варианте.
Построение СДНФ согласно таблице истинности
Если функция соответствует единице, то в случае каждого набора записывается произведение, причем с отрицанием берутся те переменные, которые равны нулю.
Нахождение СКНФ и СДНФ: примеры
Пример
Согласно таблице истинности записать логическую функцию:
Рисунок 1.
Решение:
Прибегнем к правилу построения совершенной ДНФ
Рисунок 2.
Получаем такую СДНФ
Задействовав правило её построения:
Рисунок 3.
Получаем СКНФ:
Пример
Представить функцию как СДНФ и СКНФ, при том, что она задаётся таблицей истинности.
Рисунок 4.
Решение
Для начала нужно записать логическую функцию в СДНФ. Чтобы упростить решение, добавляем к таблице столбец. Прибегнув к правилу составления СДНФ, вводим знак отрицания для переменных с нулевым значением. Инвертирование нулевых значений переменных имеет большое значение, поскольку без этого значения конъюнкций будут преобразованы в нули ключевой функции.
Рисунок 5.
Вычисленные конъюнкции из вспомогательного столбца необходимо объединить знаком дизъюнкции и получим необходимую логическую функцию, имеющую вид совершенной конъюнктивной формы нормального типа:
Запишем логическую функцию в СКНФ.
Прибегнув к правилу, по которому составляется СКНФ, нужно помнить о введения знака отрицания для переменных с единицей. Инвертирование единичных значений имеет большое значение, поскольку без этого значения дизъюнкций будут преобразованы в единицы ключевой функции.
Рисунок 6.
Вычисленные дизъюнкции из вспомогательного столбца необходимо объединить знаком конъюнкции, так как таким образом и можно получить необходимую логическую функцию, имеющую вид совершенной нормальной формы конъюнктивного типа.