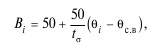Как составить шкалу оценки по тесту

Часто задаваемые вопросы

Тестовые
шкалы разрабатываются для того, чтобы
оценить индивидуальный результат
тестирования путем сопоставления его
с тестовыми нормами, полученными на
выборке стандартизации. Выборка
стандартизации специаль­но
формируется для разработки тестовой
шкалы – она должна быть репрезентативна
генеральной совокупности, для которой
планируется применять данный тест.
Впоследствии при тестировании
предполагается, что и тестируемый, и
выборка стандартизации принадлежат
одной и той же генеральной совокупности.

Исходным
принципом при разработке тестовой шкалы
является предпо­ложение о том, что
измеряемое свойство распределено в
генеральной сово­купности в соответствии
с нормальным законом. Соответственно,
измерение в тестовой шкале данного
свойства на выборке стандартизации
также должно обеспечивать нормальное
распределение. Если это так, то тестовая
шкала является метрической – точнее,
равных интервалов. Если это не так, то
свойство удалось отразить в лучшем
случае – в шкале порядка. Естественно,
что большинство стандартных тестовых
шкал являются метрическими, что позволяет
более детально интерпретировать
результаты тестирования – с учетом
свойств нормального распределения –
и корректно применять любые методы
статистического анализа. Таким
образом, основная проблема стандартизации
теста заключается в разработке такой
шкалы, в которой распределение тестовых
показателей на выборке стандартизации
соответствовало бы нормальному
распределению.

Исходные
тестовые оценки – это количество ответов
на те или иные вопросы теста, время или
количество решенных задач и т. д. Они
еще называются первичными, или «сырыми»
оценками. Итогом стандартизации являются
тестовые нормы – таблица пересчета
«сырых» оценок в стандартные тестовые
шкалы.

Существует
множество стандартных тестовых шкал,
основное назначение которых –
представление индивидуальных результатов
тестирования в удобном для интерпретации
виде. Некоторые из этих шкал представлены
на рисунке 6.5. Общим для них является
соответствие нормальному распределению,
а различаются они только двумя
показателями: средним значением и
масштабом (стандартным отклонением –
σ), определяющим дробность шкалы.

Общая
последовательность стандартизации
(разработки
тестовых норм – таблицы пересчета
«сырых» оценок в стандартные тестовые)
состоит в следующем:

1. определяется
   генеральная совокупность, для которой
   разрабатывается методика и формируется
   репрезентативная выборка стандартизации;

2. по
   результатам применения первичного
   варианта теста строится распределение
   «сырых» оценок;

3. проверяют
   соответствие полученного распределения
   нормальному закону;

4. если
   распределение «сырых» оценок соответствует
   нормальному, производится линейная
   стандартизация;

5. если
   распределение «сырых» оценок не
   соответствует нормальному, то возможны
   два варианта:

• перед
  линейной стандартизацией производят
  эмпирическую нормализацию;

• проводят
  нелинейную нормализацию.

Проверка
распределения «сырых» оценок на
соответствие нормальному закону
производится при помощи специальных
критериев, которые мы рассмотрим далее
в этой главе.

Линейная
стандартизация
заключается
в том, что определяются границы интервалов
«сырых» оценок, соответствующие
стандартным тестовым показателям. Эти
границы вычисляются путем прибавления
к среднему «сырых» оценок (или вычитания
из него) долей стандартных отклонений,
соответствующих тестовой шкале. Пример,
приведенный ниже, демонстрирует процедуру
линейной стандартизации.

Рис.
6.5. Нормальная кривая и тестовые шкалы

Пример.
Предположим,
получено распределение «сырых» оценок,
соответствующее нормальному, со средним
М_х
= 22
и стандартным отклонением σ_х
=
6. В качестве стандартной тестовой шкалы
выбрана 10-балльная шкала стенов,
предложенная Р. Кеттелом (M_st
=
5,5; σ_st
= 2). Результатом
линейной стандартизации должна являться
таблица пересчета из шкалы «сырых»
оценок в шкалу стенов. Для этого каждому
стандартному значению ставится в
соответствие интервал «сырых» оценок.
Границы интервалов определяются
следующим образом. Среднее «сырых»
оценок должно делить шкалу стенов ровно
пополам (1 – 5 – ниже среднего, 6 – 10 –
выше среднего). Следовательно, среднее
«сырых» оценок М_х=22
–
это
граница стенов 5 и 6. Следующая граница
справа – отделяющая стены 6 и 7 – отстоит
от среднего на σ_st/2.
Этой границе должна соответствовать
граница «сырых» оценок М_х
+
σ_st/2
= 22
+ 3 = 25. Так же определяются границы всех
оставшихся интервалов, а границы крайних
интервалов остаются открытыми. Результатом
являются тестовые нормы – таблица
пересчета «сырых» баллов в стандартные
тестовые оценки (табл. 6.1).

Обратите
внимание, что левая граница каждого
диапазона «сырых» оценок исключает
границу интервалов, а правая – включает
ее. Можно было бы сделать и наоборот, но
главное, чтобы границы соседних диапазонов
не совпадали во избежание недоразумений
при попада­нии индивидуального
значения на границу интервалов.

Таблица
6.1

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

Теория

ШКАЛИРОВАНИЕ ТЕСТОВЫХ РЕЗУЛЬТАТОВ

Вадим Аванесов

testolog@mail.ru

Шкалирование определяется как трансформация тестовых результатов из одной числовой системы в другую числовую систему.

Выделены шкалы классификационная (номинальная), порядка, шкала упорядоченной классификации, интервальная и пропорциональная.

Интервальная шкала представляется шкалой нормированных отклонений ^-шкалой) и производной от неё Т-шкалой. Главными условиями корректного применения Z и T шкал признаны надёжность исходных результатов тестирования и нормальное распределение данных.

Шкалирование на научной основе предполагает трансформацию исходных тестовых баллов в баллы т.н. истинных значений результатов испытуемых (в). Истинные значения тестовых баллов испытуемых определяются на латентной шкале измеряемого свойства личности.

Hn

измерения

-е-

—i—

Maranell О.М. Scaling: A Sourcebook for Behavioral Scientists. Chicago: Aldine, 1974.

Torgerson W.S. Scaling. (1958) Theory and Method of Scaling.

N-Y, Wiley.

Каргин Ю.Н. Метод независимого шкалирования результатов ЕГЭ //Педагогические измерения. 2013 №1.

Определение

В литературе приводится довольно много определений шкалирования. Это сделано в трудах МагапеП1, То^егеоп2 и других. В настоящей работе даётся самое короткое определение шкалирования: это трансформация исходных тестовых результатов из одной числовой системы в другую числовую систему.

Роль элементарной единицы учёта наличия интересующего признака выполняют контрольные задания, подобранные для определения уровня подготовленности. Объектом измерения является носитель интересующего свойства личности. Наиболее корректное средство измерения — педагогический тест. Получаемые при измерении числа позволяют глубже проникнуть в суть изучаемых явлений, что особенно важно для научно обоснованного тестового контроля.

Цель и задачи

В педагогических измерениях при разработке тестов обычно шкалируются уровни подготовленности испытуемых (0;,) уровни трудности заданий в и уровни дифференцирующей способности заданий (ар.

Шкалирование проводится с целью объективного сравне-

ния результатов испытуемых, полученным по разным тестам, с разным числом заданий, и разных систем оценивания результатов испытуемых.

Шкалирование необходимо также для решения задач формирования комплексной оценки уровня подготовленности испытуемых по результатам нескольких тестов, для определения места испытуемых, для выравнивания баллов в нескольких вариантах теста и др.

Проблемная ситуация

В настоящий момент вопросы шкалирования приобрели отчётливо спорный, если не сказать проблемно-конфликтный, характер в рамках проведения т.н. Единого государственного экзамена (ЕГЭ).

Проблемную ситуацию чётко охарактеризовал Ю.Н. Кар-гин. Он считает, что разработчики и организаторы проведения ЕГЭ кардинально изменили систему шкалирования результатов в 2011 году. Вследствие чего существующая в России система оценивания знаний из метрической области оказалась сдвинутой в область описательных характеристик и неметрических оценок3.

Ю.Н. Каргин делает вывод, что основной источник проблем действующей сейчас методики шкалирования заложен

в отсутствии какой-либо научной основы. Официальная методика носит скорее умозрительный, искусственный характер и, по-видимому, не имеет под собой ни теоретического обоснования, ни достаточного эмпирического подтверждения4. Этот автор предложил новую систему шкалирования, которая существенно лучше существующей.

Критика существующей практики шкалирования содержится также в статье Л.М. Нуриевой и С.Г. Киселёва, публикуемой в настоящем номере журнала «ПИ». Они справедливо отмечают, что учащиеся, делающие лишь единичные ошибки, МАКСИМАЛЬНО НАКАЗЫВАЮТСЯ потерей тестовых баллов5.

Например, за работу наугад на экзамене по русскому языку «непредвзятая диагностика ЕГЭ» одарит лоботряса 7-8 первичными или 15-17 тестовыми баллами. Сильных школьников, потерявших 7-8 первичных баллов из 80 возможных (10%), она обворует на пятую часть тестовых (20%). Отсюда понятной становится уже почти закономерная картина: неожиданно высокие результаты у детей, учившихся в школе на «3-4», и относительно низкие — у отличников, призеров олимпиад и различных конкурсов по предметам. Именно нелепая система оценивания

позволяет обвинять школы в «липовых» медалистах, а олимпиады и конкурсы — в слабых победителях. Собственно в этом кривом зеркале ЕГЭ и отражается состояние школьной подготовки6.

Как отметил в своём интервью газете «РУ» учитель Григория Перельмана и Станислава Смирнова, двух лауреатов Филдсовской премии, педагог, воспитавший 90 призеров и победителей международных олимпиад по математике, профессор РГПУ им. Герцена, замдиректора по науке, физмат лицея №239 Сергей Рукшин, «Ломоносовых в России уже больше не будет»7. Основную причину такого положения он видит в бюрократизации управления образованием.

Виды шкал

С.С. Стивенсу мы обязаны первой, понятной, а потому популярной классификацией шкал8. Он выделил четыре шкалы. Каждая из шкал связана с допустимостью использования цифр, чисел, с различиями в интерпретации возможного смысла чисел.

Номинальная шкала

Например, номера футболистов ничего не говорят об уровне мастерства. Потому что но-

Там же.

Нуриева Л.М, Киселёв С.

Единый государственный экзамен нуждается в существенных изменениях //Педагогические измерения. 2013. №4.

Там же.

«Ломоносовых больше не будет». Сергей Рук-шин рассказал «Газе-те^и», в чем ошибки реформы российского образования. 30 ноября 2013 г.

http://www.zavuch.info/ news/news_main/456/

Стивенс С.С. Экспериментальная психология. Т. 1. Иност. лит-ра, 1960. С. 19-89.

г»п

измерения

мера — это цифры, которые не содержат числового и операционального смысла. Цифры нельзя складывать или делить, на основе таких операций невозможно сформировать новые конструктивные суждения. Так же примерно надо относиться к нумерации комнат в гостиницах. Больший номер не обязательно указывает на более качественное помещение для проживания.

Из этих двух примеров видно, что в номинальной шкале используются цифры, а не числа. Вот почему в классификации С.С. Стивенса номинальная шкала рассматривается как необходимая прелюдия к измерениям, но не к результатам измерения.

Цифры, используемые для названия, являются обычно оцениванием объектов по признаку наличия или отсутствия интересующего признака. В психометрике уже давно сложилась традиция: наличие признака оценивать числом один, а отсутствие — числом ноль. Это случай не измерения, а оценки. Примеры оценивания: «отличники», «хорошо успевающие», «удовлетворительно подготовленные» «и получившие неудовлетворительные оценки».

При оценивании с опорой на понятие «номинальная шкала», в соответствующем векторе-столбце матрицы испытуемые одного уровня — напри-

мер, отличники оценивают обычно одним баллом. Всех прочих в этом столбце оценивают нулём. Таким образом, их отделяют от испытуемых других классов. В следующем столбце матрицы одним баллом оценивают тех, кто получил балл «хорошо»; все остальные опять получают ноль. И т.д. Каждый вектор-столбец представляет испытуемых одного класса (уровня) подготовленности. Это делается на основе сходных учебных показателей.

Однако если в процессе исследования возникает задача определить тех, у кого чаще (или больше) выражен интересующий признак, то те же единица и ноль могут быть истолкованы как числа. Тогда открывается возможность складывать проявления признака у каждого испытуемого и делать вывод о больших или меньших различиях между испытуемыми по этому признаку. Таким образам, можно выйти на раскрытие смысла понятия «уровень подготовленности. Процесс превращения цифр номинальной шкалы в числа уровневой шкалы наглядно представлен в последнем столбце табл. 1.

Порядковая шкала

По значениям чисел последнего столбца табл. 1 можно судить о некотором уровне (порядке)

Таблица 1

Теория

Пример матрицы результатов тестирования

Номера заданий

Номера испытаний 1 2 3 4 5 6 Сумма баллов

1 1 1 1 1 1 1 6

2 1 1 1 1 1 0 5

3 1 1 1 1 0 1 5

4 1 1 1 0 1 0 4

5 1 1 1 0 0 0 3

6 1 1 0 0 0 0 2

7 1 1 0 0 0 0 2

8 1 1 0 0 0 0 2

9 1 0 0 1 0 0 2

10 1 0 0 0 0 0 1

Сумма 10 8 5 4 3 2 33

баллов подготовленности испытуемых. Поэтому использование единиц, нулей и других чисел в рамках номинальной шкалы могут рассматриваться как числа, имеющие смысл для определения места испытуемого. Именно содержательный смысл в гуманитарных науках открывает возможности трансформации исходных данных в порядковую шкалу.

Порядковая шкала имеет два варианта. В подлинно по-

рядковой шкале каждый испытуемый (или интересующий объект) имеет свой, отличный от всех других испытуемых ранг. Ранг — это число, указывающее на место, занимаемое каждым испытуемым в порядковой шкале.

Пример оценки испытуемых на порядковой шкале приведён в табл. 2.

Здесь каждому испытуемому поставлен в соответствие свой ранг. У каждого испытуе-

Таблица 2

Номера заданий

Номера испытаний 1 2 3 4 5 6 Сумма баллов

1 1 1 1 1 1 1 6

2 1 1 1 1 1 0 5

3 1 1 1 0 1 0 4

4 1 1 1 0 0 0 3

5 1 1 0 0 0 0 2

6 1 0 0 0 0 0 1

Сумма 6 5 4 2 3 1 21

измерения

мого свой ранг, отличный от других испытуемых. Имеет смысл и сумма рангов. Но такая ситуация полного упорядочения случается редко.

А потому возникает необходимость введения ещё одной шкалы, не существующей в шкалах С.С. Стивенса — шкалы упорядоченной классификации.

Шкала

упорядоченной классификации

Расположение результатов испытуемых в табл. 2, на порядковой шкале, случается очень редко. Чаще бывает так, что многие, особенно средние, результаты повторяются у нескольких испытуемых. Такие повторяющиеся результаты являются неразличимыми по уровню подготовленности, а потому часть из них включается в один общий уровень (класс) испытуемых. Отсюда возникает статистическое понятие частоты (/). В табл. 3 частоты указывают, сколько человек получили одинаковый исходный тестовый балл.

Пример распределения результатов девяти, взятых для примера, испытуемых можно увидеть в табл. 3. Из неё видно, что четыре исходных тестовых балла получили двое испытуемых, а пять исходных баллов

получили трое испытуемых. Здесь нет отношений строгого порядка между испытуемыми.

В таких случаях некоторые испытуемые упорядочиваются, а некоторые классифицируются — а здесь это те, кто получили баллы 4, 5 и 6. И только затем все тестируемые упорядочиваются. При этом попавшие в один класс испытуемые получают один общий (связанный) ранг.

Результат упорядочения на основе связанных рангов представлен в последней колонке табл. 3. Тех, кто получил в данном примере четыре исходных тестовых балла, можно упорядочить с остальными, дав им девятый с половиной ранг. Тем, кто имеет 5 исходных баллов (а их трое), логично дать седьмой ранг. И наконец, тем, кто получил 6 баллов, даётся четвёртый с половиной ранг. Только в этом случае все испытуемые становятся различимыми (расставленными) на порядковой шкале, или иначе, на шкале рангов.

Интервальная шкала

В интервальной шкале фиксируется не только общее количество интересующего свойства у испытуемых, но и различия между ними по данному свойству. В этой шкале возникает необходимость иметь единицу

Таблица 3

Теория

Баллы Частоты / Сит. F Ранг

iНе можете найти то, что вам нужно? Попробуйте сервис подбора литературы.

1 1 13 13

2 1 12 12

3 1 11 11

4 2 10 9-10

5 3 8 6-8

6 2 5 4-5

7 1 3 3

8 1 2 2

9 1 1 1

измерения. В психологических и педагогических тестах это баллы теста, что даёт возможность ответить на вопрос: на сколько единиц измерения результат одного испытуемого выше результата другого испытуемого? Вследствие этого, числа, используемые в интервальной шкале, не только имеют свойства однозначности и упорядоченности, отмечавшиеся для порядковых шкал, но и свойство различий между значениями используемых чисел. В интервальной шкале уместен вопрос: на сколько баллов результат одного испытуемого отличается от баллов другого испытуемого?

В качестве средней арифметической интервальной шкалы нередко выбирается значение нуля, что имеет некоторые преимущества. Примеры использования интервальной шкалы дают нам баллы интеллектуальных (психологических) и педагогических тестов, шкала Г. Раша и др.

Как отмечают Дж. Гласс и Дж. Стэнли, измерение любой непрерывной переменной величины должно сопровождаться определением точности процесса измерения9. Этим объясняется потребность введения более дробных значений используемых шкал.

Пропорциональная шкала

Главное свойство пропорциональной шкалы — наличие бесспорного нулевого значения интересующего признака. В психофизике конца XIX и начала ХХ веков много обсуждался вопрос о возможности наличия человека с нулевым значением интеллекта. И тогда же был поставлен важный вопрос: а можно ли называть человеком лицо, имеющее нулевой интеллект? В итоге дискуссий была принята идея о невозможности создания шкалы интеллекта с нулевым значением,

Дж.Гласс, Дж. Стэнли. Статистические методы в педагогике и психологии. М.: Прогресс, 1976. С. 20.

Hn

измерения

как противоречащую сути психологических измерений.

Примерно такая же логика присуща и педагогическим измерениям. Здесь декларируемый нулевой уровень знаний может оказаться слишком субъективным, поскольку испытуемые студенты и школьники что-нибудь всё-таки знают. Оценка «ноль» в таких случаях сомнительная и спорная.

В отсутствии бесспорного нуля шкалы становятся невозможными утверждения типа «во сколько раз один испытуемый знает больше другого испытуемого». Поэтому в педагогических измерениях уже много лет назад утвердилось мнение о неперспективности создания пропорциональных шкал. Недавняя публикация Ю.Н. Каргина по альтернативному методу шкалирования результатов ЕГЭ вновь возвращает нас к вопросу о возможности создания новых шкал, соотносящихся, в той или иной мере, со свойствами пропорциональной шкалы.

Четыре науки

Почти в каждой науке существует круг исследователей, занимающихся вопросами шкалирования изучаемых там объектов, по интересующим свойствам. Например, в физике

шкалируются данные по таким величинам, как температура, длина, скорость, масса и другим. При этом температура может измеряться по шкале Фаренгейта или Цельсия, длина — в сантиметрах или футах, вес — в килограммах или фунтах. Это примеры разных шкал измерения одного и того же свойства (признака).

Вопросами шкалирования занимаются четыре науки:

1. Собственно шкалирование как прикладная специальная наука, развивающаяся в технике, педагогике, психологии, социологии и т. п. Эта наука имеет общее английское название Scaling с добавлением названия науки.

2. Педагогические, психологические и иные измерения, связанные с разработкой тестов и интерпретацией тестовых результатов. При этом обычно шкалируются баллы испытуемых, уровень трудности заданий теста и показатели дифференцирующей способности каждого задания теста.

В двухпараметрической модели математической теории измерений (Item Response Theory) в результате шкалирования получаются значения 0i — баллов испытуемых на латентной шкале, значения меры трудности заданий теста в) и значения уровня дифференцирующей способности каждого задания теста (aj), где

индекс ] означает номер задания теста.

3. Статистика, как наука, тоже занимается шкалированием исследуемых объектов по интересующему признаку. Именно в статистике используются т.н. центрирование баллов испытуемых, что означает операцию вычитания среднего арифметического из балла каждого испытуемого (Х; — М), а также статистические методы трансформации данных в различные шкалы.

4. Математика и математические методы шкалирования, вопросы непрерывности (континуума) измерения, вопросы размерности шкал, допустимости различных преобразования, аксиомы и пр.

В психометрике уже давно в качестве графического аналога континуума принимается числовая ось, простирающаяся до бесконечности, вправо и влево, от -го до

Условия

качественного

шкалирования

Задачи шкалирования обычно возникают на заключительных этапах тестового процесса, когда возникает потребность объективного сравнения результатов одного испытуемого по разным тестам, имеющим разное количество заданий.

Распространённую практику сложения всех баллов испытуемого, по всем тестам, и выведения суммы как критерия успешности, как это делается в ЕГЭ, надо признать ошибочной ввиду несопоставимости самих тестов, имеющих различающиеся средние арифметические и показатели вариации, а также разные формы распределения, выражаемые показателями эксцесса и асимметрии. Это теперь уже установлено фактически, в статье, печатаемой в данном номере10.

Для сложения таких исходных данных требуется процесс стандартизации результатов тестирования.

Предпосылкой для качественного шкалирования результатов рассматриваются качественные педагогические тесты, позволяющие получать измерения со свойствами интервальной шкалы и нормального распределения результатов, а также алгоритмы шкалирования, основанные на науке. В специальной литературе эти свойства справедливо расцениваются как признаки фундаментальности проводимых измерений.

Шкала

нормированных отклонений

В педагогических измерениях нет шкалы более популярной и полезной, чем шкала нормиро-

-10-

Нуриева Л.М., Киселёв С.

Единый государственный экзамен нуждается в существенных изменениях. Педагогические измерения. № 4. 2013.

г»п

измерения

ванных отклонений тестовых баллов испытуемых от среднего арифметического тестового балла. Это так называемая 2-шкала. Популярность объясняется функциями и свойствами этой шкалы, лёгкостью расчёта и возможностью корректного сравнения тестовых баллов испытуемых по нескольким тестам, имеющим разное число заданий. Различие в количестве заданий каждого теста обычно препятствуют объективному сравнению в таких ситуациях. Перевод данных в 2-шкалу снимает данное препятствие.

Пример расчёта z-шкалы

Для перевода результатов тестирования по любому тесту в 2-шкалу используются две операции:

• определяются значения отклонений тестовых баллов X; от среднего арифметического значения Мх. Получается значение отклонения тестового балла, X; = X; — Мх. Эту операцию иногда называют центрированием данных. Деление х;^ даёт значение нормированного отклонения тестового балла испытуемого под номером I.

Далее каждое значение отклонения X; делится на стандартное отклонение этого же теста Бх. Получается = х;Д

Эту операцию называют нормированием данных. В качестве единицы нормирования тестовых данных выступает стандартное отклонение соответствующего теста. В результате центрирования и нормирования значения любого теста переводятся в значения стандартной 2-шкалы.

Для центрирования данных необходимо знать значение среднего арифметического балла (Мх). Последний вычисляется по формуле

I X

М, = ■

N

где символы при знаке X, в числителе, означают так называемые пределы суммирования тестовых баллов всех испытуемых X;, с первого до седьмого включительно; N — число испытуемых.

Находится значение среднего арифметического балла:

„ 28 . Мх = — = 4 балла.

Для нормирования данных требуется знание значения стандартного отклонения. Стандартное отклонение (5х) вычисляется по формуле:

‘ N ‘

где является суммой квадратов отклонений от среднего арифметического значения.55х считается по формуле.

=.

X X2 —

(X *)

N

В нашем примере XX2 = 140, XX = 28, (EX)2 = 784. Подставляем в нашем примере:

SSx = 140 — Ш = 140 -112 = 28.

Результаты расчётов представлены в табл. 4

Значения z-шкалы удобно вычислять в электронных таблицах Excel.

Sx N , V 7 2.

Z1 =1-4 = -1,5, 1 2

2 — 4 Z = 2-4 = -1,0,

Z=

2

3 — 4

= -0,5,

4 — 4 Z, = 4-4 = 0,

Z=

2

5 — 4

= 0,5,

Z = 6-4 = 1,0,

Z=

2

7 — 4

= 1,5.

Свойства Е-шкалы

2-шкала обладает следующими свойствами:

1. Средняя арифметическая z-шкалы равна нулю: = 0. Доказательство:

I

M =-

N

IZ = I(X — M ) / n

N x

Но по свойству средней арифметической

X(* — M)= 0.

Следовательно,

IZ 0 = — = 0. N N

Таблица 4

iНе можете найти то, что вам нужно? Попробуйте сервис подбора литературы.

Баллы Х Z — значения баллов Х

1 -1,5z

2 -1,0z

3 -0,5z

4 0z

5 0,5z

6 1,0z

7 1,5z

ZX = 28 Zz = 0

Hn

измерения

-e-

-n-

Аванесов В.С. Дис. на соискание учёной степени д-ра пед. наук. СП-б . 1994. 339 стр.

Guilford J.P. Psychometric Methods. 2-ed, N-Y, McGraw-Hill, 1954. 597 p.; Guilford J.P. Fundamental Statistics in Psychology and Education. 3 ed. N-Y., McGraw-Hill, 1956.565 p. Guilford J.P., FruchterB. Fundamental Statistics in Psychology and Education. 5-ed. N-Y, McGraw-Hill. 1973. 564 p.

Это означает, что при переводе в 2-шкалу среднее арифметическое значение любого теста равно нулю. Среднее арифметическое в 2-шкале даёт общую точку для сравнения баллов, что очень удобно для сравнения тестовых баллов различных испытуемых по различным тестам.

2. Все значения меньше среднего арифметического в 2-шкале отрицательны, а значения больше среднего арифметического — положительны. Это вытекает из свойства среднего арифметического значения и из свойства операции вычитания X; — Mx.

3. Распределение 2 точно такое же по форме, как и распределение исходных баллов. Это линейное преобразование, не меняющее форму распределения исходных данных.

4. Дисперсия и стандартное отклонение равны единице:

Б2 = Бг = 1,0 .

Т-шкала

Потребность в Т-шкале возникла, главным образом, из трудностей общения исследователей с родителями. Последние не допускали даже мысли о том, что их дети могут получить отрицательные баллы. Поэтому родителям была предложена иная шкала, позволяющая трансформировать данные

2-шкалы в другую шкалу, которая обеспечивает перевод всех данных в область положительных значений. Это стало возможным посредством формулы, переводящей данные 2-шкалы в Т-шкалу:

Т; = 50 + 10г; [1]

Одиннадцатибалльная шкала

Для повышения дифференцирующей способности педагогических оценок автором этой статьи в своё время была предложена одиннадцатибалльная шкала, которая получается из известной в литературе шкалы стандартных девяти единиц за счёт добавления по одному интервалу в 0,5 стандартного отклонения справа и слева11.

В отличие от шкалы стандартных девяти единиц ^а-п;пе)12, здесь появляется возможность более тонкой дифференциации испытуемых. Если значениям стандартных баллов приписать оценочные эквиваленты, то соотношение между значениями нормированных отклонений 2, процентом испытуемых и оценочными эквивалентами можно представить в табл. 2.

В случае перевода системы образования с нынешней пятибалльной на более дифференцированную шкалу, одиннадцатибалльная шкала

является наиболее подходящей и рекомендуемой как по своим статистическим свойствам, так и по наличию лексических эквивалентов каждой числовой оценки13. Преимущество последней обосновано с педагогической, статистической и управленческой точек зрения14.

Соотношение между балльными оценочными эквивалентами баллами представлено в табл. 6.

Утверждение одиннадцатибалльной шкалы в качестве нормативной может дать ряд преимуществ. По сравнению с пятибалльной, повышается дифференцирующая способность педагогической оценки. Не надо вычислять до сотых долей средний балл, получен-

ный из баллов, исходная точность которых была заведомо ниже. Особенно чётко в одиннадцатибалльной шкале дифференцируется один процент лучших и худших15.

Лучшие — это чаще всего самые талантливые студенты, которых надо выявлять и затем тщательно с ними работать. Если согласиться с тем, что один хороший специалист лучше ста плохих и средних, то ясно, что в век технологий от этого одного процента зависит довольно много. С другой стороны, мы имеем 1% наименее подготовленных студентов, с которыми высшая школа может безболезненно расстаться, также как, впрочем, и с тремя процентами тех, кто в одиннадцатибалльной шкале имеет два балла.

Таблица 5

Соотношение Z-значений и процентов испытуемых

Значения 11-балльной шкалы Лексико-оценочные эквиваленты Значения 2 Процент испытуемых

1 Низшая оценка 2. < -2,25 1

2 Неудовлетворительно -2,25 < 2 < -1,75 3

3 Малоудовлетворительно 1,75 < 2 < -1,25 7

4 Удовлетворительно -1,25 < 2 < -0,75 12

5 Ниже среднего -0,75 < 2 < -0,25 17

6 Средняя оценка -0,25 < 2; < 0,25 20

7 Выше среднего 0,25 < 2; < 0,75 17

8 Хорошо 0,75 < 2 <1,25 12

9 Очень хорошо 1,25 < 2 <1,75 7

10 Отлично 1,75 < 2 <2,25 3

11 Высшая 2,25 < 2; 1

Стр. 196 указанной диссертации.

Дис.

Со стр. 195 докт. дис. В.С. Аванесова. Ук соч. С-Пб, 1994.

Hn

измерения

-е-

Аванесов ВС. Основы педагогического контроля в высшей школе //Основы педагогики и психологии высшей школы. Учебное пособие / Под. ред. А.В.Петровского. М.: МГУ, 1986. 303 с.; Аванесов ВС. Основы научной организации педагогического контроля в высшей школе: Учеб. пособ. для слушателей Учебного Центра. М.: МИСиС, 1987. 107 с.

В дополнение к этому, у одиннадцатибалльной шкалы, по сравнению с ранее описанной автором девятибалльной и

десятибалльной шкалами16, есть преимущества психологического характера. В качестве опорных точек шкалы используются три привычных каждому человеку сравнительных понятия — низшее значение «единица», хуже которой нет, среднее значение «шесть», приписываемое легко различимому и наиболее распространённому в практике среднему уровню знаний и высшая оценка «одиннадцать», посредством которой появляется возможность выделить из числа отличников самого отличного студента. Это важно для дальнейшего мотивирования учёбы тех, кто уже учится отлично, но может, при старании, показать более выдающиеся результаты, особо ценные как для развития личности самого студента, так и для пополнения интеллектуального потенциала общества.

Одна из таких важных для высшей школы сфер, где измерения ещё не использовались мало-мальски заметно — это педагогический контроль, научная организация которого на современном этапе развития науки и техники не мыслится без тестов. Применение тестов позволяет быстро и качественно собрать информацию об уровне подготовленности аби-

туриентов, студентов и выпускников вузов, обработать эту информацию, сравнить достижения, выявить тенденции, достижения и недостатки, осуществлять прогноз, внести коррекции в учебный процесс.

Критерии оценки качества шкал

Качества шкал можно оценивать по следующим критериям:

• уровень шкалы — номинальная, порядковая, интервальная и пропорциональная. Предпочтительны две последние;

• наличие общей единицы измерения, что обеспечивает сравнимость результатов различных тестов;

• размах значений, пределы значений оценок и измерений, получаемых по разным шкалам, дисперсия — желательно иметь их сопоставимыми, что обеспечивает равноценность баллов, получаемых по той или иной шкале;

• совпадающие средние значения шкальных баллов, показатели асимметрии и эксцесса позволяют корректно сравнивать распределения результатов по разным тестам.

Наиболее научно обоснованной шкалой надо признать такую, которая отражает идею измерения на латентной переменной величине. Ввиду обширности этого вопроса, его лучше изложить в отдельной статье.

Развитие и внедрение современных тестовых методов и технологий остро ставит вопрос необходимости совершенствования техники обработки результатов тестового контроля. Проблема надежности шкалирования результатов тестирования в педагогических измерениях так же важна, как подготовка качественного теста или техника тестирования.

В самом широком смысле измерение сводится в конечном счете к припис^гванию чисел измеряемым объектам или событиям согласно определенным правилам. Правила устанавливают соответствие между некоторыми свойствами объектов и чисел, позволяющее сравнивать между собой эти объекты по состоянию измеряемого свойства. В зависимости от целей измерения и сопоставления тех или иных объектов выбираются различные правила, отображающие различные свойства объектов. Переменные различаются тем, насколько хорошо они могут быть измерены или, другими словами, как много измеряемой информации обеспечивает их шкала. Всякий раз при измерениях нужного свойства выбирают соответствующую измерительную шкалу. Шкала – это средство фиксации результатов измерения определенных свойств объектов путем упорядочения их в определенную числовую систему, в которой отношение между отдельными результатами выражено в соответствующих числах. Очевидно, в каждом измерении всегда присутствует некоторая ошибка, определяющая границы «количества информации», которое можно получить. Другим фактором, определяющим количество информации, содержащейся в переменной, является тип шкалы, в которой проведено измерение.

В образовательной практике выделяют четыре основных вида шкал, получивших наиболее широкое распространение: номинальная, порядковая (ординальная), интервальная, относительная. Согласно С.С. Стивенсу, они получили следующие названия: шкала наименований, шкала порядка (ранговая шкала), интервальная шкала и шкала отношений [172]. Измерения на первых двух шкалах считаются качественными, а на двух других – количественными. Шкалы качественных измерений называют дискретными, а количественных – непрерывными. В каждой из этих шкал определены свойства чисел, приписываемых объектам. По этим признакам шкалы перечислены в таком порядке, что в каждой последующей, кроме свойств предыдущей шкалы, добавляются и новые. Поэтому чем больше порядок шкалы, тем больше арифметических действий разрешается проводить над числами, приписанными объектам на этих шкалах.

Номинальная, или шкала наименований, самая простая, например: зачет – незачет. Номинальные переменные используются только для качественной классификации. Это означает, что данные переменные могут быть измерены только в терминах принадлежности к некоторым, существенно различным классам, при этом определить количество или упорядочить эти классы невозможно. Типичные примеры номинальных переменных – пол, национальность, цвет, город и т.д. Часто номинальные переменные называют категориальными. Шкала наименований устанавливает критерии, позволяющие распределить измеряемые объекты по состоянию измеряемого свойства на несколько классов (или категорий). При этом каждый объект должен попасть в определенный класс, в котором объектам приписывается одно и то же число. Объекты одного класса считаются одинаковыми по состоянию измеряемого свойства. Примером является дихотомическая шкала: выполнившие задание получают число 1, а невыполнившие – 0. Методы обработки таких результатов оценивания знаний называют статистикой качественных признаков. Данные, соответствующие номинальным шкалам, составляют наблюдаемые значения частот появления каждой из разновидностей изучаемой переменной. Эти результаты, как правило, используются при построении матриц результатов педагогических измерений.

Порядковые шкалы (например, пятибалльная) – это шкалы, результаты измерений по которым невозможно сравнивать между собой. Порядковые переменные позволяют только ранжировать (упорядочить) объекты, указав, какие из них в большей или меньшей степени обладают качеством, выраженным данной переменной. Однако они не позволяют сказать на сколько больше или на сколько меньше один результат отличается от другого. Само расположение шкал – номинальная, порядковая, интервальная – является примером порядковой шкалы. В пределах порядковых шкал можно только упорядочить объекты в порядке возрастания или убывания оценок измеряемых параметров. На такой шкале оцениваются только качественные признаки объектов, например оценка А > В, или медианный объект, который по измеряемому свойству переходит за 50%. Число, приписываемое такому объекту, называется медианой и принимается за меру центральной тенденции грутты объектов [121].

Шкала более высокого уровня называется интервальной (или шкалой равных единиц). Интервальные переменные позволяют не только упорядочить объекты измерения, но и численно выразить и сравнить различия между ними. Например, температура, измеренная в градусах Фаренгейта или Цельсия, образует интервальную шкалу. Она позволяет сказать, что температура 40 градусов выше, чем температура 30 градусов, и что увеличение температуры с 20 до 40 градусов вдвое больше увеличения температуры с 30 до 40 градусов. Интервальная шкала – количественная, можно задать разность оценок (Х₁ – Х₂ ), абсолютное значение которой трактуется как расстояние между двумя элементами множества, выраженное в определенных единицах. Для такой шкалы характерно отсутствие начала отсчета, равного нулю, но допустимы различные арифметические действия над числами. Эта шкала задает взаимное положение измеряемых объектов относительно друг друга, но не показывает расположение объектов относительно начала координат. Так, например, разности баллов 48 – 45 и 5 – 2 одинаковы, а смысл их разности может быть различным. К результатам измерений на такой шкале применимы почти все статистические операции.

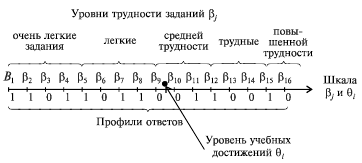
Интервальная метрическая, или нормальная, – это такая шкала, у которой задано начало отсчета. На такой шкале можно определить не только метрики (единицы измерения), как на интервальной шкале, но и понятие нормы (местоположения от начала координат). В современной теории педагогических измерений перевод «сырых» баллов («сырые» баллы дают оценки на порядковой шкале обычно в числе правильно выполненных заданий) производится на интервальную шкалу, учитывающую степень трудности выполненных заданий. Для визуализации такой шкалы можно представить уровни трудности тестовых заданий ?_j  и профили ответов, соответствующих подготовленности ?_i (рис. 14).

Рис. 14. Условный вид шкалы уровней трудности тестовых заданий и уровней подготовленности испытуемых

Шкала отношений позволяет получать самый высокий уровень измерений: допускает не только приписывание числа измеряемому объекту, но и все арифметические действия над этими числами и статистические операции, а также устанавливает равенство отношений чисел, приписываемых объектам, что вытекает из фиксированного положения нуля. Любая интервальная шкала может использоваться в качестве шкалы отношений, если в рамках проводимого измерения задать начало отсчета. Относительные переменные очень похожи на интервальные переменные. В дополнение ко всем свойствам переменных, измеренных в интервальной шкале, их характерной чертой является наличие нуля. Таким образом, для этих переменных являются обоснованными предложения типа: Х в два раза больше, чем Y. Типичными примерами шкал отношений являются измерения времени или пространства. Например, температура по Кельвину образует шкалу отношения, можно не только утверждать, что температура 200 градусов выше, чем 100 градусов, но и что она вдвое выше. Интервальные шкалы (например, шкала Цельсия) не обладают данным свойством шкалы отношения. Заметим, что в большинстве статистических процедур не делается различия между свойствами интервальных шкал и шкал отношения. На шкале отношений к полученным результатам применимы все известные понятия и методы математической статистики.

Содержательная статистическая обработка и интерпретация результатов измерений по этим шкалам могут быть только в том случае, когда методы обработки адекватны тем шкалам, к которым отнесена исходная информация. Методологией любого исследования по измерению и оценке результатов обучения является вероятностный подход, а методикой – применение аппарата математической статистики (см. приложение 3) [20, 36, 46, 89—92, 198, 233, 229]. Как понятие качества подготовленности оценка на шкале педагогических измерений имеет два основных смысла: суждение о ценности полученного знания и приблизительную характеристику некоторой величины – подготовленности [73, 183, 204].

Особенно важно использование различных шкал при тестировании, что, собственно, и делается при расчете сертификационных или тестовых баллов. При этом эффективность тестовых оценок зависит не только от качества теста, но и от используемых методов сравнения и интерпретации первичных («сырых») баллов. Стремление выявить истинные уровни знаний испытуемых, получить возможность сравнивать эти уровни между собой даже тогда, когда они определены по разным тестам, привело исследователей к разработке новых методов интерпретации результатов тестирования. Одной из сильных сторон тестового метода является не оценивание абсолютных результатов подготовленности, а измерение уровня учебных достижений обучающихся.

Это особенно важно при приеме в вузы, итоговой аттестации учащихся и диагностике качества их подготовленности.

Шкалированием принято называть комплекс вопросов, связанных с отображением на определенной шкале с единой метрикой латентных характеристик трудности всех заданий теста и выставлением каждому участнику тестирования окончательного балла, отображающего уровень его учебных достижений в заданной области знаний вне зависимости от того, в какой группе и над каким вариантом работал испытуемый.

При исследованиях предлагается учитывать ряд педагогических гипотез статистического типа: результаты выполнения одной и той же группой испытуемых различных заданий одинакового уровня не имеют существенных различий, а наблюдаемое различие объясняется случайными причинами; результаты двукратного выполнения одной и той же группой одного и того же задания существенно различаются, эти различия нельзя объяснить только случайными причинами; результаты выполнения одних и тех же заданий учащимися городских и сельских школ существенно различаются, фактор расположения школы (в определенном социуме) влияет на успеваемость учащихся.

Основной целью современного педагогического тестирования является надежное измерение уровня учебных достижений испытуемых в определенной области знаний. Традиционные методы тестирования (классические) используют порядковые шкалы, отличающиеся друг от друга длиной, масштабом и значением центрального индекса. Балл тестируемого определяется количеством правильно выполненных заданий А из общего числа заданий К. Тогда отношение А/К можно выразить в процентах и получить 100–балльную шкалу, называемую процентной.

Окончательный балл участников тестирования зависит от относительных успехов каждого по сравнению с успехами других. Такие шкалы называют процентильными. Как и процентные, они имеют ранговый смысл. Недостатком этих шкал является невозможность сравнения полученных результатов между распределением результатов разных выборок тестируемых. В этих случаях требуется стандартизация измерений, избавляющая баллы от особенностей различных выборок испытуемых и позволяющая сопоставлять баллы на единой шкале. Для этого используется нормированная шкала. Она создается путем отношения всех эмпирических частот распределения первичных баллов к одному и тому же модельному распределению (центрированному и нормированному) – нормальному. Нормы – это множество показателей, которые устанавливаются эмпирически соответственно тому, как выполняет задания теста некоторая, четко определенная выборка тестируемых. Разработка и процедуры получения этих показателей составляют процесс стандартизации теста. Наиболее распространенными являются среднее арифметическое значение и стандартное отклонение по множеству индивидуальных баллов выборки стандартизации. При этом предполагается, что эмпирическое распределение баллов мало отличается от нормального [9]. Соотнесение первичного результата с нормами теста позволяет установить, соответствует ли полученный результат среднему или нет.

К нормам предъявляют ряд требований:

• норма должна быть дифференцированной, т.е. обучающиеся по разным программам должны сравниваться исходя из разных норм;

• норма должна быть соответственной, отражающей реальный контингент и реальные требования, вытекающие из современной ситуации в образовании, отражать реальную подготовленность контингента и реальные требования;

• норма должна быть репрезентативной, обеспечивающей несмещенные нормативные оценки (для ЕГЭ – оценки федеральной выборки) [195].

Понятие нормы относительное, тесно связанное с качеством выборки, используемой для стандартизации. Поэтому формирование выборки требует особого внимания при стандартизации теста: выборка должна точно отражать категорию испытуемых, для которых предназначен тест; быть достаточно большой и сбалансированной; обеспечивать пренебрежимо малую погрешность измерений. Сохраняя репрезентативность, можно ограничиться выборкой из 200—300 испытуемых. Еще более предпочтительна стратифицированная выборка, отражающая особенности и сочетания разных признаков тестируемых (социальное положение, пол, городские, сельские, с дополнительной подготовкой и без нее и др.). Стратификация обеспечивает представление правильных пропорций страт генеральной совокупности тестируемых. Исходя из этого формирование репрезентативной выборки стандартизации теста предусматривает:

• стратификацию выборки по наиболее важным переменным не менее чем по четырем уровням или подгруппам;

• в каждой подгруппе число испытуемых должно быть одинаковым и не менее 100.

С учетом возможных сочетаний переменных и оснований для стратификации объем выборки стандартизации теста во многих странах достигает 12 000—15 000 испытуемых [76].

Наблюдаемые результаты выполнения теста дают только «сырые» баллы, не обеспечивающие решение вопросов сопоставимости. Для возможности сопоставимости необходимо произвести перевод «сырых» баллов в одну из метрических стандартных шкал при помощи математических методов и моделей, обеспечив получение тестовых баллов. В основе такого преобразования лежит стремление повысить уровень измерений на интервальной шкале, допускающей упорядочение испытуемых на шкале с фиксированной единицей измерения. Отметим, что повышение уровня измерений путем шкалирования направлено на расширение возможностей интерпретации сопоставимых тестовых баллов, и это не связано с повышением точности измерений.

Методика перевода первичных баллов в нормализованные допускает замену оценок, выраженных в логитах, на оценки другой шкалы путем линейных преобразований, не нарушающих рейтинг учащихся на логистической шкале. Теоретической основой шкалирования результатов ЕГЭ и централизованного тестирования является современная теория моделирования и параметризации педагогических тестов на основе математических моделей их создания. Можно пользоваться однопараметрической логистической моделью Г. Раша. При этом первичные баллы обеспечивают достаточную статистику. Это означает, в частности, что все испытуемые, набравшие один и тот же первичный балл, получат практически одинаковые и окончательные тестовые баллы по 100–балльной шкале (очень небольшие отклонения от этого правила возможны только за счет непараллельности различных вариантов теста). Создать идеально параллельные тесты практически невозможно. Поэтому существуют методики выравнивания непараллельности различных вариантов теста с тем, чтобы оценки испытуемых, выполнявших разные варианты теста, не зависели от того, более трудный или более легкий вариант они выполняли [134].

Недостатком модели Г. Раша является то, что обработка результатов тестирования позволяет оценить для каждого тестового задания только одну его характеристику – уровень трудности. Другая характеристика – коэффициент дискриминации – непосредственно не оценивается и заменяется коэффициентом точечной бисериальной корреляции.

Можно использовать двухпараметрическую логистическую модель А. Бирнбаума, которая позволяет для каждого задания теста непосредственно оценивать и уровень трудности, и коэффициент дискриминации. Это удобно с точки зрения составления базы калиброванных заданий. Что же касается оценок уровня подготовленности испытуемых, то участники тестирования, верно выполнившие одинаковое количество заданий теста и набравшие, таким образом, один и тот же первичный балл, получают разные окончательные тестовые баллы. В этом нет никакой ошибки, результаты соответствуют сути дела, но такие «инверсии» оценок невозможно объяснить широкой аудитории пользователей. Расчет тестового балла при этом подходе производится более изощренным способом и теоретически более обоснован.

Важно, что при таком шкалировании учитываются свойства как верно, так и неверно выполненных заданий. При этом для легких заданий:

• за неверный ответ снимается много баллов;

• за верный ответ добавляется мало баллов.

Для трудных заданий:

• за неверный снимается мало баллов;

• за верный добавляется много баллов.

Обе модели имеют серьезное теоретическое обоснование, однако их практическое использование в массовом тестировании имеет разный психологический эффект. Вместе с тем такое шкалирование отвечает сути массового педагогического тестирования как контрольно–оценочного процесса и согласуется с особенностями измерений в любой другой области. Отметим некоторые из них, отражающие специфику шкалирования результатов тестирования:

• сертификационный балл учитывает не только процент верно выполненых заданий теста, но и уровень их трудности, коэффициент дискриминации, характеристики невыполненных заданий;

• уровень трудности заданий теста и коэффициент дискриминации оцениваются после совместной обработки всех результатов тестирования.

В общем случае не существует прямой зависимости между количеством выполненных заданий (первичных баллов) и сертификационными баллами, так как невозможно практически обеспечить полную параллельность различных вариантов одного и того же теста; по первичным баллам возможно только ранжировать учащихся, но измерять уровень их знаний нельзя. С математической точки зрения это значит, что шкала, индексами которой является число заданий (число первичных, или «сырых», баллов), является только порядковой, но не метрической, а поэтому первичные баллы являются лишь индикаторами подготовленности учащихся, а не измерителями.

Окончательный балл получается после обработки результатов тестирования всех учащихся по одному и тому же варианту теста с учетом статистических оценок трудности всех его заданий. Для расчета сертификационного балла используется 100–балльная шкала, обладающая единой метрикой для всех вариантов теста. В частности, для пересчета на 100–балльную шкалу используют формулу

где: t_?  – коэффициент, значение которого выбирается так, чтобы возможность получения высших баллов была регламентирована; ? – среднее квадратичное отклонение подготовленности испытуемых нормативной выборки относительно среднего значения параметра ?_с.в; ?_i  – уровень подготовленности испытуемого [134].

Так, например, при коэффициенте 2,5 вероятность получить 100 баллов составляет около 0,01, а при коэффициенте, равном 3, – не более 0,003. Уровень подготовленности каждого участника тестирования и трудность всех заданий теста оцениваются сначала на логистической шкале в интервале от–5 до +5 логитов.

Начало шкалы логитов «закрепляется» репрезентативной выборкой из 1000 испытуемых, адекватно отражающих структуру генеральной выборки участников тестирования (по регионам, видам образовательных учреждений, городских – сельских и др.). После этого значения оценок в логитах и их средние квадратичные ошибки преобразуются (без деформации метрики) в 100–балльную шкалу для выдачи результатов учащимся и использования в образовательной статистике. Таким образом, сертификационный, или окончательный, тестовый балл является следствием учета не только качества верно выполненных заданий, но и характеристик трудности этих заданий, их дифференцирующей силы (способности к дискриминации уровня подготовленности). При пересчете на тестовые баллы с учетом трудности выполненных заданий следует учитывать, что:

• невыполнение данного задания по–разному сказывается на изменении сертификационного балла в зависимости от выполнения остальных заданий;

• верное выполнение одного и того же задания теста по–разному сказывается на росте сертификационного балла в зависимости от качеств остальных выполненных заданий;

• труднее улучшить высокий результат, чем средний и, тем более, низкий (как в спорте: чем выше планка, тем труднее повышение результата).

Такой балл имеет основные черты количественной меры, а поэтому позволяет проводить объективное сопоставление результатов, производить математико–статистический анализ, изучать динамику различных образовательных процессов в одних и тех же единицах измерения уровня подготовки учащихся и трудности заданий тестов. Кроме сертификационного балла участникам тестирования может быть присвоен рейтинг, указывающий на процент учащихся, получивших более низкий балл, чем у данного испытуемого. Это позволяет выпускникам оценивать свою конкурентоспособность при поступлении в вузы и участии в конкурсе. Сегодня можно с заранее заданной точностью оценить уровень учебных достижений каждого ученика, класса, школы, района, города, региона, страны с одинаковым подходом к требованиям оценивания результатов учебной деятельности.

Все это влечет за собой ряд существенных преобразований при определении результатов обучения, в частности перевода «сырыж» баллов в шкалу перцентильных рангов и др. [76]. Появляются сопоставимость и возможность сравнения результатов, полученных испытуемыми при выполнении тестов.

Понятно, что шкала тем лучше (т.е. тем достовернее), чем она надежнее. Один из способов сделать шкалу более достоверной – просто добавить в нее новые позиции. Однако на практике количество позиций на шкале ограничивается различными факторами (например, респонденты устали и просто не будут отвечать на большое число вопросов, полное пространство ограниченно и т.д.). Для построения надежной шкалы необходима последовательность нескольких действий.

1. Написать вопросы – исключительно творческий процесс, когда исследователь создает как можно больше вопросов, которые, как ему кажется, всесторонне описывают контролируемое содержание. Теоретически следует выбирать вопросы, связанные с заданной концепцией измерений. В области образовательного и психологического тестирования на этой стадии конструирования шкалы обычно обращают внимание на аналогичные анкеты и опросники для того, чтобы получить максимально полное представление о концепции.

2. Провести апробацию заданий на начальной выборке типичных респондентов и проанализировать результаты по каждому пункту для построения надежной шкалы и выявления уровня трудности заданий теста. В образовательных и психологических тестах обычно используют вопросы с ответами типа да/нет (или 1/0) – дихотомическая оценка. Надежная шкала состоит из вопросов (позиций), которые пропорционально разделяют ее на интервалы, их называют калиброванными заданиями, т.е. заданиями с известным уровнем трудности.

3. Из первоначального теста удалить все вопросы, дающие значительные отклонения. После удаления всех вопросов, которые не согласуются со шкалой, можно остаться без достаточного количества вопросов для того, чтобы создать полностью надежную шкалу (напомним, что чем меньше вопросов, тем менее надежна шкала).

4. Вернуться к первому действию. На практике исследователь часто несколько раз проходит через этапы создания и удаления вопросов до тех пор, пока не придет к их окончательному набору, образующему надежную шкалу.

При построении шкалы по тесту возникают определенные проблемы, связанные с ее неустойчивостью, в том случае, если тест используется в различное время учебного года либо выполняется испытуемыми различных возрастных групп. Однако и в этих случаях можно предпринять определенные шаги, способствующие повышению устойчивости тестовых шкал. При этом необходимо предположить, что приращение оцениваемого уровня подготовки по предмету происходит равномерно на протяжении всего времени изучения предмета [201].

В качестве таких шагов при конструировании шкалы зарубежные исследователи предлагают:

• получить репрезентативную выборку для вычисления устойчивых оценок уровня подготовки испытуемых с известными стандартными ошибками измерения;

• предъявить тест выборке подходящего возраста и периода обучения, объединив испытуемых выборки в одинаковые возрастные группы и разбив на трехмесячные подгруппы по периодам обучения;

• определить средний балл для каждой подгруппы, шкалировать результаты;

• интерполировать шкалированные результаты между соседними средними для тех «сырых» баллов, которые не наблюдались в выборке;

• экстраполировать результаты с учетом минимального и максимального наблюдаемых баллов для установления возможных границ шкалы по тесту;

• результаты интерполяции и экстраполяции собрать в таблицу, указывающую шкалированные эквиваленты «сырых» баллов в различных возрастных подгруппах или с учетом определенного периода обучения.

Информатизация процедур тестирования, обработки и проверки результатов привела к созданию статистических отчетов, позволяющих оперативно получать на единой шкале оценок показатели учебных достижений по различным выборкам.