Мы с вами сосредоточимся только на силлогизмах. Они отличаются тем, что и в посылках и в заключении имеют категорические атрибутивные высказывания и на основании наличия или отсутствия каких-то свойств у объектов позволяют сделать вывод о наличии или отсутствии у них других свойств.
Содержание:
- Простой категорический силлогизм
- Правила терминов
- Задачи Эйнштейна
- Энтимемы
- Сориты
- Упражнения
- Проверочные вопросы на усвоение материала
Простой категорический силлогизм
Простой категорический силлогизм – это одно из наиболее простых и часто встречающихся умозаключений. Он состоит из двух посылок. В первой посылке говорится об отношении терминов А и В, во второй – об отношениях терминов В и С. На основании этого делается вывод об отношении терминов А и С. Такой вывод возможен потому, что обе посылки содержат общий термин В, который опосредует отношение между терминами А и С.
Приведём пример:
- Все рыбы не могут жить без воды.
- Все акулы – это рыбы.
- Следовательно, все акулы не могут жить без воды.
В данном случае, термин «рыбы» – это общий термин для двух посылок, и он помогает связать термины «акулы» и «существа, способные жить без воды». Общий термин для двух посылок принято называть средним термином. Субъект заключения (в нашем примере это «акулы») называют меньшим термином. Предикат заключения («существа, способные жить без воды») называют бóльшим термином. Соответственно, посылку, содержащую меньший термин, называют меньшей посылкой («Все акулы – это рыбы»), а посылку, содержащую больший термин, – бóльшей посылкой («Все рыбы не могут жить без воды»).
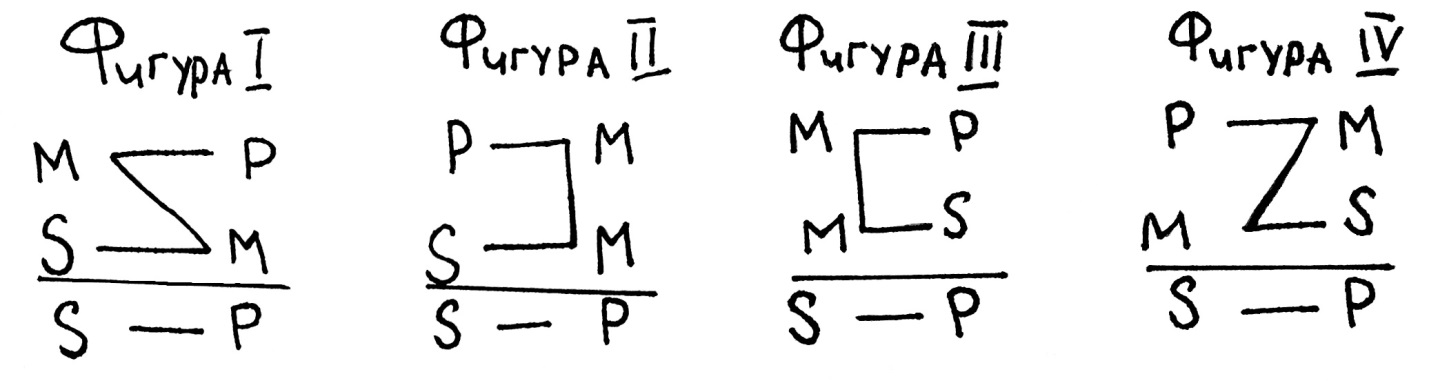
Фигура – это форма простого категорического силлогизма, которая определяется расположением среднего термина.
Сверху расположена большая посылка, за ней следует меньшая посылка, под чертой находится заключение. Буквой S обозначен меньший термин, буквой P – больший термин, буквой М – средний термин.
Далее, фигуры могут наполняться разным содержанием, то есть на место посылок и заключений могут подставляться разные типы категорических атрибутивных высказываний. Например:
- Всякий М есть P
- Всякий S есть М
- Всякий S есть P
или:
- Ни один М не есть P
- Некоторые М есть S
- Некоторые S не есть P
Эти различные сочетания высказываний в фигурах образуют так называемые модусы. Каждая фигура имеет 64 модуса, таким образом, на все четыре фигуры приходятся всего 256 модусов. Если подумать обо всём многообразии умозаключений, имеющих форму силлогизмов, то 256 модусов – это не так уж и много. Кроме того, далеко не все модусы образуют правильные умозаключения, то есть существуют такие модусы, которые при истинности посылок не гарантируют истинности умозаключения. Такие модусы называются неправильными. Правильными же называются те модусы, с помощью которых из истинных посылок мы всегда получаем истинное заключение. Всего существует 24 правильных модуса – по шесть на каждую фигуру. Это означает, что во всей классической силлогистике, которая исчерпывает львиную долю рассуждений, производимых людьми, существует всего 24 вида правильных умозаключений. Это очень маленькое число, поэтому правильные модусы не так уж и сложно запомнить.
Каждый из этих модусов ещё в Средние века получил особое мнемоническое наименование. Каждый тип категорического атрибутивного высказывания был обозначен с помощью всего одной буквы. Высказывания типа «Все S есть P» обозначили буквой «а», первой буквой в латинском слове «affirmo» («утверждаю»), и их запись превратилась в «SaP». Высказывания вида «Некоторые S есть P» записывались с помощью буквы «i», второй гласной в слове «affirmо», поэтому они выглядели как «SiP». Высказывания формы «Ни один S не есть P» обозначили буквой «е», первой гласной в латинском слове «nego» («отрицаю»), их стали записывать в виде «SeP». Как вы, наверное, уже догадались высказывания типа «Некоторые S не есть P» обозначили буквой «о», второй гласной в слове «nego», их формальная запись выглядела как «SoP». Поэтому модусы правильных силлогизмов традиционно обозначаются именно с помощью этих четырёх букв, которые для удобства запоминания представлены в виде слов. Таблица всех правильных модусов выглядит так:
|
Фигура I |
Фигура II |
Фигура III |
Фигура IV |
|
Barbara (aaa) Celarent (eae) Darii (aii) Ferio (eio) Barbari (aai) Celaront (eao) |
Baroko (aoo) Cesare (eae) Camestres (aee) Festino (eio) Camestrop (aeo) Cesaro (eao) |
Bocardo (oao) Disamis (iai) Datisi (aii) Ferison (eio) Darapti (aai) Felapton (eao) |
Camenos (aeo) Dimaris (iai) Camenes (aee) Fresison (eio) Bramantip (aai) Fesapo (eao) |
К примеру, модус второй фигуры Cesare (eae) в развёрнутом виде будет выглядеть так:
- Ни один P не есть М
- Все S есть М
- Ни один S не есть P
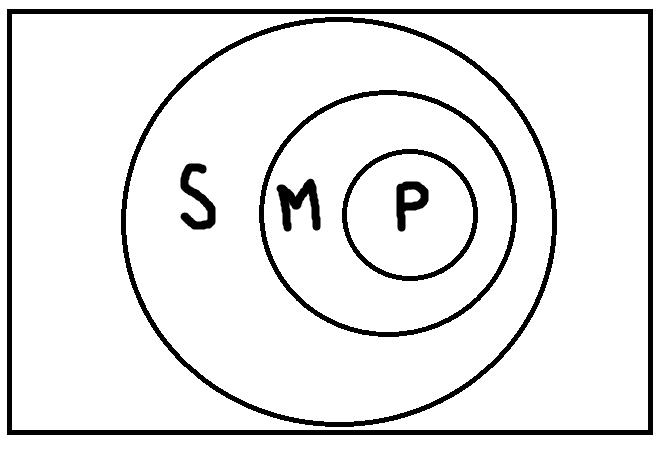
Хотя 24 модуса – это совсем не много и в таблице можно усмотреть некоторые регулярности (например, для всех фигур верны модусы eao и eio), запомнить её всё равно сложно. К счастью, это совсем и необязательно. Для проверки силлогизмов можно также пользоваться модельными схемами. Только в отличие от тех схем, которые мы строили раньше, на них уже должно присутствовать не два, а три термина: S, P, M.
Давайте возьмём модус четвёртой фигуры Bramantip (aai) и проверим его с помощью модельных схем.
- Всякий P есть М
- Всякий М есть S
- Некоторые S есть P
Сначала нужно найти такие модельные схемы, при которых обе посылки будут одновременно истинными. Таких схем всего четыре:
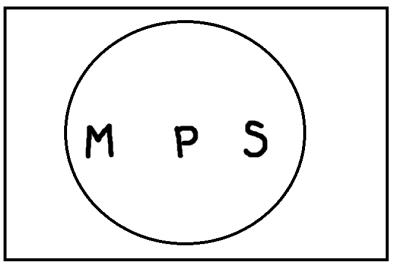
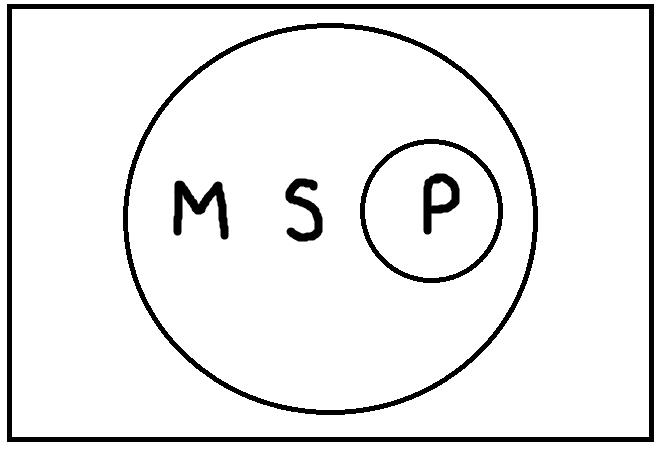
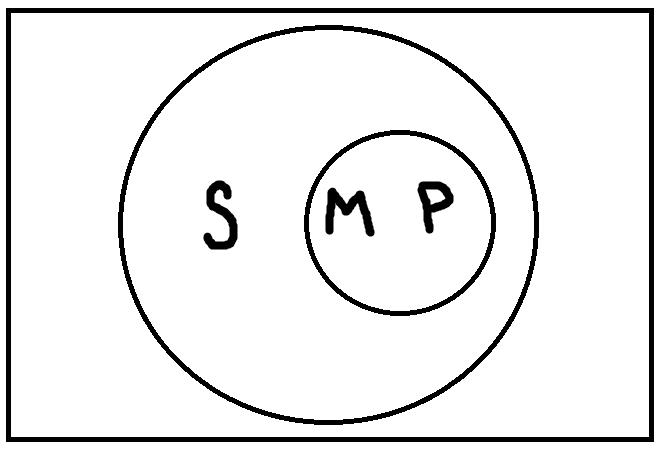
Теперь на каждой из этих схем мы должны проверить, верно ли будет высказывание «Некоторые S есть P», представляющее заключение. В результате проверки, мы обнаруживаем, что на каждой схеме это высказывание будет верным. Таким образом, умозаключение по модусу Bramantip (aai) четвёртой фигуры правильное. Если бы была хотя бы одна схема, на которой это высказывание было бы ложным, то умозаключение было бы неправильным.
Метод проверки силлогизмов с помощью модельных схем хорош, так как он позволяет представить отношения между терминами наглядно. Однако для некоторых посылок могут оказаться верными очень много схем сразу. В результате их построение и проверка будут представлять собой трудоёмкую и отнимающую много времени задачу. Таким образом, метод модельных схем не всегда удобен.
Поэтому логики разработали ещё один метод для определения, правильный силлогизм или нет. Этот метод называется синтаксическим и представляет собой два перечня правил (правила терминов и правила посылок), при соблюдении которых силлогизм будет верным.
Модус простого категорического силлогизма является правильным, если он удовлетворяет следующим условиям:
Правила терминов
- Простой категорический силлогизм должен включать только три термина.
- Средний термин должен быть распределён хотя бы в одной из посылок.
- Если больший или меньший термин не распределён в посылке, то он должен быть нераспределён и в заключении.
Правила посылок:
- Хотя бы одна из посылок должна быть утвердительной.
- Если обе посылки являются утвердительными, то и заключение должно быть утвердительным.
- Если одна из посылок отрицательная, то и заключение должно быть отрицательным.
Правила посылок понятны, а правила терминов требуют некоторых пояснений. Начнём с правила о трёх терминах. Хотя оно кажется очевидным, оно довольно часто нарушается вследствие так называемой подмены терминов. Посмотрите на следующий силлогизм:
- Золото – элемент 11 группы, шестого периода периодической системы химических элементов Д. И. Менделеева, с атомным номером 79.
- Молчание – золото.
- Молчание – элемент 11 группы, шестого периода периодической системы химических элементов Д. И. Менделеева, с атомным номером 79.
Прежде всего, если вы помните фигуры и правильные модусы, вы сразу можете сказать, что этот силлогизм неправильный, так как он относится ко второй фигуре и имеет модус aaa, который не принадлежит к списку правильных модусов для этой фигуры. Но если вы их не помните, всё равно вы можете выявить его ложность, потому что здесь явно присутствует четыре термина, вместо трёх. Термин «золото» употребляется в двух совершенно различных смыслах: как химический элемент и как нечто, обладающее ценностью. Посмотрим на более сложный пример:
- Все книги из собрания Российской государственной библиотеки нельзя прочитать за целую жизнь.
- «Отцы и дети» Ивана Тургенева – книга из собрания Российской государственной библиотеки.
- «Отцы и дети» Ивана Тургенева нельзя прочитать за целую жизнь.
Кажется, что этот силлогизм соответствует модусу Barbara первой фигуры. Однако посылки истинны, а заключение ложно.
Если бы мы заменили слово «все» на слова «каждый в отдельности», то первая посылка попросту стала бы ложной: «Каждую в отдельности книгу из собрания Российской государственной библиотеки нельзя прочитать за целую жизнь». Таким образом, мы получаем четыре термина вместо трёх, а потому это умозаключение ложно.
Теперь перейдём к правилам о распределённости терминов. Для начала объясним, что это за характеристика. Термин называют распределённым, если в высказывании речь идёт обо всех объектах, входящих в его объём. Соответственно, термин не распределён, если в высказывании речь идёт не обо всех объектах, составляющих его объём. Грубо говоря, термин распределён, если мы говорим обо всех предметах, и не распределён, если мы говорим только о некоторых предметах, о части объёма термина.
Давайте возьмём типы высказываний и посмотрим, какие термины в них распределены, а какие нет. Распределённый термин отмечается знаком «+», нераспределённый – знаком «–».
Все S+ есть P–.
Ни один S+ не есть P+.
Некоторые S– есть P–.
Некоторые S– не есть P+.
а+ есть P–.
a+ не есть P+.
Как видно, субъект всегда распределён в общих и единичных высказываниях, но не распределён в частных. Предикат всегда распределён в отрицательных высказываниях, но не распределён в утвердительных. Если теперь перенести это на наши правила для терминов, то получается, что средний термин хотя бы в одной из посылок должен быть взят во всём своём объёме.
- Пингвины – это птицы.
- Некоторые птицы не умеют летать.
- Пингвины не умеют летать.
Хотя и высказывания над чертой и высказывание под чертой истинны, умозаключение как таковое здесь отсутствует. Здесь нет логического перехода от посылок к заключению. И это можно легко выявить, так как средний термин «птицы» ни разу не берётся во всём своём объёме.
Что касается третьего правила терминов, если в посылках речь идёт только о части объектов из объёма терминов, то в заключении мы не можем ничего утверждать обо всех объектах объёма терминов. Мы не можем перейти от части к целому. Кстати, обратный переход возможен: если мы говорим обо всех элементах объёма терминов, то мы можем сделать заключение о части из них.
Задачи Эйнштейна
Эта игра является нашей версией всемирно известной «загадки Эйнштейна», в которой 5 иностранцев живут на 5 улицах, едят 5 видов еды и т.д. Подробнее про эту задачу написано здесь. В подобных заданиях вам нужно сделать правильное умозаключение на основе имеющихся посылок, которых, на первый взгляд, для этого недостаточно.
Энтимемы
Во время реальных дискуссий и споров мы довольно часто опускаем те или иные части рассуждения. Это приводит к возникновению энтимем. Энтимема – это сокращённая форма умозаключения, в которой пропущены посылки или заключение. Важно не путать энтимемы с однопосылочными умозаключениями. Энтимема – это именно многопосылочное умозаключение, просто его части в силу тех или иных причин опущены. Иногда такие пропуски оправданы, так как оба собеседника хорошо разбираются в проблеме, и им нет нужды проговаривать все шаги. Между тем, недобросовестные собеседники могут специально пользоваться энтимемами, чтобы затемнить и запутать своё рассуждение и скрыть свои истинные аргументы или выводы. Поэтому необходимо уметь отличать корректные энтимемы от некорректных. Энтимема называется корректной, если она может быть восстановлена в виде правильного модуса категорического силлогизма, и если все пропущенные посылки оказываются истинными.
Поговорим о том, как восстановить энтимему до полного силлогизма. В первую очередь нужно понять, что именно пропущено. Для этого нужно обратить внимание на слова-маркеры, обозначающие причинно-следственные связи: «таким образом», «следовательно», «так как», «потому что», «в результате» и т.д. К примеру, возьмём рассуждение: «Золото – это драгоценный металл, потому что оно практически не окисляется на воздухе». Здесь заключением является высказывание «Золото – это драгоценный металл». Одна из посылок: «Золото практически не окисляется на воздухе». Ещё одна посылка пропущена. Нужно сказать, что чаще всего пропускают именно одну из посылок. Довольно странно, если в рассуждении отсутствует самое важное – вывод.
Итак, мы установили, что именно пропущено. В нашем примере – это посылка. Большая это посылка или меньшая? Как вы помните, меньшая посылка содержит субъект заключения («золото»), а большая – предикат заключения («драгоценный металл»). Посылка, содержащая субъект заключения нам уже известна: «Золото практически не окисляется на воздухе». Значит, нам известна меньшая посылка, и не известна большая. Кроме того, благодаря известной посылке, мы можем установить и средний термин: «металлы, которые практически не окисляются на воздухе», – тот термин, который не содержится в заключении.
Теперь располагаем известную нам информацию в форме силлогизма:
- 1.
- 2. Золото практически не окисляется на воздухе.
- 3. Золото – это драгоценный металл.
Или в виде схемы:
- 1.
- 2. SaМ
- 3. SaP
В большей посылке должны находиться предикат заключения и средний термин: «драгоценные металлы» (P) и «металлы, которые окисляются на воздухе» (M). Здесь возможны два варианта:
- 1. P M
- 2. SaМ
- 3. SaP
Или:
- 1. М P
- 2. SaМ
- 3. SaP
Значит, возможен силлогизм либо второй фигуры, либо первой фигуры. Теперь смотрим на нашу табличку с правильными модусами силлогизмов. Во второй фигуре вообще нет правильных модусов, где в заключении стояло бы высказывание типа а. В первой фигуре есть только один такой модус – Barbara. Достраиваем наш силлогизм:
- 1. МаP
- 2. SaМ
- 3. SaP
Или:
- 1. Все металлы, которые практически не окисляются на воздухе, являются драгоценными.
- 2. Золото практически не окисляется на воздухе.
- 3. Золото – драгоценный металл.
Теперь проверяем, истинна ли наша восстановленная посылка. В нашем случае она истинна, поэтому энтимема была правильной.
Сориты
Термином «сориты» пользовался Льюис Кэррол для обозначения сложных силлогизмов, которые имеют более чем две посылки. По большому счёту, сорит представляет собой гибрид силлогизма и энтимемы. Он устроен следующим образом: дано множество посылок, из каждой пары посылок делаются промежуточные выводы, которые обычно опускаются, к промежуточным выводам присоединяются новые посылки, из них делаются новые промежуточные выводы, к которым опять присоединяются новые посылки и так далее, пока мы не переберём все имеющиеся посылки и не дойдём до окончательного заключения. В принципе подобным образом люди и рассуждают в повседневной жизни. Поэтому очень важно уметь решать сориты и оценивать, правильны они или нет.
Мы приведём пример сорита из книги Льюиса Кэррола «История с узелками»:
1. Все полисмены из нашей округи ужинают у нашей кухарки.
2. Человек с длинными волосами не может не быть поэтом.
3. Амос Джадд никогда не сидел в тюрьме.
4. Все кузены нашей кухарки любят холодную баранину.
5. В этой округе нет других поэтов, кроме полисменов.
6. С нашей кухаркой не ужинает никто, кроме её кузенов.
7. Все люди с короткими волосами сидели в тюрьме.
8. Амос Джадд любит холодную баранину.
Над чертой находятся посылки, под чертой – заключение.
Как же нужно решать и проверять сориты? Дадим пошаговую инструкцию. Во-первых, необходимо привести все посылки в более или менее стандартную форму:
1. Все полисмены из нашей округи ужинают у нашей кухарки.
2. Все люди с длинными волосами являются поэтами.
3. Амос Джадд не сидел в тюрьме.
4. Все кузены нашей кухарки любят холодную баранину.
5. Все поэты из нашего округа являются полисменами.
6. Все люди, ужинающие с нашей кухаркой, приходятся ей кузенами.
7. Все люди с короткими волосами сидели в тюрьме.
Теперь нужно взять две исходные посылки. По большому счёту, неважно, с каких именно посылок вы начнёте. Главное, чтобы ваши исходные посылки вместе содержали всего три термина. Это означает, что мы не можем взять посылки «Амос Джадд не сидел в тюрьме» и «Все кузены нашей кухарки любят холодную баранину». В них входят четыре разных термина, а потому мы не можем сделать из них никакого заключения. Я в качестве исходных возьму посылки 7 и 3 и сделаю из них вывод по правилам для простых категорических силлогизмов.
- 1. Все люди с короткими волосами сидели в тюрьме.
- 2. Амос Джадд не сидел в тюрьме.
- 3. Амос Джадд не является человеком с короткими волосами.
Этот силлогизм соответствует модусу Camestres (aee) второй фигуры. Теперь для удобства я переформулирую наш промежуточный вывод следующим образом: «Амос Джадд является человеком с длинными волосами». Этот промежуточный вывод я соединяю с посылкой номер 2:
- 1. Все люди с длинными волосами являются поэтами.
- 2. Амос Джадд является человеком с длинными волосами.
- 3. Амос Джадд является поэтом.
Этот силлогизм соответствует модусу Barbara (aaa) первой фигуры. Теперь я присоединяю этот промежуточный вывод к посылке номер 5:
- 1. Все поэты из нашего округа являются полисменами.
- 2. Амос Джадд является поэтом.
- 3. Амос Джадд является полисменом.
Этот силлогизм опять же соответствует модусу Barbara (aaa) первой фигуры. Присоединяем промежуточный вывод к посылке номер 1:
- 1. Все полисмены из нашей округи ужинают у нашей кухарки.
- 2. Амос Джадд является полисменом.
- 3. Амос Джадд ужинает у нашей кухарки.
Это силлогизм, как вы уже, наверное, заметили, тоже представляет собой модус Barbara (aaa) первой фигуры. Присоединяем этот вывод к посылке номер 6:
- 1. Все люди, ужинающие с нашей кухаркой, приходятся ей кузенами.
- 2. Амос Джадд ужинает у нашей кухарки.
- 3. Амос Джадд приходится кузеном нашей кухарке.
Опять Barbara, которая является одним из самых распространённых модусов. Присоединяем к нашему последнему промежуточному выводу последнюю посылку номер 4:
- 1. Все кузены нашей кухарки любят холодную баранину.
- 2. Амос Джадд приходится кузеном нашей кухарке.
- 3. Амос Джадд любит холодную баранину.
Итак, с помощью всё того же модуса Barbara мы получили наше заключение: «Амос Джадд любит холодную баранину». Таким образом, сориты решаются и проверяются с помощью пошагового разделения на простые категорические силлогизмы. В нашем примере сорит оказался правильным, но возможны и обратные ситуации. Существует два условия корректности соритов. Во-первых, каждый сорит должен разбиваться на последовательность правильных модусов силлогизмов. Во-вторых, заключение, которое вы получаете, когда все посылки исчерпаны, должно совпасть с заключением сорита. Это условие действует в тех случаях, когда вы имеете дело с чужим рассуждением, в котором уже присутствует какое-то заключение.
Итак, мы рассмотрели различные многопосылочные умозаключения на примере простых категорических силлогизмов, энтимем и соритов. По большому счёту, если вы знаете, как иметь с ними дело, то вы вооружены для любых дискуссий с любыми противниками. Единственное, что может на данный момент вызывать некоторое недовольство, это необходимость тратить много времени на проверку правильности умозаключений. Не стоит расстраиваться по этому поводу: лучше выглядеть тугодумом, который рассуждает правильно, чем блестящим демагогом, который не замечает своих и чужих ошибок. Тем более, с накоплением опыта внимательного отношения к умозаключениям у вас появится чутьё, автоматический навык, позволяющий быстро отделять корректные рассуждения от некорректных. Поэтому упражнений к этому уроку будет много, чтобы у вас была возможность набить руку.
Упражнения
Упражнения 1, 2 и 3 взяты из книги Льюиса Кэррола «История с узелками», М.: Мир, 1973.
Упражнение 1
Сделайте заключения из следующих посылок по правилам для простого категорического силлогизма. Помните, что простой категорический силлогизм должен содержать только три термина. Не забывайте приводить высказывания к стандартному виду.
1
- Зонтик – очень нужная вещь в путешествии.
- Отправляясь в путешествие, всё лишнее следует оставлять дома.
- ?
2
- Музыка, которую можно услышать, вызывает колебания воздуха.
- Музыка, которую нельзя услышать, не стоит того, чтобы за неё платили деньги.
- ?
3
- Ни один француз не любит пудинга.
- Все англичане любят пудинг.
- ?
4
- Ни один старый скряга не жизнерадостен.
- Некоторые старые скряги тощи.
- ?
5
- Все непрожорливые кролики чёрные.
- Ни один старый кролик не склонен к воздержанию в пище.
- ?
6
- Ничто разумное никогда не ставило меня в тупик.
- Логика ставит меня в тупик.
- ?
7
- Ни в одной из исследованных до сих пор стран не обитают драконы.
- Неисследованные страны пленяют воображение.
- ?
8
- Некоторые сны ужасны.
- Ни один барашек не внушает ужаса.
- ?
9
- Ни одному лысому созданию не нужна расчёска.
- Ни у одной ящерицы нет волос.
- ?
10
- Все яйца можно разбить.
- Некоторые яйца сварены вкрутую.
- ?
Упражнение 2
Проверьте, правильны ли следующие рассуждения. Попробуйте разные способы проверки. Не забывайте ставить большую посылку на первую строку.
1
- Словари полезны.
- Полезные книги высоко ценятся.
- Словари высоко ценятся.
2
- Золото тяжёлое.
- Ничто, кроме золота, не сможет заставить его замолчать.
- Ничто лёгкое не сможет заставить его замолчать.
3
- Некоторые галстуки безвкусны.
- Всё, сделанное со вкусом, приводит меня в восторг.
- Я не в восторге от некоторых галстуков.
4
- Ни одно ископаемое животное не может быть несчастно в любви.
- Устрица может быть несчастна в любви.
- Устрицы – не ископаемые животные.
5
- Ни одна горячая сдоба не полезна.
- Все булочки с изюмом неполезны.
- Булочки с изюмом – не сдоба.
6
- Некоторые подушки мягкие.
- Ни одна кочерга не мягкая.
- Некоторые кочерги – не подушки.
7
- Скучные люди невыносимы.
- Ни одного скучного человека не упрашивают остаться, когда он собирается уходить из гостей.
- Ни одного невыносимого человека не упрашивают остаться, когда он собирается уходить из гостей.
8
- Ни одна лягушка не имеет поэтической внешности.
- Некоторые утки выглядят прозаично.
- Некоторые утки – не лягушки.
9
- Все разумные люди ходят ногами.
- Все неразумные люди ходят на голове.
- Ни один человек не ходит на голове и ногах.
Упражнение 3
Найдите заключения следующих соритов.
1
- Малые дети неразумны.
- Тот, кто может укрощать крокодилов, заслуживает уважения.
- Неразумные люди не заслуживают уважения.
2
- Ни одна утка не танцует вальс.
- Ни один офицер не откажется потанцевать вальс.
- У меня нет другой птицы, кроме уток.
3
- Всякий, кто находится в здравом уме, может заниматься логикой.
- Ни один лунатик не может быть присяжным заседателем.
- Ни один из ваших сыновей не может заниматься логикой.
4
- В этой коробке нет моих карандашей.
- Ни один из моих леденцов – не сигара.
- Вся моя собственность, не находящаяся в этой коробке, состоит из сигар.
5
- Ни один терьер не блуждает среди знаков Зодиака.
- То, что не блуждает среди знаков Зодиака, не может быть кометой.
- Только у терьера хвост колечком.
6
- Никто не станет выписывать газету «Таймс», если он не получил хорошего образования.
- Ни один дикобраз не умеет читать.
- Те, кто не умеет читать, не получили хорошего образования.
7
- Никто их тех, кто действительно ценит Бетховена, не станет шуметь во время исполнения «Лунной сонаты».
- Морские свинки безнадёжно невежественны в музыке.
- Те, кто безнадёжно невежественен в музыке, не станут соблюдать тишину во время исполнения «Лунной сонаты».
8
- Вещи, продаваемые на улице, не имеют особой ценности.
- Только дрянь можно купить за грош.
- Яйца большой гагарки представляют большую ценность.
- Лишь то, что продаётся на улице, и есть настоящая дрянь.
9
- Те, кто нарушает свои обещания, не заслуживают доверия.
- Любители выпить очень общительны.
- Человек, выполняющий свои обещания, честен.
- Ни один трезвенник не ростовщик.
- Тому, кто очень общителен, всегда можно верить.
10
- Любая мысль, которую нельзя выразить в виде силлогизма, поистине смешна.
- Моя мечта о сдобных булочках не стоит того, чтобы её записывать на бумаге.
- Ни одну мою несбыточную мечту нельзя выразить в виде силлогизма.
- Мне не приходило в голову ни одной действительно смешной мысли, о которой я бы не сообщим своему другу.
- Я только и мечтаю, что о сдобных булочках.
- Я никогда не высказывал своему другу ни одной мысли, если она не стоила того, чтобы её записать на бумаге.
Упражнение 4
Проверьте правильность следующих энтимем.
- Барсик – не законопослушный кот, потому что он украл у меня сосиску.
- Ртуть жидкая, следовательно, она не может быть металлом.
- Ни один послушный ребёнок не устраивает истерик по пустякам. Поэтому Толя – непослушный ребёнок.
- Некоторые женщины глупы, значит, некоторые мужчины могут этим воспользоваться.
- Все девушки хотят выйти замуж, так как каждая из них мечтает о пышном белом платье.
- Ни один студент не хочет получить двойку на экзамене, вот почему все студенты – ботаники.
- Некто украл у меня кошелёк, поэтому у меня совсем не осталось денег.
- Павлины – самовлюблённые птицы, потому что у них большой красивый хвост.
Проверьте свои знания
Если вы хотите проверить свои знания по теме данного урока, можете пройти небольшой тест, состоящий из нескольких вопросов. В каждом вопросе правильным может быть только 1 вариант. После выбора вами одного из вариантов, система автоматически переходит к следующему вопросу. На получаемые вами баллы влияет правильность ваших ответов и затраченное на прохождение время. Обратите внимание, что вопросы каждый раз разные, а варианты перемешиваются.
← 6 Умозаключения8 Типы рассуждений →
1. Простой категорический силлогизм
Наиболее распространенной и важной формой опосредованного умозаключения из простых атрибутивных суждений выступает простой категорический силлогизм (от греч. syllogismos — умозаключение, выведение). Приводившийся выше пример с Сократом и есть классический пример такого силлогизма.
Структура простого категорического силлогизма. Он называется простым именно потому, что состоит всего из двух посылок, особым образом связанных между собой, и заключения.
В свою очередь, посылки и заключение, будучи суждениями, состоят из терминов, тоже определенным образом соотносящихся друг с другом. Принципиально важно отметить, что их всего три: меньший, больший и средний.
Меньшим термином называется субъект заключения. Поэтому он обозначается буквой «S».
Б?льшим термином именуется предикат заключения (буква «Р»).
Средний термин не входит в заключение, но входит в обе посылки, обеспечивая логическую связь между ними, выступая их посредствующим звеном и тем самым делая возможным само заключение. Обозначается буквой «М» (от лат. medius — средний).
Посылка, в которую входит больший термин, называется большей.
Посылка, включающая в себя меньший термин, — меньшая.
Вся эта структура может быть наглядно представлена на примере:
Все люди (М) смертны (Р). (Б?льшая посылка)
Сократ (S) — человек (М). (Меньшая посылка)
Следовательно, Сократ (S) смертен (Р). (Заключение)
Заметим, что все значение подобного силлогизма, который кажется ученически тривиальным и который люди до поры до времени не склонны относить к себе, обнаруживается (как это с огромной художественной силой показал Л.Толстой в повести «Смерть Ивана Ильича») лишь на смертном одре.
Аксиома силлогизма. Отражением многовековой практики мышления людей, миллиардного повторения одной и той же мыслительной конструкции служит аксиома силлогизма. В зависимости от того, рассматриваются ли посылки в объемном или содержательном плане, различаются две ее формулировки.
1. Dictum de omni et de nullo (буквально: сказанное обо всем и ни об одном): все, что утверждается или отрицается о классе предметов в целом, утверждается или отрицается и о части или отдельном элементе этого класса.
2. Nota notae est nota rei (признак признака есть признак самой вещи).
В современной логической литературе обе формулировки подвергаются критике; последняя считается даже элементарно ошибочной; но сама аксиома в целом сохраняет известный рациональный смысл. Более того, она составляет исходную логическую основу, на которой выстраивается грандиозное и стройное здание всей силлогистики.
Общие правила простого категорического силлогизма. Построение простого категорического силлогизма подчиняется ряду общих правил, без соблюдения которых даже из истинных посылок нельзя с логической необходимостью получить истинное заключение. Всего таких правил семь: три из них — это правила терминов, а четыре — правила посылок.
Каковы прежде всего правила терминов?
1. В силлогизме должно быть только три термина (S, Р и М). Нарушение этого правила ведет к логической ошибке, которая называется «quaternio terminorum» («учетверение терминов»). Так, из того, что «Собака бегает по двору», а «Кошка сидит на заборе», никакого вывода не получится. Здесь налицо четыре разных термина — два субъекта и два предиката. Среднего термина, который связывал бы оба суждения, нет.
Логическая ошибка «учетверение терминов» часто носит завуалированный характер. Это может быть связано с употреблением омонимов (т.е. одного и того же слова в разных значениях). Например, слово «закон» означает и объективную связь между предметами, и юридическое установление. Поэтому если мы построим силлогизм, где это слово выражает средний термин, то вытекающего отсюда с логической необходимостью вывода не получится.
Например:
Все законы объективны, т.е. не зависят от людей.
Конституция России — закон.
Следовательно, Конституция России не зависит от людей.
Нелепость получается именно из-за «учетверения терминов».
2. Средний термин должен быть распределен хотя бы в одной из посылок. Если это правило нарушается, то связь между большим и меньшим терминами будет неопределенной. Значит, и вывод из посылок не может следовать с логической необходимостью.
Все художники (Р) тонко чувствуют природу (М).
Петров (S) тонко чувствует природу (М).
Следовательно, Петров (S) — художник (P).
Вывод неопределенный, так как Петров может и не быть художником. Причина неопределенности в том, что средний термин (М), занимающий место предиката и в большей, и в меньшей посылках, не распределен, так как обе они утвердительные, а в утвердительных суждениях предикат, как правило, не распределен. Покажем соотношение терминов на круговой схеме:

3. Если больший или меньший термины не распределены в посылках, то они не могут быть распределены и в заключении.
Например:
Все учебники (М) полезны (Р).
Все учебники (М) — книги (S).
Следовательно, некоторые книги (S) полезны (Р).
А почему в этом случае нельзя сказать, что «Все книги полезны»? Суть в том, что субъект заключения («книги»), занимающий место предиката в меньшей посылке, не распределен, так как эта посылка утвердительная, а в утвердительных суждениях предикат, как правило, не распределен. Поэтому он не может быть взят во всем объеме и в заключении. См. круговую схему:

Нетрудно догадаться, что по этой же причине не распределен и предикат заключения.
Таковы правила терминов. А теперь о правилах посылок.
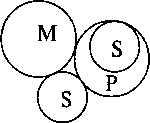
1. Из двух отрицательных посылок определенного вывода сделать нельзя. Хотя бы одна из них должна быть утвердительным суждением. Например:
Стекло (М) не проводит электричества (Р).
Резина (S) — не стекло (М).
Следовательно, резина (S) проводит электричество (P).
Вывод ложный. Если же вместо «резины» подставить, например, «железо», то он окажется истинным. В чем причина неопределенности вывода? В том, что при отрицательных посылках средний термин не может связать субъект и предикат. См. схему:
2. Если одна из посылок отрицательная, то и вывод будет отрицательным. Например:
Всякое преступление (Р) есть правонарушение (М).
Моральный проступок (S) не есть правонарушение (М).
Следовательно, моральный проступок (S) не есть преступление (Р).
См. схему:
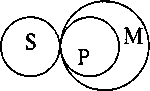
3. Из двух частных посылок определенного вывода сделать нельзя. Хотя бы одна из посылок должна быть общим суждением.
Например:
Некоторые депутаты Госдумы (М) — юристы (Р).
Некоторые артисты (S) — депутаты Госдумы (М).
Следовательно, некоторые артисты (S) — юристы (Р)
А может быть, «ни один»? А почему не «все»?
См. схему:
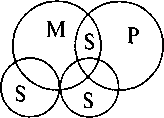
4. Если одна из посылок частная, то и вывод будет частным. Например:
Некоторые пенсионеры (Р) — работающие (М).
Все работающие (М) получают заработную плату (S).
Следовательно, некоторые получающие заработную плату (S) — пенсионеры (Р).
См. схему:

Фигуры и модусы простого категорического силлогизма. Простой категорический силлогизм имеет свои разновидности, которые называются фигурами силлогизма. Они различаются положением среднего термина (М) в посылках. Таких фигур четыре.
Первая фигура характеризуется тем, что средний термин занимает место субъекта в большей посылке и место предиката — в меньшей. Приведем соответственно ее графическое изображение и пример.

Всякое преступление (М) есть правонарушение (Р).
Кража (S) есть преступление (М).
Следовательно, кража (S) есть правонарушение (Р).
Во второй фигуре средний термин занимает место предиката в большей и меньшей посылках.
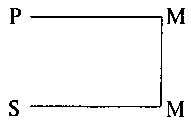
Все юристы (Р) знают логику (М).
Павлов (S) не знает логики (М).
Следовательно, Павлов (S) — не юрист (Р).
Третья фигура отличается тем, что средний термин занимает здесь место субъекта в большей и меньшей посылках.

Все учебники (М) полезны (Р).
Все учебники (М) — книги (S).
Следовательно, некоторые книги (S) полезны (Р).
Четвертой фигуре свойственно то, что средний термин занимает здесь место предиката в большей посылке и место субъекта — в меньшей.
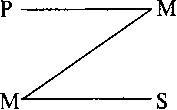
Некоторые пенсионеры (Р) — работающие (М).
Все работающие (М) получают зарплату (S).
Следовательно, некоторые получающие зарплату (S) — пенсионеры (Р).
Каждая фигура тоже имеет свои разновидности, которые называются модусами (от лат. modus — способ, образ). Они различаются количеством и качеством суждений, составляющих посылки. Каждая из посылок может быть общеутвердительной (А), общеотрицательной (Е), частноутвердительной (I) и частноотрицательной (О). Поэтому в одной фигуре возможно 16 модусов (4×4). Так, если большая посылка — общеутвердительная (А), то могут быть следующие модусы: АА, АЕ, AI, АО. Если большая посылка — общеотрицательная (Е), то возможны модусы ЕА, ЕЕ, EI, ЕО. Если большая посылка — частноутвердительная (I), то модусы будут IA, IE, II, IO. Наконец, если большая посылка — частноотрицательная (О), то могут быть модусы ОА, ОЕ, OI, OO.
Таким образом, в четырех фигурах соответственно будет 64 модуса (16?4). Но правильные из них — только 19 модусов.
Запишем их вместе с заключениями:
по первой фигуре — AAA, ЕАЕ, АII, ЕIO;
по второй фигуре — ЕАЕ, АЕЕ, ЕIO, АОО;
по третьей фигуре — AAI, IAI, АII, ЕАО, ОАО, ЕIO
и, наконец, по четвертой — AAI, АЕЕ, IAI, ЕАО, ЕIO.
Почему только эти 19 модусов являются правильными? Потому что именно они подчиняются общим правилам простого категорического силлогизма. Остальные же так или иначе не подчиняются. Например, модус ЕЕ — неправильный, так как обе посылки отрицательные, а из них определенного вывода сделать нельзя. Или модус II: в нем обе посылки частные.
Специальные правила фигур силлогизма. Каждая из фигур имеет особые, специальные правила, вытекающие из общих.
Правила первой фигуры. Большая посылка должна быть общим суждением, меньшая посылка — утвердительным. Начнем с меньшей. Если меньшая посылка — отрицательная, то и вывод, согласно одному из общих правил силлогизма, будет отрицательным. Но в отрицательных суждениях предикат всегда распределен. Следовательно, согласно одному из правил терминов, он должен быть распределен и в большей посылке. А он может быть распределен в ней лишь в том случае, если эта посылка отрицательная. Но это противоречит одному из общих правил о том, что из двух отрицательных посылок определенного вывода сделать нельзя. Значит, меньшая посылка не может быть отрицательной. Значит, она должна быть утвердительным суждением.
А почему большая посылка должна быть непременно общей? Если, как установлено, меньшая посылка — утвердительная, то средний термин, занимающий в ней место предиката, не распределен. Следовательно, согласно одному из общих правил терминов, он должен быть распределен в большей. А так как он занимает в ней место субъекта, то, значит, она должна быть общим суждением.
Вспомним, что в первой фигуре возможны следующие модусы:
АА
ЕА
IA
ОА
АЕ
ЕЕ
IE
ОЕ
AI
EI
II
OI
АО
ЕО
IO
OO
Вычеркнем вначале все те, которые не соответствуют первому правилу первой фигуры, а затем те, которые не соответствуют второму правилу. Какие же останутся? АА, ЕА, AI, EI. А какие будут заключения? В соответствии с общими правилами силлогизма — ААА, ЕАЕ, АII, ЕIO.
Какое значение имеют умозаключения по первой фигуре простого категорического силлогизма? Без преувеличения — огромное. Это наиболее распространенная и богатая форма силлогизма. На ее основе происходит типичное для дедукции применение какого-либо общего положения к частному (или единичному) случаю. Вспомним классическое: «Все люди смертны. Сократ — человек». Первая фигура дает самые различные заключения: А, Е, I, О.
Ее часто используют в юридической практике, когда на основании общей нормы, — статьи какого-либо кодекса — делается вывод о конкретном факте. Например: «Хищение в особо крупных размерах наказывается по статье такой-то. Данное хищение — в особо крупном размере. Следовательно, оно наказывается по статье такой-то».
Правила второй фигуры. Большая посылка должна быть общим суждением, одна из посылок — отрицательным. Естественно, что по второй фигуре заключение всегда носит отрицательный характер. Значение умозаключений по второй фигуре тоже велико. Она используется в тех случаях, когда частный случай не подходит под общее правило. Например, в юридической практике — когда требуется доказать чью-либо невиновность.
Правила третьей фигуры. Меньшая посылка должна быть утвердительным суждением, заключение — частным. Третья фигура — сравнительно редкая в практике мышления.
Правила четвертой фигуры. Если большая посылка — утвердительное суждение, то меньшая посылка должна быть общим. Если одна из посылок отрицательное суждение, то большая должна быть общим. Заключение по четвертой фигуре носит в значительной мере искусственный характер. Вспомним пример с работающими пенсионерами:
Некоторые пенсионеры (Р) — работающие (М).
Все работающие (М) получают зарплату (S).
Следовательно, некоторые получающие зарплату (S) — пенсионеры (Р).
Естественнее было бы, конечно, сказать: «Некоторые пенсионеры получают зарплату».
Рассмотренные выше качественные различия между фигурами силлогизма на самом деле относительны. При определенных условиях силлогизм одной фигуры может превращаться в силлогизм другой.
Особое значение имеет здесь логическая операция, которая называется сведением всех фигур силлогизма к первой фигуре, поскольку она является наиболее употребительной и важной. Покажем это на примере силлогизма третьей фигуры, уже приводившемся нами:
Все учебники (М) полезны (Р).
Все учебники (М) — книги (S).
Следовательно, некоторые книги (S) полезны (Р).
Подвергнем меньшую посылку операции обращения: «Все учебники — книги» — «Некоторые книги — учебники». В итоге получим то же самое заключение, но уже по первой фигуре:
Все учебники (М) полезны (Р).
Некоторые книги (S) — учебники (М).
Следовательно, некоторые книги (S) полезны (Р).
Сокращенная форма простого категорического силлогизма. Энтимема. Простой категорический силлогизм может быть полным и сокращенным.
В практике мышления далеко не всегда он может облекаться в полную, т. е. развернутую, языковую форму — с большей и меньшей посылками, заключением.
Нередко он принимает сокращенную форму, т. е. в нем опускается либо одна из посылок, либо заключение. Такой сокращенный категорический силлогизм называется энтимемой (от греч. «в уме»).
Существует три разновидности энтимемы:
1) силлогизм с пропущенной большей посылкой. Например: «Петров — адвокат. Следовательно, он юрист». Здесь подразумевается очевидная большая посылка: «Все адвокаты — юристы», поэтому она опускается;
2) энтимема с пропущенной меньшей посылкой. Например: «Все адвокаты — юристы. Следовательно, Петров юрист». Предполагается, что «Петров — адвокат»;
3) энтимема с пропущенным заключением. Например: «Все адвокаты — юристы. Петров — адвокат». Предполагается, что «следовательно, он юрист».
Значение энтимем состоит в том, что с их помощью достигается краткость, лаконичность речи. Кроме того, они побуждают слушателя или читателя мыслить, думать. Вот почему энтимемы довольно широко используются в устной и письменной речи. Так, древний афоризм: «Юпитер, ты сердишься, значит, ты неправ» — это энтимема. Здесь подразумевается, а поэтому опущена, большая посылка: «Всякий, кто сердится, неправ». Восстановим весь силлогизм полностью:
Всякий, кто сердится, неправ.
Юпитер сердится.
Следовательно, Юпитер неправ.
Подобную энтимему представляет замечательно краткое и сильное высказывание А. Пушкина о Е. Баратынском: «Оригинален, ибо мыслит». Здесь тоже опущена большая посылка. Восстановим полный силлогизм:
Тот, кто мыслит, оригинален.
Баратынский мыслит.
Следовательно, Баратынский оригинален.
Еще пример. «Все это говорят, а что говорят все, должно быть правдой». Пропущено заключение: «Следовательно, это правда».
Или как сказано у поэта: «Я где боль: а боль — везде». Восстановим полностью силлогизм:
Боль везде.
Я — где боль.
Следовательно, я везде.
Для чего необходимо восстанавливать полный силлогизм из энтимемы? Чтобы проверить ее правильность. Как это делается? Покажем всю процедуру на примере: «Он, должно быть, очень невежественный человек, поскольку отвечает на все вопросы, которые ему задают». Сначала находим заключение. Оно, как мы помним, стоит после слова «следовательно» и ему подобных либо перед словами «потому что» и их аналогами. В нашем примере заключением будет: «Он, должно быть, очень невежественный человек», так как стоит перед словом «поскольку». Определяем структуру этого суждения, т.е. находим в нем субъект и предикат. Субъект — «он», предикат — «невежественный человек». По субъекту или предикату заключения устанавливаем характер имеющейся налицо посылки: «Он отвечает на все вопросы…» В ней находится субъект заключения, следовательно, это меньшая посылка. По предикату заключения и среднему термину, который входит в меньшую посылку, восстанавливаем опущенную большую посылку: «Тот, кто отвечает на все вопросы, должно быть, очень невежественный человек». Получаем полный силлогизм:
Тот, кто отвечает на все вопросы, невежественный человек.
Он отвечает на все вопросы, которые ему задают.
Следовательно, он невежественный человек.
Проверим правильность этого силлогизма. Он построен по первой фигуре, оба правила этой фигуры (см. выше) соблюдены. Значит, этот силлогизм правильный. Его можно проверить также с помощью круговой схемы:
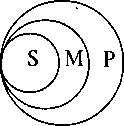
Утрировано о силлогизме можно сказать что это логический вывод, в котором частное заключение выводится из нескольких общих заключений, это своего рода выжимка или конкретизация более абстрактного понятия. Причем, умозаключение может быть не истинным, если были взяты неверные / ошибочные предпосылки под следствие. Если же правила соблюдаются, то в итоге фиксируется истинное знание.
Правила на примере: есть утверждение 1) все коты приземляются на лапы и 2) Барсик -кот → вывод: Барсик приземлится на лапы. Барсик в данном случае субъект заключения или меньший термин обозначается буквой S , упадет на лапы — предикат заключения или больший термин обозначается в схеме буквой Р. Средним является термин кот — обозначается буквой М. Этот силлогизм построен по правилу: Все М есть Р. Все S есть М. Все S есть Р.
Чтобы понять как правильно построить силлогизм пользуются схемой, которых различают 4 фигуры силлогизма
Пример силлогизма для первой фигуры:
Все люди (М) смертны (Р). я (S) — человек (М).
я смертен
**
По схеме 2фигуры построен силлогизм:
Все рыбы (Р) дышат жабрами (М). люди (S) не дышат жабрами (М).
Все люди не рыбы.
**
Пример силлогизма по 3 фигуры:
Все елки (М) имеют шишки (Р). Все елки (М) — многолетние растения (S).
Некоторые многолетние растения имеют шишки.
**
Пример силлогизма по 4фигуре:
Все люди (Р) имеют разум (М). Все имеющие разум (М) живут на Земле (S).
Некоторые имеющие разум на Земле — люди.
дляБВ
Умозаключения,
в которых с необходимостью выводится
заключение от знания большей степени
общности к знанию меньшей степени
общности, как уже говорилось, называются
дедуктивными
(от
лат. deductio
—
«выведение»).
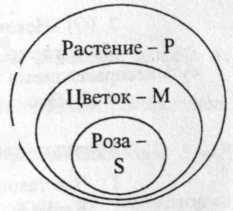
Пример:
Все
цветы — растения. Роза
— цветок.
Роза
— растение.
Типичной
формой дедуктивного умозаключения
является простой
категорический силлогизм (от
гр. sillogismos
—
«получение вывода»).
Простой
категорический силлогизм состоит из
двух посылок и заключения.
Анализ
силлогизма всегда начинают с заключения.
Субъект суждения, которым является
заключение — это меньший
термин
заключения (S),
предикат
— больший
термин
(Р).
Посылка,
в которой содержится больший термин,
называется большей
посылкой,
посылка с меньшим термином — меньшей
посылкой.
Понятие,
которое содержится в каждой из посылок,
но отсутствует в заключении, называется
средний
термин
(М)
В
вышеприведенном примере: роза (S).
растение
(Р),
а
цветы — (М).
Итак,
простой
категорический
силлогизм
—
это умозаключение об отношении большего
и меньшего терминов на основании их
связи со средним термином.
И
зобразим это графически:
Схема
графически представляет нам аксиому
силлогизма, которая лежит в основе
вывода по категорическому силлогизму:
«Все, что присуще роду, присуще и его
виду».
Общие
правила категорического силлогизма
Чтобы
с помощью силлогизма получить истинное
заключение, мы должны иметь истинные
посылки и соблюдать правила терминов,
посылок и фигур.
I.
Правила терминов.
1. В
каждом силлогизме должно быть только
3 термина (S,
Р. М). Если
правило нарушено, то ошибка называется
«учетверение термина».
Пример
такой ошибки
:
Труд
— основа жизни.
Изучение
логики — труд.
Изучение
логики — основа жизни.
Здесь
термин «труд» трактуется в разном
смысле: в большей посылке — широко, а в
меньшей — узко.
2. Средний
термин должен быть распределен, по
крайней мере, в одной из посылок:
Все
полезные вещи имеют приятный запах.
Духи
«Шанель» имеют приятный запах.
Духи
«Шанель» полезны.
Здесь
средний термин «имеют приятный запах»
(удобно записывать так: «есть имеющие
приятный запах») не распределен ни в
одной из посылок. Поэтому заключение
ложно. Поясним это графически:
Как
мы видим, и S
и
Р
затрагивают
лишь часть объема среднего термина —
«имеющие приятный запах». Следовательно,
достоверный вывод здесь получить нельзя.
-
Если
термин не распределен в посылке, то он
не может быть распределен в заключении:
Все
солдаты умеют стрелять.
Все
дети
— не
солдаты.
Все
дети не умеют стрелять.
Предикат
вывода («умеют стрелять») — распределен,
а в посылке он не распределен. Смысл
этого правила состоит в том, что при его
нарушении в заключении о большем круге
предметов, чем содержится в посылках.
II.
Правила посылок.
-
Из
двух отрицательных посылок вывод
сделать нельзя:
Все
негры — не белые.
Ни
один кусок угля — не белый.
?
Термин
«негры» и термин «кусок угля» никак не
связаны со средним термином «белый».
Все три термина находятся в отношении
несовместимости, поэтому вывод здесь
не возможен.
2.
Из двух частных посылок вывод сделать
нельзя:
Некоторые
студенты — отличники.
Некоторые
студенты — хорошие шахматисты.
?
Здесь
средний термин не распределен в обеих
посылках.
3.
Если одна из посылок отрицательная, то
и заключение должно быть отрицательным:
Все
студенты имеют зачетные книжки.
Дмитриев
— не студент.
Дмитриев
не имеет зачетной книжки.
Любая
отрицательная посылка свидетельствует
о том, что средний термин несовместим
с S
или
Р.
Отсюда
— несовместимость друг с другом большего
и меньшего терминов.
4. Если
одна из посылок частная, то и заключение
должно быть частным:
Все
десантники умеют прыгать с парашютом.
Некоторые
военнослужащие — десантники.
Некоторые
военнослужащие умеют прыгать с парашютом.
Фигуры
силлогизма и их правила
Фигуры
силлогизма
— это его формы, которые различаются
по положению среднего термина М
в
посылках. Всего фигур — четыре.
У
каждой из фигур — свои правила. I.
Первая фигура.
Все
металлы проводят электрический ток.
Медь
— металл.
Медь
проводит электрический ток.
Правила
первой фигуры: большая посылка должна
быть общей, меньшая посылка —
утвердительной.
Распространенная
ошибка: заключение делается по первой
фигуре с меньшей отрицательной посылкой.
Например.
Все
дети любят шоколад.
Петрова
— не ребенок.
Петрова
не любит шоколад.
Здесь
нарушено правило терминов: термин, не
распределенный в посылке, не может быть
распределен в заключении.
II.
Вторая фигура.
Все
приключенческие фильмы интересны.
Этот
фильм — неинтересен.
Этот
фильм — не приключенческий.
Правила
второй фигуры: большая посылка должна
быть общим суждением, а меньшая посылка
и заключение должны быть отрицательными
суждениями. Распространенная
ошибка:
заключение делается по второй фигуре
с двумя утвердительными посылками.
Например:
Все
зайцы едят морковку.
Егоров
есть морковку.
Егоров
— заяц?!
Здесь
нарушается правило терминов: средний
термин не распределен в обеих посылках.
III.Третья
фигура
Все
бамбуки цветут один раз в жизни.
Все
бамбуки — многолетние растения.
Некоторые
многолетние растения цветут один раз
в жизни. Правило
третьей фигуры: меньшая посылка должна
быть утвердительной, а заключение —
частным.
Распространенная
ошибка: заключение — общеутвердительное
суждение. Например:
Все
лисицы любят сыр.
Все
лисицы имеют длинный хвост.
Все.
кто имеет длинный хвост, любят сыр.
Ясно,
что
длинным хвостом обладают не только
лисицы.
IV.
Четвертая фигура.
Все
киты плавают.
Все
плавающие живут в воде.
Некоторые,
живущие в воде, — киты.
Четвертая
фигура не дает общеутвердительных
заключений. Эта фигура используется
редко.
Правила
четвертой
фигуры.
а) если
большая посылка является утвердительной,
то меньшая должна быть общей;
б) если
одна из посылок отрицательная, то большая
посылка должна быть общей.
Возможная
ошибка при использовании четвертой
фигуры: меньшая посылка — частная при
утвердительной большей. Например:
Все
кошки имеют усы.
Некоторые
имеющие усы пишут стихи.
Некоторые
пишущие стихи — кошки?
Модусы
категорического силлогизма
Модусы
категорического
силлогизма
— это разновидности силлогизма, которые
отличаются друг от друга количественной
и качественной характеристиками входящих
в него посылок и заключения.
В
четырех фигурах правильных модусов 19:
1-я
фигура — AAA,
ЕАЕ,
АН, ЕЮ;
2-я
фигура — А
ЕЕ,
АО
О,
ЕАЕ,
ЕЮ;
3-я
фигура — AAI.
ЕАО,
IAI,
АЛ,
ОАО,
ЕЮ;
4-я
фигура — AAL
АЕЕ,
IAI,
ЕАО,
ЕЮ.
Пример:
Все
рыбы не имеют легких.
Все
киты имеют легкие.
Ни
одна рыба — не кит.
Большая
посылка — общеутвердительное суждение
(А).
Меньшая
посылка — общеотрицательное суждение
(Е).
Заключение
— общеотрицательное суждение (Е).
Таким
образом, модус данного силлогизма —
ЕАЕ
(1-я
фигура). Определив модус и фигуры
силлогизма и соотнеся модус с таблицей
правильных модусов, мы можем быстро
определить, верен ли силлогизм.
3.
ДРУГИЕ ВИДЫ СИЛЛОГИЗМОВ Сокращенный
силлогизм
В
повседневной жизни мы часто пользуемся
силлогизмами, у которых некоторые части
выпущены. Эти силлогизмы называются
сокращенными или энтимемами (от греч.
—
«в уме»). В зависимости от того, на чем
нам необходимо сосредоточить внимание,
мы можем оставить только одну посылку
или убрать заключение.
Пример.
Если мы о ком-то говорим: «Нужно быть
непорядочным человеком, чтобы совершать
подобные поступки», — то это выражение
представляет собой силлогизм. Когда мы
этому силлогизму придадим полную форму,
он приобретет следующий вид:
Все
люди, которые совершают подобные
поступки, непорядочны.
Этот
человек совершает подобные поступки.
Следовательно,
этот человек— непорядочный.
Чтобы
восстановить энтимему в полный силлогизм,
необходимо руководствоваться следующими
правилами:
-
Найти
заключение и так его сформулировать,
чтобы меньший и больший термины были
четко выражены.
Заключение обычно идет после слов:
«значит», «следовательно» и т.п. или же
перед словами «потому, что», «ибо», «так
как». Если таких слов нет, то в энтимеме
пропущено заключение. -
Если
имеется заключение, а нет одной из
посылок, то необходимо установить —
большая или меньшая посылка присутствует.
Предикат заключения — это больший
термин. Субъект заключения — меньший
термин. По тому, какой термин содержится
в имеющейся в посылке, определяем какая
посылка. -
Итак,
мы знаем, какая посылка отсутствует,
знаем средний термин. Исходя из этого
определяем оба термина недостающей
посылки.
Энтимемы
широко используются в обыденной
разговорной речи, но следует быть
внимательным, ибо не всегда можно
заметить ошибку, которую ясно зафиксировать
в полном силлогизме. Например: «Он —
некультурный человек, так как не читал
роман Джойса «Улисс»». Разворачиваем
энтимему в полный силлогизм:
Все
некультурные люди не читали роман Джойса
«Улисс». Он
не читал роман Джойса « Улисс».
Он
— некультурный человек.
Из
двух отрицательных посылок заключения
не следует.
Сложный
силлогизм (полисиллогизм)
Это
два или несколько простых категорических
силлогизмов, связанных друг с другом
таким образом, что заключение одного
становится посылкой другого силлогизма
и т.д. Общая формула полисиллогизма
такова.
М—
P
Все, что укрепляет здоровье (М) — полезно
(Р).
С
— М. Физкультура (С) укретяет здоровье
(М).
С
— Р Физкультура (С) полезна (Р).
S
—
С Плавание
(S)
— это физкультура (С).
Следовательно,
S
— Р: Плавание (S)
— полезно (Р).
Всякое
научное мышление в развернутой или
скрытой форме являет собой полисиллогизм,
который следует из целой системы
умозаключений.
Сокращенный
сложный полисиллогизм называется
соритом. В сорите все промежуточные
заключения опускаются, приводится же
только последнее заключение.
Сложносокращенный
силлогизм, в котором посылками служат
энтимемы, называется эпихейремой.
Схема
эпихейремы:
Все
А
суть
С,
так
как А
суть
В.
Все
Д
суть
А.
так как Д
суть
Е.
Следовательно,
все Д
суть
С. Разделительно-категорический
силлогизм
В
разделительно-категорическом умозаключении
одна посылка является разделительным
суждением, а вторая посылка и заключение
— категорические суждения.
Разделительно-категорический силлогизм
имеет два модуса:
а) утверждающе-отрицающий:
б) отрицающе-утверждающий.
Общая
формула модуса а).
А
есть
или В,
или
С.
А
есть
В.
Следовательно,
А не есть С. Пример:
Войны
бывают или реакционные, или прогрессивные
.
Войны,
цель которых захват чужих земель, не
прогрессивны Следовательно,
захватнические войны не прогрессивны.
Общая
формула модуса б):
А
есть
или В,
или
С.
А
не
есть В.
Следовательно,
А
есть
С.
Пример:
Минеральные
удобрения бывают или азотными, или
фосфорными. Это
удобрение не азотное.
Следовательно,
это удобрение — фосфорное.
Условный
(гипотетический) силлогизм
Как
мы помним, кроме категорических суждений
есть условные и разделительные суждения.
Поэтому могут быть силлогизмы, в посылки
которых входят условные суждения,
разделительные суждения, или и те и
другие.
Схема
условного суждения: Если А
есть
В,
то
С есть Д.
Первое
суждение (Если А
есть
В)
называется
«основанием», а второе (С
есть
Д)
—
«следствием».
Если
в силлогизме обе посылки и заключение
являются условными суждениями, то он
называется условным.
Структура
условного умозаключения: Если А,
то
В.
Если
В.
то
С.
Если
А,
то
С.
Например:
Если
по проводнику пропустить электрический
ток, то вокруг проводника образуется
магнитное поле.
Если
вокруг проводника образуется магнитное
поле, то железные опилки располагаются
в этом
магнитном
поле вдоль силовых линий.
Следовательно,
если по проводнику пропустить электрический
ток, то железные опилки располагаются
в его магнитном поле вдоль силовых
линий.
Условно-категорический
силлогизм
Это
силлогизм, где одна посылка — условное
суждение, а вторая — простое категорическое.
При этом категорическая посылка обычно
состоит из тех же терминов, что основание
или следствие условной посылки.
Условно-категорический
силлогизм имеет два модуса: а) утверждающий
и б) отрицающий Схема утверждающего
модуса:
Если
есть А,
то
есть В.
А
есть.
Следовательно,
есть В.
Пример:
Если
это дерево ель, то оно не теряет на зиму
иголок.
Это
дерево ель.
Следовательно,
данное дерево не теряет на зиму иголок.
Схема
отрицающего модуса:
Если
есть А,
то
есть В.
В
нет.
Следовательно,
А
нет.
Пример:
Если
Богданов хороший лыжник, то он выполнит
норматив мастера спорта.
Богданов
не выполнил норматив мастера спорта по
лыжам.
Следовательно, Богданов не является
хорошими лыжником.
Обратим
внимание на следующий факт. В условных
силлогизмах можно делать заключение
только от утверждения основания к
утверждению следствия. И от отрицания
следствия к отрицанию основания. Нельзя
делать заключение от утверждения
следствия к утверждению основания и от
отрицания основания к отрицанию
следствия. Дело в том, что одно и то же
явление может вызываться разными
причинами. Если я отрицаю, что данная
причина вызвала к жизни то или иное
явление, то это не значит, что его не
могла произвести какая-то другая причина.
Если я утверждаю, что данное действие
произошло, то это не значит, что оно
порождено данной причиной — могло быть
множество других причин, которые его
могли породить.
Пример
1.
Попробуем
утверждать следствие:
Если
кто-нибудь читает хорошие книги, то он
расширяет свой кругозор.
Кузнецов
расширил кругозор.
Следует
ли отсюда, что Кузнецов читал хорошие
книги? Нет, ибо Кузнецов мог ходить на
лекции, беседовать с хорошими специалистами
и т.д. То есть причин расширения кругозора
много.
Пример
2. Попробуем отрицать основание:
Если
кто-нибудь читает хорошие книги, то он
расширяет свой кругозор.
Кузнецов
не читает хороших книг.
Можем
ли мы сказать, что Кузнецов не расширяет
свой кругозор? Нет, ибо верны в данном
случае соображения, приведенные в
примере 1. Разделительное
умозаключение
Разделительным
умозаключением называется
умозаключение, в котором одна или
несколько посылок — разделительные.
Существуют чисто разделительные и
разделительно-категорические
умозаключения.
Как
мы помним, общая форма разделительного
суждения такова: А
есть
или В,
или
С,
или
Д
или
Е.
Каждый
член разделительного суждения называется
альтернативой.
В
чисто разделительном силлогизме обе
посылки являются разделительными
суждениями.
Формула
чисто разделительного силлогизма:
S
есть
А,
или
В,
или
С,
А
есть
или А,,
или
А.
S
есть
или A,
или
А2,
или
В,
или
С.
Пример:
Всякая
философская система есть или идеализм,
или материализм.
Идеалистическая
философия есть или объективный идеализм,
или субъективный идеализм.
Следовательно,
всякая философская система есть или
объективный идеализм, или субъективный
идеализм, или материализм.
Условно-разделительный
силлогизм
Условно-разделительное
умозаключение —
это умозаключение, в котором одна посылка
состоит из двух или более условных
суждений, а другая является разделительным
суждением.
В
зависимости от числа членов в разделительной
посылке это умозаключение может быть
дилеммой
(если разделительная посылка содержит
два члена), трилеммой
(если разделительная посылка содержит
три члена) и полилеммой
(число разделительных членов больше
двух).
Дилеммы
и трилеммы бывают двух видов: конструктивные
и деструктивные; обе формы дилеммы и
трилеммы могут быть простыми и сложными.
Простая
конструктивная дилемма.
Это умозаключение состоит из двух
посылок. В первой утверждается, что из
двух разных оснований вытекает одно и
то же следствие. Во второй посылке,
которая является разделительным
суждением, утверждается, что одно или
другое из этих оснований истинно.
Схема
простой конструктивной дилеммы:
Если
А
есть
В,
то
С
есть
D;
если
Е
есть
F,
то
С есть D.
А
есть
В
или
Е
есть
F.
Следовательно,
С
есть
D.
Пример:
Если
студент ходит на лекции, то он знает
логику.
Если
студент читает учебник логики, то он
знает логику.
Студент
ходит на лекции или читает учебник
логики.
Студент знает логику.
Сложная
конструктивная дилемма.
Это умозаключение, где в первой посылке
есть два основания, из которых вытекают
два следствия. Во второй посылке
(разделительном суждении) говорится об
истинности одного или другого основания.
В заключении утверждается истинность
одного или другого следствия. Отличие
сложной конструктивной дилеммы от
простой в том, что оба следствия ее
условной посылки не одинаковы, а различны.
Схема
сложной конструктивной дилеммы:
Если
А
есть
В,
то
С
есть
D:
если
Е
есть
F,
то
G
есть
Н.
Но
или А
есть
В.
или
Е
есть
F.
Следовательно,
или С
есть
D,
или
G
есть
Н.
Пример:
Рассуждение
Штирлица в романе «Семнадцать мгновений
весны» (см.: Семенов Ю. Собр. соч. в 8 т. Т.
3. — М.. 1991. — С 567-574).
Если
я вернусь в Берлин, меня может арестовать
гестапо, если я поеду в Москву, то не
выполню задание до конца.
Но
я могу направиться в Берлин или вернуться
в Москву.
Следовательно,
или меня может арестовать гестапо, или
я не выполню задание до конца.
Более
сложные ситуации выражаются логической
формой трилеммы или даже полимеммы.
Пример
сложной конструктивной трилеммы;
Во
многих русских народных сказках говорится
о камне, который лежит на перекрестке
трех дорог. На камне надпись, содержащая
в себе трилемму:
Прямо
пойдешь — жизнь потеряешь;
Налево
пойдешь — коня потеряешь;
Направо
пойдешь — в неволю попадешь.
Герой
сказки может поехать прямо, или направо,
или налево.
Следовательно,
он или жизнь потеряет, или коня потеряет,
или в неволю попадет.
Достоверность
лемматического умозаключения находится
в зависимости от правильности условных
суждений в большей посылке и от полноты
членов деления в меньшей.
Нередко
эти условия не соблюдаются, тогда
лемматическое умозаключение делается
источником ошибок.
Причина
ошибок чаще всего — неполное перечисление
членов деления. Двумя альтернативами
не всегда можно исчерпать все возможные
случаи — альтернатив может быть много
больше. Пример подобной ошибки:
Если
студент любит учение, то он не нуждается
в поощрении. Если студент чувствует
отвращение к учению, то любое поощрение
неэффективно.
Студент
может любить учение или испытывать к
нему отвращение.
Следовательно,
поощрение в деле обучения или излишне,
или бесполезно.
Ошибка
здесь в том, что кроме «любви к учению»
и «отвращения к учению» у студента может
быть и, так сказать, нейтральная позиция
— для таких студентов поощрение учения
в какой-либо форме может оказаться
действенным.
Общие правила силлогизма и логических фигур помогают легко отличить правильные умозаключения от неправильных. Если в процессе мысленного анализа выясняется, что высказывание соответствует всем правилам, то оно логически верное. Упражнения в развитии навыка использования данных правил позволяют сформировать культуру мышления.
Общее определение силлогизма и виды терминов


Правила силлогизма вытекают из общего определения этого термина. Данное понятие является одной из форм дедуктивного мышления, для которого характерно формирование заключения из двух высказываний (называемых посылками). Наиболее распространенной и примитивной формой служит простой категорический силлогизм, построенный на 3 терминах. В качестве наглядного примера можно привести такое умозаключение:

Меньший термин S – это предмет логического суждения, входящий в заключение. В приведенном примере – «тыква» (субъект заключения). Соответственно, посылка, его содержащая, называется меньшей (номер 2).
Средний, опосредующий термин M присутствует в посылках, но не содержится в заключении («овощ»). Посылка с утверждением о нем также называется средней (номер 1).
Больший термин P, называемый предикатом заключения («растение») – это утверждение, высказанное о субъекте, который является большой посылкой (номер 3). Для облегчения анализа в логике больший термин располагается в первой посылке.
В общем смысле простой категорический силлогизм — это субъектно-предикатное умозаключение, устанавливающее взаимоотношения между меньшим и большим терминами с учетом их связи со средним термином.
Средний термин может иметь различное расположение в системе посылок. В связи с этим выделяют 4 фигуры, показанные на рисунке ниже.
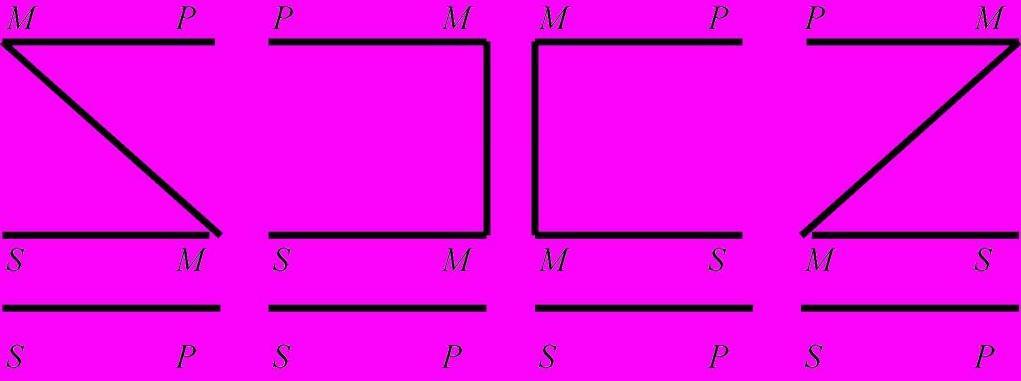

Логические отношения, показывающие взаимосвязь данных терминов, называются модусами.
Правила силлогизмов и их значение
Если отношения между посылками (модусы) построены логично, из них можно вывести обоснованное заключение, то говорят, что силлогизм построен правильно. Для выявления неправильных дедуктивных выводов существуют специальные правила. Если нарушено хотя бы одно из них, то силлогизм – неправильный.
Существует 3 группы правил силлогизмов: правила терминов, посылок и правила фигур. Всего их насчитывается двенадцать. При определении того, правильным ли является силлогизм, можно не обращать внимания на истинность самих посылок, то есть их содержание. Главное, чтобы был сделан верный вывод из них. Чтобы умозаключение стало правильным, нужно корректно связать больший и меньший термины. Поэтому различают также форму (связь между терминами) и содержание силлогизма. Так, утверждение «Тигры – травоядные. Бараны есть тигры. Следовательно, бараны – травоядные» по содержанию первой и второй посылок является ложным, но его заключение – верное.
Правилами простого категорического силлогизма являются:
1. Правила для терминов:
- «Трех терминов».
- «Распределения среднего термина».
- «Связи заключения и посылки».
2. Для посылок:
- «Трех категорических суждений».
- «Отсутствия заключения при двух отрицательных суждениях».
- «Отрицательного заключения».
- «Частных суждений».
- «Частности заключения».
Для каждой из логических фигур используют свои правила (их всего четыре), описанные ниже.
Существуют также сложные силлогизмы (сориты), которые состоят из нескольких простых. В их структурной цепочке каждое заключение служит посылкой для получения следующего вывода. Если, начиная со второго из них, меньшая посылка в выражении опущена, то такой силлогизм называется аристотелевским.
Еще в Древней Греции силлогизмы считали одним из важнейших инструментов научного познания, так как они помогают соединению понятий. Главной задачей верного научного построения умозаключения является нахождение среднего понятия, благодаря которому и осуществляется силлогизация. В результате соединения формальных понятий в уме человек может познать реальные вещи в природе.
С другой стороны, силлогизм состоит из понятий, обобщающих свойства предметов. Если понятия построены неправильно, как в примере о тиграх и баранах, то силлогизм будет не точным.
Методы проверки утверждений

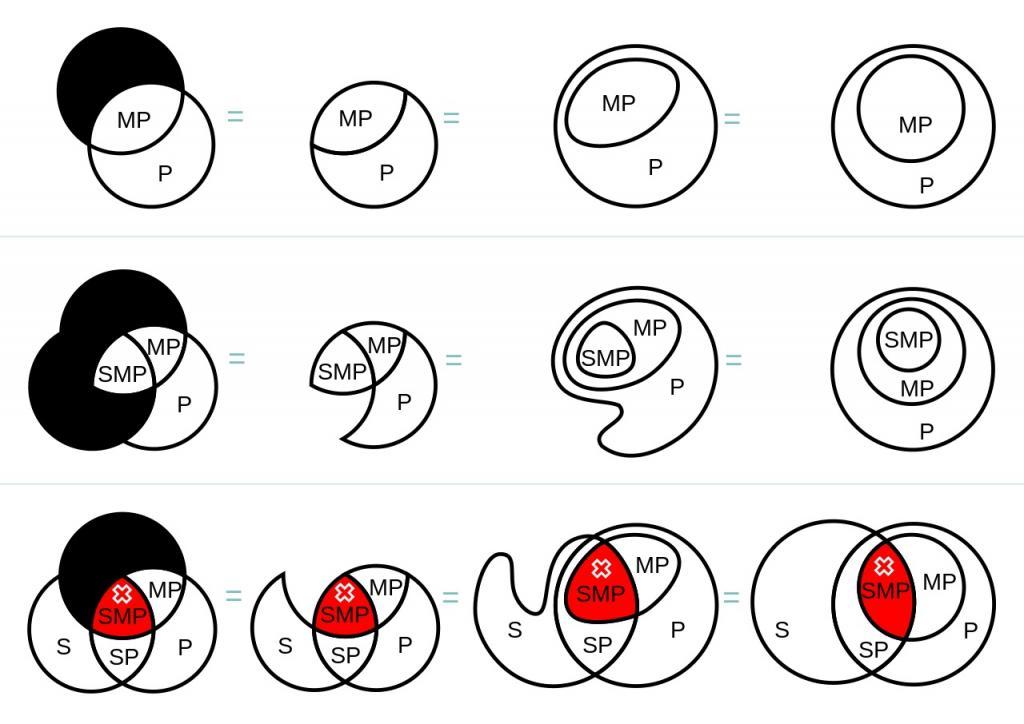
В логике применяются 3 практических метода проверки правильности силлогизмов:
- создание круговых схем (изображение объемов) с посылками и заключениями;
- составление противоположного примера;
- проверка на согласованность силлогизма с общими правилами и правилами фигур.
Наиболее наглядным и часто использующимся способом является первый.
Правило 3 терминов

Данное правило категорического силлогизма заключается в следующем: должно быть ровно 3 термина. Логическое умозаключение выстраивается на взаимоотношении большего и меньшего терминов к среднему. Если количество терминов больше, то может произойти установление полного равенства среди разных по смыслу свойств предметов, которые определяются в качестве среднего термина:
«Коса есть ручной инструмент. Эта прическа есть коса. Эта прическа есть ручной инструмент».
В этом умозаключении под словом «коса» скрываются два разных понятия – инструмент для скашивания травы и коса, сплетенная из волос. Таким образом, здесь присутствует 4 понятия, а не три. В результате происходит искажение смысла. Это общее правило силлогизмов является одним из основных в логике.
Если же терминов меньше, то из посылок невозможно сделать никаких заключений. Например: «Все кошки – млекопитающие. Все млекопитающие есть животные». Здесь логически можно понять, что результатом умозаключения будет вывод, что все кошки – это животные. Но формально такой вывод сделать нельзя, так как в силлогизме присутствует только 2 понятия.
Правило распределения среднего силлогизма
Смысл второго правила категорического силлогизма заключается в следующем: средний из терминов обязательно должен распределяться хотя бы в одной посылке.
«Все бабочки летают. Некоторые насекомые летают. Некоторые насекомые являются бабочками».
В данном случае термин М не распределен в посылках. Установить взаимосвязь между крайними терминами не представляется возможным. И хотя вывод является по смыслу верным, логически он неправильный.
Правило связи заключения и посылки
Третье правило терминов силлогизма гласит, что термин, имеющийся в заключительном выводе, необходимо распределить и в посылках. Применительно к предыдущему силлогизму это будет выглядеть так: «Все бабочки летают. Некоторые насекомые – бабочки. Некоторые насекомые – летают».
Неправильный вариант, нарушающий правило простого силлогизма: «Все бабочки летают. Ни один жук не является бабочкой. Ни один жук не летает».
Правило посылок (ПП) №1: 3 категорических суждения
Первое правило посылок силлогизмов вытекает из переформулировки определения понятия простого категорического силлогизма: должно быть 3 категорических суждения (положительных или отрицательных), которые состоят из 2 посылок и 1 заключения. Оно перекликается с первым правилом терминов.
Под категорическим суждением понимают высказывание, в котором производится утверждение или отрицание какого-либо свойства или признака предмета (субъекта).
ПП №2: отсутствие заключения при наличии двух отрицательных суждений

Второе правило, характеризующее связи между посылками логического рассуждения, гласит: из 2 посылок отрицательного характера невозможно вывести заключение. Существует также аналогичная переформулировка: хотя бы одна из посылок в выражениях должна носить утвердительный характер.
В самом деле, можно взять такой наглядный пример: «Овал не есть круг. Квадрат не есть овал». Никакого логического заключения из него вывести не получится, так как ничего нельзя получить из соотношения терминов «овал» и «квадрат». Крайние термины (больший и меньший) исключены из среднего. Следовательно, между ними нет определенного отношения.
ПП №3: условие отрицательного заключения
Правило третье: заключение отрицательно только в том случае, если одна из посылок также отрицательна. Пример применения этого правила: «Рыбы не могут жить на суше. Пескарь – рыба. Пескарь не может жить на суше».
В этом утверждении средний термин убирается из большего. В связи с этим крайний термин («рыбы»), который входит в состав среднего (второе утверждение) исключается из второго крайнего термина. Данное правило является очевидным.
ПП №4: правило частных суждений
Четвертое правило посылок аналогично первому правилу простого категорического силлогизма. Оно заключается в следующем: если в силлогизме присутствуют 2 частных суждения, то заключение получить невозможно. Под частными суждениями понимают такие, в которых производится отрицание или утверждение определенной части предметов, относящихся к группе предметов, обладающих общими признаками. Обычно они выражаются в виде утверждений: «Некоторые S не являются (или, наоборот, являются) Р».

Наглядный пример, демонстрирующий данное правило: «Некоторые спортсмены устанавливают мировые рекорды. Некоторые студенты – спортсмены». Вывести отсюда заключение о том, что часть «некоторых студентов» устанавливает мировые рекорды – невозможно. Если обратиться ко второму правилу терминов силлогизмов, то можно заметить, что средний термин не распределен в посылках. Поэтому такой силлогизм является неверным.
Когда утверждение представляет собой комбинацию из частноутвердительной и частноотрицательной посылок, то в структуре силлогизма будет распределен только предикат частноотрицательного высказывания, что также неправильно.
Если же обе посылки — частноотрицательные, то в этом случае срабатывает второе правило посылок. Таким образом, хотя бы одна из посылок в утверждении должна иметь характер общего суждения.
ПП №5: частность заключения
Согласно пятому правилу посылок силлогизмов, если хотя бы одна посылка является частным рассуждением, то заключение также становится частным.
Пример: «Все художники города приняли участие в выставке. Некоторые из работников предприятия – художники. Некоторые работники предприятия приняли участие в выставке». Это верный силлогизм.
Пример частного отрицательного заключения: «Все победители получили награды. Некоторые из присутствующих наград не имеют. Некоторые из присутствующих – не победители». В этом случае распределены как субъект, так и предикат общеотрицательного суждения.
Правила первой и второй фигур
Правила фигур категорического силлогизма были введены для того, чтобы наглядно описать критерии правильности суждений, которые характерны только для данной фигуры.
Правило первой фигуры гласит: меньшая из посылок должна носить утвердительный характер, а большая – быть общей. Примеры неверных силлогизмов по этой фигуре:
Правило, которое применяется для описания второй фигуры категорического силлогизма: большая из посылок должна носить характер общей, а одна из посылок – служить отрицанием.
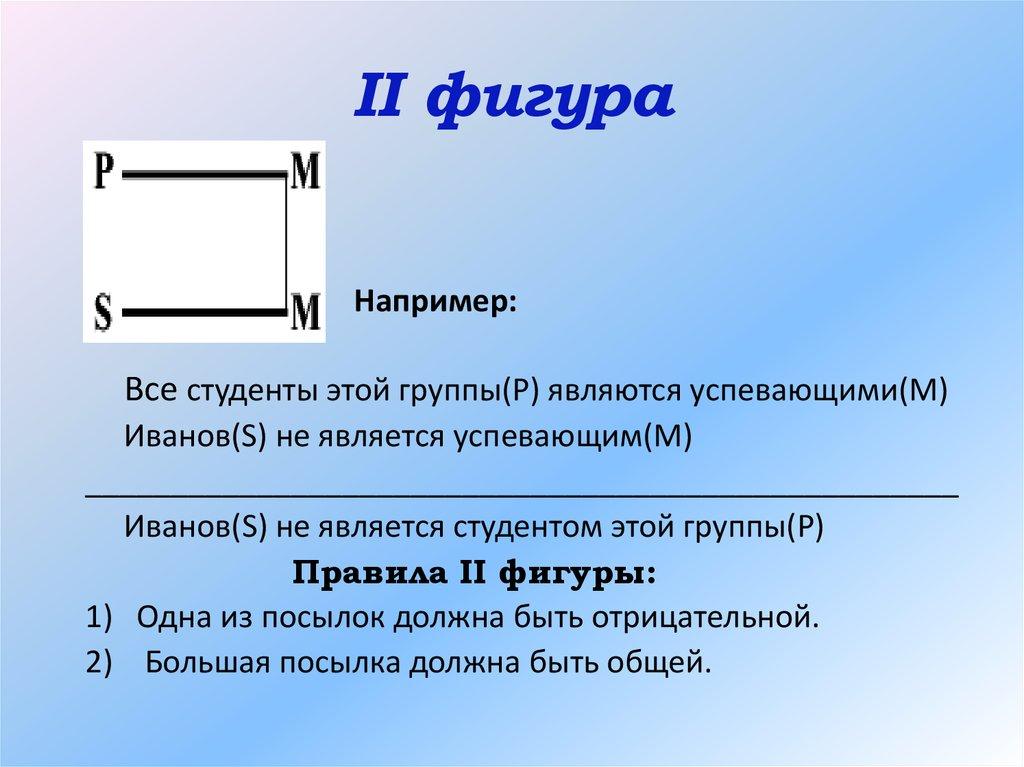
Примеры ошибочных утверждений:
Правила третьей и четвертой фигур
Третье правило фигур силлогизма связано с распределением меньшего термина силлогизма. Если такое распределение отсутствует в посылке, то оно не может быть распределенным и в заключении. Поэтому требуется выполнение следующего правила: меньшая из посылок должна быть утвердительного характера, а заключение – частным утверждением.
Пример: «Все ящерицы – пресмыкающиеся. Некоторые пресмыкающиеся не являются яйцекладущими. Некоторые яйцекладующие не являются пресмыкающимися». В этом случае меньшая из посылок — не утвердительная, а отрицательная, поэтому силлогизм является неправильным.
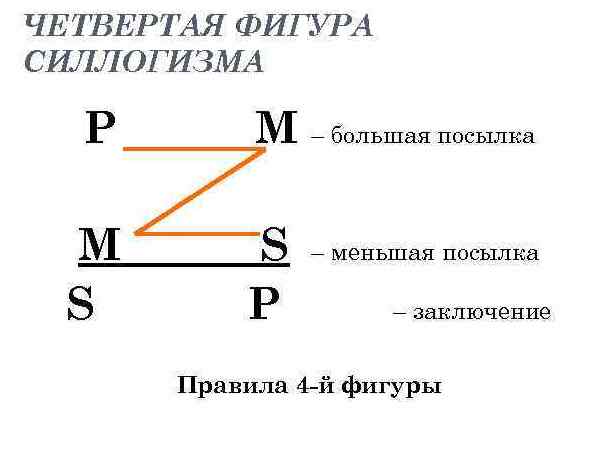
Четвертая фигура наименее распространена, так как получение заключения на основе ее посылок носит характер неестественности для процесса суждения. На практике для построения умозаключения подобного типа пользуются первой фигурой. Правило для этой фигуры заключается в следующем: в четвертой фигуре заключение не может быть общеутвердительным.