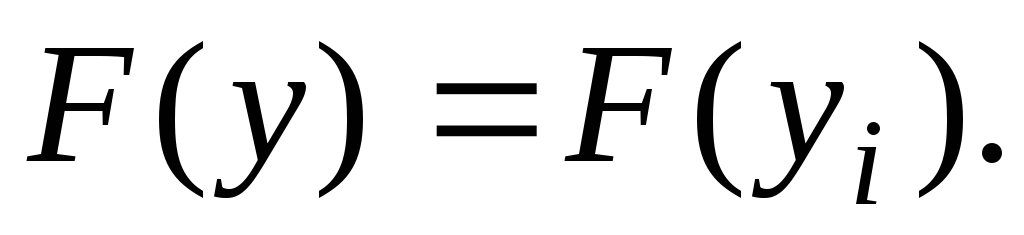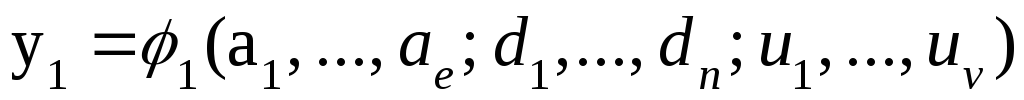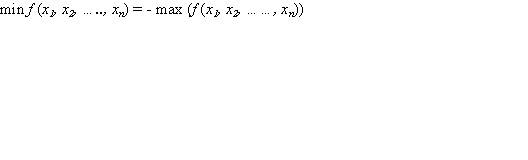Содержание:
Исследование различных процессов, в том числе и экономических, обычно начинается с их моделирования, т.е. отражения реального процесса через математические соотношения. При этом составляются уравнения или неравенства, которые связывают различные показатели (переменные) исследуемого процесса, образуя систему ограничений. В этих процессах выделяются такие переменные, меняя которые можно получить оптимальное значение основного показателя данной системы (прибыль, доход, затраты и т.д.). Соответствующие методы, позволяющие решать указанные задачи, объединяются под общим названием «математическое программирование» или математические методы исследования операций.
Математическое программирование включает в себя такие разделы математики, как линейное, нелинейное и динамическое программирование. Сюда же относят и стохастическое программирование, теорию игр, теорию массового обслуживания, теорию управления запасами и некоторые другие.
Математическое программирование — это раздел высшей математики, посвященный решению задач, связанных с нахождением экстремумов функций нескольких переменных, при наличии ограничений на переменные.
Методами математического программирования решаются задачи о распределении ресурсов, планировании выпуска продукции, ценообразования, транспортные задачи и т.д.
Построение математической модели экономической задачи включает следующие этапы:
- выбор переменных задачи;
- составление системы ограничений;
- выбор целевой функции.
Переменными задачи называются величины
Система ограничений включает в себя систему уравнений и неравенств, которым удовлетворяют переменные задачи и которые следуют из ограниченности ресурсов или других экономических или физических условий, например, положительности переменных и т.п.
Целевой функцией называют функцию переменных задачи, которая характеризует качество выполнения задачи, и экстремум которой требуется найти.
Общая задача математического программирования формулируется следующим образом: найти экстремум целевой функции: 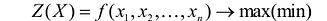
Если целевая функция и система ограничений линейны, то задача математического программирования называется задачей линейного программирования и в общем виде может быть записана следующим образом:
Данная запись означает следующее: найти экстремум целевой функции задачи и соответствующие ему переменные X = (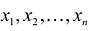
Допустимым решением (планом) задачи линейного программирования называется любойX = (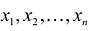
Оптимальным решением (планом) задачи линейного программирования называется такое допустимое решение задачи, при котором целевая функция достигает экстремума.
Задача линейного программирования
В общем случае задача линейного программирования записывается так, что ограничениями являются как уравнения, так и неравенства, а переменные могут быть как неотрицательными, так и произвольно изменяющимися. В случае, когда все ограничения являются уравнениями и все переменные удовлетворяют условию неотрицательности, задачу линейного программирования называют канонической. Каноническая задача линейного программирования в координатной форме записи имеет вид:
Используя знак суммирования эту задачу можно записать следующим образом:
Каноническая задача линейного программирования в векторной форме имеет вид:
В данном случае введены векторы:
Здесь С — X — скалярное произведение векторов С и X.
Каноническая задача линейного программирования в матричной форме записи имеет вид:
где:
Здесь А — матрица коэффициентов системы уравнений, X -матрица-столбец переменных задачи; 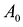
Нередко используются задачи линейного программирования, называемые симметричными, которые в матричной форме записи имеют вид:
Приведение общей задачи линейного программирования к канонической форме
В большинстве методов решения задач линейного программирования предполагается, что система ограничений состоит из уравнений и естественных условий неотрицательности переменных. Однако, при составлении математических моделей экономических задач ограничения в основном формулируются системы неравенств, поэтому возникает необходимость перехода от системы неравенств к системе уравнений. Это может быть сделано следующим образом. К левой части линейного неравенства:
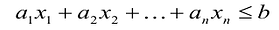
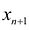
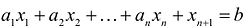
Неотрицательная переменная 
Основания для возможности такого преобразования дает следующая теорема.
Теорема. Каждому решению 
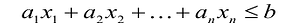
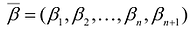
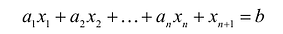
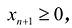

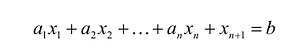

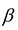
Доказательство. Пусть 
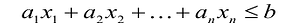
Если в уравнение 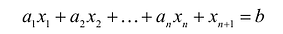
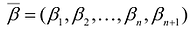
Таким образом, решение 
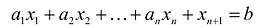

Доказана первая часть теоремы.
Пусть 
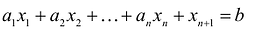

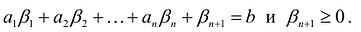
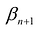
т.е. 
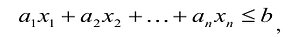
Если в левую часть неравенств системы ограничений вида
добавить переменную 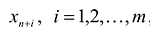
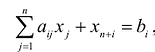
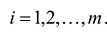
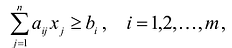
Полученная таким образом система уравнений-ограничений, вместе с условиями неотрицательности переменных, т.е. 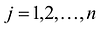
Дополнительные переменные вводятся в целевую функцию с нулевыми коэффициентами и поэтому не влияют на ее значения.
В реальных практических задачах дополнительные неизвестные имеют определенный смысл. Например, если левая часть ограничений задачи отражает расход ресурсов на производство продукции в объемах 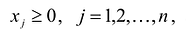
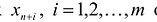
Иногда возникает также необходимость перейти в задаче от нахождения минимума к нахождению максимума или наоборот. Для этого достаточно изменить знаки всех коэффициентов целевой функции на противоположные, а в остальном задачу оставить без изменения. Оптимальные решения полученных таким образом задач на максимум и минимум совпадают, а значения целевых функций при оптимальных решениях отличаются только знаком.
Множества допустимых решений
Множество точек называется выпуклым, если оно вместе с любыми двумя своими точками содержит их произвольную выпуклую линейную комбинацию.
Выпуклой линейной комбинацией произвольных точек 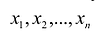
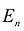
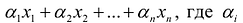
Геометрически это означает, что если множеству с любыми двумя его произвольными точками полностью принадлежит и отрезок, соединяющий эти точки, то оно будет выпуклым. Например, выпуклыми множествами являются прямолинейный отрезок, прямая, круг, шар, куб, полуплоскость, полупространство и др.
Точка множества называется граничной, если любая окрестность этой точки сколь угодно малого размера содержит точки, как принадлежащие множеству, так и не принадлежащие ему.
Граничные точки множества образуют его границу. Множество называется замкнутым, если оно содержит все свои граничные точки.
Ограниченным называется множество, если существует шар с радиусом конечной длины и центром в любой точке множества, содержащий полностью в себе данное множество. В противном случае множество будет неограниченным.
Пересечение двух или более выпуклых множеств будет выпуклым множеством, так как оно отвечает определению выпуклого множества.
Точка выпуклого множества называется угловой, если она не может быть представлена в виде выпуклой линейной комбинации двух других различных точек этого множества.
Так, угловые точки треугольника — его вершины, круга — точки окружности, ее ограничивающие, а прямая, полуплоскость, плоскость, полупространство, пространство не имеют угловых точек.
Выпуклое замкнутое ограниченное множество на плоскости, имеющее конечное число угловых точек, называется выпуклым многоугольником, а замкнутое выпуклое ограниченное множество в трехмерном пространстве, имеющее конечное число угловых точек, называется выпуклым многогранником.
Теорема. Любая тонка многоугольника является выпуклой линейной комбинацией его угловых точек.
Теорема. Область допустимых решений задачи линейного программирования является выпуклым множеством.
Уравнение целевой функции при фиксированных значениях самой функции является уравнением прямой линии (плоскости, гиперплоскости и т.д.). Прямая, уравнение которой получено из целевой функции при равенстве ее постоянной величине, называется линией уровня.
Линия уровня, имеющая общие точки с областью допустимых решений и расположенная так, что область допустимых решений находится целиком в одной из полуплоскостей, называется опорной прямой.
Теорема. Значения целевой функции в точках линии уровня увеличиваются, если линию уровня перемещать параллельно начальному положению в направлении нормали и убывают при перемещении в противоположном направлении.
Теорема. Целевая функция задачи линейного программирования достигает экстремума в угловой точке области допустимых решений; причем, если целевая функция достигает экстремума в нескольких угловых точках области допустимых решений, она также достигает экстремума в любой выпуклой комбинации этих точек.
Опорное решение задачи линейного программирования, его взаимосвязь с угловыми точками
Каноническая задача линейного программирования в векторной форме имеет вид:
Положительным координатам допустимых решений ставятся в соответствие векторы условий. Эти системы векторов зависимы, так как число входящих в них векторов больше размерности векторов.
Базисным решением системы называется частное решение, в котором неосновные переменные имеют нулевые значения. Любая система уравнений имеет конечное число базисных решений, равное 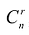
Опорным решением задачи линейного программирования называется такое допустимое решение 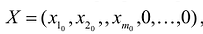
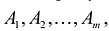
Число отличных от нуля координат опорного решения не может превосходить ранга r системы векторов условий (т.е. числа линейно независимых уравнений системы ограничений).
Если число отличных от нуля координат опорного решения равно m, то такое решение называется невырожденным, в противном случае, если число отличных от нуля координат опорного решения меньше т, такое решение называется вырожденным.
Базисом опорного решения называется базис системы векторов условий задачи, в состав которой входят векторы, соответствующие отличным от нуля координатам опорного решения.
Теорема. Любое опорное решение является угловой точкой области допустимых решений.
Теорема. Любая угловая точка области допустимых решений является опорным решением.
Пример:
Графический метод решения задачи линейной оптимизации рассмотрим на примере задачи производственного планирования при n = 2.
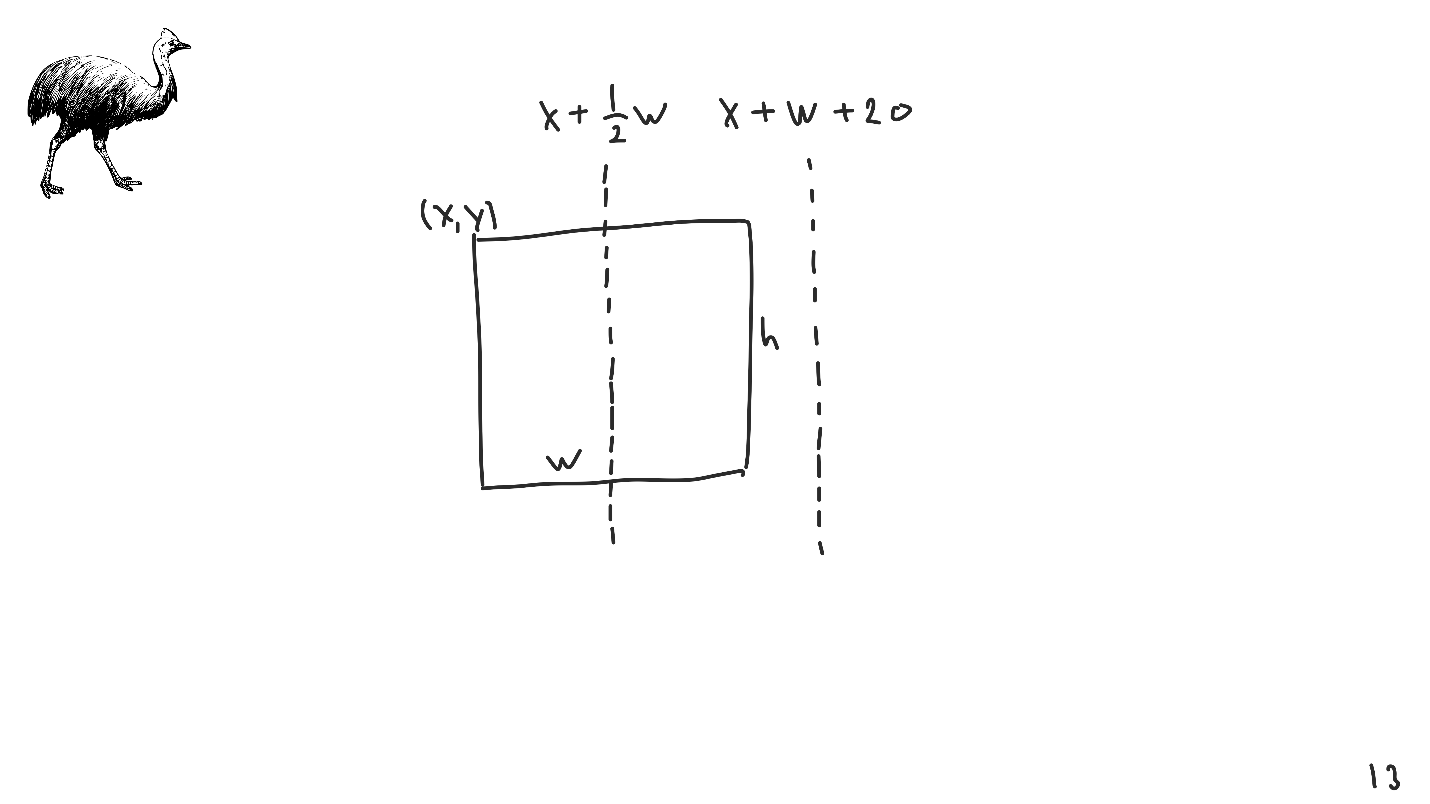
Предприятие изготавливает изделия двух видов А и В. Для производства изделий оно располагает сырьевыми ресурсами трех видов С, D и Е в объемах 600, 480 и 240 единиц соответственно. Нормы расхода ресурсов на единицу продукции каждого вида известны и представлены в табл. 14.1
Прибыль от реализации изделия А составляет 40 млн. руб., а изделия В — 50 млн.руб. Требуется найти объемы производства изделий А и В, обеспечивающие максимальную прибыль.
Построим математическую модель задачи, для чего обозначим 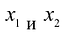
Тогда прибыль предприятия от реализации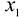
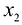
Ограничения по ресурсам будут иметь вид:
Естественно, объемы производства должны быть неотрицательными
Решение сформулированной задами найдем, используя геометрическую интерпретацию. Определим сначала многоугольник решений, для чего систему ограничений неравенств запишем в виде уравнений и пронумеруем их:
Каждое из записанных уравнений представляет собой прямую на плоскости, причем 4-я и 5-я прямые являются координатными осями.
Чтобы построить первую прямую, найдем точки ее пересечения с осями координат: 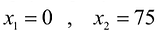
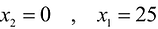
Далее нас интересует, по какую сторону от прямой будет находиться полуплоскость, соответствующая первому неравенству. Чтобы определить искомую полуплоскость, возьмем точку O(0,0) подставив ее координаты в неравенство, видим, что оно удовлетворяется. Так как точка O(0,0) лежит левее первой прямой, то и полуплоскость будет находиться левее прямой
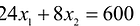
Аналогично построены 2-я и 3-я прямые и найдены полуплоскости, соответствующие 2-му и 3-му неравенству. Точки, удовлетворяющие ограничениям 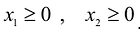
Любая точка многоугольника решений удовлетворяет системе ограничений задачи и, следовательно, является ее решением. Это говорит о том, что эта задача линейной оптимизации имеет множество допустимых решений, т.е. моговариантпа. Нам же необходимо найти решение, обеспечивающее максимальную прибыль.
Чтобы найти эту точку, приравняем функцию к нулю и построим соответствующую ей прямую. Вектор-градиент прямой функции
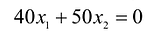
Рис. 14.1
Изобразим вектор на графике и построим прямую функции перпендикулярно вектору на рис. 14.1. Перемещая прямую функции параллельно самой себе в направлении вектора, видим, что последней точкой многоугольника решений, которую пересечет прямая функции, является угловая точка В. Следовательно, в точке В функция достигает максимального значения. Координаты точки В находим, решая систему уравнений, прямые которых пересекаются в данной точке.
Решив эту систему, получаем, что
Следовательно, если предприятие изготовит изделия в найденных объемах, то получит максимальную прибыль, равную:
Алгоритм решения задачи линейного программирования графическим методом таков:
- Строится область допустимых решений;
- Строится вектор нормали к линии уровня с точкой приложении в начале координат;
- Перпендикулярно вектору нормали проводится одна из линий уровня, проходящая через начало координат;
- Линия уровня перемещается до положения опорной прямой. На этой прямой и будут находиться максимум или минимум функции.
В зависимости от вида области допустимых решений и целевой функции задача может иметь единственное решение, бесконечное множество решений или не иметь ни одного оптимального решения.
На рис. 14.3 показан случай, когда прямая функции параллельна отрезку АВ, принадлежащему ОДР. Максимум функции Z достигается в точке А и в точке В, а, следовательно, и в любой точке отрезка АВ, т.к. эти точки могут быть выражены в виде линейной комбинации угловых точек А и В.
На рисунке 14.4 изображен случай, когда система ограничений образует неограниченное сверху множество. Функция Z в данном случае стремится к бесконечности, так как прямую функции можно передвигать в направлении вектора градиента как угодно далеко, а на рисунке 14.5 представлен случай несовместной системы ограничений.
Основные понятия симплексного метода решения задачи линейного программирования.
Среди универсальных методов решения задач линейного программирования наиболее распространен симплексный метод (или симплекс-метод), разработанный американским ученым Дж.Данцигом. Суть этого метода заключается в том, что вначале получают допустимый вариант, удовлетворяющий всем ограничениям, но необязательно оптимальный (так называемое начальное опорное решение); оптимальность достигается последовательным улучшением исходного варианта за определенное число этапов (итераций). Нахождение начального опорного решения и переход к следующему опорному решению проводятся на основе применения рассмотренного выше метода Жордана-Гаусса для системы линейных уравнений в канонической форме, в которой должна быть предварительно записана исходная задача линейного программирования; направление перехода от одного опорного решения к другому выбирается при этом на основе критерия оптимальности (целевой функции) исходной задачи.
Симплекс-метод основан на следующих свойствах задачи линейного программирования:
- Не существует локального экстремума, отличного от глобального. Другими словами, если экстремум есть, то он единственный.
- Множество всех планов задачи линейного программирования выпукло.
- Целевая функция ЗЛП достигает своего максимального (минимального) значения в угловой точке многогранника решений (в его вершине). Если целевая функция принимает свое оптимальное значение более чем в одной угловой точке, то она достигает того же значения в любой точке, являющейся выпуклой линейной комбинацией этих точек.
- Каждой угловой точке многогранника решений отвечает опорный план ЗЛП.
Рассмотрим две разновидности симплексного метода: симплекс-метод с естественным базисом и симплекс-метод с искусственным базисом (или М-метод).
- Заказать решение задач по высшей математике
Симплекс-метод с естественным базисом
Для применения этого метода задача линейного программирования должна быть сформулирована в канонической форме, причем матрица системы уравнений должна содержать единичную подматрицу размерностью mхm. В этом случае очевиден начальный опорный план (неотрицательное базисное решение).
Для определенности предположим, что первые m векторов матрицы системы составляют единичную матрицу. Тогда очевиден первоначальный опорный план:
Проверка на оптимальность опорного плана проходит с помощью критерия оптимальности, переход к другому опорному плану — с помощью преобразований Жордана-Гаусса и с использованием критерия оптимальности.
Полученный опорный план снова проверяется на оптимальность и т.д. Процесс заканчивается за конечное число шагов, причем на последнем шаге либо выявляется неразрешимость задачи (конечного оптимума нет), либо получаются оптимальный опорный план и соответствующее ему оптимальное значение целевой функции.
Признак оптимальности заключается в следующих двух теоремах.
Теорема 1. Если для некоторого вектора, не входящего в базис, выполняется условие:
то можно получить новый опорный план, для которого значение целевой функции будет больше исходного; при этом могут быть два случая:
- если все координаты вектора, подлежащего вводу в базис, неположительны, то задача линейного программирования не имеет решения;
- если имеется хотя бы одна положительная координата у вектора, подлежащего вводу в базис, то можно получить новый опорный план.
Теорема 2. Если для всех векторов выполняется условие 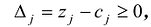
На основании признака оптимальности в базис вводится вектор Ак, давший минимальную отрицательную величину симплекс-разности:
Чтобы выполнялось условие неотрицательности значений опорного плана, выводится из базиса вектор 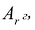
Строка 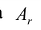
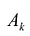
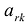
Элементы вводимой строки, соответствующей направляющей строке, в новой симплекс-таблице вычисляются по формулам:
а элементы любой другой i-й строки пересчитываются по формулам:
Значения базисных переменных нового опорного плана (показатели графы «план») рассчитываются по формулам:
Если наименьшее значение Q достигается для нескольких базисных векторов, то чтобы исключить возможность зацикливания (повторения базиса), можно применить следующий способ.
Вычисляются частные, полученные от деления всех элементов строк, давших одинаковое минимальное значение Q на свои направляющие элементы. Полученные частные сопоставляются по столбцам слева направо, при этом учитываются и нулевые, и отрицательные значения. В процессе просмотра отбрасываются строки, в которых имеются большие отношения, и из базиса выводится вектор, соответствующий строке, в которой раньше обнаружится меньшее частное.
Для использования приведенной выше процедуры симплекс -метода к минимизации линейной формы 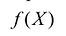
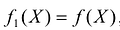
Симплексный метод с искусственным базисом (М-метод)
Симплексный метод с искусственным базисом применяется в тех случаях, когда затруднительно найти первоначальный опорный план исходной задачи линейного программирования, записанной в канонической форме.
М-метод заключается в применении правил симплекс-метода к так называемой М-задаче. Она получается из исходной добавлением к левой части системы уравнений в канонической форме исходной задачи линейного программирования таких искусственных единичных векторов с соответствующими неотрицательными искусственными переменными, чтобы вновь полученная матрица содержала систему единичных линейно-независимых векторов. В линейную форму исходной задачи добавляется в случае её максимизации слагаемое, представляющее собой произведение числа (-М) на сумму искусственных переменных, где М — достаточно большое положительное число.
В полученной задаче первоначальный опорный план очевиден. При применении к этой задаче симплекс-метода оценки А, теперь будут зависеть от числа М. Для сравнения оценок нужно помнить, что М — достаточно большое положительное число, поэтому из базиса будут выводиться в первую очередь искусственные переменные.
В процессе решения M-задачи следует вычеркивать в симплекс-таблице искусственные векторы по мере их выхода из базиса. Если все искусственные векторы вышли из базиса, то получаем исходную задачу. Если оптимальное решение М-задачи содержит искусственные векторы или М-задача неразрешима, то исходная задача также неразрешима.
Путем преобразований число вводимых переменных, составляющих искусственный базис, может быть уменьшено до одной.
Теория двойственности
Любой задаче линейного программирования можно сопоставить сопряженную или двойственную ей задачу. Причем, совместное исследование этих задач дает, как правило, значительно больше информации, чем исследование каждой из них в отдельности.
Любую задачу линейного программирования можно записать в виде:
Первоначальная задача называется исходной или прямой.
Модель двойственной задачи имеет вид:
Переменные двойственной задачи 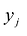
Связь исходной и двойственной задач заключается, в частности, в том, что решение одной из них может быть получено непосредственно из решения другой. Каждая из задач двойственной пары фактически является самостоятельной задачей линейного программирования и может быть решена независимо от другой.
Двойственная задача по отношению к исходной составляется согласно следующим правилам:
- Целевая функция исходной задачи формулируется на максимум, а целевая функция двойственной задачи — на минимум, при этом в задаче на максимум все неравенства в функциональных ограничениях имеют вид <, а в задаче на минимум — вид
- Матрица
, составленная из коэффициентов при неизвестных в системе ограничении исходной задачи, и аналогичная матрица
, в двойственной задаче получаются друг из друга транспонированием;
- Число переменных в двойственной задаче равно числу функциональных ограничений исходной задачи, а число ограничений в системе двойственной задачи — числу переменных в исходной задаче;
- Коэффициентами при неизвестных в целевой функции двойственной задачи являются свободные члены в системе ограничений исходной задачи, а правыми частями в ограничениях двойственной задачи — коэффициенты при неизвестных в целевой функции исходной задачи;
- Каждому ограничению одной задачи соответствует переменная другой задачи: номер переменной совпадает с номером ограничения; при этом ограничению, записанному в виде неравенства <, соответствует переменная, связанная условием неотрицательности.
Если функциональное ограничение исходной задачи является равенством, то соответствующая переменная двойственной задачи может принимать как положительные, так и отрицательные значения.
Математические модели пары двойственных задач могут быть симметричными и несимметричными. В несимметричных двойственных задачах система ограничений исходной задачи задается в виде равенств, а двойственной — в виде неравенств, причем переменные в двойственной задаче могут быть и отрицательными. В симметричных двойственных задачах система ограничений как исходной, так и двойственной задачи задается в виде неравенств, причем на двойственные переменные налагается условие неотрицательности.
где:
Рассмотрим пример, показывающий, как в реальной экономической ситуации появляются взаимно двойственные задачи линейного программирования.
На некотором предприятии после выполнения годового плана возник вопрос: как поступить с остатками сырья? Из оставшегося сырья можно наладить производство продукции и реализовать его или продать сырье.
Предположим, что имеется два вида сырья 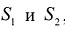
При исследовании первой возможности (наладить выпуск товаров 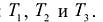
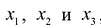
Прибыль, которую получит предприятие от реализации товара, составит:
В интересах предприятия эту прибыль максимизировать.
Это прямая задача.
Объективно обусловленными оценками двойственной задачи 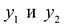
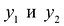
Справедливое требование со стороны продающего предприятия состоит в следующем: если взять сырье, идущее на производство единицы товара 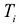
Это требование можно представить в виде системы неравенств:
В левой части каждого неравенства предполагаемая выручка от продажи сырья, необходимого для производства единицы товара 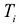
Что касается покупателя, то он заинтересован в минимизации расходов на покупку сырья, т.е. величины
Теоремы двойственности
Теоремы двойственности позволяют установить взаимосвязь между оптимальными решениями пары двойственных задач: можно либо найти оптимальное решение другой задачи, не решая ее, либо установить его отсутствие.
Возможны следующие случаи:
- обе задачи из пары двойственных имеют оптимальные решения;
- одна из задач не имеет решения ввиду неограниченности целевой функции, а другая — ввиду несовместности системы ограничений.
Первая теорема двойственности.
Для двойственных задач линейного программирования имеет место один из взаимоисключающих случаев:
- В прямой и двойственной задачах имеются оптимальные решения, при этом значения целевых функций на оптимальных решениях совпадают:
- В прямой задаче допустимое множество не пусто, а целевая функция на этом множестве не ограничена сверху. При этом у двойственной задачи будет пустое допустимое множество.
- В двойственной задаче допустимое множество не пусто, а целевая функция на этом множестве не ограничена снизу. При этом у прямой задачи допустимое множество оказывается пустым;
- Обе из рассматриваемых задач имеют пустые допустимые множества.
Вторая теорема двойственностн (теорема о дополняющей нежесткости):
Пусть 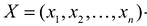
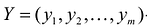
Для того, чтобы они были оптимальными решениями соответствующих взаимодвойственных задач, необходимо и достаточно, чтобы выполнялись следующие соотношения:
Эти условия устанавливают связь между оптимальными значениями прямой и двойственной задач и позволяют, зная решение одной из них, находить решение другой задачи.
Теорема об оценках:
Значения переменных 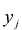
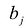
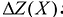
Диапазон изменения компонент вектора В, в котором сохраняется оптимальный базис, называется областью устойчивости оптимальных оценок.
Экономический смысл первой теоремы двойственности следующий. План производства X и набор ресурсов Y оказываются оптимальными тогда и только тогда, когда прибыль от реализации продукции, определенная при известных заранее ценах продукции 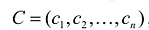
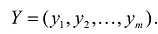
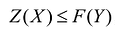
- Дифференциальное исчисление функций одной переменной
- Исследование функции
- Пространство R»
- Неопределённый интеграл
- Линейный оператор — свойства и определение
- Многочлен — виды, определение с примерами
- Квадратичные формы — определение и понятие
- Системы линейных уравнений с примерами
(Идея
симплекс-метода)
Чтобы решить задачу ЛП надо представить
ее в каноническом виде:
(4.1)

С помощью метода Жордана-Гаусса
преобразуем систему (2) и выделим базисные
переменные.
Если ,
то система имеет единственное решение,
подставляем его в целевую функцию (1) и
получаем решение задачи ЛП.
Если ,
то выражаем базисные переменные через
свободные. Пусть базисные переменные
– ,…,
,
свободные
переменные –
.
Получаем преобразованную задачу:
(4.3)

В этой задаче:
-
Система ограничений выражена через
свободные переменные; -
Целевая функция
выражена через свободные переменные; -
Все
;
-
Все
.
Это условие может
быть обеспечено только в том случае,
если система ограничений (4.2) имеет хотя
бы одно неотрицательное решение.
Одно из решений
системы (4.4) получается, если в ней
свободные неизвестные приравнять к 0.
Получаем базисное решение:
Симплекс-метод состоит
в переходе от одного базисного решения
к другому базисному решению, такому,
что целевая функция F
будет увеличиваться. При этом
рассматриваются коэффициенты целевой
функции.
Рассмотрим коэффициенты при свободных
неизвестных в целевой функции:
(4.3)
Возможны следующие случаи:
Случай 1. Среди
коэффициентов целевой функции (3) нет
положительных:
Тогда если увеличивать
любую свободную переменную, то целевая
функция (4.3) будет уменьшаться.
Т.к. ищем максимальное
решение, то уже найденное решение и
будет оптимальным. Но оно может быть не
единственным, если в целевой функции
(4.3) есть коэффициенты, равные 0.
Случай 2. Среди
коэффициентов целевой функции (4.3)
найдется хотя бы один положительный,
например .
Положим в уравнениях
(4.3) и (4.4) все свободные переменные равными
нулю, кроме .
Тогда система (4.4) и
уравнение (4.3) примут вид:
(4.5)

Если увеличивать, то будет
увеличиваться и целевая функция (4.5), но
возможность роста определяется системой
(4.6) и зависит от знаков коэффициентов
.
Возможны следующие случаи:
Случай 1. Предположим,
что среди коэффициентов нет положительных,
т.е., ,тогда
любая переменная,
либо
не изменяется (если),
либо растет (если),
с ростом ,
оставаясь положительной.
Случай 2.
Предположим, что среди коэффициентов
есть положительные, тогда требование
неотрицательности переменных приводит
к неравенствам вида:
.
Это означает, что: 
для тех индексов ,
у которых .
Максимальное значение,
которое может принимать переменная ,
равно минимальному из отношений .
Допустим, что оно
достигается при ,
т.е.:
Элемент называется
разрешающим
элементом.
уходит в разряд
базисных переменных, а
становится
свободной переменной.
Далее целевую функцию
(4.3) и систему (4.4) записываем через новые
свободные переменные.
И снова рассматривается
новая целевая функция, если какую-нибудь
переменную можно увеличить, то весь
процесс повторяется. Если все коэффициенты
при переменных (в целевой функции) не
положительны, то найдено оптимальное
решение.
Этапы решения задачи ЛП симплекс-методом:
1. Записываем систему ограничений в
каноническом виде;
2. Записываем базисное решение;
3. Выбираем переменную из целевой
функции, которую будем увеличивать;
4. Определяем возможность роста переменной
из системы ограничений;
5. Среди уравнений выбираем то, где рост
переменной минимален;
6. Делаем выбранную переменную базисной,
а базисную свободной;
7. Записываем систему ограничений и
целевую функцию через новую свободную
переменную;
8. И далее все повторяется со второго
пункта, пока можно выбирать переменную
из целевой функции.
Пример 4.1. Озеро можно
заселить двумя видами рыб А
и В.
Средняя масса рыбы для вида А
равна 2 кг и для вида В
– 1 кг. В озере имеется два вида пищи: P1
и Р2.
Средние потребности одной рыбы вида А
составляют 1 ед. корма P1
и 3 ед. корма P2
в день. Аналогичные потребности для
рыбы вида В
составляют 2 ед. P1
и 1 ед. P2.
Ежедневный запас пищи поддерживается
на уровне500 ед. P1
и 900 ед. Р2.
Как следует заселить озеро рыбами, чтобы
максимизировать общую массу рыб?
Решение. Для удобства
оформим данные задачи в таблице.
|
Вид пищи |
Кол-во корма для одной |
Ежедневный запас пищи |
|
|
Рыбы |
Рыбы |
||
|
Р1 |
1 |
2 |
500 |
|
Р2 |
3 |
1 |
900 |
|
Вес рыб (кг) |
2 |
1 |
Составим математическую модель задачи.
Введем переменные задачи:
х1
– количество рыб вида А;
x2
– количество рыб вида В.
Составим систему
ограничений:
Зададим целевую
функцию. Масса рыб
→ max.
1.Запишем эту задачу в виде основной
ЗЛП, для этого перейдем от системы
неравенств к равенствам (канонический
вид), для этого введем две дополнительные
переменные:
2. Запишем базисное решение.
F0(0;0;500;900)
= 0.
3. Выбираем
переменную
из целевой функции ,
которую будем увеличивать.
4. Определяем возможность роста переменной
из системы ограничений.
5. Выбираем второе уравнение, т.к. рост
переменной минимален.
6. Делаем выбранную переменную базисной,
а базисную свободной.
7. Записываем систему ограничений и
целевую функцию через новую свободную
переменную.
Подставим
в
и целевую функцию.
8.
Далее все повторяется со второго пункта,
пока можно выбирать переменную из
целевой функции.
2. Запишем базисное решение.
F1
(300;0;200;0) = 0.
3. Выбираем
переменную
из целевой функции ,
которую будем увеличивать.
4. Определяем возможность роста переменной
из системы ограничений.
5. Выбираем первое уравнение, т.к. рост
переменной минимален.
6. Делаем выбранную переменную базисной,
а базисную свободной.
7. Записываем систему ограничений и
целевую функцию через новую свободную
переменную.
Подставим
в
и целевую функцию.
8.
Далее все повторяется со второго пункта,
пока можно выбирать переменную из
целевой функции.
2. Запишем базисное решение.
F1
(260;120;0;0) = 640.
3. Выбираем
переменную из целевой функции ,
которую будем увеличивать. Видим,
что увеличивая любую свободную переменную,
целевая функция будет уменьшаться.
Значит уже найденное решение и будет
оптимальным.
Ответ: Для получения
максимального веса рыб 640кг, следует
заселить 260 рыб вида А
и 120 рыб вида В.
Пример 4.2. Для
изготовления различных изделий А,
В и
С предприятие
использует три различных вида сырья.
Нормы расхода сырья на производство
одного изделия каждого вида, цена одного
изделия А, В и
С, а также общее
количество сырья каждого вида, которое
может быть использовано предприятием,
приведены в таблице.
Составить план производства изделий,
при котором общая стоимость всей
произведенной продукции будет
максимальной.
|
Виды сырья |
Нормы |
Общее количество сырья |
||
|
А |
В |
С |
||
|
I |
18 |
15 |
12 |
360 |
|
II |
6 |
4 |
8 |
192 |
|
III |
5 |
3 |
3 |
180 |
|
Цена |
9 |
10 |
16 |
Решение: Составим
математическую модель. Обозначим:
–выпуск изделий
вида А;
–выпуск изделий вида
В;
–выпуск изделий вида
С.
Запишем систему ограничений:
Общая стоимость
произведенных товаров составляет: .
По экономическому
содержанию переменные ,
,
могут принимать
только неотрицательные значения.
1.Запишем эту задачу
в виде основной ЗЛП, для этого перейдем
от системы неравенств к равенствам
(канонический вид), для этого введем три
дополнительные переменные:
2. Запишем базисное решение.
F0(0;0;0;120;96;180)
= 0.
3. Выбираем
переменную
из целевой
функции ,
которую будем увеличивать.
4. Определяем возможность роста переменной
из системы ограничений.
5. Выбираем второе уравнение, т.к. рост
переменной минимален.
6. Делаем выбранную переменную базисной,
а базисную свободной.
7. Записываем систему ограничений и
целевую функцию через новую свободную
переменную.
Подставим
в ,
и целевую функцию.
8.
Далее все повторяется со второго пункта,
пока можно выбирать переменную из
целевой функции.
2. Запишем базисное решение.
F1(0;0;24;24;0;108)
= 384.
3. Выбираем
переменную
из целевой
функции ,
которую будем увеличивать.
4. Определяем возможность роста переменной
из системы ограничений.
5. Выбираем первое уравнение, т.к. рост
переменной минимален.
6. Делаем выбранную переменную базисной,
а базисную свободной.
7. Записываем систему ограничений и
целевую функцию через новую свободную
переменную.
Подставим
в ,
и целевую функцию.
8.
Далее все повторяется со второго пункта,
пока можно выбирать переменную из
целевой функции.
2. Запишем базисное решение.
F2(0;8;20;0;0;96)
= 400.
3. Выбираем
переменную из целевой функции ,
которую будем увеличивать. Видим,
что увеличивая любую свободную переменную,
целевая функция будет уменьшаться.
Значит уже найденное решение и будет
оптимальным.
Ответ: Для получения
максимальной стоимости
всей произведенной продукции
400€,
необходимо производить 0 изделий вида
А,
8 изделий вида В
и 20 изделие вида С.
-
ТАБЛИЧНАЯ ИНТЕРПРЕТАЦИЯ СИМПЛЕКСНОГО
МЕТОДА
Рассмотрим решение задач симплексным
методом используя построение симплексных
таблиц.
Пример 5.1. На приобретение
мебели для офиса предприятием было
выделено средств на сумму 70 тыс. руб.
Мебель должна быть размещена на общей
площади, не превышающей 100 м². Предприятие
может заказать мебель двух типов: А
и В,
стоимостью 15 тыс. руб. и 10 тыс. руб.
соответственно. Мебели типа А
требуется 12 м² площади (с учетом проходов),
мебели типа В
– 14 м² (с учетом проходов). Доход от
эксплуатации мебели типа А
составляет 18 тыс. руб. в месяц, В
– 12 тыс. руб. в месяц.
Найти оптимальный вариант приобретения
мебели, обеспечивающей максимум прибыли
для данного предприятия.
Решение:
Составим математическую модель задачи.
Введем переменные задачи:
х1
– количество мебели вида А,
x2
– количество мебели вида В.
Составим систему ограничений:
Зададим целевую функцию:
F(x)
= 18x1
+ 12x2
→ max
Решение. Запишем
данную задачу в форме основной задачи
линейного программирования. Для этого
перейдем от ограничений-неравенств к
ограничениям-равенствам. Введем две
дополнительные переменные, в результате
чего ограничения запишутся в виде
системы уравнений
где,
x3
— остаток
выделенных средств (тыс. руб.) на
приобретение мебели,
x4
— остаток
площади (м²) на которой размещается
мебель.
F(x)
= 18∙x1
+ 12∙x2
+ 0∙x3
+ 0∙x4→
max
— данная задача
представлена
в каноническом виде;
—
система
уравнений приведена к единичному базису;
— каждое уравнение системы ограничений
содержит базисную переменную;
— правые части всех ограничений
неотрицательны.
Строим симплекс – таблицу, имеющую
следующий вид:
|
Б.П. |
С |
b |
Ө |
||||
|
x1 |
x2 |
… |
… |
||||
|
… |
|||||||
|
… |
|||||||
|
∆к |
где
Б.П. – столбец базисных переменных
С
– содержит коэффициенты при базисных
переменных в целевой функции;
b
– столбец свободных членов;
∆к – индексная строка. По ее данным
определяется, является ли решение
оптимальным.
Заполним таблицу по данным задачи.
Вводим коэффициенты
из системы ограничений и заполняем
индексную строку коэффициентами целевой
функции, взятыми с противоположными
знаками.
В столбец Б.П. записываем
базисные (новые введенные) переменные
x3
, x4
.
В столбце С
и над переменными записываем коэффициенты
переменных целевой функции.
|
Б.П. |
С |
18 |
12 |
0 |
0 |
b |
Ө |
|
x1 |
x2 |
x3 |
x4 |
||||
|
x3 |
0 |
15 |
10 |
1 |
0 |
70 |
|
|
x4 |
0 |
12 |
14 |
0 |
1 |
100 |
|
|
∆к |
-18 |
-12 |
0 |
0 |
0 |
Проверим данный план на оптимальность.
Если целевая функция исследуется как
максимум, то в оптимальном плане все
оценки должны быть ≥ 0. Если индексная
строка не отвечает критериям оптимальности,
то план можно улучшить. У нас все оценки
отрицательны.
Используем метод Жордана – Гаусса.
Сначала выбирается разрешающий столбец
и разрешающаяся строка, на их пересечении
– разрешающий элемент.
Для выбора разрешающегося
столбца необходимо среди всех отрицательных
оценок индексной строки выбрать
наименьшее отрицательное число. В нашем
случае это -18. Если окажется, что наименьших
равных между собой элементов индексной
строки имеется несколько, то рекомендуется
выбрать первый (левый) элемент. Если в
разрешающем столбце в некоторой таблице
все коэффициенты не положительны, то
целевая функция неограничена на множестве
допустимых планов и задачу рушить
нельзя.
Разрешающий столбец показывает, какая
переменная на следующем этапе перейдет
из свободных в базисные.
Для выбора разрешающей
строки в столбцах Ө
составляем следующие отношения ,
где ai
— коэффициенты (берем только положительные)
при xi
в разрешающей строке. Т.е. Элементы
столбца свободных членов симплексной
таблицы делят на соответствующие
положительные элементы разрешающего
столбца. Выбираем минимальное значение
из данных отношений Ө
= {
}
= .
Данная строка определяет переменную,
которая на следующем этапе выйдет из
базиса и станет свободной.
Разрешающие столбец и строку обозначим
стрелками.
В нашем случае вместо
переменной x3
в базисе будет
переменная x1.
На пересечении разрешающего столбца и
строки получаем разрешающий элемент.
|
Б.П. |
С |
18 |
12 |
0 |
0 |
b |
Ө |
|
x1 |
x2 |
x3 |
x4 |
||||
|
x3 |
0 |
15 |
10 |
1 |
0 |
70 |
|
|
x4 |
0 |
12 |
14 |
0 |
1 |
100 |
|
|
∆к |
— |
-12 |
0 |
0 |
0 |
После выбора
разрешающего элемента, строится новая
симплексная таблица следующим образом:
из базиса выводится переменная разрешающей
строки, а в базис вводится переменная
разрешающего столбца и заполняется
вновь столбец С.
Разделив все элементы разрешающей
строки предыдущей таблицы на разрешающий
элемент, результаты деления вносят в
строку следующей таблицы, соответствующую
введенной в базис переменной. На месте
разрешающего элемента в следующей
таблице будет стоять единица, а в
остальных клетках разрешающего столбца,
включая клетку индексной строки, стоят
нули.
|
Б.П. |
С |
18 |
12 |
0 |
0 |
b |
|
x1 |
x2 |
x3 |
x4 |
|||
|
x1 |
18 |
1 |
|
|
0 |
|
|
x4 |
0 |
0 |
||||
|
∆к |
0 |
Oстальные элементы рассчитываются по
методу Жордана –Гаусса.
Чтобы заполнить
вторую строку, соответствующую базисной
переменной x4,
необходимо все элементы преобразованной
строки умножить на коэффициент, стоящий
на пересечении второй строки и разрешающего
столбца предыдущей таблицы и вычесть
из соответствующих элементов второй
строки этой же таблицы, а результат
записать во вторую строку новой таблицы
и т.д.
|
Б.П. |
С |
18 |
12 |
0 |
0 |
b |
|
x1 |
x2 |
x3 |
x4 |
|||
|
x1 |
18 |
1 |
|
|
0 |
|
|
x4 |
0 |
0 |
6 |
|
1 |
44 |
|
∆к |
0 |
0 |
|
0 |
84 |
Полученный план проверяем на оптимальность.
Получаем, F
= 84. Опорное решение
Х = (;
0; 0; 44) является оптимальным, т.к. для всех
векторов условий оценки в задаче на
максимум неотрицательны. Однако данное
решение не единственное, т.к. вектор
x2,
не входящий в базис, имеет нулевую
оценку. Этот вектор нужно ввести в базис
опорного решения, чтобы получить еще
одно оптимальное решение.
|
Б.П. |
С |
18 |
12 |
0 |
0 |
b |
Ө |
|
x1 |
x2 |
x3 |
x4 |
||||
|
x1 |
18 |
1 |
|
|
0 |
|
7 |
|
x4 |
0 |
0 |
6 |
|
1 |
44 |
|
|
∆к |
0 |
0 |
|
0 |
84 |
Рассчитываем по методу Жордана –Гаусса
последнюю симплекс таблицу.
|
Б.П. |
С |
18 |
12 |
0 |
0 |
b |
|
x1 |
x2 |
x3 |
x4 |
|||
|
x2 |
12 |
|
1 |
|
0 |
7 |
|
x4 |
0 |
18 |
0 |
|
1 |
2 |
|
∆к |
0 |
0 |
|
0 |
84 |
Получаем: F
= 84; Х
= (0; 7; 0; 2).
Ответ: Для того чтобы
обеспечить максимальную прибыль 84 тыс.
руб., предприятию можно приобрести
только 7 шт. мебели вида В.
Рассмотрим решение примеров 4.1. и 4.2. с
помощью симплексных таблиц.
Пример 5.2. (решение
примера 4.1.)
→max.
Перейдя от системы
неравенств к равенствам, получаем:
Решение.
Таблица 1
|
Б.П. |
С |
2 |
1 |
0 |
0 |
b |
Ө |
|
x1 |
x2 |
x3 |
x4 |
||||
|
x3 |
0 |
1 |
2 |
1 |
0 |
500 |
500 |
|
x4 |
0 |
3 |
1 |
0 |
1 |
900 |
3 |
|
∆к |
— |
-1 |
0 |
0 |
0 |
Таблица 2
|
Б.П. |
С |
2 |
1 |
0 |
0 |
b |
Ө |
|
x1 |
x2 |
x3 |
x4 |
||||
|
x3 |
0 |
0 |
|
1 |
|
200 |
1 |
|
x1 |
2 |
1 |
|
0 |
|
300 |
900 |
|
∆к |
0 |
|
0 |
|
600 |
Таблица 3
|
Б.П. |
С |
2 |
1 |
0 |
0 |
b |
|
x1 |
x2 |
x3 |
x4 |
|||
|
x2 |
1 |
0 |
1 |
|
|
120 |
|
x1 |
2 |
1 |
0 |
|
|
260 |
|
∆к |
0 |
0 |
|
|
640 |
Ответ: F(x)
= 640, X
= (260, 120, 0, 0), т.е. для
получения максимального веса рыб 640 кг,
следует заселить
260 рыб вида А
и 120 рыб вида В.
Пример 5.3. (решение
примера 4.2.)
→max
Перейдя от системы
неравенств к равенствам, получаем:
Решение.
Таблица 1
|
Б.П. |
С |
9 |
10 |
16 |
0 |
0 |
0 |
b |
Ө |
|
x1 |
x2 |
x3 |
x4 |
x5 |
x6 |
||||
|
x4 |
0 |
6 |
5 |
4 |
1 |
0 |
0 |
120 |
30 |
|
x5 |
0 |
3 |
2 |
4 |
0 |
1 |
0 |
96 |
2 |
|
x6 |
0 |
5 |
3 |
3 |
0 |
0 |
1 |
180 |
60 |
|
∆к |
-9 |
-10 |
— |
0 |
0 |
0 |
Таблица 2
|
Б.П. |
С |
9 |
10 |
16 |
0 |
0 |
0 |
b |
Ө |
|
x1 |
x2 |
x3 |
x4 |
x5 |
x6 |
||||
|
x4 |
0 |
3 |
3 |
0 |
1 |
-1 |
0 |
24 |
8 |
|
x3 |
16 |
|
|
1 |
0 |
|
0 |
24 |
48 |
|
x6 |
0 |
|
|
0 |
0 |
|
1 |
108 |
72 |
|
∆к |
3 |
— |
0 |
0 |
4 |
0 |
Таблица 3
|
Б.П. |
С |
9 |
10 |
16 |
0 |
0 |
0 |
b |
|
x1 |
x2 |
x3 |
x4 |
x5 |
x6 |
|||
|
x2 |
10 |
1 |
1 |
0 |
|
|
0 |
8 |
|
x3 |
16 |
|
0 |
1 |
|
|
0 |
20 |
|
x6 |
0 |
|
0 |
0 |
|
|
1 |
96 |
|
∆к |
5 |
0 |
0 |
|
|
0 |
400 |
Ответ: Для получения
максимальной стоимости
всей произведенной продукции
400€,
необходимо производить 0 изделий вида
А,
8 изделий вида В
и 20 изделие вида С.
Решение задачи линейного программирования методом Гомори
Введение
Задачи, которые мы решали ранее всегда давали целочисленный ответ. Это происходило
потому, что исходные данные были подобраны специальным образом. Но так бывает не всегда.
Гораздо чаще в ответе получаются дробные величины — например, нужно произвести 2,5 единицы
изделия A и 3,44 единицы изделия B. Допустимо ли такое решение? Тут все зависит от
условий задачи. Если мы производим, например, муку и сахар в килограммах — такое решение
вполне допустимо. 2,5 единицы изделия A — это 2 килограмма 500 грамм муки, а 3,44 единицы
изделия B это 3 килограмма 440 грамм сахара. Однако представьте, что изделие A — это компьютеры,
а изделие B — это MP3-плееры. Как можно произвести 3,44 единицы MP3-плеера? Очевидно, что
никак. В таких случаях говорят, что необходимо решить задачу целочисленного
линейного программирования, подразумевая, что в ответе обязательно должны получиться
целые числа.
Для решения целочисленных задач был разработан специальный метод под названием Метод
Гомори. На самом деле, метод Гомори это всего лишь «надстройка» над обычным симплекс-методом,
который мы изучили в прошлых главах. Идея метода Гомори заключается в том, что можно решить
задачу обычным симплекс-методом, получив (возможно) нецелочисленное решение, а потом для каждой
нецелочисленной переменной добавить «поправочное» ограничение, которое во-первых, сделает эту
переменную целочисленной, а во-вторых, минимальным образом повлияет на значение целевой функции.
Полезная страница? Сохрани или расскажи друзьям
Алгоритм метода Гомори
Итак, понятно, что нам необходимо сначала просто решить задачу симплекс-методом, а затем для
каждой нецелочисленной переменной в решении немного «подправить» ее значение. То есть, схема метода
Гомори примерно следующая:
- Решить исходную производственную задачу обычным симплекс-методом;
- Убедиться, что ответ получился нецелочисленным. Если он целочисленный, то задача решена;
- Умножить значения в последней строке (строка F) на -1;
- Пока в ответе остались нецелочисленные переменные, делать следующее:
- Среди нецелочисленных значений в получившемся решении выбрать переменную, для которой
необходимо составить дополнительное ограничение (как это сделать будет объяснено в нижеприведенном
примере); - К исходной задаче добавить специальным образом составленное ограничение для выбранной переменной
(опять же, в примере будет показано, как именно это сделать). Это приведет к появлению еще одной
вспомогательной переменной; - К полученной задаче применить один этап симплекс-метода, причем убрать появившуюся вспомогательную
переменную, и добавить какую-то из исходных (какую именно также будет объяснено в примере). - Предыдущий шаг (шаг 4) необходимо выполнять, пока все решение не станет целочисленным. Метод Гомори
гарантирует, что на каком-либо шаге это точно произойдет.
Решение производственной задачи методом Гомори
Решим методом Гомори ту же самую производственную задачу, которую решали ранее Симплекс-методом,
но изменим в ней одно число — чтобы решение с использованием Симплекс-метода получилось нецелочисленным:
| Ресурс | Изделие A | Изделие B | Изделие C | Сколько ресурса на складах |
| R1 | 1 | 2 | 3 | 35 |
| R2 | 4 | 3 | 2 | 45 |
| R3 | 3 | 1 | 1 | 40 |
| Прибыль | 4 | 5 | 6 |
Как обычно, запишем систему ограничений нашей задачи и целевую функцию в виде неравенств.
Обозначим за $x_A, x_B$ и $x_C$ количество производимых изделий A, B и C, соответственно. Так
как весь процесс был подробно описан ранее, приведем только результат:
$$begin{array}{l}
left{ {begin{array}{*{20}{c}}
{{x_A} + 2{x_B} + 3{x_C} le 35}\
{4{x_A} + 3{x_B} + 2{x_C} le 45}\
{3{x_A} + {x_B} + {x_C} le 40}
end{array}} right.\
{x_A},{x_B},{x_C} ge 0\
F({x_A},{x_B},{x_C}) = 4{x_A} + 5{x_B} + 6{x_C} to max
end{array}$$
Чтобы начать решать производственную задачу симплекс-методом, необходимо наши неравенства
превратить в равенства. Для этого добавим к каждому из ограничений дополнительные неотрицательные
переменные ${x_1},{x_2},{x_3}$:
$$begin{array}{l}
left{ {begin{array}{*{20}{c}}
{{x_A} + 2{x_B} + 3{x_C} + {x_1} = 35}\
{4{x_A} + 3{x_B} + 2{x_C} + {x_2} = 45}\
{3{x_A} + {x_B} + {x_C} + {x_3} = 40}
end{array}} right.\
{x_A},{x_B},{x_C},{x_1},{x_2},{x_3} ge 0\
F({x_A},{x_B},{x_C}) = 4{x_A} + 5{x_B} + 6{x_C} to max
end{array}$$
Как и в прошлых разделах, найдем «начальное решение». В производственной задаче в качестве
начального решения лучше всего выбрать такое, когда не производится ни одной единицы товара, то
есть, $x_A,x_B,x_C=0$. При этом исходя из ограничений, получаем $x_1=35,x_2=45,x_3=40$. Такое решение
можно записать в виде $(0,0,0,35,45,40)$ — то есть, в скобках просто последовательно перечислить
переменные (сначала «основные», а потом «введенные нами»).
Запишем симплекс-таблицу. Как это делается было подробно объяснено тут.
| $x_A$ | $x_B$ | $x_C$ | $x_1$ | $x_2$ | $x_3$ | B | |
| $x_1$ | 1 | 2 | 3 | 1 | 0 | 0 | 35 |
| $x_2$ | 4 | 3 | 2 | 0 | 1 | 0 | 45 |
| $x_3$ | 3 | 1 | 1 | 0 | 0 | 1 | 40 |
| F | -4 | -5 | -6 | 0 | 0 | 0 | 0 |
Итерация 1
Прежде чем выполнять очередную итерацию, необходимо проверить, может быть, наше решение
уже оптимально, и ничего делать не нужно? Для этого необходимо проверить, есть ли в последней
строке отрицательные элементы. Есть. Их три. Следовательно, наше решение не оптимально.
Выберем самое большое по модулю отрицательное значение -6 в столбце $x_C$, эту переменную необходимо
добавить к нашему базису (то есть, ввести ее в одну из строк слева). Но тогда одну из
переменных текущего базиса ($x_1,x_2,x_3$) необходимо убрать. Чтобы узнать, какую,
необходимо найти для каждой базисной переменной (каждой строки) отношение свободного
члена (значения в столбце B) к коэффициенту в строке $x_C$ (переменной, которую, как мы
решили выше, необходимо ввести в базис). Обратите внимание, что это отношение должно существовать,
и оно должно быть положительно. Если это не так, мы просто пропускаем соответствующую строку
| $x_A$ | $x_B$ | $x_C$ | $x_1$ | $x_2$ | $x_3$ | B | $frac{B}{x_C}$ | |
| $x_1$ | 1 | 2 | 3 | 1 | 0 | 0 | 35 | $frac{35}{3}approx11,67$ |
| $x_2$ | 4 | 3 | 2 | 0 | 1 | 0 | 45 | $frac{45}{2}=22,5$ |
| $x_3$ | 3 | 1 | 1 | 0 | 0 | 1 | 40 | $frac{40}{1}=40$ |
| F | -4 | -5 | -6 | 0 | 0 | 0 | 0 |
Мы нашли отношения для каждой строки, и для первой строки отношение получилось наименьшим.
Поэтому именно данную строку (то есть, переменную $x_1$) необходимо убрать из базиса, заменив,
как мы определили выше, переменной $x_C$. Как это сделать? Прежде всего, найдем значение
элемента на пересечении найденной строки и найденного столбца. Он равен 3 (в таблице выше он
подчеркнут). И нам нужно всю найденную строку на этот элемент поделить:
| $x_A$ | $x_B$ | $x_C$ | $x_1$ | $x_2$ | $x_3$ | B | |
| $frac{1}{3}$ | $frac{2}{3}$ | 1 | $frac{1}{3}$ | 0 | 0 | $frac{35}{3}$ | |
| $x_2$ | 4 | 3 | 2 | 0 | 1 | 0 | 45 |
| $x_3$ | 3 | 1 | 1 | 0 | 0 | 1 | 40 |
| F | -4 | -5 | -6 | 0 | 0 | 0 | 0 |
Обратите внимание, из первой строки исчезло название строки — $x_1$. Это потому, что
$x_1$ — больше не базисная переменная. Она была бы базисной, если бы был столбец $x_1$,
в котором была бы одна единица, а остальные нули. Но такого столбца больше нет. Теперь
первая строка не выражает никакой базисной переменной. Нам же необходимо, чтобы базисной
стала переменная $x_C$. Первое требование к базисным переменным для нее выполняется —
есть столбец $x_C$, и у него в первой строке число 1. Но вот остальные числа не равны
нулю. Так давайте их сделаем такими.
- Чтобы во второй строке, в столбце $x_C$ число 2 превратить в ноль, вычтем из второй строки две первых.
- Чтобы в третьей строке, в столбце $x_C$ число 1 превратить в ноль, вычтем из третьей строки первую.
- Чтобы в последней строке, в столбце $x_C$ число -6 превратить в ноль, добавим к последней строке шесть первых.
| $x_A$ | $x_B$ | $x_C$ | $x_1$ | $x_2$ | $x_3$ | B | |
| $x_C$ | $frac{1}{3}$ | $frac{2}{3}$ | 1 | $frac{1}{3}$ | 0 | 0 | $frac{35}{3}$ |
| $x_2$ | $4-2cdotfrac{1}{3}$ | $3-2cdotfrac{2}{3}$ | $2-2cdot1$ | $0-2cdotfrac{1}{3}$ | $1-2cdot0$ | $0-2cdot0$ | $45-2cdotfrac{35}{3}$ |
| $x_3$ | $3-frac{1}{3}$ | $1-frac{2}{3}$ | 1-1 | $0-frac{1}{3}$ | 0-0 | 1-0 | $40-frac{35}{3}$ |
| F | $-4+6cdotfrac{1}{3}$ | $-5+6cdotfrac{2}{3}$ | $-6+6cdot1$ | $0+6cdotfrac{1}{3}$ | $0+6cdot0$ | $0+6cdot0$ | $0+6cdotfrac{35}{3}$ |
Проводим математические действия и получаем итоговую таблицу.
| $x_A$ | $x_B$ | $x_C$ | $x_1$ | $x_2$ | $x_3$ | B | |
| $x_C$ | $frac{1}{3}$ | $frac{2}{3}$ | 1 | $frac{1}{3}$ | 0 | 0 | $frac{35}{3}$ |
| $x_2$ | $frac{10}{3}$ | $frac{5}{3}$ | 0 | $-frac{2}{3}$ | $1$ | $0$ | $frac{65}{3}$ |
| $x_3$ | $frac{8}{3}$ | $frac{1}{3}$ | 0 | $-frac{1}{3}$ | 0 | 1 | $frac{85}{3}$ |
| F | -2 | -1 | 0 | 2 | 0 | 0 | 70 |
Теперь первая строка у нас выражает базисную переменную $x_C$, так как действительно,
в столбце $x_C$ одно значение равно 1, а остальные — 0. Итерация выполнена.
Итерация 2
Прежде чем выполнять очередную итерацию, необходимо проверить, оптимально ли наше решение?
В последней строке есть отрицательные элементы, следовательно, наше решение не оптимально.
Выберем самое большое по модулю отрицательное значение -2 в столбце $x_A$, эту переменную необходимо
добавить к нашему базису, а одну из переменных текущего базиса ($x_C,x_2,x_3$) необходимо
убрать. Чтобы узнать, какую, необходимо найти для каждой базисной переменной отношение свободного
члена к коэффициенту в строке $x_A$ (переменной, которую, как мы решили выше, необходимо ввести в базис).
Обратите внимание, что это отношение должно существовать, и оно должно быть положительно. Если это
не так, мы просто пропускаем соответствующую строку
| $x_A$ | $x_B$ | $x_C$ | $x_1$ | $x_2$ | $x_3$ | B | $frac{B}{x_A}$ | |
| $x_C$ | $frac{1}{3}$ | $frac{2}{3}$ | 1 | $frac{1}{3}$ | 0 | 0 | $frac{35}{3}$ | $frac{35}{3}:frac{1}{3}=35$ |
| $x_2$ | $frac{10}{3}$ | $frac{5}{3}$ | 0 | $-frac{2}{3}$ | 1 | 0 | $frac{65}{3}$ | $frac{65}{3}:frac{10}{3}=frac{65}{10}=6,5$ |
| $x_3$ | $frac{8}{3}$ | $frac{1}{3}$ | 0 | $-frac{1}{3}$ | 0 | 1 | $frac{85}{3}$ | $frac{85}{3}:frac{8}{3}=frac{85}{8}=10,625$ |
| F | -2 | -1 | 0 | 2 | 0 | 0 | 70 |
Мы нашли отношения для каждой строки, и для переменной $x_2$ отношение получилось наименьшим.
Поэтому именно данную переменную необходимо убрать из базиса, заменив,
как мы определили выше, переменной $x_A$. Прежде всего, найдем значение элемента на пересечении
найденной строки и найденного столбца. Он равен $frac{10}{3}$. И нам нужно всю найденную строку
на этот элемент поделить:
| $x_A$ | $x_B$ | $x_C$ | $x_1$ | $x_2$ | $x_3$ | B | |
| $x_C$ | $frac{1}{3}$ | $frac{2}{3}$ | 1 | $frac{1}{3}$ | 0 | 0 | $frac{35}{3}$ |
| 1 | $frac{1}{2}$ | 0 | $-frac{1}{5}$ | $frac{3}{10}$ | 0 | $frac{65}{10}$ | |
| $x_3$ | $frac{8}{3}$ | $frac{1}{3}$ | 0 | $-frac{1}{3}$ | 0 | 1 | $frac{85}{3}$ |
| F | -2 | -1 | 0 | 2 | 0 | 0 | 70 |
Из второй строки исчезло название строки — $x_2$. Это потому, что
$x_2$ — больше не базисная переменная. Нам же необходимо, чтобы базисной
стала переменная $x_A$. Первое требование к базисным переменным для нее выполняется —
есть столбец $x_A$, и у него во второй строке число 1. Но вот остальные числа не равны
нулю. Так давайте их сделаем такими.
- Чтобы в первой строке, в столбце $x_A$ число $frac{1}{3}$ превратить в ноль, вычтем из первой строки вторую, умноженную на $frac{1}{3}$.
- Чтобы в третьей строке, в столбце $x_A$ число $frac{8}{3}$ превратить в ноль, вычтем из третьей строки вторую, умноженную на $frac{8}{3}$
- Чтобы в последней строке, в столбце $x_A$ число -2 превратить в ноль, добавим к последней строке две вторых.
| $x_A$ | $x_B$ | $x_C$ | $x_1$ | $x_2$ | $x_3$ | B | |
| $x_C$ | $frac{1}{3}-frac{1}{3}cdot1$ | $frac{2}{3}-frac{1}{3}cdotfrac{1}{2}$ | $1-frac{1}{3}cdot0$ | $frac{1}{3}-frac{1}{3}cdot(-frac{1}{5})$ | $0-frac{1}{3}cdotfrac{3}{10}$ | 0 | $frac{35}{3}-frac{1}{3}cdotfrac{65}{10}$ |
| 1 | $frac{1}{2}$ | 0 | $-frac{1}{5}$ | $frac{3}{10}$ | 0 | $frac{65}{10}$ | |
| $x_3$ | $frac{8}{3}-frac{8}{3}cdot1$ | $frac{1}{3}-frac{8}{3}cdotfrac{1}{2}$ | $0-frac{1}{3}cdot0$ | $-frac{1}{3}-frac{8}{3}cdot(-frac{1}{5})$ | $0-frac{8}{3}cdotfrac{3}{10}$ | $1-frac{8}{3}cdot0$ | $frac{85}{3}-frac{8}{3}cdotfrac{65}{10}$ |
| F | $-2+2cdot1$ | $-1+2cdotfrac{1}{2}$ | $0+2cdot0$ | $2+2cdot(-frac{1}{5})$ | $0+2cdotfrac{3}{10}$ | $0+2cdot0$ | $70+2cdotfrac{65}{10}$ |
Проводим математические действия и получаем итоговую таблицу.
| $x_A$ | $x_B$ | $x_C$ | $x_1$ | $x_2$ | $x_3$ | B | |
| $x_C$ | 0 | $frac{1}{2}$ | 1 | $frac{2}{5}$ | $-frac{1}{10}$ | 0 | $frac{19}{2}$ |
| $x_A$ | 1 | $frac{1}{2}$ | 0 | $-frac{1}{5}$ | $frac{3}{10}$ | 0 | $frac{13}{2}$ |
| $x_3$ | 0 | -1 | 0 | $frac{1}{5}$ | $-frac{4}{5}$ | 1 | 11 |
| F | 0 | 0 | 0 | $frac{8}{5}$ | $frac{3}{5}$ | 0 | 83 |
Теперь вторая строка у нас выражает базисную переменную $x_A$, так как действительно,
в столбце $x_A$ одно значение равно 1, а остальные — 0. Итерация выполнена.
Итерация 3
Прежде чем выполнять очередную итерацию, необходимо проверить, оптимально ли наше решение?
В последней строке нет отрицательных элементов, следовательно, наше решение оптимально. Если записать
значения интересующих нас переменных $x_A,x_B,x_C$, то получим, что $x_A=frac{13}{2};x_B=0;x_C=frac{19}{2}$.
Значения получились нецелые. Следовательно, необходимо применить метод Гомори. По методу Гомори
нам необходимо добавить еще одно ограничение к нашей задаче. Сперва необходимо определить, для какой
нецелой переменной мы будем составлять дополнительное ограничение. У нас две нецелых переменных — $x_C$ и $x_A$.
Чтобы определить, для какой именно, необходимо найти дробные части чисел, стоящих в соответствующих строках, столбце B.
- Число, стоящее в строке $x_C$, столбце B равно $frac{19}{2}$. Можно записать его как $9frac{1}{2}$. Его
дробная часть равна $frac{1}{2}$ - Число, стоящее в строке $x_A$, столбце B равно $frac{13}{2}$. Можно записать его как $6frac{1}{2}$. Его
дробная часть равна $frac{1}{2}$
Среди данных дробных частей нужно найти наибольшую, и именно для этой переменной мы будем составлять
дополнительное ограничение. Однако у нас дробные части получились равными, поэтому просто берем первую — $x_C$.
Составляем для переменной $x_C$ ограничение. Оно будет иметь вид:
$$q_C-q_{CA}cdot{x_A}-q_{CB}cdot{x_B}-q_{CC}cdot{x_C}-q_{C1}cdot{x_1}-q_{C2}cdot{x_2}-q_{C3}cdot{x_3}leq0$$
Для любой другой переменной будет точно такая же формула, только в ней индексы у коэффициентов $q$ будут не
$C$, а какие-то другие
Разберемся что тут что. Очевидно, что $x_A,x_B,x_C,x_1,x_2,x_3$ — переменные нашей задачи. Для нахождения
коэффициентов $q$ будем использовать числа первой строки, так как именно там содержатся данные по нашей
переменной $x_C$. Значение $q_C$ это просто дробная часть числа в строке $x_C$ и столбце свободных членов B. Значение
этой клетки равно $frac{19}{2}=9frac{1}{2}$. Очевидно, что целая часть здесь 9, а дробная $frac{1}{2}$.
Следовательно, $q_C=frac{1}{2}$.
- Значение коэффициента $q_{CA}$ это дробная часть числа, находящегося в строке $x_C$, столбце $x_A$.
Там находится число 0, и очевидно, что его дробная часть также равна 0. $q_{CA}=0$ - Значение коэффициента $q_{CB}$ это дробная часть числа, находящегося в строке $x_C$, столбце $x_B$.
Там находится число $frac{1}{2}$, и очевидно, что его дробная часть также равна $frac{1}{2}$. $q_{CB}=frac{1}{2}$ - Значение коэффициента $q_{CC}$ это дробная часть числа, находящегося в строке $x_C$, столбце $x_C$.
Там находится число 1, и очевидно, что его дробная часть равна 0. $q_{CC}=0$ - Значение коэффициента $q_{C1}$ это дробная часть числа, находящегося в строке $x_C$, столбце $x_1$.
Там находится число $frac{2}{5}$, и очевидно, что его дробная часть также равна $frac{2}{5}$. $q_{C1}=frac{2}{5}$ - Значение коэффициента $q_{C2}$ это дробная часть числа, находящегося в строке $x_C$, столбце $x_2$.
Там находится число $-frac{1}{10}$. Для отрицательных чисел дробная часть определяется немного не так, как
для положительных, и равна разности нашего числа и следующего целого отрицательного числа, меньшего, чем нашего.
Для числа $-frac{1}{10}$ следующее меньшее целое отрицательное число это $-1$, и, следовательно, $q_{С2}=-frac{1}{10}-(-1)=frac{9}{10}$ - Значение коэффициента $q_{C3}$ это дробная часть числа, находящегося в строке $x_C$, столбце $x_3$.
Там находится число 0, и очевидно, что его дробная часть также равна 0. $q_{C3}=0$
Подставив найденные коэффициенты, получим еще одно ограничение:
$$frac{1}{2}-frac{1}{2}cdot{x_B}-frac{2}{5}cdot{x_1}-frac{9}{10}cdot{x_2}leq0$$
Однако это ограничение в виде неравенства, а у нас все ограничения в виде равенств. Поэтому превратим данное
ограничение в равенство, добавив еще одну неотрицательную переменную $x_4$:
$$-frac{1}{2}cdot{x_B}-frac{2}{5}cdot{x_1}-frac{9}{10}cdot{x_2}+x_4=-frac{1}{2}$$
Занесем данное ограничение еще одной строкой в симплекс-таблицу, кроме того, не забудем, что появился новый
столбец $x_4$, а также изменим знак последней строки — так всегда делается при начале работы по методу Гомори:
| $x_A$ | $x_B$ | $x_C$ | $x_1$ | $x_2$ | $x_3$ | $x_4$ | B | |
| $x_C$ | 0 | $frac{1}{2}$ | 1 | $frac{2}{5}$ | $-frac{1}{10}$ | 0 | 0 | $frac{19}{2}$ |
| $x_A$ | 1 | $frac{1}{2}$ | 0 | $-frac{1}{5}$ | $frac{3}{10}$ | 0 | 0 | $frac{13}{2}$ |
| $x_3$ | 0 | -1 | 0 | $frac{1}{5}$ | $-frac{4}{5}$ | 1 | 0 | 11 |
| $x_4$ | 0 | $-frac{1}{2}$ | 0 | $-frac{2}{5}$ | $-frac{9}{10}$ | 0 | 1 | $-frac{1}{2}$ |
| F | 0 | 0 | 0 | $-frac{8}{5}$ | $-frac{3}{5}$ | 0 | 0 | -83 |
Теперь продолжаем работать по практически обычному симплекс-методу. Правда теперь будет отличаться правило
определения того, какую переменную необходимо убрать из базиса, а какую оставить. По правилам метода Гомори,
убирать надо всегда только что введенную переменную, то есть, $x_4$. А вот чтобы определить, какую необходимо ввести,
необходимо найти частные от деления значений последней строки (F) на значения предпоследней строки (так как
именно в ней переменная $x_4$). Найдем эти частные (кроме только что введенной переменной $x_4$ и столбца B, а
также тех столбцов, где приходится делить на ноль):
| $x_A$ | $x_B$ | $x_C$ | $x_1$ | $x_2$ | $x_3$ | $x_4$ | B | |
| $x_C$ | 0 | $frac{1}{2}$ | 1 | $frac{2}{5}$ | $-frac{1}{10}$ | 0 | 0 | $frac{19}{2}$ |
| $x_A$ | 1 | $frac{1}{2}$ | 0 | $-frac{1}{5}$ | $frac{3}{10}$ | 0 | 0 | $frac{13}{2}$ |
| $x_3$ | 0 | -1 | 0 | $frac{1}{5}$ | $-frac{4}{5}$ | 1 | 0 | 11 |
| $x_4$ | 0 | $-frac{1}{2}$ | 0 | $-frac{2}{5}$ | $-frac{9}{10}$ | 0 | 1 | $-frac{1}{2}$ |
| F | 0 | 0 | 0 | $-frac{8}{5}$ | $-frac{3}{5}$ | 0 | 0 | -83 |
| $frac{F}{x_4}$ | — | 0 | — | 4 | $frac{2}{3}$ | — | — | — |
Наименьшее значение мы получили для столбца с переменной $x_B$ — 0. Следовательно именно переменную $x_B$
необходимо ввести в базис. Определяем, какое число стоит на пересечении строки $x_4$ и столбца $x_B$ — это
число $-frac{1}{2}$. Поэтому делим всю строку $x_4$ на это число:
| $x_A$ | $x_B$ | $x_C$ | $x_1$ | $x_2$ | $x_3$ | $x_4$ | B | |
| $x_C$ | 0 | $frac{1}{2}$ | 1 | $frac{2}{5}$ | $-frac{1}{10}$ | 0 | 0 | $frac{19}{2}$ |
| $x_A$ | 1 | $frac{1}{2}$ | 0 | $-frac{1}{5}$ | $frac{3}{10}$ | 0 | 0 | $frac{13}{2}$ |
| $x_3$ | 0 | -1 | 0 | $frac{1}{5}$ | $-frac{4}{5}$ | 1 | 0 | 11 |
| 0 | 1 | 0 | $frac{4}{5}$ | $frac{9}{5}$ | 0 | -2 | 1 | |
| F | 0 | 0 | 0 | $-frac{8}{5}$ | $-frac{3}{5}$ | 0 | 0 | -83 |
Из четвертой строки исчезло название строки — $x_4$. Это потому, что
$x_4$ — больше не базисная переменная. Нам же необходимо, чтобы базисной
стала переменная $x_B$. Первое требование к базисным переменным для нее выполняется —
есть столбец $x_B$, и у него в четвертой строке число 1. Но вот остальные числа не равны
нулю. Так давайте их сделаем такими.
- Чтобы в первой строке, в столбце $x_B$ число $frac{1}{2}$ превратить в ноль, вычтем из первой строки четвертую, умноженную на $frac{1}{2}$.
- Чтобы во второй строке, в столбце $x_B$ число $frac{1}{2}$ превратить в ноль, вычтем из второй строки четвертую, умноженную на $frac{1}{2}$
- Чтобы в третьей строке, в столбце $x_B$ число $-1$ превратить в ноль, добавим к третьей строке четвертую
- Последнюю строку не трогаем, так как в последней строке, столбце $x_B$ и так ноль
| $x_A$ | $x_B$ | $x_C$ | $x_1$ | $x_2$ | $x_3$ | $x_4$ | B | |
| $x_C$ | $0-frac{1}{2}cdot0$ | $frac{1}{2}-frac{1}{2}cdot1$ | $1-frac{1}{2}cdot0$ | $frac{2}{5}-frac{1}{2}cdotfrac{4}{5}$ | $-frac{1}{10}-frac{1}{2}cdotfrac{9}{5}$ | $0-frac{1}{2}cdot0$ | $0-frac{1}{2}cdot(-2)$ | $frac{19}{2}-frac{1}{2}cdot1$ |
| $x_A$ | $1-frac{1}{2}cdot0$ | $frac{1}{2}-frac{1}{2}cdot1$ | $0-frac{1}{2}cdot0$ | $-frac{1}{5}-frac{1}{2}cdotfrac{4}{5}$ | $frac{3}{10}-frac{1}{2}cdotfrac{9}{5}$ | $0-frac{1}{2}cdot0$ | $0-frac{1}{2}cdot(-2)$ | $frac{13}{2}-frac{1}{2}cdot1$ |
| $x_3$ | 0+0 | -1+1 | 0+0 | $frac{1}{5}+frac{4}{5}$ | $-frac{4}{5}+frac{9}{5}$ | 1+0 | 0-2 | 11+1 |
| $x_B$ | 0 | 1 | 0 | $frac{4}{5}$ | $frac{9}{5}$ | 0 | -2 | 1 |
| F | 0 | 0 | 0 | $-frac{8}{5}$ | $-frac{3}{5}$ | 0 | 0 | -83 |
Проводим математические действия и получаем итоговую таблицу.
| $x_A$ | $x_B$ | $x_C$ | $x_1$ | $x_2$ | $x_3$ | $x_4$ | B | |
| $x_C$ | 0 | 0 | 1 | 0 | -1 | 0 | 1 | 9 |
| $x_A$ | 1 | 0 | 0 | $-frac{3}{5}$ | $-frac{3}{5}$ | 0 | 1 | 6 |
| $x_3$ | 0 | 0 | 0 | 1 | 1 | 1 | -2 | 12 |
| $x_B$ | 0 | 1 | 0 | $frac{4}{5}$ | $frac{9}{5}$ | 0 | -2 | 1 |
| F | 0 | 0 | 0 | $-frac{8}{5}$ | $-frac{3}{5}$ | 0 | 0 | -83 |
Проверяем, получили ли мы целочисленное решение. Да, получили. Мы получили решение $x_A=6,x_B=1,x_C=9$, причем
значение целевой функции (правая нижняя клетка таблицы с противоположным знаком) равно 83, что, кстати, совпадает
со значением целевой функции в исходной (нецелочисленной) задачи. Поэтому, можно сказать, что переход к целочисленности не изменяет значения дохода фирмы. Так, однако бывает не всегда, и чаще всего доход фирмы при переходе к целочисленности немного падает.
Выводы
Так как мы получили целочисленное решение, то задача решена. Если бы какие-то из переменных снова были бы
нецелочисленными, процесс нужно было бы повторить — найти одну из нецелочисленных переменных, составить для нее
дополнительное ограничение, получив еще одну вспомогательную переменную, а затем сделать шаг симплекс-метода, уберя
ее из базиса. После какого-то шага мы бы точно получили целочисленное решение (как и в этом случае).
Мы научились решать производственную задачу, и умеем выдавать такой результат, который обеспечивает
максимальную прибыль. Однако при этом мы совсем не учитываем остатки на складах. То есть, мы конечно гарантируем,
что используем не больше ресурсов, чем есть, однако вполне возможно, что на складах останутся излишки. Что обычно
делают предприятия, если у них на складах образуются излишки ресурсов? На самом деле, можно много чего сделать:
- Можно их продать, и тем самым повысить прибыль (целевую функцию);
- Можно поменять одни ресурсы на другие (если такое возможно), и, может быть, тогда прибыль увеличится;
- Можно обдумать выпуск нового товара, который потребляет как раз тот ресурс, которого у нас излишек.
Может быть, тогда наша прибыль увеличится.
Обычное решение производственной задачи не дает ответов на вопросы подобного рода. Однако существуют методы, позволяющие получить такие ответы. Один из этих методов — решение «двойственной» задачи. Его мы рассмотрим в следующем разделе.
Полезное по теме
- Примеры решений задач ЛП в целых числах
- Решенные контрольные по линейному программированию
- Заказать решение целочисленной задачи ЛП
Ограниченияитранспортнаязадача
Здесь a и b — постоянные числа, заданные условиями задачи.[2] Если по условиям задачи вместо равенств предполагаются неравенства, то для неравенства вида «≤» для преобразования его в равенство надо добавить дополнительную переменную xn+1
или несколько таких переменных (xn+2
и т.д. по числу неравенств). Аналогично, для неравенств вида «≥» дополнительную неотрицательную переменную xn+i
следует вычесть (или, что то же самое, прибавить с коэффициентом –1).
Транспортная задача (задача Монжа — Канторовича) — математическая задача линейного программирования специального вида. Её можно рассматривать как задачу об оптимальном плане перевозок грузов из пунктов отправления в пункты потребления, с минимальными затратами на перевозки.
Транспортная задача по теории сложности вычислений входит в класс сложности P. Когда суммарный объём предложений (грузов, имеющихся в пунктах отправления) не равен общему объёму спроса на товары (грузы), запрашиваемые пунктами потребления, транспортная задача называется несбалансированной (открытой).
Транспортная задача (классическая) — задача об оптимальном плане перевозок однородного продукта из однородных пунктов наличия в однородные пункты потребления на однородных транспортных средствах (предопределённом количестве) со статичными данными и линеарном подходе (это основные условия задачи).
Для классической транспортной задачи выделяют два типа задач: критерий стоимости (достижение минимума затрат на перевозку) или расстояний и критерий времени (затрачивается минимум времени на перевозку). Под названием транспортная задача, определяется широкий круг задач с единой математической моделью, эти задачи относятся к задачам линейного программирования и могут быть решены оптимальным методом. Однако, спец.метод решения транспортной задачи позволяет существенно упростить её решение, поскольку транспортная задача разрабатывалась для минимизации стоимости перевозок.
Пример транспортной задачи
Составить математическую модель транспортной задачи, исходные данные которой приведены в таблице 34.2
Решение:
1. Вводим переменные задачи (матрицу перевозок):

2. Записываем матрицу стоимостей:
3. Целевая функция задачи равняется сумме произведений всех соответствующих элементов матриц C и X.
Данная функция, определяющая суммарные затраты на все перевозки, должна достигать минимального значения.
4. Составим систему ограничений задачи.
Сумма всех перевозок, стоящих в первой строке матрицы X, должна равняться запасам первого поставщика, а сумма перевозок во второй строке матрицы X равняться запасам второго поставщика:

Это означает, что запасы поставщиков вывозятся полностью.
Суммы перевозок, стоящих в каждом столбце матрицы X, должны быть равны запросам соответствующих потребителей:

Это означает, что запросы потребителей удовлетворяются полностью.
Необходимо также учитывать, что перевозки не могут быть отрицательными:
Ответ: Таким образом, математическая модель рассматриваемой задачи записывается следующим образом:
Найти переменные задачи, обеспечивающие минимум целевой функции (1) и удовлетворяющие системе ограничений (2) и условиям неотрицательности (3).
Линейное программирование и целевая функция
Линейное программирование — наиболее разработанный и широко применяемый раздел математического программирования. Это объясняется следующим:
· математические модели очень большого числа экономических задач линейны относительно искомых переменных;
· эти типы задач в настоящее время наиболее изучены;
· для них разработаны специальные конечные методы, с помощью которых эти задачи решаются, и соответствующие стандартные программы для их решения на ЭВМ;
· многие задачи линейного программирования, будучи решенными, нашли уже сейчас широкое практическое применение в народном хозяйстве;
· некоторые задачи, которые в первоначальной формулировке не являются линейными, после ряда дополнительных ограничений и допущений могут стать линейными или могут быть приведены к такой форме, что их можно решать методами линейного программирования.
Итак, Линейное программирование – это направление математического программирования, изучающее методы решения экстремальных задач, которые характеризуются линейной зависимостью между переменными и линейным критерием.
Необходимым условием постановки задачи линейного программирования являются ограничения на наличие ресурсов, величину спроса, производственную мощность предприятия и другие производственные факторы.
Сущность линейного программирования состоит в нахождении точек наибольшего или наименьшего значения некоторой функции при определенном наборе ограничений, налагаемых на аргументы и образующих систему ограничений, которая имеет, как правило, бесконечное множество решений. Каждая совокупность значений переменных (аргументов функции F), которые удовлетворяют системе ограничений, называется допустимым планом задачи линейного программирования. Функция F, максимум или минимум которой определяется, называется целевой функцией задачи. Допустимый план, на котором достигается максимум или минимум функции F, называется оптимальным планом задачи.
Система ограничений, определяющая множество планов, диктуется условиями производства. Задачей линейного программирования (ЗЛП) является выбор из множества допустимых планов наиболее выгодного (оптимального).
В общей постановке задача линейного программирования выглядит следующим образом:
Имеются какие-то переменные х = (х1 , х2 , … хn ) и функция этих переменных f(x) = f (х1 , х2 , … хn ), которая носит название целевой функции. Ставится задача: найти экстремум (максимум или минимум) целевой функции f(x) при условии, что переменные x принадлежат некоторой области G:
В зависимости от вида функции f(x) и области G и различают разделы математического программирования: квадратичное программирование, выпуклое программирование, целочисленное программирование и т.д. Линейное программирование характеризуется тем, что
а) функция f(x) является линейной функцией переменных х1 , х2 , … хn
б) область G определяется системой линейных равенств или неравенств.
Математическая модель любой задачи линейного программирования включает в себя:
· максимум или минимум целевой функции (критерий оптимальности);
· систему ограничений в форме линейных уравнений и неравенств;
· требование неотрицательности переменных.
В других ситуациях могут возникать задачи с большим количеством переменных, в систему ограничений которых, кроме неравенств, могут входить и равенства. Поyтому в наиболее общей форме задачу линейного программирования формулируют следующим образом:
Коэффициенты ai,j, bi, cj, j = 1, 2, . , n, i =1, 2, . , m – любые действительные числа (возможно 0).
Итак, решения, удовлетворяющие системе ограничений (2.4) условий задачи и требованиям неотрицательности (2.5), называются допустимыми, а решения, удовлетворяющие одновременно и требованиям минимизации (максимализации) (2.6) целевой функции, — оптимальными.
Выше описанная задача линейного программирования (ЗЛП) представлена в общей форме, но одна и та же (ЗЛП) может быть сформулирована в различных эквивалентных формах. Наиболее важными формами задачи линейного программирования являются каноническая и стандартная.
В канонической форме задача является задачей на максимум (минимум) некоторой линейной функции F, ее система ограничений состоит только из равенств (уравнений). При этом переменные задачи х1, х2, . хnявляются неотрицательными:
К канонической форме можно преобразовать любую задачу линейного программирования.
Правило приведения ЗЛП к каноническому виду:
1. Если в исходной задаче некоторое ограничение (например, первое) было неравенством, то оно преобразуется в равенство, введением в левую часть некоторой неотрицательной переменной, при чем в неравенства «≤» вводится дополнительная неотрицательная переменная со знаком «+»; в случаи неравенства «≥» — со знаком «-»
 |
(2.10) |

Тогда неравенство (2.10) запишется в виде:
 |
(2.11) |
В каждое из неравенств вводится своя “уравнивающая” переменная, после чего система ограничений становится системой уравнений.
2. Если в исходной задаче некоторая переменная не подчинена условию неотрицательности, то ее заменяют (в целевой функции и во всех ограничениях) разностью неотрицательных переменных
 |
, l — свободный индекс |
3. Если в ограничениях правая часть отрицательна, то следует умножить это ограничение на (-1)
4. Наконец, если исходная задача была задачей на минимум, то введением новой целевой функции F1 = -F мы преобразуем нашу задачу на минимум функции F в задачу на максимум функции F1.
Таким образом, всякую задачу линейного программирования можно сформулировать в канонической форме.
В стандартной форме задача линейного программирования является задачей на максимум (минимум) линейной целевой функции. Система ограничений ее состоит из одних линейных неравенств типа « = ». Все переменные задачи неотрицательны.
Всякую задачу линейного программирования можно сформулировать в стандартной форме. Преобразование задачи на минимум в задачу на максимум, а также обеспечение не отрицательности переменных производится так же, как и раньше. Всякое равенство в системе ограничений равносильно системе взаимопротивоположных неравенств:
Существует и другие способы преобразования системы равенств в систему неравенств, т.е. всякую задачу линейного программирования можно сформулировать в стандартной форме.
Поперечные профили набережных и береговой полосы: На городских территориях берегоукрепление проектируют с учетом технических и экономических требований, но особое значение придают эстетическим.
Опора деревянной одностоечной и способы укрепление угловых опор: Опоры ВЛ — конструкции, предназначенные для поддерживания проводов на необходимой высоте над землей, водой.
Действие системы, ее поведение характеризуются не только установлением факта достижения цели, но и степенью ее достижения, определяемой с помощью целевой функции.
Целевая функция – есть обобщенный показатель системы, который характеризует степень достижения системой ее цели. Составление целевой функции одна из важнейших задач при проектировании системы. Однако нет общей теории построения целевых функций, есть только некоторые рекомендации.
Целевая функция составляется по указаниям ТЗ о критерии оптимизации путем анализа внешних параметров системы и ограничений на них.
Целевая функция должна существенно зависеть от внешних параметров или части их. В противном случае оптимизация по данной целевой функции не имеет смысла. Целевая функция представляет вектор в m-мерном пространстве внешних параметров системы
Обычно целевая функция задается в скалярном виде.
Используются следующие четыре формы целевой функции.
1. Наиболее часто используется целевая функция одного внешнего параметра
В этом случае целевая функция просто равна одному из внешних параметров или его обратной величине
Все остальные (m – 1) внешних параметров переводятся в систему ограничений.
Физический смысл целевой функции приведенных видов заключается в том, что чем больше (или меньше) параметр yi, тем лучше при прочих равных условиях данная система, причем равенство прочих условий понимается в смысле ограничений на остальные внешние параметры. Типичные задачи с приведенной формой целевой функции: оптимизация системы по надежности (y = P(t)), помехоустойчивости, стоимости и другим внешним параметрам. Такая целевая функция имеет ясный физический (технический или экономический) смысл, объективно характеризует систему и поэтому часто используется. То есть в этом случае целевой функцией является внешний параметр системы. Он и называется целевой функцией системы. Это могут быть: точность, быстродействие, время, стоимость, надежность, масса, габариты, какой-то технологический показатель и т.п.
2. Вторая форма целевой функции – это сумма параметров одной размерности или сумма функций от этих параметров
Такая форма характерна при оптимизации по экономическим критериям, по критериям сложности и т.п.
Например, при минимизации годовых приведенных затрат на систему целевая функция представляет собой сумму двух внешних параметров: годовых эксплуатационных расходов и капитальных затрат, отнесенных к сроку окупаемости системы. В этом случае каждый из этих внешних параметров системы является сложной функцией ее внутренних (подлежащих нахождению) параметров.
Целевые функции задач оптимизации по критерию сложности также имеют вторую форму, т.к. они представляются в виде суммы сложностей отдельных подсистем или блоков системы.
3. Третья форма целевой функции – ранжированная форма – представляет собой упорядоченную совокупность целевых функций первой формы с приоритетами
Первая целевая функция наиболее важная, последняя целевая функция наименее важная.
В частном случае целевая функция этого вида записывается так:
Пример ранжирования – это (например) такая последовательность целевых функций: точность, надежность, стоимость. Смысл целевой функции третьей формы состоит в следующем. Самым главным – первым по рангу – признается некоторый i-й параметр системы – yi (например, точность). Если у некоторой системы этот i-ый параметр больше, чем у всех других систем, то независимо от значений других параметров (если только они удовлетворяют ограничениям) данная система считается лучшей. Затем по второму параметру и т.д.
Процедура оптимизации в этом случае, как правило, является многошаговой. Такая оптимизация часто неосознанно применяется в технических системах. Сначала выбирают систему лучшую по точности, при одинаковой точности нескольких систем – более надежную, а затем – более дешевую. На каждом шаге при оптимизации используется только один критерий, что не противоречит концепции системного подхода (оптимизация по одному единственному критерию, см. далее).
4. Четвертая – наиболее общая – форма целевой функции представляет собой произвольную зависимость от всех или части (но не меньше двух) разнородных внешних параметров
При этом разнородные параметры преобразуются в безразмерные (или одноразмерные) и целевая функция формируется как некоторая композиция (например, среднее арифметическое) полученных безразмерных показателей.
Единую целевую функцию четвертой формы можно получить из целевых функций третьей формы путем умножения их на весовые коэффициенты и последующего суммирования [13]:
Однако, как указывается там же, определение весовых коэффициентов отдельных целевых функций является очень сложным.
Экстремальное значение полученной суммы будет считаться оптимальным.
Таким образом, можно указать, что в большинстве случаев (1-я и 3-я формы) показатели качества системы оцениваются численными значениями компонентов векторной целевой функции, которые носят названия функционалов:

Так как системы работают в условиях случайных воздействий, то значения функционалов часто оказываются случайными величинами. Это неудобно при использовании функционалов в виде показателей качества. Поэтому в таких случаях обычно пользуются средними значениями соответствующих функционалов. Например: среднее количество изделий, выпускаемых за смену; средняя стоимость продукции и т.д.
В некоторых случаях показатели качества представляют собой вероятности некоторых случайных событий. При этом в качестве целевой функции выбирается вероятность 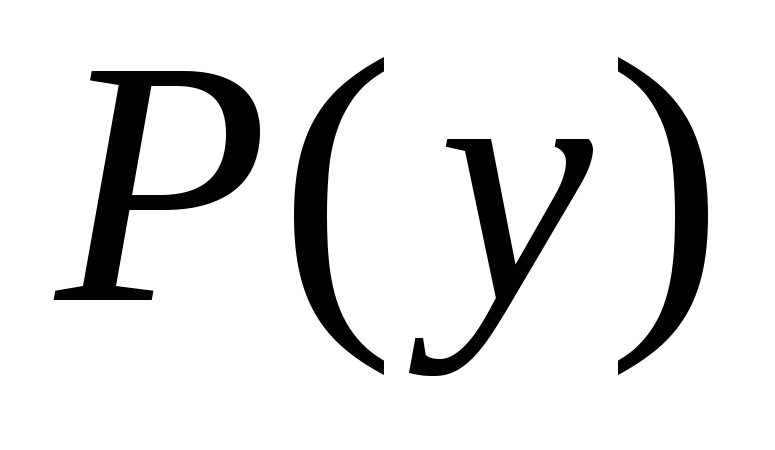
Например, вероятность обнаружения цели радиолокатором и т.п.
60. Задание << 27 >> ТЗ № 27
Отметьте правильный ответ
Критерий оптимальности — это:
+ целевая функция, глобальный экстремум которой отыскивается при заданных ограничениях
£ функция, максимум которой отыскивается
£ ограничение задачи линейного программирования
£ функция, минимум которой отыскивается
61. Задание << 28 >> ТЗ № 28
Отметьте правильный ответ
Задача линейного программирования
с · х-> max (или min)
+ в матричном виде
£ в векторной форме
62. Задание << 29 >> ТЗ № 29
Отметьте правильный ответ
Оптимальным решением (оптимальным планом) задачи математического программирования называется допустимое решение
£ удовлетворяющее всем ограничениям
£ удовлетворяющее большинству ограничений
+ доставляющее целевой функции максимальное или минимальное значение
£ удовлетворяющее хотя бы одному из ограничений
63. Задание << 30 >> ТЗ № 30
Отметьте правильный ответ
Целевая функция задачи математического программирования — это функция,
£ входящая в систему ограничений
£ включающая все ограничения задачи с весовыми коэффициентами
+ экстремальное значение которой нужно найти в условиях экономических возможностей
£ зависящая от свободных членов системы ограничений
64. Задание << 31 >> ТЗ № 31
Отметьте правильный ответ
Модель задачи математического программирования включает:
£ уравнения и неизвестные величины
£ неизвестные величины и целевую функцию
+ совокупность неизвестных величин, целевую функцию и систему ограничений
£ совокупность неизвестных величин и систему неравенств
65. Задание << 32 >> ТЗ № 32
Отметьте правильный ответ
Планом или решением задачи математического программирования называется:
+ совокупность неизвестных величин, удовлетворяющая системе ограничений
£ совокупность неизвестных величин, удовлетворяющая большей части ограничений
£ любая совокупность неизвестных величин
£ совокупность переменных, принадлежащая области определения целевой функции
66. Задание << 33 >> ТЗ № 33
Отметьте правильный ответ
Целевая функция задачи математического программирования позволяет:
£ найти допустимое решение задачи
£ определить опорный план задачи
+ выбрать наилучший план из множества возможных
£ найти вырожденное решение задачи
67. Задание << 34 >> ТЗ № 34
Отметьте правильный ответ
Наилучший план задачи математического программирования доставляет целевой функции:
68. Задание << 35 >> ТЗ № 35
Отметьте правильный ответ
Условия, налагаемые на неизвестные величины в задачах математического программирования, следуют:
+ из ограниченности ресурсов, из необходимости удовлетворения насущных потребностей, из условий производственных и технологических процессов;
£ из математических соображений
£ из способностей и желания человека, составляющего модель
£ из политических соображений
69. Задание << 36 >> ТЗ № 36
Отметьте правильный ответ
Математически ограничения выражаются в виде:
+ уравнений и неравенств
70. Задание << 37 >> ТЗ № 37
Отметьте правильный ответ
Область допустимых решений — это:
£ все пространство, на котором рассматривается задача
+ совокупность всех уравнений и неравенств системы ограничений
£ совокупность только уравнений системы ограничений
£ совокупность только неравенств системы ограничений
71. Задание << 38 >> ТЗ № 38
Отметьте правильный ответ
Оптимальное решение задачи математического программирования
£ всегда существует и единственно
+ не обязательно единственно, возможны случаи, когда оно не существует или имеется конечное или бесконечное множество оптимальных решений.
£ не единственно, а их бесконечное множество
£ зависит от разработчика модели
72. Задание << 39 >> ТЗ № 39
Отметьте правильный ответ
Линейная функция это
+ линейная комбинация переменных
£ выпуклая комбинация переменных
£ комбинация переменных с коэффициентами в первой степени
73. Задание << 40 >> ТЗ № 40
Отметьте правильный ответ
В линейной функции может присутствовать константа
+ в зависимости от условий задачи
£ в зависимости от разработчика модели
74. Задание << 41 >> ТЗ № 41
Отметьте правильный ответ
Равенство является линейным, если оно выполняется для
£ комбинации переменных с коэффициентами в первой степени
£ любой комбинации переменных
£ выпуклой комбинации переменных
75. Задание << 42 >> ТЗ № 42
Отметьте правильный ответ
Неравенство является линейным если оно выполняется для
£ комбинации переменных с коэффициентами в первой степени
+ линейной комбинации переменных
£ любой комбинации переменных
£ выпуклой комбинации переменных
76. Задание << 43 >> ТЗ № 43
Отметьте правильный ответ
Для задачи линейного программирования в общем виде оптимальный план доставляет целевой функции
77. Задание << 44 >> ТЗ № 44
Отметьте правильный ответ
Линейное программирование — это раздел математического программирования, применяемый при разработке методов отыскания экстремума:
+ линейных функций нескольких переменных при дополнительных линейных ограничениях, налагаемых на переменные
£ линейных функций при нелинейных ограничениях
£ нелинейной функции при линейных ограничениях
78. Задание << 45 >> ТЗ № 45
Отметьте правильный ответ
Особенностью задач линейного программирования является то, что экстремума целевая функция
£ достигает во внутренней точке области допустимых решений
£ достигает вне области допустимых решений
+ достигает на границе области допустимых решений
79. Задание << 46 >> ТЗ № 46
Отметьте правильный ответ
£ в канонической форме
+ в симметрической форме
£ в матричной форме
80. Задание << 47 >> ТЗ № 47
Отметьте правильный ответ
£ в матричной форме
£ в канонической форме
+ в симметрической форме
81. Задание << 48 >> ТЗ № 48
Отметьте правильный ответ
£ в стандартной форме
+ в канонической форме
£ в векторной форме
82. Задание << 65 >> ТЗ № 65
Отметьте правильный ответ
В линейном программировании используются функции, уравнения и неравенства
£ в зависимости от решаемой задачи
83. Задание << 66 >> ТЗ № 66
Отметьте правильный ответ
Методы линейного программирования позволяют определить оптимальное экономическое решение
+ да, если оно существует
£ линейное программирование предназначено для других целей
84. Задание << 67 >> ТЗ № 67
Отметьте правильный ответ
Конкретный план в линейном программировании представляется
£ интегральной кривой возможных потерь
85. Задание << 68 >> ТЗ № 68
Отметьте правильный ответ
Оптимальный план задачи ЛП это
£ любой допустимый план
+ допустимый план, которому соответствует максимум выручки
£ любой опорный план
86. Задание << 69 >> ТЗ № 69
Отметьте правильный ответ
Система ограничений задачи ЛП это система
£ только строгих неравенств
+ равенств и неравенств
87. Задание << 70 >> ТЗ № 70
Отметьте правильный ответ
Допустимыми являются планы
£ любые с положительными значениями
+ удовлетворяющие системе ограничений
£ любые с ненулевыми значениями
88. Задание << 71 >> ТЗ № 71
Отметьте правильный ответ
Целевая функция задачи линейного программирования должна быть
89. Задание << 72 >> ТЗ № 72
Отметьте правильный ответ
Математическая модель задачи линейного программирования это
+ целевая функция и набор ограничений
90. Задание << 73 >> ТЗ № 73
Отметьте правильный ответ
Методом линейного программирования решаются задачи поиска экстремума
£ нелинейной функции при линейных ограничениях
£ линейной функции при нелинейных ограничениях
+ линейной функции при линейных ограничениях
91. Задание << 74 >> ТЗ № 74
Отметьте правильный ответ
Допустимым планом задачи является
+ любой план, обеспечивающий выполнение ограничений
£ это зависит от конкретного содержания задачи
£ любой план с ненулевыми значениями
92. Задание << 75 >> ТЗ № 75
Отметьте правильный ответ
Оптимальным планом задачи является план
£ любой, обеспечивающий выполнение ограничений
£ доставляющий экстремум целевой функции
+ доставляющий экстремум целевой функции при выполнении ограничений
£ любой с ненулевыми значениями
93. Задание << 76 >> ТЗ № 76
Отметьте правильный ответ
В задаче линейного программирования допустимо количество ограничений
+ не более числа переменных
£ равное числу переменных
94. Задание << 77 >> ТЗ № 77
Отметьте правильный ответ
Если вся выпускаемая продукция или ее часть реализуется комплектами, то в модели задачи необходимо изменить
£ целевую функцию и систему ограничений
£ только целевую функцию
+ только систему ограничений
95. Задание << 78 >> ТЗ № 78
Если предприятие может пополнять объемы ресурсов, неся связанные с этим затраты, но и расширяя свои производственные возможности, то в модели задачи необходимо изменить
£ только целевую функцию
+ целевую функцию и систему ограничений
£ только систему ограничений
96. Задание << 79 >> ТЗ № 79
При динамическом планировании определяется
£ последовательность оптимальных планов
+ оптимальная последовательность планов
97. Задание << 49 >> ТЗ № 49
Отметьте правильный ответ
£ не опорным решением
£ не допустимым решением
98. Задание << 50 >> ТЗ № 50
Отметьте правильный ответ
При необходимости задачу минимизации можно заменить задачей максимизации, воспользовавшись формулой:
+
£
£
£
99. Задание << 51 >> ТЗ № 51
Отметьте правильный ответ
£
+
£
100. Задание << 52 >> ТЗ № 52
Отметьте правильный ответ
+
£
£
101. Задание << 53 >> ТЗ № 53
Отметьте правильный ответ
£
£
+
102. Задание << 54 >> ТЗ № 54
Отметьте правильный ответ
£ к их правым частям нужно прибавить дополнительные переменные
+ к их левым частям нужно прибавить дополнительные неотрицательные переменные
£ от обеих частей нужно отнять дополнительные переменные
£ к обеим частям нужно прибавить дополнительные переменные
103. Задание << 55 >> ТЗ № 55
Отметьте правильный ответ
£ к левой части прибавить дополнительные переменные
£ от правой части отнять дополнительные переменные
£ от обеих частей нужно отнять дополнительные переменные
+ от левой части отнять дополнительные неотрицательные переменные
104. Задание << 56 >> ТЗ № 56
Отметьте правильный ответ
При преобразовании задачи линейного программирования к каноническому виду, дополнительные переменные вводятся в целевую функцию с коэффициентами,
£ равными очень большим положительным числам
£ равными правым частям соответствующих ограничений
105. Задание << 57 >> ТЗ № 57
Отметьте правильный ответ
£ в скалярной форме
+ в векторной форме
£ в стандартной форме
106. Задание << 58 >> ТЗ № 58
Отметьте правильный ответ
Для задачи о наилучшем использовании ресурсов дополнительные переменные показывают:
+ величину неиспользованного ресурса
£ величину ресурса, использованного в оптимальном плане
£ дополнительную прибыль от сэкономленного ресурса
£ стоимость соответствующего потребляемого ресурса
107. Задание << 59 >> ТЗ № 59
Отметьте правильный ответ
Для задачи о смесях дополнительная переменная показывает:
£ потребление соответствующего питательного вещества в пределах нормы
+ потребление соответствующего питательного вещества в оптимальном плане сверх нормы
£ стоимость соответствующего потребляемого вещества
£ величину ресурса, использованного в оптимальном плане
108. Задание << 60 >> ТЗ № 60
Отметьте правильный ответ
В задаче о рационе требуется:
+ минимизация общей стоимости всех кормов
£ максимизация содержания питательных веществ в кормах
£ минимизация количества кормов
£ минимизация стоимости всех питательных веществ
109. Задание << 61 >> ТЗ № 61
Отметьте правильный ответ
£
+
£
£
110. Задание << 62 >> ТЗ № 62
Отметьте правильный ответ
£
£
+
£
111. Задание << 63 >> ТЗ № 63
Отметьте правильный ответ
+
£
£
£
112. Задание << 64 >> ТЗ № 64
Отметьте правильный ответ
Линейное программирование это
£ один из приемов разработки программного обеспечения ЭВМ
+ математический метод оптимизации
£ определение последовательности действий при проведении общественных мероприятий
£ составление программ линейной структуры
113. Задание << 292 >> ТЗ № 26
Отметьте правильный ответ
Целевая функция задачи линейного программирования имеет следующий вид
Не нашли то, что искали? Воспользуйтесь поиском:
Лучшие изречения: Увлечёшься девушкой-вырастут хвосты, займёшься учебой-вырастут рога 9987 — 

91.146.8.87 © studopedia.ru Не является автором материалов, которые размещены. Но предоставляет возможность бесплатного использования. Есть нарушение авторского права? Напишите нам | Обратная связь.
Отключите adBlock!
и обновите страницу (F5)
очень нужно
Многие разработчики считают, что Auto Layout — это тормозная и проблемная штука, и крайне сложно заниматься его отладкой. И хорошо, если этот вывод сделан на основе собственного опыта, а то бывает и просто «я слышал, не буду даже и пытаться с ним подружиться».
Но возможно, причина не снаружи, а внутри. Например, самые опасные птицы в мире казуары не будут атаковать людей без причины, только ради самообороны. Поэтому попробуйте на секунду предположить, что это не Auto Layout плохой, а вы его не достаточно хорошо понимаете и не умеете готовить. Так поступил Антон Сергеев и углубился в теорию, чтобы во всем точно разобраться. Нам предлагается готовая выжимка про математические основы Auto Layout.
Auto Layout — это система верстки. Прежде, чем углубиться в неё, поговорим о современной верстке вообще. Затем займемся Auto Layout — разберемся какую задачу он решает и как это делает. Рассмотрим особенности в имплементации Auto Layout в iOS, и попробуем выработать практические советы, которые могут помочь в работе с ним.
Этот рассказ будет очень близок к математической статье, поэтому сначала договоримся об обозначениях, чтобы говорить на одном языке.
О спикере: Антон Сергеев (antonsergeev88) работает в команде Яндекс.Карт, занимается мобильным клиентом для Карт на iOS. До мобильной разработки занимался системами управления электростанциями, где цена ошибок в коде слишком высока, чтобы их допускать.
Обозначения
Системы линейных уравнений знакомы нам еще со школы — обозначаются фигурной скобкой, а их решение — уже без. Также у систем линейных уравнений есть сущности, которыми оперирует Auto Layout — ограничения. Обозначаются прямой линией.
Странная и, как мы уже знаем, опасная птица не случайно нарисована в верхнем углу слайда. В честь казуара (лат. Cassowary), который, конечно, обитает в Австралии, во всех наших Айфонах назван алгоритм.
В Auto Layout есть свои ограничения, будем обозначать их цветами по порядку приоритета: красный — required; желтый — high; синий — low.
Верстка
Когда я верстал презентацию, то располагал различные элементы на экране, например, казуара. Чтобы это сделать, я определил, что казуар — это прямоугольная картинка. Расположить ее нужно на листе, который имеет оси и свою систему координат, и для этого я определил координаты левого верхнего угла, ширину и высоту.
Знать эти четыре значения достаточно, чтобы представить любую View.
Алгоритм № 1
Пока располагали казуара на листе, мы ненавязчиво описали первый алгоритм верстки:
- определяем координаты и размеры;
- применяем их к UIView.
Алгоритм работает, но достаточно сложен в применении, поэтому дальше будем его упрощать.
Предположим, что ниже — решение некоторой системы линейных уравнения.
Система линейных уравнений особенна тем, что над ней определена масса операций: складывание строк, умножение их на константы и т.д. Эти операции называются линейными преобразованиями, и с их помощью система приводится к произвольной форме.
Прелесть линейных преобразований в том, что они обратимы. Это подводит нас к интересной и довольно тонкой идее, с которой начинается вся современная верстка.
Пусть есть View — прямоугольник со своими координатами и размером. Мы хотим расположить ее так, чтобы центр совпадал с заданной точкой. Центр мы смоделируем с помощью линейных преобразований — координата левого верхнего угла + половина ширины.
Мы смоделировали центр линейным преобразованием, его не было: были только координаты левой верхней точки, ширина и высота.
Аналогично можно смоделировать любые другие отступы, например, 20 точек от правого угла.
Именно идея линейных преобразований позволяет нам создавать различные системы верстки.
Рассмотрим на элементарном примере. Выпишем систему, с помощью которой установим координаты середины и правой стороны, ширину и соотношение между шириной и высотой. Решим систему и получим ответ.
Так мы подошли ко второму алгоритму.
Алгоритм № 2
Вторая итерация алгоритма состоит из таких пунктов:
- составляем систему линейных уравнений;
- решаем ее;
- применяем решение к UIView.
Представим, что мы попали в ХХ век, в то время, когда только зарождалась компьютерная техника, и оказались первыми, кто дошел до создания своей системы верстки. Придумали, запаковали, отдали пользователю, и он начинает ее использовать — заполняет начальные параметры и передает в нашу систему.
Появляется проблема — у этой системы не существует ни одного решения. Проблема не исключительная, с ней сталкиваются абсолютно все системы верстки, и называется отсутствием решения.
Выходов из этой ситуации не так уж и много:
- Можно упасть — это очень распространенный метод. Кто работает с MacOS, знает, что NSLayoutConstraintManager так и поступает.
- Возвращать значение по умолчанию. В контексте вёрстки, мы всегда можем вернуть все нули.
- Более известный и деликатный способ — не допускать некорректный ввод. Этим способом пользуются популярные системы верстки, например, Yoga, известная под названием Flex Layout. Такие системы стараются создать интерфейс, который не допустит некорректный ввод.
- Существует еще один способ в решении абсолютно всех задач — это переосмыслить все с самого начала и изначально не допустить возникновения этой проблемы. Auto Layout пошел именно этим путем.
Auto Layout. Постановка и решение задачи
У нас есть прямоугольная картинка и чтобы однозначно ее определить, нам необходимы 4 параметра:
- координаты левого верхнего угла;
- ширина и высота.
Auto Layout очень многословный. По сравнению с системой линейных уравнений, с ним гораздо сложнее все поместить на экран. Поэтому мы будем рассматривать, не теряя общности, одномерный случай.
Все очень просто: пространство — это прямая, а все объекты, которые в нем могут разместиться — точки на прямой. Одного значения: X = XP достаточно, чтобы определить положение точки.
Рассмотрим подход Auto Layout. Есть пространство, в котором задаются ограничения. Решение, которое мы хотим получить — это X = X0, и никакое другое.
Есть проблема — у нас не определены операции с ограничениями. Мы не можем напрямую сделать вывод из записи, что X = X0, не можем ни на что умножить и ни с чем сложить. Для этого нам нужно преобразовать ограничение в то, с чем мы умеем работать — в систему уравнений и неравенств.
Auto Layout преобразует систему уравнений и неравенств следующим образом.
- Сначала вводит 2 дополнительных переменных, которые не отрицательны и зависят друг от друга. Хотя бы одна из них равна нулю.
- Само ограничение преобразуется в запись X = X0 + a+ — a—.
Точка X0 — решение системы: если a+ и a— будут равны нулю, то это будет верно. Но и любая другая точка на этой прямой будет решением.
Следовательно, надо среди всего множества решений найти лучшее. Для этого введем функционал — обычную функцию, которая возвращает число, а числа мы умеем сравнивать. Нарисуем график и заметим, что решение, которое мы изначально хотели получить является минимумом.
Получили задачу линейного программирования. Именно таким образом Auto Layout поступает с ограничениями, которые бывают не только в виде равенств, но и неравенств.
Ограничения в виде неравенств
В случае ограничений-неравенств преобразование происходит так же, как и с равенствами: вводятся две дополнительные переменные и все это собирается в систему. Отличается лишь функционал, и он равен a—.
На графике выше видно, почему это так — любое значение a+ при a— = 0 (от X0 до +∞) будет оптимальным решением для задачи.
Попробуем совместить эти два ограничения уравнений и неравенств в одно — ведь ограничения живут не замкнуто, они вместе применяются ко всей системе.
Для каждого ограничения дополнительно вводится по паре переменных, и составляется функционал. Так как мы хотим, чтобы все эти ограничения выполнялись одновременно, то функционал будет равен сумме всех функционалов от каждого ограничения.
Собираем функцию f и видим, что решение — это X1. Как мы и ожидали, составляя ограничения. Так мы подошли к третьему алгоритму.
Алгоритм № 3
Чтобы что-то сверстать, нужно:
- составить систему линейных ограничений;
- преобразовать ее в задачу линейного программирования;
- решить задачу любым известным способом, например, симплекс-методом, который используется в Auto Layout;
- применить решение к UIView.
Кажется, что этого алгоритма достаточно, но рассмотрим такой случай: изменим начальный набор ограничений так, что второе ограничение теперь X ≥ X2.
Какое решение мы ожидаем увидеть?
- X1? Ведь в первом ограничении так и написано: X = X1, и это решение конфликтует со вторым ограничением.
- X2? Будет конфликт уже с первым ограничением.
Для выхода из ситуации мы выполним преобразования, которые уже делать умеем.
График нового функционала выглядит по-другому: любая точка из промежутка от X1 до X2 будет корректным валидным решением системы. Это называется неопределенность.
Неопределенность
У Auto Layout есть механизм для решения таких задач — приоритеты. Напоминаю, что желтым будем обозначать высокий приоритет, а синим — низкий.
Преобразуем ограничения. Обратите внимание, что полученная система просто черного цвета. Мы умеем с ней работать, и в ней нет никакой информации об ограничениях. Она есть в функционалах, которых здесь будет целых два. Auto Layout сначала будет минимизировать первый, а затем второй.
В задачах линейного программирования мы ищем не само решение, а область допустимых решений. Разумеется, мы хотим, чтобы эта область составляла лишь одну точку, и Auto Layout действует таким же способом. Сначала он минимизирует самый приоритетный функционал на (— ∞, +∞) и на выходе получает область допустимых решений. Вторую задачу линейного программирования Auto Layout решает уже на полученной области допустимых значений. Такой механизм называется иерархией ограничений, и дает в этой задаче точку X2.
Алгоритм № 4
- Составить иерархию линейных ограничений;
- преобразовать её в задачу линейного программирования;
- решить последовательно задачу линейного программирования — от наиболее приоритетной к наименее приоритетной.
- применить решение к UlView.
Давайте еще раз посмотрим на предыдущую задачу. Мы не математики, а инженеры, и любого инженера должно здесь кое-что смущать.
Здесь есть серьезная проблема — бесконечность, и я не знаю, что это такое.
Алгоритм Cassowary под капотом Auto Layout не был уже существующим механизмом, который удобно лег на задачу Auto Layout, а придумывался как инструмент верстки, и в нем были предусмотрены специальные механизмы, чтобы уходить от бесконечностей еще в самом начале. Именно для этого были придуманы несколько типов ограничений:
- Параметры — это те ограничения, с которыми мы работали. В оригинале они называются preferences, иногда в документации Apple — optional constraints.
- Требования или requirements — ограничения с приоритетом required.
Посмотрим, как требования с такими приоритетами преобразовываются с точки зрения математики.
У нас опять прямая с двумя точками, и первое ограничение — X = X1. На слайде оно красное, то есть это ограничение с приоритетом required — будем называть его требованием.
Auto Layout преобразует его в систему линейных уравнений, содержащую одно уравнение X = X1. Больше ничего нет — никаких задач линейного программирования, никаких оптимизаций.
С неравенствами ситуация схожа, но немного сложнее — ведь появится дополнительная переменная, которая может принимать любые значения больше 0. При любом ее значении больше 0 это ограничение будет удовлетворяться. Обратите внимание, что и здесь нет никаких задач линейного программирования и оптимизаций.
Попробуем совместить все это вместе, собрать два требования и преобразовать их в одну систему. Внимательный читатель, заметил, что мы пришли к тому же самому вопросу, с которого начинали — требования должны быть непротиворечивыми.
Ограничения типа required или требования, — это очень сильный инструмент, но не основной, а вспомогательный. Он был специально введен в Auto Layout для решения проблемы бесконечных интервалов, использовать его нужно осторожно.
Попробуем совместить все типы ограничений, с которыми мы познакомились, в одну систему. Допустим, мы хотим решить задачу не на всей прямой, а лишь между X0 и X3. Преобразовывая все это в систему линейных уравнений и неравенств, получим следующее.
Относительно прошлой системы добавились две дополнительные переменные — c и d, но в функционалы они не попадут, так как ограничения типа required никак не влияют на функционал в его первоначальном виде.
Кажется, что задача почти не изменилась — минимизируем то же самое, что и раньше, но меняется исходная область допустимых значений, теперь она от X0 до X3.
С математической точки зрения требования — ограничения типа required — это возможность внедрить дополнительные уравнения внутрь системы, при этом не модифицируя ее функционалы.
С этим нужно быть очень аккуратным, потому что излишнее злоупотребление required constraints приведет к задаче без решений, и Auto Layout с ней не справится.
Мы приходим к последнему пятому алгоритму.
Алгоритм № 5
- Определить необходимые ограничения — требования к верстке;
- составить иерархию линейных ограничений;
- преобразовать все ограничения в задачу линейного программирования;
- решить задачу линейного программирования;
- применить решение к UlView.
Мы рассмотрели Cassowary — алгоритм, который находится внутри Auto Layout, но при его реализации возникают различные особенности.
Особенности в iOS
В layoutSubviews() нет расчетов.
Когда же они производятся? Ответ: всегда, в любой момент времени Auto Layout посчитан. Расчет происходит ровно тогда, когда мы добавляем constraints на нашу view, либо активируем их с помощью современных методов работы API с constraints.
Наши view — это прямоугольники, но проблема в том, что внутри Казуара эта информация не содержится, ее нужно туда дополнительно внедрить. У нас есть механизм внедрения дополнительных ограничений. Если введем для каждой view набор ограничений с положительными шириной и высотой, то на выходе всегда будем получать прямоугольники. Именно поэтому мы не можем сверстать с помощью Auto Layout view с отрицательными размерами.
Вторая особенность — это intrinsicContentSize — свойственный размер, который можно задать каждой view.
Это простой интерфейс для создания 4 дополнительных ограничений-неравенств, которые будут помещены в систему. Этот механизм очень удобен, он позволяет уменьшать количество явных ограничений, что упрощает использование Auto Layout. Последний и самый тонкий момент, про который часто забывают — это TranslateAutoresizingMaskIntoConstraints.
Это костыль, который ввели еще во времена iOS 5, чтобы старый код после появления Auto Layout не поломался.
Представьте ситуацию: мы верстаем view на constraints. Внутри view мы используем view, которая про constraints ничего не знает, верстает все на фреймах, но внутри себя она верстает view, которую уже давно перевели на constraints.
Напоминаю, внутрь задачи Auto Layout Казуара никакие фреймы не приходят, только ограничения.
Размер и положение view, которая была сверстана на фреймах, полностью не определяются через constraints. При расчете размера и положения всех других view будут учитываться некорректные размеры, даже несмотря на то, что после Auto Layout мы применим туда корректные фреймы.
Чтобы избежать этой ситуации, если значение переменной TranslateAutoresizingMaskIntoConstraints равно true, то внедряется дополнительное ограничение каждой view, сверстанной на фрейме. Этот набор ограничений может отличаться от запуска к запуску. Про этот набор известно лишь одно — его решением будет именно тот фрейм, который был передан.
Совместимость старого кода, написанного без constraints, и нового, написанного с constraints, часто может страдать из-за неправильного использования этого свойства. Эти ограничения обязательно имеют приоритет требований, поэтому если мы вдруг на такой view наложим constraint, у которого очень высокий приоритет, например, требование, то можем случайно создать не консистентную систему, которая не будет иметь решений.
Важно знать:
- Если мы создаем view из Interface Builder, то значение по умолчанию для этого свойства будет false.
- Если же мы создаем view непосредственно из кода, то оно будет true.
Идея очень простая — старый код, в котором создавались view, ничего про Auto Layout не знал, и необходимо было сделать так, что если вдруг view использовали где-то в новом месте, то она бы работала.
Практические советы
Всего совета будет три и начнем с самого важного.
Оптимизация
Важно локализовать проблему.
Вы когда-нибудь сталкивались с проблемой оптимизации экрана, который сверстан на Auto Layout? Скорее всего нет, чаще вы сталкивались с проблемой оптимизации верстки ячеек внутри таблицы или Сollection View.
Auto Layout достаточно оптимизирован, чтобы сверстать любой экран и любой интерфейс, но сверстать сразу 50 или 100 для него проблема. Чтобы ее локализовать и оптимизировать, посмотрим на эксперимент. Цифры взяты из статьи , где Казуар впервые был описан.
Задача такая: создаем цепочку view одну за одной, и каждую последующую связываем с предыдущей. Таким образом выстраивалась последовательность из 1000 элементов. После замерили различные операции, время указано в миллисекундах. Значения достаточно велики, потому что Auto Layout был придуман еще на стыке 80-х и 90-х годов.
Собирая такую цепочку, можно действовать следующим образом:
- Последовательно добавлять по одному constraint и каждый раз решать. При этом будет затрачено 38 секунд.
- Можно добавить сразу все ограничения единовременно, и только потом решать систему. Это решение эффективнее. По старым данным эффективность возрастает на 70%, но в текущей реализации на современных устройствах будет всего 20%. Но качественно единовременное добавление ограничений всегда будет эффективнее.
- Когда вся цепочка собрана, можно добавить еще одно ограничение. Как видно из таблицы, это операция достаточно дешевая.
- Самое интересное: если мы не добавляем никакие новые ограничения, а изменяем какую-то константу в одном из существующих — это на порядок эффективнее, чем удалять или создавать новое ограничение.
Первые два пункта можно описать как первичный расчет интерфейсов, два последних — как последующий.
Первичный расчет интерфейса
Здесь можно воспользоваться методами массового добавления constraints для оптимизации:
- NSLayoutConstraints.activate(_:) — при создании view собирать все constraints последовательно в массив, кэшировать и только потом единовременно добавить.
- Либо создавать ячейки в Interface Builder. Он все сделает за нас, и проведет дополнительную оптимизацию, что часто бывает удобно.
Последующие расчеты интерфейса
Добавление или изменение constraint — это сложная операция, поэтому лучше не изменять набор ограничений, а изменять только константы в существующих ограничениях. Для этого есть следующие приемы:
- Скрывать UIView — самый интересный и малоиспользуемый прием. При удалении view чистится весь кэш, который был сохранен в Auto Layout. Если мы ее просто скроем, то кэш не сотрется, но при этом можно сверстать view, которая будет иметь другое отображение.
- Управлять приоритетами свойственных ограничений — IntrinsicContentSize. Эффективный метод, который позволяет хорошо справляться с ячейками, но про него часто забывают.
- Создавать больше типов ячеек. Если ваши ячейки очень сильно различаются одна от другой, возможно, они разных типов.
Чтобы познакомиться подробно с приемами, советую посмотреть сессию WWDC 2018S220 High Performance Auto Layout. Она уникальна — Apple глубоко забирается в реализацию и описывает много удобных механизмов, которые позволяют создавать ячейки оптимально.
Проектирование ограничений
Дальше я дам несколько практических советов, которые могут помочь в работе с constraints.
Начните с приоритетов
Чем больше required ограничений, требований — тем больше вероятность, что вы однажды придете к противоречивой системе, которая не будет иметь решения. У вас возникнут проблемы.
В любой непонятной ситуации понижайте приоритет, что бы ни случилось.
Здесь действуют очень простые правила:
- Чем меньше компоненты, тем больше приоритеты. Чем меньше вы верстаете компонент (кнопку или loader) — тем выше должен быть приоритет.
- Чем больше компоненты, тем меньше приоритеты. Если вы делаете огромный экран, то приоритеты должны быть низкие.
Замораживайте требования
Все мы знаем, что ходить по воде и работать по требованию одинаково легко, когда они заморожены.
Когда создаете constraint с приоритетом required, не меняйте его в рантайме. Если его нужно поменять, значит, вы ошиблись в проектировании, и на самом деле это не требование. Переформулируйте вашу систему так, чтобы вы меняли уже опциональные ограничения.
Неочевидный вывод — чем ниже приоритет, тем дешевле модификация ограничения. Это напрямую исходит из того, что задачи в иерархии приоритетов решаются последовательно — от более приоритетных к низкоприоритетным. Если мы что-то меняем в низком приоритете, то на решение верхних это никак не отразится, и область допустимых значений не изменится. Auto Layout это понимает и решает систему оптимально, если вы меняете только низкоприоритетные ограничения.
Случайно создать противоречивые требования крайне просто, если вы будете их менять в рантайме. Вы это можете даже не заметить. Более того, это может быть не конечная ваша точка, когда требования станут приоритетными, а лишь промежуточная. В итоге вы построите тот же самый layout, но ситуация, когда система не разрешима, крайне дорога с точки зрения производительности. Поэтому лучше этого избегать еще на этапе дизайна.
Используйте неравенства
Неравенства — это классный инструмент, который позволяет использовать Auto Layout, так как мы не можем использовать многие другие системы верстки, и пренебрегать им просто неправильно.
Плюсы неравенства, типа required, в том, что с ними гораздо сложнее создать противоречия. Приемы достаточно простые:
- Чем выше приоритет, тем больше должно быть неравенств.
- И наоборот, чем меньше приоритет, тем больше можно использовать равенств.
Самое главное, что я хотел донести в этой статье, это понимание того, как мы приходим к ограничениям.
Сначала мы преобразовали требования в систему линейных уравнений и пришли к проблемам, а затем пошли совсем другим путем. Поэтому, когда возникают проблемы или баги, мы пытаемся анализировать их с точки зрения системы линейных уравнений, и пытаемся ее решать. Это неверно, ограничения — это не уравнения. Подходить к ним таким образом ошибочно.
Требования и параметры — это принципиально разные вещи. Мы привыкли работать с ограничениями так, как будто они бывают просто разных приоритетов, но важно понимать и помнить, что принципиально — и с точки зрения математики, и внутри при решении — ограничения типа required и все остальные решаются принципиально по-разному.
Полезные ссылки:
Solving Linear Arithmetic Constraints for User Interface Applications
The Cassowary Linear Constraint Solving Algorithm
Constraints as s Design Pattern
Auto Layout Guide by Apple
WWDC 2018 Session 220 High Performance Auto Layout
Магия UILabel или приватное API Auto Layout — Александр Горемыкин
Блог Яндекс.Карт на Medium
Кстати, мы уже приняли доклад Антона в программу AppsConf 2019. Напомню, мы перенесли AppsConf с осени на весну, и следующая самая полезная конференция для мобильных разработчиков пройдет 22 и 23 апреля. Пора-пора задуматься о теме для выступления и подать доклад, или обсудить с руководителем важность походов на конференцию и забронировать билет.

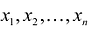
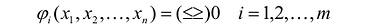
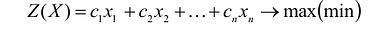
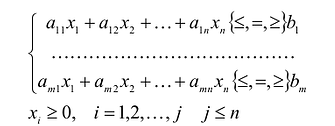
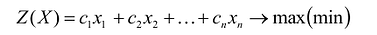
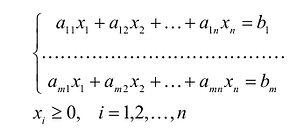
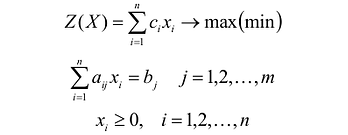
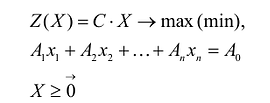
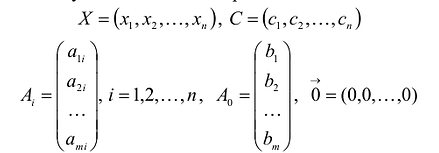
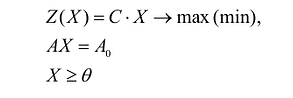
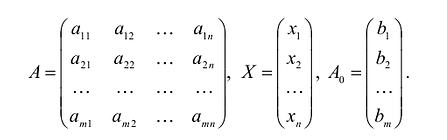
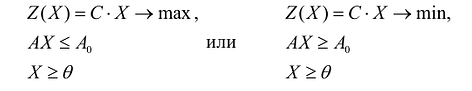
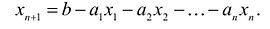
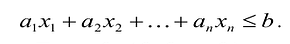
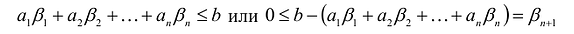
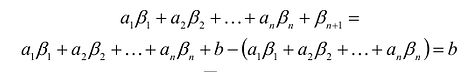
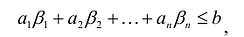
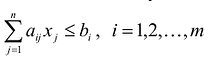
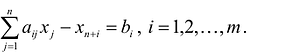
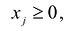
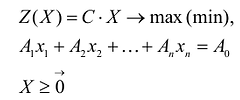
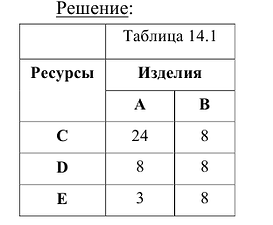
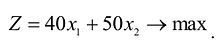
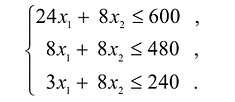
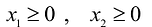
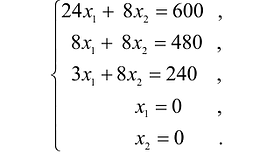
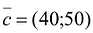
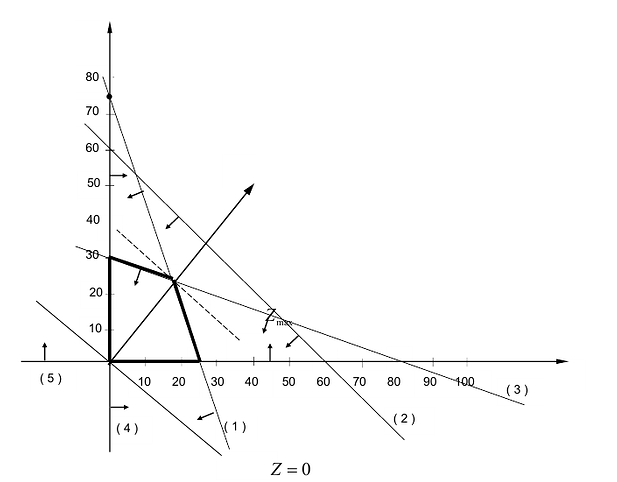
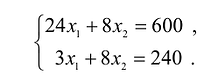
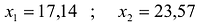
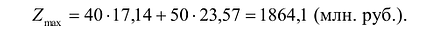
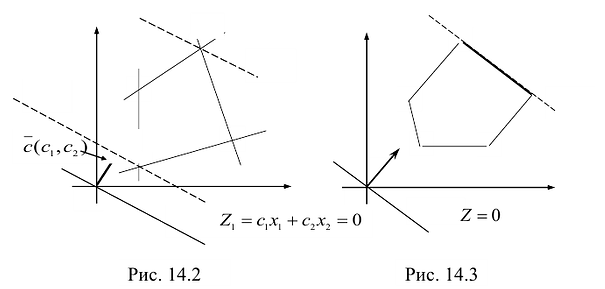
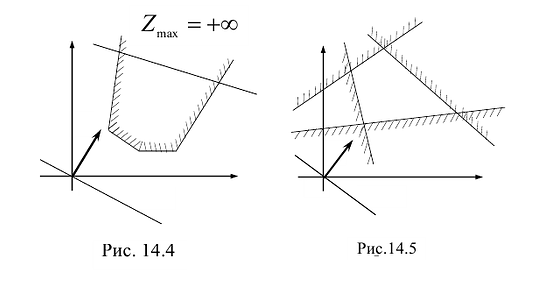
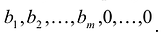
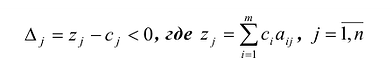
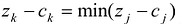
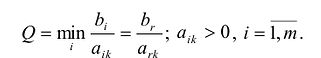
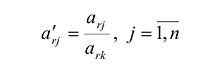
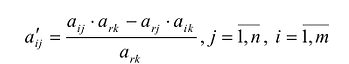
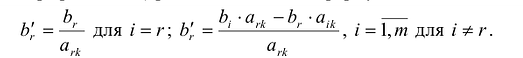
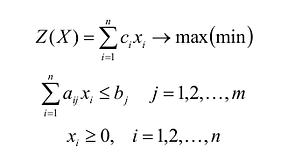
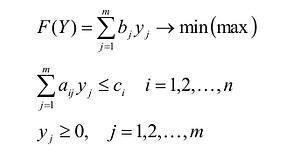
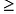
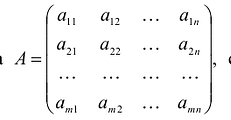 , составленная из коэффициентов при неизвестных в системе ограничении исходной задачи, и аналогичная матрица
, составленная из коэффициентов при неизвестных в системе ограничении исходной задачи, и аналогичная матрица 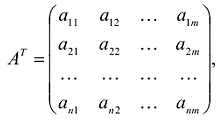 , в двойственной задаче получаются друг из друга транспонированием;
, в двойственной задаче получаются друг из друга транспонированием;
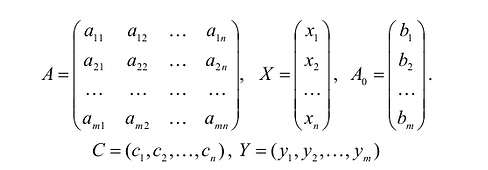
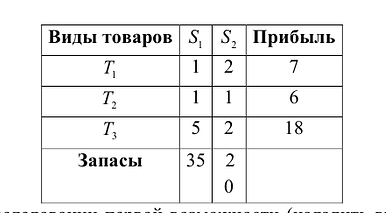
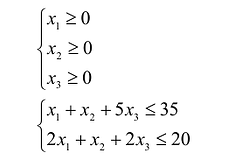
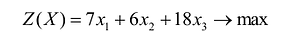
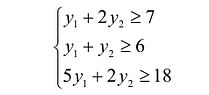
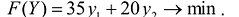
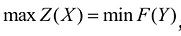
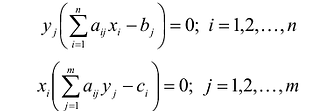
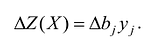
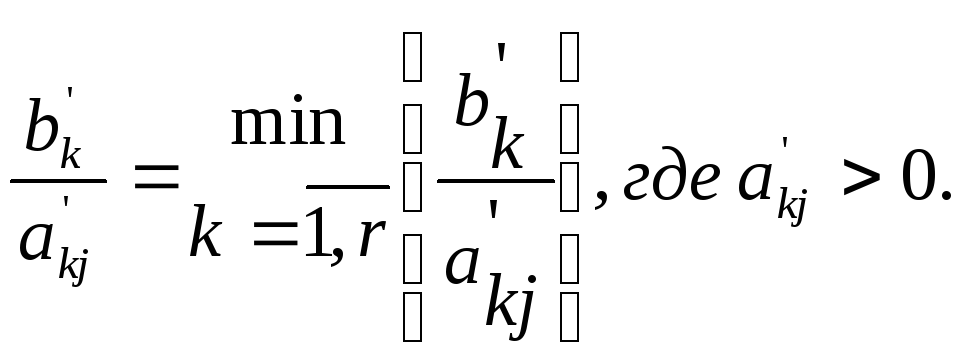
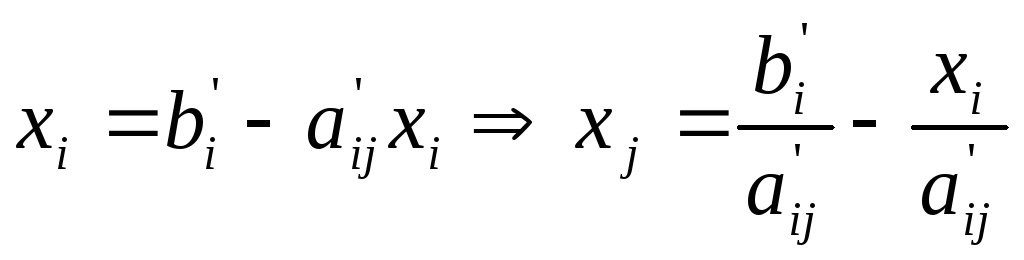


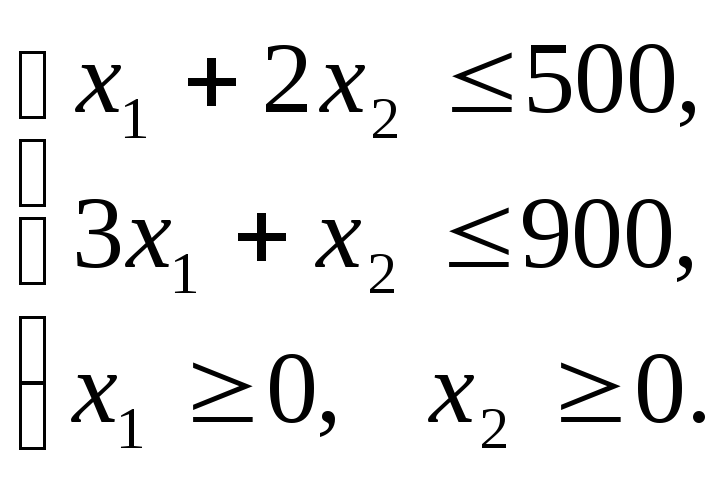




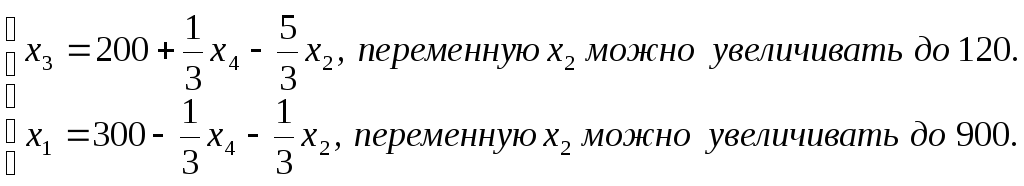








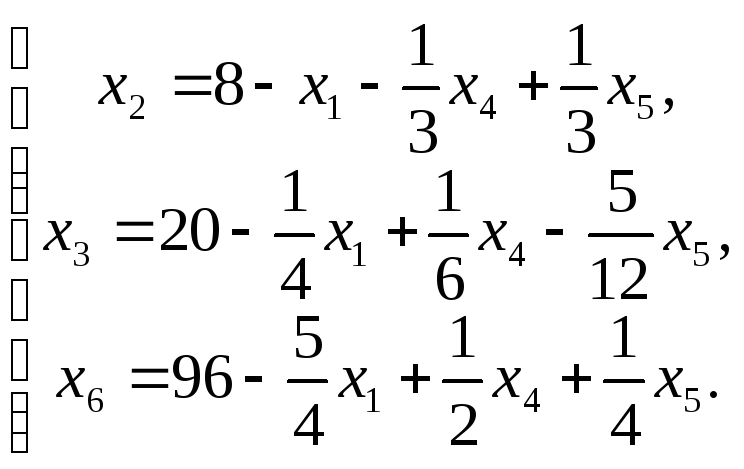

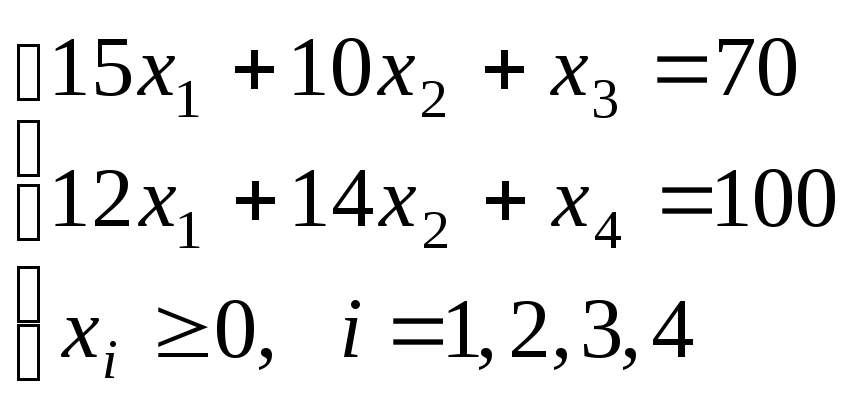

 18
18
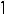
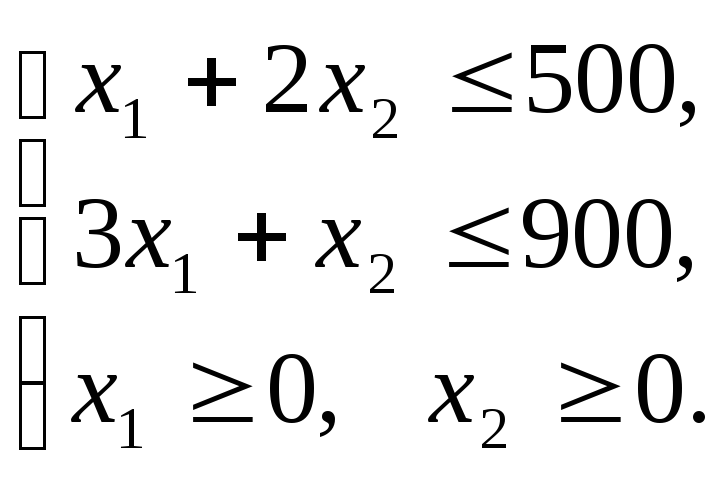
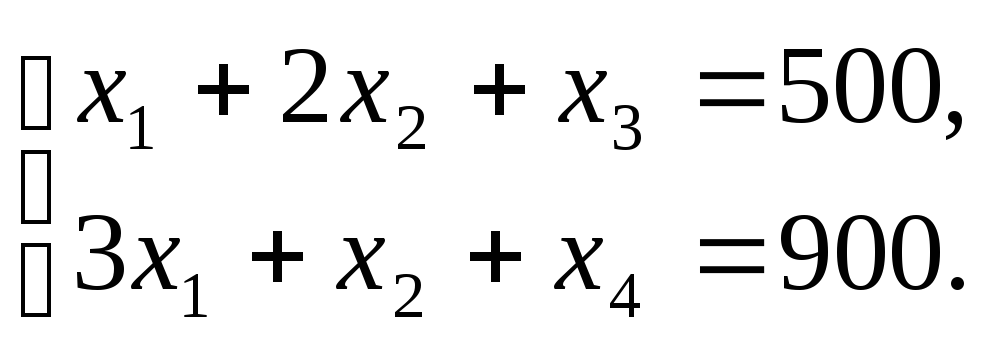
 00
00 2
2 20
20

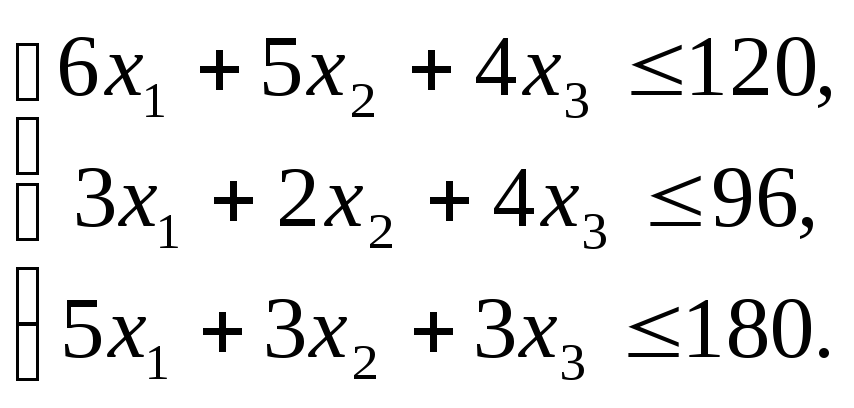

 4
4 16
16
 2
2