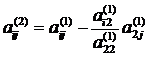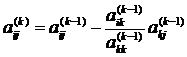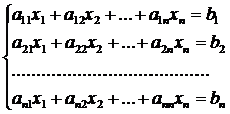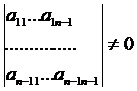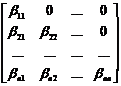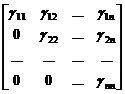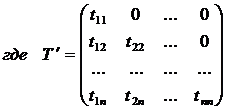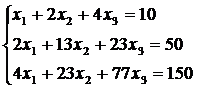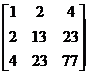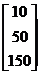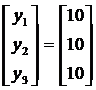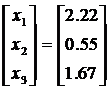Как составить систему уравнений по корням

Как решать систему уравнений

О чем эта статья:

8 класс, 9 класс, ЕГЭ/ОГЭ

Основные понятия

Алгебра в 8 и 9 классе становится сложнее. Но если изучать темы последовательно и регулярно практиковаться в тетрадке и онлайн — ходить на уроки математики будет не так страшно.

Уравнение — это математическое равенство, в котором неизвестна одна или несколько величин. Значение неизвестных нужно найти так, чтобы при их подстановке в исходное уравнение получилось верное числовое равенство.

Например, возьмем 3 + 4 = 7. При вычислении левой части получается верное числовое равенство, то есть 7 = 7.

Уравнением можно назвать, например, равенство 3 + x = 7 с неизвестной переменной x, значение которой нужно найти. Результат должен быть таким, чтобы знак равенства был оправдан, и левая часть равнялась правой.

Система уравнений — это несколько уравнений, для которых надо найти значения неизвестных, каждое из которых соответствует данным уравнениям.

Так как существует множество уравнений, составленных с их использованием систем уравнений также много. Поэтому для удобства изучения существуют отдельные группы по схожим характеристикам. Рассмотрим способы решения систем уравнений.

Линейное уравнение с двумя переменными

Уравнение вида ax + by + c = 0 называется линейным уравнением с двумя переменными x и y, где a, b, c — числа.

Решением этого уравнения называют любую пару чисел (x; y), которая соответствует этому уравнению и обращает его в верное числовое равенство.

Теорема, которую нужно запомнить: если в линейном уравнение есть хотя бы один не нулевой коэффициент при переменной — его графиком будет прямая линия.

Вот алгоритм построения графика ax + by + c = 0, где a ≠ 0, b ≠ 0:

Дать переменной 𝑥 конкретное значение x = x₁, и найти значение y = y₁ при ax₁ + by + c = 0.

Дать x другое значение x = x₂, и найти соответствующее значение y = y₂ при ax₂ + by + c = 0.

Построить на координатной плоскости xy точки: (x₁; y₁); (x₂; y₂).

Провести прямую через эти две точки и вуаля — график готов.

Нужно быстро привести знания в порядок перед экзаменом? Записывайтесь на курсы ЕГЭ по математике в Skysmart!

Система двух линейных уравнений с двумя переменными

Для ax + by + c = 0 можно сколько угодно раз брать произвольные значение для x и находить значения для y. Решений в таком случае может быть бесчисленное множество.

Система линейных уравнений (ЛУ) с двумя переменными образуется в случае, когда x и y связаны не одним, а двумя уравнениями. Такая система может иметь одно решение или не иметь решений совсем. Выглядит это вот так:

Из первого линейного уравнения a₁x + b₁y + c₁ = 0 можно получить линейную функцию, при условии если b₁ ≠ 0: y = k₁x + m₁. График — прямая линия.

Из второго ЛУ a₂x + b₂y + c₂ = 0 можно получить линейную функцию, если b₂ ≠ 0: y = k₂x + m₂. Графиком снова будет прямая линия.

Можно записать систему иначе:

Множеством решений первого ЛУ является множество точек, лежащих на определенной прямой, аналогично и для второго ЛУ. Если эти прямые пересекаются — у системы есть единственное решение. Это возможно при условии, если k₁ ≠ k₂.

Две прямые могут быть параллельны, а значит, они никогда не пересекутся и система не будет иметь решений. Это возможно при следующих условиях: k₁ = k₂ и m₁ ≠ m₂.

Две прямые могут совпасть, и тогда каждая точка будет решением, а у системы будет бесчисленное множество решений. Это возможно при следующих условиях: k₁ = k₂ и m₁ = m₂.

Метод подстановки

Разберем решение систем уравнений методом подстановки. Вот алгоритм при переменных x и y:

Выразить одну переменную через другую из более простого уравнения системы.

Подставить то, что получилось на место этой переменной в другое уравнение системы.

Решить полученное уравнение, найти одну из переменных.

Подставить поочередно каждый из найденных корней в уравнение, которое получили на первом шаге, и найти второе неизвестное значение.

Записать ответ. Ответ принято записывать в виде пар значений (x; y).

Потренируемся решать системы линейных уравнений методом подстановки.

Пример 1

Решите систему уравнений:

x − y = 4
x + 2y = 10

Выразим x из первого уравнения:

x − y = 4
x = 4 + y

Подставим получившееся выражение во второе уравнение вместо x:

x + 2y = 10
4 + y + 2y = 10

Решим второе уравнение относительно переменной y:

4 + y + 2y = 10
4 + 3y = 10
3y = 10 − 4
3y = 6
y = 6 : 3
y = 2

Полученное значение подставим в первое уравнение вместо y и решим уравнение:

x − y = 4
x − 2 = 4
x = 4 + 2
x = 6

Ответ: (6; 2).

Пример 2

Решите систему линейных уравнений:

x + 5y = 7
3x = 4 + 2y

Сначала выразим переменную x из первого уравнения:

x + 5y = 7
x = 7 − 5y

Выражение 7 − 5y подставим вместо переменной x во второе уравнение:

3x = 4 + 2y
3 (7 − 5y) = 4 + 2y

Решим второе линейное уравнение в системе:

3 (7 − 5y) = 4 + 2y
21 − 15y = 4 + 2y
21 − 15y − 2y = 4
21 − 17y = 4
17y = 21 − 4
17y = 17
y = 17 : 17
y = 1

Подставим значение y в первое уравнение и найдем значение x:

x + 5y = 7
x + 5 = 7
x = 7 − 5
x = 2

Ответ: (2; 1).

Пример 3

Решите систему линейных уравнений:

x − 2y = 3
5x + y = 4

Из первого уравнения выразим x:

x − 2y = 3
x = 3 + 2y

Подставим 3 + 2y во второе уравнение системы и решим его:

5x + y = 4
5 (3 + 2y) + y = 4
15 + 10y + y = 4
15 + 11y = 4
11y = 4 − 15
11y = −11
y = −11 : 11
y = −1

Подставим получившееся значение в первое уравнение и решим его:

x − 2y = 3
x − 2 (−1) = 3
x + 2 = 3
x = 3 − 2
x = 1

Ответ: (1; −1).

Метод сложения

Теперь решим систему уравнений способом сложения. Алгоритм с переменными x и y:

При необходимости умножаем почленно уравнения системы, подбирая множители так, чтобы коэффициенты при одной из переменных стали противоположными числами.

Складываем почленно левые и правые части уравнений системы.

Решаем получившееся уравнение с одной переменной.

Находим соответствующие значения второй переменной.

Запишем ответ в в виде пар значений (x; y).

Система линейных уравнений с тремя переменными

Системы ЛУ с тремя переменными решают так же, как и с двумя. В них присутствуют три неизвестных с коэффициентами и свободный член. Выглядит так:

Решений в таком случае может быть бесчисленное множество. Придавая двум переменным различные значения, можно найти третье значение. Ответ принято записывать в виде тройки значений (x; y; z).

Если x, y, z связаны между собой тремя уравнениями, то образуется система трех ЛУ с тремя переменными. Для решения такой системы можно применять метод подстановки и метод сложения.

Решение задач

Разберем примеры решения систем уравнений.

Задание 1. Как привести уравнение к к стандартному виду ах + by + c = 0?

5x − 8y = 4x − 9y + 3

5x − 8y = 4x − 9y + 3

5x − 8y − 4x + 9y = 3

Задание 2. Как решать систему уравнений способом подстановки

Выразить у из первого уравнения:

Подставить полученное выражение во второе уравнение:

Найти соответствующие значения у:

Задание 3. Как решать систему уравнений методом сложения

1. Решение систем линейных уравнений начинается с внимательного просмотра задачи. Заметим, что можно исключить у. Для этого умножим первое уравнение на минус два и сложим со вторым:

1. Решаем полученное квадратное уравнение любым способом. Находим его корни:

1. Найти у, подставив найденное значение в любое уравнение:

1. Ответ: (1; 1), (1; -1).

Задание 4. Решить систему уравнений

Решим второе уравнение и найдем х = 2, х = 5. Подставим значение переменной х в первое уравнение и найдем соответствующее значение у.

Задание 5. Как решить систему уравнений с двумя неизвестными

При у = -2 первое уравнение не имеет решений, при у = 2 получается:

Решение систем линейных уравнений алгоритмы общих и частных методов нахождения корней, основные правила и теоремы и примеры их использования, онлайн калькулятор

Совокупность математических записей, из которых каждая является линейным алгебраическим равенством первой степени, называется системой линейных уравнений. Её решение — это классическая задача алгебры, определяющая объекты и методы. Существует несколько принципиально разных способов нахождения ответа. Каждый из них имеет достоинства и недостатки, но выбор метода зависит лишь только от личных предпочтений решающего.

Понятия и обозначения

Для измерения геометрических или физических величин в математике используют действительное число — вещественное. В уравнении под ним понимают все свободные члены или неизвестные переменные. Вычисление линейных алгебраических уравнений играет важную роль в различных математических задачах: численных методах, программировании, эконометрике.

Общий вид системы линейных уравнений (СЛАУ) в классическом понимании представляют следующим образом:

a11 * n 1 + a 12 * n 2 + …+a 1x n x = c 1.

a21 * n 1 + a 22 * n 2 + …+a 2x n x = c 2.

as1 * n 1 + a 12 * n 2 + …+a 1x n x = c s.

В этой записи s — это количество уравнений, x — число переменных, а n — переменная которую необходимо вычислить. Предполагается что a и b это известные свободные члены. Индексы обозначают порядковый номер уравнения. Первый символ — расположение строчки, а второй — позиция произведения переменной и свободного члена.

Если эти члены отличные от нуля, то система называется неоднородной, в ином же случае однородной. Квадратной системой называется совокупность уравнений, когда их число совпадает с количеством неизвестных. Существует понятие и неопределённой системы. Это совокупность, при которой неизвестных больше числа уравнений. Если наоборот, то система считается переопределенной. В литературе её ещё часто называют прямоугольной.

Система считается решаемой, когда множество членов X соответствует такому набору чисел, что при их подстановке вместо n вся система обратится в тождество. Если существует хотя бы одно решение, система называется совместной. Ответы, превращающие уравнения в равенства, при которых переменные не совпадают, считаются различными.

Существует четыре способа развязывания системы уравнений:

• способ подстановки;
• использование новых переменных;
• алгебраическое сложение;
• матричный метод.

Вид используемого алгоритма зависит от типа примера. Метод алгебраического сложения применяют, когда в задании лишь одно неизвестное, а коэффициенты противоположны или равны. Если же хотя бы в одной из формул коэффициент равен единице, то удобнее будет решить систему уравнений методом подстановки. В иных случаях используют матрицы.

Алгебраическое сложение

Способ заключается в сложении или вычитании выражений. Это довольно простой способ и в то же время эффективный. Алгоритм нахождения ответа для равенств с двумя переменными n и m сводится к следующему:

• уравниванию модулей коэффициентов при любом из неизвестных;
• сложению или вычитанию равенства;
• вычисления составленного выражения;
• прогонки каждого найденного корня через первую или вторую строчку системы уравнений;
• нахождению второго неизвестного.

То есть после выполнения арифметических действий с уравнениями должно получиться одно выражение с одним неизвестным. Затем находят значение этой переменной и в него подставляют полученный корень. Например, нужно узнать, какие корни системы, состоящей из двух строчек, превращают её в тождество:

В первую очередь необходимо сложить равенства между собой. В итоге получится:

Подставив поочерёдно в каждое равенство найденные корни можно найти второе неизвестное. Для корня n = – 5 ответом будет:

Соответственно, корнями будут числа два и минус два. Аналогичные действия необходимо выполнить и для корня другого знака n = 5. В итоге получится, что пары (− 5; − 2), (− 5; 2), (5; − 2), (5 ; 2) являются нужным ответом. При достаточном опыте подробно описывать решение не обязательно.

Существуют системы, требующие подготовительного этапа. Например, такого вида:

Исключить здесь сразу переменную не выйдет. Если умножить все члены первой строчки на тройку, а второй на четвёрку, получится запись:

9 * n – 12 * m = 15.

8 * n + 12 * m = 28.

Теперь равенства можно сложить, тем самым исключив переменную m. Затем система решается по базисному алгоритму. Чтобы понять, можно ли решить систему этим методом, следует предварительно её проанализировать. Необходимое условие заключается в том, что коэффициенты второй переменной должны быть одинаковыми по модулю, но противоположными по знаку.

Метод подстановки

Систему равенств возможно решить и способом подстановки. Используя любое из уравнений, можно выразить любую из неизвестных переменных, а затем подставить её в другое равенство. Алгоритм использования метода следующий:

• через n в одном из уравнений выражают m;
• подставляют полученное равенство вместо n в другое тождество;
• решают уравнение и находя m;
• поочерёдно подставляют найденные корни и получают ответ.

Например, нужно проверить, все ли целые корни могут быть у системы:

10 * n + 3 * m = 17.

Выразив m через n можно записать равенство: n = (8* m + 16) / 5. Так как n одинаково в обоих уравнениях, то следует подставить полученное тождество и записать: 10* n + 3*(8* n +16) / 5 = 17. Отсюда уже просто найти корень. Он будет равен дроби 1/2. Подставив его вместо n легко вычислить и второй корень: m = (8 * n + 16) / 5 = 4. Таким образом, у системы будет только один целый корень. При желании проверить ответ можно решить систему другим методом.

Использование матриц

Для систем с произвольным числом уравнений и неизвестных используют другие методы. Если система состоит из нелинейных дифференциальных уравнений с постоянными коэффициентами, то используют матричный способ. Этот метод предполагает применение обратной матрицы.

Пусть дана система с тремя неизвестными х1, х2, х3. Нужно найти значения, при которых равенства станут верными. Для нахождения решений используют три матрицы:

• Коэффициент системы. При этом её определитель не должен быть равным нулю.
• Вектора неизвестных. Именно его понадобится найти.
• Столбца свободных членов.

Базисное решение строят на произведении первой и второй матрицы. В результате получают матрицу размером три на один. То есть вектор-столбец с тремя элементами. После выполнения действия получится, что системный вектор будет равен левой части системы и соответствовать третьей матрице. Таким образом, обозначив матрицы буквами А, Б, В, можно записать выражение А * Б = В и найти необходимую Б.

При умножении на А-1 (обратную матрицу) получают равенство: Е * Б = А-1 * В, где Е – единичная матрица получена из совместимости прямой и обратной. Так как при произведении с единичной матрицей значения не изменяются, то решением системы будет формула: Б = А-1 * В.

Способ Гаусса-Жордана

Частным случаем решения системы является Метод Гаусса — Жордана. Суть решения основана на составлении специальной таблицы. В первый столбец заносятся известные значения, то есть величины, расположенные после равно, а в три других коэффициенты, стоящие после неизвестных. Чтобы приступить к решению, необходимо выполнить три шага:

• выбрать ключевой элемент из первых трёх столбцов;
• переписать строчку с ключевым значением, предварительно разделив все элементы на это значение;
• переписать оставшиеся элементы, при этом вычитая из него произведение соответствующих ему чисел.

В полученной новой матрице снова выбирают ключевой элемент и выполняют все действия снова. Шаги повторяют до тех пор, пока не получится матрица, состоящая из нулей и единиц. Значения корней системы будут находиться на пересечении столбцов со строчками напротив единиц.

Этот метод используют только при выполнении условия совместности. Его ещё называют способом простой итерации. Он был доказан и оптимизирован Зейделем. С помощью итерационного метода можно посчитать систему А* Б = В с точностью “е”. Составляют n уравнение на сходимость, а затем на точность. Затем из первого уравнения выражают n1, второго n2, третьего n3 и так далее. Новые n с индексом i +1 считаются через старые i. Зейдель предложил расширить решение и добавить снова для счёта индекс i+1.

Это фундаментальные способы решения сложных систем уравнений. Они трудные, требуют опыта и внимательности. Поэтому существуют специальные онлайн-калькуляторы по методу Гаусса с подробным решением, помогающие исследовать систему любой численности.

Теорема Кронекера — Капелли

Применяется она при проведении исследований без непосредственного решения. То есть для записи эквивалентной совокупности алгебраических уравнений с их минимальным числом. Теорема говорит о следующем: система уравнений А * Б = В имеет решение только тогда, когда ранг А равен (А, В), где последнее расширенная матрица, полученная из первого члена путём приписывания столбца В.

Это утверждение обобщает различные виды СЛАУ:

• Несовместные – которые определяют при условии, что их ранг меньше ранга расширенной матрицы. Существование корней невозможно.
• Совместные неопределённые – системы, имеющие бесконечное множество решений. В этом случае ранги равны, а количество неизвестных будет меньше.
• Совместно определённые – в этом случае ранг равен расширенной матрице и количеству неизвестных. Точное решение будет одно.

Выводом из этой теоремы является то, что число главной переменной совокупности будет всегда равно рангу системы. При этом столбец свободных членов представляет собой линейную комбинацию столбцов матрицы А.

Решение Крамера

Пожалуй, это один из самых простых способов нахождения корней уравнений. Для решения строят несколько матриц. Основная получается из коэффициентов, стоящих при неизвестных. Она обозначается символом дельта. Вторую, дельта-икс, образуют из основной матрицы заменой первого столбца на ответы уравнений. Следующая, дельта-игрек, строится с заменой в основной матрице второго столбца на значения ответов и так далее.

Затем вычисляют дискриминант этих матриц, то есть их определитель. Для его поиска можно использовать способ треугольника или разложения. Первый подходит для простых матриц. Находят его как разницу умножения чисел, стоящих в матрице крест-накрест. Второй же применим для матриц, содержащих три и более строк. При нахождении выбирают одну из них и раскладывают матрицу.

Как только все дискриминанты найдены, используют правило Крамера: n = Δn/ Δ. Подставляют значения, находят ответ. Стоит отметить, что много интернет-порталов, предлагающих услугу расчётов СЛАУ, используют для вычислений онлайн-метод Крамера.

Удобные онлайн-калькуляторы

В некоторых случаях решение СЛАУ онлайн будет хорошим подспорьем для того, чтобы разобраться в различных правилах, используемых при решениях. Из популярных интернет-сервисов, позволяющих найти корни систем, можно отметить: kontrolnaya-rabota, mathsolution, planetcalc, allcalc. Использовать эти сайты-решатели смогут даже слабо подготовленные пользователи, имеющие общее представление о методах решений.

Для выполнения расчёта необходимо ввести параметры системы и нажать кнопку «Рассчитать». При этом можно выбрать метод, на базе которого будут проводиться вычисления. Удобным является и то, что полученный расчёт сопровождается объяснениями.

На этих порталах также можно посмотреть примеры и правила решений. Некоторые калькуляторы могут построить и график системы. Например, kontrolnaya-rabota. Для этого на сайте нужно выбрать раздел «Графическое решение уравнений онлайн» и ввести исследуемую систему равенств.

Системы линейных уравнений

Линейные уравнения с двумя переменными

У школьника имеется 200 рублей, чтобы пообедать в школе. Пирожное стоит 25 рублей, а чашка кофе 10 рублей. Сколько пирожных и чашек кофе можно накупить на 200 рублей?

Обозначим количество пирожных через x , а количество чашек кофе через y . Тогда стоимость пирожных будет обозначаться через выражение 25x , а стоимость чашек кофе через 10y .

25x — стоимость x пирожных
10y — стоимость y чашек кофе

Итоговая сумма должна равняться 200 рублей. Тогда получится уравнение с двумя переменными x и y

Сколько корней имеет данное уравнение?

Всё зависит от аппетита школьника. Если он купит 6 пирожных и 5 чашек кофе, то корнями уравнения будут числа 6 и 5.

Говорят, что пара значений 6 и 5 являются корнями уравнения 25x + 10y = 200 . Записывается как (6; 5) , при этом первое число является значением переменной x , а второе — значением переменной y .

6 и 5 не единственные корни, которые обращают уравнение 25x + 10y = 200 в тождество. При желании на те же 200 рублей школьник может купить 4 пирожных и 10 чашек кофе:

В этом случае корнями уравнения 25x + 10y = 200 является пара значений (4; 10) .

Более того, школьник может вообще не покупать кофе, а купить пирожные на все 200 рублей. Тогда корнями уравнения 25x + 10y = 200 будут значения 8 и 0

Или наоборот, не покупать пирожные, а купить кофе на все 200 рублей. Тогда корнями уравнения 25x + 10y = 200 будут значения 0 и 20

Попробуем перечислить все возможные корни уравнения 25x + 10y = 200 . Условимся, что значения x и y принадлежат множеству целых чисел. И пусть эти значения будут бóльшими или равными нулю:

Так будет удобно и самому школьнику. Пирожные удобнее покупать целыми, чем к примеру несколько целых пирожных и половину пирожного. Кофе также удобнее брать целыми чашками, чем к примеру несколько целых чашек и половину чашки.

Заметим, что при нечетном x невозможно достичь равенства ни при каком y . Тогда значениями x будут следующие числа 0, 2, 4, 6, 8. А зная x можно без труда определить y

Таким образом, мы получили следующие пары значений (0; 20), (2; 15), (4; 10), (6; 5), (8; 0). Эти пары являются решениями или корнями уравнения 25x + 10y = 200 . Они обращают данное уравнение в тождество.

Уравнение вида ax + by = c называют линейным уравнением с двумя переменными. Решением или корнями этого уравнения называют пару значений ( x; y ), которая обращает его в тождество.

Отметим также, что если линейное уравнение с двумя переменными записано в виде ax + b y = c , то говорят, что оно записано в каноническом (нормальном) виде.

Некоторые линейные уравнения с двумя переменными могут быть приведены к каноническому виду.

Например, уравнение 2(16x + 3y − 4) = 2(12 + 8x − y) можно привести к виду ax + by = c . Раскроем скобки в обеих частях этого уравнения, получим 32x + 6y − 8 = 24 + 16x − 2y . Слагаемые, содержащие неизвестные сгруппируем в левой части уравнения, а слагаемые свободные от неизвестных — в правой. Тогда получим 32x − 16x + 6y + 2y = 24 + 8 . Приведём подобные слагаемые в обеих частях, получим уравнение 16x + 8y = 32. Это уравнение приведено к виду ax + by = c и является каноническим.

Рассмотренное ранее уравнение 25x + 10y = 200 также является линейным уравнением с двумя переменными в каноническом виде . В этом уравнении параметры a , b и c равны значениям 25, 10 и 200 соответственно.

На самом деле уравнение ax + by = c имеет бесчисленное множество решений. Решая уравнение 25x + 10y = 200, мы искали его корни только на множестве целых чисел. В результате получили несколько пар значений, которые обращали данное уравнение в тождество. Но на множестве рациональных чисел уравнение 25x + 10y = 200 будет иметь бесчисленное множество решений.

Для получения новых пар значений, нужно взять произвольное значение для x , затем выразить y . К примеру, возьмем для переменной x значение 7. Тогда получим уравнение с одной переменной 25 × 7 + 10y = 200 в котором можно выразить y

Пусть x = 15 . Тогда уравнение 25x + 10y = 200 примет вид 25 × 15 + 10y = 200. Отсюда находим, что y = −17,5

Пусть x = −3 . Тогда уравнение 25x + 10y = 200 примет вид 25 × (−3) + 10y = 200. Отсюда находим, что y = 27,5

Система двух линейных уравнений с двумя переменными

Для уравнения ax + by = c можно сколько угодно раз брать произвольные значение для x и находить значения для y . Отдельно взятое такое уравнение будет иметь бесчисленное множество решений.

Но бывает и так, что переменные x и y связаны не одним, а двумя уравнениями. В этом случае они образуют так называемую систему линейных уравнений с двумя переменными. Такая система уравнений может иметь одну пару значений (или по-другому: «одно решение»).

Может случиться и так, что система вовсе не имеет решений. Бесчисленное множество решений система линейных уравнений может иметь в редких и в исключительных случаях.

Два линейных уравнения образуют систему тогда, когда значения x и y входят в каждое из этих уравнений.

Вернемся к самому первому уравнению 25x + 10y = 200 . Одной из пар значений для этого уравнения была пара (6; 5) . Это случай, когда на 200 рублей можно можно было купить 6 пирожных и 5 чашек кофе.

Составим задачу так, чтобы пара (6; 5) стала единственным решением для уравнения 25x + 10y = 200 . Для этого составим ещё одно уравнение, которое связывало бы те же x пирожных и y чашечек кофе.

Поставим текст задачи следующим образом:

«Школьник купил на 200 рублей несколько пирожных и несколько чашек кофе. Пирожное стоит 25 рублей, а чашка кофе 10 рублей. Сколько пирожных и чашек кофе купил школьник, если известно что количество пирожных на одну единицу больше количества чашек кофе?»

Первое уравнение у нас уже есть. Это уравнение 25x + 10y = 200 . Теперь составим уравнение к условию «количество пирожных на одну единицу больше количества чашек кофе» .

Количество пирожных это x , а количество чашек кофе это y . Можно записать эту фразу с помощью уравнения x − y = 1. Это уравнение будет означать, что разница между пирожными и кофе составляет 1.

Либо второе уравнение можно записать как x = y + 1 . Это уравнение означает, что количество пирожных на единицу больше, чем количество чашек кофе. Поэтому для получения равенства, к количеству чашек кофе прибавлена единица. Это легко можно понять, если воспользоваться моделью весов, которые мы рассматривали при изучении простейших задач:

Получили два уравнения: 25x + 10y = 200 и x = y + 1. Поскольку значения x и y , а именно 6 и 5 входят в каждое из этих уравнений , то вместе они образуют систему. Запишем эту систему. Если уравнения образуют систему, то они обрамляются знаком системы. Знак системы это фигурная скобка:

Давайте решим данную систему. Это позволит увидеть, как мы придём к значениям 6 и 5. Существует много методов решения таких систем. Рассмотрим наиболее популярные из них.

Метод подстановки

Название этого метода говорит само за себя. Суть его заключается в том, чтобы одно уравнение подставить в другое, предварительно выразив одну из переменных.

В нашей системе ничего выражать не нужно. Во втором уравнении x = y + 1 переменная x уже выражена. Эта переменная равна выражению y + 1 . Тогда можно подставить это выражение в первое уравнение вместо переменной x

После подстановки выражения y + 1 в первое уравнение вместо x , получим уравнение 25(y + 1) + 10y = 200 . Это линейное уравнение с одной переменной. Такое уравнение решить довольно просто:

Мы нашли значение переменной y . Теперь подставим это значение в одно из уравнений и найдём значение x . Для этого удобно использовать второе уравнение x = y + 1 . В него и подставим значение y

Значит пара (6; 5) является решением системы уравнений, как мы и задумывали. Выполняем проверку и убеждаемся, что пара (6; 5) удовлетворяет системе:

Пример 2. Решить методом подстановки следующую систему уравнений:

Подставим первое уравнение x = 2 + y во второе уравнение 3x − 2y = 9 . В первом уравнении переменная x равна выражению 2 + y . Это выражение и подставим во второе уравнение вместо x

Теперь найдём значение x . Для этого подставим значение y в первое уравнение x = 2 + y

Значит решением системы является пара значение (5; 3)

Пример 3. Решить методом подстановки следующую систему уравнений:

Здесь в отличие от предыдущих примеров, одна из переменных не выражена явно.

Чтобы подставить одно уравнение в другое, сначала нужно выразить одну из переменных.

Выражать желательно ту переменную, которая имеет коэффициент единицу. Коэффициент единицу имеет переменная x , которая содержится в первом уравнении x + 2y = 11 . Эту переменную и выразим.

После выражения переменной x , наша система примет следующий вид:

Теперь подставим первое уравнение во второе и найдем значение y

Подставим y в первое уравнение и найдём x

Значит решением системы является пара значений (3; 4)

Конечно, выражать можно и переменную y . Корни от этого не изменятся. Но если выразить y, получится не очень-то и простое уравнение, на решение которого уйдет больше времени. Выглядеть это будет следующим образом:

Видим, что в данном примере выражать x намного удобнее, чем выражать y .

Пример 4. Решить методом подстановки следующую систему уравнений:

Выразим в первом уравнении x . Тогда система примет вид:

Подставим первое уравнение во второе и найдём y

Подставим y в первое уравнение и найдём x . Можно воспользоваться изначальным уравнением 7x + 9y = 8 , либо воспользоваться уравнением , в котором выражена переменная x . Этим уравнением и воспользуемся, поскольку это удобно:

Значит решением системы является пара значений (5; −3)

Метод сложения

Метод сложения заключается в том, чтобы почленно сложить уравнения, входящие в систему. Это сложение приводит к тому, что образуется новое уравнение с одной переменной. А решить такое уравнение довольно просто.

Решим следующую систему уравнений:

Сложим левую часть первого уравнения с левой частью второго уравнения. А правую часть первого уравнения с правой частью второго уравнения. Получим следующее равенство:

Приведем подобные слагаемые:

В результате получили простейшее уравнение 3x = 27 корень которого равен 9. Зная значение x можно найти значение y . Подставим значение x во второе уравнение x − y = 3 . Получим 9 − y = 3 . Отсюда y = 6 .

Значит решением системы является пара значений (9; 6)

Пример 2. Решить следующую систему уравнений методом сложения:

Сложим левую часть первого уравнения с левой частью второго уравнения. А правую часть первого уравнения с правой частью второго уравнения. В получившемся равенстве приведем подобные слагаемые:

В результате получили простейшее уравнение 5 x = 20, корень которого равен 4. Зная значение x можно найти значение y . Подставим значение x в первое уравнение 2 x + y = 11 . Получим 8 + y = 11 . Отсюда y = 3 .

Значит решением системы является пара значений (4;3)

Процесс сложения подробно не расписывают. Его нужно выполнять в уме. При сложении оба уравнения должны быть приведены к каноническому виду. То есть к виду ax + by = c .

Из рассмотренных примеров видно, что основная цель сложения уравнений это избавление от одной из переменных. Но не всегда удаётся сразу решить систему уравнений методом сложения. Чаще всего систему предварительно приводят к виду, при котором можно сложить уравнения, входящие в эту систему.

Например, систему можно сразу решить методом сложения. При сложении обоих уравнений, слагаемые y и −y исчезнут, поскольку их сумма равна нулю. В результате образуется простейшее уравнение 11x = 22 , корень которого равен 2. Затем можно будет определить y равный 5.

А систему уравнений методом сложения сразу решить нельзя, поскольку это не приведёт к исчезновению одной из переменных. Сложение приведет к тому, что образуется уравнение 8x + y = 28 , имеющее бесчисленное множество решений.

Если обе части уравнения умножить или разделить на одно и то же число, не равное нулю, то получится уравнение равносильное данному. Это правило справедливо и для системы линейных уравнений с двумя переменными. Одно из уравнений (или оба уравнения) можно умножить на какое-нибудь число. В результате получится равносильная система, корни которой будут совпадать с предыдущей.

Вернемся к самой первой системе , которая описывала сколько пирожных и чашек кофе купил школьник. Решением этой системы являлась пара значений (6; 5) .

Умножим оба уравнения, входящие в эту систему на какие-нибудь числа. Скажем первое уравнение умножим на 2, а второе на 3

В результате получили систему
Решением этой системы по-прежнему является пара значений (6; 5)

Это значит, что уравнения входящие в систему можно привести к виду, пригодному для применения метода сложения.

Вернемся к системе , которую мы не смогли решить методом сложения.

Умножим первое уравнение на 6, а второе на −2

Тогда получим следующую систему:

Сложим уравнения, входящие в эту систему. Сложение компонентов 12x и −12x даст в результате 0, сложение 18y и 4y даст 22y , а сложение 108 и −20 даст 88. Тогда получится уравнение 22y = 88 , отсюда y = 4 .

Если первое время тяжело складывать уравнения в уме, то можно записывать как складывается левая часть первого уравнения с левой частью второго уравнения, а правая часть первого уравнения с правой частью второго уравнения:

Зная, что значение переменной y равно 4, можно найти значение x. Подставим y в одно из уравнений, например в первое уравнение 2x + 3y = 18 . Тогда получим уравнение с одной переменной 2x + 12 = 18 . Перенесем 12 в правую часть, изменив знак, получим 2x = 6 , отсюда x = 3 .

Пример 4. Решить следующую систему уравнений методом сложения:

Умножим второе уравнение на −1. Тогда система примет следующий вид:

Сложим оба уравнения. Сложение компонентов x и −x даст в результате 0, сложение 5y и 3y даст 8y , а сложение 7 и 1 даст 8. В результате получится уравнение 8y = 8 , корень которого равен 1. Зная, что значение y равно 1, можно найти значение x .

Подставим y в первое уравнение, получим x + 5 = 7 , отсюда x = 2

Пример 5. Решить следующую систему уравнений методом сложения:

Желательно, чтобы слагаемые содержащие одинаковые переменные, располагались друг под другом. Поэтому во втором уравнении слагаемые 5y и −2x поменяем местами. В результате система примет вид:

Умножим второе уравнение на 3. Тогда система примет вид:

Теперь сложим оба уравнения. В результате сложения получим уравнение 8y = 16 , корень которого равен 2.

Подставим y в первое уравнение, получим 6x − 14 = 40 . Перенесем слагаемое −14 в правую часть, изменив знак, получим 6x = 54 . Отсюда x = 9.

Пример 6. Решить следующую систему уравнений методом сложения:

Избавимся от дробей. Умножим первое уравнение на 36, а второе на 12

В получившейся системе первое уравнение можно умножить на −5, а второе на 8

Сложим уравнения в получившейся системе. Тогда получим простейшее уравнение −13y = −156 . Отсюда y = 12 . Подставим y в первое уравнение и найдем x

Пример 7. Решить следующую систему уравнений методом сложения:

Приведем оба уравнения к нормальному виду. Здесь удобно применить правило пропорции в обоих уравнениях. Если в первом уравнении правую часть представить как , а правую часть второго уравнения как , то система примет вид:

У нас получилась пропорция. Перемножим её крайние и средние члены. Тогда система примет вид:

Первое уравнение умножим на −3, а во втором раскроем скобки:

Теперь сложим оба уравнения. В результате сложения этих уравнений, мы получим равенство, в обеих частях которого будет ноль:

Получается, что система имеет бесчисленное множество решений.

Но мы не можем просто так взять с неба произвольные значения для x и y . Мы можем указать одно из значений, а другое определится в зависимости от значения, указанного нами. Например, пусть x = 2 . Подставим это значение в систему:

В результате решения одного из уравнений, определится значение для y , которое будет удовлетворять обоим уравнениям:

Получившаяся пара значений (2; −2) будет удовлетворять системе:

Найдём еще одну пару значений. Пусть x = 4. Подставим это значение в систему:

На глаз можно определить, что значение y равно нулю. Тогда получим пару значений (4; 0), которая удовлетворяет нашей системе:

Пример 8. Решить следующую систему уравнений методом сложения:

Умножим первое уравнение на 6, а второе на 12

Перепишем то, что осталось:

Раскроем скобки в обоих уравнениях и приведём подобные слагаемые:

Первое уравнение умножим на −1. Тогда система примет вид:

Теперь сложим оба уравнения. В результате сложения образуется уравнение 6b = 48 , корень которого равен 8. Подставим b в первое уравнение и найдём a

Система линейных уравнений с тремя переменными

В линейное уравнение с тремя переменными входит три переменные с коэффициентами, а также свободный член. В каноническом виде его можно записать следующим образом:

Данное уравнение имеет бесчисленное множество решений. Придавая двум переменным различные значения, можно найти третье значение. Решением в этом случае является тройка значений (x; y; z) которая обращает уравнение в тождество.

Если переменные x, y, z связаны между собой тремя уравнениями, то образуется система трех линейных уравнений с тремя переменными. Для решения такой системы можно применять те же методы, которые применяются к линейным уравнениям с двумя переменными: метод подстановки и метод сложения.

Пример 1. Решить следующую систему уравнений методом подстановки:

Выразим в третьем уравнении x . Тогда система примет вид:

Теперь выполним подстановку. Переменная x равна выражению 3 − 2y − 2z . Подставим это выражение в первое и второе уравнение:

Раскроем скобки в обоих уравнениях и приведём подобные слагаемые:

Мы пришли к системе линейных уравнений с двумя переменными. В данном случае удобно применить метод сложения. В результате переменная y исчезнет, и мы сможем найти значение переменной z

Теперь найдём значение y . Для этого удобно воспользоваться уравнением −y + z = 4. Подставим в него значение z

Теперь найдём значение x . Для этого удобно воспользоваться уравнением x = 3 − 2y − 2z . Подставим в него значения y и z

Таким образом, тройка значений (3; −2; 2) является решением нашей системы. Проверкой убеждаемся, что эти значения удовлетворяют системе:

Пример 2. Решить систему методом сложения

Сложим первое уравнение со вторым, умноженным на −2.

Если второе уравнение умножить на −2, то оно примет вид −6x + 6y − 4z = −4 . Теперь сложим его с первым уравнением:

Видим, что в результате элементарных преобразований, определилось значение переменной x . Оно равно единице.

Вернемся к главной системе. Сложим второе уравнение с третьим, умноженным на −1. Если третье уравнение умножить на −1, то оно примет вид −4x + 5y − 2z = −1 . Теперь сложим его со вторым уравнением:

Получили уравнение x − 2y = −1 . Подставим в него значение x , которое мы находили ранее. Тогда мы сможем определить значение y

Теперь нам известны значения x и y . Это позволяет определить значение z . Воспользуемся одним из уравнений, входящим в систему:

Таким образом, тройка значений (1; 1; 1) является решением нашей системы. Проверкой убеждаемся, что эти значения удовлетворяют системе:

Задачи на составление систем линейных уравнений

Задача на составление систем уравнений решается путем ввода нескольких переменных. Далее составляются уравнения на основании условий задачи. Из составленных уравнений образуют систему и решают её. Решив систему, необходимо выполнить проверку на то, удовлетворяет ли её решение условиям задачи.

Задача 1. Из города в колхоз выехала машина «Волга». Обратно она возвращалась по другой дороге, которая была на 5 км короче первой. Всего в оба конца машина проехала 35 км. Сколько километров составляет длина каждой дороги?

Решение

Пусть x — длина первой дороги, y — длина второй. Если в оба конца машина проехала 35 км, то первое уравнение можно записать как x + y = 35. Это уравнение описывает сумму длин обеих дорог.

Сказано, что обратно машина возвращалась по дороге которая была короче первой на 5 км. Тогда второе уравнение можно записать как x − y = 5. Это уравнение показывает, что разница между длинами дорог составляет 5 км.

Либо второе уравнение можно записать как x = y + 5 . Этим уравнением и воспользуемся.

Поскольку переменные x и y в обоих уравнениях обозначают одно и то же число, то мы можем образовать из них систему:

Решим эту систему каким-нибудь из изученных ранее методов. В данном случае удобно воспользоваться методом подстановки, поскольку во втором уравнении переменная x уже выражена.

Подставим второе уравнение в первое и найдём y

Подставим найденное значение y в во второе уравнение x = y + 5 и найдём x

Длина первой дороги была обозначена через переменную x . Теперь мы нашли её значение. Переменная x равна 20. Значит длина первой дороги составляет 20 км.

А длина второй дороги была обозначена через y . Значение этой переменной равно 15. Значит длина второй дороги составляет 15 км.

Выполним проверку. Для начала убедимся, что система решена правильно:

Теперь проверим удовлетворяет ли решение (20; 15) условиям задачи.

Было сказано, что всего в оба конца машина проехала 35 км. Складываем длины обеих дорог и убеждаемся, что решение (20; 15) удовлетворяет данному условию: 20 км + 15 км = 35 км

Следующее условие: обратно машина возвращалась по другой дороге, которая была на 5 км короче первой . Видим, что решение (20; 15) удовлетворяет и этому условию, поскольку 15 км короче, чем 20 км на 5 км: 20 км − 15 км = 5 км

При составлении системы важно, чтобы переменные обозначали одни и те же числа во всех уравнениях, входящих в эту систему.

Так наша система содержит два уравнения. Эти уравнения в свою очередь содержат переменные x и y , которые обозначают одни и те же числа в обоих уравнениях, а именно длины дорог, равных 20 км и 15 км.

Задача 2. На платформу были погружены дубовые и сосновые шпалы, всего 300 шпал. Известно, что все дубовые шпалы весили на 1 т меньше, чем все сосновые. Определить, сколько было дубовых и сосновых шпал отдельно, если каждая дубовая шпала весила 46 кг, а каждая сосновая 28 кг.

Решение

Пусть x дубовых и y сосновых шпал было погружено на платформу. Если всего шпал было 300, то первое уравнение можно записать как x + y = 300 .

Все дубовые шпалы весили 46x кг, а сосновые весили 28y кг. Поскольку дубовые шпалы весили на 1 т меньше, чем сосновые, то второе уравнение можно записать, как 28y − 46x = 1000 . Это уравнение показывает, что разница масс между дубовыми и сосновыми шпалами, составляет 1000 кг.

В результате получаем два уравнения, которые образуют систему

Решим данную систему. Выразим в первом уравнении x . Тогда система примет вид:

Подставим первое уравнение во второе и найдём y

Подставим y в уравнение x = 300 − y и узнаем чему равно x

Значит на платформу было погружено 100 дубовых и 200 сосновых шпал.

Проверим удовлетворяет ли решение (100; 200) условиям задачи. Для начала убедимся, что система решена правильно:

Было сказано, что всего было 300 шпал. Складываем количество дубовых и сосновых шпал и убеждаемся, что решение (100; 200) удовлетворяет данному условию: 100 + 200 = 300.

Следующее условие: все дубовые шпалы весили на 1 т меньше, чем все сосновые . Видим, что решение (100; 200) удовлетворяет и этому условию, поскольку 46 × 100 кг дубовых шпал легче, чем 28 × 200 кг сосновых шпал: 5600 кг − 4600 кг = 1000 кг.

Задача 3. Взяли три куска сплава меди с никелем в отношениях 2 : 1 , 3 : 1 и 5 : 1 по массе. Из них сплавлен кусок массой 12 кг с отношением содержания меди и никеля 4 : 1 . Найдите массу каждого исходного куска, если масса первого из них вдвое больше массы второго.

Решение

Пусть x — масса первого куска, y — масса второго куска, z — масса третьего куска. Если из этих кусков сплавлен кусок массой 12 кг, то первое уравнение можно записать как x + y + z = 12 .

Масса первого куска вдвое больше массы второго куска. Тогда второе уравнение можно записать как x = 2y .

Полученных двух уравнений недостаточно для решения данной задачи. Если второе уравнение подставить в первое, то мы получим уравнение 2y + y + z = 12 , откуда 3y + z = 12 . Это уравнение имеет бесчисленное множество решений.

Составим ещё одно уравнение. Пусть это уравнение будет описывать количество меди, взятого с каждого сплава и сколько меди оказалось в получившемся сплаве.

Если первый сплав имеет массу x , а медь и никель находится нём в отношении 2 : 1 , то можно записать, что в новом сплаве содержится меди от первого куска.

Если второй сплав имеет массу y , а медь и никель находится в нём в отношении 3 : 1 , то можно записать, что в новом сплаве содержится меди от второго куска.

Если третий сплав имеет массу z , а медь и никель находится в отношении 5 : 1 , то можно записать, что в новом сплаве содержится меди от третьего куска.

Полученный сплав имеет имеет массу 12 кг, а медь и никель находится в нём в отношении 4 : 1 . Тогда можно записать, что в полученном сплаве содержится меди.

Сложим , , и приравняем эту сумму к 9,6. Это и будет нашим третьим уравнением:

Попробуем решить данную систему.

Для начала упростим третье уравнение. Подставим в него второе уравнение и посмотрим, что из этого выйдет:

Теперь в главной системе вместо уравнения запишем уравнение, которое мы сейчас получили, а именно уравнение 25y + 10z = 115,2

Подставим второе уравнение в первое:

Умножим первое уравнение на −10 . Тогда система примет вид:

Сложим оба уравнения. Тогда получим простейшее уравнение −5y = −4,8 откуда найдём y равный 0,96 . Значит масса второго сплава составляет 0,96 кг .

Теперь найдём x . Для этого удобно воспользоваться уравнением x = 2y. Значение y уже известно. Осталось только подставить его:

Значит масса первого сплава составляет 1,92 кг .

Теперь найдём z . Для этого удобно воспользоваться уравнением x + y + z = 12 . Значения x и y уже известны. Подставим их куда нужно:

Значит масса третьего сплава составляет 9,12 кг.

п.1. Решение иррациональных систем уравнений

Внимание!
При решении иррациональных систем уравнений следует помнить, что для корней четных степеней должно выполняться требование ОДЗ: $$ mathrm{y=sqrt[n]{f(x)}, n — text{чётное}Leftrightarrow} left{ begin{array}{ l } mathrm{f(x) geq 0} & \ mathrm{ygeq 0} & \ mathrm{f(x) =y^n} & end{array}right. $$

Например:
$$ left{ begin{array}{ l } mathrm{y=sqrt{2x-3}} & \ mathrm{y-x=-3} & end{array}right.Rightarrow left{ begin{array}{ l } mathrm{y=sqrt{2x-3}} & \ mathrm{y=x-3} & end{array}right.Rightarrow left{ begin{array}{ l } mathrm{2x-3geq 0} & \ mathrm{x-3geq 0} & \ mathrm{y^2=(x-3)^2=2x-3} & end{array}right. $$ Решаем неравенства ОДЗ: ( left{ begin{array}{ l } mathrm{2x-3geq 0} & \ mathrm{x-3geq 0} & end{array}right.Rightarrow left{ begin{array}{ l } mathrm{xgeq 1,5} & \ mathrm{xgeq 3} & end{array}right.Rightarrow mathrm{xgeq 3} )
Решаем нижнее уравнение: begin{gather*} mathrm{x^2-6x+9=2x-3Rightarrow x^2-8x+12 = 0Rightarrow (x-2)(x-6)=0}\ mathrm{x_1=2, x_2=6} end{gather*} По требованию ОДЗ оставляем только второй корень.
Решение системы: ( left{ begin{array}{ l } mathrm{x=6} & \ mathrm{y=x-3=3} & end{array}right. )

Ответ: (6; 3).

п.2. Решение иррациональных систем неравенств

Подробней о решении иррациональных неравенств, см. §11 данного справочника.

Например:
Найти решение системы: ( left{ begin{array}{ l } mathrm{sqrt{x+2}gt x+1} & \ mathrm{|y-1|leq 2} & end{array}right. ) и изобразить его на координатной плоскости.
Решаем верхнее неравенство: begin{gather*} left[begin{array}{ l } left{begin{array}{ l } mathrm{x+1lt 0} & \ mathrm{x+2geq 0} & end{array}right. & \ left{ begin{array}{ l } mathrm{x+1geq 0} & \ mathrm{x+2gt (x+1)^2} & end{array}right. & end{array}right.Rightarrow left[begin{array}{ l } left{begin{array}{ l } mathrm{xlt -1} & \ mathrm{xgeq -2} & end{array}right. & \ left{ begin{array}{ l } mathrm{xgeq -1} & \ mathrm{x+2gt x^2+2x+1} & end{array}right. & end{array}right.Rightarrow left[begin{array}{ l } mathrm{-2leq xlt -1} & \ left{ begin{array}{ l } mathrm{xgeq -1} & \ mathrm{x^2+x-1lt 0} & end{array}right. & end{array}right.Rightarrow \ left[begin{array}{ l } mathrm{-2leq xlt -1} & \ left{ begin{array}{ l } mathrm{xgeq -1} & \ mathrm{x_{1,2}=frac{-1pmsqrt{5}}{2}, x_1lt xlt x_2} & end{array}right. & end{array}right.Rightarrow left[begin{array}{ l } mathrm{-2leq xlt -1} & \ mathrm{-1leq xltfrac{sqrt{5}-1}{2}} & end{array}right.Rightarrow mathrm{-2leq xlt frac{sqrt{5}-1}{2}} end{gather*}
Решаем нижнее неравенство: ( mathrm{|y-1|leq 2Rightarrow -2leq y-1leq 2Rightarrow -1leq yleq 3} )

п.3. Примеры

Пример 1. Решите систему уравнений: a) ( left{ begin{array}{ l } mathrm{sqrt[3]{x}-sqrt{y}=1} & \ mathrm{x-y=55} & end{array}right. )
Требования ОДЗ: y ≥ 0.
Замена переменных: ( left{ begin{array}{ l } mathrm{a=sqrt[3]{x}} & \ mathrm{b=sqrt{y}geq 0} & end{array}right. )
Подставляем: $$ left{ begin{array}{ l } mathrm{a-b=1} & \ mathrm{a^3-b^2=55} & end{array}right.Rightarrow left{ begin{array}{ l } mathrm{b=a-1} & \ mathrm{a^3-(a-1)^2=55} & end{array}right. $$ Решаем нижнее уравнение: begin{gather*} mathrm{ a^3-a^2+2a-1-55=0Rightarrow a^3-a^2+2a-56=0 }\ mathrm{ a^3-4a^2+3a^2-12a+14a-56=0 }\ mathrm{ a^2(a-4)+3a(a-4)+14(a-4)=0 }\ mathrm{ (a-4)(a^2+3a+14)=0 } end{gather*} Дискриминант второй скобки D = 9 — 56 < 0. Уравнение имеет одно решение: $$ mathrm{ a=4Rightarrow b=a-1=3 } $$
Возвращаемся к исходным переменным: ( left{ begin{array}{ l } mathrm{x=a^3=4^3=64} & \ mathrm{y=b^3=3^2=9} & end{array}right. )

Ответ: (64; 9).

б) ( left{ begin{array}{ l } mathrm{xsqrt{x}-ysqrt{y}=37} & \ mathrm{xsqrt{y}-ysqrt{x}=12} & end{array}right. )
Требования ОДЗ: x ≥ 0, y ≥ 0.
Кроме того, из первого уравнения: ( mathrm{xsqrt{x} gt ysqrt{y}Rightarrow x gt y} )
Замена переменных: ( left{ begin{array}{ l } mathrm{a=sqrt{x} geq 0} & \ mathrm{b=sqrt{y}geq 0} & end{array},right. ) при этом a > b.
Подставляем: $$ left{ begin{array}{ l } mathrm{a^3-b^3=37} & \ mathrm{a^2b-b^2a=12} & end{array}right.Rightarrow left{ begin{array}{ l } mathrm{(a-b)(a^2+ab+b^2)=37} & \ mathrm{ab(a-b)=12} & end{array}right. $$ Разделим верхнее равенство на нижнее, сократим на (a – b): begin{gather*} mathrm{ frac{a^2+ab+b^2}{ab}=frac{37}{12}Rightarrow 12(a^2+ab+b^2)-37ab=0 }\ mathrm{ 12a^2-25ab+12b^2=0 |:b^2 }\ mathrm{ 12left(frac{a}{b}right)^2-25left(frac{a}{b}right)+12=0 }\ mathrm{ D=25^2-4cdot 12cdot 12=49=7^2, left(frac{a}{b}right)=frac{25pm 7}{24}=} left[begin{array}{ l } mathrm{frac12} & \ mathrm{frac43} & end{array}right. end{gather*} Т.к. a > b оставляем решение ( mathrm{frac{a}{b}=frac43Rightarrow a=frac43 b.} )
Подставляем в нижнее уравнение: begin{gather*} mathrm{ frac43 bcdot bcdotleft(frac43 b-bright)=12Rightarrowfrac49 b^3=12Rightarrow b^3=12cdot frac94=27Rightarrow b=3 }\ a=frac43 b=4 end{gather*} Возвращаемся к исходным переменным: ( left{ begin{array}{ l } mathrm{sqrt{x}=a=4} & \ mathrm{sqrt{y}=b=3} & end{array}right.Rightarrow left{ begin{array}{ l } mathrm{x=16} & \ mathrm{y=9} & end{array}right. )

Ответ: (16; 9).

в) ( left{ begin{array}{ l } mathrm{sqrt{2-x}+sqrt{5-y}=3} & \ mathrm{5x+2y-xy=6} & end{array}right. )
Требования ОДЗ: ( left{ begin{array}{ l } mathrm{xleq 2} & \ mathrm{y leq 5} & end{array}right. )
Замена переменных: ( left{ begin{array}{ l } mathrm{a=sqrt{2-x} geq 0} & \ mathrm{b=sqrt{5-y}geq 0} & end{array},right. )
Заметим, что ( mathrm{a^2b^2=(2-x)(5-y)=10-5x-2y+xy} )
Тогда нижнее уравнение: begin{gather*} mathrm{xy-2y-5x+6=0Rightarrow xy-2y-5x+10=4Rightarrow a^2b^2=4Rightarrow}\ mathrm{Rightarrow (ageq 0, bgeq 0)ab=2} end{gather*}
Подставляем: $$ left{begin{array}{ l } mathrm{a+b=3} & \ mathrm{ab=2} & end{array}right.Rightarrow left[begin{array}{ l } left{ begin{array}{ l } mathrm{a=1} & \ mathrm{b=2} & end{array}right. & \ left{ begin{array}{ l } mathrm{a=2} & \ mathrm{b=1} & end{array}right. & end{array}right. $$ Возвращаемся к исходным переменным: $$ left[begin{array}{ l } left{ begin{array}{ l } mathrm{sqrt{2-x}=1} & \ mathrm{sqrt{5-y}=2} & end{array}right. & \ left{ begin{array}{ l } mathrm{sqrt{2-x}=2} & \ mathrm{sqrt{5-y}=1} & end{array}right. & end{array}right.Rightarrow left[begin{array}{ l } left{ begin{array}{ l } mathrm{2-x=1} & \ mathrm{5-y=4} & end{array}right. & \ left{ begin{array}{ l } mathrm{2-x=4} & \ mathrm{5-y=1} & end{array}right. & end{array}right.Rightarrow left[begin{array}{ l } left{ begin{array}{ l } mathrm{x=1} & \ mathrm{y=1} & end{array}right. & \ left{ begin{array}{ l } mathrm{x=-2} & \ mathrm{y=4} & end{array}right. & end{array}right. $$ Получили два решения.

Ответ: {(1; 1); (–2; 4)}.

Пример 2. Решите систему неравенств и изобразите решение на координатной плоскости: $$ left{ begin{array}{ l } mathrm{3sqrt[6]{x+3}-sqrt[3]{x+3}geq 2} & \ mathrm{ylt x+3} & end{array}right. $$ Найдите пару решений с натуральными x и y, для которых сумма x + y минимальна.
Решаем верхнее неравенство.
Замена переменных: ( mathrm{a=sqrt[3]{x+3}}. ) Ограничений по ОДЗ нет. Подставляем: ( mathrm{3a^2-ageq 2Rightarrow 3a^2-a-2geq 0Rightarrow (3a+1)(a-2)geq 0Rightarrow aleq -frac13cup ageq 2} )
Возвращаемся к исходной переменной: begin{gather*} mathrm{sqrt[3]{x+3}leq-frac13cup sqrt[3]{x+3}geq 2Rightarrow x+3leq -frac{1}{27}cup x+3geq 8}\ mathrm{xleq -3frac{1}{27}cup xgeq 5Rightarrow xin left(-infty; -3frac{1}{27}right]cup [5; +infty)} end{gather*} Для второй переменной: y < x + 3

Искомая точка (5; 1), минимальная сумма 5 + 1 = 6.

Метод квадратного корняоснован
на пред­став­­лении матрицыА,
составленной из ко­эф­фи­ци­­ентов
сис­темы в форме произведения
тре­у­голь­ных мат­риц, что
позволят свести решение за­дан­ной
сис­те­мы к по­сле­довательному
решению двух сис­­тем с тре­у­голь­ны­ми
матрицами.

Метод квадратного корня применяется
для ре­ше­­ния сис­темы линейных
уравнений, ко­эф­фи­ци­ен­ты
ко­торой об­ра­зуют эрмитову
сим­мет­ри­чес­кую мат­ри­цу
(эр­ми­то­ва мат­­рица
совпадает с ком­­плек­с­­но-со­пря­женной
тран­с­­по­ни­ро­ваннойA^*=A).

Представим матрицу Ав видеА=S^*D
S, гдеS — верх­няя
треугольная матрица с по­ло­жи­тель­ны­ми
эле­мен­тами на главной диагонали;S^*— транс­по­ни­ро­ван­ная
к матрицеS;D— ди­а­го­наль­ная
мат­ри­ца, на ди­агонали ко­торой
на­хо­дят­ся чис­ла (+1) или (—
1).

Если матрицы SиD
найдены, то заданная сис­­те­маAХ= = F может быть
решена следующим пу­­тем:

AX = S^*
D S X = (S^*
D) S X = B
Y = F, (1.28)

где S^*D = Весть нижняя треугольная матрица и
Y = S X— вспомогательный
вектор.

Таким об­ра­зом, ре­шение системы
АX = Fрав­но­­силь­но
ре­ше­нию двух треугольных систем ВY = Fи SX
=Y.

Пусть S
= (s_ik)
при i
> k и s_ik
№
0, s_ii
> 0;
S^* = ();
D = =(d_ik), d
=1;
i № k. Тогда
из срав­не­ния мат­риц АиS^*DSпо­лучим

.

Ограничение в сумме получается из
учета то­го фак­­­та, что в
матрице Sниже главной ди­а­го­на­ли
эле­­менты об­ра­ща­ются в
нуль. Последнее ра­венс­т­во
можно пе­ре­пи­сать не­сколько
иначе, при­няв для оп­ределенностиk= min(k,l):

;

,

откуда окончательно получим формулы
для вы­чис­­ления элементов матриц
SиD:

(1.29)

Единственным условием возможности
опре­де­ле­­ния s_ikявляетсяs_kk №
0. Для по­стро­е­ния мат­­риц
по­лагаемk = 1 и
последовательно вы­чис­ля­­емвсе эле­менты первой строкиsпо
формуле (1.29); за­т­ем по­лагаемk= 2- и определяем
эле­мен­ты вто­рой стро­­ки
и т.д. Когдаk=n, тогда
най­де­ны все эле­­мен­тыматрицS
иD,а
следовательно иS^*.
За­тем последовательно вы­пол­ня­­ем
вы­чис­ления (1.28):

S^*Z = F;
D Y = Z; S X
= Y

обыч­ным ходом по формулам

(1.30)

при i = 2,
3, …, n.

Попутно заметим, что определитель
матрицы А можно вычислить
из выражения

.
(1.31)

Этот метод экономичен, требует n³/3
ариф­ме­­тических действий и при
большихn(n> 50) вдвое бы­стрее
метода Га­усса. Если за основу
про­цедуры при­нять алгоритм П5.6
Дья­конова [1987], то тогда метод
квад­ратного кор­ня мо­жет быть
ре­а­­ли­зован c помощью сле­дующей
про­це­ду­ры:

procedure
KVK (M, N : integer;

aa:
array of real; bb : array of real;

var C:
array of real);

type
mas1=array [0..4] of real;

mas=array
[0..4] of mas1;

var a :
mas; j, k, i : integer; s, c1 : real;

begin

i := 0;

for j := 1
to m do

for k :=
1 to n do

begin
Inc (i); a[j,k] := aa [i]; end;

for
j := 1 to N do

begin

for k :=
j to N do

begin

s :=
0.0;

for
i := 1 to M do s := s + a[i,j] * a[i,k];

c[k] := s;

end;

c1 :=
0.0;

for
i := 1 to M do с1 := c1 + a[i,j]*Bb[i];

for
i := j to N do a[i,j] := c[i];

c[J]
:= c1;

end;

a[1,1] :=
sqrt (a[1,1]);

for
j := 2 to N do a[1,j] := a[j,1] / a[1,1];

for
i := 2 to n do

begin

s :=
0.0;

for k :=
1 to i-1 dо s := s + a[k,i]*a[k,i];

a[i,i]
:= sqrt (a[i,i] — S);

for
j := i+1 to N do

begin

s :=
0.0;

for k
:= 1 to i-1 do

S := S
+ A[K,I]*A[K,J];

A[I,J]
:= (A[J,I] — S) / A[I,I];

end;

end;

c[1] :=
c[1] / a[1,1];

for i
:= 2 to N do

begin
s := 0.0;

for k :=
1 to i-1do

s := s
+ a[k,i] * c[k];

c[i] :=
(c[i] — s) / a[i,i];

end;

c[n] :=
c[n] / a[n,n];

for i
:= n-1 downto 1 do

begin
s := 0.0;

for
k := i+1 to N do s := s + a[i,k] * c[k];

c[i] :=
(c[i] — s) / a[i,i];

end;

еnd.

Формальные параметры процедуры.Входные:
m, N(типinteger) —mуравнений
иnне­из­вест­ных оп­ре­де­ляют
раз­мер матрицыА.Для этой
про­це­ду­рыобя­за­тельно
вы­пол­не­ние m
> n,
т.е. ко­ли­чествоурав­­не­ний
долж­но быть боль­­­­ше
ко­личества не­из­вест­­ных
(сис­­те­ма пе­ре­о­пре­делена),
пре­дель­­ныйраз­­­ре­шен­ный
слу­чай m =
n;
а — мат­рица,
со­став­­­лен­­наяиз
ко­эф­фи­ци­ен­тов при
не­из­вест­­ных;В — мас­сив,
со­став­­ленный из стол­бца
сво­бод­ных чле­­нов.Вы­ход­ные:С — массив, в ко­­то­ром
со­дер­жит­ся решение сис­темы.

Для проверки правильности работы
про­це­ду­ры ре­­ша­лась
система 4´4 линейных
уравнений ме­то­дом квад­рат­ных
корней с точностью 0.0001:

0.68X₁
+ 0.05X₂
+ 0.11X₃
+ 0.08X₄
= 2.15 ;

0.05X₁
+ 0.13X₂
+ 0.27X₃
+ 0.80X₄
= 0.44 ;

0.11X₁
+ 0.27X₂
+ 0.28X₃
+ 0.06X₄
= 0.83 ;

0.08X₁
+ 0.80X₂
+ 0.06X₃
+ 0.12X₄
= 1.16 ,

решение которой, полученное методом
квад­рат­ных кор­ней, будет
следующим

Х
₁
= 2.97; Х₂
= 1.11; Х₃
= 0.74; Х₄
= -0.07.

Соседние файлы в папке GLAVA1_1

• #
• #
• #
• #

Страница находится по новому адресу

http://mathhelpplanet.com/static.php?p=chislennyye-metody-resheniya-slau

Математический форум (помощь с решением задач, обсуждение вопросов по математике).

Если заметили ошибку, опечатку или есть предложения, напишите в комментариях.

Прямые методы решения линейных систем. Метод квадратного корня

Введение

Три четверти прикладных математических задач в
конечном итоге сводятся к решению систем алгебраических и трансцендентных
уравнений, причем подавляющее большинство из них — линейные алгебраические
системы, имеющие единственное решение.

Современная вычислительная математика обладает
большим арсеналом методов, а математическое обеспечение ЭВМ — многими пакетами
прикладных программ, позволяющих решать различные линейные системы. Казалось
бы, этого достаточно, но на практике при решении линейных систем возникает
множество разных проблем.

Поэтому ввиду большой важности и практической
значимости задача решения линейных систем до сих пор привлекает внимание
математиков. Создано большое количество разных методов решения этой задачи и
сопутствующих ей задач (вычисление определителей, обратных матриц). Среди этих
методов можно выделить две большие группы: прямые (или точные) и итерационные
методы [4].

Прямые методы приводят к точному решению системы
(если не учитывать вычислительные погрешности округлений), причем за конечное
число шагов. К ним относятся методы Гаусса, LU-разложение, квадратного корня,
методы прогонки, вращений и т.п. [2,4].

Итерационные методы позволяют получить
приближенное решение системы с заданной точностью, используя идею
последовательных приближений. К ним относятся методы простой итерации, Зейделя,
релаксации, установления, спуска и т. п.[2,4].

Каждый из существующих методов решения линейных
систем имеет свою сферу применения, где он является наиболее эффективным.
Эффективность же названных численных методов зависит в основном от свойств
матрицы системы (порядка, симметричности, меры обусловленности, заполненности).

Целью данной курсовой работы является:

обзор литературы по прямым методам решения
линейных систем;

реализация метода квадратного корня средствами
системы программирования Turbo Pascal.

Курсовая работа содержит две главы. Первая глава
посвящена таким прямым методам решения линейных систем, как метод Гаусса,
LU-разложение, метод прогонки для решения линейных систем с трехдиагональными
матрицами коэффициентов и метод вращений для решения линейных систем. Во второй
главе отдельно рассматривается метод квадратного корня для решения линейных
систем, а именно: приведены теоретические основы метода, а также произведена
его реализация в системе программирования Turbo Pascal.

Глава 1. Прямые методы решения
линейных систем

.1 Постановка задачи

К решению систем линейных уравнений сводятся
многочисленные практические задачи. В данной курсовой работе изучается вопрос о
численном решении систем вида [4]:

 (1.1.1)

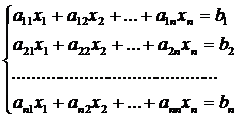
Совокупность коэффициентов (aij), неизвестных
(хi) и свободных членов (bi) этой системы запишем в виде матриц [4]:

=, x=,
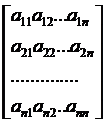
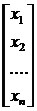
b=
(1.1.2)

Помимо введенной матрицы А мы введем еще и
расширенную матрицу системы, получающуюся из матрицы А добавлением столбца
правых частей:

 (1.1.3)

Матрица системы А и столбец правых частей b
считаются заданными, а столбец x ищется, при этом определитель матрицы не
должен равняться 0.

1.2 Метод Гаусса

Данный метод является наиболее простым и
популярным способом решения линейных систем вида (1.1.1). Он основан на
последовательном исключении неизвестных [5].

Итак, пусть дана система (1.1.1). Для удобства
можно представить её в виде (1.1.3). На первом этапе разделим все коэффициенты
первой строки, а также свободный член на первый коэффициент. Таким образом
перед х1 в первой строке получится единица. Теперь наша задача — исключить
переменную х1 из остальных строк, другими словами сделать коэффициенты перед х1
нулевыми. Для этого заменяем все уравнения, начиная со второго, уравнениями,
полученными сложением каждого из них с первым, умноженным на —,
—,…,
—.
Таким образом, получаем [2]:

 (1.2.1)

В общем виде формулы для данного этапа выглядят
следующим образом [2]:

 ,

 , (i,j=2…n)

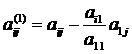
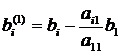
На втором этапе проделаем то же самое, только
первую строку в расчет не берем. Делим все элементы второй строки на ,
а затем исключаем переменную х2 из оставшихся строк путем опять же замены всех
уравнений, начиная с третьего, уравнениями, полученными сложением каждого из
них со вторым, умноженным на —, —,…,
—.
Таким образом, получаем [2]:

 (1.2.2)

Формулы в общем виде[2]:

 , (i,j=3…n)

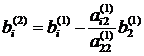
Этот процесс продолжается до тех пор, пока
матрица не будет приведена к виду [2]:

 (1.2.3)

Коэффициенты данной системы получены по формулам
[2]:

 , (i, j=k+1…n,
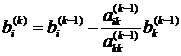
k=1…n-1)

Все рассмотренные выше этапы называются прямым
ходом метода Гаусса. Далее идет обратный ход: значения х вычисляются снизу
вверх по формуле [2]:

, (k=n,n-1,…,1)

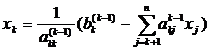
1.3 LU-разложение матриц

Данный метод напрямую связан с методом Гаусса. В
предыдущем пункте решение линейной системы сводилось к тому, что матрицу
(1.1.3) путем элементарных преобразований сводили к верхней треугольной матрице
(1.2.3). Заметим, что, умножая исходную матрицу на матрицу (1.2.3), получится
нижняя треугольная матрица с единицами на главной диагонали [5]. Учитывая эту
взаимосвязь, можно подойти к решению линейной системы иначе, то есть, разложив
исходную матрицу в произведение двух треугольных матриц А=LU [5, 7]:

 (1.3.1)

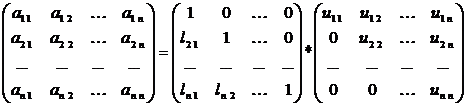
То есть систему Ax=b можно переписать в виде:

LUx=b (1.3.2)

Введем вектор вспомогательных переменных 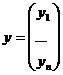 и
(1.3.2) перепишем в виде [2, 7]:

 (1.3.3)

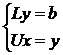
Очевидно, чтобы найти х, нужно сначала найти у.
Для этого запишем первое уравнение (1.2.3) в развернутом виде:

 (1.3.4)

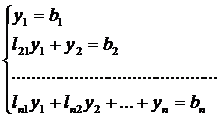
Найти у можно сверху вниз по формуле [7]:

 при i=1,2,…,n.
(1.3.5)

Аналогично для второго уравнения (1.3.3):

 (1.3.6)

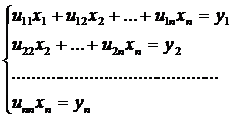
Найти у можно снизу вверх по формуле [7]:

 при i=n,n-1,…,1
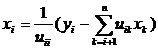
(1.3.7)

1.4 Метод прогонки решения систем с
трехдиагональными матрицами коэффициентов

Данный метод удобно применять для так называемых
ленточных трёхдиагональных матриц вида [10]:

*= (1.4.1)

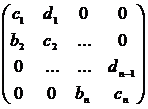
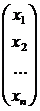
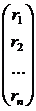
Каждое уравнение такой системы связывает три
«соседних» неизвестных [2, 10]:

, где i=1…n; b1=0;
dn=0. (1.4.2)

Предположим, что существуют такие наборы чисел  и
 (i=1…n),
при которых [10]

 (1.4.3)

Уменьшим индекс на единицу, подставим полученное
в (1.4.2) и выразим хi [2,10] :

 (1.4.4)

Сравнив (1.4.3) и (1.4.4), получаем, что [10]:

 (1.4.5)

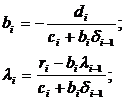
при i=1…n — прямая прогонка,

при i=n…1 — обратная прогонка.

Эти коэффициенты называются прогоночными. Найдя
их по формулам (1.4.5), можно найти хi из формулы (1.4.3).

1.5 Метод вращений решения линейных
систем

Цель данного метода — привести систему (1.1.1) к
треугольному виду (как в методе Гаусса).

 (1.5.1)

На введенные параметры накладываются 2 условия
[8]:

условие обнуления (исключения х1 из второго
уравнения)

=0 (1.5.2)

условие нормировки. За  и
 можно
принять соответственно

,  (1.5.3)

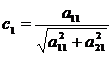
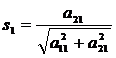
Отсюда система (1.1.1) принимает вид [8]:

 (1.5.4)

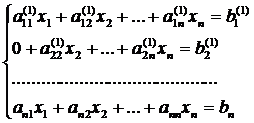
Где  (j=1…n)
 

 (j=2…n)

Далее первое уравнение системы (1.5.4)
заменяется новым, полученным сложением результатов умножения первого и третьего
уравнений на [8]:

 и  

А третье уравнение системы (1.5.4) заменим
полученным сложением результатов умножения тех же уравнений, умноженных на —
и .
Таким образом, получаем систему [8]:

 (1.5.5)

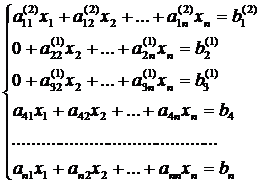
где  (j=1…n)

 (j=2…n)

Проделав такие преобразования n-1 раз мы обнулим
коэффициенты при х1 в первом столбце, кроме первой строчки. Затем проделаем
аналогичные преобразования с остальными столбцами и в конечном итоге получим
треугольную матрицу. После этого можно будет найти неизвестные. Это делается
точно так же как в обратном методе Гаусса.

Глава 2. Метод квадратного корня для
решения линейных систем

.1 Краткая характеристика метода

Метод квадратного корня применяется в том
случае, когда матрица А симметричная, то есть:

= aji (i, j = 1, 2, …, n).

Кроме того, матрица должна быть невырожденной,
то есть её определитель не должен равняться нулю (det(A)¹0).
Таким образом, система будет иметь единственное решение.

Метод квадратного корня дает большой выигрыш во
времени по сравнению с другими методами (например, методом Гаусса), так как,
во-первых, существенно уменьшает число умножений и делений (почти в два раза
для больших n), во-вторых, позволяет накапливать сумму произведений без записи
промежуточных результатов.

Всего метод квадратных корней требует [2,3]  операций
умножения и деления (примерно в два раза меньше, чем метод Гаусса), а также n
операций извлечения корня.

2.2 Постановка задачи

К решению систем линейных уравнений сводятся
многочисленные практические задачи. Запишем еще раз систему (1.1.1) n линейных
алгебраических уравнений с n неизвестными [4]:

Совокупность коэффициентов (aij), неизвестных
(хi) и свободных членов (bi) этой системы запишем в виде матриц (1.1.2) [4]:

=, X=,
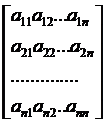
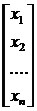
B=

Используя понятие матрицы , систему уравнений
(1.1.1) можно записать в матричном виде:

=b (2.2.1)

Таким образом, задача состоит в том, чтобы
вычислить столбец неизвестных, используя метод квадратного корня.

2.3 Теоретическая основа метода
квадратного корня для решения линейных систем

Пусть дана симметричная система линейных
уравнений в матричном виде (2.2.1): Ах=b

К ee решению может быть применена идея
разложения матрицы А в произведение двух матриц специального вида. Основанием для
этого служит следующая теорема [3]:

Теорема. Какова бы ни была матрица А с отличными
от нуля глав­ными минорами:

 ,
… ,

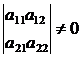
ее всегда можно разложить в произведение двух
треугольных матриц:=BC,

где В — левая треугольная матрица:

В=

С — правая треугольная матрица:

С=

Так как данная матрица (2.2.1) симметрична, то
она раскладывается на произведение двух взаимно транспонированных треугольных
матриц[1,2,3]:

А = Т¢ Т, (2.3.1)

 

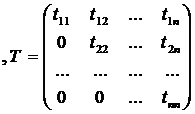
Найдем элементы tij матрицы Т. Для этого
перемножим T и T’ между собой и приравняем полученное к исходной матрице [2]:

t211 = a11 , t11 t12 =a12 , … , t11
t1n = a1n ,+ t222= a22 , … , t12 t1n + t22 t2n= a2n ,

…………………………………………………………………..n + t22n +…+ t2nn =
ann

Получим следующие формулы для определения tij
[3]:

 (2.3.2)

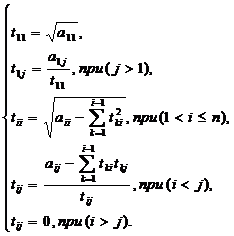
Далее, решение системы сводится к решению двух
треугольных систем. Действительно, равенство (2.2.1) равносильно двум
равенствам:

’y=b и Tx=y. (2.3.3)

Запишем в развернутом виде системы (2.3.3)
[1,3]:

 (2.3.4)

 (2.3.5)

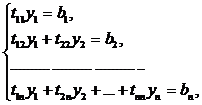
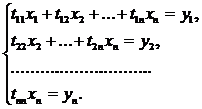
И из этих систем (2.3.4) и (2.3.5)
последовательно находим [1,2,3]:

, ,
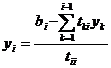
при (i>1) (2.3.6)

, ,
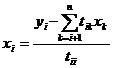
при (i<n). (2.3.7)

2.4 Реализация метода квадратного
корня для решения линейных систем. Тестирование программы

В данном пункте описано тестирование программы,
посвященной методу квадратного корня решения линейных систем. Код программы
составлен на языке Pascal и находится в приложении.

Для того, чтобы удостовериться, что программа
работает правильно, решим конкретный пример вручную, а затем сравним полученный
результат с результатом программы.

Задача 1.Пусть дана система линейных уравнений:

Этой системе соответствуют: матрица
коэффициентов А и столбец свободных членов b:

А=
b=

В коде программы прописано, что пользователь
может ввести матрицу размерности не более, чем 10×10,
но, вводя коэффициенты, необходимо помнить о том, что матрица должна быть
симметричной. В противном случае программа сработает неправильно.

Найдем элементы матрицы Т. Это действие
оформлено в коде программы в качестве процедуры PROCEDURE Tij, которая
вычисляет коэффициенты матрицы Т из разложения (2.3.1) по формулам (2.3.2).
Таким
образом,
получим:

t211 = 1  t11
= 1, t12 =2  t12 = 2,t13 = 4  t13
= 4,+ t222= 13  t22 = 3,t13 + t22
t23= 23  t23
=5,+ t223 +t233 = 77  t33 =6

Таким образом, матрица А раскладывается в
произведение матриц T’ и Т (2.3.1):

Решим систему T’y=b. В коде программы данному
действию соответствует процедура PROCEDURE Yi , которая описывает процесс
вычисления вспомогательного столбца у по формулам (2.3.6) из нижней треугольной
матрицы (2.3.4).

 

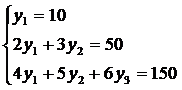
Решим систему Тх=у. Данное действие представлено
в коде программы в виде процедуры PROCEDURE Хi, которая считает искомый столбец
х по формулам (2.3.7) из верхней треугольной матрицы (2.3.5). По завершении
этого этапа программа выводит на экран значения х1…xn, а также выполняется
проверка правильности найденного решения. Суть её состоит в том, что полученные
значения х подставляются в исходную матрицу и высчитывается значение столбца
свободных членов b. Если оно совпадает с исходным, то решение найдено верно.

 

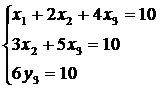
Результаты, которые вывела на экран программа
при вводе тех же самых значений элементов матрицы А и столбца b, совпадают с
результатами, полученными в данном пункте и находятся на рис.1.

Программа отлажена и готова к работе.

Рис. 1 — Реализация задачи

Задача 2. Протестируем эту же программу для
других значений. Зададим очень маленькое значение Е. Входные данные, а также
результат, полученный в ходе программы отражен на рисунке 2. По полученным
результатам можно сделать вывод: значение Е не влияет на результат. И это не
случайно. Ведь метод квадратного корня относится к группе точных методов.

Рис. 2

Заключение

В данной работе были рассмотрены прямые методы
решения линейных систем: метод Гаусса, метод LU-разложения, метод прогонки,
метод вращений и метод квадратного корня. К основным результатам курсовой
работы можно отнести:

обзор литературы, связанной с прямыми методами
решения линейных систем.

Реализация метода квадратного корня средствами
системы программирования Turbo Pascal.

Более подробно был проанализирован один из
методов решения систем линейных алгебраических уравнений: метод квадратных
корней. Метод был предложен для решения системы Ax=b, где матрица A —
симметрическая.

Также в данной системе были проанализированы
разного рода матрицы, и их влияние на точность полученного решения. Основываясь
на полученных выводах, можно контролировать в каких конкретно моментах удобно
решать систему линейных алгебраических уравнений методом квадратных, а когда
лучше использовать другой метод.

Список используемой литературы

1.       Бахвалов
Н.С., Жидков Н.П., Кобельков Г.М. Численные методы. М.: Наука, 2001.

2.      Вержбицкий
В.М. Основы численных методов. М.: Высшая школа. 2002.

.        Крылов
В.И. и др. Вычислительные методы, т.I. М.: Наука, 1976.

.        Трубников
С.В Численные методы. Часть 1: Теория погрешностей. Решение алгебраических и
трансцендентных уравнений и систем: Учебное пособие для студентов вузов. —
Брянск: Изд-во БГУ, 2005.

.        Фаддеев
Д.К., Фаддеева В.Н. Вычислительные методы линейной алгебры. М., Л.: изд-во
физ.-мат. лит-ры, 1963.

.        Лапчик
М.П., рагулина М.И., Хернер Е.К. Численные методы.- М.: Наука, 2007.

.        Заварыкин
В.М., Житомирский Г.В. Численные методы.- М.: Просвещение 1990.

.        Березин
И.С., Жидков Н.П. Методы вычислений, том 1. М.: Наука, 1966.

.        Березин
И.С., Жидков Н.П. Методы вычислений, том 2. М.: Наука, 1966.

.        Воеводин
В.В., Кузнецов Ю.А., Матрицы и вычисления.- М.: Наука, 2007.

.        Программирование
в среде Turbo Pascal 7.0: А. М. Епанешников, В. А. Епанешников — Москва,
Диалог-МИФИ, 2004 г.- 368 с.

Приложение

линейный система матрица программа

Листинг программы, реализующей метод
квадратного корня для решения линейных систем

Program KvadrKoren;crt;= record

d: real;

y: real;

end;= array [1..10] of complex; {массив
для
задания
вектор-столбцов
}= array [1..10, 1..10] of complex; {массив
для
задания
матриц}

Y, X, B: Vector;{вектор-столбцы:
вспомогательный, искомый и свободных членов}, T: Massiv;{матрицы: исходная и
матрица из разложения (2.3.1)}, j, n: integer; {индексы}, s, f: complex;
{вспомогательные переменные}: array [1..10] of real; {вспомогательный
вектор-столбец}: real; {погрешность}SUM (a,b: complex; var c: complex);
{процедуры SUM-KOR — это заранее описанные математические операции, .d
:=a.d+b.d; используемые в программе}

c.y:=a.y+b.y;;RAZ (a,b: complex; var
c: complex);.d :=a.d-b.d;.y:=a.y-b.y;;UMN (a,b: complex; var c: complex);.d
:=a.d*b.d — a.y*b.y;.y:=a.d*b.y + a.y*b.d;;DIL (a,b: complex; var c:
complex);.d :=(a.d*b.d + a.y*b.y)/(b.d*b.d + b.y*b.y);.y:= (b.d*a.y —
a.d*b.y)/(b.d*b.d + b.y*b.y);;KOR (a: complex; var c: complex);r, f: real;:=
sqrt (a.d*a.d + a.y*a.y);.d :=sqrt(r)*sqrt((a.d/r+1)/2);.y:=
sqrt(r)*sqrt((1-a.d/r)/2)

END;Tij; {нахождение матрицы Т из разложения
(2.3.1) по формулам (2.3.2)}

var k, i, j: integer;

BEGIN(A[1,1], T[1,1]); {нахождение 1 элемента по
1 формуле из (2.3.2)}i:= 1 to n do {нахождение элементов1 строки и главной
диагонали по 3 формуле из (2.3.2)}

for j:=1 to n do(i=j) and
(i<>j) then

begin.d:= 0;{вспомогательные переменные}

s.y:=
0;

for
k:=1 to
i-1 do

begin(T[k, i], T[k, i], p);(s, p,
s);;(A[i, j], s, p);(p, T[i, j]); i<j then
{нахождение оставшихся элементов}

begin.d:= 0;.y:= 0;k:= 1 to i-1 do(T[k,
i], T[k, i], p);(s, p, s);;(A[i, j], s, p);

DIL(p, T[i, j], T[i, j]);

endi>j then {так как матрица Т — верхняя
треугольная, то все элементы под главной диагональю — нулевые}[i, j].d := 0;

T[i, j].y := 0;;;

PROCEDURE Yi {нахождение столбца у по формулам
(2.3.6) из k, i: integer; из нижней треугольной системы (2.3.4)}

BEGIN(b[1], T[1, 1], y[1]);{находим
у1}

for i:= 2 to n do{находим все остальные у}.d:=
0;{вспомогательные переменные}

s.y:= 0;k:= 1 to i-1 do(T[k, i],
y[k], p);(s, p, s);;(b[i], s, p);(p, T[i, i], y[i]);;

END;Xi {нахождение искомого вектор-столбца х k,
i: integer; по формулам (2.3.7) из верхней треугольной матрицы (2.3.5)}(y[n],
T[n,n], x[n]); {нахождение хn}i:= n-1 downto 1 do {нахождение остальных х} .d:=
0;{вспомогательные переменные}

s.y:= 0;k:= i+1 to n do(T[i,k],
x[k], p);(s, p, s);;(y[i], s, p);(p, T[i, i], x[i]);;

END;PROVERKA;{подставляем полученные значения в
исходную i, j: integer; систему и считаем столбец свободных членов заново. Эти
значения заносим во вспомогательный вектор- i:=1 to n do столбец свободных
членов z. Сравниваем этот столбец с исходным столбцом b. Если они совпали,
[i]:= 0; то система решена правильно. }

for j:=1 to n do[i]:=z[i] +
a[i,j].d*x[j].d;(‘b’, i, ’=’, z[i]:7:7);;;; {очистить
экран}(‘vvedite
razmernost matritsy n=’);

readln(n); {ввод размерности матрицы}

write(‘vvedite pogreshnost
vychislenia e=’);(e); {ввод погрешности}(‘vvedite
koefficienty matritsy’);

for i:=1 to n do{ввод коэффициентов матрицы}

for j:=1 to n do(‘a[’, I, ‘,’, j,
‘]=’);(a[i,j].d);;(‘vvedite stolbets svobodnyh chlenov’);

for i:=1 to n do {ввод столбца свободных членов}

begin(‘b[’, i, ‘]=’);(b[i].d);;

Tij; {нахождение матрицы Т}; {нахождение
вектор-столбца y}; {нахождение решения x}i:=1 to n do(‘proverka
pravilnosty’);{процедура проверки};;.