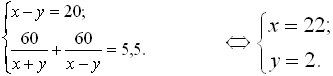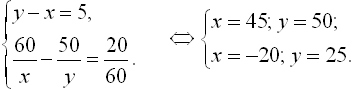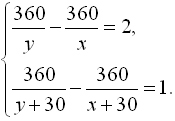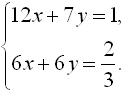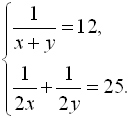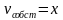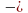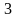Решая задачи при помощи уравнений, мы искали, как правило, одно неизвестное. Но встречаются и задачи, где есть несколько неизвестных. Такие задачи принято решать посредством составления систем уравнений.

Навстречу друг другу из одного города в другой, расстояние между которыми составляет 30 км, едут два велосипедиста. Предположим, что если велосипедист 1 выедет на 2 ч раньше своего товарища, то они встретятся через 2,5 часа после отъезда велосипедиста 2; если же велосипедист 2 выедет 2мя часами ранее велосипедсита 1, то встреча произойдет через 3 часа после отъезда первого. С какой скоростью движется каждый велосипедист?
Решение.
1. Определим скорость велосипедиста 1 как х км/ч, а скорость велосипедиста 2 как у км/ч.
2. Если первый велосипедист выедет на 2 ч раньше второго, то, согласно условию, он будет ехать до встречи 4,5 ч, тогда как второй 2,5 часа. За 4,5 ч первый проедет путь 4,5х км, а за 2,5 ч второй проедет путь 2,5у км.
3. Встреча двух велосипедистов означает, что суммарно они проехали путь 30 км, т.е. 4,5х + 2,5 у = 30. Это и есть наше первое уравнение.
4. Если второй выедет на 2 ч раньше первого, то, согласно условию, он будет ехать до встречи 5 ч, тогда как первый – 3 ч. Используя рассуждения, аналогичные изложенным выше рассуждениям, приходим к уравнению:
3х + 5у = 30.
5. Итак, мы получили систему уравнений
{4,5х + 2,5 у = 30,
{3х + 5у = 30.
6. Решив полученную систему уравнений, мы найдем корни: х = 5, у = 3.
Т.о., первый велосипедист едет со скоростью 5 км/ч, а второй – 3 км/ч.
Ответ: 5 км/ч, 3 км/ч.
Задача 2.
Вкладчику на его сбережения через год было начислено 6 $ процентных денег. Добавив 44 $, вкладчик оставил деньги еще на год. По истечении года вновь было произведено начисление процентов, и теперь вклад вместе с процентами составил 257,5 $. Какая сумма составляла вклад первоначально и сколько процентов начисляет банк?
Решение.
1. Пусть х ($) – первоначальный вклад, а у (%) – это проценты, которые начисляются ежегодно.
2. Тогда к концу года к первоначальному вкладу добавится (у/100) ∙ х $.
Из условия получаем уравнение (ух/100) = 6.
3. По условию известно, что в конце года вкладчик внес еще 44 $, так что вклад в начале второго года составил х + 6 + 44, т.е. (х + 50) $. Таким образом, сумма, полученная к концу второго года с учетом начисления, равнялась (х + 50 + (у/100)(х + 50)) $. По условию эта сумма равна 275,5 $. Это позволило нам составить второе уравнение:
х + 50 + (у/100)(х + 50) = 257,5
4. Итак, мы получили систему уравнений:
{(ух/100) = 6,
{х + 50 + (у/100)(х + 50) = 257,5
После преобразования системы уравнений мы получим:
{ху = 600,
{100х + 50у + ху = 20750.
Решив систему уравнений, мы нашли два корня: 200 и 1,5. Только первое значение удовлетворяет нашему условию.
Подставим значение х в уравнение и найдем значение у:
если х = 200, то у = 3.
Таким образом, первоначальный вклад составлял 200 $, а банк в год производит начисление а размере 3 %.
Ответ: 200 $; 3 %.
© blog.tutoronline.ru,
при полном или частичном копировании материала ссылка на первоисточник обязательна.
Алгоритм решения задачи с помощью системы линейных уравнений
- Обозначить неизвестные величины переменными («от смысла к буквам»).
- По условию задачи записать уравнения, связывающие обозначенные переменные.
- Решить полученную систему уравнений.
- Истолковать результат в соответствии с условием задачи («от букв к смыслу»).
Например:
Задуманы два числа. Если от первого отнять второе, то получается 10. Если к первому прибавить удвоенное второе, то получается 91. Найдите задуманные числа.
Шаг 1
«От смысла к буквам»:
Пусть x и y — задуманные числа.
Шаг 2
Уравнения по условию задачи::
${left{ begin{array}{c} x-y = 10 \ x+2y = 91 end{array} right.}$
Шаг 3
Решение системы уравнений:
$(-) {left{ begin{array}{c} x-y = 10 \ x+2y = 91 end{array} right.} Rightarrow {left{ begin{array}{c} -3y = -81 \ x = y+10 end{array} right.} Rightarrow$
$ Rightarrow {left{ begin{array}{c} x = 37 \ y = 27 end{array} right.} $
Шаг 4
«От букв к смыслу»:
Задуманы числа 37 и 27.
Примеры
Пример 1. Периметр прямоугольника равен 48 см. Его длина больше ширины в 3 раза.
Найдите стороны прямоугольника.
Пусть a и b — длина и ширина прямоугольника.
По условию:
$$ {left{ begin{array}{c} P = 2(a+b) = 48 \ a = 3b end{array} right.} Rightarrow {left{ begin{array}{c} a+b = 24 \ a = 3b end{array} right.} Rightarrow {left{ begin{array}{c} 3b+b = 24 \ a = 3b end{array} right.} Rightarrow {left{ begin{array}{c} 4b = 24 \ a = 3b end{array} right.} Rightarrow {left{ begin{array}{c} a = 18 \ b = 6 end{array} right.} $$
Ответ: длина прямоугольника 18 см, ширина 6 см.
Пример 2. Два программиста из Бомбея, работающие в одном проекте, написали 100500 строк кода. Первый работал 70 дней, второй – 100 дней. Сколько строк писал каждый программист ежедневно, если за первые 30 дней первый написал на 5550 строк больше, чем второй?
Пусть x — ежедневное количество строк для 1-го программиста, y- для 2-го.
По условию:
$$ {left{ begin{array}{c} 70x+100y = 100500 |:10 \ 30x-30y = 5550 |:30 end{array} right.} (-) Rightarrow {left{ begin{array}{c} 7x+10y = 10050 \ x-y=185 | times 10 end{array} right.}$$
$$ Rightarrow (+) {left{ begin{array}{c} 7x+10y = 10050 \ 10x-10y = 1850 end{array} right.} Rightarrow {left{ begin{array}{c} 17x = 11900 \ y = x-185 end{array} right.} Rightarrow {left{ begin{array}{c} x = 700 \ y = 515 end{array} right.} $$
Ответ: 700 строк и 515 строк
Пример 3. За 2 кг конфет и 3 кг печенья заплатили 1540 руб. Сколько стоит 1 кг конфет и 1 кг печенья, если 2 кг печенья дороже 1 кг конфет на 210 руб.?
Пусть x — цена за 1 кг конфет, y — за 1 кг печенья.
По условию:
$$ {left{ begin{array}{c} 2x+3y = 1540 \ 2y-x = 210 | times 2 end{array} right.} Rightarrow (+) {left{ begin{array}{c} 2x+3y = 1540 \ -2x+4y = 420 end{array} right.} Rightarrow {left{ begin{array}{c} 7y = 1960 \ x = 2y-210 end{array} right.} Rightarrow {left{ begin{array}{c} x = 350 \ y = 280 end{array} right.} $$
Ответ: 1 кг конфет — 350 руб. и 1 кг печенья — 280 руб.
Пример 4. Катер за 3 ч движения против течения реки и 2 часа по течению проходит 73 км. Найдите собственную скорость катера и скорость течения, если за 4 ч движения по течению катер проходит на 29 км больше, чем за 3 ч движения против течения.
Пусть v — скорость катера (км/ч), u — скорость течения (км/ч).
По условию:
$$ {left{ begin{array}{c} 3(v-u)+2(v+u) = 73 \ 4(v+u)-3(v-u) = 29 end{array} right.} Rightarrow {left{ begin{array}{c} 3v-3u+2v+2u = 73 \ 4v+4u-3v+3u = 29 end{array} right.}$$
$$ Rightarrow {left{ begin{array}{c} 5v-u = 73 \ v+7u = 29 end{array} right.} Rightarrow {left{ begin{array}{c} 5(29-7u)-u = 73 \ v = 29-7u end{array} right.} Rightarrow {left{ begin{array}{c} 145-35u-u = 73 \ v = 29-7u end{array} right.} Rightarrow$$
$$ Rightarrow {left{ begin{array}{c} -36u = -72 \ v = 29-7u end{array} right.} Rightarrow {left{ begin{array}{c} v = 15 \ u = 2 end{array} right.} $$
Ответ: скорость катера 15 км/ч и скорость течения 2 км/ч
Пример 5. 5 карандашей и 3 тетрадки вместе стоили 170 руб. После того, как карандаши подешевели на 20%, а тетрадки подорожали на 30%, за 3 карандаша и 5 тетрадок заплатили 284 руб. Найдите первоначальную цену карандаша и тетрадки.
Пусть x – первоначальная цена карандаша, y — тетрадки.
По условию:
$$ {left{ begin{array}{c} 5x+3y = 170 \ 3cdot0,8x+5cdot1,3y = 284 end{array} right.} Rightarrow {left{ begin{array}{c} 5x+3y = 170 |times frac{2,4}{5} \ 2,4x+6,5y = 284 end{array} right.} Rightarrow (-) {left{ begin{array}{c} 2,4x+1,44y = 81,6 \ 2,4x+6,5y = 284 end{array} right.} $$
$$ Rightarrow {left{ begin{array}{c} (6,5-1,44)y = 284-81,6 \ x = frac{170-3y}{5} end{array} right.}Rightarrow {left{ begin{array}{c} y = 202,4:5,06 = 40 \ x = frac{170-120}{5} = 10 end{array} right.} $$
Ответ: карандаш сначала стоил 10 руб., тетрадка — 40 руб.
Пример 6*. Велосипедист планирует добраться из пункта А в пункт В. Если он будет ехать на 3 км/ч быстрее, чем обычно, он доберётся на 1 час раньше. А если он будет ехать на 2 км/ч медленней, чем обычно, то – на 1 час позже. Найдите обычную скорость велосипедиста и время поездки при этой скорости.
Пусть v – обычная скорость велосипедиста (км/ч), t — обычное время (ч).
Расстояние между А и В неизменно, и по условию равно:
$$ s_{AB} = vt = (v+3)(t-1) = (v-2)(t+1) $$
Получаем систему:
$$ {left{ begin{array}{c} vt = (v+3)(t-1) \ vt = (v-2)(t+1) end{array} right.} Rightarrow (-) {left{ begin{array}{c} vt = vt-v+3t-3 \ vt = vt+v-2t-2 end{array} right.} Rightarrow (+) {left{ begin{array}{c} v-3t = -3 \ -v+2t = -2 end{array} right.} Rightarrow $$
$$ Rightarrow {left{ begin{array}{c} -t = -5 \ v = 2t+2 end{array} right.} Rightarrow {left{ begin{array}{c} t = 5 \ v = 12 end{array} right.} $$
Ответ: обычная скорость 12 км/ч, время 5 ч
Пример 7*. В одной бочке налито 12 л, во второй – 32 л. Если первую бочку доверху наполнить водой из второй, то вторая бочка будет наполнена ровно наполовину своего объёма. Если вторую бочку доверху наполнить водой из первой, то первая бочка будет наполнена на 1/6 своего объёма. Найдите объём каждой бочки.
Пусть x — объём первой бочки (л), y – объём второй (л).
Пусть a л перелито из второй бочки, и первая наполнилась до краёв, а во второй воды осталось наполовину:
$$ (+) {left{ begin{array}{c} 12+a = x \ 32-a = frac{1}{2} y end{array} right.} Rightarrow x+ frac{1}{2} y = 44 $$
Теперь пусть b л перелито из первой бочки, и вторая наполнилась до краёв, а в первой воды осталось на 1/6:
$$ (+) {left{ begin{array}{c} 32+b = y \ 12-b = frac{1}{6} x end{array} right.} Rightarrow frac{1}{6}x+y = 44 $$
Получаем систему:
$$ {left{ begin{array}{c} x+ frac{1}{2} y = 44 | times 2 \ frac{1}{6} x+y = 44 end{array} right.} Rightarrow (-) {left{ begin{array}{c} 2x+y = 88 \ frac{1}{6} x+y = 44 end{array} right.} Rightarrow (+) {left{ begin{array}{c} 1frac{5}{6} x = 44 \ y = 88-2x end{array} right.} Rightarrow $$
$$ {left{ begin{array}{c} x = 44: frac{11}{6} = 44cdot frac{6}{11} = 24 \ y = 88-2cdot24 = 40 end{array} right.} $$
Ответ: первая бочка 24 л, вторая – 40 л
Пример 8*. Если школьник едет в школу на автобусе, а возвращается домой пешком, то он тратит на всю дорогу полтора часа. Если он едет туда и обратно на автобусе, то он тратит полчаса. Сколько времени потратит школьник, если он пойдёт туда и обратно пешком?
Пусть s — расстояние между домом и школой, v — скорость автобуса, u — скорость школьника, t — искомое время, потраченное на дорогу туда и обратно пешком.
По условию задачи:
$$ {left{ begin{array}{c} 1,5 = frac{s}{v} + frac{s}{u} \ 0,5 = frac{2s}{v} \ t = frac{2s}{u} end{array} right.} $$
Из второго уравнения $ frac{s}{v} = frac{0,5}{2} = 0,25 $. Подставляем в первое уравнение:
$$ frac{s}{u} = 1,5-frac{s}{v} = 1,5-0,25 = 1,25 $$
И тогда искомое время:
$$ t = frac{2s}{v} = 2cdot1,25 = 2,5 (ч) $$
Ответ: 2,5 ч
Цели урока:
- Совершенствование навыков решения текстовых задач.
- Продолжить формирование знаний учащихся по решению систем уравнений с
двумя неизвестными. - Развитие математической грамотности.
Ход урока
Приложение
1. Актуализация знаний учащихся (5 минут).
Устный счет:
1. Найдите решение системы уравнений:
Ответы: 1) (1;3); 2) (0;3); 3) (1;2); 4) (2;1).
2. Выразите из уравнения 3х + 2у = 5 переменную х через
переменную у.
Ответы:
1)
2)
3) х = 3(5 – 2у);
4) х = 3(5 + 2у).
2. Объяснение нового материала (8 минут).
Алгоритм решения задач на движение и на производительность:
- Ввести неизвестные величины.
- Составить краткую запись задачи в таблице (скорость, путь, время) или
(производительность, работа, время). - Исходя из условия задачи, составить систему двух уравнений с двумя
неизвестными. - Решить систему уравнений, исключив те корни, которые не подходят по
условию задачи. - Записать ответ по вопросу задачи.
Задача №475.
Расстояние между двумя пристанями 60 км. Теплоход проходит это расстояние по
течению и против течения за 5,5 часов. Найдите скорость теплохода в стоячей воде
и скорость течения, если одна из них больше другой на 20 км/ч.
Краткая запись: пусть скорость теплохода х км/ч, а скорость течения
реки у км/ч, тогда
| Скорость, км/ч | Путь, км | Время, ч | |
| По течению | х + у | 60 | 60/(х + у) |
| Против течения | х – у | 60 | 60/(х – у) |
Зная, что теплоход проходит это расстояние по течению и против течения реки
за 5,5 часов и скорость катера больше скорости течения реки, составим систему
двух уравнений с двумя неизвестными:
Ответ: 22 км/ч – скорость теплохода, 2 км/ч – скорость течения реки.
3. Решение задач (30 минут).
Задача №478.
Фермер отправился на машине в город, находящийся на расстоянии 110 км от
фермы. Через 20 минут из города на ферму выехал его сын, который проезжал в час
на 5 км больше. Встреча произошла в 50 км от города. С какой скоростью ехал
фермер?
Краткая запись: пусть скорость фермера х км/ч, а скорость сына у,
тогда
| Скорость, км/ч | Путь, км | Время, ч | |
| Фермер | х | 110 – 50 = 60 | 60/х |
| Сын | у | 50 | 50/у |
Зная, что встреча произошла в 50 км от города, и сын выехал на 20 минут
позже, составим систему уравнений с двумя неизвестными:
Второе решение не подходит по условию задачи.
Ответ: 45 км/ч скорость фермера.
Задача №494.
Расстояние в 360 км легковой автомобиль прошел на 2 часа быстрее, чем
грузовой. Если скорость каждого автомобиля увеличить на 30 км/ч, то грузовой
затратит на весь путь на 1 час больше, чем легковой. Найдите скорость каждого
автомобиля.
Краткая запись: пусть скорость легкового автомобиля х км/ч, а скорость
грузового у км/ч, тогда:
1 случай
| Скорость, км/ч | Путь, км | Время, ч | |
| Легковой | х | 360 | 360/х |
| Грузовой | у | 360 | 360/у |
2 случай
| Скорость, км/ч | Путь, км | Время, ч | |
| Легковой | х + 30 | 360 | 360/(х + 30) |
| Грузовой | у + 30 | 360 | 360/(у + 30) |
Зная, что в первом случае легковой автомобиль приезжает на 2 часа раньше, а
во втором на 1 час раньше, составим систему уравнений с двумя переменными:
Ответ: 90 км/ч скорость легкового автомобиля, 60 км/ч скорость грузового
автомобиля.
Задача №489.
Бассейн наполнится. Если первую трубу открыть на 12 минут, а вторую – на 7
минут. Если же обе трубы открыть на 6 минут. То наполнится 2/3 бассейна. За
сколько минут наполнится бассейн, если открыть только вторую трубу?
Краткая запись: пусть весь объем воды в бассейне равен 1, производительность
1 трубы х , а второй – у, тогда:
1 случай
| Производительность | Работа | Время, мин | |
| 1 труба | х | 12х | 12 |
| 2 труба | у | 7у |
2 случай
| Производительность | Работа | Время, мин | |
| 1 труба | х | 6х | 6 |
| 2 труба | у | 6у | 6 |
Зная, что в первом случае бассейн наполнится полностью, а во втором только
2/3, составим систему двух уравнений с двумя неизвестными.
Ответ: за 15 минут вторая труба заполнит весь бассейн.
Задача №492.
Двое рабочих могут выполнить задание за 12 дней. Если сначала один из них
сделает половину всей работы, а потом остальное сделает другой, то им
потребуется 25 дней. За сколько дней каждый рабочий, работая один, может
выполнить задание?
Краткая запись: пусть производительность 1 рабочего х, а второго у,
тогда:
| Производительность | Работа | Время | |
| 1 рабочий | х | 1/2 | 1/2х |
| 2 рабочий | у | 1/2 | 1/2у |
Зная, что вместе они сделают работу за 12 дней, а работая по очереди и
выполнив по половине работы, им потребуется 25 дней, составим систему уравнений
с двумя неизвестными:
Ответ: один рабочий выполнит всю работу за 30 дней, а другой за 20 дней.
4. Подведение итогов урока (2 минуты).
Домашнее задание: п. 22, №476, 479, 491.
Используемая литература:
- Учебник «Алгебра 9», автор Макарычев Ю.Н., Миндюк Н.Г., Нешков К.И.,
Феоктистов И.Е.
Решение текстовых задач. 9-й класс
Разделы: Математика
Класс: 9
- Совершенствование навыков решения текстовых задач.
- Продолжить формирование знаний учащихся по решению систем уравнений с двумя неизвестными.
- Развитие математической грамотности.
1. Актуализация знаний учащихся (5 минут).
1. Найдите решение системы уравнений:
Ответы: 1) (1;3); 2) (0;3); 3) (1;2); 4) (2;1).
2. Выразите из уравнения 3х + 2у = 5 переменную х через переменную у.
1)
2)
2. Объяснение нового материала (8 минут).
Алгоритм решения задач на движение и на производительность:
- Ввести неизвестные величины.
- Составить краткую запись задачи в таблице (скорость, путь, время) или (производительность, работа, время).
- Исходя из условия задачи, составить систему двух уравнений с двумя неизвестными.
- Решить систему уравнений, исключив те корни, которые не подходят по условию задачи.
- Записать ответ по вопросу задачи.
Расстояние между двумя пристанями 60 км. Теплоход проходит это расстояние по течению и против течения за 5,5 часов. Найдите скорость теплохода в стоячей воде и скорость течения, если одна из них больше другой на 20 км/ч.
Краткая запись: пусть скорость теплохода х км/ч, а скорость течения реки у км/ч, тогда
| Скорость, км/ч | Путь, км | Время, ч | |
| По течению | х + у | 60 | 60/(х + у) |
| Против течения | х – у | 60 | 60/(х – у) |
Зная, что теплоход проходит это расстояние по течению и против течения реки за 5,5 часов и скорость катера больше скорости течения реки, составим систему двух уравнений с двумя неизвестными:
Ответ: 22 км/ч – скорость теплохода, 2 км/ч – скорость течения реки.
3. Решение задач (30 минут).
Фермер отправился на машине в город, находящийся на расстоянии 110 км от фермы. Через 20 минут из города на ферму выехал его сын, который проезжал в час на 5 км больше. Встреча произошла в 50 км от города. С какой скоростью ехал фермер?
Краткая запись: пусть скорость фермера х км/ч, а скорость сына у, тогда
| Скорость, км/ч | Путь, км | Время, ч | |
| Фермер | х | 110 – 50 = 60 | 60/х |
| Сын | у | 50 | 50/у |
Зная, что встреча произошла в 50 км от города, и сын выехал на 20 минут позже, составим систему уравнений с двумя неизвестными:
Второе решение не подходит по условию задачи.
Ответ: 45 км/ч скорость фермера.
Расстояние в 360 км легковой автомобиль прошел на 2 часа быстрее, чем грузовой. Если скорость каждого автомобиля увеличить на 30 км/ч, то грузовой затратит на весь путь на 1 час больше, чем легковой. Найдите скорость каждого автомобиля.
Краткая запись: пусть скорость легкового автомобиля х км/ч, а скорость грузового у км/ч, тогда:
| Скорость, км/ч | Путь, км | Время, ч | |
| Легковой | х | 360 | 360/х |
| Грузовой | у | 360 | 360/у |
| Скорость, км/ч | Путь, км | Время, ч | |
| Легковой | х + 30 | 360 | 360/(х + 30) |
| Грузовой | у + 30 | 360 | 360/(у + 30) |
Зная, что в первом случае легковой автомобиль приезжает на 2 часа раньше, а во втором на 1 час раньше, составим систему уравнений с двумя переменными:
Ответ: 90 км/ч скорость легкового автомобиля, 60 км/ч скорость грузового автомобиля.
Бассейн наполнится. Если первую трубу открыть на 12 минут, а вторую – на 7 минут. Если же обе трубы открыть на 6 минут. То наполнится 2/3 бассейна. За сколько минут наполнится бассейн, если открыть только вторую трубу?
Краткая запись: пусть весь объем воды в бассейне равен 1, производительность 1 трубы х , а второй – у, тогда:
| Производительность | Работа | Время, мин | |
| 1 труба | х | 12х | 12 |
| 2 труба | у | 7у |
| Производительность | Работа | Время, мин | |
| 1 труба | х | 6х | 6 |
| 2 труба | у | 6у | 6 |
Зная, что в первом случае бассейн наполнится полностью, а во втором только 2/3, составим систему двух уравнений с двумя неизвестными.
Ответ: за 15 минут вторая труба заполнит весь бассейн.
Двое рабочих могут выполнить задание за 12 дней. Если сначала один из них сделает половину всей работы, а потом остальное сделает другой, то им потребуется 25 дней. За сколько дней каждый рабочий, работая один, может выполнить задание?
Краткая запись: пусть производительность 1 рабочего х, а второго у, тогда:
| Производительность | Работа | Время | |
| 1 рабочий | х | 1/2 | 1/2х |
| 2 рабочий | у | 1/2 | 1/2у |
Зная, что вместе они сделают работу за 12 дней, а работая по очереди и выполнив по половине работы, им потребуется 25 дней, составим систему уравнений с двумя неизвестными:
Ответ: один рабочий выполнит всю работу за 30 дней, а другой за 20 дней.
4. Подведение итогов урока (2 минуты).
Домашнее задание: п. 22, №476, 479, 491.
- Учебник «Алгебра 9», автор Макарычев Ю.Н., Миндюк Н.Г., Нешков К.И., Феоктистов И.Е.
Решение уравнений с двумя неизвестными
В математике большая часть задач ориентирована на решение стандартных уравнений, в которых представлена одна переменная. Однако, некоторые из них, помимо числовых выражений, содержат одновременно две неизвестные. Перед тем как приступить к решению такого уравнения, стоит изучить его определение.
Определение
Итак, уравнением с двумя неизвестными называют любое равенство следующего типа:
a*x + b*y =с, где a, b, c — числа, x, y — неизвестные переменные.
Ниже приведены несколько примеров:
Уравнение с двумя неизвестными точно так же, как и с одной, имеет решение. Однако такие выражения, как правило, имеют бесконечное множество разных решений, поэтому в алгебре их принято называть неопределенными.
Решение задач
Чтобы решить подобные задачи, необходимо отыскать любую пару значений x и y, которая удовлетворяла бы его, другими словами, обращала бы уравнение с неизвестными x и y в правильное числовое равенство. Найти удовлетворяющую пару чисел можно при помощи метода подбора.
Для наглядности объяснений подберем корни для выражения: y-x = 6.
При y=5 и x=-1 равенство становится верным тождеством 5- (-1) = 6. Поэтому пару чисел (-1; 5) можно считать корнями выражения y-x = 6. Ответ: (-1; 5).
Необходимо отметить, что записывать полученный ответ по правилам необходимо в скобках через точку с запятой. Первым указывается значение х, вторым — значение y.
У равенств такого вида может и не быть корней. Рассмотрим такой случай на следующем примере: x+y = x+y+9
Приведем исходное равенство к следующему виду:
В результате мы видим ошибочное равенство, следовательно, это выражение не имеет корней.
При решении уравнений можно пользоваться его свойствами. Первое их них: каждое слагаемое можно вынести в другую часть выражения. Вместе с этим обязательно нужно поменять знак на обратный. Получившееся равенство будет равнозначно исходному.
Например, из выражения 20y — 3x = 16 перенесем неизвестное y в другую его часть.
Оба равенства равносильны.
Второе свойство: допустимо умножать или делить части выражения на одинаковое число, не равное нолю. В итоге получившиеся равенства будут равнозначны.
Оба уравнения также равносильны.
Система уравнений с двумя неизвестными
Система уравнений представляет собой некоторое количество равенств, выполняющихся одновременно. В большинстве задач приходится находить решение системы, состоящей из двух равенств с двумя переменными.
Для решения системы уравнений необходимо найти пару чисел, обращающих оба уравнения системы в правильное равенство. Решением может служить одна пара чисел, несколько пар чисел или вовсе их отсутствие.
Решить подобные системы уравнений можно, применяя следующие методы.
Метод подстановки
- Выражаем неизвестное из любого равенства через вторую переменную.
- Подставляем получившееся выражение неизвестного во второе равенство и решаем его.
- Делаем подстановку полученного значения неизвестного и вычисляем значение второго неизвестного.
Метод сложения
- Приводим к равенству модули чисел при каком-либо неизвестном.
- Производим вычисление одной из переменных, произведя сложение или вычитание полученных выражений.
- Подставляем найденное значение в какое-либо уравнение в первоначальной системе и вычисляем вторую переменную.
Графический метод
- Выражаем в каждом равенстве одну переменную через другую.
- Строим графики двух имеющихся уравнений в одной координатной плоскости.
- Определяем точку их пересечения и ее координаты. На этом шаге у вас может получиться три варианта: графики пересекаются — у системы единственно верный вариант решения; прямые параллельны друг другу — система решений не имеет; графики совпадают — у системы бесконечно много решений.
- Делаем проверку, подставив полученные значения в исходную систему равенств.
При нахождении корней у одной системы всеми этими способами у вас обязательно должен получиться одинаковый результат, если вы, конечно, все сделали правильно.
В настоящее время есть возможность решения подобных задач с помощью встроенных средств офисной программы Excel, а также на специализированных онлайн-ресурсах и калькуляторах. С помощью них вы легко можете проверить правильность своих вычислений и результатов.
Надеемся, что наша статья помогла вам в освоении этой базовой темы школьной математики. Если же вы пока не можете справиться с решением уравнений такого вида, не расстраивайтесь. Для понимания и закрепления изученной темы рекомендуется как можно больше практиковаться, и тогда у вас без труда получится решать задачи любой сложности. Желаем вам удачи в покорении математических вершин!
Видео
Из этого видео вы узнаете, как решать уравнения с двумя неизвестными.
Решение задач с помощью систем линейных уравнений
Алгоритм решения задачи с помощью системы линейных уравнений
- Обозначить неизвестные величины переменными («от смысла к буквам»).
- По условию задачи записать уравнения, связывающие обозначенные переменные.
- Решить полученную систему уравнений.
- Истолковать результат в соответствии с условием задачи («от букв к смыслу»).
Задуманы два числа. Если от первого отнять второе, то получается 10. Если к первому прибавить удвоенное второе, то получается 91. Найдите задуманные числа.
«От смысла к буквам»:
Пусть x и y — задуманные числа.
Уравнения по условию задачи::
Решение системы уравнений:
«От букв к смыслу»:
Задуманы числа 37 и 27.
Примеры
Пример 1. Периметр прямоугольника равен 48 см. Его длина больше ширины в 3 раза.
Найдите стороны прямоугольника.
Пусть a и b — длина и ширина прямоугольника.
$$ <left< begin P = 2(a+b) = 48 \ a = 3b end right.> Rightarrow <left< begin a+b = 24 \ a = 3b end right.> Rightarrow <left< begin 3b+b = 24 \ a = 3b end right.> Rightarrow <left< begin 4b = 24 \ a = 3b end right.> Rightarrow <left< begin a = 18 \ b = 6 end right.> $$
Ответ: длина прямоугольника 18 см, ширина 6 см.
Пример 2. Два программиста из Бомбея, работающие в одном проекте, написали 100500 строк кода. Первый работал 70 дней, второй – 100 дней. Сколько строк писал каждый программист ежедневно, если за первые 30 дней первый написал на 5550 строк больше, чем второй?
Пусть x — ежедневное количество строк для 1-го программиста, y- для 2-го.
$$ <left< begin 70x+100y = 100500 |:10 \ 30x-30y = 5550 |:30 end right.> (-) Rightarrow <left< begin 7x+10y = 10050 \ x-y=185 | times 10 end right.>$$
$$ Rightarrow (+) <left< begin 7x+10y = 10050 \ 10x-10y = 1850 end right.> Rightarrow <left< begin 17x = 11900 \ y = x-185 end right.> Rightarrow <left< begin x = 700 \ y = 515 end right.> $$
Ответ: 700 строк и 515 строк
Пример 3. За 2 кг конфет и 3 кг печенья заплатили 1540 руб. Сколько стоит 1 кг конфет и 1 кг печенья, если 2 кг печенья дороже 1 кг конфет на 210 руб.?
Пусть x — цена за 1 кг конфет, y — за 1 кг печенья.
$$ <left< begin 2x+3y = 1540 \ 2y-x = 210 | times 2 end right.> Rightarrow (+) <left< begin 2x+3y = 1540 \ -2x+4y = 420 end right.> Rightarrow <left< begin 7y = 1960 \ x = 2y-210 end right.> Rightarrow <left< begin x = 350 \ y = 280 end right.> $$
Ответ: 1 кг конфет — 350 руб. и 1 кг печенья — 280 руб.
Пример 4. Катер за 3 ч движения против течения реки и 2 часа по течению проходит 73 км. Найдите собственную скорость катера и скорость течения, если за 4 ч движения по течению катер проходит на 29 км больше, чем за 3 ч движения против течения.
Пусть v — скорость катера (км/ч), u — скорость течения (км/ч).
$$ Rightarrow <left< begin 5v-u = 73 \ v+7u = 29 end right.> Rightarrow <left< begin 5(29-7u)-u = 73 \ v = 29-7u end right.> Rightarrow <left< begin 145-35u-u = 73 \ v = 29-7u end right.> Rightarrow$$
Ответ: скорость катера 15 км/ч и скорость течения 2 км/ч
Пример 5. 5 карандашей и 3 тетрадки вместе стоили 170 руб. После того, как карандаши подешевели на 20%, а тетрадки подорожали на 30%, за 3 карандаша и 5 тетрадок заплатили 284 руб. Найдите первоначальную цену карандаша и тетрадки.
Пусть x – первоначальная цена карандаша, y — тетрадки.
$$ <left< begin 5x+3y = 170 \ 3cdot0,8x+5cdot1,3y = 284 end right.> Rightarrow <left< begin 5x+3y = 170 |times frac<2,4> <5>\ 2,4x+6,5y = 284 end right.> Rightarrow (-) <left< begin 2,4x+1,44y = 81,6 \ 2,4x+6,5y = 284 end right.> $$
Ответ: карандаш сначала стоил 10 руб., тетрадка — 40 руб.
Пример 6*. Велосипедист планирует добраться из пункта А в пункт В. Если он будет ехать на 3 км/ч быстрее, чем обычно, он доберётся на 1 час раньше. А если он будет ехать на 2 км/ч медленней, чем обычно, то – на 1 час позже. Найдите обычную скорость велосипедиста и время поездки при этой скорости.
Пусть v – обычная скорость велосипедиста (км/ч), t — обычное время (ч).
Расстояние между А и В неизменно, и по условию равно:
Ответ: обычная скорость 12 км/ч, время 5 ч
Пример 7*. В одной бочке налито 12 л, во второй – 32 л. Если первую бочку доверху наполнить водой из второй, то вторая бочка будет наполнена ровно наполовину своего объёма. Если вторую бочку доверху наполнить водой из первой, то первая бочка будет наполнена на 1/6 своего объёма. Найдите объём каждой бочки.
Пусть x — объём первой бочки (л), y – объём второй (л).
Пусть a л перелито из второй бочки, и первая наполнилась до краёв, а во второй воды осталось наполовину:
Теперь пусть b л перелито из первой бочки, и вторая наполнилась до краёв, а в первой воды осталось на 1/6:
$$ <left< begin x+ frac<1> <2>y = 44 | times 2 \ frac<1> <6>x+y = 44 end right.> Rightarrow (-) <left< begin 2x+y = 88 \ frac<1> <6>x+y = 44 end right.> Rightarrow (+) <left< begin 1frac<5> <6>x = 44 \ y = 88-2x end right.> Rightarrow $$
Ответ: первая бочка 24 л, вторая – 40 л
Пример 8*. Если школьник едет в школу на автобусе, а возвращается домой пешком, то он тратит на всю дорогу полтора часа. Если он едет туда и обратно на автобусе, то он тратит полчаса. Сколько времени потратит школьник, если он пойдёт туда и обратно пешком?
Пусть s — расстояние между домом и школой, v — скорость автобуса, u — скорость школьника, t — искомое время, потраченное на дорогу туда и обратно пешком.
По условию задачи:
Из второго уравнения $ frac = frac<0,5> <2>= 0,25 $. Подставляем в первое уравнение:
И тогда искомое время:
$$ t = frac<2s> = 2cdot1,25 = 2,5 (ч) $$
http://liveposts.ru/articles/education-articles/matematika/reshenie-uravnenij-s-dvumya-neizvestnymi
http://reshator.com/sprav/algebra/7-klass/resheniya-zadachi-s-pomoshchyu-sistemy-linejnyh-uravnenij/
Решение задач с использованием систем линейных уравнений с двумя переменными.
Переходим теперь к практическому применению систем линейных уравнений с двумя переменными. Часто бывает, что в задачах неизвестны два, а то и три-четыре компонента. И в этом случае обозначение какого-то одного компонента переменной не облегчает решение задачи. Тогда нужно ввести две или три переменные. Вот здесь нам как раз и понадобится система уравнений и способы её решения. Приведём пример с полным описанием.
Например, решить задачу. Лодка за 3 ч движения по течению и 4 ч против течения проходит 114 км. Найдите скорость лодки по течению и её скорость против течения, если за 6 ч движения против течения она проходит такой же путь, как за 5 ч по течению.
Решение. В задаче описывается движение по воде. А значит, должна быть собственная скорость лодки и скорость течения реки. Они нам и не известны, поэтому обозначим через 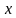
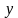

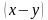
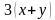
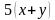
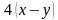

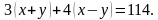
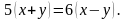
Для наглядности составим условие задачи в виде таблицы.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Имеем два линейных уравнения с двумя переменными, которые должны выполняться при одних и тех же значениях переменных, значит, составляем систему:
Раскроем сначала скобки и приведём подобные слагаемые.
Уравнения получились достаточно простые, поэтому можно использовать или способ подстановки, или способ сложения. Приведём оба способа решения, чтобы показать, что выбор только за вами, сложность одинакова.
|
Способ подстановки |
Способ сложения |
|
|
|
Значит, собственная скорость лодки равна км/ч, а скорость течения реки —
км/ч.
Тогда скорость лодки по течению реки: км/ч.
Скорость лодки против течения реки: км/ч.
Ответ: 18 км/ч; 15 км/ч.
Рассмотрим ещё одну задачу.
Есть две металлические отливки, одна из которых содержит 30% меди, а вторая – 70% меди. Сколько килограммов каждой отливки надо взять, чтобы получить 120 кг сплава, содержащего 40% меди?
Решение. Пусть 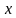
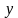
кг, а во второй —
кг. По условию задачи известно, что после сплава этих двух отливок, масса станет равной 120 кг, поэтому
. Кроме того известно, что полученный сплав будет содержать 40% меди, составляем уравнение: . Запишем и решим систему двух уравнений.
Решим систему способом сложения. Умножим первое уравнение на и почленно сложим два уравнения.
Значит, первого сплава нужно взять 90 кг, а второго – 30 кг.
Ответ: 90 кг; 30 кг.
Задачи на стоимость.
-
За 7 кг апельсинов и 4 кг лимонов заплатили 1120 рублей. Сколько стоит 1 кг апельсинов и сколько 1 кг лимонов, если 5 кг апельсинов дороже, чем 2 кг лимонов, на 390 рублей?
-
За 2 стола и 6 стульев заплатили 10620 рублей. После того, как столы подешевели на 10%, а стулья – на 20%, за один стол и два стула заплатили 4135,5 рублей. Какова была начальная цена одного стола и одного стула?
-
За 4 футбольных и 3 волейбольных мяча заплатили 6700 рублей. После того, как футбольный мяч подешевел на 20%, а волейбольный подорожал на 10%, за один футбольный и один волейбольный мячи заплатили 1830 рублей. Какова была начальная цена каждого мяча?
-
За 5 ручек и 4 карандаша заплатили 300 рублей. Сколько стоит одна ручка и сколько стоит один карандаш, если 3 ручки дороже, чем 2 карандаша, на 70 рублей?
-
За 7 тетрадей и 4 ручки заплатили 300 рублей. После того, как тетради подешевели на 40%, а ручки – на 20%, одна ручка стала дороже одной тетради на 20 рублей. Какими были первоначальные цены тетради и ручки?
-
Магазин закупил конфеты двух сортов в упаковках по 240 г и 250 г, причём конфет первого вида было куплено на 600 г больше. Сколько купили конфет каждого вида, если упаковок с конфетами первого сорта было на 20 больше?
-
Таня за 3 тетради и 2 карандаша заплатила 58 рублей, а Лена за 5 таких же тетрадей и 1 такой же карандаш заплатила 78 рублей. Сколько стоит тетрадь и сколько карандаш?
-
У Толи 18 монет по 2 руб. и по 5 руб. на сумму 97 руб. Сколько монет каждого достоинства у Толи?
-
Банк продал предпринимателю г-ну Разину 8 облигаций по 2000 руб. и 3000 руб. Сколько облигаций каждого номинала купил г-н Разин, если за все облигации было заплачено 19 000 рублей?
-
За 15 акций компании «Трансгаз» и 10 акций компании «Суперсталь» заплатили 35 000 руб. Сколько стоит одна акция каждой компании, если акция «Трансгаза» на 1000 руб. дешевле акции «Суперстали»?
-
За 4 блокнота и 3 карандаша заплатили 181 руб., а за такие же 2 блокнота и 5 карандашей заплатили 115 руб. Сколько стоит один блокнот и один карандаш?
-
За 5 пачек творога и 2 банки сметаны заплатили 210 руб., а за такие же 3 пачки творога и 3 банки сметаны заплатили 171 руб. Сколько стоит одна пачка творога и одна банка сметаны?
-
Шапка и шарф вместе стоили 1200 руб. После того, как шапка подешевела на 20%, а шарф – на 10%, их суммарная стоимость составила 1005 руб. Сколько стоила шапка и сколько стоил шарф до снижения цен?
-
Сумка и ремень вместе стоили 2300 руб. После того как сумка подешевела на 15%, а ремень – на 5%, их суммарная стоимость составила 2005 руб. Сколько стоила сумка и сколько стоил ремень до снижения цен?
-
Три ватрушки и пять плюшек стоят 45 руб., а пять ватрушек и три плюшки стоят 43 руб. Сколько стоит ватрушка и сколько стоит плюшка?
-
Три марки и пять конвертов стоят 39 руб., а четыре марки и два конверта стоят 24 руб. Сколько стоит марка и сколько стоит конверт?
-
Пять открыток и четыре конверта стоят 44 руб., а две открытки и три конверта стоят 26 руб. Сколько стоит открытка и сколько стоит конверт?
-
Стоимость 50 экземпляров учебника физики для 10 класса и 25 экземпляров учебника физики для 11 класса составляет 10 000 рублей. С учётом скидки в размере 20% на учебники для 10 класса и 10% на учебники для 11 класса стоимость покупки снизилась на 17%. Сколько стоит один учебник физики для 10 класса с учётом скидки?
-
За 1 кг апельсинов и 1 кг яблок заплатили 120 рублей. После подорожания апельсинов на 30%, а яблок на 20% такая же покупка будет стоить 151 руб. Найдите первоначальную стоимость 1 кг апельсинов и 1 кг яблок.
-
За 1 кг огурцов и 1 кг помидоров заплатили 150 руб. После того как огурцы подешевеют на 30%, а помидоры на 20%, такая же покупка будет стоить 113 руб. Найдите первоначальную стоимость 1 кг огурцов и 1 кг помидоров.
-
За 1 рюкзак и 1 пенал заплатили 850 руб. Если рюкзак подорожает на 10%, а пенал на 20%, такая же покупка будет стоить 950 руб. Найдите первоначальную стоимость 1 рюкзака и 1 пенала.
-
Три пирожка и две булки стоят 40 руб., а два пирожка и три булки стоят 45 руб. Сколько стоит пирожок, сколько стоит булка?
Задачи на количество.
-
В двух ящиках лежали яблоки. Если из одного ящика переложить во второй 45 яблок, то в обоих ящиках их станет поровну. Если же из второго ящика переложить в первый 20 яблок, то в первом станет в 3 раза больше яблок, чем во втором. Сколько яблок было в каждом ящике?
-
В двух шкафах стояли книги. Если из первого шкафа переставить во второй 10 книг, то в обоих шкафах книг станет поровну. Если же из второго шкафа переставить в первый 44 книги, то в нём останется в 4 раза меньше книг, чем в первом. Сколько книг было в каждом шкафу?
-
У двух мальчиков были марки. Если один из них отдаст второму 10 марок, то у обоих мальчиков марок станет поровну. Если же первый отдаст второму 50 марок, то у него останется в 5 раз меньше марок, чем станет у второго. Сколько марок было у каждого мальчика?
-
В туристический поход ребята взяли двухместные и трёхместные палатки. Сколько человек разместилось в трёхместных палатках, если на 26 человек ребята взяли 10 палаток?
-
В копилку складывали двухрублёвые и пятирублёвые монеты. Когда копилку вскрыли, в ней оказалось 178 рублей, причём пятирублёвых монет было на 12 штук меньше, чем двухрублёвых. Сколько денег пятирублёвыми монетами было в копилке?
-
В гостинице 25 номеров. Есть четырёхместные и двухместные номера. Сколько каких номеров, если всего в гостинице могут поместиться 70 человек?
-
В первый день в школьную библиотеку привезли 4 пачки учебников по геометрии и 3 пачки учебников по алгебре: всего 96 книг. Во второй день привезли 5 пачек учебников по геометрии и 6 пачек учебников по алгебре, причём учебников по геометрии на 3 больше, чем по алгебре. Сколько учебников по геометрии привезли в библиотеку?
-
В магазин привезли 3 коробки с пачками чая и 4 коробки с пачками кофе, всего 76 пачек. В другой день привезли 6 таких же коробок чая и 5 коробок кофе, причём чая на 22 пачки больше. Сколько пачек чая привезли?
-
В первом отряде летнего лагеря было 25 подростков. В течение смены число девочек увеличилось на 10%, а число мальчиков уменьшилось на 20%, в результате в отряде стало 23 подростка. Сколько девочек и сколько мальчиков стало в первом отряде в конце смены?
-
На дворе было 20 кроликов и кур, у которых 52 ноги. Сколько было кроликов и сколько было кур на дворе?
-
Для кормления 5 лошадей и 25 коров ежедневно отпускают 220 кг сена, для 3 лошадей и 35 коров отпускают 272 кг сена. Найдите дневную норму сена для лошади и для коровы.
-
Летели галки и сели на палки. Если на каждую палку сядет по галке, то одной галке не хватит палки. Если на каждую палку сядут по две галки, то одна палка останется без галок. Сколько было галок и сколько палок?
-
Школьники отправились в поход в составе 57 человек, при этом у них были только трёхместные и четырёхместные палатки. Сколько трёхместных палаток и сколько четырёхместных, если всего в поход взяли 16 палаток?
-
83 подарка были упакованы в большие и маленькие коробки. В большие коробки помещается по 8 подарков, а в маленькие – по 5. Всего использовали 13 коробок. Сколько было коробок каждого вида?
-
В гостинице группа из 27 туристов была размещена в двухместных и трёхместных номерах. Всего туристы заняли 10 номеров. Сколько было занято трёхместных и сколько двухместных номеров?
-
В классе 36 учеников. Девочек на 3 меньше, чем мальчиков. Сколько девочек и сколько мальчиков было в классе?
-
В магазине продаются тетради по 96 листов и по 24 листа. Во всех тетрадях, купленных Сашей, 528 листов. Сколько толстых и сколько тонких тетрадей купил Саша, если все купленные им толстые тетради содержат на 48 листов больше, чем все тонкие?
-
В физкультурном зале 35 учеников. Мальчиков в 1,5 раза больше, чем девочек. Сколько мальчиков и сколько девочек в физкультурном зале?
-
В первой рукописи на 60 страниц больше, чем во второй. Корректор, вычитывающий первую рукопись, выполнив 60% всей работы, вычитал на 12 страниц меньше, чем корректор, вычитывающий вторую рукопись и выполнивший 80% всей работы. Сколько страниц в каждой рукописи?
-
На турбазе имеются палатки и домики, вместе их 25. В каждом домике живут 4 человека, а в палатке – 2. Сколько на турбазе палаток и сколько домиков, если турбаза рассчитана на 70 человек?
-
В классе 24 человека. Чтобы девочкам выдать по три тетради, а мальчиками по две тетради, потребуется 59 тетрадей. Сколько в классе мальчиков и сколько девочек?
-
В классе 25 человек. Чтобы девочкам выдать по три тетради, а мальчикам по две тетради, потребуется 62 тетради. Сколько в классе мальчиков и сколько девочек?
-
На двух полках стояло 210 книг. Если с первой полки убрать половину книг, а на второй увеличить их число вдвое, то на двух полках будет 180 книг. Сколько книг стояло на каждой полке первоначально?
-
В двух коробках лежало 210 карандашей. Если в первой коробке число карандашей уменьшить вдвое, а во второй их число увеличить в 2 раза, то в двух коробках станет 240 карандашей. Сколько карандашей было в каждой коробке первоначально?
-
Если раздать детям по 3 яблока, то 7 яблок останется, а чтобы раздать каждому по 5 яблок, не хватит 3 яблок. Сколько было детей?
-
Если раздать детям по 5 конфет, то 13 конфет останется, а чтобы раздать каждому по 8 конфет, не хватит 5 конфет. Сколько было детей?
-
В 5 пакетов и 4 коробки расфасовали 1 650 г печенья. В каждую коробку уместилось на 75 г печенья больше, чем в пакет. Сколько граммов печенья расфасовали в коробки?
-
К новогоднему празднику семиклассники клеили бумажные гирлянды и ёлочные игрушки. Каждый мальчик склеил по 4 гирлянды и 3 игрушки, а каждая девочка по 3 гирлянды и 5 игрушек. Мальчики склеили на 22 гирлянды больше, чем девочки. Игрушек всего было сделано 118. Сколько мальчиков и девочек в этом классе?
-
В физкультурный зал школы привезли 5 сеток с баскетбольными мячами и 2 сетки с волейбольными мячами, всего 23 мяча. Через неделю – 3 такие же сетки с баскетбольными мячами и одну сетку с волейбольными мячами, причём баскетбольных мячей на 5 больше, чем волейбольных. Сколько мячей в каждой сетке?
-
В магазин привезли 3 упаковки с пачками чая и 4 упаковки с пачками кофе, всего 85 пачек. В другой день – 5 таких же упаковок с пачками чая и 4 упаковки с пачками кофе, всего 107 пачек. Сколько пачек чая и сколько пачек кофе в каждой упаковке?
-
Группа туристов, в которой 21 человек, отправилась в поход на байдарках. Они взяли с собой двухместные и трёхместные байдарки, всего 9 лодок. Сколько байдарок каждого типа взяли с собой туристы?
-
Десант из 130 человек был доставлен к месту назначения на 4 тяжёлых и 2 лёгких вертолётах. Один тяжёлый и один лёгкий вертолёты вместе вмещают 36 десантников. Сколько десантников можно перевезти в каждом вертолёте?
-
Две мастерские сшили в первый день 110 костюмов. Во второй день первая мастерская увеличила выпуск костюмов на 20%, а вторая – на 10%, в результате во второй день было сшито на 16 костюмов больше, чем в первый день. Сколько костюмов сшила каждая мастерская во второй день?
-
Масса туриста с рюкзаком в 5 раз больше массы одного рюкзака. Определите массы рюкзака и туриста в отдельности, если сумма масс двух рюкзаков и массы туриста равна 120 кг.
-
Шесть метров новой верёвки имеют такую же массу, как и пять метров старой. Найдите массу одного метра новой и старой верёвки в отдельности, если 13 м новой и 12 м старой верёвки вместе весят 5 кг 480 г.
-
В одном баке было 28 л бензина, а в другом – 42 л. Если первый бак долить доверху из второго бака, то второй бак станет наполненным наполовину. Если второй бак дополнить доверху из первого бака, то в нём останется только четвёртая часть объёма. Найдите объём каждого бака.
-
У Лены 8 монет по 10 руб. и 5 руб. Сколько у неё десятирублёвых и сколько пятирублёвых монет, если всего у неё 65 рублей?
-
На получение пирожка в автомате нужно 5 жетонов, а на получение булочки – 1 жетон. Таня получила в автомате несколько пирожков и булочек, отдав за всю покупку 25 жетонов. Сколько пирожков и сколько булочек получила Таня, если за булочки она отдала на 15 жетонов меньше, чем за пирожки?
Задачи с геометрическими фигурами.
-
Если ширину прямоугольника уменьшить на 2 см, а длину увеличить на 3 см, то его площадь уменьшится на 8 см2. Если же каждую сторону данного прямоугольника увеличить на 4 см, то площадь исходного прямоугольника увеличится на 80 см2. Найдите стороны данного прямоугольника.
-
Если длину прямоугольника уменьшить на 2 м, а ширину увеличить на 4 м, то его площадь увеличится на 12 м2. Если же каждую его сторону уменьшить на 1 м, то площадь исходного прямоугольника уменьшится на 13 м2. Найдите стороны данного прямоугольника.
-
Периметр прямоугольника равен 32 см. Если его длину увеличить на 5 см, а ширину уменьшить на 2 см, то площадь прямоугольника увеличится на 7 см2. Найдите стороны данного прямоугольника.
-
Одна сторона прямоугольника на 4 см больше другой. Если меньшую сторону увеличить в 2 раза, а большую оставить без изменения, то периметр нового прямоугольника будет равен 56 см. Найдите стороны данного прямоугольника.
-
Периметр прямоугольника равен 48 см. Если одну его сторону увеличить в 2 раза, а другую уменьшить на 6 см, то периметр нового прямоугольника будет равен 64 см. Найдите стороны данного прямоугольника.
-
Периметр прямоугольника равен 56 см. Найдите его стороны, если известно, что длина прямоугольника на 14,2 см больше ширины.
-
Периметр прямоугольника 400 м. Длина его в 3 раза больше ширины. Найдите длину и ширину этого прямоугольника.
-
Периметр равнобедренного треугольника 17 см. Основание треугольника на 2 см меньше, чем боковая сторона. Найдите стороны этого треугольника.
-
Боковая сторона равнобедренного треугольника на 4 см длиннее основания. Найти стороны треугольника, если его периметр равен 26 см.
-
Ширина прямоугольника на 5 см короче его длины. Найдите длину и ширину прямоугольника, если его периметр равен 38 см.
Задачи с числами.
-
Сумма цифр двузначного числа равна 8. Если поменять местами его цифры, то получим число, которое больше данного на 18. Найдите данное число.
-
Цифра в разряде десятков данного трёхзначного числа равна нулю, а удвоенное количество сотен на 2 меньше, чем количество единиц. Число, записанное теми же цифрами в обратном порядке, на 495 больше данного. Найдите данное число.
-
Сумма удвоенного количества десятков и количества единиц некоторого двузначного числа равна 11. Если поменять местами цифры этого числа, то получим число, которое на 9 меньше данного. Найдите данное число.
-
Сумма двух чисел равна 77. Найдите эти числа, если
первого числа равны
второго числа.
-
Разность двух чисел равна 12. Найдите эти числа, если
первого числа равны
второго числа.
-
Сумма цифр двузначного числа равна 8. Если к данному числу прибавить 18, то получится двузначное число, записанное теми же цифрами, но в обратном порядке. Найдите данное число.
-
Разность между двузначным числом и числом, записанным теми же цифрами, но в обратном порядке, равна 27. Разность между квадратами таких чисел равна 1485. Найдите данное число.
-
Разность между двузначным числом и числом, записанным теми же цифрами, но в обратном порядке, равна 45. Разность между квадратами таких чисел равна 5445. Найдите данное число.
-
Сумма чисел равна 98, а из разность – 42,4. Найдите эти числа.
-
Найдите двузначное число, сумма цифр которого равна 15, а разность цифр равна 3.
-
Даны два числа. Если к первому числу прибавить половину второго, то получится 65, а если из второго вычесть третью часть первого, то получится первое число. Найдите эти числа.
-
Если к первому числу добавить четверть второго числа, получится 129, а если увеличить второе число в 5 раз и отнять от него половину первого числа, то получится первое число. Найдите эти числа.
-
Разность квадратов двух натуральных чисел равна 21, а сумма этих чисел равна 7. Найдите эти числа.
-
Сумма двух чисел равна 76, а 3/4 первого числа составляют 5/6 второго числа. Найдите эти числа.
-
Среднее арифметическое двух чисел равно 11. Если большее число разделить на меньшее, то в частном получится 3, а в остатке 2. Найдите эти числа.
-
При сложении двузначного числа с суммой его цифр получится 50. Если от этого числа отнять число, записанное теми же цифрами в обратном порядке, то получится 9. Найдите это число.
-
Если к числителю и знаменателю несократимой дроби прибавить по 1, то получится
, а если вычесть из них по 1, то получится
. Найдите эту дробь.
-
Задумали два числа. Если сложить 70% первого числа и 20% второго, то получится 20. Если же первое число уменьшить на 20%, а второе увеличить на 30%, а затем сложить полученные результаты, то получится55. Чему равно каждое из чисел?
-
Задумали два числа. Если сложить 30% первого числа и 40% второго, то получится 10. Если же первое число увеличить на 10%, а второе уменьшить на 20%, а затем сложить полученные результаты, то получится 26. Чему равно каждое из чисел?
-
Задумали два числа. Если сложить 40% первого числа и 20% второго, то получится 18. Если же первое число увеличить на 20%, а второе уменьшить на 10%, а затем сложить полученные результаты, то получится 69. Чему равно каждое из чисел?
-
Сумма двух чисел равна 17. Одно из чисел на 7 меньше другого. Найдите эти числа.
-
Разность двух чисел равна 12. Одно из них больше другого в 4 раза. Найдите эти числа.
-
4 боксёра тяжёлого веса и 5 боксёров лёгкого веса вместе весят 730 кг. Спортсмен тяжёлого веса весит на 70 кг больше спортсмена лёгкого веса. Найдите вес каждого боксёра.
-
Среднее арифметическое двух чисел равно 22,5; а
их разности равна
Найдите эти два числа.
-
Одно число на 215 больше другого; 80% большего числа на 129 больше 60% меньшего из них. Найдите эти числа.
-
В трёхзначном числе сумма цифр равна 16. Цифра разряда сотен в 4 раза меньше цифры разряда десятков и на 4 меньше цифры разряда единиц. Найдите это число.
-
Сумма двух чисел равна 81. а их разность равна 15. Найдите эти числа.
-
Сумма двух чисел равна 36. Одно из них в 2 раза больше другого. Найдите эти числа.
-
Три яблока и две груши весят вместе 1 кг 200 г. Яблоко легче груши на 100 г. Сколько весит одно яблоко и сколько одна груша?
-
Среднее арифметическое двух чисел равно 36, а
их разности равна 0,8. Найдите эти числа.
-
Одно число на 140 меньше другого; 60% большего числа на 64 больше 70% меньшего числа. Найдите эти числа.
-
В трёхзначном числе сумма цифр равна 10. Цифра разряда сотен в 2 раза больше цифры разряда десятков и на 5 больше цифры разряда единиц. Найдите это число.
-
Если к числителю дроби прибавить 1, а к знаменателю 2, то дробь не изменится. Если же к числителю дроби прибавить 2, а из знаменателя вычесть 1, то дробь увеличится в 6 раз. Найдите эту дробь.
-
Сумма цифр двузначного числа равна 9. Если это число разделить на разность его цифр, то получится 54. Найдите исходное число.
-
Если к числителю дроби прибавить 2, а к знаменателю дроби прибавить 3, то получится ½. Числитель дроби в 3 раза меньше знаменателя. Найдите исходную дробь.
-
Разность цифр двузначного числа равна 6. Если это число разделить на сумму его цифр, то получится 8,2. Найдите исходное число.
-
Разность двух чисел равна 16, а их сумма равна 26. Найдите эти числа.
-
Сумма двух чисел равна 47, а их разность равна 29. Найдите эти числа.
-
Коля задумал два числа. Удвоенное первое число в 3 раза больше второго. Если же первое из задуманных чисел уменьшить на 49, оно станет в 3 раза меньше второго. Найдите задуманные числа.
-
Андрей задумал два числа. Утроенное первое число в 2 раза больше второго. Если же первое из задуманных чисел уменьшить на 11, оно станет в 2 раза меньше второго. Найдите задуманные числа.
-
Саша задумал два числа. Утроенное первое число в 4 раза больше второго. Если же первое из задуманных чисел уменьшить на 26, оно станет в 4 раза меньше второго. Найдите задуманные числа.
-
Андрей задумал два числа. Удвоенное первое число в 5 раз больше второго. Если же первое из задуманных чисел уменьшить на 69, оно станет в 5 раз меньше второго. Найдите задуманные числа.
-
Сумма двух чисел равна 35. Если одно из них увеличить в 4 раза, а другое – на 30, то сумма полученных чисел будет равна 125. Найдите эти числа.
Задачи на работу.
-
На заводе изготовили два вида деталей. Масса 8 деталей одного вида и 6 деталей другого вида составляет вместе 29 кг. Найдите массу детали каждого вида, если масса 4 деталей второго вида на 1 кг больше, чем масса двух деталей первого вида.
-
Саша и Витя вскапывают грядку за 10 мин, а один Витя – за 15 мин. За сколько минут вскапывает грядку один Саша?
-
Игорь и Олег вскапывают грядку за 12 мин, а один Игорь – за 20 мин. За сколько минут вскапывает грядку один Олег?
-
Миша вскапывает грядку за 10 мин, Саша – за 12 мин, Олег – за 15 мин. За сколько минут они скопают грядку втроём?
-
Миша вскапывает грядку за 6 мин, Саша – за 20 мин, Олег – за 30 мин. За сколько минут они вскопают грядку втроём?
-
Если половину заказа выполнит мастер, а оставшуюся часть закончит ученик, то вся работы будет сделана за 10 ч. Если мастер выполнит ¾ работы, а оставшуюся часть выполнит ученик, то всё будет сделано за 9 ч. За какое время мог бы выполнить работу каждый из них, работая один?
-
Четыре одинаковых насоса, работая вместе, наполнили нефтью первый танкер и треть второго танкера (другого объёма) за 11 ч. Если бы три насоса наполнили первый танкер, а затем один из насосов наполнил бы четверть второго танкера, то работа заняла бы 18 ч. За сколько часов три насоса могут наполнить второй танкер?
-
Три каменщика (разной квалификации) выложили кирпичную стену, причём первый каменщик работал 6 ч, второй – 4 ч, а третий – 7 ч. Если бы первый каменщик работал 4 ч, второй – 2 ч, а третий – 5 ч, то они выполнили бы 2/3 всей работы. За сколько часов каменщики закончили бы кладку, если бы они работали все вместе одно и то же время?
-
Три бригады вспахали два поля общей площадью 96 га. Первое поле было вспахано за 3 дня, причём все три бригады работали вместе. Второе поле было вспахано за 6 дней второй и третьей бригадами. Если бы все три бригады проработали на втором поле 1 день, то оставшуюся часть второго поля первая бригада могла вспахать за 8 дней. Сколько гектаров в день вспахивает первая бригада?
-
Три одинаковых комбайна, работая вместе, убрали первое поле, а затем два из них убрали второе поле (другой площади). Вся работа заняла 12 ч. Если бы три комбайна выполнили половину всей работы, а затем оставшуюся часть сделал бы один из них, то работа заняла бы 20 ч. За какое время два комбайна могут убрать первое поле?
-
Две бригады вместе должны изготовить 270 изделий. К середине дня первая бригада выполнила 60% своего задания, а вторая – 70% своего. При этом первая бригада изготовила на 6 изделий больше, чем вторая. Сколько изделий должна изготовить каждая бригада?
-
Два токаря изготовили 172 детали. Первый работал 3 ч, а второй – 2 ч. Если бы первый работал 1 ч, а второй – 4 ч, то они изготовили бы 198 деталей. Сколько деталей изготовил каждый токарь?
-
Маша и Даша могут вымыть окно за 1 ч, работая вместе. За сколько часов может вымыть окно Даша, если известно, что Маша работает в 3 раза быстрее Даши?
-
Андрей и Иван могут покрасить забор за 2 ч, работая вместе. За сколько часов может покрасить забор Иван, если известно, что он работает медленнее Андрея в 4 раза?
-
Первый рабочий работал 7 дней, а второй – 9 дней. Вместе они изготовили 174 детали. Сколько деталей в день изготавливал каждый рабочий, если первый рабочий за 1 день изготавливал на 8 деталей меньше, чем второй за 2 дня?
-
Две наборщицы подготовили к печати 171 страницу текста. Первая работала 8 ч, а вторая – 7 ч. Сколько страниц текста готовила за 1 ч каждая наборщица, если вторая за 3 ч работы подготовила на 29 страниц больше, чем первая за 1 ч работы?
-
Токарь и его ученик за 3 ч обтачивают 75 деталей. Если токарь будет работать 2 ч, а его ученик – 4 ч, то вместе они обточат 70 деталей. Сколько деталей обтачивает каждый из них за 1 ч?
-
Токарь и его ученик за 2 ч обтачивают 54 детали. Если токарь будет работать 3 ч, а его ученик – 4 ч, то вместе они обточат 92 детали. Сколько деталей обтачивает каждый из них за 1 ч?
-
Мастер и его ученик вместе могут изготовить за 1 час 17 деталей. До обеда мастер проработал 4 часа, а ученик 2 часа и изготовили вместе 54 детали. Сколько деталей изготавливал каждый из них за 1 час?
Задачи на движение.
-
Из двух городов, расстояние между которыми 52 км, одновременно выехали навстречу друг другу два велосипедиста и встретились через 2 ч. Найдите скорость каждого велосипедиста, если известно, что второй велосипедист проезжает за 3 ч на 18 км больше, чем первый за 2 ч.
-
Из двух сёл одновременно вышли навстречу друг другу два пешехода и встретились через 3 ч. Расстояние между сёлами 30 км. Один из пешеходов прошёл до встречи на 6 км больше, чем другой. Найдите скорость каждого пешехода.
-
По окружности, длина которой 100 см, движутся равномерно две точки. Они встречаются каждые 4с, двигаясь в противоположных направлениях, и через каждые 20 с, двигаясь в одном направлении. Найдите скорости этих точек.
-
По окружности, длина которой 200 см, движутся равномерно две точки. Они встречаются каждые 5 с, двигаясь противоположных направлениях, и через каждые 20 с, двигаясь в одном направлении. Найдите скорости этих точек.
-
Из пункта А в пункт В, расстояние между которыми 18 км, вышел турист. Через 1,5 ч из пункта В ему навстречу вышел другой турист, и они встретились через 1 ч 20 мин. Если бы они вышли одновременно, то встретились бы через 2 ч. Какова скорость каждого туриста?
-
Автомобиль за 3,5 ч проехал на 10 км больше, чем мотоциклист за 2,5 ч. Скорость мотоциклиста на 20 км/ч больше скорости автомобиля. Найдите скорость автомобиля и скорость мотоциклиста.
-
Турист прошёл 50 км за 3 дня. Во второй день он прошёл на 10 км меньше, чем в первый, и на 5 км больше, чем в третий. Сколько километров проходил турист каждый день?
-
Из двух пунктов А и В, расстояние между которыми 15 км, одновременно навстречу друг другу выехали два велосипедиста и через 30 мин встретились. Если бы они поехали в одном направлении, то один догнал бы другого через 2 ч 30 мин. Найдите скорость каждого велосипедиста.
-
Два велосипедиста выехали одновременно навстречу друг другу из двух городов, расстояние между которыми 90 км. Через 3 ч они встретились, причём первый велосипедист проехал на 6 км больше второго. Найдите скорость каждого велосипедиста.
-
Пешеход сначала шёл в горку со скоростью 3 км/ч, а затем спускался с неё со скоростью 5 км/ч. Найдите общий путь, проделанный пешеходом, если дорога в горку на 1 км длиннее спуска, а затраченное на весь путь время равно 3 ч.
-
Пешеход спускался со скоростью 4 км/ч, а затем поднимался в горку со скоростью 3 км/ч. Найдите общий путь, проделанный пешеходом, если спуск был на 5 км длиннее подъёма, а затраченное на весть путь время равно 3 ч.
-
Расстояние между домами, где живут Андрей и Борис, равно 1500 м. Школа находится между домами мальчиков, причём от дома Андрея она на 300 м дальше, чем от дома Бориса. На каком расстоянии от школы находится дом каждого мальчика?
-
Поезд прошёл первый перегон за 2 ч, а второй за 3 ч. Всего за это время он прошёл 330 км. Найдите скорость поезда на каждом перегоне, если на втором перегоне она была на 10 км/ч больше, чем на первом.
-
Расстояние между Москвой и Санкт-Петербургом по шоссе 700 км. Великий Новгород находится между этими городами, причём от Москвы на 300 км дальше, чем от Санкт-Петербурга. На каком расстоянии от Москвы и на каком от Санкт-Петербурга находится Великий Новгород?
-
Туристы прошли 24 км, причём 3 ч дорога шла в гору, а 2 ч – под гору. С какой скоростью туристы шли в гору и с какой под гору, если на первом участке они проходили в час на 2 км меньше, чем на втором?
-
Велосипедист ехал 2 ч по лесной дороге и 1 ч по шоссе, всего он проехал 40 км. Скорость его на шоссе была на 4 км/ч больше, чем скорость на лесной дороге. С какой скоростью велосипедист ехал по шоссе и с какой по лесной дороге?
-
Из посёлка на станцию, расстояние между которыми 32 км, выехал велосипедист. Через 0,5 ч навстречу ему со станции выехал мотоциклист и встретил велосипедиста через 0,5 ч после своего выезда. Известно, что скорость мотоциклиста на 28 км/ч больше скорости велосипедиста. Найдите скорость каждого из них.
-
Из пункта А в пункт В, расстояние между которыми 17 км, вышел пешеход. Через 0,5 ч навстречу ему из пункта В вышел второй пешеход и встретился с первым через 1,5 ч после своего выхода. Найдите скорость каждого пешехода, если известно, что скорость первого на 2 км/ч меньше скорости второго.
-
Из двух городов, расстояние между которыми по трассе равно 294 км, выехали одновременно навстречу друг другу автомобилист и мотоциклист. Через 3 ч они встретились. Если бы в начале движения автомобилист увеличил скорость вдвое, а мотоциклист увеличил свою скорость на 7 км/ч, то они встретились бы через 2 ч. Найдите скорость автомобилиста и скорость мотоциклиста.
-
На трассе, протянувшейся с севера на юг, расположены посёлки А и В, расстояние между которыми 90 км. Из посёлка А, находящегося севернее посёлка В, на юг выехал автомобилист. Одновременно с ним из посёлка В на ют выехал велосипедист. Через 1,5 ч автомобилист догнал велосипедиста. Если бы автомобилист увеличил скорость на 26 км/ч, а велосипедист уменьшил свою скорость в 1,5 раза, то автомобилист догнал бы велосипедиста через час после начала движения. Найдите скорость автомобилиста и скорость велосипедиста.
-
Сельчанин может добраться от своего дома до города двумя способами. В первом случае ему придётся 1 час 30 минут идти пешком и 4 часа ехать поездом, и он преодолеет в общей сложности 206 км. Во втором случае ему придётся 2 часа идти пешком и 3 часа ехать поездом (оба поезда движутся с одинаковыми скоростями). Длина второй дороги 158 км. С какой скоростью сельчанин ходит?
-
В 10 часов утра грузовой и легковой автомобили выехали навстречу друг другу из городов, расстояние между которыми 840 км. Они встретились в 16 часов. Если бы грузовой автомобиль выехал в 8 часов утра, а легковой автомобиль в 12 часов, то в 16 часов им оставалось бы проехать до встречи 40 км. Найдите скорость легкового автомобиля.
-
Туристическая группа ехала 2 ч на электричке и шла 3 ч пешком, преодолев в общей сложности пусть в 165 км. Скорость электрички была на 70 км/ч больше скорости движения пешком. Какое расстояние группа прошла пешком?
-
Туристическая группа ехала 3 ч на автобусе и шла 4 ч пешком, преодолев в общей сложности путь в 200 км. Скорость автобуса была на 55 км/ч больше скорости движения пешком. Какое расстояние группа прошла пешком?
Задачи на движение по воде.
-
Катер за 4 ч движения по течению реки и 3 ч движения по озеру прошёл 148 км. За 5 ч движения против течения реки он прошёл на 50 км больше, чем за 2 ч по озеру. Найдите скорость катера в стоячей воде и скорость течения реки.
-
Моторная лодка за 2 ч движения по течению реки и 5 ч движения против течения реки прошла 120 км. За 7 ч движения против течения она прошла на 52 км больше, чем за 3 ч движения по течению. Найдите скорость лодки по течению и её скорость против течения.
-
По течению реки лодка за 3 ч 20 мин проходит расстояние 30 км, а против течения за 4 ч – расстояние 28 км. Какое расстояние по озеру пройдёт лодка за 5 ч?
-
По течению реки лодка за 3,5 ч проходит расстояние 42 км, а против течения за 4 ч – расстояние 32 км. Какое расстояние по озеру пройдёт лодка за 6 ч?
-
Скорость теплохода по течению реки 45,2 км/ч, а против течения – 36,2 км/ч. Найдите скорость течения реки.
-
Путь в 30 км катер прошёл по течению за 2 ч, а против течения – за 3 ч. Найдите собственную скорость катера и скорость течения.
-
Скорость моторной лодки по течению реки равна 14,3 км/ч, а против течения реки – 12,1 км/ч. Найдите скорость течения реки и собственную скорость лодки.
-
Скорость теплохода по течению реки равна 45,2 км/ч, а против течения реки – 36,2 км/ч. Найдите скорость течения реки и собственную скорость теплохода.
-
Скорость моторной лодки по течению реки равна 25,6 км/ч, а против течения реки – 16,2 км/ч. Найдите скорость течения реки и собственную скорость лодки.
-
Скорость моторной лодки по течению реки равна 17,7 км/ч, а против течения реки – 14,9 км/ч. Найдите скорость течения реки и собственную скорость лодки.
-
Из порта одновременно в противоположных направлениях вышли два катера. Через 3 ч расстояние между ними составило 96 км. Найдите скорость первого катера, если она на 10 км/ч больше скорости второго катера.
-
Моторная лодка прошла по течению реки 8 км, а против течения – 3 км, затратив на весь путь 45 мин. Найдите собственную скорость лодки, если скорость течения реки равна 2 км/ч.
-
Моторная лодка прошла по течению реки 20 км, а против течения 30 км. Найдите собственную скорость лодки, если скорость течения реки равна 3 км/ч, а на весь путь затрачено 6 ч 40 мин.
-
Моторная лодка плыла по течению реки 3 ч, а на тот же путь против течения реки моторная лодка затратила 5 ч. Найдите собственную скорость лодки, если скорость течения реки равна 10 км/ч.
-
Теплоход за 4 ч по течению реки прошёл 60 км, а за 6 ч против течения прошёл 54 км. Какова была собственная скорость теплохода и скорость течения реки?
-
Расстояние, равное 24 км, лодка проплыла по течению за 4 ч, а против течения за 6 ч. Найдите собственную скорость лодки и скорость течения реки.
-
Из двух пунктов реки одновременно навстречу друг другу вышли две моторные лодки. Через 1,2 ч они встретились. Собственная скорость лодки, которая шла по течению реки, равна 18 км/ч, а лодки, которая шла против течения реки, 16 км/ч. До встречи одна лодка прошла на 9,6 км больше другой. Найдите скорость течения реки.
-
Из двух пунктов реки одновременно навстречу друг другу движутся две моторные лодки, собственные скорости которых равны. Скорость течения реки равна 2 км/ч. До встречи лодка, идущая по течению, шла 0,9 ч, а другая лодка шла 1 ч. Найдите собственную скорость лодок, если лодка, идущая по течению, прошла на 2 км больше, чем другая лодка.
-
По течению реки катер прошёл за 7 ч столько же, сколько он проходит за 8 ч против течения. Собственная скорость катера 30 км/ч. Сколько км проплывём за 4 ч спичка, брошенная в эту реку?
-
Моторная лодка вышла из пункта А в пункт В и, двигаясь против течения, потратила на путь до пункта В 4 ч, затем она повернула обратно и прибыла в пункт А ещё через 3 часа. Собственная скорость лодки 14 км/ч. Сколько км проплывёт плот за 5 ч по этой реке?
-
Лодка 2 ч двигалась по течению и 3 ч против течения, пройдя за это время 36 км. Скорость лодки против течения составляет 2/3 скорость лодки по течению. Какое расстояние пройдёт лодка за это время в стоячей воде, если будет двигаться с той же собственной скоростью?
-
За 3 ч против течения реки лодка проплыла на 5 км больше, чем за 2 ч по течению. Скорость лодки против течения составляет 0,75 её скорости по течению. Какое расстояние прошла лодка за это время?
-
Расстояние между двумя пристанями равно 60 км. Это расстояние лодка проплывает по течению реки за 4 ч, а против течения реки – за 5 ч. Найдите собственную скорость лодки скорость течения реки.
-
Расстояние между двумя пристанями равно 80 км. Это расстояние лодка проплывает по течению реки за 5 ч, а против течения реки – за 8 ч. Найдите собственную скорость лодки и скорость течения реки.
-
Моторная лодка в первый день прошла 120 км по течению реки за 5 ч, а во второй день она прошла 72 км против течения за 6 ч. Найдите собственную скорость лодки и скорость течения реки.
-
Расстояние между двумя пристанями равно 75 км. Катер прошёл это расстояние по течению реки за 3 ч, а против течения за 5 ч. Найдите собственную скорость катера и скорость течения реки.
Задачи на смеси и сплавы.
-
Сколько граммов трёхпроцентного и сколько граммов восьмипроцентного растворов соли надо взять, чтобы получить 260 г пятипроцентного раствора?
-
Есть металлолом двух сортов, содержащих 12% и 30% меди. Сколько килограммов лома каждого вида надо взять, чтобы получить 180 кг сплава, содержащего 25% меди?
-
Сколько граммов 75%-го и 15%-го растворов кислоты надо смешать, чтобы получить 72 г 50%-го раствора кислоты?
-
Сколько граммов 15%-го и 60%-го растворов кислоты надо смешать, чтобы получить 90 г 40%-го раствора кислоты?
-
В одном ведре находится молоко жирностью 30%, а в другом – сливки жирностью 18%. Сколько нужно взять молока и сколько сливок, чтобы получить 10 л молока жирностью 6%?
-
В одной бочке находится смесь спирта с водой в отношении 3:7 соответственно, а в другой – 40%-ная спиртовая смесь. Сколько следует взять спиртовой смеси из каждой бочки, чтобы получить 16 л смеси, в которой спирт и вода были в отношении 5:11?
Задачи на возраст.
-
Если сложить возраст отца и возраст сына, то получится 52. Через 8 лет отношение возраста отца к возрасту сына будет равно 3. Сколько лет отцу и сколько сыну в настоящий момент?
-
Если сложить возраст отца и возраст сына, то получится 30. Через 7 лет отношение возраста отца к возрасту сына будет равно 3. Сколько лет отцу и сколько сыну в настоящий момент?
-
Мальчик на вопрос о том, сколько лет ему и его отцу, ответил так: «Вместе нам 44 года. Через 2 года отец будет старше меня в 3 раза». Сколько лет каждому из них сейчас?
-
Мальчик на вопрос о том, сколько лет ему и его брату, ответил так: «Вместе нам 20 лет. 4 года назад я был в 2 раза старше своего брата». Сколько лет каждому из них сейчас?
Задачи повышенной сложности.
-
* В корзине лежат 35 шаров, среди которых есть шары белого и чёрного цвета. Сколько шаров каждого цвета лежит в корзине, если известно, что среди каждых 17 шаров есть хотя бы один белый, а среди каждых 20 шаров есть хотя бы 1 чёрный?
-
* Коля и Вася получили за сентябрь по 64 оценки, причём Коля получил пятёрок столько же, сколько Вася – четвёрок, четвёрок столько же, сколько Вася – троек, троек столько же, сколько Вася – двоек и двоек столько же, сколько Вася – пятёрок. Кроме того оказалось, что их средние баллы совпадают. Сколько и Коли двоек?
5