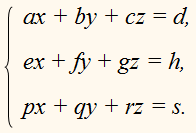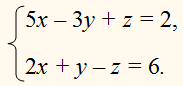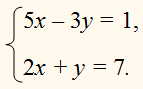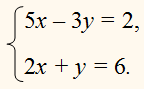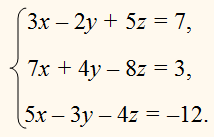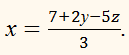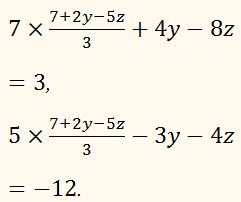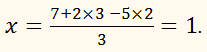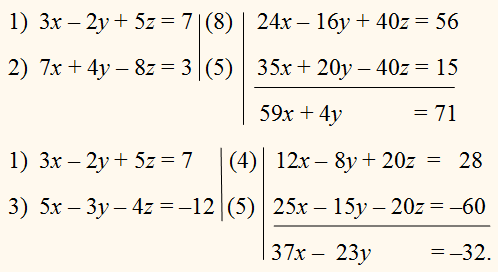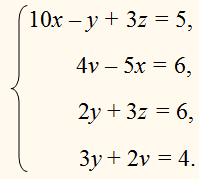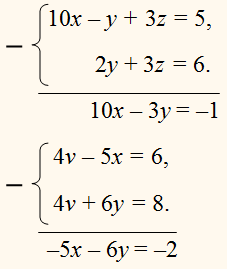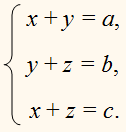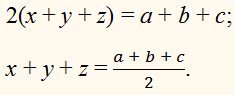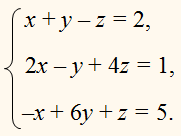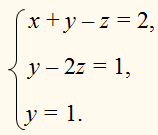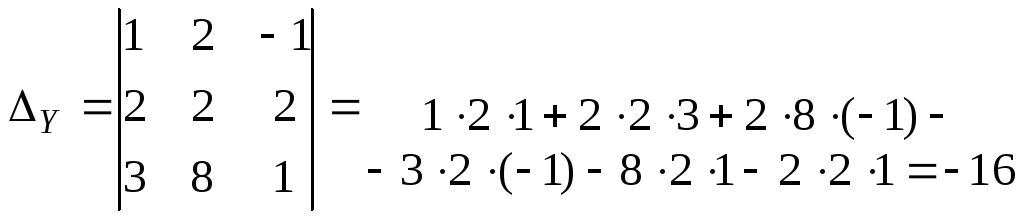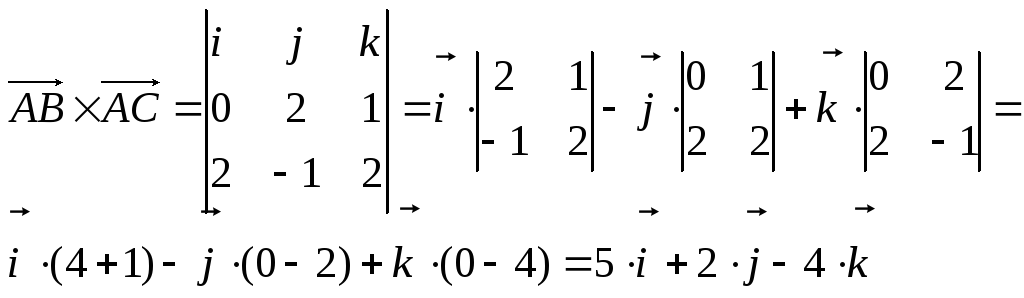Как составить систему уравнений с тремя неизвестными - Исправление недочетов и поиск решений вместе с Examum.ru

Линейное уравнение с тремя переменными и его решение

Уравнение вида ax+by+cz = d , где a, b, c, d — данные числа, называется линейным уравнением с тремя переменными x, y и z.

Например: $2x+5y+z = 8; -x+1, 5y+2z = 0; frac{1}{2} x-8y-5z = 7$

Уравнение с тремя переменными может быть не только линейным, т.е. содержать не только первые степени переменных x,y и z.

Например: $2x^2+xz+y^2+yz^2 = 3,x-5y^2+z^3 = 1, 7x^3+y+xyz = 7$

Решением уравнения с тремя переменными называется упорядоченная тройка значений переменных (x,y,z), обращающая это уравнение в тождество.

О тождествах – см. §3 данного справочника

Например: для уравнения 2x+5y+z=8 решениями являются тройки x = -2, y = 1, z = 7; x = -1, y = 1, 6 , z = 2; x = -3, y = 2, 4, z = 2 и т.д. Уравнение имеет бесконечное множество решений.

Геометрическим представлением линейного уравнения с тремя переменными является плоскость в трёхмерном координатном пространстве.

Решение системы линейных уравнений с тремя переменными методом подстановки

Алгоритм метода подстановки для системы уравнений с тремя переменными аналогичен алгоритму для двух переменных (см.§45 данного справочника)

Например: решить систему

$$ {left{ begin{array}{c} 3x+2y-z = 8 \ x-y+z = -2 \ 2x-3y-5z = 1 end{array} right.} Rightarrow {left{ begin{array}{c} 3(y-z-2)+2y-z = 8 \ x = y-z-2 \ 2(y-z-2)-3y-5z = 1 end{array} right.} Rightarrow $$

$$ Rightarrow {left{ begin{array}{c} x = y-z-2 \ 5y-4z = 14 \ -y-7z = 5 end{array} right.} Rightarrow {left{ begin{array}{c} x = y-z-2 \ y = -7z-5 \ 5(-7z-5)-4z = 14 end{array} right.} Rightarrow {left{ begin{array}{c} x = y-z-2 \ y = -7z-5 \ -39z = 39 end{array} right.} Rightarrow $$

$$ Rightarrow {left{ begin{array}{c} x = 2-(-1)-2 = 1 \ y = -7cdot(-1)-5 = 2 \ z = -1 end{array} right.} Rightarrow {left{ begin{array}{c} x = 1 \ y = 2 \ z = -1 end{array} right.} $$

Ответ: (1;2;-1)

Решение системы линейных уравнений с тремя переменными методом Крамера

Метод Крамера для системы уравнений с 2-мя переменными рассмотрен в §48 данного справочника.

Для системы с 3-мя переменными действуем по аналогии.

Дана система 3-х линейных уравнений с 3-мя переменными:

$$ {left{ begin{array}{c} a_1 x+b_1 y+c_1 z = d_1 \ a_2 x+b_2 y+c_2 z = d_2 \ a_3 x+b_3 y+c_3 z = d_3 end{array} right.} $$

Определим главный определитель системы:

$$ Delta = begin{vmatrix} a_1 & b_1 & c_1 \ a_2 & b_2 & c_2 \ a_3 & b_3 & c_3 end{vmatrix} $$

и вспомогательные определители:

$$ Delta_x = begin{vmatrix} d_1 & b_1 & c_1 \ d_2 & b_2 & c_2 \ d_3 & b_3 & c_3 end{vmatrix}, Delta_y = begin{vmatrix} a_1 & d_1 & c_1 \ a_2 & d_2 & c_2 \ a_3 & d_3 & c_3 end{vmatrix}, Delta_z = begin{vmatrix} a_1 & b_1 & d_1 \ a_2 & b_2 & d_2 \ a_3 & b_3 & d_3 end{vmatrix} $$

Тогда решение системы:

$$ {left{ begin{array}{c} x = frac{Delta_x}{Delta} \ y = frac{Delta_y}{Delta} \ z = frac{Delta_z}{Delta} end{array} right.} $$

Соотношение значений определителей, расположения плоскостей и количества решений:

$ Delta neq 0 $

$ Delta = 0, Delta _x neq 0, Delta_y neq 0, Delta_z neq 0 $

$ Delta = 0$ некоторые вспомогательные определители равны 0

Три плоскости пересекаются в одной точке

Три плоскости параллельны

Две или три плоскости совпадают или пересекаются по прямой

Одно решение

Нет решений

Бесконечное множество решений

Осталось определить правило вычисления определителя 3-го порядка.

Таких правил несколько, приведём одно из них (так называемое «раскрытие определителя по первой строке»):

$$ Delta = begin{vmatrix} a_1 & b_1 & c_1 \ a_2 & b_2 & c_2 \ a_3 & b_3 & c_3 end{vmatrix} = a_1 = begin{vmatrix} b_2 & c_2 \ b_3 & c_3 end{vmatrix} — b_1 = begin{vmatrix} a_2 & c_2 \ a_3 & c_3 end{vmatrix} + c_1 = begin{vmatrix} a_2 & b_2 \ a_3 & b_3 end{vmatrix} = $$

$$ = a_1 (b_2 c_3-b_3 c_2 )-b_1 (a_2 c_3-a_3 c_2 )+c_1 (a_2 b_3-a_3 b_2 )$$

Примеры

Пример 1. Найдите решение системы уравнений методом подстановки:

$ а) {left{ begin{array}{c} 3x+2y-z = 13 \ 2x-y+3z = -2 \ x+2y-z = 9 end{array} right.} $

$${left{ begin{array}{c} z = 3x+2y-13 \ 2x-y+3(3x+2y-13) = -2 \ x+2y-(3x+2y-13) = 9 end{array} right.} Rightarrow {left{ begin{array}{c} z = 3x+2y-13 \ 11x+5y = 37 \ -2x = -4 end{array} right.} Rightarrow $$

$$Rightarrow {left{ begin{array}{c} z = 3cdot2+2cdot3-13 = -1 \ y = frac{37-11cdot2}{5} = 3 \ x = 2 end{array} right.} Rightarrow {left{ begin{array}{c} x = 2 \ y = 3 \ z = -1 end{array} right.} $$

Ответ: (2;3;-1)

$ б) {left{ begin{array}{c} x+y+3z = 6 \ 2x-5y-z = 5 \ x+2y-5z = -11 end{array} right.} $

$$ {left{ begin{array}{c} x = -y-3z+6 \ 2(-y-3z+6)-5y-z = 5\ (-y-3z+6)+2y-5z = -11 end{array} right.} Rightarrow {left{ begin{array}{c} x = -y-3z+6 \ -7y-7z = -7 |:(-7) \ y-8z = -17 end{array} right.} Rightarrow $$

$$ Rightarrow {left{ begin{array}{c} x = -y-3z+6 \ y+z = 1 \ y-8z = -17 end{array} right.} Rightarrow {left{ begin{array}{c} x = -y-3z+6 \ 9z = 18 \ y = 1-z end{array} right.} Rightarrow {left{ begin{array}{c} x = 1-6+6 = 1 \ z = 2 \ y = 1-2 = -1 end{array} right.} Rightarrow$$

$$ Rightarrow {left{ begin{array}{c} x = 1 \ y = -1 \ z = 2 end{array} right.} $$

Ответ: (1;-1;2)

Пример 2. Найдите решение системы уравнений методом Крамера:

$а) {left{ begin{array}{c}3x+2y-z = 13 \ 2x-y+3z = -2 \ x+2y-z = 9 end{array} right.} $

$$ Delta = begin{vmatrix} 3 & 2 & -1 \ 2 & -1 & 3\ 1 & 2 & -1 end{vmatrix} = 3 = begin{vmatrix} -1 & 3 \ 2 & -1 \ end{vmatrix} — 2 = begin{vmatrix} 2 & 3 \ 1 & -1 \ end{vmatrix} — 1 = begin{vmatrix} 2 & -1 \ 1 & 2 \ end{vmatrix} = $$

$$= 3(1-6)-2(-2-3)-(4+1) = -15+10-5 = -10$$

$$ Delta_x = begin{vmatrix} 13 & 2 & -1 \ -2 & -1 & 3 \ 9 & 2 & -1 \ end{vmatrix} = 13 = begin{vmatrix} -1 & 3 \ 2 & -1 \ end{vmatrix} — 2 = begin{vmatrix} -2 & 3 \ 9 & -1 \ end{vmatrix} — 1 = begin{vmatrix} -2 & -1 \ 9 & 2 \ end{vmatrix} = $$

$$ = 13(1-6)-2(2-27)-(-4+9) = -65+50-5=-20 $$

$$ Delta_y = begin{vmatrix} 3 & 13 & -1 \ 2 & -2 & 3 \ 1 & 9 & -1 \ end{vmatrix} = 3 = begin{vmatrix} -2 & 3 \ 9 & -1 \ end{vmatrix} — 13 = begin{vmatrix} 2 & 3 \ 1 & -1 \ end{vmatrix} — 1 = begin{vmatrix} 2 & -2 \ 1 & 9 \ end{vmatrix} = $$

$$ = 3(2-27)-13(-2-3)-(18+2) = -75+65-20 = -30 $$

$$ Delta_z = begin{vmatrix} 3 & 2 & 13 \ 2 & -1 & -2 \ 1 & 2 & 9 \ end{vmatrix} = 3 = begin{vmatrix} -1 & -2 \ 2 & 9 \ end{vmatrix} — 2 = begin{vmatrix} 2 & -2 \ 1 & 9 \ end{vmatrix} + 13 = begin{vmatrix} 2 & -1 \ 1 & 2 \ end{vmatrix} = $$

$$ = 3(-9+4)-2(18+2)+13(4+1) = -15-40+65 = 10 $$

$$ x = frac{Delta_x}{Delta} = frac{-20}{-10} = 2, y = {Delta_y}{Delta} = frac{-30}{-10} = 3, z = {Delta_z}{Delta} = frac{10}{-10} = -1$$

Ответ: (2;3;-1)

$б) {left{ begin{array}{c} x+y+3z = 6 \ 2x-5y-z = 5 \ x+2y-5z = -11 end{array} right.} $

$$ Delta = begin{vmatrix} 1 & 1 & 3 \ 2 & -5 & -1\ 1 & 2 & -5 end{vmatrix} = 1 = begin{vmatrix} -5 & -1 \ 2 & -5 \ end{vmatrix} — 1 = begin{vmatrix} 2 & -1 \ 1 & -5 \ end{vmatrix} + 3 = begin{vmatrix} 2 & -5 \ 1 & 2 \ end{vmatrix} = $$

$$= (25+2)—(-10+1)+3(4+5) = 27+9+27 = 63$$

$$ Delta_x = begin{vmatrix} 6 & 1 & 3 \ 5 & -5 & -1 \ -11 & 2 & -5 \ end{vmatrix} = 6 = begin{vmatrix} -5 & -1 \ 2 & -5 \ end{vmatrix} — 1 = begin{vmatrix} 5 & -1 \ -11 & -5 \ end{vmatrix} + 3 = begin{vmatrix} 5 & -5 \ -11 & 2 \ end{vmatrix} = $$

$$ = 6(25+2)—(-25-11)+3(10-55) = 162+36-135 = 63 $$

$$ Delta_y = begin{vmatrix} 1 & 16 & 3 \ 2 & 5 & -1 \ 1 & -11 & -5 \ end{vmatrix} = 1 = begin{vmatrix} 5 & -1 \ -11 & -5 \ end{vmatrix} — 6 = begin{vmatrix} 2 & -1 \ 1 & -5 \ end{vmatrix} + 3 = begin{vmatrix} 2 & 5 \ 1 & -11 \ end{vmatrix} = $$

$$ = (-25-11)—6(-10+1)+3(-22-5) = -36+54-81 = -63 $$

$$ Delta_z = begin{vmatrix} 1 & 1 & 6 \ 2 & -5 & 5 \ 1 & 2 & -11 \ end{vmatrix} = 1 = begin{vmatrix} -5 & 5 \ 2 & -11 \ end{vmatrix} — 1 = begin{vmatrix} 2 & 5 \ 1 & -11 \ end{vmatrix} + 6 = begin{vmatrix} 2 & -5 \ 1 & 2 \ end{vmatrix} = $$

$$ = (55-10)—(-22-5)+6(4+5) = 45+27+54 = 126 $$

$$ x = frac{Delta_x}{Delta} = frac{63}{63} = 1, y = {Delta_y}{Delta} = frac{-63}{63} = -1, z = {Delta_z}{Delta} = frac{126}{63} = 2$$

Ответ: (1;-1;2)

Пример 3*. Решите систему уравнений относительно x,y,и z:

$$ {left{ begin{array}{c} a^3+a^2 x+ay+z = 0 \ b^3+b^2 x+by+z = 0 \ c^3+c^2 x+cy+z = 0 end{array} right.} $$

$$ a neq b, b neq c, a neq c $$

Решаем методом замены:

$$ {left{ begin{array}{c} z = -(a^3+a^2 x+ay)\ b^3+b^2 x+by-(a^3+a^2 x+ay) = 0 \ c^3+c^2 x+cy-(a^3+a^2 x+ay) = 0 end{array} right.} Rightarrow {left{ begin{array}{c}z = -(a^3+a^2 x+ay)\ (b^2-a^2 )x+(b-a)y = a^3-b^3 \ (c^2-a^2 )x+(c-a)y = a^3-c^3 end{array} right.} $$

Т.к. $ a neq b$ второе уравнение можно сократить на $(a-b) neq 0$

Т.к.$ a neq c$ третье уравнение можно сократить на $(a-с) neq 0 $. В третьем уравнении после сокращения поменяем знаки:

$$ {left{ begin{array}{c} z = -(a^3+a^2 x+ay) \ -(a-b)(a+b)x-(a-b)y = (a-b)(a^2+ab+b^2 ) \ -(a-c)(a+c)x-(a-c)y = (a-c)(a^2+ac+c^2 ) end{array} right.} $$

$$ {left{ begin{array}{c} z = -(a^3+a^2 x+ay) \ -(a+b)x-y = a^2+ab+b^2 \ (a+c)x+y = -(a^2+ac+c^2 ) end{array} right.} $$

$$ {left{ begin{array}{c} z = -(a^3+a^2 x+ay) \ -(a+b)x+(a+c)x = (a^2+ab+b^2 ) — (a^2+ac+c^2 ) \ y = -(a+c)x-(a^2+ac+c^2 ) end{array} right.} $$

Из второго уравнения получаем:

$$x = frac{ab+b^2-ac-c^2}{c-b} = -frac{a(b-c)+(b^2-c^2 )}{b-c} = — frac{(b-c)(a+b+c)}{b-c} $$

Т.к. $b neq c$ можно сократить на $(b-c) neq 0$:

$$ x = -(a+b+c)$$

Подставляем:

$$ y = -(a+c)x-(a^2+ac+c^2 ) = (a+c)(a+b+c)-(a^2+ac+c^2 ) = $$

$$ = a^2+ab+ac+ac+bc+c^2-a^2-ac-c^2 = ab+ac+bc $$

$$ z = -(a^3+a^2 x+ay) = -a^3+a^2 (a+b+c)-a(ab+ac+bc) = $$

$$ = -a^3+a^3+a^2 b+a^2 c-a^2 b-a^2 c-abc = -abc $$

Ответ:$ {left{ begin{array}{c} x = -(a+b+c) \ y = ab+ac+bc \ z = -abc end{array} right.} $

Источник

Системы линейных уравнений с тремя переменными

Линейным уравнением называется уравнение вида:

В этом уравнении — неизвестные, а — действительные (или комплексные) числа. При этом называются коэффициентами уравнения, а — свободным членом.

Рассмотрим систему трех линейных уравнений с тремя неизвестными:

Из трех способов решения этих систем: графического, способа подстановки и способа сложения остается два последних способа. Графический способ уже не проходит, так как пришлось бы находить точку пересечения трех плоскостей. А это трудно изобразить.

Способ подстановки для трех уравнений похож на способ подстановки для двух уравнений с двумя неизвестными, только у этого способа на один шаг больше. Первое: выражаем одно из неизвестных из одного уравнения через два остальных неизвестных и подставляем это выражение в оставшиеся два уравнения. Эти оставшиеся два уравнения составляют систему из двух уравнений с двумя неизвестными. А дальше решаем эту полученную систему и находим два неизвестных, а затем, зная их, и третье неизвестное.

Пример 1 Решить систему уравнений: способом подстановки.

Выразим из первого уравнения через остальные неизвестные и свободный член. Найденное выражение подставим в остальные уравнения.

Далее, оставляя первое уравнение в покое, решаем систему из двух получившихся уравнений с неизвестными и (предварительно разделив обе части второго уравнения на ).

Получили единственное решение системы

Рассмотрим теперь способ сложения. Так же как и для двух уравнений с двумя неизвестными, нужно при помощи сложения уравнений добиться, чтобы одно из неизвестных пропало.Приведем пример.

Пример 2 Решить систему уравнений: способом сложения.

Постараемся получить два уравнения с двумя неизвестными. Избавимся от неизвестной . Для этого удвоенное первое уравнение сложим почленно с удвоенным вторым уравнением, а удвоенное второе уравнение прибавим к третьему уравнению:

Далее производим почленное сложение двух уравнений с двумя неизвестными, исключая неизвестную :

Из последнего уравнения системы находим . Подставляя найденное значение во второе уравнение, находим . Наконец из первого уравнения находим . Итак — единственное решение системы.

В заключении решим задачу, которая приводится к системе с тремя неизвестными.

Задача В трех урнах — шариков. В первой урне шариков больше чем во второй на столько, сколько шариков в третьей урне. Число шариков во второй урне относится к числу шариков в третьей урне как . Сколько шариков в каждой урне?

Обозначим число шариков в 1-й, 2-й и 3-й урнах через соответственно. Тогда первое условие задачи дает уравнение , второе условие — , а третье условие — . Запишем три полученные уравнения в систему, сделав предварительно третье уравнение линейным:

Складывая почленно первые два уравнения находим .Решаем систему из двух оставшихся уравнений:

Итак, в урнах соответственно и шариков.

Длины волн инфракрасного света достаточно велики, чтобы перемещаться сквозь облака, которые в противном случае блокировали бы наш обзор. Используя большие инфракра сные телескопы, астрономы смогли заглянуть в ядро нашей галактики. Большое количество звезд излучают часть своей электромагнитной энергии в виде видимого света, крошечной части спектра, к которой чувствительны наши глаза.

Так как длина волны коррелирует с энергией, цвет звезды говорит нам, насколько она горячая. Используя телескопы, чувствительные к различным диапазонам длин волн спектра, астрономы получают представление о широком круге объектов и явлений во вселенной.

Пример №1 Постройте центральную симметрию тетраэдра, относительно точки O, изображенных на рисунке 3.

Для построения такой центральной симметрии сначала проведем через все точки тетраэдра прямые, каждая из которых будет проходить через точку O. На них построим отрезки, удовлетворяющие условиям |AO|=|A?O|, |BO|=|B?O|, |CO|=|C?O|, |DO|=|D?O| Таким образом, и получим искомую симметрию (рис. 4).

В ряду разных механических движений особенным значением обладают колебания. Это движения и процессы, имеющие периодичность во времени.

В среде электромагнитных явлений также значительное место заняли электромагнитные колебания. В этих колебаниях заряды, токи, электрические и магнитные поля изменяются согласно периодическим законам.

Совет №1 Велосипедист, имеющий скорость 300 м/с, или идеальный газ, оказывающий давление 100 паскалей в большой тепловой машине — это странно.

Нужна помощь с курсовой или дипломной работой?

Система линейных уравнений с тремя переменными

Линейное уравнение с тремя переменными и его решение

Уравнение вида ax+by+cz = d , где a, b, c, d — данные числа, называется линейным уравнением с тремя переменными x, y и z.

Например: $2x+5y+z = 8; -x+1, 5y+2z = 0; frac<1> <2>x-8y-5z = 7$

Например: $2x^2+xz+y^2+yz^2 = 3,x-5y^2+z^3 = 1, 7x^3+y+xyz = 7$

О тождествах – см. §3 данного справочника

Решение системы линейных уравнений с тремя переменными методом подстановки

Например: решить систему

$$ <left< begin 3x+2y-z = 8 \ x-y+z = -2 \ 2x-3y-5z = 1 end right.> Rightarrow <left< begin 3(y-z-2)+2y-z = 8 \ x = y-z-2 \ 2(y-z-2)-3y-5z = 1 end right.> Rightarrow $$

$$ Rightarrow <left< begin x = y-z-2 \ 5y-4z = 14 \ -y-7z = 5 end right.> Rightarrow <left< begin x = y-z-2 \ y = -7z-5 \ 5(-7z-5)-4z = 14 end right.> Rightarrow <left< begin x = y-z-2 \ y = -7z-5 \ -39z = 39 end right.> Rightarrow $$

$$ Rightarrow <left< begin x = 2-(-1)-2 = 1 \ y = -7cdot(-1)-5 = 2 \ z = -1 end right.> Rightarrow <left< begin x = 1 \ y = 2 \ z = -1 end right.> $$

Решение системы линейных уравнений с тремя переменными методом Крамера

Для системы с 3-мя переменными действуем по аналогии.

Дана система 3-х линейных уравнений с 3-мя переменными:

$$ <left< begin a_1 x+b_1 y+c_1 z = d_1 \ a_2 x+b_2 y+c_2 z = d_2 \ a_3 x+b_3 y+c_3 z = d_3 end right.> $$

Определим главный определитель системы:

$$ Delta = begin a_1 & b_1 & c_1 \ a_2 & b_2 & c_2 \ a_3 & b_3 & c_3 end $$

и вспомогательные определители :

$$ Delta_x = begin d_1 & b_1 & c_1 \ d_2 & b_2 & c_2 \ d_3 & b_3 & c_3 end, Delta_y = begin a_1 & d_1 & c_1 \ a_2 & d_2 & c_2 \ a_3 & d_3 & c_3 end, Delta_z = begin a_1 & b_1 & d_1 \ a_2 & b_2 & d_2 \ a_3 & b_3 & d_3 end $$

Тогда решение системы:

Соотношение значений определителей, расположения плоскостей и количества решений:

Три плоскости пересекаются в одной точке

Три плоскости параллельны

Две или три плоскости совпадают или пересекаются по прямой

Бесконечное множество решений

Осталось определить правило вычисления определителя 3-го порядка.

Таких правил несколько, приведём одно из них (так называемое «раскрытие определителя по первой строке»):

$$ Delta = begin a_1 & b_1 & c_1 \ a_2 & b_2 & c_2 \ a_3 & b_3 & c_3 end = a_1 = begin b_2 & c_2 \ b_3 & c_3 end — b_1 = begin a_2 & c_2 \ a_3 & c_3 end + c_1 = begin a_2 & b_2 \ a_3 & b_3 end = $$

$$ = a_1 (b_2 c_3-b_3 c_2 )-b_1 (a_2 c_3-a_3 c_2 )+c_1 (a_2 b_3-a_3 b_2 )$$

Примеры

Пример 1. Найдите решение системы уравнений методом подстановки:

$$<left< begin z = 3x+2y-13 \ 2x-y+3(3x+2y-13) = -2 \ x+2y-(3x+2y-13) = 9 end right.> Rightarrow <left< begin z = 3x+2y-13 \ 11x+5y = 37 \ -2x = -4 end right.> Rightarrow $$

$$Rightarrow <left< begin z = 3cdot2+2cdot3-13 = -1 \ y = frac<37-11cdot2> <5>= 3 \ x = 2 end right.> Rightarrow <left< begin x = 2 \ y = 3 \ z = -1 end right.> $$

$$ <left< begin x = -y-3z+6 \ 2(-y-3z+6)-5y-z = 5\ (-y-3z+6)+2y-5z = -11 end right.> Rightarrow <left< begin x = -y-3z+6 \ -7y-7z = -7 |:(-7) \ y-8z = -17 end right.> Rightarrow $$

$$ Rightarrow <left< begin x = -y-3z+6 \ y+z = 1 \ y-8z = -17 end right.> Rightarrow <left< begin x = -y-3z+6 \ 9z = 18 \ y = 1-z end right.> Rightarrow <left< begin x = 1-6+6 = 1 \ z = 2 \ y = 1-2 = -1 end right.> Rightarrow$$

Пример 2. Найдите решение системы уравнений методом Крамера:

$$ Delta = begin 3 & 2 & -1 \ 2 & -1 & 3\ 1 & 2 & -1 end = 3 = begin -1 & 3 \ 2 & -1 \ end — 2 = begin 2 & 3 \ 1 & -1 \ end — 1 = begin 2 & -1 \ 1 & 2 \ end = $$

$$ Delta_x = begin 13 & 2 & -1 \ -2 & -1 & 3 \ 9 & 2 & -1 \ end = 13 = begin -1 & 3 \ 2 & -1 \ end — 2 = begin -2 & 3 \ 9 & -1 \ end — 1 = begin -2 & -1 \ 9 & 2 \ end = $$

$$ Delta_y = begin 3 & 13 & -1 \ 2 & -2 & 3 \ 1 & 9 & -1 \ end = 3 = begin -2 & 3 \ 9 & -1 \ end — 13 = begin 2 & 3 \ 1 & -1 \ end — 1 = begin 2 & -2 \ 1 & 9 \ end = $$

$$ Delta_z = begin 3 & 2 & 13 \ 2 & -1 & -2 \ 1 & 2 & 9 \ end = 3 = begin -1 & -2 \ 2 & 9 \ end — 2 = begin 2 & -2 \ 1 & 9 \ end + 13 = begin 2 & -1 \ 1 & 2 \ end = $$

$$ Delta = begin 1 & 1 & 3 \ 2 & -5 & -1\ 1 & 2 & -5 end = 1 = begin -5 & -1 \ 2 & -5 \ end — 1 = begin 2 & -1 \ 1 & -5 \ end + 3 = begin 2 & -5 \ 1 & 2 \ end = $$

$$ Delta_x = begin 6 & 1 & 3 \ 5 & -5 & -1 \ -11 & 2 & -5 \ end = 6 = begin -5 & -1 \ 2 & -5 \ end — 1 = begin 5 & -1 \ -11 & -5 \ end + 3 = begin 5 & -5 \ -11 & 2 \ end = $$

$$ = 6(25+2)—(-25-11)+3(10-55) = 162+36-135 = 63 $$

$$ Delta_y = begin 1 & 16 & 3 \ 2 & 5 & -1 \ 1 & -11 & -5 \ end = 1 = begin 5 & -1 \ -11 & -5 \ end — 6 = begin 2 & -1 \ 1 & -5 \ end + 3 = begin 2 & 5 \ 1 & -11 \ end = $$

$$ Delta_z = begin 1 & 1 & 6 \ 2 & -5 & 5 \ 1 & 2 & -11 \ end = 1 = begin -5 & 5 \ 2 & -11 \ end — 1 = begin 2 & 5 \ 1 & -11 \ end + 6 = begin 2 & -5 \ 1 & 2 \ end = $$

Пример 3*. Решите систему уравнений относительно x,y,и z:

$$ a neq b, b neq c, a neq c $$

Решаем методом замены:

$$ <left< begin z = -(a^3+a^2 x+ay)\ b^3+b^2 x+by-(a^3+a^2 x+ay) = 0 \ c^3+c^2 x+cy-(a^3+a^2 x+ay) = 0 end right.> Rightarrow <left< beginz = -(a^3+a^2 x+ay)\ (b^2-a^2 )x+(b-a)y = a^3-b^3 \ (c^2-a^2 )x+(c-a)y = a^3-c^3 end right.> $$

Т.к. $ a neq b$ второе уравнение можно сократить на $(a-b) neq 0$

Т.к.$ a neq c$ третье уравнение можно сократить на $(a-с) neq 0 $. В третьем уравнении после сокращения поменяем знаки:

Из второго уравнения получаем:

Т.к. $b neq c$ можно сократить на $(b-c) neq 0$:

$$ z = -(a^3+a^2 x+ay) = -a^3+a^2 (a+b+c)-a(ab+ac+bc) = $$

$$ = -a^3+a^3+a^2 b+a^2 c-a^2 b-a^2 c-abc = -abc $$

Системы линейных уравнений

Линейные уравнения (уравнения первой степени) с двумя неизвестными

Системы из двух линейных уравнений с двумя неизвестными

Системы из трех линейных уравнений с тремя неизвестными

Линейные уравнения (уравнения первой степени) с двумя неизвестными

Определение 1 . Линейным уравнением (уравнением первой степени) с двумя неизвестными x и y называют уравнение, имеющее вид

где a , b , c – заданные числа.

Определение 2 . Решением уравнения (1) называют пару чисел (x ; y) , для которых формула (1) является верным равенством.

Пример 1 . Найти решение уравнения

Решение . Выразим из равенства (2) переменную y через переменную x :

Из формулы (3) следует, что решениями уравнения (2) служат все пары чисел вида

где x – любое число.

Замечание . Как видно из решения примера 1, уравнение (2) имеет бесконечно много решений. Однако важно отметить, что не любая пара чисел (x ; y) является решением этого уравнения. Для того, чтобы получить какое-нибудь решение уравнения (2), число x можно взять любым, а число y после этого вычислить по формуле (3).

Системы из двух линейных уравнений с двумя неизвестными

Определение 3 . Системой из двух линейных уравнений с двумя неизвестными x и y называют систему уравнений, имеющую вид

Определение 4 . В системе уравнений (4) числа a₁ , b₁ , a₂ , b₂ называют коэффициентами при неизвестных , а числа c₁ , c₂ – свободными членами .

Определение 5 . Решением системы уравнений (4) называют пару чисел (x ; y) , являющуюся решением как одного, так и другого уравнения системы (4).

Определение 6 . Две системы уравнений называют равносильными (эквивалентными) , если все решения первой системы уравнений являются решениями второй системы, и все решения второй системы являются решениями первой системы.

Равносильность систем уравнений обозначают, используя символ «»

Системы линейных уравнений решают с помощью метода последовательного исключения неизвестных , который мы проиллюстрируем на примерах.

Пример 2 . Решить систему уравнений

Решение . Для того, чтобы решить систему (5) исключим из второго уравнения системы неизвестное х .

С этой целью сначала преобразуем систему (5) к виду, в котором коэффициенты при неизвестном x в первом и втором уравнениях системы станут одинаковыми.

Если первое уравнение системы (5) умножить на коэффициент, стоящий при x во втором уравнении (число 7 ), а второе уравнение умножить на коэффициент, стоящий при x в первом уравнении (число 2 ), то система (5) примет вид

Теперь совершим над системой (6) следующие преобразования:

первое уравнение системы оставим без изменений;
из второго уравнения вычтем первое уравнение и заменим второе уравнение системы на полученную разность.

В результате система (6) преобразуется в равносильную ей систему

Из второго уравнения находим y = 3 , и, подставив это значение в первое уравнение, получаем

Пример 3 . Найти все значения параметра p , при которых система уравнений

а) имеет единственное решение;

б) имеет бесконечно много решений;

в) не имеет решений.

Решение . Выражая x через y из второго уравнения системы (7) и подставляя полученное выражение вместо x в первое уравнение системы (7), получим

Следовательно, система (7) равносильна системе

Исследуем решения системы (8) в зависимости от значений параметра p . Для этого сначала рассмотрим первое уравнение системы (8):

y (2 – p) (2 + p) = 2 + p

(9)

Если , то уравнение (9) имеет единственное решение

Следовательно, система (8) равносильна системе

Таким образом, в случае, когда , система (7) имеет единственное решение

Если p = – 2 , то уравнение (9) принимает вид

и его решением является любое число . Поэтому решением системы (7) служит бесконечное множество всех пар чисел

где y – любое число.

Если p = 2 , то уравнение (9) принимает вид

и решений не имеет, откуда вытекает, что и система (7) решений не имеет.

Системы из трех линейных уравнений с тремя неизвестными

Определение 7 . Системой из трех линейных уравнений с тремя неизвестными x , y и z называют систему уравнений, имеющую вид

Определение 9 . Решением системы уравнений (10) называют тройку чисел (x ; y ; z) , при подстановке которых в каждое из трех уравнений системы (10) получается верное равенство.

Пример 4 . Решить систему уравнений

Решение . Будем решать систему (11) при помощи метода последовательного исключения неизвестных .

Для этого сначала исключим из второго и третьего уравнений системы неизвестное y , совершив над системой (11) следующие преобразования:

первое уравнение системы оставим без изменений;
ко второму уравнению прибавим первое уравнение и заменим второе уравнение системы на полученную сумму;
из третьего уравнения вычтем первое уравнение и заменим третье уравнение системы на полученную разность.

В результате система (11) преобразуется в равносильную ей систему

Теперь исключим из третьего уравнения системы неизвестное x , совершив над системой (12) следующие преобразования:

первое и второе уравнения системы оставим без изменений;
из третьего уравнения вычтем второе уравнение и заменим третье уравнение системы на полученную разность.

В результате система (12) преобразуется в равносильную ей систему

Из системы (13) последовательно находим

Пример 5 . Решить систему уравнений

Решение . Заметим, что из данной системы можно получить удобное следствие, сложив все три уравнения системы:

Если числа (x ; y ; z) являются решением системы (14), то они должны удовлетворять и уравнению (15). Однако в таком случае числа (x ; y ; z) должны также быть решением системы, которая получается, если из каждого уравнения системы (14) вычесть уравнение (15):

Поскольку мы использовали следствие из системы (14), не задумываясь о том, являются ли сделанные преобразования системы (14) равносильными, то полученный результат нужно проверить. Подставив тройку чисел (3 ; 0 ; –1) в исходную систему (14), убеждаемся, что числа (3 ; 0 ; –1) действительно являются ее решением.

Замечание . Рекомендуем посетителю нашего сайта, интересующемуся методами решения систем уравнений, ознакомиться также c разделом справочника «Системы с нелинейными уравнениями» и нашим учебным пособием «Системы уравнений».

источники:

http://reshator.com/sprav/algebra/7-klass/sistema-linejnyh-uravnenij-s-tremya-peremennymi/

http://www.resolventa.ru/spr/algebra/system.htm

Источник

Системы трёх
линейных уравнений с тремя неизвестными имеют вид:

Где a, b, c, d, e, f, g, h, p, q,
r, s – заданные числа; x,
y, z – неизвестные.
Числа a, b, c, e, f, g, p, q, r –
коэффициенты при неизвестных; d, h, s – свободные члены.

Нормальный вид уравнения первой степени с тремя
неизвестными.

Если
в уравнении 1-й степени с 3 неизвестными х, у и z, сделать
определённые преобразования, то мы приведем уравнение к такому виду
(называемому нормальным), при котором в левой части уравнения находятся только
три члена: один с х, другой с у и третий с
z, а в правой части будет один член, не
содержащий неизвестных.

ПРИМЕР:

Уравнение:

5х – 3у – 4z = –12.

Общий вид его есть следующий:

ах + by + cz = d,
где а,
b, с и d какие-нибудь относительные числа.

Неопределенность двух и одного уравнения с тремя
неизвестными.

ПРИМЕР:

Предположим, нам дана система 2 уравнений
с 3 неизвестными:

Назначим одному неизвестному, например z, какое-нибудь произвольное число, предположим
1, и подставим это
число на место z:

Мы получили таким образом систему 2 уравнений
с 2 неизвестными. Решив
ее каким-нибудь способом, найдем:

х = 2, у = 3;

значит, данная система с 3 неизвестными
удовлетворяется при

х = 2; у = 3;
z =1.

Дадим теперь неизвестному z какое-нибудь иное значение, например z =
0, и подставим это значение в данную
систему уравнений, получим:

Мы снова получим систему 2 уравнений с 2 неизвестными. Решив ее каким-нибудь
способом, найдем:

х = ²⁰/₁₁ = 1⁹/₁₁;
у = 2⁴/₁₁.

Значит, данная система удовлетворяется при

х = 1⁹/₁₁;
у = 2⁴/₁₁ и
z = 0.

Назначив для z еще какое-нибудь (третье) значение, мы снова
получим систему 2 уравнений с 2 неизвестными,
из которой найдем новые значения для х и у. Так как для z мы можем назначать сколько угодно
различных чисел, то и для х и у можем получить сколько угодно значений (соответствующих взятым значениям z). Значит, 2 уравнения с 3 неизвестными допускают бесчисленное множество
решений; другими словами, такая
система неопределенна.

Еще
большая неопределенность будет, если имеется всего 1 уравнение
c 3 неизвестными. Тогда можно будет для
каких-нибудь 2 неизвестных назначить произвольные
числа; третье же неизвестное найдется из данного уравнения, если подставить в
него значения, взятые произвольно для двух неизвестных.
Для
того, чтобы можно было найти определенные численные значения для трех
неизвестных х, у и z, необходимо,
чтобы была задана система 3 уравнений. Такая система может быть решена
способом подстановки, а также и способом сложения или вычитания уравнений.
Покажем применение этих способов на следующем примере (каждое уравнение
предварительно приведено к нормальному виду):

ПРИМЕР:

Способ подстановки.

Из какого-нибудь уравнения, например из
первого, определим одно
неизвестное, например х, как функцию от двух остальных неизвестных:

Так как во всех уравнениях х означает одно и то же число, то мы можем
подставить найденное выражение на место
х в остальные уравнения:

Мы приходим таким образом к системе 2 уравнений
с 2 неизвестными у и z. Решив эту систему по какому-нибудь из
способов, указанных раньше, найдем численные значения для у и z. В нашем
примере это будут значения: у
= 3, z = 2; подставив эти
числа в выражение, выведенное нами для х, найдем и это неизвестное:

Таким образом, предложенная система имеет
решение

х = 1, у = 3, z
= 2

(в чем можно убедиться поверкою).

Способ сложения или вычитания.

Из 3 данных уравнений возьмем
какие-нибудь два, напр. 1-е и 2-е, и, уравняв в них
коэффициенты перед одним неизвестным, напр., перед z, исключим из них это неизвестное способом
сложения или вычитания; от
этого получим одно уравнение c 2 неизвестными х и у. Потом, возьмем какие-нибудь два других
уравнения из 3 данных, напр. 1-е и 3-е (или
2-е и 3-е), и тем же способом исключим из них то же неизвестное
т. е. z; от этого получим еще одно уравнение с х и у:

Решим получившиеся два уравнения:

x =
1, у = 3.

Вставим эти числа в одно из трех данных
уравнений, например, в первое:

3 ×
1 – 2 × 3 + 5z = 7;
5z = 7 – 3 + 6 =
10;
z = 2.

Замечание.

Теми
же двумя способами мы можем привести систему 4 уравнений с 4 неизвестными к системе 3 уравнений с 3 неизвестными (а эту систему – к системе 2 уравнений с 2 неизвестными
и т. д.). Вообще систему m уравнений
с m неизвестными
мы можем привести к системе m – 1 уравнений с
m – 1 неизвестными
(а эту систему к системе m – 2 уравнений с
m – 2 неизвестными
и т. д.).

Некоторые особые случаи систем
уравнений.

Случай, когда не все неизвестные входят в каждое из данных уравнений.

ПРИМЕР:

В этом случае система решается быстрее, чем
обыкновенно, так как в некоторых уравнениях уже исключены те или другие
неизвестные. Надо только сообразить, какие неизвестные и из каких уравнений
следует исключить, чтобы возможно скорее дойти до одного уравнения с одним
неизвестным. В нашем примере, исключив z из 1-го и 3-го уравнений и v из 2-го и 1-го, получим 2 уравнения с х и у:

Решив эти уравнения, найдем:

х = 0, y = ¹/₃.

Теперь вставим эти числа во 2-е и 3-е уравнения, тогда получим:

v = ³/₂,
z = ¹⁶/₉= 1⁷/₉.

Случай, когда полезно все данные уравнения сложить.

ПРИМЕР:

Сложив все три уравнения, найдем:

Вычтя из последнего уравнения каждое из
данных, получим:

ПРИМЕР:

Решить систему уравнений:

РЕШЕНИЕ:

При решении систем линейных уравнений удобно
пользоваться методом Гаусса, который состоит в преобразовании системы к
треугольному виду.

Умножаем первое уравнение системы на –2 и, складывая полученный результат со вторым
уравнением, получаем

– 3у + 6z = –3.

Это уравнение можно переписать в виде

у – 2z = 1.

Складывая первое уравнение с третьим, получаем 7у
= 7, или у = 1.

Таким образом, система приобрела треугольный вид:

Подставляя у = 1 во второе
уравнение, находим z =
0. Подставляя у = 1 и z = 0 в первое
уравнение, находим х = 1.

ОТВЕТ: (1; 1; 0)

Задания к уроку 16

Источник

Для системы
составляем
главный определитель

и вычисляем его.

Затем составляем
дополнительные определители

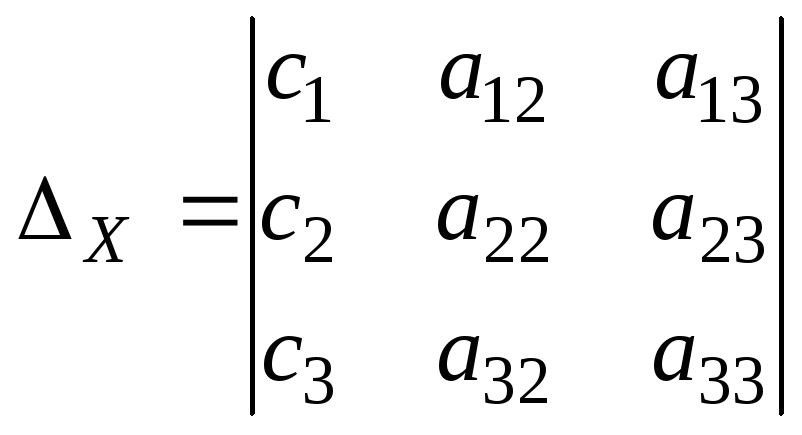
и вычисляем их.

По правилу Крамера
решение системы находят по формулам

; ;

,если

Примеры:

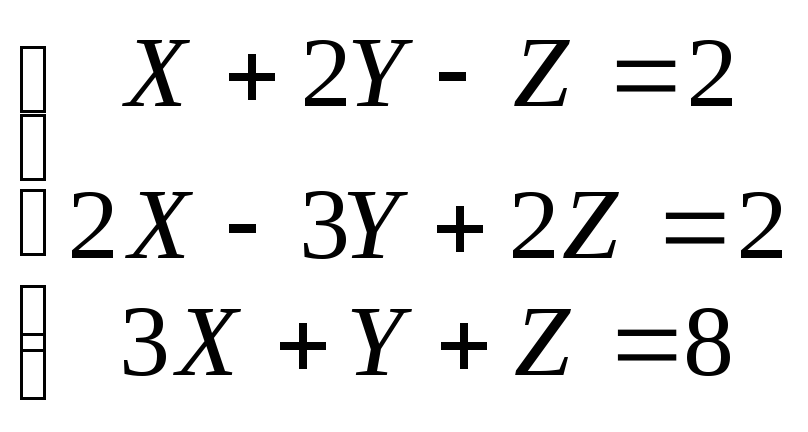
Вычислим:

По формулам Крамера
находим:

Ответ: (1; 2; 3)

Вычислим:

Так как главный
определитель
,
а хотя бы один дополнительный не равен
нулю (в нашем случае
),
то решения у системы нет.

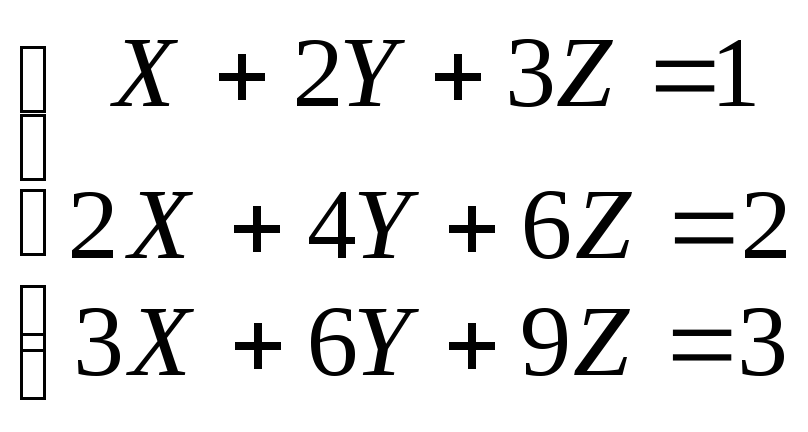
Вычислим:

Так как все
определители равны нулю, то система
имеет бесконечное множество решений,
которое можно найти так

Решите самостоятельно
системы:

а)
б)

Ответ: а) ( 1; 2; 5 )
б)
;;

Практическое
занятие № 3 на тему:

Скалярное произведение двух векторов и его приложение

1. Если дан
и,
то скалярное произведение находим по
формуле:∙

2.Если,
то скалярное произведение этих двух
векторов находим по формуле

Примеры:

1. Даны два вектора
и

Их скалярное
произведение находим так:

2. Даны два вектора:

={2;3;–4}

={1;
–5; 6}

скалярное
произведение находят так:

3.,

3.1 Нахождение работы постоянной силы на прямолинейном участке пути

Примеры:

1) Под действием
силы в 15Н тело переместилось по прямой
на 2 метра. Угол между силой и направлением
перемещения =60⁰.
Вычислить работу силы по перемещению
тела.

Дано:

Решение:

2) Дано:

Найти А.

Решение:

3) Из точки М(1; 2; 3)
в точку N(5;
4; 6) переместилось тело под действием
силы 60Н. Угол между направлением силы
и вектором перемещения =45⁰.
Вычислить работу, совершаемую этой
силой.

Решение: находим
вектор перемещения

Находим модуль
вектора перемещения:

По формуле

находим работу:

3.2 Определение ортогональности двух векторов

Два вектора
ортогональны, если
,
то есть

так как

Примеры:

–не ортогональны

–ортогональны

3) Определить, при
каком 
векторы
и

взаимно-ортогональны.

Так как
,
то
,
значит

Решите самостоятельно:

а)

.
Найти их скалярное произведение.

б) Вычислить, какую
работу производит сила
,
если точка ее приложения, двигаясь
прямолинейно, переместилась из точки
M
(5; -6; 1) в точку N
(1; -2; 3)

в) Определить,
ортогональны ли вектора
и

Ответы: а) 1 б)
16 в) да

3.3.Нахождение угла между векторами

Примеры:

.
Найти
.

Решение:

Находим

подставляем в
формулу:

1). Даны вершины
треугольника А(3;
2; –3), В(5; 1; –1), С(1; –2; 1).
Найти угол при вершине А.

Решение:

Находим

Подставим в формулу:

Решите самостоятельно:

Даны вершины
треугольника А(3;
5; -2), В(5; 7; -1), С(4; 3; 0).
Определить внутренний угол при вершине
А.

Ответ: 90^о

Практическое
занятие № 4 на тему:

ВЕКТОРНОЕ
ПРОИЗВЕДЕНИЕ ДВУХ ВЕКТОРОВ И ЕГО
ПРИЛОЖЕНИЕ.

Формула для
нахождения векторного произведения
двух векторов:

имеет
вид

Примеры:

1) Найти модуль
векторного произведения:

Решение:

Составим определитель
и вычислим его (по правилу Саррюса или
по теореме о разложении определителя
по элементам первой строки).

1-ый способ: по
правилу Саррюса

2-й способ: разложим
определитель по элементам первой строки.

2)
Найти модуль
векторного произведения:

4.1. ВЫЧИСЛЕНИЕ
ПЛОЩАДИ ПАРАЛЛЕЛОГРАММА, ПОСТРОЕННОГО
НА ДВУХ ВЕКТОРАХ.

Примеры:

1) Вычислить площадь
параллелограмма, построенного на
векторах

Решение.

2). Найти векторное
произведение и его модуль

Ответ:

4.2. ВЫЧИСЛЕНИЕ
ПЛОЩАДИ ТРЕУГОЛЬНИКА

Пример: даны вершины
треугольника А(1; 0; -1), В(1; 2; 0), С(3; -1; 1).
Вычислить площадь треугольника.

Решение:

Сначала найдем
координаты двух векторов, выходящих из
одной вершины.

Найдем их векторное
произведение

найдем

4.3. ОПРЕДЕЛЕНИЕ
КОЛЛИНЕАРНОСТИ ДВУХ ВЕКТОРОВ

Если вектора
иколлинеарны, то

, т. е. координаты
векторов должны быть пропорциональны.

Примеры:

а) Даны вектора::

Они коллинеарны
потому, что
и

после сокращения
каждой дроби получается соотношение

б) Даны вектора:
.

Они не коллинеарны,
потому, что

или

Решите самостоятельно:

а) При каких
значениях m
и n
вектора

коллинеарны?

Ответ:
;

б) Найти векторное
произведение и его модуль
,

Ответ:

Практическое
занятие № 5 на тему:

ПРЯМАЯ ЛИНИЯ НА
ПЛОСКОСТИ

Примеры:

Задача № 1. Найти
уравнение прямой, проходящей через
точку А(-2; 3) параллельно прямой

Решение:

1. Найдем угловой
коэффициент прямой
.

— это уравнение
прямой с угловым коэффициентом и
начальной ординатой ().
Поэтому
.

2. Так как прямые
MN
и АС
параллельны, то их угловые коэффициенты
равны, т.е.
.

3. Для нахождения
уравнения прямой АС
воспользуемся уравнением прямой,
проходящей через точку с данным угловым
коэффициентом:

.
В эту формулу вместо

и

подставим координаты точки А(-2; 3), вместо
подставим
– 3. В результате подстановки получим:

Ответ:

Задача №2. Найти
уравнение прямой, проходящей через
точку К(1; –2)
параллельно прямой
.

Решение:

1. Найдем угловой
коэффициент прямой
.

—
это общее уравнение прямой, которое в
общем виде задается формулой
.
Сравнивая уравнения

и

находим, что А
= 2, В = –3. Угловой
коэффициент прямой, заданной уравнением

,
находится по формуле
.
Подставив в эту формулу А = 2 и В = –3,
получим угловой коэффициент прямой MN.
Итак,
.

2. Так как прямые
MN
и КС параллельны, то их угловые коэффициенты
равны:
.

3. Для нахождения
уравнения прямой КС воспользуемся
формулой уравнения прямой, проходящей
через точку с данным угловым коэффициентом

.
В эту формулу вместо

и

подставим координаты точки К(–2; 3),
вместо
подставим

.
В результате подстановки получим:

Ответ:

Задача № 3. Найти
уравнение прямой, проходящей через
точку К(–1; –3) перпендикулярно прямой

Решение:

1.

– это общее уравнение прямой, которое
в общем виде задается формулой
.

и

находим, что А
= 3, В = 4.

Угловой коэффициент
прямой, заданной уравнением
,
находится по формуле:
.
Подставив в эту формулу А
= 3 и В = 4, получим
угловой коэффициент прямой MN: