Как составить систему уравнения для функции

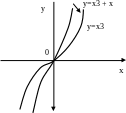
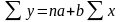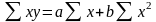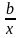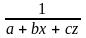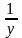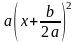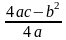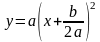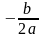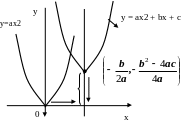Как решать систему уравнений с графиком функции

Другими словами, если задано несколько уравнений с одной, двумя или больше неизвестными, и все эти уравнения (равенства) должны одновременно выполняться , такую группу уравнений мы называем системой.

Объединяем уравнения в систему с помощью фигурной скобки:

Графический метод

Недаром ответ записывается так же, как координаты какой-нибудь точки.

Ведь если построить графики для каждого уравнения в одной системе координат, решениями системы уравнений будут точки пересечения графиков.

Например, построим графики уравнений из предыдущего примера.

Пример 1

Для этого сперва выразим y y y в каждом уравнении, чтобы получить функцию (ведь мы привыкли строить функции относительно x x x ):

Для того чтобы графически решить систему уравнений с двумя переменными нужно:

1) построить графики уравнений в одной системе координат;
2) найти координаты точек пересечения этих графиков (координаты точек пересечения графиков и есть решения системы);

Разберем это задание на примере.

Решить графически систему линейных уравнений.

Графическое решение системы уравнений с двумя переменными сводится к отыскиванию координат общих точек графиков уравнений.

Пример 2

Графиком линейной функции является прямая. Две прямые на плоскости могут пересекаться в одной точке, быть параллельными или совпадать. Соответственно система уравнений может:

а) иметь единственное решение;

б) не иметь решений;

в) иметь бесконечное множество решений.

2) Решением системы уравнений является точка (если уравнения являются линейными) пересечения графиков.

Пример 3

Графическое решение системы

Пример 4

Решить графическим способом систему уравнений.

Графиком каждого уравнения служит прямая линия, для построения которой достаточно знать координаты двух точек. Мы составили таблицы значений х и у для каждого из уравнений системы.

Прямую y=2x-3 провели через точки (0; -3) и (2; 1).

Прямую y=x+1 провели через точки (0; 1) и (2; 3).

Графики данных уравнений системы 1) пересекаются в точке А(4; 5). Это и есть единственное решение данной системы.

Пример 5

Выражаем у через х из каждого уравнения системы 2), а затем составим таблицу значений переменных х и у для каждого из полученных уравнений.

Прямую y=2x+9 проводим через точки (0; 9) и (-3; 3). Прямую y=-1,5x+2 проводим через точки (0; 2) и (2; -1).

Наши прямые пересеклись в точке В(-2; 5).

ОБЯЗАТЕЛЬНО: Познакомимся с видео, где нам объяснят как решаются системы линейных уравнений графическим способом. РАССКАЖУТ, КАК РЕШАТЬ СИСТЕМЫ ГРАФИЧЕСКИ.

Видео YouTube

Решение систем уравнений

Содержание:

Графический метод решения систем уравнений

Вспоминаем то, что знаем

Что такое график уравнения с двумя неизвестными?

Что представляет собой график линейного уравнения с двумя неизвестными?

Решите графическим методом систему линейных уравнений:

Открываем новые знания

Решите графическим методом систему уравнений:

Как можно решить систему двух уравнений с двумя неизвестными с помощью графиков уравнений этой системы? Отвечаем, проверяем себя по тексту

В курсе алгебры 7-го класса вы изучали системы линейных уравнений.

Для их решения вы применяли три метода: графический, метод подстановки и метод алгебраического сложения. Эти же методы служат и для решения других систем двух уравнений с двумя неизвестными, в которых могут содержаться уравнения второй степени или другие рациональные уравнения — как целые, так и дробные.

По этой ссылке вы найдёте полный курс лекций по высшей математике:

Начнём с графического метода

Этот метод основан на том, что каждому уравнению с двумя неизвестными соответствует некоторое множество точек координатной плоскости (график этого уравнения). Построив графики уравнений, мы найдём точки пересечения этих графиков (если они есть), и пары чисел — координаты точек пересечения — будут представлять собой решения системы уравнений.

Найденные решения будут, вообще говоря, приближёнными, в зависимости от точности построений соответствующих графиков.

Таким образом, решить графически систему уравнений — значит найти общие точки графиков уравнений, входящих в систему.

Возможно вам будут полезны данные страницы:

Примеры с решением

Пример 1:

Решим систему уравнений:

Построим графики уравнений

Графиком первого уравнения является парабола, с вершиной в точке (0; 1) и ветвями, направленными вверх, графиком второго — прямая, проходящая через точки (0; 3) и (-3; 0).

Парабола и прямая пересекаются в точках А(2; 5) и В(— 1; 2).

Проверкой убеждаемся, что найденные пары чисел действительно являются решениями системы.

Ответ: (2; 5) и (-1; 2).

Пример 2:

Выясним количество решений системы уравнений:

Построим графики уравнений

Графики этих уравнений — окружности. Центр первой окружности — начало координат, а её радиус равен 2; центр второй окружности — точка Р(1; — 1), её радиус равен 3.

Окружности пересекаются в двух точках М и N, координаты которых можно найти приближённо. Поскольку нам нужно определить только количество решений, мы делать этого не будем.

Ответ: Два решения.

Решение систем уравнений методом подстановки

Вспоминаем то, что знаем

Расскажите, как решить систему двух линейных уравнений с двумя неизвестными методом подстановки.

Решите систему линейных уравнений методом подстановки:

Открываем новые знания

Как вы думаете, можно ли применять метод подстановки при решении систем, где не все уравнения являются линейными? При каком условии это удастся сделать?

Решите систему уравнений методом подстановки:

Как решить систему двух уравнений с двумя неизвестными методом подстановки?

Всякую ли систему двух уравнений с двумя неизвестными можно решить методом подстановки?

Ранее вы решали системы уравнений первой степени.

Теперь познакомимся с системами, в которых хотя бы одно уравнение не является линейным. Как и прежде, распространённым методом решения систем является метод подстановки.

Пример 3:

Пусть (х; у) — решение системы.

Выразим х из уравнения

Подставим найденное выражение в первое уравнение:

Решим полученное уравнение:

Убедиться, что найденные пары чисел действительно являются решениями системы, можно подстановкой.

Чуть сложнее дело обстоит в следующем примере.

Пример 4:

Решим систему уравнений:

Пусть (х; у) — решение системы.

Выразим у из линейного уравнения:

Подставим найденное выражение в первое уравнение системы:

После преобразований получим:

Ответ: (-0,5; 0,5), (4; 5).

Если это целесообразно, то можно осуществлять подстановку некоторого выражения «в целом».

Пример 5:

Подставим во второе уравнение тогда его можно переписать в виде:

Теперь выразим х через у из первого уравнения системы:

Подставим в полученное ранее уравнение ху = 2:

Корни этого уравнения:

.

Иногда решить систему можно, используя метод алгебраического сложения.

Пример 6:

Сложим уравнения, предварительно умножив первое уравнение на —1. В результате получим:

.

Корни этого уравнения:

Подставим найденные значения в первое уравнение. Рассмотрим два случая:

1)

2) , получим уравнение корней нет.

Иногда упростить решение удаётся, используя различные варианты замены неизвестных.

Пример 7:

Решим систему уравнений:

Обозначим

Второе уравнение системы примет вид:

Решим полученное уравнение. Получим, умножая обе части на 2а:

Осталось решить методом подстановки линейные системы:

Ответ: (2; 1), (1; 2). Решение задач с помощью систем уравнений Знакомимся с новыми знаниями

Напомним, что при решении задач обычно действуют следующим образом:

1) обозначают буквами какие-нибудь неизвестные величины, выражают через них другие величины, составляют систему уравнений;

2) решают полученную систему;

3) отвечают на вопрос задачи.

Пример 8:

Периметр прямоугольника равен 34 см, а его диагональ 13 см. Найдите стороны прямоугольника.

Пусть х см — длина, у см — ширина (х у), тогда периметр прямоугольника — см.

Воспользуемся теоремой Пифагора:

Решим систему. Выразим из первого уравнения у:

Подставим во второе уравнение:

Корни уравнения:

Найдём

С учётом условия получим ответ: длина — 12 см, ширина — 5 см.

Пример 9:

Если произведение двух положительных чисел увеличить на первое из них, то получится 128. Если это же произведение увеличить на второе из них то получится 135. Найдите эти числа.

Пусть х — первое число, у — второе число.

Тогда: — произведение, увеличенное на первое число, ху 4-у — произведение, увеличенное на второе число.

Вычтем из второго уравнения первое. Получим:

Дальше будем решать методом подстановки:

Подставим в первое уравнение выражение для у:

Корни уравнения: (не подходит по смыслу задачи).

Найдём у из уравнения:

Получим ответ: 16 и 7.

Симметричные системы уравнений с двумя неизвестными

Уравнение с двумя неизвестными называется симметричным, если при перестановке этих неизвестных местами уравнение не меняется. Например, уравнение симметричное, так как при перестановке входящих в него неизвестных оно приобретает вид , то есть не меняется. А вот уравнение не симметричное, так как при перестановке входящих в него неизвестных оно приобретает вид , то есть меняется.

Система двух уравнений с двумя неизвестными называется симметричной, если каждое уравнение этой системы симметричное.

ПРЕДУПРЕЖДЕНИЕ. В определении симметричной системы уравнений требуется, чтобы каждое уравнение в отдельности не менялось.

Например, если в системе уравнений

переставить местами неизвестные х и у, то получим систему:

Видно, что система в целом не изменилась (уравнения поменялись местами по сравнению с первоначальной системой). Но такая система не является симметричной, так как каждое из уравнений в отдельности изменилось.

Убедитесь, что симметричные системы с двумя неизвестными х и у можно решать с помощью замены неизвестных:

Сначала научитесь выражать через неизвестные выражения:

Присылайте задания в любое время дня и ночи в ➔

Официальный сайт Брильёновой Натальи Валерьевны преподавателя кафедры информатики и электроники Екатеринбургского государственного института.

Все авторские права на размещённые материалы сохранены за правообладателями этих материалов. Любое коммерческое и/или иное использование кроме предварительного ознакомления материалов сайта natalibrilenova.ru запрещено. Публикация и распространение размещённых материалов не преследует за собой коммерческой и/или любой другой выгоды.

Сайт предназначен для облегчения образовательного путешествия студентам очникам и заочникам по вопросам обучения . Наталья Брильёнова не предлагает и не оказывает товары и услуги.

6.9.1. Решение систем линейных уравнений графическим способом

Примеры. Решить графическим способом систему уравнений.

Графиком каждого уравнения служит прямая линия, для построения которой достаточно знать координаты двух точек. Мы составили таблицы значений х и у для каждого из уравнений системы.

Прямую y=2x-3 провели через точки (0; -3) и (2; 1).

Прямую y=x+1 провели через точки (0; 1) и (2; 3).

Графики данных уравнений системы 1) пересекаются в точке А(4; 5). Это и есть единственное решение данной системы.

Ответ: (4; 5).

Выражаем у через х из каждого уравнения системы 2), а затем составим таблицу значений переменных х и у для каждого из полученных уравнений.

Прямую y=2x+9 проводим через точки (0; 9) и (-3; 3). Прямую y=-1,5x+2 проводим через точки (0; 2) и (2; -1).

Существует
определенное правило составления
системы стандартных уравнений:

1.
Записывается исходное уравнение:

y
= a + bx.

2.
Перемножаются все члены уравнения на
коэффициент при первом неизвестном и
суммируются. Одновременно первый член
(а) умножается на (n),
т.е. на число наблюдений:

.

3.
Далее в системе перемножаются все члены
уравнения на коэффициент при втором
неизвестном и также суммируются:

и
т.д.

Итак,
система стандартных уравнений для
функции у
= а + bx имеет
вид:

Для
параболы второй степени у
= а + bх + сх²
система стандартных уравнений имеет
вид:

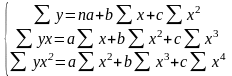
Для
параболы третьей степени у
= а + bх + сх²
+ dx³:

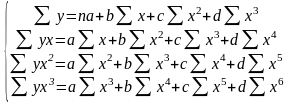
Для
функции у
= а +

система стандартных уравнений имеет
вид:

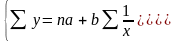
Для
функции у
=

система стандартных уравнений записывается
следующим образом:

=
а + bx + cz

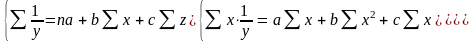
Для
функции у
= а + а₁х₁
+ а₂х₂
+ а₃х₃
система стандартных уравнений имеет
вид:

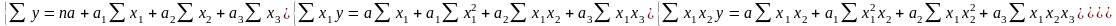
1.6.
Наиболее привлекательные функции для
измерения

экономических
процессов (спроса, выпуска продукции,

ценообразования
и других)

Для
количественной оценки технико-экономических
показателей, в частности спроса,
предложения (выпуска продукции) и других
возможно применение не только линейных,
но и различных более усложненных функций.

1.6.1.
Квадратичная функция

Зависимость
между спросом и насыщенностью
потребительского рынка вполне может
выражаться функцией вида:

y
= aх²
+ bx
+ с,

где
х
— насыщенность рынка;

у
— спрос;

а,
b,
с — параметры
системы.

Предположим,
что b
= 0, с
= 0. Тогда функция примет вид:

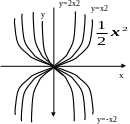
y
= ax².

График,
последней функции в зависимости от
величины коэффициентов а
— принимает вид

Рис.
2

Осуществим
преобразования функции:

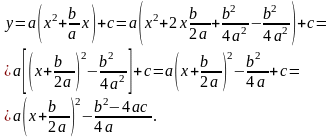
Итак,

Первая
часть равенства есть сумма двух слагаемых,
из которых

зависит
от переменной х,

не
зависит от х,
следовательно, имеет постоянное значение.

Чтобы
получить график функции

,
имея график у
= ах²,
достаточно сдвинуть график у
= ах²
вдоль оси
абсцисс на отрезок, равный

,
а затем достаточно произвести перенос
вдоль оси ординат на величину

.

Т
аким
образом, чтобы получить график функции
у = ах²
+ bx
+ c
надо сдвинуть
график у =
ах²
сначала вдоль оси абсцисс на отрезок

,
а затем вдоль оси ординат на

.
На рис. 3 показаны графики функции у
= ах²
+ bx
+ c:

Рис.
3

1.6.2. Биквадратная функция

Функция
вида

у
= ах⁴
+ bx²
+ c
(а ≠
0)

называется
биквадратной.

После
преобразования получим:

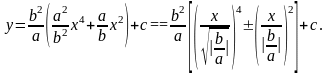
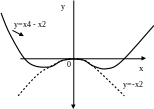
Если
b
≠
0, то график функции получается либо из
графика функции у
= х⁴
+ х²,
либо из графика у
= х⁴
— х².

График
функции у
= х⁴
+ х²,
есть сумма графиков функции у
= х⁴,
у = х².
На рис. 4 показан график данной функции:

Рис.
4.

1.6.3. Кубическая функция

Функция
вида у = ах³
+ bх²
+ cx
+ d,
где a
≠
0, b,
c
и d
— любые числа, называется кубической. В
зависимости от конкретных обстоятельств
данную функцию также возможно использовать
для оценки основных технико-экономических
показателей, и в том числе спроса,
предложения, равновесных цен и других.

Функция
у = х³.
Если а
= 1,
b
= c
= d
= 0.
В данном
случае график функции имеет вид:

Рис.
5.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

Как составить систему уравнений

Уравнением называют аналитическую запись задачи о разыскании значений аргументов, при которых значения двух данных функций равны. Система – это совокупность уравнений, для которых требуется найти значения неизвестных, удовлетворяющих одновременно всем этим уравнениям. Так как успешное решение задачи невозможно без правильно составленной системы уравнений, необходимо знать основные принципы составления подобных систем.

Инструкция

Во-первых, определите неизвестные величины, которые требуется найти в данной задаче. Обозначьте их через переменные. Наиболее распространенные переменные, используемые при решении систем уравнений, это x, y и z. В отдельных задачах удобнее применять общепринятые обозначения, например, V для обозначения объема, или a для обозначения ускорения.

Пример. Пусть гипотенуза прямоугольного треугольника равна 5 м. Необходимо определить катеты, если известно, что после того, как один из них увеличить в 3 раза, а другой в 4, то сумма их длин составит 29 м. Для данной задачи необходимо обозначить длины катетов через переменные x и y.

Далее внимательно читайте условие задачи и связывайте неизвестные величины уравнениями. Иногда взаимосвязь между переменными будет очевидна. Например, в приведенном выше примере, катеты связывает следующее соотношение.Если «один из них увеличить в 3 раза» (3 * x), «а другой в 4» (4 * y), «то сумма их длин составит 29 м»: 3 * x + 4 * y = 29.

Другое уравнение для данной задачи менее очевидно. Оно кроется в условии задаче о том, что дан прямоугольный треугольник. Значит, можно применить теорему Пифагора. Т.е. x^2 + y^2 = 25. Итого получается два уравнения:
3 * x + 4 * y = 29 и x^2 + y^2 = 25.Для того чтобы система имела однозначное решение, количество уравнений должно быть равно количеству неизвестных. В приведенном примере имеется две переменных и два уравнения. Значит, система имеет одно конкретное решение: x = 3 м, y = 4 м.

При решении физических задач «неочевидные» уравнения могут заключаться в формулах, связывающих физические величины. Например, пусть в условии задачи необходимо найти скорости пешеходов Va и Vb. Известно, что пешеход A проходит расстояние S на 3 часа медленнее, чем пешеход B. Тогда можно составить уравнение, воспользовавшись формулой S = V * t, где S – это расстояние, V – скорость, t – время: S / Va = S / Vb + 3. Здесь S / Va — это время, за которое пройдет заданное расстояние пешеход A. S / Vb — время, за которое пройдет заданное расстояние пешеход B. По условию это время на 3 часа меньше.

Видео по теме

Обратите внимание

Все уравнения в системе должны поставлять дополнительную независимую от других уравнений информацию. Иначе система будет недоопределена и однозначного решения найти будет не возможно.

Полезный совет

После решения системы уравнений подставьте найденные значения в исходную систему и проверьте, что они удовлетворяют всем уравнениям.

Войти на сайт

или

Забыли пароль?
Еще не зарегистрированы?

Прежде чем перейти к разбору как решать системы уравнений, давайте разберёмся, что называют системой уравнений
с двумя неизвестными.

Например, система уравнений может быть задана следующим образом.

Чтобы решить систему уравнений, нужно найти и «x», и «y».

Как решить систему уравнений

Существуют два основных способа решения систем уравнений. Рассмотрим оба способа решения.

Способ подстановки
или
«железобетонный» метод

Первый способ решения системы уравнений называют способом подстановки или «железобетонным».

Название «железобетонный» метод получил из-за того, что с помощью этого метода практически всегда можно
решить систему уравнений. Другими словами, если у вас не получается решить систему уравнений,
всегда пробуйте решить её методом подстановки.

Разберем способ подстановки на примере.

Выразим из первого уравнения «x + 5y = 7»
неизвестное «x».

Перенесём в первом уравнении «x + 5 y = 7» всё что
содержит «x» в левую часть,
а остальное в правую часть по
правилу переносу.

При «x» стоит коэффициент равный единице, поэтому дополнительно делить уравнение
на число не требуется.

Теперь, вместо «x» подставим во второе уравнение полученное выражение
«x = 7 − 5y» из первого уравнения.

	x = 7 − 5y
3(7 − 5y) − 2y = 4

Подставив вместо «x» выражение «(7 − 5y)»
во второе уравнение,
мы получили обычное линейное уравнение с одним неизвестным «y».
Решим его по правилам
решения линейных уравнений.

Чтобы каждый раз не писать всю систему уравнений заново, решим полученное уравнение
«3(7 − 5y) − 2y = 4» отдельно.
Вынесем его решение отдельно с помощью
обозначения звездочка (*).

	x = 7 − 5y
3(7 − 5y) − 2y = 4  (*)

(*)   3(7 − 5y) − 2y = 4
21 − 15y − 2y = 4
− 17y = 4 − 21
                 − 17y = − 17     | :(−17)
y = 1

Мы нашли, что «y = 1».
Вернемся к первому уравнению «x = 7 − 5y» и вместо «y» подставим в него полученное числовое значение.
Таким образом можно найти «x».
Запишем в ответ оба полученных значения.

Ответ: x = 2; y = 1

Способ сложения

Рассмотрим другой способ решения системы уравнений. Метод называется способ сложения.
Вернемся к нашей системе уравнений еще раз.

По правилам математики уравнения системы можно складывать. Наша задача в том, чтобы сложив исходные
уравнения, получить такое уравнение, в котором останется только одно неизвестное.

Давайте сейчас сложим уравнения системы и посмотрим, что из этого выйдет.

	x + 5y = 7		(x + 5y) + (3x − 2y) = 7 + 4
	+          =>	x + 5y + 3x − 2y = 11
3x − 2y = 4		4x + 3y = 11

При сложении уравнений мы получили уравнение «4x + 3y = 11».
По сути, сложение уравнений в исходном виде нам ничего
не дало, так как в полученном уравнении мы по прежнему имеем оба неизвестных.

Вернемся снова к исходной системе уравнений.

Чтобы при сложении неизвестное «x» взаимноуничтожилось,
нужно сделать так, чтобы в первом уравнении при «x» стоял коэффициент
«−3».

Для этого умножим первое уравнение на «−3».

	x + 5y = 7 | ·(−3)
3x − 2y = 4

	x ·(−3) + 5y · (−3) = 7 · (−3)
3x − 2y = 4

	−3x −15y = −21
3x − 2y = 4

Теперь сложим уравнения.

	−3x −15y = −21		(−3x −15y ) + (3x − 2y) = −21 + 4
	+          =>	−3x −15y + 3x − 2y = −21 + 4
3x − 2y = 4		−17y = −17 |:(−17)
		y = 1

Мы нашли «y = 1».
Вернемся к первому уравнению и подставим вместо «y» полученное числовое
значение и найдем «x».

Ответ: x = 2; y = 1

Пример решения системы уравнения
способом подстановки

Выразим из первого уравнения «x».

Подставим вместо «x» во второе уравнение полученное выражение.

	x = 17 + 3y
(17 + 3y) − 2y = −13 (*)

(*) (17 + 3y) − 2y = −13
17 + 3y − 2y = −13
17 + y = −13
y = −13 − 17
y = −30

Подставим в первое уравнение полученное числовое значение «y = −30» и
найдем «x».

	x = 17 + 3 · (−30)
y = −30

Ответ: x = −73; y = −30

Пример решения системы уравнения
способом сложения

Рассмотрим систему уравнений.

	3(x − y) + 5x = 2(3x − 2)
4x − 2(x + y) = 4 − 3y

Раскроем скобки и упростим выражения в обоих уравнениях.

	3x − 3y + 5x = 6x − 4
4x − 2x − 2y = 4 − 3y

	8x − 3y = 6x − 4
2x −2y = 4 − 3y

	8x − 3y − 6x = −4
2x −2y + 3y = 4

Мы видим, что в обоих уравнениях есть «2x».
Наша задача, чтобы при сложении уравнений «2x» взаимноуничтожились и в
полученном уравнении осталось только «y».

Для этого достаточно умножить первое уравнение на «−1».

	2x − 3y = −4      |·(−1)
2x + y = 4

	2x · (−1) − 3y · (−1) = −4 · (−1)
2x + y = 4

Теперь при сложении уравнений у нас останется только «y» в уравнении.

	−2x + 3y = 4		(−2x + 3y ) + (2x + y) = 4 + 4
	+          =>	−2x + 3y + 2x + y = 4 + 4
2x + y = 4		4y = 8         | :4
		y = 2

Подставим в первое уравнение полученное числовое значение «y = 2» и
найдем «x».

Ответ: x = 1; y = 2

---

Ваши комментарии

Оставить комментарий:

---

Решение системы линейных уравнений графическим способом

Графиком линейной функции является прямая. Две прямые на плоскости могут пересекаться в одной точке, быть параллельными или совпадать. Соответственно система уравнений может: 

а) иметь единственное решение; 

б) не иметь решений; 

в) иметь бесконечное множество решений.

2) Решением системы уравнений является точка (если уравнения являются линейными) пересечения графиков.

Пример 3

Графическое решение системы 

Пример 4

Выражаем у через х из каждого уравнения системы 2), а затем составим таблицу значений переменных х и у для каждого из полученных уравнений.

Прямую y=2x+9 проводим через точки (0; 9) и (-3; 3). Прямую y=-1,5x+2 проводим через точки (0; 2) и (2; -1).

Наши прямые пересеклись в точке В(-2; 5).

Ответ: (-2; 5).

ОБЯЗАТЕЛЬНО: Познакомимся с видео, где нам объяснят как решаются системы линейных уравнений графическим способом. РАССКАЖУТ, КАК РЕШАТЬ СИСТЕМЫ ГРАФИЧЕСКИ.

ДОМАШНЯЯ РАБОТА: ВЫПОЛНЯТЬ ВСЕ ШАГИ ПОСТРОЕНИЯ, КАК ПОКАЗАНО В ВИДЕО РАЗБОРАХ И ПРИМЕРАХ. В УЧЕБНИКЕ ТЕОРИЯ НА СТРАНИЦАХ СТР 195-199. ВСЕ ИЗУЧИТЬ, ТЕМА ОЧЕНЬ ВАЖНАЯ.