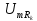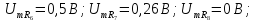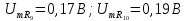Практическое применение преобразования Фурье для анализа сигналов. Введение для начинающих
Время на прочтение
9 мин
Количество просмотров 255K
1. Преобразование Фурье и спектр сигнала
Во многих случаях задача получения (вычисления) спектра сигнала выглядит следующим образом. Имеется АЦП, который с частотой дискретизации Fd преобразует непрерывный сигнал, поступающий на его вход в течение времени Т, в цифровые отсчеты — N штук. Далее массив отсчетов подается в некую программку, которая выдает N/2 каких-то числовых значений (программист, который утянул из инета написал программку, уверяет, что она делает преобразование Фурье).
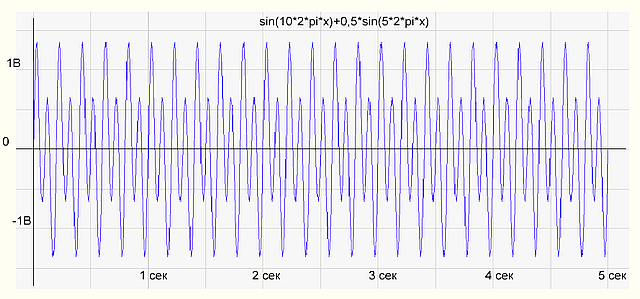
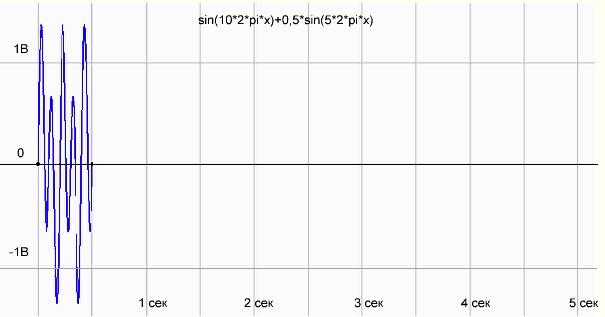
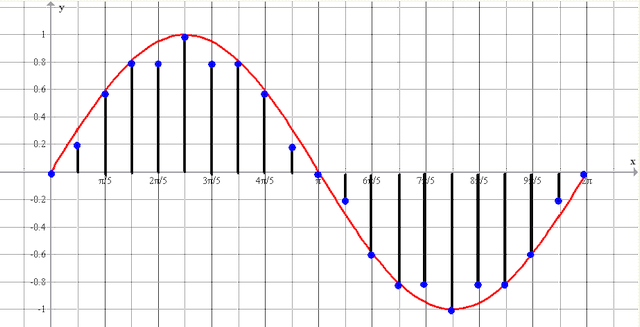
Чтобы проверить, правильно ли работает программа, сформируем массив отсчетов как сумму двух синусоид sin(10*2*pi*x)+0,5*sin(5*2*pi*x) и подсунем программке. Программа нарисовала следующее:
рис.1 График временной функции сигнала
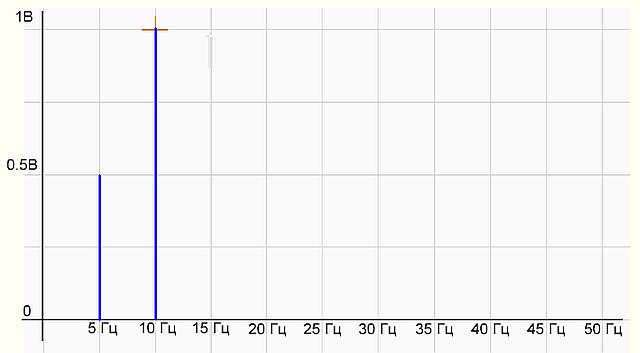
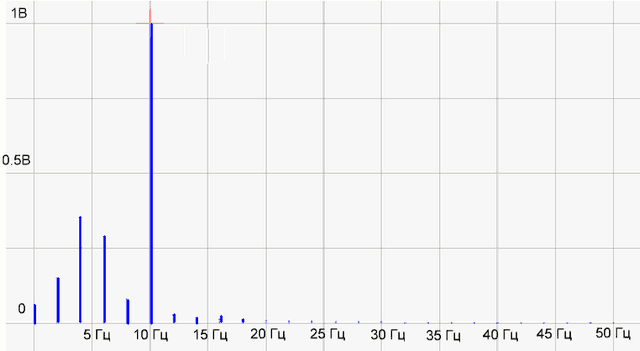
рис.2 График спектра сигнала
На графике спектра имеется две палки (гармоники) 5 Гц с амплитудой 0.5 В и 10 Гц — с амплитудой 1 В, все как в формуле исходного сигнала. Все отлично, программист молодец! Программа работает правильно.
Это значит, что если мы подадим на вход АЦП реальный сигнал из смеси двух синусоид, то мы получим аналогичный спектр, состоящий из двух гармоник.
Итого, наш реальный измеренный сигнал, длительностью 5 сек, оцифрованный АЦП, то есть представленный дискретными отсчетами, имеет дискретный непериодический спектр.
С математической точки зрения — сколько ошибок в этой фразе?
Теперь
начальство решило
мы решили, что 5 секунд — это слишком долго, давай измерять сигнал за 0.5 сек.
рис.3 График функции sin(10*2*pi*x)+0,5*sin(5*2*pi*x) на периоде измерения 0.5 сек
рис.4 Спектр функции
Что-то как бы не то! Гармоника 10 Гц рисуется нормально, а вместо палки на 5 Гц появилось несколько каких-то непонятных гармоник. Смотрим в интернетах, что да как…
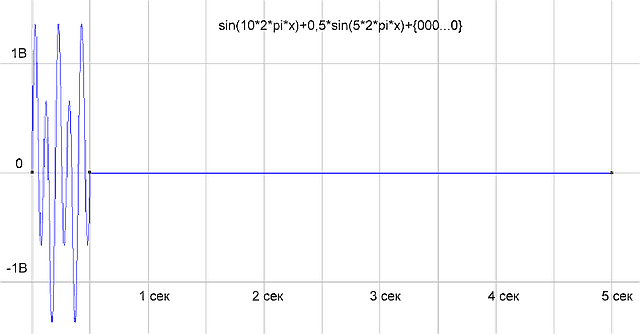
Во, говорят, что в конец выборки надо добавить нули и спектр будет рисоваться нормальный.
рис.5 Добили нулей до 5 сек
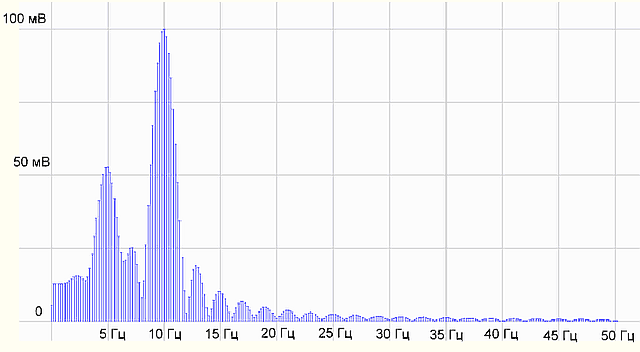
рис.6 Получили спектр
Все равно не то, что было на 5 секундах. Придется разбираться с теорией. Идем в Википедию — источник знаний.
2. Непрерывная функция и представление её рядом Фурье
Математически наш сигнал длительностью T секунд является некоторой функцией f(x), заданной на отрезке {0, T} (X в данном случае — время). Такую функцию всегда можно представить в виде суммы гармонических функций (синусоид или косинусоид) вида:
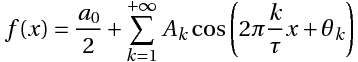
k — номер тригонометрической функции ( номер гармонической составляющей, номер гармоники)
T — отрезок, где функция определена (длительность сигнала)
Ak — амплитуда k-ой гармонической составляющей,
θk- начальная фаза k-ой гармонической составляющей
Что значит «представить функцию в виде суммы ряда»? Это значит, что, сложив в каждой точке значения гармонических составляющих ряда Фурье, мы получим значение нашей функции в этой точке.
(Более строго, среднеквадратичное отклонение ряда от функции f(x) будет стремиться к нулю, но несмотря на среднеквадратичную сходимость, ряд Фурье функции, вообще говоря, не обязан сходиться к ней поточечно. См. https://ru.wikipedia.org/wiki/Ряд_Фурье.)
Этот ряд может быть также записан в виде:
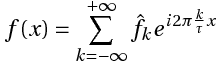
где 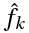
или
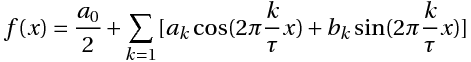
Связь между коэффициентами (1) и (3) выражается следующими формулами:
и
Отметим, что все эти три представления ряда Фурье совершенно равнозначны. Иногда при работе с рядами Фурье бывает удобнее использовать вместо синусов и косинусов экспоненты мнимого аргумента, то есть использовать преобразование Фурье в комплексной форме. Но нам удобно использовать формулу (1), где ряд Фурье представлен в виде суммы косинусоид с соответствующими амплитудами и фазами. В любом случае неправильно говорить, что результатом преобразования Фурье действительного сигнала будут комплексные амплитуды гармоник. Как правильно говорится в Вики «Преобразование Фурье (ℱ) — операция, сопоставляющая одной функции вещественной переменной другую функцию, также вещественной переменной.»
Итого:
Математической основой спектрального анализа сигналов является преобразование Фурье.
Преобразование Фурье позволяет представить непрерывную функцию f(x) (сигнал), определенную на отрезке {0, T} в виде суммы бесконечного числа (бесконечного ряда) тригонометрических функций (синусоид иили косинусоид) с определёнными амплитудами и фазами, также рассматриваемых на отрезке {0, T}. Такой ряд называется рядом Фурье.
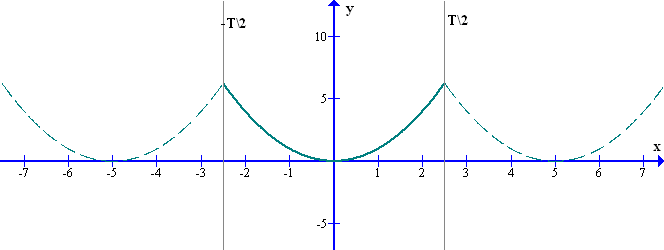
Отметим еще некоторые моменты, понимание которых требуется для правильного применения преобразования Фурье к анализу сигналов. Если рассмотреть ряд Фурье (сумму синусоид) на всей оси Х, то можно увидеть, что вне отрезка {0, T} функция представленная рядом Фурье будет будет периодически повторять нашу функцию.
Например, на графике рис.7 исходная функция определена на отрезке {-T2, +T2}, а ряд Фурье представляет периодическую функцию, определенную на всей оси х.
Это происходит потому, что синусоиды сами являются периодическими функциями, соответственно и их сумма будет периодической функцией.
рис.7 Представление непериодической исходной функции рядом Фурье
Таким образом:
Наша исходная функция — непрерывная, непериодическая, определена на некотором отрезке длиной T.
Спектр этой функции — дискретный, то есть представлен в виде бесконечного ряда гармонических составляющих — ряда Фурье.
По факту, рядом Фурье определяется некоторая периодическая функция, совпадающая с нашей на отрезке {0, T}, но для нас эта периодичность не существенна.
Далее.
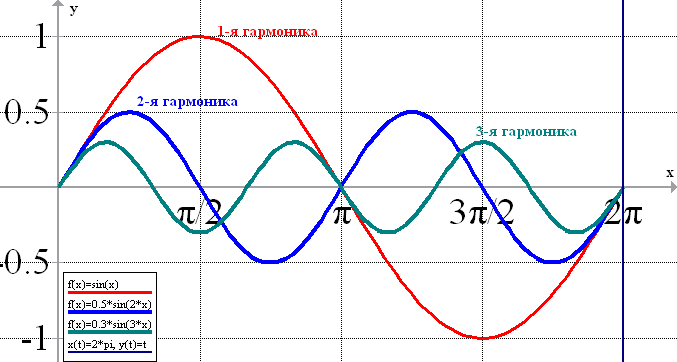
Периоды гармонических составляющих кратны величине отрезка {0, T}, на котором определена исходная функция f(x). Другими словами, периоды гармоник кратны длительности измерения сигнала. Например, период первой гармоники ряда Фурье равен интервалу Т, на котором определена функция f(x). Период второй гармоники ряда Фурье равен интервалу Т/2. И так далее (см. рис. 8).
рис.8 Периоды (частоты) гармонических составляющих ряда Фурье (здесь Т=2π)
Соответственно, частоты гармонических составляющих кратны величине 1/Т. То есть частоты гармонических составляющих Fk равны Fk= кТ, где к пробегает значения от 0 до ∞, например к=0 F0=0; к=1 F1=1T; к=2 F2=2T; к=3 F3=3T;… Fk= кТ (при нулевой частоте — постоянная составляющая).
Пусть наша исходная функция, представляет собой сигнал, записанный в течение Т=1 сек. Тогда период первой гармоники будет равен длительности нашего сигнала Т1=Т=1 сек и частота гармоники равна 1 Гц. Период второй гармоники будет равен длительности сигнала, деленной на 2 (Т2=Т/2=0,5 сек) и частота равна 2 Гц. Для третьей гармоники Т3=Т/3 сек и частота равна 3 Гц. И так далее.
Шаг между гармониками в этом случае равен 1 Гц.
Таким образом сигнал длительностью 1 сек можно разложить на гармонические составляющие (получить спектр) с разрешением по частоте 1 Гц.
Чтобы увеличить разрешение в 2 раза до 0,5 Гц — надо увеличить длительность измерения в 2 раза — до 2 сек. Сигнал длительностью 10 сек можно разложить на гармонические составляющие (получить спектр) с разрешением по частоте 0,1 Гц. Других способов увеличить разрешение по частоте нет.
Существует способ искусственного увеличения длительности сигнала путем добавления нулей к массиву отсчетов. Но реальную разрешающую способность по частоте он не увеличивает.
3. Дискретные сигналы и дискретное преобразование Фурье
С развитием цифровой техники изменились и способы хранения данных измерений (сигналов). Если раньше сигнал мог записываться на магнитофон и храниться на ленте в аналоговом виде, то сейчас сигналы оцифровываются и хранятся в файлах в памяти компьютера в виде набора чисел (отсчетов).
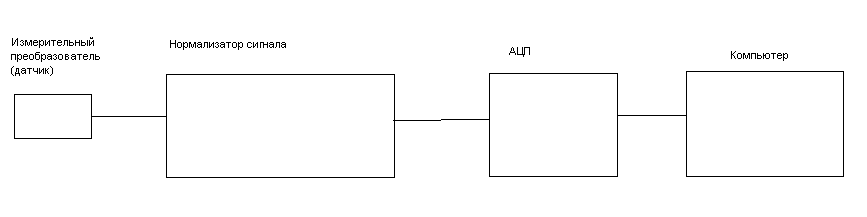
Обычная схема измерения и оцифровки сигнала выглядит следующим образом.
рис.9 Схема измерительного канала
Сигнал с измерительного преобразователя поступает на АЦП в течение периода времени Т. Полученные за время Т отсчеты сигнала (выборка) передаются в компьютер и сохраняются в памяти.
рис.10 Оцифрованный сигнал — N отсчетов полученных за время Т
Какие требования выдвигаются к параметрам оцифровки сигнала? Устройство, преобразующее входной аналоговый сигнал в дискретный код (цифровой сигнал) называется аналого-цифровой преобразователь (АЦП, англ. Analog-to-digital converter, ADC) ( Wiki).
Одним из основных параметров АЦП является максимальная частота дискретизации (или частота семплирования, англ. sample rate) — частота взятия отсчетов непрерывного во времени сигнала при его дискретизации. Измеряется в герцах. (( Wiki))
Согласно теореме Котельникова, если непрерывный сигнал имеет спектр, ограниченный частотой Fмакс, то он может быть полностью и однозначно восстановлен по его дискретным отсчетам, взятым через интервалы времени 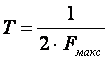
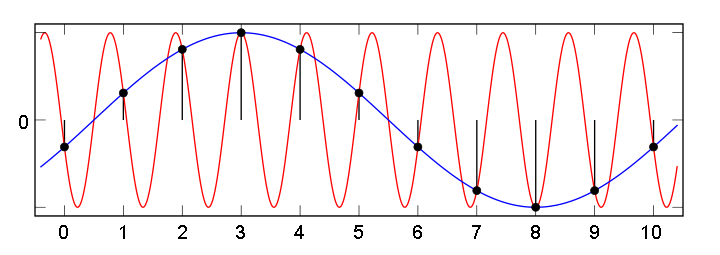
А что будет, если мы будем брать отсчеты с меньшей частотой, чем требуется по теореме Котельникова?
В этом случае возникает эффект «алиасинга» (он же стробоскопический эффект, муаровый эффект), при котором сигнал высокой частоты после оцифровки превращается в сигнал низкой частоты, которого на самом деле не существует. На рис. 11 красная синусоида высокой частоты — это реальный сигнал. Синяя синусоида более низкой частоты — фиктивный сигнал, возникающий вследствие того, за время взятия отсчета успевает пройти больше, чем пол-периода высокочастотного сигнала.
Рис. 11. Появление ложного сигнала низкой частоты при недостаточно высокой частоте дискретизации
Чтобы избежать эффекта алиасинга перед АЦП ставят специальный антиалиасинговый фильтр — ФНЧ (фильтр нижних частот), который пропускает частоты ниже половины частоты дискретизации АЦП, а более высокие частоты зарезает.
Для того, чтобы вычислить спектр сигнала по его дискретным отсчетам используется дискретное преобразование Фурье (ДПФ). Отметим еще раз, что спектр дискретного сигнала «по определению» ограничен частотой Fмакс, меньшей половине частоты дискретизации Fd. Поэтому спектр дискретного сигнала может быть представлен суммой конечного числа гармоник, в отличие от бесконечной суммы для ряда Фурье непрерывного сигнала, спектр которого может быть неограничен. Согласно теореме Котельникова максимальная частота гармоники должна быть такой, чтобы на нее приходилось как минимум два отсчета, поэтому число гармоник равно половине числа отсчетов дискретного сигнала. То есть если в выборке имеется N отсчетов, то число гармоник в спектре будет равно N/2.
Рассмотрим теперь дискретное преобразование Фурье (ДПФ).
Сравнивая с рядом Фурье
видим, что они совпадают, за исключением того, что время в ДПФ имеет дискретный характер и число гармоник ограничено величиной N/2 — половиной числа отсчетов.
Формулы ДПФ записываются в безразмерных целых переменных k, s, где k – номера отсчетов сигнала, s – номера спектральных составляющих.
Величина s показывает количество полных колебаний гармоники на периоде Т (длительности измерения сигнала). Дискретное преобразование Фурье используется для нахождения амплитуд и фаз гармоник численным методом, т.е. «на компьютере»
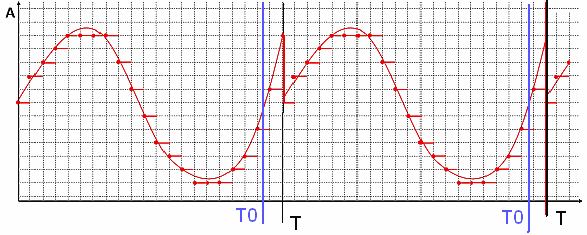
Возвращаясь к результатам, полученным в начале. Как уже было сказано выше, при разложении в ряд Фурье непериодической функции (нашего сигнала), полученный ряд Фурье фактически соответствует периодической функции с периодом Т. (рис.12).
рис.12 Периодическая функция f(x) с периодом Т0, с периодом измерения Т>T0
Как видно на рис.12 функция f(x) периодическая с периодом Т0. Однако из-за того, что длительность измерительной выборки Т не совпадает с периодом функции Т0, функция, получаемая как ряд Фурье, имеет разрыв в точке Т. В результате спектр данной функции будет содержать большое количество высокочастотных гармоник. Если бы длительность измерительной выборки Т совпадала с периодом функции Т0, то в полученном после преобразования Фурье спектре присутствовала бы только первая гармоника (синусоида с периодом равным длительности выборки), поскольку функция f(x) представляет собой синусоиду.
Другими словами, программа ДПФ «не знает», что наш сигнал представляет собой «кусок синусоиды», а пытается представить в виде ряда периодическую функцию, которая имеет разрыв из-за нестыковки отдельных кусков синусоиды.
В результате в спектре появляются гармоники, которые должны в сумме изобразить форму функции, включая этот разрыв.
Таким образом, чтобы получить «правильный» спектр сигнала, являющегося суммой нескольких синусоид с разными периодами, необходимо чтобы на периоде измерения сигнала укладывалось целое число периодов каждой синусоиды. На практике это условие можно выполнить при достаточно большой длительности измерения сигнала.
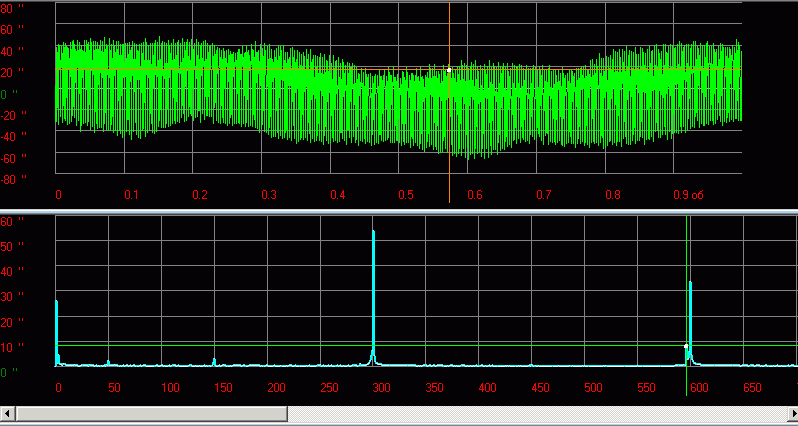
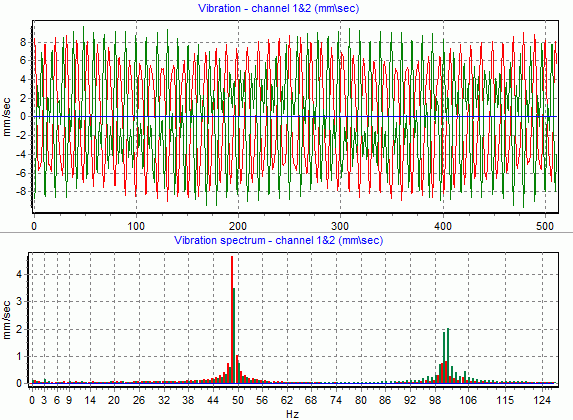
Рис.13 Пример функции и спектра сигнала кинематической погрешности редуктора
При меньшей длительности картина будет выглядеть «хуже»:
Рис.14 Пример функции и спектра сигнала вибрации ротора
На практике бывает сложно понять, где «реальные составляющие», а где «артефакты», вызванные некратностью периодов составляющих и длительности выборки сигнала или «скачками и разрывами» формы сигнала. Конечно слова «реальные составляющие» и «артефакты» не зря взяты в кавычки. Наличие на графике спектра множества гармоник не означает, что наш сигнал в реальности из них «состоит». Это все равно что считать, будто число 7 «состоит» из чисел 3 и 4. Число 7 можно представить в виде суммы чисел 3 и 4 — это правильно.
Так и наш сигнал… а вернее даже не «наш сигнал», а периодическую функцию, составленную путем повторения нашего сигнала (выборки) можно представить в виде суммы гармоник (синусоид) с определенными амплитудами и фазами. Но во многих важных для практики случаях (см. рисунки выше) действительно можно связать полученные в спектре гармоники и с реальными процессами, имеющими циклический характер и вносящими значительный вклад в форму сигнала.
Некоторые итоги
1. Реальный измеренный сигнал, длительностью T сек, оцифрованный АЦП, то есть представленный набором дискретных отсчетов (N штук), имеет дискретный непериодический спектр, представленный набором гармоник (N/2 штук).
2. Сигнал представлен набором действительных значений и его спектр представлен набором действительных значений. Частоты гармоник положительны. То, что математикам бывает удобнее представить спектр в комплексной форме с использованием отрицательных частот не значит, что «так правильно» и «так всегда надо делать».
3. Сигнал, измеренный на отрезке времени Т определен только на отрезке времени Т. Что было до того, как мы начали измерять сигнал, и что будет после того — науке это неизвестно. И в нашем случае — неинтересно. ДПФ ограниченного во времени сигнала дает его «настоящий» спектр, в том смысле, что при определенных условиях позволяет вычислить амплитуду и частоту его составляющих.
Использованные материалы и другие полезные материалы.
FourierScope — программа для построения радио сигналов и их спектрального анализа.
Graph — программа с открытым кодом, предназначенная для построения математических графиков.
ДИСКРЕТНОЕ ПРЕОБРАЗОВАНИЕ ФУРЬЕ – КАК ЭТО ДЕЛАЕТСЯ
Дискретное преобразование Фурье (ДПФ)
Как построить спектр
Одни источники излучают свет с непрерывным спектром, у других он является линейчатым. Даже у двух источников, цвета которых кажутся совершенно одинаковыми, спектры могут выглядеть совершенно по-разному. Для их наблюдения предназначен прибор, называемый спектроскопом.

Инструкция
Возьмите большую картонную коробку. В ее боковой стенке прорежьте вертикальную щель высотой в несколько сантиметров и шириной от 3 до 5 миллиметров. Она будет придавать потоку света форму тонкой полоски, простирающейся в вертикальной плоскости.
На противоположной стенке коробки разместите чистый компакт-диск типа CD-R.
Теперь в боковой стенке коробки прорежьте отверстие под трубку для наблюдения спектра. Несмотря на то, что трубка имеет круглое сечение, отверстие должно быть овальным, чтобы ее можно было поворачивать в горизонтальной плоскости.
Вставьте трубку в отверстие.
Направьте щель на источник света.
Загляните в трубку, и, поворачивая ее, найдите спектр и рассмотрите его.
Попробуйте пронаблюдать с помощью спектроскопа спектры различных источников света: солнца, лампы накаливания, люминесцентной лампы, свечи, светодиодов разных цветов. Сформулируйте их отличие друг от друга и попробуйте найти в учебниках и интернете информацию о принципах работы этих источников света.
Спектры, полученные при помощи спектроскопа, можно фотографировать веб-камерой, цифровым фотоаппаратом и мобильным телефоном. Полученные снимки вы сможете помещать в отчеты о выполнении школьных лабораторных работ или просто использовать в составе, например, коллажей или стенгазет.
При желании, интенсивность той или иной линии спектра можно измерить. Изготовьте примитивный фотометр, состоящий из фоторезистора и мультиметра, работающего в режиме омметра. Затемнив датчик, попробуйте фокусировать на нем линзой те или иные линии спектра. Следите за показаниями прибора: чем меньше сопротивление фоторезистора, тем ярче он освещен.
Теперь, получив данные об интенсивности линий спектра, можно построить на бумаге соответствующий график (по горизонтали — длина волны, по горизонтали — интенсивность). Поскольку наш фотометр не отградуирован, интенсивность будет выражаться в условных единицах. А вот длину волны с достаточной точностью можно определить на глаз — по цвету:
690 нм — темно-красный;
635 нм — красный;
620 нм — красно-оранжевый;
600 нм — оранжевый;
580 нм — желтый;
590 нм — салатовый;
550 нм — зеленый;
520 нм — изумрудный;
480 нм — синий;
420 нм — фиолетовый.
Обратите внимание
Осторожно обращайтесь со свечами.
Источники:
- Самодельные спектроскопы
Войти на сайт
или
Забыли пароль?
Еще не зарегистрированы?
This site is protected by reCAPTCHA and the Google Privacy Policy and Terms of Service apply.
МИНИСТЕРСТВО
ОБРАЗОВАНИЯ НАУКИ
РОССИЙСКОЙ
ФЕДЕРАЦИИ
ФЕДЕРАЛЬНО
ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ ОБРАЗОВАТЕЛЬНОЕ
УЧРЕЖДЕНИЕ
ВЫСШЕГО
ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ
МОСКОВСКИЙ
ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ
ПРИБОРОСТРОЕНИЯ
И ИНФОРМАТИКИ
В.
В. Филинов
Электроника
и схемотехника.
Расчёт
спектров электрических сигналов.
Учебно-методическое
пособие
Москва
— 2014
УДК
621.38
ББК
32.85
Рекомендовано
к изданию в качестве учебно-методического
пособия редакционно-издательским
советом МГУПИ
Рецензент:
д.т.н.
профессор Шкатов П. Н. (МГУПИ)
Филинов
В.В.
Электроника
и схемотехника. Расчет спектров
электрических сигналов.
Учебно-методическое пособие. М.: МГУПИ,
2014
Учебно-методическое
пособие предназначено для студентов
(бакалавров и специалистов) специальностей
по радиоэлектронике и информационной
безопасности, изучающих курс лекций
“Электроника и схемотехника”,
предназначено при подготовке к выполнению
практических и расчетно-графических
работ (РГР) по теме “Расчет спектров
электрических сигналов”. Приведены
примеры расчета спектров периодических
и непериодических сигналов, а также
задания для выполнения РГР. Полезно для
магистров и аспирантов технических
направлений МГУПИ.
Утверждено
и рекомендовано решением УМС факультета
«Приборостроения и радиоэлектроники»
МГУПИ в качестве учебно-методического
пособия.
©
Московский Государственный Университет
Приборостроения и Информатики, 2014
©
Филинов В.В., 2014
Оглавление
Стр.
Введение.
Необходимые формулы
………………………………………4
-
Спектры
амплитуд и фаз периодических сигналов
..…………6
Пример
1 ……………………………………………………………………6
Пример
2 …………………………………………………………………..10
Пример
3 …………………………………………………………………..11
Пример
4 …………………………………………………………………..12
Пример
5 …………………………………………………………………..13
Пример
6 …………………………………………………………………..14
Пример
7 …………………………………………………………………..16
Пример
8 …………………………………………………………………..17
Пример
9 …………………………………………………………………..18
Пример
10 …………………………………………………………………23
Пример
11 …………………………………………………………………24
-
Спектральная
плотность амплитуд и фаз периодических
сигналов
……..….…………..………………………..…….………………27
Пример
12 …………………………..……………………….……………27
Пример
13 …………………………..……………………….……………29
Пример
14 …………………………..……………………….……………31
Пример
15 …………………………..……………………….……………31
Пример
16 …………………………..……………………….……………33
Пример
17 …………………………..……………………….……………34
Пример
18 …………………………..……………………….……………36
Пример
19 …………………………..……………………….……………37
-
Литература
……………………………………………………………….39 -
Задания
для расчетно-географических
работ…………..………39
Необходимые
формулы.
Применительно
к периодическому гармоническому
напряжению
можно использовать разложение в ряд
Фурье:
(1)
Простейшим
периодическим сигналом является
гармоническое колебание вида
Разложение
последовательности прямоугольных
импульсов рис. 1.1 имеет вид:
(2)
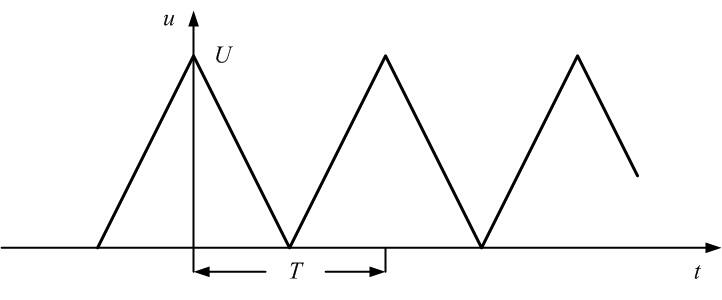
Разложение
последовательности пилообразных
импульсов рис. 1.2 имеет вид:
(3)
Две
равнозначные записи ряда Фурье:
Ряд Фурье в
комплексной форме:
Выражение
для комплексного спектра сигнала:
Ряд
Фурье периодической последовательности
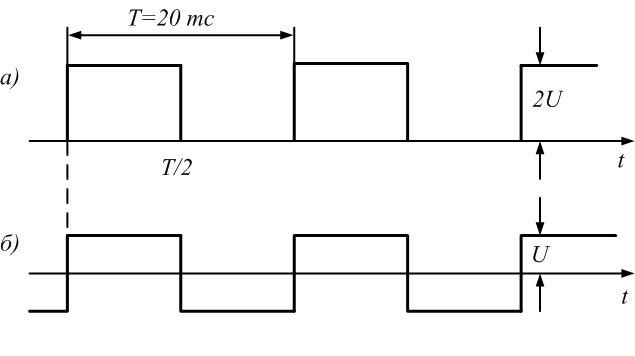
прямоугольных импульсов амплитудой U
(рис. 1.5а)
имеет вид:
Напряжение
на участках цепи находят, используя
принцип суперпозиции, например напряжение
на резисторах:
Расчет
цепи от отдельных постоянной и
гармонических составляющих напряжения
проводится в символической форме. При
этом нужно иметь в виду, что на k-й
гармонике сопротивление индуктивности

а сопротивление емкости
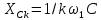
Интеграл
Фурье:
Уравнения
(10) и (11) являются основными в теории
спектров непериодических сигналов,
причем (10) называется прямым,
а (11) –
обратным
преобразованием Фурье (интегралом
Фурье).
Комплексная
придаточная функция по напряжению:
Из
выражений:
следует,
что спектральная плотность амплитуд
реакции цепи равна произведению
спектральной плотности амплитуд
воздействия АЧХ
цепи, а спектральная плотность фаз
реакции цепи равна сумме спектральной
плотности фаз
воздействия и ФЧХ
цепи.
-
Спектры амплитуд и фаз периодических сигналов.
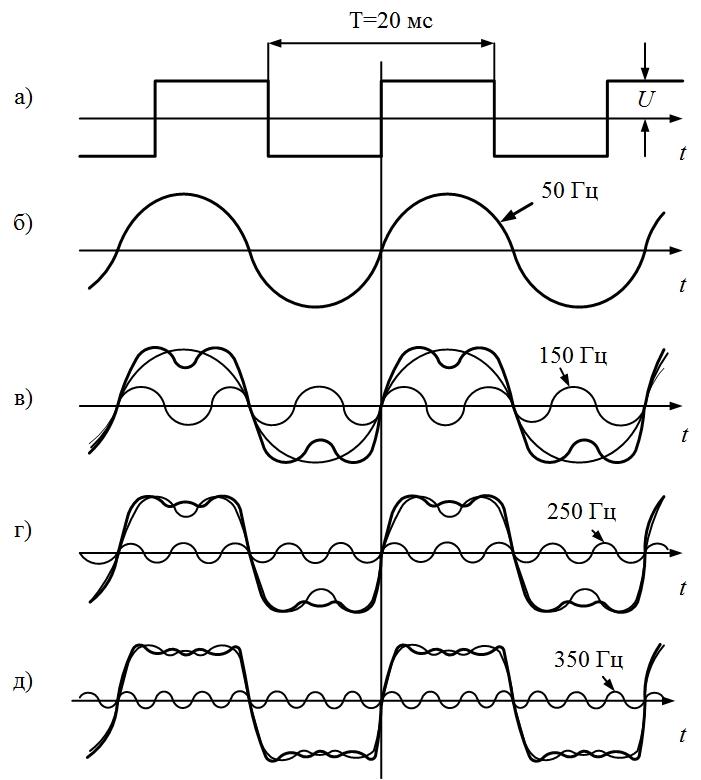
Пример
1.
Определим параметры синусоид, формирующих
последовательности прямоугольных (рис.
1.1, а) и пилообразных (рис. 1.2, а) импульсов,
имеющих амплитуду U = 10 В
и период Т = 20 мс.
а)
Для формирования периодической
последовательности прямоугольных
импульсов амплитуда основной синусоиды
должна быть
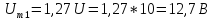
Частота
колебаний этой синусоиды обратно
пропорциональна периоду:
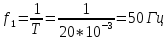
Круговая
частота

Таким образом, основная синусоида
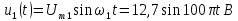
Все
последующие синусоиды в соответствии
с (2) должны иметь амплитуды в нечетное
количество раз меньшие, а частоты — в
это же нечетное количество раз большие,
чем у основной синусоиды:

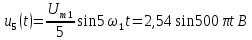
и
т.д.
Последовательность
прямоугольных импульсов, изображенных
на рис. 1.1, а,
—
это сумма синусоид:
.
Сигнал
изображен
на рис. 1.1, д.
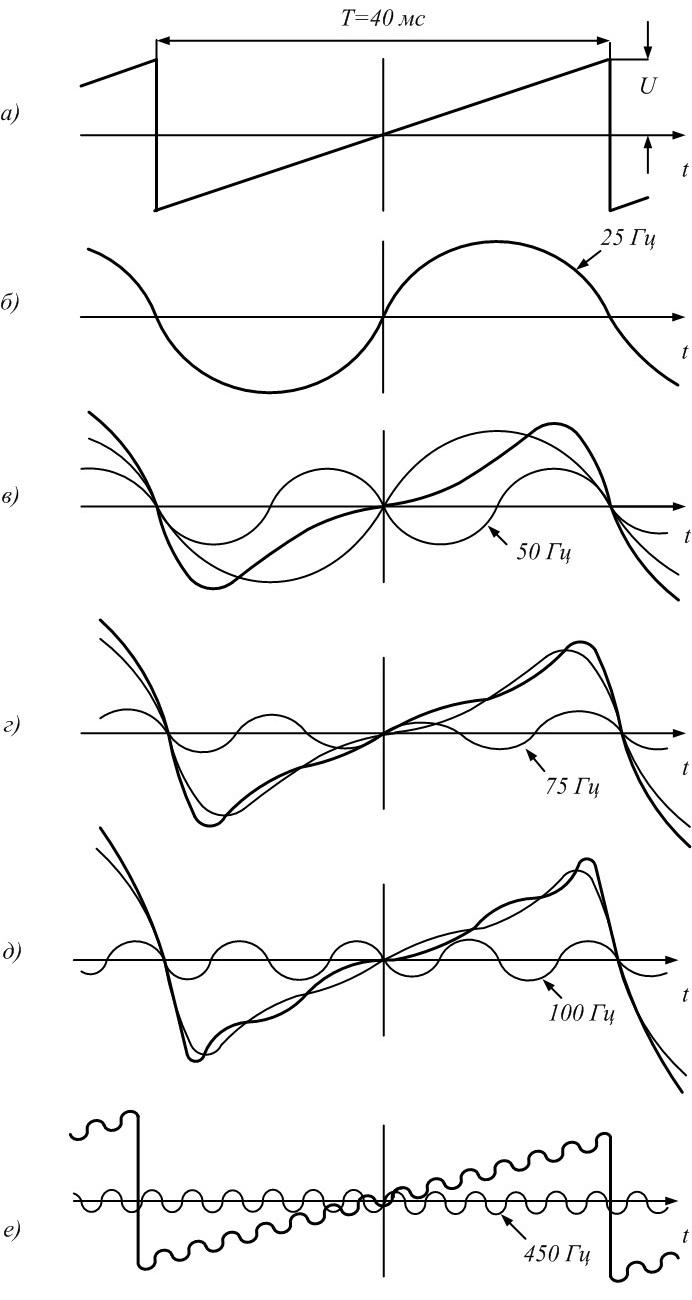
6)
Для формирования последовательности
пилообразных импульсов необходимо,
чтобы амплитуда основной синусоиды
была, как мы уже знаем [1, 3], равна
Частота
основной синусоиды

Таким
образом,
Рис.
1.1. Последовательность прямоугольных
импульсов и образующие ее синусоиды
Рис.
1.2. Последовательность пилообразных
импульсов и образующие ее синусоиды
Таблица
1.1. Ряды Фурье наиболее часто встречающихся
сигналов
|
Сигнал |
Ряд |
|
|
|
|
|
|
|
|
|
|
|
k-четные; |
|
|
k-четные; |
|
|
|
Последующие
синусоиды в соответствии с (3) будут
иметь вид
и
т.д.
Последовательность
пилообразных импульсов — это сумма
синусоид:
.
Чем
больше синусоид используется при
формировании сигнала, тем ближе его
форма к пилообразной (рис. 1.е).
Пример
2.
Определим гармонический состав
последовательности треугольных
импульсов, изображенных на рис. 1.3,
имеющих амплитуду, U
= 10 B
и период Т = 10 мс.
Периодический
сигнал на рис. 1.3 отличается от сигнала
во второй строке табл. 1.1 на величину
постоянной составляющей
Частота
основной составляющей сигнала
или
Амплитуда
основной составляющей сигнала
рассчитывается по формуле, приведенной
в табл. 1.1, или по одной из формул (1):
Четная
функция (рис. 1.3) содержит только
косинусоиды, амплитуды и частоты
которых определяются по формулам,
приведенным во второй строке табл. 1.1.
Амплитуда
и частота третьей гармоники:
Рис.
1.3. Последовательность треугольных
импульсов
Амплитуда
и частота пятой гармоники:
Амплитуда
и частота седьмой гармоники:
и
т.д.
Гармонический
состав последовательности треугольных
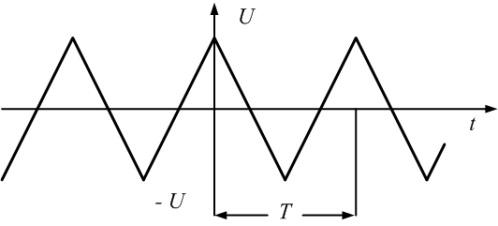
импульсов (рис.1.3) имеет вид:
Пример
3.
Представим переменное напряжение,
выпрямленное двухполупериодным
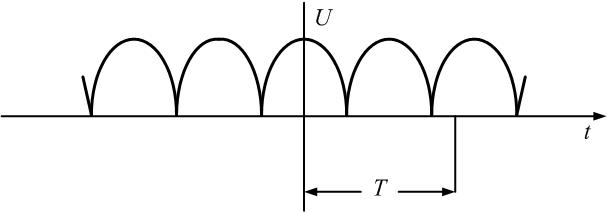
выпрямителем (пятая строка табл. 1.1),
рядом Фурье в тригонометрической форме
(5).
Из
табл. 1.1 следует, что переменное напряжение
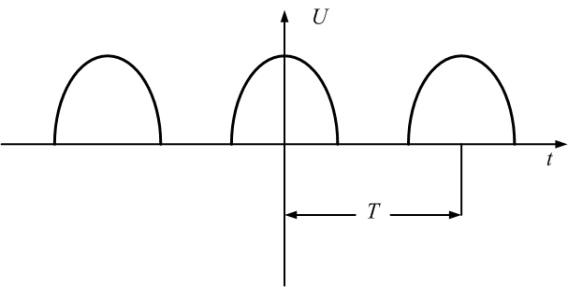
u(t) представлено рядом Фурье:
k
– четные.
Постоянная
составляющая напряжения u(
t)
рассчитывается по формуле

0,635U.
Нечетные
гармоники отсутствуют в ряде Фурье,
поскольку функция u(
t)—
четная.
Для
расчета амплитуд четных гармоник
нео6ходимо определить

1,27U.
Тогда амплитуда второй гармоники
Начальная
фаза второй гармоники равна нулю:
Амплитуда
четвертной гармоники
Фаза
четвертой гармоники
, так как в ряде Фурье перед слагаемым
стоит знак «минус».
Амплитуда
шестой гармоники
а
ее фаза, а также фазы десятой, четырнадцатой
и т.д. гармоник равны нулю.
Амплитуда
восьмой гармоники
а
ее начальная фаза, так же как и фазы
гармоник с номерами 12, 16, 20 и т.д., равна
180˚.
Тригонометрическая
форма ряда Фурье рассматриваемого
напряжения имеет вид:
.
Пример
4.
Представим ряд Фурье, полученный в
примере 3, в комплексной форме, ограничив
его восьмой гармоникой.
В
соответствии с (6) значения постоянной
составляющей и амплитуд гармоник
уменьшаются в 2 раза по сравнению со
значениями, которые 6ыли рассчитаны в
примере 3. Поэтому ряд Фурье в комплексной
форме имеет вид
Пример
5.
Построим спектр амплитуд и фаз
выпрямленного напряжения
(строка
5 табл, 1.1), имеющего амплитуду U
= 10 В и период Т = 10 мс.
При
решении примера 3 была получена
тригонометрическая форма ряда Фурье,
соответствующая выпрямленному напряжению:
.
Частота
основной составляющей сигнала
определяется
периодом колебаний:
В
спектре сигнала отсутствуют нечетные
гармоники, так как само колебание
является четной функцией. Частоты высших
гармоник с четными номерами кратны этим
номерам: частота второй гармоники равна
2
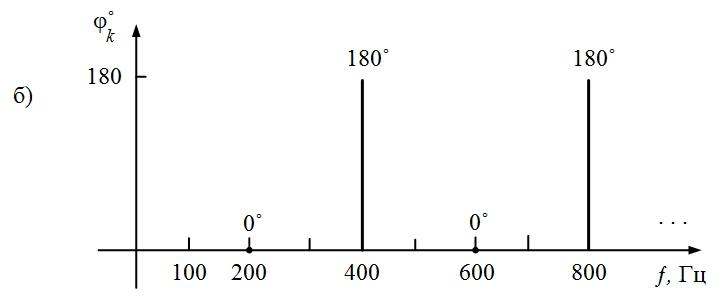
= 200 Гц, четвертой, шестой, восьмой гармоник
— 400, 600, 800 Гц соответственно и т.д.
Постоянная
составляющая
Амплитуды
четных гармоник спектра в соответствии
с выражениями, полученными для ряда
Фурье, имеют следующие значения:
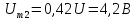

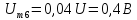
и
т.д.
Фазы
гармоник поочередно принимают значения
0 и 180˚.
Рис.
1.4. Спектры амплитуд и фаз выпрямленного
напряжения
Пример
6.
Рассмотрим периодическую последовательность
прямоугольных импульсов, показанную
на рис. 1.5, а:
Рис.
1.5. Последовательности прямоугольных
импульсов
Она
имеет постоянную составляющую, равную
в соответствии с (1)
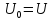
Коэффициенты
вычисляются
по формуле (1):
Здесь
6ыло учтено, что

1/Т.
Коэффициенты
вычисляются по формуле (1):
Выражение
удовлетворяет соотношению
Поэтому
Форма
ряда Фурье будет содержать только
синусоиды с нечетными гармоническими
частотами:
что,
естественно, с точностью до постоянной
составляющей U
совпадает с полученным ранее выражением
(2).
Переход
к форме ряда Фурье (5) дает
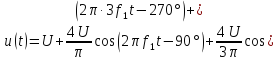
Спектр
такого сигнала без постоянной составляющей
показан на рис. 1.6:
Рис.
1.6. Спектры амплитуд и фаз сигнала рис.
1.5а
Пример
7.
Представим спектр сигнала
из примера 6 в комплексной форме.
Комплексный
спектр периодической последовательности
прямоугольных импульсов рассчитывается
по формуле (7):
Функция
имеет значения
Это
значит, что комплексный спектр
существует только для нечетных гармоник:
Заметим,
что в спектре
нет постоянной составляющей

которая рассчитывается по формуле (1) и
равна U.
Полученный
комплексный спектр
соответствует спектрам амплитуд и фаз,
изображенным на рис. 1.6.
Пример
8.
Найдем спектр последовательности
прямоугольных импульсов, изображенных
на рис. 1.7.
Сигнал,
изображенный на рис. 1.7, имеет следующие
параметры: амплитуда U
= 10 В, длительность импульса τ= 10 мс,
период повторения импульсов Т
= 40 мс, скважность q
= Т/τ = 4. Спектр этого сигнала в форме
(Табл. 1.1, строка 6) имеет вид
Постоянная
составляющая
Частота
первой гармоники
Частоты
высших гармоник кратны 100 Гц. Амплитуды
первых шести гармоник, рассчитываемые
по формуле (3.28)
имеют
следующие значения:
Фазы
первой, второй, третьей гармоник равны
0˚, фазы пятой и шестой гармоник равны
180˚, так как при расчете
и
получены отрицательные значения.
Амплитуды и фазы последующих гармоник
рассчитывают аналогичным образом.
Причем, амплитуды гармоник, кратных
скважности q, т.е. четвертой, восьмой,
двенадцатой, шестнадцатой гармоник и
т.д., равны нулю. Спектры амплитуд и фаз
сигнала, изображенного на рис. 1.7,
приведены на рис. 1.8.
Рис.
1.7. Последовательность прямоугольных
импульсов со скважностью q = 4
Рис.
1.8. Спектр последовательности прямоугольных
импульсов со скважностью q = 4
Пример
9.
Определим напряжение на резисторе
в
последовательном колебательном контуре,
на который подается последовательность
прямоугольных импульсов (рис. 1.10).
Параметры элементов контура и сигнала
заданы: R = 2 Ом; L = 0,704 мГн; С = 4 мкФ; U = 5
В; Т = 1 мс; τ = 0,5 мс.
Найдем
параметры постоянной и гармонических
составляющих сигнала (рис. 1.10),
представленного рядом Фурье (8). Частота
первой гармоники
или
Частоты
третьей, пятой и т.д. гармоник равны
соответственно: 3
= 18,84 рад/с; 3
= 3 кГц; 5
= 31,4 рад/с; 5
= 5 кГц; … .
Амплитуды
четных гармоник равны нулю. Амплитуды
нечетных гармоник рассчитываются по
формуле (1):
.
Ряд
Фурье сигнала имеет вид:
Рис.
1.9. Последовательный колебательный
контур с источником периодического
сигнала
Рис.
1. 10. Последовательность прямоугольных
импульсов
Определим
резонансную частоту
и
контура
(рис. 1.9):
Резонанс
в контуре наступает на частоте третьей
гармоники входного напряжения.
Добротность
контура
Определим
гармонические составляющие тока в цепи
и напряжения на резисторе в каждой из
составляющих ряда Фурье схем, изображенных
на рис. 1.9.
Схема
последовательного колебательного
контура с источником постоянного
напряжения

= 2,5 В приведена на рис. 1.11. В этой цепи
сопротивление индуктивности равно
нулю, а сопротивление конденсатора
равно бесконечности, поэтому
= 0;
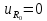
В
цепи, изображенной на рис. 1.12, в контур
включен источник напряжения, соответствующий
напряжению первой гармоники. Синусоидальное
напряжение
заменено
на комплексное

На частоте
= 1 кГц (
)
сопротивление индуктивности
а
сопротивление емкости
Рис.
1.11. Контур с источником постоянного
напряжения
Рис.
1.12. Контур с источником напряжения
первой гармоники
Комплексное
сопротивление цепи
Определим
комплексные значения тока
и напряжение
:
Это
соответствует составляющей синусоидального
напряжения (9) в исходной цепи:
На
третьей гармонике синусоидальный
источник заменяется источником
комплексного напряжения
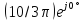
В результате имеем цепь, изображенную
на рис. 1.13.
На
частоте
= 3 кГц (
)
в цепи наступает резонанс напряжений.
Сопротивления индуктивности и емкости
равны по величине и противоположны по
знаку:
Комплексное
сопротивление цепи
= R = 2 Ом. Ток
Рис.
1.13. Контур с источником третьей гармоники
Рис.
1.14. Контур с источником напряжения
пятой гармоники
Напряжение
на резисторе
равно входному напряжению:

пятой гармонике синусоидальный источник
заменяется
источником комплексного напряжения
(рис. 1.14). На частоте
= 5 кГц (
)
сопротивления индуктивности и емкости
равны соответственно
и
Комплексное
сопротивление цепи
рассчитаем
по формуле:
Напряжение
на резисторе
Таким
образом, ряд Фурье напряжения на резисторе
имеет вид,
Рис.
1.15. Спектры амплитуд и фаз входного
напряжения и напряжения на резисторе
в колебательном контуре
Спектры
амплитуд и фаз этого напряжения изображены
на рис. 1.15
( 6, в).
Анализ спектра
показывает, что колебательный контур
выделил третью гармонику из входной
последовательности и подавил остальные
гармоники, т.е. явление резонанса можно
использовать для, выделения отдельных
гармоник из периодического несинусоидального
сигнала.
Пример
10.
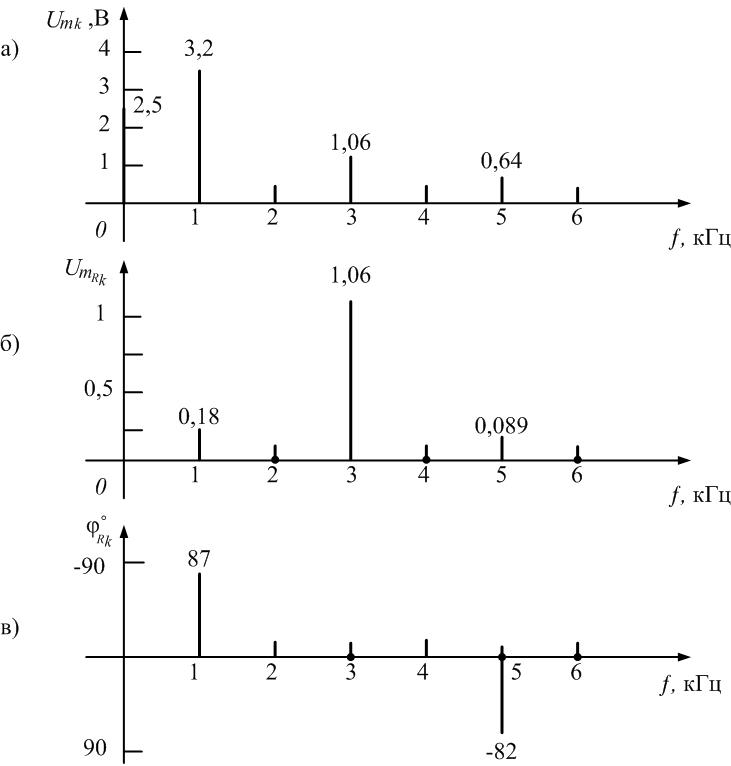
Сравним спектры амплитуд (рис. 1.15) входной
последовательности прямоугольных
импульсов
и напряжения
на резисторе колебательного контура
из примера 9, чтобы определить коэффициенты
передачи по напряжению цепи на частотах
гармоник.
В
соответствии с формулой и рис. 1.15 (а),
постоянная составляющая
в спектре напряжения
равна 2,5 В. Амплитуды первой, третьей и
пятой гармоник имеют значения:
Постоянная
составляющая в спектре напряжения
на резисторе (рис. 3.15, б)
равна нулю, а амплитуды нечетных гармоник
равны соответственно
Коэффициенты
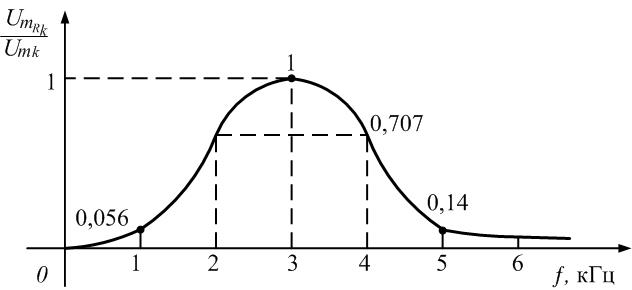
передачи по напряжению
на частотах гармоник рассчитаем по
формуле
На
частоте f
= 0 кГц получаем
= 0/2,5 = 0. На частоте f
= 1 кГц (частота основной составляющей)
= 0,18/3,2 = 0,056.
Рис.
1.16. Коэффициенты передачи по напряжению
на резисторе R на частотах гармоник
На
частоте
f=3
кГц (третья гармоника)
= 1,06/1,06 = 1.
На
частоте f=
5 кГц (пятая гармоника)
= 0,089/0,64= 0,14.
На
рис. 1.16 приведен график зависимости
коэффициента передачи контура от частоты
гармоник. На частоте резонанса коэффициент
передачи максимален и равен 1. На частотах
первой и пятой гармоник коэффициент
передачи резко уменьшается.
Пример
11.
Определим спектр амплитуд напряжения
на резисторе в цепи, изображенной на
рис. 1.17, а,
на вход которой поступает периодическая
последовательность прямоугольных
импульсов (рис. 1.17, б),
если заданы R
= 50 Ом, L
= 10 мГн, U
= 10 В, τ = 1 мс, Т = 4 мс.
Рис.
1.17. RL-цепь
и сигнал на ее входе
Найдем
комплексный спектр входного сигнала
u(t),
воспользовавшись (7):
Применив
формулу Эйлера, получим
Вычислим
амплитуды спектральных составляющих
Амплитуда
постоянной составляющей
Частота
основной составляющей
а
ее амплитуда
Аналогичным
образом определяются частоты и амплитуды
высших гармоник:
|
При |
k=2 |
2 |
|
|
k=3 |
3 |
|
|
|
k=4 |
4 |
|
|
|
k=5 |
5 |
|
|
|
k=6 |
6 |
|
|
|
k=7 |
7 |
|
|
|
k=8 |
8 |
|
|
|
k=9 |
9 |
|
|
|
k=10 |
10 |
|
Спектр
амплитуд
входного сигнала изображен на рис.
1.18, а.
Огибающая спектра амплитуд прямоугольных
импульсов изменяется по закону

нули спектра расположены на частотах,
кратных
=1 кГц (четвертая, восьмая, двенадцатая
и т.д. гармоники). Комплексная передаточная
функция цепи (рис. 1.17, а) определяется
по формуле
|
При |
k=0 |
|
|
k=1 |
|
|
|
k=2 |
|
|
|
k=3 |
|
|
|
k=4 |
|
|
|
k=5 |
|
|
|
k=6 |
|
|
|
k=7 |
|
|
|
k=8 |
|
|
|
k=9 |
|
|
|
k=10 |
|
Рис.
1.18. Спектры амплитуд последовательности
прямоугольных импульсов и напряжения
на резисторе в RL-цепи
и коэффициенты передачи цепи
График
зависимости коэффициента передачи
RL-цепи
от частоты изображен на рис. 3.18 (б).
Спектр
амплитуд
напряжения на резисторе, рассчитываем
в виде:
принимает
значения:
и
приведен на рис. 1.18 (в).
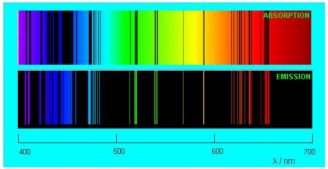
Если пропустить солнечный свет через стеклянную призму или дифракционную решётку, то на экране получится хорошо известный нам спектр. Спектр, который вы видите ниже, называется непрерывным спектром. Он представляет собой сплошную полосу, состоящую из разных цветов, плавно переходящих друг в друга.
Непрерывный (сплошной) спектр — разновидность спектра, в которой присутствуют все длины волн видимого диапазона (от красной границы до фиолетовой).
Излучения, обладающие непрерывным спектром:
- свет, излучаемый Солнцем;
- искусственный свет от лампы дневного освещения;
- любые твердые и жидкие тела, плотные газы, нагретые до высокой температуры.
Пример №1. Будет ли излучать свет в непрерывном спектре спираль работающей электроплиты?
В данном случае да, поскольку спирать — твердое тело, нагретое до высокой температуры.
Линейчатый спектр и его виды
Картина резко меняется, когда мы наблюдаем свечение, излучаемое разреженными газами. Спектр перестает быть непрерывным: в нём появляются разрывы, которые увеличиваются по мере разрежения газа. В предельном случае чрезвычайно разреженного атомарного газа спектр становится линейчатым.
Линейчатый спектр — спектр, который состоит из отдельных достаточно тонких линий.
Линейчатый спектр бывает двух видов:
- спектр испускания;
- спектр поглощения.
Спектр испускания
Предположим, что газ состоит из атомов некоторого химического элемента и разрежен настолько, что атомы почти не взаимодействуют друг с другом. Раскладывая в спектр излучение такого газа (нагретого до очень высокой температуры), мы сможем наблюдать такую картину, как на картинке ниже.
Спектр испускания — линейчатый спектр, который состоит из тонких изолированных разноцветных линий, соответствующих тем длинам волн света, который излучается атомами.
Любой атомарный разреженный газ излучает свет с линейчатым спектром. Но наибольшую важность имеет то, что для любого химического элемента спектр испускания является уникальным. Поэтому по нему можно устанавливать, какой химический элемент находится перед нами. Он является своего рода идентификатором.
Поскольку газ разрежен и атомы мало взаимодействуют друг с другом, мы можем сделать следующий вывод:
Свет излучают атомы сами по себе. Следовательно, каждый атом характеризуется дискретным, строго определённым набором длин волн излучаемого света. У каждого химического элемента этот набор свой.
Спектр поглощения
Атомы излучают свет в процессе перехода из возбуждённого состояния в основное. Но вещество может не только излучать, но и поглощать свет. При поглощении света атом совершает обратный процесс — он переходит из основного состояния в возбуждённое.
Снова рассмотрим разреженный атомарный газ, но теперь в охлажденном состоянии (при довольно низкой температуре). Свечения газа в этом случае мы не увидим. В не нагретом состоянии газ не излучает свечение, так как атомов в возбуждённом состоянии оказывается для этого слишком мало.
Если сквозь охлажденный газ пропустить свет с непрерывным спектром, мы увидим следующую картину (см. рисунок ниже).
Спектр поглощения — темные линии на фоне непрерывного спектра, соответствующие тем длинам волн света, которые поглощаются атомами и излучаются впоследствии при сильном нагревании.
Объясним, откуда берутся темные линии. Под действием падающего света газовые атомы переходят в возбуждённое состояние. При этом оказывается, что для возбуждения атомов нужны не любые длины волн, а лишь некоторые, строго определённые для данного вида газа. Именно эти длины волн газ поглощает из падающего на него света.
Внимание! Газ поглощает те длины волн, которые излучает сам. Поэтому, цветные линии на спектре испускания соответствуют темным линиям на спектре поглощения. Если их сложить, можно получить непрерывный спектр.
На рисунке ниже сопоставлены спектры испускания и поглощения разреженных паров натрия.
Глядя на спектры испускания и поглощения, ученые XIX века пришли к выводу, что атом не является неделимой частицей и обладает некоторой внутренней структурой. Ведь что-то внутри атома должно обеспечивать процессы излучения и поглощения света.
Кроме того, уникальность атомных спектров говорит о том, что этот механизм различен у атомов разных химических элементов. Поэтому атомы разных химических элементов должны отличаться по своему внутреннему устройству.
Спектральный анализ
Использование линейчатых спектров в качестве идентификаторов химических элементов лежит в основе спектрального анализа.
Спектральный анализ — метода исследования химического состава вещества по его спектру.
Идея спектрального анализа заключается в следующем. Спектр излучения исследуемого вещества сопоставляется с эталонными спектрами химических элементов. Затем делается вывод о присутствии или отсутствии различных химических элементов в исследуемом образце. При определённых условиях посредством спектрального анализа можно определить химический состав не только качественно, но и количественно.
В результате наблюдения различных спектров были открыты новые химические элементы. Первыми из таких элементов были цезий и рубидий. Названия эти элементы получили по цвету линий своего спектра. Так, в спектре цезия больше всего выражены две линии небесно-синего цвета, который на латинском языке звучит как caesius. Рубидий же даёт две отчетливые линии рубинового цвета.
В 1868 году в спектре солнечного света были обнаружены линии, не соответствующие ни одному из известных химических элементов. Этот элемент был назван гелием (от греческого гелиос — солнце). Впоследствии гелий был найден в атмосфере нашей планеты. Спектральный анализ излучения Солнца и других звезд показал, что все входящие в их состав входят элементы имеются и на Земле. Таким образом, оказалось, что все объекты Вселенной собраны из одного и того же набора элементов.
Пример №2. Какую картинку можно получить, если провести спектральный анализ вещества, состоящего из двух химических элементов?
Спектры испускания и спектры поглощения будут накладываться друг на друга. В итоге можно будет получить спектр испускания, в котором будут присутствовать все длины волн, соответствующие тем, что испускаются первым и вторым химическим элементом. В спектре поглощения эти же длины волн будут отсутствовать.
Задание EF18348
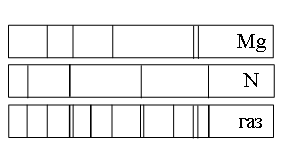
Ответ:
а) азота (N), магния (Mg) и другого неизвестного вещества
б) только азота (N)
в) только магния (Mg)
г) только магния (Mg) и азота (N)
Алгоритм решения
- Определить, при каком условии можно считать, что данный химический элемент входит в состав неизвестного газа.
- Сравнить спектр поглощения неизвестного газа и магния. Сделать вывод о том, присутствует ли магний в газе.
- Сравнить спектр поглощения неизвестного газа и азота. Сделать вывод о том, присутствует ли азот в газе.
- Установить, содержит ли неизвестный газ какие-либо еще элементы.
Решение
Если спектр поглощения неизвестного газа содержит все линии, которые есть на спектре известного элемента, то этот газ содержит этот элемент.
Видно, что спектр поглощения неизвестного газа включает в себя все линии, которые есть в спектре поглощения магния. Следовательно, этот газ содержит магний.
Видно, что спектр поглощения неизвестного газа включает в себя все линии, которые есть в спектре поглощения азота. Следовательно, этот газ также содержит азот.
Но кроме линий, соответствующих азоту и магнию, на спектре поглощения газа наблюдаются другие линии. Следовательно, газ содержит как минимум еще один элемент.
Ответ: а
pазбирался: Алиса Никитина | обсудить разбор
Задание EF18254
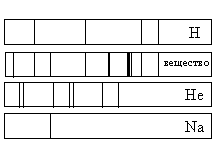
Ответ:
а) только натрий (Na) и водород (Н)
б) только водород (Н) и гелий (Не)
в) водород (Н), гелий (Не) и натрий (Na)
г) натрий (Na), водород (H) и другие элементы, но не гелий (He)
Алгоритм решения
- Определить, при каком условии можно считать, что данный химический элемент входит в состав неизвестного газа.
- Сравнить спектр поглощения неизвестного вещества и водорода. Сделать вывод о том, присутствует ли водород в веществе.
- Сравнить спектр поглощения неизвестного вещества и гелия. Сделать вывод о том, присутствует ли гелий в веществе.
- Сравнить спектр поглощения неизвестного вещества и натрия. Сделать вывод о том, присутствует ли натрий в веществе.
- Установить, содержит ли неизвестный газ какие-либо еще элементы.
Решение
Если спектр поглощения неизвестного газа содержит все линии, которые есть на спектре известного элемента, то этот газ содержит данный элемент.
Видно, что спектр поглощения неизвестного вещества включает в себя все линии, которые есть в спектре поглощения водорода и натрия. Но линий, соответствующих спектру поглощения гелия, в нем нет. Следовательно, это вещество содержит водород, натрий, но не содержит гелий.
Кроме линий, соответствующих водороду и натрию, на спектре поглощения вещества наблюдаются другие линии. Следовательно, оно содержит как минимум еще один элемент.
Ответ: г
pазбирался: Алиса Никитина | обсудить разбор
Задание EF17744

Можно утверждать, что в неизвестном образце
Ответ:
а) не содержится стронция
б) не содержится кальция
в) содержатся кальций и ещё какие-то элементы
г) содержится только кальций
Алгоритм решения
- Определить, при каком условии можно считать, что данный химический элемент входит в состав неизвестного образца.
- Сравнить спектр излучения неизвестного образца и стронция. Сделать вывод о том, присутствует ли стронций в составе образца.
- Сравнить спектр излучения неизвестного образца и кальция. Сделать вывод о том, присутствует ли кальций в составе образца.
- Установить, содержит ли неизвестный газ какие-либо еще элементы.
- Выбрать подходящее утверждение.
Решение
Если спектр излучения неизвестного образца содержит все линии, которые есть на спектре излучения известного элемента, то этот образец содержит данный элемент.
Видно, что спектр излучения неизвестного образца включает в себя все линии, которые есть в спектре излучения стронция. Но линий, соответствующих спектру излучения кальция, в нем нет. Следовательно, этот образец не содержит кальций.
Кроме линий, соответствующих стронцию, на спектре излучения неизвестного образца наблюдаются другие линии. Следовательно, он содержит как минимум еще один элемент.
Из всех перечисленных утверждений верным является только одно — образец не содержит кальция.
Ответ: б
pазбирался: Алиса Никитина | обсудить разбор
Алиса Никитина | Просмотров: 6.6k
Любой сигнал можно разложить на составляющие. Такое разложение сигнала называется спектральным. При этом сигнал можно представить в виде графика зависимости параметров сигнала от частоты, такая диаграмма называется спектральной или спектром сигнала.
Спектр сигнала — это совокупность простых составляющих сигнала с определенными амплитудами, частотами и начальными фазами.
Между спектром сигнала и его формой существует жесткая взаимосвязь: изменение формы сигнала приводит к изменению его спектра и наоборот, любое изменение спектра сигнала приводит к изменению его формы. Это важно запомнить, поскольку при передаче сигналов в системе передачи, они подвергаются преобразованиям, а значит, происходит преобразование их спектров.
Различают два вида спектральных диаграмм:
— спектральная диаграмма амплитуд;
— спектральная диаграмма фаз.
В спектральной диаграмме амплитуд — отображаются все составляющие со своими амплитудами и частотами.
В спектральной диаграмме фаз — отображаются все составляющие со своими начальными фазами и частотами.
Любой сигнал имеет одну спектральную диаграмму амплитуд и одну спектральную диаграмму фаз, в составе которых может содержаться множество составляющих.
Не зависимо от того, какой спектр (амплитуд или фаз), он изображается в виде множества линий — составляющих. В спектре амплитуд высота спектральной линии равна амплитуде составляющей сигнала, а в спектре фаз — начальной фазе составляющей. Причем: в спектре амплитуд все составляющие имеют положительные значения, а в спектре фаз как положительные, так и отрицательные. Если амплитуда спектральной составляющей имеет отрицательный знак, то в спектре амплитуд она берется по модулю, а в спектре фаз знак составляющей изменяется на противоположный.
Классификация спектров сигналов.
1. По виду спектры бывают дискретными (линейчатыми) или сплошными.
Дискретным является спектр, у которого можно выделить отдельные составляющие.
Сплошным является спектр, у которого нельзя выделить отдельные составляющие, так как они расположены настолько близко, что сливаются друг с другом.
2. По диапазону частот различают спектры ограниченные и неограниченные.
Ограниченным является спектр, у которого вся энергия сигнала (все спектральные составляющие) находятся в ограниченном диапазоне частот (fmax ? ?).
Неограниченным является спектр, у которого вся энергия сигнала находится в неограниченном диапазоне частот (fmax ? ?). На практике такие спектры ограничивают.
Спектральное представление периодических сигналов
1. Гармоническое колебание.
Математическая модель гармонического колебания имеет вид:
u(t)=Ums sin (?st+?s) (11)
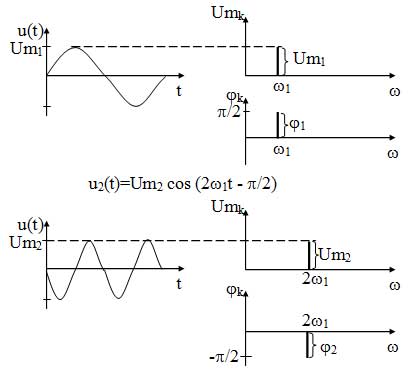
Как видно из математической модели, в спектре данного колебания присутствует одна гармоническая составляющая, которая находится на частоте ?s. Высота составляющей в спектре амплитуд равна амплитуде колебания Ums, а в спектре фаз — начальной фазе колебания ?s. Причем при построении спектра необходимо учитывать связь между временной диаграммой сигнала и спектром амплитуд. Амплитуда составляющей спектра должна по высоте соответствовать амплитуде колебания на временной диаграмме.
Необходимо отметить, что при увеличении частоты сигнала, его составляющая будет удаляться по оси частот от нуля (рисунок 13).
Рисунок 13 — Спектральное представление гармонических колебаний
Как видно из рисунков, спектр гармонического колебания является дискретным и ограниченным.
2. Периодические, негармонические сигналы.
Основной особенностью спектрального представления таких сигналов является наличие в их спектре множества спектральных составляющих. Такие сигналы могут быть описаны рядом Фурье, согласно которому:
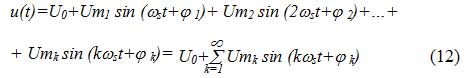
Преобразуем данный ряд, используя тригонометрическое свойство
sin(x+y) = sin x cos y + cos x sin y (13)
Полагая что x=?k и y=k?ct получим:

Umk sin ? k = ak; Umk cos ?k = bk (15)
Тогда ряд примет вид:
Параметры ряда можно определить через коэффициенты ak и bk:
где k=1, 2, 3 …
Амплитуда постоянной составляющей и коэффициенты могут быть определены через значение сигнала u(t):

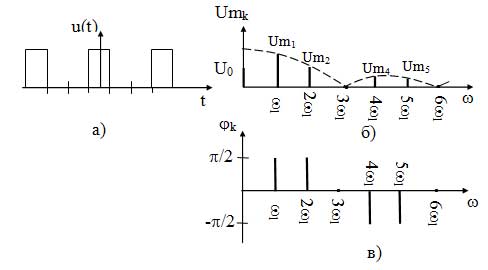
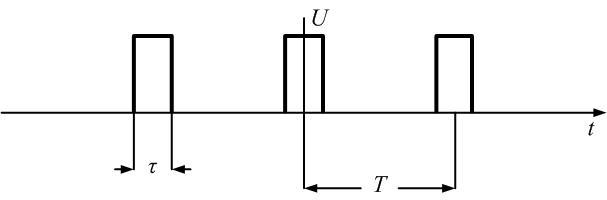
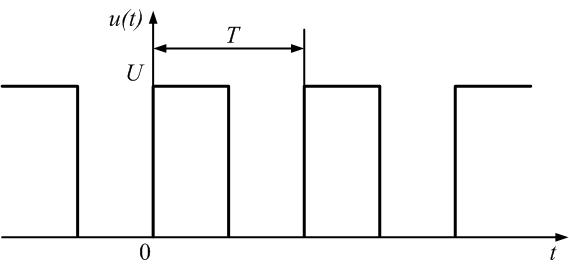
Рассмотрим спектральное представление периодических, негармонических сигналов на примере периодической последовательности прямоугольных импульсов (ПППИ).
При построении спектра необходимо рассчитать следующие параметры:
а) скважность сигнала:
q = T/?и (21)
б) значение постоянной составляющей:
U0=Ums/q (22)
I0=Ims/q
в) частоту первой гармоники спектра, которая равна частоте сигнала:
f1=fs=1/T (23)
г) амплитуды гармонических составляющих спектра:
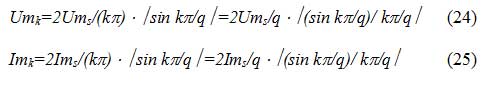
1. Все гармонические составляющие находятся на частотах, кратных частоте первой гармоники (2?1, 3?1, 4?1 и т. д.);
2. Для спектра амплитуд:
а) спектр ПППИ имеет лепестковый характер, т. е. в спектре можно выделить множество «лепестков»;
б) количество гармонических составляющих в лепестке зависит от скважности и равно q — 1;
в) амплитуды гармонических составляющих, находящихся на частотах, кратных скважности, равны нулю;
г) форма спектра обозначается огибающей — пунктирной линией, плавно соединяющей вершины гармонических составляющих;
д) точка, из которой исходит огибающая, равна 2U0 или 2I0.
3. Для спектра фаз:
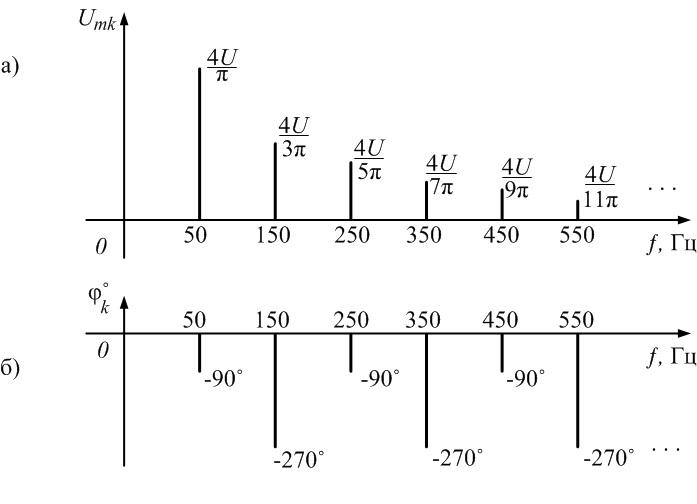
а) все гармонические составляющие, на частотах, не кратных скважности, имеют одинаковую высоту, равную ?/2 (90°);
б) все гармонические составляющие в одном лепестке имеют одинаковый знак, а в соседних противоположный.
в) составляющие на частотах кратных скважности имеют начальную фазу равную нулю.
Спектры ПППИ при скважности q=3 представлены на рисунке 14.
Как видно из диаграмм спектр ПППИ является дискретным и неограниченным. Поэтому за ширину спектра принимают диапазон частот, в пределах которого находится два первых лепестка, т. к. в них содержится около 95% энергии сигнала:
?fs = 2/?и. (26)
Рисунок 14 — Спектральное представление ПППИ: а) временная диаграмма; б) спектральная диаграмма амплитуд; в) спектральная диаграмма фаз
Как видно из формулы ширина спектра ПППИ зависит только от длительности импульса и не зависит от его периода.
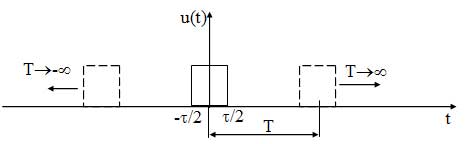
3. Непериодические сигналы.
Поскольку в непериодических сигналах нельзя выделить период, т. к. Т??, то рассчитать и построить спектр тем же методом, что и для периодических сигналов нельзя. Однако знать спектр таких сигналов необходимо, т. к. все информационные сигналы являются непериодическими. Для построения спектра непериодического сигнала производят следующую процедуру: сигнал мысленно представляют как периодический с произвольным периодом, ддля которого строят спектр. Затем осуществляют предельный переход устремляя период к бесконечности (Т??) (рисунок 15). При этом частота первой гармоники и, соответственно, расстояние между гармоническими составляющими стремится к нулю (f1=1/Т), поэтому все составляющие сливаются друг с другом и образуют сплошной спектр.
Рисунок 15 — Импульсный сигнал u(t) и его представление периодическим сигналом
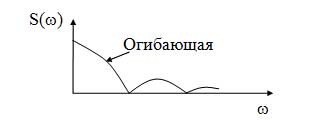
Форма спектра непериодических сигналов обозначается огибающей (сплошной линией) (рисунок 16).
Рисунок 16 — Спектральная диаграмма непериодического сигнала
Ряд Фурье, для таких сигналов, также нельзя записать, т. к. в этом случае амплитуда постоянной составляющей и коэффициенты ak и bk равны нулю. В этом случае значение сигнала в любой момент времени также равно нулю, что является не верным. Поэтому для таких сигналов используют преобразования Фурье:
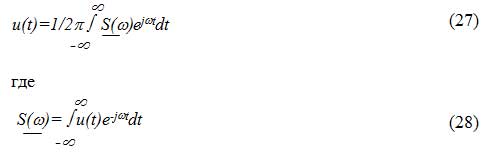
Величина S(?) является комплексной спектральной плотностью непериодического сигнала u(t). Она равна:
S(?) = S(?)e ^(-j?(?)) (29)
где S(?) спектральная плотность амплитуд или амплитудный спектр непериодического сигнала, а ?(?) — фазовый спектр непериодического сигнала.
Спектральная плотность амплитуд непериодического сигнала на любой частоте ? равна суммарной амплитуде составляющих находящихся в малой полосе ?? в окрестностях частоты ? пересчитанных на 1 Герц.
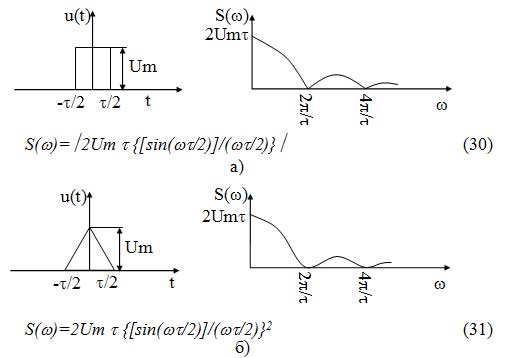
Временные диаграммы и спектральные плотности амплитуд для прямоугольного и треугольного импульсов представлены на рисунке 18:
Рисунок 18 — Спектральное представление непериодических сигналов: а) прямоугольный импульс; б) треугольный импульс

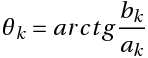

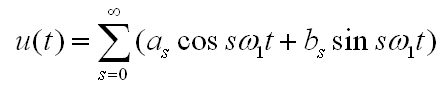

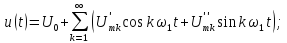
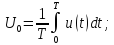
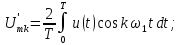

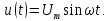
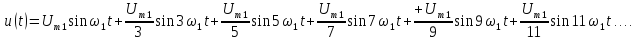
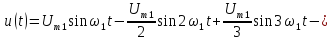
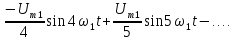


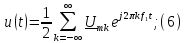

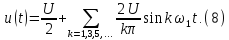

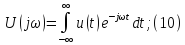
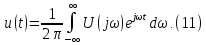
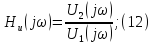
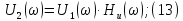
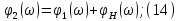


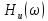
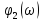

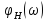

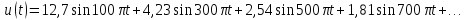

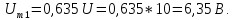



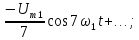
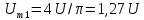
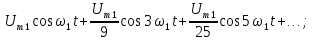


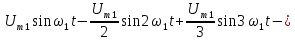

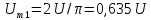
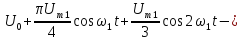
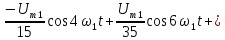


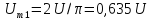
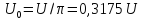
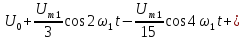

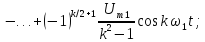
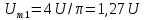

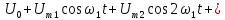
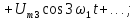
 ;
; ;
;
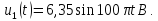

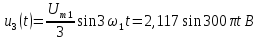
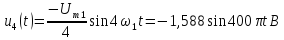
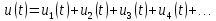

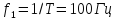
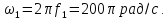
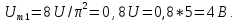



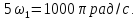
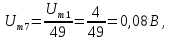


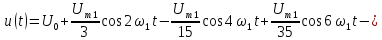

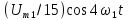


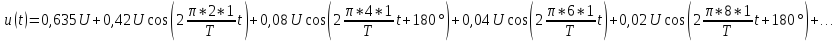
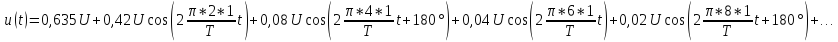
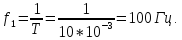
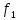
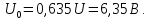


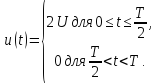
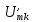



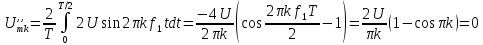
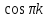
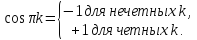
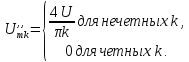
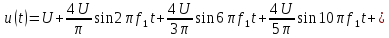








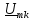
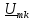
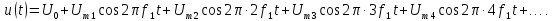
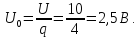

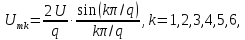

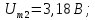

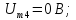
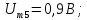
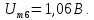
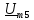


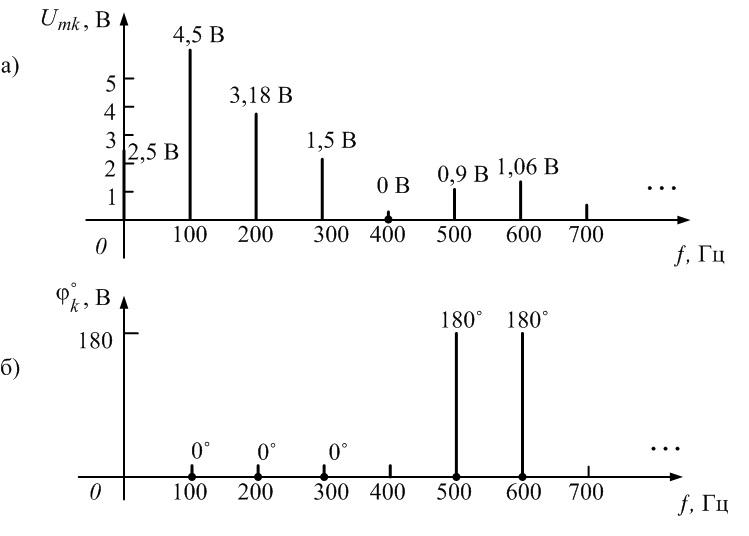
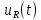
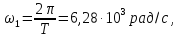
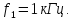

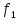



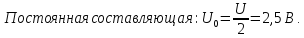
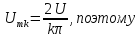
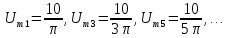

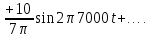

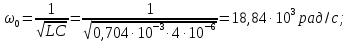



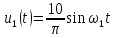
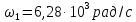
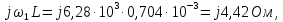
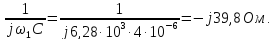


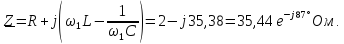






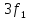
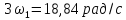


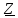

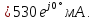




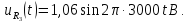
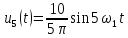





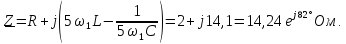
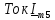
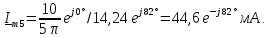
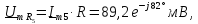
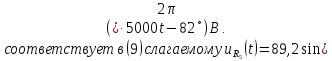

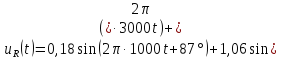

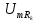
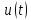

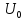

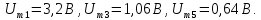
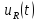
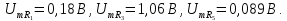

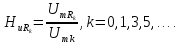

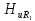
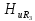
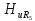

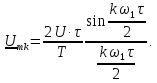
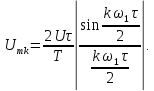
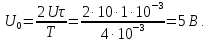

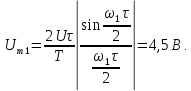
 =0,5
=0,5 =3,28
=3,28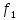 =0,75
=0,75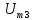 =1,5
=1,5 =1
=1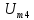 =0
=0 =1,25
=1,25 =0,9
=0,9 =1,5
=1,5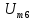 =1,06
=1,06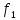 =1,75
=1,75 =0,64
=0,64 =2,0
=2,0 =0
=0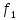 =2,25
=2,25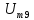 =0,5
=0,5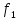 =2,5
=2,5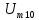 =0,64
=0,64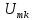

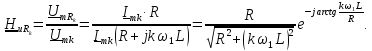
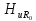 =1;
=1; =0,95;
=0,95;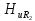 =0,85;
=0,85;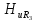 =0,73;
=0,73; =0,62;
=0,62; =0,54;
=0,54;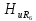 =0,47;
=0,47;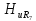 =0,41;
=0,41;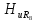 =0,37;
=0,37;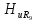 =0,33;
=0,33; =0,3.
=0,3.