Способы задания множеств
I. Перечисление
(список элементов).
II. Порождающая
процедура.
III. Разрешающая
процедура (описание характеристических
свойств, которыми должны обладать
элементы).
I. Задание множества списком
Списком можно
задать лишь множества, содержащие
несколько элементов. Задание типа
N = 1, 2, 3 . . .
не список, а условное
обозначение, допустимое, когда оно
заведомо не вызывает разногласий.
Пример:
Определим А как
множество все целых чисел х строго
между 6 и 10. Это можно записать следующим
образом:
и прочитать как :
“А —
множество, содержащее 7, 8, 9”.
Множества часто
рассматриваются как “неупорядоченные
совокупности элементов”, хотя иногда
полезно подчеркнуть, что, например,
.
Мы не делаем никакой
оговорки о порядке,
в котором рассматриваются элементы,
поэтому было бы неправильно
допускать какой-либо определенный
порядок.
Выясним далее,
какие из приведенных определений верные:
.
Если число членов
множества В легко вычисляется, и среди
элементов множества нет повторений, то
определение верно.
Множество С также
выглядит правильным, за исключением
лишь того, что число 6 повторяется дважды.
Мы можем проверить, принадлежит ли
элемент или нет. Таким образом, это
наиболее важное требование в определении
множества выполнено. Следовательно, мы
можем рассматривать эту запись как
верную и эквивалентную
.
Однако в этой ситуации возникают
следующие проблемы. Если мы рассмотрим
первоначальное определение С
и выбросим
одно из чисел 6 из множества, то мы,
очевидно, будем иметь
и
.
Возникает противоречие. Поэтому мы
будем рассматривать повторение символов
в определении множеств как упоминание
одного и того же символа, а его дублирование
как недосмотр.
Определение D также
справедливо. Заметим, что это множество
множеств, такое, что оно имеет только
два элемента, в частности,
,
даже еслии
.
Это легко проверить, так каки только В и С являются элементами D.
II. Порождающая процедура
Описывает способ
получения элементов множества из уже
полученных элементов либо других
объектов. Тогда элементы множества —
все объекты, которые могут быть получены
(построены) с помощью такой процедуры.
Примеры:
1) Описание
множества
(множество всех чисел вида
),
где исходные объекты для построения
множества — натуральные числа, а
порождающая процедура для вычисления
описана формулой.
2) Множество
Порождающая
процедура определяется двумя правилами:
а) ;
б) если,
то.
Правила, описанные
таким образом, называются индуктивными
или рекурсивными.
3) Множество
,
заданное следующим образом.
Пусть имеется
процедура вычисления цифр разложения
числа
в бесконечную десятичную дробь
= 3,1415926536 . . .
По мере вычисления
будем образовывать из последовательности
цифр данной десятичной дроби трехзначные
числа
314, 159, 265 и т. д.
Множество всех
таких чисел образует множество
.
4) Распространенная
порождающая процедура — образование
новых множеств из других множеств с
помощью операций над множествами.
III. Задание множества описанием его элементов (разрешающая процедура)
Примеры:
— множество всех
натуральных чисел (N).
— множество всех
решений уравнения
.
— множество всех
действительных чисел.
— множество всех
чисел
,
гдеможно интерпретировать как описание
свойства его элементов, заключающегося
в возможности представить их в виде.
—
заданное как “множество всех целых
чисел, являющихся степенью двойки”,
.
Такой способ задания множества
применяется, когда свойство элементов
М может быть описано коротким выражением.
Например, P(x) читается: «х обладает
свойством Р», то М задается при помощи
обозначениячитается:
«М — множество элементов х, обладающих
свойством Р».
Пример:
1) .
2) .
Требования к
описанию свойств
— точность и недвусмысленность.
Пример:
Множество всех
красивых первокурсниц математического
факультета 2002 г. не строго определено,
так как у разных людей – различные
критерии отбора.
Надежный способ
точно описать свойства элементов данного
множества — задание распознающей
(разрешающей)
процедуры, которая для любого объекта
устанавливает, обладает он свойством
или нет (т. е. является элементом
множества или нет).
Пример:
Для
,
то есть для свойства, быть степенью
двойкиразрешающей
процедурой
является любой метод
разложения целых
чисел на простые множители. Здесь
разрешающая процедура не является
порождающей. Но ее нетрудно таковой
сделать: например, порождающая процедура
может быть таковой. Берем последовательно
все натуральные числа и каждые из них
разлагаем на простые множители: те
числа, которые не содержат множителей,
отличных от двойки, включаем в
.
С другой стороны
порождающая процедура может не быть
разрешающей. Например, при получении
действует порождающая процедура. Но с
ее помощью нельзя определить, будет ли
произвольное трехзначное число
принадлежатьили нет, т. е. множество
бесконечно, и если при построении
n — чисел множества некоторое
(проверяемое) число не встретилось, то
еще нельзя утверждать, что оно не
принадлежит.
Обобщение:
Суть
порождающей процедуры в том, что с ее
помощью из уже полученных элементов
множества или других объектов получают
(или могут получить) все последующие
элементы.
Суть
разрешающей процедуры в том, что она
разрешает (или не разрешает) предложенному
для проверки объекту быть или не быть
элементом данного множества в зависимости
от его свойств.
Понятие “точно
заданное множество” нуждается в
уточнении. Одна из основных трудностей
задания множества (даже из множеств,
точность описания которых не вызывает
сомнения) с помощью вполне, казалось
бы, законных средств — в том, что можно
сконструировать описание множеств,
которые приводят к противоречиям —
“парадоксам теории множеств”. Например,
множество всех подмножеств по смыслу
своего описания этого множества должно
содержать все мыслимые множества. Но
оно само содержится в множестве своих
подмножеств в качестве элемента.
Перед дальнейшим
изложением будет удобно определить два
специальных множества.
Определение:
Пустое
множество
(обозначается
)
есть множество, обладающее свойством:
при любом х.
Другое множество,
определение которого зависит от задачи,
называют универсальным множеством.
Определение:
Универсальное
множество
(обозначается U) есть множество всех
рассматриваемых в данной задаче
элементов.
Рассмотрим теперь
множество.
Оно имеет n элементов. Будем говорить,
что мощность этого множества есть n.
Определение:
Мощностью
(длиной, размерностью)
множества называется число элементов
этого множества. Обозначим
.
Далее любое
множество В, которое имеет то же число
элементов, что и А, имеет такую же
мощность, и естественно, эти элементы
не надо пересчитывать. Для небольших
множеств достаточно легко пересчитать
элементы, но для других множеств, например
N, это может быть невозможно. Далее
следует строгое, но неформальное
определение количества элементов.
Определение:
Говорят, что множество Х конечно,
если
или для некоторого
существует
множествотакое,
что оно имеет то же самое число элементов,
что и X. Еслии никакого n не может быть найдено, то Х
называютбесконечным.
Соседние файлы в папке Методичка
- #
- #
- #
Понятие множества
Что такое «множество», мы понимаем интуитивно. В этом смысле это понятие первично, так же как «точка» или «плоскость».
Создатель теории множеств Г.Кантор описывал множество как «многое, мыслимое нами как единое».
Приведём примеры множеств:
Множество людей в салоне самолёта
Множество деревьев в парке
Множество планет Солнечной системы
Множество электронов в атоме
Множество натуральных чисел
Множество «синих-синих презелёных красных шаров»
1,2,3,….$infty$
$varnothing$
Конечное, бесконечное и пустое множества
Людей в салоне самолёта легко посчитать, это множество конечно.
С деревьями в парке, планетами и электронами – сложней. Скорее всего, мы не сможем назвать точное количество элементов этих множеств в данный момент времени. Однако, и эти множества конечны.
Натуральное число – это идеальный объект, абстракция. Множество натуральных чисел бесконечно. Как оказалось, человек может оперировать и абстракциями, и бесконечностями.
Можно себе представить даже то, «чего на свете вообще не может быть». Поскольку таких объектов нет, их множество будет пустым. Пустое множество является частью любого другого множества.
Конечные множества
Бесконечные множества
Пустые множества
Игроки на поле
Помидоры на грядке
Пчёлы в улье
Числа (натуральные, рациональные, действительные и т.д.)
Количество рациональных чисел на отрезке [0;1]
Полосатые летающие слоны
Все точки пересечения двух параллельных прямых на плоскости
Способы задания множеств
1) Перечисление – в списке задаются все элементы множества.
Например:
Множество всех континентов Земли:
{Евразия,Северная Америка,Южная Америка,Африка,Австралия,Антарктида}
Множество букв слова «математика»: {м,а,т,е,и,к}
Множество натуральных чисел меньших 5: {1,2,3,4}
2) Характеристическое свойство – указывается особенность элементов множества.
Например:
A = ${x|x gt 0, x in Bbb R}$ — множество всех действительных положительных x
B = ${n|n⋮5,n in Bbb N}$ — множество всех натуральных n, кратных 5
C = ${(x,y)|x^2+y^2 ge 1,x in Bbb R,y in Bbb R}$ – множество всех действительных точек координатной плоскости (x,y), расстояние от которых до начала координат не больше 1 (круг с центром в начале координат, радиусом 1).
D = {k|k-материк Земли} – множество всех материков планеты Земля
3) Графическое изображение – визуальное моделирование с помощью различных диаграмм (круги Эйлера, интервалы, графики и т.п.)
Подмножества
Множество A называют подмножеством множества B (A $subseteq$ B), если всякий элемент множества A также является элементом множества B:
$$ A subseteq B iff (a in Bbb A Rightarrow a in Bbb B) $$
Говорят, что B содержит A, или B покрывает A.
Пустое множество является подмножеством любого множества.
Знак $subseteq$ является аналогом $ge$, т.е. «нестрогим» неравенством. Это значит, что множества A и B могут и совпадать (любое множество является подмножеством самого себя).
Между множествами можно также ввести отношение «строгое подмножество», $A subset B$, в котором B заведомо «шире» множества A (аналог строгого неравенства $lt$).
Примеры подмножеств:
Множество людей является подмножеством приматов, живущих на Земле.
Множество натуральных чисел меньших 5 является подмножеством натуральных чисел меньших $10: A = {n|n lt 5, n in Bbb N}, B = {m|m lt 10, m in Bbb N}, A subseteq B$
Множество квадратов является подмножеством прямоугольников.
Множество полосатых летающих слонов – как пустое множество — является подмножеством чего угодно: приматов, чисел, прямоугольников. Что удобно для размышлений о смысле всего.
Множество всех подмножеств данного множества A называют булеаном или степенью множества A.
Булеан конечного множества из n элементов содержит $2^n$ элементов:
$$ |A| = n, |P(A)| = 2^n$$
Примеры
Пример 1. Запишите данное множество с помощью перечисления элементов:
а) $A = {x|x^2 lt 5, x in Bbb Z}$
Задано множество целых чисел, квадрат которых меньше 5. Перечисляем:
A = {-2;-1;0;1;2}
б) $B = {x||x| ge 3, x in Bbb Z}$
Задано множество целых чисел, модуль которых не больше 3. Перечисляем:
B = {-3;-2;-1;0;1;2;3}
в) $ C = {x|(x-1)(2x+5) = 0, x in Bbb Q}$
Задано множество рациональных чисел, являющихся корнями уравнения
(x-1)(2x+5) = 0. Перечисляем:
C = {1;-2,5}
г) $D = {n|9 lt n ge 12, n in Bbb N}$
Задано множество натуральных чисел, входящих в полуинтервал $9 lt n le 12$.
Перечисляем:
D = {10;11;12}
Пример 2. Запишите данное множество с помощью характеристического свойства:
а) Множество всех натуральных чисел меньше 10
$$ A = {n|n lt 10, n in Bbb N} $$
б) Множество всех действительных чисел, кроме 0
$$ B = {x|x neq 0, x in Bbb R} $$
в) Множество всех точек с целыми координатами, принадлежащих прямой y = 2x+1
$$C = {(x,y)|y = 2x+1, x in Bbb Z, y in Bbb Z}$$
г) Множество всех целых решений уравнения $x^3+x^2+4 = 0$
$$ D = {x|x^3+x^2+4 = 0, x in Bbb Z} $$
Пример 3. Изобразите на графике в координатной плоскости данное множество:
а) $A = {(x,y)|y = x+2, x le 3, x in Bbb N}$
Задано конечное множество точек, которое можно представить перечислением:
A = {(1;3);(2;4);(3;5) }
На графике:
б)$ B = {(x,y)|y = frac{4}{x},-4 le x le -1, x in Bbb R}$
Задано бесконечное множество точек, принадлежащих данной гиперболе $y = frac{4}{x}$ в данном интервале $-4 le x le -1$. На графике:
Пример 4. Укажите и запишите с помощью перечисления одно из непустых конечных подмножеств для данного множества:
а) A = {k|k-электронное устройство}
$B subseteq A, B$ = {компьютер, смартфон, планшет}
б) A = {m|m-четырёхугольник}
$B subseteq A, B$ = {квадрат, ромб, прямоугольник}
в) A = {p|p-музыкальный инструмент}
$B subseteq A, B$ = {пианино, скрипка, виолончель}
г) A = {t|t-средство передвижения}
$B subseteq A, B$ = {автомобиль,автобус,поезд}
Пример 5*. Найдите булеан данного множества:
а) A = {5;10;27}
$$ P(A) = {{varnothing},{5},{10},{27},{5;10},{5;27},{10;27},{5;10;27} } $$
Исходное множество состоит из n = 3 элементов, булеан состоит из $2^3 = 8$ элементов.
б) B = {1;{2;16} }
$$ P(B) = {{varnothing},{1},{2;16},{1;{2;16} } } $$
Исходное множество состоит из n = 2 элементов, булеан состоит из $2^2 = 4$ элементов.
Пояснительная записка
Программа данного элективного курса
рассчитана на 9 часов. Подобранный материал
способствует расширению объема сведений по
математике, а также обучению подростков навыкам
анализа нестандартных ситуаций, самостоятельной
работе с литературой, развитию математической
речи.
В настоящее время большинство разделов
математики построены на базе
теоретико-множественных идей. Использование
множеств и операций над ними позволяет осветить
с современных позиций целый ряд разделов
школьной математики. В то же время основные
понятия теории множеств настолько просты и ясны,
что их можно начинать преподавать с начальной
школы.
При проведении занятий по теории множеств
большое внимание уделяется разбору примеров
множеств из окружающего мира. Надо научить
школьников видеть конкретные примеры множеств,
подмножеств, пересечений и объединений множеств
и т.д. В то же время следует разобрать достаточное
число примеров из уже известных школьникам
вопросов математики, научить подходить к этим
вопросам с теоретико-множественных позиций.
Такие понятия, как система уравнений и
неравенств, совокупность уравнений и неравенств,
получают естественное истолкование на языке
теории множеств.
Цель курса: познакомить учащихся с
элементами теории множества.
Задачи курса:
- познакомить учащихся с понятием множества;
- познакомить учащихся с основными операциями:
объединение и пересечение множеств; - дать определение подмножества;
- рассмотреть конечные, бесконечные, числовые
множества; - рассмотреть число элементов объединения и
пересечения двух конечных множеств; - предоставить учащимся возможность,
проанализировать свои способности к математике.
Распределение часов
|
№ |
Тема занятия |
Кол-во часов |
Виды деятельности учащихся |
| 1. | Понятие множества. Элемент множества. Пустое множество. |
1 |
Составление конспекта. Коллективное решение задач. Работа со справочной литературой. |
| 2. | Понятие подмножества. |
1 |
Деятельность учащихся направлена на выработку умения, отличать множества от подмножества. |
| 3. | Пересечение и объединение множеств. |
1 |
Выполнение тренировочных упражнений на отработку определений пересечения и объединения множеств. Проводятся тренировочные упражнения в устной форме на применение терминов из теории с целью развития математической речи. |
| 4. | Конечные и бесконечные множества. |
1 |
Используя навыки определения множества и подмножества, учащиеся самостоятельно пытаются |
| 5. | Число элементов объединения и пересечения двух конечных множеств |
1 |
На конкретных примерах учащиеся самостоятельно формулируют свойства, записывают их в тетрадь. Выполняют тренировочные упражнения, которые помогают закрепить полученные знания. |
| 6. | Числовые множества. Числовые промежутки. |
1 |
Деятельность учащихся направлена на выработку умения, правильно записывать числовые промежутки. Упражнения выполняются в письменной форме. |
| 7. | Взаимно однозначное соответствие между множествами. |
1 |
Конспект лекции, работа со справочной литературой. Отработка полученного материала с записью в тетради. |
| 8. | Разность множеств. |
1 |
Составление опорного конспекта, оформление рисунков на доске, сообщение учеников по данной теме. |
| 9. | Проверочная работа. |
1 |
Обобщение знаний и проверка с помощью выполнения письменной работы составленной по аналогии с пройденным материалом. |
Дидактический материал
Тема 1. Понятие множества. Элемент
множества. Пустое множество
Цель: ввести понятие множества, его
элементов.
Справочный материал
В повседневной жизни постоянно различные
совокупности предметов называют, одним словом.
Совокупность документов называют архивом;
собрание музыкантов – оркестром; группу лошадей
– табуном; родителей, детей и их родственников –
семьей; большую группу людей – толпой или
очередью; собрание книг – библиотекой и т.д.
Математическим понятием, отражающим
объединение некоторых объектов, предметов или
понятий в одну единую совокупность является
понятие множества. Это понятие не определяется,
подобно понятиям точки, числа, и является
первичным.
Предметы (объекты), составляющие некоторое
множество, называются его элементами. Все
множества можно записывать с помощью заглавных
букв латинского алфавита:
А – множество квадратов;
В – множество чисел.
Элементы множества можно записать с помощью
маленьких букв: х является элементом множества А.
Это можно записать так: хА (читают: х есть элемент множества А,
или х принадлежит А, или х содержится в А, или А
содержит х). Если объект х не является элементом
множества А, то это записывают так: хА (читается: х не
есть элемент множества А, или х не принадлежит А,
или х не содержится в А).
Например: Если множество В – множество
натуральных чисел, то 2В, –7
В, муха
В и т.д.
Множество можно иногда задавать перечислением
его элементов. Например: множество стран на
земном шаре задается их списком в географическом
атласе, множество учеников в классе – их списком
в классном журнале. Если множество задано
списком, то названия всех элементов множества
записывают в фигурные скобки, разделяя запятой.
Например: если множество С состоит из трех
элементов:1,9 и –4, то это записывают так: С ={1,9; –4}.
Но не все множества можно записывать списком.
Если множество содержит бесконечно много
элементов, то такой список составить нельзя.
Множество считается заданным, если указано
некоторое свойство, которым обладают все его
элементы и не обладают ни какие другие объекты.
Такое свойство называют характеристическим
свойством множества. Например: множество {2, 4}
может быть задано:
а)множество четных чисел, удовлетворяющих
неравенству 1 < х < 5;
б)множество корней квадратного уравнения х2 –
6х + 8 = 0.
Задание множества его характеристическим
свойством записывают и в геометрии. Например:
биссектриса угла есть геометрическое место
точек плоскости, лежащих внутри этого угла и
равноудаленных от его сторон.
Множество элементов обладающих
характеристическим свойством записывают так:
А = {х: –3 < х < 4} означает, что
множество А состоит из всех чисел х,
удовлетворяющих неравенству –3 < х <
4.
Упражнения
№ 1. Как называется множество
артистов, работающих в одном театре?
№ 2. Как называется множество царей
данной страны, принадлежащих одному семейству?
№ 3. Пусть А множество всех
многочленов от одной переменной х, все
коэффициенты которых целые.
Верна ли запись:
а) х – 15 х + 6А;
б) х3
– 1А;
в) х2 + у2 – 1А.
№ 4. На координатной плоскости
расположен квадрат АВСД, где А(10; 10), В(–10; 10), С(–10;
–10), Д(10, –10). Сколько точек с целыми координатами,
расположено на сторонах квадрата или внутри его?
Дома
№ 1. Запишите известные вам названия
множеств военнослужащих.
№ 2. На координатной плоскости
расположен треугольник АВС, где А(–3; –2), В(0; 8),
С(10; –5). Сколько точек с целыми координатами,
расположено на сторонах треугольника или внутри
его?
Тема 2. Понятие подмножества
Цель: ввести понятие подмножества, его
элементов.
Справочный материал.
При помощи операций над множествами можно
получать новые множества. Рассмотрим операцию пересечение
множеств.
Пересечение множеств А и В есть множество,
которое состоит из элементов, принадлежащих
каждому из множеств А и В.
Обозначается операция пересечения: АВ.
Например: А = {1; 2; 3}и В ={2; 3; 4; 5}, то АВ = {2; 3}.
Наглядно представить расположение множеств в
различных случаях можно при помощи
геометрических фигур.
Множества называются не пересекающимися, если
у них нет общих элементов, т. е. их пересечение
пусто.
Если заданы два множества, то можно образовать
новое множество, включив в него, во-первых,
элементы первого множества и, во-вторых, элементы
второго множества, не совпадающие с элементами
первого. Рассмотрим операцию объединение
множеств.
Объединение множеств А и В представляет собой
множество, состоящее из элементов, принадлежащих
хотя бы одному из множеств А и В. Обозначается
операция объединения: АВ.
Например: А = {1; 2; 3}, В = {2; 3; 4}, то А B = {1; 2; 3;
4}.
Упражнения.
№ 1. На координатной плоскости даны
три множества:
- А – множество точек А(х; у), у которых | x
| = 1; - В – множество точек В(х; у), таких, что | y
| = 1; - С – множество, равное графику функции у = 2х.
Изобразите множества:
a) A
B;
б) А
В;
в) А
С;
г) В
С;
д) А
ВС
№ 2.Назовите 5 подмножеств в множестве
слов русского языка.
№ 3. Каким свойством выделяется
подмножество млекопитающих в множестве всех
живых существ?
Дома.
Пусть А – множество четных чисел из промежутка
[100;1000], а В – множество чисел, кратных 5, из того же
промежутка.
Сколько чисел в множестве: а) A B; б) А
В
Тема 3. Пересечение и объединение
множеств.
Цель: ввести понятия пересечения и
объединения множеств.
Справочный материал.
Если каждый элемент множества В является в то
же время элементом множества А, то говорят, что В –>
подмножество в А, и пишут
ВА. Каждое
непустое множество имеет по крайней мере два
подмножества: пустое множество и само
множество А. Таким образом, пустое множество
является подмножеством любого множества.
Упражнения.
№ 1. Даны множества:
а) Множество А всех тетрадей.
б) Множество В всех прямоугольников.
в) Множество С всех четырехугольников.
г) Множество D всех квадратов.
д) Множество Е всех параллелограммов.
е) Множество F всех многоугольников.
Выписать буквы, обозначающие эти множества, в
таком порядке, чтобы каждая следующая обозначала
подмножество предыдущего.
№ 2. Даны множества:
а) Множество А всех рациональных чисел.
б) Множество В всех целых чисел.
в) Множество С всех действительных чисел.
г) Множество D всех четных натуральных чисел.
д) Множество Е всех натуральных чисел.
е) Множество F всех натуральных чисел, делящихся
на 12.
Выписать буквы, обозначающие эти множества, в
таком порядке, чтобы каждая следующая обозначала
подмножество предыдущего.
№ 3. Даны множества:
а) Множество А учеников 8-го класса данной
средней школы.
б) Множество В всех учеников данной средней
школы.
в) Множество С учеников 8-го класса этой средней
школы, посещающие факультативные занятия по
математики.
г) Множество Е всех учащихся средней школы в
России.
д) Множество D всех учащихся средних школ города
Салехард.
е) Множество F мальчиков из 8 класса, посещающих
факультативные занятия по математике.
Выписать буквы, обозначающие эти множества, в
таком порядке, чтобы каждая следующая обозначала
подмножество предыдущего.
Дома.
Даны множества:
а) Множество А всех позвоночных животных.
б) Множество В всех животных.
в) Множество С всех млекопитающих животных.
г) Множество D всех волков.
д) Множество Е всех хищных млекопитающих.
Выписать буквы, обозначающие эти множества, в
таком порядке, чтобы каждая следующая обозначала
подмножество предыдущего.
Тема 4. Конечные и бесконечные
множества.
Цель: ввести понятие конечного и
бесконечного множества, научить оперировать
этими понятиями при решении задач.
Справочный материал.
Множество, элементы которого можно
пересчитать называется конечным множеством.
Конечное множество можно задавать двумя
способами:
- указанием на некоторое свойство, которому
удовлетворяют его элементы; - перечислением его элементов.
Например: А = {х: –3 < х < 4}
означает, что множество А состоит из всех чисел х,
удовлетворяющих неравенству –3 < х <
4.
Пустое множество считается конечным.
Свойство: Подмножество конечного множества
само конечно.
Множество, элементы которого невозможно
пересчитать называется бесконечным.
Свойство: Если множество В содержит
бесконечное подмножество, то В бесконечно.
Упражнения
№ 1. Пусть конечное множество А
содержит n элементов. Подсчитать, сколько
подмножеств имеет это множество.
№ 2. Угадай по какому закону
составлено бесконечное множество, содержащие
числа:
а { ,
,
,
,…};
б) {,
,
,
,…}
в) {,
,
,
,
,
,…}
г) {2, 12, 36, 80, 150,…}
№ 3. Как называется множество точек
земной поверхности, равноудаленных от северного
полюса?
№ 4. Пусть Е – множество, состоящее из
таких чисел х, что 4 < х2 < 9.
Проверьте, что [2; 3] Е. Верно ли, что [2; 3] = Е?
Дома.
№ 1. На координатной плоскости
расположен квадрат АВСД, где А(10;10), В(–10;10),
С(–10;–10), Д(10;–10). Сколько точек с целыми
координатами, расположено на сторонах квадрата
или внутри его?
№ 2. Как называется множество точек
земной поверхности, равноудаленных от обоих
полюсов? Поясните ответ.
Тема 5. Число элементов объединения и
пересечения двух конечных множеств
Цель: определить число элементов
объединения и пересечения двух конечных
множеств.
Справочный материал.
Нам уже известно, что пересечением двух не
пустых множеств является новое множество,
состоящее из элементов принадлежащих каждому из
множеств. Если говорить о двух конечных
множествах, то можно заметить, что их пересечение
есть тоже конечное множество, состоящее из
элементов принадлежащих каждому из множеств.
Можно сказать и об объединении двух конечных
множеств, оно тоже конечно.
Упражнения
№ 1. Пусть А – множество корней
квадратного уравнения: х2 – 7х + 12 =
0.
Составьте список элементов множества А.
№ 2. Пусть А – множество делителей
числа 60.
Составьте список элементов множества А.
№ 3. Составьте список элементов
множества, заданных свойствами:
а) А = {х : х2 – 8х + 12 = 0};
б) В = {х : хN, –11 < х < –3}.
№ 4. Запишите с помощью фигурных
скобок множество, состоящее из:
а) целы чисел, таких, что –3,71 < х < 4;
б) натуральных делителей числа 124 числа 30;
Дома.
№ 1. Запиши с помощью фигурных скобок
множество корней уравнения:
а) 5х – 17 = 3;
б) (х – 1)(х – 2) = 0;
в) х2 + 9 = 0.
№ 2. В следующих множествах все
элементы, кроме одного, обладают некоторым
свойством. Найдите элементы не обладающие этим
свойством:
а) {2; 6; 15; 84; 156};
б) {2; 7; 13; 16; 29}
Ответ поясните.
№ 3. Назовите отличия записи множества
А = {2; 4} от множества [2; 4].
Тема 6. Числовые множества. Числовые
промежутки.
Цель: ввести понятие “числовые
промежутки” и “числовые множества”, учить
применять на практике.
Справочный материал.
Некоторые числовые множества имеют особые
названия. Если даны два числа а и b, а
< b, то множество всех чисел,
удовлетворяющих неравенству, а < х
< b, называют числовым отрезком и
обозначают [а; b]. На числовой оси ему
соответствует отрезок с концами а и b.
а
b
Множество чисел, удовлетворяющих неравенству, а
< х < b, называют числовым
промежутком и обозначают (а, b). На
числовой оси это множество изображается
отрезном у которого отброшены концы.
Иногда встречаются множества чисел,
удовлетворяющие неравенствам, а < х
< b или а < х < b. Их
называют числовыми полуотрезками и
обозначают [а; b), или (а; b].
Квадратная скобка обозначает, что
соответствующий конец включается в множество, а
круглая – что он исключается.
Числовые отрезки, полуотрезки и промежутки
имеют конечную длину. Рассмотрим множество
чисел, удовлетворяющих неравенству а <
х < +. Такое
множество называется числовым лучом.
Числовой луч имеет бесконечную длину. Числовыми
лучами называют и множества чисел,
удовлетворяющих неравенствам вида а < х
< +, –
< х < а,
– < х < а
числовые лучи обозначают так: [а; +), (а; +
), (–
; а], (–
; а). С
числовыми множествами приходится иметь дело при
решении уравнений и неравенств.
Упражнения.
№ 1. Найдите область допустимых
значений (ОДЗ) уравнения:
.
№ 2.Найдите ОДЗ для уравнений:
а);
б) х2 + 5х + 7 + = 1 +
.
№ 3. Совпадают ли ОДЗ уравнений: х
+ 5 = 15 – х и х + 5 +.
Дома.
№ 1. Найдите ОДЗ для уравнений: .
№ 2. Придумайте и запишите элементы
множества, используя рисунок.
А) 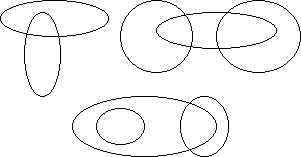
В)
Тема 7. Взаимнооднозначное
соответствие между множествами
Цель: ввести понятие взаимного
однозначного соответствия между множествами.
Справочный материал.
Между множествами А и В установлено
взаимно-однозначное соответствие, если каждому
элементу а из А поставлен в соответствие b из В, и
при этом соответствии каждый элемент b из В
соответствует одному и только одному элементу а
из А.
Например: в случае, когда на танцевальной
площадке танцуют все, между множеством юношей и
множеством девушек устанавливается
соответствие, обладающее следующими свойствами:
1) Каждому юноше соответствует одна и только
одна девушка – его партнерша.
2) Каждой девушке соответствует один и только
один юноша – ее партнер.
Понятие взаимнооднозначное соответствие
весьма важное при изучении функции. Рассмотрим
функцию: у = . Когда х изменяется на отрезке [–1; 2], то у
изменяется на отрезке [–1; 8]. При этом каждому
числу х из отрезка [–1; 2] соответствует одно и
только одно значение у, принадлежащее
отрезку[–1;8], а каждому значению у из отрезка [–1;
8] – одно и только одно значение х из отрезка [–1;
2]. Иными словами, функция у = устанавливает взаимнооднозначное
соответствие между точками отрезков [–1; 8] и [–[1;
2]. Эта функция устанавливает и взаимно
однозначное соответствие между точками числовых
прямых х и у. Отсюда следует, что каждому значению
у соответствует единственное значение х, такое,
что х= у.
Упражнения.
№ 1. Приведите пример функции, которая
не задает взаимно однозначного соответствия.
Ответ объясните.
№ 2. Каждой параболе, ось которой
параллельна оси ординат, ставится в соответствие
ее уравнение вида у = а+ bх + с.
Является ли это соответствие взаимно
однозначным?
№ 3. Пусть А – множество всех
окружностей на плоскости и В – множество всех
квадратов плоскости. Каждому квадрату ставят в
соответствие вписанную в него окружность.
Является ли это соответствие взаимно
однозначным?
№ 4. Пусть А – множество всех
окружностей на плоскости и В – множество всех
точек этой плоскости. Каждой окружности ставится
в соответствие ее центр. Является ли это
соответствие взаимно однозначным?
№ 5. Найдите объединение корней
уравнений (3х + 5) + (8х + 1) = 17 и 2х = 20.
Дома.
№ 1. Каждому квадратному уравнению
вида (а
и b — положительные числа) ставится в
соответствие его положительный корень. Является
ли это соответствие взаимно однозначным?
№ 2. Найдите пересечение двух прямых у
= х и у = 2- х. Ответ запишите в виде
множества состоящего из элементов.
Тема 8. Разность множеств
Цель: ввести понятие разности множеств и
научить применять его на практике.
Справочный материал.
Разностью двух множеств А и В называется
такое множество, в которое входят все элементы из
множества А, не принадлежащие множеству В.
Разность множеств А и В обозначают АВ. Если
рассмотреть разность множеств А и В с помощью
диаграмм Эйлера-Вена, то видим АВ = когда А = В.
В случае, когда В — есть подмножество множества
А, разность АВ называют дополнением множества В
в множестве А и обозначают САВ*.
Например, дополнением множества четных чисел в
множестве всех целых чисел является множество
нечетных чисел. Дополнением множества всех
квадратов в множестве прямоугольников является
множество всех прямоугольников с неравными
сторонами. Разность множеств используется при
решении уравнений с переменными в знаменателе.
Упражнения.
№ 1. Что представляет собой множество:
а) САА;
б) СА ?
№ 2. Пусть А = [1; 4], В = [2; 6]. Найдите
множества АВ и ВА. Чему равно множество (АВ)(ВА)?
Найдите дополнение множества правильных
треугольников в множестве всех треугольников;
всех правильных многоугольников.
Дома.
Пусть А = {х/х = 2м — 1, м — целое
число}, В = {х/х = 4к + 1, к — целое
число}. Опишите множество АВ.
Тема 9. Проверочная работа
Цель: проверить знания и умения, учащихся по
элементам теории множеств.
Справочный материал.
ВАРИАНТ 1.
№ 1. Даны множества:
А = {12; 4; 2; 78}, В = {15; 3; 24; 5}, С = {15; 3; 5; 21; 76}.
Найдите:
а) А
В; б) А В; в) В
С; г) А
С; д) В
.
№ 2.Пусть А — множество делителей числа 80.
№ 3. Даны множества:
а) Множество В всех прямоугольников;
б) Множество С всех четырехугольников;
в) Множество D всех квадратов;
г) Множество Е всех параллелограммов;
д) Множество F всех многоугольников.
Выписать буквы, обозначающие эти множества, в
таком порядке, чтобы каждая следующая обозначала
подмножество предыдущего.
№ 4.. На координатной плоскости расположен
треугольник АВС,
где А(0; 8), В(2; -4), С(-6; -2). Сколько точек с целыми
координатами, расположено на сторонах
треугольника или внутри его?
№ 5.Найдите пересечение двух прямых у = 3х
и у = х + 2. Ответ запишите в виде
множества состоящего из элементов.
№ 6.Запиши с помощью фигурных скобок
множество корней уравнения:
а) 2х -17 = 3;
б) (х — 4)(х — 3) = 0;
в) х2 + 16 = 0.
№ 7.Пусть Е — множество, состоящее из таких
чисел х, что 9 = х2 = 25.
Проверьте, что [3; 5]Е. Верно ли, что [3; 5] = Е?
№ 8. Найдите ОДЗ для уравнений: а).
ВАРИАНТ 2.
№ 1. Даны множества: А = {1; 5; 7; 13}, В = {15; 3; 7; 23}, С
= {17; 23; 2; 15; 3}.
Найдите:
а) А
В; б) А В; в) В
С; г) А
С; д) В
.
№ 2. Пусть А — множество делителей числа 60.
№ 3. Даны множества:
а) Множество А всех рациональных чисел.
б) Множество В всех целых чисел.
в) Множество С всех действительных чисел.
г) Множество D всех четных натуральных чисел.
д) Множество Е всех натуральных чисел.
е) Множество F всех натуральных чисел, делящихся
на 12.
Выписать буквы, обозначающие эти множества, в
таком порядке, чтобы каждая следующая обозначала
подмножество предыдущего.
№ 4. На координатной плоскости расположен
треугольник АВС, где А(3; 1), В(-2; -8), С(-4; 7).
Сколько точек с целыми координатами, расположено
на сторонах треугольника или внутри его?
№ 5. Найдите пересечение двух прямых у =
х и у = 2 — х. Ответ запишите в виде
множества состоящего из элементов.
№ 6. Запиши с помощью фигурных скобок
множество корней уравнения:
а) 5х — 17 = 3;
б) (х — 1)(х — 2) = 0;
в) х2 + 9 = 0.
№ 7. Пусть Е — множество, состоящее из таких
чисел х, что 4 = х2 = 9. Проверьте, что
[2; 3]Е. Верно ли,
что [2; 3] = Е?
№ 8. Найдите ОДЗ для уравнений: а).
Дополнительные упражнения.
№ 1. Каждая семья, живущая в нашем доме,
выписывает или газету, или журнал, или то и другое
вместе. 75 семей выписывают газету, а 27 семей
выписывают журнал и лишь 13 семей выписывают и
журнал, и газету. Сколько семей живет в нашем
доме?
№ 2. Из 40 учащихся нашего класса 32
любят молоко, 21 — лимонад, а 15 — и молоко, и
лимонад. Сколько ребят в нашем классе не любят ни
молоко, ни лимонад?
№ 3.В одном классе 25 учеников. Из них 7
любят груши, 11 — черешню. Двое любят груши и
черешню; 6 — груши и яблоки; 5 — яблоки и черешню.
Но есть в классе два ученика, которые любят все и
четверо таких, что не любят фруктов вообще.
Сколько учеников этого класса любят яблоки?
№ 4.Из 100 человек 85 знают английский
язык, 80 — испанский, 75 — немецкий. Все владеют, по
крайней мере, одним иностранным языком. Среди них
нет таких, которые знают два иностранных языка,
но есть владеющие тремя иностранными языками.
Сколько человек из этих 100 знают 3 языка?
№ 5. Учитель задал на уроке сложную
задачу. В результате количество мальчиков,
решавших задачу, оказалось равно количеству
девочек, ее не решивших. Кого в классе больше —
решивших задачу или девочек?
№ 6. Сколько человек участвовало в
прогулке, если известно, что 16 из них взяли с
собой бутерброды с ветчиной, 24 — с колбасой, 15 — с
сыром, 11 — с ветчиной и с колбасой, 8 — с ветчиной
и с сыром, 12 — с колбасой и с сыром, 6 — бутерброды
всех трех видов, а 5 — вместо бутербродов взяли с
собой пирожки?
Литература:
- И.Л. Никольская. «Факультативный курс по
математике», учебное пособие для 7-9-х классов
средней школы. М., «Просвещение», 1991. - К.П. Сикорский. «Дополнительные главы по
курсу математики 7-8 классов для факультативных
занятий», М., «Просвещение», 1969. - Н.А. Виленкин. «Алгебра» учебник для
учащихся 8 класса с углубленным изучением
математики, М., «Просвещение», 2005. - И.Н. Бронштейн, К.А. Семендяев. «Справочник
по математике для инженеров и учащихся «, М.,
«Наука», 1986. - А.Г.Ципкин. «Справочник по математике», для
средних учебных заведений, М., «Наука», 1988.








