Все, что познается, имеет число, ибо невозможно ни понять ничего, ни познать без него – Пифагор
В этой статье:
Матрица смежности
Матрица инцидентности
Список смежности (инцидентности)
Взвешенный граф (коротко)
Итак, мы умеем задавать граф графическим способом. Но есть еще два способа как можно задавать граф, а точнее представлять его. Для экономии памяти в компьютере граф можно представлять с помощью матриц или с помощью списков.
Матрица является удобной для представления плотных графов, в которых число ребер близко к максимально возможному числу ребер (у полного графа).
Другой способ называется списком. Данный способ больше подходит для более разреженных графов, в котором число ребер намного меньше максимально возможного числа ребер (у полного графа).
Перед чтением материала рекомендуется ознакомится с предыдущей статьей, о смежности и инцидентности, где данные определения подробно разбираются.
Матрица смежности
Но тем кто знает, но чуть забыл, что такое смежность есть краткое определение.
Смежность – понятие, используемое только в отношении двух ребер или в отношении двух вершин: два ребра инцидентные одной вершине, называются смежными; две вершины, инцидентные одному ребру, также называются смежными.
Матрица (назовем ее L) состоит из n строк и n столбцов и поэтому занимает n^2 места.
Каждая ячейка матрицы равна либо 1, либо 0;
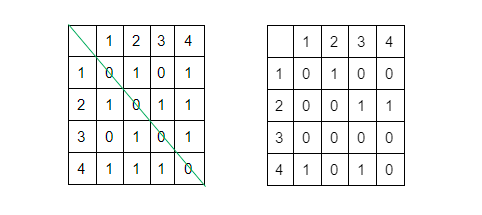
Ячейка в позиции L (i, j) равна 1 тогда и только тогда, когда существует ребро (E) между вершинами (V) i и j. Если у нас положение (j, i), то мы также сможем использовать данное правило. Из этого следует, что число единиц в матрице равно удвоенному числу ребер в графе. (если граф неориентированный). Если ребра между вершинами i и j не существует, то ставится 0.
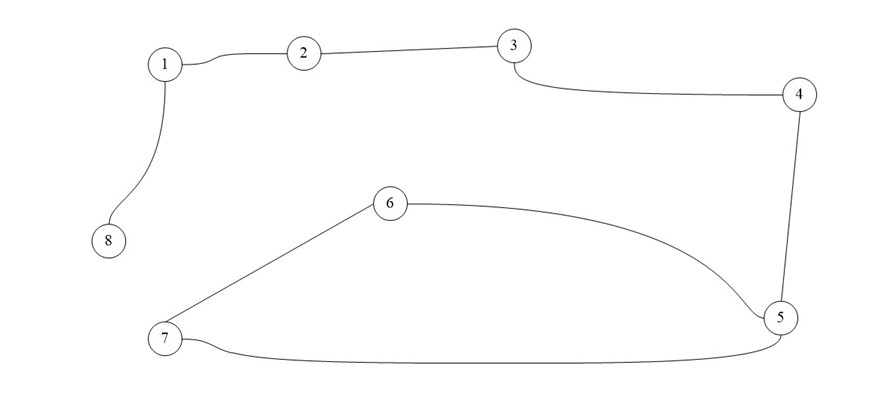
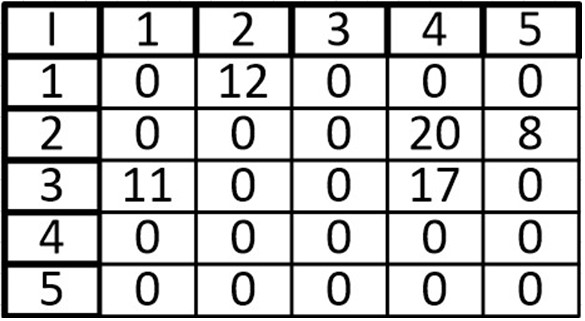
Для практического примера возьмем самый обыкновенный неориентированный граф:
А теперь представим его в виде матрицы:
Ячейки, расположенные на главной диагонали всегда равны нулю, потому что ни у одной вершины нет ребра, которое и начинается, и заканчивается в ней только если мы не используем петли. То есть наша матрица симметрична относительно главной диагонали. Благодаря этому мы можем уменьшить объем памяти, который нам нужен для хранения.
С одной стороны объем памяти будет:
Но используя вышеописанный подход получается:
Потому что нижнюю часть матрицы мы можем создать из верхней половины матрицы. Только при условии того, что у нас главная диагональ должна быть пустой, потому что при наличии петель данное правило не работает.
Если граф неориентированный, то, когда мы просуммируем строку или столбец мы узнаем степень рассматриваемой нами вершины.
Если мы используем ориентированный граф, то кое-что меняется.
Здесь отсутствует дублирование между вершинами, так как если вершина 1 соединена с вершиной 2, наоборот соединена она не может быть, так у нас есть направление у ребра.
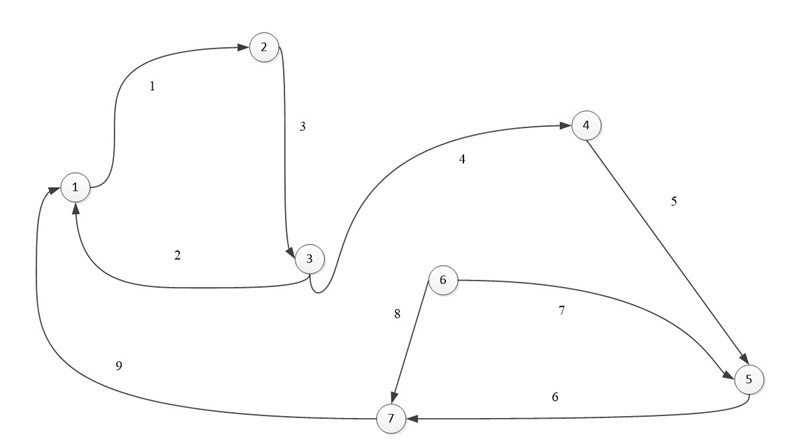
Возьмем в этот раз ориентированный граф и сделаем матрицу смежности для него:
В виде матрицы:
Если мы работаем со строкой матрицы, то мы имеем элемент из которого выходит ребро, в нашем случаи вершина 1 входит в вершину 2 и 8. Когда мы работаем со столбцом то мы рассматриваем те ребра, которые входят в данную вершину. В вершину 1 ничего не входит, значит матрица верна.
Объем памяти:
Если бы на главной диагонали была бы 1, то есть в графе присутствовала петля, то мы бы работали уже не с простым графом, с каким мы работали до сих пор.
Используя петли мы должны запомнить, что в неориентированном графе петля учитывается дважды, а в ориентированном — единожды.
Матрица инцидентности
Инцидентность – понятие, используемое только в отношении ребра и вершины: две вершины (или два ребра) инцидентными быть не могут.
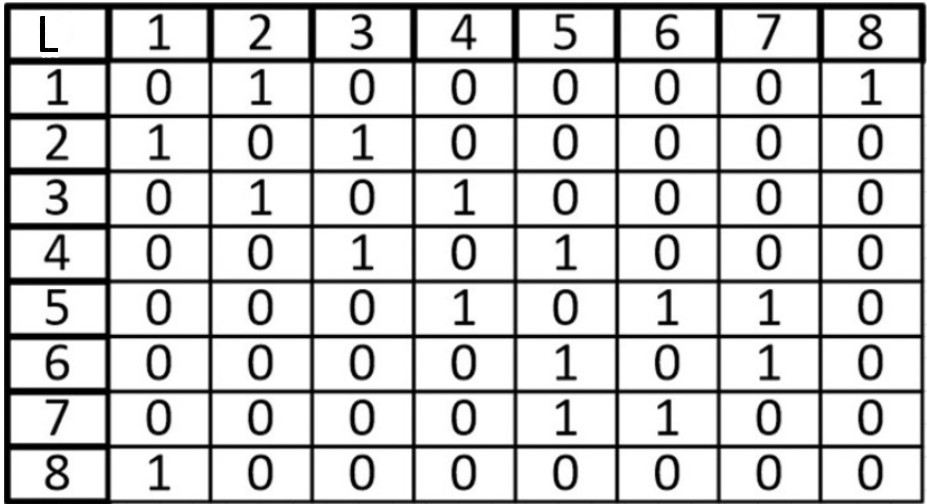
Матрица (назовем ее I) состоит из n строк которое равно числу вершин графа, и m столбцов, которое равно числу ребер. Таким образом полная матрица имеет размерность n x m. То есть она может быть, как квадратной, так и отличной от нее.
Ячейка в позиции I (i, j) равна 1 тогда, когда вершина инцидентна ребру иначе мы записываем в ячейку 0, такой вариант представления верен для неориентированного графа.
Сразу же иллюстрируем данное правило:
В виде матрицы:
Сумма элементов i-ой строки равна степени вершины.
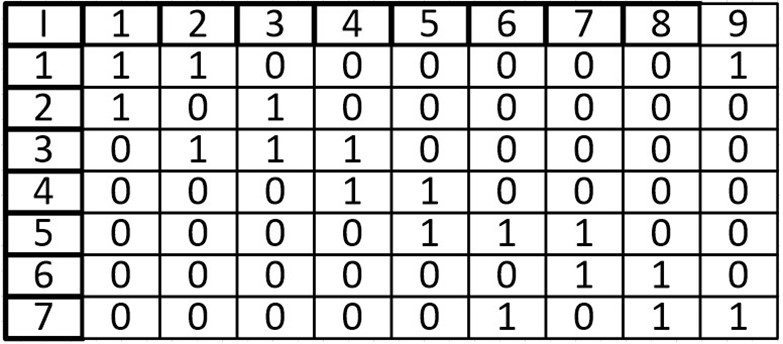
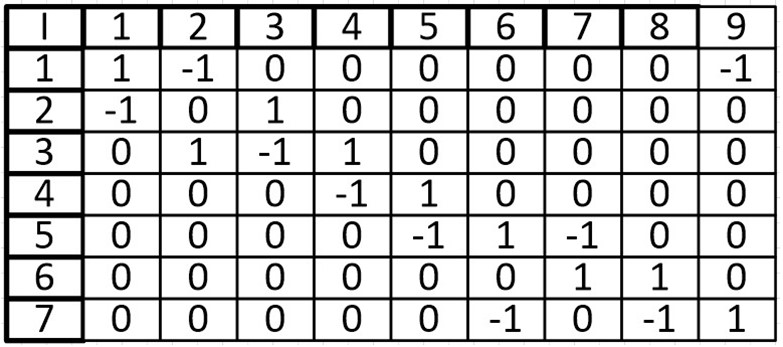
При ориентированным графе, ячейка I (i, j) равна 1, если вершина V (i) начало дуги E(j) и ячейка I (i, j) равна -1 если вершина V (i) конец дуги E (j), иначе ставится 0.
Ориентированный граф:
В виде матрицы:
Одной из особенностей данной матрицы является то, что в столбце может быть только две ненулевых ячейки. Так как у ребра два конца.
При суммировании строки, ячейки со значением -1, могут складываться только с ячейками, также имеющими значение -1, то же касается и 1, мы можем узнать степень входа и степень выхода из вершины. Допустим при сложении первой вершины, мы узнаем, что из нее исходит 1 ребро и входят два других ребра. Это является еще одной особенностью (при том очень удобной) данной матрицы.
Объем памяти:
Список смежности (инцидентности)
Список смежности подразумевает под собой, то что мы работаем с некоторым списком (массивом). В нем указаны вершины нашего графа. И каждый из них имеет ссылку на смежные с ним вершины.
В виде списка это будет выглядеть так:
Неважно в каком порядке вы расположите ссылку так как вы рассматриваете смежность относительно первой ячейки, все остальные ссылки указывают лишь на связь с ней, а не между собой.
Так как здесь рассматривается смежность, то здесь не обойдется без дублирования вершин. Поэтому сумма длин всех списков считается как:
Объем памяти:
Когда мы работаем с ориентированным графом, то замечаем, что объем задействованной памяти будет меньше, чем при неориентированном (из-за отсутствия дублирования).
В виде списка:
Сумма длин всех списков:
Объем памяти:
Со списком инцидентности все просто. Вместо вершин в список (массив) вы вставляете рёбра и потом делаете ссылки на те вершины, с которыми он связан.
К недостатку списка смежности (инцидентности) относится то что сложно определить наличие конкретного ребра (требуется поиск по списку). А если у вас большой список, то удачи вам и творческих успехов! Поэтому, чтобы работать максимальной отдачей в графе должно быть мало рёбер.
Взвешенность графа
Взвешенный граф — это граф, в котором вместо 1 обозначающее наличие связи между вершинами или связи между вершиной и ребром, хранится вес ребра, то есть определённое число с которым мы будем проводить различные действия.
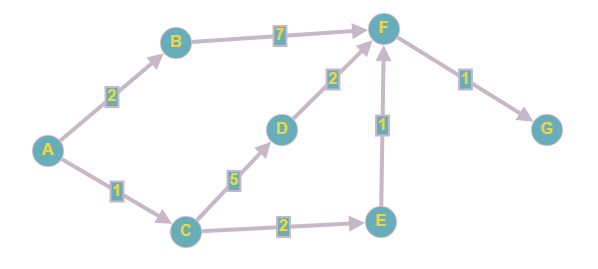
К примеру, возьмем граф с весами на ребрах:
И сделаем матрицу смежности:
В ячейках просто указываем веса ребра, а в местах где отсутствует связь пишем 0 или -∞.
Более подробно данное определение будет рассмотрено при нахождении поиска кратчайшего пути в графе.
Итак, мы завершили разбор представления графа с помощью матрицы смежности и инцидентности и списка смежности (инцидентности). Это самые известные способы представления графа. В дальнейшем мы будем рассматривать и другие матрицы, и списки, которые в свою очередь будут удобны для представления графа с определёнными особенностями.
Если заметили ошибку или есть предложения пишите в комментарии.
Только зарегистрированные пользователи могут участвовать в опросе. Войдите, пожалуйста.
На каком языке программирования проводить операции с графами
21.28%
Использовать оба
10
Проголосовали 47 пользователей.
Воздержались 8 пользователей.
- 1. Представление списка смежности
- 2. Структура списка смежности
- 3. Список смежности C ++
- 4. Список смежности Java
- 5. Список смежности Python
- 6. Код списка смежности в C
- 7. Код списка смежности в C++
- 8. Код списка смежности Java
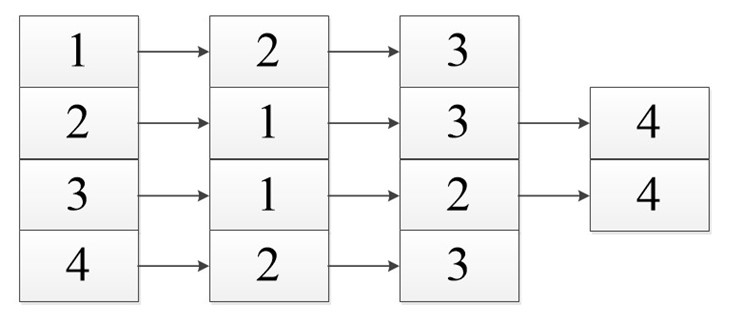
Список смежности
представляет граф в виде массива связанного списка.
Индекс массива представляет вершину и каждый элемент в его связанном списке, а также представляет другие вершины, которые образуют ребро с вершиной.
Представление списка смежности
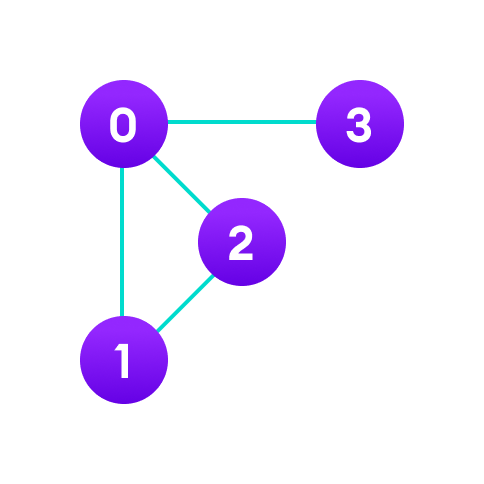
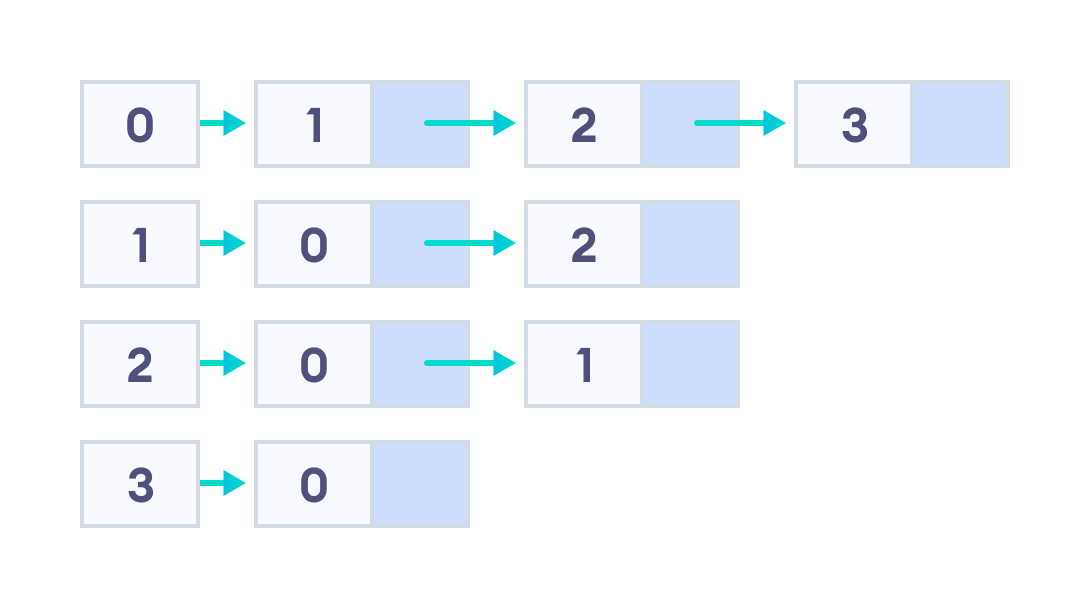
Граф и его эквивалентное представление списка смежности показаны ниже.
Список смежности эффективен с точки зрения хранения, потому что нам нужно хранить только значения для ребер. Для разреженного графа с миллионами вершин и ребер это может означать много сэкономленного пространства.
Структура списка смежности
Самому простому списку смежности требуется структура данных узла для хранения вершины и структура данных графа для организации узлов.
Мы приближаемся к основному определению графа — совокупности вершин и ребер {V, E}. Для простоты мы используем немаркированный граф, а не помеченный, то есть вершины идентифицируются по их индексам 0,1,2,3.
Давайте рассмотрим структуру данных ниже.
struct node { int vertex; struct node* next; }; struct Graph { int numVertices; struct node** adjLists; };Не позволяйте struct node*
adjLists ошеломить вас.
Нам нужно сохранить указатель struct node
. Потому, как мы не знаем, сколько вершин будет в графе, и поэтому не можем создать массив связанных списков во время компиляции.Список смежности C ++
Это та же самая структура, но с помощью встроенного списка структур данных STL в C ++ мы делаем структуру немного чище. Мы также можем абстрагировать детали реализации.
class Graph { int numVertices; list<int> *adjLists; public: Graph(int V); void addEdge(int src, int dest); };Список смежности Java
Мы используем Java Collections для хранения массива связанных списков.
class Graph { private int numVertices; private LinkedList<integer> adjLists[]; }Тип LinkedList определяет, какие данные вы хотите сохранить в нем. Для помеченного графа вы можете хранить словарь вместо целого значения.
Список смежности Python
Есть причина, по которой Python получает так много «любви». Простой словарь вершин и его ребер является достаточным представлением графа. Вы можете сделать вершину настолько сложной, насколько захотите.
graph = {'A': set(['B', 'C']), 'B': set(['A', 'D', 'E']), 'C': set(['A', 'F']), 'D': set(['B']), 'E': set(['B', 'F']), 'F': set(['C', 'E'])}Код списка смежности в C
#include <stdio.h> #include <stdlib.h> struct node { int vertex; struct node* next; }; struct node* createNode(int); struct Graph { int numVertices; struct node** adjLists; }; struct Graph* createGraph(int vertices); void addEdge(struct Graph* graph, int src, int dest); void printGraph(struct Graph* graph); int main() { struct Graph* graph = createGraph(6); addEdge(graph, 0, 1); addEdge(graph, 0, 2); addEdge(graph, 1, 2); addEdge(graph, 1, 4); addEdge(graph, 1, 3); addEdge(graph, 2, 4); addEdge(graph, 3, 4); addEdge(graph, 4, 6); addEdge(graph, 5, 1); addEdge(graph, 5, 6); printGraph(graph); return 0; } struct node* createNode(int v) { struct node* newNode = malloc(sizeof(struct node)); newNode->vertex = v; newNode->next = NULL; return newNode; } struct Graph* createGraph(int vertices) { struct Graph* graph = malloc(sizeof(struct Graph)); graph->numVertices = vertices; graph->adjLists = malloc(vertices * sizeof(struct node*)); int i; for (i = 0; i < vertices; i++) graph->adjLists[i] = NULL; return graph; } void addEdge(struct Graph* graph, int src, int dest) { // Add edge from src to dest struct node* newNode = createNode(dest); newNode->next = graph->adjLists[src]; graph->adjLists[src] = newNode; // Add edge from dest to src newNode = createNode(src); newNode->next = graph->adjLists[dest]; graph->adjLists[dest] = newNode; } void printGraph(struct Graph* graph) { int v; for (v = 0; v < graph->numVertices; v++) { struct node* temp = graph->adjLists[v]; printf("n Adjacency list of vertex %dn ", v); while (temp) { printf("%d -> ", temp->vertex); temp = temp->next; } printf("n"); } }Код списка смежности в C++
#include <iostream> #include <list> using namespace std; class Graph { int numVertices; list *adjLists; public: Graph(int V); void addEdge(int src, int dest); }; Graph::Graph(int vertices) { numVertices = vertices; adjLists = new list[vertices]; } void Graph::addEdge(int src, int dest) { adjLists[src].push_front(dest); } int main() { Graph g(4); g.addEdge(0, 1); g.addEdge(0, 2); g.addEdge(1, 2); g.addEdge(2, 3); return 0; }Код списка смежности Java
import java.io.*; import java.util.*; class Graph { private int numVertices; private LinkedList<Integer> adjLists[]; Graph(int vertices) { numVertices = vertices; adjLists = new LinkedList[vertices]; for (int i = 0; i < vertices; i++) adjLists[i] = new LinkedList(); } void addEdge(int src, int dest) { adjLists[src].add(dest); } public static void main(String args[]) { Graph g = new Graph(4); g.addEdge(0, 1); g.addEdge(0, 2); g.addEdge(1, 2); g.addEdge(2, 3); } }
In this tutorial, you will learn what an adjacency list is. Also, you will find working examples of adjacency list in C, C++, Java and Python.
An adjacency list represents a graph as an array of linked lists. The index of the array represents a vertex and each element in its linked list represents the other vertices that form an edge with the vertex.
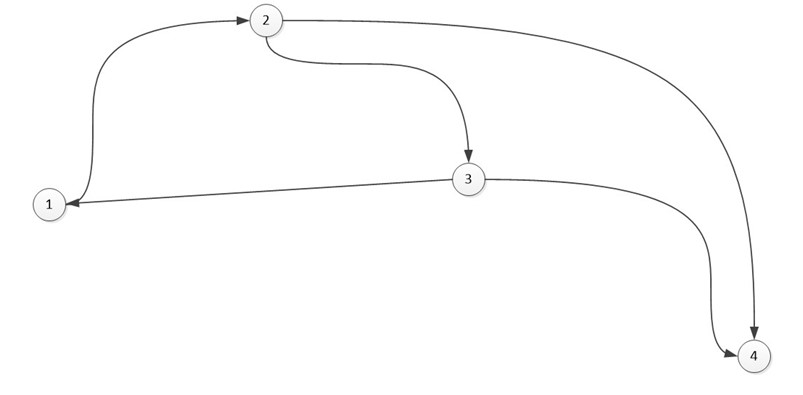
For example, we have a graph below.
We can represent this graph in the form of a linked list on a computer as shown below.
Here, 0, 1, 2, 3 are the vertices and each of them forms a linked list with all of its adjacent vertices. For instance, vertex 1 has two adjacent vertices 0 and 2. Therefore, 1 is linked with 0 and 2 in the figure above.
Pros of Adjacency List
- An adjacency list is efficient in terms of storage because we only need to store the values for the edges. For a sparse graph with millions of vertices and edges, this can mean a lot of saved space.
- It also helps to find all the vertices adjacent to a vertex easily.
Cons of Adjacency List
- Finding the adjacent list is not quicker than the adjacency matrix because all the connected nodes must be first explored to find them.
Adjacency List Structure
The simplest adjacency list needs a node data structure to store a vertex and a graph data structure to organize the nodes.
We stay close to the basic definition of a graph — a collection of vertices and edges {V, E}. For simplicity, we use an unlabeled graph as opposed to a labeled one i.e. the vertices are identified by their indices 0,1,2,3.
Let’s dig into the data structures at play here.
struct node{
int vertex;
struct node* next;
};
struct Graph{
int numVertices;
struct node** adjLists;
};Don’t let the struct node** adjLists overwhelm you.
All we are saying is we want to store a pointer to struct node*. This is because we don’t know how many vertices the graph will have and so we cannot create an array of Linked Lists at compile time.
Adjacency List C++
It is the same structure but by using the in-built list STL data structures of C++, we make the structure a bit cleaner. We are also able to abstract the details of the implementation.
class Graph{
int numVertices;
list<int> *adjLists;
public:
Graph(int V);
void addEdge(int src, int dest);
};Adjacency List Java
We use Java Collections to store the Array of Linked Lists.
class Graph{
private int numVertices;
private LinkedList<integer> adjLists[];
}The type of LinkedList is determined by what data you want to store in it. For a labeled graph, you could store a dictionary instead of an Integer
Adjacency List Python
There is a reason Python gets so much love. A simple dictionary of vertices and its edges is a sufficient representation of a graph. You can make the vertex itself as complex as you want.
graph = {'A': set(['B', 'C']),
'B': set(['A', 'D', 'E']),
'C': set(['A', 'F']),
'D': set(['B']),
'E': set(['B', 'F']),
'F': set(['C', 'E'])}Adjacency List Code in Python, Java, and C/C++
# Adjascency List representation in Python
class AdjNode:
def __init__(self, value):
self.vertex = value
self.next = None
class Graph:
def __init__(self, num):
self.V = num
self.graph = [None] * self.V
# Add edges
def add_edge(self, s, d):
node = AdjNode(d)
node.next = self.graph[s]
self.graph[s] = node
node = AdjNode(s)
node.next = self.graph[d]
self.graph[d] = node
# Print the graph
def print_agraph(self):
for i in range(self.V):
print("Vertex " + str(i) + ":", end="")
temp = self.graph[i]
while temp:
print(" -> {}".format(temp.vertex), end="")
temp = temp.next
print(" n")
if __name__ == "__main__":
V = 5
# Create graph and edges
graph = Graph(V)
graph.add_edge(0, 1)
graph.add_edge(0, 2)
graph.add_edge(0, 3)
graph.add_edge(1, 2)
graph.print_agraph()// Adjascency List representation in Java
import java.util.*;
class Graph {
// Add edge
static void addEdge(ArrayList<ArrayList<Integer>> am, int s, int d) {
am.get(s).add(d);
am.get(d).add(s);
}
public static void main(String[] args) {
// Create the graph
int V = 5;
ArrayList<ArrayList<Integer>> am = new ArrayList<ArrayList<Integer>>(V);
for (int i = 0; i < V; i++)
am.add(new ArrayList<Integer>());
// Add edges
addEdge(am, 0, 1);
addEdge(am, 0, 2);
addEdge(am, 0, 3);
addEdge(am, 1, 2);
printGraph(am);
}
// Print the graph
static void printGraph(ArrayList<ArrayList<Integer>> am) {
for (int i = 0; i < am.size(); i++) {
System.out.println("nVertex " + i + ":");
for (int j = 0; j < am.get(i).size(); j++) {
System.out.print(" -> " + am.get(i).get(j));
}
System.out.println();
}
}
}// Adjascency List representation in C
#include <stdio.h>
#include <stdlib.h>
struct node {
int vertex;
struct node* next;
};
struct node* createNode(int);
struct Graph {
int numVertices;
struct node** adjLists;
};
// Create a node
struct node* createNode(int v) {
struct node* newNode = malloc(sizeof(struct node));
newNode->vertex = v;
newNode->next = NULL;
return newNode;
}
// Create a graph
struct Graph* createAGraph(int vertices) {
struct Graph* graph = malloc(sizeof(struct Graph));
graph->numVertices = vertices;
graph->adjLists = malloc(vertices * sizeof(struct node*));
int i;
for (i = 0; i < vertices; i++)
graph->adjLists[i] = NULL;
return graph;
}
// Add edge
void addEdge(struct Graph* graph, int s, int d) {
// Add edge from s to d
struct node* newNode = createNode(d);
newNode->next = graph->adjLists[s];
graph->adjLists[s] = newNode;
// Add edge from d to s
newNode = createNode(s);
newNode->next = graph->adjLists[d];
graph->adjLists[d] = newNode;
}
// Print the graph
void printGraph(struct Graph* graph) {
int v;
for (v = 0; v < graph->numVertices; v++) {
struct node* temp = graph->adjLists[v];
printf("n Vertex %dn: ", v);
while (temp) {
printf("%d -> ", temp->vertex);
temp = temp->next;
}
printf("n");
}
}
int main() {
struct Graph* graph = createAGraph(4);
addEdge(graph, 0, 1);
addEdge(graph, 0, 2);
addEdge(graph, 0, 3);
addEdge(graph, 1, 2);
printGraph(graph);
return 0;
}// Adjascency List representation in C++
#include <bits/stdc++.h>
using namespace std;
// Add edge
void addEdge(vector<int> adj[], int s, int d) {
adj[s].push_back(d);
adj[d].push_back(s);
}
// Print the graph
void printGraph(vector<int> adj[], int V) {
for (int d = 0; d < V; ++d) {
cout << "n Vertex "
<< d << ":";
for (auto x : adj[d])
cout << "-> " << x;
printf("n");
}
}
int main() {
int V = 5;
// Create a graph
vector<int> adj[V];
// Add edges
addEdge(adj, 0, 1);
addEdge(adj, 0, 2);
addEdge(adj, 0, 3);
addEdge(adj, 1, 2);
printGraph(adj, V);
}Applications of Adjacency List
- It is faster to use adjacency lists for graphs having less number of edges.
Table of Contents
- Introduction
- Pros of Adjacency List
- Cons of Adjacency List
- Adjacency List Structure
- Adjacency List C++
- Adjacency List Java
- Adjacency List Python
- Adjacency List Code in Python, Java, and C/C++
- Applications of Adjacency List
Если хочешь подтянуть свои знания, загляни на наш курс «Алгоритмы и структуры данных», на котором ты:
- углубишься в решение практических задач;
- узнаешь все про сложные алгоритмы, сортировки, сжатие данных и многое другое.
Ты также будешь на связи с преподавателем и другими студентами.
В итоге будешь браться за сложные проекты и повысишь чек за свою работу 🙂
***
Продолжаем изучать популярные алгоритмы и структуры данных и их реализацию на JavaScript. В предыдущей статье мы разобрались с деревьями – нелинейными иерархическими структурами. В этой копнем еще глубже и познакомимся со старшими братьями деревьев – графами.
Другие статьи цикла:
- Часть 1. Основные понятия и работа с массивами
- Часть 2. Стеки, очереди и связные списки
- Часть 3. Деревья
- Часть 5. Объекты и хеширование
- Часть 6. Полезные алгоритмы для веб-разработки
Граф – это нелинейная структура, состоящая из конечного множества вершин, соединенных между собой ребрами. Порядок соединения может быть любым.
Количество вершин определяет порядок графа, а количество ребер – его размер.
Если две вершины графа соединены одним ребром, они называются соседними, или смежными. В графе также могут быть отдельно стоящие вершины, не связанные с другими, они называются изолированными. Количество ребер, исходящих из вершины, определяют ее степень связности.
Значение и применение структуры
Основная задача графа – отображать связи (ребра) между разными сущностями (вершины). Самый простой пример – карта метро, на которой станции являются вершинами графа, а связывающие их перегоны – ребрами.
Деревья, которые мы разбирали в предыдущей части цикла, также являются графами.
С помощью графов можно представить связи между пользователями социальной сети (подписки) или ссылки между разными страницами одного сайта (перелинковка). В таких графах ребра будут иметь направление – пользователь А подписан на пользователя Б, а не наоборот. Это ориентированные графы.
Любой набор объектов, между которыми есть связи, можно изобразить в виде графа.
В настоящее время это очень востребованная структура данных, так как она позволяет работать с большими объемами плохо структурированной информации. На графах, например, основываются разнообразные системы рекомендаций и ранжирования контента.
Итак, зачем нужны графы, разобрались, но остается неясным, как их использовать. В JavaScript мы не можем просто нарисовать несколько вершин и соединить их ребрами – нужен какой-то способ представления.
Список смежности
Самый простой способ – для каждой вершины графа хранить список вершин, смежных с ней (или вершин, в которые можно попасть из текущей вершины). Это и есть список смежности.
При его составлении для ориентированного графа важно учитывать направление ребер.
Для первого (неориентированного) графа список смежности будет выглядеть так:
const graph = {
1: [2,4],
2: [1,3,4],
3: [2,4]
4: [1,2,3]
}
Мы представили его в виде JavaScript-объекта с четырьмя свойствами, каждое из которых соответствует вершине графа. В качестве значений – массивы смежных вершин:
- из вершины 1 можно попасть в 2 и 4;
- из вершины 2 можно попасть в 1, 3 и 4;
- из вершины 3 можно попасть в 2 и 4;
- из вершины 4 можно попасть в 1, 2, 3.
Ориентированный граф выглядит почти так же, но список смежности у него другой:
const graph = {
1: [2],
2: [3,4],
3: [],
4: [1,3]
}
Из вершины 3 не выходит ни одно ребро, поэтому из нее нельзя никуда попасть – ее массив смежных вершин пуст.
Матрица смежности
Еще один распространенный способ представления графа – матрица смежности. Ее можно представить в виде таблицы. По обеим осям матрицы располагаются вершины графа, а на их пересечении указывается, есть ли связь между этими вершинами.
Связь определяется построчно. Первая строка соответствует вершине 1, нужно определить, есть ли путь из нее в вершины, представленные столбцами таблицы.
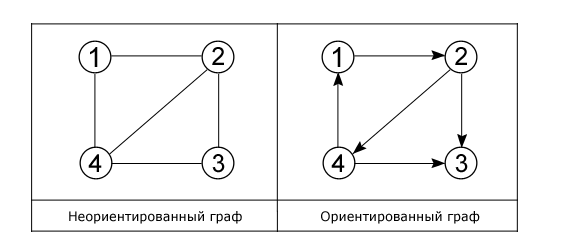
У неориентированного графа матрица смежности симметрична, а у ориентированного – нет.
На JavaScript граф можно представить в виде двумерного массива:
const graph = [
[ 0, 1, 0, 0 ],
[ 0, 0, 1, 1 ],
[ 0, 0, 0, 0 ],
[ 1, 0, 1, 0 ],
]
Сравнение способов
Список смежности – более компактный способ представления графа, он требует меньше памяти и особенно удобен для «разреженных» графов, у которых немного ребер.
В то же время матрица – более наглядная и удобная структура, позволяющая быстро определить, есть ли связь между двумя вершинами. Для «плотных» графов с большим количеством ребер матрица обычно выгоднее, чем список.
Способ представления структуры данных следует выбирать в зависимости от задачи и требований к использованию памяти и вычислительной сложности.
Например, операция проверки наличия связи между двумя вершинами a и b в матрице занимает константное время – достаточно лишь проверить элемент graph[a][b]. В списке смежности же это будет сложнее – потребуется поиск элемента b в массиве graph[a].
Помимо списка и матрицы смежности можно использовать и более абстрактные представления, например, хранить отдельно множество вершин и отдельно множество ребер.
Реализация на JavaScript
Напишем класс для самого простого неориентированного графа с хранением данных в виде списка смежности.
class Graph {
constructor() {
this.vertices = {}; // список смежности графа
}
addVertex(value) {
if (!this.vertices[value]) {
this.vertices[value] = [];
}
}
addEdge(vertex1, vertex2) {
if (!(vertex1 in this.vertices) || !(vertex2 in this.vertices)) {
throw new Error('В графе нет таких вершин');
}
if (!this.vertices[vertex1].includes(vertex2)) {
this.vertices[vertex1].push(vertex2);
}
if (!this.vertices[vertex2].includes(vertex1)) {
this.vertices[vertex2].push(vertex1);
}
}
}
Основные методы графа:
addVertex– добавление новой вершины;addEdge– добавление нового ребра.
Так как граф неориентированный, новое ребро является двусторонней связью, поэтому мы добавляем новые записи в списки обеих смежных вершин. Для ориентированного графа нужно лишь немного изменить метод addEdge, чтобы новая связь шла лишь в одном направлении.
Основные алгоритмы на графах
Мы разберем лишь две востребованные в программировании задачи: обход графа (в т.ч. поиск в графе) и нахождение кратчайшего пути между двумя вершинами.
- 🌌 10 анимированных алгоритмов на графах
Обход графа
Как и в случае с деревьями, у нас есть два способа обхода графов с разным порядком перебора вершин: поиск в ширину и поиск в глубину. Принципиально они не отличаются от алгоритмов обхода деревьев.
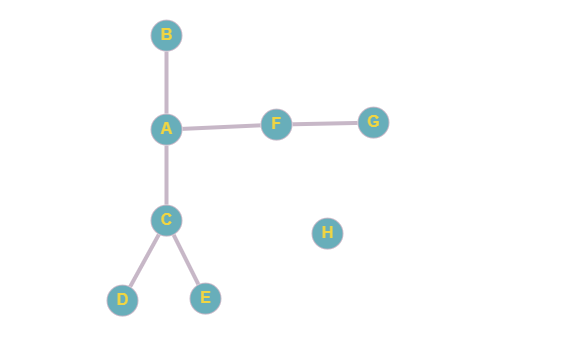
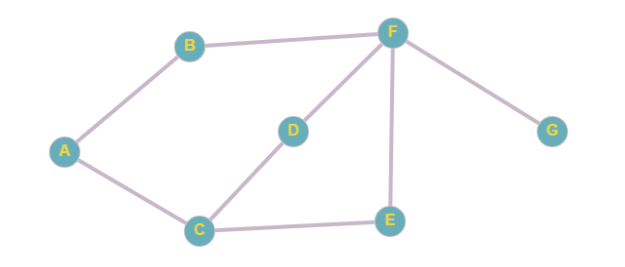
Создадим тестовый граф для демонстрации работы алгоритмов:
Перенесем его представление в JavaScript:
const graph = new Graph();
graph.addVertex('A');
graph.addVertex('B');
graph.addVertex('C');
graph.addVertex('D');
graph.addVertex('E');
graph.addVertex('F');
graph.addVertex('G');
graph.addVertex('H');
graph.addEdge('A', 'B');
graph.addEdge('A', 'C');
graph.addEdge('C', 'D');
graph.addEdge('C', 'E');
graph.addEdge('A', 'F');
graph.addEdge('F', 'G');
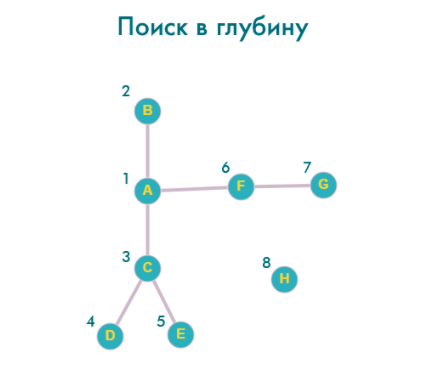
Поиск в глубину (depth-first search)
Алгоритм поиска в глубину движется последовательно по ветвям графа от начала до конца.
Когда мы разбирали этот алгоритм на примере деревьев, то использовали его рекурсивную реализацию – функция поиска для одного узла вызывала сама себя для его дочерних узлов. Это, вероятно, более очевидный и понятный путь, но он может приводить к переполнению стека вызовов для больших графов. Поэтому сейчас для разнообразия мы рассмотрим итеративную реализацию поиска в глубину.
Для этого нам понадобится вспомогательная структура данных – стек, мы уже знакомились с ним во второй части цикла. В стеке мы будем хранить вершины, которые нужно посетить.
Кроме того, нужно отмечать вершины, которые уже были посещены, чтобы не перебирать их повторно. В дереве нам не требовалось делать это, но графы имеют более сложную структуру, в которой могут встречаться циклы.
Перебор может начинаться с любой вершины графа. Стартовую вершину сразу же отмечаем как посещенную и добавляем ее в стек, а дальше начинается собственно алгоритм:
- Берем вершину с конца стека. В соответствии с описанием структуры данных стек это будет вершина, добавленная в него последней.
- Получаем все ее смежные вершины.
- Отбрасываем те вершины, которые уже были посещены ранее.
- Остальные отмечаем как посещенные, добавляем в стек и возвращаемся к пункту 1.
Таким образом мы будем двигаться в глубину ветки, обрабатывая сначала «более глубокие» вершины, а когда в ней закончатся непосещенные вершины, просто перейдем к следующей ветке.
На JavaScript это может выглядеть так:
class Graph {
// ..
dfs(startVertex, callback) {
let list = this.vertices; // список смежности
let stack = [startVertex]; // стек вершин для перебора
let visited = { [startVertex]: 1 }; // посещенные вершины
function handleVertex(vertex) {
// вызываем коллбэк для посещенной вершины
callback(vertex);
// получаем список смежных вершин
let reversedNeighboursList = [...list[vertex]].reverse();
reversedNeighboursList.forEach(neighbour => {
if (!visited[neighbour]) {
// отмечаем вершину как посещенную
visited[neighbour] = 1;
// добавляем в стек
stack.push(neighbour);
}
});
}
// перебираем вершины из стека, пока он не опустеет
while(stack.length) {
let activeVertex = stack.pop();
handleVertex(activeVertex);
}
// проверка на изолированные фрагменты
stack = Object.keys(this.vertices);
while(stack.length) {
let activeVertex = stack.pop();
if (!visited[activeVertex]) {
visited[activeVertex] = 1;
handleVertex(activeVertex);
}
}
}
}
Несколько важных моментов:
- Для хранения посещенных вершин мы используем не массив, а объект, так как наличие свойства в объекте проверить проще, чем наличие элемента в массиве.
- При добавлении смежных вершин в стек, мы используем метод
reverse, то есть добавляем их в обратном порядке. Это нужно для того, чтобы перебор веток происходил в том же порядке, в котором они были добавлены. - После того, как стек опустел, мы дополнительно проверяем все вершины графа на предмет посещенности. Это необходимо, так как в графе могут быть изолированные вершины или подграфы, например, в нашем тестовом графе такая вершина есть. Непосещенные вершины обрабатываем. Если в графе нет изолированных фрагментов, то эту часть можно опустить.
Запустим этот метод для нашего тестового графа:
graph.dfs('A', v => console.log(v));
Порядок перебора вершин:
A -> B -> C -> D -> E -> F -> G -> H
Поиск в глубину напоминает поиск пути в лабиринте, алгоритм идет по ветке, пока не упрется в «стену», после этого он возвращается назад.
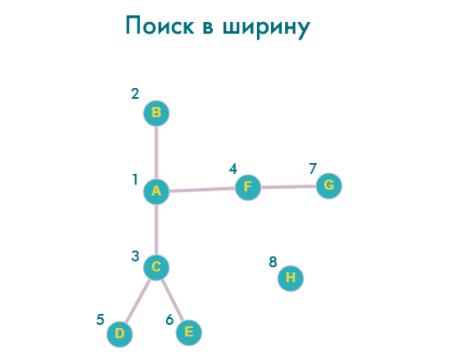
Поиск в ширину (breadth-first-search)
Алгоритм поиска в ширину сначала перебирает все смежные вершины, затем смежные вершины смежных вершин и так далее по уровням.
В алгоритме DFS мы использовали стек для временного хранения вершин, которые нужно перебрать. Поиск в ширину же использует очередь.
Первый узел, в которого начинается обход, отмечается как посещенный и помещается в очередь. Далее совершаем следующие действия:
- Берем вершину с начала очереди. В соответствии с описанием структуры данных очередь это будет вершина, добавленная в нее самой первой.
- Получаем все ее смежные вершины.
- Отбрасываем те вершины, которые уже были посещены ранее.
- Остальные отмечаем как посещенные, добавляем в стек и возвращаемся к пункту 1.
Обратите внимание, алгоритм абсолютно такой же, как и алгоритм поиска в глубину – разница только в порядке извлечения узлов. Вот так выбор простейшей структуры данных (стека или очереди) влияет на результат выполнения задачи.
На JavaScript поиск в ширину выглядит примерно так:
class Graph {
// ..
bfs(startVertex, callback) {
let list = this.vertices; // список смежности
let queue = [startVertex]; // очередь вершин для перебора
let visited = { [startVertex]: 1 }; // посещенные вершины
function handleVertex(vertex) {
// вызываем коллбэк для посещенной вершины
callback(vertex);
// получаем список смежных вершин
let neighboursList = list[vertex];
neighboursList.forEach(neighbour => {
if (!visited[neighbour]) {
visited[neighbour] = 1;
queue.push(neighbour);
}
});
}
// перебираем вершины из очереди, пока она не опустеет
while(queue.length) {
let activeVertex = queue.shift();
handleVertex(activeVertex);
}
queue = Object.keys(this.vertices);
// Повторяем цикл для незатронутых вершин
while(queue.length) {
let activeVertex = queue.shift();
if (!visited[activeVertex]) {
visited[activeVertex] = 1;
handleVertex(activeVertex);
}
}
}
}
В этой реализации мы не переворачиваем массив смежных вершин, так как из очереди они и так будут извлекаться в правильном порядке.
После перебора основного дерева обязательно повторяем процедуру для всех изолированных вершин.
Запустим этот метод для нашего тестового графа:
graph.bfs('A', v => console.log(v));
Порядок перебора вершин:
A -> B -> C -> F -> D -> E -> G -> H
Рисунок поиска в ширину напоминает круги на воде – сначала исследуются вершины в границах маленького круга, затем он увеличивается.
Поиск кратчайшего пути
Одной из базовых задач при работе с графами является определение кратчайшего пути между двумя вершинами. Такие алгоритмы очень востребованы, например, в картографических сервисах (Google maps) для прокладывания маршрута между двумя точками.
Вариантов постановки этой задачи очень много, мы начнем с самого простого.
Представьте, что вам требуется построить маршрут, проходящий через наименьшее количество станций или населенных пунктов.
Например, в этом графе из точки A в точку G можно попасть тремя разными способами. Как выяснить, какой из них самый быстрый?
Сначала создадим JavaScript-представление этой структуры:
let graph = new Graph();
graph.addVertex('A');
graph.addVertex('B');
graph.addVertex('C');
graph.addVertex('D');
graph.addVertex('E');
graph.addVertex('F');
graph.addVertex('G');
graph.addVertex('H');
graph.addEdge('A', 'B');
graph.addEdge('B', 'F');
graph.addEdge('F', 'G');
graph.addEdge('A', 'C');
graph.addEdge('C', 'D');
graph.addEdge('D', 'F');
graph.addEdge('C', 'E');
graph.addEdge('E', 'F');
Для решения нашей задачи подойдет уже знакомый нам алгоритм поиска в ширину с некоторыми модификациями.
Необходимо по ходу работы алгоритма сохранять дополнительную информацию, чтобы затем восстановить путь из исходной вершины в искомую. Мы будем сохранять расстояние каждой вершины от исходной, а также для каждой вершины – предыдущую вершину, из которой мы пришли.
class Graph {
// ..
bfs2(startVertex) {
let list = this.vertices;
let queue = [startVertex];
let visited = { [startVertex]: 1 };
// кратчайшее расстояние от стартовой вершины
let distance = { [startVertex]: 0 };
// предыдущая вершина в цепочке
let previous = { [startVertex]: null };
function handleVertex(vertex) {
let neighboursList = list[vertex];
neighboursList.forEach(neighbour => {
if (!visited[neighbour]) {
visited[neighbour] = 1;
queue.push(neighbour);
// сохраняем предыдущую вершину
previous[neighbour] = vertex;
// сохраняем расстояние
distance[neighbour] = distance[vertex] + 1;
}
});
}
// перебираем вершины из очереди, пока она не опустеет
while(queue.length) {
let activeVertex = queue.shift();
handleVertex(activeVertex);
}
return { distance, previous }
}
}
Обработка изолированных фрагментов графа здесь не требуется. Между изолированными подграфами пути нет, ни кратчайшего, ни какого-либо другого, мы и так это увидим.
Опробуем обновленный алгоритм:
let data = graph.bfs2('A');
/*
{
distance: {
A: 0,
B: 1,
C: 1,
D: 2,
E: 2,
F: 2,
G: 3
},
previous: {
A: null,
B:'A',
C:'A',
D:'C',
E: 'C',
F:'B',
G: 'F'
},
}
*/
В свойстве distance хранятся кратчайшие расстояния от вершины А до всех остальных вершин графа. Выходит, что до вершины G можно добраться всего за три шага. А восстановить этот путь поможет свойство previous, которое хранит всю цепочку шагов:
class Graph {
// ...
findShortestPath(startVertex, finishVertex) {
let result = this.bfs2(startVertex);
if (!(finishVertex in result.previous))
throw new Error(`Нет пути из вершины ${startVertex} в вершину ${finishVertex}`);
let path = [];
let currentVertex = finishVertex;
while(currentVertex !== startVertex) {
path.unshift(currentVertex);
currentVertex = result.previous[currentVertex];
}
path.unshift(startVertex);
return path;
}
}
Запустим алгоритм поиска:
graph.findShortestPath('A', 'G'); // ['A', 'B', 'F', 'G']
graph.findShortestPath('A', 'Z'); // Error: Нет пути из вершины A в вершину Z
Взвешенные графы
Зачастую нам интересен не только факт наличия связи между двумя сущностями (смежность вершин, наличие ребра между ними), но и некоторые характеристики этой связи.
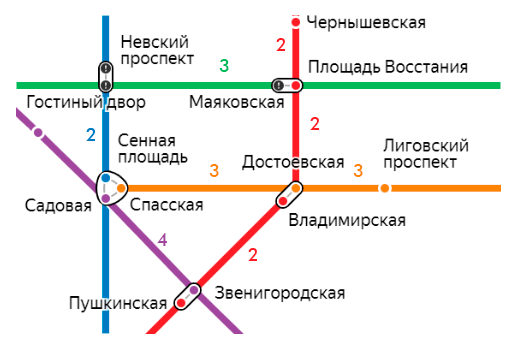
Для примера возьмем карту метро. Перегоны между станциями отличаются расстоянием.
В этом графе каждому ребру (перегон) соответствует число, равное времени в пути в минутах между смежными станциями. Это число называют весом ребра, а сам граф взвешенным.
Представление взвешенного графа
Для взвешенного графа необходимо хранить не только факт связи, но и вес ребра, соединяющего две вершины.
Попробуем перенести в JavaScript вот такой граф:
Если мы используем матрицу смежности, то веса можно подставлять вместо единиц и нулей (наличие или отсутствие связи).
| A | B | C | D | E | F | G | |
| A | 0 | 2 | 1 | 0 | 0 | 0 | 0 |
| B | 0 | 0 | 0 | 0 | 0 | 7 | 0 |
| C | 0 | 0 | 0 | 5 | 2 | 0 | 0 |
| D | 0 | 0 | 0 | 0 | 0 | 2 | 0 |
| E | 0 | 0 | 0 | 0 | 0 | 1 | 0 |
| F | 0 | 0 | 0 | 0 | 0 | 0 | 1 |
| G | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
В списках смежности нужно поставить в соответствие каждой смежной вершине вес ребра, ведущего к ней. Для этого мы можем использовать, например, вложенные массивы:
let graph = {
a: [ [b, 2], [c, 1] ],
b: [ [f, 7] ],
c: [ [d, 5], [e, 2] ],
d: [ [f, 2] ],
e: [ [f, 1] ],
f: [ [g, 1] ],
g: [ ]
}
Первым элементом в массиве идет сама смежная вершина, вторым – длина пути до нее (вес ребра).
Или можно представить то же самое с помощью объектов JavaScript:
let graph = {
a: { b: 2, c: 1 },
b: { f: 7 },
c: { d: 5, e: 2 },
d: { f: 2 },
e: { f: 1 },
f: { g: 1 },
g: { },
}
Дальше мы будем использовать именно такое представление.
Кратчайший путь во взвешенном графе
Задача поиска кратчайшего пути во взвешенном графе встречается еще чаще, чем в невзвешенном. Например, для построения самого быстрого маршрута между двумя станциями метро или для сетевых протоколов маршрутизации. И здесь все намного интереснее. Мы не можем полагаться на количество ребер между вершинами, а значит, поиск в ширину нам не поможет.
В графе на картинке выше более короткий (по количеству ребер) путь ABFG весит 10, а вот более длинный ACEFG – всего 5, и он оказывается выгоднее.
Для поиска кратчайшего пути во взвешенных графах существует множество алгоритмов. Некоторые из них могут работать даже с отрицательными весами. Мы рассмотрим один из самых популярных.
Алгоритм Дейкстры
Алгоритм Дейкстры предназначен для нахождения кратчайших путей во взвешенных графах с неотрицательными весами ребер.
Он похож на поиск в ширину – мы начинаем со стартовой вершины и перебираем ее смежные вершины. На каждом шаге мы рассчитываем все возможные пути до вершины и выбираем среди них самый короткий.
Изначально полагается, что путь до каждой вершины неизвестен и равен бесконечности, кроме пути до стартовой вершины, который равен нулю.
На каждом шаге выбирается самая близкая из известных вершин. На первом шаге это стартовая вершина, так как о других мы просто ничего не знаем.
Для выбранной вершины мы можем получить ее смежные вершины и расстояния до них (вес ребер). А зная расстояние от стартовой вершины до текущей и расстояния от текущей вершины до ее смежных вершин, мы можем рассчитать и расстояния от стартовой вершины до смежных.
Текущая вершина отмечается как посещенная и в дальнейших манипуляциях не участвует.
Затем все действия повторяются: мы выбираем самую близкую из известных вершин, не считая посещенных. Теперь известных вершин стало больше, поэтому есть из чего выбирать. Находим смежные вершины и обновляем расстояния до них.
Если расстояние для какой-то вершины уже было определено на предыдущих шагах, мы должны сравнить его с новым и выбрать минимальное.
Чтобы восстановить кратчайший путь до нужной вершины, мы дополнительно должны сохранять предыдущую вершину в этом пути, как мы уже делали для невзвешенного графа.
Реализация алгоритма Дейкстры на JavaScript
Для реализации алгоритма Дейкстры на потребуется вспомогательная функция для поиска ближайшей вершины из известных:
function findNearestVertex(distances, visited) {
let minDistance = Infinity;
let nearestVertex = null;
Object.keys(distances).forEach(vertex => {
if (!visited[vertex] && distances[vertex] < minDistance) {
minDistance = distances[vertex];
nearestVertex = vertex;
}
});
return nearestVertex;
}
Она принимает объект distances, в котором каждой вершине соответствует известное на данный момент расстояние, и объект visited, в котором отмечены посещенные вершины.
Сам алгоритм выглядит так:
function dijkstra(graph, startVertex) {
let visited = {};
let distances = {}; // кратчайшие пути из стартовой вершины
let previous = {}; // предыдущие вершины
let vertices = Object.keys(graph); // список вершин графа
// по умолчанию все расстояния неизвестны (бесконечны)
vertices.forEach(vertex => {
distances[vertex] = Infinity;
previous[vertex] = null;
});
// расстояние до стартовой вершины равно 0
distances[startVertex] = 0;
function handleVertex(vertex) {
// расстояние до вершины
let activeVertexDistance = distances[vertex];
// смежные вершины (с расстоянием до них)
let neighbours = graph[activeVertex];
// для всех смежных вершин пересчитать расстояния
Object.keys(neighbours).forEach(neighbourVertex => {
// известное на данный момент расстояние
let currentNeighbourDistance = distances[neighbourVertex];
// вычисленное расстояние
let newNeighbourDistance = activeVertexDistance + neighbours[neighbourVertex];
if (newNeighbourDistance < currentNeighbourDistance) {
distances[neighbourVertex] = newNeighbourDistance;
previous[neighbourVertex] = vertex;
}
});
// пометить вершину как посещенную
visited[vertex] = 1;
}
// ищем самую близкую вершину из необработанных
let activeVertex = findNearestVertex(distances, visited);
// продолжаем цикл, пока остаются необработанные вершины
while(activeVertex) {
handleVertex(activeVertex);
activeVertex = findNearestVertex(distances, visited);
}
return { distances, previous };
}
Запустим алгоритм для нашего взвешенного графа:
dijkstra(graph, 'a');
/*
{
distances: {
a: 0,
b: 2,
c: 1,
d: 6,
e: 3,
f: 4,
g: 5
},
previuos: {
a: null,
b: 'a',
c: 'a',
d: 'c',
e: 'c',
f: 'e',
g: 'f',
}
}
*/
Кратчайший путь от A до G составляет 5 и проходит через вершины ACEFG (Алгоритм восстановления пути по объекту previous рассмотрен выше).
Заключение
В современном информационном мире графы – одна из важнейших структур данных, которая позволяет отобразить связи между объектами. Одновременно это одна из самых сложных структур. Существует множество разновидностей графов: кроме взвешенных и ориентированных графов, с которыми мы познакомились, существуют, например, псевдографы (графы, в структуре которых содержатся петли). Соответственно, существует и множество алгоритмов, работающих с графами.
Мы разобрали практически все популярные структуры данных, которые могут пригодиться JavaScript-разработчику в работе или на собеседовании: массивы, связные списки, стеки и очереди, а также деревья и графы.
В следующей статье цикла мы поговорим про еще одну очень важную структуру – хеш-таблицу.
Лекция 7. Графы и деревья
1. Способы задания графа в программировании
1.1. Неформальное определение понятия графа
Если говорить не формально, то граф представляет собой какое-либо множество (обычно конечное) вершин (изображаемых точками), некоторые из которых соединенны дугами (реберами).
При этом какие-либо две вершины могут быть соедениены несколькими дугами (такие дуги называют кратными, или мульти-дугами). Кроме того, концы дуг могут совпадать — такие ребра называют петлями. Также иногда рассматривают ребра, один конец которых присоединен к некоторый вершине, а другой — свободный, т.е. ни к какой вершине не присоединенный (такие ребра называются висячими — их не надо путать с висячими вершинами, см. ниже).
При изображении графа взаимное расположение вершин и форма соединяющих их дуг (ребер) значения не имеют, важен только факт соединения или его отсутсвие.
Ребрам графа может приписываться некоторая ориентация (при изображении на дугах ставится «стрелочка») — в этом случае граф называется ориентированным. В противном случае граф называется неориентированным.
Иногда каждому ребру графа приписывается некоторое число (вес, стоимость). В этом случае граф называют взвешенным.
Кроме того, иногда вершинам графа приписываются некоторые значения (данные). В этом случае можно, например, все вершины графа проиндесировать значениями 1,2,3,...,n (начиная с 1 и заканчивая числом вершин n, без пропусков). Тогда данные, связанные с вершинами могут хранится в отдельном одномерном массиве длины n, каждый i-ый элемент которого должен соответствовать i-ой вершине графа.
1.2. Формальные определения
Хотя мы могли бы и обойтись без формального определения графа: для практического программирования сказанного в предыдущем разделе достаточно, однако всё же полезно это сделать.
Графы бывают ориентированные, неориентированные, простые, с петлями, с кратными рёбрами, с висячими рёбрами. В большинстве источников эти понятия определяются по отдельности, мы же дадим одно самое общее определение.
Прежде всего, чтобы в одном определении охватить и случай графа с кратными ребрами, нам понадобится понятие мультимножества.
Определение. Говорят, что над множеством $A$ определено мультимножество, если на этом множестве задана функция принадлежности $mu: A to {{0,1,2,…}}$, причем $a in A Leftrightarrow mu(a)>0$, при этом значение $mu(a)$ называется кратностью элемента $a$.
В частном случае, когда кратнасти элементов некоторого мультимножества не превышают 1, имеем обычное множество.
Перейдем теперь к понятию графа. Пусть $V$ — множество вершин (некоторое абстрактное множество), и пусть $overline{V}=Vcup{}$, где $$ — это символ, обозначающий факт отсутствия вершины (иногда отсутствующую вершину $*$ называют еще внешней вершиной).
Определение. Ориентированным мультиграфом называется пара $(V, varepsilon)$, где $varepsilon$ — некоторе отображение $overline{V} times overline{V} to {0,1,2,…}$.
При этом $E={(u,v)inoverline{V} times overline{V} |varepsilon((u,v))ne 0}$ — множестово всех ребер графа.
Употребляя термин — граф, мы имеем ввиду сейчас самый общий случай: ориенированный мультиграф. Граф часто обозначают одной буквой, например $G=(V, varepsilon)$.
В частности, если ребра ориентированного мультиграфа не имеют кратностей больших 1, то можно считать, что $G=(V,E)$, т.е. — что граф представляет собой пару множеств: множество вершин и множество ребер.
В любом случае, при условии $varepsilon((u,v)) ne 0$, $(u,v)$ — это обычное ребро. При этом, считается, что ребра $(u,v)$ и $(v,u)$ имеют противоположную ориентацию.
При этом ${(u,) | u in V, varepsilon((u,))ne 0} cup {(,v) |v in V, varepsilon((,v))ne 0 }$ — это множество всех висячих ребер.
Не надо путать понятие висячего ребра с понятием висячей вершины: вершина называется висячей если она соединена только с одним ребром (если она инцидентна только одному ребру).
Ребро вида $(u,u)$ называется петлей.
Граф без петель, без кратных и висячих ребер называется простым графом. Именно с простыми графами чаще всего приходится иметь дело.
Неориентированный граф. В частности, если ориетированный простой граф обладает следующим свойством:
$(u,v) in E Leftrightarrow (v,u) in E (une v)$, то такой граф можно считать неориентированным графом, если каждую пару противонаправленных ребер рассматривать как одно ненаправленное ребро.
1.3. Способы задания графа
Из сказанного в предыдущем разделе должно быть ясно, что задать граф — означает задать множество его вершин $V$ и функцию принадлежности $varepsilon: overline{V} times overline{V} to {0,1,2,…}$.
Обычно считается, что $V={1,2,3,…,n}$, тогда функция принадлежности $varepsilon$ может быть задана квадратной матрицей размера $ntimes n$, в которой $i,j$-элемент равет $varepsilon((i,j))$.
В случае отсутствия кратных ребер в графе такая матрица называется матрицей смежности.
Функцию принадлежности можно задать также с помощью матрицы инциденций, т.е. с помощью прямоугольной матрицы, строки которой индексируются номерами вершин графа, а столбцы — номерами ребер (имеется ввиду, что множество $E$ каким-либо образом, безразлично каким, упорядочено), при этом её $i,j$-элемент равен 0, если только $e_j[1]ne i$, и $varepsilon((i,e_j[2]))$, в противном случае.
Здесь по умолчанию предполагалось следующее соглашение об обозначениях: если $e_j=(u,v)$, то $e_j[1]=u, e_j[2]=v$.
В программировании матрица инциденций обычно не используется (в наиболее популярных алгоритмах, по крайней мере), в отличии от матрицы смежностей.
1.4. Использование разреженных матриц
Если число вершин в графе очень большое и если при этом граф является слабосвзанным, т.е. в его матрице смежности очень много нулей, то использование такой матрицы в программе может оказаться не слишком экономичным, в смысле расходования компьютерной памяти.
Однако в современных языках программирования, ориентированных на математические вычисления, существуют так называемые разреженные матрицы. Разреженные матрицы — это матрицы с большим числом нулей, и для их компактного представления требуется специальный тип.
Для Julia имеется соответствующий пакет SparseArrays (требующий предварительной установки), в котором для представления разреженных матриц определен специальный тип SparseMatrixCSC, позволяющий экономномить расходование компьютерной памяти, и при этом выполнять с такими матрицами привычные операции.
Например,
using SparseArrays I=[1, 2, 5, 4, 5] # - индексы строк с ненулевыми значениями J=[2, 2, 2, 3, 5] # - индексы столбцов с ненулевыми значениями V=[10, 10, 10, 20, 30] # - сами не нулевые значения A=sparse(I,J,V)
Тогда вывод разреженной матрицы A на экран будет иметь вид:
5×5 SparseMatrixCSC{Int64, Int64} with 5 stored entries: ⋅ 10 ⋅ ⋅ ⋅ ⋅ 10 ⋅ ⋅ ⋅ ⋅ ⋅ ⋅ ⋅ ⋅ ⋅ ⋅ 20 ⋅ ⋅ ⋅ 10 ⋅ ⋅ 30
где точками отмечены позиции с нулевыми значениями.
При этом если бы среди элементов вектора V были бы нули, то эти нули не формально рассматривались бы как ненулевые значения, в том сысле, что они бы всё равно реально размещались в памяти компьютера. Например:
I = [1, 2, 5, 4, 5] J = [2, 2, 2, 3, 5] V = [10, 0, 10, 20, 30] A = sparse(I,J,V) 5×5 SparseMatrixCSC{Int64, Int64} with 5 stored entries: ⋅ 10 ⋅ ⋅ ⋅ ⋅ 0 ⋅ ⋅ ⋅ ⋅ ⋅ ⋅ ⋅ ⋅ ⋅ ⋅ 20 ⋅ ⋅ ⋅ 10 ⋅ ⋅ 30
(новое нулевое значение в выводе не заменено точкой, это означает, что оно реально размещено в памяти).
Работать с разреженными матрицами формально можно точно как же, как и с обычными мартицами, для них переопределены все стандартные операции и функции.
При этом, если требуется перебрать все формально ненулевые элементы (реально размещенные в памяти) разреженной матрицы, то для этого дополнительно имеются специальные функции rowvals, nonzeros и nzrange, позволяющие это делать экономично, с учетом структуры разреженной матрицы, например:
rows = rowvals(A) # rowvals(A) - возвращает вектор индексов строк A, содержащих ФОРМАЛЬНО не нулевые значения vals = nonzeros(A) # nonzeros(A) - возвращает вектор значений всех ФОРМАЛЬНО не нулевых элементов матрицы A m, n = size(A) for j = 1:n for i in nzrange(A, j) #= если в j-ом столбце нет формально не нулевых элементов, то диапазон индексов, возвращаемых функцией nzrange(A, j) будет пустым =# index_row = rows[i] val = vals[i] # val - очередное ФОРМАЛЬНО не нулевое значение, которое в матрице A имеет индексы (index_row, j) end end
1.5. Список смежностей
Всё отмеченное в предыдущем разделе делает возможным эффективно использовать разреженные матрицы в том числе и для представления графов.
Однако во многих случаях вполне можно обходиться и без разреженных матриц, если для представления графа использовать так называемый список смежностей.
Список смежностей представляет собой вектор, индексы которого суть номера вершин графа, в каждой позиции содержащий вектор, элементами которого являются индексы вершин, смежных с данной (её индекс — это индекс данной позиции).
При этом, если рассматривается мультиграф, то кратные ребра в этом случае могут быть представлены путем дублирования индексов смежных вершин требуемое число раз.
Рассмотрим, например, полный граф с 5 вершинами (простой граф называется полным, если в нём каждая вершина смежна со всеми остальными). Представление этого графа списком смежностей будет иметь вид:
G=[[2,3,4,5], [1,3,4,5], [1,2,4,5], [1,2,3,5], [1,2,3,4]]
Если бы мы захотели изобразить этот граф, то из каждой вершины следовалобы направить ориентированное ребро во все остальные. При этом мы можем считать, что пара проивонаправленных ребер эквивалентна одному ненаправленному ребру.
Пусть теперь, например, в некотором графе из некоторой вершины не исходит ни одного ориентированного ребра, тогда соответствующий ей вектор с индексами смежных вершин должен быть пустым.
Вот пример такого графа (ориентированного)
G=[[2,3,4,5], [], [1,2,4,5], [1,2,3,5], [1,2,3,4]]
У этого графа во вторую вершину направлены ребра из всех остальных вершин, но из ней в обратном направлении нет ни одного исходящего ребра.
В некоторых случаях список смежностей удобно представлять не в виде одномерного массива (вектора), а в виде значения типа Dict, т.е. в виде словаря. Словарь состоит из пар типа Pair (есть в Julia такой тип данных), при этом каждая пара типа Pair задается в виде: key => value_of_key (ключ => значение_соответствующее_ключу). Тип Dict, как и тип Pair, является двухпараметрическим, первый параметр определяет тип ключа, а второй — тип соответствующего значения.
Например, представление графа из предыдущего примера в виде словаря будет выглядеть так:
G=Dict{Int,Vector{Int}}([ 1=>[2,3,4,5], 2=>[], 3=>[1,2,4,5], 4=>[1,2,3,5], 5=>[1,2,3,4] ])
Аргументом функции Dict{Int,Vector{Int}} в данном случае является вектор типа `Vector{Pair{Int, Vector{Int}}}.
Чтобы теперь, наоборот, из словаря G получить вектор из содержащихся в нём пар (если это вдруг понадобится), надо воспользоваться стандартной функцией collect:
collect(G) |> println # [1=>[2,3,4,5], 2=>[], 3=>[1,2,4,5], 4=>[1,2,3,5], 5=>[1,2,3,4]]
Тот же самый словарь G можно было бы создать и динамически:
G=Dict{Int, Vector{Int}}() # - создан пустой словарь нужного типа G[1]=[2,3,4,5] G[2]=[] G[3]=[1,2,4,5] G[4]=[1,2,3,5], G[5]=[1,2,3,4]
В отличие от массива, в словарь можно добавлять новые пары вида индекс => вектор_смежных_индексов динамически, причем необязательно, чтобы соблюдался порядок следования индексов, т.е. необязательно, чтобы сначала добавилась пара 1 => [...], затем — 2 => [...] и т.д. В словарь такие пары можно будет добавлять в произвольном порядке, по мере того, как они будут определяться при обходе дерева.
1.6. Представление графа со взвешенными ребрами
Если рассматривается взвешенный граф (без кратных и висячих ребер), т.е. если его ребрам приписаны некоторые числа (веса), то его можно представить с помощью так называемой весовой матрицы, подобной матрице смежностей, только вместо единичек в весовой матрице нахоядися веса ребер.
В этом есть одна особенность, состоящая в том, что предполагается, что веса ребер не могут быть нулевыми, и поэтому нули матрицы рассматриваются как информация об отсутствии соответствующих ребер в графе.
Такое допущение приемлемо для многих алгоритмов на графах. Если же, однако, в какой-либо задаче всё же понадобится учитывать фактическое наличие рёбер с нулевым весом, то это можно всегда сделать, если факт отсутствия ребра кодировать не нулем, а, например, значенем Inf (бесконечно большую стоимость ребра естественно интерпретировать как его отсутствие). Это решение годится, если используются обычные (не разреженные) матрицы.
Если же использовать разреженные матрицы, то необходимость в использовании значения Inf отпадает (более того, использование этого значения не желательно, поскольку это снизит до предела эффект от использования разреженных матриц). Это благодаря тому, что при работе с разреженными матрицами имеется возможность различать нулевые элементы реально размещаемые в памяти и не размещаемые в памяти. Т.о. последние можно интерпретировать как факт отсутствия соответствующих ребер.
В любом случае обычную матрицу смежностей можно трактовать как весовую матрицу графа, в котором все его ребра имеют единичный вес.
2. Способы задания корневых деревьев в программировании
Валентностью (или, по другому, степенью) вершины графа называется число инцидентных ей (присоединенных к ней) ребер.
Валентностью по выходу вершины ориентирванного графа называется число его ребер, для которых она является начальной.
Валентностью по входу вершины ориентированного графа называется число его ребер, для которых она является конечной.
Таким образом, валентность любой вершины графа равна сумме ее валентностей по входу и по выходу.
Говорят, что в графе вершина $v$ достижима из вершины $u$, если существует последовательность ребер графа $(v,v_1), (v_1,v_2),…,(v_n,u)$, в которой конец предшествующего ребра является началом последующего.
Корневым деревом называется ориентированный граф, у которого
- имеется ровно одна вершина, называемая корнем, валентность по входу которой равна 0;
- любая другая его вершина достижима из корня, и её валентоность по входу равна 1.
Очевидно, что
-
в любом корневом дереве имеются вершины, валентности по выходу которых равны 0 (т.к. число вершин конечно); такие вершины называются листьями;
-
никакое дерево не содержит циклов.
Представление корневого дерева списком смежностей.
Поскольку корневое дерево — это простой ориентированный граф, то теоретически для задания дерева можно использовать любой из способов задания простого ориентированного графа. Например, для его задания можно использовать список смежностей.
Однако важным отличием от задания графа общего вида является то, что у корневого дерева имеется выделенная вершина, называемая корнем, с которой всегда должен осуществляться обход дерева. Поэтому для задания корневого дерева кроме собственно списка смежностей требуется указывать еще индекс корневой вершины.
Помимо этого, существуют еще некоторые специфические способы задания корневого дерева можно.
Представление корневого дерева вложенными векторами.
Рассмотрим это на примерах:
-
Int[]— пустое дерево (не содержащее ни одной вершины); -
[1]— тривиальное дерево, состоящее только из корня; -
[[2], [3], 1]— дерево с корнем 1, которому соответствует список смежностей
[[2, 3], Int[], Int[]]; -
[[[4], [5], [6], 2], [[7], [8], 3], 1]— дерево с корнем 1, которому соответствует список смежностей[[2, 3], [4, 5, 6], [7, 8], Int[], Int[], Int[], Int[], Int[]];
Замечание. Бывают деревья, у вершин которых имеются специализированные валентности, например, — двоичные деревья, в каждом узле которых имеется зафиксированная позиция для корня левого поддерева и зафиксированная позиция для корня правого поддерев. При этом если в нкотрой вершине отсутствует какое-то одно из из двух поодеревьев (левое или правое), то способ кодирования дерева должен обеспечивать возможность определять какое же поддерево присутствует. В случае вложенных массивов это можно обеспечить используя пустые массивы для фиксации позиции отсутствующего поддерева. А в случае использования списка смежностей это можно сделать используя значение 0 (предполагается, что никакая вершина дерева не может иметь индекса 0).
Например:
-
Int[]— пустое дерево (не содержащее ни одной вершины); -
[Int[], Int[], 1]— тривиальное дерево, состоящее только из корня; -
[[Int[], Int[], 2], [Int[], Int[], 3], 1]— дерево с корнем 1, которому соответствует список смежностей[[2, 3], [0, 0], [0, 0]]; -
[[[Int[], Int[], 4], Int[], 2], [Int[], [Int[], Int[], 5], 3], 1]— дерево с корнем 1, которому соответствует список смежностей[[2, 3], [4, 0], [0, 5], [0,0], I[0,0]].
Представление дерева связанными структурами.
Структура, представляющая узел бинарного дерева:
mutable struct BiTree{T} index::T left::Union{BiTree{T},Nothing} right::Union{BiTree{T},Nothing} BiTree{T}(index) where T = new(index,nothing,nothing) end
BTI = BiTree{Int}
t = BTI(1)
t.left = BTI(2)
t.right = BTI(3)
Структура, представляющая узел дерева с произвольной валентностью (по выходу):
struct Tree{T} index::T sub::Vector{Tree{T}}} Tree(index)=new(index, Tree{T}[]) end
Структура, представляющая узел дерева с фиксированной валентностью по выходу:
struct NTree{N,T} index::T sub::Vector{<:Union{NTree{N,T}, Nothing}} NTree{N,T}(index) where {N,T} = new(index, [nothing for _ in 1:N]) end
Замечание. Было бы ошибкой аннотировать тип поля sub так
sub::Vector{Union{NTree{N,T}, Nothing}}
Потому что тип Union является абстрактным типом, и, следовательно, невозможно будет впоследствии создать конкретный вектор типа Vector{Union{NTree{N,T}, Nothing}}, чтобы инициализировать поле subtees каким-либо значением, тип которого соответствовал бы такой аннотации.
3. Алгоритмы обхода корневых деревьев
Дерево по своей природе являеися рекурсивной структурой: с его корнем связано нескосколько поддеревьев, каждое из котрых устроено точно также, т.е. каждое поддерево является деревом.
Задача обхода дерева заключается в последовательой «обработке» всех поддеревьев данного дерева, включая и само дерево.
Под «обработкой» в самом общем смысле понимается извлечение информации как из структуры поддеревьев, так из значения каждого узла дерева (корня соответствующего поддерева). Последовательность, в которой обрабатыаются поддеревья может быть различной. Различают обход дерева сверху-вниз и снизу-вверх.
Вне зависимости от конкретного способа представления корневого дерева алгоритм обхода (обработки) сверху-вниз может быть записан рекурсивно так:
- обработать корень
- поочередно обработать каждое поддерево, непосредственно связанное с корнем
Соответственно, обход (обработка) снизу-вверх рекурсивно записывается так:
- поочередно обработать каждое поддерево, непосредственно связанное с корнем
- обработать корень
Например, если дерево представлено вложенными векторами, и под обработкой корня понимать просто вывод на печать значения его индекса, то в случае обхода сверху-вниз программный код будет выглядеть так:
function toptrace(tree::Vector) println(tree[end]) # на последней позиции в tree находится индекс корня for subtree in tree[1:end-1] # с первой до предпоследней поциции нахоятся поддеревья toptrace(subtree) end end
Соответственно обход (обработка) снизу-вверх будет выглядеть так:
function downtrace(tree::Vector) for subtree in tree[1:end-1] downtrace(subtree) end println(tree[end]) end
При всех других способах кодирования деревьев алгоритмы обхода будут выглядеть подобным образом, различаясь лишь в мелких деталях, связанных со спецификой выбранного способа кодирования.
Напимер, если дерево представлено типом NTree{N,T}, то тот же самый обход сверху-вниз записывается так:
function toptrace(tree::NTree{N,T}) where {N,T} println(tree.index) for i in 1:N toptrace(tree.sub[i]) end end
А если дерево представлено типом Tree{T}, то — так:
function toptrace(tree::Tree{T}) where T println(tree.index) for sub in tree.sub toptrace(tree.sub) end end
В случае же, если дерево представлено списком смежностей, код будет выглядеть так:
ConnectList{T} = Vector{Vector{T}}
function toptrace(rootindex::T, tree::ConnectList{T}) where T
println(rootindex)
for subindex in tree[rootindex]
toptrace(subindex, tree)
end
end
4. Метод рекуррентных соотношения для корневых деревьев
Многие задачи обработки деревьев могут быть элегантно решены на основе соответствующих рекуррентных соотношений. Рассмотрим конкретные прмеры.
4.1. Вычисление высоты дерева
Высота дерева — это набольшая длина пути к его концевым вершинам (листьям); по определению длина пути к корню дерева равна 1.
Пусть имеется некоторое дерево с $n$ поддеревьми, непосредственно связанных с его корнем, и нусть известно, что высоты этих поддеревьев равны $h_1,h_2,…,h_n$. Тогда для высоты $h$ всего дерева справедлива рекуррентная вормула:
$$
h=max{h_1,…,h_n}+1
$$
Этой формуле соответствует следующая рекурсивная функция:
function height(tree::Tree) h=0 for sub in tree.sub h = max(h,height(sub)) end return h+1 end
4.2. Подсчет всех вершин дерева
При подсчете числа всех вершин поступим аналогично: сначала запишем требуемую рекурреную формулу, из которой затем выведем соответствующую ей рекурсивную функцию.
Пусть $N_1,…N_n$ — числа вершин всех $n$ поддеревьев, связанных с корнем некоторого дерева. Тогда число вершин $N$ самого дерева, очевидно, равно:
$$
N=N_1+…+N_n+1
$$
Полученной рекуррентной формуле соответствует следующая рекурсивная функция:
function vernumber(tree::Tree) N=1 for sub in tree.sub N += vernumber(sub) end return N end
4.3. Подсчет числа листьев дерева
Пусть $N_1,…N_n$ — числа листьев во всех $n$ поддеревьях, связанных с корнем некоторого дерева. Тогда число листьев $N$ в самом дереве, очевидно, равно:
$$
N=begin{cases}
1 &, если дерево состоит только из корня
N_1+…+N_n &, в противном случае
end{cases}
$$
Полученной рекуррентной формуле соответствует следующая рекурсивная функция:
function leavesnumber(tree::Tree) if isempty(tree.sum) return 1 end N=0 for sub in tree.sub N += leavesnumber(sub) end return N end
4.4. Определение максимальной валентности вершин дерева
Пусть $p_1,…p_n$ — наибольшие валентности по выходу во всех $n$ поддеревьях, связанных с корнем некоторого дерева. Тогда наибольшая валентность по выходу $p$ в самом дереве, очевидно, равна:
$$
p=max{max{p_1,…,p_n}, валентность_корня}
$$
Этой рекуррентной формуле соответствует следующая рекурсивная функция:
function maxvalence(tree::Tree) p=length(tree.sub) for i in tree.sub p = max(p, maxvalence(sub)) end return p end
4.5. Вычисление средней длины пути к вершинам дерева
Практическая важность величины среднего пути к вершинам дерева определяется тем, что она пропорциональна среднему времени доступа к данным, хранящимся в узлах дерева.
Чтобы её найти потребуется сначала вычислить суммарную длину пути ко всем вершинам и число всех вершин. После чего, поделив первое на второе, получим искомую характеристику.
Рекуррентная формула для вычисления числа всех вершин нам уже известна:
$$
N=N_1+…+N_n+1
$$
где $N_1,…N_n$ — числа вершин всех $n$ поддеревьев, связанных с корнем некоторого дерева.
Рекуррентная формула для суммарной длины длины пути:
$$
S=S_1+…+S_n+N
$$
где $S_1,…,S_n$ суммы длин путей к каждой вершине всех поддеревьев, $N$ — число вершин во всём дереве. К сумме длин путей в каждом из поддеревьев по отдельности $S_1+…+S_n$ надо прибавить ещё число всех вершин дерева $N$ потому, что длины путей ко всем вершинам каждого поддерева, отсчитываемых от его корня, при переходе к отсчету от корня самого дерева увеличиваются на 1 (включая сам корень, так как длина пути к корню считается равной 1).
Соответствующая функция, возвращающая кортеж из величин $S, N$ записывается так:
function sumpath_numver(tree::Tree) N=1 S=0 for sub in tree.sub s, n = sumpath_numver(sub) S += s N += n end return S, N end
Поскольку эта функция самостоятельного значения не имеет, то её можно обернуть во внешнюю не рекурсивную функцию, возвращающую уже требуемый результат:
function meanpath(tree::Tree) function sumpath_numver() N=1 S=0 for sub in tree.sub s, n = sumpath_numver(sub) S += s N += n end return S, N end S, N = sumpath_numver() return S/N end
Задача о нахождении ближайшей родительской вершины для заданного набора вершин корневого дерева
Пусть имеется некоторое дерево и задано некоторое подмножество индексов его вершин. Требуется найти индекс ближайшей к этим вершинам и общей для всех них родительской вершины.
Идея решения состоит в следующем. Будем рекурсивно обрабатывать дерево сверху-вниз. При этом будем использовать две внешних по отношению к рекурсивной процедуре переменных:
-
number_visited— cчетчик числа посещённых вершин из заданного набораsetver -
general— переменная, в которой будет находиться индекс ближайщей общей родительской вершины для всех тех вершин из заданного набораsetver, которые на данный момент были уже посещены (при рекурсивном обходе сверху-вниз)
Внешняя переменная general перед началом обхода инициализируется некоторым значением (не важно каким именно), но за пределами всех возможных значений индексов вершин, например, значением 0.
Рекурсивная процедура обхода дерева, назовем её recursrtace, будет иметь дополнительный второй аргумент parent, через который в неё будет в неё передаваться индекс корня дерева, очередное поддерево которого передаётся в качестве первого аргумента (назовем его tree).
Идея алгоритма состоит в следующем:
-
как только (после обработки всех поддеревьев, т.е. на возвратном движении к корню) обнаруживается, что корень текущего дерева (поддерева) принадлежит заданному набору
setver, счетчик числа посещенных вершинnumber_visitedувеличивается на 1, и если при этом это случилось первый раз, то значению индекса ближайшей первой родительской вершины (переменнойgeneral) присваивается индекс этого корня; -
при последующих посещениях вершин из заданного набора (на возвратном движении) значение переменной
generalможет изменяться, а может и оставаться прежним — это зависит от того, где именно (в иерархическом отношении) была обнаружена очередная вершина заданного набора: если текущее значение переменнойgeneralявляется индексом какой-либо её родительской (прародительской, прапрародительской и т.д.), то это значение остаётся неизменным, а в противном случае оно должно быть заменено индексом вершины, являющейся родительской (непосредственно) для очередной обнаруженной вершины заданного набора; -
для обеспечения последнего в рекурсивной процедуре обхода используется локальная логическая переменная (флаг)
is_mutable_general, которая при входе в очередное поддерево (при движении от корня к переферии) принимает значениеfalse, запрещающее изменять значение внешней переменнойgeneral, а на возвратном движении, как только произойдет возврат в вершину с индексом содержащимся в текущий момент времени в переменнойgeneral, флагis_mutable_generalдолжен принимать значениеtrue, разрешающее изменение переменнойgeneral; -
при всём этом, при возвратном движении по подереву (от переферии к корню), если только изменение внешней переменной
generalразрешено (is_mutable_general = true), то её значение будет заменяться на значение индекса непосредственной родительской вершины (parent) для корня текущего дерева (поддерева,tree), но лишь в случае если счетчик числа посещенных вершинnumber_visitedне достиг ещё числа всех элементов заданного набораsetver.
Пусть, например, дерево представлено вложенными векторами tree, а подмножество индексов его вершин — множеством setver, тогда следующая функция возвращает индекс искомой ближайшей общей родительской вершины.
function find_general(tree::Vector, setver::Set) number_visited = 0 # - cчетчик числа посещённых вершин из набора setver general = 0 # - в этой переменной формируется результат (начальное значение не должно только входить в диапазон индексов вершин дерева) function recurstrace(tree, parent=0) # - выполняет рекурсивную обработку дерева сверху-вниз is_mutable_general = false # при движение по дереву вглубь от корня внешнюю переменную general изменять не надо for subtree in tree[begin:end-1] if number_visited < length(setver) recurstrace(subtree, tree[end]) end end # number_visited = число ранее посещенных вершин из заданного набора setver if tree[end] in setver number_visited +=1 if number_visited == 1 general = tree[end] end end # теперь - обратное движение по дереву - из глубины к корню if general==tree[end] is_mutable_general = true # т.е. при движении к корню, внешнюю переменную general снова нужно отслеживать end if is_mutable_general && number_visited < length(setver) general = parent end println((current=tree[end],parent=parent,general=general)) # - это для отладки end recurstrace(tree) return general end #-------------- TEST: ----------- tree=[[[[4],[5],[6],3],[[9],[[[17],[18],16],[19],10],7],2],[[11],[[14],[15],12],8],1] #find_general(tree,Set((3,4,6,7))) |> println # 2 find_general(tree,Set((6,10,16))) |> println # 2
Отладочный вывод при этом получится таким:
(current = 4, parent = 3, general = 0) (current = 5, parent = 3, general = 0) (current = 6, parent = 3, general = 3) (current = 3, parent = 2, general = 2) (current = 9, parent = 7, general = 2) (current = 17, parent = 16, general = 2) (current = 18, parent = 16, general = 2) (current = 16, parent = 10, general = 2) (current = 19, parent = 10, general = 2) (current = 10, parent = 7, general = 2) (current = 7, parent = 2, general = 2) (current = 2, parent = 1, general = 2) (current = 1, parent = 0, general = 2) 2