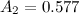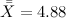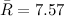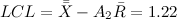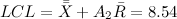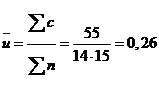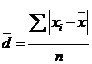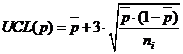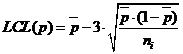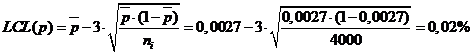Практикум использования контрольных карт Шухарта
Время на прочтение
3 мин
Количество просмотров 94K
Недавно я публиковал здесь свой слайдкаст с рассказом о 6-сигмах, контрольных картах Шухарта и людях снежинках, где достаточно простым языком, местами злоупотребляя сквернословием, под 20-ти минутный хохот слушателей рассказывал о том, как отделить системные вариации от вариаций, вызванных особыми причинами.
Теперь хочу подробно разобрать пример построения контрольной карты Шухарта на основе реальных данных. В качестве реальных данных я взял историческую информацию о завершенных личных задачах. Эта информация у меня есть благодаря адаптации под себя модели личной эффективности Дэвида Аллена Getting Things (про это у меня тоже есть старый слайдкаст в трех частях: Часть 1, Часть 2, Часть 3 + Excel-табличка с макросами для анализа задач из Outlook ).
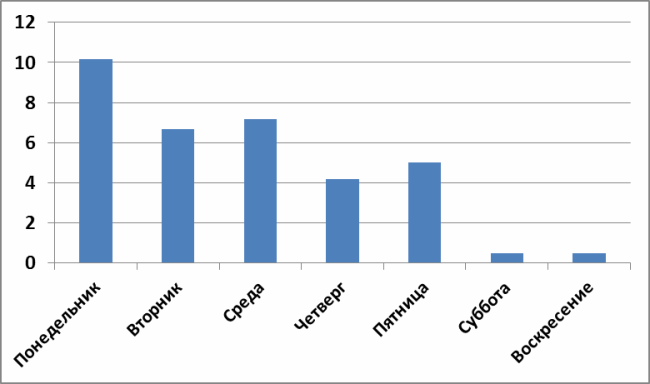
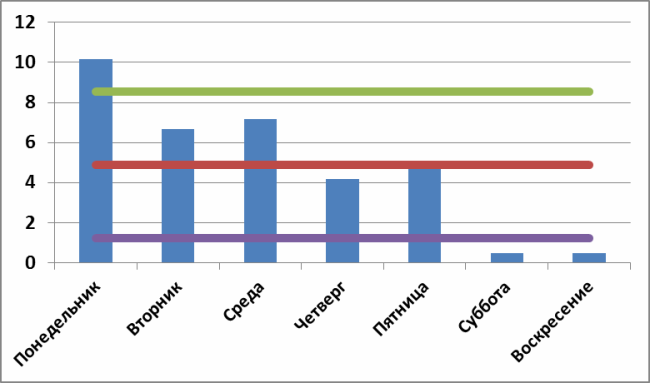
Постановка задачи выглядит так. У меня имеется распределение среднего числа завершенных задач в зависимости от дня недели (ниже на графике) и нужно ответить на вопрос: «есть ли что-то особенное в понедельниках или это всего лишь погрешность системы?»
Ответим на этот вопрос при помощи контрольной карты Шухарта – основного инструмента статистического управления процессами.
Итак, критерий Шухарта наличия особой причины вариации достаточно прост: если какая-то точка выходит за контрольные пределы, рассчитанные особым образом, то она свидетельствует об особой причине. Если точка лежит внутри этих пределов, то отклонение обусловлено общими свойствами самой системы. Грубо говоря, является погрешностью измерений.
Формула для вычисления контрольных пределов выглядит так:
Где
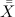
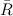
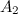
Все формулы и табличные коэффициенты можно найти, например, в ГОСТ 50779.42-99, где кратко и понятно изложен подход к статистическому управлению (честно, сам не ожидал, что есть такой ГОСТ. Более подробно тема статистического управления и его места в оптимизации бизнеса раскрыта в книге Д. Уилера).
В нашем случае мы группируем количество выполненных задач по дням недели – это и будет подгруппами нашей выборки. Я взял данные о числе завершенных задач за 5 недель работы, то есть, размер подгруппы равен 5. При помощи таблицы 2 из ГОСТа находим значение инженерного коэффициента:
Вычисление среднего значения и размаха (разницы между минимальным и максимальным значениями) по подгруппе (в нашем случае по дню недели) задача достаточно простая, в моем случае результаты такие:
| День недели | Групповое среднее | Размах |
|---|---|---|
| Понедельник | 10.2 | 8 |
| Вторник | 6.7 | 10 |
| Среда | 7.2 | 11 |
| Четверг | 4.2 | 9 |
| Пятница | 5.0 | 10 |
| Суббота | 0.5 | 2 |
| Воскресенье | 0.5 | 3 |
Центральной линией контрольной карты будет являться среднее групповых средних, то есть:
Так же вычисляем средний размах:
Теперь мы знаем, что нижний контрольный предел для числа выполненных задач будет равен:
То есть, те дни, в которые я в среднем завершаю меньшее число задач, с точки зрения системы являются особенными.
Аналогично получаем верхний контрольный предел:
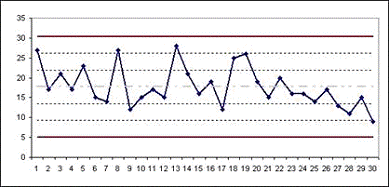
Теперь нанесем на график центральную линию (красная), верхний контрольный предел (зеленая) и нижний контрольный предел (фиолетовая):
И, о, чудо! Мы видим три явно особенные группы, выходящие за контрольные пределы, в которых присутствуют явно не системные причины вариаций!
По субботам и воскресеньям я не работаю. Факт. А понедельник оказался действительно особенным днем. И теперь можно думать и искать что же такого реально особенного в понедельниках.
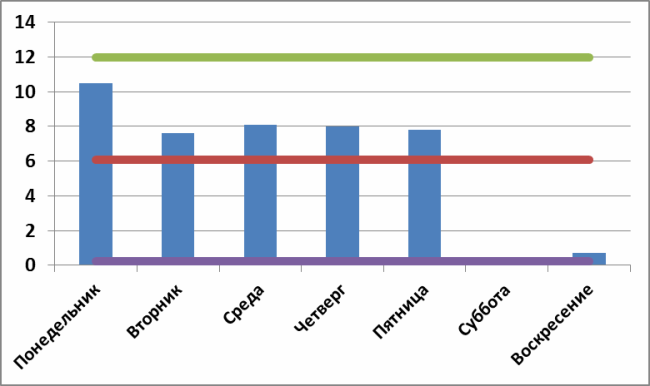
Однако если бы среднее число выполненных в понедельник задач находилось внутри контрольных пределов и пусть даже сильно выделялось на фоне остальных точек, то с точки зрения Шухарта и Деминга искать какие-то особенности в понедельниках было бы бессмысленным занятием, так как подобное поведение обуславливается исключительно общими причинами. Например, я построил контрольную карту для других 5-ти недель в конце прошлого года:
И вроде как есть какое-то ощущение того, что понедельник как-то выделяется, но согласно критерию Шухарта — это всего-лишь флуктуация или погрешность самой системы. Согласно Шухарту, в данном случае можно сколь угодно долго исследовать особые причины понедельников — их просто нет. С точки зрения статистического управления, на этих данных понедельник ничем не отличается от любого другого рабочего дня (даже воскресенья).
Построение контрольных карт в статистике
Введение
Роль статистики в нашей жизни настолько значительна, что
люди, часто не задумываясь и не осознавая, постоянно используют элементы
статистической методологии не только в трудовых процессах, но и в повседневном
быту. Работая и отдыхая, делая покупки, знакомясь с другими людьми, принимая
какие-то решения, человек пользуется определённой системой имеющихся у него
сведений, сложившихся вкусов и привычек, фактов, систематизирует, сопоставляет
эти факты, анализирует их, делает выводы и принимает определённые решения,
предпринимает конкретные действия. Таким образом, в каждом человеке заложены
элементы статистического мышления, представляющего собой способности к анализу
и синтезу информации об окружающем нас мире.
Можно без преувеличения сказать, что статистическими методами
сегодня пронизана вся наша жизнь [1].
В ХХ в. статистику обычно рассматривают как самостоятельную
научную дисциплину. Статистика есть совокупность методов и принципов, согласно
которым проводится сбор, анализ, сравнение, представление и интерпретация
числовых данных (1925). В 1954 г. академик АН УССР Б.В. Гнеденко дал следующее
определение: «Статистика состоит из трех разделов:
1) сбор статистических сведений, т.е. сведений,
характеризующих отдельные единицы каких-либо массовых совокупностей;
2) статистическое исследование полученных данных,
заключающееся в выяснении тех закономерностей, которые могут быть установлены
на основе данных массового наблюдения;
) разработка приемов статистического наблюдения и
анализа статистических данных. Последний раздел, собственно, и составляет
содержание математической статистики».
Термин «статистика» употребляют еще в двух смыслах.
Во-первых, в обиходе под «статистикой» часто понимают набор количественных
данных о каком-либо явлении или процессе. Во-вторых, в специальной литературе
статистикой называют функцию от результатов наблюдений, используемую для
оценивания характеристик и параметров распределений и проверки гипотез [2].
В условиях постоянно расширяющегося ассортимента выпускаемой
продукции основным фактором, определяющим целесообразность приобретения изделий
потребителем, является качество [3].
Качество стало залогом успеха и основным условием,
предопределяющим увеличение объема продукции, поставляемой на национальные и
международные рынки. Тщательно разработанные и эффективно функционирующие
системы управления качеством продукции обеспечивают рентабельность фирм и
получение значительных прибылей на инвестированный капитал. В результате
внедрения систем управления качеством предприятия увеличивают объем выпускаемой
продукции, добиваются повышения производительности труда, обеспечивают
существенное снижение расходов на качество и повышают свою
конкурентоспособность [3].
Однако далеко не все предприятия добиваются равнозначного
эффекта от реализации своей продукции на рынках сбыта. Так, качество продукции,
выпускаемой одними фирмами, существенно отличается от качества продукции,
выпускаемой другими [3].
В настоящее время понятие качества стало намного шире
восприниматься производителями и потребителями. Уже недостаточным условием
успешной работы предприятия является только производство качественной
продукции, так как производитель, не обеспечивший на высоком уровне договорные
и сопроводительные мероприятия по реализации своей продукции потребителям, рискует
в будущем уступить конкурентам [3].
При таком положении дел потребитель, который в настоящее
время может легко отличить более качественную продукцию от менее качественной,
отдает, естественно, предпочтение продукции более высокого качества [3].
Стремление фирм во всем мире повысить качество выпускаемой
продукции объясняется наличием различных уровней качества. В связи с этим
методы и средства, обеспечивающие улучшение качества продукции, приобретают
первостепенное значение и играют решающую роль в производственной деятельности
[3].
К одному из таких методов относится организация работы
предприятия по общепринятым нормам или стандартам, которые помогают
организовать работу предприятия в направлении повышения качества продукции или
услуги. В настоящее время одними из таких стандартов являются международные
стандарты ISO 9000, в соответствии с которыми можно создавать систему качества
на предприятии [3].
В методологическом плане принципиально важным для всего
семейства стандартов ISO серии 9000 является введенное положение о том, что вся
работа, выполняемая организацией, рассматривается как совокупность
взаимосвязанных процессов. Соответственно общее руководство качеством
достигается через управление процессами, реализуемыми в организации и умением
применять статистические методы [3].
Основным результатом работы систем менеджмента качества
является завоевание изготовителем соответствующего доверия в отношении его
способности обеспечивать качество, как самого продукта, так и всех процессов
его создания [3].
Системы ISO 9000 являются моделью СМК, то есть их задача
состоит в организации системы управления качеством [4].
Стандарты ISO 9000, в том числе устанавливают возможность и
необходимость принятия обоснованных решений в области качества на базе
достоверной информации — принцип «Принятие решений, основанное на фактах». Этот
принцип может быть реализован, если возможно будет осуществить следующие
действия:
1) проведение измерений, сбор данных и информации на
всех этапах технологического цикла продукции;
2) обеспечение точности, надежности и доступности данных
и информации;
) проведение соответствующего анализа и информации с
помощью различных методов [4].
Поскольку в реальных условиях часто затруднено использование
детермированных параметров, используют методы математической статистики
(статистического анализа) [4].
Статистические методы подразумевают работу со случайными
величинами [4].
В системе стандартов ISO указывается, что должна
обеспечиваться возможность реализации статистических методов для подтверждения возможности
производства и достижения требуемых характеристик продукции. В целом,
статистические методы рассматриваются как средства измерений, описания,
анализа, интерпретации и моделирования изменчивости качества при наличии
определенного количества данных [4].
Основные этапы выполнения статистического анализа:
1. Сбор и первичный анализ информации. При кажущейся
тривиальности данный этап по трудоемкости является наиболее весомым и во многом
определяет достоверность получаемых результатов.
2. Описательная статистика и первичная обработка
выборки. Целью является выявление и устранение грубых погрешностей, расчет
числовых характеристик и установление вида распределения, как правило,
подтверждение нормальности распределения (распределение Гаусса).
. Дисперсионный анализ одно- или двухфакторного
комплекса. На данном этапе качественно устанавливается или опровергается
гипотеза о зависимости (влиянии) параметров управления на параметры состояний
[4].
Фактически, нужно дать ответ на вопрос — влияет или не влияет на
(
— параметры управления, то есть факторы,
которыми можно варьировать; — результат процесса, параметры состояния) [4].
. Корреляционный анализ — количественно (численно)
устанавливается степень влияния на
.
. Регрессионный анализ — устанавливается конечная
математическая зависимость между и
, которая в дальнейшем позволяет, варьируя
значениями , получать значений
.
. Анализ полученных результатов и возможностей
использования (построение контрольных карт, диаграмм, корректировка
технологического процесса, осуществление организационных мероприятий, внесение
изменений в нормативную документацию и др.) [4].
Рассмотрим подробнее этап описательной статистики.
1.
Статистическая обработка данных
1.1
Теоретические сведения
статистический контрольный карта
Описательная статистика применяется для систематизации и
описания данных наблюдения. Задачи, которые решает описательная статистика —
это, прежде всего, задачи соединения и обобщения данных. Цель здесь состоит не
только в том, чтобы извлечь и представить в самом сжатом виде существенную
информацию об изделии или процессе, придав ей форму некоторой системы данных
[3].
Описание данных обычно является начальным этапом в анализе
количественных данных и часто — первым шагом к использованию других
статистических процедур [3].
В качестве данных для описательной статистики может быть
любая информация, которая отражает содержание наблюдений: опросы общественного
мнения, показатели экономической и финансовой деятельности, характеристики
производственных процессов и т.д. Характеристики выборочных данных могут
служить основанием для выводов относительно характеристик всей совокупности
данных. И какова бы ни была генеральная совокупность наблюдений, из которой
черпаются данные, описательная статистика предлагает наиболее целесообразные
способы, с помощью которых можно не только быстро выделить основное содержание
полученной информации, но и провести дальнейший ее анализ с минимальной
трудоемкостью [3].
На этапе описательной статистики определяются следующие
основные характеристики выборки:
1. Минимум и максимум. Максимум — самое большое значение
из анализируемого набора данных, минимум — самое маленькое (может быть и
отрицательным числом). Это крайние значения в совокупности данных, обозначающие
границы их вариации [5].
2. Размах выборки — обозначается буквой R. Это самый
простой показатель, который можно получить для выборки — разность между
максимальной и минимальной величинами данного конкретного вариационного ряда,
т.е.
[5].
3. Среднее арифметическое выборки характеризует средний
уровень значений изучаемой случайной величины в наблюдавшихся случаях и
вычисляется путем деления суммы отдельных величин исследуемого признака на
общее число наблюдений:
,
где — выборочное среднее,
— объем выборки,
— i-й элемент выборки [5].
4. Медиана представляет собой срединное значение
упорядоченного массива чисел. Если массив не содержит повторяющихся чисел, то
половина его элементов окажется меньше, а половина — больше медианы. Если
выборка содержит экстремальные значения, для оценки среднего значения лучше использовать
не среднее арифметическое, а медиану. Чтобы вычислить медиану выборки, ее
сначала необходимо упорядочить.
элемент упорядоченного массива [5].
Эта формула неоднозначна. Ее результат зависит от четности или
нечетности числа :
если выборка содержит нечетное количество элементов, медиана равна
(n+1)/2-му элементу;
если выборка содержит четное количество элементов, медиана лежит
между двумя средними элементами выборки и равна среднему арифметическому,
вычисленному по этим двум элементам [5].
5. Мода. Термин был впервые введен Пирсоном в 1894 г.
Мода — это число, которое чаще других встречается в выборке (наиболее модное).
Мода хорошо описывает, например, типичную реакцию водителей на сигнал светофора
о прекращении движения. Классический пример использования моды — выбор размера
выпускаемой партии обуви или цвета обоев. Если распределение имеет несколько
мод, то говорят, что оно мультимодально или многомодально (имеет два или более
«пика»). Мультимодальность распределения дает важную информацию о природе
исследуемой переменной. Например, в социологических опросах, если переменная
представляет собой предпочтение или отношение к чему-то, то мультимодальность
может означать, что существуют несколько определенно различных мнений.
Мультимодальность также служит индикатором того, что выборка не является
однородной и наблюдения, возможно, порождены двумя или более «наложенными»
распределениями. В отличие от среднего арифметического, выбросы на моду не
влияют. Для непрерывно распределенных случайных величин, например, для
показателей среднегодовой доходности взаимных фондов, мода иногда вообще не
существует (или не имеет смысла). Поскольку эти показатели могут принимать
самые разные значения, повторяющиеся величины встречаются крайне редко [5].
6. Дисперсия и стандартное отклонение. Эти показатели
позволяют оценить степень колебания данных вокруг среднего значения. Выборочная
дисперсия является приближением среднего арифметического, вычисленного на
основе квадратов разностей между каждым элементом выборки и выборочным средним.
Для выборки выборочная дисперсия, обозначаемая
символом , задается следующей формулой:
[5].
В общем случае выборочная дисперсия — это сумма квадратов
разностей между элементами выборки и выборочным средним, деленная на величину,
равную объему выборки минус один:
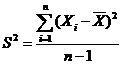
Наиболее практичной и широко распространенной оценкой разброса
данных является стандартное выборочное отклонение. Этот показатель обозначается
символом и равен квадратному корню из выборочной
дисперсии:
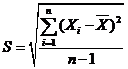
Ни выборочная дисперсия, ни стандартное выборочное отклонение не
могут быть отрицательными. Единственная ситуация, в которой показатели и
могут быть нулевыми, — если все элементы выборки равны между
собой [5].
7. Асимметрия распределения — качественное свойство
кривой распределения, указывающее на отличие от симметричного распределения.
Асимметрия распределения положительна (отрицательна), если коэффициент
асимметрии положителен (отрицателен). При положительной (отрицательной)
асимметрии распределения более «длинная» часть кривой плотности распределения
лежит правее (левее) моды [6].
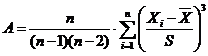
где — общее количество выборки,
— стандартное выборочное отклонение.
8. Эксцесс — характеризует остроконечность или
сглаженность функции распределения:
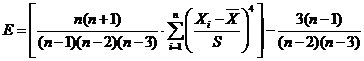
Различают относительную и кумулятивную частоты. В общем случае,
частота — это количество значений случайной величины в выборке [4].
Относительная частота:
.
где — частота отдельных значений в выборке
[4].
Кумулятивная частота:
[4].
В первом приближении совпадает с вероятностью [4].
Относительная кумулятивная частота:
[4].
Причем
[4].
Как правило, оперируют не с отдельными значениями, а с интервалами
(подгруппами) по правилу:
[4].
.2
Практическая часть
Исходные данные: содержание марганца в сварочной проволоке
Св-08Г2С
|
1,78 |
1,79 |
1,81 |
1,88 |
1,80 |
1,79 |
1,82 |
1,78 |
1,75 |
1,81 |
1,81 |
1,81 |
1,77 |
1,83 |
1,81 |
|
1,90 |
1,79 |
1,79 |
1,89 |
1,79 |
1,80 |
1,82 |
1,88 |
1,81 |
1,84 |
1,87 |
1,81 |
1,86 |
1,80 |
1,80 |
|
1,83 |
1,77 |
1,80 |
1,83 |
1,71 |
1,78 |
1,85 |
1,75 |
1,82 |
1,82 |
1,81 |
1,82 |
1,81 |
1,77 |
1,80 |
|
1,85 |
1,79 |
1,79 |
1,80 |
1,83 |
1,81 |
1,82 |
1,78 |
1,80 |
1,78 |
1,87 |
1,81 |
1,80 |
1,79 |
1,77 |
|
1,85 |
1,91 |
1,86 |
1,95 |
1,88 |
1,78 |
1,79 |
1,90 |
1,80 |
1,78 |
1,89 |
1,82 |
1,79 |
1,76 |
1,74 |
|
1,78 |
1,94 |
1,92 |
1,80 |
1,81 |
1,80 |
1,81 |
1,89 |
1,83 |
1,84 |
1,87 |
1,83 |
1,82 |
1,77 |
1,78 |
|
1,87 |
1,79 |
1,79 |
1,78 |
1,85 |
1,86 |
1,75 |
1,81 |
1,80 |
1,81 |
1,88 |
1,90 |
1,77 |
1,81 |
1,81 |
|
1,76 |
1,85 |
1,86 |
1,82 |
1,77 |
1,82 |
1,82 |
1,86 |
1,82 |
1,88 |
1,92 |
1,88 |
1,77 |
1,81 |
1,83 |
|
1,86 |
1,86 |
1,80 |
1,81 |
1,82 |
1,90 |
1,83 |
1,88 |
1,82 |
1,87 |
1,81 |
1,88 |
1,82 |
1,79 |
1,81 |
|
1,78 |
1,85 |
1,86 |
1,81 |
1,82 |
1,82 |
1,80 |
1,75 |
1,79 |
1,83 |
1,79 |
1,87 |
1,84 |
1,82 |
1,83 |
|
1,88 |
1,87 |
1,83 |
1,77 |
1,84 |
1,87 |
1,78 |
1,80 |
1,79 |
1,81 |
1,89 |
1,87 |
1,83 |
1,81 |
1,80 |
|
1,85 |
1,89 |
1,81 |
1,88 |
1,76 |
1,76 |
1,77 |
1,86 |
1,84 |
1,85 |
1,85 |
1,85 |
1,85 |
1,81 |
1,79 |
|
1,83 |
1,94 |
1,81 |
1,75 |
1,81 |
1,82 |
1,83 |
1,85 |
1,83 |
1,87 |
1,80 |
1,89 |
1,82 |
1,79 |
1,83 |
|
1,83 |
1,98 |
1,82 |
1,78 |
1,85 |
1,79 |
1,84 |
1,87 |
1,75 |
1,82 |
1,80 |
1,82 |
1,83 |
1,82 |
1,81 |
|
1,79 |
1,85 |
1,79 |
1,80 |
1,81 |
1,78 |
1,78 |
1,82 |
1,77 |
1,84 |
1,83 |
1,87 |
1,82 |
1,79 |
1,81 |
|
1,82 |
1,80 |
1,82 |
1,81 |
1,84 |
1,86 |
1,79 |
1,79 |
1,80 |
1,84 |
1,83 |
1,88 |
1,82 |
1,80 |
1,86 |
|
1,78 |
1,78 |
1,87 |
1,81 |
1,85 |
1,78 |
1,79 |
1,78 |
1,80 |
1,75 |
1,75 |
1,83 |
Определить:
1. Максимальное и минимальное значение выборки.
2. Размах варьирования.
. Частоту отдельных значений.
. Признак или интервал группирования.
. Групповую или частную частоту.
. Относительную групповую или частную частоту.
. Кумулятивную абсолютную групповую или частную
частоту.
. Кумулятивную относительную групповую или частную
частоту.
. Среднее арифметическое выборки.
. Медиану выборки.
. Моду выборки.
. Дисперсию выборки.
. Среднее квадратическое отклонение выборки.
. Вероятность.
. Теоретическую вероятность.
. Дать графическое изображение (если возможно)
указанных ранее величин, функций.
. Какими программными пакетами может быть обработана
данная выборка.
|
Максимальное |
1,98 |
|
Минимальное |
|
|
Размах |
0,27 |
|
Интервал |
0,027 |
|
Среднее |
1,82115 |
|
Медиана выборки |
1,815 |
|
Мода выборки |
1,81 |
|
Дисперсия |
0,00171 |
|
Среднее |
0,04131 |
|
Объем выборки |
252 |
|
Асимметрия |
0,6474 |
|
Эксцесс |
0,76369 |
|
Интервалы |
Частота |
Относительная |
Относительная |
|
1,71-1,737 |
1 |
0,003968 |
0,003968 |
|
1,737-1,764 |
13 |
0,051587 |
0,055556 |
|
1,764-1,791 |
55 |
0,218254 |
0,27381 |
|
1,791-1,818 |
5 |
0,22619 |
0,5 |
|
1,818-1,845 |
59 |
0,234127 |
0,734127 |
|
1,845-1,872 |
39 |
0,154762 |
0,888889 |
|
1,872-1,899 |
17 |
0,06746 |
0,956349 |
|
1,899-1,926 |
7 |
0,027778 |
0,984127 |
|
1,926-1,953 |
3 |
0,011905 |
0,996032 |
|
1,953-1,98 |
1 |
0,003968 |
1 |
|
Сумма значений |
252 |
1 |
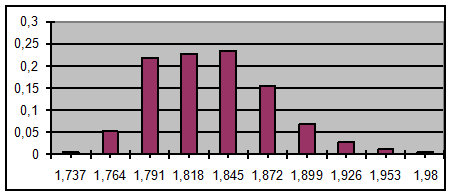
Рисунок 1 — График распределения относительных частот по
интервалам
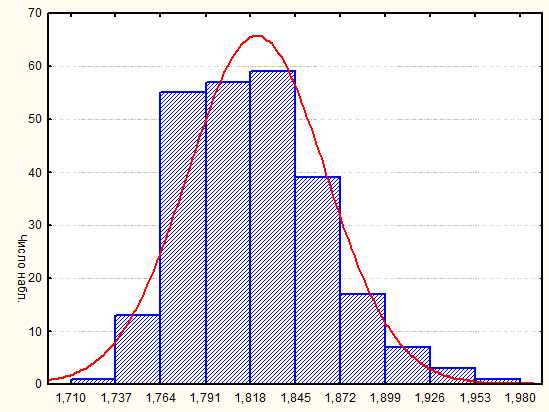
Рисунок 2 — График распределения частот отдельных значений по
интервалам
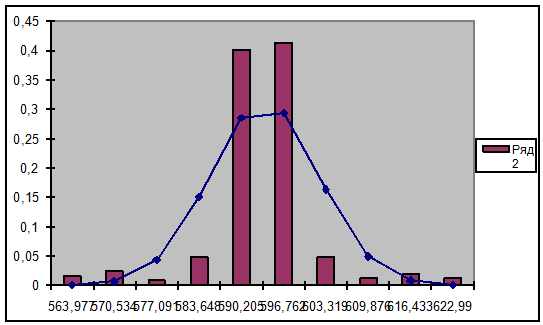
Рассчитаем теоретические частоты. Для этого из нижней границы
каждого интервала вычитаем среднее арифметическое выборки и делим полученное
выражение на среднее квадратическое отклонение выборки. Затем построим
стандартное нормальное интегральное распределение, для каждого из полученных
значений. После этого, попарно вычитая найденные значения друг из друга,
умножаем полученные результаты на 100 и строим график распределения
теоретических частот по интервалам, представленный на рисунке 3.
|
-2,03698318 |
0,020826 |
0,020826 |
2,082586 |
|
-1,38341186 |
0,083269 |
0,062443 |
6,244345 |
|
-0,72984053 |
0,232744 |
0,149475 |
14,94745 |
|
-0,0762692 |
0,469602 |
0,236859 |
23,68586 |
|
0,577302128 |
0,718132 |
0,24853 |
24,85298 |
|
1,230873457 |
0,890815 |
0,172683 |
17,26826 |
|
1,884444785 |
0,970248 |
0,079433 |
7,943268 |
|
2,538016113 |
0,994426 |
0,024178 |
2,417828 |
|
3,191587441 |
0,999293 |
0,004867 |
0,486668 |
|
3,845158769 |
0,99994 |
0,000647 |
0,064723 |
Рисунок 3 — График распределения теоретических частот по
интервалам
2.
Контрольные карты
2.1
Теоретические сведения
Контрольные карты считают одним из наиболее важных
инструментов статистического управления качеством. Они представляют собой
относительно простое графическое средство оценки управляемости (стабильности)
процесса по результатам сравнения отдельных измерений с заданными контрольными
границами.
Контрольные карты — инструмент, позволяющий отслеживать ход
протекания процесса и воздействовать на него (с помощью соответствующей
обратной связи), предупреждая его отклонения от предъявляемых к процессу
требований.
У.А. Шухарт считал, что контрольные карты должны отвечать
трем главным требованиям:
Определять требуемый
уровень или номинал процесса, на достижение которого должен быть нацелен
персонал предприятия.
Использоваться как
вспомогательное средство для достижения этого номинала.
Служить в качестве основы
для определения соответствия номиналу и допускам.
Таким образом, принципы построения контрольных карт Шухарта
охватывают круг понятий, связанных со стабилизацией производственного процесса,
его производительностью и оценкой качества, а реализация этих принципов
способствует взаимоувязке различных направлений хозяйственной деятельности.
Общий подход к построению различных карт сводится к
следующему:
Проводятся
последовательные измерения значений контролируемого показателя. Измерения
группируются в выборки, состоящие из нескольких измерений.
Для каждой выборки
рассчитывается некоторая числовая характеристика, анализ которой позволяет
оценить соответствие процесса определенным требованиям. Важно иметь в виду, что
характеристика представляет собой не абсолютные значения контролируемого
показателя качества, а статистическую оценку его изменчивости.
Устанавливаются
центральная или средняя линия процесса (CL — center line), а также верхняя (UCL — upper control limit) и нижняя (LCL — lower control limit) контрольные границы для
анализируемой числовой характеристики.
Если числовая
характеристика выходит за контрольные границы, или в расположении точек
наблюдаются некоторые тенденции, то делается вывод о потере качества на
соответствующей выборке.
Наблюдаемые на контрольных картах отклонения изучаемой
характеристики (например — показателя качества) происходят под воздействием
различных причин, которые могут быть классифицированы на две группы: обычные и
особые. К обычным причинам относят естественные возмущения, такие, как
вибрации, колебания питающих напряжений, температуры, влажности и т.п. Особыми
причинами являются возмущения, которые проявляются при нарушении условий
нормальной организации или нормального осуществления процесса (сдвиг шкалы
измерительного прибора, разладка или поломка технологического оборудования,
несоответствие сырья или комплектующих техническим условиям по номинальному
значению).
Средняя линия и границы регулирования отображают закономерности
вариации контролируемой характеристики при нормальном осуществлении процесса,
т.е. при отсутствии особых причин. Ордината средней линии соответствует
статистической оценке положения, а контрольные границы — наибольшему и
наименьшему пределам объективно присущего ей интервала варьирования. Если
оценку положения контролируемой характеристики условно обозначить как , а стандартное отклонение данной оценки
контролируемой характеристики как , то можно записать:
;
;
,
где и
— коэффициенты, значения которых зависят от доверительной
вероятности и особенностей распределения контролируемой характеристики.
Основная цель использования контрольных карт — обнаружить и
отделить случайные отклонения, связанные с обычными причинами, от отклонений,
вызванных действием особых причин.
Существуют два типа контрольных карт: один предназначен для
контроля параметров качества, представляющих собой непрерывные случайные
величины, значения которых являются количественными данными параметра качества
(значения размеров, масса, электрические и механические параметры и т.п.), а
второй — для контроля параметров качества, представляющих собой дискретные
(альтернативные) случайные величины значения, которые являются качественными
данными (годен — не годен, соответствует — не соответствует, дефектное —
бездефектное изделие и т.п.).
В зависимости от вида данных и методов их статистической обработки
выделяют различные типы контрольных карт, основные из которых представлены на
рисунке 4.
Все перечисленные карты относятся к категории карт Шухарта,
которые широко применяются в Европе и Японии. Как правило, при анализе
процессов метод контрольных карт используется совместно с гистограммами и
расслоением данных.
Что важнее всего в процессе управления, так это точное понимание
состояния объекта управления с помощью чтения контрольных карт и быстрое
осуществление соответствующих действий, как только в объекте обнаружилось
что-нибудь необычное, неслучайное. Контролируемое состояние объекта — это такое
состояние, когда процесс стабилен, а его среднее и разброс не меняются.
Дискретная случайная величина принимает лишь отдельные,
изолированные одно от другого значения. Таким свойством обладают атрибутивные
признаки (цвет предмета, сорт продукции, годное или бракованное изделие и
т.д.).
Непрерывная случайная величина принимает любые значения от
некоторого свойственного ей числового интервала. Таким свойством обладают
количественные признаки (механические свойства материала, фактические размеры
продукции, производительность агрегата при обработке конкретного профилеразмера
и т.п.).
В литературе, посвященной управлению качеством с применением
контрольных карт, указывают на следующие достоинства карт по альтернативному
признаку:
отображают состояние
производства с учетом всех аспектов качества анализируемой продукции;
иногда позволяют обойтись
без применения дорогих точных приборов и длительных измерительных процедур;
более понятны менеджерам,
которые не разбираются в особенностях статистических характеристик.
Применительно к картам по количественному признаку указывают,
что они являются наиболее чувствительными индикаторами ухудшения качества и
предупреждают о возможных проблемах задолго до того, как в процессе
производства резко возрастет доля бракованных изделий.
Выход из контролируемого состояния определяется по
контрольной карте на основании следующих критериев:
1) Выход точек за контрольные пределы.
2) Серия — это проявление такого состояния, когда точки
неизменно оказываются по одну сторону от средней линии; число таких точек
называется длиной серии. Серия длиной в семь точек рассматривается как
неслучайная. Даже если длина серии оказывается менее шести, в ряде случаев
ситуацию следует рассматривать как неслучайную, например, когда:
а) не менее 10 из 11 точек оказываются по одну сторону
от центральной линии;
б) не менее 12 из 14 точек оказываются по одну сторону
от центральной линии;
в) не менее 16 точек из 20 оказываются по одну сторону
от центральной линии.
3) Тренд (дрейф) Если точки образуют непрерывно
повышающуюся или понижающуюся кривую, говорят, что имеет место тренд.
4) Приближение к контрольным «зонам» пределам.
Рассматриваются точки, которые приближаются к 3-сигмовым контрольным пределам,
причем если 2 или 3 точки оказываются за 2-сигмовыми линиями, то такой случай
надо рассматривать как ненормальный.
Приближение к центральной линии. Когда большинство точек концентрируется внутри
центральных полуторосигмовых линий, что обусловлено неподходящим способом
разбиения на подгруппы. Приближение к центральной линии вовсе не означает, что
достигнуто контролируемое состояние, напротив, это значит, что в подгруппах
смешиваются данные из различных распределений, что делает размах контрольных
пределов слишком широким. В таком случае надо изменить способ разбиения на
подгруппы.
Одним из важных этапов при составлении контрольных карт
является способ определения контрольных границ (границ регулирования). Для
определения контрольных границ необходимо собрать большое количество данных,
характеризующих состояние процесса, и на их основе рассчитать по установленной
формуле контрольные нормативы. Обычно диапазон от средней до границ
регулирования содержит трехкратное среднее квадратичное отклонение.
Контрольные карты для количественного признака применяют в
тех случаях, когда при регистрации данных фиксируют измеренные значения
характеристик процесса. Контрольные карты для количественного признака
предпочтительны по следующим причинам:
1. Численное значение (например, диаметр равен 16.45 мм)
содержит больше информации, чем регистрация альтернативных событий «да-нет»
(например диаметр внутри поля допуска или вне поля допуска)
2. Общие затраты на измерения в некоторых случаях
оказываются ниже, хотя получение одного отдельного измерения дороже, чем получение
единицы данных в виде «да — нет», так как для
получения достаточной информации о процессе зачастую требуется измерить меньшее
число единиц продукции, чем при контроле по альтернативному признаку
. Благодаря меньшему числу единиц продукции,
подлежащих контролю, сокращается время между изготовлением продукции и
корректирующими действиями, если по результатам контроля они необходимы
. Улучшение процесса может быть оценено количественно,
даже если все индивидуальные значения лежат внутри установленного допуска. Это
важно при проведении анализа и дальнейшего непрерывного совершенствования
процесса.
. С помощью контрольных карт по количественному
признаку можно объяснить поведение процесса как по разбросу (изменение от
единицы к единице), так и по расположению уровня процесса (среднему процесса).
Благодаря этому контрольные карты по количественному признаку можно
анализировать попарно: одна карта для среднего процесса, другая — для разброса.
Контрольные карты для альтернативных признаков могут
использоваться по следующим причинам.
1. Альтернативные данные можно получить в результате
работы любого технического и административного процесса. Самая трудная задача
при этом — создать точные рабочие определения несоответствия (что это такое,
как измерить, при каких условиях и т.п.).
2. Получение альтернативных данных (при контроле,
ремонте сортировке и т.п.) не требует дополнительных затрат; необходимо только
нанести эти данные на контрольную карту.
. Необходимы оперативность, простота и небольшие
затраты при сборе данных, например, с использованием простых калибров (типа «да
— нет») не требуется специального обучения.
. Отчеты для руководства содержат альтернативные
данные. Например, процент изделий, принятых с первого предъявления объем брака,
число отклонений при проверке качества изделий и материалов Контрольные карты
могут быть полезны при анализе этих отчетов, благодаря возможности различать
изменчивость от обычных и особых причин.
При введении контрольных карт в организации важно определить
первоочередные проблемы и использовать карты там, где они наиболее необходимы.
Сигналы о проблемах могут исходить от системы управления издержками, претензий
потребителей и т.п. Применение контрольных карт для альтернативных признаков по
основным показателям качества продукции может указать на возможное
использование конкретных карт для количественного [7].
Х-карта. Отображает изменчивость выборочных характеристик
положения показателя качества (среднего или медианы
). Позволяет контролировать смещения
фактических показателей от целевого значения.
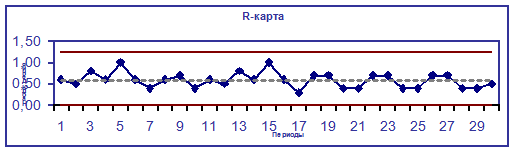
R-карта. Отображает изменчивость фактического интервала
варьирования (размаха). Позволяет контролировать соответствие размаха полю
допуска.
S-карта. Отображает изменчивость выборочного стандартного
отклонения. Позволяет контролировать динамику степени изменчивости
анализируемого показателя.
S2-карта. Отображает изменчивость выборочной
дисперсии. Позволяет контролировать динамику степени изменчивости
анализируемого показателя.
С-карта. Отображает изменчивость числа дефектов (в партии, в
день, на один станок и т.п.) в тех случаях, когда обнаружение дефекта является
редким событием.
U-карта. Отображает изменчивость относительной частоты
дефектов (т.е. отношения числа обнаруженных дефектов к числу проверенных единиц
продукции) в тех случаях, когда вероятность дефекта является редким событием.
Удобно использовать при анализе партий различного объема.
Np-карта. Отображает изменчивость числа дефектов,
когда обнаружение дефекта не является редким событием (например, происходит
более, чем у 5% проверенных единиц продукции).
P-карта. Отображает изменчивость процента обнаруженных
дефектных изделий (в расчете на партию, в день, на станок и т.д.), когда
обнаружение дефекта не является редким событием [7].
.2
Построение контрольных карт
— и R-карты
Карты для количественных данных отражают состояние процесса через
разброс (изменчивость от единицы к единице) и через расположение центра
(среднее процесса). Поэтому контрольные карты для количественных данных почти
всегда применяют и анализируют парами — одна карта для расположения и одна —
для разброса. Наиболее часто используют пару — и
-карту [8].
1. По осям x на обеих картах наносим моменты времени, по
которым мы располагаем данными и на протяжении которых мы хотим изучить
ситуацию (обычно 20 или больше периодов). Например, январь, февраль, март, …
или 1-й час, 2-й час, 3-й час, и т.д. [9]
2. По осям y создаем шкалу, соответствующую измерениям
(вес, температура…) [9].
3. По каждому моменту времени, на X-карте отобразим средние
значения в выборках и на R-карте размах в выборках () [9].
. Посчитаем центральную линию для Х-карты: [9].
. Посчитаем центральную линию для R-карты: [9].
,
где n — количество элементов в выборке [9].
.
. Посчитаем верхний и нижний
пределы для Х-карты, верхний
и нижний
пределы для R-карты [9].
Значение констант ,
,
зависят от n (количества
элементов в выборке) и находятся по таблице 1.
Таблица 1 — Коэффициенты для вычисления линий контрольных
карт [8]
|
Число |
Коэффициенты |
Коэффициенты |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
2,121 |
1,880 |
2,659 |
0,000 |
3,267 |
0,000 |
2,606 |
0,000 |
3,686 |
0,000 |
3,267 |
0,7979 |
1,2533 |
1,128 |
0,8865 |
|
3 |
1,732 |
1,023 |
1,954 |
0,000 |
2,568 |
0,000 |
2,276 |
0,000 |
4,358 |
0,000 |
2,574 |
0,8886 |
1,1284 |
1,693 |
0,5907 |
|
4 |
1,500 |
0,729 |
1,628 |
0,000 |
2,266 |
0,000 |
2,088 |
0,000 |
4,696 |
0,000 |
2,282 |
0,9213 |
1,0854 |
2,059 |
0,4857 |
|
5 |
1,342 |
0,577 |
1,427 |
0,000 |
2,089 |
0,000 |
1,964 |
0,000 |
4,918 |
0,000 |
2,114 |
0,9400 |
1,0638 |
2,326 |
0,4299 |
|
6 |
1,225 |
0,483 |
1,287 |
0,030 |
1,970 |
0,029 |
1,874 |
0,000 |
5,078 |
0,000 |
2,004 |
0,9515 |
1,0510 |
2,534 |
0,3946 |
|
7 |
1,134 |
0,419 |
1,182 |
0,118 |
1,882 |
0,113 |
1,806 |
0,204 |
5,204 |
0,076 |
1,924 |
0,9594 |
1,0423 |
2,704 |
0,3698 |
|
8 |
1,061 |
0,373 |
1,099 |
0,185 |
1,815 |
0,179 |
1,751 |
0,388 |
5,306 |
0,136 |
1,864 |
0,9650 |
1,0363 |
2,847 |
0,3512 |
|
9 |
1,000 |
0,337 |
1,032 |
0,239 |
1,761 |
0,232 |
1,707 |
0,547 |
5,393 |
0,184 |
1,816 |
0,9693 |
1,0317 |
2,970 |
0,3367 |
|
10 |
0,949 |
0,308 |
0,975 |
0,284 |
1,716 |
0,276 |
1,669 |
0,687 |
5,469 |
0,223 |
1,777 |
0,9727 |
1,0281 |
0,3249 |
|
|
11 |
0,905 |
0,285 |
0,927 |
0,321 |
1,679 |
0,313 |
1,637 |
0,811 |
5,535 |
0,256 |
1,744 |
0,9754 |
1,0252 |
3,173 |
0,3152 |
|
12 |
0,866 |
0,266 |
0,886 |
0,354 |
1,646 |
0,346 |
1,610 |
0,922 |
5,594 |
0,283 |
1,717 |
0,9776 |
1,0229 |
3,258 |
0,3069 |
|
13 |
0,832 |
0,249 |
0,850 |
0,382 |
1,618 |
0,374 |
1,585 |
1,025 |
5,647 |
0,307 |
1,693 |
0,9794 |
1,0210 |
3,336 |
0,2998 |
|
14 |
0,802 |
0,235 |
0,817 |
0,406 |
1,594 |
0,399 |
1,563 |
1,118 |
5,696 |
0,328 |
1,672 |
0,9810 |
1,0194 |
3,407 |
0,2935 |
|
15 |
0,775 |
0,223 |
0,789 |
0,428 |
1,572 |
0,421 |
1,544 |
1,203 |
5,741 |
0,347 |
1,653 |
0,9823 |
1,0180 |
3,472 |
0,2880 |
|
16 |
0,750 |
0,212 |
0,763 |
0,448 |
1,552 |
0,440 |
1,526 |
1,282 |
5,782 |
0,363 |
1,637 |
0,9835 |
1,0168 |
3,532 |
0,2831 |
|
17 |
0,728 |
0,203 |
0,739 |
0,466 |
1,534 |
0,458 |
1,511 |
1,356 |
5,82 |
0,378 |
1,622 |
0,9845 |
1,0157 |
3,588 |
0,2784 |
|
18 |
0,707 |
0,194 |
0,718 |
0,482 |
1,518 |
0,475 |
1,496 |
1,424 |
5,856 |
0,391 |
1,608 |
0,9854 |
1,0148 |
3,640 |
0,2747 |
|
19 |
0,688 |
0,187 |
0,698 |
0,497 |
1,503 |
0,490 |
1,483 |
1,487 |
5,891 |
0,403 |
1,597 |
0,9862 |
1,0140 |
3,689 |
0,2711 |
|
20 |
0,671 |
0,180 |
0,680 |
0,510 |
1,490 |
0,504 |
1,470 |
1,549 |
5,921 |
0,415 |
1,585 |
0,9869 |
1,0133 |
3,735 |
0,2677 |
|
21 |
0,655 |
0,173 |
0,663 |
0,523 |
1,477 |
0,516 |
1,459 |
1,605 |
5,951 |
0,425 |
1,575 |
0,9876 |
1,0126 |
3,778 |
0,2647 |
|
22 |
0,640 |
0,167 |
0,647 |
0,534 |
1,466 |
0,528 |
1,448 |
1,659 |
5,979 |
0,434 |
1,566 |
0,9882 |
1,0119 |
3,819 |
0,2618 |
|
23 |
0,626 |
0,162 |
0,633 |
0,545 |
1,455 |
0,539 |
1,438 |
1,710 |
6,006 |
0,443 |
1,557 |
0,9887 |
1,0114 |
3,858 |
0,2592 |
|
24 |
0,612 |
0,157 |
0,619 |
0,555 |
1,445 |
0,549 |
1,429 |
1,759 |
6,031 |
0,451 |
1,548 |
0,9892 |
1,0109 |
3,895 |
0,2567 |
|
25 |
0,600 |
0,153 |
0,606 |
0,565 |
1,434 |
0,559 |
1,420 |
1,806 |
6,056 |
0,459 |
1,541 |
0,9896 |
1,0105 |
3,931 |
0,2544 |
|
Примечание — |
Уточнения к формулам: Контрольные границы для X-карты вычисляются как , где оценка стандартного отклонения равна [9]:
.
Значение находится по таблице 1 [9].
Если исследователю известно, что процесс не имеет трендов, то
можно достичь лучших результатов, используя следующую оценку [9]:
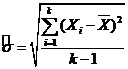
где — это все измерения по всем выборкам [9].
. На X-карте
отобразим ,
и
как линии, параллельные оси x [9].
. На R-карте
отобразим ,
и
[9].
. Подобно нижней и верхней границам, на X-карте посчитаем и отобразим пределы первого и второго
сигма-уровней [9].
— пределы первого сигма-уровня [9].
— пределы второго сигма-уровня [9].
— пределы третьего сигма-уровня, они же контрольные границы [9].
Приведем пример [9].
Размер выборки: 5
Константы:
U-карта
U — карта контроля числа несоответствий на одно изделие в
выборке (применяются как при постоянном, так и при переменном объеме выборки).
Методика построения контрольных карт U типа:
1. В зависимости от того заданы ли стандартные значения
показателя качества или нет, первый этап разбивается на два варианта:
I. Стандартные значения не заданы:
· Соберите предварительные данные о
протекании процесса. Для этого зафиксируйте наличие или отсутствие выбранных
признаков у каждого изделия рассматриваемой подгруппы.
· Определите:
— число несоответствий на единицу в подгруппе;
где — индекс измеренного показателя качества
в подгруппе;
— число несоответствий в подгруппе;
— индекс подгруппы;
— количество изделий в подгруппе;
· Рассчитайте среднеарифметическое значение,
вычисленного на предыдущем шаге статистического показателя:
— среднеарифметическое значение несоответствий на единицу во всех
подгруппах;
где — количество подгрупп.
· Вычислите значения для центральной линии,
нижнего и верхнего контрольного пределов
. Стандартные значения заданы (т.е. заданы ):
· Вычислите значения для центральной линии,
нижнего и верхнего контрольного пределов:
Когда объем выборки меняется незначительно (не более ±25% среднего
объема подгруппы), то можно ограничиться одним набором контрольных границ,
рассчитанным для среднего объема подгруппы. Если объем выборки меняется
существенно, то для каждой подгруппы рассчитывают свои контрольные границы.
1) Начертите вертикальную ось. Выберите масштаб и
отображаемый диапазон значений, разметьте в соответствии с ними ось.
2) Начертите горизонтальную ось и разбейте ее на
интервалы, представляющие собой подгруппы.
) Нанесите на карту вычисленные в п. 1 центральную
линию, нижний и верхний контрольные пределы.
) В соответствии с получаемыми данными наносите точки
контролируемых параметров показателя качества и проводите анализ контрольной
карты.
Пример построения контрольной карты U типа.
На заводе по производству шин каждые полчаса контролировали
15 шин и записывали общее число несоответствий и их число на единицу. Было решено
применить U-карту
для числа несоответствий на единицу, чтобы определить состояние процесса.
Данные приведены в таблице 2.
Завод по производству шин. Число несоответствий на единицу
(единицы проверялись по 14 подгруппам, объемом n = 15 каждая)
Таблица 2
|
Номер подгруппы |
Число |
Число |
Номер подгруппы |
Число |
Число |
|
1 |
4 |
0,27 |
9 |
2 |
0,13 |
|
2 |
5 |
0,33 |
10 |
4 |
0,27 |
|
3 |
3 |
0,20 |
11 |
7 |
0,47 |
|
4 |
6 |
0,40 |
12 |
5 |
0,33 |
|
5 |
2 |
0,13 |
13 |
2 |
0,13 |
|
6 |
1 |
0,07 |
14 |
3 |
0,20 |
|
7 |
5 |
0,33 |
Всего |
55 |
|
|
8 |
6 |
0,40 |
Среднее значений u подсчитывалось из таблицы делением общего числа
несоответствий (из ряда с-значений) на общее число проконтролированных единиц
(т.е. 14: 15).
центральная линия: ;
;
(т.к. отрицательные значения невозможны, нижняя граница
отсутствует).
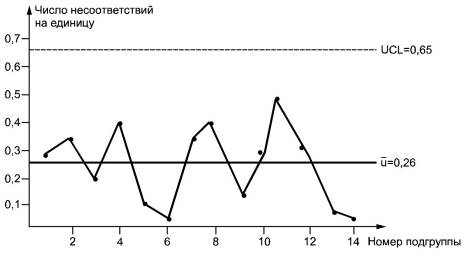
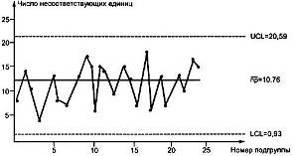
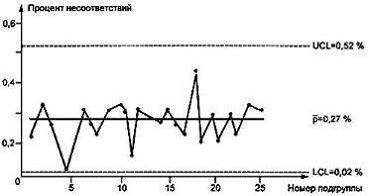
Данные и контрольные линии нанесены на рисунке 5. Карта
показывает, что процесс находится в состоянии статистической управляемости.
Рисунок 5 — U-карта по
данным таблицы 2
Отметим, что поскольку объемы подгрупп постоянны, можно применить
и с-карту.
C-карта
В таких контрольных картах строится график
числа дефектов (в партии, в день, на один станок, в расчете на 100 футов трубы
и т.п.). При использовании карты этого типа делается предположение, что дефекты
контролируемой характеристики продукции встречаются сравнительно редко, при
этом контрольные пределы для данного типа карт рассчитываются на основе свойств
распределения Пуассона (распределения редких событий).
При использовании С- и U-карт принимается
предположение о том, что дефекты контролируемой характеристики продукции
встречаются сравнительно редко и контрольные пределы для данных типов карт рассчитываются
на основе свойств распределения Пуассона (распределения редких событий).
При этом на С- и Np-картах отображается число дефектов (в
партии, в день, на один станок), а на U- и P-картах отображается относительная
частота дефектов, то есть отношение числа обнаруженных дефектов к числу
проверенных единиц продукции.
Методика построения контрольных карт C типа:
1. В зависимости от того заданы ли стандартные значения
показателя качества или нет первый этап разбивается на два варианта:
I. Стандартные значения не заданы:
· Соберите предварительные данные о
протекании процесса. Для этого зафиксируйте наличие или отсутствие выбранных
признаков у каждого изделия рассматриваемой подгруппы.
— число несоответствий в подгруппе;
. Рассчитайте среднеарифметическое значеник вычисленного на
предыдущем шаге статистического показателя :
— среднеарифметическое значение несоответствий во всех подгруппах;
где — количество подгрупп.
· Вычислите значения для центральной линии,
нижнего и верхнего контрольного пределов
Стандартные значения заданы (т.е. заданы ):
. Вычислите значения для центральной линии, нижнего и верхнего
контрольного пределов
Когда объем выборки меняется незначительно (не более ±25% среднего
объема подгруппы), то можно ограничиться одним набором контрольных границ,
рассчитанным для среднего объема подгруппы. Если объем выборки меняется
существенно, то для каждой подгруппы рассчитывают свои контрольные границы.
1) Начертите вертикальную ось. Выберите масштаб и
отображаемый диапазон значений, разметьте в соответствии с ними ось.
2) Начертите горизонтальную ось и разбейте ее на
интервалы, представляющие собой подгруппы.
) Нанесите на карту вычисленные в п. 1 центральную
линию, нижний и верхний контрольные пределы.
) В соответствии с получаемыми данными наносите точки
контролируемых параметров показателя качества и проводите анализ контрольной
карты.
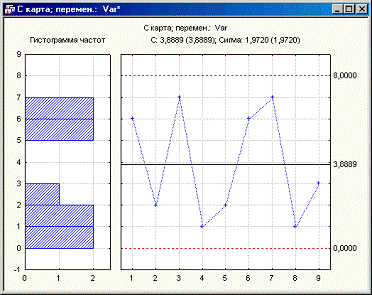
На этой С-карте показан хорошо управляемый технологический
процесс: количество бракованной продукции в каждой выборке находится в рамках
контрольных пределов.
А в этом примере на C-карте наблюдается выброс (первая
выборка). Однако соответствующие статистики по остальным выборкам находятся в
рамках контрольных пределов. Таким образом, на основании этой карты, исключив
первую выборку, можно считать процесс управляемым. Если проблемная выборка
отражает начало реального технологического процесса, то, скорее всего, ее
неудовлетворительное качество связано с первоначальной настройкой процесса. В
этом случае рекомендуется провести дополнительный анализ качества продукции,
выпущенной на начальном этапе и, исключив имеющийся выброс, признать процесс
управляемым.
Np-карта
Np-карта — (контрольная карта количества брака) используется
при контроле некоторого свойства детали, которое достаточно часто встречается в
измерениях
Контрольная np-карта служит для отображения изменения числа
дефектов по выборкам (партиям) i, i=1,…, N, при условии равенства объемов
выборок, большом количестве дефектов (более 5%) и биномиальном распределении
переменной величины.
В контрольных картах этого типа строится график для числа
дефектов (в партии, в день, на станок), как и в случае С-карты. Однако,
контрольные пределы этой карты рассчитываются на основе биномиального распределения,
а не распределения редких событий Пуассона. Поэтому данный тип карт должен
использоваться в том случае, когда обнаружение дефекта не является редким
событием (например, когда обнаружение дефекта происходит более чем у 5%
проверенных единиц продукции). Этой картой можно воспользоваться, например, при
контроле числа единиц продукции, имеющих небольшой брак.
Например, с помощью Np-карты можно отслеживать число единиц продукции в
партии, у которых обнаружены потемнения.
Контрольные пределы для Np-карты считаются на
основе Биномиального распределения
Рисунок 6 — Пример контрольной карты на основе биноминального
распределения
Биномиальное распределение:
Вероятность в n испытаниях с вероятностью успеха p и неудачи 1-p получить ровно k успехов и n-k
неудач.карта строится в случаях, когда объем выборки постоянный. Только в этом
случае имеет смысл сравнивать количество брака для разных партий.
Основные области применения контрольных карт:
· уменьшение отклонений процесса.
· контроль результатов процесса.
· установление общего языка для обсуждения
показателей процесса.
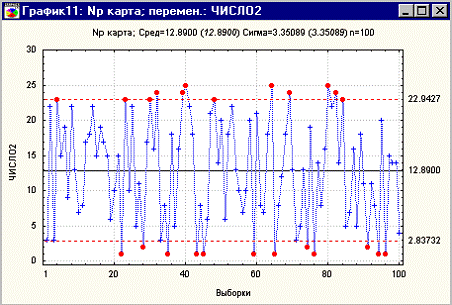
Построение: np =4,7 UCL=11,0 LCL=0,0 n=100 np =4,7 UCL=11,0
LCL=0,0 n=100
Рисунок 7 — Количество дефектов
Таблица 3 — Данные для построения np-карты
|
Период |
1 |
|
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
12 |
13 |
14 |
15 |
16 |
17 |
18 |
19 |
20 |
21 |
22 |
23 |
24 |
25 |
26 |
27 |
28 |
29 |
30 |
|
Кол-во дефектов |
2 |
7 |
5 |
1 |
4 |
3 |
2 |
6 |
8 |
4 |
2 |
5 |
7 |
4 |
3 |
1 |
9 |
3 |
4 |
5 |
2 |
8 |
7 |
10 |
6 |
8 |
2 |
4 |
6 |
2 |
|
CL |
4,7 |
4,7 |
4,7 |
4,7 |
4,7 |
4,7 |
4,7 |
4,7 |
4,7 |
4,7 |
4,7 |
4,7 |
4,7 |
4,7 |
4,7 |
4,7 |
4,7 |
4,7 |
4,7 |
4,7 |
4,7 |
4,7 |
4,7 |
4,7 |
4,7 |
4,7 |
4,7 |
4,7 |
4,7 |
4,7 |
|
UCL |
11,0 |
11,0 |
11,0 |
11,0 |
11,0 |
11,0 |
11,0 |
11,0 |
11,0 |
11,0 |
11,0 |
11,0 |
11,0 |
11,0 |
11,0 |
11,0 |
11,0 |
11,0 |
11,0 |
11,0 |
11,0 |
11,0 |
11,0 |
11,0 |
11,0 |
11,0 |
11,0 |
11,0 |
11,0 |
11,0 |
|
LCL |
0,0 |
0,0 |
0,0 |
0,0 |
0,0 |
0,0 |
0,0 |
0,0 |
0,0 |
0,0 |
0,0 |
0,0 |
0,0 |
0,0 |
0,0 |
0,0 |
0,0 |
0,0 |
0,0 |
0,0 |
0,0 |
0,0 |
0,0 |
0,0 |
0,0 |
0,0 |
0,0 |
0,0 |
0,0 |
0,0 |
|
+1у |
6,8 |
6,8 |
6,8 |
6,8 |
6,8 |
6,8 |
6,8 |
6,8 |
6,8 |
6,8 |
6,8 |
6,8 |
6,8 |
6,8 |
6,8 |
6,8 |
6,8 |
6,8 |
6,8 |
6,8 |
6,8 |
6,8 |
6,8 |
6,8 |
6,8 |
6,8 |
6,8 |
6,8 |
6,8 |
6,8 |
|
+2у |
8,9 |
8,9 |
8,9 |
8,9 |
8,9 |
8,9 |
8,9 |
8,9 |
8,9 |
8,9 |
8,9 |
8,9 |
8,9 |
8,9 |
8,9 |
8,9 |
8,9 |
8,9 |
8,9 |
8,9 |
8,9 |
8,9 |
8,9 |
8,9 |
8,9 |
8,9 |
8,9 |
8,9 |
8,9 |
8,9 |
|
-1у |
2,6 |
2,6 |
2,6 |
2,6 |
2,6 |
2,6 |
2,6 |
2,6 |
2,6 |
2,6 |
2,6 |
2,6 |
2,6 |
2,6 |
2,6 |
2,6 |
2,6 |
2,6 |
2,6 |
2,6 |
2,6 |
2,6 |
2,6 |
2,6 |
2,6 |
2,6 |
2,6 |
2,6 |
2,6 |
2,6 |
|
-2у |
0,4 |
0,4 |
0,4 |
0,4 |
0,4 |
0,4 |
0,4 |
0,4 |
0,4 |
0,4 |
0,4 |
0,4 |
0,4 |
0,4 |
0,4 |
0,4 |
0,4 |
0,4 |
0,4 |
0,4 |
0,4 |
0,4 |
0,4 |
0,4 |
0,4 |
0,4 |
0,4 |
0,4 |
0,4 |
0,4 |
1. 1. По оси x нанесите моменты времени, по которым
вы располагаете данными и на протяжении которых вы хотите изучить ситуацию
(обычно 20 или больше периодов). Например, январь, февраль, март, … или 1-й
час, 2-й час, 3-й час, и т.д.
2. По оси y создайте шкалу соответствующую измерениям
(процент дефектов, количество дефектов, количество дефектов на одну единицу
продукции).
. Отобразите данные по каждому моменту времени.
. В зависимости от карты, которую вы используете,
посчитаете соответствующую центральную линию CL.
Центральная линия, определяющая среднее число дефектных
изделий для N-го количества выборок:
,
где — количество выборок,
— количество дефектных единиц в i-ой выборке,
5. Посчитать соответствующие верхний UCL и нижний LCL
пределы.
Комментарии. Контрольные границы вычисляются как 3
стандартных отклонения от среднего значения данных.
6. На карте отобразите CL, UCL и LCL как линии
параллельные оси x.
7. Подобно нижней и верхней границам, посчитайте и
отобразите пределы первого и второго сигма уровней.
Пределы первого сигма уровня — одно отклонение от среднего.
Пределы второго сигма уровня — два отклонения от среднего.
Пределы третьего сигма уровня они же контрольные границы —
три отклонения от среднего.
Пример np-карты.
В таблице 4 указано число несоответствующих единиц в час с
учетом неисправностей, найденных при сплошном контроле небольших выключателей с
помощью устройств автоматического контроля. Выключатели производят на
автоматической сборочной линии. Поскольку неисправность серьезна, для
определения момента выхода сборочной линии из статистически управляемого
состояния используют контрольную карту процента несоответствующих единиц.
Таблица 4 — Выключатели. Предварительные данные
|
Номер подгруппы |
Число |
Число |
Процент |
|
1 |
4000 |
8 |
0,200 |
|
2 |
4000 |
14 |
0,350 |
|
3 |
4000 |
10 |
0,250 |
|
4 |
4000 |
4 |
0,100 |
|
5 |
4000 |
13 |
0,325 |
|
6 |
4000 |
9 |
0,225 |
|
7 |
4000 |
7 |
0,175 |
|
8 |
4000 |
11 |
0,275 |
|
9 |
4000 |
15 |
0,375 |
|
10 |
4000 |
13 |
0,325 |
|
11 |
4000 |
5 |
0,126 |
|
12 |
4000 |
14 |
0,350 |
|
13 |
4000 |
12 |
0,300 |
|
14 |
4000 |
8 |
0,200 |
|
15 |
4000 |
15 |
0,375 |
|
16 |
4000 |
11 |
0,275 |
|
17 |
4000 |
9 |
0,225 |
|
18 |
4000 |
18 |
0,450 |
|
19 |
4000 |
6 |
0,150 |
|
20 |
4000 |
12 |
0,300 |
|
21 |
4000 |
6 |
0,150 |
|
22 |
4000 |
12 |
0,300 |
|
23 |
4000 |
8 |
0,200 |
|
24 |
4000 |
15 |
0,375 |
|
25 |
4000 |
14 |
0,350 |
|
Всего |
100000 |
269 |
0,269 |
Отметим, что для приведенных данных в той же степени пригодна
np-карта, поскольку объемы
всех выборок равны. Вычисления для np-карты даны в таблице 4, карта представлена на
рисунке 8.
Рисунок 8 — np-Карта по данным таблицы 4
np-Карта:
;
;
.
S — карта
Контрольная карта средних значений и средних
квадратичных отклонений (X—S). Данная карта практически идентична карте (X — R),
но точнее её и может рекомендоваться при отладке технологических процессов при
массовом производстве ответственных деталей. Её можно применить в случаях,
когда имеется система встроенного контроля с автоматическим вводом данных в
ЭВМ, используемые для автоматического управления процессом.
В картах X — S вместо размаха R используется более
эффективная статистическая характеристика рассеивания наблюдаемых значений —
среднее квадратичное отклонение (S).
Она показывает, насколько тесно группируются отдельные
значения вокруг средней арифметической или как они рассеиваются вокруг неё.
Среднее квадратичное отклонение определяется по формуле:
В остальном построение и применение карты (X — S) не отличается
от карты (X — R).
Иногда для контроля используется карта (Me — R) — контрольная карта медиан и размахов.
Медиана — это среднее значение в выборке, если все значения расположены в
порядке возрастания или убывания. В выборке из трёх значений медиана — второе
значение, в выборке из пяти значений медиана занимает третье место. Такая карта
менее точна, чем карта (X — R), но она проще в пользовании и нередко применяется.
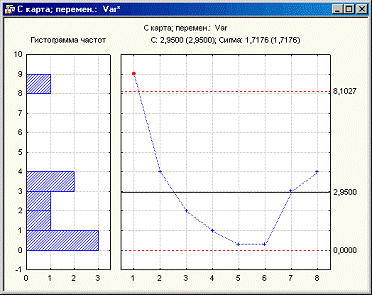
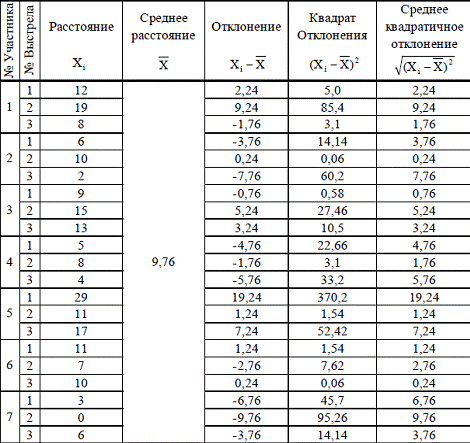
Пример. В
качестве примера контрольной карты средних значений и средних квадратичных
отклонений рассмотрим контроль точности попадания в мишень на спортивных
соревнованиях с участием 7 стрелков. Объект измерения и контроля — расстояние
места попадания от центра мишени. Радиус мишени составляет 15 сантиметров. Если
расстояние между местом попадания и центром составляет более 15 сантиметров,
говорят, что спортсмен попал в «молоко» и не засчитывают ему очки за этот
выстрел. Каждому стрелку предоставляется по 3 выстрела, и его результат определяется
как сумма набранных баллов.
Точность стрельбы представлена в таблице 5.
Для построения контрольной карты необходимо вычислить:
При вычислении необходимо использовать коэффициенты ,
,
, значения которых берём из таблицы 1.
Таблица 5
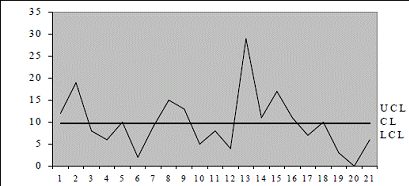
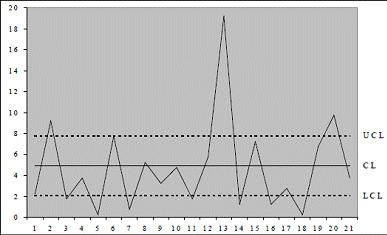
Нанесём полученные контрольные границы и значения параметра на
контрольные карты (рис. 9, 10):
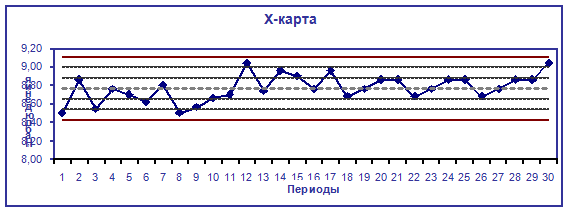
Рисунок 9 — Контрольная карта X — типа
Рисунок 10 — Контрольная карта S-типа
Построенные диаграммы позволяют сделать следующее заключение:
исследуемый процесс не является статистически управляемым (множественные выходы
значений за контрольные пределы). Из чего следует, что в соревнованиях
принимали участие спортсмены разной квалификации. Максимальное отклонение на
тринадцатом выстреле свидетельствует о полной неготовности спортсмена к
соревнованиям или о каком-то серьёзном происшествии (помехе выстрелу). В
качестве рекомендаций можно выдать введение в систему отборочных туров.
P-карта
Обычно p — карту используют для определения
среднего процента несоответствующих единиц, обнаруженных за определенный период
времени. Она привлекает внимание персонала процесса и управляющих к любым
изменениям этого среднего. Процесс признается находящимся в состоянии
статистической управляемости так же, как и при использовании — и
-карт. Если все выборочные точки ложатся внутри пробных
контрольных границ без выбросов, указывающих на наличие особых причин, то о
процессе можно сделать заключение, что он управляем. В этом случае средняя доля
несоответствующих единиц берется как стандартное значение
для доли несоответствующих единиц .
Построение p-карты:
1. По оси x нанесите моменты времени, по которым вы
располагаете данными и на протяжении которых вы хотите изучить ситуацию (обычно
20 или больше периодов). Например, январь, февраль, март, … или 1-й час, 2-й
час, 3-й час, и т.д.
2. По оси y создайте шкалу, соответствующую измерениям
(процент дефектов, количество дефектов, количество дефектов на одну единицу
продукции).
3. Отобразите данные по каждому моменту времени.
4. Посчитаем центральную линию для p-карты
,
где — количество выборок,
— процент дефекта в
-ой выборке,
. Посчитаем верхний и нижний
пределы для p-карты
— количество элементов в выборках (p-карты могут использоваться
для выборок разного размера).
Комментарии. Контрольные границы вычисляются как 3 стандартных
отклонения от среднего значения данных.
6. На карте отобразите CL, UCL и LCL как линии
параллельные оси x.
7. Подобно нижней и верхней границам, посчитайте и
отобразите пределы первого и второго сигма уровней.
Пределы первого сигма уровня — одно отклонение от среднего.
Пределы второго сигма уровня — два отклонения от среднего.
Пределы третьего сигма уровня они же контрольные границы —
три отклонения от среднего
Пример p-карты. В таблице 6 указано число
несоответствующих единиц в час с учетом неисправностей, найденных при сплошном
контроле небольших выключателей с помощью устройств автоматического контроля.
Выключатели производят на автоматической сборочной линии. Поскольку
неисправность серьезна, для определения момента выхода сборочной линии из
статистически управляемого состояния используют контрольную карту процента
несоответствующих единиц. Карта получена при сборе предварительных данных по 25
подгруппам каждая из 4000 выключателей (таблица 6).
Таблица 6 — Выключатели. Предварительные данные
|
Номер подгруппы |
Число |
Число |
Процент |
|
1 |
4000 |
8 |
0,200 |
|
2 |
4000 |
14 |
0,350 |
|
3 |
4000 |
10 |
0,250 |
|
4 |
4000 |
4 |
0,100 |
|
5 |
4000 |
13 |
0,325 |
|
6 |
4000 |
9 |
0,225 |
|
7 |
4000 |
7 |
0,175 |
|
8 |
4000 |
11 |
0,275 |
|
9 |
4000 |
15 |
0,375 |
|
10 |
4000 |
13 |
0,325 |
|
11 |
4000 |
5 |
0,126 |
|
12 |
4000 |
14 |
0,350 |
|
13 |
4000 |
12 |
0,300 |
|
14 |
4000 |
8 |
0,200 |
|
15 |
4000 |
15 |
0,375 |
|
16 |
4000 |
11 |
0,275 |
|
17 |
4000 |
9 |
0,225 |
|
18 |
4000 |
18 |
0,450 |
|
19 |
4000 |
6 |
0,150 |
|
20 |
4000 |
12 |
0,300 |
|
21 |
4000 |
6 |
0,150 |
|
22 |
4000 |
12 |
0,300 |
|
23 |
4000 |
8 |
0,200 |
|
24 |
4000 |
15 |
0,375 |
|
25 |
4000 |
14 |
0,350 |
|
Всего |
100000 |
269 |
0,269 |
Центральная линия и контрольные границы вычислены ниже и
приведены на рисунке 11.
Рисунок 11 — p-карта по данным таблицы 6
p—карта:
центральная линия:
Карта показывает, что качество выключателей находится в
управляемом состоянии, хотя процент несоответствий, видимо, слишком велик.
Данные контрольные границы могут быть использованы для будущих подгрупп до тех
пор, пока процесс не изменится или выйдет из статистически управляемого
состояния. Когда же процесс находится в состоянии статистической управляемости,
вряд ли удастся какое-либо усовершенствование без изменения самого процесса.
Если сделано улучшение процесса, надо вычислить новые
контрольные границы для будущих подгрупп, чтобы учесть измененное качество
процесса. Если процесс улучшен (значение уменьшилось), то нужно
использовать новые границы. Если процесс был ухудшен (значение увеличилось), надо найти
дополнительные неслучайные причины.
Список
использованных источников
1. http://festival.1september.ru/articles/634553/
2. http://producm.ru/books/books_statistic/book16/p2/
. http://venec.ulstu.ru/lib/disk/2012/Efimov5.pdf
. лекции
5. http://baguzin.ru/wp/? p=5381
. http://dic.academic.ru/dic.nsf/enc_mathematics/295/АСИММЕТРИЯ
7. учебник
. ГОСТ Р 50779.42-99 (ИСО 8258-91)
Статистические методы. Контрольные карты Шухарта.
9. http://www.six-sigma.ru/index.php?
id=278
Каждая организация сталкивается со сбоями в бизнес-процессах. Поиск и устранение причин отнимают не только время, но и деньги. Важно отслеживать изменение процесса в реальном времени и обеспечивать стабильность его работы. Контрольные карты Шухарта позволяют решить эту задачу и значительно сократить издержки.
- Что такое контрольные карты Шухарта
- Виды контрольных карт Шухарта
- Построение контрольных карт
- Эффективное управление бизнес-процессами
- Преимущества использования контрольных карт
Одной из причин убытка американской компании Nvidia по итогам 2-го квартала 2010-2011 финансового года стал массовый выпуск бракованных видеокарт. Нарушение при изготовлении одной детали привело к серьезным проблемам всего бизнеса: некачественные корпуса микросхем приводили к их быстрому нагреву и выходу из строя. Ремонт и замена обошлись компании в 315 миллионов долларов, что в 12 раз превысило стоимость обычного обслуживания.
Как избежать таких ситуаций на реальном производстве, на котором проходят тысячи процессов? Очевидно, что решение проблем постфактум приводит к скачкообразному росту издержек. Поэтому помочь может только предиктивная аналитика.
Если все процессы находятся в стабильном состоянии, то можно предсказать их поведение в будущем. Это заметно упрощает процесс управления бизнесом. Например, если можно предсказать примерный объем работы, то гораздо легче заранее рассчитать количество требующегося персонала.
То же самое касается и оборудования на производстве. При прогнозируемости нагрузки есть возможность равномерно распределить ее по имеющимся станкам, не допустив простоя или перегрузки, которые в обоих случаях ведут к финансовым потерям.
Как предсказать поведение процесса?
Эту задачу в 1924 году решил американский ученый Уолтер Эндрю Шухарт или, как его называют, «отец современного контроля качества». Он изучал статистическую теорию и поставил себе задачу применить ее на благо промышленности.
В результате был разработан специальный графический инструмент, который позволяет отслеживать отступления от нормы и тенденции возникновения ошибок до того, как на производстве появится брак. Это стало революцией в области контроля качества продукции.
Изначально карты Шухарта были созданы для контроля брака на производстве. Но они показали свою универсальность для любых процессов, которые имеют регулярный характер. Сейчас они получили широкое распространение во всех сферах бизнеса. Например, в сфере услуг в качестве брака могут рассматриваться претензии от потребителей.
Что такое контрольные карты Шухарта
Контрольные карты Шухарта — это временной график изменения параметров процесса для осуществления статистического контроля его стабильности.
Их основная задача — определить, возможно ли использовать последовательность данных для того, чтобы предсказать поведение процесса в будущем. В случае, если данные использовать нельзя, карты сигнализируют о его нестабильности, а если их применение возможно, являются основой для построения прогноза.
В этом подходе основным критерием процесса является его устойчивость, которая в свою очередь, напрямую зависит от причин изменчивости.
У изменчивости может быть 2 причины:
- Специальная (особая) — внешние воздействия на систему, процесс неустойчивый.
- Общая (случайная) — часть системы, процесс считается устойчивым.
Контрольные карты Шухарта строятся для того, чтобы исключить специальные причины появления изменчивости. Тогда процесс становится стабильным и предсказуемым. Кроме того, повышается его качество и уменьшаются издержки.
По вертикальной оси графика откладываются множественные значения параметра процесса, а по горизонтальной — номера подгрупп, для которых актуальны данные значения.
Важно учитывать, что этот метод применим для регулярных (исполняемых через определенный промежуток времени) процессов, т.к. для построения нужно большое количество значений его параметра.
На рисунке представлено, как выглядит контрольная карта.
Контрольная карта Шухарта
CL — центральная линия. Соответствует опорному значению характеристики. Обычно определяется как среднее арифметическое значение. Причем в зависимости от задачи управления это может быть и намеченное (желаемое) целевое значение.
UCL и LCL — верхняя и нижняя контрольные границы. Расположены по обе стороны от центральной линии, задают коридор значений параметра процесса. Пока параметры не выходят за его границы, считается, что процесс находится в стабильном состоянии.
Важно правильно задать контрольные границы. Если они расположены слишком близко к центральной линии, это приводит к обнаружению проблем там, где их нет. Если, наоборот, коридор окажется слишком широким, особые причины изменчивости могут быть не выявлены.
Поэтому Шухарт установил границы на расстоянии ±3σ от центральной линии, где σ — истинное значение стандартного отклонения процесса. При нормальном распределении 99.7% значений попадут внутрь границ, если процесс управляемый.
Т.к. контрольные карты выявляют и фиксируют точки выхода из стабильного состояния, то часто на них устанавливают «предупреждающие» границы на расстоянии ±2σ, которые сигнализируют о возможном приближении выхода процесса из границ.
Особое преимущество этих карт — не чувствительность к малым сдвигам уровня процесса. Это значит, что они будут реагировать только на аномальное поведение, которое как раз и ведет к нестабильной работе внутри процесса.
Виды контрольных карт Шухарта
Контрольные карты классифицируются в зависимости от типа данных, которые в них отражаются:
- Для количественных данных. Измерения результатов процесса.
- Для альтернативных данных. Характеризуются дискретными значениями процесса (да/нет).
Чаще всего на практике предпочтение отдается первому виду карт. Хотя сбор данных для них осуществить сложнее.
Преимущества контрольных карт для количественных данных:
- Основная масса процессов имеет характеристики, которые могут быть измерены.
- Измеренное значение содержит больше информации, чем простое утверждение «да/нет».
- Есть возможность проанализировать характеристики отдельно от установленных требований.
Значения параметров процесса для каждой контрольной карты могут быть:
- Не заданы. В этом случае анализ данных процесса производят на основании значений самого процесса. Ведется поиск отклонений, которые могут быть вызваны только неслучайными причинами.
- Заданы. Обычно они взяты из требований или получены в результате анализа данных на длительном интервале времени. В этом случае сравниваем наблюдаемые значения с заданными.
Отличием этих двух типов карт, является то, что во втором случае присутствуют дополнительные критерии расположения центральной линии и контрольных границ.
Построение контрольных карт
Когда контрольные карты строятся впервые, часто оказывается, что сам процесс статистически нестабильный. Поэтому его надо привести в управляемое состояние.
Построение карт ведется в 2 этапа:
- Установка параметров контрольной карты. Собирается и обрабатывается большое количество данных для того, чтобы опытным путем узнать значения центральной линии и границ процесса. Т.к. достоверно неизвестно, находился ли данный процесс в состоянии статистической управляемости на момент сбора данных, они считаются пробными. Необходимо раз за разом выявлять происхождение специальных причин вариативности до тех пор, пока карта не покажет отсутствие сигналов. Это будет гарантией того, что процесс стал стабильным.
- Поддержка процесса в состоянии статистической управляемости. Значения, полученные на первом этапе, становятся параметрами контрольной карты для следующего этапа. На этом этапе основным становится поддержание управляемости процесса и быстрое выявление специальных причин, которые влияют на него.
Основные критерии нарушения стабильности процесса:
- Выход значения параметра за пределы контрольных границ.
- От семи и более точек, которые расположены последовательно по одну сторону от центральной линии.
- Семь точек, которые последовательно убывают или возрастают.
- Участок с очевидно неслучайным изменением значений.
Критерии нестабильного процесса
Изначально при оценке результатов рекомендуется ориентироваться на первый критерий — само правило Шухарта. Остальные могут добавляться по необходимости, в зависимости от характера исследуемого процесса.
Кроме того, при долгосрочном анализе обычно выявляются уникальные критерии выхода процесса из стабильного состояния, которые также могут быть учтены. Но нужно иметь ввиду, что с каждым добавленным критерием возрастает вероятность ложных тревог.
Эффективное управление бизнес-процессами
Из-за склонности процессов к изменчивости необходимо их контролировать, а при выходе из стабильного состояния — оперативно применять управленческие решения.
Когда операции единичные, наблюдать за их ходом можно вручную. Если же речь идет о регулярных процессах, то очевидно, что объем информации для исследования будет настолько большим, что необходимо будет автоматизировать анализ.
Например, в банк ежедневно приходят тысячи заявок на кредит. Процесс принятия решений о выдаче кредита стандартизирован, но все равно подвержен изменчивости. Имея данные о показателях за предыдущие периоды можно вычислить контрольный коридор и быстро выявить точки выхода за его пределы.
На рисунке представлен график, который иллюстрирует работу реального процесса. Точки расположены хаотично, большинство вне контрольного коридора.
Нестабильный процесс
На следующем графике процесс перешел в управляемое состояние. Все точки находятся в пределах контрольных границ, появилась структура. Теперь можно прогнозировать его работу в перспективе.
Cтабильный процесс
Последний график иллюстрирует этап контроля за состоянием процесса для предотвращения его перехода в нестабильное состояние. Точка 7 вышла за пределы контрольного коридора, что служит сигналом для применения управляющего воздействия.
Управление процессом
Преимущества использования контрольных карт
Резюмируя, можно сделать вывод, что контрольные карты Шухарта — универсальный инструмент автоматизированного контроля процессов.
Стоит отметить следующие плюсы их применения:
- Быстро реагируют на выход процесса из стабильного состояния. Позволяют оперативно начать устранять проблему.
- Уменьшают изменчивость внутри процесса. После приведения процесса в стабильное состояние снижается общее количество вариаций значений его параметра.
- Показывают тенденцию поведения процесса. Появляется возможность управлять процессом и предсказывать его работу.
Создание сценария Loginom для автоматизированного контроля работы линии техподдержки будет описано в статье «Построение контрольных карт Шухарта в Loginom».
Другие материалы по теме:
Роботизация аналитических бизнес-процессов с помощью Loginom
Сбор данных для анализа
Аналитика в управлении запасами с помощью Loginom. Кейс Русклимат
План:
10.1 Основы контрольных
карт Шухарта
10.2 Типы контрольных
карт Шухарта
10.1 Основы контрольных карт Шухарта
Задача статистического
управления процессами — обеспечение
и поддержание процессов на приемлемом
и стабильном уровне, гарантируя
соответствие продукции и услуг
установленным требованиям.
Главный статистический инструмент,
используемый для этого, — контрольная
карта. Метод
контрольных карт помогает определить,
действительно ли процесс
достиг статистически управляемого
состояния на правильно заданном уровне
или остается в этом
состоянии, а затем поддерживать управление
и высокую степень однородности важнейших
характеристик
продукции или услуги посредством
непрерывной записи информации о качестве
продукции в процессе производства.
Использование контрольных карт и их
тщательный анализ ведут к лучшему
пониманию
и совершенствованию процессов.
Контрольные карты
Шухарта (ККШ) являются основным
инструментом статистического управления
качеством. ККШ применяют для сравнения
получаемой по выборкам информации о
текущем состоянии процесса с контрольными
границами, представляющими пределы
собственной изменчивости (разброса)
процесса. ККШ используют для оценки
того, находятся или не находятся
производственный процесс, процесс
обслуживания или административного
управления в статистически управляемом
состоянии. Первоначально ККШ были
разработаны для применения в промышленном
производстве. В настоящее время их
широко используют в сфере обслуживания
и других областях.
Контрольная
карта – это
графический способ представления и
сопоставления информации, основанный
на последовательности выборок, отражающих
текущее состояние процесса, с границами,
установленными на основе внутренне
присущей процессу изменчивости.
Теория контрольных
карт различает два вида изменчивости.
Первый вид – изменчивость из-за «случайных
(обычных величин), обусловленная
бесчисленным набором разнообразных
причин, присутствующих постоянно,
которые нелегко или невозможно выявить.
Каждая из таких причин составляет очень
малую долю общей изменчивости, и не одна
из них не значима сама по себе.
Тем не менее, сумма всех этих причин
измерима и предполагается, что она
внутренне
присуща процессу. Исключение или
уменьшение влияния обычных причин
требует управленческих
решений и выделения ресурсов на улучшение
процесса и системы. Второй
вид — реальные перемены в процессе. Они
могут быть следствием некоторых
определяемых
причин, не присущих процессу внутренне,
и могут быть устранены.
Эти выявляемые причины рассматриваются
как «неслучайные» или «особые» причины
изменения. К
ним могут быть отнесены поломка
инструмента, недостаточная однородность
материала, производственного
или контрольного оборудования,
квалификация персонала, невыполнение
процедур и т. д.
Цель
контрольных карт — обнаружить
неестественные изменения в данных из
повторяющихся процессов
и дать критерии для обнаружения отсутствия
статистической управляемости. Процесс
находится в статистически управляемом
состоянии, если изменчивость вызвана
только случайными причинами.
При определении этого приемлемого
уровня изменчивости любое отклонение
от него считают результатом действия
особых причин, которые следует выявить,
исключить или ослабить.
Карта
Шухарта требует данных, получаемых
выборочно из процесса через примерно
равные
интервалы. Интервалы могут быть заданы
либо по времени (например ежечасно),
либо по
количеству продукции (каждая партия).
Обычно каждая подгруппа состоит из
однотипных
единиц продукции или услуг с одними и
теми же контролируемыми показателями,
и
все подгруппы имеют равные объемы. Для
каждой подгруппы определяют одну или
несколько характеристик,
таких как среднее арифметическое
подгруппы
и размах подгруппы R
или выборочное стандартное
отклонение S.
Карта Шухарта — это
график значений определенных характеристик
подгрупп в зависимости от их номеров.
Она имеет центральную линию (CL),
соответствующую
эталонному значению характеристики.
При оценке того, находится ли процесс
в статистически управляемом состоянии,
эталонным обычно служит среднее
арифметическое рассматриваемых данных.
При управлении процессом эталонным
служит долговременное значение
характеристики, установленное
в технических условиях, или ее номинальное
значение, основанное на предыдущей
информации
о процессе, или намеченное целевое
значение характеристики продукции или
услуги. Карта Щухарта
имеет две статистические определяемые
контрольные границы относительно
центральной линии,
которые называются верхней контрольной
границей (UCL)
и нижней контрольной границей (LCL)
(рисунок 9 ).
1
2 3 4
5 6
Порядковый
номер выборки
USL
CL
LCL
Рисунок
9 — Вид контрольной карты
Контрольные
границы на карте Шухарта находятся на
расстоянии Зот центральной линии,где
— генеральное стандартное
отклонение используемой статистики.
Изменчивость внутри подгрупп является
мерой случайных вариаций. Для получения
оценки
вычисляют выборочное
стандартное отклонение
или умножают выборочный размах на
соответствующий коэффициент. Эта мера
не включает
межгрупповых вариаций, а оценивает
только изменчивость внутри подгрупп.
Границы
±3указывают, что около 99,7 % значений
характеристики подгрупп попадут в этипределы
при условии, что процесс находится в
статистически управляемом состоянии.
Другими словами,
есть риск, равный 0,3 % (или в среднем три
на тысячу случаев), что нанесенная точка
окажется вне
контрольных границ, когда процесс
стабилен. Употребляется слово
«приблизительно», поскольку отклонения
от исходных предположений, таких как
вид распределения данных, будут влиять
на значения
вероятности.
Некоторые
консультанты предпочитают вместо
множителя, равного 3, значение 3,09, чтобы
обеспечить номинальное значение
вероятности 0,2 % (в среднем два вводящих
в заблуждение наблюдения на тысячу),
но Шухарт выбрал число 3, чтобы не давать
поводов к рассмотрению точных
вероятностей.
Аналогично некоторые консультанты
применяют фактические значения
вероятностей для карт, основанных
на ненормальных распределениях, таких
как карты размахов и долей несоответствий,
и в этом случае в
карте Шухарта также используют границы
на расстоянии ± 3вместо вероятностных
пределов,
упрощая эмпирическую интерпретацию.
Вероятность
того, что нарушение границ в самом деле
случайное событие, а не реальный сигнал,
считается
столь малой, что при появлении точки
вне границ следует предпринять
определенные действия.
Так как действие предпринимается именно
в этой точке, то Зконтрольные границы иногданазываются
«границами действий».
Часто
на контрольной карте границы проводят
еще и на расстоянии 2.Тогда
любое выборочное значение, попадающее
за границы 2а,
может
служить предостережением о грозящей
ситуации выхода процесса
из состояния статистической управляемости.
Поэтому границы ±2иногда называют «предупреждающими»
.
При применении
контрольных карт возможны два вида
ошибок: первого и второго рода.
Ошибка
первого рода возникает, когда процесс
находится в статистически управляемом
состоянии,
а точка выскакивает за контрольные
границы случайно. В результате неправильно
решают, что процесс
вышел из состояния статистической
управляемости, и делают попытку найти
и устранить причину
несуществующей проблемы.
Ошибка
второго рода возникает, когда
рассматриваемый процесс не управляем,
а точки случайно
оказываются внутри контрольных границ.
В этом случае неверно заключают, что
процесс статистически
управляем и упускают возможность
предупредить рост выхода несоответствующей
продукции. Риск
ошибки второго рода — функция трех
факторов: ширины контрольных границ,
степени неуправляемости
и объема выборки. Их природа такова, что
можно сделать лишь общее утверждение
о величине
ошибки.
Система
карт Шухарта учитывает только ошибки
первого рода, равные 0,3 % в пределах
границ 3.
Поскольку в общем случае непрактично
делать полную оценку потерь от ошибки
второго рода в конкретной ситуации, а
удобно произвольно брать малый объем
подгруппы (4 или 5 единиц), целесообразно
использовать границы на расстоянии ±
Зи сосредоточивать внимание в основном
на управлении
и улучшении качества самого процесса.
Если
процесс статистически управляем,
контрольные карты реализуют метод
непрерывной статистической проверки
нулевой гипотезы о том, что процесс не
изменился и остается стабильным. Но
поскольку
значение конкретного отклонения
характеристики процесса от цели, которое
могло бы привлечь внимание, обычно
нельзя определить заранее, как и риск
ошибки второго рода, и объем выборки
не рассчитывается для удовлетворения
соответствующего уровня риска, то карту
Шухарта не стоит
рассматривать с точки зрения проверки
гипотез. Шухарт подчеркивал именно
эмпирическую
полезность контрольных карт для
установления отклонений от состоянии
статистической управляемости,
а не их вероятностную интерпретацию.
Некоторые пользователи применяют кривые
оперативных
характеристик как средства для
интерпретации проверок гипотез.
Когда
наносимое значение выходит за любую из
контрольных границ или серия значений
проявляет необычные
структуры, состояние статистической
управляемости подвергается сомнению.
В этом случае надо исследовать и
обнаружить неслучайные (особые) причины,
а процесс можно остановить
или скорректировать. Как только особые
причины найдены и исключены, процесс
снова готов
к продолжению работы. При возникновении
ошибки первого рода можно не найти
никакой особой
причины. Тогда считают, что выход точки
за границы представляет собой достаточно
редкое случайное
явление при нахождении процесса в
статистически управляемом состоянии.
Если
контрольную карту процесса строят
впервые, то часто оказывается, что
процесс статистически
неуправляем. Контрольные границы,
рассчитанные на основе данных такого
процесса, будут иногда приводить к
ошибочным заключениям, поскольку они
могут оказаться слишком широкими.
Следовательно,
прежде чем устанавливать постоянные
параметры контрольных карт, надо привести
процесс
в статистически управляемое состояние.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #