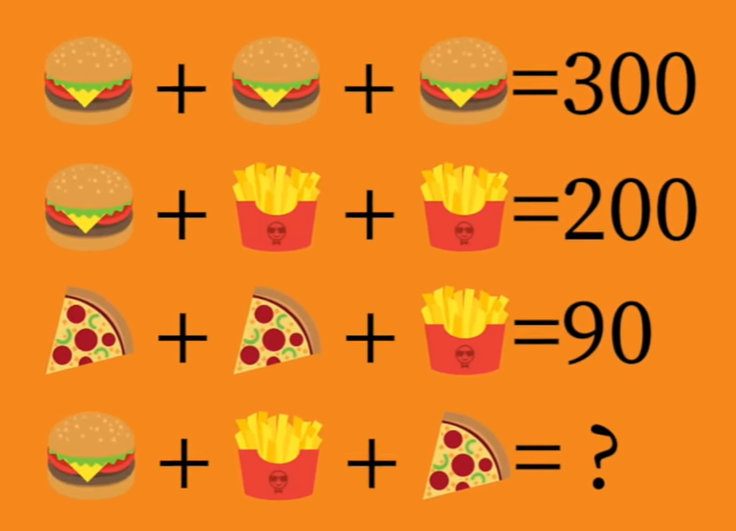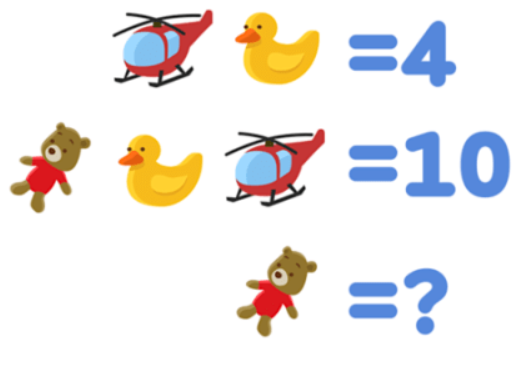Логические задачи
- Авторы
- Руководители
- Файлы работы
- Наградные документы
Носков Я.Д. 1
1МБОУ «Средняя общеобразовательная школа №13» г. Калуги
Регеда Е.А. 1
1МБОУ «Средняя общеобразовательная школа №13» г.Калуги
Текст работы размещён без изображений и формул.
Полная версия работы доступна во вкладке «Файлы работы» в формате PDF
Введение
Развитию творческой активности, инициативы, любознательности, смекалки способствует решение нестандартных задач, логических.
Логические задачи – это неотъемлемая часть сегодняшнего дня. Они не покидают ученика в течение всего обучения в школе.
Логические задачи вызывают массу трудностей у школьников. Чтобы помочь справиться с этими задачами надо изучить типы логических задач и способы их решения. Только решение трудной, нестандартной задачи приносит радость победы. При решении логических задач предоставляется возможность подумать над необычным условием, рассуждать. Это вызывает и сохраняет интерес к математике.
В наше время очень часто успех человека зависит от его способности четко мыслить, логически рассуждать и ясно излагать свои мысли. Без приобретения навыков умственного труда, культуры мышления невозможно успешное овладение основами наук.
Поэтому целью этой работы является изучение видов логических задач, методов их решения, а также возможности развивать свои способности, умения рассуждать и делать правильные выводы.
Задачи:
1. Ознакомление с понятиями «логика» и «математическая логика».
2. Используя литературу, изучить типы логических задач.
3. Изучение основных методов решения логических задач.
4. Проведение диагностики на выявление уровня логического мышления учащихся 6 класса.
Актуальность темы очевидна, так как логические задачи помогают расширить свой кругозор и развить логическое мышление.
I. Что такое логика?
Итак, логика — одна из древнейших наук. Отдельные истоки логического учения можно обнаружить еще в Индии, в конце II тысячелетия до н. э. Основоположником логики как науки является древнегреческий философ и ученый Аристотель. Именно он обратил внимание на то, что в рассуждениях мы из одних утверждений выводим другие, исходя не из конкретного содержания утверждений, а из определенной взаимосвязи между их формами, структурами.
Чтобы правильно рассуждать, надо изучить правильные способы и методы рассуждении. Научится правильно составлять высказывания, или, как говориться в математической логике, выполнять операции над высказываниями. При этом необходимо знать, вытекает ли истинность сложных высказываний из истинности составляющих их более простых предложений. Анализом методов рассуждений занимается наука логика, а исследованием и изучением математических рассуждений – математическая логика.Логика служит одним из инструментов почти любой науки.
II. Типы логических задач.
Нечисловые задачи очень разнообразны по сложности, содержанию и способности решения. Логическиезадачи составляют обширный класс нестандартных задач. Сюда относятся, прежде всего, текстовые задачи, в которых требуется распознать объекты или расположить их в определенном порядке по имеющимся свойствам. При этом часть утверждений условия задачи может выступать с различной истинностной оценкой (быть истинной или ложной).
Все логические задачи делятся на определенные группы (типы):
Истинноностные задачи
Задачи, решаемые с конца
Задачи на переливание
Задачи на взвешивание
Задачи типа «Кто есть кто?»
Задачи на пересечение и объединение множеств
Математические ребусы
III. Методы решения логических задач.
Решать логические задачи очень увлекательно. В них вроде бы нет никакой математики — нет ни чисел, ни треугольников, а есть только лжецы и мудрецы, истина и ложь. В то же время дух математики в них чувствуется ярче всего — половина решения любой математической задачи (а иногда и гораздо больше половины) состоит в том, чтобы как следует разобраться в условии, распутать все связи между участвующими объектами.
При решении определенного типа задач существует свой оптимальный метод решения:
|
Истинноностные задачи |
При решении задач данного типа лучше всего использовать метод рассуждений. Он позволяет проводить рассуждения, используя последовательно все условия задачи, и приходить к выводу, который и будет являться ответом задачи. |
|
Задачи на пересечение и объединение множеств |
Это тип задач, в которых требуется найти некотороепересечение множеств или их объединение, соблюдая условия задачи. Метод Эйлера является незаменимым при решении задач этого типа, а также упрощает рассуждения. Однако, прежде чем приступить к решению задачи, нужно проанализировать условие. |
|
Задачи на переливание |
При решении текстовых логических задач на переливание применяется метод построения таблиц. Таблицы не только позволяют наглядно представить условие задачи или ее ответ, но в значительной степени помогают делать правильные логические выводы в ходе решения задачи. |
|
Задачи на взвешивание |
В таких задачах от решающего требуется локализовать отличающийся от остальных предмет по весу за ограниченное число взвешиваний. Поиск решения в этом случае осуществляется путем операций сравнения, правда, не только одиночных элементов, но и групп элементов между собой. Задачи данного типа чаще всего решаются методом рассуждений. |
|
Математические ребусы |
Записи восстанавливаются на основании логических рассуждений. При этом нельзя ограничиваться отысканием только одного решения. Испытание нужно доводить до конца, чтобы убедиться, что нет других решений, или найти все решения. |
|
Задачи, решаемые с конца |
Такие задачи очень часто ребята задают друг другу в виде головоломок на задуманное число. Задачи решаются методом математических вычислений, основанных на конечном результате в условии. |
|
Задачи типа «Кто есть кто?» |
Смысл задач под кодовым названием «Кто есть кто?» довольно прост. Нам даются отношения между предметами и следуя по цепочке этих отношений, мы приходим к правильному результату. Задачи данного типа чаще всего решаются методом графов. |
IV. Подробное рассмотрение трёх способов решения логических задач.
Разнообразие логических задач очень велико. Способов их решения тоже немало. Рассмотрим три самых часто используемых способов решения логических задач:
— метод графов;
-круги Эйлера;
— табличный;
1) Метод графов.
Даны отношения между предметами и следуя по цепочке этих отношений, мы приходим к правильному результату. Граф – это несколько точек, часть которых соединены друг с другом отрезками или стрелками. Рассмотрим метод графов на примере решения задачи.
Задача “Любимые мультфильмы”: Жила-была одна дружная семья: мама, папа и сын. Они все любили делать вместе. Но вот мультфильмы любили разные: «Ну, погоди!», «Покемоны», «Том и Джерри». Определите, какой мультфильм любит каждый из них, если мама, папа и любитель мультфильма «Покемоны» никогда не унывают, а папа и любитель мультфильма «Том и Джерри» делают зарядку по утрам?
Решение.Рассмотрим множество людей: мама, папа, сын и множество мультфильмов «Ну, погоди!», «Покемоны», «Том и Джерри». Обозначим элементы этих двух множеств точками.
Поэтому граф на рисунке будет выглядеть следующим образом:
Если точке из одного множества соответствует точка другого множества, будем соединять эти точки сплошной линией, если не соответствует – то штриховой. Заметим, что по условию задачи у человека только один любимый мультфильм. Поэтому нужно найти единственно возможное соответствие между элементами двух множеств.
Правило: если какая-то точка оказывается соединенной с двумя точками другого множества штриховыми линиями, то с третьей точкой она должна быть соединена сплошной.
Поэтому граф на рисунке будет выглядеть следующим образом:
Теперь мы установили, что папа любит мультфильм «Ну, погоди!», сын – «Покемоны». В обеих множествах остается только по одной точке, следовательно мама любит мультфильм «Том и Джерри».
Задача решена.
2) Круги Эйлера. Второй способ, которым решаются такие задачи круги Эйлера – задачи на пересечение или объединение множеств.
Это новый тип задач, в которых требуется найти некоторое пересечение множеств или их объединение, соблюдая условия задачи.
Круги Эйлера — геометрическая схема, с помощью которой можно изобразить отношения между подмножествами, для наглядного представления.
Метод Эйлера является незаменимым при решении некоторых задач, а также упрощает рассуждения. Однако, прежде чем приступить к решению задачи, нужно проанализировать условие. Иногда с помощью арифметических действий решить задачу легче.
Задача «Обитаемый остров» и «Стиляги» : Некоторые ребята из нашего класса любят ходить в кино. Известно, что 15 ребят смотрели фильм «Обитаемый остров», 11 человек – фильм «Стиляги», из них 6 смотрели и «Обитаемый остров», и «Стиляги». Сколько человек смотрели только фильм «Стиляги»?
Решение. Чертим два множества таким образом:
6 человек, которые смотрели фильмы «Обитаемый остров» и «Стиляги», помещаем в пересечение множеств.
15 – 6 = 9 – человек, которые смотрели только «Обитаемый остров».
11 – 6 = 5 – человек, которые смотрели только «Стиляги».
Получаем:
Ответ: 5 человек смотрели только «Стиляги».
3) Решение логических задач табличным способом.
Основной прием, который используется при решении текстовых логических задач, заключается в построении таблиц. Таблицы не только позволяют наглядно представить условие задачи или ее ответ, но в значительной степени помогают делать правильные логические выводы в ходе решения задачи. Рассмотрим способ решения на конкретной задаче.
Задача. Три клоуна Бим, Бам и Бом вышли на арену в красной, зеленой и синей рубашках. Их туфли были тех же цветов. У Бима цвета рубашки и туфель совпадали. У Бома ни туфли, ни рубашка не были красными. Бам был в зеленых туфлях, а в рубашке другого цвета. Как были одеты клоуны?
Решение. Составим таблицу, в столбцах которой отметим возможные цвета рубашек и туфель клоунов. Будем заполнять таблицу, используя условия задачи. Туфли Бама зеленые, а рубашка не является зеленой. Следовательно, у Бима и Бома туфли уже не могут быть зелеными, так же как не могут быть туфли Бама синими или красными.
Отметим все это в таблице:
Ответ: Бом – в синих туфлях и зелёной рубашке, Бим – во всём красном, Бам – в зеленых туфлях и синий рубашке.
V. Интересны ли логические задачи учащимся 6 класса ?
В практической части моей научной работы я подобрал несколько логических задач типа «Кто есть кто?», соответствующие уровню 6 класса, и раздал их для решения своим одноклассникам. Задачи были решены. После чего мною были проанализированы полученные результаты.
Задачи следующего содержания:
Задача 1. Леня, Женя и Миша имеют фамилию Орлов, Соколов и Ястребов. Какую фамилию имеет каждый мальчик, если Женя, Миша и Соколов — члены математического кружка, а Миша и Ястребов занимаются музыкой? (Ответ: Алёша Соколов, Женя Ястребов, Миша Орлов).
Задача 2. В семье четверо детей им 5, 8, 13 и 15 лет.
Зовут их Таня, Юра, Света и Лена.
Сколько лет каждому из них, если одна девочка ходит в детский сад, Таня старше, чем Юра, а сумма лет Тани и Светы делится на 3? (Ответ: Свете 5, Юре 8, Тане 13, Лене 15).
Среди учеников моего класса, в количестве 30 человек, с двумя предложенными задачами типа «Кто есть кто?» справилось 19 человек, среди которых 11 девочек и 8 мальчиков. С первой задачей справились почти все учащиеся. Вторая задача, вызвала у затруднения.
Результаты решения представлены на диаграмме:
Из диаграммы видно, что 63% (19 человек) успешно справились с двумя задачами, только с первой задачей — 73% (22 человека). Не решили ни одну из задач верно — 27%
(8 человек).
Ребята со всей ответственностью и большим интересом отнеслись к решению логических задач. Несмотря на то, что с задачами справились не все ученики, этот процесс их очень увлек. Подводя итог, можно сделать вывод, что если при обучении математике использовать решение нестандартных задач, то это приведет к повышению интереса к урокам математики и развитию математических способностей учащихся.
VI. Логические задачи на уроках математики в общеобразовательных школах.
Я решил составить таблицу соответствия некоторых логических задач темам, изучаемым на уроках математики.
Вот, что у меня получилось:
|
Логические задачи |
Тема урока по математике |
|
1. Деду, отцу и сыну вместе 100 лет. Отцу и сыну вместе 45 лет. Сын на 25 лет моложе отца. Сколько кому лет? Решение: деду 100-45=55 лет; сыну10 лет; отцу 35 лет. |
Устный счет |
|
2. Разделите 5 яблок поровну между шестью детьми, не разрезав никакое яблоко больше, чем на 3 части Решение: 3 яблока разрезать на две равные части. 2 яблока на три. Получим 6 половин и 6 третей. Дать каждому половину и треть. |
Дроби |
|
3. Белка за 20 минут приносит орех в гнездо. Далеко ли орешник от гнезда, если известно, что налегке белка бежит со скоростью 5 м/с , а с орехом — 3 м/с? Решение: Пусть х – искомый путь. 20мин=20∙60=1200с. |
Средняя скорость |
|
4. Решите: К · О · Т = У · Ч · Ё · Н · Ы · Й Решение: 8х9х10=1х2х3х4х5х6 720=720 |
Разложение на множители |
|
5. Груша тяжелее яблока,а яблоко тяжелее персика. Что тяжелее: груша или персик? Решение: Груша тяжелее всех, затем яблоко, и самый лёгкий это персик |
Неравенства |
Основные выводы: применение логических задач на уроках математики в общеобразовательных школах помогает развитию логического мышления у учащихся, расширяет математический кругозор, а также способствуют развитию силы воли, трудолюбия, настойчивости в преодолении трудностей, упорства в достижении целей.
VII. Заключение
В данной работе мы познакомились с понятием «логика» и «математическая логика», изучили логические задачи. Узнали на какие типы они делятся, какие бывают методы и способы их решения. Некоторые методы мы рассмотрели более подробно. Из этого можно сделать вывод, что применяя только изученные способы решения логических задач, невозможно решить все математические задачи. Мною была составлена таблица соответствия некоторых логических задач с темами, изучаемыми на уроках математики. Также, я предложил своим одноклассникам решить пару нестандартных логических задач. Несмотря, на то что не все ученики с ними справились, это задание вызвало у них большой интерес.
Из вышеизложенного можно сделать вывод — необходимо включить изучение логических задач в программу по математике в общеобразовательных школах. Так как это способствует повышению интереса учащихся к данному предмету, развитию нестандартного мышления, трудолюбия и внимания.
VIII. Библиография:
1.Математическая логика // Википедия /http://ru.wikipedia.org.
2.Тысяча и одна задача по математике: Кн. Для учащихся 5-7 кл./А.В.Спивак.-3-е изд.-М.: Просвещение, 2010.-207 с.: ил.-ISBN 978-5-09-023442-9.
3. Кэрролл Л. Логическая игра. – М., 1991.
4. Интернет-ресурсы:
http://wiki.iteach.ru
http://dic.academic.ru
http://bibliofond.ru
http://tolkslovar.ru
Просмотров работы: 12440

Принцип 1: Наглядность
В сюжете задачи используйте объекты, знакомые ребёнку. В соответствии с возрастом малыша это могут быть:
- предметы обихода: посуда, игрушки, книжки, одежда, канцелярские товары;
- карточки с изображением знакомых объектов: предметов, природных явлений, эмоциональных состояний;
- сюжетные картинки;
- словесное описание знакомых объектов (образы).
Принцип 2: Систематичность
Решайте логические задачи ежедневно или хотя бы как можно чаще. Не обязательно оформлять это как полноценное самостоятельное занятие. Используйте любое подходящее время, когда ребёнок открыт для интеллектуальной работы, когда он не устал физически, не расстроен и не слишком возбуждён. Например:
- по дороге в детский сад/магазин/поликлинику/гости;
- на прогулке;
- во время монотонной для вас домашней работы, когда ребёнок находится рядом: готовка, глажка, мытьё посуды;
- во время монотонных для ребёнка занятий: лечебные процедуры, наведение порядка в игрушках, возможно — рисование*.
*Под монотонностью в данном случае понимается ситуация, при которой выполняются некоторые действия, не требующие концентрации внимания. Т.е. те ситуации, при которых внимание может быть успешно распределено.
Принцип 3: Вариативность
Используйте одни и те же схемы задач снова и снова, меняя только исходные данные:
- Замените в задаче белочек на мишек или кукол на машинки;
- Вчера искали красные пуговицы, а сегодня ищем жёлтые кнопки и т. д.
Если ребёнок уже демонстрировал успехи в решении логических задач определённого типа, не забывайте периодически возвращаться к ним, чуть усложняя и обновляя условия.
Принцип 4: Последовательность
Не забывайте главный принцип любого обучения. Продвижение от простого к сложному должно быть:
- поступательным;
- равномерным.
Скорость движения формируется в зависимости от способностей малыша к обучению и ваших педагогических талантов. Но даже если очевидные успехи воодушевляют, не поддавайтесь соблазну и не форсируйте события. Детская психика — система гибкая, но довольно хрупкая. Вы укрепите её, заставляя работать, но можете навлечь неприятности, если перегрузите чрезмерным усердием.
Принцип 5: Научность

- время: времена года, месяц, сутки, неделя, час, минута, распорядок дня и пр.;
- пространство: далеко/близко, над/под, за/перед, слева/справа;
- цветовосприятие: изучение основных и дополнительных цветов и оттенков
и пр.
Принцип 6: Воспитательная ценность
Ярые приверженцы раннего развития иногда забывают, что развитие — это не только обучение. Это работа над всеми аспектами личности. Грамотно составленные логические задачи делают эту работу более успешной и плодотворной. Они учат:
- распознавать эмоции — свои и чужие;
- проявлять сострадание, сопереживание;
- общаться, дружить.
Принцип 7: Развивающая ценность
Придумывая задания для того, чтобы развить логику у ребёнка, не забывайте: эффективное развитие дошкольника подразумевает гармоничный симбиоз различных познавательных процессов:
- восприятие;
- память;
- воображение;
- мышление.
Чем большей активности требует выполнение задания, тем выше окажется ожидаемый результат. Разумеется, при условии, что вы учли остальные принципы составления логических задач.
Вы можете воспользоваться готовыми заданиями от НИИ «Эврика», которые помогут вам развить логическое мышление ребёнка. А затем по образцу, освоив главные принципы, составлять задания на развитие логики самостоятельно.
Счастливого вам родительства!
В книге “Занимательная логика” Э.Кольмана и
О.Зиха имеется много интересных логических
задач. Вот одна из них.
1. В кафе встретились три друга: скульптор Белов,
скрипач Чернов и художник Рыжов. “Замечательно,
что один из нас имеет белые, один черные и один
рыжие волосы, но ни у одного из нас нет волос того
цвета, на который указывает его фамилия”, —
заметил черноволосый. “Ты прав”, — сказал Белов. Какой
цвет волос у художника?
Решение. Для решения подобных логических задач
полезно составить таблицу.
| Белов | Чернов | Рыжов | |
| блондин | |||
| брюнет | |||
| рыжий |
Ответ.
| Белов | Чернов | Рыжов | |
| блондин | — | + | — |
| брюнет | — | — | + |
| рыжий | + | — | — |
В бутылке, стакане, кувшине и банке находятся
молоко, лимонад, квас и вода. Известно, что вода и
молоко не в бутылке, сосуд с лимонадом стоит
между кувшином и сосудом с квасом, в банке – не
лимонад и не вода. Стакан стоит около банки и
сосуда с молоком.
Куда налита каждая жидкость?
Ответ.
| бутылка | стакан | кувшин | банка | |
| Молоко | — | — | + | — |
| Лимонад | + | — | — | — |
| Квас | — | — | — | + |
| вода | — | + | — | — |
3. В течение последних четырех лет Алексеев,
Фомин, Дементьев и Иванов получали очередной
отпуск в мае, июне, июле или в августе. Причем,
если один из них отдыхал в мае, то другой — в июне,
третий – в июле, а четвертый – в августе. Каждый
их них получал отпуск в эти четыре года в разные
месяцы. Так в первый год Дементьев отдыхал в июле,
во второй год – в августе. Алексеев во второй год
отдыхал в мае, Иванов в третий год – в июне, а
Фомин в четвертый год – в июле.
Кто в каком месяце отдыхал в каждом из этих
четырех лет?
Ответ.
| 1 –й год | 2 –й год | 3 –й год | 4 –й год | |
| Алексеев | июнь | май | июль | август |
| Фомин | май | июнь | август | июль |
| Дементьев | июль | август | май | июнь |
| Иванов | август | июль | июнь | май |
Три подруги вышли в белом, зеленом и синем
платьях. Их туфли тоже были белого, зеленого и
синего цветов. Известно, что только у Ани цвет
платья и туфель совпадали. Ни платье, ни туфли
Вали не были белыми, Наташа была в зеленых туфлях.
Определить цвет платья и туфель каждой из
подруг.
Решение: можно решать, составляя две таблицы, а
можно таблицы объединить в одно целое.
| Аня | Валя | Наташа | Аня | Валя | Наташа | |||
| Белые туфли | + | — | — | Белое платье | + | — | — | |
| Зеленые туфли | — | — | + | Зеленое платье | — | + | — | |
| Синие туфли | — | + | — | Синее платье | — | — | + |
| белое платье | зеленое платье | синее платье | белые туфли | зеленые туфли | синее платье | |
| Аня | ||||||
| Валя | ||||||
| Наташа | ||||||
| белые туфли | ||||||
| зеленые туфли | ||||||
| синие туфли |
5. Три друга – спортсмена — Алеша, Вася и
Сережа – учились в одном классе. Каждый из них
увлекался двумя видами спорта из следующих
шести: футбол, волейбол, баскетбол, теннис,
плавание и велоспорт. Известно, что:
- все трое – Сережа, теннисист и пловец ходят из
школы домой вместе, - пловец и футболист – соседи по дому,
- Алеша самый старший из троих, а теннисист старше
велосипедиста, - Наиболее интересные спортивные передачи по
телевизору все трое – Алеша, велосипедист и
волейболист – смотрят вместе.
Надо узнать, кто каким спортом увлекается.
Ответ.
- Алеша – баскетбол и плавание,
- Вася – волейбол и теннис,
- Сережа – футбол и велоспорт.
6. На школьном вечере четыре юноши: Валентин,
Николай, Владимир и Алексей все из разных
классов, и их одноклассницы танцевали танец, но
каждый юноша танцевал не своей одноклассницей.
Лена танцевала с Валентином, Аня – с
одноклассником Наташи, Николай — с
одноклассницей Владимира, а Владимир танцевал с
Олей.
Ответ.
Танцевали Лена с Валентином, Оля с Владимиром,
Аня с Николаем, Наташа с Алексеем.
Учатся в одних классах Аня и Владимир, Оля и
Валентин, Лена и Алексей, Наташа и Николай.
Кто с кем танцевал?
А вот эту задачу придумали дети после
очередного занятия математического кружка в 6
классе.
7. В одном поселке живут три товарища: Саша,
Коля и Петя, которые осваивают новую профессию.
Один из них готовится стать дизайнером, другой —
садоводом, третий — парикмахером. Кроме того, все
они имеют и другую профессию: один строитель,
другой – руководитель драмкружка, а третий ведет
дискотеки. В разное время они сказали разные
фразы:
- Петя, ты меня не жди, я должен доделать прическу,
- Эх, Коля, вести дискотеку – сложно, но мне очень
нравится, - Завтра, Коля, ко мне не приходи, я буду на
конкурсе парикмахеров, - На днях я получу новый диск “ Комнатные
растения”.Для меня, как для будущего садовода, он
будет интересным и полезным. - Наблюдал я вчера за тобой во время репетиции и
подумал, что тебе поставить пьесу не легче, чем
мне вывести новый сорт роз. - С применением новых технологий в строительстве
я совершенно не знаком, хотя как дизайнеру надо
сними познакомиться.
Попробуйте по этим фразам установить, кто из
друзей осваивает какую профессию и какую
профессию они уже имеют?
Ответ.
- Саша – парикмахер и строитель,
- Коля – дизайнер и руководитель драмкружка,
- Петя — садовод и ведущий дискотек.
8. Сокровиша.
Три пирата: Нытик, Стрелец и Барс зарыли свои
сокровища на одном острове. Один из них зарыл
возле дерева лимона, другой – банана, а третий –
абрикоса. Ёмкость для хранения тоже у каждого
была своя: один использовал сундучок, второй –
большую морскую ракушку, а третий – кожаный
мешочек.
Определите имя пирата, а также где и чем
хранил свои сокровища каждый из них, если
известно, что:
- Ракушку использовал не Нытик.
- Тот, кто закопал сокровища под абрикосом,
использовал мешочек. - Барс закопал сундучок, но не под лимоном.
| банан | абрикос | лимон | сундучок | ракушка | мешочек | |
| Нытик | ||||||
| Стрелец | ||||||
| Барс | ||||||
| сундучок | ||||||
| ракушка | ||||||
| мешочек |
Ответ.
| имя | дерево | тара |
| Нытик | абрикос | мешочек |
| Стрелец | лимон | ракушка |
| Барс | банан | сундучок |
9. После традиционного вечера встречи с бывшими
выпускниками школы в стенгазете появилась
заметка о трех бывших учениках школы. В этой
заметке было написано, что Иван, Борис и Андрей
стали учителями. Теперь они преподают разные
дисциплины: один – математику, второй – физику,
третий – химию. Живут они тоже в разных городах:
Минске, Витебске и Харькове. В заметке было еще
написано, что первоначальные их планы
осуществились не полностью: Иван работает не в
Минске, Андрей – не в Витебске; житель Минска
преподает не математику, Андрей преподает не
физику. Повезло только жителю Витебска: он
преподает любимую им химию. Кто есть кто?
Ответ.
- Иван – химик — Витебск
- Борис — физик — Минск
- Андрей — математик – Харьков
10. Арташ, Отар, Гурам и Сурен занимаются в разных
спортивных секциях. Один из них играет в
баскетбол, другой – в волейбол, третий – в
футбол, четвертый – в теннис. У них различные
увлечения: один из них любит кино, другой – театр,
третий – эстраду, а четвертый – цирк. Арташ не
играет ни в волейбол, ни в баскетбол. Отар играет
в футбол и любит театр. Сурен не играет в
волейбол. Тот из ребят, кто играет в волейбол,
любит ходить в кино, а тот, кто играет в баскетбол,
не любит цирк. Какое у каждого из них
увлечение, и каким видом спорта занимается
каждый?
Ответ.
- Арташ – теннис – цирк, Отар – футбол – театр,
- Гурам – волейбол – кино, Сурен – баскетбол –
эстрада.
11. Первоклашки.
Год назад с нашего двора первый раз в первый
класс пошли 5 мальчиков. Их имена: Петя, Коля,
Ваня, Гена и Миша. Получилось так, что все
пятеро попали в разные классы: один в класс “А”,
другой – в “Б”, третий – в “В”, четвертый — в “Г”,
пятый – в “Д”. Каждому из ребят досталась в
качестве классного руководителя добрая
учительница: Лидия Михайловна, Елена
Анатольевна. Екатерина Кирилловна. Татьяна
Григорьевна и Виктория Николаевна. Дети учились
прекрасно, напротив их фамилий ( Анисин,
Белов, Кукушкин, Степанов и Харитонов) всегда
были практически одни пятерки.
Определите имя, фамилию, класс и добрую
учительницу для каждого из первоклашек, если
известно, что
- Ваня учится у Татьяны Григорьевны и его фамилия
не Степанов. - В классе “Д” преподает не Екатерина
Кирилловна. - Коля учится в классе “Б”. Он старше на 1месяц,
чем Белов, и младше на 12 дней, чем тот, кто учится у
Татьяны Григорьевны. - Елена Анатольевна преподает в классе “Г” и у
нее нет ученика по фамилии Белов. - Харитонов Гена дружит с Петей и с тем, кто ходит
в класс “А”. - Кукушкин учится в классе “А”. Его учительница
не Лидия Михайловна и не Екатерина Кирилловна. - Анисин учится в классе “В” и его имя не Петя и
не Миша.
| Имя |
Учительница |
Класс | ||||||||||||||
| Петя | Коля | Ваня | Гена | Миша | Лидия Михайловна |
Елена Анатольевна |
Екатерина Кирилловна |
Татьяна Григорьевна |
Виктория Николаевна |
А | Б | В | Г | Д | ||
| Фамилия | Анисин | |||||||||||||||
| Белов | ||||||||||||||||
| Кукушкин | ||||||||||||||||
| Степанов | ||||||||||||||||
| Харитонов | ||||||||||||||||
| Класс | А | |||||||||||||||
| Б | ||||||||||||||||
| В | ||||||||||||||||
| Г | ||||||||||||||||
| Д | ||||||||||||||||
| Учительница | Лидия Михайловна |
|||||||||||||||
| Елена Анатольевна |
||||||||||||||||
| Екатерина Кирилловна |
||||||||||||||||
| Татьяна Григорьевна |
||||||||||||||||
| Виктория Николаевна |
Ответ.
| фамилия | имя | учительница | класс |
| Анисин | Ваня | Татьяна Григорьевна | В |
| Белов | Петя | Лидия Михайловна | Д |
| Кукушкин | Миша | Виктория Николаевна | А |
| Степанов | Коля | Елена Анатольевна | Б |
| Харитонов | Гена | Елена Анатольевна | Г |
На математическую олимпиаду в город Киров
поехало четыре девятиклассника: Лева, Коля, Миша
и Петя. В первый день они решили позавтракать в
разных местах: один пошел в кафе, другой – в
столовую, третий – в закусочную, четвертый – в
буфет. После завтрака они снова собрались вместе.
Разговор, естественно, зашел о том, кто как
позавтракал. Выяснилось, что все они пили разные
напитки, так как в каждом из этих мест, где они
завтракали, оказалось в наличии только по одному
напитку: в одном месте – только кофе, в другом –
только молоко, в третьем – только ряженка, в
четвертом – только чай. В буфете, например, было
только молоко, а в столовой не было ряженки. Петя
рассказал, что он был в столовой, но пил там не
чай. Лева рассказал, что он пил ряженку, а Миша
сказал, что он не был ни в закусочной, ни в буфете. Кто
из ребят где завтракал и что пил?
Ответ.
- Лева – закусочная – ряженка,
- Коля – буфет – молоко,
- Миша – кафе – чай,
- Петя – столовая – кофе.
Задачи для самостоятельного решения.
1. В начале учебного года пятиклассники
избрали старосту, председателя совета отряда,
звеньевых первого, второго и третьего звеньев. Их
имена: Аня, Боря, Вася, Гриша и Дина. Звеньевая
первого звена решила подружиться со звеньевой
второго звена. Дина удивилась, узнав, что
председатель совета отряда и звеньевая второго
звена брат и сестра. Гриша дружит с председателем
совета отряда и со старостой. У Васи нет сестер.
Назовите имена каждого из избранных.
Ответ.
- Вася – староста, Боря – председатель отряда,
- Дина – звеньевая 1 –го звена, Аня – 2-го звена,
Гриша — 3-го звена.
2. Петя, Гена, Дима и Вова занимаются в детской
спортивной школе в разных секциях:
гимнастической, баскетбольной, волейбольной и
легкой атлетики. Петя, Дима и волейболист
занимаются в одном классе. Петя и Гена на
тренировки ходят пешком вместе, а гимнаст ездит
на автобусе. Легкоатлет не знаком ни с
баскетболистом, ни с волейболистом.
Кто в какой секции занимается?
Ответ.
- Петя – баскетболист, Гена – волейболист,
- Дима – гимнаст. Вова – легкоатлет.
3. Пять человек живут в одном городе. Их имена:
Леонид, Владимир, Николай, Олег и Петр. Их Фамилии:
Степанов, Борисов, Козин, Дроздов и Истомин.
Известно, что
- Козин знаком только с двумя, а с Козиным знаком
только один человек, - Петр знаком со всеми, кроме одного, а Леонид
знает только одного из всех, - Николай и Истомин знают друг друга с детства.
- Владимир, Николай и Олег знакомы между собой,
- Дроздов и Владимир незнакомы,
- Олег, Николай и Борисов Часто вместе ходят на
работу,
Назовите имена и фамилии каждого.
Ответ. Борисов Владимир, Степанов Николай,
Козин Леонид, Дроздов Петр. Истомин Олег.
В детстве в учебниках по математике всегда были задачи, помеченные звездочкой, так называемые «задачи повышенной сложности». Некоторые учителя по какой-то причине их либо пропускали, либо уделяли очень мало внимания, либо оставляли на самостоятельный разбор в качестве домашнего задания, либо просто не располагали временем для их разбора. На самом деле эти задачи активно развивают мышление ребенка, его интеллектуальные способности, в особенности логику.
«Зачем вообще развивать логику?» – спросите вы. К примеру, человек работает бухгалтером или филологом, биологом или тренером в спортивном зале. Вот, к чему в его практике акцентировать внимание на логическом мышлении? Ответ прост: развитая логика означает развитое мышление, способность видеть очевидные вещи, приходить к ним самостоятельно, а не с чьей-то помощью, делать практические выводы, которые помогают в обыденных ситуациях. Иногда логически поразмыслив, мы приходим к, казалось бы, простым и очевидным вещам, хотя до этого их не замечаем.
Кстати, развитие логического мышления, а также других навыков поможет вам учиться быстрее, эффективнее и интереснее. Этот же результат вы получите по прохождении нашей 5-недельной онлайн-программы «Лучшие техники самообразования».
Хорошо. Допустим, момент с задачками со звездочкой упущен, не вернешь былые школьные годы. Означает ли это, что нам уже никак не получится развить логику, действительно ли поезд с интеллектуальным капиталом ушел? Однозначно нет! И в этой статье мы попытаемся потренировать нашу логику. Так что включайтесь в работу и айда решать задачки на развитие логического мышления.
Ниже вы увидите ряд заданий. Не торопитесь открывать окошко с ответом, подумайте над решением, попытайтесь подойти к решению нестандартно, рассмотрите возможные варианты, перенесите смысловые акценты в задании, в общем, постарайтесь мыслить с разнопланово. В любом случае, не отчаивайтесь, если не придете к правильному ответу. Терпение и труд все перетрут. А мы желаем вам успехов!
Итак,
Задача №1
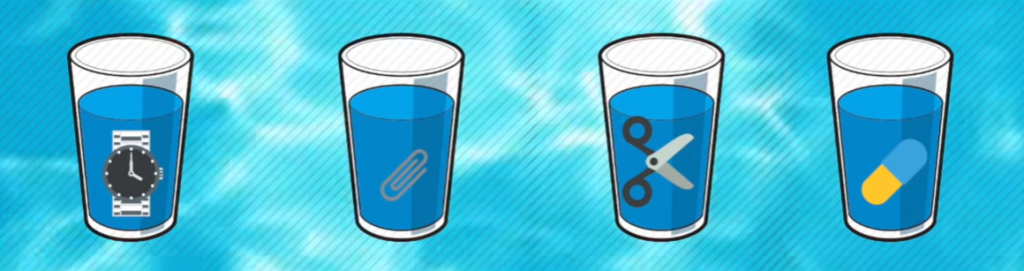
Представьте, перед вами четыре стакана, наполненных водой. В каждом стакане находятся предметы. Так:
- в первом стакане – металлические наручные часы;
- во втором стакане – канцелярская скрепка;
- в третьем стакане – металлические ножницы;
- в четвертом стакане – ластик.
При этом уровень воды во всех стаканах одинаковый. Визуально это выглядит следующим образом:
Вопрос: в каком стакане воды больше, чем в остальных?
Ответ
Размялись? Согласитесь, это было несложно. Продолжаем…
Задача №2
Давайте немного вспомним арифметические действия и применим их к задаче.
В кафе быстрого питания зашли четыре посетителя. При этом:
- первый посетитель купил три бургера и заплатил 300 рублей;
- второй посетитель купил один бургер и две порции картофеля фри и заплатил 200 рублей;
- третий посетитель купил два куска пиццы и одну порцию картофеля фри и заплатил 90 рублей;
- четвертый посетитель купил один бургер, одну порцию картофеля фри и один кусок пиццы.
Схематично эту ситуацию можно представить так:
Вопрос: сколько заплатил четвертый посетитель?
Ответ
Задача №3
Жарим котлеты.
Мы располагаем сковородой, на которую помещается две колеты. Нам необходимо пожарить три котлеты за 3 минуты, при том, что одна сторона котлеты жарится ровно 1 минуту (котлеты необходимо прожарить с обеих сторон).
Вопрос: Как прожарить котлеты?
Ответ
Задача №4
Еще немного о еде.
Предположим, у нас имеется круглый торт. Нам нужно разрезать его на восемь кусков, при этом сделав только три надреза.
Вопрос: как это сделать?
Ответ
Задача №5
Мудрецы и колпаки.
Царь решил проверить своих троих мудрецов на мудрость, пригласил их и сказал: «Мудрецы, у меня есть 5 колпаков – 3 из них черные, а 2 белые. Сейчас вы закроете глаза, и я надену на ваши головы эти колпаки, при этом вы не будете знать, колпак какого цвета у вас на голове, но будете видеть колпаки других мудрецов». После осуществленных действий мудрецы открыли глаза и долго-долго молчали. Затем один из мудрецов произнес: «На моей голове черный колпак!» И он был прав.
Вопрос: как мудрец догадался?
Ответ
Да, такая вот интересная задача.
Помимо задач хотелось бы предложить загадки с подвохом. По возможности уделите время их решению, это будет увлекательно.
Загадка 1
Изначально в аквариуме плавает 10 рыбок. Однако спустя неделю 2 из них утонули, 4 – уплыли, а еще 3 – погибли. Сколько рыбок осталось в аквариуме?
Ответ
Загадка 2
Что проходит по полям и городам, но остается неподвижным?
Ответ
Загадка 3
Возраст матери и дочери вместе составляет 77 лет. При этом возраст одной можно получить, если поменять цифры возраста другой. Сколько лет матери и сколько лет дочери?
Ответ
Загадка 4
Перечислите 5 дней подряд, не пользуясь числами или названиями дней недели.
Ответ
Загадка 5
Все пять сестер чем-то заняты:
- Катя играет на пианино.
- Маша стирает.
- Ольга играет в шахматы.
- Алиса готовит пирог.
Вопрос: Чем занята Наташа?
Ответ
Помимо задачек для взрослых хотелось бы предложить задачи на логику для детей, ведь важно развивать логические мышление уже на ранних стадиях. Поэтому зовите своих детей, сестер, братьев и племянников младшего возраста, устраивайтесь поудобнее и начинайте думать.
Задача 1
Профессор всегда мечтал о домашнем животном, и он решил изобрести механических хомячков:
Хомячки, как видно, разного окраса: черный, рыжий и пятнистый. Профессор дал им имена: Уголёк, Рыжик и Пятнышко. Но цвет и имя не совпадают.
Вопрос: Как зовут хомячков, если самого темного зовут Пятнышко?
Ответ
Задача 2
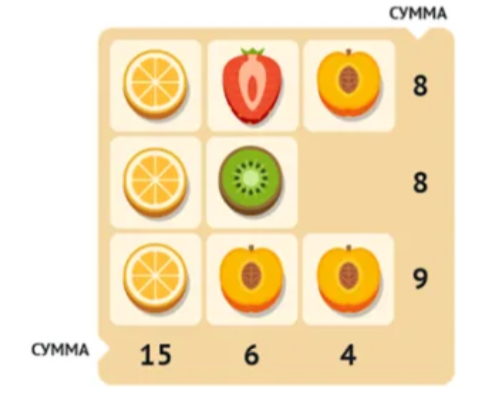
Сумма фруктов по вертикали и по горизонтали представлена на картинке:
Вопрос: сколько стоит клубника?
Ответ
Задача 3
Каждой из четырёх девочек подарили одну куклу:
У Ани и Маши куклы с голубыми волосами, а у Оли и Даши – с желтыми. У Маши и Даши куклы в платьях, а у Ани и Оли – в блузках с юбками.
Вопрос: кому принадлежит какая кукла?
Ответ
Задача 4
Давайте обратимся к примерам:
Вопрос: сколько стоит мишка?
Ответ
Задача 5
Вновь обратимся к рисунку и посмотрим, что говорят Правдиш и Вруниш:
Правдиш всегда говорит правду.
Вруниш всегда говорит ложь.
Правдиш смотрит на пирамиду сбоку, а Вруниш – сверху.
Правдиш говорит, что нижнее кольцо красного цвета.
Вруниш говорит, что видит все кольца.
Вопрос: на какую пирамиду смотрят Правдиш и Вруниш?
Ответ
Задача 6
Люда собирается на вечеринку. Она смотрит на свой гардероб:
Люда располагает четырьмя платьями и тремя парами туфель. Сколько вариантов наряда есть у Люды?
Ответ
На этом мы заканчиваем наши задачки. Если вам понравилось решать подобные задания, обратите внимание на это видео:
Тут приводятся десять загадок, которые помогут поработать над логикой.
Помните, что логическое мышление имеет большое значение при принятии жизненных решений. Поэтому не ленитесь – проводите свое время за решением нескучных и полезных задачек.
Желаем вам успехов!
Знаете, какой самый эффективный способ на время остановить работу целого отдела в IT-компании или научном коллективе? Подкинуть сотрудникам интересную, незнакомую математическую или логическую задачку. А какой самый простой и распространённый способ оценить кандидата на должность программиста или аналитика в ходе короткого собеседования? Предложить ему интересную, незнакомую математическую или логическую задачку.
В сети, в книгах, в журналах мы все периодически встречаем задачи различного типа сложности. Задачи попроще — немного размять мозговые извилины или же посложнее — на многочасовое или даже многодневное обдумывание. Удовольствие от успешного решения какой-нибудь особенно непростой задачи, пожалуй, сравнимо с чувством, когда твоя сложная программа наконец заработала без ошибок и стала выдавать правильный результат. Подобные задачи — это своего рода тренажёр для мозга. Они позволяют отвлечься от трудовой рутины и поразмышлять над какой-нибудь нестандартной проблемой.
Работодатели давно взяли на заметку, что несложные логические или математические задачи — это хороший способ проверить сообразительность, знание законов логики и умение рассуждать. Именно поэтому такие задачи называют «типовыми» для собеседований.
В статье «16 вопросов с собеседований, которые означают не то, что вы думаете» Елена Лыбина, руководитель отдела найма и адаптации Bercut, рассказывает:
«Прежде всего скажу, что мы ведём открытую коммуникацию с кандидатами. У нас нет цели создать стрессовую ситуацию, кого-то на чём-то «поймать» или что-то выведать. Мы изучаем опыт и мотивацию кандидата в процессе свободной доброжелательной беседы и ловушек никому не устраиваем. Но для некоторых позиций, особенно Junior, в Bercut важна способность мыслить нестандартно. Это сложно определить в ходе стандартного интервью. Поэтому мы используем логические задачки. Нам интересен ход размышлений кандидата, и мы просим озвучивать его процесс решения. Иногда ход решения важнее правильного результата. А иногда способность решить простую логическую задачу является для нас показателем того, что кандидат может собраться и в стрессовой ситуации выдать быстрый результат. Если такие качества обязательны для позиции, на которую мы ищем кандидата, то задачка становится вопросом с подвохом».
В ноябре 2019 года Bercut выступил партнером конференции SECR (Software Engineering Conference Russia). Где специалисты Bercut предложили посетителям выставки поучаствовать в квестах по решению задач. Хотя, с решением полного набора задач справилось всего несколько человек, сама викторина вызвала большой интерес.
Также часто работодатели предлагают задачи на составление программ по заранее заданным условиям, но в этой статье мы их рассматривать не будем — здесь интересны лишь те, которые можно решить за непродолжительное время, не прибегая к программированию. Именно такие задачи лучше всего подходят для получасового собеседования, а задачи на составление программ идеальны для тестовых заданий.
В сети есть много сборников математических и логических задач. Проблема в том, что эти сборники читают не только работодатели, но и их потенциальные работники. Зачастую бывает так, что решение какой-нибудь интересной задачи уже известно многим. Так не годится, ведь нужно проверять не только способность хорошо запоминать прочитанное, но и умение решать новые, неизвестные кейсы. Да и вы, наверное, не захотите, чтобы вас снова спросили, как взвесить Боинг-747 или сколько будет 2 в степени 64. Правильные ответы на подобные популярные вопросы выучили наизусть даже офисные пальмы и фикусы в «переговорках», где проводятся собеседования. Нужно больше новых интересных задач.
Эта статья написана о том, как составлять новые задачи. Давайте подойдём к этому вопросу творчески, но системно: попробуем придумать алгоритмы для создания новой задачи того или иного типа, а потом, воспользовавшись этими алгоритмами, составим абсолютно новые, ещё никому не известные задачи.
Для каждого типа задач я буду приводить примеры уже известных — из журнала «Наука в фокусе», из книги Якова Перельмана «Занимательные задачи и опыты» и из других источников. Вообще, книги по математике и научно-популярные журналы (например, многие могут вспомнить журнал «Квант» для школьников, интересующихся математикой) — это неиссякаемые источники интересных задач.
Я опишу алгоритм сочинения новых задач для каждого типа и приведу примеры тех, которые составил, пользуясь этим алгоритмом. Думаю, задачи, приведённые в этой статье, покажутся вам не сложными. Главное — это понять принцип и разложить процесс на составляющие. А дальше — уже дело техники.
Александр Клименков, ведущий технический писатель Bercut
1. Задачи с конечным множеством чисел
Первый тип задач, о котором я хочу рассказать, про числа в реальном мире. Нас окружает множество устройств, предметов и объектов, на которых нарисованы или отображаются цифры. Это и часы, и календари, и номера машин. Обычно значение чисел или количество цифр в таких объектах конечно. Почему бы не сделать это предметом размышлений? Вот пример двух таких задач.
Задача о неточных часах
В доме трое часов. 1 января все они показывали верное время. Но верно идут только первые часы. Вторые отстают на 1 минуту в сутки. Третьи спешат на 1 минуту в сутки. Если часы будут продолжать так идти, через какое время все вместе будут снова показывать верное время?
Ответ:
Через 720 суток.
За это время вторые часы отстанут на 720 минут, то есть ровно на 12 часов; третьи часы на столько же уйдут вперёд. Тогда все часы будут показывать то же, что и 1 января, то есть верное время.
Задача о годе рождения профессора
Профессор Кумле в 1971 году сообщил своим студентам: «Мне было n лет в n² году». В каком году родился профессор?
Ответ:
Профессор родился в 1892 году. В 1936 году ему было 44 года: 44²=1936.
Алгоритм составления задач с конечным множеством чисел:
1. Берём любое распространённое устройство или объект, на котором отображаются или написаны цифры.
2. Выбираем характерное, однозначно определяемое число из множества допустимых чисел, отображаемых на этом устройстве или объекте. Например, максимальное или минимальное возможное число. Также можно описать какую-то характерную комбинацию цифр.
3. Просим назвать устройство, рассчитать количество комбинаций или определить какой-то вариант числа, обладающих характерными особенностями.
Давайте попробуем придумать такие задачи. Для начала возьмём какой-нибудь объект, опишем характерную особенность его чисел и попросим угадать, что это за объект.
Новая задача 1
В нём бывает разное количество чисел. Разница между минимальной и максимальной суммой чисел в нём равна 90. Его традиционно делят на части, в первой из которых бывает до четырёх простых чисел. Что это такое?
Ответ:
Это календарный месяц.
Его делят на недели. Если первая неделя начинается с понедельника, то в ней четыре простых числа: 2, 3, 5 и 7. Минимальная сумма чисел в месяце — 406, максимальная — 496.
Теперь давайте попробуем придумать новую задачу про цифровые часы.
Новая задача 2
Винни-Пух посмотрел на свои цифровые часы: было 12:45. «Все цифры разные, самое время перекусить», — подумал он. Сколько раз за сутки Винни-Пуху можно перекусить? На цифровых часах Винни-Пуха отображаются четыре цифры — только часы и минуты.
Эту задачу можно решать разными способами. Один из самых очевидных — взять и всё посчитать.
Нам нужно перебрать все варианты, вроде 01:23. Конечно, при этом не нужно забывать, что количество минут не может быть больше 59, а количество часов не может быть больше 23.
Для начала посчитаем количество возможных вариантов для 10-минутного промежутка. Например: 01:23, 01:24, 01:25, 01:26, 01:27, 01:28, 01:29 — всего 7 штук. Это количество всегда будет постоянным, ведь смена одной цифры в часах «уберёт» некоторые варианты минут, но добавит столько же других вариантов. Например: 07:21, 07:23, 07:24, 07:25, 07:26, 07:28, 07:29. Или: 16:20, 16:23, 16:24, 16:25, 16:27, 16:28, 16:29.
Теперь посчитаем, сколько таких десятиминутных наборов будет в часе. Для нашей задачи их будет меньше 6:
1. Для часов от 01 до 05, от 10 до 15 и от 20 до 23 количество наборов — 4. Так получается, потому что мы должны исключить наборы, начинающиеся с каждой из двух цифр часов. Например, для 12 часов не будет наборов минут 10–19 и 20–29. Часы 00, 11 и 22 не рассматриваем — цифры в часах не могут повторяться. В итоге для всего этого множества имеем (5+5+3)×4×7=364 варианта.
2. Для часов от 06 до 09 и от 16 до 19 количество наборов — 5. В часе 60 минут, значит нужно исключить только 10 минут, начинающиеся с первой цифры часов — от 00 до 09 или от 10 до 19. Для всего этого множества имеем (4+4)×5×7=280 вариантов.
Ответ:
Всего в сумме имеем 364+280=644 варианта. Это значит, что Винни-Пуху за сутки можно перекусить 644 раза. Наверное, поэтому он такой упитанный.
Ещё один неиссякаемый источник задач — это телефонные номера. Для нас в Bercut это вообще «родная» тема, ведь большинство продуктов Bercut предназначены для автоматизации и решения различных бизнес-задач операторов мобильной связи.
Новая задача 3
У оператора мобильной связи есть новый пул семизначных телефонных номеров. Пока ещё все номера этого пула доступны. В офис оператора пришёл клиент с необычной просьбой: подобрать ему телефонный номер, в котором сумма всех семи цифр равна его счастливому числу 62. Сотрудник оператора предложил клиенту распечатать все такие номера на выбор. Сколько номеров будет в распечатке?
При решении этой задачи можно начать вспоминать формулы комбинаторики, а можно выполнить всего одно простейшее арифметическое действие. Для начала давайте просто найдём максимальное число, которое можно получить суммируя все цифры семизначного номера: 9×7=63. Оказывается, это число на единицу больше счастливого числа клиента. Значит, в искомом телефонном номере все цифры будут девятками, кроме одной восьмёрки.
Ответ:
Таких телефонных номеров всего 7 — по одному на каждую позицию восьмёрки в номере.
2. Задачи с поиском закономерностей в последовательностях
Следующий тип задач — на поиск закономерностей. Их великое множество и сочинить новый вариант совсем не сложно. Последовательность можно придумать самостоятельно или взять из реального мира. Приведу пару примеров ранее опубликованных задач этого типа.
Задача о первой загадочной последовательности
Каким будет сотый член в последовательности, которая начинается числами: 81, 73, 52, 42, 34, 22, 18, …?
Последовательность строится по следующему принципу: 81−(8×1)=73, 73−(7×3)=52 и далее до 18−(1×8)=10. Поскольку 10−(1×0)=10, это число повторяется бесконечно.
Ответ:
Это будет число 10.
Задача о второй загадочной последовательности
Дана последовательность чисел: 11, 7, 5, 7, 7, 7. Продолжите последовательность ещё одним числом.
Эта последовательность, описывающая объект реального мира, а именно — дни недели. В ней перечислено количество букв в названиях дней недели: понедельник — 11, вторник — 7, среда — 5, четверг — 7, пятница — 7, суббота — 7. Следующий и последний день недели — воскресенье.
Ответ:
Значит, в последовательность нужно добавить число 11.
Алгоритм составления задач с поиском закономерностей в последовательностях:
1. Берём любую последовательность с чётко заданными правилами изменения элементов. Правила не обязательно должны быть связаны с математикой.
2. Вносим в эту последовательность одно, и только одно, изменение. Этот шаг можно пропустить.
3. Просим восстановить или продолжить последовательность.
Попробуем воспользоваться этим алгоритмом и сочинить новые задачи.
Новая задача 4
Математик Матвей, работая над диссертацией, задумчиво глядел в окно и считал ворон на крышах соседних домов. На первой крыше сидело 11 ворон, на второй — 16, на третьей — 7, на четвёртой — 21, на пятой вообще не было ворон, а на шестой сидело 34 вороны. «Глупые птицы», — подумал Матвей. За что Матвей критиковал ворон?
Количество ворон на крышах — это последовательность, каждый следующий член которой изменяется по сравнению с предыдущим на число Фибоначчи. Начальный член последовательности — 11, начальное число Фибоначчи — 5 (это сумма 2+3=5). При этом очередное число Фибоначчи то прибавляется, то вычитается из предыдущего члена последовательности. Получается такая закономерность:
1) Начальный член последовательности: 11.
2) Число Фибоначчи: 2+3=5. Действие — сложение. Член последовательности: 11+5=16.
3) Число Фибоначчи: 3+5=8. Действие — вычитание. Член последовательности: 16−8=8.
4) Число Фибоначчи: 5+8=13. Действие — сложение. Член последовательности: 8+13=21.
5) Число Фибоначчи: 8+13=21. Действие — вычитание. Член последовательности: 21−21=0.
6) Число Фибоначчи: 13+21=34. Действие — сложение. Член последовательности: 0+34=34.
Ответ:
Матвей критиковал ворон за то, что на третьей крыше по правилам последовательности должно сидеть 8, а не 7 ворон.
В следующей задаче придумаем более сложную последовательность. Пусть это будут связанные пары чисел. На этот раз сама последовательность достаточно сложна, чтобы ещё и угадывать место, в которое нужно вставить недостающий член. Поэтому попросим просто её продолжить.
Новая задача 5
Финский программист Юкка, стоя в пробке, от нечего делать разглядывал номера встречных машин. Сначала проехала машина с номером 22-34, потом с номером 42-28, дальше были машины с номерами 34-50, 58-40 и 46-66. «Однако, тенденция», — подумал Юкка. Какой номер будет у следующей машины?
Последовательность номеров машин подчиняется трём правилам:
1) Разница между числами в паре на каждом шаге увеличивается на 2: 12, 14, 16, 18, 20.
2) Минимальное число в паре на каждом шаге увеличивается на 6: 22, 28, 34, 40, 46.
3) На каждом шаге меньшее и большее число в паре меняются местами.
Ответ:
По этим правилам следующий номер будет такой: 74-52.
3. Задачи на элементарную логику
Логика — это важнейший инструмент любого человека интеллектуальной профессии. Самый простой способ проверить знание логики — это задачи с оценкой истинности утверждений. Вот пример одной такой задачи из теста на логическое мышление. Я немного перефразировал её условие.
Задача про пингвинов
Некоторые пингвины — птицы. Каждая птица имеет три крыла.
Какое из следующих утверждений является истинным:
1) Пингвины с двумя крыльями не являются птицами.
2) Птицы, которые являются пингвинами, иногда имеют три крыла.
3) Птицы с двумя крыльями иногда являются пингвинами.
4) Пингвинов не птиц, с тремя крыльями не бывает.
5) Пингвины имеют три крыла, потому что они птицы.
6) Ни одно из вышеперечисленного.
Ответ:
Истинно только первое утверждение.
Алгоритм составления задач на элементарную логику:
1. Придумываем набор любых не очень сложных логических утверждений, задающих условия пересечения нескольких множеств.
2. Заменяем объекты множеств другими объектами, делающими заданные утверждение абсурдным на уровне житейской логики.
3. Придумываем ряд утверждений, которые с учётом заданных условий являются ложными. И одно или несколько утверждений, которые являются истинными.
4. Просим указать истинные утверждения.
По такому алгоритму можно придумать огромное количество весёлых оригинальных задачек.
Новая задача 6
Коты знают информатику. Все коты любят музыку.
Какое из следующих утверждений является истинным:
1) Все, кто знают информатику, любят музыку.
2) Информатику знают только коты.
3) Коты, которые знают информатику, не любят музыку.
4) Некоторые знатоки информатики любят музыку.
5) Все знатоки информатики не любят музыку.
6) Коты, которые любят музыку, не знают информатику.
Ответ:
Истинно только четвёртое утверждение.
Новая задача 7
Некоторые астрофизики любят апельсины. Все любители апельсинов живут на Кипре.
Какие из следующих утверждений являются истинными:
1) Все астрофизики живут на Кипре.
2) Некоторые жители Кипра — астрофизики.
3) Все жители Кипра любят апельсины.
4) Все любители апельсинов — астрофизики.
5) Некоторые астрофизики, которые не любят апельсины, могут жить на Кипре.
6) Некоторые любители апельсинов могут жить не на Кипре.
Ответ:
Истинны только второе и пятое утверждения.
4. Задачи на выполнение расчётов и решение уравнений
Этот тип задач, пожалуй, самый распространённый. Ещё с глубокой древности подобные задачи были включены в книги и учебники по арифметике. Многим они покажутся довольно простыми, на уровне школьной программы. Но не забывайте, что наша цель — проверить умение рассуждать и оперировать некоторым количеством цифр, а не открыть в соискателе гениального математика.
Вот пример такой задачи.
Задача про кенгуру
В австралийском зоопарке 35% всех кенгуру серые. 13% всех животных зоопарка — кенгуру, но не серые. Сколько процентов от всех животных в зоопарке составляют кенгуру?
Введём обозначения:
– a — общее количество животных в зоопарке;
– s — количество серых кенгуру;
– k — количество всех кенгуру.
Первое утверждение из задачи можно записать так: 0,35×k=s.
Второе утверждение из задачи можно записать так: 0,13×a=k−s. Или: 0,13×a=k−0,35×k.
Последовательно упростим это уравнение: 0,13×a=0,65×k.
Получаем a=5×k или k=1/5×a. То есть k составляет 20% от a.
Ответ:
Значит, в зоопарке 20% животных — это кенгуру.
Вот ещё одна весьма любопытная задача.
Задача об основном вопросе Вселенной
Из книги «Автостопом по Галактике» мы знаем формулировку основного вопроса жизни, Вселенной и всего остального: «Что получится, если умножить шесть на девять?» Известен также и знаменитый ответ на этот вопрос — 42. В какой системе счисления этот ответ будет верным?
Ответ:
В тринадцатеричной системе счисления: 6×9=4×13+2.
Алгоритм составления задач на выполнение расчётов и решение уравнений:
1. Придумываем один или несколько ответов — целые числа.
2. Составляем систему из одного или нескольких уравнений, решением которых будут числа, полученные на шаге 1, или выполняем ряд несложных математических или иных преобразований с этими числами. В итоге получаем коэффициенты уравнений или результаты математических преобразований.
3. Придумываем историю, описывающую коэффициенты или результаты преобразований.
4. Просим решить задачу, не упоминая при этом, что она связана с уравнением или преобразованиями.
Новая задача 8
Перед выпуском нового релиза системы два тестировщика — Фаддей и Фиона — проверили 100 тестов. Тестировщик Фаддей работал на 5 часов дольше Фионы и проверил на 10 тестов больше. Но Фиона работает быстрее Фаддея на 50%. Сколько времени работал каждый тестировщик?
Сначала найдём скорость работы Фаддея 10/5=2 теста в час. Фиона работает быстрее Фаддея на 50%, значит скорость её работы — 3 теста в час. Когда Фиона и Фаддей работали вместе, они проверили 100−10=90 тестов. Каждый час оба тестировщика проверяют 2+3=5 тестов. Разделим 90 на 5 и получим 18 часов — это время совместной работы Фионы и Фаддея. Но Фаддей работал дольше на 5 часов: 18+5=23 часа.
Ответ:
Фиона работала 18 часов, Фаддей — 23 часа.
Проверяем: 3×18+2×23=100.
Новая задача 9
В магазине электроники новая модель телефона сначала подорожала на 10%, а потом подешевела на 10%. После этого телефон стал стоить 93555 рублей. Сколько телефон стоил до подорожания?
После подорожания телефон стоил 110%, то есть 1,1 от первоначальной цены. После удешевления его цена будет равна: 1,1×0,9=0,99. То есть 99% процентов от начальной цены.
Ответ:
Значит, до подорожания телефон стоил 93555/0,99=94500 рублей.
5. Задачи на поиск оптимального алгоритма действий
Этот тип, пожалуй, наиболее интересный. Это именно те задачи, которые гуляют по сети и знакомы почти всем: задача про три лампочки и три выключателя, задача про маляров и перчатки, задача про мост и фонарик. Приведу два давно известных примера.
Задача о варке яиц
Как проще всего отмерить 15 минут, необходимые для варки яиц, имея под рукой семи- и одиннадцатиминутные песочные часы?
Ответ
Для простоты обозначим часы цифрами «7» и «11». Алгоритм будет такой:
1. Кладём яйцо в воду, запускаем одновременно часы «7» и «11».
2. Когда в часах «7» закончится песок, переворачиваем их. Всего прошло 7 минут.
3. Когда в часах «11» закончится песок, переворачиваем часы «7». Всего прошло 11 минут. В часах «7» к этому времени собралось песка на 4 минуты. Когда мы перевернём часы «7», они начнут отмерять эти 4 минуты.
4. Когда в часах «7» закончится песок, пройдёт 11+4=15 минут.
Задача об автоматах с мороженым
Перед вами три автомата с мороженым. Первый выдаёт ванильное мороженое, второй — шоколадное. Третий автомат действует случайно — выдаёт ванильное или шоколадное мороженое. Мороженое стоит одну монету. На всех трёх автоматах есть надписи: «Ванильное», «Шоколадное», «Случайное». Но надписи перепутаны — все три надписи неправильные. Сколько нужно потратить монет, чтобы выяснить, где какой автомат?
Ответ:
Понадобится всего одна монета!
Алгоритм действий такой:
1. Опускаем монету в автомат с надписью «Случайный». Автомат не может быть случайным. Получив мороженное мы узнаем, что это за автомат: с ванильным или шоколадным вкусом. Пусть это будет ванильное мороженое.
2. Осталось два автомата с надписями «Ванильное» и «Шоколадное». Но автомат с ванильным мороженым мы уже нашли. Значит оставшиеся автоматы на самом деле выдают шоколадное и случайное мороженое.
3. Помним, что все три надписи — неправильные. Значит автомат с надписью «Шоколадное» не может выдавать шоколадное мороженое. Это на самом деле автомат со случайным мороженым.
4. Оставшийся автомат с надписью «Ванильное» на самом деле выдаёт шоколадное мороженое.
Алгоритм составления задач на поиск оптимального алгоритма действий:
1. Придумываем систему, в которой есть несколько элементов с разными значениями одного и того же параметра. Например, время, вес или объём.
2. Придумываем искусственные ограничения, накладываемые на систему.
3. Придумываем показатель, который нужно минимизировать.
4. Просим найти оптимальный алгоритм решения задачи.
Кстати, когда вы сочините задачу на поиск оптимального алгоритма действий, может так случиться, что вы и сами не будете знать лучший ответ на свою же задачу. Сами сочиняете, сами решаете — замечательное развлечение для субботнего вечера! При этом нет никакой гарантии, что вы найдёте самое оптимальное решение. Бывают такие задачи, над которыми можно размышлять неделями.
Следующие две задачи могут показаться вам достаточно простыми. Однако я столкнулся с некоторыми трудностями в процессе придумывания этих «творческих» задачек. С уточнением условий новой задачи под номером 10 мне помог один мой коллега — мудрый и рассудительный человек, тоже любящий разные логические задачи.
Новая задача 10
У бассейна в зоопарке отдыхают пять бегемотов. Бассейн полон воды и достаточно большой, чтобы в нём поместились все бегемоты разом. У вас нет никаких измерительных инструментов. Вы — главный начальник бегемотов и можете решать, кому из них что нужно сделать. Как найти самого толстого бегемота?
Ответ:
По сути это задача на нахождение максимального элемента в массиве массивных бегемотов. Погружаем в воду первого бегемота. Он вытеснит определённое количество воды. Воды в бассейне станет меньше. Пока считаем его самым толстым. Затем последовательно погружаем в воду по одному всех остальных бегемотов. Если какой-то из бегемотов снова заставит воду перелиться через край, значит он толще предыдущего лидера. Звание самого толстого бегемота переходит к нему. Так мы выясним, какой из бегемотов толще всех, и сможем наградить его кочаном вкусной капусты.
Новая задача 11
Жители одного тропического острова в Тихом океане приплыли к жителям другого острова на лодках. Гости привезли груз манго и хотят обменять его на такой же по объёму груз авокадо. Как им это сделать, если у островитян под рукой нет ни весов, ни линеек, ни других средств точного измерения? И ещё одно важное условие: верования туземцев не позволяют им рыть ямы.
Ответ:
А лодки на что? Эта задача чем-то похожа на предыдущую. Вытаскиваем лодку на берег, нагружаем в лодку манго, оставшийся объём лодки до краёв заливаем водой. Вынимаем из лодки манго и постепенно наполняем её авокадо до тех пор, пока вода снова не достигнет краёв лодки. Островитяне останутся довольны справедливым обменом.
Следующая задача уже посложнее.
Новая задача 12
На далёкую планету роботов «Железяка» прилетел грузовой транспорт с 230 литрами машинного масла на борту. На данный момент на планете проживает 5 роботов. Как за минимальное количество шагов поделить машинное масло поровну между роботами, если у них на планете остались только две канистры ёмкостью 17 и 21 литр?
Ответ:
Каждому роботу нужно отмерить 230/5=46 литра масла. Для начала отмерим первому роботу 21 литр из большой канистры. Недостающие 25 литров можно отмерить так:
1. Наливаем в большую канистру 21 литр, затем переливаем из неё 17 литров в маленькую канистру. В большой канистре остаётся 21−17=4 литра.
2. Отливаем 17 литров роботу из маленькой канистры.
3. Переливаем 4 литра из большой в маленькую канистру.
4. Снова наливаем в большую канистру 21 литр и доливаем из неё масло в маленькую канистру масло до краёв. В маленькой канистре уже есть 4 литра, значит из большой канистры туда перельётся 17−4=13 литров. В большой канистре останется 21−13=8 литров. Отливаем их роботу.
В результате этих шагов робот получит ещё 17+8=25 литров.
Теперь мы можем перелить остаток из маленькой канистры обратно в большую и дополнить её до 21 литра, чтобы выдать их следующему роботу и повторить алгоритм.
В этой статье описаны только пять типов задач. Безусловно, их гораздо больше. Да и алгоритмы составления можно придумать гораздо более сложные и разветвлённые. Важен сам принцип сочинения: в обратном направлении — от готового решения к интересному и загадочному условию. Кстати, должен вам признаться, что автор этой статьи непосредственно в режиме собеседования может и не решил бы некоторые из приведённых здесь задач — как известных, так и новых. Но я уверен, что читатели умеют легко решать подобные задачки, как на собеседованиях, так и для развлечения!
Составление новых задач лично для меня оказалось даже интереснее их решения. Для новой задачи нужно не только придумать её математическую или логическую основу, но и изобрести вокруг неё свою историю и персонажей, чтобы её захотелось тут же решить. Вполне возможно, что при составлении новых задач вы почувствуете себя автором детективного жанра, который заранее знает ответ на загадку, но должен искусно скрыть этот ответ от читателя, выстраивая ловушки и ложные тупиковые линии. Если всё это сделать как следует, то получится по-настоящему интересная задача. Предлагаю вам заняться составлением и публикацией собственных задач — это не только полезное, но и очень захватывающее занятие. Пусть у нас будет больше новых интересных задач!
Александр Клименков, ведущий технический писатель Bercut
Тем, кто дочитал статью до конца — небольшой бонус: три задачки с реальных собеседований в Bercut.
Бонусная задача 1
Рядом с офисом Bercut стоят два дома. Высота каждого — 10 метров. Между ними с крыши на крышу перекинут телекоммуникационный кабель длиной 12 метров. Кабель прогибается под своей тяжестью и в месте максимального прогиба расстояние от кабеля до земли составляет 4 метра. Найдите расстояние между домами.
Бонусная задача 2
На одном этаже офиса Bercut есть сотрудники без мониторов, с одним монитором и с двумя мониторами. У всех вместе 100 мониторов. Сотрудников без монитора столько же, сколько сотрудников с двумя мониторами. Сколько всего сотрудников работает на этом этаже?
Бонусная задача 3
1,5 разработчика за 1,5 минуты пишут 1,5 строки кода. Сколько строк напишут 2 разработчика за 2 минуты?