Содержание
- Типы частот
- Шаги по составлению таблицы распределения частот
- Шаг 1
- Шаг 2
- Шаг 3
- Шаг 4
- Шаг 5
- Шаг 6
- Шаг 7
- Шаг 8
- Шаг 9
- Шаг 10
- Пример построения стола
- Упражнение решено
- Ссылки
А Распределение частоты В статистике это относится к тенденции, за которой следуют данные, организованные в группы, категории или классы, когда каждому присваивается номер, называемый частотой, который указывает, сколько данных находится в каждой группе.
Как правило, наблюдается, что эти частоты распределяются вокруг центральной группы: группы с наибольшим количеством данных.
Группы, которые находятся выше или ниже этой центральной категории, постепенно уменьшают свою частоту, становясь очень маленькими или незначительными для категорий, наиболее удаленных от категории с более высокой частотой.
Чтобы узнать частотное распределение набора данных, сначала создайте категории, а затем составьте таблицу частот. Визуальное представление частотной таблицы называется гистограммой.
Типы частот
Есть несколько типов частот:
1.- Абсолютная частота: он самый простой, и из него строятся остальные. Он просто состоит из общего количества данных, соответствующих категории.
2.- Относительная частота: абсолютная частота каждой категории, деленная на общее количество данных.
3.- Частота в процентах: это та же относительная частота, но умноженная на сто, указывающая процент появления значений в каждой категории.
4.- Накопленная частота: это сумма абсолютных частот категорий ниже или равных рассматриваемой категории.
5.- Кумулятивная частота в процентах: это сумма процентных частот категорий ниже или равных наблюдаемой категории.
Шаги по составлению таблицы распределения частот
Чтобы построить таблицу частотного распределения, необходимо выполнить несколько шагов.
Прежде всего, должны быть доступны данные, которые могут быть разного типа: возраст детей в школе, количество правильных ответов в тесте, рост сотрудников компании, длина листов. дерева и др.
Шаг 1
Определите минимальное значение xmin и максимальное значение xmax в наборе данных Икс.
Шаг 2
Рассчитайте диапазон R, который определяется как разница между максимальным значением минус минимальное значение: R = xmax — xmin.
Шаг 3
Определить количество k интервалов или классов, которые можно задать заранее. Номер k определит количество строк в частотной таблице.
Шаг 4
Если количество интервалов k ранее не указывалось, то оно должно быть установлено в соответствии со следующими руководящими принципами: наименьшее количество рекомендуемых категорий — 5, но оно может быть больше, и в этом случае предпочтительнее выбрать нечетное число.
Шаг 5
Есть формула, которая называется правило осетров что дает нам количество интервалов k рекомендуется для набора, состоящего из N данные:
k = [1 + 3,322⋅Log N]
Поскольку результат внутри скобки обязательно будет действительным числом, скобка говорит нам, что его необходимо округлить до ближайшего нечетного целого числа, чтобы получить целое значение k.
Шаг 6
Амплитуда рассчитывается К каждого интервала (классов или категорий), беря частное между диапазоном р и количество интервалов k: А = R / k. Если исходные данные являются целыми числами, то A округляется до ближайшего целого числа, в противном случае его реальное значение остается.
Шаг 7
Определите нижние пределы Li и верхние пределы Ls для каждого интервала или класса. Первый интервал или самый низкий класс имеет нижний предел Li наименьшего из исходных данных, то есть Li = xmin, а верхний предел — минимальное значение плюс ширина интервала, то есть Ls = xmin + A.
Шаг 8
Последовательные интервалы:
[xmin, xmin + A), [ xmin + A, xmin + 2⋅A), …, [ xmin + (k-1) A, xmin + k⋅A).
Шаг 9
Оценка класса Xc определяется для каждого интервала по следующей формуле: Xc = (Ls — Li) / 2 + Li.
Шаг 10
Размещается заголовок таблицы частот, который состоит из строки со следующими метками: классы, метка класса Xc, частота f, относительная частота fr (или процентная частота f%) и накопленная частота F (или накопленная частота в процентах). F%).
У нас будет следующее:
Первый столбец частотной таблицы— Содержит интервалы или классы, на которые были разделены данные.
Второй столбец: содержит метку класса (или среднюю точку) каждого подынтервала.
Третий столбец: содержит абсолютную частоту f каждого класса или категории.
Четвертая и пятая колонки: помещаются значения, соответствующие относительной частоте (или проценту) и накопленной частоте F (или накопленному проценту).
Пример построения стола
Следующие данные соответствуют правильным ответам анкеты из 100 вопросов, примененной к группе из 52 студентов:
65, 70, 70, 74, 61, 77, 85, 36, 70, 62, 62, 77, 80, 89, 39, 43, 70, 77, 79, 77, 88, 52, 85, 1, 55, 47, 73, 63, 59, 51, 56, 65, 85, 79, 53, 79, 3, 71, 7, 54, 8, 61, 61, 77, 67, 58, 61, 45, 48, 64, 15, 50.
Мы будем следовать шагам, чтобы построить таблицу частот:
1.- Минимальное и максимальное значения Xmin = 1, Xmax = 89.
2.- Диапазон: R = 89 — 1 = 88
3.- Определение количества интервалов по правило осетров: k = [1 + 3,322⋅Журнал 52] = [6,70] = 7.
4.- Расчет ширины интервалов: A = R / k = 88/7 = 12,57 ≈ 13.
5.- Интервалы: [1,14), [14, 27), [27, 40), [40, 53), [53, 66), [66, 79), [79, 92 ».
6.- Определяются оценки классов каждого интервала: 8, 21, 34, 47, 60, 73 и 86.
7.- Таблица сделана:
График частот для различных интервалов или категорий показан на рисунке 1.
Упражнение решено
Учитель записывает процент достижений целей по курсу физики для каждого студента. Однако оценка для каждого студента, хотя и зависит от процента достигнутых целей, ограничена определенными категориями, ранее установленными в правилах обучения университета.
Давайте рассмотрим конкретный случай: в разделе физики у нас есть процент достижений целей для каждого из 52 студентов:
15, 50, 62, 58, 51, 61, 62, 74, 65, 79, 59, 56, 77, 8, 55, 70, 7, 36, 79, 61, 77, 52, 35, 43, 61, 65, 70, 89, 64, 54, 85, 61, 39, 63, 70, 85, 70, 79, 48, 77, 73, 67, 45, 77, 71, 53, 88, 85, 47, 73, 77, 80.
В этом примере категории или классы соответствуют итоговой оценке, которая выставляется в соответствии с процентной долей x достигнутых целей:
1.- Очень плохо: 1 ≤ x <30
2.- Недостаточно: 30 ≤ x <50
3.- Достаточно: 50 ≤ x <70
4.- Хорошо: 70 ≤ x <85
5.- Отлично: 85 ≤ x ≤ 100
Чтобы составить частотную таблицу, данные упорядочиваются от наименьшего к наибольшему, и подсчитывается количество данных, соответствующих каждой категории, что и будет оценкой, которую студент получит за курс физики:
1.- Очень плохо: 4 ученика.
2.- Плохо: 6 учеников.
3.- Достаточно: 20 учеников.
4.- Хорошо: 17 учеников.
5.- Отлично: 5 учеников.
Ниже представлена гистограмма оценок, построенная на основе приведенной выше таблицы:
Ссылки
- Беренсон, М. 1985. Статистика для управления и экономики. Interamericana S.A.
- Канавос, Г. 1988. Вероятность и статистика: приложения и методы. Макгроу Хилл.
- Деворе, Дж. 2012. Вероятность и статистика для техники и науки. 8-е. Издание. Cengage.
- Левин, Р. 1988. Статистика для администраторов. 2-й. Издание. Прентис Холл.
- Шпигель, М. 2009. Статистика. Серия Шаум. 4-й Издание. Макгроу Хилл.
- Уолпол, Р. 2007. Вероятность и статистика для инженерии и науки. Пирсон.
Продолжаем изучать элементарные задачи по математике. Сегодня мы поговорим о статистике.
Статистика — это раздел математики в котором изучаются вопросы сбора, измерения и анализа информации, представленной в числовой форме. Происходит слово статистика от латинского слова status (состояние или положение дел).
Так, с помощью статистики мы можем узнать свое положение дел, касающихся финансов. С начала месяца можно вести дневник расходов и по окончании месяца, воспользовавшись статистикой, узнать сколько денег в среднем мы тратили каждый день или какая потраченная сумма была наибольшей в этом месяце либо узнать какую сумму мы тратили наиболее часто.
На основе этой информации можно провести анализ и сделать определенные выводы: следует ли в следующем месяце немного сбавить аппетит, чтобы тратить меньше денег, либо наоборот позволить себе не только хлеб с водой, но и колбасу.
Выборка. Объем. Размах
Что такое выборка? Если говорить простым языком, то это отобранная нами информация для исследования. Например, мы можем сформировать следующую выборку — суммы денег, потраченных в каждый из шести дней. Давайте нарисуем таблицу в которую занесем расходы за шесть дней
Выборка состоит из n-элементов. Вместо переменной n может стоять любое число. У нас имеется шесть элементов, поэтому переменная n равна 6
n = 6
Элементы выборки обозначаются с помощью переменных с индексами . Последний
элемент является шестым элементом выборки, поэтому вместо n будет стоять число 6.
Обозначим элементы нашей выборки через переменные
Количество элементов выборки называют объемом выборки. В нашем случае объем равен шести.
Размахом выборки называют разницу между самым большим и маленьким элементом выборки.
В нашем случае, самым большим элементом выборки является элемент 250, а самым маленьким — элемент 150. Разница между ними равна 100
Среднее арифметическое
Понятие среднего значения часто используется в повседневной жизни.
Примеры:
- средняя зарплата жителей страны;
- средний балл учащихся;
- средняя скорость движения;
- средняя производительность труда.
Речь идет о среднем арифметическом — результате деления суммы элементов выборки на их количество.
Среднее арифметическое — это результат деления суммы элементов выборки на их количество.
Вернемся к нашему примеру
Узнаем сколько в среднем мы тратили в каждом из шести дней:
Средняя скорость движения
При изучении задач на движение мы определяли скорость движения следующим образом: делили пройденное расстояние на время. Но тогда подразумевалось, что тело движется с постоянной скоростью, которая не менялась на протяжении всего пути.
В реальности, это происходит довольно редко или не происходит совсем. Тело, как правило, движется с различной скоростью.
Когда мы ездим на автомобиле или велосипеде, наша скорость часто меняется. Когда впереди нас помехи, нам приходиться сбавлять скорость. Когда же трасса свободна, мы ускоряемся. При этом за время нашего ускорения скорость изменяется несколько раз.
Речь идет о средней скорости движения. Чтобы её определить нужно сложить скорости движения, которые были в каждом часе/минуте/секунде и результат разделить на время движения.
Задача 1. Автомобиль первые 3 часа двигался со скоростью 66,2 км/ч, а следующие 2 часа — со скоростью 78,4 км/ч. С какой средней скоростью он ехал?
Сложим скорости, которые были у автомобиля в каждом часе и разделим на время движения (5ч)
Значит автомобиль ехал со средней скоростью 71,08 км/ч.
Определять среднюю скорость можно и по другому — сначала найти расстояния, пройденные с одной скоростью, затем сложить эти расстояния и результат разделить на время. На рисунке видно, что первые три часа скорость у автомобиля не менялась. Тогда можно найти расстояние, пройденное за три часа:
66,2 × 3 = 198,6 км.
Аналогично можно определить расстояние, которое было пройдено со скоростью 78,4 км/ч. В задаче сказано, что с такой скоростью автомобиль двигался 2 часа:
78,4 × 2 = 156,8 км.
Сложим эти расстояния и результат разделим на 5
Задача 2. Велосипедист за первый час проехал 12,6 км, а в следующие 2 часа он ехал со скоростью 13,5 км/ч. Определить среднюю скорость велосипедиста.
Скорость велосипедиста в первый час составляла 12,6 км/ч. Во второй и третий час он ехал со скоростью 13,5. Определим среднюю скорость движения велосипедиста:
Мода и медиана
Модой называют элемент, который встречается в выборке чаще других.
Рассмотрим следующую выборку: шестеро спортсменов, а также время в секундах за которое они пробегают 100 метров
Элемент 14 встречается в выборке чаще других, поэтому элемент 14 назовем модой.
Рассмотрим еще одну выборку. Тех же спортсменов, а также смартфоны, которые им принадлежат
Элемент iphone встречается в выборке чаще других, значит элемент iphone является модой. Говоря простым языком, носить iphone модно.
Конечно элементы выборки в этот раз выражены не числами, а другими объектами (смартфонами), но для общего представления о моде этот пример вполне приемлем.
Рассмотрим следующую выборку: семеро спортсменов, а также их рост в сантиметрах:
Упорядочим данные в таблице так, чтобы рост спортсменов шел по возрастанию. Другими словами, построим спортсменов по росту:
Выпишем рост спортсменов отдельно:
180, 182, 183, 184, 185, 188, 190
В получившейся выборке 7 элементов. Посередине этой выборки располагается элемент 184. Слева и справа от него по три элемента. Такой элемент как 184 называют медианой упорядоченной выборки.
Медианой упорядоченной выборки называют элемент, располагающийся посередине.
Отметим, что данное определение справедливо в случае, если количество элементов упорядоченной выборки является нечётным.
В рассмотренном выше примере, количество элементов упорядоченной выборки было нечётным. Это позволило нам быстро указать медиану
Но возможны случаи, когда количество элементов выборки чётно.
К примеру, рассмотрим выборку в которой не семеро спортсменов, а шестеро:
Построим этих шестерых спортсменов по росту:
Выпишем рост спортсменов отдельно:
180, 182, 184, 186, 188, 190
В данной выборке не получается указать элемент, который находился бы посередине. Если указать элемент 184 как медиану, то слева от этого элемента будут располагаться два элемента, а справа — три. Если как медиану указать элемент 186, то слева от этого элемента будут располагаться три элемента, а справа — два.
В таких случаях для определения медианы выборки, нужно взять два элемента выборки, находящихся посередине и найти их среднее арифметическое. Полученный результат будет являться медианой.
Вернемся к нашим спортсменам. В упорядоченной выборке 180, 182, 184, 186, 188, 190 посередине располагаются элементы 184 и 186
Найдем среднее арифметическое элементов 184 и 186
Элемент 185 является медианой выборки, несмотря на то, что этот элемент не является членом исходной и упорядоченной выборки. Спортсмена с ростом 185 нет среди остальных спортсменов. Рост в 185 см используется в данном случае для статистики, чтобы можно было сказать о том, что срединный рост спортсменов составляет 185 см.
Поэтому более точное определение медианы зависит от количества элементов в выборке.
Если количество элементов упорядоченной выборки нечётно, то медианой выборки называют элемент, располагающийся посередине.
Если количество элементов упорядоченной выборки чётно, то медианой выборки называют среднее арифметическое двух чисел, располагающихся посередине этой выборки.
Медиана и среднее арифметическое по сути являются «близкими родственниками», поскольку и то и другое используют для определения среднего значения. Например, для предыдущей упорядоченной выборки 180, 182, 184, 186, 188, 190 мы определили медиану, равную 185. Этот же результат можно получить путем определения среднего арифметического элементов 180, 182, 184, 186, 188, 190
Но медиана в некоторых случаях отражает более реальную ситуацию. Например, рассмотрим следующий пример:
Было подсчитано количество имеющихся очков у каждого спортсмена. В результате получилась следующая выборка:
0, 1, 1, 1, 2, 1, 2, 3, 5, 4, 5, 0, 1, 6, 1
Определим среднее арифметическое для данной выборки — получим значение 2,2
По данному значению можно сказать, что в среднем у спортсменов 2,2 очка
Теперь определим медиану для этой же выборки. Упорядочим элементы выборки и укажем элемент, находящийся посередине:
0, 0, 1, 1, 1, 1, 1, 1, 2, 2, 3, 4, 5, 5, 6
В данном примере медиана лучше отражает реальную ситуацию, поскольку половина спортсменов имеет не более одного очка.
Частота
Частота это число, которое показывает сколько раз в выборке встречается тот или иной элемент.
Предположим, что в школе проходят соревнования по подтягиваниям. В соревнованиях участвует 36 школьников. Составим таблицу в которую будем заносить число подтягиваний, а также число участников, которые выполнили столько подтягиваний.
По таблице можно узнать сколько человек выполнило 5, 10 или 15 подтягиваний. Так, 5 подтягиваний выполнили четыре человека, 10 подтягиваний выполнили восемь человек, 15 подтягиваний выполнили три человека.
Количество человек, повторяющих одно и то же число подтягиваний в данном случае являются частотой. Поэтому вторую строку таблицы переименуем в название «частота»:
Такие таблицы называют таблицами частот.
Частота обладает следующим свойством: сумма частот равна общему числу данных в выборке.
Это означает, что сумма частот равна общему числу школьников, участвующих в соревнованиях, то есть тридцати шести. Проверим так ли это. Сложим частоты, приведенные в таблице:
4 + 5 + 10 + 8 + 6 + 3 = 36
Относительная частота
Относительная частота это в принципе та же самая частота, которая была рассмотрена ранее, но только выраженная в процентах.
Относительная частота равна отношению частоты на общее число элементов выборки.
Вернемся к нашей таблице:
Пять подтягиваний выполнили 4 человека из 36. Шесть подтягиваний выполнили 5 человек из 36. Восемь подтягиваний выполнили 10 человек из 36 и так далее. Давайте заполним таблицу с помощью таких отношений:
Выполним деление в этих дробях:
Выразим эти частоты в процентах. Для этого умножим их на 100. Умножение на 100 удобно выполнить передвижением запятой на две цифры вправо:
Теперь можно сказать, что пять подтягиваний выполнили 11% участников, 6 подтягиваний выполнили 14% участников, 8 подтягиваний выполнили 28% участников и так далее.
Понравился урок?
Вступай в нашу новую группу Вконтакте и начни получать уведомления о новых уроках
Возникло желание поддержать проект?
Используй кнопку ниже

Many types of companies use frequency tables and excel as a frequency calculator. They are a mathematical calculation that shows the distribution of responses to a question in a survey, for example.
They could also show the frequency distribution of occurrences within a data set.
For example, temperature data over the course of the year could be grouped into ranges to see climate data trends. Learning how to make frequency tables using Excel is a bit challenging at first, but it becomes very easy after you have done it a few times.
Make Frequency Data Ranges
Load your data into Excel. It is easiest to have the data in columns per question, and the responses from the different participants in rows.
For example, you might have 100 responses to a survey in your data set. Start numbering your first row with the question numbers, and the respondent responses in the first column in cell A2.
Cell A1 would be blank, but cell A2 would have the first respondent’s answers to the questions going across. Cell A2 would have the first question’s results, cell A3 would be the second question, and so on, to the end of the questionnaire.
Look over your spreadsheet after all of the data have been entered, then determine the range of the data. If you have 100 respondents in your data set, you will have 100 rows of data, ending on row 101. (Remember, the first row is the question number.)
So your first column’s data range will be A2:A101. Your second question will be data range will be B2:B101.
Use the simple formula for counting. Say you have six possible responses to your first question. The formula would read as follows:
=countif(a2:a101,1)
This formula tells Excel to count the times that the number 1 occurs in the data range found in column A from row 2 to row 101.
The formula to count all the 2’s in column A would read as follows:
=countif(a2:a101,2)
The formula for the 3’s would be countif(b2:b101,3), and so on through all your possible responses to the question.
Simplify the process by pasting the first counting formula—countif(a2:a101,1)—into the cells for the number of possible responses you have.
For example, if you have six possible responses, copy that formula into the first six cells in the area of your spreadsheet where you are doing your counting.
Change the criteria manually from 1 in the second cell to 2, and the third to 3, and so on. Once you have made all the changes to 1 through 6, put in the formula for calculating the percent distributions.
Total the count of column results in the first cell below your count.
For example, if you are using A105 through A110 to do your counting, you would either use the sum button on the formula toolbar in Excel to sum the column, or this formula: =sum(a105:a110). You would use cell A111 to put in the formula.
Use the following formula to calculate the frequency distributions of the results in A105 through A110, starting it in cell A112: =a105/a111). This will give you a decimal response, which you can reformat into a percentage for easier viewing.
Simply copy the formula in A112 and apply it to the five cells that fall below A112 to get the percentage distribution of all the responses.
Make a Frequency Table Using Data Ranges
Create or find the data that you want to summarize.
Determine the ranges you want.
For example, if your data set goes from 1 to 100, you would probably want to break it into 10 segments, 1 to 10, 11 to 20, 21 to 30, and so on. Let’s assume your data are in column A, and rows 1 to 100.
Type in the following numbers in B1 through B10, in a column next to the data series: 10, 20, 30, 40, 50, 60, and so on, with each number in a separate cell.
Select 10 cells with the mouse in the column C next to the data range (column B).
Position the mouse in the function bar above the spread sheet (where it says «fx»), then type in your formula. The formula for counting frequencies is pretty easy: =frequency(b1:b100b1:b10).
Since this is an array function, you have to hold down control shift while you hit enter. Otherwise you will get an error like «=NAME?» or something like that. If you have entered your formula correctly, the results will be shown in Column C1 through C10.
Total the results of C1through C10 as discussed in Section 1, Step 5, but using the cells in C1 through C10.
Use the following formula to calculate the frequency distributions of the results in C1 through C10, starting it in cell C11: =c1/b$b11). This will give you a decimal response, which you can reformat into a percentage for easier viewing.
Simply copy the formula in C1 and apply it to the nine cells that fall below C1 to get the percentage distribution of all the ranges.
План урока:
Понятие выборки и генеральной совокупности
Среднее арифметическое выборки
Упорядоченный ряд и таблица частот
Размах выборки
Мода выборки
Медиана выборки
Ошибки в статистике
Понятие выборки и генеральной совокупности
Слово статистика, образованное от латинского status(состояние дел), появилось только в 1746 году, когда его употребил немец Готфрид Ахенвалль. Однако ещё в Древнем Китае проводились переписи населения, в ходе которых правители собирали информацию о своих владениях и жителях, проживающих в них.
В основе любого статистического исследования лежит массив информации, который называют выборкой данных. Покажем это на примере. Пусть в классе, где учится 20 учеников, проводился тест по математике, содержавший 25 вопросов. В результате учащиеся показали следующие результаты:
Ряд чисел, приведенный во второй строке таблицы (12, 19, 19, 14, 17, 16, 18, 20, 15, 25, 13, 20, 25, 16, 17, 12, 24, 13, 21, 13), будет выборкой. Также ее могут называть рядом данных или выборочной совокупностью.
В примере с классом выборка состоит из 20 чисел. Эту величину (количество чисел в ряду) называют объемом выборки. Каждое отдельное число в ряду именуют вариантой выборки.
В примере со школьным классом в выборку попали все его ученики. Это позволяет точно определить, насколько хорошо учащиеся написали математический тест. Однако иногда необходимо проанализировать очень большие группы населения, состоящие из десятков и даже сотен миллионов человек. Например, необходимо узнать, какая часть населения страны курит. Опросить каждого жителя государства невозможно, поэтому в ходе исследования опрашивают лишь его малую часть. В этом случае статистики выделяют понятие генеральная совокупность.
Так, если с помощью опроса 10 тысяч человек ученые делают выводы о распространении курения в России, то все российское население будет составлять генеральную совокупность исследования, а опрошенные 10 тысяч людей вместе образуют выборку.
Среднее арифметическое выборки
Сбор информации о выборке является лишь первой стадией статистического исследования. Далее ее необходимо обобщить, то есть получить некоторые цифры, характеризующие выборку. Самой часто используемой статистической характеристикой является среднее арифметическое.
Другими словами, для подсчета среднего арифметического необходимо просто сложить все числа в ряде данных, а потом поделить получившееся значение на количество чисел в ряде. Так, в примере с тестом по математике (таблица 1) средний балл учащихся составит: (12+19+19+14+17+16+18+20+15+25+13+20+25+16+17+12+24+13+21+13):20=
= 349:20 = 17,45.
Среднее арифметическое позволяет одним числом характеризовать какое-либо качество всех объектов группы. Чем больше средний балл учащихся в классе, тем выше их успеваемость. Чем меньше среднее количество голов, пропускаемых футбольной командой за один матч, тем лучше она играет в обороне. Если средняя зарплата программистов в городе составляет 90 тысяч рублей, а дворников – 25 тысяч рублей, то это значит, что программисты значительно более востребованы на рынке труда, а потому при выборе будущей профессии лучше предпочесть именно эту специальность.
Упорядоченный ряд и таблица частот
В ряде данных в таблице 1 числа приведены в произвольном порядке. Перепишем ряд так, чтобы все числа шли в неубывающем порядке, то есть от самого маленького к самому большому:
12, 12, 13, 13, 13, 14, 15, 16, 16, 17, 17, 18, 19, 19, 20, 20, 21, 24, 25, 25.
Такую запись называют упорядоченным рядом данных.
Его характеристики ничем не отличаются от изначальной выборки, однако с ним удобнее работать. С его помощью можно видеть, что ни одному ученику не удалось набрать 22 или 23 балла на тесте, но сразу двое учащихся дали 25 правильных ответов. На основе упорядоченного ряда данных несложно составить таблицу частот, в которой будет указано, как часто та или иная варианта выборки встречается в ряде. Выглядеть она будет так:
При составлении этой таблицы мы исключили из нее те варианты количества набранных баллов, частота которых равна нулю (от 0 до 12, 22 и 23).Заметим, что сумма чисел в нижней строке таблицы частот должна равняться объему выборки. Действительно,
2+3+1+1+2+2+1+2+2+1+1+2 = 20.
С помощью таблицы частот можно быстрее посчитать среднее арифметическое выборки. Для этого каждую варианту надо умножить на ее частоту, после чего сложить полученные результаты и поделить их на объем выборки:
(12•2+13•3+14•1+15•1+16•2+17•2+18•1+19•2+20•2+21•1+24•1+25•2):20 =
(24+39+14+15+32+34+18+38+40+42+24+50):20 = 349:20 = 17,45.
Размах выборки
Следующий важная характеристика ряда данных – это размах выборки.
Если выборка представлена в виде упорядоченного ряда данных, то достаточно вычесть из последнего числа ряда первое число. Так, размах выборки результатов теста в классе равен:
25 – 12 = 13,
так как самые лучшие ученики смогли решить все 25 заданий, а наихудший учащийся ответил правильно только на 13 вопросов.
Размах выборки характеризует стабильность, однородность исследуемых свойств. Например, пусть два спортсмена-стрелка в ходе соревнований производят по 5 выстрелов по круговой мишени, где за попадание начисляют от 0 до 10 очков. Первый стрелок показал результаты 8, 9, 9, 8, 9 очков. Второй же спортсмен в своих попытках показал результаты 7, 10, 10, 6, 10. Средние арифметические этих рядов равны:
(8+9+9+8+9):5 = 43:5 = 8,6;
(7+10+10+6+10):5 = 43:5 = 8,6.
Получается, что в среднем оба стрелка стреляют одинаково точно, однако первый спортсмен демонстрирует более стабильные результаты. У его выборки размах равен
9 – 8 = 1,
в то время как размах выборки второго спортсмена равен
10 – 6 = 4.
Размах выборки может быть очень важен в метеорологии. Например, в Алма-Ате и Амстердаме средняя температура в течение года почти одинакова и составляет 10°С. Однако в Алма-Ате в январе и феврале иногда фиксируются температуры ниже -30°С, в то время как в Амстердаме за всю историю наблюдений она никогда не падала ниже -20°С.
Мода выборки
Иногда важно знать не среднее арифметическое выборки, а то, какая из ее вариант встречается наиболее часто. Так, при управлении магазином одежды менеджеру не важен средний размер продаваемых футболок, а необходима информация о том, какие размеры наиболее популярны. Для этого используется такой показатель, как мода выборки.
В примере с математическим тестом сразу 3 ученика набрали по 13 баллов, а частота всех других вариант не превысила 2, поэтому мода выборки равна 13. Возможна ситуация, когда в ряде есть сразу две или более вариант, которые встречаются одинаково часто и чаще остальных вариант. Например, в ряде
1, 2, 3, 3, 3, 4, 5, 5, 5
варианты 3 и 5 встречаются по три раза. В таком случае ряд имеет сразу две моды – 3 и 5, а всю выборку именуют мультимодальной. Особо выделяется случай, когда в выборке все варианты встречаются с одинаковой частотой:
6, 6, 7, 7, 8, 8.
Здесь числа 6, 7 и 8 встречаются одинаково часто (по два раза), а другие варианты отсутствуют. В таких случаях говорят, что ряд не имеет моды.
Медиана выборки
Иногда, например, при расчете средней зарплаты, среднее арифметическое не вполне адекватно отражает ситуацию. Это происходит из-за наличия в выборке чисел, очень сильно отличающихся от среднего. Так, из-за огромных зарплат некоторых начальников большинство рядовых сотрудников компаний обнаруживают, что их зарплата ниже средней. В таких случаях целесообразно использовать такую характеристику, как медиану ряда. Это такое значение, которое делит ряд данных пополам. В упорядоченном ряде 2, 3, 6, 8, 8, 12, 15, 15, 18, 19, 25 медианой будет равна 12, так как именно она находится в середине ряда:
Однако таким образом можно найти только медиану ряда, в котором находится нечетное количество чисел. Если же их количество четное, то за медиану условно принимают среднее арифметическое двух средних чисел. Так, для ряда 2, 3, 6, 8, 8, 12, 15, 15, 18, 19, 25, 30, содержащего 12 чисел, медиана будет равна среднему значению 12 и 15, которые занимают 6-ое и 7-ое место в ряду:
Вернемся к примеру с математическим тестом в школе. Так как его сдавали 20 учеников, а 20 – четное число, то для расчета медианы следует найти среднее арифметическое 10-ого и 11-ого числа в упорядоченном ряде
12, 12, 13, 13, 13, 14, 15, 16, 16, 17, 17, 18, 19, 19, 20, 20, 21, 24, 25, 25.
Эти места занимают числа 17 и 17 (выделены жирным шрифтом). Медиана ряда будет равна
(17+17):2 = 34:2 = 17.
Три приведенные основные статистические характеристики выборки, а именно среднее арифметическое, мода и медиана, называются мерами центральной тенденции. Они позволяют одним числом указать значение, относительно которого группируются все числа ряда.
Рассмотрим для наглядности ещё один пример. Врач в ходе диспансеризации измерил вес мальчиков в классе. В результате он получил 10 значений (в кг):
39, 41, 67, 36, 60, 58, 46, 44, 39, 69.
Найдем среднее арифметическое, размах, моду и медиану для этого ряда.
Решение. Сначала перепишем ряд в упорядоченном виде:
36, 39, 39, 41, 44, 46, 58, 60, 67, 69.
Так как в ряде 10 чисел, то объем выборки равен 10. Найдем среднее арифметическое. Для этого сложим все числа в ряде и поделим их на объем выборки (то есть на 10):
(36+39+39+41+44+46+58+60+67+69):10 =
= 499:10 = 49,9 кг.
Размах выборки равен разнице между наибольшей и наименьшей вариантой в ней. Самый тяжелый мальчик весит 69 кг, а самый легкий – 36 кг, а потому размах ряда равен
69 – 36 = 33 кг.
В упорядоченном ряде только одно число, 39, встречается дважды, а все остальные числа встречаются по одному разу. Поэтому мода ряда будет равна 39 кг.
В выборке 10 чисел, а это четное число. Поэтому для нахождения медианы надо найти два средних по счету значение найти их среднее. На 5-ом и 6-ом месте в ряде находятся числа 44 и 46. Их среднее арифметическое равно
(44+46):2 = 90:2 = 45 кг.
Поэтому и медиана ряда будет равна 45 кг.
Ошибки в статистике
Статистика является очень мощным инструментом для исследований во всех областях человеческой деятельности. Однако иногда ее иронично называют самой точной из лженаук. Известно и ещё одно высказывание, приписываемое политику Дизраэли, согласно которому существует просто ложь, наглая ложь и статистика. С чем же связана такая репутация этой дисциплины?
Дело в том, что некоторые люди и организации часто манипулируют данными статистики, чтобы убедить других в своей правоте или преимуществах товара, которые они продают. Требуются определенные навыки, чтобы правильно пользоваться статистикой. Одна из самых распространенных ошибок – это неправильный выбор выборки.
В 1936 году перед президентскими выборами в США был проведен телефонный опрос, который показал, что с большим преимуществом победу должен одержать Альфред Лендон. Однако на выборах Франклин Рузвельт набрал почти вдвое больше голосов. Ошибка была связана с тем, что в те годы телефон могли позволить себе только богатые люди, которые в большинстве своем поддерживали Лендона. Однако бедные люди (а их, конечно же, больше, чем богатых) голосовали за Рузвельта.
Ещё один пример – это агитация в конце XIX века в США к службе на флоте. Пропагандисты в своей рекламе указывали, что, согласно статистике, смертность на флоте во время войны (испано-американской) составляет 0,09%, в то время как среди населения Нью-Йорка она равнялась 0,16%. Получалось, что служить на флоте в военное время безопаснее, чем жить мирной жизнью. Однако на самом деле причина таких цифр заключается в том, что во флот всегда отбирали молодых мужчин с хорошим здоровьем, которые не могли умереть от «старческих» болезней, в то время как в население Нью-Йорка входят больные и старые люди.
При указании среднего значения исследователь может использовать разные характеристики – среднее арифметическое, медиана, мода. При этом почти всегда среднее арифметическое несколько больше медианы. Именно поэтому большинство людей, узнающих о средней зарплате в стране, удивляются, так как они столько не зарабатывают. Правильнее ориентироваться на медианную зарплату.
Ну и наконец, нельзя забывать, что любая статистика может показать только корреляцию между двумя величинами, но это не всегда означает причинно-следственную связь. Так, известно, что чем больше в городе продается мороженого, тем больше в это же время людей тонет на пляжах. Означает ли это, что поедание мороженого увеличивает риск во время плавания? Нет. Дело в том, что оба этих показателя, продажи мороженого и количество утонувших, зависят от третьей величины – температуры в городе. Чем жарче на улице, тем большее количество людей ходят на пляж и тем больше мороженого продается в магазинах.
HR-Инструменты Учебник по STATISTICA
- Вводный
обзор - Таблицы
частот - Таблицы
сопряженности и таблицы флагов и заголовков - Таблицы
флагов и заголовков - Статистики
таблиц сопряженности - Статистики,
основанные на рангах - Многомерные
отклики и дихотомии - Многомерные
отклики - Многомерные
дихотомии - Кросстабуляция
многомерных откликов и дихотомий - Парная
кросстабуляция переменных с многомерными откликами - Средства
построения таблиц системы STATISTICA. - Таблицы
частот - Таблицы
сопряженности и таблицы флагов и заголовков - Многомерные
отклики и дихотомии - Примеры
- Пример
1. Таблицы частот - Пример
2. Таблицы флагов и заголовков - Пример
3. Таблицы сопряженности - Пример
4. Табулирование многомерных откликов и дихотомий - Пример
(анализ продаж)
Вводный обзор
Одним из первых шагов анализа является табуляция данных. Табуляция данных может быть очень изощренной, например, как в показанной выше таблице, где на самом деле объединено несколько таблиц.
Мы начнем с самых простых таблиц. Приведенная ниже таблица называется одномерной таблицей частот:
|
Цвет рубашки |
|
|
Желтый |
5 |
|
Черный |
3 |
|
Цвет морской волны |
1 |
|
Зеленый |
1 |
|
Белый |
7 |
|
Другие |
10 |
|
Всего |
27 |
В этой таблице табулирована переменная цвета рубашки у 27 встреченных мужчин. Таблица называется одномерной, так как в ней табулирована только одна переменная — цвет рубашки. Так как таблица показывает, насколько часто встречается тот или другой цвет, она называется
также таблицей частот. Вы можете видеть, насколько удобно табличное представление.
Табулируя, например, доход, можно проанализировать различные группы населения по уровню дохода.
Наблюдаемые данные могут быть измерены в разнообразных шкалах (интервальных, порядковых, номинальных), поэтому исследование зависимостей между ними может быть затруднено (например, зависимости могут быть нелинейными, данные — неоднородными и т. д.). Отсюда следует, что вначале разумно сгруппировать данные, разбив на достаточно однородные группы (классы, категории — в данном контексте эти слова рассматриваются как синонимы), интуитивно ожидая, что зависимости в отдельных группах будут более отчетливыми.
Таким образом, возникают категоризованные переменные. Часто категоризованную переменную можно рассматривать как некоторую классификацию исходной числовой переменной. Например, количество посетителей сайта в течение дня можно отнести к определенным временным отрезкам, например, к часам. Вы легко можете построить соответствующую группировку.
Однако имеется много ситуаций, когда категоризованная переменная не выражается в терминах какой-либо исходной числовой переменной, а определяется самой природой данных. Например, на книжном рынке можно выделить категории книг по Windows, Windows-приложениям (Word, Excel и др.), Internet, книги, посвященные языкам программирования, научным программам и т. д. В свою очередь, пользователи могут быть разбиты на классы: начинающие пользователи, продвинутые пользователи, профессионалы и т. д.
Пример категоризации данных. Рассмотрим файл данных о продажах.
Эти данные измерены в количественной шкале.
Предположим, что нас интересует только факт покупки данного товара. Тогда количественная шкала явно избыточна. Перейдем к категориальным переменным. Покажем, как это сделать в системе STATISTICA. Дважды щелкнем на имени переменной КОЛБАСЫ. Это
1-я переменная в файле данных. Определим новую переменную формулой:
(v1>0). Это уже категориальная переменная, принимающая два значения: значение 0, если
v1<0 (то есть покупатель не купил товар), и значение 1, если
v1>0 (покупатель купил товар).
Такие переменные называют также индикаторными, т. к. они являются индикатором определенного события (в данном случае факта покупки).
Построенная категориальная переменная разбивает покупателей на два класса: покупатели, купившие продукт (значение переменной равно 1), и покупатели, не купившие продукт (значение переменной равно 0).
После того как мы записали формулу, значения переменной
v1 будут пересчитаны, и мы получим следующий столбец:
Подобную категоризацию можно выполнить для всего списка товаров. В итоге получим файл данных, состоящий из значений 0 и 1.
Единица показывает, что данный покупатель (строка) купил данный товар (столбец).
Заметим, что подобного рода таблицы, содержащие индикаторные переменные, весьма часто появляются в медицинских исследованиях. В них строка — пациент, переменные — симптомы болезни. Единица отмечает, что у данного пациента присутствует данный симптом, 0 — симптом отсутствует.
Такого типа таблицы будут подробно рассмотрены также в главе Анализ соответствий.
Теперь ещё раз напомним идею категоризации, потому что эта идея является ключевой.
Итак, идея состоит в том, чтобы разбить множество разнородных наблюдений на однородные группы с помощью определенных признаков, отражающих существо задачи, и провести дальнейшее исследование в каждой группе отдельно. Такие группы гораздо проще анализировать, чем исходную корзину с разнородными данными.
Например, множество всех покупателей можно поделить на две группы — купивших и не купивших мороженое, или на четыре группы — купивших мороженое и купивших сыр, купивших мороженое и не купивших сыр, не купивших мороженое и купивших сыр, не купивших мороженое и не купивших сыр и т. д.
В STATISTICA таблицы строятся в модуле Основные статистики и таблицы. Конкретный способ построения таблиц зависит от целей исследования.
Врач может табулировать частоты различных симптомов заболевания в зависимости от возраста и пола пациентов, социолог имеет возможность построить сводную таблицу результатов опроса и оценить связи между ответами мужчин и женщин отдельно. В области образования можно табулировать число учащихся, покинувших среднюю школу, в зависимости от возраста, пола и этнического происхождения. Экономисту может понадобиться свести в таблицу количество банкротств в зависимости от вида промышленности, региона и начального капитала, а исследователю спроса классифицировать потребителей в зависимости от доходов. Менеджеры, размещающие рекламу в Internet, могут интересоваться частотой посещения различных сайтов в отдельные дни недели.
Более серьезной задачей является установление цен на продукцию с целью эффективного способа организации продаж: имеются разные категории пользователей, например, учебные заведения, государственные организации, коммерческие структуры и т. д. Покупательские возможности разных категорий различны, поэтому разбиение на группы, когда вы имеете дело не со средним покупателем, а с покупателем из определенной группы, выглядит совершенно естественно.
Далее в одной таблице можно табулировать значения двух переменных, тогда возникают таблицы сопряженности. Пример такой таблицы, которую мог бы поместить в свою записную книжку метрдотель ресторана, показан ниже:
| Дни недели | Количество посетителей ресторана «Табу» в 9 часов вечера | ||
|
Мужчины |
Женщины |
Всего |
|
|
Понедельник |
9 |
11 |
20 |
|
Вторник |
7 |
8 |
15 |
|
Среда |
11 |
7 |
18 |
|
Четверг |
9 |
16 |
25 |
|
Пятница |
15 |
7 |
22 |
|
Суббота |
17 |
5 |
22 |
|
Воскресенье |
17 |
9 |
26 |
|
Всего |
85 |
63 |
148 |
Вы видите, как естественно организована таблица: дни недели сопряжены с количеством посетителей ресторана, отсюда и название таблицы — таблица сопряженности: на пересечении строки дня недели и столбца показано количество посетителей (мужчин и женщин) в выбранный день недели. В крайнем правом столбце с литером ВСЕГО даются суммы значений по строкам таблицы. В последней строке показаны суммы значений, подсчитанные по столбцам. Это так называемые маргинальные частоты.
Удобство таблиц. Удобство таблиц очевидно. Метрдотелю достаточно взглянуть на таблицу, чтобы представить, сколько было посетителей разного пола в различные дни недели. Вместо того чтобы скользить глазами по длинному списку посетителей, он просто бросает взгляд на таблицу. В нижней строке и правом столбце количество посетителей просуммировано. Возможно, метрдотелю интересно знать, сколько всего посетителей было в субботу, и ему вовсе не нужно суммировать частоты в двух столбцах (мужчины и женщины), а достаточно посмотреть на крайний столбец и строку
Суббота.
В таблице табулированы значения двух переменных, поэтому она называется двухвходовой. Если табулируется несколько переменных, то имеют дело с многовходовыми (многомерными) таблицами (от английского термина multy-way) с двумя или более факторами. Заметьте, что табулированные переменные на сленге анализа данных называют также факторами.
Другой типичный пример таблицы сопряженности показан ниже:
В этой таблице табулированы переменные пол и программа телевидения. Таблица построена из исходного файла данных, в котором отмечался выбор программ ТВ респондентами разного пола.
Итак, представление данных в виде таблиц компактно, удобно и наглядно. Вместо того чтобы иметь дело с файлом исходных данных, содержащим сотни и тысячи наблюдений, вы имеете одну таблицу.
Для проверки факта зависимости между табулированными переменными (например, Пол и ТВ) и оценки степени зависимости или, как иногда выражаются, тесноты связи, разработаны специальные методы.
Анализ таблиц связан с определенным сленгом, который стоит запомнить. Переменные, табулированные в таблице, называются также факторами. Значения факторов называются уровнями. Например, переменная пол имеет два уровня — мужчина и женщина, переменная TV также два уровня — 1 и 2. Конечно, количеством уровней и числом табулируемых переменных можно управлять. Можно, например, ввести дополнительные переменные — возраст, профессию и т. д.
В анализе таблиц также употребляется несколько архаичный термин вход таблицы (от английского way) для обозначения табулированной переменной. Если табулируются две переменные, то говорят о двухвходовой таблице (таблицы с двумя входами), если табулируется три переменные — о трехвходовой таблице и т. д.
Несмотря на кажущуюся простоту идеи, техника работы с таблицами за много лет развилась и стала чрезвычайно изощренной.
Альтернативные методы. Вначале таблицы строятся и анализируются в модуле
Основные статистики и таблицы. Однако имеются модули
Логлинейный анализ и Анализ соответствий, в которых также можно исследовать таблицы сопряженности.
Методы Логлинейного анализа (loglinear analysis) позволяют глубоко исследовать сложные многомерные таблицы, возникающие, например, при проведении массовых обследований.
Анализ соответствий (correspondence analysis) — это разведочный метод анализа двухвходовых и многовходовых таблиц, позволяющий визуализировать таблицы и исследовать их структуру. Ясно, что гораздо проще анализировать таблицу визуально, чем исследовать в численном виде. Этот разведочный метод анализа применяется в разнообразных областях: в социологии, эконометрике, маркетинге, медицине (см. например, Thomas Werani: Correspondence Analysis as a Means for Developing City Marketing Strategies, 3rd International Conference on Recent Advances in Retailing and Services Science, pp. 22-25, Juni 1996, Telfs-Buchen (Osterreich) Werani, Thomas, werani@market.uni-linz.ac.at, http://www.market.uni-linz.ac.at).
Продвинутый метод исследования таблиц — анализ соответствий — будет подробно описан в отдельной главе.
В данной главе рассмотрим классические методы анализа, реализованные в модуле Основные статистики и таблицы. Обзор различных типов таблиц начнем с наиболее простой таблицы — таблицы частот.
Таблицы частот
Частоты, или одновходовые таблицы, представляют собой простейший метод анализа категориальных или искусственно категоризованных непрерывных переменных. Часто их используют как одну из процедур разведочного анализа, чтобы посмотреть, каким образом различные группы данных распределены в выборке. Например, изучая зрительский интерес к разным видам спорта (возможно для целей рекламы), вы могли бы представить ответы респондентов в следующей таблице:
Таблица отображает число и кумулятивную (суммарную) долю респондентов, характеризующих свой интерес к просмотру футбольных матчей в следующей шкале: 1) Всегда интересуюсь — Always interested, 2) Обычно интересуюсь — Usually interested, 3) Иногда интересуюсь — Sometimes interested или 4) Никогда не интересуюсь — Never interested.
Точно так же мы могли бы представить информацию о том, насколько часто респондент использует в своей работе Интернет:
STATISTICA обеспечивает разнообразные возможности, позволяющие описать различные категории наблюдений в таблице частот (например, используя «все отличные между собой значения» переменных).
Любая переменная из множества данных может быть проанализирована и представлена в виде таблицы частот. Исследователь может также ввести определенные коды для таблицы, задать интервалы и даже определить ряд логических условий, позволяющих отнести наблюдение к определенной группе.
Практически каждый исследовательский проект начинается с построения таблиц частот. Например, в социологических опросах таблицы частот могут отображать количество мужчин и женщин, число респондентов из определенной этнической группы и т. д. Ответы, измеренные в определенной шкале (например, в шкале интерес к футболу), можно также свести в таблицу частот.
Ниже на графике показана табуляция частоты посещения магазина.
В медицинских исследованиях можно табулировать пациентов с определенными симптомами. В промышленности — частоту выхода из строя элементов, приведших к авариям или отказам всего устройства при испытаниях на прочность (например, для определения, какие детали телевизора действительно надежны после эксплуатации в аварийном режиме и при большой температуре, а какие нет). Обычно если в данных имеются категориальные переменные, то для них всегда вычисляются таблицы частот для каждой переменной.
Таблицы сопряженности и таблицы флагов и заголовков
Это более сложные таблицы, так как они содержат частоты нескольких переменных. Процесс построения таблицы частот для одной переменной называется табуляцией, для нескольких переменных — кросстабуляцией. На самом деле кросстабуляция — это процесс объединения двух (или нескольких) таблиц частот так, что каждая ячейка (клетка) в построенной таблице представляется единственной комбинацией значений кросстабулированных переменных.
Таким образом, кросстабуляция позволяет совместить частоты появления наблюдений на разных уровнях рассматриваемых факторов. Исследуя эти частоты, можно определить зависимости между кросстабулированными переменными.
Идея проверки независимости табулированных переменных очень проста. Рассмотрим двухвходовую таблицу сопряженности {v(i, j),1
< i < k, 1 < j < m}, в которой табулированы значения двух переменных (X, Y).
Частоты v(i, j)/n являются оценками вероятностей p(i,j).
При гипотезе независимости эти вероятности обладают свойством мультипликативности:
P(i,j) = P(i)×p(j),
p(i)=p(1,i) + p(2,i) + …+ p(m,i)
P(j)=p(1,j) + p(2,j) + …+ p(k,j)
При наличии зависимости между табулированными переменными это равенство нарушается.
Критерием проверки гипотезы независимости в таблицах сопряженности является хи-квадрат Пирсона, который сравнивает наблюдаемые частоты в реальной таблице с ожидаемыми, рассчитанными при условии независимости табулированных переменных (си. далее).
Пример. Рассмотрим файл данных с информацией о прививках (см. Вступительное эссе).
Построим таблицу сопряженностей признаков ПРИВИВКА, БОЛЕЗНЬ.
Посмотрим на хи-квадрат:
По результатам применения хи-квадрат критерия можно сделать вывод, что есть серьезные основания для того, чтобы отвергнуть гипотезу о независимости признаков.
Общая схема рассуждений
- Шаг 1. Проверьте гипотезу о независимости признаков.
- Шаг 2. Если гипотеза о независимости отвергается, используйте специальные меры связи, например, статистику гамма, чтобы оценить степень зависимости между табулированными переменными.
Обычно кросстабулируются номинальные переменные или переменные с относительно небольшим числом значений.
Если вы хотите кросстабулировать непрерывные переменные (например, доход), то вначале их следует категоризоватъ, разбив диапазон изменения на небольшое число интервалов (например, низкий, средний, высокий).
Таблицы 2×2. Простейшая форма кросстабуляции — это таблица 2× 2, в которой значения двух переменных «пересечены» (сопряжены) и каждая переменная принимает только два значения, то есть имеет два уровня (поэтому таблица и называется 2
× 2). Рассмотрим поясняющий пример. Предположим, проводится простое исследование, в котором мужчин и женщин спрашивают, какой напиток они предпочитают (газированную воду марки А или газированную воду марки В); файл данных показан ниже:
|
ПОЛ |
ГАЗ. ВОДА |
|
|
наблюдение 1 |
МУЖЧИНА |
А |
|
наблюдение 2 |
ЖЕНЩИНА |
В |
|
наблюдение 3 |
ЖЕНЩИНА |
В |
|
наблюдение 4 |
ЖЕНЩИНА |
А |
|
наблюдение 5 |
МУЖЧИНА |
В |
Результаты кросстабуляции выглядят следующим образом:
|
ГАЗ. ВОДА:А |
ГАЗ. ВОДА: В |
||
|
ПОЛ: МУЖЧИНА |
20(40%) |
30(60%) |
50(50%) |
|
ПОЛ: ЖЕНЩИНА |
30(60%) |
20(40%) |
50(50%) |
|
50(50%) |
50(50%) |
100(100%) |
Каждая ячейка таблицы содержит единственную комбинацию значений двух кросстабулированных переменных (в строке указана переменная ПОЛ, в столбце — переменная ГАЗ. ВОДА). Каждая ячейка стоит на пересечении столбца и строки. Числа в каждой ячейке на пересечении определенной строки и определенного столбца показывают, сколько наблюдений соответствует данным значениям. Посмотрите на таблицу. Таблица показывает, что женщины больше мужчин предпочитают газированную воду марки А, мужчины больше предпочитают марку В. Таким образом, пол и предпочтение могут быть зависимыми (позже будет показано, как эту зависимость измерить).
Маргинальные частоты. Значения, расположенные на краях таблицы, — это просто одномерные таблицы частот для всех рассматриваемых переменных. Эти значения важны, т. к. позволяют оценить распределение частот в отдельных столбцах и строках. Например, 40% и 60% мужчин и женщин (соответственно), выбравших марку А (см. первый столбец таблицы), не могли бы показать какой-либо связи между переменными ПОЛ и ГАЗ. ВОДА — Soda, если бы маргинальные частоты переменной ПОЛ были также 40% и 60%. В этом случае они просто отражали бы разную долю мужчин и женщин, участвующих в опросе. Таким образом, различия в распределении частот в строках (или столбцах) отдельных переменных и в соответствующих маргинальных частотах дают информацию о зависимости кросстабулированных переменных.
Проценты по столбцам, по строкам и кумулятивные проценты. Приведенный пример показывает, что для оценки зависимости между кросстабулированными переменными необходимо сравнивать маргинальные доли и индивидуальные доли в столбцах и строках. Такие сравнения легче провести с использованием процентов.
Процедура Итоговые таблицы позволяет выдать кросстабулированные частоты в таблице результатов вместе с числом наблюдений, попавших в ячейку, процентами в столбцах и строках, а также суммарными процентами.
Можно построить итоговую объединенную таблицу, в которой каждая ячейка содержит эти числа.
Графическое представление кросстабуляций. Отдельные строки и столбцы таблицы удобно представить в виде графиков. Полезно также отобразить целую таблицу на отдельном графике. Имеется несколько способов сделать это с помощью процедуры
Таблицы сопряженности. Таблицы с двумя входами можно визуально представить
ЗМ гистограммой.
Другой способ визуализации таблиц сопряженности — построение категоризованной гистограммы, в которой каждая переменная представлена индивидуальными гистограммами, разбитыми на каждом уровне другой переменной (см. ниже).
Преимущество ЗМ гистограммы в том, что она позволяет представить на одном графике таблицу полностью. Достоинство категоризованного графика заключается в том, что он дает возможность точно оценить специфические частоты в каждой ячейке.
Таблицы флагов и заголовков
Таблицы флагов и заголовков, или, кратко, таблицы заголовков, позволяют отобразить несколько двухмерных таблиц сопряженности в сжатом виде как одну таблицу. Этот тип таблиц поясняется на примере файла, отражающего интерес к спорту.
В данной таблице результатов представлены три двухвходовые таблицы, в которых интерес к Футболу — Football сопряжен с интересом к Бейсболу — Baseball, Теннису — Tennis и Боксу — Boxing. Таблица содержит информацию о процентах по столбцам, поэтому суммы по строкам равны 100%. Например, число в левом верхнем углу таблицы результатов (85,71) показывает, что 85,71 процентов всех респондентов ответили, что им всегда интересно смотреть футбол и всегда интересно смотреть бейсбол. Рассмотрите первый столбец приведенной таблицы. Вы видите, например, что имеется 2 респондента, обычно интересующихся футболом и всегда интересующихся бейсболом. Также 2 (других) респондента иногда интересуются футболом и всегда интересуются бейсболом. Нет ни одного респондента, которому был бы всегда интересен бейсбол и никогда не интересен футбол. Аналогично интерпретируются другие столбцы. Если вы прокрутите таблицу вправо, то увидите, что процент тех, кому всегда интересно смотреть футбол и всегда интересно смотреть теннис, равен 38,46; для бокса этот процент составляет 70,0 (см. таблицы ниже).
Проценты в столбце (Всего по строке), показанные после каждого набора переменных, всегда связаны с общим числом наблюдений. В диалоговом окне
Результаты кросстабуляции имеется множество процедур, позволяющих построить таблицы заголовков в различных форматах. Например, можно одновременно отображать число наблюдений в ячейках, строках, столбцах и общие проценты в одной
и той же таблице.
Многовходовые таблицы с контрольными переменными. Когда кросстабулируются только две переменные, результирующая таблица называется двухвходовой (двухмерной). Конечно, общую идею кросстабулирования можно обобщить на большее число переменных. В примере с «газированной водой» добавим третью переменную с информацией о штате, в котором проводилось исследование (Небраска или Нью-Йорк).
|
ПОЛ |
ГАЗ. ВОДА |
ШТАТ |
|
наблюдение 1 |
МУЖЧИНА А |
НЕБРАСКА |
|
наблюдение 2 |
ЖЕНЩИНА В |
НЬЮ-ЙОРК |
|
наблюдение 3 |
ЖЕНЩИНА В |
НЕБРАСКА |
|
наблюдение 4 |
ЖЕНЩИНА А |
НЕБРАСКА |
|
наблюдение 5 |
МУЖЧИНА В |
НЬЮ-ЙОРК |
Кросстабуляция этих трех переменных представлена в следующей таблице:
|
ШТАТ: НЬЮ-ЙОРК ШТАТ: НЕ БРАСКА |
||||||
| ГАЗ. ВОДА А | ГA3 .ВОДА В |
ГАЗ. ВОДА
А |
ГАЗ.ВОДА В | |||
|
П: МУЖЧИНА |
20 |
30 |
50 |
5 |
45 |
50 |
| П: ЖЕНЩИНА | 30 | 20 | 50 | 45 | 5 | 50 |
| 50 | 50 | 100 | 50 | 50 | 100 |
Теоретически любое число переменных может быть кросстабулировано в одной многовходовой таблице. Однако на практике возникают сложности с проверкой и «пониманием» таких таблиц, если они содержат более четырех переменных.
Статистики таблиц сопряженности
Таблицы сопряженности позволяет исследовать зависимость между кросстабулированными переменными. Следующая таблица отчетливо показывает очень сильную зависимость между двумя переменными: переменная ВОЗРАСТ
(ВЗРОСЛЫЙ или РЕБЕНОК) и переменная предпочитаемый сорт ПЕЧЕНЬЕ (сорт А или сорт В).
|
ПЕЧЕНЬЕ: А |
ПЕЧЕНЬЕ: В |
||
|
ВОЗРАСТ: ВЗРОСЛЫЙ |
50 |
0 |
50 |
|
ВОЗРАСТ: РЕБЕНОК |
0 |
50 |
50 |
|
50 |
50 |
100 |
Из этой таблицы видно, что все взрослые выбирают печенье А, а все дети —печенье В. В данном случае нет никаких оснований сомневаться в надежности этого факта.
Невозможно поверить, что данная структура частот носит случайный характер. Мало кто усомнится, что между предпочтениями детей и взрослых имеется отчетливое различие. Однако в реальной обстановке зависимости между переменными значительно слабее, и поэтому возникает вопрос, как их измерить и оценить надежность (статистическую значимость).
Далее обсуждаются общие меры зависимости между двумя группирующими переменными.
Итак, вначале проверяется гипотеза: имеется ли зависимость между представленными в таблице переменными?
Критерий хи-квадрат Пирсона. Хи-квадрат Пирсона — это наиболее простой критерий проверки значимости зависимостей между группирующими переменными. Критерий Пирсона основывается на том, что в двухвходовой таблице ожидаемые частоты при гипотезе, что между переменными нет зависимости, можно непосредственно вычислить.
Критерий хи-квадрат — это непараметрический критерий, его применение никак не связано с распределением табулированных переменных.
Идея критерия очень проста.
Рассмотрим двухмерную таблицу сопряженности
(v(i,j)}, i = 1, 2 …r, j = 1, 2 … s, состоящую из г строк и s столбцов.
Обозначим
Итак, v(i)- сумма элементов в i-й строке, v(j)-
сумма элементов в j-м столбце, n- общее число
наблюдений ( сумма всех частот в таблице). v(i),
v(j) называются также маргинальными
частотами, т.к. они располагаются по краям
таблицы. Из частоты, стоящей в ячейке (это
наблюдаемая частота), вычтите ожидаемую
частоту ( она вычисляется перемножением
маргинальных частот и делением их на общее
число наблюдений). Полученную разность
возведите в квадрат и разделите на
ожидаемую частоту. Далее проделайте то же
самое со всеми ячейками и результаты
сложите.
Это и есть знаменитая статистика хи-квадрат. Статистика хи-квадрат замечательна тем, что при достаточно большом числе наблюдений ее распределение можно приблизить распределением хи-квадрат и, значит, вычислить приближенный
р-уровень критерия.
Формально статистика хи-квадрат вычисляется по формуле:
где суммирование производится по всем индексам i, j. y(i,j) = v(i) * v(j)/n — ожидаемая частота в ячейке i, j.
Большие значения хи-квадрат свидетельствуют против проверяемой гипотезы о независимости признаков, табулированных в таблице.
Представьте, что опрошено 20 мужчин и 20 женщин относительно выбора газированной воды (марка А или марка В). Если между выбором и полом нет зависимости, то естественно ожидать равного выбора марки А и марки В для каждого пола.
Распределение хи-квадрат при проверке независимости можно аппроксимировать хи-квадрат распределением с числом степеней свободы (r-l)*(s-l). Однако качество этой аппроксимации ухудшается, если число наблюдений в ячейках мало (см. ниже).
Критерий хи-квадрат становится высокозначимым при отклонении реально наблюдаемых частот в таблице от ожидаемых, иными словами, когда выбор мужчин и женщин различен. Значение статистики хи-квадрат и ее уровень значимости определяется общим числом наблюдений и количеством ячеек в таблице.
Иногда используют статистику хи-квадрат в форме максимального правдоподобия:
По существу, эти две статистики эквивалентны.
Имеется только единственное существенное ограничение использования критерия хи-квадрат (кроме очевидного предположения о случайном выборе наблюдений) — ожидаемые частоты должны быть не слишком малы (см. пример ниже). Это ограничение возникает потому, что хи-квадрат сравнивает наблюдаемые частоты и вероятности в каждой ячейке, и когда частоты в ячейках малы, например, меньше 5 или даже 10, эти вероятности нельзя оценить с достаточной точностью (см. например, Everitt B.S. (1977) The analysis of contingency tables, London: Chapman&Hall).
Замечание.
Статистика хи-квадрат Пирсона позволяет строить также критерии согласия и однородности (см. главу 4 Подгонка вероятностных распределений).
Поправка Йетса для таблиц 2×2. Для важного класса таблиц 2×2, содержащих ячейки с малыми частотами, аппроксимация распределения статистики хи-квадрат может быть улучшена понижением абсолютного значения разностей между ожидаемыми и наблюдаемыми частотами на величину 0,5 перед возведением в квадрат (поправка Йетса).
Поправка Йетса, делающая оценку более умеренной, применяется в случаях, когда таблица содержит ячейки с малыми частотами. Принято считать, что наименьшая ожидаемая частота, позволяющая применять критерий хи-квадрат без поправок, должна равняться 5. Из приведенной ниже таблицы видно, как могут отличаться
р-уровни критерия хи-квадрат без поправки и с поправкой Йетса. Исходная таблица сопряженности имеет вид:
В таблице сопряжены два признака: покупка мороженого и орехов. Статистики для этой таблицы сопряженности имеют вид:
Используя хи-квадрат без поправки Йетса, мы совершили бы грубую ошибку.
Точный критерий Фишера. Этот критерий применим только для таблиц 2×2. Критерий основан на следующем рассуждении. Даны маргинальные частоты в таблице. Предположим, что оба фактора в таблице независимы. Зададимся вопросом: какова вероятность получения наблюдаемых в таблице частот исходя из маргинальных? Эта вероятность вычисляется точно исходя из данных маргинальных частот. Таким образом, критерий Фишера вычисляет точную вероятность появления наблюдаемых частот при нулевой гипотезе. Вычисляются односторонние и двусторонние вероятности.
Макнемара хи-квадрат. Этот критерий применяется, когда частоты в таблице 2×2 представляют зависимые выборки. Например, наблюдения одних и тех же индивидуумов до и после эксперимента. Вы можете подсчитывать число студентов, имеющих минимальные успехи по математике в начале и в конце семестра. Вычисляются два значения хи-квадрата:
A/D и В/С. A/D хи-квадрат проверяет гипотезу о том, что частоты в ячейках А и D (верхняя левая, нижняя правая) одинаковы. В/С
хи-квадрат проверяет гипотезу о равенстве частот в ячейках В и С (верхняя правая, нижняя левая).
Коэффициент фи. Фи-квадрат представляет собой меру зависимости между двумя группирующими переменными в таблице 2×2. Его значения изменяются от 0 (нет зависимости между факторами; хи-квадрат — 0,0) до 1 (абсолютная зависимость между двумя факторами в таблице).
Тетрахорическая корреляция. Эта статистика вычисляется (и применяется) только для таблиц сопряженности 2×2. Если таблица
2×2 может рассматриваться как результат (искусственного) разбиения двух непрерывных переменных на два класса, то коэффициент тетрахорической корреляции будет оценивать зависимость между двумя этими переменными.
Коэффициент сопряженности С. Коэффициент сопряженности представляет собой основанную на статистике хи-квадрат меру зависимости между двумя группирующими переменными (предложенную Пирсоном). Преимущество этого коэффициента перед обычным хи-квадрат состоит в том, что он легче интерпретируется, т. к. диапазон его изменения от 0 до 1 (где 0 означает полную независимость).
Недостаток заключается в том, что верхний предел «ограничен» размером таблицы; С может достигать значения 1, только если число классов не ограничено.
Интерпретация мер сопряженности. Существенный недостаток мер зависимости в трудности их интерпретации в обычных терминах вероятности или «доли вариации», как в случае коэффициента корреляции
r Пирсона.
Статистики, основанные на рангах
Во многих случаях классы, используемые в кросстабуляции, содержат информацию о ранговом упорядочивании объектов; иными словами, имеются измерения лишь в порядковой шкале. Предположим, вы опросили некоторое множество респондентов для того, чтобы выяснить их отношение к некоторым видам спорта. Затем представили измерения в 4-точечной шкале со следующими градациями: 1) всегда — always, 2) обычно — usually, 3) иногда — sometimes и 4) никогда — never interested. Очевидно, что ответ иногда интересуюсь — sometimes interested показывает меньший интерес, чем обычно интересуюсь — usually interested, обычно интересуюсь — usually interested меньший интерес, чем всегда интересуюсь — always interested, и т. д.
Для таких переменных имеются свои типы корреляции, позволяющие численно выразить зависимости между ними (см. главу Непараметрическая статистика).
Многомерные отклики и дихотомии
Переменные типа многомерных откликов или многомерных дихотомий возникают в ситуациях, когда исследователя интересуют не только «простые» частоты событий, но также некоторые (часто неструктурированные) качественные свойства событий. Типичным примером является опрос общественного мнения, где вопросы, по крайней мере частично, имеют так называемые «открытые концы» (не подразумевая однозначного ответа), и респондент делает выбор из неограниченного (или очень большого) списка ответов. Вопрос состоит в том, как разумным способом закодировать ответы. Природу многомерных переменных (факторов) лучше всего рассмотреть на примерах.
Многомерные отклики
Представьте, что в процессе большого исследования вы попросили пользователей назвать три лучших, с их точки зрения, сайта. Обычный вопрос может выглядеть следующим образом:
Напишите ниже три ваших сайта:
1:______ 2:______ 3:______
Анкета содержит от 0 до 3 ответов. Очевидно, список может быть очень большим. Ваша цель — свести результаты в таблицу, в которой, например, будет подсчитан процент респондентов, предпочитающих определенный сайт.
Следующий шаг после получения анкет — занесение ответов в файл данных. Предположим, в ответах упоминалось 50 различных сайтов. Вы могли бы, конечно, создать 50 переменных — одну для каждого сайта, рассмотреть респондентов как наблюдения (строки таблицы), ввести код / для респондента и переменной, если он предпочитают данный сайт (0, если нет); например:
|
Сайт1 |
Сайт 2 |
Сайт3 |
|
|
наблюдение 1 |
0 |
1 |
0 |
|
наблюдение 2 |
1 |
1 |
0 |
|
наблюдение 3 |
0 |
0 |
1
|
Такой метод кодирования откликов, т. е. приписывания им конкретных значений, очевидно, «расточителен». Заметим, что каждый респондент дает максимум три ответа; однако для кодирования используется 50 переменных. (Если вы интересуетесь только тремя сайтами, то такой метод кодирования будет успешным. Чтобы табулировать предпочтения в выборе сайта, следует рассмотреть 3 переменные как одну многомерную дихотомию; см. ниже.)
Кодирование многомерных откликов. Более разумным является следующий подход. Введите 3 переменные и определите схему кодирования для 50 сайтов. Затем введите соответствующие коды (альфа-метки) для значений переменных и получите таблицу вида:
|
Ответ_1 |
Ответ 2 |
Ответ_3 |
|
|
набл. 1 |
сайт1 |
сайт 17 |
сайт 13 |
|
набл. 2 |
сайт 2 |
сайт 21 |
сайт 77 |
|
набл. 3 |
сайт 19 |
сайт1 |
сайт 4 |
Теперь, чтобы получить число респондентов, предпочитающих определенный сайт, рассмотрите переменные Ответ 1 — Ответ 3 как переменную с многомерным откликом. Само название переменной показывает, что она принимает многомерные значения. Таблица значений такой переменной имеет вид:
|
N=500 Категория |
Число |
Процент ответов |
Процент наблюдений |
|
сайт1 |
44 |
5,23 |
8,80 |
|
сайт 2 |
5 |
1 |
2,60 |
|
сайтЗ |
81 |
9,62 |
16,20 |
|
сайт 4 |
74 |
8,79 |
14,80 |
|
Всего |
|||
|
Ответов |
842 |
100,00 |
168,40 |
Интерпретация таблиц частот с многомерными откликами. Итак, общее число респондентов в опросе
n=500. Заметьте, что числа в первой колонке таблицы не составляют в сумме 500, как можно было бы ожидать, а равны 842. Вы поймете, почему это так, если вспомните, что каждый респондент может дать несколько ответов, так как у него может быть несколько любимых сайтов. Число, приведенное внизу в первом столбце (на границе таблицы), — это общее число ответов. Каждый респондент может дать до трех ответов, поэтому общее число ответов в действительности больше . числа респондентов.
Вторые и третьи столбцы таблицы содержат проценты относительного числа ответов (второй столбец) и респондентов (третий столбец). Таким образом, вход 8,80 в первой строке последнего столбца таблицы означает, что 8,8% всех респондентов назвали сайт1 в числе лучших.
Как учитывать повторяющиеся ответы в одной и той же анкете? В отличие от других популярных программ, строящих таблицы для многомерных откликов, процедура Кросстабуляция в модулеОсновные статистики и таблицы по умолчанию игнорирует одинаковые отклики. Например, если респондент ответил; сайт 1, сайт 1, сайт 1, то система STATISTICA учтет из его ответа сайт 1 только один раз. Следовательно, этот респондент в таблице частот будет учтен только один раз в группе сайт 1, иными словами, в эту группу будет добавлена единица, а не тройка.
Многомерные дихотомии
Предположим, вас интересуют только сайт А, сайт В и сайт С. Как отмечалось, одним из способов кодирования является следующий:
|
сайт А |
сайт В |
сайт C |
|
|
наблюдение 1 |
1 |
||
|
наблюдение 2 |
1 |
1 |
|
|
наблюдение 3 |
1 |
Здесь каждая переменная используется для одного сайта. Код 1 будет введен в таблицу всякий раз, когда соответствующий респондент указал ее в своем ответе. Заметим, что каждая переменная является дихотомией, т. к. принимает только два значения: «1» и «не 1» (можно ввести 1 и 0, но так обычно не делается, можно просто рассматривать 0 как пустую ячейку или пропуск). Когда табулируются такие значения, вы получите итоговую таблицу, очень похожую на ту, которая была показана ранее для переменных с многомерными откликами; из нее вы можете вычислить число и процент респондентов (и ответов) для каждого сайта. Таким образом, вы компактно представили три переменные сайт А, сайт В, сайт С одной переменной (Любимые сайты) — многомерной дихотомией. Заметьте, для кодирования трех сайтов использовано 3 одномерные дихотомии, для кодирования десяти напитков понадобится 10 одномерных дихотомий и т. д.
Кросстабуляция многомерных откликов и дихотомий
Процедура Кросстабуляция модуля Основные статистики и таблицы
позволяет определить простые группирующие переменные (например, ПОЛ:
МУЖЧИНА или ЖЕНЩИНА), многомерные отклики и многомерные дихотомии. Все эти типы переменных можно использовать в таблицах сопряженности. Например, вы можете «сопрячь» многомерную дихотомию Сайт (закодированную, как описано выше) с многомерным откликом Телевидение (со многими категориями, например, ПРОГРАММА 1, ПРОГРАММА 2 и т. д.), а также с простой группирующей переменной ПОЛ.
Как и в таблице частот для обычных переменных, в таблице частот для многомерных переменных можно вычислить проценты и маргинальные суммы либо по общему числу респондентов, либо по общему числу ответов (откликов). Например, рассмотрим следующего респондента:
|
ПОЛ |
сайт 7 |
сайт 3 |
сайт 9 |
ТВ |
ТВ |
|
ЖЕНЩИНА |
1 |
1 |
1 |
2 |
Этот респондент ЖЕНЩИНА назвал своими любимыми сайт 7 и сайт 3 и программы ТВ 1 и ТВ2. В полной таблице сопряженности этот респондент будет представлен следующими наборами:
|
ТВ Общеечисло ответов |
||||
|
ПОЛ |
Сайт |
ТВ1 |
ТВ2 |
|
|
ЖЕНЩИНА |
сайт7 |
X |
X |
2 |
|
сайт 3 |
X |
X |
2 |
|
|
сайт 9 |
||||
|
МУЖЧИНА |
сайт 7 |
|||
|
сайт 3 |
||||
|
сайт 9 |
Данный респондент учитывается в таблице четыре раза. Дополнительно он будет считаться дважды в столбце ЖЕНЩИНА -сайт 7 маргинальных частот, если этот столбец запрошен для представления общего числа откликов. Если пользователь запрашивает маргинальные суммы, вычисленные как общее число респондентов, этот респондент будет учитываться только один раз.
Парная кросстабуляция переменных с многомерными откликами
Лучше всего показать ее на простом примере. Предположим, проводится обследование нынешних и бывших домовладений респондента. Вы попросили респондента описать три последних дома, которыми он владел (включая тот, которым он владеет в данный момент). Естественно, для некоторых из респондентов нынешний дом является самым первым (если до этого они не приобретали дома в частную собственность). Для каждого дома респондента запрашивается количество квартир и число жильцов — членов семьи. Ниже показано, как ответ одного респондента (скажем, наблюдение 112) может быть введен в файл данных:
|
№ набл |
Комнаты 1 2 3 |
Число жильцов 1 2 3 |
|
1 1 2 |
|
|
Респондент имел три дома: первый из трех комнат, второй также из трех комнат, третий из четырех комнат. Количество членов семьи также росло: в первом доме жили 2 человека, во втором — 3, в третьем — 5.
Допустим, вы хотите кросстабулировать число комнат с числом жильцов для всех респондентов (например, чтобы понять, как количество комнат связано с числом жильцов). Один из способов — создать три различные таблицы с двумя входами, одну таблицу для одного дома. Вы можете также рассмотреть два фактора в этом исследовании (Число комнат, Число жильцов) как переменные со многими откликами. Однако очевидно, что нет никакого смысла в приведенном примере с респондентом 112 учитывать значения 3 и 5 в ячейке Комнаты — Жильцы в таблице сопряженности (которые вы могли бы учитывать, если бы рассматривали два эти фактора как одинарные переменные с многомерными откликами). Другими словами, вы хотите игнорировать комбинацию жильцов в третьем доме с числом комнат в первом. Скорее всего, нужно рассматривать переменные попарно; вы хотели бы рассмотреть число комнат в первом доме вместе с числом жильцов в первом доме, число комнат во втором доме вместе с числом жильцов в нем и т. д. Именно так и происходит, когда программа выполняет парную кросстабуляцию многомерных переменных.
Иногда при создании сложных таблиц сопряженности с переменными типа многомерных откликов и дихотомий возникает следующий вопрос (в ваших вычислениях): какую «выбрать дорогу», или как точно будут учитываться наблюдения в файле данных. Лучший способ проверить, как программа строит соответствующую таблицу, — рассмотреть простой пример и увидеть, каким образом учитывается каждое наблюдение (какой оно вносит вклад).
Средства построения таблиц системы STATISTICA
Таблицы частот
Данная процедура позволяет вычислить таблицы частот (и гистограммы). В этих таблицах представляются частоты попадания значений переменной (наблюдений) в разные классы (приводятся численные или численно-буквенные значения и их метки). STATISTICA предлагает различные процедуры для определения категорий (классов) в таблицах частот (например, целые интервалы, определенные коды и т. д.). Пользователь может табулировать данные с помощью определенных условий, заданных в виде логических выражений.
Например, в показанном выше окне мы включили в категорию 1 только наблюдения с номерами строго больше 10, для которых значения v7 строго меньше 3. Таблицы частот для этой группы данных имеет вид:
Таблицы сопряженности и таблицы флагов и заголовков
Это процедуры позволяют кросстабулировать данные (таблицы с числом входов до 6; многовходовые таблицы более высокого уровня можно строить, используя условия выбора) и строить разнообразные таблицы сопряженности. Здесь также доступно большое количество статистик (например,
критерии хи-квадрат, фи-квадрат, гамма и т. д.).
Многомерные отклики и дихотомии
Модуль Основные статистики и таблицы имеет разнообразные возможности построения итоговых таблиц для переменных с многомерными откликами, а также для многомерных дихотомий. Обычно группирующие переменные или факторы делят выборку на непересекающиеся (эксклюзивные) группы, например, группу мужчин и женщин. Очевидно, достаточно только одной группирующей переменной, чтобы закодировать пол субъекта. Однако в некоторых исследованиях категории не исключают друг друга (пересекаются).
Например, в маркетинговых исследованиях респонденту можно задать вопрос о трех самых любимых безалкогольных напитках. Предположим, 60 различных напитков присутствует в ответах, которые можно закодировать тремя группирующими переменными (первые три предпочтения). В этом случае категории, очевидно, не являются взаимоисключающими. Действительно, человек может отметить 3 различных напитка как предпочтительные. Следовательно, если наблюдение — это субъект, то для трех различных группирующих переменных это наблюдение является общим (не эксклюзивным). Такие группирующие переменные называют переменными с многомерными откликами (многомерные дихотомии по существу схожи с ними). Эти переменные легко анализировать в модуле Основные статистики и таблицы.
Примеры
Пример 1. Таблицы частот
Пример основан на модельных данных опроса об использовании Интернет. Проводился опрос 100 человек относительно степени использования ими сети Интернет. Каждый респондент получил список из семи разделов с просьбой определить свой интерес: 1) Всегда интересуюсь — Always interested, 2) Обычно интересуюсь — Usually interested, 3) Иногда интересуюсь — Sometimes interested и 4) Никогда не интересуюсь — Never interested.
Ниже приведен файл SPORTS.sta.
Можно щелкнуть по кнопке Отображение числовых/текстовых значений панели инструментов таблицы исходных данных, чтобы переключиться в численное представление значений переменных в таблице.
Напомним, STATISTICA всегда обрабатывает данные в численном формате, однако для удобства пользователя можно ввести текстовые значения и установить взаимно однозначное соответствие между текстовыми и числовыми значениями переменных. Это очень удобно для представления и ввода данных и интерпретации результатов. Например, вместо того чтобы вводить значение ALWAYS, можно вводить значение 1, вместо SOMETIMES — 3 и т. д.
Таблицы частот
Из стартовой панели Основные статистики и таблицы выберите процедуру
Таблицы частот, чтобы открыть диалоговое окно
Таблицы частот. В этом окне щелкните по кнопке Переменные и выберите первые три переменные. Диалоговое окно
Таблицы частот появится на экране в следующем виде:
Это диалоговое окно предлагает множество настроек, позволяющих изменять вид и группировку в таблицах частот, а также проверять нормальность распределения, в том числе и графическими способами. В этом примере используется принятый по умолчанию метод группировки (в частности, Все различные значения, с текстовыми значениями) и опции отображения (Кумулятивные частоты, Проценты (относительные частоты), Кумулятивные проценты, 100% минус кумулятивные проценты, логит-преобразование, пробит-преобразование), как показано в диалоговом окне выше.
Как можно видеть, 99% респондентов отметили, что они всегда
интересуются результатами футбольных
матчей , 55% — обычно и т. д. Всего 81% респондентов попали в категории всегда — always, обычно — usually, иногда — sometimes и только
19% сказали никогда — never.
Большинство результатов в электронной таблице результатов понятно исходя из здравого смысла. Разъясним, что такое логит и пробит значения. Это специальные преобразования частот, которые часто используются на практике.
Логит — это преобразование вида: ln(х/(1-х)), тех — относительная частота (процент), наблюдаемая в ячейке.
Пробит переменной х — это стандартное нормализующее преобразование переменной х. Пробит относительных частот — это обратное нормальное преобразование, примененное к относительным частотам в ячейках. Итак, с помощью пробит-преобразования из частот получаются величины, имеющие нормальное распределение. Такое преобразование применяется в медицинских исследованиях типа «доза — эффект».
Имея вероятностный калькулятор STATISTICA, можно легко понять идею этого преобразования (см. также главу Вероятностные распределения).
Посмотрите на таблицу результатов. Например, в первой строке таблицы имеется частота 19 (относительная частота 0,19). Вычислим ее пробит.
Откройте вероятностный калькулятор. Выберите в списке распределений нормальное распределение. Далее отметьте опцию
Обратная функция распределения и введите в поле
р относительную частоту 0,19. Нажмите кнопку
Вычислить. В поле Z вы увидите пробит введенной частоты, он равен — 0,877896.
Точно такое же значение приведено в электронной таблице для соответствующей частоты.
Построение гистограмм. Визуализируем таблицы, построив на их базе гистограммы. Заметим, что можно без труда построить гистограммы всех выбранных переменных, если вернуться обратно в диалоговое окно
Таблицы частот и нажать кнопку Гистограммы. Каскад гистограмм, по одной гистограмме для каждой выбранной переменной, мгновенно появится на экране.
В системе STATISTICA можно распечатать (или сохранить в файле) результаты анализа либо автоматически (когда содержимое каждой выводимой на экран таблицы результатов одновременно направляется на принтер и/или вОкно текста/вывода), либо вручную (когда пользователь сам выбирает какую таблицу результатов или часть какой таблицы результатов распечатать). Перед тем как распечатать результаты анализа, программа попросит вас уточнить направление вывода (то есть Текст, файл, Принтер, Нет, и/или Окно) в окне Параметры страницы/вывода (выберите установкуПараметры страницы/вывода
в выпадающем меню Файл, настройку Принтер в выпадающем меню
Сервис или дважды щелкните на поле Вывод строки состояния).
В этом окне можно также определить дополнительную информацию для печати вместе с таблицей результатов. Доступны следующие формы выводимого отчета: Минимальный, Краткий, Средний или Полный.
Если в окнеПараметры страницы/вывода была выбрана настройка
Авт. печать всех таблиц результатов (автоотчет), то дополнительная информация (количество которой определяется установленным в этом же окне форматом отчета), а также все результаты анализа будут автоматически выведены на принтер или в файл (в зависимости от того, выбрана ли установка
Окно в левой верхней части этого диалогового окна). Этот режим печати полезен, если вы хотите получить полную сводку всех результатов, выведенных на экран в процессе анализа.
Графические процедуры. Практически все результаты могут быть отображены на графиках с помощью графических процедур, доступных в данном окне. Прежде всего щелкните по кнопке
Диаграмма размаха для всех переменных, в появившемся диалоговом окне выберите
Средние/ст.ош./ст.откл. и затем нажмите ОК, чтобы построить график.
Печать графиков в пакетном режиме. Если в диалоговом окне Параметры страницы/вывода выбрана установка Автоматически печатать все графики, STATISTICA автоматически направит создаваемые графики или на печать, или в окно вывода (или сохранит в файле вывода, если выбрана
Печать в файл в диалоговом окне Печать графика).
Пример 2. Таблицы флагов и заголовков
Таблицы флагов и заголовков являются экономным способом представления нескольких двухвходовых (двухмерных) таблиц в одной. Работая с данными, нам интересно узнать, имеют те же самые респонденты, которые проявили наивысший интерес к бизнесу, также наивысший интерес к новостям в Интернет.
Описание анализа
Используемый файл данных SPORTS.sta описан в предыдущем примере. Из стартовой панели Основные статистики и таблицы выберите процедуру Таблицы и заголовки и откройте диалоговое окно
Задайте таблицы.
Таблица флагов и заголовков по существу содержит несколько двухмерных таблиц, собранных вместе. Лучший способ понять эти таблицы — рассмотреть конкретный пример. В диалоговом окне Задайте таблицы нажмите кнопку
Задать таблицы под заголовком Таблицы флагов и заголовков. Программа запросит ввод переменных для таблицы.
Теперь диалоговое окно Задайте таблицы будет выглядеть следующим образом:
Нажмите ОК в этом диалоговом окне, чтобы открыть диалоговое окно
Результаты кросстабуляции.
В этом диалоговом окне нажмите кнопкуТаблица флагов и заголовков, чтобы отобразить таблиц}7результатов.
Вы можете рассматривать построенную таблицу как объединение нескольких двухвходовых таблиц. Например, в четырех начальных строках таблицы показаны частоты двухмерной таблицы
FOOTBALL — TRACK. Другой способ состоит в том, что значения в четырех начальных строках и четырех начальных столбцах таблицы рассматриваются как совместное распределение 100 респондентов в 4*4=16 ячейках, созданных пересечением интереса к футболу с интересом к бейсболу. Теперь рассмотрим различные способы представления результатов.
Частоты по строке. По умолчанию таблица флагов и заголовков отображает частоты в строке. Таким образом, видно, например, что
7 (из 100) респондентов всегда интересуются
FOOTBALL и всегда интересуются TRACK. Посмотрите на четвертую строку таблицы, вы увидите, что из тех респондентов, которые никогда не интересуется
FOOTBALL, 13 {3+1+9} интересуются TRACK всегда — always (3), обычно — usually
(1) или иногда — sometimes (9).
Проценты. Снова вернемся в диалоговое окно Результаты кросстабуляции. Диалоговое окно содержит настройки, позволяющие выразить результаты в процентах. Проценты могут быть вычислены относительно общего числа наблюдений в строке, относительно общего числа наблюдений в столбце или относительно общего числа наблюдений.
Вы также можете включить в таблицу ожидаемые и/или остаточные частоты (разность наблюдаемых и ожидаемых частот). Выберите настройку Проценты по строке и снова нажмите кнопку Таблица флагов и заголовков.
После того как выбрана настройка Проценты по строке, станет доступна настройка
Отображать выбранные % в отдельных таблицах. Так как в одной таблице может быть слишком много информации, выбор этой настройки помещает проценты в отдельную таблицу результатов. Мы рассмотрим общую таблицу.
Из таблицы результатов следует, что из тех респондентов, которые всегда интересуются — always interested
FOOTBALL (все респонденты в первой строке), 17,95% также всегда интересуются — always interested
TRACK.
Поэтому FOOTBALL и TRACK тесно между собой связаны (в этих данных).
Так же можно найти темы, не связанные между собой.
Статистики
Рассмотрим некоторые из этих статистик, представленные в диалоговом окне Результаты кросстабуляции. Наиболее употребляемая статистика — хи-квадрат.
Мерой зависимости между переменными подобно коэффициенту корреляции г Пирсона является ранговая корреляция R Спирмена (см. главу Непараметрическая статистика, где систематически описаны ранговые корреляции). Эта мера предполагает, что значения переменных содержат, по крайней мере, ранжированную информацию. Такое предположение разумно в данном примере, так как ответы респондентов упорядочены по степени интереса.
Выберите опцию Корреляция Спирмена. Диалоговое окно
Результаты кросстабуляции примет следующий вид:
После того как выбраны Статистики, нажмите кнопку
Подробные двухвходовые таблицы для того, чтобы выбрать таблицы для анализа.
На экране появится диалоговое окно Выбор таблиц для просмотра, в котором приводится список всех двухмерных таблиц:
Можно воспользоваться параметром Все таблицы, чтобы построить каскад двухвходовых таблиц.
В данном примере выберите таблицу FOOTBALL —
TRACK и нажмите
ОК. Для каждой выбранной таблицы будут построены две таблицы результатов.
Первая содержит наблюдаемые частоты и все остальные характеристики, выбранные в поле Таблицы диалогового окна
Результаты кросстабуляции (в частности, Проценты от общего числа).
Вторая таблица содержит результаты хи-квадрат и корреляции Спирмена.
Значение статистики хи-квадрат для этой таблицы равно
9, что является низкозначимым. FOOTBALL и TRACK являются
независимыми. Степень зависимости дает R Спирмена, равная
0,08.
В дополнение к этим методам вы можете построить графики, нажав кнопкуГрафики взаимодействий для
частот диалогового окна Результаты кросстабуляции
(из диалогового окна Результаты кросстабуляции), чтобы визуально исследовать частоты в выбранных двухмерных таблицах.
Пример 3. Таблицы сопряженности
Для углубленного анализа результатов опроса (см. предыдущий пример) рассмотрим некоторые таблицы более высокого порядка. В частности, определим процент респондентов, являющихся «фанатами
спорта».
Иными словами, найдем число тех респондентов, которые всегда интересуются — always interested
и FOOTBALL, и TRACK, и BASEBALL в Интернет.
Задание анализа
В стартовой панели модуля Основные статистики и таблицы
выберите процедуру Таблицы и заголовки. Для определения таблицы нажмите на кнопку
Задать таблицы в разделе Многовходовые таблицы сопряженности диалогового окна
Задайте таблицы. Откроется стандартное окно выбора переменных.
В открывшемся окне выбора переменных выберите группирующие переменные (можно выбрать до шести списков группирующих переменных).
Вы можете выбрать одну и более переменных в каждом из шести списков, чтобы создать таблицы со многими входами. Теперь диалоговое окно
Задайте таблицы будет выглядеть следующим образом:
Нажмите ОК в диалоговом окне Задайте таблицы, после этого откроется диалоговое окно
Результаты кросстабуляции.
Это то же диалоговое окно, что и в примере с таблицами флагов и заголовков, единственное отличие — неактивна кнопка
Таблицы флагов и заголовков.
Выберите еще раз параметры таблицы (например, Проценты по строке, Проценты от общего числа и т. д.) и статистики (например, Хи-квадрат, корреляции и т. д.), нажав либо кнопку Просмотреть итоговые таблицы, либо кнопку Подробные двухвходовые таблицы.
В любом случае на экране появится промежуточное диалоговое окно, в котором можно выбрать таблицу из уже выбранных. Если использована команда Все таблицы, то каскад таблиц результатов будет построен для каждой таблицы, показанной в этом диалоговом окне.
Для Примера 3 процедура Подробные двухвходовые таблицы дает следующую таблицу:
Как можно заметить, 7 респондентов из 100 сообщили, что они всегда интересуются — always interested
football, track.
Развитие этого примера очевидно. Например, в маркетинговых исследованиях таким образом можно находить группы клиентов, которые всегда покупают определенный набор продуктов.
«Работая руками», перебирая множество вариантов, вы добиваетесь четкого представления данных и открываете нетривиальные связи.
Пример 4. Табулирование многомерных откликов и дихотомий
Пример показывает, как обращаться с многомерными откликами и дихотомиями, часто возникающими в массовых опросах, а также какие возможности для анализа этих переменных имеются в модуле Основные статистики и таблицы. При проведении массовых опросов имеется своя кухня, с некоторыми рецептами которой мы сейчас познакомимся. Пример с результатами гипотетического опроса находится в папке Примеры.
На основе рассматриваемых данных покажем, как табулируются следующие типы переменных:
- простые группирующие переменные;
- переменные с многомерными откликами;
- многомерные дихотомии.
Термин многомерный отклик на сленге анализа данных означает многомерный ответ, то есть ответ, содержащий в себе несколько ответов (а не один вариант ответа), например, респонденту, возможно, нравится, несколько типов машин, а не одна машина, или несколько фильмов, а не один из числа предложенных, несколько развлекательных сайтов, а не один и т. д. Для того чтобы не заключать отвечающих в жесткие рамки, при проведении опроса может допускаться несколько ответов. Число их заранее оговаривается.
Дихотомия (от греческого- разделять или рассекать на две части) — это переменная, принимающая два значения, 0 или 1, а в текстовом виде — нет или да. Соответственно многомерная дихотомия представляет собой набор нулей и единиц.
Вначале расскажем, как строятся простые таблицы частот для описанных переменных, затем построим и исследуем таблицы сопряженности для них.
Описание файла данных
Представьте, что проводится исследование покупательских предпочтений молодых людей. Задаются следующие вопросы: 1) какую систему быстрого питания вы предпочитаете; 2) какой тип автомобиля вы предпочитаете; 3) какой местный ресторан вы посещали в течение последних двух недель. Дополнительно записывается пол респондента. Эти ответы записаны в файл Fastfood.sta, переменные которого описаны ниже.
Пол (простая группирующая переменная). Пол респондента записывается в группирующую переменную Пол — Gender (Мужчина — Male, Женщина — Female).
Лучшая «быстрая» еда (многомерный отклик). Вопросник, используемый в данном исследовании, предлагает респондентам выбрать любимое «быстрое» блюдо (до трех блюд) из следующего списка:
1) Гамбургер — Hamburger
2) Сэндвич — Sandwiches
3) Цыплёнок — Chicken
4) Пицца — Pizza
5) Мексиканские блюда — Mexican fast-food
6) Китайские блюда — Chinese fast-food
7) Еда из морепродуктов — Seafood
Другие национальные блюда — other ethnic or regionally popular fast-food
У каждого человека может быть несколько любимых блюд. Поэтому выбор каждого респондента вводится в файл как переменная с многомерными значениями. Например, первый пункт ответа записывается в столбец Еда_1 — Food_1 (первое предпочтение), второй пункт (если он имеется) — в переменную Еда_2 — Food_2 и третий — в переменную Еда_3 — Food_3. Таким образом, в данном опросе мы имеем одну переменную, принимающую три значения.
При анализе переменная Еда_1 — Food_1 может рассматриваться как простая группирующая переменная. Далее можно задать вопрос: какое число респондентов (или их доля) назвало определенный тип системы быстрого питания своим любимым — favorite? Однако интерес может представлять также и то, сколько респондентов выбрали определенную систему быстрого питания как одну из любимых. Такой вопрос приводит нас к тому, чтобы рассматривать переменные Еда_1 — Еда_3 (Food_1 — Food_3) как одну переменную с многомерным откликом. Такие переменные можно называть также многомерными.
Любимый автомобиль (переменная с многомерными откликами). В этом опросе вас просят назвать три самых любимых типа автомашины (фактор денег, стоимость машины, не учитывается, просто спрашивается о некотором идеальном воображаемом автомобиле). Эти ответы (определенные марки и модели) закодированы следующим образом:
1) Отечественный спортивный автомобиль — Domestic sports car
2) Отечественный седан (закрытый автомобиль) — Domestic sedan
3) Иностранная спортивная машина — Foreign sports car
4) Иностранный седан — Foreign sedan.
Данная переменная рассматривается как переменная с многомерными откликами подобно переменной любимая система быстрого питания — favorite fast-food. Это означает, что ответы респондентов были введены как значения переменных Машина _1 — Машина_3 (Саг_1 — Саг_3).
Например, если респондент называл три любимых блюда Гамбургер — Hamburger, Гамбургер — Hamburger и Гамбургер — Hamburger, тогда значение Гамбургер —
Hamburger, будет учитываться только один раз (в переменную Еда_1 — Food_1), а соответствующие ячейки переменных Еда_2 — Food_2nEda_3 — Food_3 рассматривались как пустые.
Рестораны (многомерная дихотомия). Посетителей ресторана попросили назвать, какие из четырех ресторанов они посещали за последние две недели. Полученные данные были введены в файл так, что для каждого ресторана имелась своя переменная. Всего использовано четыре переменные Хозяин_1 — Хозяин _4 (Burger_1 — Burger_4) для следующих ресторанов:
1) Бутерброд Мейстер — Burger Meister
2) Лучшие бутерброды у Билла — Bill’s Best Burgers
3) Гамбургер «Блаженство» — Hamburger Heaven
4) Большой бутерброд — Bigger Burger
Если респондент сообщил, что в течение двух недель обедал в одном или нескольких ресторанах, то в соответствующий столбец (столбцы) ставилась единица, если нет, столбец оставался пустым. Таким образом, переменная представляет собой многомерную дихотомию (со значениями Да или пропуск), которую желательно табулировать, то есть указать число (или долю) респондентов, обедавших в каждом из четырех ресторанов.
Заметьте, что можно было бы рассмотреть эту переменную как переменную с многомерными откликами. Однако для этого нужно создать не менее четырех переменных, например, Еда_1 — Еда_4 (Eat_1 — Eat_4), и затем ввести названия ресторанов, например, Бургер_1 — Burger_1, Бургер_2 — Burger_2…, как значения этих переменных в столбцы таблицы (аналогично переменным любимая машина — favorite car и любимая система быстрого питания — favorite fast-food, см. выше).
Ниже представлены несколько первых наблюдений файла данных Fastfood.sta.

Для того чтобы показать, каким образом каждый опрашиваемый респондент введен в файл, посмотрите на первое наблюдение. Первый респондент — женщина, поэтому в переменную Пол — Gender введено значение Женщина — Female. Самое любимое быстро приготовленное блюдо — Пицца — Pizza (введено в переменную Еда_1 — Food_1), второе по предпочтению блюдо — Еда из морепродуктов — Seafood (введено в переменную Еда_2 — Food_2), третий вид еды не указан, поэтому в переменной Еда_3 — Food_3 стоит пропуск.
Далее этот респондент выбрал следующие три типа автомобилей: 1) домашний седан — domestic sedan, 2) домашний спортивный автомобиль — domestic sports car, 3) снова домашний спортивный автомобиль — domestic sports — переменные Саг_1, Саг_2, Саг_3, — Саг_1, Саг_2, Саг_3 соответственно. Наконец, он ответил, что последние две недели обедал в двух ресторанах Burger_1 (Burger Meister) и Burger_3 (Hamburger Heaven), таким образом Да — Yes было записано в ячейках соответствующих переменных, значения двух других переменных Burger остались пустыми.
Всего было опрошено 200 респондентов.
Начнем с вычисления таблиц частот для простой группирующей переменной Пол — Gender и переменных с многомерными откликами. Так как имеются пропущенные значения во всех переменных Burger_1 — Burger_4, таблица для них будет определена позже.
По умолчанию наблюдения со всеми пропусками в переменных Burger исключаются из анализа, и частоты будут вычисляться лишь для респондентов, посетивших, по крайней мере, один из четырех ресторанов. Другой способ обработки пропусков состоит в том, чтобы сделать отметку в поле
Включить ПД как дополнительную категорию для каждого фактора.
Выберите Таблицы и заголовки в стартовой панели. В появившемся окне
Задайте таблицы выберите Таблицы для многомерных откликов в списке
Анализ, при этом откроется диалоговое окно
Таблицы многомерных откликов. В этом окне можно определить три типа группирующих переменных: простые группирующие переменные (Пол — Gender в нашем примере), переменные с многомерными откликами (Еда_1 — Food_1 (Еда_3 — Food_3)wmMauiuHa_1 — Саг_1 (Маишна_3 — Саг_3)) и многомерные дихотомии (Burger_1 — 4).
Нажмите кнопкуЗадать таблицы для того, чтобы определить переменные в диалоговом окне:
В окне можно выбрать до шести многомерных факторов (простых группирующих переменных, многомерных откликов или дихотомий) для одной таблицы. В первой колонке выберите только переменную Пол — Gender, программа автоматически рассматривает единственную выбранную переменную как простую группирующую (простая группирующая является частным случаем переменной с многомерными откликами, для нее число откликов равно 1). Во второй колонке выберите переменные Еда_1 — Еда_3 (Food_1 — Food_3), в третьей — Машина_1 — Машина_3 (Саг_1 — Саг_3). Сначала обратите внимание на простые таблицы частот для всех выбранных факторов (таблица частот для Burger_ 1 —
Burger_4 будет исследована позже). Нажмите ОК, чтобы завершить выбор. Теперь в окне Таблицы многомерных откликов можно видеть выбранные переменные.
Термин фактор используется для общего обозначения всех типов переменных (например, такая переменная, как любимая еда — food preference, в действительности состоит из нескольких переменных). Мы употребляем термин многомерный фактор и для простых переменных, и для переменных с многомерными откликами, и для многомерных дихотомий. Заметим, что по умолчанию фактору присваивается имя (как длинное, так и короткое) первой переменной в соответствующем списке.
Определение факторов. Расположенная рядом с каждым фактором опция позволяет определить его тип. Первая переменная Пол — Gender — это простая группирующая переменная. Для второго и третьего факторов выберите опцию
Многомерный отклик.
Далее выберите коды для определения различных категорий. Выберите коды, чтобы идентифицировать пол респондента Мужчина — Male и Женщина — Female (переменная Пол — Gender), а также различные типы «быстрой» еды в переменных Еда_ 1 — Еда_3 (Food_1 — Food_3) и различные типы автомобилей в Машина_1 — Машина_3 (CarJ — CarJ).
Если вы не зададите коды явно (просто нажмете
OK, программа возьмет их из первой переменной в каждом факторе. Данный способ обычно позволяет определить все коды, однако может случиться так, что определенный код не присутствует в первой переменной, а присутствует только во второй или в третьей. В этом случае способ по умолчанию не применим, т. к. ряд значений окажутся неучтенными.
Лучше задать все используемые коды точно. После нажатия одной из кнопок
Коды, расположенной рядом с каждым фактором, можно ввести коды для фактора.
В данном примере не так интересно знать, все ли три выбранные машины были определенного типа (в связи с чем чрезмерно увеличивается число идентичных откликов). Интереснее определить число респондентов, предпочитающих, например, домашнюю закрытую машину. Заметим, что переменные, составляющие фактор Еда — Food, содержат только взаимно исключающие ответы (непересекающиеся категории), т. к. респондентам не разрешалось давать идентичные ответы (например, Гамбургер — Hamburger, Гамбургер — HamburgerриГамбургер — Hamburger). Их просили сделать выбор из восьми типов быстрой еды без повторения. Поэтому для фактора Еда — Food данная опция не имеет значения.
Нажмите ОК в диалоговом окне Таблицы многомерных откликов, чтобы начать анализ и открыть окно Результаты таблицы многомерных откликов.
Вначале рассмотрим простой вывод Таблицы частот.
Введите в редактируемое поле Выделить частоты число 100 (что приведет к тому, что все частоты больше 100 будут выделены в таблице результатов). Затем нажмите кнопку
Таблицы частот.
Таблица частот для переменной Пол — Gender интерпретируется обычным образом, и на ней мы останавливаться не будем. Таблицы частот для других двух факторов показаны ниже.

Всего в исследовании было опрошено 200 респондентов (число опрошенных N=200 отображается в верхнем левом углу таблицы).
Столбец Частота показывает число респондентов, назвавших данный способ питания как один из любимых. Напомним, что учитываются только уникальные ответы (см. выше) и, таким образом, ответ каждого респондента может быть посчитан только один раз в этом столбце. Отсюда вы можете прийти к заключению, что Пицца — Pizza была самой популярной системой быстрого питания, указанной либо в первой, либо во второй, либо в третьей позиции 138 респондентами, Гамбургер — Hamburger был вторым по популярности (114). Все типы систем быстрого питания отметили только 40-50 респондентов.
Во втором столбце таблицы результатов вычислены относительные частоты, соответствующие числам первого столбца. Можно сказать, например, что 26,44% (100*138/522) всех указанных в ответах предпочтений составляет Пицца — Pizza. В отличие от этой колонки третья колонка таблицы показывает проценты респондентов, отметивших соответствующий тип еды как первый, второй или третий. Пиццу — Pizza как лучшую систему быстрого питания выбрали 69% (100* 138/200) всех респондентов.
Аналогично рассматривается таблица частот для фактора Машина —
Саr. Иностранные спортивные машины отмечены 157 респондентами на одной из трех позиций (учитываются только различные ответы); отечественные спортивные машины отмечены 123 респондентами. Вторая колонка показывает 37,38% ответов для иностранных спортивных машин; эти числа не так легко проинтерпретировать, т. к. подсчитывались только различные ответы (несколько одинаковых ответов рассматривались как один). Таким образом, если респондент указал в анкете три иностранные спортивные машины, то этот ответ учтен только один раз. Числа в третьей колонке (Процент набл.) более информативны; из них, например, видно, что 78,5% всех респондентов назвали иностранные спортивные машины в числе трех самых любимых.
Возвратимся в диалоговое окно Таблицы многомерных откликов (нажмите
Отмена в окне Результаты), чтобы задать многомерную дихотомию в обследовании посетителей ресторанов. Нажмите кнопкуЗадать таблицы, отмените предыдущий выбор и выберите Burger_1 — Burger_4 как переменные первого множества.
Далее установите опцию Многомерная дихотомия
рядом с первым фактором в диалоговом окне Таблицы многомерных откликов. Как и ранее, можете использовать опцию
Длинные метки факторов для того, чтобы ввести подходящее имя фактора. Например, можно назвать этот фактор Patron: Recently patronized restaurants — Хозяин: Недавно посещенные рестораны.
Вам также необходимо задать код, который использовался в факторе многомерной дихотомии Patron для того, чтобы определить, обедал или нет респондент в соответствующем ресторане в течение двух недель перед опросом. Задайте нужный код в поле Счетчик ниже списка факторов. Так как код, равный 1 (числовой эквивалент значения Да — Yes; см. Управление данными, глава 7), использовался для того, чтобы определить, какой ресторан посещался респондентом, то можно просто принять код, предложенный по умолчанию.
Напомним, каким образом многомерные дихотомии интерпретируются программой. Переменные, из которых построен фактор, рассматриваются как его уровни, затем подсчитывается число уровней со значениями, равными значению, указанному в счетчике. Все значения, не равные этому значению, игнорируются. Вы можете строить более «сложные» схемы кодирования (а не просто 1 -0, как в этом примере), задавая подходящие значения в поле
Счетчик.
Например, можно использовать отдельный код (отличный от 1) для обозначения ответа: «даже никогда не думал там обедать». Вы могли бы ввести код 2 в переменные Burger_1 — Burger_4 для обозначения таких резко отрицательных ответов в отношении определенных ресторанов, задать этот код в поле
Счетчик и табулировать ответы. Таким образом, задавая различные значения для кодов многомерной дихотомии, можно идентифицировать взаимоисключающие ответы.
Из диалогового окна Результаты снова выберите процедуру
Таблицы частот. Интерпретация чисел, представленных в этой таблице, аналогична таблицам для многомерных откликов.
Всего 157 респондентов обедали в одном из четырех ресторанов (n = 157); 60 респондентов обедали в Burger Meister, 68 — в Bill’s Best Burgers и т. д. Значения во второй колонке (Процент откликов) выражают эти числа в процентах от общего числа респондентов, обедавших хотя бы в одном ресторане (то есть от 157 респондентов).
Предполагается, что четыре (воображаемых) ресторана делят рынок быстрого питания в городе и что 157 респондентов (из 200) в большей или меньшей степени представляют мнение общего рынка. Поэтому значения во второй колонке таблицы показывают долю рынка, которым владеет каждый ресторан.
Например, из всех мест (где подаются гамбургеры), которые посещались респондентами в течение двух недель до опроса, Burger Meister посещали 24,19%, Bill’s Best Burger — 27,42% и т. д. Третья колонка (Процент набл.) содержит процент респондентов, обедавших последние две недели в соответствующих ресторанах.
Напомним, что проценты вычислены для n = 157, то есть относительно числа респондентов, обедавших, по крайней мере, в одном из четырех ресторанов. Поэтому можно сказать, что 38,22% респондентов, обедавших в каком-то одном из четырех ресторанов, где подают гамбургеры, обедали также в Burger Meister — 43,31%, обедали в Bill’s Best Burger и т. д.
Заметим, что можно легко построить линейные графики или гистограммы частот и процентов с помощью процедур меню
Пользовательские графики.
Покажем, как строить таблицы сопряженности для переменных с многомерными откликами и многомерных дихотомий. Нажмите
Отмена в диалоговом окне Результаты для того, чтобы вернуться в диалоговое окно
Таблицы многомерных откликов. Прежде всего, посмотрим на таблицу сопряженности Пол — Gender и Машина — Саг. Иными словами, исследуем интерес к различным типам машин у Мужчин — Males и Женщин — Females. Нажмите кнопку
Задать таблицы и в открывшемся диалоговом окне выберите Пол — Gender как единственную переменную в первом множестве, а переменные Машина_1 — Машина_3 (Саr_1 —
Саr_3) как переменные во втором множестве.
Нажмите ОК и вернитесь в диалоговое окноТаблицы многомерных откликов. Задайте далее коды для фактора Машина —
Саr, чтобы идентифицировать четыре различных типа автомобилей. Возможно, вы захотите изменить описание фактора, тогда воспользуйтесь кнопкой
Длинные метки факторов.
Для этой таблицы отмените опциюСчитать только уникальные отклики.
Напомним, что назначение этой опции — исключить одинаковые ответы (одинаковые ответы одного и того же респондента на разные пункты считаются как один ответ). В данном примере, напротив, вы можете захотеть включить такие ответы в таблицу. Получившаяся таблица сопряженности будет показывать общее число различных типов машин, определенных респондентом как первая, либо как вторая, либо как третья, разбитых на классы значениями переменной Пол — Gender. Нажмите
ОК и откройте диалоговое окно Результаты таблицы многомерных откликов.
Нажмите кнопку Просмотреть итоговые таблицы. В результате будет построена следующая таблица:
По умолчанию Быстрым статистическим графиком для этой таблицы является ЗМ гистограмма. Нажмите правую кнопку мыши и выберите в меню опцию
ЗМ гистограмма.
Рассмотрев приведенную выше таблицу, можно прийти к выводу, что и мужчины, и женщины отмечали спортивные машины чаще, чем седаны. Разницу в общем числе Уашин, отмеченных мужчинами и женщинами, можно объяснить тем, что число мужчин и женщин в выборке существенно различается (если вы посмотрите на таблицу частот переменной Пол — Gender, то увидите, что в выборке присутствует только 36 женщин).
Вместо ЗМ гистограммы можно использовать линейный график. Вернитесь в диалоговое окно результатов и выберите опцию
Графики взаимодействий частот.
Здесь разница в предпочтении спортивных машин более отчетлива у мужчин, чем у женщин (линия, соответствующая женщинам, более сглаженная, чем линия мужчин).
Пример (анализ продаж)
Рассмотрим данные о продажах в магазине. Мы хотим провести разведочный анализ этих данных и построить модель покупателя.
Категоризируем исходные данные (способ категоризации количественных переменных в системе STATISTICA описан выше).
В этом файле первая переменная — день недели, каждая оставшаяся переменная принимает два значения: 0, если данный покупатель не купил данный товар, и 1, если данный покупатель купил данный товар. Покупатели записаны в строках, товары в столбцах.
Для данного покупателя 1 означает, что он купил соответствующий товар.
Мы хотели построить модель покупателя. Для этого нам нужно знать, как распределены покупки и как они связаны между собой.
Работаем в модуле Основные статистики. Введите показанные данные в свой файл пли сгенерируйте нечто похожее, чтобы повторить действия.
Несколько тонких вопросов будут отмечены в ходе анализа и указаны альтернативные способы исследования.
Распределение числа покупок. Вначале введем переменную (в наших данных это будет переменная var24), подсчитывающую общее число покупок, сделанных покупателем (она равна сумме всех индикаторов покупок).
Вначале посмотрим, как распределено число покупок. Откройте процедуры описательной статистики.
Выберите все переменные, в которых записаны покупки различных
продуктов и нажмите кнопку Подробные описательные статистики
. На экране появится таблица с описательными статистиками.
Таблица с описательными статистиками имеет вид:
В этой таблице для нас прежде всего интересен второй столбец, в котором показано, как часто покупались различные продукты. Но вначале построим гистограмму числа покупок N.
Из гистограммы видно, что наибольшее число покупателей делает от одной до четырех покупок.
Редактор данных графика позволяет просмотреть данные графика в численном виде. Нажмите кнопку
Редактор данных графика, и вы увидите данные в численном виде.
Итак, общее число покупателей равно 674. Из них 90 сделали одну покупку, 110 сделали 2 покупки, 110 сделали 3 покупки, 102 сделали 4 покупки и т. д.
Случай одной покупки. Рассмотрим покупателей, сделавших только одну покупку. Для этого введем условие выбора наблюдений.
Группировка по дням недели. Рассмотрим, как распределены покупатели, сделавшие одну покупку, по дням недели. Выберите переменную День и постройте гистограмму.
Из гистограммы следует, что наиболее часто единичные покупки делаются в среду.
Какие продукты наиболее часто относятся к одиночным покупкам?
Найдем, какие продукты наиболее часто являются «одиночными». Выберем все переменные из файла, кроме первой. Вычислим средние величины.
Из таблицы следует, что если покупатель сделалтолько одну
покупку, то, скорее всего, это было мясо, хлеб, овощи, кондитерские изделия или колбасы. Вероятность сделать одиночную покупку из оставшейся части списка практическая нулевая.
Заметьте, что средние, приведенные во втором столбце таблицы с результатами, представляют собой оценки вероятностей покупки данного товара.
Таким образом, если покупатель пришел в магазин и решил сделать только одну покупку, то с вероятностью 0,26 он купит мясо, с вероятностью 0,133 купит хлеб, с вероятностью 0,11 купит овощи, с вероятностью 0,11 купит кондитерские изделия, с вероятностью 0,9 купит колбасные изделия.
Вероятность того, что покупатель сделает только 1 покупку, равна90/677= 0,13 (см. таблицу с распределением N).
Модель покупателя, делающего одну покупку. С вероятностью 0,13 покупатель, пришедший в магазин, делает одну покупку. С вероятностью 0,26 он покупает мясо, с вероятностью 0,133 — хлеб, с вероятностью 0,11 — овощи, с вероятностью 0,11 — кондитерские изделия, с вероятностью 0,9 — колбасные изделия.
Случай двух покупок. Рассмотрим покупателей, сделавших две покупки.
Число таких покупателей равно 110.
Для этих покупателей N=2. Изменим условие выбора случаев. Заметьте, в условии выбора наблюдений можно употреблять имя переменной, что и было сделано в данном случае.
Вычислим описательные статистики при условии, что
N=2.
Из этой таблицы видно, что если покупатель сделал две покупки, то наиболее вероятно, что в эти покупки вошли овощи, хлеб, молоко, кондитерские изделия, колбасы, мясо.
Поставим вопрос, какие пары покупок наиболее вероятны.
Ответ на этот вопрос можно получить с помощью простейших действий.
Всего переменных 22. Конечно, мы не будем перебирать все 22*21 = 462 пары переменных и строить для них таблицы.
С помощью некоторых разумных приемов, например, рассмотрев корреляции переменных, можно существенно сократить процедуру поиска.
За несколько минут можно найти наиболее вероятные пары покупок
.
Полезными здесь являются гамма-статистики, массив которых сразу для всех переменных можно вычислить с помощью непараметрических процедур (не забудьте при вычислении поставить условие N
= 2).
Просматривая таблицу и выбирая максимальные коэффициенты, можно определить наиболее вероятные парные покупки.
Так же можно определить несовместимые пары.
Вероятность того, что покупатель сделает две покупки, равна 110/677= 0,16 (см. таблицу с распределением N).
В принципе те же самые действия можно провести для остальных N, при этом полезно использовать язык STATISTICA BASIC.
Однако очевидно, здесь мы сталкиваемся с довольно сложной переборной задачей, поэтому наметим различные подходы к ее решению.
В частности, используем анализ соответствий и геометрическую интерпретацию частот.
Здесь же рассмотрим, какие дополнительно возможности имеются в модуле
Основные статистики и таблицы.
Случай трех и четырех покупок. Воспользуемся процедурами группировки. Не забудьте отменить условия выбора случаев, назначенные ранее.
В диалоге Группировка и однофакторная ANOVA прежде всего выберите переменные для анализа. Группирующие переменные — день и N. Все остальные переменные определите как зависимые.
Выберем коды для группирующих переменных, как показано ниже. Конечно, можно было бы выбрать все коды для N, но мы ограничимся тремя и четырьмя покупками как наиболее типичными.
Нажмите ОК и проанализируйте результаты.
Прежде всего нажмите кнопку Итоговая таблица средних.
На экране появится таблица средних, вычисленная для каждой группы данных. Всего имеются 14 групп: 7 дней недели, умноженные на 2 (мы задали два кода переменной N — группа покупателей, сделавших три покупки, и группа покупателей, сделавших четыре покупки).
Ориентироваться в этой таблице очень просто. Рассмотрим, например, переменную КОЛБАСЫ.
Вы видите, что в понедельник покупатель, сделавший три покупки, с вероятностью 0,25 покупает колбасу, а покупатель, сделавший четыре покупки, покупает ее с вероятностью 0,75.
Рассмотрев вероятности по строке, можно видеть, что в понедельник покупатель, сделавший три покупки (первая строка таблицы), скорее всего, купил хлеб, кондитерские изделия или молоко.
Связи между покупками. Рассмотрим таблицы сопряженности хлеб и колбаса при числе покупок, равном 3.
Значение гамма-статистики 0,38 говорит о наличии неярко выраженной связи между признаками.
После того как гипотеза о независимости отвергается с помощью критерия хи-квадрат или точного критерия Фишера, необходимо измерить силу связи признаков.
Одной из таких мер принято считать гамма-статистику.
- Если модуль меры больше 0,8, то мы имеем сильную связь табулированных переменных.
- Если модуль меры связи принимает значения от 0,3 до 0,8, то говорят о неярко выраженной связи.
- Меньшие значения модуля меры связи свидетельствуют об отсутствии связи. Как и во всех задачах, связанных с оценкой зависимости, здесь очень полезна визуализация.
Рассмотрим при трех покупках степень связи между переменными: хлеб и молоко.
Из приведенной таблицы следует, что при трех покупках из 55 человек, купивших хлеб, 21 купили молоко, 34 не купили молоко (вторая строка таблицы).
Из 55 человек, не купивших хлеб, 24 купили молоко, 31 не купили молоко.
С помощью критерия хи-квадрат проверим гипотезу о независимости табулированных переменных.
Критерий хи-квадрат не позволяет отвергнуть гипотезу о независимости. Как понимать это положение?
Рассмотрим внутренние ячейки таблицы с покупками хлеба и молока при трех сделанных покупках.
Из таблицы получим следующие оценки вероятностей (при условии трех покупок!). Вероятность того, что покупатель:
1) не купит ни молока, ни хлеба — 31/110 = 0,28;
2) не купит молоко, но купит хлеб — 24/110 = 0,22;
3) купит хлеб, не купит молоко — 34/110 = 0,31;
4) купит хлеб и молоко — 21/110 — 0,19.
Эти оценки получены из наблюдаемых частот.
Рассмотрим маргинальные частоты, эти частоты располагаются по краям таблицы и при гипотезе независимости позволяют оценить ожидаемые частоты.
Имеем (см. таблицу):
- Покупатель, пришедший в магазин и сделавший три покупки, с вероятностью 65/110 = 0,59 не купит молоко, а с вероятностью 45/110 = 0,41 купит молоко.
- Покупатель, пришедший в магазин и сделавший три покупки, с вероятностью 55/110 = 0,5 купит хлеб, с вероятностью 55/110 = 0,5 не купит хлеб.
Перемножая эти вероятности, получаем:
- 0,59 × 0,5 = 0,295 — вероятность того, что покупатель не купит ни молока, ни хлеба;
- 0,59×0,5 = 0,295 — вероятность того, что покупатель не купит молоко, но купит хлеб;
- 0,5 × 0,41 = 0,205 — вероятность того, что покупатель купит хлеб, но не купит молоко;
- 0,5× 0,41 = 0,205 — вероятность того, что покупатель купит хлеб и купит молоко.
Можно видеть, что эти вероятности очень близки к вероятностям, вычисленным ранее в 1-4.
Критерий хи-квадрат как раз и измеряет «расстояние» между этими частотами.
Итак, если покупатель делает три покупки, то покупка молока и покупка хлеба независимы.
Заметим, что продвинутый анализ покупателей, сделавших даже три покупки, связан с очевидными трудностями. В частности, не так просто найти группы товаров, наиболее вероятно объединяющиеся в тройки.
Далее мы применим к данным о продажах разведочные методы анализа соответствий (см. главу Анализ соответствий).








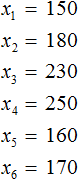
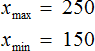
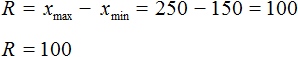






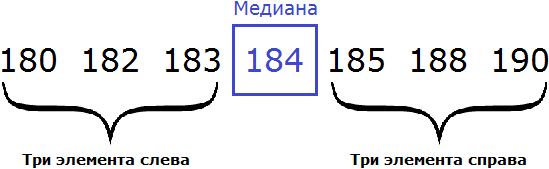



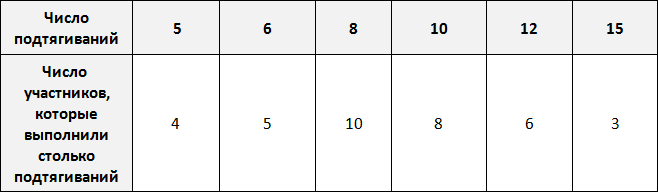







































































 Другие национальные блюда — other ethnic or regionally popular fast-food
Другие национальные блюда — other ethnic or regionally popular fast-food



















