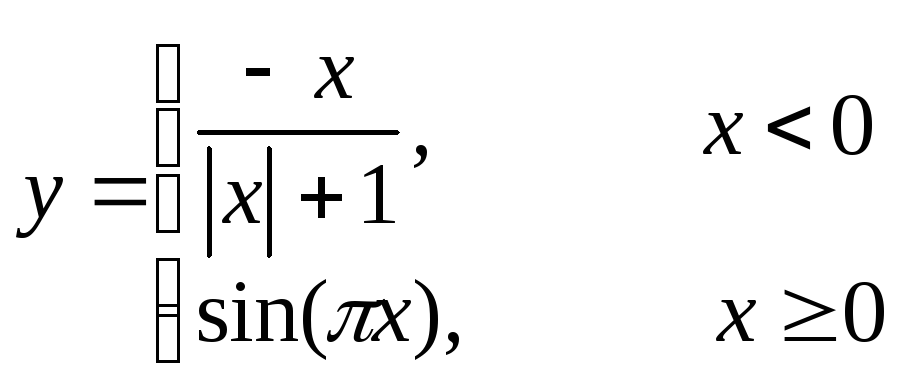Содержание статьи (кликните для открытия/закрытия)
- Построение графика линейной функции в Excel
- Подготовка расчетной таблицы
- Построение графика функции
- Построение графиков других функций
- Квадратичная функция y=ax2+bx+c
- Кубическая парабола y=ax3
- Гипербола y=k/x
- Построение тригонометрических функций sin(x) и cos(x)
Построение графика зависимости функции является характерной математической задачей. Все, кто хотя бы на уровне школы знаком с математикой, выполняли построение таких зависимостей на бумаге. В графике отображается изменение функции в зависимости от значения аргумента. Современные электронные приложения позволяют осуществить эту процедуру за несколько кликов мышью. Microsoft Excel поможет вам в построении точного графика для любой математической функции. Давайте разберем по шагам, как построить график функции в excel по её формуле
Построение графиков в Excel 2016 значительно улучшилось и стало еще проще чем в предыдущих версиях. Разберем пример построения графика линейной функции y=kx+b на небольшом интервале [-4;4].
Подготовка расчетной таблицы
В таблицу заносим имена постоянных k и b в нашей функции. Это необходимо для быстрого изменения графика без переделки расчетных формул.
Далее строим таблицу значений линейной функции:
- В ячейки A5 и A6 вводим соответственно обозначения аргумента и саму функцию. Запись в виде формулы будет использована в качестве названия диаграммы.
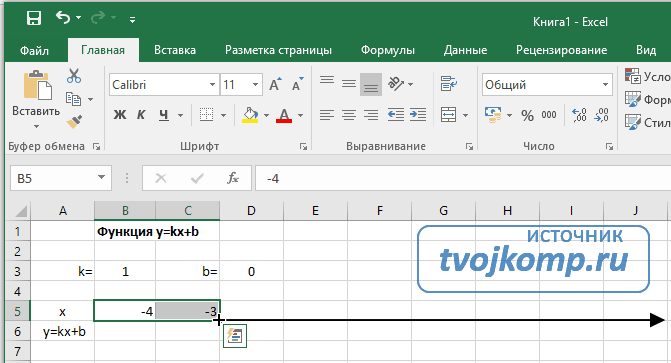
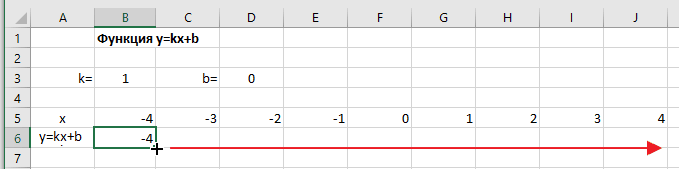
- Вводим в ячейки B5 и С5 два значения аргумента функции с заданным шагом (в нашем примере шаг равен единице).
- Выделяем эти ячейки.
- Наводим указатель мыши на нижний правый угол выделения. При появлении крестика (смотри рисунок выше), зажимаем левую кнопку мыши и протягиваем вправо до столбца J.
Ячейки автоматически будут заполнены числами, значения которых различаются заданным шагом.
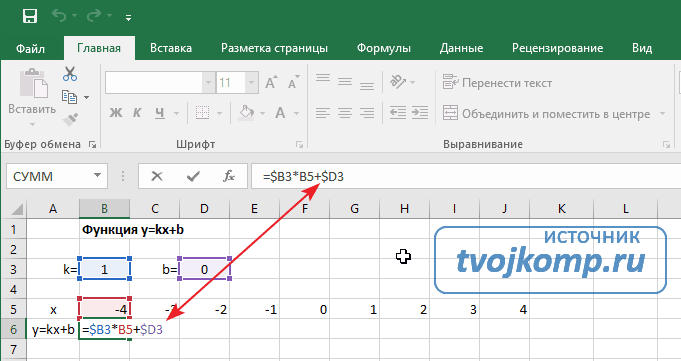
Далее в строку значений функции в ячейку B6 записываем формулу =$B3*B5+$D3
Внимание! Запись формулы начинается со знака равно(=). Адреса ячеек записываются на английской раскладке. Обратите внимание на абсолютные адреса со знаком доллара.
Чтобы завершить ввод формулы нажмите клавишу Enter или галочку слева от строки формул вверху над таблицей.
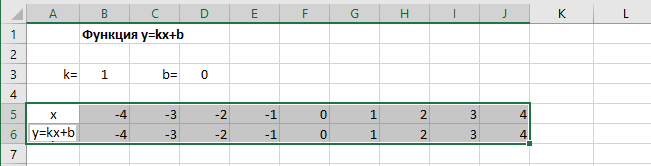
Копируем эту формулу для всех значений аргумента. Протягиваем вправо рамку от ячейки с формулой до столбца с конечными значениями аргумента функции.
Построение графика функции
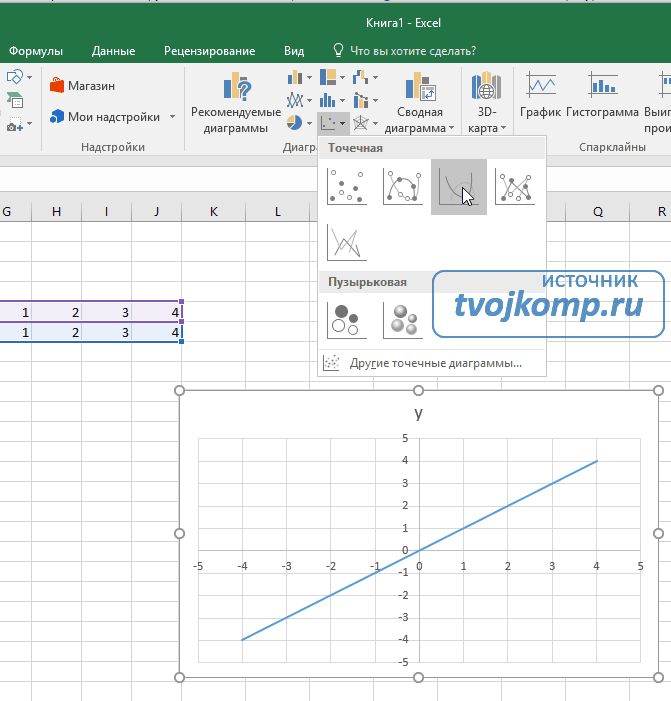
Выделяем прямоугольный диапазон ячеек A5:J6.
Переходим на вкладку Вставка в ленте инструментов. В разделе Диаграмма выбираем Точечная с гладкими кривыми (см. рисунок ниже).Получим диаграмму.
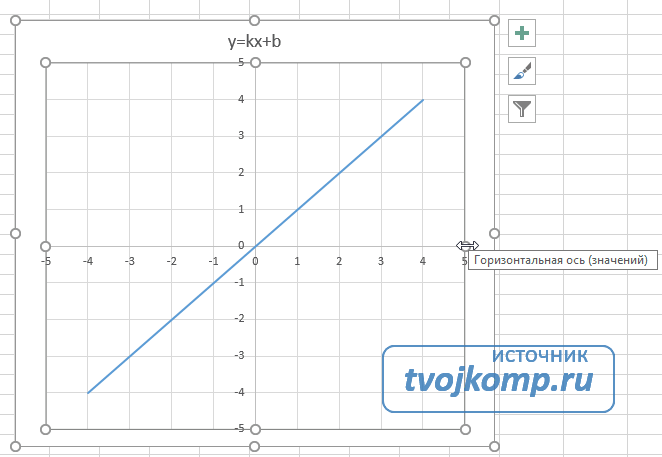
После построения координатная сетка имеет разные по длине единичные отрезки. Изменим ее перетягивая боковые маркеры до получения квадратных клеток.
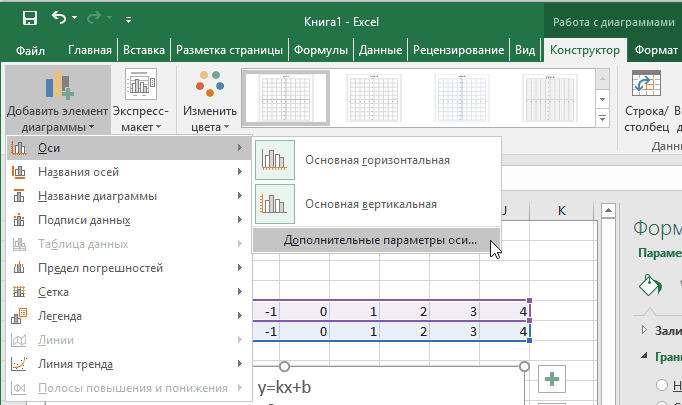
Теперь можно ввести новые значения постоянных k и b для изменения графика. И видим, что при попытке изменить коэффициент график остается неизменным, а меняются значения на оси. Исправляем. Кликните на диаграмме, чтобы ее активировать. Далее на ленте инструментов во вкладке Работа с диаграммами на вкладке Конструктор выбираем Добавить элемент диаграммы — Оси — Дополнительные параметры оси..
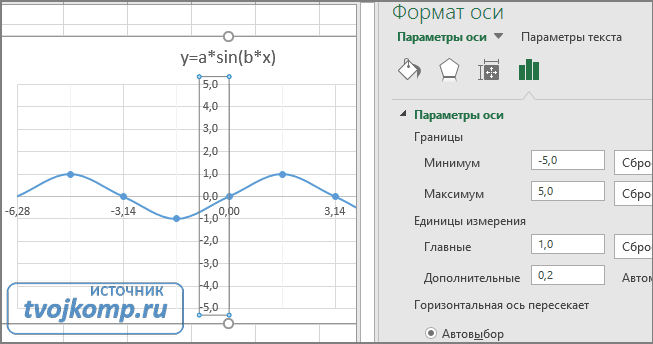
В правой части окна появиться боковая панель настроек Формат оси.
- Кликните на раскрывающийся список Параметры оси.
- Выберите Вертикальная ось (значений).
- Кликните зеленый значок диаграммы.
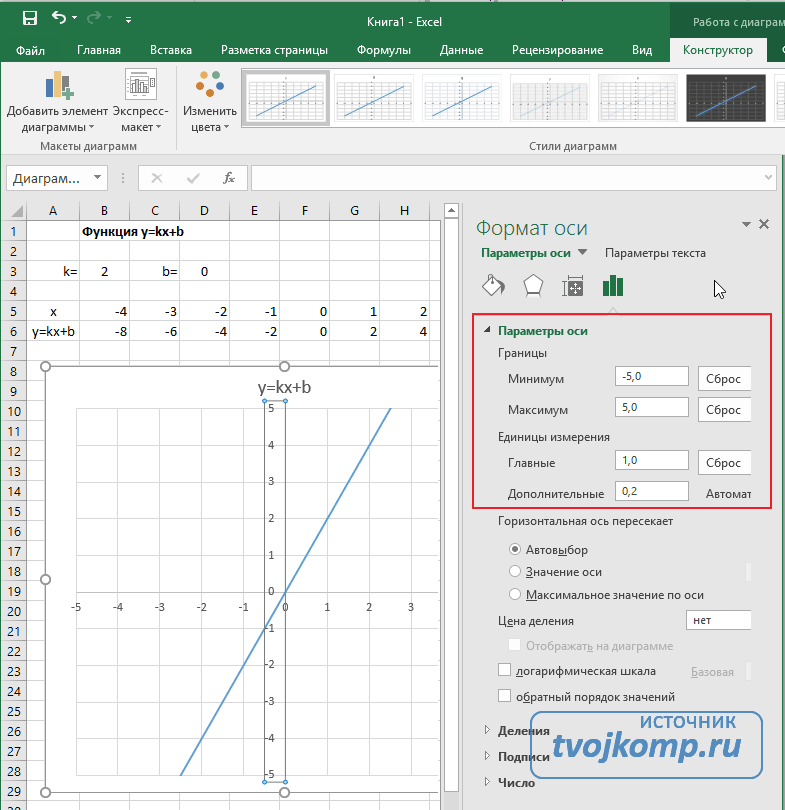
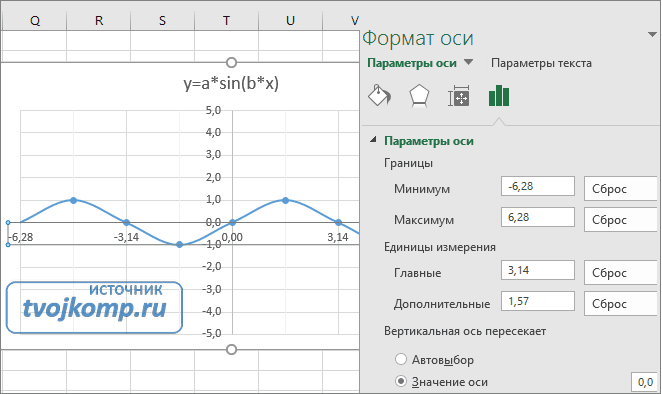
- Задайте интервал значений оси и единицы измерения (обведено красной рамкой). Ставим единицы измерения Максимум и минимум (Желательно симметричные) и одинаковые для вертикальной и горизонтальной осей. Таким образом, мы делаем мельче единичный отрезок и соответственно наблюдаем больший диапазон графика на диаграмме.И главную единицу измерения — значение 1.
- Повторите тоже для горизонтальной оси.
Теперь, если поменять значения K и b , то получим новый график с фиксированной сеткой координат.
Построение графиков других функций
Теперь, когда у нас есть основа в виде таблицы и диаграммы, можно строить графики других функций, внося небольшие корректировки в нашу таблицу.
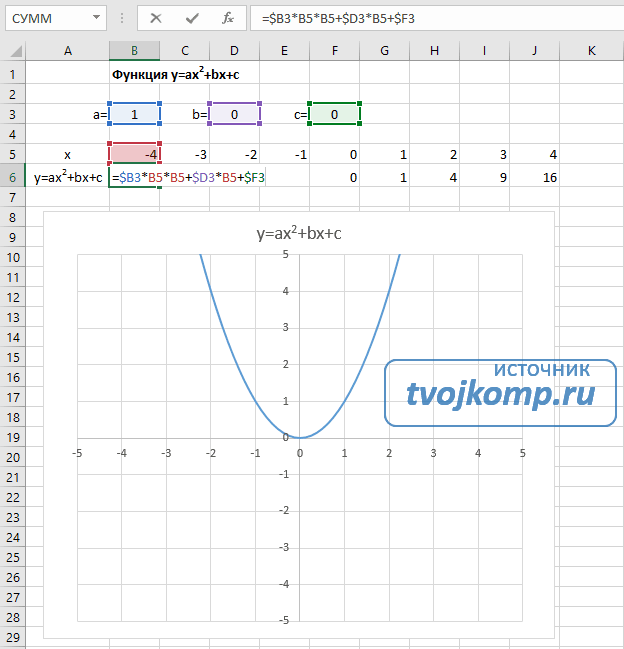
Квадратичная функция y=ax2+bx+c
Выполните следующие действия:
- В первой строке меняем заголовок
- В третьей строке указываем коэффициенты и их значения
- В ячейку A6 записываем обозначение функции
- В ячейку B6 вписываем формулу =$B3*B5*B5+$D3*B5+$F3
- Копируем её на весь диапазон значений аргумента вправо
Получаем результат
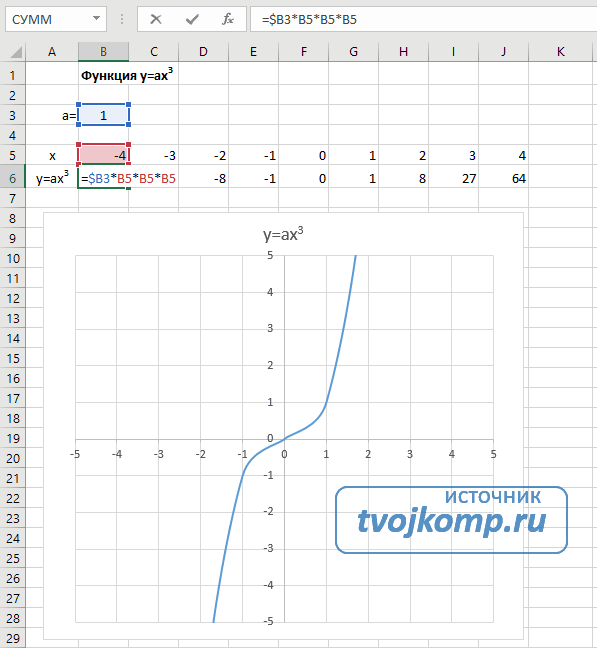
Кубическая парабола y=ax3
Для построения выполните следующие действия:
- В первой строке меняем заголовок
- В третьей строке указываем коэффициенты и их значения
- В ячейку A6 записываем обозначение функции
- В ячейку B6 вписываем формулу =$B3*B5*B5*B5
- Копируем её на весь диапазон значений аргумента вправо
Получаем результат
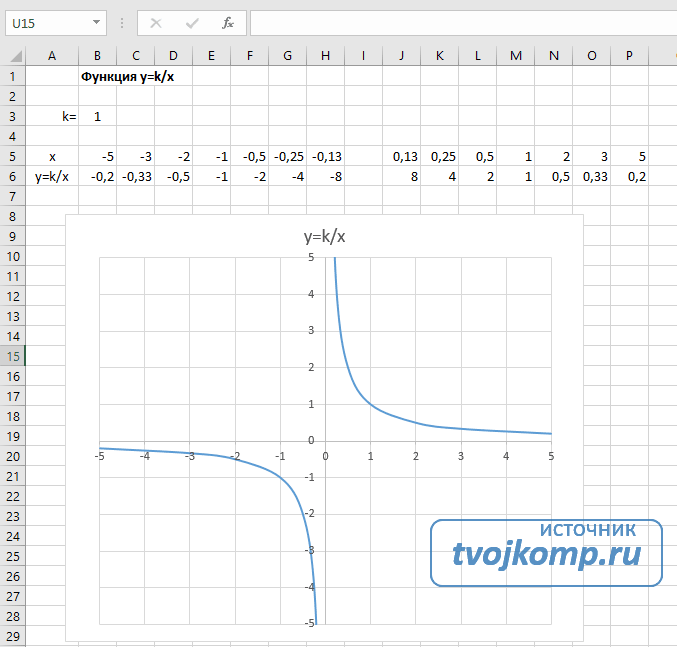
Гипербола y=k/x
Для построения гиперболы заполните таблицу вручную (смотри рисунок ниже). Там где раньше было нулевое значение аргумента оставляем пустую ячейку.
Далее выполните действия:
- В первой строке меняем заголовок.
- В третьей строке указываем коэффициенты и их значения.
- В ячейку A6 записываем обозначение функции.
- В ячейку B6 вписываем формулу =$B3/B5
- Копируем её на весь диапазон значений аргумента вправо.
- Удаляем формулу из ячейки I6.
Для корректного отображения графика нужно поменять для диаграммы диапазон исходных данных, так как в этом примере он больше чем в предыдущих.
- Кликните диаграмму
- На вкладке Работа с диаграммами перейдите в Конструктор и в разделе Данные нажмите Выбрать данные.
- Откроется окно мастера ввода данных
- Выделите мышкой прямоугольный диапазон ячеек A5:P6
- Нажмите ОК в окне мастера.
Получаем результат
Построение тригонометрических функций sin(x) и cos(x)
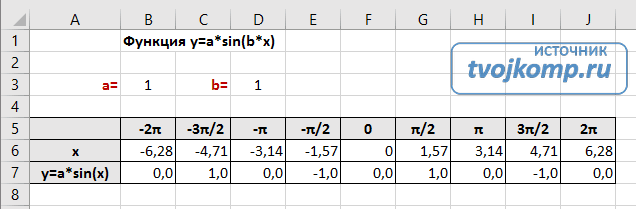
Рассмотрим пример построения графика тригонометрической функции y=a*sin(b*x).
Сначала заполните таблицу как на рисунке ниже
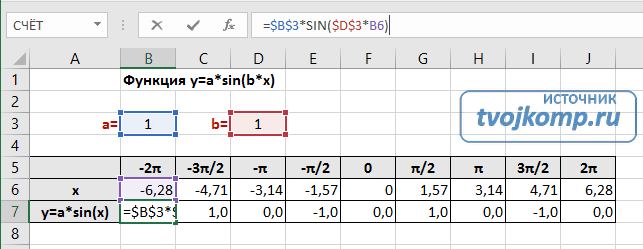
В первой строке записано название тригонометрической функции.
В третьей строке прописаны коэффициенты и их значения. Обратите внимание на ячейки, в которые вписаны значения коэффициентов.
В пятой строке таблицы прописываются значения углов в радианах. Эти значения будут использоваться для подписей на графике.
В шестой строке записаны числовые значения углов в радианах. Их можно прописать вручную или используя формулы соответствующего вида =-2*ПИ(); =-3/2*ПИ(); =-ПИ(); =-ПИ()/2; …
В седьмой строке записываются расчетные формулы тригонометрической функции.
В нашем примере =$B$3*SIN($D$3*B6). Адреса B3 и D3 являются абсолютными. Их значения – коэффициенты a и b, которые по умолчанию устанавливаются равными единице.
После заполнения таблицы приступаем к построению графика.
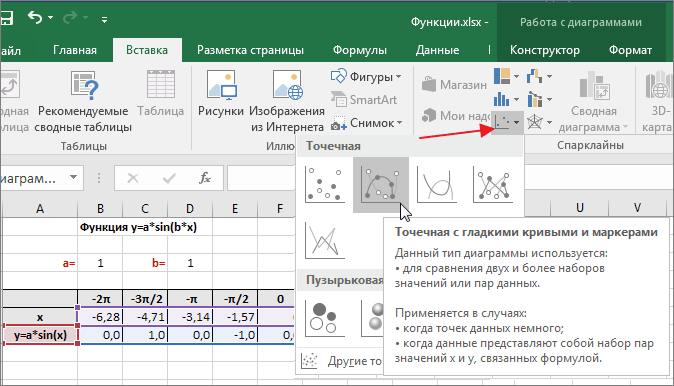
Выделяем диапазон ячеек А6:J7. В ленте выбираем вкладку Вставка в разделе Диаграммы указываем тип Точечная и вид Точечная с гладкими кривыми и маркерами.
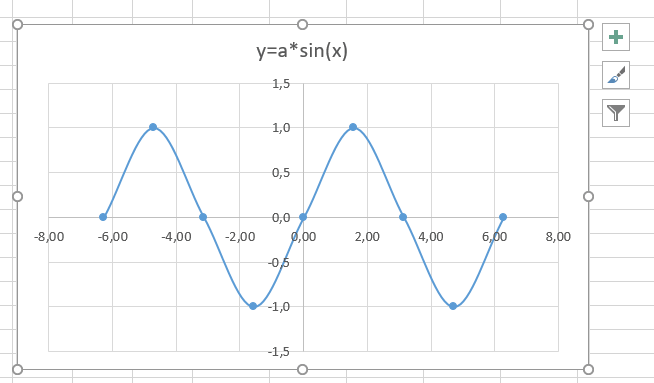
В итоге получим диаграмму.
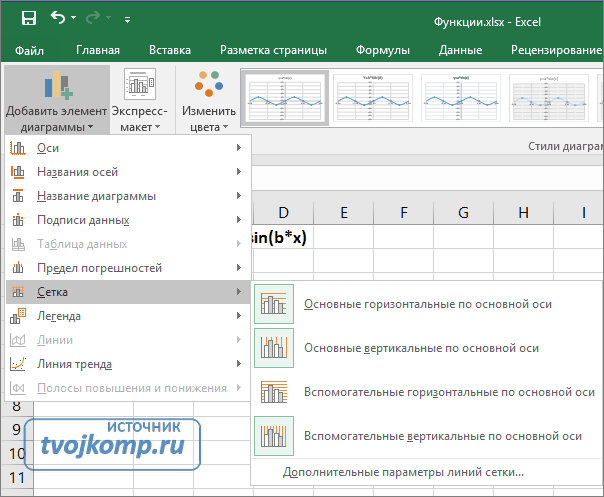
Теперь настроим правильное отображение сетки, так чтобы точки графика лежали на пересечении линий сетки. Выполните последовательность действий Работа с диаграммами –Конструктор – Добавить элемент диаграммы – Сетка и включите три режима отображения линий как на рисунке.
Теперь зайдите в пункт Дополнительные параметры линий сетки. У вас появится боковая панель Формат области построения. Произведем настройки здесь.
Кликните в диаграмме на главную вертикальную ось Y (должна выделится рамкой). В боковой панели настройте формат оси как на рисунке.
Кликните главную горизонтальную ось Х (должна выделится) и также произведите настройки согласно рисунку.
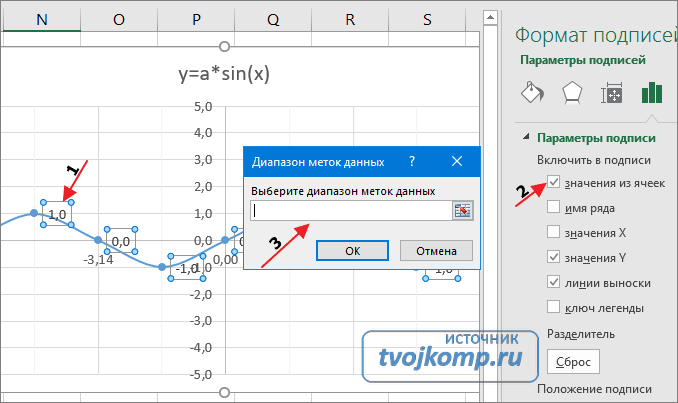
Теперь сделаем подписи данных над точками. Снова выполняем Работа с диаграммами –Конструктор – Добавить элемент диаграммы – Подписи данных – Сверху. У вас подставятся значения числами 1 и 0, но мы заменим их значениями из диапазона B5:J5.
Кликните на любом значении 1 или 0 (рисунок шаг 1) и в параметрах подписи поставьте галочку Значения из ячеек (рисунок шаг 2). Вам будет сразу же предложено указать диапазон с новыми значениями (рисунок шаг 3). Указываем B5:J5.
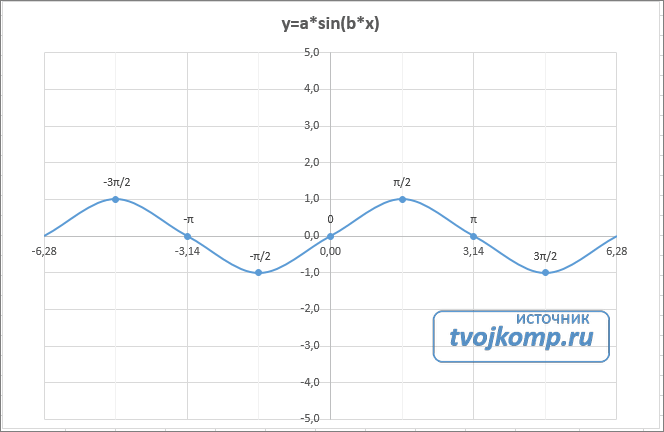
Вот и все. Если сделали правильно, то и график будет замечательным. Вот такой.
Чтобы получить график функции cos(x), замените в расчетной формуле и в названии sin(x) на cos(x).
Аналогичным способом можно строить графики других функций. Главное правильно записать вычислительные формулы и построить таблицу значений функции. Надеюсь, что вам была полезна данная информация.
Дополнительные статьи по теме:
- Знакомство с таблицами в Excel
- Изменение строк и столбцов в Excel
- Работа с ячейками: объединение, изменение, защита…
- Ошибки в формулах: почему excel не считает
- Использования условий в формулах Excel
- Функция CЧЕТЕСЛИМН
- Работа с текстовыми функциями Excel
- Все уроки по Microsoft Excel
Дорогой читатель! Вы посмотрели статью до конца.
Получили вы ответ на свой вопрос? Напишите в комментариях пару слов. Если ответа не нашли, укажите что искали или откройте содержание блога.
ОЧЕНЬ ВАЖНО! Оцени лайком или дизлайком статью!

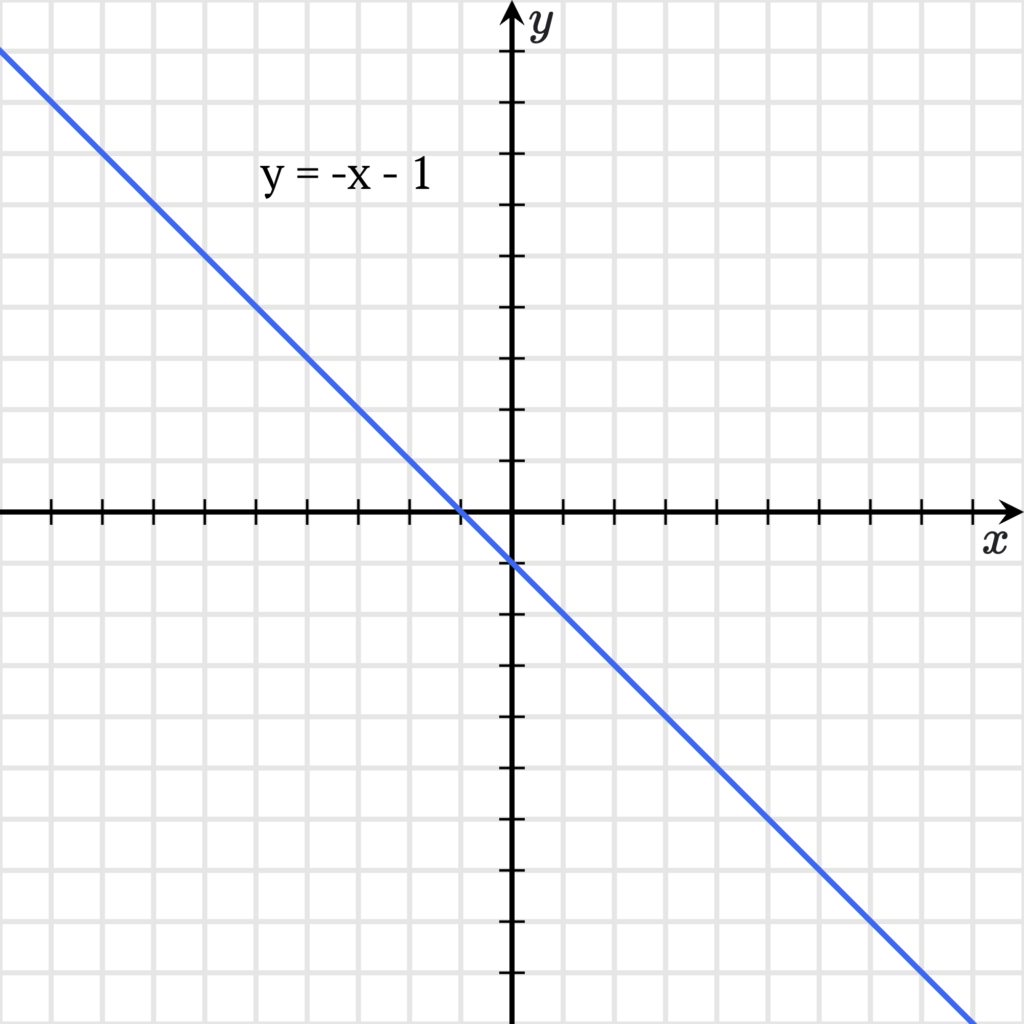
построить график линейной функции:
a)
y=13x+1,x∈−6;3
; b)
y=13x+1,x∈−6;3
.
Составим таблицу значений функции:
| (x) | (-6) | (3) |
| (y) | (-1) | (2) |
Построим на координатной плоскости (xOy) точки ((-6;-1)) и ((3;2)) и
проведём через них прямую.
Далее выделим отрезок, соединяющий построенные точки.
Этот отрезок и есть график линейной функции
y=13x+1,x∈−6;3
.
Точки ((-6); (-1)) и ((3); (2)) на рисунке отмечены тёмными кружочками.
b) Во втором случае функция та же, только значения (x=-6) и (x=3) не рассматриваются, так как они не принадлежат интервалу ((-6;3)).
Поэтому точки ((-6); (-1)) и ((3); (2)) на рисунке отмечены светлыми кружочками.
По графику линейной функции, можно определить наибольшее и наименьшее значения линейной функции на заданном отрезке.
В случае
a)
y=13x+1,x∈−6;3
, имеем:
yнаиб
(= 2) и
yнаим
(= -1);
b)
y=13x+1,x∈−6;3
, концы отрезка не рассматриваются, поэтому наибольшего и наименьшего значений нет.
In mathematics, a function defines a relationship between an independent variable and a dependent variable. In simple words, a function is a relationship between inputs and outputs in which each input is connected to exactly one output. If every element in set A has exactly one and only one image in set B, then the relation is said to be a function. Every function has a domain and a codomain, where a domain is a set of input values and a codomain, or range, is the set of possible output values for which the function is defined. The domain and codomain of a function are non-empty sets. If there exists a function from A → B and (a, b) ∈ f, then f (a) = b, where “a” is the image of “b” under “f” and “b” is the preimage of “b” under “f” and set A is the domain of the function and set B is its co-domain.
Examples of a function
- The formula for the circumference/perimeter of a circle is P = 2πr, where r is the radius of a circle. We can say that circumference/perimeter (P) is dependent on the radius (r) of the circle. In the language of functions, we say that P is defined as a function of r.
- The area (A) of a square A is a function of its side length. The dependence of A on s is given by A = 4s2.
Table Values of a Function
The table values of a function are referred to as the list of numbers that can be used to substitute for the given variable. By using this variable within the equation or in the other function, it is simple to determine the value of the other variable or the equation’s missing integer. In the table of values of a function, there are two kinds of variables, namely an independent variable and a dependent variable. For any equation of a function, an independent variable is selected independently to determine the value of a dependent variable, which is the output of the given function. The table of values is unique for every function. A graph of the given function can be plotted easily after the determination of the values of the independent and dependent variables. There are many uses and applications for tables of values of a function. These are used in the fields of mathematics, physics, and engineering.
How to make the Table of Values of a Function?
A function is typically represented by f(x), where x is the input, and its general representation is y = f(x).
- Create the table first, then choose a range of input values.
- In the left-hand side column, substitute each input value into the given equation.
- To determine the output value, evaluate the equation in the middle column. (A middle column is optional as the table of values just contains the input (independent variable) and output (dependent variable) pair.)
- Now, note down the output values in the right-hand side column.
Let us solve an example to understand the concept better.
Example: Write the table of the value for the function y = √x.
Here, the input is x and the output is y, where y = √x.
x value
Equation
y = √x
y value
0
y = √0 = 0
0
1
y = √1 = 1
1
4
y = √4 = 2
2
9
y = √9 = 3
3
16
y = √16 = 4
4
25
y = √25 = 5
5
Sample Problems
Problem 1: Write the table of values for the function y = 3x + 5.
Solution:
Here, the input is x and the output is y, where y = 3x + 5.
x value
Equation
y = 3x +5
y value
-2
y = 3(-2) + 5 = -6 + 5 = -1
-1
-1
y = 3(-1) + 5 = -3 + 5 = 2
2
0
y = 3(0) + 5 = 0 + 5 = 5
5
1
y = 3(1) + 5 = 3 + 5 = 8
8
2
y = 3(2) + 5 = 6 + 5 = 11
11
Problem 2: Write the table of values for the function P = 4s, where P is the perimeter of a square and a is its side length.
Solution:
Here, the input is s and the output is P, where P = 4s.
s value
Equation
P = 4s
P value
1
4 × 1 = 4
4
2
4 × 2 = 8
8
3
4 × 3 = 12
12
4
4 × 4 =16
16
5
4 × 5 = 20
20
Problem 3: Write the table of values for the function y = 2x + 3x.
Solution:
Here, the input is x and the output is y, where y = 2x + 3x .
x value
Equation
y = 2x + 3x
y value
-2
y = 2-2 + 3-2 = 1/22 + 1/32 = 1/4 + 1/9 = 13/36 = 0.3611
0.3611
-1
y = 2-1 + 3-1 = 1/2 + 1/3 = 5/6 = 0.834
0.834
0
y = 20 + 30 = 1 + 1 = 2
2
1
y = 21 + 31 = 2 + 3 = 5
5
2
y = 22 + 32 = 4 + 9 = 13
13
3
y = 23 + 33 = 8 + 27 = 35
35
Problem 4: Write the table values for the function y = cos x × sin x.
Solution:
Here, the input is x and the output is y, where y = cos x × sin x.
x value
Equation
y = cos x × sin x
y value
0°
y = cos 0 sin 0 = 1 × 0 = 0
0
30°
y = cos 30 sin 30 = √3/2 × 1/2 = 3/4
√3/4
45°
y = cos 45 sin 45 = 1/√2 × 1/√2 = 1/2
1/2
60°
y = cos 60 sin 60 = 1/2 × √3/2 = 3/4
√3/4
90°
y = cos 90 sin 90 = 0 × 1 = 0
0
180°
y = cos 180 sin 180 = -1 × 0 = 0
0
Problem 5: Write the table values for the function y = x2 – 5x + 6.
Solution:
Here, the input is x and the output is y, where y = x2 – 5x + 6.
x value
Equation
y = x2 – 5x + 6
y value
-3
y = (-3)2 – 5(-3) + 6 = 9 + 15 + 6 = 30
30
-2
y = (-2)2 – 5(-2) + 6 = 4 + 10 + 6 = 20
20
-1
y = (-1)2 – 5(-1) + 6 = 1 + 5 + 6 = 12
12
0
y = 02 – 5(0) + 6 = 0 – 0 + 6 = 6
6
1
y = 12 – 5(1) + 6 = 1 – 5 + 6 = 2
2
2
y = 22 – 5(2) + 6 = 4 – 10 + 6 = 10- 10 = 0
0
3
y = 32 – 5(3) + 6 = 9 – 15 + 6 = 15 – 15 = 0
0
Last Updated :
19 Jul, 2022
Like Article
Save Article
Определить правило, по которому зависимая величина будет меняться, значит задать функцию. Вариантов задания функции несколько:
- Словесно, например: «игрек равен двум х». Запись будет выглядеть так: $у = 2times x$
- Аналитический способ, то есть сразу с помощью записи формулы, например: $f(x) = x-3$
- Графический способ
- Табличный способ
Графический способ
Графический способ подразумевает чертеж на прямоугольной координатной плоскости, например:
Линия, изображенная на рисунке, называется графиком функции.
Определение:
Графиком функции называется множество точек плоскости, абсциссы которых равны значениям аргумента $x$, а ординаты – соответствующим значениям функции $y$.
Линия может быть разной: прямой или кривой.
Функция (и ее график) может быть:
- возрастающей (линия идет вверх, как на рисунке выше), если вторая зависимая величина увеличивается вместе с первой;
- убывающей (линия идет вниз), если вторая величина уменьшается при увеличении первой, например:
Функция (и ее график) может быть убывающей или возрастающей как на всей области определения, так и на определенном промежутке:
Графический способ не дает возможности предельно точного определения численных значений $x$ и $у$, но он наглядно показывает поведение функции (убывает или возрастает, максимум, минимум, непрерывность и т. д.) и является важным способом ее исследования.
Подробный урок о том, как строить график линейной функции.
Табличный способ
Часто используется табличный (то есть в виде таблицы) способ задания функции. В таблице для каждого значения аргумента $x$ указывается соответствующее ему конкретное значение функции $y$, например:
| $x$ | $1$ | $2$ | $3$ | $5$ |
| $y$ | $10$ | $20$ | $30$ | $50$ |
Каждое значение аргумента и функции нумеруется. В данном случае в таблице значению $x_1$, равному $1$, соответствует единственное значение $у_1$, равное $10$. Значению $x_2$, равному $2$, соответствует $у_2$, равное $20$ и т. д.
Не трудно догадаться, что в таблице выше отражена зависимость
$y = 10x$.
Ее можно продолжить для любых значений $x$, так при
$x_{100} = 100$
$y_{100}$ будет равен $1000$.
Табличный способ позволяет быстро найти конкретные значения $x$ и $у$.
Заполним таблицу для функции
Попробуем заполнить таблицу функции $у=3x+2$, для значений $x$, равных $1$, $3$, $4$, $8$.
Подставим в формулу $у=3x+2$ значения $x_1$, $x_2$, $x_3$, $x_4$.
Получим:
$у_1 = 3times 1 + 2 = 5$
$у_2 = 3times 3 + 2 = 11$
$у_3 = 3times 4 + 2 = 14$
$у_4 = 3times 8 + 2 = 26$
Заполним таблицу:
| $x$ | $1$ | $3$ | $4$ | $8$ |
| $у$ | $5$ | $11$ | $14$ | $26$ |
Пример
1. ( Функция
одной переменной для шагового аргумента).
Построить
таблицу значений функции
для аргумента x,
изменяющегося от 0 до 1,5 с шагом 0,1.
Построить график функции.
Решение.
Решение
разбивается на два основных этапа:
построение таблицы значений функции и
построение графика функции.
Построение
таблицы
-
Наберем заголовки
столбцов для x
и y
в ячейках A1,
B1. -
Наберем первое
значение x,
равное 0, в ячейку A2. -
Выполним команду
Правка|Заполнить|Прогрессия,
зададим в диалоге Расположение
в столбце,
Арифметическая
прогрессия, Шаг
0,1, Предельное
значение 2.
Заполнятся ячейки A4:A22. -
В ячейку B2
введем формулу: =SIN(4*A2)^2/(A2+1)
и скопируем ее в ячейки B3:B22 -
Выполним
форматирование данных (чисел) и обрамление
таблицы. Фрагмент рабочего листа с
таблицей показан на рис.5.1.
П
остроение
графика функции. Для
построения графика выделим диапазон
данных (ячейки A1:B22)
и построим точечную диаграмму, вид
которой представлен на рис. 5.2.
Рис.
5.1. Таблица значений функции для примера
1
Рис. 5.2. График
(точечная диаграмма) примера 1
Пример
2. (Функция,
заданная различными аналитическими
выражениями (сложная функция)). Построить
таблицу значений и график функции
для аргумента x
, изменяющегося от -2 до 2 с шагом 0,2
Решение
Построение
таблицы.
Решение
выполним
в том же файле, что и предыдущий пример,
но
на новом листе Excel.
Последовательность заполнения ячеек
аналогична примеру 1.
В
ячейку B2
введем формулу:
=ЕСЛИ(A2<0;-A2/(ABS(A2)+1);SIN(ПИ()*A2))
и скопируем ее в
нижележащие ячейки для всех значений
x
.
П
Рис. 5.4. График
сложной функции
Рис.
5.3. Таблица значений сложной функции
остроение
графика функции также
полностью аналогично построению
предыдущего примера, если заданная
функция непрерывна.
Замечание.
Если функция терпит разрыв при переходе
от одного аналитического выражения к
другому, то нужно построить на одной
диаграмме два графика, каждый из которых
отвечает области непрерывности функции.
В случае разрывной функции можно строить
один график, если выбрать вид графика
из отдельных точек
Пример
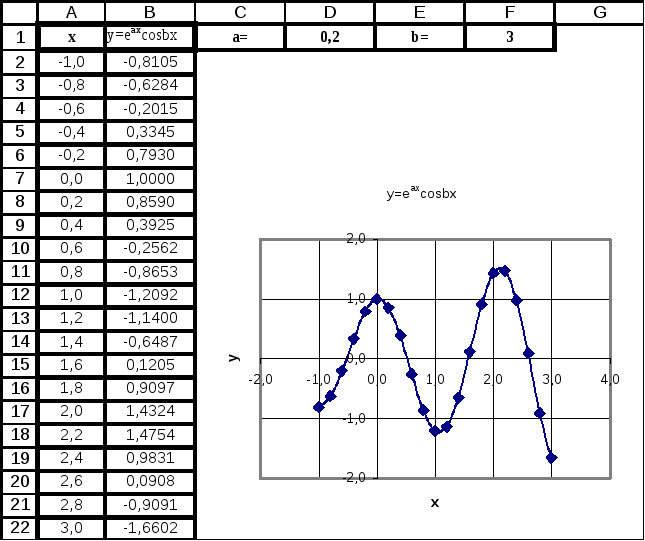
3. (Функция,
зависящая от параметра). Построить
таблицу значений и график функции
для аргумента x
, изменяющегося
от -1 до 3 с шагом 0,2 при заданных значениях
a
и b.
Решение
-
Введем заголовки
столбцов для x
и y
в ячейки A1,
B1
и значения a,
b
в отдельные ячейки D1,
F1. -
Заполним столбец
A2:A22
значениями x. -
Введем формулу
для y
в ячейку B2
=EXP($D$1*A2)*COS($F$1*A2)
и скопируем ее в ячейки B3:B22.
-
П
Рис. 5.5. Таблица и
график функции, зависящей от параметра
остроим
график аналогично примеру 1 (см. рис.5.5)
Замечание.
Меняя значения параметров, можно получить
совершенно другое поведение функции.
Рекомендуется проанализировать поведение
функции при a>0
и a<0,
а также
рассмотреть уменьшение и увеличение
b.
Пример
4. (Функция,
заданная параметрическими уравнениями).
Вычислить
таблицу значений функции, заданной
параметрическими уравнениями и построить
ее график. В качестве примера рассмотрим
построение окружности.
Параметрические
уравнения окружности рассмотрим для
значений параметра, пробегающих полный
оборот вокруг начала координат:

Построение
таблицы значений функции
-
Перейдем на новый
рабочий лист. -
Зададим заголовки
столбцов t,
x,
y. -
Заполним первый
столбец значениями t,
применив еще один способ задания
аргумента: каждое последующее значение
вычислим через предыдущее, добавляя
шаг. В ячейке D2
вычислим
по формуле =ПИ()/16. В ячейку A2
введем 0, в ячейку A3
введем формулу =A2+$D$2,
которую копируем вниз до значения 2. -
Введем в ячейку
B2
формулу =COS(A2);
в ячейку C2
формулу =SIN(A2) -
Выделим ячейки
B2,
C2
и копируем их для всех значений t
с помощью заполнения. -
Форматируем
таблицу по образцу.
Построение
графика функции
-
Выделим диапазон
B1:C22 -
Вызовем Мастер
диаграмм и
построим точечную диаграмму. В процессе
построения зададим заголовки диаграммы
и осей, уберем легенду, назначим линии
сетки. -
Затем отредактируем
диаграмму: по команде Формат
оси зададим
точность – один знак после запятой, по
команде Формат
области построения укажем
рамку Невидимая. -
Выполним
растяжение-сжатие диаграммы, так чтобы
получилась окружность, а не эллипс.
Результат
построения показан на рис. 5.7.
Рис.
5.7. График функции, заданной параметрическими
уравнениями
Рис.
5.6. Таблица функции, заданной
параметрическими уравнениями
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #