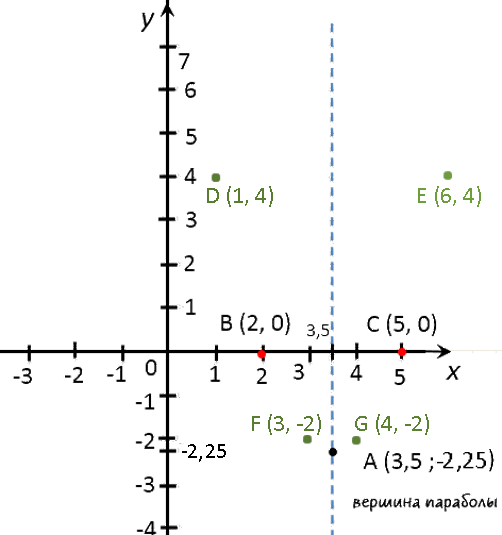Как составить таблицу для графика функции ветвь параболы - Исправление недочетов и поиск решений вместе с Examum.ru

Прежде чем перейти к разбору квадратичной функции рекомендуем вспомнить, что называют
функцией в математике.

Если вы прочно закрепите общие знания о функции (способы задания, понятие графика)
дальнейшее изучение других
видов функций будет даваться значительно легче.

Что называют квадратичной функцией

Запомните!

Квадратичная функция — это функция вида

y = ax² + bx + c,

где a,
b и с — заданные числа.

Другими словами можно сказать, что если в функции старшая (то есть самая большая) степень,
в которой стоит «x» — это «2»,
то перед нами квадратичная функция.

Рассмотрим примеры квадратичных функций и определим, чему в них равны коэффициенты «a»,
«b» и «с».

Квадратичная функция	Коэффициенты
y = 2x² − 7x + 9	a = 2 b = −7 с = 9
y = 3x² − 1	a = 3 b = 0 с = −1
y = −3x² + 2x	a = −3 b = 2 с = 0

Как построить график квадратичной функции

Запомните!

График квадратичной функции называют параболой.

Парабола выглядит следующим образом.

Также парабола может быть перевернутой.

Существует четкий алгоритм действий при построении графика квадратичной функции.
Рекомендуем при построении параболы всегда следовать этому порядку действий, тогда вы сможете избежать ошибок при построении.

Чтобы было проще понять этот алгоритм, сразу разберем его на примере.

Построим график квадратичной функции «y = x² −7x + 10».

Направление ветвей параболы

Запомните!

Если «a > 0», то ветви направлены вверх.

Если «a < 0», то ветви направлены вниз.

В нашей функции «a = 1», это означает, что ветви параболы направлены вверх.
Координаты вершины параболы

Запомните!

Чтобы найти «x₀»
(координата вершины по оси «Ox»)
нужно использовать формулу:

Найдем «x₀» для нашей функции «y = x² −7x + 10».

Теперь нам нужно найти «y₀»
(координату вершины по оси «Oy»).
Для этого нужно подставить найденное значение «x₀» в исходную функцию.
Вспомнить, как найти значение функции можно в уроке
«Как решать задачи на функцию» в подразделе
«Как получить значение функции».

y₀(3,5) =
(3,5)² − 7 ·3,5 + 10 = 12,25 − 24,5 + 10 =

−12,25 + 10 = −2,25

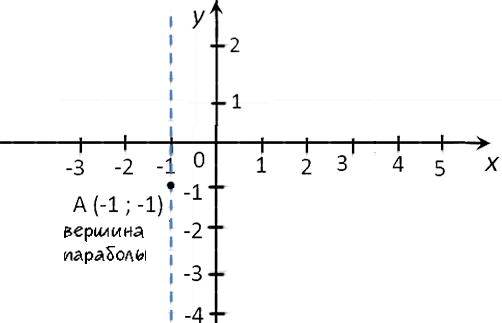
Выпишем полученные координаты вершины параболы.

(·) A (3,5; −2,25) — вершина параболы.

Отметим вершину параболы на системе координат.
Проведем через отмеченную точку ось симметрии, так как парабола — это симметричный график
относительно оси «Oy».

Нули функции

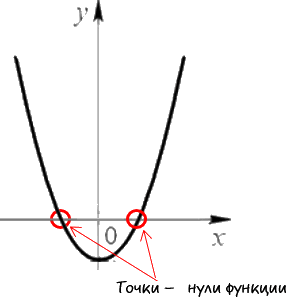
Для начала давайте разберемся, что называют нулями функции.

Запомните!

Нули функции — это точки пересечения графика функции с осью «Ox»
(осью абсцисс).

Наглядно нули функции на графике выглядят так:

Свое название нули функции получили из-за того, что у этих точек координата
по оси «Oy» равна нулю.

Теперь давайте разберемся, как до построения графика функции рассчитать координаты точек нулей функции.

Запомните!

Чтобы найти координаты точек нулей функции, нужно в исходную функцию подставить вместо
«y = 0».

Подставим в заданную функцию «y = x² −7x + 10»
вместо «y = 0» и решим полученное
квадратное уравнение
относительно
«x» .

0 = x² −7x + 10
x² −7x + 10 = 0

x_1;2 =

7 ±
√49 − 4 · 1 · 10

2 · 1

x_1;2 =

x₁ =	x₂ =
x₁ =	x₂ =
x₁ = 5	x₂ = 2

Мы получили два корня в уравнении, значит, у нас две точки пересечения
с осью «Ox».
Назовем эти точки и выпишем их координаты.

(·) B (5; 0)
(·) C (2; 0)

Отметим полученные точки («нули функции») на системе координат.

Дополнительные точки для построения графика

Возьмем четыре произвольные числовые значения для «x».
Целесообразно брать целые числовые значения на оси «Ox»,
которые наиболее близки к оси
симметрии. Числа запишем в таблицу в порядке возрастания.

x	1	3	4	6
y

Для каждого выбранного значения «x»
рассчитаем «y».

y(1) = 1² − 7 · 1 + 10 = 1 − 7 + 10 =
4
y(3) = 3² − 7 · 3 + 10 = 9 − 21 + 10 =
−2
y(4) = 4² − 7 · 4 + 10 = 16 − 28 + 10 =
−2
y(6) = 6² − 7 · 6 + 10 = 36 − 42 + 10 =
4

Запишем полученные результаты в таблицу.

x	1	3	4	6
y	4	−2	−2	4

Отметим полученные точки графика на системе координат (зеленые точки).

Теперь мы готовы построить график.
На забудьте после построения подписать график функции.

Краткий пример построения параболы

Рассмотрим другой пример построения графика квадратичной функции.
Только теперь запишем алгоритм построения коротко без подробностей.

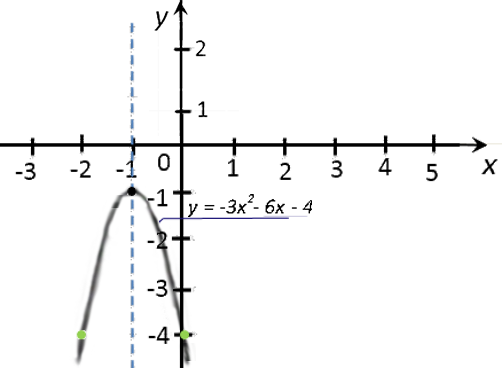
Пусть требуется построить график функции
«y = −3x² − 6x − 4».

Направление ветвей параболы

«a = −3» — ветви параболы направлены вниз.

Координаты вершины параболы

x₀ =
x₀ = =

= −1

y₀(−1) = (−3) · (−1)² − 6 · (−1) − 4 =
−3 · 1 + 6 − 4 = −1

(·) A (−1; −1)

— вершина параболы.
Нули функции
Точки пересечения с осью «Ox» (y = 0).

0 = −3x² − 6x − 4

−3x² − 6x − 4 = 0 |·(−1)

3x² + 6x + 4 = 0

x_1;2 =

−6 ±
√6² − 4 · 3 · 4

2 · 1

x_1;2 =

x_1;2 =

Ответ: нет действительных корней.

Так как корней нет, значит, график функции не пересекает ось
«Ox».

Вспомогательные точки для: «x = −3»;
«x = −2»;
«x = 0»;
«x = 1». Подставим в исходную функцию
«y = −3x² − 6x − 4».

y(−3) = −3 · (−3)² − 6 · (−3) − 4
= −3 · 9 + 18 − 4 = −27 + 14 = −13

y(−2) = −3 · (−2)² − 6 · (−2) − 4
= −3 · 4 + 12 − 4 = −12 + 12 − 4 = −4

y(0) = −3 · 0² − 6 · 0 − 4
= −4

y(1) = −3 · 1² − 6 · 1 − 4
= −3 −6 − 4 = −13

x	−3	−2	0	1
y	−13	−4	−4	−13

Отметим вспомогательные точки. Отмечаем на системе координат только те точки, которые
не выходят за масштаб нашей системы координат, то есть точки
«(−2; −4)» и «(0; −4)».
Построим и подпишем график функции.

Ваши комментарии

Важно!

Чтобы оставить комментарий, вам нужно войти на наш сайт при помощи

«ВКонтакте».

Оставить комментарий:

Источник

Функция вида , где называется квадратичной функцией.

График квадратичной функции – парабола.

Рассмотрим случаи:

I СЛУЧАЙ, КЛАССИЧЕСКАЯ ПАРАБОЛА

, то есть , ,

Для построения заполняем таблицу, подставляя значения x в формулу:

Отмечаем точки (0;0); (1;1); (-1;1) и т.д. на координатной плоскости (чем с меньшим шагом мы берем значения х ( в данном случае шаг 1 ), и чем больше берем значений х, тем плавнее будет кривая), получаем параболу:

Нетрудно заметить, что если мы возьмем случай , , , то есть , то мы получим параболу, симметричную относительно оси (ох). Убедиться в этом несложно, заполнив аналогичную таблицу:

II СЛУЧАЙ, «a» ОТЛИЧНО ОТ ЕДИНИЦЫ

Что же будет, если мы будем брать , , ? Как изменится поведение параболы? При парабола изменит форму, она “похудеет” по сравнению с параболой (не верите – заполните соответствующую таблицу – и убедитесь сами):

На первой картинке (см. выше) хорошо видно, что точки из таблицы для параболы (1;1), (-1;1) трансформировались в точки (1;4), (1;-4), то есть при тех же значениях ордината каждой точки умножилась на 4. Это произойдет со всеми ключевыми точками исходной таблицы. Аналогично рассуждаем в случаях картинок 2 и 3.

А при парабола «станет шире» параболы :

Давайте подитожим:

III СЛУЧАЙ, ПОЯВЛЯЕТСЯ «С»

Теперь давайте введем в игру (то есть рассматриваем случай, когда ), будем рассматривать параболы вида . Нетрудно догадаться (вы всегда можете обратиться к таблице), что будет происходить смещение параболы вдоль оси вверх или вниз в зависимости от знака :

IV СЛУЧАЙ, ПОЯВЛЯЕТСЯ «b»

Когда же парабола “оторвется” от оси и будет, наконец, “гулять” по всей координатной плоскости? Когда перестанет быть равным .

Здесь для построения параболы нам понадобится формула для вычисления вершины: $x_o=frac{-b}{2a}$ , .

Так вот в этой точке (как в точке (0;0) новой системы координат) мы будем строить параболу , что уже нам по силам. Если имеем дело со случаем , то от вершины откладываем один единичный отрезок вправо, один вверх, – полученная точка – наша (аналогично шаг влево, шаг вверх – наша точка); если имеем дело с , например, то от вершины откладываем один единичный отрезок вправо, два – вверх и т.д.

Например, вершина параболы :

$x_o=frac{4}{2}=2$ , . Теперь главное уяснить, что в этой вершине мы будем строить параболу по шаблону параболы , ведь в нашем случае.

При построении параболы после нахождения координат вершины очень удобно учитывать следующие моменты:

1) парабола обязательно пройдет через точку . Действительно, подставив в формулу x=0, получим, что . То есть ордината точки пересечения параболы с осью (оу), это . В нашем примере (выше), парабола пересекает ось ординат в точке , так как .

2) осью симметрии параболы является прямая $x=frac{-b}{2a}$ , поэтому все точки параболы будут симметричны относительно нее. В нашем примере, мы сразу берем точку (0; -2) и строим ей симметричную относительно оси симметрии параболы, получим точку (4; -2), через которую будет проходить парабола.

3) Приравнивая к , мы узнаем точки пересечения параболы с осью (ох). Для этого решаем уравнение . В зависимости от дискриминанта, будем получать одну (, $x=-frac{b}{2a}$ ), две (, $x_{1,2}=frac{-bpmsqrt{b^2-4ac}}{2a}$ ) или нИсколько () точек пересечения с осью (ох). В предыдущем примере у нас корень из дискриминанта – не целое число, при построении нам особо нет смысла находить корни, но мы видим четко, что две точки пересечения с осью (ох) у нас будут (так как ), хотя, в общем, это видно и без дискриминанта.

Итак, давайте выработаем

Алгоритм для построения параболы, если она задана в виде

1) определяем направление ветвей ( а>0 – вверх, a<0 – вниз)

2) находим координаты вершины параболы по формуле $x_o=frac{-b}{2a}$ , .

3) находим точку пересечения параболы с осью (оу) по свободному члену , строим точку, симметричную данной относительно оси симметрии параболы (надо заметить, бывает, что эту точку невыгодно отмечать, например, потому, что значение велико… пропускаем этот пункт…)

4) В найденной точке – вершине параболы (как в точке (0;0) новой системы координат) строим параболу . Если , то парабола становится у’же по сравнению с , если , то парабола расширяется по сравнению с

5) Находим точки пересечения параболы с осью (оу) (если они еще сами “не всплыли”), решая уравнение

Пример 1

Пример 2

Замечание 1. Если же парабола изначально нам задана в виде , где – некоторые числа (например, ), то построить ее будет еще легче, потому что нам уже заданы координаты вершины . Почему?

Возьмем квадратный трехчлен и выделим в нем полный квадрат: $ax^2+bx+c=a(x^2+frac{b}{a}x+frac{c}{a})=a((x^2+2frac{b}{2a}x+frac{b^2}{4a^2})-frac{b^2}{4a^2}+frac{c}{a})=a(x+frac{b}{2a})^2-frac{b^2}{4a}+c.$ Посмотрите, вот мы и получили, что $m=frac{-b}{2a}$ , $n=-frac{b^2}{4a}+c=y(frac{-b}{2a})$ . Мы с вами ранее называли вершину параболы , то есть теперь , .

Например, $y=-frac{1}{3}{(x+2)}^2+6$ . Отмечаем на плоскости вершину параболы , понимаем, что ветви направлены вниз, парабола расширена (относительно ). То есть выполняем пункты 1; 3; 4; 5 из алгоритма построения параболы (см. выше).

Замечание 2. Если парабола задана в виде, подобном этому (то есть представлен в виде произведения двух линейных множителей), то нам сразу видны точки пересечения параболы с осью (ох). В данном случае – (0;0) и (4;0). В остальном же действуем согласно алгоритму, раскрыв скобки.

Источник

В этой статье мы поговорим о том, что такое квадратичная функция, научимся строить ее график и определять вид графика в зависимости от знака дискриминанта и знака старшего коэффициента.
Итак.

Функция вида , где называется квадратичной функцией.

В уравнении квадратичной функции:

a — старший коэффициент

b — второй коэффициент

с — свободный член.

Графиком квадратичной функции является квадратичная парабола, которая для функции y=x^2 имеет вид:

Обратите внимание на точки, обозначенные зелеными кружками — это, так называемые «базовые точки». Чтобы найти координаты этих точек для функции y=x^2 , составим таблицу:

Внимание! Если в уравнении квадратичной функции старший коэффициент a=1 , то график квадратичной функции имеет ровно такую же форму, как график функции y=x^2 при любых значениях остальных коэффициентов.

График функции y=-x^2 имеет вид:

Для нахождения координат базовых точек составим таблицу:

Обратите внимание, что график функции y=-x^2 симметричен графику функции y=x^2 относительно оси ОХ.

Итак, мы заметили:

Если старший коэффициент a>0, то ветви параболы напрaвлены вверх.

Если старший коэффициент a<0, то ветви параболы напрaвлены вниз.

Второй параметр для построения графика функции — значения х, в которых функция равна нулю, или нули функции. На графике нули функции f(x) — это точки пересечения графика функции y=f(x) с осью ОХ.

Поскольку ордината (у) любой точки, лежащей на оси ОХ равна нулю, чтобы найти координаты точек пересечения графика функции с осью ОХ, нужно решить уравнение .

В случае квадратичной функции нужно решить квадратное уравнение .

Теперь внимание!

В процессе решения квадратного уравнения мы находим дискриминант: , который определяет число корней квадратного уравнения.

И здесь возможны три случая:

1. Если D<0 ,то уравнение не имеет решений, и, следовательно, квадратичная парабола не имеет точек пересечения с осью ОХ. Если a>0 ,то график функции выглядит как-то так:

2. Если D=0 ,то уравнение имеет одно решение, и, следовательно, квадратичная парабола имеет одну точку пересечения с осью ОХ. Если a>0 ,то график функции выглядит примерно так:

3. Если D>0 ,то уравнение имеет два решения, и, следовательно, квадратичная парабола имеет две точки пересечения с осью ОХ:

$x_1={-b+sqrt{D}}/{2a}$ , $x_2={-b-sqrt{D}}/{2a}$

Если a>0 ,то график функции выглядит примерно так:

Следовательно, зная направление ветвей параболы и знак дискриминанта, мы уже можем в общих чертах определить, как выглядит график нашей функции.

Следующий важный параметр графика квадратичной функции — координаты вершины параболы:

$x_0=-{b/{2a}}$

$y_0=-{D/{4a}}=y(x_0)$

Прямая, проходящая через вершину параболы параллельно оси OY является осью симметрии параболы.

И еще один параметр, полезный при построении графика функции — точка пересечения параболы с осью OY.

Поскольку абсцисса любой точки, лежащей на оси OY равна нулю, чтобы найти точку пересечения параболы с осью OY, нужно в уравнение параболы вместо х подставить ноль: y(0)=c .

То есть точка пересечения параболы с осью OY имеет координаты (0;c).

Итак, основные параметры графика квадратичной функции показаны на рисунке:

Рассмотрим несколько способов построения квадратичной параболы. В зависимости от того, каким образом задана квадратичная функция, можно выбрать наиболее удобный.

1. Функция задана формулой .

Рассмотрим общий алгоритм построения графика квадратичной параболы на примере построения графика функции

1. Направление ветвей параболы.

Так как a=2>0 ,ветви параболы направлены вверх.

2. Найдем дискриминант квадратного трехчлена

Дискриминант квадратного трехчлена больше нуля, поэтому парабола имеет две точки пересечения с осью ОХ.

Для того, чтобы найти их координаты, решим уравнение:

$x_1={-3+7}/4=1$ , $x_1={-3-7}/4=-2,5$

3. Координаты вершины параболы:

$x_0=-{b/{2a}}=-3/4 =-0,75$

$y_0=-{D/{4a}}=-49/8=-6,125$

4. Точка пересечения параболы с осью OY: (0;-5),и ей симметричная относительно оси симметрии параболы.

Нанесем эти точки на координатную плоскость, и соединим их плавной кривой:

Этот способ можно несколько упростить.

1. Найдем координаты вершины параболы.

2. Найдем координаты точек, стоящих справа и слева от вершины.

Воспользуемся результатами построения графика функции

Кррдинаты вершины параболы

$x_0=-{b/{2a}}=-3/4 =-0,75$

$y_0=-{D/{4a}}=-49/8=-6,125$

Ближайшие к вершине точки, расположенные слева от вершины имеют абсциссы соответственно -1;-2;-3

Ближайшие к вершине точки, расположенные справа имеют абсциссы соответственно 0;1;2

Подставим значения х в уравнение функции, найдем ординаты этих точек и занесем их в таблицу:

Нанесем эти точки на координатную плоскость и соединим плавной линией:

2. Уравнение квадратичной функции имеет вид — в этом уравнении x_0;y_0 — координаты вершины параболы

или в уравнении квадратичной функции a=1 , и второй коэффициент — четное число.

Построим для примера график функции .

Вспомним линейные преобразования графиков функций. Чтобы построить график функции , нужно

сначала построить график функции ,
затем одинаты всех точек графика умножить на 2,
затем сдвинуть его вдоль оси ОХ на 1 единицу вправо,
а затем вдоль оси OY на 4 единицы вверх:

Теперь рассмотрим построение графика функции . В уравнении этой функции a=1 , и второй коэффициент — четное число.

Выделим в уравнении функции полный квадрат:

Следовательно, координаты вершины параболы: . Старший коэффициент равен 1, поэтому построим по шаблону параболу с вершиной в точке (-2;1):

3. Уравнение квадратичной функции имеет вид y=(x+a)(x+b)

Построим для примера график функции y=(x-2)(x+1)

1. Вид уравнения функции позволяет легко найти нули функции — точки пересечения графика функции с осью ОХ:

(х-2)(х+1)=0, отсюда

2. Координаты вершины параболы: $x_0={x_1+x_2}/2={2-1}/2=1/2$

$y_0=y(-1)=({1/2}-2)({1/2}+1)=-9/4=-2,25$

3. Точка пересечения с осью OY: с=ab=(-2)(1)=-2 и ей симметричная.

Нанесем эти точки на координатную плоскость и построим график:

График квадратичной функции.

Перед вами график квадратичной функции вида .

Кликните по чертежу.
Подвигайте движки.
Исследуйте зависимость
— ширины графика функции от значения коэффициента ,
— сдвига графика функции вдоль оси от значения ,

— сдвига графика функции вдоль оси от значения
— направления ветвей параболы от знака коэффициента
— координат вершины параболы от значений и :

Скачать таблицу квадратичная функция

И.В. Фельдман, репетитор по математике.

Источник

Функция вида

y=ax2+bx+c

, где (a), (b), (c) — реальные числа, (a)

≠

(0), называется квадратичной функцией.

Графиком квадратичной функции является парабола.

Область определения функции (D(f)) — все действительные числа.

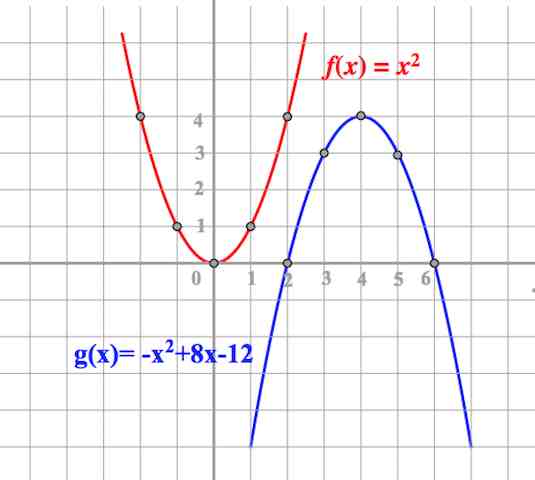
Рассмотрим для примера две квадратичные функции.

Пример 1.

y=x2−2x−1

(рис. (1)).

Пример 2.

y=−2×2+4x

(рис. (2)).

Область значений функции (E(f)) считывается с графика, она зависит от координаты (y), вершины параболы и направления ветвей параболы.
(1) пример —

E(f)=[−2;+∞)

;
(2) пример —

E(f)=(−∞;2]

Параметр (a) определяет направление ветвей параболы:
если (a > 0), то ветви направлены вверх (см. пример (1));
если (a < 0), то ветви направлены вниз (см. пример (2)).

Параметр (c) указывает, в какой точке парабола пересекает ось (Oy).

Чтобы построить график квадратичной функции, необходимо:

1) вычислить координаты вершины параболы:

x0=−b2aиy0

— которую находят, подставив значение

в формулу функции;

2) отметить вершину параболы на координатной плоскости, провести ось симметрии параболы;

3) определить направление ветвей параболы;

4) отметить точку пересечения параболы с осью (Oy);

5) составить таблицу значений, выбрав необходимые значения аргумента (x).

Решив квадратное уравнение

ax2+bx+c=0

, получаем точки пересечения параболы с осью (Ox), или корни функции (если дискриминант (D > 0));

если (D < 0), то точек пересечения параболы с осью (Ox) не существует;

если (D = 0), то вершина параболы находится на оси (Ox).

Но не всегда точки пересечения с осью (Ox) являются рациональными числами; если невозможно точно вычислить корень из (D), то такие точки не используют для построения графика.

1. Построй график функции

y=x2−2x−1

x0=−b2a=22=1;y0=12−2⋅1−1=−2.

Ветви параболы направлены вверх, т. к.

(a = 1 > 0).

Парабола пересекает ось (Oy) в точке ((0; -1)).

(x)	(2)	(3)	(4)
(y)	(-1)	(2)	(7)

Симметрично строим левую сторону параболы

Рис. (1). График функции

y=x2−2x−1

2. Построй график функции

y=−2×2+4x

В данном случае легко вычислить корни:

−2×2+4x=0;x(−2x+4)=0;x=0,или−2x+4=0;x=2;x1=0;x2=2.

Координаты вершины параболы:

x0=−42⋅−2=1;y0=−2⋅12+4⋅1=2.

В таблице достаточно одного значения:

если (x = 3), то

Симметрично, если (x = -1),

то (y = -6)

Рис. (2). График функции

y=−2×2+4x

Источник

Данная статья не содержит графических
иллюстраций. Поэтому знакомиться с ее
содержанием будет удобнее, имея под рукой лист
бумаги и карандаш.

1. Линейная функция

При изучении линейной функции на уроках алгебры в 7-м
классе учащиеся довольно успешно осваивают
способ построения прямой по двум точкам. При этом
составляется таблица, в которой задаются
значения х и вычисляются соответствующие
значения y. Однако при построении прямой
часто допускаются неточности: из-за того, что
выбранные точки очень близко расположены друг к
другу, построенная прямая “уходит в сторону”.
Построить график линейной функции можно гораздо
быстрее, если заметить определенные
закономерности. Рассмотрим примеры.

Пример 1. Построить график функции .

Решение Составим таблицу значений функции.

Порядковый №	1	2	3	4	5
x	0	1	2	3	4
y	-3	-1	1	3	5

Первая точка выбирается традиционно – точка
пересечения прямой с осью ординат. А дальше
обратим внимание, что разность значений функции , т.е. совпадает
со значением углового коэффициента заданной
функции. А значит, для построения точек на
координатной плоскости вся информация заложена
в коэффициентах заданной линейной функции.
Алгоритм построения точек следующий:

строим первую точку ;
переносим ее на 1 единицу вправо и две единицы
вверх (это вторая точка, принадлежащая прямой):
вторую точку снова перемещаем на 1 единицу
вправо и две единицы вверх и получаем третью
точку искомой прямой;
далее все повторяется любое число раз.

Пример 2. Построить график функции .

Решение Первая точка имеет координаты . Каждая
следующая получается из предыдущей смещением на
1 единицу вправо и на 3 единицы вниз.

Рассмотрим теперь случай, когда угловой
коэффициент линейной функции задается дробью.

Пример 3. Построить график функции .

Решение Составим таблицу значений функции.
Чтобы получить точки прямой с целочисленными
координатами, возьмем значения х, кратные
трем. Ну. а первая точка, по-прежнему, – точка
пересечения прямой с осью ординат.

x	0	3	6	9	12
y	-4	-2	0	2	4

Построим точки на координатной плоскости.
Видно, что каждая следующая точка получается из
предыдущей сдвигом на 3 единицы вправо и 2 единицы
вверх. Проводим прямую.

Пример 4. Построить график функции .

Решение Первая точка имеет координаты . Заметим, что
угловой коэффициент прямой . Значит, каждая следующая точка
прямой будет получена из предыдущей смещением на
5 единиц вправо и на 4 единицы вниз. Строим точки и
проводим прямую.

Обратите внимание, что в случае дробного
углового коэффициента линейной функции
знаменатель дроби указывает количество единиц
для перемещения точки вправо, а числитель –
количество единиц, на которые переместится точка
вверх (при )
или вниз (при k<0).

2. Квадратичная функция

2.1. С графиком квадратичной функции учащиеся
знакомятся еще в седьмом классе. При этом, для
построения параболы, как правило, записывается
таблица значений функции для , затем полученные точки строят
на координатной прямой и рисуют параболу. Более
продвинутые ученики записывают таблицу только
для , строят
полученные точки и проводят правую ветвь
параболы. Затем, воспользовавшись симметрией
графика относительно оси ординат, строят точки
параболы для
и рисуют вторую ветвь параболы.

Записи таблицы можно избежать, если заметить
одну закономерность в расположении указанных
точек. Посмотрим таблицу значений функции :

В третьей строке таблицы записана разность
двух последующих значений функции. Видно, что
полученные числа образуют последовательность
нечетных чисел (легко убедиться, что эта
закономерность выполняется и далее, например, ). Этот факт
легко запоминается. А с учетом этой
закономерности построить характеристические
точки параболы можно так:

первая точка – начало координат;
вторая точка получается из первой смещением на
одну единицу вправо и на одну единицу вверх;
третья получается смещением второй точки на
один вправо и три вверх;
четвертая точка получается переносом третьей
на один вправо и пять вверх;
затем строятся точки левой ветви параболы за
счет симметрии графика относительно оси ординат.

Остается провести плавную линию через
полученные точки, и парабола построена.

2.2. Перейдем теперь к квадратичной
функции вида ,
которая изучается уже в восьмом классе. Учащиеся
узнают, что коэффициент а определяет
направление ветвей параболы, а также растяжение
или сжатие графика вдоль оси ординат. А для
построения графика все равно просчитывают
координаты точек. Но без этого можно обойтись,
если знать указанную выше закономерность
построения точек параболы . И если для нее сдвиг точек вдоль
оси OY задавался последовательностью чисел , то для функции эта
последовательность чисел будет .

Пример 5. Построить график функции .

Решение Графиком функции служит парабола,
ветви которой направлены вниз, а вершина
находится в начале координат. Для построения
других точек параболы вспомним про нечетные
числа ,
умножим их на ,
получаем последовательность чисел Знак говорит о том , что смещение
точек будет сделано вниз. На словах алгоритм
построения звучит так: от начала координат одна
единица вправо и две вниз; от новой точки одна
единица вправо и шесть вниз; строим точки,
симметричные полученным относительно оси
ординат; проводим параболу.

Пример 6. Построить график функции .

Решение Графиком функции – парабола, ветви
которой направлены вверх. Вершина параболы
находится в начале координат. Для построения
других точек воспользуемся последовательностью При получаем
следующий порядок перемещений вдоль оси ординат . Строим точки
на координатной плоскости: от точки 1 клетка вправо и
полклетки вверх, от полученной точки снова одна
клетка вправо и полторы клетки вверх, потом от
новой точки опять одна клетка вправо и две с
половиной клетки вверх и т.д. (ясно, что в
указанном случае за единичный отрезок на осях
координат принимается одна клеточка в тетрадном
листе). Затем строим точки левой ветви параболы
за счет симметрии графика относительно оси OY и
рисуем параболу.

2.3. В 9-м классе учащиеся изучают
квадратичную функцию . Для построения ее графика с учетом
выше сказанного можно применять следующий
алгоритм:

найти координаты вершины параболы ;
построить в системе координат полученную точку
и провести оси вспомогательной системы
координат (прямые и );
по коэффициенту а определить направление
ветвей параболы;
построить во вспомогательной системе координат
характеристические точки функции , следуя алгоритму пункта
2.2.
провести плавную линию через указанные точки.
График готов.

Пример 7. Построить график функции .

Решение Графиком функции – парабола.

Вычисляем координаты вершины параболы: .
Строим точку
и проводим пунктиром вспомогательные оси
координат (прямые проходят через указанную точку
и параллельны осям ОХ и ОY).
Коэффициент при х² в данной функции
равен 1. Значит, для построения
характеристических точек параболы применим ряд
чисел 1,3,5,…. , т.е. строим стандартную параболу, но
во вспомогательной системе координат (пункт 2.1.).
Проводим плавную линию через полученные точки.
Парабола построена.

ПРИМЕРЫ ДЛЯ САМОСТОЯТЕЛЬНОГО РЕШЕНИЯ

Постройте графики указанных функций:

Источник