Как составить таблицу для задачи на движение 4 класс

Чтобы быстро решить задачи на движение, в том числе сложные и запутанные, нужно составить к ней схему или таблицу данных.

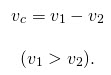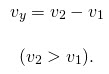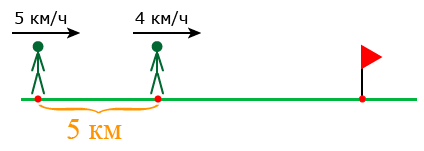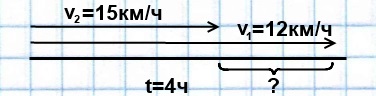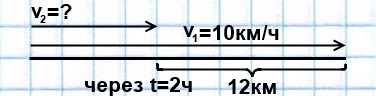
• Схемы задач на движение помогают представить наглядно условие задачи и найти верное решение.
• Таблица к задачам на движение позволяет структурировать данные, чтобы наглядно видеть исходные данные и неизвестные величины.

Поэтому, чтобы решить сложные задачи на движение, нужно нарисовать схему, а в дополнение к схеме рекомендуется нарисовать таблицу, где в шапке параметры скорости, времени и расстояния. При этом везде применяется основная формула:

Рассмотрим решение следующих типов задач:

• простые задачи на скорость, время и расстояние;
• задачи на движение в разных направлениях: сближение и удаление;
• задачи на движение в одном направлении: сближение и удаление;
• решение задач на движение по реке.

Решить простые задачи на движение

Для решения простых задач на движение, как правило, схема или таблица не требуется, в них применяется формула нахождения скорости, времени или расстояния. Но иногда, чтобы не запутаться в решении, лучше воспользоваться каким-либо методом. Рассмотрим схему и таблицу, чтобы вы смогли выбрать наиболее удобный для себя способ разобраться в задаче.

Задача 1. Средняя скорость

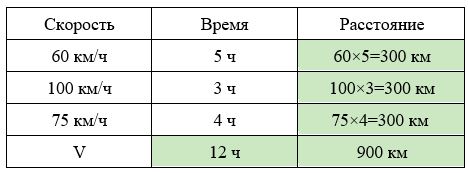
Первые 5 часов автомобиль ехал со скоростью 60 км/ч, следующие 3 часа — со скоростью 100 км/ч, а последние 4 часа — со скоростью 75 км/ч. Найдите среднюю скорость автомобиля на протяжении всего пути.

Решение.
Нарисуем схему движения.

Заполним все исходные данные в таблице. Также заполним другие ячейки таблицы по возможности (такие ячейки выделены зеленым цветом) 

Средняя скорость — это отношение пройденного пути ко времени, за который пройден этот путь.

• Найдем общее расстояние: 900 км.
• Найдем время в пути: 5 + 3 + 4 = 12 часов.
• Найдем среднюю скорость автомобиля: 900:12 = 75 км/ч.

Задача 2. Движение с остановкой

В 9:00 велосипедист выехал из пункта А в пункт Б. Доехав до пункта Б, он сделал остановку на полчаса, а в 11:30 выехал обратно с прежней скоростью. В 13:00 ему оставалось проехать 8 км до пункта А. Найдите расстояние между пунктами А и Б.

Решение.
Нарисуем схему движения.

Заполним все исходные данные в таблице. Также заполним другие ячейки таблицы по возможности.

• Найдем скорость: 8 : 0,5 = 16 км/ч
• Найдем расстояние: 16×2=32 км.

Задача 3. Уровень ЕГЭ.

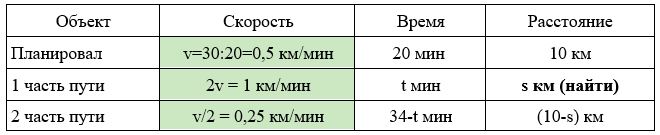
Лыжник планировал проехать 10 км с горы за 20 минут с постоянной скоростью v. Вместо этого первые несколько километров он проехал в два раза быстрее, чем планировал, а оставшиеся километры он проехал в два раза медленнее, чем планировал. В итоге весь путь занял у него 34 минуты. Сколько километров лыжник проехал в два раза быстрее, чем планировал?

Решение.
Нарисуем схему движения.

Заполним все исходные данные в таблице. Также заполним другие ячейки таблицы по возможности (такие ячейки выделены зеленым цветом)

• Найдем скорость, с которой лыжник планировал скатиться: 10 : 20 = 0,5км/мин
• Найдем скорости, с которыми лыжник скатывался: 3км/мин и 0,25км/мин.
• Составим систему уравнений:
  1) 1×t=s  → t=s
  2) 0,25×(34-t)=10-s → 0,25×(34-s)=10-s → s=2 км.

Решить задачи на движение в разных направлениях: сближение и удаление

Задача 4. Скорость удаления

Два автомобиля выехали одновременно из одного и того же пункта в противоположных направлениях. Скорость первого автомобиля  100  км/ч, скорость второго —  70  км/ч. Какое расстояние будет между автомобилями через  4  часа?

Решение.
Нарисуем схему движения.

Заполним все исходные данные в таблице. Также заполним другие ячейки таблицы по возможности (такие ячейки выделены зеленым цветом) /

Способ 1.
1) 100× 4 = 400 (км)  — проехал первый автомобиль,
2) 70 × 4 = 280 (км)  — проехал второй автомобиль.
3) 400 + 280 = 680 (км).

Способ 2.
1)  (100 + 70),  170  км/ч — это скорость удаления автомобилей.
2) 170× 4 = 680 км.

Задача 5. Скорость сближения

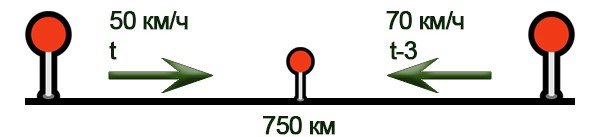
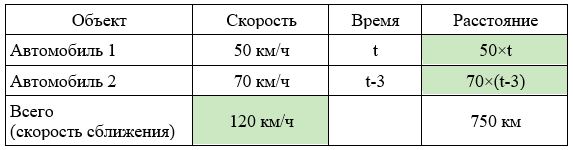
Расстояние между городами А и В равно 750 км. Из города А в город В со скоростью 50 км/ч выехал первый автомобиль, а через три часа после этого навстречу ему из города В выехал со скоростью 70 км/ч второй автомобиль. На каком расстоянии от города А автомобили встретятся?

Решение.
Нарисуем схему движения.

Заполним все исходные данные в таблице. Также заполним другие ячейки таблицы по возможности (такие ячейки выделены зеленым цветом)

Способ 1.

• Составим уравнение: 50×t + 70×(t-3) =750
• Решим уравнение: 120t=960; t=8 часов.
• По условиям задачи нужно найти расстояние от пункта А, то есть расстояние для первого автомобиля: 50×8=400км.

Способ 2.

• За первые три часа пути автомобиль, выехавший из города А, проехал 150 километров и расстояние от него до города В стало равным 600 км.
• Скорость сближения двух автомобилей равна 120 км/ч, значит, они встретятся через 5 часов после выезда второго автомобиля: 600:120=5 часов.
• Таким образом, первый автомобиль всего ехал  8 часов: 50×8=400км.

Задача 6. Скорость сближения

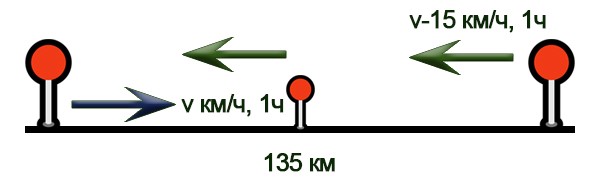
Расстояние между пунктами А и В равно 135 км. Из пункта А в пункт В выехал легковой автомобиль. Одновременно с ним из пункта В в пункт А выехал грузовой автомобиль, скорость которого на 15 км/ч меньше скорости легкового. Через час после начала движения они встретились. Через сколько минут после встречи грузовой автомобиль прибыл в пункт А?

Решение.
Нарисуем схему движения.

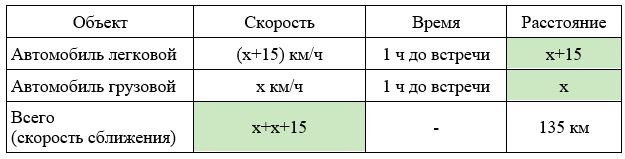
Заполним все исходные данные в таблице. Также заполним другие ячейки таблицы по возможности (такие ячейки выделены зеленым цветом)

• Пусть x км/ч — скорость грузового автомобиля, тогда (x + 15) км/ч — скорость легкового автомобиля. Получаем уравнение: x+x+15=135; x=60км/ч. 
• Найдем сколько времени грузовой автомобиль затратил на весь путь: 135:60=2,25 часов.
• Найдем сколько времени грузовой автомобиль затратил на путь после встречи: 2,25-1=1,25 часов или 75 минут (1,25*60).
• Ответ: 75 мин.

Задача 7. Уровень ЕГЭ.

Два поезда движутся навстречу друг другу – один со скоростью 70 км/ч, другой со скоростью 80 км/ч. Пассажир, сидящий во втором поезде, заметим, что первый поезд прошел мимо него за 12 секунд. Какова длина первого поезда? Ответ дайте в метрах.

Решение.
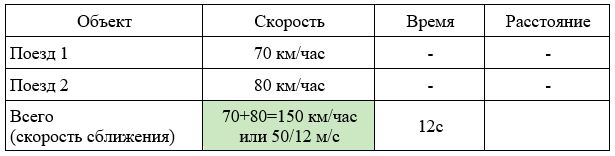
Заполним все исходные данные в таблице. Также заполним другие ячейки таблицы по возможности (такие ячейки выделены зеленым цветом)

• Найдем скорость сближения: 70+80=150км/ч.
• Переведем ее в другие единицы измерения: 150 км/ч = 150000/3600 = 50/12 м/с
• Заметим, что фраза “первый поезд прошел мимо пассажира за 12с” означает, что с того момента, как пассажир увидел голову поезда, до того момента, как он увидел хвост поезда, прошло 12с.
  
• Найдем расстояние 50/12 × 12 =50 метров.

Решить задачи на движение в одном направлении: сближение и удаление

Задача 8. Скорость сближения

Поезд, двигаясь равномерно со скоростью 63 км/ч, проезжает мимо идущего в том же направлении параллельно путям со скоростью 3 км/ч пешехода за 57 секунд. Найдите длину поезда в метрах.

Решение.
Нарисуем схему движения.

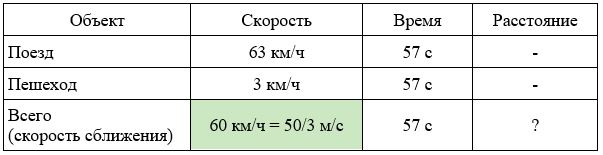
Заполним все исходные данные в таблице. Также заполним другие ячейки таблицы по возможности (такие ячейки выделены зеленым цветом)

• Найдем скорость поезда относительно пешехода: 63 − 3 = 60 км/ч
• Переведем скорость сближения в другие единицы измерения: 60 км/ч = 60000/3600=50/3 м/с.
• Найдем длину поезда (расстояние, которое проехал поезд): (50/3)*57=950 м.

Задача 9. Скорость сближения

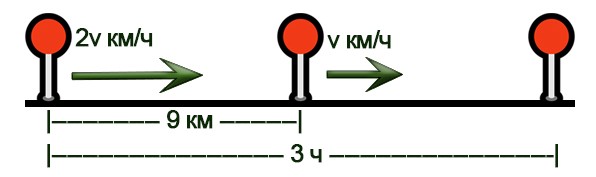
Два туриста одновременно вышли в одном направлении в город N. При этом вышли они из разных городов, расстояние между которыми 9 км. Известно, что турист, изначально находившийся дальше от города N, шёл со скоростью, в два раза превышающей скорость другого туриста. В город N они прибыли одновременно, через 3 часа после начала движения. Найдите скорость туриста, который шёл быстрее. Ответ дайте в км/ч.

Решение.
Нарисуем схему движения.

Заполним все исходные данные в таблице. Также заполним другие ячейки таблицы по возможности (такие ячейки выделены зеленым цветом)

• Найдем скорость сближения туристов: 9:3=3 км/ч.
• По формуле сближения получаем: 2v-v=3  → v=3 →2v=6 км/ч.
• Ответ: 6

Задача 10. Скорость удаления

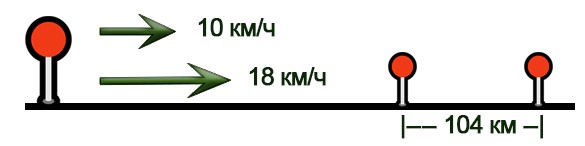
Два велосипедиста выехали из одного места в одном направлении. Скорость первого – 10 км/ч, а второго – 18 км/ч. Через сколько часов расстояние между велосипедистами будет равно 104 км?

Решение.
Нарисуем схему движения.

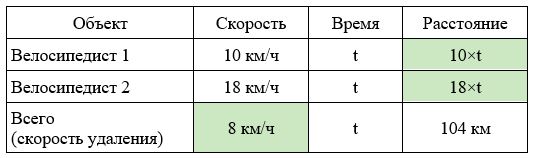
Заполним все исходные данные в таблице. Также заполним другие ячейки таблицы по возможности (такие ячейки выделены зеленым цветом)

• Найдем скорость удаления: 18-10=8 км/ч
• Найдем время в пути: 108:8=13 часов.
• Ответ: 13

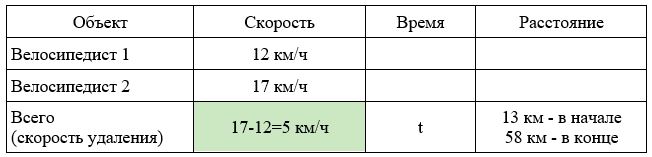
Задача 11. Скорость удаления

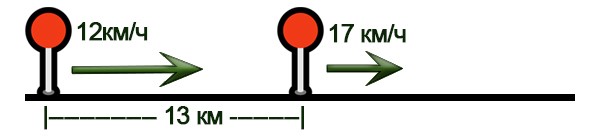
Два велосипедиста выехали в одном направлении из мест, находящихся на расстоянии 13 км друг от друга. Скорость первого – 12 км/ч, а второго – 17 км/ч, причем второй находился в начале движения впереди. Через сколько часов расстояние между велосипедистами будет равно 58 км?

Решение.
Нарисуем схему движения.

Заполним все исходные данные в таблице. Также заполним другие ячейки таблицы по возможности (такие ячейки выделены зеленым цветом)

• Найдем скорость удаления: 17-12=5 км/ч
• Найдем расстояние, на которое они удались друг от друга: 58-13=45 км.
• Найдем время: 45:5=9 часов. 

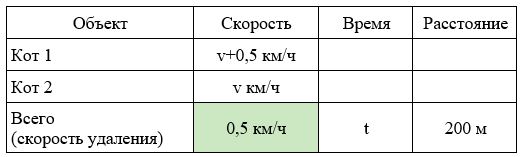
Задача 12. Уровень ЕГЭ

Два кота одновременно выбегают в одном направлении из одного и того же подъезда. Скорость первого на 0,5 км/ч больше скорости второго. Через сколько минут расстояние между котами станет равным 200 метрам?

Решение.
Заполним все исходные данные в таблице. Также заполним другие ячейки таблицы по возможности (такие ячейки выделены зеленым цветом)

• Скорость удаления будет 0,5 км/ч — это скорость, с которой первый кот бежит быстрее второго.
• Найдем время: 0,2 : 0,5 = 0,4 часа
• Переведем время в другие единицы измерения: 0,4 ч = 0,4*60 = 24 мин.

Решить задачи на движение по реке

Задача 13.

Яхта движется по стоячей воде, ее собственная скорость равна 30 км/ч. Встречный ветер каждую минуту сносит яхту на 20 метров. За сколько часов яхта пройдет 259200 метров?

Решение.
Заполним все исходные данные в таблице. Также заполним другие ячейки таблицы по возможности (такие ячейки выделены зеленым цветом)

• Переведем скорость яхты в другие единицы измерения: 30 км/ч = 500 м/с.
• Найдем скорость удаления: 500-20=480 м/с.
• Найдем время: 259200 :480=540 минут = 9 часов.

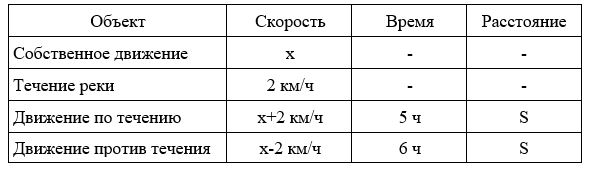
Задача 14.

Расстояние от пристани А до пристани Б по течению реки катер прошёл за 5 часов, а на обратный путь он затратил на 1 час больше. Найдите скорость катера в неподвижной воде (собственную скорость), если скорость течения реки 2 км/ч. 

Решение.
Заполним все исходные данные в таблице. Также заполним другие ячейки таблицы по возможности (такие ячейки выделены зеленым цветом)

• Пусть скорость катера в неподвижной воде равна x км/ч.
• Составим уравнение: 5×(x+2)=6×(x-2); x=22 км/ч.

Правильность решения задач вы можете проверить на сайте intmag24.ru с помощью калькулятора решения задач на движение.

Советы для решения задач на движения

• В процессе решения задач на движение может быть составлена формула квадратного уравнения, которое будет иметь два корня. В этом случае нужно взять тот ответ, который  будет логичен для задачи (положительный). Отрицательный корень не берется во внимание.
• Внимательно следите, чтобы в задаче все данные измерялись одними величинами. Если это не так, нужно се привести к единым единицам измерения.

Памятка «Учимся решать задач на движение»

В задачах на движение  рассматриваются три взаимосвязанные величины:

S — расстояние (пройденный путь),

t — время движения и

V — скорость – расстояние, пройденное за единицу времени.

Расстояние – это произведение скорости на время движения

S = V ● t

Скорость  — это частное от деления расстояния на время движения

V = S : t

Время – это частное от деления расстояния на скорость движения

t = S : V

Задачи на встречное движение

Скорость сближения – это сумма скоростей, движущихся навстречу друг другу тел. V сближ. = 1V + 2V

 Пример 1. Два велосипедиста одновременно выехали навстречу друг другу из двух посёлков и встретились через 3 часа. Первый велосипедист ехал со скоростью 12 км/ч, а второй – 14 км/ч. На каком расстоянии находятся посёлки?

Схема к задаче:

 

Решение:

S = V ● t

V сближ. = 1V + 2V

1 способ:

1) 12 • 3 = 36 (км) – проехал первый велосипедист до встречи

2) 14 • 3 = 42 (км) – проехал второй велосипедист до встречи

3) 36 + 42 = 78 (км)

2 способ:

1) 12 + 14 = 26 (км/ч) – скорость сближения

2) 26 • 3 = 78 (км)

Ответ: расстояние между посёлками 78 км.

 Пример 2. Из двух городов навстречу друг другу выехали две машины. Скорость первой – 80 км/ч, скорость второй – 60 км/ч. Через, сколько часов машины встретятся, если расстояние между городами 280 км?

Схема к задаче:

 

Решение:

V сближ. = 1V + 2V

t = S : V

1) 80 + 60 = 140 (км/ч) – скорость сближения

2) 280 : 140 = 2 (ч)

Ответ: машины встретятся через  2 часа.

 Пример 3. Из двух городов, расстояние между которыми 340 км, выехали одновременно навстречу друг другу две машины. Скорость первой – 80 км/ч. С какой скоростью ехала вторая машина, если встретились они через 2 часа?

Схема к задаче:

 

Решение:

V = S : t

2V = V сближ. — 1V

1) 340 : 2 = 170 (км/ч) – скорость сближения

2) 170 – 80 = 90 (км/ч)

Ответ: 90 км/ч. скорость второй машины

Задачи на движение в противоположных направлениях

Скорость удаления – это расстояние, которое проходят тела за 1 ч при движении в противоположных направлениях. 

V удал. = 1V + 2V

 Пример 1. Два лыжника одновременно вышли из пункта А в противоположных направлениях. Первый лыжник шёл со скоростью 12 км/ч, а второй – 14 км/ч. На каком расстоянии друг от друга они будут через 3 ч?

Схема к задаче:

 Решение:

S = V ● t

1 способ

1)12 • 3 = 36 (км) – расстояние, которое прошёл первый лыжник за 3 ч

2)14 • 3 = 42 (км) – расстояние, которое прошёл второй лыжник за 3 ч

3)36 + 42 = 78 (км) 

2 способ

V удал. = 1V + 2V

S = V ● t

1)12 + 14 = 26 (км/ч) – скорость удаления

2)26 • 3 = 78 (км)

Ответ: через 3 ч они будут друг от друга на расстоянии 78 км.

 Пример 2. Из города в противоположных направлениях выехали две машины. Скорость первой – 80 км/ч, скорость второй – 60 км/ч. Через сколько часов расстояние между машинами будет 280 км?

Схема к задаче:

 

Решение:

V удал. = 1V + 2V

t = S : V

1) 80 + 60 = 140 (км/ч) – скорость удаления

2) 280 : 140 = 2 (ч)

Ответ: через 2 часа расстояние между машинами будет 280 км

Пример 3. Из города одновременно в противоположных направлениях выехали две машины. Скорость первой – 80 км/ч. С какой скоростью ехала вторая машина, если через 2 часа расстояние между ними было 340 км?

Схема к задаче:

  

Решение:

V = S : t

2V = V удал. — 1V

1) 340 : 2 = 170 (км/ч) – скорость удаления машин

2) 170 – 80 = 90 (км/ч)

Ответ: скорость второй машины 90 км/ч.

Схемы задач на движение очень просто нарисовать. Они помогают представить наглядно условие задачи и найти верное решение. В дополнение к схеме в сложных случаях или когда ученик затрудняется с решением рекомендуется рисовать таблицу, где в шапке параметры скорости, времени и расстояния. Об этом подробнее ниже.

Узнайте также, как составить схемы к задачам по математике для 2 класса

Простые задачи на движение

Простые задачи про путников, лыжников, мотоциклистов и другие движущиеся объекты (встречаются даже задачки про черепах) начинают решать еще в начальных классах. Именно на этих примерах удобно разбирать составление схем.  

Задача 1. Пешеход вышел из пункта А в пункт Б со скоростью 5 км/ч. Через 3 часа он добрался до пункта Б. Какое расстояние между этими двумя пунктами?

Рисуем схему к задаче: прямая линия, соединяющая точки А и Б — это весь путь. Стрелкой обозначаем направление движения путника. Над стрелкой отмечаем скорость, если известна. Время или расстояние отмечаем под (или над) отрезком:

Если со схемой вы не смогли решить задачу, то предлагаю вам воспользоваться таблицей:

скорость	время	расстояние
5 км/ч	3 ч	? км

Чтобы решать с помощью таблицы, запомните правила:

• Чтобы найти расстояние, нужно скорость умножить на время: S = V x t
• Чтобы найти скорость, нужно расстояние разделить на время, (это производное из первой формулы:
  V = S : t )
• чтобы найти время, необходимо расстояние разделить на скорость. (также просто вывести из первой формулы:
  t = S : t

Решение

5 х 3 = 15 км — расстояние между пунктами А и Б

Обратные задачи на движение

Как найти скорость, если известно время и расстояние

Чтобы не путать вас разными условиями задачи состав задачу, обратную первому примеру:

Задача 2. Расстояние между пунктами А и Б равно 15 км. Путник преодолел это расстояние за 3 часа. С какой скоростью шел пешеход?

скорость	время	расстояние
? км/ч	3 ч	15 км

Решение

15 : 3 = 5 км/ч

Как найти время, когда известны скорость и расстояние

Задача 3. Расстояние между пунктами 15 км. Пешеход шел со скоростью 5 км/ч. За какое время пешеход преодолеет весь путь?

Скорость	время	расстояние
5 км/ч	? ч	15 км

Решение

15 : 5 = 3 часа

Схемы задач на встречное движение

Чтобы начертить встречное движение, мы рисуем стрелочки из двух пунктов навстречу. Флажком обозначаем место встречи

Когда задачи со встречным или удаляющимся движением — это задачи на общую скорость. Скоро будет подробный урок о них на моем сайте. 

Задача 4. Два пешехода вышли одновременно из пунктов А и Б навстречу друг другу. Скорость одного — 5 км/ч, другого — 3 км/ч. Через какое время они встретятся, если известно, что расстояние между пунктами 24 км?

Решение

1 способ:

5 + 3 =8 км/ч — общая скорость

24 : 8 = 3 часа

Задачи на движение в одном направлении

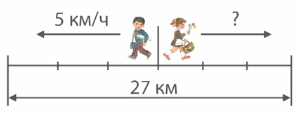
Задача 5. Два пешехода вышли из пунктов А и Б одновременно в одном направлении. Пешеход, который шел впереди, двигался со скоростью 3 км/ч, а второй — со скоростью 5 км/ч. Через какое время второй пешеход догонит первого, если расстояние между пунктами 2 км?

Здесь нужно выяснить скорость сближения. Так как один пешеход шел быстрее второго, то расстояние между ними сокращалось на 2 км/ч (мы посчитали так: 5 — 3 = 2 км/ч). Так как первоначальное расстояние между пунктами 2 км, то найдем время:

2км : 2 км/ч = 1 час.

Через 1 час пешеходы встретятся. 

Шпаргалка по решению задач на скорость, время и расстояние

Вы можете воспользоваться данной памяткой при решении этого типа задач. Кликните для просмотра в полном размере и распечатайте, нажав на клавиатуре клавиши CTRL + P.

Кому и для чего будет полезна статья?

• Статья о задачах на движение полезна учащимся 4 класса, родителям и учителям.
• Помогает развить логическое мышление и математические навыки.
• Предоставляет примеры и объяснения простых задач на движение.
• Улучшает понимание концепций расстояния, времени и скорости.
• Дает полезные советы и подходы к решению задач.
• Помогает учителям подготовить уроки и объяснить материал ученикам.
• Способствует активному и интересному изучению физики и математики.
• Развивает навыки и готовит к дальнейшему изучению наук.

Существует несколько типов задач на движение. Примеры решения всех типов задач с пояснениями мы рассмотрим в этой статье.

Задачи на нахождение скорости, времени и расстояния

Ниже вы найдете базовые задачи по теме движения с ответами, которые школьники проходят в 4 классе.

Скорость

Рассмотрим простую задачу на движение в 4 классе:

Андрей пробежал расстояние 200 метров за 40 секунд. Какова была его скорость?

Решение:

Для решения задачи используем формулу скорости:

Скорость = Расстояние / Время

В данной задаче известны расстояние (200 метров) и время (40 секунд). Подставляем эти значения в формулу:

Скорость = 200 м / 40 с = 5 м/с

Таким образом, скорость Андрея равна 5 метров в секунду.

Время

Рассмотрим простую задачу на нахождение времени в 4 классе:

Вася пробежал расстояние 300 метров со скоростью 10 м/с. За какое время он пробежал это расстояние?

Решение:

Для решения задачи используем формулу времени:

Время = Расстояние / Скорость

В данной задаче известны расстояние (300 метров) и скорость (10 м/с). Подставляем эти значения в формулу:

Время = 300 м / 10 м/с = 30 секунд

Таким образом, Вася пробежал расстояние 300 метров за 30 секунд.

Расстояние

Давай рассмотрим простую задачу на нахождение расстояния в 4 классе:

Петя прошел пешком 15 метров за 5 секунд. Какое расстояние он пройдет за 10 секунд?

Решение:

Для решения задачи используем формулу расстояния:

Расстояние = Скорость × Время

В данной задаче известны скорость (15 метров за 5 секунд) и время (10 секунд). Подставляем эти значения в формулу:

Расстояние = 15 м/с × 10 с = 150 метров

Таким образом, Петя пройдет 150 метров за 10 секунд.

Задачи на движение в одном направлении

Задачи на движении в одном направлении относятся к одному из трех основных видов задач на движение.
Если два объекта выехали из одного пункта одновременно, то, поскольку они имеют разные скорости, объекты удаляются друг от друга. Чтобы найти скорость удаления, надо из большей скорости вычесть меньшую:

Если из одного пункта выехал один объект, а спустя некоторое время в том же направлении вслед за ним выехал другой объект, то они могут как сближаться, так и удаляться друг от друга.
Если скорость объекта, движущегося впереди, меньше движущегося вслед за ним объекта, то второй догоняет первого и они сближаются.
Чтобы найти скорость сближения, надо из большей скорости вычесть меньшую:

Если скорость объекта, который идет впереди, больше скорости объекта, который движется следом, то второй не сможет  догнать первого и они удаляются друг от друга.
Скорость удаления находим аналогично — из большей скорости вычитаем меньшую:

Задачи на скорость сближения

Задача 1

Из города выехал автомобиль со скоростью 40 км/ч. Через 4 часа вслед за ним выехал второй автомобиль со скоростью 60 км/ч. Через сколько часов второй автомобиль догонит первый?

Решение:

Так как на момент выезда второго автомобиля из города первый уже был в пути 4 часа, то за это время он успел удалится от города на:

40 · 4 = 160 (км)

Второй автомобиль движется быстрее первого, значит каждый час расстояние между автомобилями будет сокращаться на разность их скоростей:

60 — 40 = 20 (км/ч) – это скорость сближения автомобилей

Разделив расстояние между автомобилями на скорость их сближения, можно узнать, через сколько часов они встретятся:

160 : 20 = 8 (ч)

Решение задачи по действиям можно записать так:

1) 40 · 4 = 160 (км) – расстояние между автомобилями

2) 60 — 40 = 20 (км/ч) – скорость сближения автомобилей

3) 160 : 20 = 8 (ч)

Ответ: Второй автомобиль догонит первый через 8 часов.

Задача 2

Из двух посёлков между которыми 5 км, одновременно в одном направлении вышли два пешехода. Скорость пешехода, идущего впереди, 4 км/ч, а скорость пешехода, идущего позади 5 км/ч. Через сколько часов после выхода второй пешеход догонит первого?

Решение: 

Так как второй пешеход движется быстрее первого, то каждый час расстояние между ними будет сокращаться. Значит можно определить скорость сближения пешеходов:

5 — 4 = 1 (км/ч)

Оба пешехода вышли одновременно, значит расстояние между ними равно расстоянию между посёлками (5 км). Разделив расстояние между пешеходами на скорость их сближения, узнаем через сколько второй пешеход догонит первого:

5 : 1 = 5 (ч)

Решение задачи по действиям можно записать так:

1) 5 — 4 = 1 (км/ч) – это скорость сближения пешеходов

2) 5 : 1 = 5 (ч)

Ответ: Через 5 часов второй пешеход догонит первого.

Задача 3

Из одного села в одном направлении одновременно выехали два велосипедиста. Скорость одного из них — 15 км/ч, скорость другого — 12 км/ч. Какое расстояние будет через ними через 4 часа?

Решение:

1) 15-12=3 (км/ч) скорость удаления велосипедистов

2) 3∙4=12 (км) такое расстояние будет между велосипедистами через 4 часа.

Ответ: Через 4 часа расстояние между велосипедистами составит 12 км.

Задача 4

Из села на станцию одновременно вышел пешеход и выехал велосипедист. Через 2 часа велосипедист опережал пешехода на 12 км. Найти скорость пешехода, если скорость велосипедиста 10 км/ч.

Решение:

1) 12:2=6 (км/ч) скорость удаления велосипедиста и пешехода

2) 10-6=4 (км/ч) скорость пешехода.

Ответ: Скорость пешехода составляет 4 км/ч.

Задачи на скорость удаления

Задача 1

Два автомобиля выехали одновременно из одного и того же пункта в одном направлении. Скорость первого автомобиля 80 км/ч, а скорость второго – 40 км/ч.

1. Чему равна скорость удаления между автомобилями?
2. Какое расстояние будет между автомобилями через 3 часа?
3. Через сколько часов расстояние между ними будет 200 км?

Решение:

Сначала узнаем скорость удаления автомобилей друг от друга, для этого вычтем из большей скорости меньшую:

80 — 40 = 40 (км/ч)

Каждый час автомобили отдаляются друг от друга на 40 км. Теперь можно узнать сколько километров будет между ними через 3 часа, для этого скорость удаления умножим на 3:

40 · 3 = 120 (км)

Чтобы узнать через сколько часов расстояние между автомобилями станет 200 км, надо расстояние разделить на скорость удаления:

200 : 40 = 5 (ч)

Ответ:

1. Скорость удаления между автомобилями равна 40 км/ч.
2. Через 3 часа между автомобилями будет 120 км.
3. Через 5 часов между автомобилями будет расстояние в 200 км.

Движение навстречу друг другу

Если два объекта движутся навстречу друг другу, то они сближаются. Чтобы найти скорость сближения двух объектов, движущихся навстречу друг другу, надо сложить их скорости:  

Скорость сближения больше, чем скорость каждого из них.

Задача 1

Из поселка и города навстречу друг другу, одновременно выехали два автобуса. Один автобус до встречи проехал 100 км со скоростью 25 км/час. Сколько километров до встречи проехал второй автобус, если его скорость 50 км/час.

Решение:

1) 100 : 25 = 4 (часа ехал один автобус)

2) 50 * 4 = 200

Решение в виде выражения: 50 * (100 : 25) = 200

Ответ: второй автобус проехал до встречи 200 км.

Расстояние между двумя пристанями 90 км. От каждой из них одновременно навстречу друг другу вышли два теплохода. Сколько часов им понадобится чтобы встретиться, если скорость первого 20 км/час, а второго 25 км/час?

Решение:

1) 25 + 20 = 45 (сумма скоростей теплоходов)

2) 90 : 45 = 2

Решение в виде выражения:90 : (20 + 25) = 2

Ответ: Теплоходы встретятся через 2 часа.

Задача 3

От двух станций, расстояние между которыми 564 км., одновременно навстречу друг другу вышли два поезда. Скорость одного из них 63 км/час. Какова скорость второго, если поезда встретились через 4 часа?

Решение:

1) 63 * 4 = 252 (прошел 1 поезд)

2) 564 — 252 =312 (прошел 2 поезд)

3) 312 : 4 = 78

Решение в виде выражения (63 * 4 — 252) : 4 = 78

Ответ: Скорость второго поезда 78 км/час.

Задача 4

Два велосипедиста выехали навстречу друг другу. Скорость одного из низ 12 км/ч, а другого — 10 км/ч. Через 3 часа они встретились. Какое расстояние было между ними в начале пути?

Решение:

1) 12+10=22 (км/ч) скорость сближения велосипедистов

2) 22∙3=66 (км) было между велосипедистами в начале пути.

Ответ: Расстояние между велосипедистами в начале пути было 66 км.

Задача 5

Два поезда идут навстречу друг другу. Скорость одного из них 50 км/ч, скорость другого —  60 км/ч. Сейчас между ними 440 км. Через сколько часов они встретятся?

Решение:

1) 60+50=110 (км/ч) скорость сближения поездов

2) 440:110=4 (ч) время, через которое поезда встретятся.

Ответ: Поезда встретятся через 4 часа.

Движение в противоположных направлениях

Если два объекта движутся в противоположных направлениях, то они удаляются. Чтобы найти скорость удаления, надо сложить скорости этих объектов:

Скорость удаления больше скорости любого из них.

Задача 1

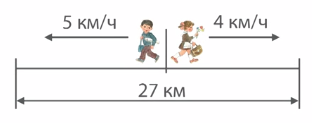
Из поселка вышли одновременно в противоположных направлениях два пешехода. Средняя скорость одного пешехода – 5 км/ч, другого – 4 км/ч. Через сколько часов расстояние между ними будет 27 км ?

Решение:

Чтобы найти время движения пешеходов, нужно знать расстояние и скорость пешеходов. Мы знаем, что за каждый час один пешеход удаляется от поселка на 5 км, а другой пешеход удаляется от поселка на 4 км. Можем найти их скорость удаления.

1. 

 (км/ч)

Мы знаем скорость удаления и знаем все расстояние – 27 км. Можем найти время, через которое пешеходы удалятся друг от друга на 27 км, для этого нужно расстояние разделить на скорость.

2. 

 (ч)

Ответ: Через три часа расстояние между переходами будет 27 км.

Задача 2

Из поселка вышли одновременно в противоположных направлениях два пешехода. Через 3 часа расстояние между ними было 27 км. Первый пешеход шел со скоростью 5 км/ч. С какой скоростью шел второй пешеход ?

Решение:

Чтобы узнать скорость второго пешехода, надо знать расстояние, которое он прошел, и его время в пути. Чтобы узнать, какое расстояние прошел второй пешеход, надо знать, какое расстояние прошел первый пешеход и общее расстояние. Общее расстояние мы знаем. Чтобы найти расстояние, которое прошел первый пешеход, надо знать его скорость и его время в пути. Средняя скорость движения первого пешехода – 5 км/ч, его время в пути – 3 часа. Если среднюю скорость умножить на время в пути, получим расстояние, которое прошел пешеход:

1. 

 (км)

Мы знаем общее расстояние и знаем расстояние, которое прошел первый пешеход. Можем теперь узнать, какое расстояние прошел второй пешеход.

2. 

 (км)

Теперь мы знаем расстояние, которое прошел второй пешеход, и время, проведенное им в пути. Можем найти его скорость.

3. 

 (км/ч)

Ответ: Скорость второго пешехода – 4 км/ч.

Задача 3

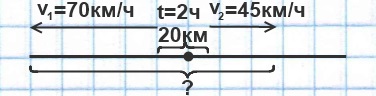
Товарный и пассажирский поезда движутся в противоположных направлениях. Скорость товарного 45 км/ч, скорость пассажирского — 70 км/ч. Сейчас между ними 20 км. Какое расстояние будет между ними через 2 часа ?

Решение:

1) 70+45=115 (км/ч) скорость удаления поездов

2) 115∙2=230 (км) пройдут поезда вместе за 2 часа

3) 230+20=250 (км) такое расстояние между поездами будет через 2 часа.

Ответ: Через 2 часа расстояние между поездами составит 250 км.

Задача 4

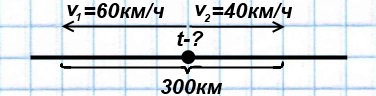
Из одного пункта одновременно в противоположных направлениях выехали два мотоциклиста. Скорость одного из них — 60 км/ч, скорость другого — 40 км/ч. Через какое время расстояние между ними станет равным 300 км?

Решение:

1) 60+40=100 (км/ч) скорость удаления мотоциклистов

2) 300:100=3 (ч) через такое время расстояние между ними будет 300 км.

Ответ: Расстояние между мотоциклистами станет 300 км через 3 часа.

Что мы узнали?

В статье были рассмотрены различные варианты задач и примерами их решений, которые пригодятся всем четвероклассникам.

• В 4 классе школьники решают простые задачи на движение, связанные с понятиями расстояния, времени и скорости.

• Они изучают задачи, которые требуют определения скорости по известному расстоянию и времени, или определения времени по известной скорости и расстоянию.

• Школьники решают задачи, связанные с равномерным прямолинейным движением, где известны расстояние и время, и нужно найти скорость.

• Они также могут сталкиваться с задачами, где требуется определить расстояние по известной скорости и времени.

• Задачи на движение помогают ребятам развить навыки анализа и применения математических концепций к реальным ситуациям.

Пример №1

Допустим, из точки ( displaystyle A) и из точки ( displaystyle B) навстречу друг другу выехали две машины. Скорость одной машины – ( displaystyle 60) км/ч, а скорость ( displaystyle 2) машины – ( displaystyle 40) км/ч. Они встретились через ( displaystyle 1,2) часа.

Какое расстояние между пунктами ( displaystyle A) и ( displaystyle B)?

1 вариант решения

Можно рассуждать так: машины встретились, значит расстояние между городами – это сумма расстояния, которая прошла первая машина, и расстояния, которое прошла вторая.

( displaystyle 60cdot 1,2text{ }=text{ }72) (км) – путь, который проехала первая машина

( displaystyle 40cdot 1,2text{ }=text{ }48) (км) – путь, который проехала вторая машина

( displaystyle 72 + 48 = 120) (км) – расстояние, которое проехали обе машины, то есть, расстояние между пунктами ( displaystyle A) и ( displaystyle B).

2 вариант решения (более рациональный)

А можно просто воспользоваться очень логичной формулой о сложении скоростей.

Проверим, работает ли она:

( displaystyle 60 + 40 = 100) (км/ч) – скорость сближения машин

( displaystyle 100cdot 1,2text{ }=text{ }120) (км) – расстояние, которые проехали машины, то есть, расстояние между пунктами ( displaystyle A) и ( displaystyle B).

Оба решения являются верными. Второе просто более рациональное.

Пример №3

Итак, задача:

Из пункта ( displaystyle A) и пункта ( displaystyle B) машины движутся навстречу друг другу со скоростями ( displaystyle 50) км/ч и ( displaystyle 80) км/ч. Расстояние между пунктами – ( displaystyle 195) км.

Через сколько времени машины встретятся?

1 вариант решения

Пусть ( displaystyle x) – время, которое едут машины, тогда путь первой машины – ( displaystyle 50x), а путь второй машины – ( displaystyle 80x).

Их сумма и будет равна расстоянию между пунктами ( A) и ( B) – ( displaystyle 50x+80x=195).

2 вариант решения (более рациональный)

( displaystyle 50 + 80 = 130) (км/ч) – скорость сближения машин;

( displaystyle 195:130 = 1,5) (ч) – время, которое машины были в пути.

Задача решена.

Пример №4

Из пунктов A и B одновременно навстречу друг другу выехали два автомобиля со скоростями ( displaystyle 60) км/ч и ( displaystyle 40) км/ч. Через сколько минут они встретятся. Если расстояние между пунктами ( displaystyle 100) км?

2 способа решения:

I способ

Относительная скорость автомобилей ( displaystyle 60+40=100) км/ч. Это значит, что если мы сидим в первом автомобиле, то он нам кажется неподвижным, но второй автомобиль приближается к нам со скоростью ( displaystyle 100) км/ч. Так как между автомобилями изначально расстояние ( displaystyle 100) км, время, через которое второй автомобиль проедет мимо первого:

( displaystyle t=frac{100}{100}=1 час=60 минут).

II способ

Время от начала движения до встречи у автомобилей, очевидно, одинаковое. Обозначим его ( displaystyle t). Тогда первый автомобиль проехал путь ( displaystyle 60t), а второй – ( displaystyle 40t).

В сумме они проехали все ( displaystyle 100) км. Значит,

( displaystyle 60t+40t=100Rightarrow t=1 час=60 минут).

Из пункта ( displaystyle A) в пункт ( displaystyle B), расстояние между которыми ( displaystyle 30) км, одновременно выехал велосипедист и мотоциклист. Известно, что в час мотоциклист проезжает на ( displaystyle 65) км больше, чем велосипедист.

Определите скорость велосипедиста, если известно, что он прибыл в пункт ( displaystyle B) на ( displaystyle 156) минут позже, чем мотоциклист.

Вот такая вот задача. Соберись, и прочитай ее несколько раз. Прочитал? Начинай рисовать – прямая, пункт ( displaystyle A), пункт ( displaystyle B), две стрелочки…

В общем рисуй, и сейчас сравним, что у тебя получилось.

Пустовато как-то, правда? Рисуем таблицу.

Как ты помнишь, все задачи на движения состоят из ( displaystyle 3) компонентов: скорость, время и путь. Именно из этих граф и будет состоять любая таблица в подобных задачах.

Правда, мы добавим еще один столбец – имя, про кого мы пишем информацию – мотоциклист и велосипедист.

Так же в шапке укажи размерность, в какой ты будешь вписывать туда величины. Ты же помнишь, как это важно, правда?

У тебя получилась вот такая таблица?

	Скорость, км/ч	Время t, часов	Путь S, км
велосипедист
мотоциклист

Теперь давай анализировать все, что у нас есть, и параллельно заносить данные в таблицу и на рисунок.

Первое, что мы имеем – это путь, который проделали велосипедист и мотоциклист. Он одинаков и равен ( displaystyle 30) км. Вносим!

	Скорость, км/ч	Время t, часов	Путь S, км
велосипедист			( displaystyle 30)
мотоциклист			( displaystyle 30)

Рассуждаем дальше. Мы знаем, что мотоциклист проезжает на ( displaystyle 65) км/ч больше, чем велосипедист, да и в задаче нужно найти скорость велосипедиста…

Возьмем скорость велосипедиста за ( displaystyle x), тогда скорость мотоциклиста будет ( displaystyle x+65)…

Если с такой переменной решение задачи не пойдет – ничего страшного, возьмем другую, пока не дойдем до победного. Такое бывает, главное не нервничать!

	Скорость, км/ч	Время t, часов	Путь S, км
велосипедист	( displaystyle x)		( displaystyle 30)
мотоциклист	( displaystyle x+65)		( displaystyle 30)

Таблица преобразилась. У нас осталась не заполнена только одна графа – время. Как найти время, когда есть путь и скорость?

Правильно, разделить путь на скорость. Вноси это в таблицу.

	Скорость, км/ч	Время t, часов	Путь S, км
велосипедист	( displaystyle x)	( displaystyle frac{30}{x})	( displaystyle 30)
мотоциклист	( displaystyle x+65)	( displaystyle frac{30}{65+x})	( displaystyle 30)

Вот и заполнилась наша таблица, теперь можно внести данные на рисунок.

Что мы можем на нем отразить?

Молодец. Скорость передвижения мотоциклиста и велосипедиста.

Еще раз перечитаем задачу, посмотрим на рисунок и заполненную таблицу.

Какие данные не отражены ни в таблице, ни на рисунке?

Верно. Время, на которое мотоциклист приехал раньше, чем велосипедист. Мы знаем, что разница во времени – ( displaystyle 156) минут.

Что мы должны сделать следующим шагом? Правильно, перевести данное нам время из минут в часы, ведь скорость дана нам в км/ч.

( displaystyle 156) минут / ( displaystyle 60) минут = ( displaystyle 2,6) часа.

И что дальше, спросишь ты? А дальше числовая магия!

Взгляни на свою таблицу, на последнее условие, которое в нее не вошло и подумай, зависимость между чем и чем мы можем вынести в уравнение?

Правильно. Мы можем составить уравнение, основываясь на разнице во времени!

( displaystyle frac{30}{x}-frac{30}{65+x}=2,6)

Логично? Велосипедист ехал больше, если мы из его времени вычтем время движения мотоциклиста, мы как раз получим данную нам разницу.

Это уравнение – рациональное. Если не знаешь, что это такое, прочти тему «Рациональные уравнения».

Приводим слагаемые к общему знаменателю:

( displaystyle frac{30cdot left( 65+x right)}{xcdot left( 65+x right)}-frac{30x}{xcdot left( 65+x right)}=2,6)

Раскроем скобки и приведем подобные слагаемые: Уф! Усвоил? Попробуй свои силы на следующей задаче.

( displaystyle frac{1950}{xcdot left( 65+x right)}=2,6)

Из этого уравнения мы получаем следующее:

( displaystyle 2,6cdot xcdot left( 65+x right)=1950)

( displaystyle xcdot left( 65+x right)=frac{1950}{2,6})

( displaystyle xcdot left( 65+x right)=750)

Раскроем скобки и перенесем все в левую часть уравнения:

( displaystyle {{x}^{2}}+65{x}-750=0)

Вуаля! У нас простое квадратное уравнение. Решаем!

( displaystyle {{x}^{2}}+65{x}-750=0)

( displaystyle D={{b}^{2}}-4ac)

( displaystyle D={{65}^{2}}-4cdot 1cdot left( -750 right)=4225+3000=7225)

( displaystyle sqrt{D}=sqrt{7225}=85)

( displaystyle {{x}_{1,2}}=frac{-bpm sqrt{D}}{2a})

( displaystyle {{x}_{1}}=frac{-65+85}{2}=10)

( displaystyle {{x}_{2}}=frac{-65-85}{2}=-75)

Мы получили два варианта ответа. Смотрим, что мы взяли за ( displaystyle x)? Правильно, скорость велосипедиста.

Вспоминаем правило «3Р», конкретнее «разумность». Понимаешь, о чем я? Именно! Скорость не может быть отрицательной, следовательно, наш ответ – ( displaystyle 10) км/ч.

Пример №9

Два велосипедиста одновременно отправились в ( displaystyle 165)-километровый пробег. Первый ехал со скоростью, на ( displaystyle 5) км/ч большей, чем скорость второго, и прибыл к финишу на ( displaystyle 5,5) часов раньше второго.

Найти скорость велосипедиста, пришедшего к финишу вторым. Ответ дайте в км/ч.

Напоминаю:

• Прочитай задачу пару раз – усвой все-все детали. Усвоил?
• Начинай рисовать рисунок – в каком направлении они двигаются? какое расстояние они прошли? Нарисовал?
• Проверь, все ли величины у тебя одинаковой размерности, и начинай выписывать кратко условие задачи, составляя табличку (ты же помнишь, какие там графы?).
• Пока все это пишешь, думай, что взять за ( displaystyle x)? Выбрал? Записывай в таблицу!
• Ну а теперь просто: составляем уравнение и решаем. Да, и напоследок – помни о «3Р»!

Все сделал? Молодец! У меня получилось, что скорость велосипедиста – ( displaystyle 10) км/ч.

Пример №10

Из пункта ( displaystyle A) круговой трассы выехал велосипедист. Через ( displaystyle 40) минут он еще не вернулся в пункт ( displaystyle A) и из пункта ( displaystyle A) следом за ним отправился мотоциклист.

Через ( displaystyle 20) минут после отправления он догнал велосипедиста в первый раз, а еще через ( displaystyle 40) минут после этого догнал его во второй раз.

Найдите скорость велосипедиста, если длина трассы равна ( displaystyle 50) км. Ответ дайте в км/ч.

Попробуй нарисовать рисунок к этой задаче и заполнить для нее таблицу. Вот что получилось у меня:

Пусть скорость велосипедиста будет ( displaystyle x), а мотоциклиста – ( displaystyle y). До момента первой встречи велосипедист был в пути ( displaystyle 60) минут, а мотоциклист – ( displaystyle 20).

При этом они проехали равные расстояния:

( displaystyle 60x=20y (1))

Между встречами велосипедист проехал расстояние ( displaystyle 40x), а мотоциклист – ( displaystyle 40y).

Но при этом мотоциклист проехал ровно на один круг больше, это видно из рисунка:

(Надеюсь, ты понимаешь, что по спирали они на самом деле не ездили – спираль просто схематически показывает, что они ездят по кругу, несколько раз проезжая одни и те же точки трассы.)

Значит,

( displaystyle 40x+50=40y (2))

Полученные уравнения решаем в системе:

( displaystyle left{ begin{array}{l}60x=20y\40x+50=40yend{array} right.Leftrightarrow left{ begin{array}{l}y=3x\4x+5=4yend{array} right.Rightarrow text{4}x+5=12xRightarrow )

( displaystyle Rightarrow x=frac{5}{8}=0,625frac{text{км}}{мин}=0,625cdot 60frac{text{км}}{text{ч}}=37,5frac{text{км}}{text{ч}})

Ответ: ( displaystyle 37,5).

Разобрался? Попробуй решить самостоятельно следующие задачи:

Представь, что у тебя есть плот, и ты спустил его в озеро. Что с ним происходит? Правильно. Он стоит, потому что озеро, пруд, лужа, в конце концов, – это стоячая вода.

Скорость течения в озере равна ( displaystyle 0).

Плот поедет, только если ты сам начнешь грести. Та скорость, которую он приобретет, будет собственной скоростью плота. Неважно куда ты поплывешь – налево, направо, плот будет двигаться с той скоростью, с которой ты будешь грести.

Это понятно? Логично же.

А сейчас представь, что ты спускаешь плот на реку, отворачиваешься, чтобы взять веревку…, поворачиваешься, а он … уплыл…

Это происходит потому что у реки есть скорость течения, которая относит твой плот по направлению течения.

Его скорость при этом равна нулю (ты же стоишь в шоке на берегу и не гребешь) – он движется со скоростью течения.

Разобрался? Тогда ответь вот на какой вопрос – «С какой скоростью будет плыть плот по реке, если ты сидишь и гребешь?» Задумался?

Здесь возможно два случая:

1 случай – ты плывешь по течению, и тогда ты плывешь с собственной скоростью + скорость течения. Течение как бы помогает тебе двигаться вперед.

2 случай – ты плывешь против течения. Тяжело? Правильно, потому что течение пытается «откинуть» тебя назад. Ты прилагаешь все больше усилий, чтобы проплыть хотя бы ( displaystyle 100) метров, соответственно скорость, с которой ты передвигаешься, равна собственная скорость – скорость течения.