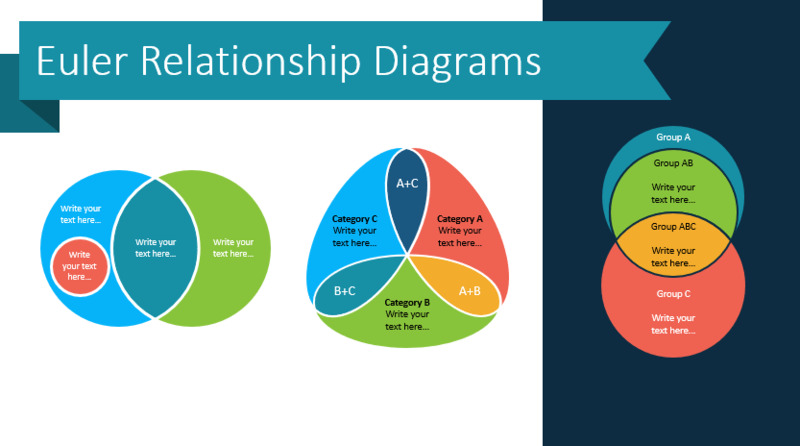
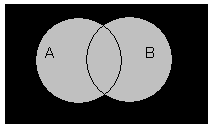
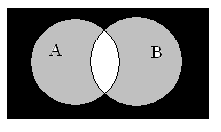
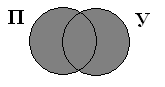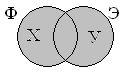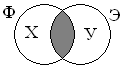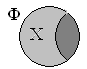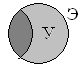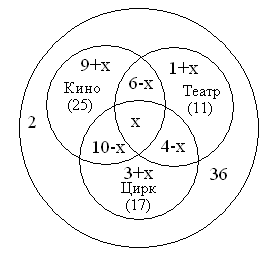Что это такое? Диаграмма Эйлера кажется чем-то очень сложным на первый взгляд. Однако на самом деле это круги, накладываемые друг на друга при решение определенных задач. Их применяют в алгебре, информатике и даже в жизни, столкнувшись с каким-то выбором.
Как строить? Для начала нужно представить универсальное множество в виде прямоугольника. Внутри него будут эллипсы или круги, которые могут пересекаться, а могут и нет. Их можно дополнять, объединять, пересекать. Давайте рассмотрим все это на примере ниже.
В статье рассказывается:
- Что собой представляет диаграмма Эйлера
- Разница между диаграммой Эйлера и диаграммой Эйлера-Венна
- Задачи, решаемые диаграммой Эйлера
- Принцип построения диаграммы
- Применение диаграмм для доказательства логических равенств
- Пример решения задачи с помощью кругов Эйлера
-
Пройди тест и узнай, какая сфера тебе подходит:
айти, дизайн или маркетинг.Бесплатно от Geekbrains
Что собой представляет диаграмма Эйлера
Так называется геометрическое изображение, которое используют, чтобы смоделировать множества и схематично отразить отношения между ними. На диаграмме Эйлера наглядно показаны утверждения о данных множествах.
При этом универсальное множество обозначено прямоугольником, а подмножества изображены в виде кругов. Поэтому диаграмму называют также «круги Эйлера». Такое схематичное изображение применяют при решении математических и логических задач, а также в менеджменте и различных прикладных целях.
Автор этого способа – математик XVIII века Леонард Эйлер, который хотел таким образом помочь размышлениям. Автором кругов является известный математик Леонард Эйлер, который считал, что они необходимы, чтобы облегчить размышления человека. Диаграмма Эйлера стала признанным методом с момента своего появления.
Биография Леонарда Эйлера связана со Швейцарией, Пруссией и Россией. Этот учёный оказал огромное влияние на развитие математики, механики, физики. Его научные работы (более 850 трудов) затрагивают теорию чисел, теорию музыки, оптику, баллистику, небесную механику. Среди его трудов имеется ряд основополагающих монографий. Около половины жизни Эйлер провёл в России, работал в Петербургской Академии наук и много вложил в развитие российской науки.
Скачать
файл
В дальнейшем в работах многих учёных используется диаграмма Эйлера для множеств: это математики Бернард Больцано и Эрнест Шредер; философ и логик Джон Венн и другие. В наши дни эту методику применяют для развития мышления как при очном обучении, так и на различных онлайн-курсах.
Разница между диаграммой Эйлера и диаграммой Эйлера-Венна
Диаграммы Эйлера-Венна – это частный случай кругов Эйлера, который показывает все 2π{displaystyle 2^{n}} комбинаций π{displaystyle n} свойств, то есть конечную булеву алгебру. При π = 3 диаграмма Эйлера-Венна обычно выглядит как три круга, имеющих одинаковый радиус, их центры совпадают с вершинами равностороннего треугольника, стороне которого приблизительно равны радиусы.
Если определённая комбинация свойств соответствует пустому множеству, на схеме эту область закрашивают. Диаграммы Эйлера могут быть не типичны, а иногда эквивалентны диаграммам Венна. Закрашенный участок схемы указывает на то, что это множество не содержит элементов, то есть пустое.
Задачи, решаемые диаграммой Эйлера
Прикладное значение, которое имеет диаграмма Эйлера: задачи на соотношение множеств в математике, логике, информатике, статистике становятся понятнее при её использовании. Круги Эйлера можно применять и в жизни, находя с их помощью взаимосвязи и отвечая на возникающие насущные вопросы.
Круги Эйлера можно разделить на такие группы:
- равнозначные;
- пересекающиеся;
- подчиненные;
- соподчиненные;
- противоречащие;
- противоположные.

Читайте также
Выполняя упражнения на развитие мышления, чаще всего можно столкнуться с двумя их видами:
- Круги, изображающие объединяющиеся понятия и вложенные один в другой, чтобы это показать.
- Круги, иллюстрирующие пересечения различных множеств, которые имеют те или иные общие признаки.
Топ-30 самых востребованных и высокооплачиваемых профессий 2023
Поможет разобраться в актуальной ситуации на рынке труда
Подборка 50+ ресурсов об IT-сфере
Только лучшие телеграм-каналы, каналы Youtube, подкасты, форумы и многое другое для того, чтобы узнавать новое про IT
ТОП 50+ сервисов и приложений от Geekbrains
Безопасные и надежные программы для работы в наши дни
Уже скачали 20958
Приведём пример использования кругов при выборе профессии. Можно перебирать варианты, обдумывая наиболее подходящий, а можно начертить схему, изобразив в виде кругов то, что вам нравится делать, что вы умеете, и что хорошо оплачивается. Получится диаграмма Эйлера. Пересечение этих трёх кругов и показывает, что будет наиболее вам подходить.
Метод прост в применении и подходит для всех. Его используют и при работе с дошкольниками в детском саду с 4-5 лет, и при обучении студентов (например, можно увидеть подобные задачи в ЕГЭ по информатике), и в научной среде.
Принцип построения диаграммы
При построении диаграммы Эйлера сначала рисуют большой прямоугольник, обозначающий универсальное множество U. Внутри этого прямоугольника располагают фигуры, которые являются изображением множеств: круги (если их не больше трёх) или круги и эллипсы (когда множеств четыре и больше). Фигуры пересекаются различными способами, в зависимости от условий задачи.
Допустим, у нас имеется выражение А. Изображаем на диаграмме круг, обозначающий множество А. Пространство внутри круга показывает значения, при которых выражение А будет истинным, а область снаружи обозначает ложь. Чтобы отобразить на схеме логическую операцию, заштрихуем те части диаграммы, в которых значения истинны. В результате мы отмечаем область, где множества пересекаются.
Можно доказать любой закон алгебры, представив его в виде графической схемы при помощи диаграммы Эйлера. Алгоритм действий таков:
- Сначала чертим диаграмму и заштриховываем все множества, которые находятся с левой стороны от знака «равно».
- Затем нужно начертить другую диаграмму и на ней заштриховать множества, находящиеся справа от знака равенства.
- Если на диаграммах окажется заштрихованной одна и та же область, тождество будет истинным.
Сильнее углубимся в тему.
Дополнение множества
Дополнением к множеству A будет множество Его элементы не относятся к множеству А.
= {x | x ∉ A}
Но в включаются не все элементы, не относящиеся к А. По условиям применения диаграммы Эйлера, все множества, о которых идёт речь в задаче, будут включены в универсальное множество U, то есть являются его подмножествами. С учётом этого дополнение будет определяться так:
=U∖A
Объединение множеств
Объединением двух множеств (назовём их А и В) будет множество A ∪ B, состоящее из элементов, которые включаются хотя бы в одно из них.
Это можно записать так:
A ∪ B={x |x ∈ A или x ∈ B}
Пересечение множеств
Пересечение множеств A и B это множество A ∩ B. Оно состоит из элементов, которые входят и в множество А, и в то же время в множество В.
Только до 29.05
Скачай подборку тестов, чтобы определить свои самые конкурентные скиллы
Список документов:



Чтобы получить файл, укажите e-mail:
Подтвердите, что вы не робот,
указав номер телефона:
Уже скачали 7503
Записывается пересечение множеств так:
A ∩ B = {x | x ∈ A и x ∈ B}
Симметричная разность множеств
Симметричная разность – это множество A B, в которое включаются элементы, которые входят только в одно из множеств А и В, но не в оба сразу.
Запись симметричной разности выглядит таким образом:
A △ B = (A ∖ B) ∪ (B ∖ A)
Разность множеств
Разностью A B являются элементы множества A, не входящие в B.
Записанная разность множеств выглядит так:
A ∖ B = {x | x ∈ A и x ∉ B}
Применение диаграмм для доказательства логических равенств
Давайте рассмотрим, как применяется диаграмма Эйлера на примере доказательства логического равенства.
Представим, что мы имеем конъюнкцию множеств A ∧ B.
Сначала работаем с левой частью равенства. Нужно с помощью диаграммы Эйлера построить множества А и В, заштриховать оба круга цветом и таким образом выделим дизъюнкцию.
Дальше нужно показать инверсию с помощью штриховки области за пределами этих множеств.
Теперь переключаемся на правую часть равенства. Сперва показываем цветной штриховкой за пределами круга А инверсию этого множества.
То же самое действие выполняем для множества В.
Штрихуем чёрным цветом все области пересечения и получаем графическое отображение конъюкции инверсий множеств А и В.
Сравнивая области, отображающие правую и левую части равенства, убеждаемся, что они равны. Таким образом, истинность логического равенства доказана при помощи диаграммы Эйлера.
Пример решения задачи с помощью кругов Эйлера
В демонстрационном тесте ЕГЭ по информатике и ИКТ была представлена задача, которую мы решим с применением этого метода.
Условия задачи:
В языке запросов поискового применяется символ «|» для логической операции «или» и символ «&», чтобы обозначить логическую операцию «и».
Таблица, приведённая ниже, отражает запросы в некотором сегменте сети Интернет и количество найденных страниц по этим запросам.
| Запрос | Найдено страниц (в тысячах) |
| Крейсер | Линкор | 7000 |
| Крейсер | 4800 |
| Линкор | 4500 |
Вопрос: какое количество страниц (в тысячах) найдётся, если запрос будет сформулирован в виде Крейсер & Линкор?
Принимаем версию, что все запросы выполняются в один отрезок времени, поэтому набор страниц, которые включают искомые слова, остался неизменным.
Решение:
Покажем условие задачи при помощи диаграммы Эйлера. Используем цифры 1, 2 и 3 для обозначения полученных областей.

Читайте также
Используя условия задачи, составляем уравнения:
- Крейсер | Линкор: 1 + 2 + 3 = 7000
- Крейсер: 1 + 2 = 4800
- Линкор: 2 + 3 = 4500
Искомая область Крейсер & Линкор обозначенная на чертеже цифрой 2, находится путём подстановки уравнения (2) в уравнение (1). Получаем следующее:
4800 + 3 = 7000, откуда получаем область 3, равную 2200.
Полученный результат мы подставляем в уравнение (3). Получаем результат:
Область 2 + 2200 = 4500, значит, она равна 2300.
Ответ: будет найдено 2300 страниц по запросу Крейсер & Линкор.
Этот пример показывает, что можно решать с помощью диаграммы Эйлера задачи, являющиеся достаточно сложными или запутанными.
Можно сделать вывод, что круги Эйлера не просто занимательный, но и полезный в плане решения учебных и бытовых задач метод. Многие вещи можно представить в виде множеств, а поможет наглядно представить их пересечение или объединение диаграмма Эйлера.
Любопытно, что современная массовая культура применяет круги Эйлера для создания мемов, а также их можно встретить в таких сериалах, как «Теория большого взрыва» и «4исла».
Советуем применять этот метод для решения задач и непременно поделитесь этим полезным и наглядным способом с друзьями.
Как составить диаграмму Эйлера-Венна
Содержание:
- Диаграмма Эйлера-Венна — что из себя представляет, где используется
-
Принципы построения, как изобразить множества
- Дополнение множества
- Объединение множеств
- Пересечение множеств
- Разность множеств
- Симметричная разность множеств
- Использование диаграмм Эйлера-Венна для доказательства логических равенств
-
Решение задачи поиска информации в Интернет с помощью диаграмм Эйлера-Венна
- Как логические операции связаны с теорией множеств
- Примеры задач с решением
Диаграмма Эйлера-Венна — что из себя представляет, где используется
Определение
Диаграмма Эйлера-Венна представляет собой геометрическую схему, предназначенную для представления моделей множеств и схем их взаимосвязей.
Благодаря данной диаграмме, приводят наглядное объяснение разных фактов о множествах. При таком методе универсальное множество представляют в виде прямоугольника, а для изображения подмножества используют круги. Широкое применение диаграммы Эйлера-Венна нашли в таких дисциплинах, как математика, логика, менеджмент, финансы и другие прикладные направления.
Примечание
Способы отражения отношений между множествами ранее отличались. Джон Венн применял в качестве обозначения множеств замкнутые фигуры, а Эйлер – круги.
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
Диаграммы Эйлера-Венна представляют собой важный частный случай кругов, которые изображал Эйлер. На диаграммах представлены все 2n комбинаций n свойств, что является конечной булевой алгеброй. Если n = 3, на диаграмме, как правило, изображают три круга с центрами, которые расположены в углах равностороннего треугольника, и совпадающими радиусами, ориентировочно равными длине сторон этого многоугольника.
Принципы построения, как изобразить множества
Определение
Построить диаграмму Эйлера-Венна – значит, составить большой прямоугольник, представляющий универсальное множество U, и разместить внутри него замкнутые фигуры в качестве обозначения множеств.
В том случае, когда требуется строить на диаграмме не более трех множеств, целесообразно использовать круги. Для изображения свыше четырех множеств применяют эллипсы. Пересечение фигур соответствует максимально общему случаю, согласно условиям задачи, и изображается должным образом на диаграмме.
Если предположить, что диаграмма содержит круг, обозначающий множество А, его центральная часть будет отражать истинность выражения А, а область вне круга – обозначать ложь. Те области, которые соответствуют истинным значениям, заштриховывают, что является отражением логической операции на диаграмме.
Согласно алгебре логики, конъюнкция множеств А и В соответствует истине в том случае, когда истинны оба эти множества. При этом на диаграмме отмечают участок пересечения множеств.
Применяя диаграммы Эйлера-Венна, доказывают любые алгебраические законы с помощью их графического изображения. Алгоритм построения:
- изображение диаграммы с заштрихованными множествами, которые представлены в левой части выражения;
- чертеж другой диаграммы с заштрихованными множествами, расположенными в правой части уравнения;
- сравнение заштрихованных областей на диаграммах: если это одна и та же область, то можно говорить об истинности тождества.
Данные диаграммы являются эффективным методом визуализации операций с множествами. Отдельные множества изображают в виде кругов, а универсальное множество представляют прямоугольником.
Дополнение множества
Объединение множеств
Пересечение множеств
Разность множеств
Симметричная разность множеств
Использование диаграмм Эйлера-Венна для доказательства логических равенств
В качестве доказательства логического равенства подходит способ построения диаграмм Эйлера-Венна. Для примера можно представить доказательства следующего выражения: ¬(АvВ) = ¬А&¬В. Равенство демонстрирует запись закона де Моргана. В первую очередь следует наглядно изобразить левую часть уравнения. Для этого необходимо последовательно заштриховать серым цветом все круги, то есть применить дизъюнкцию. Отобразить инверсию можно с помощью закрашивания черным цветом области вне этих кругов.
Далее следует визуально представить правую часть выражения. Последовательность действий в этом случае такова: необходимо заштриховать область, в которой отображается инверсия (¬А), с использованием серого цвета и аналогично закрасить область ¬В; отобразить конъюнкцию в виде пересечения этих серых областей. Результат такого наложения будет окрашен черным цветом.
На рисунке видно, что области, в которых отображены левая и правая части уравнения, равны друг другу. Таким образом, закономерность доказана.
Решение задачи поиска информации в Интернет с помощью диаграмм Эйлера-Венна
Изучая тему поиска информации в глобальной сети Интернет, нельзя обойтись без примеров поисковых запросов, в которых использованы логические связки. Как правило, их смысл аналогичен союзам «и», «или» из русского языка. Принцип действия можно понять, если изобразить логические связи с помощью графической схемы или диаграммы Эйлера-Венна.
Как логические операции связаны с теорией множеств
Используя диаграммы Эйлера-Венна, принято наглядно демонстрировать связь логических действий и теории множеств. Операции логики можно задать с помощью таблиц истинности. В этом случае следует руководствоваться общим принципом.
На диаграмме в виде области круга под названием А отображают истинность определения А, то есть теоретически круг А обозначает все элементы, которые включены в данное множество. Таким образом, область за пределами круга А будет обозначать ложь соответствующего утверждения.
Понимание, какая область диаграммы отражает логическую операцию, возникает после того, как будут заштрихованы только те области, в которых значения логической операции на наборах А и В соответствуют истине. К примеру, импликация истинна при (00, 01 и 11).
Необходимо заштриховать сначала область за пределами пары пересекающихся кругов в соответствии со значениями А=0, В=0. Затем закрасить область в круге В, которая относится к значениям А=0, В=1, и область, соответствующую и кругу А, и кругу В, то есть участок пересечения, отображающий значения А=1, В=1. Эти три области в комплексе являются графическим представлением логической импликации.
Примеры задач с решением
Диаграммы Эйлера-Венна могут содержать три и более круга. Преимуществом данного графического способа представления выражений является его высокая эффективность и наглядность. К примеру, можно изобразить диаграмму пересечений букв из русского, латинского и греческого алфавита:
Понять суть методики удобно на практике. Можно решить несколько задач с применением диаграмм Эйлера-Венна.
Задача 1
По условию есть таблица поисковых запросов. В ней представлены страницы по некоторому сегменту. Требуется определить, сколько страниц в тысячах будет отображаться по запросу «Эсминец». Следует отметить, что запросы выполнялись практически в одно время, поэтому набор страниц с искомыми словами не менялся в процессе выполнения запросов.
Решение
Допустим, что:
Ф – является числом страниц (в тысячах) в соответствии с запросом «Фрегат»;
Э – является числом страниц (в тысячах) в соответствии с запросом «Эсминец»;
Х – представляет собой число страниц (в тысячах) по запросу, в котором присутствует «Фрегат» и отсутствует «Эсминец»;
У – определяет число страниц (в тысячах) по запросу, в котором указано слово «Эсминец» и отсутствует слово «Фрегат».
Диаграмма для каждого поискового запроса будет иметь следующий вид:
Исходя из информации по диаграммам, получим:
Х+900+У = Ф+У = 2100+У = 3400
Таким образом:
У = 3400-2100 = 1300
Э = 900+У = 900+1300= 2200
Ответ: по запросу «Эсминец» будет найдено 2200 страниц
Задача 2
Класс состоит из 36 учеников. Дети ходят на занятия в рамках математического, физического, химического кружка. Факультатив по математике посещают 18 учащихся, по физике – 14, по химии – 10. Также известно, что 2 ученика ходят на все три кружка, 8 – на математику и физику, 5 – на математику и химию, 3 – на физику и химию. Необходимо определить количество учеников, которые не посещают ни одного кружка.
Решение
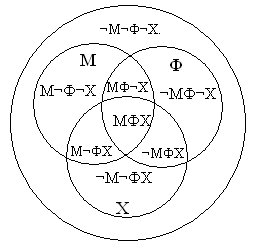
Решить данную задачу можно с помощью удобного и наглядного метода в виде кругов Эйлера. Наибольшим кругом следует обозначить множество всех учащихся класса. Внутри этой окружности необходимо изобразить пересекающиеся множества в виде учащихся на факультативе по математике (М), физике (Ф), химии (Х).
Допустим, что:
МФХ – является множеством учеников, каждый из которых ходит на занятия во все три кружка;
МФ¬Х – определяет множество учащихся, которые посещают факультативы по математике и физике, но не ходят на занятия по химии.
¬М¬ФХ – представляет собой множество людей, каждый из которых посещает химический факультатив, но отказался от дополнительных занятий по физике и математике.
По аналогичному принципу можно ввести множества: ¬МФХ, М¬ФХ, М¬Ф¬Х, ¬МФ¬Х, ¬М¬Ф¬Х.
Согласно условиям задачи, пара учеников записаны во все три кружка. Поэтому в область МФХ требуется вписать число 2. Исходя из того, что 8 учащихся посещают факультативы по математике и физике, а из них двое школьников ходят во все кружки, то в области МФ¬Х следует отметить 6 человек (8-2). Аналогичным способом можно определить число учеников в остальных множествах:
Далее требуется определить сумму учеников по всем областям:
7+6+3+2+4+1+5=28
Таким образом, всего 28 учащихся посещают факультативные занятия.
Поэтому:
36 – 28 = 8
Ответ: 8 учеников из класса не посещают ни одного кружка.
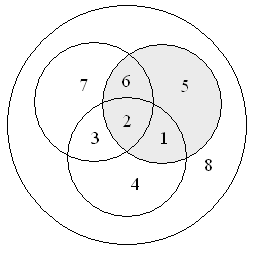
Задача 3
Когда закончились зимние каникулы, преподаватель поинтересовался у учеников, кто из них посещал театр, кино или цирк. Всего в классе 36 человек. По полученной информации, два ребенка не были ни в кино, ни в театре, ни в цирке. Кино посетили 25 школьников, театр – 11, цирк – 17. И в кино, и в театр сходили 6 человек, и в кино, и в цирк – 10, и в театр, и в цирк – 4. Необходимо посчитать, какое количество учащихся из класса посетили и кино, и театр, и цирк.
Решение
Предположим, что х представляет собой число учеников, которые посетили и кино, и театр, и цирк. В таком случае, можно изобразить диаграмму и определить число школьников для каждой области:
Ответ: 1 ученик побывал и в кино, и в театре, и в цирке.
Overlapping definitions and complex hierarchies are often classified using diagrams that can clearly show the relationship between different sets. One of these models is the Euler diagram, which is often used for differentiating between sets to understand the relevant relationship between them. In this article, we shall explore what defines an Euler diagram and how to construct one.
What is an Euler Diagram?
An Euler diagram is a visual representation of the relationship between different sets and is used for understanding complex hierarchies and validating arguments. The diagram is used by presenting connections among sets using shapes. It is similar to a Venn diagram. However, unlike a Venn diagram, it only shows relevant relationships between sets. The Euler diagram provides a great way of explaining complex hierarchies and overlapping definitions while presenting only relevant information.
Euler diagrams depict closed shapes using a two-dimensional plane, each showing a category. The overlapping of these shapes demonstrates the relationship between sets. Euler diagrams are used across various fields, such as for the purpose of business analysis and concept modeling, mathematics, biology, etc.
History of the Euler Diagram
The use of the Euler diagram is attributed to Leonhard Euler, who was an 18th-century Swiss mathematician. He is considered one of the greatest mathematicians to have ever lived.
Euler made contributions in the field of mathematics, mechanics, optics, astronomy, and fluid dynamic. He is credited with the earliest use of the circular diagrams to explain relationships, which Euler used for the purpose of illustrating syllogistic reasoning with the help of closed curves. In the 20th century, the Euler and Venn diagrams were incorporated in the United States as a part of set theory instructions during the 1960s.
Why Use Euler Diagrams?
There are numerous uses of the Euler diagram across various fields. Some of the common reasons for using Euler diagrams are mentioned below.
Explain Complex Hierarchies
Euler diagrams are important for explaining complex hierarchies and overlapping definitions. By using an Euler diagram, you can represent sets and show relevant information in the form of relationships between sets.
Visually Organize Information
Euler diagrams can help visually organize information for analysis and study, as the sets can be clearly differentiated in a diagrammatic form.
Comparison of Relevant Information
Euler diagrams can help organize and visualize relevant information to help better understand and compare it. Such a diagram can enable breaking down information to identify where sets intersect and overlap.
Example of How to Construct an Euler Diagram
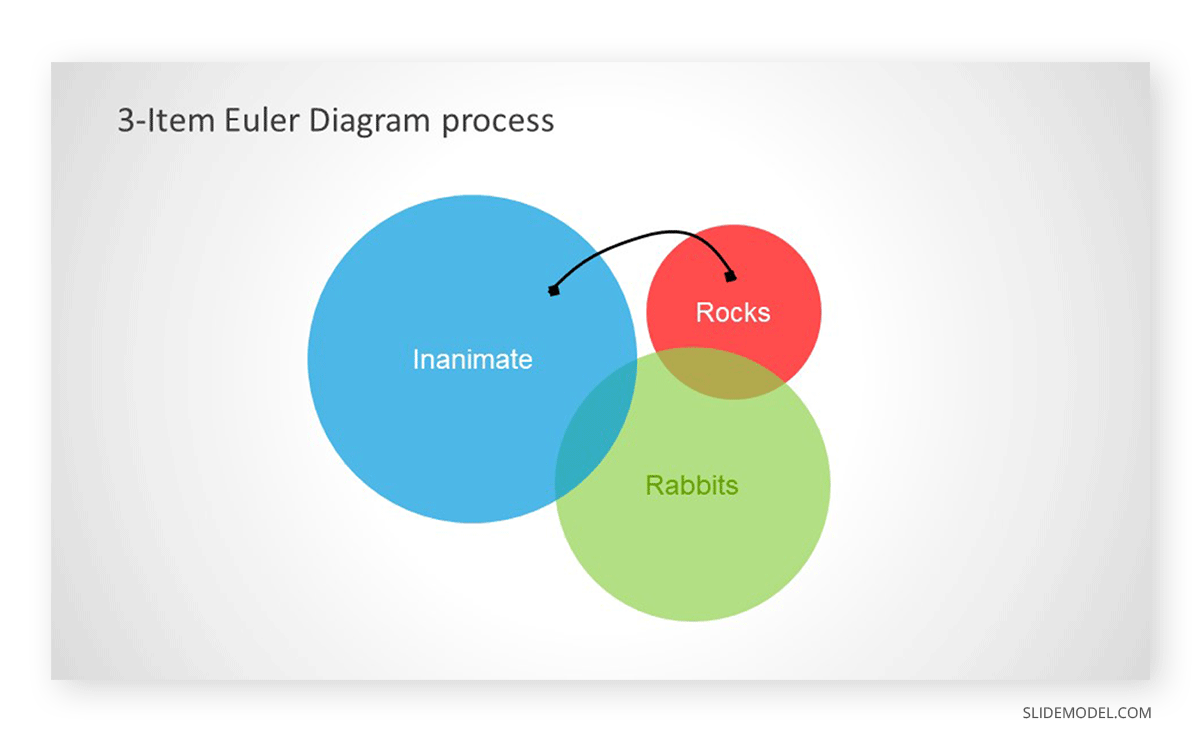
By following the example given below, you can construct an Euler diagram. We will draw an Euler diagram to represent this statement:
- All rocks are inanimate.
- No rabbits are rocks.
- No rocks are rabbits.
Step 1. Represent 3 Categories
In this example of an Euler diagram, we will construct 3 circles to represent 3 categories (rocks, rabbits, and inanimate).
Step 2. Move the Corresponding Circle According to The First Statement
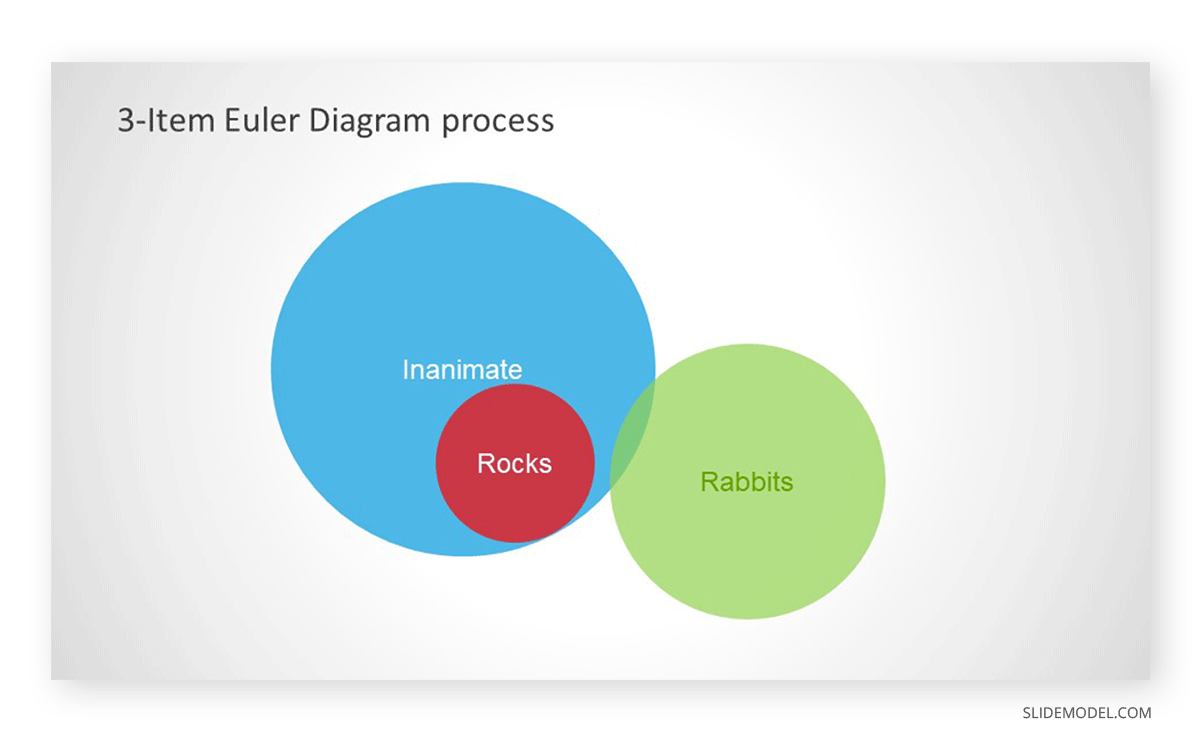
Read the statement above and move circles accordingly. Since ‘all rocks are inanimate,’ this means that the entire rocks’ circle needs to be inside the inanimate circle.
Step 3. Move the Corresponding Circle According to The Second Statement
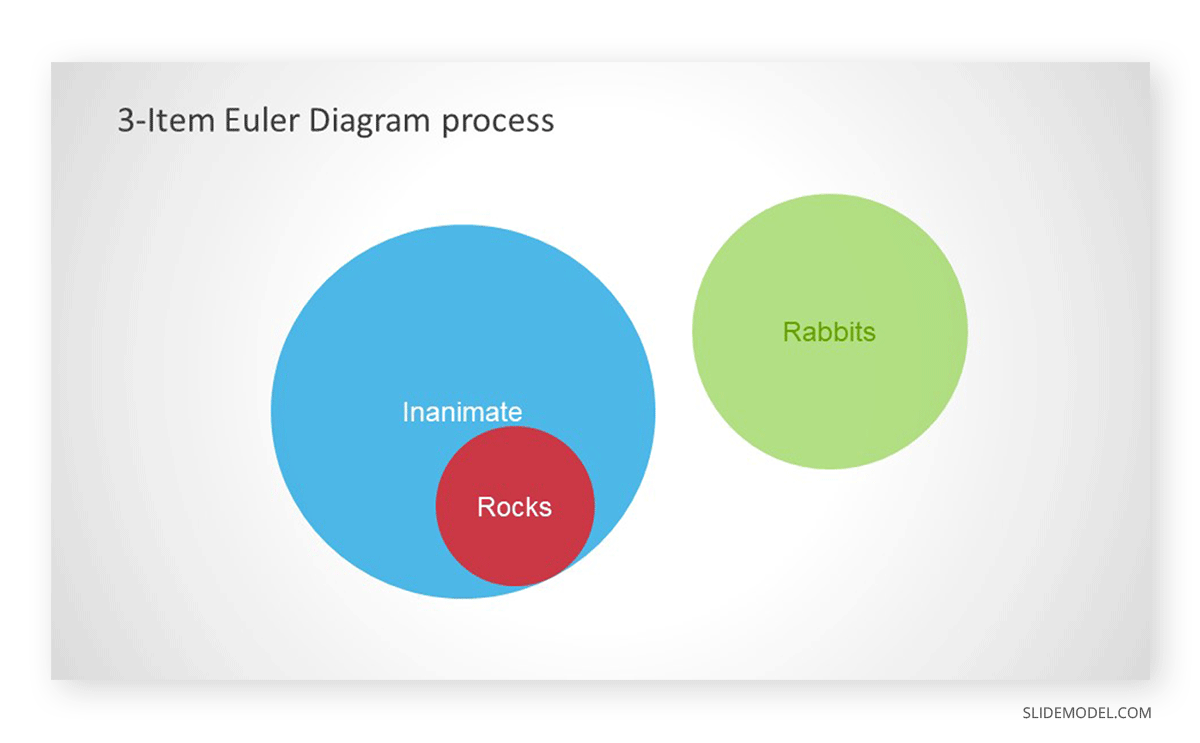
Read the second statement and then move the corresponding circle to represent information. Since ‘no rabbits are rocks,’ this means that the entire rabbits’ circle will be outside the rocks circle.
Step 4. Move the corresponding circle according to the third statement
Read the last statement and move the circle accordingly. Since ‘no rocks are rabbits,’ the entire rabbits’ circle should be outside the inanimate circle. As this circle is already outside, we have correctly constructed the Euler diagram.
Differences Between Euler Diagram and Venn Diagram
While Venn and Euler diagrams can appear similar, there are a number of differences between them.
The difference in Representation of Relationships Between Sets
The most significant difference between a Venn and Euler diagram is that a Venn diagram represents all possible relations between sets. However, an Euler diagram shows only relevant relationships.
The complexity of Visual Representation
A Venn diagram becomes far more complex than an Euler diagram beyond three sets. This is because of the representation of all possible relations in a Venn diagram, unlike an Euler diagram which focuses on relevant relationships only.
Intersection Requirements
In an Euler diagram, only intersections that aren’t empty are represented. However, in a Venn diagram, each intersection between each set is represented.
Using Euler Diagrams (Real World Applications + Examples)
To better understand the use of Euler diagrams, let’s take a look at a few real-world applications and examples.
Analyzing Arguments with Euler Diagrams
Euler diagrams are used for analyzing and validating arguments. This is perhaps the most common reason for using Euler diagrams. By using deductive reasoning with the help of an Euler diagram, you can validate an argument by following a few simple steps. Other than the Euler diagram example mentioned earlier, the below video provides a few additional examples of how you can validate an argument by constructing an Euler diagram.
Euler Diagram for Concept Modeling
As mentioned earlier, one of the applications of Euler diagrams is for concept modeling. A conceptual model is a representation of a system where concepts are used to help understand and simulate subjects associated with the model. For example, Euler diagrams can help business analysts to understand the complexity of different relationships between various concepts.
Euler Diagrams in Education
Since Euler diagrams have mathematical applications, they are also commonly used to educate students, such as for solving math problems or to show the relationship between sets in a simplified manner. Explaining complex hierarchies using a simple diagrammatic representation.
Tools for Creating an Euler Diagram
Euler diagrams are so easy to construct that you can use a number of tools to construct them. There are a number of cross-platform and web apps available that can help you create Euler diagrams.
Adobe Photoshop/Illustrator
If you are good with using complex apps like Adobe Photoshop or Adobe Illustrator, you can construct an Euler diagram quite easily. Since both softwares use layers, it can also be easy to move around the shapes as you try to validate an argument or find relationships between sets.
Inkscape
Inkscape is a famous cross-platform application for making scalable vector images. You can also use Inkscape to draw diagrams. Inkscape also provides the utility of transforming shapes by moving, scaling, or rotating them. While Inkscape is a complex tool, with a bit of skill, it can help you create visually appealing Euler diagrams. Other than Windows and Mac, the app is also available for Linux and FreeBSD.
Microsoft Paint
One of the easiest methods of creating an Euler diagram is by using shapes in Microsoft Paint. Since Euler diagrams are usually constructed using circles, you can pick the circle shape in MS Paint to create an Euler diagram and label it using text. However, since moving shapes isn’t possible using layers in MS Paint, you might find it harder to use.
Google Drawings
Google’s drawing app available in Google Drive can be another good option for drawing an Euler diagram. The drawing app can be particularly useful for people who are good with freeform drawing. You can also export your drawings in PNG, JPG, SVG, and PDF format.
Google Slides and PowerPoint
If you find it difficult to construct Euler diagrams on your own, you can also use readymade PowerPoint templates or use shapes in PowerPoint or Google Slides to construct your diagram.
Since both platforms are extremely easy to use and allow moving around slide objects, you can also look to validate arguments as you find relationships between sets using a presentation slide. Diagrams constructed this way might also be easier to present compared to static images since you can also animate objects.
Final Words
Euler diagrams have applications across various fields and can be a simple method for identifying relevant relationships between sets. While a Venn diagram can become too complex due to its limitation of incorporating all possible relations when depicting sets, the Euler diagram resolves this issue by focusing only on more specific information.
Euler diagrams are also great for validating arguments. However, the use of these diagrams in mathematics can be a bit complex. Therefore, if you are new to the concept, you can start with a basic diagram to validate an argument to better grasp the construction of such a diagram before moving on to visually deconstructing more complex hierarchies and relationships between different sets.
(...) — задание скобок; A — отрицание, инверсия, дополнение (NOT); ∪ — дизъюнкция, объединение (OR); ∩ — конъюнкция, пересечение (AND); = — эквивалентность (тождество) (↔); → — импликация (следование); — относительное дополнение (разность); △ — симметрическая разность.
Для вложенного отрицания необходимо использовать знак !. Например, A ∪ B = !(A ∪ B) или A ∪ B = A ∪ !B
Чтобы доказать равенство, например, (AB)C∩B = (AC)(BC), необходимо отдельно ввести (AB)C∩B и (AC)(BC), а затем сравнить их результаты.
Введеное выражение также можно упростить, используя законы логики высказываний (на следующем шаге выбрать параметр Упростить выражение
).
Здесь будет показано решение
Множества изображаются в виде кругов или эллипсов, помещенных в прямоугольник (универсум).
Рисование кругов Эйлера
С помощью этого инструмента можно будет вручную создавать круги Венна с индивидуальным оформлением. Чтобы заштриховать требуемую область, нажмите на кнопку Заштриховать область, а затем выберите номер области. Для снятия штриховки, повторно нажмите на этот же номер.
Количество переменных (кругов)
Оформление кругов
Цвет линии
Цвет штриховки
Использовать сетку
ABC
(0)(1)(2)(3)(4)(5)(6)(7)
1. Введение
В курсе Информатики и ИКТ основной и старшей
школы рассматриваются такие важные темы как
“Основы логики” и “Поиск информации в
Интернет”. При решении определенного типа задач
удобно использовать круги Эйлера (диаграммы
Эйлера-Венна).
Математическая справка. Диаграммы Эйлера-Венна
используются прежде всего в теории множеств как
схематичное изображение всех возможных
пересечений нескольких множеств. В общем случае
они изображают все 2n комбинаций n свойств.
Например, при n=3 диаграмма Эйлера-Венна обычно
изображается в виде трех кругов с центрами в
вершинах равностороннего треугольника и
одинаковым радиусом, приблизительно равным
длине стороны треугольника.
2. Представление логических связок в поисковых
запросах
При изучении темы “Поиск информации в
Интернет” рассматриваются примеры поисковых
запросов с использованием логических связок,
аналогичным по смыслу союзам “и”, “или”
русского языка. Смысл логических связок
становится более понятным, если
проиллюстрировать их с помощью графической
схемы – кругов Эйлера (диаграмм Эйлера-Венна).
| Логическая связка | Пример запроса | Пояснение | Круги Эйлера |
| & — “И” | Париж & университет | Будут отобраны все страницы, где упоминаются оба слова: Париж и университет |
Рис.1
|
| | — “ИЛИ” | Париж | университет | Будут отобраны все страницы, где упоминаются слова Париж и/или университет |
Рис.2
|
3. Связь логических операций с теорией множеств
С помощью диаграмм Эйлера-Венна можно наглядно
представить связь логических операций с теорией
множеств. Для демонстрации можно
воспользоваться слайдами в Приложение
1.
Логические операции задаются своими таблицами
истинности. В Приложении 2
подробно рассматриваются графические
иллюстрации логических операций вместе с их
таблицами истинности. Поясним принцип
построения диаграммы в общем случае. На
диаграмме – область круга с именем А отображает
истинность высказывания А (в теории множеств
круг А – обозначение всех элементов, входящих в
данное множество). Соответственно, область вне
круга отображает значение “ложь”
соответствующего высказывания. Что бы понять
какая область диаграммы будет отображением
логической операции нужно заштриховать только
те области, в которых значения логической
операции на наборах A и B равны “истина”.
Например, значение импликации равно “истина”
в трех случаях (00, 01 и 11). Заштрихуем
последовательно: 1) область вне двух
пересекающихся кругов, которая соответствует
значениям А=0, В=0; 2) область, относящуюся только к
кругу В (полумесяц), которая соответствует
значениям А=0, В=1; 3) область, относящуюся и к кругу
А и к кругу В (пересечение) – соответствует
значениям А=1, В=1. Объединение этих трех областей
и будет графическим представлением логической
операции импликации.
4. Использование кругов Эйлера при
доказательстве логических равенств (законов)
Для того, чтобы доказать логические равенства
можно применить метод диаграмм Эйлера-Венна.
Докажем следующее равенство ¬(АvВ) = ¬А&¬В (закон
де Моргана).
Для наглядного представления левой части
равенства выполним последовательно:
заштрихуем оба круга (применим дизъюнкцию) серым
цветом, затем для отображения инверсии
заштрихуем область за пределами кругов черным
цветом:
Рис.3 
Для визуального представления правой части
равенства выполним последовательно:
заштрихуем область для отображения инверсии (¬А)
серым цветом и аналогично область ¬В также серым
цветом; затем для отображения конъюнкции нужно
взять пересечение этих серых областей (результат
наложения представлен черным цветом):
Рис.5 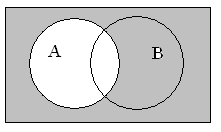
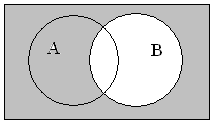
Видим, что области для отображения левой и
правой части равны. Что и требовалось доказать.
5. Задачи в формате ГИА и ЕГЭ по теме: “Поиск
информации в Интернет”
Задача №18 из демо-версии ГИА 2013.
В таблице приведены запросы к поисковому
серверу. Для каждого запроса указан его код –
соответствующая буква от А до Г. Расположите коды
запросов слева направо в порядке убывания количества
страниц, которые найдет поисковый сервер по
каждому запросу.
| Код | Запрос |
| А | (Муха & Денежка) | Самовар |
| Б | Муха & Денежка & Базар & Самовар |
| В | Муха | Денежка | Самовар |
| Г | Муха & Денежка & Самовар |
Решение:
Для каждого запроса построим диаграмму
Эйлера-Венна:
| Запрос А
Рис.8 |
Запрос Б
Рис. 9 |
Запрос В
Рис. 10 |
Запрос Г
Рис. 11 |
Ответ: ВАГБ.
Задача В12 из демо-версии ЕГЭ-2013.
В таблице приведены запросы и количество
найденных по ним страниц некоторого сегмента
сети Интернет.
| Запрос | Найдено страниц (в тысяч) |
| Фрегат | Эсминец | 3400 |
| Фрегат & Эсминец | 900 |
| Фрегат | 2100 |
Какое количество страниц (в тысячах) будет
найдено по запросу Эсминец?
Считается, что все запросы выполнялись
практически одновременно, так что набор страниц,
содержащих все искомые слова, не изменялся за
время выполнения запросов.
Решение:
Пусть
Ф – количество страниц (в тысячах) по запросу Фрегат;
Э – количество страниц (в тысячах) по запросу Эсминец;
Х – количество страниц (в тысячах) по запросу, в
котором упоминается Фрегат и не упоминается
Эсминец;
У – количество страниц (в тысячах) по запросу, в
котором упоминается Эсминец и не
упоминается Фрегат.
Построим диаграммы Эйлера-Венна для каждого
запроса:
| Запрос | Диаграмма Эйлера-Венна | Количество страниц |
| Фрегат | Эсминец | Рис.12
|
3400 |
| Фрегат & Эсминец | Рис.13
|
900 |
| Фрегат | Рис.14
|
2100 |
| Эсминец | Рис.15
|
? |
Согласно диаграммам имеем:
- Х+900+У = Ф+У = 2100+У = 3400. Отсюда находим У = 3400-2100 = 1300.
- Э = 900+У = 900+1300= 2200.
Ответ: 2200.
6. Решение логических содержательных
задач методом диаграмм Эйлера-Венна
Задача 1.
В классе 36 человек. Ученики этого класса
посещают математический, физический и
химический кружки, причем математический кружок
посещают 18 человек, физический — 14 человек,
химический — 10. Кроме того, известно, что 2
человека посещают все три кружка, 8 человек — и
математический и физический, 5 и математический и
химический, 3 — и физический и химический.
Сколько учеников класса не посещают никаких
кружков?
Решение:
Для решения данной задачи очень удобным и
наглядным является использование кругов Эйлера.
Самый большой круг – множество всех учеников
класса. Внутри круга три пересекающихся
множества: членов математического (М),
физического (Ф), химического (Х) кружков.
Пусть МФХ – множество ребят, каждый из
которых посещает все три кружка. МФ¬Х –
множество ребят, каждый из которых посещает
математический и физический кружки и не
посещает химический. ¬М¬ФХ — множество ребят,
каждый из которых посещает химический кружок и
не посещает физический и математический кружки.
Аналогично введем множества: ¬МФХ, М¬ФХ,
М¬Ф¬Х, ¬МФ¬Х, ¬М¬Ф¬Х.
Известно, что все три кружка посещают 2
человека, следовательно, в область МФХ впишем
число 2. Т.к. 8 человек посещают и математический и
физический кружки и среди них уже есть 2 человека,
посещающих все три кружка, то в область МФ¬Х впишем
6 человек (8-2). Аналогично определим количество
учащихся в остальных множествах:
| Круги Эйлера с названиями непересекающихся множеств: Рис. 16 |
Круги Эйлера с количественной информацией: Рис. 17 Например, количество человек, которые посещают |
Просуммируем количество человек по всем
областям: 7+6+3+2+4+1+5=28. Следовательно, 28 человек из
класса посещают кружки.
Значит, 36-28 = 8 учеников не посещают кружки.
Ответ: 8.
Задача 2.
После зимних каникул классный руководитель
спросил, кто из ребят ходил в театр, кино или цирк.
Оказалось, что из 36 учеников класса двое не были
ни в кино. ни в театре, ни в цирке. В кино побывало
25 человек, в театре — 11, в цирке 17 человек; и в кино,
и в театре — 6; и в кино и в цирке — 10; и в театре и в
цирке — 4.
Сколько человек побывало и в кино, и в театре, и
в цирке?
Решение:
Пусть х – количество ребят, которые побывали и
в кино, и в театре, и в цирке.
Тогда можно построить следующую диаграмму и
посчитать количество ребят в каждой области:
|
Рис.18. |
В кино и театре побывало 6 чел., значит, только в кино и театре (6-х) чел. Аналогично, Только в театре и цирке (4-х) чел. В кино побывало 25 чел., значит, из них только в Аналогично, только в театре были (1+х) чел. Только в цирке были (3+х) чел. Не были в театре, кино и цирке – 2 чел. Значит, 36-2=34 чел. побывали на мероприятиях. С другой стороны можем просуммировать (9+х)+(1+х)+(3+х)+(10-х)+(6-х)+(4-х)+х = 34 33+х = 34. Отсюда следует, что только один человек побывал |
Ответ: 1.
Таким образом, круги Эйлера (диаграммы
Эйлера-Венна) находят практическое применение
при решении задач в формате ЕГЭ и ГИА и при
решении содержательных логических задач.
Литература
- В.Ю. Лыскова, Е.А. Ракитина. Логика в информатике.
М.: Информатика и Образование, 2006. 155 с. - Л.Л. Босова. Арифметические и логические основы
ЭВМ. М.: Информатика и образование, 2000. 207 с. - Л.Л. Босова, А.Ю. Босова. Учебник. Информатика и
ИКТ для 8 класса: БИНОМ. Лаборатория знаний, 2012. 220
с. - Л.Л. Босова, А.Ю. Босова. Учебник. Информатика и
ИКТ для 9 класса: БИНОМ. Лаборатория знаний, 2012. 244
с. - Сайт ФИПИ: http://www.fipi.ru/