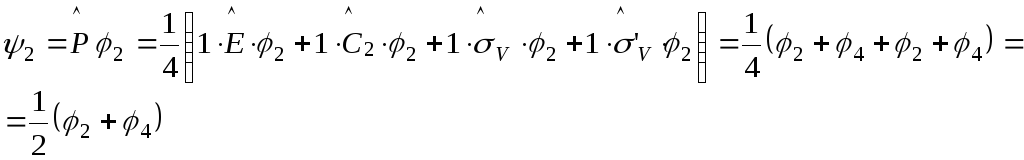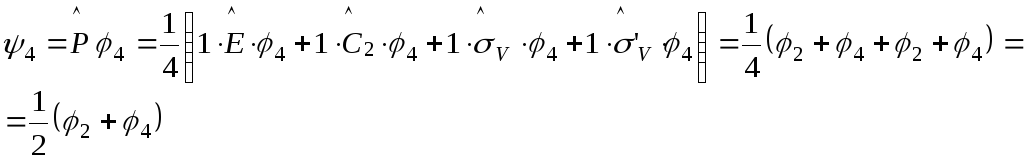Как составить таблицу характеров

Для применения теории
групп необходимо знать неприводимые
представления, для которых волновые
функции молекулы являются базисными
функциями. Их можно определить из таблиц
характеров неприводимых представлений,
известных из теории групп.

Можно
доказать, что для определения неприводимых
представлений группы достаточно знать
след (равный сумме диагональных элементов)
матриц, представляющих операции
симметрии. В теории групп след матриц
представлений часто называют характером.
Для всех представлений и операций группы
они сведены в таблицу характеров. Пример
одной из наиболее часто употребляемых
групп, С_2v,
приведен ниже.

C2v	E	C2	v(x,z)	‘v(yz)
A1 A2 B1 B2	1 1 1 1	1 1 -1 -1	1 -1 1 -1	1 -1 -1 1

Такие таблицы
составлены для всех точечных групп и
будут в рамках данного курса использоваться
без вывода. В этих таблицах
+1 означает симметричность (неизменность)
свойства функций базисного набора
представления при осуществлении операции
симметрии, а –1 – антисимметричность.
Операции антисимметрии преобразуют
предметы, обладающие двумя возможными
значениями какого-либо свойства, так,
что одно значение переходит в другое.
Пример: знак функции.

Важным свойством
характеров неприводимых представлений
является то, что таблица их умножения
соответствует таблице умножения групп.

Ниже приведены
таблицы характеров наиболее часто
встречающихся групп симметрии.

С2	Е	С2
А В	1 1	1 -1

Сi	Е	i
Аg Au	1 1	1 -1

Сs	Е	
А’ A»	1 1	1 -1

С2h	Е	С2	h	i
Аg Вg Au Bu	1 1 1 1	1 -1 1 -1	1 -1 -1 1	1 1 -1 -1

D2	Е	С2(z)	C2(y)	C2(x)
А1 В3 В1 B2	1 1 1 1	1 -1 1 -1	1 -1 -1 1	1 1 -1 -1

С3v	Е	2С3	3h
А1 A2 E	1 1 2	1 1 -1	1 -1 0

D3	Е	2С3	3C21
А1 A2 E	1 1 2	1 1 -1	1 -1 0

C4v	Е	С2	2C4	2v	2’v
А1 A2 B1 B2 E	1 1 1 1 2	1 1 1 1 -2	1 1 -1 -1 0	1 -1 1 -1 0	1 -1 -1 1 0

D4	Е	С2	2C4	2C’2	2C»2
А1 A2 B1 B2 E	1 1 1 1 2	1 1 1 1 -2	1 1 -1 -1 0	1 -1 1 -1 0	1 -1 -1 1 0

D2d	Е	С2	2S4	2C’2	2d
А1 A2 B1 B2 E	1 1 1 1 2	1 1 1 1 -2	1 1 -1 -1 0	1 -1 1 -1 0	1 -1 -1 1 0

C5v	Е	2С5	2C52	5v
А1 A2 E1 E2	1 1 2 2	1 1 2cosx 2cos2x	1 1 2cos2x 2cos4x	1 -1 0 0 x = 2/5

C6v	Е	С2	2C3	2C6	3v	3’v
А1 A2 B2 B1 E1 E2	1 1 1 1 2 2	1 1 -1 -1 -2 2	1 1 1 1 -1 -1	1 1 -1 —1 1 -1	1 -1 1 -1 0 0	1 -1 -1 1 0 0

D3h	Е	h	2C3	2S3	3C’2	3’v
А’1 A’2 A»1 A»2 E» E’	1 1 1 1 2 2	1 1 -1 -1 -2 2	1 1 1 1 -1 -1	1 1 -1 —1 1 -1	1 -1 1 -1 0 0	1 -1 -1 1 0 0

Td	Е	8С3	3C2	6d	6S4
А1 A2 E T1 T2	1 1 2 3 3	1 1 -1 0 0	1 1 2 -1 -1	1 -1 0 -1 1	1 -1 0 1 -1

В
теории групп вводится еще одно полезное
для химии понятие: понятие о прямом
произведении.

Пусть
Г₁
– n₁-мерное,
а Г₂
– n₂-мерное
представления группы G.
Тогда матрицы размера (n₁n₂)
x
(n₁n₂),
получаемые как прямые произведения
матриц из Г₁
и
Г₂,
образуют n₁n₂-мерное
представление группы G,
так называемое прямое (кронекеровское)
произведение
.

Прямое
произведение
матрицыразмераm
x n и
матрицы
размераm’
x n’
есть матрица

(1.46)

размера
mm’
x nn’,
где индекс j
означает порядковый номер пары (i,i‘)
в последовательности (1,1), (1,2), … , (1,m’),
(2,1), (2,2), … , (m,m’), а индекс h
–
порядковый
номер пары (k,k’)
в аналогичной последовательности.

Характер
представленияравен произведению характерапредставленияи характерапредставления:

(1.47)

В качестве
примера рассмотрим прямые произведения
характеров неприводимых представлений
в группе С_3v.

С3v	Е	2С3	3h
А1 A2 E	1 1 2	1 1 -1	1 -1 0

	11	11	-11	=
	21 21 22 11 11	-11 -11 -1(-1) 11 11	01 0(-1) 00 11 (-1)(-1)	= = =

Для того, чтобы
закончить с описанием начал теории
представлений, покажем два полезных
приема: определение состава приводимого
представления (разложения его на
неприводимые) и использование операторов
проектирования.

Разложение
приводимого представления на неприводимые.

Можно
показать, что разложение любого
приводимого представления осуществляется
единственным образом, причем число
вхождений неприводимого представления
i
в приводимое представление Г, определяется
по формуле:

(1.48)

Здесь
a_i
–сколько раз i-ое
неприводимое представление встречается
в приводимом представлении, h
– число элементов группы G;
R
– оператор симметрии группы;
— характер операцииR
в приводимом представлении;
— характер операцииR
в i-том
неприводимом представлении.

Характер
приводимого представления в точечной
группе определяется как число элементов
базисного набора (представления) группы,
которые остаются неподвижными при
операции симметрии.

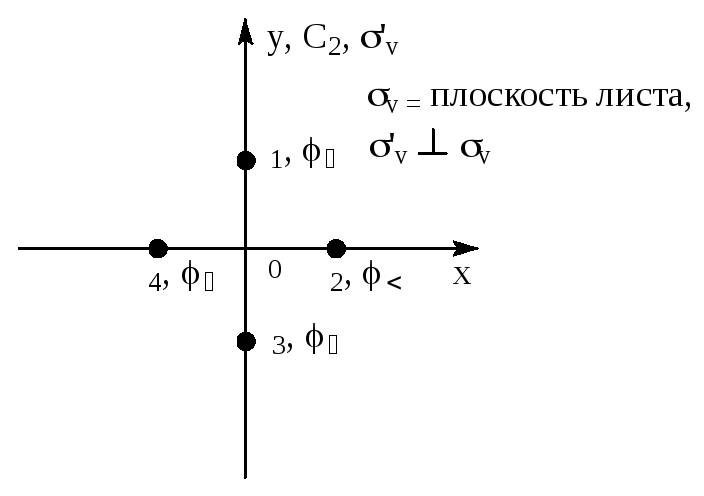
Рассмотрим
систему точек 1 … 4.

C2V	E	C2(y)	Vпл.	Vпл.(y)
A1	1	1	1	1
A2	1	1	-1	-1
B1	1	-1	1	-1
B2	1	-1	-1	1
	4	2	4	2

Тогда

Отсюда,
структуру приводимого представления
можно записать как

Последняя
запись означает, что в базисный набор
функций приводимого представления
входят 3 функции, преобразующиеся по
представлению А₁
и одна – по представлению В₁.

Часто
при применении теории групп для решения
физических и химических задач используют
метод операторов проектирования. Он
позволяет преобразовать произвольный
базис таким образом, чтобы он принадлежал
к определенному неприводимому
представлению группы симметрии. По
определению, базис имеет вид:

Здесь
h
– число элементов симметрии в группе;
i
– неприводимое представление группы;
— операция группы;— характер операциивi-том
неприводимом представлении.

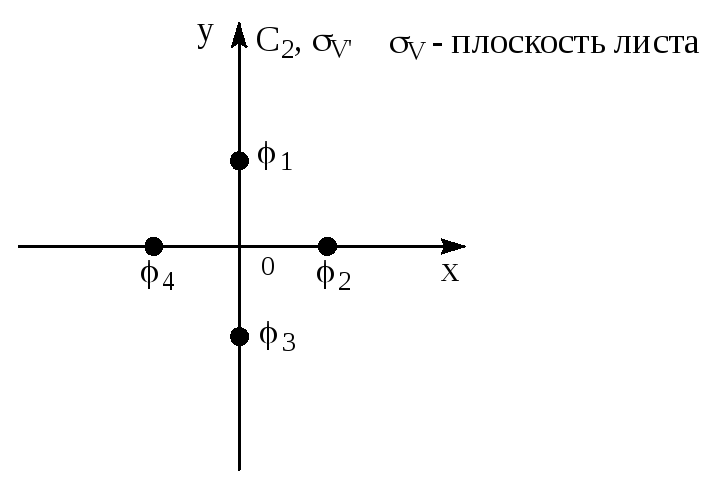
Пусть
_i
–
волновая функция атома в точке i:

Рис.2

C2V	E	C2	V	V ‘
A1	1	1	1	1
A2	1	1	-1	-1
B1	1	-1	1	-1
B2	1	-1	-1	1

Тогда
волновые функции системы атомов 1-4,
удовлетворяющие группе С_2V,
будут находиться следующим образом.

Представление
А₁:

Таким
образом ₄
= ₂,
т.е. всего образовано 3 волновых функции,
преобразующиеся по представлению А₁
группы С_2V.

Представление
В₁.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

Таблица характеров — это двумерная таблица, строки которой соответствуют неприводимым представлениям группы, а столбцы которой соответствует классам сопряжённости элементов группы. Элементы матрицы состоят из характеров, следов матриц, представляющих группу элементов класса столбца в определяемом строкoй представлении группы.

В химии, кристаллографии и спектроскопии используются таблицы характеров точечных групп^[en] для классификации, например, колебаний молекул согласно их симметрии и предсказания, будет ли переход из одного состояния в другое запрещено по причинам симметрии.

Определение и пример

Неприводимые комплексные характеры конечной группы образуют таблицу характеров, в которой закодировано много полезной информации о группе G в компактной форме. Каждая строка помечена неприводимым характером, а элементами строки являются значения характера на представлениях соответствующих классов сопряжённости группы G (поскольку характеры являются функциями классов^[en]). Столбцы помечены (представителями) классов сопряжённости группы G. Обычно первая строка помечается тривиальным характером, а первый столбец помечается (классом сопряжённости) нейтрального элемента. Элементами первого столбца являются значения неприводимых характеров на нейтральном элементе, степени неприводимых характеров. Характеры степени 1 известны как линейные характеры.

Ниже представлена таблица характеров C₃ = <u> для циклической группы с тремя элементами и генератором u:

	(1)	(u)	(u2)
1	1	1	1
[math]displaystyle{ chi_1 }[/math]	1	[math]displaystyle{ omega }[/math]	[math]displaystyle{ omega^2 }[/math]
[math]displaystyle{ chi_2 }[/math]	1	[math]displaystyle{ omega^2 }[/math]	[math]displaystyle{ omega }[/math]

где [math]displaystyle{ omega }[/math] — это примитивный кубический корень из единицы. Таблица характеров для циклических групп общего вида является (с точностью до скаляра) DFT матрицей^[en].

Другой пример — таблица характеров группы [math]displaystyle{ S_3 }[/math]:

	(1)	(12)	(123)
[math]displaystyle{ chi_{triv} }[/math]	1	1	1
[math]displaystyle{ chi_{sgn} }[/math]	1	[math]displaystyle{ — }[/math]1	1
[math]displaystyle{ chi_{stand} }[/math]	2	0	[math]displaystyle{ — }[/math]1

где (12) представляет класс сопряжённости, состоящий из (12),(13),(23), а (123) представляет класс сопряжённости, состоящий из (123),(132). О таблицах характеров симметрических групп можно почитать в статье Теория линейных представлений симметрических групп.

Первая строка таблицы характеров всегда состоит из единиц и соответствует тривиальному представлению^[en] (одномерное представление, состоящее из матриц 1×1, содержащих в качестве единственного элемента 1). Далее таблица характеров всегда квадратная, поскольку (1) неприводимые характеры попарно ортогональны и (2) никакой другой нетривиальный класс функций не ортогонален всем характерам. Это связано с важным фактом, что неприводимые представления конечной группы G имеют биекцию с её классами сопряжённости. Эта биекция также следует из того, что суммы классов образуют базис для центра групповой алгебры группы G, которая имеет размерность, равную числу неприводимых представлений группы G.

Отношения ортогональности

Пространство комплекснозначных функций классов конечной группы G имеет естественное скалярное произведение:

[math]displaystyle{ left langle alpha, betaright rangle := frac{1}{ left | G right | }sum_{g in G} alpha(g) overline{beta(g)} }[/math],

где [math]displaystyle{ overline{beta(g)} }[/math] означает комплексное сопряжение значения [math]displaystyle{ beta }[/math] на g. С учётом этого скалярного произведения неприводимые характеры образуют ортонормальный базис для пространства функций классов и дают отношение ортогональности для строк характеров таблицы:

[math]displaystyle{ left langle chi_i, chi_j right rangle = begin{cases} 0 & i ne j, \ 1 & i = j. end{cases} }[/math]

Для [math]displaystyle{ g, h in G }[/math] отношение ортогональности для столбцов следующее:

[math]displaystyle{ sum_{chi_i} chi_i(g) overline{chi_i(h)} = begin{cases} left | C_G(g) right |, & g = overline{h} \ 0 & g ne overline{h} end{cases} }[/math]

где суммирование ведётся по всем неприводимым характерам [math]displaystyle{ chi_i }[/math] группы G и символ [math]displaystyle{ left | C_G(g) right | }[/math] означает порядок централизатора [math]displaystyle{ g }[/math].

Неизвестный характер [math]displaystyle{ chi_i }[/math] неприводим тогда и только тогда, когда [math]displaystyle{ left langle chi_i, chi_i right rangle =1 }[/math].

Отношения ортогональности могут использоваться:

• Для разложения неизвестного характера в виде линейной комбинации неприводимых характеров.
• Для построения полной таблицы характеров, если известны лишь некоторые из неприводимых характеров.
• Для нахождения порядков централизаторов представителей классов сопряжённости группы.
• Для нахождения порядка группы.

Более конкретно, рассмотрим регулярное представление, которое является перестановкой на конечной группе G. Характерами этого представления являются [math]displaystyle{ chi(e) =left | G right| }[/math] и [math]displaystyle{ chi(g) = 0 }[/math] для g не равного единице. Тогда для неприводимого представления [math]displaystyle{ V_i }[/math],

[math]displaystyle{ left langle chi_{text{reg}}, chi_i right rangle =frac{1}{ left | G right | }sum_{g in G} chi_i(g) overline{chi_{text{reg}}(g)} = frac{1}{ left | G right | } chi_i(1) overline{chi_{text{reg}}(1)} = operatorname{dim} V_i }[/math].

Разложив регулярные представления в виде суммы неприводимых представлений группы G, мы получим [math]displaystyle{ V_{text{reg}} = oplus V_i^{operatorname{dim} V_i} }[/math]. Отсюда мы заключаем

[math]displaystyle{ left | G right | = operatorname{dim} V_{text{reg}} = sum(operatorname{dim} V_i)^2 }[/math]

по всем неприводимым представлениям [math]displaystyle{ V_i }[/math]. Сумма может помочь уменьшить размерность неприводимых представлений в таблице характеров. Например, если группа имеет порядок 10 и 4 класса сопряжённости (например, диэдральная группа порядка 10), то единственным способом выразить порядок группы в виде суммы четырёх квадратов является [math]displaystyle{ 10 = 1^2+1^2+2^2+2^2 }[/math], так что мы знаем размерности всех неприводимых представлений.

Свойства

Комплексное сопряжение действует на таблице характеров — поскольку комплексное сопряжение представления снова является представлением, это же верно и для характеров, а тогда характеры, принимающие нетривиальные комплексные значения, имеют сопряжённые характеры.

Некоторые свойства группы G могут быть выведены из таблицы характеров:

• Порядок группы G определяется суммой квадратов элементов первого столбца (степеней неприводимых характеров). (См. Применение леммы Шура^[en].) Более обще, сумма квадратов абсолютных значений элементов любого столбца даёт порядок централизатора элемента соответствующего класса сопряжённости.
• Все нормальные подгруппы группы G (а также является ли группа G простой) могут быть распознаны из таблицы характеров. Ядром характера [math]displaystyle{ chi }[/math] служит множество элементов g группы G, для которых [math]displaystyle{ chi (g) = chi(1) }[/math]. Это нормальная подгруппа группы G. Любая нормальная подгруппа группы G является пересечением ядер некоторых неприводимых характеров G.
• Порождённая подгруппа группы G является пересечением ядер линейных характеров группы G. В частности, G абелева тогда и только тогда, когда все её неприводимые характеры линейны.
• Из некоторых результатов Ричарда Брауэра в теории модулярных представлений^[en] вытекает, что простые делители порядков элементов каждого класса сопряжённости конечной группы могут быть выведены из таблицы характеров группы (наблюдение Грэма Хигмана).

Таблица характеров в общем случае не определяет группу с точностью до изоморфизма. Например, группа кватернионов Q и диэдральная группа из 8 элементов (D₄) имеют одну и ту же таблицу характеров. Брауэр задал вопрос, определяет ли таблица характеров, вместе со знанием, как распределены степени элементов классов сопряжённости, конечную группу с точностью до изоморфизма. В 1964 на вопрос ответил отрицательно Е. К. Дейд.

Линейные характеры образуют группу характеров^[en], которая имеет важную связь с теорией чисел.

Внешние автоморфизмы

Группа внешних автоморфизмов^[en] действует на таблице характеров путём перестановки столбцов (классов сопряжённости) и, соответственно, строк, которые дают другую симметрию таблице. Например, абелевы групп имеет внешний автоморфизм [math]displaystyle{ g mapsto g^{-1} }[/math], являющийся нетривиальным, за исключением элементарных абелевых 2-групп^[en], и внешним, поскольку абелевы группы — это в точности те, для которых сопряжения (внутренние автоморфизмы) действуют тривиально. В примере [math]displaystyle{ C_3 }[/math] выше, это отображение переводит [math]displaystyle{ u mapsto u^2, u^2 mapsto u, }[/math] и, соответственно, переключает [math]displaystyle{ chi_1 }[/math] и [math]displaystyle{ chi_2 }[/math] (переставляет их значения [math]displaystyle{ omega }[/math] и [math]displaystyle{ omega^2 }[/math]).Заметим, что этот автоморфизм (обратный в абелевых группах) согласуется с комплексным сопряжением.

Формально, если [math]displaystyle{ phicolon G to G }[/math] является автоморфизмом группы G и [math]displaystyle{ rho colon G to operatorname{GL} }[/math] является представлением, тогда [math]displaystyle{ rho^phi := g mapsto rho(phi(g)) }[/math] является представлением. Если [math]displaystyle{ phi = phi_a }[/math] является внутренним автоморфизмом (сопряжение с некоторым элементом a), тогда он действует тривиально на представлениях, поскольку представления являются классами функций (сопряжение не меняет их значение). Это даёт класс внешних автоморфизмов, который действует на характеры.

Это отношение можно использовать двумя путями: если дан внешний автоморфизм, можно сделать новые представления и наоборот, можно сузить возможные внешние автоморфизмы, основываясь на таблице характеров.

Примечания

Литература

2) Для групп типа Z4xZ2 всё просто: неприводимые представления только одномерны, их 8. Для образующих Z4 и Z2 произвольно загадываем пару корней из 1 степени 4 и 2 соответственно. Это даёт 8 вариантов; каждый определяется парой (типа (i,1), (-1,-1), и так для всех возможных комбинаций.

1) Для D4 мы знаем коммутант (в нём — тождественное преобразование и центральная симметрия). Одномерных представлений 4, как для фактора по коммутанту, изоморфного Z2xZ2. Строятся они как в предыдущем пункте.

Классов сопряжённости здесь 5, они легко перечисляются. Неодномерных неприводимых представлений будет одна штука; степень равна 2 (из соображений суммы квадратов). Оно легко строится из соображений геометрии в виде матриц линейных преобразований. Их можно выписать явно, и посмотреть на следы.

Для случая D_n меняется сама группа, и там в принципе тоже возможно полное описание, но оно сложнее описывается. Меняется и число характеров, и их вид. Простой связи с частным случаем n=4 тут нет.