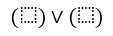Построение таблиц истинности
Екатерина Андреевна Гапонько
Эксперт по предмету «Информатика»
Задать вопрос автору статьи
Определение 1
Логическая функция – функция, переменные которой принимают одно из двух значений: $1$ или $0$.
Любую логическую функцию можно задать с помощью таблицы истинности: набор всех возможных аргументов записывается в левой части таблицы, а соответствующие значения логической функции – в правой части.
Определение 2
Таблица истинности – таблица, которая показывает, какие значения примет составное выражение при всех возможных наборах значений простых выражений, входящих в него.
Определение 3
Равносильными называются логические выражения, последние столбцы таблиц истинности которых совпадают. Равносильность обозначается с помощью знака $«=»$.
При составлении таблицы истинности важно учитывать следующий порядок выполнения логических операций:
Рисунок 1.
Приоритетом в выполнении порядка выполнения операций пользуются скобки.
Алгоритм построения таблицы истинности логической функции
-
Определяют количество строк: кол-во строк = $2^n + 1$ (для строки заголовка), $n$ – количество простых выражений. Например, для функций двух переменных существует $2^2 = 4$ комбинации наборов значений переменных, для функций трех переменных – $2^3 = 8$ и т.д.
-
Определяют количество столбцов: кол-во столбцов = кол-во переменных + кол-во логических операций. При определении количества логических операций учитывают также порядок их выполнения.
-
Заполняют столбцы результатами выполнения логических операций в определенной последовательности, учитывая таблицы истинности основных логических операций.
«Построение таблиц истинности» 👇
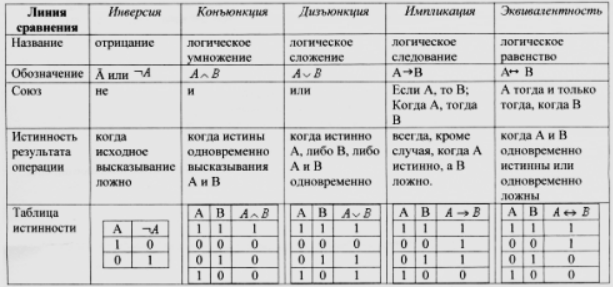
Рисунок 2.
Пример 1
Составить таблицу истинности логического выражения $D=bar{A} vee (B vee C)$.
Решение:
-
Определим количество строк:
Количество простых выражений – $n=3$, значит
кол-во строк = $2^3 + 1=9$.
-
Определим количество столбцов:
Количество переменных – $3$.
Количество логических операций и их последовательность:
- инверсия ($bar{A}$);
- дизъюнкция, т.к. она находится в скобках ($B vee C$);
-
дизъюнкция ($overline{A}vee left(Bvee Cright)$) – искомое логическое выражение.
Кол-во столбцов = $3 + 3=6$.
-
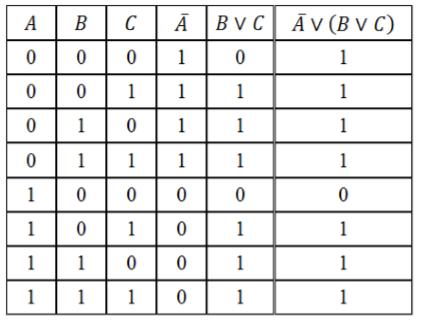
Заполним таблицу, учитывая таблицы истинности логических операций.
Рисунок 3.
Пример 2
По данному логическому выражению построить таблицу истинности:
[F=overline{(Avee B)bigwedge overline{C}}vee overline{(Avee C)bigwedge B}]
Решение:
-
Определим количество строк:
Количество простых выражений – $n=3$, значит
кол-во строк = $2^3 + 1=9$.
-
Определим количество столбцов:
Количество переменных – $3$.
Количество логических операций и их последовательность:
- отрицание ($bar{C}$);
- дизъюнкция, т.к. она находится в скобках ($A vee B$);
- конъюнкция ($(Avee B)bigwedge overline{C}$);
- отрицание, которое обозначим $F_1$ ($overline{(Avee B)bigwedge overline{C}}$);
- дизъюнкция ($A vee C$);
- конъюнкция ($(Avee C)bigwedge B$);
- отрицание, которое обозначим $F_2$ ($overline{(Avee C)bigwedge B}$);
-
дизъюнкция – искомая логическая функция ($overline{(Avee B)bigwedge overline{C}}vee overline{(Avee C)bigwedge B}$).
Кол-во столбцов = $3 + 8 = 11$.
-
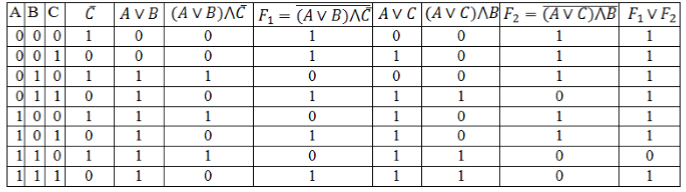
Заполним таблицу, учитывая таблицу истинности логических операций.
Рисунок 4.
Алгоритм построения логической функции по ее таблице истинности
- Выделяют в таблице истинности строки со значением функции, равным $1$.
- Выписывают искомую формулу как дизъюнкцию нескольких логических выражений. Количество этих выражений равно количеству выделенных строк.
- Каждое логическое выражение в этой дизъюнкции записать как конъюнкцию аргументов функции.
- В случае, когда значение какого-то из аргументов функции в соответствующей строке таблицы принимает значение $0$, то этот аргумент записать в виде его отрицания.
Пример 3
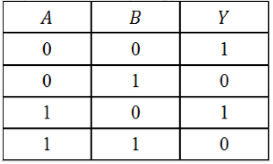
По данной таблице истинности некоторой логической функции $Y(A,B)$ cоставить соответствующую логическую функцию.
Рисунок 5.
Решение:
- Значение функции равно $1$ в $1$-й и $3$-й строках таблицы.
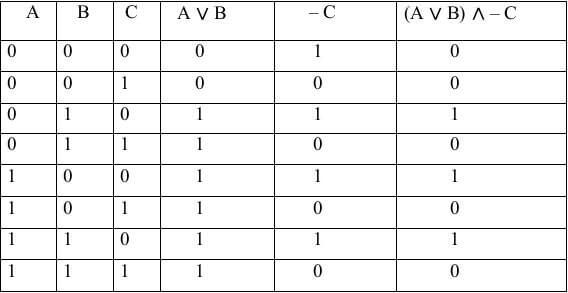
- Поскольку имеем $2$ строки, получим дизъюнкцию двух элементов:
Рисунок 6.
- Каждое логическое выражение в этой дизъюнкции запишем как конъюнкцию аргументов функции $A$ и $B$: $left(Awedge Bright)vee left(Awedge Bright)$
- В случае, когда значение в соответствующей строке таблицы равно $0$, запишем этот аргумент с отрицанием, получим искомую функцию:[Yleft(A,Bright)=left(overline{A}wedge overline{B}right)vee left(Awedge overline{B}right).]
Находи статьи и создавай свой список литературы по ГОСТу
Поиск по теме
Дата написания статьи: 12.04.2016
Формулы алгебры высказываний
Построение сложных высказываний
С помощью логических операций, рассмотренных в предыдущей лекции, из простейших высказываний можно строить высказывания более сложные. Например, из высказываний можно построить такое высказывание: «Если Саратов находится на берегу Невы и все люди смертны, то А.С. Пушкин — великий русский математик». Построенное высказывание символически записывается так:
. Конечно, оно звучит несколько странно, поскольку соединяет в себе столь разнородные понятия, которые обычно существуют раздельно друг от друга. Но нас, еще раз подчеркиваем, интересует не содержание этого высказывания, а его логическое значение. Оно может быть определено, исходя из логических значений исходных высказываний
и той схемы, по которой из исходных высказываний построено сложное высказывание. Так как
, то, используя соотношения (1.4), (1.2) и определения 1.7, 1.3, находим:
Итак, высказывание истинно.
Для конструирования данного сложного высказывания из простейших высказываний и
нужно применить операцию конъюнкции к первым двум высказываниям, а затем к полученному высказыванию и к третьему исходному высказыванию применить операцию импликации. Это словесное описание схемы конструирования данного сложного высказывания можно заменить описанием символическим:
, где
— некоторые символы (переменные), вместо которых можно подставить любые конкретные высказывания. Такая схема конструирования составного высказывания может быть применена к различным конкретным высказываниям, а не только к высказываниям
. Например, по этой схеме» из высказываний
построим высказывание «Если Сократ — человек и снег — белый, то
«. Находим его логическое значение:
Таким образом, та же самая схема построения составного высказывания привела к ложному высказыванию. Однако ввиду разнородности понятий, которыми оперируют исходные высказывания , трудно на интуитивной основе судить об истинности высказывания
.
По рассматриваемой схеме построено и следующее высказывание: «Если 100 делится на 5 и 100 делится на 2, то 100 делится на 10». Формальное вычисление логического значения данного высказывания показывает, что оно истинно, с чем вполне согласуются наши интуитивные представления об этом высказывании.
Итак, символическая запись является своего рода формулой. Конечно, более привычны формулы типа
(формула площади круга),
(формула потенциальной энергии тела) и им подобные. Тем не менее выражение
также можно считать формулой — формулой схемы конструирования составных высказываний из более простых.
Понятие формулы алгебры высказываний
В формулу вместо переменных
можно подставлять конкретные высказывания, после чего вся формула будет превращаться в некоторое составное высказывание. Переменные, вместо которых можно подставлять высказывания, т.е. переменные, пробегающие множество высказываний, называют пропозициональными переменными, или высказывательными переменными, или переменными высказываниями. Будем обозначать пропозициональные переменные заглавными буквами латинского алфавита
или такими же буквами с индексами
Теперь дадим точное определение формулы алгебры высказываний.
Определение 2.1
1. Каждая отдельно взятая пропозициональная переменная есть формула алгебры высказываний.
2. Если и
— формулы алгебры высказываний, то выражения также являются формулами алгебры высказываний:
3. Никаких других формул алгебры высказываний, кроме получающихся согласно пунктам 1 и 2, нет.
Определения такого типа называются индуктивными. В них имеются прямые пункты (в данном случае п. 1 и п. 2), где задаются объекты, которые в дальнейшем именуются определяемым термином (в данном случае — формулами алгебры высказываний), и косвенный пункт (в данном случае п. 3), в котором говорится, что такие объекты исчерпываются объектами, заданными в прямых пунктах. Среди прямых пунктов имеются базисные пункты (в данном случае п. 1), где указываются некоторые конкретные объекты, именуемые в дальнейшем определяемым термином, и индуктивные пункты (в данном случае п. 2), где даются правила получения определяемых объектов, в частности из объектов, перечисленных в базисных пунктах.
В данной лекции формулы алгебры высказываний будем называть просто формулами. Есть и другие названия для понятия формулы: правильно построенная формула или правильно построенное выражение, но они представляются менее предпочтительными. Само определение формулы, носящее индуктивный характер, на первых порах кажется непривычным. Определения такого типа вам ранее не встречались. Лучшее понимание этого определения наступит, когда вы научитесь применять его для определения того, является или не является формулой последовательность символов (слово), составленная из пропозициональных переменных, символов логических операций и скобок.
К этому полезно добавить следующее. Для каждой формулы должна существовать конечная последовательность всех ее подформул, т.е. такая конечная последовательность, которая начинается с входящих в данную формулу пропозициональных переменных, заканчивается самой этой формулой, и каждый член этой последовательности, не являющийся пропозициональной переменной, есть либо отрицание уже имеющегося члена этой последовательности, либо получается из двух уже имеющихся членов этой последовательности их соединением с помощью одного из знаков и заключением полученного выражения в скобки. Такую последовательность всех подформул данной формулы иногда называют порождающей последовательностью для данной формулы. Наличие такой последовательности у логического выражения служит критерием того, что выражение является формулой. Это свойство отличает формулы.
Приведем примеры формул. На основании п. 1 определения 2.1 формулами будут пропозициональные переменные:
Далее на основании п. 2 того же определения из этих формул построим следующие:
Из построенных формул также на основании п. 2 строим еще более сложные формулы:
Ясно, что процесс построения все более сложных формул может продолжаться безгранично.
Приведем примеры выражений, не являющихся формулами. Это в каком-то смысле нелепые выражения. К примеру, выражение было бы формулой на основании п. 2 определения 2.1, если бы формулами были выражения
и
. Выражение
есть пропозициональная переменная и потому на основании п. 1 определения 2.1 является формулой. Рассмотрим выражение
. Оно было бы формулой, если бы между формулами
и
стоял один из знаков логических связок. Но такого знака нет. Следовательно, выражение
не формула, и исходное выражение
формулой также не является.
Таким образом, индуктивный характер определения 2.1 дает возможность эффективно решать для каждого выражения, является оно формулой алгебры высказываний или нет.
Вот еще примеры выражений, не являющихся формулами (убедитесь в этом самостоятельно):
То, что последнее выражение не является формулой, может сначала вызвать недоумение. Но после сопоставления его с п. 2 определения 2.1 отмечаем, что в последнем выражении недостает внешних скобок для того, чтобы считать его формулой. Действительно, если бы мы сочли данное выражение формулой, то на основании п. 2 формулой было бы и выражение . Но оно бессмысленно, потому что неопределенно: неизвестно, какую операцию нужно выполнять первой, импликацию или эквивалентность. А от этого, как можно проверить (проверьте!), будет зависеть логическое значение составного высказывания (см. п. 3), получающегося из последнего выражения, если его превратить в формулу указанием последовательности действий и придать пропозициональным переменным
и
конкретные значения (высказывания). Если бы в исходном выражении стояли внешние скобки, т.е. если бы оно было формулой
, то проделанное в предыдущем абзаце построение привело бы к формуле
.
Итак, требование внешних скобок у формулы не является излишним формализмом. Тем не менее внешние скобки придают формуле громоздкость и, если данная формула не входит составной частью в более сложную формулу, не несут никакой информации и смысловой нагрузки. Поэтому внешние скобки в окончательно записанной формуле договариваются опускать. Например, формулу будем записывать в виде
, а вместо формулы
будем писать
. Но если данная формула должна будет войти составной частью в более сложную формулу, то сначала заключаем ее во внешние скобки и только потом отправляем в процедуру построения новой формулы.
Логическое значение составного высказывания
Если в формулу алгебры высказываний вместо пропозициональных переменных
подставить конкретные высказывания
соответственно, то получится некоторое новое составное высказывание
. Оно называется конкретизацией формулы
на выборе высказываний
. Как определить логическое значение
полученного составного высказывания, если известны логические значения
исходных высказываний
?
Прежде чем сформулировать в следующей теореме ответ на поставленный вопрос, введем одно понятие. Ранее отмечалось, что только логические значения высказываний, а не их содержание рассматриваются в алгебре высказываний. Это дает возможность несколько упростить обозначения и терминологию. Так, каждое ложное высказывание можно рассматривать как элемент 0, а каждое истинное — как элемент 1 двухэлементного множества , и писать вместо
или
лишь только
или
соответственно. Далее, если формула
при подстановке вместо ее пропозициональных переменных
высказываний
с логическими значениями
превращается в высказывание
с логическим значением
, то будем говорить, что формула
принимает значение а, если ее переменные
принимают значения
соответственно, и писать
и
, где
. Для нахождения значения
нужно подставить в формулу
вместо пропозициональных переменных
значения
соответственно и в полученном выражении последовательно проделать все действия с нулями и единицами, предписываемые правилами таблиц из определений 1.1, 1.3, 1.5, 1.7, 1.9. В результате получим 0 или 1. Полученное значение будем обозначать
и называть значением данной формулы
на данном наборе нулей и единиц
. Например, вычислим значение формулы
на наборе
Теорема 2.2. Логическое значение составного высказывания равно значению формулы
на наборе
логических значений составляющих высказываний
, т.е.
Доказательство. Докажем утверждение методом полной математической индукции по числу символов логических операций, входящих в формулу .
Если формула содержит 0 символов логических операций, то она представляет собой просто пропозициональную переменную, скажем,
, т.е.
(знак
обозначает абсолютную тождественность двух формул, графическую одинаковость левой и правой частей). Тогда доказываемое соотношение сводится к тривиальному равенству:
.
Если формула содержит лишь один символ логической операции, то она является одной из следующих формул:
В этих случаях доказываемое равенство есть одно из равенств (1.1)–(1.5).
Предположим теперь, что утверждающееся в теореме равенство верно для всех формул алгебры высказываний, содержащих не более к символов логических операций. Докажем, что оно верно для формулы , содержащей
символов логических операций. На основании определения 2.1 формула
имеет один из следующих видов:
где и
— некоторые формулы, каждая из которых содержит уже не более к символов логических операций. Нужно провести доказательство для всех пяти случаев. Но в силу принципиальной идентичности этих доказательств проделаем его, например, для случая
. Вычисляем:
В проделанных вычислениях второе равенство основано на определении 1.3 логической операции конъюнкции. Третье равенство основано на предположении индукции о том, что для формул и
соотношение теоремы выполняется. Наконец четвертое равенство записано на основании того, что
.
Аналогичным образом соотношение теоремы доказывается и во всех остальных случаях конструирования формулы из формул
и
.
Следовательно, утверждение теоремы верно для любой формулы алгебры высказываний.
Итак, здесь необходимо понять, что логическое значение составного высказывания по существу является значением некоторого (логического) выражения при некотором наборе конкретных значений всех входящих в него (пропозициональных) переменных. При этом пропозициональные переменные могут принимать значения 0 или 1, само выражение принимает значение 0 или 1, и вычисляется это значение (в силу теоремы 2.2) посредством применения к значениям 0 и 1 предписываемых данным выражением логических действий. Логические действия над величинами 0 и 1 выполняются по правилам, определяемым таблицами истинности этих действий (операций) — отрицания, конъюнкции, дизъюнкции, импликации и эквивалентности. Таким образом, мы фактически начинаем иметь дело с некой новой (логической) алгеброй, или алгеброй логики, которая как бы «параллельна» привычной школьной алгебре. Сравним компоненты этих двух алгебр с помощью следующей таблицы:
Аналогия со школьной алгеброй будет продолжена при рассмотрении равносильных преобразований в алгебре логики.
Составление таблиц истинности для формул
На основании теоремы 2.2 можно для данной формулы алгебры высказываний найти логические значения всех тех высказываний, в которые формула превращается при подстановке вместо всех ее пропозициональных переменных различных конкретных высказываний. При этом говорят о логическом значении самой формулы и о логических значениях ее пропозициональных переменных. При нахождении логических значений формулы, соответствующих всевозможным наборам значений ее пропозициональных переменных, удобной формой записи является табличная форма. Рассмотрим примеры.
Пример 2.3. Составим таблицу истинности для формулы . В первых двух столбцах таблицы выпишем всевозможные пары логических значений, которые могут принимать пропозициональные переменные
и
(точнее, те высказывания, которые могут быть подставлены в формулу вместо пропозициональных переменных
и
). В последующих столбцах выписываем логические значения формул
и
, образующих так называемую порождающую последовательность для данной формулы. Руководствуемся при этом определениями логических операций импликации и дизъюнкции. В результате получаем таблицу:
Первые два столбца и последний столбец составленной таблицы задают соответствия между логическими значениями исходных высказываний и логическим значением составного высказывания, получаемого по данной формуле. Эти три столбца и образуют таблицу истинности данной формулы. Остальные два столбца (для логических значений и
носят вспомогательный, промежуточный характер.
Пример 2.4. Составим таблицу истинности для формулы . Она содержит три пропозициональные переменные, для которых имеются точно восемь различных наборов значений истинности. Таблица истинности для рассматриваемой формулы вместе с промежуточными столбцами выглядит следующим образом:
Таблицу истинности формулы можно составлять в сокращенном виде.
Пример 2.5. Составим, например, такую таблицу для формулы: (внешние скобки у формулы, согласно договоренности, опущены). В первой строке таблицы выпишем данную формулу. Под переменными
и
выписываем всевозможные наборы их логических значений. Далее столбец под первым знаком
заполним логическими значениями формулы
, исходя из соответствующих значений переменной
, а столбец под знаком
— логическими значениями формулы
, исходя из соответствующих логических значений формул
и
. Затем заполняем столбец под вторым знаком
значениями формулы
и столбец под знаком
— значениями формулы
. Наконец заполняем столбец под знаком
логическими значениями данной формулы. В итоге получаем
Выделенные жирным шрифтом табулированные значения представляют собой столбец логических значений данной формулы.
Практика составления довольно большого числа таблиц истинности есть наилучший способ прочно запомнить определения логических связок (отрицания, конъюнкции, дизъюнкции, импликации, эквивалентности) и довести до автоматизма выдачу значений любой из этих операций. Это знание необходимо для решения более содержательных задач алгебры высказываний.
Классификация формул алгебры высказываний
Формулы алгебры высказываний подразделяются на следующие типы: выполнимые, тавтологии, опровержимые и тождественно ложные.
Формула алгебры высказываний называется выполнимой, если некоторая ее конкретизация является истинным высказыванием, т.е. существуют такие конкретные высказывания
, которые, будучи подставленными в эту формулу вместо переменных
соответственно, превращают ее в истинное высказывание. Таким образом,
выполнима, если существуют такие конкретные высказывания
, что
. Выполнимой формулой является, в частности, формула, рассмотренная в примере 2.4. Она превращается в истинное высказывание, если, например, вместо пропозициональных переменных
подставить ложные высказывания. Выполнима также формула
, конкретизация которой рассмотрена в начале этой лекции.
Формула называется тавтологией, или тождественно истинной, если она превращается в истинное высказывание при всякой подстановке вместо переменных конкретных высказываний
, т.е. если
для любых высказываний
. Формула из примера 2.3 является тавтологией. Для обозначения тавтологии используется знак
, который ставится перед формулой, являющейся тавтологией. Таким образом, запись
означает, что формула
является тавтологией. В частности, для указанного примера можем записать
.
Формула называется опровержимой, если существуют такие конкретные высказывания
, которые превращают данную формулу в ложное высказывание
, т.е.
. Другими словами, опровержимые формулы — это формулы, не являющиеся тавтологиями. Опровержимой является формула, рассмотренная в примере 2.4. Она обращается в ложное высказывание лишь тогда, когда вместо всех переменных
подставлены истинные высказывания. Формула
также опровержима.
Наконец, формула называется тождественно ложной, или противоречием, если
для любых конкретных высказываний
. Другими словами, тождественно ложные формулы — это такие формулы, которые не являются выполнимыми.
При решении задач на классификацию формул полезно отказаться от механического составления таблиц истинности и научиться решать их методом анализа структуры формулы и нахождения тех отдельных наборов значений переменных, в случае которых формула принимает определяющее значение.
Мышление и математическая логика
В заключение следует отметить, что мы приступили к фундаментальному процессу исследования математическими методами такой сферы, как область человеческого мышления. Начало процессу математизации логики положено математизацией языка. Фактически построена своеобразная знаковая система (символический язык логики высказываний), с помощью которой можно попытаться отразить человеческую мысль и проследить оформление мыслительного процесса. Этот язык основывается на алфавите, состоящем из следующих символов:
1) пропозициональных букв: ;
2) символов логических операций: ;
3) технических знаков: .
Словами построенного языка являются формулы логики высказываний. Предложения обычного (русского) языка могут быть «переведены» на символический язык логики высказываний, где они представляются формулами логики высказываний. Следует иметь в виду, что при таком переводе сохраняются логическое содержание, логическая структура предложения, но, конечно же, теряются его языковая красота и психологические оттенки. Формула представляет собой формальную последовательность знаков, составленную по строгим правилам, нарушение которых недопустимо. Такой перевод высказывания естественного языка на символический язык называется его формализацией. В частности, перевод высказывания на символический язык логики высказываний есть его формализация в рамках символической логики высказываний. Получаемая формула показывает способ соединения простых высказываний в составное при помощи логических союзов. Она представляет как бы в «чистом виде» логическую структуру составного высказывания.
Формула логики высказываний сама по себе не имеет никакого содержания. В частности, она не является ни истинной, ни ложной. Она превращается в высказывание, истинное или ложное, при всякой подстановке вместо всех ее пропозициональных переменных любых конкретных высказываний. Такой процесс подстановки называется интерпретацией данной формулы алгебры высказываний.
Таким образом, имеются два взаимно-обратных процесса (две процедуры): формализация и интерпретация. Если имеется формула и высказывание
есть результат ее интерпретации, то сама формула
будет формализацией высказывания
. Обратно, если имеется высказывание
и формула
есть его формализация, то высказывание
будет одной из интерпретаций формулы
. Итак, формализация — это переход от высказывания естественного языка к формуле логики высказываний, а интерпретация — переход от формулы логики высказываний к высказыванию естественного языка. Таблица истинности или таблица значений формулы логики высказываний — это таблица, которая указывает логическое значение формулы при любой ее интерпретации.
Осознание этих понятий исключительно важно на данном этапе, поскольку они являются ключевыми для изучения в дальнейшем более глубоких разделов математической логики. На данном этапе делается первый шаг на пути формализации — важнейшего метода математической логики.
Математический форум (помощь с решением задач, обсуждение вопросов по математике).
Если заметили ошибку, опечатку или есть предложения, напишите в комментариях.
Логическая функция одно из основополагающих понятий математической логики. Она зависит от логических переменных и принимает значения из множества, от которого находится в зависимости. Логические функции булевых переменных могут принимать только два значения – 1 или 0.
Понятие таблиц истинности
Задаваться логическая функция может числовым способом, словесным описанием, картами Карно, аналитическим выражением и с помощью таблиц истинности. В последнем случае все аргументы функции следует записать в левой части таблицы, а значения, которые им соответствуют, в правой.
Определения 1 — 2
Таблица истинности – это таблица, просто и наглядно показывающая, какие значения будут у логического выражения при всевозможных наборах переменных функции.
Равносильными именуют те логические выражения с совпадающими последними столбцами таблицы истинности. Обозначают равносильные функции знаком «=».
Правила того, как следует проводить построение таблицы истинности
Несоблюдение хотя бы одного из них ведёт к очень грубой ошибке. Вот эти правила:
- Число строк таблицы должно совпадать с числом комбинаций всевозможных n логических переменных, то есть быть равным 2n;
- Количество столбцов таблицы должно равняться сумме числа логических переменных и числа логических операций;
- В построенный шаблон таблицы истинности должны вписываться все значения исходных переменных;
- Построение таблицы истинности выражения происходит по её столбцам, при этом обязательно учитываются правила логических операций.
Порядок действий при построении таблицы истинности для логических выражений
Порядок действий при построении таблицы истинности, какой бы ни была логическая функция, следующий:
- Определить, какое число строк и столбцов будет в будущей таблице. Делается подобное по формулам
X = n + m, Y = 2n+1.
Где n – число переменных, m – чило логических операций. - Заполнить самую верхнюю строку таблицы переменными и логическими операциями, идя слева направо. При этом приоритетность логических операций следует учитывать обязательно, иначе получится совсем не то, что нужно;
- В первых столбцах перечислить всевозможные комбинации входных значений;
- Выполняя заданные логические операции, заполнить все оставшиеся ячейки;
Ответом следует считать последний заполненный столбец таблицы.
О порядке логических операций
Лучше его представить списком. Логические операции выполняют в следующей последовательности: сначала идёт инверсия, затем конъюнкция, после этого дизъюнкция, после неё импликация, по её выполнении эквиваленция.
После них идут Штрих Шеффера и Стрелка Пирса. Первым может быть выполнено как то, так и другое.
Далее приведём несколько поучительных задач на построение таблиц истинности
Задачи 1 — 3
Сделать построение таблицы истинности для функции ((A→B) ∧ A) ↔ B
Решение:
-
- Определяем сколько будет у нас столбцов. Количество переменных у нас 2, логических операций 4, число столбцов равно сумме 2+4 = 6.
- Определяем, сколько будет у на строк. Оно равно 2n, плюс ещё одна строка для обозначения переменных и логических операций. У нас будет 2n+1 = 22 + 1= 5;
- Заполняем первую строку. Прописываем символы переменные и логических операций;
- В двух первых столбцах записываем возможные значения переменных;
- В далее идущих столбцах записываем, какие значения принимают промежуточные функции;
- В самом последнем из столбцов записываем итоговые значения функции.
В результате всего этого у нас должно получиться:
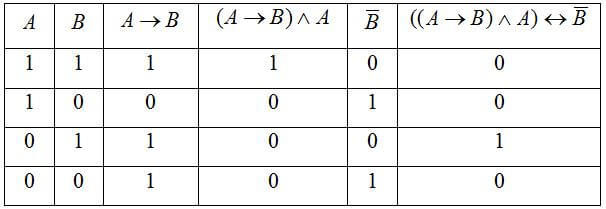
Провести построение таблицы истинности функции (A ∨ B) ∧ – C
Решение:
- Определяем сколько будет столбцов. Количество переменных у нас 3, количество логических операций 3. Складываем то и другое: 3+3 = 5.
- Определяем, количество строк. Оно равно 2n, плюс ещё одна строка для обозначения переменных и логических операций.В итоге будет 2n+1 = 23 + 1= 9;
- Заполняем первую строку. Прописываем символы переменные и логических операций;
- В два первые столбца вносим возможные значения наших переменных;
- В далее следующие столбцы записываем, какие значения принимают промежуточные функции;
- В последнем столбце записываем итоговые значения функции.
В итоге получим таблицу:
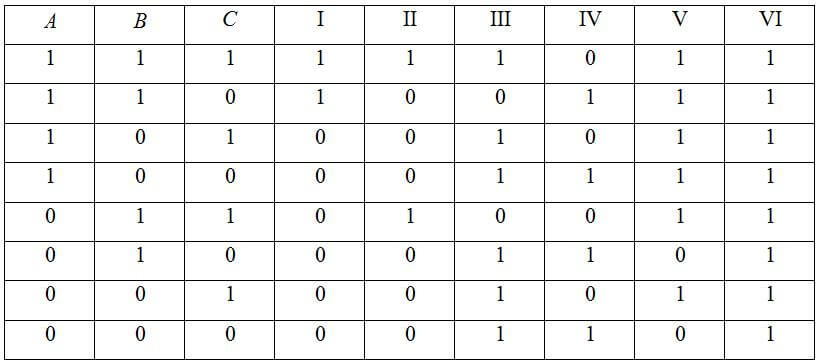
Сделать таблицу истинности для
(A ∧ B ↔ B ∧ C) ∨ (C → A)
Функция посложнее и таблица получится значительно больше, чем предыдущая.
- Считаем столбцы. Количество переменных 3, количество логических операций 6. Значит столбцов будет 3+6=9;
- Считаем строки. Их количество будет 23+1= 9;
- Заполняем первую строку таблицы;
- В первых столбцах записываем все допустимые значения наших переменных;
- В остающихся столбцах пишем, какие наша функция принимает промежуточные значения
- В последний столбец пишем итоговые значения данной нам функции.
В итоге у нас получается таблица:
Нет времени решать самому?
Наши эксперты помогут!
Построения функции, если известна её таблица истинности
Совершенной дизъюнктивной нормальной формой считают такую нормальную форму, в которой отсутствуют одинаковые элементарные конъюкции и все конъюкции включают один и тот же набор переменных, куда каждая из них входит не более одного раза.
Алгоритм действий для получения СДНФ по таблице истинности:
- Отметьте в таблице строки, в которых значение функции равняется 1
- Выпишете для каждой отмеченной строки конъюкцию всех переменных. Если переменная равна 1, в конъюкцию следует включить саму эту переменную. Если переменная равняется 0, то её отрицание;
- Все полученные конъюкции свяжите в дизъюкцию.
Аналогичным образом определяется СКНФ
В строках, в последнем столбце которых функция равна 0, запишите дизъюкции всех переменных. Если значение переменной в данной строке будет 0, в дизъюкцию следует включить саму эту переменную. Если значение функции равно 1, то включить нужно её отрицание.
Правило + задача
СДНФ всегда равно СКНФ. СДНФ = СКНФ.
Дана таблица истинности:
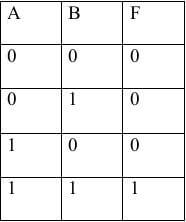
Выделяем в ней цветом строку
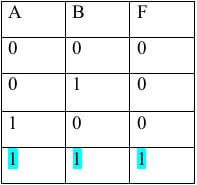
Заполняем столбцы с СДНФ и с СКНФ
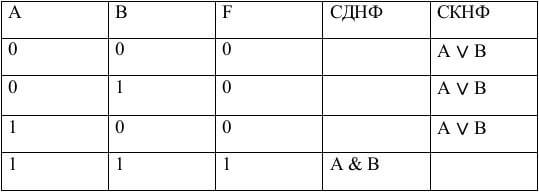
Записываем СДНФ
СДНФ = A & B
Записываем СКНФ
СКНФ = (A ∨ B) & (A ∨ B) & (A ∨ B)
Запись утверждений на языке алгебры высказываний. Формулы алгебры высказываний
Простые и составные высказывания
Бывают два вида высказываний: простые и составные. Составные высказывания получаются из простых с помощью логических символов %%overline, land, lor, rightarrow, leftrightarrow%%. Рассмотрим высказывание «Иванов окончил школу и поступил в институт». Оно образовано из простых высказываний «Иванов окончил школу» и «Иванов поступил в институт» с помощью операции конъюнкции. Обозначим эти высказывания через %%A%% и %%B%% соответственно, тогда сложное высказывание «Иванов окончил школу и поступил в институт» имеет вид %%A land B%%. При этом высказывания %%A%% — «Иванов окончил школу» и %%B%% — «Иванов поступил в институт» нельзя представить ввиде составных высказываний. Поэтому они простые (элементарные).
Пример
Дано высказывание «Если число %%a%% делится на число %%c%% и число %%b%% делится на число %%c%%, то их сумма %%a+b%% делится на число %%c%%». Обозначить буквами простые высказывания и, используя логические символы, выразить данное высказывание через простые.
Обозначим:
- %%A%%: «число %%a%% делится на число %%c%%»;
- %%B%%: «число %%b%% делится на число %%c%%»;
- %%C%%: «сумма %%a+b%% делится на число %%c%%».
Тогда высказывание, с учетом замены, примет вид: «Если %%A%% и %%B%%, то %%C%%», которое на языке алгебры высказываний выглядит
$$
(A land B) rightarrow C.
$$
Формулы алгебры высказываний
Для определения понятия формулы нам необходимо понять, какие переменные используются в алгебре высказываний.
Пропозициональная переменная, или переменная для высказываний, — переменная, котороя может принимать одно из двух истинностных значений: «истина» или «ложь». Далее будем их называть просто переменными.
С помощью логических знаков (%%overline{ }, land, lor, rightarrow, leftrightarrow%%) и переменных можно составлять сложные высказывания, которые и будем называть формулами алгебры высказываний.
Например, формула %%X = (A land B) rightarrow (A lor B)%% получена так: сначала построены формулы %%A land B%% и %%A lor B%%, затем из этих двух формул получена исходная с помощью применения знака %%rightarrow%%.
Вместо переменных в формулу можно подставлять произвольные значения переменных. При вычислении значения формулы неважно как сформулированы входящие в нее высказывания, важно лишь их значения: «истина» или «ложь».
Порядок построения формулы позволяет составить таблицу истинности для формулы %%X%%. Для этого переберем всевозможные комбинации значений переменных %%A%% и %%B%% (каждая строка в таблице) и найдем значение интересующей нас формулы.
| %%A%% | %%B%% | %%A land B%% | %%A lor B%% | %%(A land B) rightarrow (A lor B)%% |
|---|---|---|---|---|
| %%0%% | %%0%% | %%0%% | %%0%% | %%1%% |
| %%0%% | %%1%% | %%0%% | %%1%% | %%1%% |
| %%1%% | %%0%% | %%0%% | %%1%% | %%1%% |
| %%1%% | %%1%% | %%1%% | %%1%% | %%1%% |
Таблица истинности для формулы %%X%%
В курсе математической логики дается следующее определение формулы алгебры высказываний:
- Переменные являются формулами.
- Если %%A%% и %%B%% — формулы, то выражения
$$
overline{A}, A land B, A lor B, A rightarrow B, A leftrightarrow B
$$
являются формулами. - Всякая формула есть либо переменная или образуется из переменных последовательным применением правила %%2%%.
Пример
Показать, что выражение %%X = (A lor B) rightarrow ((C land D) leftrightarrow overline{A})%% является формулой.
Действительно, %%A, B, C, D%% — переменные, следовательно, формулы по правилу %%1%%. Так как %%A%% — формула, то %%overline{A}%% — формула по правилу %%2%%. Так как %%A,B,C,D%% формулы, %%A lor B%% и %%C land D%% — формулы по правилу %%2%%. Так как %%C land D%% и %%overline{A}%% формулы, то %%(C land D) leftrightarrow overline{A}%% формула по правилу %%2%%. Так как %%A lor B%% и %%(C land D) leftrightarrow overline{A}%% формулы, то %%X%% — формула по правилу %%2%%.
Подформулы
Выражения, полученные при «сборке» формулы называются ее частями или подформулами. Например, формула %%X = (A lor B) rightarrow ((C land D) leftrightarrow overline{A})%% имеет следующие подформулы:
$$
A,B,C,D, overline{A}, A lor B, C land D, (C land D) leftrightarrow overline{A}, (A lor B) rightarrow ((C land D) leftrightarrow overline{A})
$$
Правила записи формул
При записи формул придерживаются следующих правил.
- Внешние скобки в формуле можно опускать. Например, вместо %%(A lor B)%% пишем %%A lor B%%.
-
Как и в арифметике, в алгебре высказываний у каждой операции есть свой приоритет. Приоритеты логических знаков, расположенные в порядке убывания, следующие:
$$
overline{ }, land, lor, rightarrow, leftrightarrow.
$$Приоритеты логических операций можно изменить, используя скобки.
Каждый предшествующий знак является «сильнее» последующего. Поэтому вместо записи %%(A land B) lor C%% можно писать %%A land B lor C%%, вместо записи %%A leftrightarrow (B lor C)%% — %%A leftrightarrow B lor C%%.
3. Если в формуле %%X = A land B land C land ldots land Z%% опущены скобки, то подрузамевается левосторонняя расстановка скобок и считается, что %%X = bigg(Big((A land B) land CBig) land ldotsbigg)land Z%%. Аналогично для подобных формул, имеющих знак %%lor%%, %%rightarrow%% или %%leftrightarrow%%.
Примеры
Пользуясь правилами %%1-3%% восстановить скобки в формуле
$$
X = A lor B land C leftrightarrow A rightarrow B rightarrow C
$$
По правилам %%1-3%% имеем %%X = Bigg(Big(A lor (B land C)Big) leftrightarrow Big((A rightarrow B) rightarrow CBig)Bigg)%%.
Пользуясь правилами %%1-3%% опустить лишние скобки в формуле
$$
X = Bigg((A leftrightarrow B) lor Big((A land B) land CBig) rightarrow Big((B lor C) land ABig)Bigg)
$$
Решение, над знаком равно будут указаны номера правил которые применяются.
$$
begin{array}{ll}
X &= Bigg((A leftrightarrow B) lor Big((A land B) land CBig) rightarrow Big((B lor C) land ABig)Bigg) overset{1}{=}\
&overset{1}{=} (A leftrightarrow B) lor Big((A land B) land CBig) rightarrow Big((B lor C) land ABig) overset{3}{=}\
&overset{3}{=} (A leftrightarrow B) lor (A land B land C) rightarrow Big((B lor C) land ABig) overset{2}{=}\
&overset{2}{=} (A leftrightarrow B) lor A land B land C rightarrow Big((B lor C) land ABig) overset{2}{=}\
&overset{2}{=} (A leftrightarrow B) lor A land B land C rightarrow (B lor C) land A.
end{array}
$$
Виды формул
Формула %%X%% называется тождественно истинной (или тавтологией), если она принимает значение «истина» при любых значениях входящих в нее переменных.
Например, формула %%X = (A land B) rightarrow (A lor B)%% является тождественно истинной, т.к. при любых значениях %%A%% и %%B%% она является истинной.
Существует две причины, по которым мы считаем высказывание истинным или ложным. Первое, на основе различных свойств объекта. Например, «Москва — столица Австрии» ложно, так как она ею не является. Точно также в случае «%%2 cdot 3 = 6%%» значение «истина» установлено из свойств рассматриваемых объектов. Второе, когда приписывается значение «истина» или «ложь» вне зависимости от свойств обсуждаемых объектов. Это и есть логическая истинность.
Рассмотрим утверждение «верно, что завтра пойдет дождь или завтра не пойдет дождь». Очевидно, что это утверждение является истинным, даже не зная погоды на завтрашний день. В данном случае мы имеем дело с утверждениями вида %%A lor overline{A}%%. Так как формула %%A lor overline{A}%% является тождественно истинной, то независимо от переменной %%A%%, утверждение истинно.
Формула %%X%% называется тождественно ложной, если она принимает значение «ложь» при любых значениях входящих в нее переменных.
Формула, не являющаяся тождественно ложной и тождественно истинной, называется выполнимой.
Пример
Определить вид (тождественно истинная, тождественно ложная, выполнимая) формулы:
$$
X = A lor B rightarrow A land B
$$
Составим таблицу истинности для формулы %%X%%.
| %%A%% | %%B%% | %%A land B%% | %%A lor B%% | %%(A lor B) rightarrow (A land B)%% |
|---|---|---|---|---|
| %%0%% | %%0%% | %%0%% | %%0%% | %%1%% |
| %%0%% | %%1%% | %%0%% | %%1%% | %%0%% |
| %%1%% | %%0%% | %%0%% | %%1%% | %%0%% |
| %%1%% | %%1%% | %%1%% | %%1%% | %%1%% |
Поскольку формула не является тождественно истинной или тождественно ложной, то %%X%% — выполнимая формула.
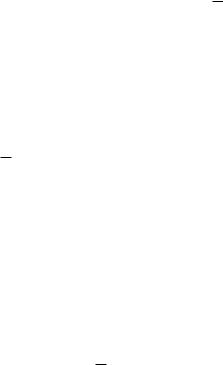
13
4.1.Логические выражения
Каждое составное высказывание можно выразить в виде формулы (логического выражения), в которую входят логические переменные, обозначающие высказывания, и знаки логических операций, обозначающие логические функции.
Для записи составного высказывания в виде логического выражения на формальном языке (языке алгебры логики) в составном высказывании нужно выделить простые высказывания и логические связи между ними.
Запишем в форме логического выражения составное высказывание
«(2·2=5 или 2·2=4) и (2·2≠5 или 2·2≠4)».
Проанализируем составное высказывание. Оно содержит два простых высказывания:
А = «2•2=5»—ложно (0), В = «2•2=4»—истинно (1).
Тогда составное высказывание можно записать в следующей форме: «(А или В) и (Ā или В)».
Теперь необходимо записать высказывание в форме логического выражения с учётом последовательности выполнения логических операций. При выполнении логических операций определён следующий порядок их выполнения:
инверсия, конъюнкция, дизъюнкция.
Для изменения указанного порядка могут использоваться скобки:
F = (A v В) & (Ā v В).
Истинность или ложность составных высказываний можно определять чисто формально, руководствуясь законами алгебры высказываний, не обращаясь к смысловому содержанию высказываний.
Подставим в логическое выражение значения логических переменных и, используя таблицы истинности базовых логических операций, получим значение логической функции:
F = (A v В) & (Ā v В) = (0 v 1) & (1 v 0) = 1 & 1 = 1.
14
4.2.Таблицы истинности
Таблицы, в которых логические операции отражают результаты вычислений сложных высказываний при различных значениях исходных простых высказываний, называются таблицами истинности.
Простые высказывания обозначаются переменными (например, A и B).
При построении таблиц истинности целесообразно руководствоваться определённой последовательностью действий:
1) необходимо определить количество строк в таблице истинности. Оно равно количеству возможных комбинаций значений логических переменных, входящих в логическое выражение. Если количество логических переменных равно п, то:
количество строк = 2n.
В нашем случае логическая функция 
2)необходимо определить количество столбцов в таблице истинности, которое равно количеству логических переменных плюс количество логических операций.
В нашем случае количество переменных равно двум: А и В, а количество логических операций — пяти (таблица 8), то есть количество столбцов таблицы истинности равно семи;
3)необходимо построить таблицу истинности с указанным количеством строк и столбцов, обозначить столбцы и внести в таблицу возможные наборы значений исходных логических переменных;
4)необходимо заполнить таблицу истинности по столбцам, выполняя базовые логические операции в необходимой последовательности и в соответствии с их таблицами истинности.
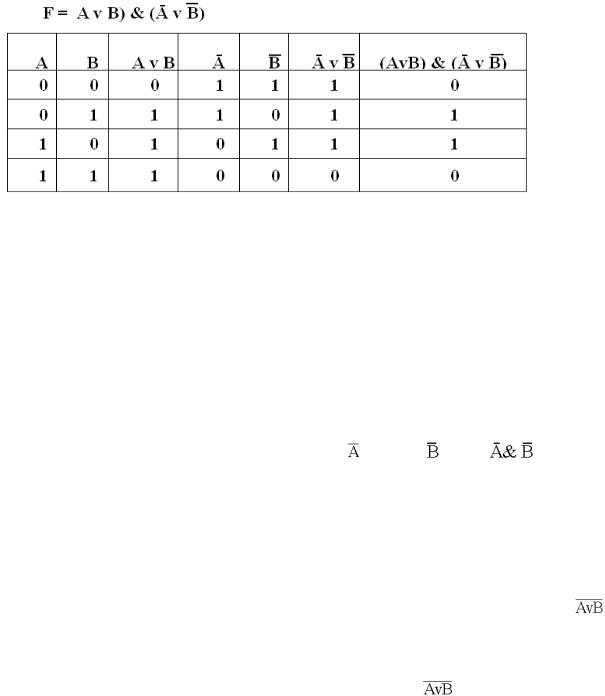
Теперь мы можем определить значение логической функции для любого набора значений логических переменных.
15
Таблица 8 – Таблица истинности логической функции
4.3.Равносильные логические выражения
Логические выражения, у которых последние столбцы таблиц истинности сов-
падают, называются равносильными. Для обозначения равносильных логических выражений используется знак «=».
Докажем, что логические выражения 

ца 9).
Таблица 9 – Таблица истинности логического выражения
|
А |
В |
|||
|
0 |
0 |
1 |
1 |
1 |
|
0 |
1 |
1 |
0 |
0 |
|
1 |
0 |
0 |
1 |
0 |
|
1 |
1 |
0 |
0 |
0 |
Теперь построим таблицу истинности логического выражения (таблица 10).
Таблица 10 – Таблица истинности логического выражения
|
А |
В |
А v В |
|
|
0 |
0 |
0 |
1 |
|
0 |
1 |
1 |
0 |
|
1 |
0 |
1 |
0 |
|
1 |
1 |
1 |
0 |
Значения в последних столбцах таблиц истинности совпадают, следовательно, логические выражения равносильны:

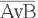
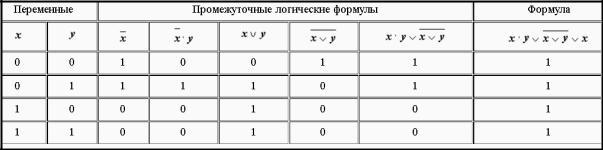
16
5. Построение таблиц истинности для сложных выражений
Согласно определению, таблица истинности логической формулы выражает соответствие между всевозможными наборами значений переменных и значениями формулы.
Для формулы, которая содержит две переменные, таких наборов значений
|
переменных всего четыре: |
|||
|
(0, 0), |
(0, 1), |
(1, 0), |
(1, 1). |
Если формула содержит три переменные, то возможных наборов значений
|
переменных восемь: |
|||||||
|
(0, 0, 0), |
(0, 0, 1), |
(0, 1, 0), |
(0, 1, 1), |
(1, 0, 0), |
(1, 0, 1), |
(1, 1, 0), |
(1, 1, 1). |
Количество наборов для формулы с четырьмя переменными равно шестнадцати и т.д.
Удобной формой записи при нахождении значений формулы является таблица, содержащая кроме значений переменных и значений формулы также и значения промежуточных формул.
Пример 1 1. Составим таблицу истинности для формулы, которая содержит две пере-
менные X и Y. В первых двух столбцах таблицы запишем четыре возможных пары значений этих переменных, в последующих столбцах — значения промежуточных формул и в последнем столбце — значение формулы. В результате получим таблицу 11:
Таблица 11 – Таблица истинности для формулы с переменными Х и У
Пример 2
Cоставить таблицу истинности сложного логического выражения: D = неA & (B+C).
А, В, С – три простых высказывания, поэтому:
количество строк = 23 +2 = 10 (n=3, т.к. на входе три элемента А, В, С) количество столбцов (таблица 12):
1)А,
2)В,
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #