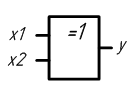Как составить таблицу истинности для шифратора

Федеральное
агентство связи

Ордена
Трудового Красного Знамени федеральное
государственное бюджетное образовательное
учреждение высшего образования

«Московский
технический университет связи и
информатики»

ПРАКТИЧЕСКАЯ
РАБОТА №2

«Шифратор»

Выполнили:
студенты гр. «Сортирный Союз»

лох

чмо

чукча

                               
  Проверила: Воронкова
М.Н.

Москва
2021

Цель
работы:
ознакомление с основными характеристиками
интегральных преобразователей кодов,
получение навыков проектирования
шифраторов.

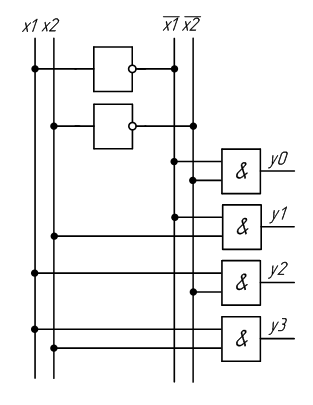
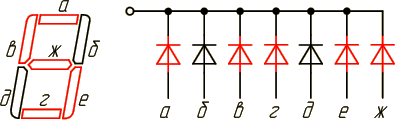
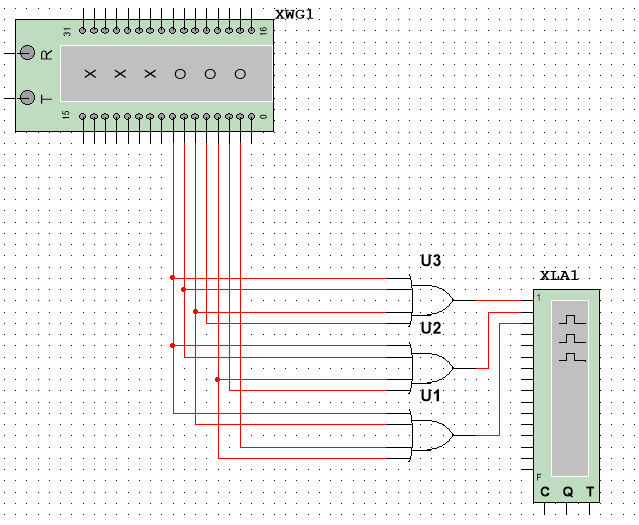
1.
По данной таблице истинности шифратора
(кодера) составить для него систему
уравнений и начертить блок-схему на
логических элементах.

Анализ
таблицы истинности шифратора показывает,
что разряд у1 принимает значение лог.1
в том случае, когда лог.1 имеют входные
сигналы х1;x3;x5;x7:

y1=x1+x3+x5+x7

Разряд
y2
принимает значение лог.1 в том случае,
когда лог.1 имеют входные сигналы х2, х3,
х6, х7:

y2=
х2+ х3+х6+х7

И,
наконец, разряд у3 принимает значение
лог.1 в том случае, когда лог.1 имеют
входные сигналы х4, х5, х6, х7:

y3=
х4+х5+х6+х7

Из
анализа полученных выражений можно
сделать вывод, что схема шифратора 8 на
3 состоит из трех четырехвходовых ЛЭ
«ИЛИ».

Следует
отметить, что разряд х0 не участвует в
формировании выходных сигналов y3—y1,
так как при хо = 1 сигналы у3=y2
= у1= 0.

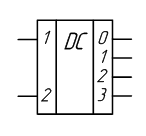
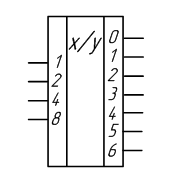
Для
обозначения шифратора служат буквы CD

Условное
обозначение шифратора 8 на 3

Скриншот
из Multisim

2.
По таблице истинности (согласно варианту)
шифратора (кодера) составить для него
систему уравнений и начертить блок-схему
на логических элементах.

Вариант
1

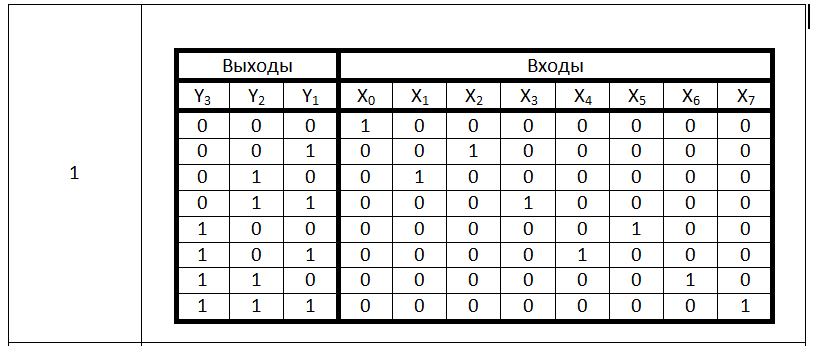
Анализ
таблицы истинности шифратора показывает,
что разряд у1 принимает значение лог.1
в том случае, когда лог.1 имеют входные
сигналы х2;x3;x4;x7:

y1=x2+x3+x4+x7

Разряд
y2
принимает значение лог.1 в том случае,
когда лог.1 имеют входные сигналы х1, х3,
х6, х7:

y2=
х1+ х3+х6+х7

И,
наконец, разряд у3 принимает значение
лог.1 в том случае, когда лог.1 имеют
входные сигналы х4, х5, х6, х7:

y3=
х4+х5+х6+х7

Из
анализа полученных выражений можно
сделать вывод, что схема шифратора 8 на
3 состоит из трех четырехвходовых ЛЭ
«ИЛИ».

Следует
отметить, что разряд х0 не участвует в
формировании выходных сигналов y3—y1,
так как при хо = 1 сигналы у3=y2
= у1= 0.

Для
обозначения шифратора служат буквы CD

Условное
обозначение шифратора 8 на 3

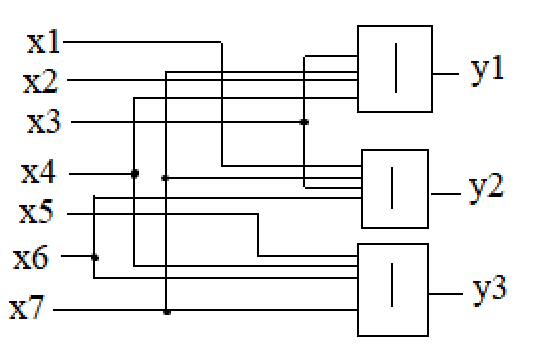
Скриншот
из Multisim

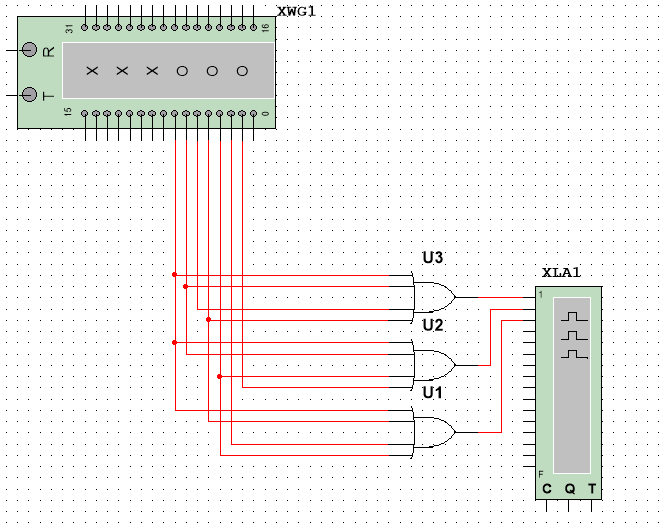
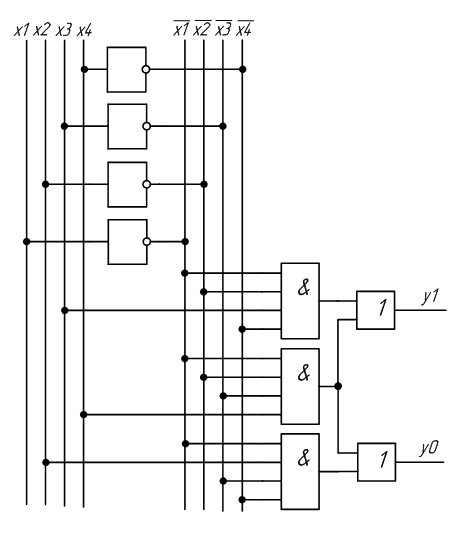
3.
Согласно заданию №1 практической работы
1 взять булеву функцию и ее таблицу
истинности, построить таблицу истинности
шифратора, составить для него систему
уравнений и начертить блок-схему на
логических элементах.

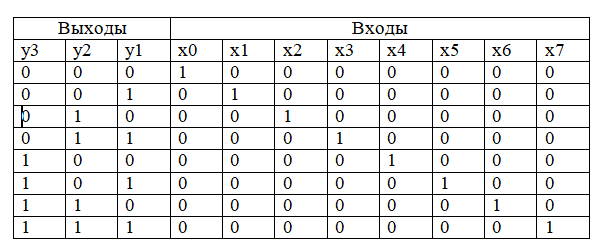
Анализ
таблицы истинности шифратора показывает,
что разряд у1 принимает значение лог.1
в том случае, когда лог.1 имеют входные
сигналы х1;x3;x5;x7:

y1=x1+x3+x5+x7

Разряд
y2
принимает значение лог.1 в том случае,
когда лог.1 имеют входные сигналы х2, х3,
х6, х7:

y2=
х2+ х3+х6+х7

И,
наконец, разряд у3 принимает значение
лог.1 в том случае, когда лог.1 имеют
входные сигналы х4, х5, х6, х7:

y3=
х4+х5+х6+х7

Из
анализа полученных выражений можно
сделать вывод, что схема шифратора 8 на
3 состоит из трех четырехвходовых ЛЭ
«ИЛИ».

Следует
отметить, что разряд х0 не участвует в
формировании выходных сигналов y3—y1,
так как при хо = 1 сигналы у3=y2
= у1= 0.

Для
обозначения шифратора служат буквы CD

Условное
обозначение шифратора 8 на 3

Скриншот
из Multisim

Лабораторная
работа 2.2 Шифраторы

Основные
теоретические положения

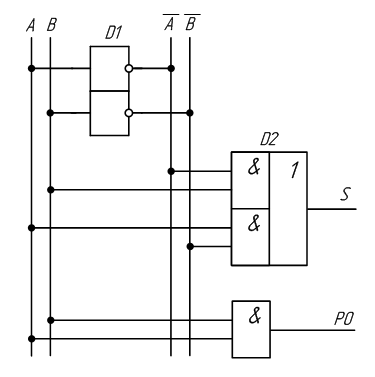
Шифраторомназывается
устройство, предназначенное для преобразования чисел, например, из десятичной
системы в двоичную систему счисления. Основное применение шифраторов – это
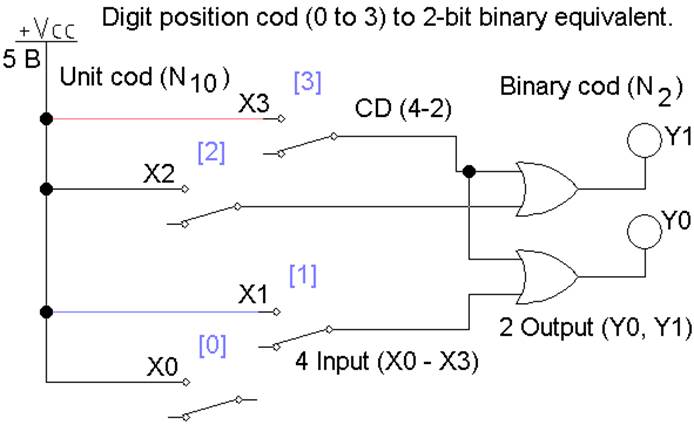
введение информации с клавиатуры. Обозначение CD(n—m), где n – количество входов, m – число выходов.

Схема и
таблица истинности CD(4 – 2) представлены на рис. 1 и в табл.
1, где X₀, X₁…X₃ входные сигналы, номер которых представляет
десятичный код. Выходные значения Y₀,
Y₁ в двоичном коде, старший разряд Y₁.

Файлы для
моделирования этих элементов расположены в папке Lab_2_2Модели.

Таблица истинности CD(4 – 2)                         Таблица 1

Номер входа X (N10)	Выходной код Y (N2)
Y1	Y0
0	0	0
1	0	1
2	1	0
3	1	1

Рис. 1 Шифратор CD(4-2) на логических элементах ИЛИ

Уравнения работы шифратора CD(4-2):

 

Задание 1. С помощью комбинаций
входных сигналов изучить работу CD(4-2) файл
L2_CD_01.ewb, и его таблицу истинности.

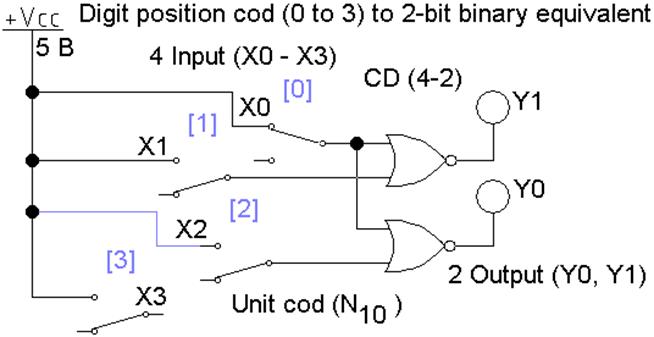
Задание 2. Составить
таблицу истинности (табл. 2) шифратора CD(4-2),
изображенного на рис. 2.

Таблица истинности CD(4 – 2)                         Таблица 2

Номер входа X (N10)	Выходной код Y (N2)
Y1	Y0
0
1
2
3

Рис. 2 Шифратор CD(4-2) на логических элементах ИЛИ-НЕ (файл L2_CD_04.ewb)

1
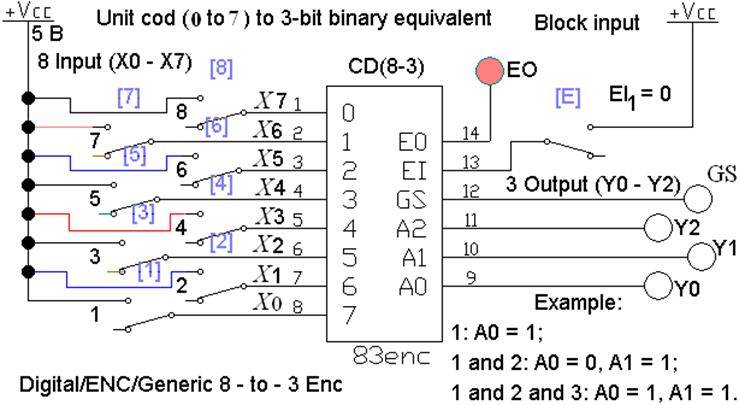
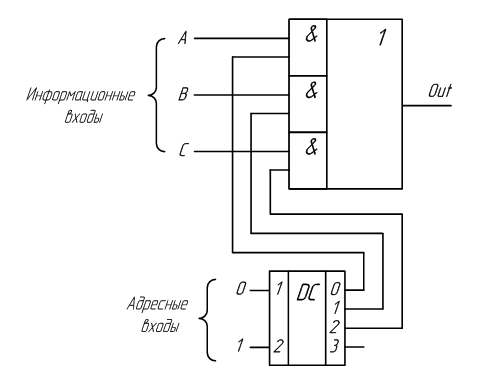
Приоритетный шифратор

Шифратор
называют приоритетным, если он формирует код, определяющий номер единицы,
стоящей в старшем разряде, из других имеющихся единиц.

Таким
шифратором является CD(8-3) выполненный на
микросхеме (рис. 3), файл L2_CD_02.ewb.

Шифратор имеет служебные входы и выходы:

• Разрешающий вход (инверсный) EI=0 – шифратор преобразует входной код, если  EI =1, то на всех информационных выходах
  шифратора появляются единицы.
• Выход GS в данном шифраторе указывает на использование
  всех разрядов шифратора и его переполнение (все единицы).
• Выход EO= 1 определяет отсутствие сигналов на всех
  информационных выходах.

Особенность данной
схемы: номер старшей единицы преобразуется в код, если имеются единицы во всех
младших разрядах. Область применения – аналого-цифровые преобразователи (АЦП).

Рис. 3 Приоритетный
шифратор CD (8-3)

Задание 3. Заполнить
таблицу истинности (табл. 3) приоритетного шифратора CD(8-3)
используя модель: файл L2_CD_02.ewb.

Клетки таблицы
в разделе «Информационные входы», где может находиться 0 или 1, не оказывая
влияния на результат шифрации в разделе «Выходы», заполнить знаком «Х».

Таблица истинности CD(8 – 3)                                                                        Таблица
3

№	Служебный вход	Информационные входы	Выходы
EI	X7	X6	X5	X4	X3	X2	X1	X0	EO	Y2	Y1	Y0
0	0									1	0	0	0
1	0									1	0	0	1
2	0									1	0	1	0
3	0									1	0	1	1
4	0									1	1	0	0
5	0									1	1	0	1
6	0									1	1	1	0
7	0									1	1	1	1
8	0									0	1	1	1
9	1										1	1	1

Вывод:

— Если при
достижении амплитудного значения изменяющегося во времени аналогового сигнала
уровней 1, 2…7 (столбец «№» табл. 3) будет замыкаться соответствующий ключ – на
выходе приоритетного шифратора получим цифровой код для этого значения сигнала.
Этот принцип использован в параллельных АЦП.Вход EI в таблице 3 и модели инверсный.

— Шифраторы
являются преобразователями кодов, причем результирующий код более компактен,
чем исходный.

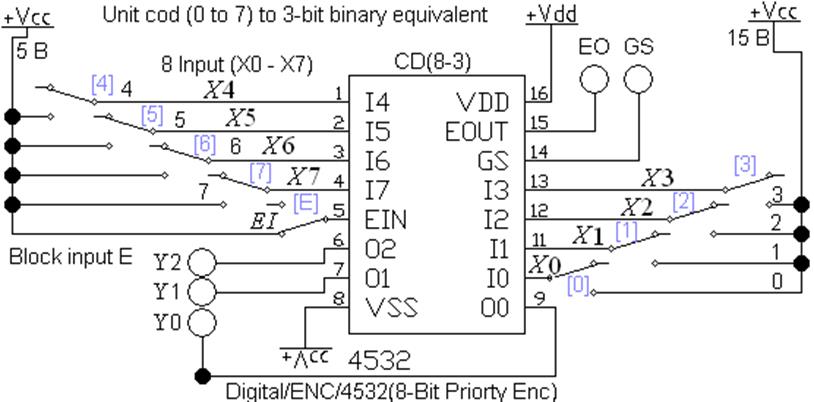
2 Указатель
старшей единицы

Приоритетный
шифратор CD(8-3) выполнен на микросхеме (рис. 4),
файл L2_CD_03.ewb. Шифратор
выявляет старшую (левую) единицу, в отличие от предыдущей схемы в младших разрядах, при этом, могут быть также
нули, и формирует двоичный код соответствующего единице десятичного номера.

Он называется указателем старшей единицы и исключает
ошибки, например, при одновременном нажатии двух клавиш клавиатуры, применяется
в работе светофоров и т.д.

Выход GSшифратора, указывает на наличие информационного сигнала хотя бы на
одном входе. Для разрешения работы на вход подается единица EI=1.

Рис. 4 Указатель
старшей единицы CD (8-3)

Задание 4

Заполнить
таблицу истинности (табл. 4) указателя старшей единицы CD(8-3),
используя модель: файл L2_CD_03.ewb.

Клетки таблицы
в разделе «Информационные входы», где может находиться 0 или 1, не оказывая
влияния на результат шифрации в разделе «Выходы», заполнить знаком «Х».

Таблица истинности CD(8 – 3)                                                                           Таблица
4

№	Служебный вход	Информационные входы	Служебные выходы	Информационные выходы
EI	X7	X6	X5	X4	X3	X2	X1	X0	EO	GS	Y2	Y1	Y0
0	1											0	0	0
1	1											0	0	0
2	1											0	0	1
3	1											0	1	0
4	1											0	1	1
5	1											1	0	0
6	1											1	0	1
7	1											1	1	0
8	1											1	1	1
9	0

Задание 5. Перечислить,
где и для каких целей применяются шифраторы.

Выводы:          

Шифраторы
являются преобразователями кодов, причем результирующий код более компактен,
чем исходный.

Служебные входы и выходы шифраторов используются для
расширения их функциональных возможностей:

— вход EI(бывает прямым или инверсным) служит для определения
момента времени, когда шифратор должен преобразовать код. Это позволяет
согласовать его работу с другими устройствами, когда они готовы передавать и
считывать информацию с шифратора.

— выходы GSи EO  используются с целью увеличения разрядности путем
выработки сигналов для подключения  дополнительных шифраторов.  

Шифраторы применяются, например, для преобразования
десятичного кода двоичный при вводе информации с клавиатуры в
компьютер (калькулятор, сотовый телефон), в аналового-цифровых преобразователях
и т.д.   

Лабораторная работа выполняется с помощью учебного лабораторного стенда LESO2.

1 Цель работы

Целью работы является изучение принципов действия комбинационных схем: дешифратора, шифратора, преобразователя кода для семисегментного индикатора, мультиплексора, сумматора.

2 Краткие теоретические сведения

2.1 Дешифратор (декодер)

Дешифратор (декодер) служит для преобразования n-разрядного позиционного двоичного кода в единичный выходной сигнал на одном из 2n выходов. При каждой входной комбинации сигналов на одном из выходов появляется 1. Таким образом, по единичному сигналу на одном из выходов можно судить о входной кодовой комбинации. Таблица истинности для декодера с двумя входами изображена в таблице 2.1.

Таблица 2.1 – Таблица истинности двухразрядного дешифратора

x1	x2	y0	y1	y2	y3
0	0	1	0	0	0
0	1	0	1	0	0
1	0	0	0	1	0
1	1	0	0	0	1

Для построения схемы декодера по таблице истинности воспользуемся методикой, изложенной в лабораторной работе №1, выполняемой на стенде LESO2. Например, устройство должно иметь 4 выхода. Для каждого выхода записываем логическое выражение. На основе СДНФ:

y0 = x1·x2

y1 = x1·x2

y2 = x1·x2

y3 = x1·x2

По этой системе выражений несложно построить схему требуемого дешифратора (рисунок 2.1).

Рисунок 2.1 – Схема дешифратора

Условное графическое обозначение такого дешифратора изображено на рисунке 2.2.

Рисунок 2.2 – Условное графическое обозначение дешифратора

2.2 Шифратор (кодер)

Шифратор выполняет функцию, обратную декодеру (дешифратору), то есть преобразует непозиционный (унитарный) двоичный 2n разрядный код в n разрядный позиционный код. При подаче на один из входов единичного сигнала на выходе формируется соответствующий двоичный код. Составим таблицу истинности шифратора при n = 2.

Таблица 2.2 – Таблица истинности шифратора при n = 2

x1	x2	x3	x4	y1	y0
1	0	0	0	0	0
0	1	0	0	0	1
0	0	1	0	1	0
0	0	0	1	1	1

Синтезируем шифратор. Для этого запишем систему его собственных функций:

y1 = x1 · x2 · x3 · x4 + x1 · x2 · x3 ·x4

y0 = x1 · x2 · x3 · x4 + x1 · x2 · x3 ·x4

Рисунок 2.3 – Схема шифратора

 

Рисунок 2.4 – Условное графическое обозначение шифратора

2.3 Преобразователь кода для семисегментного индикатора

Наиболее широко преобразователи кодов известны применительно к цифровым индикаторам. Например, преобразователь 4-х разрядного позиционного двоичного кода в десятичные цифры. Имеется семи сегментный индикатор и с его помощью требуется высветить десять цифр.

Рисунок 2.5 – Семи сегментный индикатор

Очевидно, что двоичный код должен иметь не менее 4 — х разрядов (2^4 = 16, что больше 10). Составим таблицу истинности работы такого преобразователя.

Таблица 2.3 – Таблица истинности преобразователя

Цифра	Двоичный код 8-4-2-1	a	б	в	г	д	е	ж
0	0	0	0	0	1	1	1	1	1	1	0
1	0	0	0	1	0	1	1	0	0	0	0
2	0	0	1	0	1	1	0	1	1	0	1
3	0	0	1	1	1	1	1	1	0	0	1
4	0	1	0	0	0	1	1	0	0	1	1
5	0	1	0	1	1	0	1	1	0	1	1
6	0	1	1	0	1	0	1	1	1	1	1
7	0	1	1	1	1	1	1	0	0	0	0
8	1	0	0	0	1	1	1	1	1	1	1
9	1	0	0	1	1	1	1	1	0	1	1

По ТИ несложно составить систему собственных функций для всех выходов, т.е. СДНФ, минимизировать её и составить принципиальную схему.

Рисунок 2.6 – Условное графическое обозначение преобразователя кода

2.4 Мультиплексор

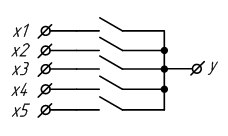
Мультиплексор – устройство, которое позволяет коммутировать один из 2^n информационных входов X на один выход Y под действием n управляющих (адресных) сигналов. На рисунке. 2.7 изображена упрощенная функциональная схема мультиплексора на идеализированных электронных ключах.

Рисунок 2.7 – Схема мультиплексора на идеализированных электронных ключах

В цифровых схемах требуется управлять ключами при помощи логических уровней. Поэтому желательно подобрать устройство, которое могло бы выполнять функции электронного ключа с управлением цифровым сигналом. Попробуем «заставить» работать в качестве электронного ключа уже знакомые нам логические элементы. Рассмотрим ТИ логического элемента «И». При этом один из входов логического элемента «И» будем рассматривать как информационный вход электронного ключа, а другой вход – как управляющий. Так как оба входа логического элемента «И» эквивалентны, то не важно какой из них будет управляющим входом. Пусть вход X будет управляющим, а Y – информационным. Для простоты рассуждений, разделим ТИ на две части в зависимости от уровня логического сигнала на управляющем входе X.

Таблица 2.4 – Таблица истинности

y	x	Out
0 0	0 1	0 0
1 1	0 1	0 1

По таблице истинности отчётливо видно, что если на управляющий вход X подан нулевой логический уровень, сигнал, поданный на вход Y, на выход Out не проходит. При подаче на управляющий вход X логической единицы, сигнал, поступающий на вход Y, появляется на выходе Out. Это означает, что логический элемент «И» можно использовать в качестве электронного ключа. При этом не важно, какой из входов элемента «И» будет использоваться в качестве управляющего входа, а какой – в качестве информационного. Остается только объединить выходы элементов «И» на один общий выход. Это делается при помощи логического элемента «ИЛИ» точно так же как и при построении схемы по произвольной таблице истинности. Получившийся вариант схемы коммутатора с управлением логическими уровнями приведён на рисунке 2.8.

Рисунок 2.8 – Принципиальная схема мультиплексора, выполненная на логических элементах

В схемах, приведенных на рисунках 2.7 и 2.8, можно одновременно включать несколько входов на один выход. Однако обычно это приводит к непредсказуемым последствиям. Кроме того, для управления таким коммутатором требуется много входов, поэтому в состав мультиплексора обычно включают двоичный дешифратор, как показано на рисунке 2.9. Такая схема позволяет управлять переключением информационных входов мультиплексора при помощи двоичных кодов, подаваемых на его управляющие входы. Количество информационных входов в таких схемах выбирают кратным степени числа два.

Рисунок 2.9 – Принципиальная схема мультиплексора, управляемого двоичным кодом

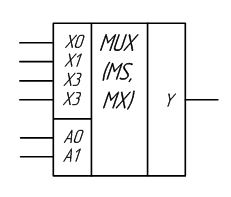
Условное графическое обозначение 4–х входового мультиплексора с управлением двоичным кодом приведено на рисунке 2.10. Входы A0 и A1 являются управляющими входами мультиплексора, определяющими адрес информационного входного сигнала, который будет соединён с выходным выводом мультиплексора Y. Информационные входные сигналы обозначены: X0, X1, X2 и X3.

Рисунок 2.10 – Условное графическое обозначение 4-х входового мультиплексора

В условном графическом обозначении названия информационных входов A, B, C и D заменены названиями X0, X1, X2 и X3, а название выхода Out заменено на название Y. Такое обозначение входов и выходов мультиплексора более распространено в отечественной литературе. Адресные входы обозначены как A0 и A1.

Об особенностях реализации мультиплесоров на языке Verilog можно почитать в статье:
Архитектура ПЛИС. Часть 2. Мультиплексор

2.5 Сумматор

Сумматор – узел компьютера, предназначенный для сложения двоичных чисел. Построение двоичных сумматоров обычно начинается с сумматора по модулю 2.

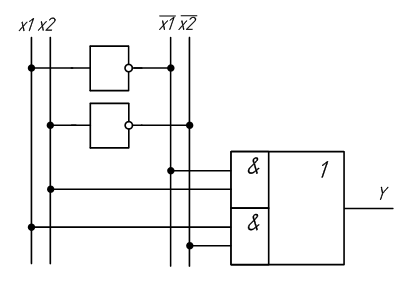
Сумматор по модулю 2

Схема сумматора по модулю 2 совпадает со схемой исключающее «ИЛИ».

Таблица 2.5 – Таблица истинности сумматора по модулю 2

x1	x2	y
0	0	0
0	1	1
1	0	1
1	1	0

Логическое выражение, описывающее сумматор по модулю 2:

y = x1 · x2 + x1 · x2

Рисунок 2.11 – Условное графическое обозначение сумматора по модулю 2

На основе логического уравнения, описывающего этот элемент можно синтезировать схему:

Рисунок 2.12 – Схема сумматора по модулю 2

Сумматор по модулю 2 выполняет суммирование без учёта переноса. В обычном двоичном сумматоре требуется учитывать перенос, поэтому требуются схемы, позволяющие формировать перенос в следующий двоичный разряд. Таблица истинности такой схемы, называемой полусумматором, приведена в таблице 2.6.

Таблица 2.6 – Таблица истинности полусумматора

A	B	S	P0
0	0	0	0
0	1	1	0
1	0	1	0
1	1	0	1

Здесь A и B – слагаемые;
S – сумма;
P0 – перенос в старший разряд (выход переноса Pout).
Запишем систему собственных функций для полусумматора:

S = A · B + A · B
P0 = A · B

Рисунок 2.13 – Принципиальная схема, реализующая таблицу истинности полусумматора

 

Рисунок 2.14 – Изображение полусумматора на схемах

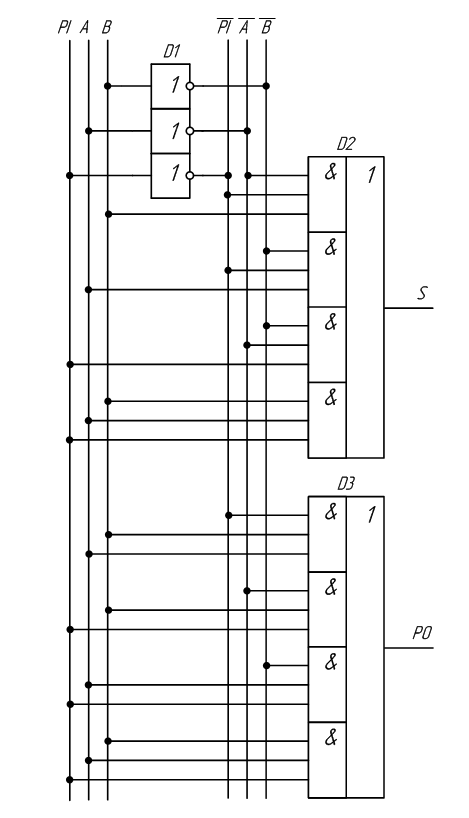
Полный сумматор.

Схема полусумматора формирует перенос в старший разряд, но не может учитывать перенос из младшего разряда. При сложении многоразрядных двоичных чисел необходимо складывать три цифры в каждом разряде – 2 слагаемых и единицу переноса из предыдущего разряда PI.

Таблица 2.7 – Таблица истинности полного сумматора

PI	A	B	S	PO
0	0	0	0	0
0	0	1	1	0
0	1	0	1	0
0	1	1	0	1
1	0	0	1	0
1	0	1	0	1
1	1	0	0	1
1	1	1	1	1

 
PI – вход 1 переноса из предыдущего разряда,
PO – выход 1 переноса в старший разряд.

На основании таблицы истинности запишем систему собственных функций для каждого выхода:

S = A · B · PI + A · B · PI + A · B · PI + A · B · PI

PO = A · B · PI + A · B · PI + A · B · PI + A · B · PI

В результате получим схему полного сумматора (рисунок 2.15).

Рисунок 2.15 – Принципиальная схема, реализующая таблицу истинности полного двоичного одноразрядного сумматора

 

Рисунок 2.16 – Изображение полного двоичного одноразрядного сумматора на схемах

3 Задание к работе

3.1 Исследовать принцип работы дешифратора 2 x 4

Сконфигурировать ПЛИС в соответствии с рисунком 3.1. Подключить к входам X0 и X1 переключатели S7 и S8, а к выходам Y0, Y1, Y2, Y3 светодиодные индикаторы LED5, LED6, LED7, LED8. Для этого подключить входы и выходы дешифратора к соответствующим ножкам ПЛИС.

Рисунок 3.1 – Схема дешифратора

Подавая все возможные комбинации логических уровней на входы X0, X1 с помощью ключей S7, S8 и наблюдая за состояниями светодиодных индикаторов LED5, LED6, LED7, LED8, заполните таблицу истинности дешифратора.

Таблица 3.1 – Таблица дешифратора

x1	x2	y0	y1	y2	y3
0	0
0	1
1	0
1	1

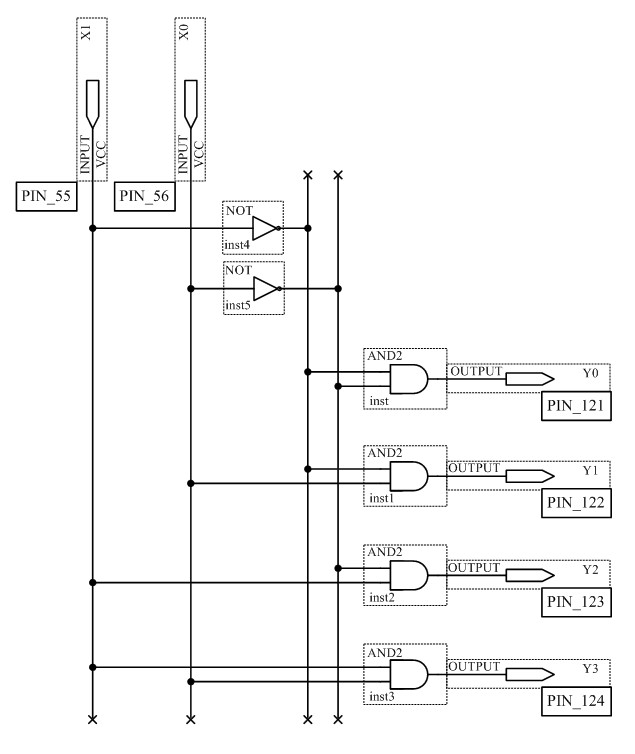
3.2 Исследовать принцип работы шифратора 4×2
Сконфигурировать ПЛИС в соответствии с рисунком 3.2.

Рисунок 3.2 – Схема шифратора 4×2

Подключить к входам X1, X2, X3, X4 переключатели S8, S7, S6, S5, а к выходам Y0, Y1 светодиодные индикаторы LED8, LED7. Для этого подключить входы и выходы дешифратора к соответствующим ножкам ПЛИС. Подавая все возможные комбинации логических уровней на входы X1, X2, X3, X4 с помощью ключей S8, S7, S6, S5 и наблюдая за состояниями светодиодных индикаторов LED7, LED8, заполните таблицу истинности шифратора.

Таблица 3.2 – Таблица истинности шифратора

x1	x2	x3	x4	y1	y0
1	0	0	0
0	1	0	0
0	0	1	0
0	0	0	1

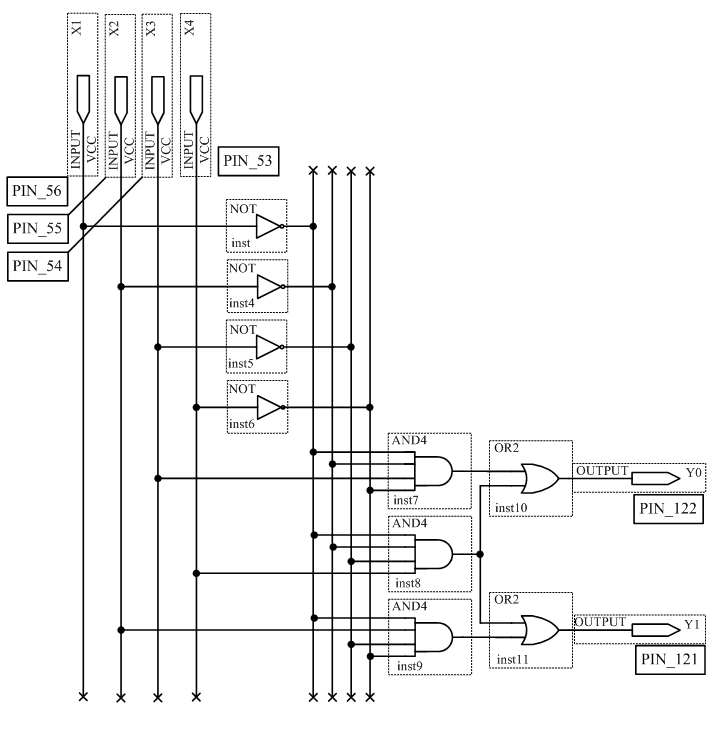
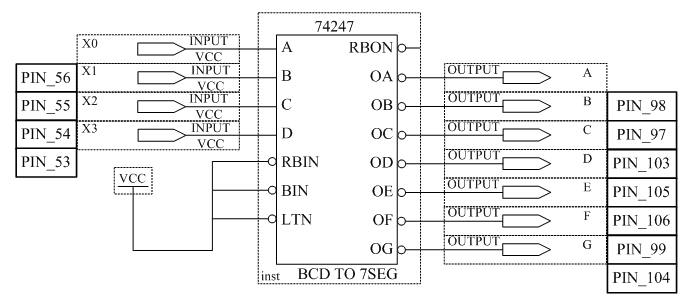
3.3 Исследовать работу преобразователя кода для семисегментного индикатора.

Составить таблицу истинности преобразователя кода (таблица. 3.3).
Собрать схему, изображенную на рисунке 3.3.

Таблица 3.3 – Таблица истинности преобразователя

x3	x2	x1	x0	A	B	C	D	E	F	G
0	0	0	0
0	0	0	1
0	0	1	0
0	0	1	1
0	1	0	0
0	1	0	1
0	1	1	0
0	1	1	1
1	0	0	0
1	0	0	1

 

Рисунок 3.3 – Схема преобразователя кода для семисегментного индикатора

Подавая с помощью ключей S8, S7, S6, S5 различные кодовые комбинации на входы X0, X1, X2, X3 определить цифры, высвечиваемые на индикаторе. По результатам эксперимента заполнить таблицу 3.4.

Таблица 3.4 – Таблица, описывающая работу преобразователя кода для семисегментного индикатора

x3	x2	x1	x0	Показание индикатора
0	0	0	0
0	0	0	1
0	0	1	0
0	0	1	1
0	1	0	0
0	1	0	1
0	1	1	0
0	1	1	1
1	0	0	0
1	0	0	1

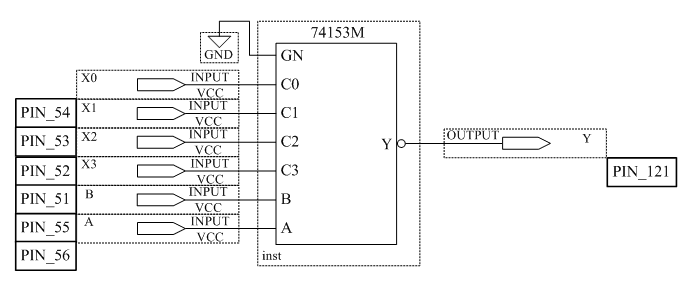
3.4 Исследовать работу мультиплексора 4×1

Сконфигурировать ПЛИС в соответствии с рисунком 3.4.

Рисунок 3.4 – Схема мультиплексора 4×1

Поочередно устанавливая все возможные кодовые комбинации на адресных входах A и B, определите номера коммутируемых каналов. Номер коммутируемого канала определяется путем поочерёдного подключения к входам X0, X2, X3, X4 уровня логической единицы и наблюдения за выходом Y. Заполните таблицу 3.5.

Таблица 3.5 – Таблица, описывающая работу мультиплексора

B	A	Номер коммутируемого канала
0	0
0	1
1	0
1	1

3.5 Исследовать схему сумматора

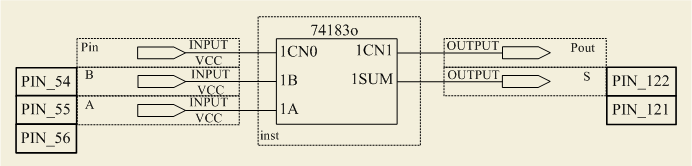
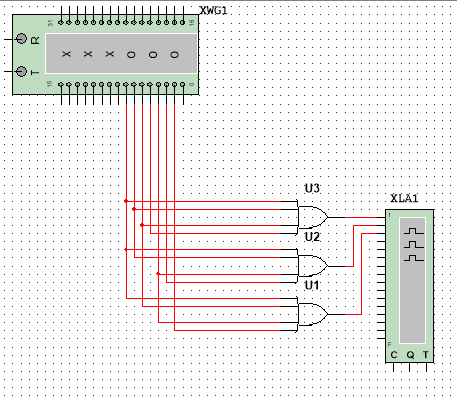
Сконфигурировать ПЛИС в соответствии с рисунком 3.5. Здесь Pin, Pout соответственно вход и выход единицы переноса, A и B – слагаемые, S – сумма.

Рисунок 3.5 – Схема сумматора

Заполнить таблицу истинности сумматора (таблица 3.6).

Таблица 2.7 – Таблица истинности полного сумматора

Pin	B	A	Pout
0	0	0
0	0	1
0	1	0
0	1	1
1	0	0
1	0	1
1	1	0
1	1	1

4 Содержание отчета

1. Цель работы.
2. Схемы исследования дешифратора, шифратора, преобразователя кода для семисегментного индикатора, мультиплексора, сумматора.
3. Таблицы истинности для каждой схемы.
4. Выводы по каждому заданию.

5 Контрольные вопросы

1. Принцип работы дешифратора?
2. Как синтезировать дешифратор с произвольной разрядностью?
3. Как работает шифратор?
4. Изобразите таблицу истинности шифратора.
5. Как работает преобразователь кода для семисегментного индикатора?
6. Как устроен семи сегментный индикатор?
7. Как работает мультиплексор?
8. Как в лабораторной работе проводилось исследование мультиплексора?
9. Как работает сумматор?
10. Изобразите таблицу истинности шифратора.
11. Что такое единица переноса?

Мы рассмотрели одноступенчатый дешифратор (линейный) – он является наиболее быстродействующим, но его реализация при значительной разрядности входного слова затруднена, поскольку требует применения логических элементов с большим числом входов, что сопровождается большой нагрузкой на источники входных сигналов. Обычно одноступенчатыми выполняются дешифраторы на небольшое число входов, определяемое возможностями элементов применяемой серии микросхем. Поэтому зачастую количества выводов дешифратора не хватает для выбора необходимого количества устройств микропроцессорной техники. Используя два дешифратора с разрешающим входом Е, можно реализовать дешифратор с количеством выходов N = 2 n+1 (рис. 2.11.3).

Рис. 2.11.3. Дешифратор 3х8 на основе двух дешифраторов 2х4

На рис. 2.11.3 приведена схема комбинированного дешифратора 3х8, реализованная на двух полных дешифраторах 2х4. Таким образом можно из 2-х дешифраторов 3х8 создать дешифратор 4х16 и т.д. Разрешающий вход Е используется, как адресный разряд. При Е = 0 работает верхний дешифратор, при Е = 1 работает нижний дешифратор, при этом все выходы верхнего дешифратора равны 0.

Широко используется еще каскадный (пирамидальный) способ построения дешифраторов с большим числом выходов на микросхемах дешифраторов с меньшим числом выходов (рис.2.11.4) .

Для разрешения работы одного из дешифраторов 3х8 (DC2, DC3, DC4, DC5) на вход Е каждого дешифратора подается разрешающий или запрещающий сигнал от дешифратора DC1 (первый каскад), который управляется адресными разрядами А3, А4.

Рис. 2.11.4. Схема каскадного (пирамидального) включения дешифраторов

Адресные разряды А0, А1, А2 параллельно подаются на дешифраторы 2-го каскада. Общее число адресных разрядов увеличилось на 2 разряда.

Шифраторы. Шифраторы это устройства, предназначенные для преобразования унитарного кода в двоичный.

На выходе шифратора появляется многоразрядный двоичный код, соответствующий десятичному номеру входа, на который подан активный логический уровень. Двоичные шифраторы выполняют операцию, обратную операции дешифраторов.

Шифратор иногда называют «кодером» (от англ. coder) и используют, например, для перевода десятичных чисел, набранных на клавиатуре кнопочного пульта управления, в двоичные числа. Если количество входов настолько ве­лико, что в шифраторе используются все возможные ком­бинации сигналов на выходе, то такой шифратор называ­ется полным. Число входов и выходов в полном шифраторе связано соотношением N = 2 n , где N — число входов, n — число выходов. Так, для пре­образования кода кнопочного пульта в четырехразрядное двоичное число достаточно использовать лишь 10 входов, в то время как полное число возможных входов будет рав­но 16 (n = 2 4 = 16), поэтому шифратор 10×4 будет неполным.

Рассмотрим пример построения шифратора для преоб­разования десятиразрядного единичного кода (десятичных чисел от 0 до 9) в двоичный код. При этом предполагает­ся, что сигнал, соответствующий логической единице, в каждый момент времени подается только на один вход.

Таблица истинности для шифратора приведена в таблице 2.11.3.

Используя данную таблицу, запишем логические выражения для выходных переменных, включая в логическую сумму те входные переменные, ко­торые соответствуют единице соответствующей выходной пере­менной.

Таблица истинности для дешифратора

Таблица 2.11.3.

Входы

Выходы

№

X0

X1

X2

X3

X4

X5

X6

X7

X8

X9

A3

A2

A1

A0

Запишем логические уравнения для выходных переменных А0, А1, А2, А3:

А0 = X1 v X3 v X5 v X7 v X9

A1 = X2 v X3 v X6 v X7

A2 = X4 v X5 v X6 v X7

Для такого шифратора легко построить схему на логических элементах «ИЛИ» (рис. 2.11.5).

Рис. 2.11.5. Схема неполного шифратора 10х4

Методические указания к выполнению работы:

Запишите в отчете, как обычно, название работы, цель работы. Приведите определение дешифратора. Составьте таблицу истинности для дешифратора, имеющего 3 адресных входа. Запишите уравнения для каждого из 8-ми выходов дешифратора. Постройте схему. Соберите схему, реализующую функции дешифратора в Multisim. Исследуйте её работу.

Исследуйте работу микросхемы дешифратора 2х4. Соберите схему дешифратора, приведенную на рис. 2.11.4 используя только дешифраторы 2х4.
Получите временные диаграммы работы схемы. Чтобы показать все входные и выходные сигналы дешифратора используйте 2 анализатора.

Зарисуйте схему и поясните в отчете принцип ее работы. Приведите временные диаграммы. Временные диаграммы надо привести на одной странице, нельзя продолжать связанные по времени графики на другой странице. Все связи между сигналами должны быть наглядными.

Составьте таблицу истинности для полного шифратора 8х3. Запишите логические функции выходных переменных. Постройте и исследуйте схему шифратора. В отчете приведите таблицу истинности, уравнения, построенную по уравнениям схему, временные диаграммы.

Запишите соответствующие каждому пункту выполненной работы выводы.

Вопросы для подготовки к отчету:

1. Дайте определение дешифратора.

2. Дайте определение шифратора.

3. Что понимают под унитарным кодом?

4. Чем отличается полный дешифратор от неполного?

5. Чем отличается полный шифратор от неполного?

6. В чем отличие линейного дешифратора от пирамидального?

7. Больше быстродействие у линейного дешифратора или пирамидального?

8. Больше аппаратных затрат требуется для реализации линейного дешифратора или пирамидального?

9. Для чего применяют в вычислительной технике дешифраторы и шифраторы?

12. Лабораторная работа №12

Исследование мультиплексоров и демультиплексоров

Цель работы:
Изучить принципы синтеза и работы мультиплексоров и демультиплексоров.

Задание:
Произвести синтез схемы мультиплексора, исследовать работу схемы. Исследовать микросхему мультиплексора, построить и исследовать работу пирамидальной схемы. Произвести синтез схемы демультиплексора, исследовать работу схемы. Исследовать совместную работу мультиплексора и демультиплексора.

Теоретическое введение

Мультиплексором
называется комбинационное логическое устройство, предназначенное для управляемой передачи данных от нескольких источников информации в один выходной канал. Входы мультиплексора подразделяются на информационные Д
0 , Д
1 , …… и управляющие (адресные) А
0 , А
1 , …, А
n-1 .

Код, подаваемый на адресные входы, определяет, какой из информационных входов в данный момент передается на выход схемы. Поскольку n
-разрядный двоичный код может принимать 2 n значений, то, если число адресных входов мультиплексора равно n
, число его информационных входов должно равняться 2 n .

Построим таблицу истинности, отображающую работу мультиплексора с двумя адресными входами на основе определения. Обозначим в таблице A0 и A1 – адресные входы. D0, D1, D2, D3 – входы 4-х потоков данных, при установке адреса соответствующие данные будут передаваться на единственный выход мультиплексора Y (таблица 2.12. 1) .

Таблица имеет следующий вид:

Таблица 2.12. 1

Адрес	Данные	Выход
А1	А0	D0	D1	D2	D3	Y
		D0	D1	D2	D3	D0
		D0	D1	D2	D3	D1
		D0	D1	D2	D3	D2
		D0	D1	D2	D3	D3

Запишем уравнение для функции Y:

Y = A1*A0*D0 v A1*A0 D1 v A1 A0*D2 v A1 A0 D3.

Схема, реализующая функцию Y, может быть построена на 2-х инверторах, 4-х трехвходовых элементах «И» и четырехвходовом элементе «ИЛИ» (рис. 12.2.1).

Рис. 12.2.1. Схема мультиплексора 4-1

Можно для реализации этой же схемы собрать дешифратор, и с его помощью осуществлять переключение входов на выход Y (рис. 2.12.2).

Рис. 2.12.2. Схема мультиплексора и его условное обозначение

В тех случаях, когда функциональные возможности ИС мультиплексоров не удовлетворяют разработчиков по числу информационных входов, прибегают к их каскадированию с целью наращивания числа входов до требуемого значения. Наиболее универсальный способ наращивания размерности мультиплексора состоит в построении пирамидальной структуры, состоящей из нескольких мультиплексоров. При этом первый ярус схемы представляет собой столбец, содержащий столько мультиплексоров, сколько необходимо для получения нужного числа информационных входов. Все мультиплексоры этого столбца коммутируются одним и тем же адресным кодом, составленным из соответствующего числа младших разрядов общего адресного кода. Старшие разряды адресного кода используются во втором ярусе, мультиплексор которого обеспечивает поочередную работу мультиплексоров первого яруса на общий выход. Каскадная схема мультиплексора «16-1», построенная на мультиплексорах «4-1», показана на рис. 2.12.3.

Рис. 2.12.3. Каскадная схема мультиплексора 16-1

Типовое применение мультиплексора — это передача информации от нескольких разнесенных в пространстве источников (датчиков) информации на вход одного приемника.

Предположим, что измеряется температура окружающей среды в нескольких помещениях и результаты этих измерений должны быть введены в одно регистрирующее устройство, например ЭВМ. При этом, так как температура изменяется медленно, для получения достаточной точности совсем не обязательно измерять ее постоянно. Достаточно иметь информацию через некоторые фиксированные промежутки времени.

Функцию подключения различных источников информации к одному приемнику по заданной команде и выполняет мультиплексор.

Мультиплексор можно использовать в качестве универсального логического элемента для реализации любой логической функции от числа аргументов, равного числу адресных входов мультиплексора. Покажем это на примере логической функции, заданной таблицей истинности (табл. 2.12.2).

Таблица2.12.2

№	A2	A1	A0	Y	№	A2	A1	A0	Y

Схема, реализующая данную функцию показана на рис. 2.12.4.

Рис. 2.12.4. Реализация комбинационной схемы при помощи мультиплексора

Демультиплексор
– это комбинационная схема, имеющая один информационный вход (D), n управляющих (адресных) входов (А0, А1, …, Аn-1) и N = 2 n выходов (Y0, Y1, …, YN-1). Двоичный код, поступающий на адресные входы, определяет один из N выходов, на который передается значение переменной с информационного входа D. Демультиплексор реализует функцию, обратную функции мультиплексора. Он предназначен для разделения потока данных одного источника информации в несколько выходных каналов.

Таблица функционирования демультиплексора (табл.2.12.2), имеющего 4 информационных выхода (Y0, Y1, Y2, Y3) и n = 2 адресных входа (А0, А1), представлена ниже.

Таблица 2.12.2

Инф.вход	Адрес	Информационные выходы
D	A1	A0	Y0	Y1	Y2	Y3
D			D
D				D
D					D
D						D

Уравнения, описывающие работу демультиплексора:

Y0 = D A1* A0*; Y1 = D A1*A0; Y2 = A1 A0*; Y3 = A1 A0.

Схема демультиплексора, построенная по данным уравнениям и его графическое изображение представлены на рис. 2.12.5.

Рис. 2.12.5. Схема демультиплексора «1-4» и его условное изображение

Функция демультиплексора легко реализуется с помощью дешифратора, если его вход “Разрешение” – Е использовать в качестве информационного входа демультиплексора, а входы 1, 2, 4 … — в качестве адресных входов демультиплексора А0, А1, А2, … Действительно, при активном значении сигнала на входе Е избирается выход, соответствующий коду, поданному на адресные входы. Поэтому интегральные схемы дешифраторов, имеющих разрешающий вход, иногда называют не просто дешифраторами, а дешифраторами-демультиплексорами.

Термином “мультиплексирование” называют процесс передачи данных от нескольких источников по общему каналу. В качестве устройства, осуществляющего на передающей стороне операцию сведения данных в один канал применяют мультиплексор. Подобное устройство способно осуществлять временное разделение сигналов, поступающих от нескольких источников, и передавать их в канал (линию) связи друг за другом в соответствии со сменой кодов на своих адресных входах.

На приемной стороне обычно требуется выполнить обратную операцию – демультиплексирование, т.е. распределение порций данных, поступивших по каналу связи в последовательные моменты времени, по своим приемникам. Эту операцию выполняет демультиплексор. Совместное использование мультиплексора и демультиплексора для передачи данных от 4-х источников к

4-м приемникам по общей линии иллюстрирует рис. 2.12.6.

Рис. 2.12.6. Совместное использование мультиплексора и демультиплексора для передачи данных

Похожая информация.

Дешифраторы
– цифровые устройства функционального
назначения, предназначенные для
распознавания двоичных кодов.

Двоичные
дешифраторы являясь преобразователем
кодов, преобразует двоичный код прямого
назначения в код “1 из N».
В такой кодовой комбинации только один
разряд занят единицей, а все остальные
– нулевые. Таблица истинности для
дешифратора, предназначенного для
распознавания четырехразрядного
двоичного кода представлена табл. 2.1

Таблица
2. 1

Из
таблицы 1 видно, что в зависимости от
входного двоичного кода на выходе
дешифратора в возбужденном состоянии
находится только один из его выходов.
Из этой же таблицы следует, что двоичный
дешифратор на n
входов должен иметь 2 n
выходов,
соответствующих числу кодовых комбинаций
n-разрядного
двоичного кода. Такой дешифратор
называется полным

,
в отличие от неполного

,
у которого часть входных кодовых
комбинаций не используется, а число
выходов у которого
меньше2 n .

В
основном поле условного обозначения
дешифраторов (Рис.2.5) проставляются
буквы DC
(от английского слова Decoder).
Входы дешифратора принято обозначать
их двоичными весами. Кроме информационных
входов дешифратор имеет обычно один
или более входов разрешения работы,
обозначаемых как Е (Enable).
При наличии разрешающего сигнала на
этом входе дешифратор работает в
соответствии с таблицей истинности,
при его отсутствии все выходы дешифратора
пассивны.

Функционирование
дешифратора описывается системой
булевых выражений:

С
хемотехническое
решение дешифраторов представлено на
рис.2.6.

Как
видно из рис. 2.6., дешифратор состоит из
2n
инверторов входного кода, образующих
прямые и инверсные значения переменных
входного кода, двух инверторов на входе
разрешения и 2 n -1
конъюнкторов, образующих выходы схемы.
Малоразрядность серийных дешифраторов
ставит вопрос и наращивании их
разряд-ности. Из малоразрядных
дешифраторов можно построить схему,
эквивалентную дешифратору большой
разрядности. С этой целью входное слово
делится на поля, при этом разрядность
поля младших разрядов соответствует
разрядности имеющихся дешифраторов.
Оставшееся поле старших разрядов служит
для получения сигнала разрешения работы
одного из дешифраторов, декодирующих
поле младших разрядов.

В
качестве примера на рис. 2.7 приведена
схема дешифрации пятиразрядного кода
с помощью дешифраторов «3-8» и «2-4». Для
получения нужных 32 выходов составляется
столбец второго яруса из четырех
дешифраторов «3-8»DC1-DC4.
Дешифратор «2-4» принимает два старших
разряда входного кода. Возбужденный
выход этого дешифратора открывает по
входу разрешения один из дешифраторов
столбца и выбранный дешифратор декодирует
младшие разряды входного слова. Каждому
входному слову соответствует возбуждение
одного из выходов F 0 -F 31 .
Например, при дешифрации слова
х 4 х 3 х 2 х 1 х 0 =11001 2 =25 10
на входе дешифратора первого яруса
имеется код 11, возбуждающий его выход
номер три (помечен крестиком), что
разрешает работу дешифратора DC4.
На входе DC4 действует код 001, поэтому
будет возбужден его первый выход, т.е.
25 выход схемы. Общее разрешение или
запрещение работы схемы осуществляется
по входу Е дешифратора первого яруса.

Наряду
с применением дешифраторов по своему
прямому назначению они могут использоваться
для реализации произвольных логических
функций, поскольку на выходах дешифратора
вырабатываются все конъюктивные термы,
которые можно составить из данного
числа аргументов. Логическая функция
в СДНФ есть дизъюнкция некоторого числа
таких термов. Объединяя их по схеме
ИЛИ, можно получить любую функцию
данного числа аргументов.

На
рис.2.8 в качестве примера показана
аппаратная реализация функции сумматора
по модулю два.

3.1.2 Шифраторы

Шифрирование
это способ сжатия данных за счет преобразования m
-разрядного
унитарного (десятичного) кода в n
-разрядный
двоичный или двоично-десятичный код (m
> n
). Шифраторы
(CD
, coder
) выполняют
функцию, обратную функции дешифратора. При поступлении сигнала на один из
входов шифратора на его выходах формируется код, соответствующий номеру этого
входа.

Полный
шифратор (m
– n
) имеет m
= 2 n
входов и n
выходов, если m
< 2 n
, то шифратор не полный. Также он может
быть неприоритетным, если разрешена подача только одного активного сигнала или приоритетным,
если допускается подача одновременно нескольких активных сигналов на входы.

Принцип работы полного неприоритетного шифратора (4
– 2) поясняется таблицей истинности (таблица 1).

Таблица истинности неприоритетного шифратора (4 –
2) Таблица 1

набора	Информационные входы	Выходы
X 3	X 2	X 1	X 0	F 1	F 0

Карты Карно для минимизации схемы шифраторов обычно
не используются вследствие сложности составления при большом количестве
переменных.

Из таблицы (1) следует, что младший разряд
F

0
кода на выходе шифратора равен единице, когда на
нечетных входах присутствует единица:

Старший разряд
F

1
кода на выходе шифратора равен единице, когда на
входах
X

3
,
X

2
присутствует единица:

Следовательно, схема шифратора (4 – 2) может быть
реализована с помощью двух элементов 2ИЛИ (рис. 1, а).

Рис. 1 Схемы неприоритетного шифратора (4 – 2) на
элементах 2ИЛИ (а), 2ИЛИ-НЕ (б)

Для инверсной записи (рис. 1, б):

Один из
входных сигналов шифратора обязательно имеет единичное значение (таблица 1). Если
на входах X

1
,
X

2
,
X

3
нулевые
значения, это означает, ч
то
на входеX

0
логическая
единица, соответствующая набору 0, и этот вход к
схеме может быть не подключен (рис. 1, а). Аналогично для
X

3
в схеме
шифратора на рис. 1, б. Схемы шифраторов на рисунке
отличаются зеркальной перестановкой входов (в обоих случаях младший разряд
X

0
,
старший
X

3
) и инвертированием выходных сигналов (рис.1, б).

У шифраторов обычно имеются служебные входы и выходы:

— Разрешающий (стробирующий) вход
EI

(EN

) для выбора времени срабатывания шифратора при
условии
EI

=1, также для наращивания разрядности входного
кода.

— Разрешающий выход
EO

(EN

), определяет отсутствие сигналов на всех
информационных выходах (EO

= 1). Используется для увеличения разрядности путем
подключения дополнительных шифраторов, условие подключения
EO

=1.

— Разрешающий выход
GS

(CS

), указывает на наличие информационного сигнала хотя
бы на одном входе, принимая значение
GS

= 1. Обеспечивает согласование работы шифратора и
внешних устройств (микропроцессор). Может применяться в схеме наращивания
разрядности шифратора для исключения ошибок преобразования кодов.

Одно из основных назначений шифратора – ввод данных
в цифровые устройства с помощью клавиатуры. Шифраторы, которые при
одновременном нажатии нескольких клавиш вырабатывают код только старшей цифры,
называют приоритетными. Если эти шифраторы выявляют старшую (левую) единицу и
формируют двоичный код соответствующего единице десятичного номера, то
называются указателями старшей единицы (обозначение элемента
HPR

1/
BIN

).

В таблице истинности указателя старшей единицы
(таблица 2) символом «Х» обозначены значения входных переменных, которые не
важны для устройства и могут быть равны 0 или 1.
Интерес
представляют единицы в старшем разряде соответствующего набора.

Символом « – » обозначены значения переменных,
которые не поступают в шифратор, т.к. на разрешающем входе
EI

сигнал логического нуля,
на выходе
F

1
F

0
= 00.

Пример
:
если нажата клавиша старшего разряда Х
3
(набор 5), что соответствует кодам 3 10
= 11 2 , нажатие других клавиш
должно игнорироваться.

Таблица истинности указателя старшей единицы (4 – 2) Таблица 2
набора	Служебные	Информационные
вход	выходы	Входы	Выходы
EI	GS	EO	X 3	X 2	X 1	X 0	F 1	F 0

В
соответствии с правилом склеивания для выхода F

1
.

Лабораторная работа выполняется с помощью учебного лабораторного стенда LESO2 .

1 Цель работы

Целью работы является изучение принципов действия комбинационных схем: дешифратора, шифратора, преобразователя кода для семисегментного индикатора, мультиплексора, сумматора.

2 Краткие теоретические сведения

2.1
Дешифратор (декодер)

Дешифратор (декодер) служит для преобразования n-разрядного позиционного двоичного кода в единичный выходной сигнал на одном из 2n выходов. При каждой входной комбинации сигналов на одном из выходов появляется 1. Таким образом, по единичному сигналу на одном из выходов можно судить о входной кодовой комбинации. Таблица истинности для декодера с двумя входами изображена в таблице 2.1.

Таблица 2.1 – Таблица истинности двухразрядного дешифратора

x1	x2	y0	y1	y2	y3
0	0	1	0	0	0
0	1	0	1	0	0
1	0	0	0	1	0
1	1	0	0	0	1

Для построения схемы декодера по таблице истинности воспользуемся методикой, изложенной в лабораторной работе №1 , выполняемой на стенде LESO2 . Например, устройство должно иметь 4 выхода. Для каждого выхода записываем логическое выражение. На основе СДНФ:

y0 = x1
·x2

y1 = x1
·x2

y2 = x1·x2

По этой системе выражений несложно построить схему требуемого дешифратора (рисунок 2.1).

Рисунок 2.1 – Схема дешифратора

Условное графическое обозначение такого дешифратора изображено на рисунке 2.2.

Рисунок 2.2 – Условное графическое обозначение дешифратора

2.2
Шифратор (кодер)

Шифратор выполняет функцию, обратную декодеру (дешифратору), то есть преобразует непозиционный (унитарный) двоичный 2n разрядный код в n разрядный позиционный код. При подаче на один из входов единичного сигнала на выходе формируется соответствующий двоичный код. Составим таблицу истинности шифратора при n = 2.

Таблица 2.2 – Таблица истинности шифратора при n = 2

x1	x2	x3	x4	y1	y0
1	0	0	0	0	0
0	1	0	0	0	1
0	0	1	0	1	0
0	0	0	1	1	1

Синтезируем шифратор. Для этого запишем систему его собственных функций:

y1 = x1
· x2
· x3 · x4
+ x1
· x2
· x3
·x4

y0 = x1
· x2 · x3
· x4
+ x1
· x2
· x3
·x4

Рисунок 2.3 – Схема шифратора

Рисунок 2.4 – Условное графическое обозначение шифратора

2.3
Преобразователь кода для семисегментного индикатора

Наиболее широко преобразователи кодов известны применительно к цифровым индикаторам. Например, преобразователь 4-х разрядного позиционного двоичного кода в десятичные цифры. Имеется семи сегментный индикатор и с его помощью требуется высветить десять цифр.

Рисунок 2.5 – Семи сегментный индикатор

Очевидно, что двоичный код должен иметь не менее 4 — х разрядов (2^4 = 16, что больше 10). Составим таблицу истинности работы такого преобразователя.

Таблица 2.3 – Таблица истинности преобразователя

Цифра	Двоичный код 8-4-2-1	a	б	в	г	д	е	ж
0	0	0	0	0	1	1	1	1	1	1	0
1	0	0	0	1	0	1	1	0	0	0	0
2	0	0	1	0	1	1	0	1	1	0	1
3	0	0	1	1	1	1	1	1	0	0	1
4	0	1	0	0	0	1	1	0	0	1	1
5	0	1	0	1	1	0	1	1	0	1	1
6	0	1	1	0	1	0	1	1	1	1	1
7	0	1	1	1	1	1	1	0	0	0	0
8	1	0	0	0	1	1	1	1	1	1	1
9	1	0	0	1	1	1	1	1	0	1	1

По ТИ несложно составить систему собственных функций для всех выходов, т.е. СДНФ, минимизировать её и составить принципиальную схему.

Рисунок 2.6 – Условное графическое обозначение преобразователя кода

2.4
Мультиплексор

Мультиплексор – устройство, которое позволяет коммутировать один из 2^n информационных входов X на один выход Y под действием n управляющих (адресных) сигналов. На рисунке. 2.7 изображена упрощенная функциональная схема мультиплексора на идеализированных электронных ключах.

Рисунок 2.7 – Схема мультиплексора на идеализированных электронных ключах

В цифровых схемах требуется управлять ключами при помощи логических уровней. Поэтому желательно подобрать устройство, которое могло бы выполнять функции электронного ключа с управлением цифровым сигналом. Попробуем «заставить» работать в качестве электронного ключа уже знакомые нам логические элементы. Рассмотрим ТИ логического элемента «И». При этом один из входов логического элемента «И» будем рассматривать как информационный вход электронного ключа, а другой вход – как управляющий. Так как оба входа логического элемента «И» эквивалентны, то не важно какой из них будет управляющим входом. Пусть вход X будет управляющим, а Y – информационным. Для простоты рассуждений, разделим ТИ на две части в зависимости от уровня логического сигнала на управляющем входе X.

Таблица 2.4 – Таблица истинности

y	x	Out
0 0	0 1	0 0
1 1	0 1	0 1

По таблице истинности отчётливо видно, что если на управляющий вход X подан нулевой логический уровень, сигнал, поданный на вход Y, на выход Out не проходит. При подаче на управляющий вход X логической единицы, сигнал, поступающий на вход Y, появляется на выходе Out. Это означает, что логический элемент «И» можно использовать в качестве электронного ключа. При этом не важно, какой из входов элемента «И» будет использоваться в качестве управляющего входа, а какой – в качестве информационного. Остается только объединить выходы элементов «И» на один общий выход. Это делается при помощи логического элемента «ИЛИ» точно так же как и при построении схемы по произвольной таблице истинности. Получившийся вариант схемы коммутатора с управлением логическими уровнями приведён на рисунке 2.8.

Рисунок 2.8 – Принципиальная схема мультиплексора, выполненная на логических элементах

В схемах, приведенных на рисунках 2.7 и 2.8, можно одновременно включать несколько входов на один выход. Однако обычно это приводит к непредсказуемым последствиям. Кроме того, для управления таким коммутатором требуется много входов, поэтому в состав мультиплексора обычно включают двоичный дешифратор, как показано на рисунке 2.9. Такая схема позволяет управлять переключением информационных входов мультиплексора при помощи двоичных кодов, подаваемых на его управляющие входы. Количество информационных входов в таких схемах выбирают кратным степени числа два.

Рисунок 2.9 – Принципиальная схема мультиплексора, управляемого двоичным кодом

Условное графическое обозначение 4–х входового мультиплексора с управлением двоичным кодом приведено на рисунке 2.10. Входы A0 и A1 являются управляющими входами мультиплексора, определяющими адрес информационного входного сигнала, который будет соединён с выходным выводом мультиплексора Y. Информационные входные сигналы обозначены: X0, X1, X2 и X3.

Рисунок 2.10 – Условное графическое обозначение 4-х входового мультиплексора

В условном графическом обозначении названия информационных входов A, B, C и D заменены названиями X0, X1, X2 и X3, а название выхода Out заменено на название Y. Такое обозначение входов и выходов мультиплексора более распространено в отечественной литературе. Адресные входы обозначены как A0 и A1.

Об особенностях реализации мультиплесоров на языке Verilog можно почитать в статье:
Архитектура ПЛИС. Часть 2. Мультиплексор

2.5
Сумматор

Сумматор – узел компьютера, предназначенный для сложения двоичных чисел. Построение двоичных сумматоров обычно начинается с сумматора по модулю 2.

Сумматор по модулю 2

Схема сумматора по модулю 2 совпадает со схемой исключающее «ИЛИ».

Таблица 2.5 – Таблица истинности сумматора по модулю 2

x1	x2	y
0	0	0
0	1	1
1	0	1
1	1	0

Логическое выражение, описывающее сумматор по модулю 2:

y = x1
· x2 + x1 · x2

Рисунок 2.11 – Условное графическое обозначение сумматора по модулю 2

На основе логического уравнения, описывающего этот элемент можно синтезировать схему:

Рисунок 2.12 – Схема сумматора по модулю 2

Сумматор по модулю 2 выполняет суммирование без учёта переноса. В обычном двоичном сумматоре требуется учитывать перенос, поэтому требуются схемы, позволяющие формировать перенос в следующий двоичный разряд. Таблица истинности такой схемы, называемой полусумматором, приведена в таблице 2.6.

Таблица 2.6 – Таблица истинности полусумматора

A	B	S	P0
0	0	0	0
0	1	1	0
1	0	1	0
1	1	0	1

Здесь A
и B
– слагаемые;
S
– сумма;
P0
– перенос в старший разряд (выход переноса Pout).
Запишем систему собственных функций для полусумматора:

S = A
· B + A · B

P0 = A · B

Рисунок 2.13 – Принципиальная схема, реализующая таблицу истинности полусумматора

Рисунок 2.14 – Изображение полусумматора на схемах

Полный сумматор.

Схема полусумматора формирует перенос в старший разряд, но не может учитывать перенос из младшего разряда. При сложении многоразрядных двоичных чисел необходимо складывать три цифры в каждом разряде – 2 слагаемых и единицу переноса из предыдущего разряда PI.

PI	A	B	S	PO
0	0	0	0	0
0	0	1	1	0
0	1	0	1	0
0	1	1	0	1
1	0	0	1	0
1	0	1	0	1
1	1	0	0	1
1	1	1	1	1

PI
– вход 1 переноса из предыдущего разряда,
PO
– выход 1 переноса в старший разряд.

На основании таблицы истинности запишем систему собственных функций для каждого выхода:

S = A
· B · PI
+ A · B
· PI + A
· B
· PI + A · B · PI

PO = A · B · PI
+ A
· B · PI + A · B
· PI + A · B · PI

В результате получим схему полного сумматора (рисунок 2.15).

Рисунок 2.15 – Принципиальная схема, реализующая таблицу истинности полного двоичного одноразрядного сумматора

Рисунок 2.16 – Изображение полного двоичного одноразрядного сумматора на схемах

3 Задание к работе

3.1
Исследовать принцип работы дешифратора 2 x 4

Сконфигурировать ПЛИС в соответствии с рисунком 3.1. Подключить к входам X0 и X1 переключатели S7 и S8, а к выходам Y0, Y1, Y2, Y3 светодиодные индикаторы LED5, LED6, LED7, LED8. Для этого подключить входы и выходы дешифратора к соответствующим ножкам ПЛИС.

Рисунок 3.1 – Схема дешифратора

Подавая все возможные комбинации логических уровней на входы X0, X1 с помощью ключей S7, S8 и наблюдая за состояниями светодиодных индикаторов LED5, LED6, LED7, LED8, заполните таблицу истинности дешифратора.

Таблица 3.1 – Таблица дешифратора

x1	x2	y0	y1	y2	y3
0	0
0	1
1	0
1	1

3.2
Исследовать принцип работы шифратора 4×2
Сконфигурировать ПЛИС в соответствии с рисунком 3.2.

Рисунок 3.2 – Схема шифратора 4×2

Подключить к входам X1, X2, X3, X4 переключатели S8, S7, S6, S5, а к выходам Y0, Y1 светодиодные индикаторы LED8, LED7. Для этого подключить входы и выходы дешифратора к соответствующим ножкам ПЛИС. Подавая все возможные комбинации логических уровней на входы X1, X2, X3, X4 с помощью ключей S8, S7, S6, S5 и наблюдая за состояниями светодиодных индикаторов LED7, LED8, заполните таблицу истинности шифратора.

Таблица 3.2 – Таблица истинности шифратора

x1	x2	x3	x4	y1	y0
1	0	0	0
0	1	0	0
0	0	1	0
0	0	0	1

3.3
Исследовать работу преобразователя кода для семисегментного индикатора.

Составить таблицу истинности преобразователя кода (таблица. 3.3).
Собрать схему, изображенную на рисунке 3.3.

Таблица 3.3 – Таблица истинности преобразователя

x3	x2	x1	x0	A	B	C	D	E	F	G
0	0	0	0
0	0	0	1
0	0	1	0
0	0	1	1
0	1	0	0
0	1	0	1
0	1	1	0
0	1	1	1
1	0	0	0
1	0	0	1

Рисунок 3.3 – Схема преобразователя кода для семисегментного индикатора

Подавая с помощью ключей S8, S7, S6, S5 различные кодовые комбинации на входы X0, X1, X2, X3 определить цифры, высвечиваемые на индикаторе. По результатам эксперимента заполнить таблицу 3.4.

Таблица 3.4 – Таблица, описывающая работу преобразователя кода для семисегментного индикатора

x3	x2	x1	x0	Показание индикатора
0	0	0	0
0	0	0	1
0	0	1	0
0	0	1	1
0	1	0	0
0	1	0	1
0	1	1	0
0	1	1	1
1	0	0	0
1	0	0	1

3.4
Исследовать работу мультиплексора 4×1

Сконфигурировать ПЛИС в соответствии с рисунком 3.4.

Рисунок 3.4 – Схема мультиплексора 4×1

Поочередно устанавливая все возможные кодовые комбинации на адресных входах A и B, определите номера коммутируемых каналов. Номер коммутируемого канала определяется путем поочерёдного подключения к входам X0, X2, X3, X4 уровня логической единицы и наблюдения за выходом Y. Заполните таблицу 3.5.

Таблица 3.5 – Таблица, описывающая работу мультиплексора

3.5
Исследовать схему сумматора

Сконфигурировать ПЛИС в соответствии с рисунком 3.5. Здесь Pin
, Pout
соответственно вход и выход единицы переноса, A
и B
– слагаемые, S
– сумма.

Рисунок 3.5 – Схема сумматора

Заполнить таблицу истинности сумматора (таблица 3.6).

Таблица 2.7 – Таблица истинности полного сумматора

Pin	B	A	Pout
0	0	0
0	0	1
0	1	0
0	1	1
1	0	0
1	0	1
1	1	0
1	1	1

1. Цель работы.
2. Схемы исследования дешифратора, шифратора, преобразователя кода для семисегментного индикатора, мультиплексора, сумматора.
3. Таблицы истинности для каждой схемы.
4. Выводы по каждому заданию.

5 Контрольные вопросы

1. Принцип работы дешифратора?
2. Как синтезировать дешифратор с произвольной разрядностью?
3. Как работает шифратор?
4. Как работает преобразователь кода для семисегментного индикатора?
5. Как устроен семи сегментный индикатор?
6. Как работает мультиплексор?
7. Как в лабораторной работе проводилось исследование мультиплексора?
8. Как работает сумматор?
9. Изобразите таблицу истинности шифратора.
10. Что такое единица переноса?

ШИФРАТОРЫ/ДЕШИФРАТОРЫ

Шифраторы.

Шифратор, (называемый так же кодером) — устройство, осуществляющее преобразование десятичных чисел в двоичную систему счисления. Пусть в шифраторе имеется m входов, последовательно пронумерованных десятичными числами (0, 1, 2, 3, …, m — 1), и n выходов. Подача сигнала на один из входов приводит к появлению на выходах n- разрядного двоичного числа, соответствующего номеру возбужденного входа.

рис 5.17

рис 5.18

Очевидно, трудно строить шифраторы с очень большим числом входов m, поэтому они используются для преобразования в двоичную систему счисления относительно небольших десятичных чисел. Преобразование больших десятичных чисел осуществляется методами, приведенными в справочнике «Системы счисления»

Шифраторы широко используются в разнообразных устройствах ввода информации в цифровые системы. Такие устройства могут снабжаться клавиатурой, каждая клавиша которой связана с определенным входом шифратора. При нажатии выбранной клавиши подается сигнал на определенный вход шифратора, и на его выходе возникает двоичное число, соответствующее выгравированному на клавише символу.

Таблица 5.5
Десятичное число	Двоичный код 8421
x 8	x 4	x 2	x 1

Таблица 5.6
Входной код 8421	Номер выхода
x 8	x 4	x 2	x 1

На рис. 5.17 приведено символическое изображение шифратора, преобразующего десятичные числа 0, 1, 2, …, 9 в двоичное представление в коде 8421. Символ CD образован из букв, входящих в английское слово CODER. Слева показано 10 входов, обозначенных десятичными цифрами 0, 1, …, 9. Справа показаны выходы шифратора: цифрами 1, 2, 4, 8 обозначены весовые коэффициенты двоичных разрядов, соответствующих отдельным выходам.

Из приведенного в табл. 5.5 соответствия десятичного и двоичного кодов следует, что переменная x 1 на выходной шине 1 имеет уровень лог. 1, если имеет этот уровень одна из входных переменных y 1 , у 3 , у 5 , у 7 , у 9 . Следовательно, x 1 = y l / y 3 / y 5 / y 7 / y 9 .

Для остальных выходов x 2 = y 2 / y 3 / y 6 / y 7 ; x 4 = y 4 / y 5 / y 6 / y 7 ; x 8 = y 8 / y 9 .

Этой системе логических выражений соответствует схема на рис. 5.18,а. На рис. 5.18,б изображена схема шифратора на элементах ИЛИ-НЕ.

Шифратор построен в соответствии со следующими выражениями:

При этом шифратор имеет инверсные выходы.

При выполнении шифратора на элементах И-НЕ следует пользоваться следующей системой логических выражений:

В этом случае предусмотрена подача на входы инверсных значений, т. е. для получения на выходе двоичного представления некоторой десятичной цифры необходимо на соответствующий вход подать лог. 0, а на остальные входы — лог.1. Схема шифратора, выполненная на элементах И-НЕ, приведена на рис. 5.18,в.

Изложенным способом могут быть построены шифраторы, выполняющие преобразование десятичных чисел в двоичное представление с использованием любого двоичного кода,

Дешифраторы.

Для обратного преобразования двоичных чисел в небольшие по значению десятичные числа используются дешифраторы (называемые также декодерами). Входы дешифратора предназначаются для подачи двоичных чисел, выходы последовательно нумеруются десятичными числами. При подаче на входы двоичного числа появляется сигнал на определенном выходе, номер которого соответствует входному числу.

Дешифраторы имеют широкое применение. В частности, они используются в устройствах, печатающих на бумаге выводимые из цифрового устройства числа или текст. В таких устройствах двоичное число, поступая на вход дешифратора, вызывает появление сигнала на определенном его выходе. С помощью этого сигнала производится печать символа, соответствующего входному двоичному числу.

На рис. 5.19,а приведено символическое изображение дешифратора. Символ DС образован из букв английского слова DECODER. Слева показаны входы, на которых отмечены весовые коэффициенты двоичного кода. Справа — выходы, пронумерованные десятичными числами, соответствующими отдельным комбинациям входного двоичного кода. На каждом выходе образуется уровень лог. 1 при строго определенной комбинации входного кода.

Дешифратор может иметь парафазные входы для подачи наряду с входными переменными их инверсий, как показано на рис. 5.19,б.

По способу построения различают линейные и прямоугольные дешифраторы.

Линейный дешифратор.

Рассмотрим построение дешифратора, осуществляющего преобразование, заданное табл. 5.6.

(5.22)	(5.23)

Значения выходных переменных определяются следующими логическими выражениями:

В линейном дешифраторе выходные переменные формируются по (5.22) либо (5.23). При выполнении дешифратора на элементах И-НЕ пользуются (5.23), получая инверсии выходных функций. В этом случае каждой комбинации входного кода будет соответствовать уровень лог. 0 на строго определенном выходе, на остальных выходах устанавливается уровень лог. 1. На рис. 5.20 показана структура дешифратора, построенного на элементах И-НЕ, и его изображение в схемах. Структура имеет особенности, характерные для дешифраторов в интегральном исполнении:

для уменьшения числа входов формирование инверсий входных переменных осуществляется в самом дешифраторе;

рис 5.20

рис 5.21

подключенные непосредственно ко входам дополнительные инверторы уменьшают нагрузку со стороны дешифратора на его входные цепи.

Дешифратор с 16 выходами для дешифрирования всех возможных комбинаций четырехразрядного двоичного кода 8421 можно построить из двух рассмотренных дешифраторов с 10 выходами. На рис. 5.21 показана структура такого дешифратора. В каждом из дешифраторов используется по 8 выходов, которые и образуют требуемые 16 выходов (y 0 , y 1 , …, y 15).

рис 5.22

Прямоугольный дешифратор.

Рассмотрим принцип построения прямоугольного дешифратора на примере дешифратора с 4 входами и 16 выходами.

Разобьем входные переменные x 8 , x 4 , x 2 , x 1 на две группы по две переменные в каждой: x 8 , x 4 , и x 2 , x 1 . Каждую пару переменных используем в качестве входных переменных отдельного линейного дешифратора на четыре выхода, как показано на рис. 5.22,а. Выходные переменные линейных дешифраторов определяются следующими логическими выражениями:

Эти дешифраторы выполняют функции первой ступени дешифратора.

Выходные переменные y 0 , y 1 , …, y 15 прямоугольного дешифратора можно представить логическими выражениями, используя в них в качестве аргументов выходные переменные y» 0 , …, y» 3 и y»» 0 , …, y»» 3 линейных дешифраторов:

Эти логические операции выполняются в отдельном дешифраторе второй ступени, называемом матричным и состоящим из двух — входовых элементов. На рис. 5.22,б показано условное изображение матричного дешифратора, где помеченные десятичными числами две группы входов служат для подключения к выходам двух предварительных ступеней дешифрации. На рис. 5.22,в представлена структура прямоугольного дешифратора с использованием символов линейного и матричного дешифраторов.

Могут быть построены прямоугольные дешифраторы с числом ступеней, большим двух.

Применение прямоугольного дешифратора может оказаться более выгодным, чем использование линейного дешифратора, в тех случаях, когда велико число входов и нежелательно использование требующихся для построения линейного дешифратора элементов с большим числом входов. Однако прохождение сигналов последовательно через несколько ступеней в прямоугольном дешифраторе приводит к большей задержке распространения сигнала в нем.

Таблица 5.7
Код 8421	Код 2421
x 4	x 3	x 2	x 1	y 4	y 3	y 2	y 1

Преобразователи кодов

В цифровых устройствах часто возникает необходимость преобразования числовой информации из одной двоичной системы в другую (из одного двоичного кода в другой). Примером такого преобразования может служить преобразование чисел из двоичного кода 8421, в котором выполняются арифметические операции, в двоичный код 2 из 5 для передачи по линии связи. Эта задача выполняется устройствами, называемыми преобразователями кодов. Для преобразования кодов можно пользоваться двумя методами:

основанным на преобразовании исходного двоичного кода в десятичный и последующем преобразовании десятичного представления в требуемый двоичный код;

основанным на использовании логического устройства комбинационного типа, непосредственно реализующего данное преобразование.

Первый метод структурно реализуется соединением дешифратора и шифратора и удобен в случаях, когда можно использовать стандартные дешифраторы и шифраторы в интегральном исполнении.

Рассмотрим подробнее второй метод на конкретных примерах преобразования двоичных кодов.

Преобразование

кода 8421
в

код 2421.

Обозначим переменные, соответствующие отдельным, разрядам кода 8421, x 4 , x 3 , x 2 , x 1 , то же для кода 2421 y 4 , y 3 , y 2 , y 1 . В табл. 5.7 приведено соответствие комбинаций обоих кодов.

Каждая из переменных y 4 , y 3 , y 2 , y 1 может рассматриваться функцией аргументов x 4 , x 3 , x 2 , x 1 и, следовательно, может быть представлена через эти аргументы соответствующим логическим выражением. Для получения указанных логических выражений представим переменные y 4 , y 3 , y 2 , y 1 таблицами истинности в форме таблицы Вейча (рис 5.24.1).

рис 5.23	рис 5.24

рис 5.24.1

Получим минимальную форму логических выражений, представленных через операции И, ИЛИ, НЕ и через операцию И-НЕ:

На рис. 5.23 приведена логическая структура преобразователя кодов, построенная на элементах И-НЕ с использованием полученных логических выражений.

Преобразование

кода 2421
в

код 8421.

Для реализации данного преобразования (обратного по отношению к рассмотренному выше) требуется получить логические выражения для переменных x 4 , x 3 , x 2 , x 1 , используя в качестве аргументов переменные y 4 , y 3 , y 2 , y 1.

Таблицы Вейча для переменных x 4 , x 3 , x 2 , x 1 представлены на рис. 5.24.2. Логические выражения для переменных x 4 , x 3 , x 2 , x 1:

Логическая структура преобразователя приведена на рис. 5.24.

Преобразователь для цифровой индикации.

Один из способов цифровой индикации состоит в следующем.

Таблица 5.10
Десятичная цифра	Двоичный код 8421	Состояние элементов (z 1 , …, z 7) и значение управляющих сигналов (y 1 , …, y 7)
x 4	x 3	x 2	x 1	1	2	3	4	5	6	7
y 1	y 2	y 3	y 4	y 5	y 6	y 7

Имеется семь элементов, расположенных так, как показано на рис. 5.25,а. Каждый элемент может светиться либо не светиться, в зависимости от значения соответствующей логической переменной, управляющей его свечением. Вызывая свечение элементов в определенных комбинациях, можно получить изображение десятичных цифр 0, 1, 9 (рис. 5.25.б).

Десятичные цифры, отображение которых необходимо вызвать, задаются обычно в двоичном коде. При этом возникает задача формирования логических переменных y 1 , y 2 , …, y 7 для управления отдельными элементами в устройстве индикации. Таблица истинности для этих переменных представлена в табл.5.10.

рис 5.25

При построении таблицы были приняты следующие условия: если элемент индикатора светится, то это означает, что он находится в состоянии лог. 1, если погашен, то он находится в состоянии лог. 0; управление элементом осуществляется таким образом, что высокий уровень лог. 1 на некотором входе индикатора вызывает гашение соответствующего элемента (т. е. чтобы i-й элемент был погашен и z i = 0, необходимо подать на 1-й вход индикатора управляющий сигнал y i = l). Таким образом, y i = i . Например, для высвечивания цифры 0 необходимо погасить 7-й элемент (z 7 =0), оставив остальные элементы в состоянии свечения; следовательно, при этом управляющий сигнал y 7 = l, остальные управляющие сигналы y l , …, y 6 должны иметь уровень лог. 0.

рис 5.26

Формирование управляющих сигналов производится логическим устройством, для синтеза которого на рис. 5.26 построены таблицы истинности в форме таблиц Вейча отдельно для каждой переменной y l , …, y 7 . Синтезируемое устройство является устройством с несколькими выходами и для получения минимальной схемы необходимо в таблицах Вейча построить минимальное число областей, обеспечивающих покрытие клеток, содержащих 1, во всех семи таблицах. Построение этих областей имеет следующие особенности. В таблицах переменных у 5 и y 6 использованы области 1 и V, которые используются в таблицах других переменных. Если вместо этих областей в таблицах переменных у 5 и y 6 построить области с большим охватом клеток, это вызовет увеличение общего количества областей и, следовательно, увеличится количество логических элементов, требуемых для формирования соответствующих им логических выражений. Выделенным областям соответствуют следующие логические выражения:

Теперь нетрудно записать логические выражения для выходных величин y l , …, y 7:

Построенная в соответствии с этими выражениями схема преобразователя приведена на рис. 5.25,в.

Таблица 5.12
Тип логического элемента	Число элементов в корпусе микросхемы	Число элементов в преобразователе	Число корпусов микросхем
Инверторы
Двухвходовые элементы И-НЕ
Трехвходовые элементы И-НЕ
Четырехвходовые элементы И-НЕ
Общее количество корпусов микросхем	5 5 / 12

Определим количество микросхем, необходимых для построения преобразователя. При этом следует учитывать, что в корпусе выпускаемых промышленностью микросхем может содержаться несколько логических элементов. В табл. 12 приведен расчет количества корпусов микросхем.

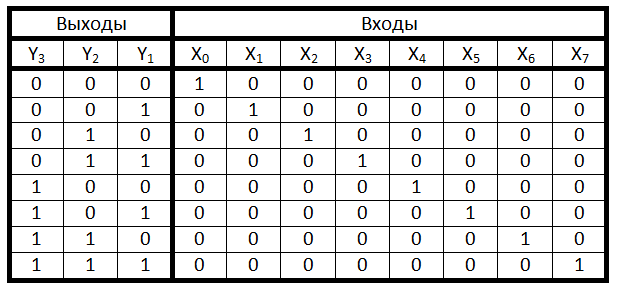
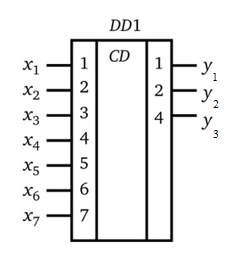
Таблица истинности для шифратора

Шифратор

Рассмотрим следующее устройство – шифратор. Его назначение – преобразовать код с единицей в одной позиции в обычный позиционный код. Таблица истинности для трехразрядного шифратора приведена ниже

Таблица истинности для шифратора

е7	e6	e5	e4	e3	e2	e1	e0	l2	l1	l0

Количество выходов определяется соотношением 

m = log₂n,

где m – число выходов, n – количество входов.

 Схема трехразрядного шифратора показана ниже. Она непосредственно следует из таблицы истинности. Заметим, что без шины e0 в принципе можно обойтись.

Схема трехразрядного шифратора

Условное изображение трехразрядного шифратора представлено на рисунке

Условное изображение трехразрядного шифратора

Отметим, что шифратор будем называть по числу выходов, так для четырехразрядного шифратора количество входов будет 2⁴=16 и т.п.           

Мультиплексор

Мультиплексор подключает один из информационных входов к единственному выходу. Используется весьма часто в электронных устройствах и устройствах связи – когда требуется по одному каналусвязипередать информацию от нескольких источников информации. При этом возможно временное мультиплексирование, частотное мультиплексирование. Здесь мы рассмотрим и в дальнейшем промоделируем простой вариант комбинационного мультиплексора, который подключает один из 8 информационных входов к выходу устройства, причем для указания номера подключаемого сигнала служат три управляющих сигнала. При этом соблюдается приведенное ранее соотношение m = 2, но здесь m иn имеют другой смысл – соответственно это число информационных и управляющих входов мультиплексора. Так, с помощью трех управляющих сигналов можно подключить 8 информационных входов, с помощью четырех – 16 и т. д. Указанное выше соотношение показывает максимально возможное значение информационных входов при данном количестве управляющих. Однако ничего не мешает, например, при четырех управляющих сигналах подключить не 16, а 10 информационных входов, просто ряд комбинаций управляющих сигналов не будут использованы. Схема и условное обозначение мультиплексора представлены на рисунках.

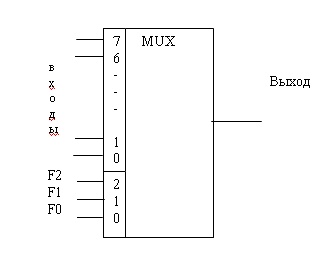
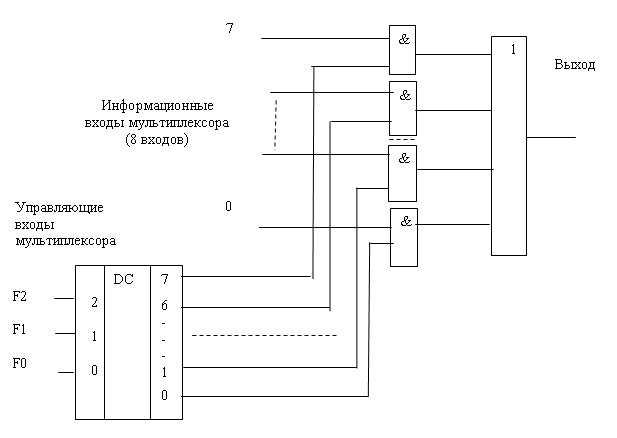
Схема мультиплексора на 8 информационных входов

Схема мультиплексора на 8 информационных входов

Условное обозначение мультиплексора на 8 информационных входов: