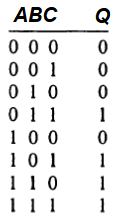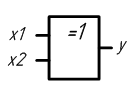КОМБИНАЦИОННЫЕ ЛОГИЧЕСКИЕ СХЕМЫ
Комбинационные логические схемы — это такие логические устройства, в которых состояние выхода зависит только от текущего состояния их выходов в некотором предопределенном виде. Комбинационные схемы могут быть построены с применением одних лишь вентилей и не требуют наличия памяти в какой-либо форме (триггер).
Логические тождества
Любое обсуждение комбинационной логики будет неполным, если не рассматривать логические тождества, представленные ниже:
Логические тождества
АВС = (АВ) С = А(ВС)
АВ = ВА
АА = А
А1 = А
А0 = 0
А(В + С) = АВ + АС
А + АВ = А
А + ВС = (А + В)(А + С)
А + В + С =(А + В) + С = А + (В + С)
А + В = В + А
А + А = А
А + 1 = 1
А + 0 = А
1′ = 0
0′ = 1
А + А’= 1
АА’ = 0
(А’)’ = А
А + А’В = А + В
(А + В)’ = А’ В’
(АВ)’ = А’ + В’
Большинство соотношений очевидны. Два последних составляют теорему Моргана, наиболее важную для построения схем.Для возбуждения шины нельзя использовать вентили (или другие схемы) с активным выходом. Потому, что их нельзя отключить от общих информационных линий.
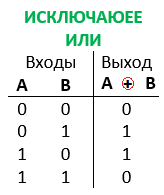
Пример: вентиль Исключающее ИЛИ. Следующий пример иллюстрирует использование логических тождеств. Построим схему Исключающее ИЛИ с помощью обычных вентилей. Таблица истинности для Исключающего ИЛИ представлена на рисунке
Изучив ее и поняв, что «1» на выходе существует только тогда, когда (А, В) = (0,1) или (1,0), мы можем написать
Соответствующая схемная реализация представлена на рисунке
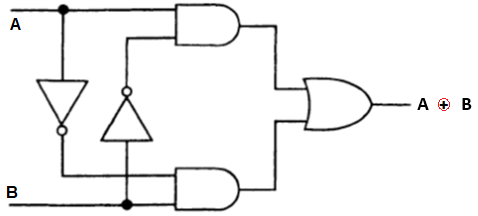
Однако эта реализация не является единственной. Используя логические тождества, мы находим, что
где
(На первом шаге мы прибавили две величины, равные нулю, а на третьем применили теорему Моргана). Схемная реализация для этого случая показана на рисунке
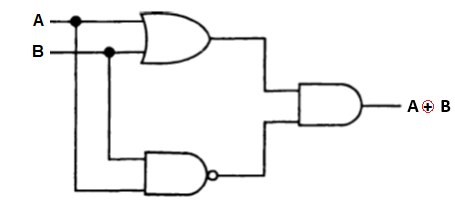
Однако эта реализация не является единственной. Используя логические тождества, мы находим, что
Минимизация и карты Карно
Поскольку логическую функцию, даже такую простую, как Исключающее ИЛИ, можно реализовать различными способами, часто бывает нужно найти для нее самое простое решение, или, возможно, наиболее удобное схемное решение. Над этой проблемой бились многие светлые умы. В настоящее время существует несколько способов ее разрешения, включая алгебраические методы, реализуемые с помощью ЭВМ. При числе входов, не превышающем четырех, наилучшим методом является составление карты Карно. Этот метод позволяет также найти логическое выражение по таблице истинности.
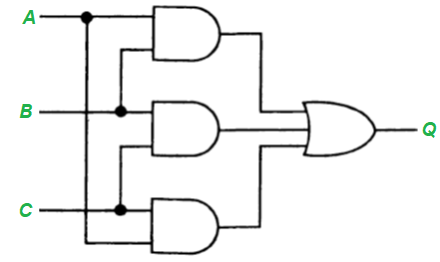
Проиллюстрируем этот метод с помощью примера. Предположим, что требуется построить схему для мажоритарного подсчета голосов при баллотировке. Будем считать, что имеются три входа, работающие в положительной логике и выход (0 или 1). На любом из входов может быть 1 или 0. Выход равен 1, если 1 присутствует не менее чем на двух входах.
Шаг 1. Составим таблицу истинности
Здесь должны быть представлены все возможные сочетания и соответствующие им состояния выхода (или выходов). В том случае, когда состояние входа не оказывает влияния на выход, ставится X (любое значение).
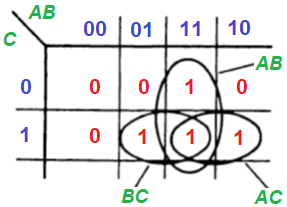
Шаг 2. Составим карту Карно. Она представляет собой нечто очень близкое к таблице истинности, но содержит переменные, которые расположены по двум осям. Переменные должны быть расположены таким образом, чтобы при переходе от каждого квадрата к соседнему менялось бы состояние только одного входа.
Шаг 3. Отметим на карте группы, содержащие единицы. Можно также использовать и группы, содержащие нули. Три овала на рисунке определяют логические выражения АВ, АС и ВС. Далее получим требуемую функцию
Q = АВ + АС + ВС,
схемная реализация ее показана на рисунке:
Этот результат кажется очевидным, когда он уже получен. Можно было бы составить выражение для нулей и вместо этого получить
Q’ = A’B’ + A’C’ + B’C’
Это выражение может оказаться полезным для случая, когда в каких-либо точках схемы имеются дополнения А’, В’ и С’.
Комментарии к картам Карно.
- Ищите группы, содержащие 2, 4, 8 и т.д. квадратов. Они имеют простые логические выражения.
- Логика будет тем проще, чем крупнее блок вы опишете.
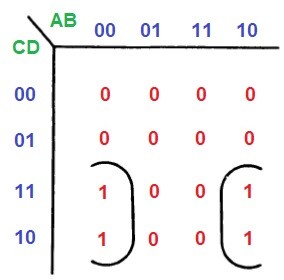
- Состыкуйте края карты Карно. Например, карта на рисунке ниже описывается выражением Q=В’С.
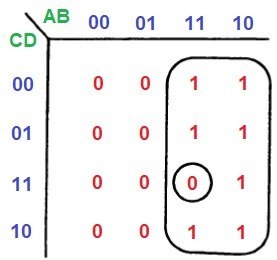
4. Блок «единиц», содержащий один или два «нуля», лучше всего описывается с помощью группировки:
Этому блоку соответствует логическое выражение Q = A (BCD)’.
5. Места, содержащие X (любое значение), представляют собой «карт-бланш». Записывайте в них «нули» или «единицы» так, чтобы можно было получить простейшую логику.
- Карта Карно может и не привести к лучшему решению. Иногда более сложное логическое выражение имеет более простую схемную реализацию. Например, в случае, когда некоторые члены выражения уже сформированы схемой в виде логических сигналов, которые можно использовать в качестве входных. Кроме того, реализации «Исключающего ИЛИ» не очевидны из карты Карно. Наконец, при выборе логической структуры схемы определенную роль играют ограничения, связанные с конструкцией ИМС. Например, когда в одном корпусе содержатся четыре 2-входовых вентиля. Когда используются такие программируемые логические устройства как ПМЛ для конструирования логических функций, их внутренняя структура сдерживает полноценную реализацию.
Комбинационные функциональные схемы, реализованные на стандартных ИМС
С помощью карт Карно можно построить логику, чтобы выполнять достаточно сложные функции. Например, двоичное сложение и сравнение величин, контроль по паритету, мультиплексирование (выбор одного из нескольких входов, который определяется двоичным адресом) и т.п. В реальности сложные функции, которые используются наиболее часто, реализуются в виде функциональных ИМС средней степени интеграции (до 100 вентилей в корпусе). Хотя в состав многих из этих ИС входят триггеры, большинство из них выполняют чисто комбинационные функции и состоят целиком из одних вентилей.
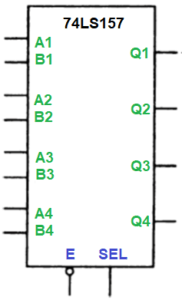
Когда вход ВЫБОР (SEL на рисунке) имеет низкий уровень, сигналы на выходах Q поступают с соответствующих входов А. При высоком уровне на входе SEL — со входов В. Когда высокий уровень действует на входе РАЗРЕШЕНИЕ (ENABLE-E на рисунке), все выходы устройства принудительно устанавливаются в состояние низкого уровня. Приведем лишь таблицу истинности, в которой X означает, что состояние данного входа не имеет значения, В-высокий уровень, Н-низкий уровень.
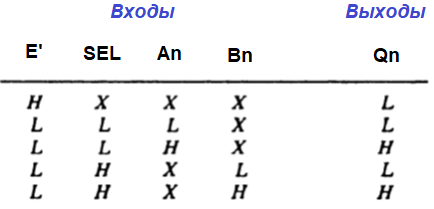
Хотя в некоторых случаях функцию выборки можно реализовать с помощью механического переключателя, тем не менее, по ряду причин предпочтительнее использовать вентили. Вентильная схема обладает следующими преимуществами:
а) она дешевле;
б) коммутация всех каналов производится быстро и одновременно;
в) с помощью логических сигналов, сформированных в устройстве, можно производить переключение практически мгновенно;
г) для того, чтобы избежать воздействия помехи и снижений уровней за счет влияния емкостей, логические сигналы лучше не пропускать через кабели и переключатели. Так как избираемый вентиль отпирается уровнем постоянного напряжения, логические сигналы управления могут быть взяты с той же платы, на которой он расположен. Это позволяет сократить внешние связи. Достаточно одной линии с нагрузкой, коммутируемой на землю с помощью однополюсного тумблера.
Такой способ управления логической схемой с помощью внешних уровней постоянного напряжения называют «холодной коммутацией». Он оказывается более предпочтительным, чем непосредственное управление сигналами от ключей, потенциометров и т.п. Кроме прочих преимуществ холодная коммутация позволяет вести управляющие линии, шунтированные конденсаторами. При этом подавляются взаимные наводки, в то время как сигнальные линии в общем случае шунтировать конденсаторами нельзя.
Передающие вентили. С помощью элементов КМОП можно построить «передающий вентиль». Это два параллельно включенных комплементарных ключа на полевых МОП-транзисторах. Через эти транзисторы входной (аналоговый) сигнал, лежащий в пределах от 0 до Ucc, может либо непосредственно подаваться на выход через низкое сопротивление (несколько сотен омов), либо быть оторванным (выходное сопротивление фактически равно бесконечности). Такие устройства являются двунаправленными. Для них не имеет значения, какой из выходов используется в качестве входа, а какой в качестве выхода. Передающие вентили прекрасно работают с цифровыми уровнями КМОП и широко применяются в КМОП-схемах. На рисунке показана структурная схема счетверенного двухстороннего КМОП- ключа типа 4066.
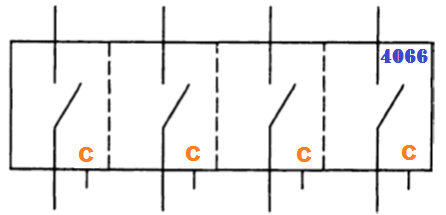
Каждый ключ имеет индивидуальный управляющий вход. Высокий уровень замыкает ключ, а низкий — размыкает. Передающие вентили являются просто ключами, и поэтому не обладают способностью к разветвлению по выходу. Они просто пропускают входной логический уровень. Они не обеспечивают дополнительную нагрузочную способность с возможностью усиления.
С помощью передающих вентилей можно построить схемы выборки на 2 и более входов для цифровых уровней КМОП и аналоговых сигналов. Связку передающих вентилей можно использовать для того, чтобы производить выбор одного из нескольких входов. Для этого вырабатываются управляющие сигналы с помощью дешифратора. Эта логическая функция настолько широко используется, что получила официальное название «мультиплексора».
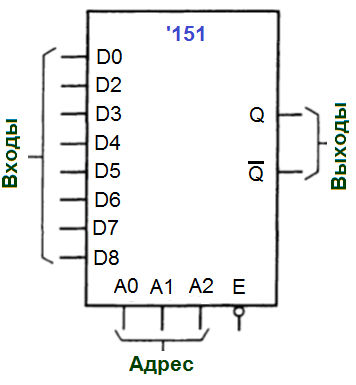
Мультиплексоры. Вентиль выборки на два входа известен также под названием 2-входового мультиплексора. Промышленностью выпускаются также мультиплексоры на 4, 8 и 16 входов. Устройства на 4 входа выпускаются сдвоенными, т. е. по 2 в одном корпусе. Двоичный адрес служит для выбора входа, сигнал с которого должен поступать на выход. Например, мультиплексор, имеющий 8 информационных входов, использует для адресации к ним 3-разрядный адресный вход. Это показано на рисунке, где представлен цифровой мультиплексор типа ‘151.
Он имеет стробирующий (или разрешающий) вход Е, а также прямой и инверсный выходы. Если устройство закрыто (на входе Е действует высокий уровень), выход Q будет иметь низкий уровень, a Q‘ — высокий независимо от состояния адресных и информационных входов.
В семействе КМОП имеются два типа мультиплексоров. Первый применяется только для работы с цифровыми сигналами. Он имеет входной порог и регенерирует на выходе «чистые» уровни, которые соответствуют входному состоянию. Таким же образом работают все функциональные элементы ТТЛ. Примером является микросхема Т53-ТТЛ-мультиплексор.
К другому типу устройств относятся аналоговые и двунаправленные КМОП мультиплексоры. Они фактически представляют собой набор передающих вентилей, КМОП-мультиплексоры 4051 и 4053 работают таким образом. Логика, выполненная из передающих вентилей, не может разветвляться. Передающие вентили являются двунаправленными и могут использоваться в качестве «демультиплексоров или дешифраторов»
Расширение числа входов мультиплексора. Иногда при разработке логических устройств может оказаться, что потребуется производить набор из большего числа входов, чем имеются в мультиплексоре.
Этот вопрос относится к общей задаче расширения микросхем. Он заключается в использовании нескольких микросхем с небольшими индивидуальными возможностями. Применяется для построения дешифраторов, памяти, регистров сдвига, арифметически-логических и других устройств. Как видно из рисунка, расширение выполняется очень просто.
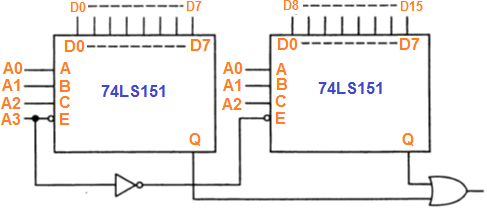
Здесь показано, как имея два мультиплексора на 8 входов 74LS51 построить мультиплексор на 16 входов. Конечно, в схемах имеется дополнительный адресный бит, который вы используете для выбора одного устройства или другого. На не выбранном мультиплексоре ‘151 выход Q поддерживается на низком уровне, что позволяет произвести объединение через вентиль ИЛИ. Если выходы имеют три состояния, то расширение производится еще проще: для этого достаточно непосредственно объединить выходы.
Демультиплексоры и дешифраторы. Входной сигнал принимается демультиплексором. Принятый сигнал направляется им на один из нескольких выходов в соответствии с двоичным кодом, действующим на адресных входах. Остальные выходы в этом случае находятся либо в неактивном состоянии, либо в состоянии разомкнутой цепи. Аналогично работает и дешифратор. Единственное отличие состоит в том, что на входы подается только адрес, возбуждающий один из n возможных выходов. На рисунке ниже показан такой пример:
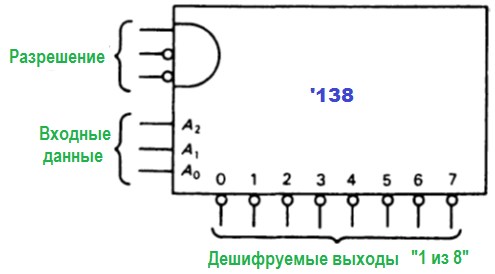
Дешифратор ‘138 — «1 из 8» (даташит) имеет низкий уровень на выходе. Этот уровень соответствует входному 3-разрядному коду (адресу). На остальных выходах при этом — высокий уровень. Этот дешифратор имеет три входа разрешение, все из которых должны быть активны (два — низкого и один — высокого уровня). Иначе на всех выходах будет высокий уровень. Основное применение дешифратора — заставить происходить различные события. Эти события зависят от состояния «счетчика», который ими управляет.
Дешифраторы обычно используются при сопряжении с микропроцессором, когда необходимо выполнить различные действия в зависимости от адреса.
Другим применением общего использования дешифратора является организация (разрешение) последовательности действий, согласно достигнутого адреса, заданного выходом двоичного счетчика. На рисунке ниже показано, как использовать два дешифратора “1 из 8” типа ‘138 для получения дешифратора «1 из 16».
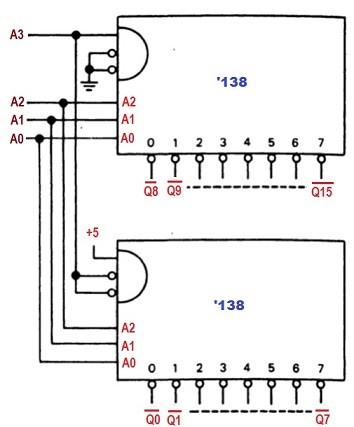
Как видно из рисунка, внешние элементы не требуются. В самой схеме ‘138 имеются входы разрешения обеих полярностей (низкого и высокого уровней).
В КМОП-логике мультиплексоры, которые используют передающие вентили, также являются демультиплексорами. Все, потому что передающие вентили являются двунаправленными. Когда они используются таким образом, важно сознавать, что выходы, которые не выбраны, отключены. Нагрузочный резистор, или эквивалентный ему, должен быть использованы для обеспечения правильного функционирования логики с такими выходами. Те же требования, что и с ТТЛ-вентилями с открытым коллектором.
Существует другой тип дешифраторов, который обычно входит в состав всех логических семейств. Примером такого дешифратора служит преобразователь двоично-десятичного кода в семисегментный. Такая схема в соответствии с двоично-десятичным кодом на входе, формирует сигналы на всех выходных линиях. Выходные линии связанны с входами семисегментного цифрового индикатора для воспроизведения десятичного символа. Устройство такого типа фактически является преобразователем кодов, но в обычной практике используется название дешифратор.
Сумматоры и другие арифметические устройства. На рисунке изображен 4-разрядный полный сумматор.
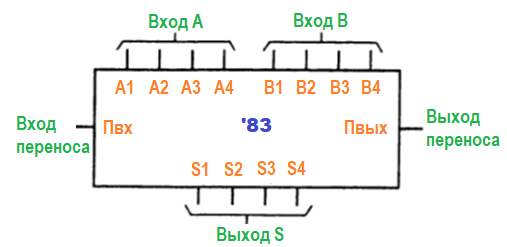
Он прибавляет 4-разрядное двоичное число An к 4-разрядному числу Bn. На выходе вырабатывает 4-разрядную сумму S и разряд переноса Пвых. Для суммирования больших величин сумматоры можно наращивать. Для этой цели предусмотрен вход Пвх, на который поступает выходной сигнал переноса от предыдущего (младшего) сумматора. На рисунке ниже показано, как строится схема для суммирования двух 8-разрядных двоичных чисел.
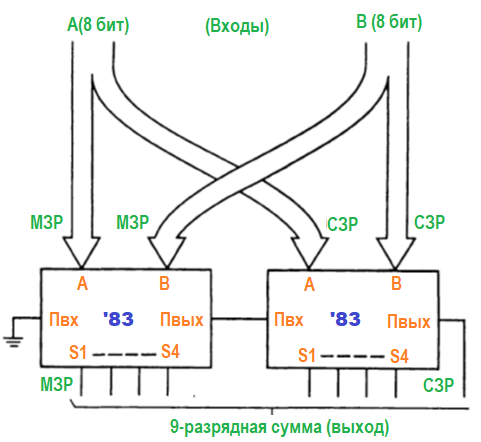
Часто в качестве сумматоров используются арифметико-логические устройства (АЛУ). Эти устройства фактически предназначены для выполнения целого ряда различных функций. В частности, 4-разрядная АЛУ ‘181 (арифметически-логическое устройство — даташит) может выполнять сложение, вычитание, сдвиг двоичных разрядов, сравнение величин и некоторые другие функции. Время выполнения арифметических операций в сумматорах и АЛУ находится в пределах от наносекунд до десятков наносекунд. Все зависит от типа логического семейства.
Интегральные умножители выпускаются в конфигурациях 8х8 бит или 16х16 бит. Разновидностью умножителей, которые в основном используются для цифровой обработки сигналов, являются так называемые умножители-накопители. Их задача накапливать сумму произведений. Они также выполняются в размерах 32 х 32 с 64-битовым произведением плюс несколько дополнительных бит для сохранения суммы от переполнения. Умножители-накопители и умножители выпускаются с временем 25-50 нс. У ЭСЛ-умножителей время меньше — 5 нс (типично) для умножителей 16 х 16.
Другим арифметическим устройством, которое используется в цифровой обработке сигналов, является коррелятор. Он сравнивает соответствующие биты двух цепочек битов, вычисляя число совпавших битов. Типовой интегральный коррелятор сравнивает два 64-разрядных, которые могут сдвигаться во внутренних регистрах сдвига. Какой-либо набор бит может игнорироваться («маскироваться») в корреляции. Типовые времена составляют 30 нс. Т. е. лента бит может тактироваться с частотой 35 МГц, с разрешением 7 бит в корреляции для каждого такта. Вычисляется отклонение вместо суммы (с переносом) попарносвязанных произведений двух цепочек целых чисел. Типичные размеры — целые числа от 4 до 10 бит при длине от 3 до 8 слов. Имеются возможности расширения.
Наиболее сложными арифметическими кристаллами являются процессоры с плавающей запятой. Они осуществляют сравнение, суммирование, умножение, вычисление тригонометрических функций, экспонент и корней. Обычно такие процессоры используются совместно с определенными микропроцессорами. Работают они в стандарте, известном как IEED754, который определяет размеры слов (до 80 бит), формат и т. д.
Компараторы. На рисунке показан 4-разрядный компаратор чисел. Он определяет относительные значения чисел Л и В и вырабатывает на выходе сигналы результатов сравнения: А < В, А = В и А > В.
Схема формирования и контроля бита паритета. Это устройство предназначено для выработки паритетного бита. Этот бит добавляется к информационному «слову» при передаче (или записи) данных, а также для проверки правильности паритета при восстановлении этих данных. Паритет может быть четным или нечетным. При нечетном паритете для каждого символа общее число битов (разрядов), содержащих 1, нечетно.
Программируемые логические устройства. Каждый может строить собственные комбинационные (и даже последовательные) логические схемы на кристалле. Для этого можно использовать интегральные схемы, которые содержат массив вентилей с программируемыми перемычками. Существуют несколько вариантов таких устройств, из которых наиболее популярными являются ПМЛ (программируемая матричная логика-PAL) и ПЛМ (программируемая логическая матрица-PLA). ПМЛ, в частности, крайне недорогие и гибкие устройствами.
Некоторые другие незнакомые функции. Существует много других комбинационных схем средней степени интеграции, представляющих несомненный интерес. Например, в семействе КМОП есть схема — «мажоритарная логика», которая говорит, что возбуждена большая часть входов. Имеется также двоично-десятичное устройство дополнения до 9, назначение которого не требует пояснений. Существует схема «барабан — сдвигатель», которая сдвигает входное число на задаваемое количество разрядов и может наращиваться до любой длины.
Произвольные таблицы истинности
К счастью, большинство из проектов цифровых схем не состоит из набора бесконечных устройств на вентилях для реализации сложных логических функций. Однако временами, когда нужно связать несколько сложных таблиц истинности, число вентилей может стать слишком большим. Возникает вопрос, нельзя ли найти какой-то другой путь. Таких путей существует несколько.
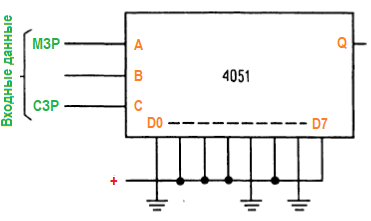
Мультиплексоры в качестве реализаций обобщенных таблиц истинности. Нетрудно видеть, что n-входовый мультиплексор может быть использован для генерации любой таблицы истинности на п входов. При этом нет необходимости применения каких-либо внешних компонентов. Просто на их входы нужно подать соответствующие высокие и низкие уровни. Схема ниже говорит, является ли входное 3-разрядное двоичное число простым.
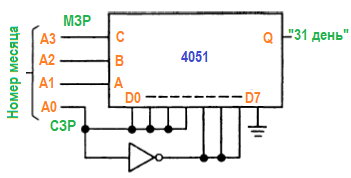
Не столь очевидно, что мультиплексор на п входов с помощью только одного инвертора может быть использован для генерации таблицы истинности на 2п входов. Например, на рисунке ниже показана схема, которая определяет, имеет или нет данный месяц года 31 день. Месяц (от 1 до 12) задается 4-битовым входом. (Даташит 4051)
Хитрость в том, чтобы заметить, что для данного состояния адресных битов, прикладываемых к мультиплексору, выход (как функция оставшегося входного бита) должен быть равен Н, L, А0 или А’0. Соответственно вход мультиплексора связывается с логическим высоким, логическим низким, А или А’0.
Данную таблицу истинности можно реализовать только с одним вентилем «исключающее или». Для этого нужно использовать для несуществующих месяцев знак X (любое значение)!
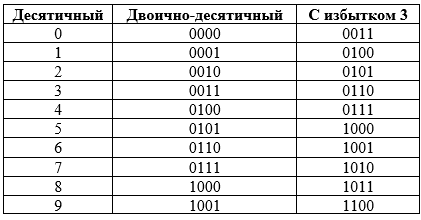
Дешифраторы как обобщенные таблицы истинности. Дешифраторы также позволяют упростить комбинационную логику. Особенно это характерно для тех случаев, когда нужно получить несколько одновременно действующих выходных сигналов. В качестве примера попробуем составить схему преобразования двоично-десятичного кода в код с избытком 3 (код устарел). Таблица истинности для такого преобразования имеет вид:
Здесь используется 4-разрядный (в двоично-десятичном коде) вход как адрес для дешифратора. Выходы дешифратора (в отрицательной логике) служат в качестве входов для нескольких вентилей ИЛИ, формирующих выходные биты, как показано на рисунке:
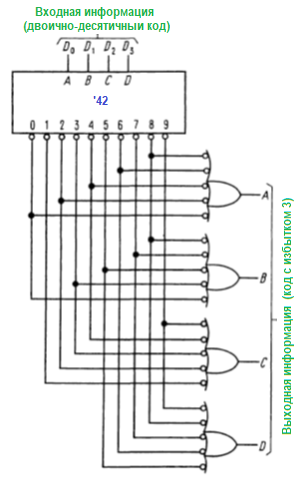
Заметим, что в этой схеме выходные биты не являются взаимно исключающими. Аналогичную схему можно использовать в качестве устройства для задания рабочих циклов в стиральной машине. При каждом состоянии входа выполняются различные функции — подача воды, заполнение, вращение барабана и т. д. Индивидуальные выходы дешифратора носят название «минтермы» и соответствуют позициям на карте Карно.
ПЗУ и программируемая логика
Эти ИС позволяют вам программировать их внутренние связи. В этом смысле они фактически являются устройствами с памятью. Однако после программирования они становятся строго комбинационными.
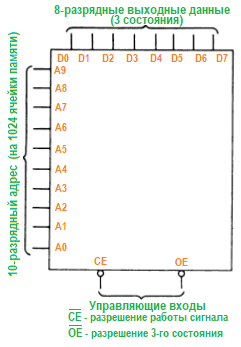
ПЗУ (постоянное запоминающее устройство) содержит битовый образ для каждого конкретного адреса, приложенного к входу. Например, 1 К х 8 ПЗУ выдает восемь выходных бит на каждое из 1024 входных состояний, определяемых 10-разрядным входным адресом:
Любая комбинационная таблица истинности может быть запрограммирована в ПЗУ, обеспечивающем достаточное число входных линий (адреса). Например, ПЗУ 1 К х 8 можно использовать для реализации умножителя 4 х 4. В этом случае ограничение на «ширину» (8 разрядов), не действует (так как имеется 10 разрядов).
ПЗУ (а также программируемые логические устройства) являются энергонезависимым устройством, т. е. хранимая информация остается даже тогда, когда питание пропадает.
ПЗУ подразделяются на несколько типов, в зависимости от их метода программирования:
а) «Масочнопрограммируемые ПЗУ» имеют свое битовое содержание, созданное во время изготовления.
б) «Программируемые ПЗУ» (ППЗУ) программируются пользователем. ПЗУ имеют тонкие перемычки, которые могут пережигаться (подобно предохранителям) посредством подачи адреса и управляющих сигналов. Они обладают высоким быстродействием (25- 50 нс), относительно большим потреблением (биполярные 0,5-1 Вт), размерами от малых до средних (от 32 х 8 до 8 К х х 8).
в) «Стираемые программируемые ПЗУ» (СППЗУ) хранят свои биты как заряды на плавающих МОП-вентилях. Информация в них может стираться посредством облучения их интенсивным ультрафиолетовым светом в течение нескольких минут (они имеют прозрачное кварцевое стекло). Выполняются по n-МОП и КМОП-технологии. Значительно медленнее (200 нс) при низком потреблении (частично в режиме хранения), имеют достаточно большой размер (8 К х 8 и 128 К х 8). Некоторые КМОП СППЗУ достигают быстродействия биполярных ПЗУ (35 нс). Известен вариант — «однократно-программируемый» (ОКП). Он содержит идентичный кристалл, но не имеет кварцевого окна для экономии и простоты.
г) «Электрические стираемые программируемые ПЗУ» (ЭСППЗУ). Подобны СППЗ, но могут программироваться и стираться электрически прямо в схеме. Для этого используются стандартные напряжения питания ( + 5 В).
ПЗУ находят широкое использование в компьютерах и микропроцессорах, где они используются для сохранения законченных программ и таблиц данных. Необходимо помнить о небольших ПЗУ, как о замене сложных вентильных матриц.
Программируемая логика. ПМЛ (программируемая матричная логика PAL) и ПЛМ (программируемые логические матрицы) являются двумя основными видами программируемой логики. Они являются ИС со многими вентилями. Связи между вентилями могут программироваться (подобно ПЗУ) для формирования желательных логических функций. Выполняются как в биполярном, так и в КМОП-вариантах. Первые используют прожигаемые перемычки (однократнопрограммируемые), вторые — плавающие вентильные КМОП схемы (ультрафиолетового или электрического стирания). Невозможно запрограммировать любые связи. Здесь мы будем ограничены встроенной структурой. Рисунок ниже показывает основные схемы комбинационных (не регистровых) ПЛМ и ПМЛ.
Для простоты на этом рисунке вентили И или ИЛИ нарисованы с одним входом. В действительности они являются многовходовыми вентилями с входом для каждого перекрестия.
Каждый выход (с 3 состояниями) комбинационной ПМЛ выводится от вентиля ИЛИ, а каждый вход подсоединяется к вентилю И с дюжинами входов.
ПЛМ подобна ПМЛ, но обладает большей гибкостью. Выходы вентилей И могут связываться со входами вентилей ИЛИ в любой комбинации (т. е. программироваться). Это предпочтительней, чем жесткое присоединение, как в ПМЛ.
Заметим, что ПМЛ и ПЛМ, описанные выше, являются комбинационными устройствами (т. е. выполнены только на вентилях, без памяти).
Для использования ПМЛ и ПЛМ должен быть программатор, как часть аппаратного обеспечения. Программатор знает, как прожигать перемычки (или другие типы программируемых средств) и проверять окончательный результат. Все программаторы имеют связь через последовательный порт с компьютером, на котором вы работаете с программным обеспечением программатора. Некоторые из современных программаторов включают одноплатный компьютер, который работает с собственным программным обеспечением.
Простейшее программное обеспечение просто позволяет выбрать перемычки для прожигания. Рисунок ниже показывает простой пример для функции «ИСКЛЮЧАЮЩЕЕ ИЛИ» на два входа на одном из выходов ПМЛ.
Хорошие программаторы позволяют вам задавать буквы выражения (если они вам известны) или таблицы истинности. Программное обеспечение затем делает остальное, включая минимизацию, моделирование и программирование.
Хотя ПЛМ более гибкие, фаворитом в современном проектировании являются ПМЛ. Это из-за того, что они быстрее (так как сигнал проходит только через один массив перемычек), дешевле и обычно удовлетворяют задаче. Более новые ПМЛ, использующие «макроячейки» и «складную архитектуру». Они дают некоторую дополнительную гибкость в проектировании на ПМЛ с фиксированными «ИЛИ-вентилями». Таким образом, ПМЛ представляют собой гибкую и компактную альтернативу интегральных схем с фиксированными функциями и не должны выпадать из виду у серьезного проектировщика схем.
Смотрите также:
Лабораторная
работа № 1
Изучение
методов синтеза и анализа комбинационных схем
Цель
работы: изучить методы синтеза и анализа комбинационных схем, методы
минимизации, макетирования и испытания комбинационных схем, изучить
одноразрядный комбинационный сумматор.
Задание
для подготовки к лабораторной работе
1.Изучить
теоретические положения, используя рекомендованную литературу и
лекционный материал.
2.
Подготовиться к выполнению работы, составив для каждого пункта задания таблицы
истинности реализуемых функций, выполнить необходимую по заданию минимизацию,
составить схемы с учётом имеющихся моделей элементов. При использовании
компьютера в отчёт необходимо представить копии набранных схем, временные
диаграммы работы схемы с комментарием. Временные диаграммы могут быть построены
путём перебора состояний входных сигналов тумблерами и контролем при этом
состояний выходного сигнала или могут быть сформированы на экране осциллографа
или логического анализатора в автоматическом режиме.
Порядок
выполнения работы
Синтезируемые
в процессе выполнения работы схемы должны быть ориентированы на элементы,
имеющиеся на стенде. Это элементы типа ЛА3, ЛА4, ЛА1, ЛР1(ЛР11), ЛР3(ЛР13). При выполнении работы на
компьютере следует использовать иностранные аналоги отечественных элементов.
Таблица соответствия иностранных и отечественных элементов предложена в
приложении. Если аналог не найден, используйте имеющиеся модели элементов, на
которых, как вы считаете, возможно решение поставленной задачи. При этом вы
должны самостоятельно или с помощью преподавателя разобраться в работе
используемой микросхемы, при необходимости обращаясь к помощи (F1) при отмеченном цветом
изображении элемента.
З
а н я т и е п е р в о е
1.
а) Используя логические возможности элементов стенда, разработать схемы для
представленных ниже функций, реализовать их на стенде и проверить правильность
функционирования с помощью таблиц истинности, составленных по исходным
выражениям:
Таблицы
истинности
|
|
|
|
x |
x̅ |
|
0 |
1 |
|
1 |
0 |
|
|
||||
|
X1 |
X2 |
X3 |
X1X2X3 |
|
|
0 |
0 |
0 |
0 |
1 |
|
0 |
0 |
1 |
0 |
1 |
|
0 |
1 |
0 |
0 |
1 |
|
0 |
1 |
1 |
0 |
1 |
|
1 |
0 |
0 |
0 |
1 |
|
1 |
0 |
1 |
0 |
1 |
|
1 |
1 |
0 |
0 |
1 |
|
1 |
1 |
1 |
1 |
0 |
|
|
|||||||
|
X1 |
X2 |
X3 |
X4 |
X1X2 |
X3X4 |
X1X2+X3X4 |
X1X2 v X3X4 |
|
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
|
0 |
0 |
0 |
1 |
0 |
0 |
0 |
1 |
|
0 |
0 |
1 |
0 |
0 |
0 |
0 |
1 |
|
0 |
0 |
1 |
1 |
0 |
1 |
1 |
0 |
|
0 |
1 |
0 |
0 |
0 |
0 |
0 |
1 |
|
0 |
1 |
0 |
1 |
0 |
0 |
0 |
1 |
|
0 |
1 |
1 |
0 |
0 |
0 |
0 |
1 |
|
0 |
1 |
1 |
1 |
0 |
1 |
1 |
0 |
|
1 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
|
1 |
0 |
0 |
1 |
0 |
0 |
0 |
1 |
|
1 |
0 |
1 |
0 |
0 |
0 |
0 |
1 |
|
1 |
0 |
1 |
1 |
0 |
1 |
1 |
0 |
|
1 |
1 |
0 |
0 |
1 |
0 |
1 |
0 |
|
1 |
1 |
0 |
1 |
1 |
0 |
1 |
0 |
|
1 |
1 |
1 |
0 |
1 |
0 |
1 |
0 |
|
1 |
1 |
1 |
1 |
1 |
1 |
1 |
0 |
|
|
||
|
X1 |
X2 |
X1 v X2 |
|
0 |
0 |
0 |
|
0 |
1 |
1 |
|
1 |
0 |
1 |
|
1 |
1 |
1 |
|
|
||
|
X1 |
X2 |
X1 / X2 |
|
0 |
0 |
0 |
|
0 |
1 |
0 |
|
1 |
0 |
0 |
|
1 |
1 |
1 |


б)*
Измерить быстродействие инвертора (), подав на его вход
импульсы F или F2 и
наблюдая с помощью двухканального осциллографа одновременно входной и выходной
сигналы инвертора.
2. а)
Произвести синтез аналитически заданной в табл. 1 схемы, учитывая номер
варианта и максимально используя возможности имеющихся в библиотеке элементов
или ориентируясь при необходимости на элементы И-НЕ (с помощью правила де
Моргана исключив применение дизъюнкторов). Составить таблицу истинности по
исходному выражению и проверить функционирование схемы в статике, задавая
входные переменные с помощью моделей тумблеров (файл «gen—slov.ewb») или с
помощью генератора слов (файл «word—generator.ewb»).
Отрицания переменных следует сформировать с помощью дополнительных инверторов.
Таблица 1
|
|
||||||||||
|
X1 |
X2 |
X3 |
X̅1 |
X̅2 |
X̅3 |
X̅1X3 |
X1X3 |
X1X̅2X̅3 |
X̅1X3+X1X3+X1X̅2X̅3 |
y1 |
|
0 |
0 |
0 |
1 |
1 |
1 |
0 |
0 |
0 |
0 |
1 |
|
0 |
0 |
1 |
1 |
1 |
0 |
1 |
0 |
0 |
1 |
0 |
|
0 |
1 |
0 |
1 |
0 |
1 |
0 |
0 |
0 |
0 |
1 |
|
0 |
1 |
1 |
1 |
0 |
0 |
1 |
0 |
0 |
1 |
0 |
|
1 |
0 |
0 |
0 |
1 |
1 |
0 |
0 |
1 |
1 |
0 |
|
1 |
0 |
1 |
0 |
1 |
0 |
0 |
1 |
0 |
1 |
0 |
|
1 |
1 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
1 |
|
1 |
1 |
1 |
0 |
0 |
0 |
0 |
1 |
0 |
1 |
0 |

|
X1 |
X2 |
X3 |
X̅1 |
X̅3 |
X̅1 X̅3 |
X2 X̅3 |
Y1 |
|
0 |
0 |
0 |
1 |
1 |
1 |
0 |
1 |
|
0 |
0 |
1 |
1 |
0 |
0 |
0 |
0 |
|
0 |
1 |
0 |
1 |
1 |
1 |
1 |
1 |
|
0 |
1 |
1 |
1 |
0 |
0 |
0 |
0 |
|
1 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
|
1 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
|
1 |
1 |
0 |
0 |
1 |
0 |
1 |
1 |
|
1 |
1 |
1 |
0 |
0 |
0 |
0 |
0 |
б)*
Исследовать динамические свойства синтезированной схемы, используя для
формирования двоичных переменных сигналы с генератора стенда с учётом заданного
в таблице 1 соответствия переменных x1, x2, x3 сигналам
F, F2, F4, F8, F16 и
усложнив при необходимости выбранную схему входными инверторами для
формирования отрицаний переменных.
Необходимо
построить с помощью осциллографа временные диаграммы входных и выходных
сигналов всех используемых логических элементов. Измерить задержки в
формировании фронтов выходного сигнала. Синхронизацию осциллографа следует
брать от входного сигнала с минимальной частотой.
3. Реализовать
предложенную в табл. 2 схему, максимально используя возможности стенда,
допуская минимальные изменения. Составить по схеме таблицу истинности,
аналитические выражения и проверить правильность функционирования схемы.
Таблица 2
|
схема |
|
|
|
X1 |
X2 |
X3 |
X̅3 |
X̅3X1 |
X1+X2 |
X̅3X1 |
X̅3X1 (X1+X2) |
F=((C’A)'(A+B))’ |
|
0 |
0 |
0 |
1 |
0 |
0 |
1 |
0 |
1 |
|
0 |
0 |
1 |
0 |
0 |
0 |
1 |
0 |
1 |
|
0 |
1 |
0 |
1 |
0 |
1 |
1 |
1 |
0 |
|
0 |
1 |
1 |
0 |
0 |
1 |
1 |
1 |
0 |
|
1 |
0 |
0 |
1 |
1 |
1 |
0 |
0 |
1 |
|
1 |
0 |
1 |
0 |
0 |
1 |
1 |
1 |
0 |
|
1 |
1 |
0 |
1 |
1 |
1 |
0 |
0 |
1 |
|
1 |
1 |
1 |
0 |
0 |
1 |
1 |
1 |
0 |

4. Произвести
минимизацию полученных в пунктах 2 и 3 выражений и синтезировать новые
комбинационные схемы. Работоспособность синтезированных схем проверить на
стенде.

|
X1 |
X2 |
X3 |
X̅1 |
X̅2 |
X̅3 |
X̅1 X̅2 |
X1 X̅3 |
X̅1 X̅2+ X1 X̅3 |
|
0 |
0 |
0 |
1 |
1 |
1 |
1 |
0 |
1 |
|
0 |
0 |
1 |
1 |
1 |
0 |
1 |
0 |
1 |
|
0 |
1 |
0 |
1 |
0 |
1 |
0 |
0 |
0 |
|
0 |
1 |
1 |
1 |
0 |
0 |
0 |
0 |
0 |
|
1 |
0 |
0 |
0 |
1 |
1 |
0 |
1 |
1 |
|
1 |
0 |
1 |
0 |
1 |
0 |
0 |
0 |
0 |
|
1 |
1 |
0 |
0 |
0 |
1 |
0 |
1 |
1 |
|
1 |
1 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
З
а н я т и е в т о р о е
5. Произвести
минимизацию представленных в табл. 3 логических функций, осуществить синтез
схем, составить таблицы истинности и проверить моделированием на стенде.
|
Таблица 3 Функция |
||||||||||
|
X1 |
X2 |
X3 |
X̅1 |
X̅2 |
X̅3 |
X̅1X2 X̅3 |
X1X̅2X3 |
X1X2 X̅3 |
X1X2X3 |
Y3=X̅1X2 X̅3+ X1X̅2X3+ |
|
0 |
0 |
0 |
1 |
1 |
1 |
0 |
0 |
0 |
0 |
0 |
|
0 |
0 |
1 |
1 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
|
0 |
1 |
0 |
1 |
0 |
1 |
1 |
0 |
0 |
0 |
1 |
|
0 |
1 |
1 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
1 |
0 |
0 |
0 |
1 |
1 |
0 |
0 |
0 |
0 |
0 |
|
1 |
0 |
1 |
0 |
1 |
0 |
0 |
1 |
0 |
0 |
1 |
|
1 |
1 |
0 |
0 |
0 |
1 |
0 |
0 |
1 |
0 |
1 |
|
1 |
1 |
1 |
0 |
0 |
0 |
0 |
1 |
0 |
1 |
1 |
|
A’BC’+AB’C+ABC’+ABC |

|
X1 |
X2 |
X3 |
X̅3 |
X2X̅3 |
X1X3 |
X2X̅3+ X1X3 |
|
0 |
0 |
0 |
1 |
0 |
0 |
0 |
|
0 |
0 |
1 |
0 |
0 |
0 |
0 |
|
0 |
1 |
0 |
1 |
1 |
0 |
1 |
|
0 |
1 |
1 |
0 |
0 |
0 |
0 |
|
1 |
0 |
0 |
1 |
0 |
0 |
0 |
|
1 |
0 |
1 |
0 |
0 |
1 |
1 |
|
1 |
1 |
0 |
1 |
1 |
0 |
1 |
|
1 |
1 |
1 |
0 |
0 |
1 |
1 |
6. Для
функций, заданных в табл. 4, составить совершенные дизъюнктивные формы,
осуществить минимизацию, синтезировать и реализовать на компьютере полученные схемы.
Функции задаются номерами тех наборов, на которых функции равны единице.
Таблица 4
|
Номера |
|
0,1,4,5 A’B’C’+A’B’C+AB’C’+AB’C |
Запишем эту функцию в виде логического выражения:
F(X1,X2,X3)=( X̅1 X̅2 X̅3)+( X̅1 X̅2 X3)+( X1 X̅2 X̅3)+(X1 X̅2 X3). Проведем минимизацию
заданной функции.
(X̅1 X̅2 X̅3+X̅1 X̅2 X3)+( X1 X̅2 X̅3+X1 X̅2 X3)= X̅1 X̅2( X̅3+X3)+
+ X1 X̅2(X̅3+X3)= X̅1 X̅2+ X1 X̅2= (X̅1+X1)X̅2= X̅2

7.
Синтезировать схему одноразрядного комбинационного сумматора, собрать и проверить
функционирование по таблице истинности (Таблица истинности и булевы функции
суммы и переноса предложены в приложении 2).
Рассмотрим
задачу синтеза комбинационного одноразрядного двоичного сумматора, имеющего три
эквивалентных входа: ai,bi,pi и два выхода:
выход сигнала переноса в старший разряд pi+1 и выход
суммы в данном разряде si (рис.
32,а).
Функционирование сумматора можно задать таблицей истинности.
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||
|
а) |
б) |
|||||||||||||||||||||||||||||||||||||||||||||
|
Рис. |
3
8.
Составить таблицу истинности, синтезировать и испытать комбинационную схему с
двумя входами (x1, x2) 12211и
четырьмя выходами (y1, y2, y3, y4), которая
для каждого набора значений переменных формирует нуль на одном выходе,
соответствующем данному набору, а на остальных выходах при этом формирует единицу.
|
X1 |
X2 |
Y1 |
Y2 |
Y3 |
Y4 |
|
0 |
0 |
1 |
0 |
0 |
0 |
|
0 |
1 |
0 |
1 |
0 |
0 |
|
1 |
0 |
0 |
0 |
1 |
0 |
|
1 |
1 |
0 |
0 |
0 |
1 |


9*.
Составить таблицу истинности, синтезировать и испытать схему с двумя информационными
входами (x1, x2), одним
управляющим входом Z и одним выходом y, которая
пропускает на выход x1, если Z=0 (то
есть y=x1), и пропускает
на выход x2, если Z=1 (при
этом y=x2).
|
X1 |
X2 |
Z |
Y |
|
0 |
0 |
0 |
0 |
|
0 |
1 |
0 |
0 |
|
1 |
0 |
0 |
1 |
|
1 |
1 |
0 |
1 |
|
0 |
0 |
1 |
0 |
|
0 |
1 |
1 |
1 |
|
1 |
0 |
1 |
0 |
|
1 |
1 |
1 |
1 |


10*.
Составить таблицу истинности, синтезировать и испытать схему с информационным
входом x,
управляющим входом Z и выходом y, которая
реализует функцию, если Z=0 и
функцию при Z=1.
|
X |
Z |
Y |
|
0 |
0 |
0 |
|
0 |
1 |
1 |
|
1 |
0 |
1 |
|
1 |
1 |
0 |
11*.
Составить таблицы истинности и синтезировать комбинационные схемы,
функционирование которых задаётся словесным описанием (табл. 5). Выходной
сигнал y равен
единице при выполнении заданных условий. Под X и Z понимаются
двухразрядные двоичные числа: ;
. Таблицы истинности
составляются для четырех переменных: x1, x2; z1, z2.
Поскольку схема может оказаться сложной, проверку правильности работы её
целесообразно осуществить на компьютере.
Таблица 5
|
Условие: X>Z+01 |
|||||||
|
X1 |
X2 |
Z1 |
Z2 |
X |
Z |
Y |
|
|
0 |
0 |
0 |
0 |
00 |
00 |
0 |
|
|
0 |
0 |
0 |
1 |
00 |
01 |
0 |
|
|
0 |
0 |
1 |
0 |
00 |
10 |
0 |
|
|
0 |
0 |
1 |
1 |
00 |
11 |
0 |
|
|
0 |
1 |
0 |
0 |
01 |
00 |
0 |
|
|
0 |
1 |
0 |
1 |
01 |
01 |
0 |
|
|
0 |
1 |
1 |
0 |
01 |
10 |
0 |
|
|
0 |
1 |
1 |
1 |
01 |
11 |
0 |
|
|
1 |
0 |
0 |
0 |
10 |
00 |
1 |
|
|
1 |
0 |
0 |
1 |
10 |
01 |
0 |
|
|
1 |
0 |
1 |
0 |
10 |
10 |
0 |
|
|
1 |
0 |
1 |
1 |
10 |
11 |
0 |
|
|
1 |
1 |
0 |
0 |
11 |
00 |
1 |
|
|
1 |
1 |
0 |
1 |
11 |
01 |
1 |
|
|
1 |
1 |
1 |
0 |
11 |
10 |
0 |
|
|
1 |
1 |
1 |
1 |
11 |
11 |
0 |
|
Выводы. В данной лабораторной работе
изучили различные способы синтеза комбинационных
схем, разработаны схемы для заданных функций, выполнена проверка
правильности функционирования с помощью таблиц истинности, составленных по
исходным выражениям.
Дмитрий Михайлович Беляев
Эксперт по предмету «Информатика»
Задать вопрос автору статьи
Определение 1
Построение комбинационных схем — это реализация схемы при помощи набора логических элементов на основе таблицы истинности.
Введение
Формирование выходного сигнала на основании обработки входных данных в любом компьютерном оборудовании выполняется формирователями или цифровыми автоматами двух типов:
- Выполненными на основе комбинационных схем.
- Выполненными на основе схем с памятью.
Комбинационными схемами называются схемы, у которых сигналы на выходе $Y = (у_1, у_2,…, у_m)$ в каждый дискретный временной промежуток единообразно задаются набором сигналов на входе $X = (x_1, х_2,…, х_n)$, поступивших в этот же временной момент t. Используемый в комбинационных схемах метод информационной обработки является комбинационным, так как итоги обработки имеют зависимость только лишь от комбинационного набора входных сигналов и они образуются сразу при появлении сигналов на входе. И это обстоятельство объясняет главное достоинство комбинационных схем, а именно высокое быстродействие. Информационные преобразования могут быть однозначно описаны функциями логики типа Y = f(X).
Сдай на права пока
учишься в ВУЗе
Вся теория в удобном приложении. Выбери инструктора и начни заниматься!
Получить скидку 3 000 ₽
Все виды логических функций и реализующие их комбинационные схемы делятся на регулярные и нерегулярные структуры. Регулярные структуры подразумевают формирование схем так, что все их выходы реализуются аналогично предыдущим. В нерегулярных структурах такой аналогии нет. В области практической реализации проектов компьютеров специалистами приобретён громадный опытный потенциал по синтезированию разнообразных схем. Большинство регулярных структурных построений заложено в основание реализации некоторых интегральных схем малой и средней интеграционной степени или функциональных составляющих больших и сверх больших интегральных схем. Самыми распространёнными комбинационными схемами являются шифраторы и дешифраторы, модули сравнения, комбинационные сумматоры и многие другие.
Дешифраторы
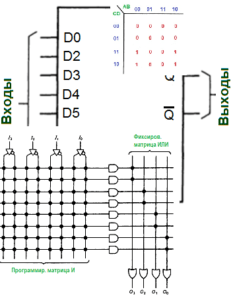
Дешифраторами являются комбинационные схемы, имеющие n входов и $т = 2^n$ выходов. Одиночный сигнал, сформированный на каком либо из m выходов, является однозначным соответствием комбинированного набора входных сигналов. К примеру, рассмотрим структуру дешифратора при n = 3, согласно таблице истинности, приведённой на рисунке ниже:
«Построение комбинационных схем» 👇
Рисунок 1. Таблица истинности. Автор24 — интернет-биржа студенческих работ
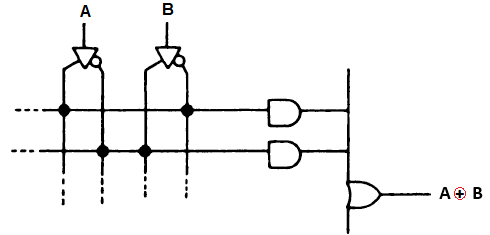
Дешифраторы повсеместно применяются в компьютерном оборудовании для того, чтобы выбрать информацию по заданному адресу, расшифровать код операции и так далее. Ниже приведены логические формулы данного дешифратора:
Рисунок 2. Логические формулы дешифратора. Автор24 — интернет-биржа студенческих работ
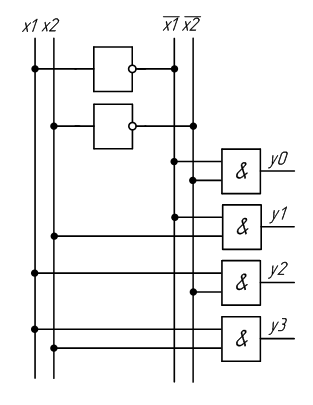
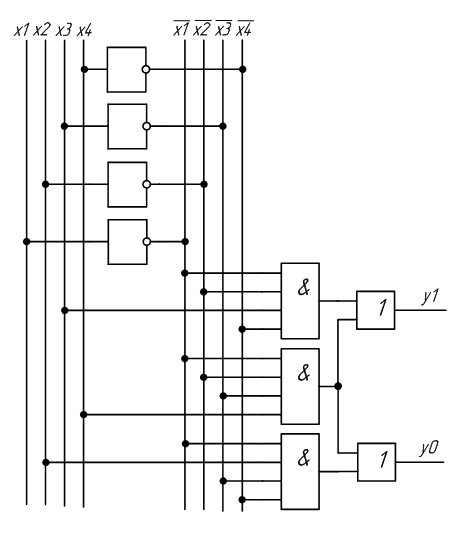
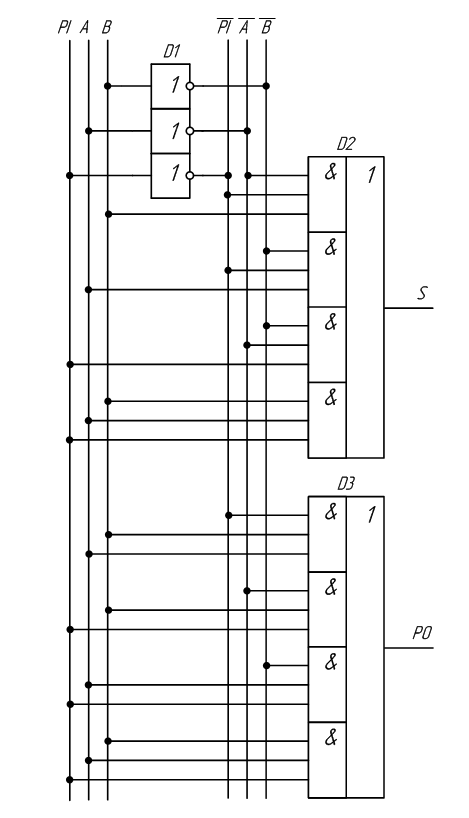
Данный дешифратор может быть реализован на основе логических элементов (И, НЕ), где кружки на выходе логических элементов обозначают логическое отрицание функций, которые реализуют элементы. Структурная схема дешифратора приведена на рисунке ниже и там же показано, как он отображается на принципиальной схеме электронной вычислительной машины:
Рисунок 3. Схема ЭВМ. Автор24 — интернет-биржа студенческих работ
Шифраторы осуществляют решение задачи, обратной дешифрации, то есть по нумерации сигнала на входе выполняется формирование однозначного комбинационного набора сигналов на выходе.
Сумматоры
Комбинационные сумматоры тоже считаются часто применяемым в компьютерном оборудовании элементом. Структурная организация и принцип действия сумматора определяются законами бинарного сложения. Принцип работы многоразрядного сумматора базируется на правилах одноразрядного суммирования двоичных чисел. Рассмотрим пример сумматора, который выполняет суммирование двух одноразрядных чисел аi и bi при отсутствии переноса из предыдущих разрядов. То есть, это может быть, к примеру, суммирование младшего разряда в бинарном коде. Таблица истинности для такой операции суммирования, приведена ниже:
Рисунок 4. Таблица истинности. Автор24 — интернет-биржа студенческих работ
Логические формулы сумматора:
Рисунок 5. Логические формулы сумматора. Автор24 — интернет-биржа студенческих работ
Здесь $S_i$ является функцией суммы одного разряда, а $Р_i$ является функцией наличия переноса. Она принимает значение, равное единице, то есть присутствует перенос в следующий разряд, когда $a_i = 1$ и $b_i = 1$.
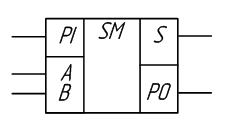
Схема такого полусумматора (а) и его обозначение в схеме компьютера (б) представлены на следующем рисунке:
Рисунок 6. Схема полусумматора. Автор24 — интернет-биржа студенческих работ
Формулы, заложенные в основание одноразрядных сумматоров, применяются и при реализации сумматоров, рассчитанных на большое количество разрядов. Отличие таблиц истинности одноразрядного сумматора (полусумматора) от таблицы истинности сумматоров, которые учитывают переносы, заключается в наличии дополнительного входа р, являющегося обозначением переноса из предыдущего разряда.
Схемы с памятью
Схемы с памятью считаются более сложными информационными преобразователями. Присутствие элемента памяти в схемной организации даёт возможность запоминания промежуточных состояний работы с сигналами и учёта их величин при последующих действиях. Формирование выходных сигналов $Y = (y_1,y_2,…,y_m)$ в таких схемных организациях осуществляется, помимо учёта набора входных сигналов $X = (х_1,х_2,…,х_п)$, ещё и с учётом набора состояний схем памяти $Q = (q_1,q_2,…,q_k)$. Для правильного учёта этого обстоятельства, вводится отличие текущего дискретного момента времени t и следующего временного момента (t+1). Обобщённая структурная организация схемы, имеющей внутреннюю память, представлена на рисунке ниже.
Рисунок 7. Обобщённая структурная организация схемы, имеющей внутреннюю память. Автор24 — интернет-биржа студенческих работ
Осуществление передачи величины Q между временными моментами t и (t+1) выполняется, как правило, с использованием памяти, имеющей две ступени, и специальных синхроимпульсов. Простейшим элементом памяти в компьютерном оборудовании являются триггерные схемы. В своё время эти компоненты заменили в электронных вычислительных машинах запоминающие элементы памяти, работающие на основе остаточной намагниченности ферритовых сердечников.
Рассмотрим пример построения элемента памяти на триггерной основе, который имеет два входа:
- R (Reset, что означает сброс), предназначенный для сброса триггера в исходное состояние.
- S (Set, что означает установка), предназначенный для перевода триггера в состояние запоминания единицы.
Если на триггер не поступают входные сигналы, то он обязан в том же состоянии до момента, пока не поступит сигнал на один из входов. На рисунке а) показана схема триггера, на рисунке б) обозначение на общих схемах и на рисунке в) диаграмма работы триггера.
Рисунок 8. Схемы и диаграмма. Автор24 — интернет-биржа студенческих работ
Находи статьи и создавай свой список литературы по ГОСТу
Поиск по теме

1 Цель работы
Целью работы является изучение принципов действия комбинационных схем: дешифратора, шифратора, преобразователя кода для семисегментного индикатора, мультиплексора, сумматора.
2 Краткие теоретические сведения
2.1 Дешифратор (декодер)
Дешифратор (декодер) служит для преобразования n-разрядного позиционного двоичного кода в единичный выходной сигнал на одном из 2n выходов. При каждой входной комбинации сигналов на одном из выходов появляется 1. Таким образом, по единичному сигналу на одном из выходов можно судить о входной кодовой комбинации. Таблица истинности для декодера с двумя входами изображена в таблице 2.1.
Таблица 2.1 – Таблица истинности двухразрядного дешифратора
| x1 | x2 | y0 | y1 | y2 | y3 |
| 0 | 0 | 1 | 0 | 0 | 0 |
| 0 | 1 | 0 | 1 | 0 | 0 |
| 1 | 0 | 0 | 0 | 1 | 0 |
| 1 | 1 | 0 | 0 | 0 | 1 |
Для построения схемы декодера по таблице истинности воспользуемся методикой, изложенной в лабораторной работе №1, выполняемой на стенде LESO2. Например, устройство должно иметь 4 выхода. Для каждого выхода записываем логическое выражение. На основе СДНФ:
y0 = x1·x2
y1 = x1·x2
y2 = x1·x2
y3 = x1·x2
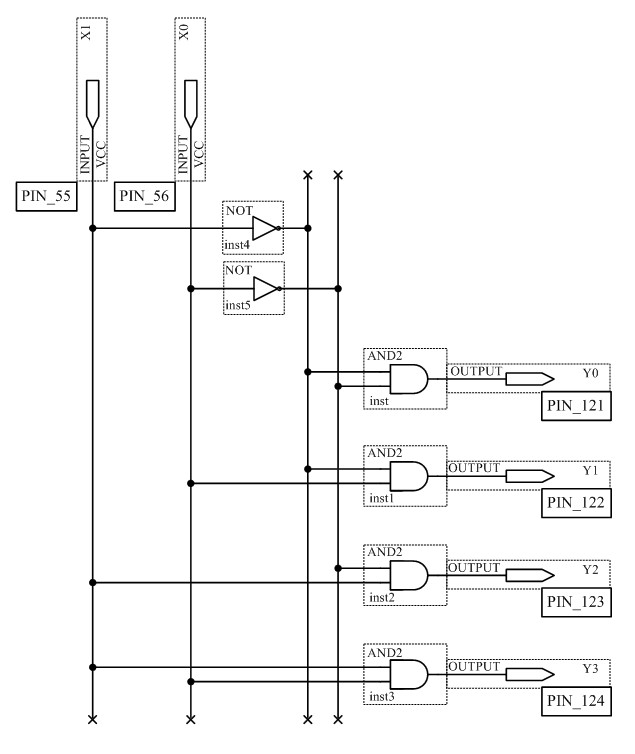
По этой системе выражений несложно построить схему требуемого дешифратора (рисунок 2.1).
Рисунок 2.1 – Схема дешифратора
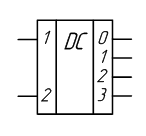
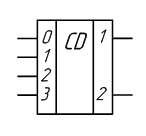
Условное графическое обозначение такого дешифратора изображено на рисунке 2.2.
Рисунок 2.2 – Условное графическое обозначение дешифратора
2.2 Шифратор (кодер)
Шифратор выполняет функцию, обратную декодеру (дешифратору), то есть преобразует непозиционный (унитарный) двоичный 2n разрядный код в n разрядный позиционный код. При подаче на один из входов единичного сигнала на выходе формируется соответствующий двоичный код. Составим таблицу истинности шифратора при n = 2.
Таблица 2.2 – Таблица истинности шифратора при n = 2
| x1 | x2 | x3 | x4 | y1 | y0 |
| 1 | 0 | 0 | 0 | 0 | 0 |
| 0 | 1 | 0 | 0 | 0 | 1 |
| 0 | 0 | 1 | 0 | 1 | 0 |
| 0 | 0 | 0 | 1 | 1 | 1 |
Синтезируем шифратор. Для этого запишем систему его собственных функций:
y1 = x1 · x2 · x3 · x4 + x1 · x2 · x3 ·x4
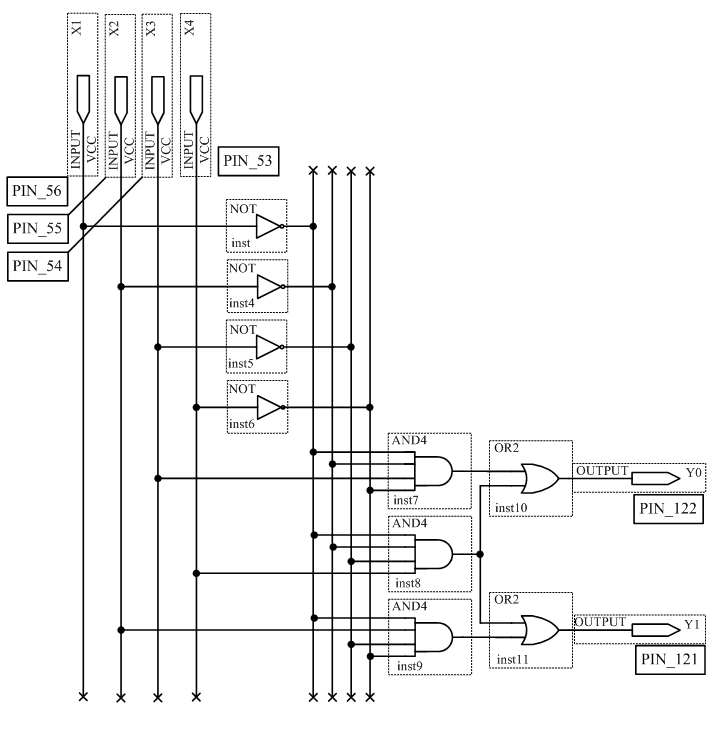
y0 = x1 · x2 · x3 · x4 + x1 · x2 · x3 ·x4
Рисунок 2.3 – Схема шифратора
Рисунок 2.4 – Условное графическое обозначение шифратора
2.3 Преобразователь кода для семисегментного индикатора
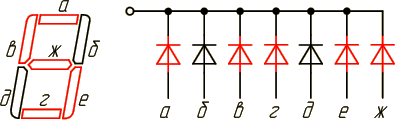
Наиболее широко преобразователи кодов известны применительно к цифровым индикаторам. Например, преобразователь 4-х разрядного позиционного двоичного кода в десятичные цифры. Имеется семи сегментный индикатор и с его помощью требуется высветить десять цифр.
Рисунок 2.5 – Семи сегментный индикатор
Очевидно, что двоичный код должен иметь не менее 4 — х разрядов (2^4 = 16, что больше 10). Составим таблицу истинности работы такого преобразователя.
Таблица 2.3 – Таблица истинности преобразователя
| Цифра | Двоичный код 8-4-2-1 | a | б | в | г | д | е | ж | |||
| 0 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 0 |
| 1 | 0 | 0 | 0 | 1 | 0 | 1 | 1 | 0 | 0 | 0 | 0 |
| 2 | 0 | 0 | 1 | 0 | 1 | 1 | 0 | 1 | 1 | 0 | 1 |
| 3 | 0 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 0 | 0 | 1 |
| 4 | 0 | 1 | 0 | 0 | 0 | 1 | 1 | 0 | 0 | 1 | 1 |
| 5 | 0 | 1 | 0 | 1 | 1 | 0 | 1 | 1 | 0 | 1 | 1 |
| 6 | 0 | 1 | 1 | 0 | 1 | 0 | 1 | 1 | 1 | 1 | 1 |
| 7 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 0 | 0 | 0 | 0 |
| 8 | 1 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
| 9 | 1 | 0 | 0 | 1 | 1 | 1 | 1 | 1 | 0 | 1 | 1 |
По ТИ несложно составить систему собственных функций для всех выходов, т.е. СДНФ, минимизировать её и составить принципиальную схему.
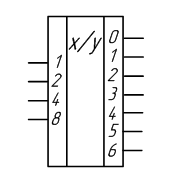
Рисунок 2.6 – Условное графическое обозначение преобразователя кода
2.4 Мультиплексор
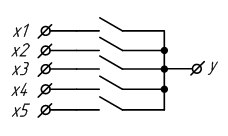
Мультиплексор – устройство, которое позволяет коммутировать один из 2^n информационных входов X на один выход Y под действием n управляющих (адресных) сигналов. На рисунке. 2.7 изображена упрощенная функциональная схема мультиплексора на идеализированных электронных ключах.
Рисунок 2.7 – Схема мультиплексора на идеализированных электронных ключах
В цифровых схемах требуется управлять ключами при помощи логических уровней. Поэтому желательно подобрать устройство, которое могло бы выполнять функции электронного ключа с управлением цифровым сигналом. Попробуем «заставить» работать в качестве электронного ключа уже знакомые нам логические элементы. Рассмотрим ТИ логического элемента «И». При этом один из входов логического элемента «И» будем рассматривать как информационный вход электронного ключа, а другой вход – как управляющий. Так как оба входа логического элемента «И» эквивалентны, то не важно какой из них будет управляющим входом. Пусть вход X будет управляющим, а Y – информационным. Для простоты рассуждений, разделим ТИ на две части в зависимости от уровня логического сигнала на управляющем входе X.
Таблица 2.4 – Таблица истинности
| y | x | Out |
| 0 0 |
0 1 |
0 0 |
| 1 1 |
0 1 |
0 1 |
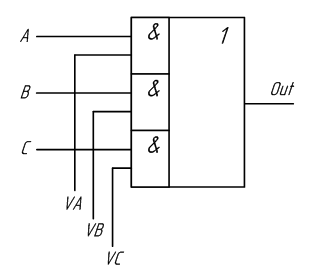
По таблице истинности отчётливо видно, что если на управляющий вход X подан нулевой логический уровень, сигнал, поданный на вход Y, на выход Out не проходит. При подаче на управляющий вход X логической единицы, сигнал, поступающий на вход Y, появляется на выходе Out. Это означает, что логический элемент «И» можно использовать в качестве электронного ключа. При этом не важно, какой из входов элемента «И» будет использоваться в качестве управляющего входа, а какой – в качестве информационного. Остается только объединить выходы элементов «И» на один общий выход. Это делается при помощи логического элемента «ИЛИ» точно так же как и при построении схемы по произвольной таблице истинности. Получившийся вариант схемы коммутатора с управлением логическими уровнями приведён на рисунке 2.8.
Рисунок 2.8 – Принципиальная схема мультиплексора, выполненная на логических элементах
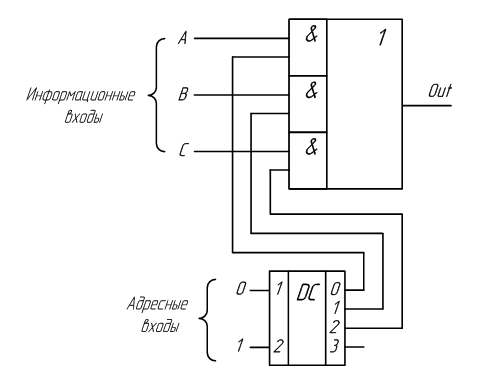
В схемах, приведенных на рисунках 2.7 и 2.8, можно одновременно включать несколько входов на один выход. Однако обычно это приводит к непредсказуемым последствиям. Кроме того, для управления таким коммутатором требуется много входов, поэтому в состав мультиплексора обычно включают двоичный дешифратор, как показано на рисунке 2.9. Такая схема позволяет управлять переключением информационных входов мультиплексора при помощи двоичных кодов, подаваемых на его управляющие входы. Количество информационных входов в таких схемах выбирают кратным степени числа два.
Рисунок 2.9 – Принципиальная схема мультиплексора, управляемого двоичным кодом
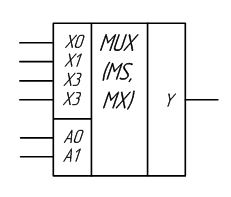
Условное графическое обозначение 4–х входового мультиплексора с управлением двоичным кодом приведено на рисунке 2.10. Входы A0 и A1 являются управляющими входами мультиплексора, определяющими адрес информационного входного сигнала, который будет соединён с выходным выводом мультиплексора Y. Информационные входные сигналы обозначены: X0, X1, X2 и X3.
Рисунок 2.10 – Условное графическое обозначение 4-х входового мультиплексора
В условном графическом обозначении названия информационных входов A, B, C и D заменены названиями X0, X1, X2 и X3, а название выхода Out заменено на название Y. Такое обозначение входов и выходов мультиплексора более распространено в отечественной литературе. Адресные входы обозначены как A0 и A1.
Об особенностях реализации мультиплесоров на языке Verilog можно почитать в статье:
Архитектура ПЛИС. Часть 2. Мультиплексор
2.5 Сумматор
Сумматор – узел компьютера, предназначенный для сложения двоичных чисел. Построение двоичных сумматоров обычно начинается с сумматора по модулю 2.
Сумматор по модулю 2
Схема сумматора по модулю 2 совпадает со схемой исключающее «ИЛИ».
Таблица 2.5 – Таблица истинности сумматора по модулю 2
| x1 | x2 | y |
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
Логическое выражение, описывающее сумматор по модулю 2:
y = x1 · x2 + x1 · x2
Рисунок 2.11 – Условное графическое обозначение сумматора по модулю 2
На основе логического уравнения, описывающего этот элемент можно синтезировать схему:
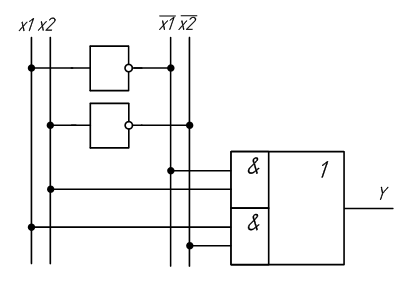
Рисунок 2.12 – Схема сумматора по модулю 2
Сумматор по модулю 2 выполняет суммирование без учёта переноса. В обычном двоичном сумматоре требуется учитывать перенос, поэтому требуются схемы, позволяющие формировать перенос в следующий двоичный разряд. Таблица истинности такой схемы, называемой полусумматором, приведена в таблице 2.6.
Таблица 2.6 – Таблица истинности полусумматора
| A | B | S | P0 |
| 0 | 0 | 0 | 0 |
| 0 | 1 | 1 | 0 |
| 1 | 0 | 1 | 0 |
| 1 | 1 | 0 | 1 |
Здесь A и B – слагаемые;
S – сумма;
P0 – перенос в старший разряд (выход переноса Pout).
Запишем систему собственных функций для полусумматора:
S = A · B + A · B
P0 = A · B
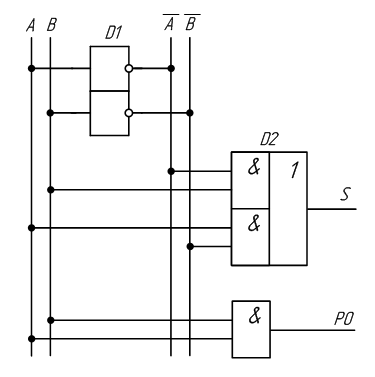
Рисунок 2.13 – Принципиальная схема, реализующая таблицу истинности полусумматора
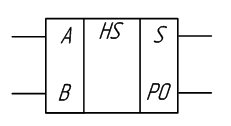
Рисунок 2.14 – Изображение полусумматора на схемах
Полный сумматор.
Схема полусумматора формирует перенос в старший разряд, но не может учитывать перенос из младшего разряда. При сложении многоразрядных двоичных чисел необходимо складывать три цифры в каждом разряде – 2 слагаемых и единицу переноса из предыдущего разряда PI.
Таблица 2.7 – Таблица истинности полного сумматора
| PI | A | B | S | PO |
| 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 1 | 0 |
| 0 | 1 | 0 | 1 | 0 |
| 0 | 1 | 1 | 0 | 1 |
| 1 | 0 | 0 | 1 | 0 |
| 1 | 0 | 1 | 0 | 1 |
| 1 | 1 | 0 | 0 | 1 |
| 1 | 1 | 1 | 1 | 1 |
PI – вход 1 переноса из предыдущего разряда,
PO – выход 1 переноса в старший разряд.
На основании таблицы истинности запишем систему собственных функций для каждого выхода:
S = A · B · PI + A · B · PI + A · B · PI + A · B · PI
PO = A · B · PI + A · B · PI + A · B · PI + A · B · PI
В результате получим схему полного сумматора (рисунок 2.15).
Рисунок 2.15 – Принципиальная схема, реализующая таблицу истинности полного двоичного одноразрядного сумматора
Рисунок 2.16 – Изображение полного двоичного одноразрядного сумматора на схемах
3 Задание к работе
3.1 Исследовать принцип работы дешифратора 2 x 4
Сконфигурировать ПЛИС в соответствии с рисунком 3.1. Подключить к входам X0 и X1 переключатели S7 и S8, а к выходам Y0, Y1, Y2, Y3 светодиодные индикаторы LED5, LED6, LED7, LED8. Для этого подключить входы и выходы дешифратора к соответствующим ножкам ПЛИС.
Рисунок 3.1 – Схема дешифратора
Подавая все возможные комбинации логических уровней на входы X0, X1 с помощью ключей S7, S8 и наблюдая за состояниями светодиодных индикаторов LED5, LED6, LED7, LED8, заполните таблицу истинности дешифратора.
Таблица 3.1 – Таблица дешифратора
| x1 | x2 | y0 | y1 | y2 | y3 |
| 0 | 0 | ||||
| 0 | 1 | ||||
| 1 | 0 | ||||
| 1 | 1 |
3.2 Исследовать принцип работы шифратора 4×2
Сконфигурировать ПЛИС в соответствии с рисунком 3.2.
Рисунок 3.2 – Схема шифратора 4×2
Подключить к входам X1, X2, X3, X4 переключатели S8, S7, S6, S5, а к выходам Y0, Y1 светодиодные индикаторы LED8, LED7. Для этого подключить входы и выходы дешифратора к соответствующим ножкам ПЛИС. Подавая все возможные комбинации логических уровней на входы X1, X2, X3, X4 с помощью ключей S8, S7, S6, S5 и наблюдая за состояниями светодиодных индикаторов LED7, LED8, заполните таблицу истинности шифратора.
Таблица 3.2 – Таблица истинности шифратора
| x1 | x2 | x3 | x4 | y1 | y0 |
| 1 | 0 | 0 | 0 | ||
| 0 | 1 | 0 | 0 | ||
| 0 | 0 | 1 | 0 | ||
| 0 | 0 | 0 | 1 |
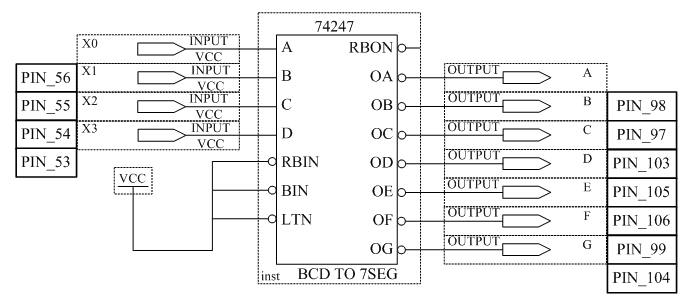
3.3 Исследовать работу преобразователя кода для семисегментного индикатора.
Составить таблицу истинности преобразователя кода (таблица. 3.3).
Собрать схему, изображенную на рисунке 3.3.
Таблица 3.3 – Таблица истинности преобразователя
| x3 | x2 | x1 | x0 | A | B | C | D | E | F | G |
| 0 | 0 | 0 | 0 | |||||||
| 0 | 0 | 0 | 1 | |||||||
| 0 | 0 | 1 | 0 | |||||||
| 0 | 0 | 1 | 1 | |||||||
| 0 | 1 | 0 | 0 | |||||||
| 0 | 1 | 0 | 1 | |||||||
| 0 | 1 | 1 | 0 | |||||||
| 0 | 1 | 1 | 1 | |||||||
| 1 | 0 | 0 | 0 | |||||||
| 1 | 0 | 0 | 1 |
Рисунок 3.3 – Схема преобразователя кода для семисегментного индикатора
Подавая с помощью ключей S8, S7, S6, S5 различные кодовые комбинации на входы X0, X1, X2, X3 определить цифры, высвечиваемые на индикаторе. По результатам эксперимента заполнить таблицу 3.4.
Таблица 3.4 – Таблица, описывающая работу преобразователя кода для семисегментного индикатора
| x3 | x2 | x1 | x0 | Показание индикатора |
| 0 | 0 | 0 | 0 | |
| 0 | 0 | 0 | 1 | |
| 0 | 0 | 1 | 0 | |
| 0 | 0 | 1 | 1 | |
| 0 | 1 | 0 | 0 | |
| 0 | 1 | 0 | 1 | |
| 0 | 1 | 1 | 0 | |
| 0 | 1 | 1 | 1 | |
| 1 | 0 | 0 | 0 | |
| 1 | 0 | 0 | 1 |
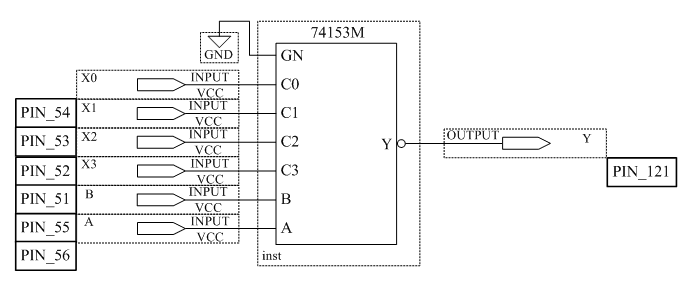
3.4 Исследовать работу мультиплексора 4×1
Сконфигурировать ПЛИС в соответствии с рисунком 3.4.
Рисунок 3.4 – Схема мультиплексора 4×1
Поочередно устанавливая все возможные кодовые комбинации на адресных входах A и B, определите номера коммутируемых каналов. Номер коммутируемого канала определяется путем поочерёдного подключения к входам X0, X2, X3, X4 уровня логической единицы и наблюдения за выходом Y. Заполните таблицу 3.5.
Таблица 3.5 – Таблица, описывающая работу мультиплексора
| B | A | Номер коммутируемого канала |
| 0 | 0 | |
| 0 | 1 | |
| 1 | 0 | |
| 1 | 1 |
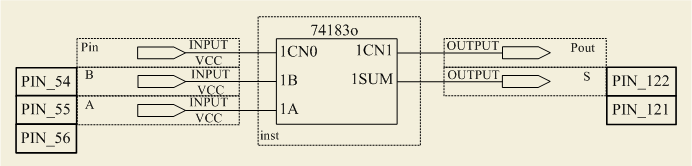
3.5 Исследовать схему сумматора
Сконфигурировать ПЛИС в соответствии с рисунком 3.5. Здесь Pin, Pout соответственно вход и выход единицы переноса, A и B – слагаемые, S – сумма.
Рисунок 3.5 – Схема сумматора
Заполнить таблицу истинности сумматора (таблица 3.6).
Таблица 2.7 – Таблица истинности полного сумматора
| Pin | B | A | Pout |
| 0 | 0 | 0 | |
| 0 | 0 | 1 | |
| 0 | 1 | 0 | |
| 0 | 1 | 1 | |
| 1 | 0 | 0 | |
| 1 | 0 | 1 | |
| 1 | 1 | 0 | |
| 1 | 1 | 1 |
4 Содержание отчета
- Цель работы.
- Схемы исследования дешифратора, шифратора, преобразователя кода для семисегментного индикатора, мультиплексора, сумматора.
- Таблицы истинности для каждой схемы.
- Выводы по каждому заданию.
5 Контрольные вопросы
- Принцип работы дешифратора?
- Как синтезировать дешифратор с произвольной разрядностью?
- Как работает шифратор?
- Изобразите таблицу истинности шифратора.
- Как работает преобразователь кода для семисегментного индикатора?
- Как устроен семи сегментный индикатор?
- Как работает мультиплексор?
- Как в лабораторной работе проводилось исследование мультиплексора?
- Как работает сумматор?
- Изобразите таблицу истинности шифратора.
- Что такое единица переноса?
Построение таблицы истинности. СДНФ. СКНФ. Полином Жегалкина.
Онлайн калькулятор позволяет быстро строить таблицу истинности для произвольной булевой функции или её вектора, рассчитывать совершенную дизъюнктивную и совершенную конъюнктивную нормальные формы, находить представление функции в виде полинома Жегалкина, строить карту Карно и классифицировать функцию по классам Поста.
Калькулятор таблицы истинности, СКНФ, СДНФ, полинома Жегалкина
введите функцию или её вектор
Скрыть клавиатуру
∨
∧
¬
⊕
→
≡
↓
↑
0
1
a
b
c
x
y
z
(
)
X1
X2
X3
X4
X5
X6
Показать настройки
Таблица истинности
СКНФ
СДНФ
Полином Жегалкина
Классификация Поста
Минимизация, карта Карно
Фиктивные переменные
С решением
Построить
Построено таблиц, форм:
Как пользоваться калькулятором
- Введите в поле логическую функцию (например, x1 ∨ x2) или её вектор (например, 10110101)
- Укажите действия, которые необходимо выполнить с помощью переключателей
- Укажите, требуется ли вывод решения переключателем «С решением»
- Нажмите на кнопку «Построить»
Видеоинструкция к калькулятору
Используемые символы
В качестве переменных используются буквы латинского и русского алфавитов (большие и маленькие), а также цифры, написанные после буквы (индекс переменной). Таким образом, именами переменных будут: a, x, a1, B, X, X1, Y1, A123 и так далее.
Для записи логических операций можно использовать
как обычные символы клавиатуры (*, +, !, ^, ->, =), так и символы, устоявшиеся в литературе (∧, ∨, ¬, ⊕, →, ≡). Если на вашей клавиатуре отсутствует нужный символ операции, то используйте клавиатуру калькулятора (если она не видна, нажмите «Показать клавиатуру»), в которой доступны как все логические операции, так и набор наиболее часто используемых переменных.
Для смены порядка выполнения операций используются круглые скобки ().
Обозначения логических операций
- И (AND):
&•∧* - ИЛИ (OR):
∨+ - НЕ (NOT):
¬! - Исключающее ИЛИ (XOR):
⊕^ - Импликация:
->→=> - Эквивалентность:
=~≡<=> - Штрих Шеффера:
↑| - Стрелка Пирса:
↓
Что умеет калькулятор
- Строить таблицу истинности по функции
- Строить таблицу истинности по двоичному вектору
- Строить совершенную конъюнктивную нормальную форму (СКНФ)
- Строить совершенную дизъюнктивную нормальную форму (СДНФ)
- Строить полином Жегалкина (методами Паскаля, треугольника, неопределённых коэффициентов)
- Определять принадлежность функции к каждому из пяти классов Поста
- Строить карту Карно
- Минимизировать ДНФ и КНФ
- Искать фиктивные переменные
Что такое булева функция
Булева функция f(x1, x2, ... xn) — это любая функция от n переменных x1, x2, … xn, в которой её аргументы принимают одно из двух значений: либо 0, либо 1, и сама функция принимает значения 0 или 1. То есть это правило, по которому произвольному набору нулей и единиц ставится в соответствие значение 0 или 1. Подробнее про булевы функции можно посмотреть на Википедии.
Что такое таблица истинности?
Таблица истинности — это таблица, описывающая логическую функцию, а именно отражающую все значения функции при всех возможных значениях её аргументов. Таблица состоит из n+1 столбцов и 2n строк, где n — число используемых переменных. В первых n столбцах записываются всевозможные значения аргументов (переменных) функции, а в n+1-ом столбце записываются значения функции, которые она принимает на данном наборе аргументов.
Довольно часто встречается вариант таблицы, в которой число столбцов равно n + число используемых логических операций. В такой таблице также первые n столбцов заполнены наборами аргументов, а оставшиеся столбцы заполняются значениями подфункций, входящих в запись функции, что позволяет упростить расчёт конечного значения функции за счёт уже промежуточных вычислений.
Логические операции
Логическая операция — операция над высказываниями, позволяющая составлять новые высказывания путём соединения более простых. В качестве основных операций обычно называют конъюнкцию (∧ или &), дизъюнкцию (∨ или |), импликацию (→), отрицание (¬), эквивалентность (=), исключающее ИЛИ (⊕).
Таблица истинности логических операций
Как задать логическую функцию
Есть множество способов задать булеву функцию:
- таблица истинности
- характеристические множества
- вектор значений
- матрица Грея
- формулы
Рассмотрим некоторые из них:
Чтобы задать функцию через вектор значений необходимо записать вектор из 2n нулей и единиц, где n — число аргументов, от которых зависит функция. Например, функцию двух аргументов можно задать так: 0001 (операция И), 0111 (операция ИЛИ).
Чтобы задать функцию в виде формулы, необходимо записать математическое выражение, состоящее из аргументов функции и логических операций. Например, можно задать такую функцию: a∧b ∨ b∧c ∨ a∧c
Способы представления булевой функции
С помощью формул можно получать огромное количество разнообразных функций, причём с помощью разных формул можно получить одну и ту же функцию. Иногда бывает весьма полезно узнать, как построить ту или иную функцию, используя лишь небольшой набор заданных операций или используя как можно меньше произвольных операций. Рассмотрим основные способы задания булевых функций:
- Совершенная дизъюнктивная нормальная форма (СДНФ)
- Совершенная конъюнктивная нормальная форма (СКНФ)
- Алгебраическая нормальная форма (АНФ, полином Жегалкина)
Совершенная дизъюнктивная нормальная форма (ДНФ)
Простая конъюнкция — это конъюнкция некоторого конечного набора переменных, или их отрицаний, причём каждая переменная встречается не более одного раза.
Дизъюнктивная нормальная форма (ДНФ) — это дизъюнкция простых конъюнкций.
Совершенная дизъюнктивная нормальная форма (СДНФ) — ДНФ относительно некоторого заданного конечного набора переменных, в каждую конъюнкцию которой входят все переменные данного набора.
Например, ДНФ является функция ¬abc ∨ ¬a¬bc ∨ ac, но не является СДНФ, так как в последней конъюнкции отсутствует переменная b.
Совершенная конъюнктивная нормальная форма (КНФ)
Простая дизъюнкция — это дизъюнкция одной или нескольких переменных, или их отрицаний, причём каждая переменная входит в неё не более одного раза.
Конъюнктивная нормальная форма (КНФ) — это конъюнкция простых дизъюнкций.
Совершенная конъюнктивная нормальная форма (СКНФ) — КНФ относительно некоторого заданного конечного набора переменных, в каждую дизъюнкцию которой входят все переменные данного набора.
Например, КНФ является функция (a ∨ b) ∧ (a ∨ b ∨ c), но не является СДНФ, так как в первой дизъюнкции отсутствует переменная с.
Алгебраическая нормальная форма (АНФ, полином Жегалкина)
Алгебраическая нормальная форма, полином Жегалкина — это форма представления логической функции в виде полинома с коэффициентами вида 0 и 1, в котором в качестве произведения используется операция конъюнкции, а в качестве сложения — исключающее ИЛИ.
Примеры полиномов Жегалкина: 1, a, a⊕b, ab⊕a⊕b⊕1
Алгоритм построения СДНФ для булевой функции
- Построить таблицу истинности для функции
- Найти все наборы аргументов, на которых функция принимает значение 1
- Выписать простые конъюнкции для каждого из наборов по следующему правилу: если в наборе переменная принимает значение 0, то она входит в конъюнкцию с отрицанием, а иначе без отрицания
- Объединить все простые конъюнкции с помощью дизъюнкции
Алгоритм построения СКНФ для булевой функции
- Построить таблицу истинности для функции
- Найти все наборы аргументов, на которых функция принимает значение 0
- Выписать простые дизъюнкции для каждого из наборов по следующему правилу: если в наборе переменная принимает значение 1, то она входит в дизъюнкцию с отрицанием, а иначе без отрицания
- Объединить все простые дизъюнкции с помощью конъюнкции
Алгоритм построения полинома Жегалкина булевой функции
Есть несколько методов построения полинома Жегалкина, в данной статье рассмотрим наиболее удобный и простой из всех.
- Построить таблицу истинности для функции
- Добавить новый столбец к таблице истинности и записать в 1, 3, 5… ячейки значения из тех же строк предыдущего столбца таблицы истинности, а к значениям в строках 2, 4, 6… прибавить по модулю два значения из соответственно 1, 3, 5… строк.
- Добавить новый столбец к таблице истинности и переписать в новый столбец значения 1, 2, 5, 6, 9, 10… строк, а к 3, 4, 7, 8, 11, 12… строкам аналогично предыдущему пункту прибавить переписанные значения.
- Повторить действия каждый раз увеличивая в два раза количество переносимых и складываемых элементов до тех пор, пока длина не станет равна числу строк таблицы.
- Выписать булевы наборы, на которых значение последнего столбца равно единице
- Записать вместо единиц в наборах имена переменных, соответствующие набору (для нулевого набора записать единицу) и объединить их с помощью операции исключающего ИЛИ.
Примеры построения различных представлений логических функций
Построим совершенные дизъюнктивную и дизъюнктивную нормальные формы, а также полином Жегалкина для функции трёх переменных F = ¬ab∨¬bc∨ca
1. Построим таблицу истинности для функции
Построение совершенной дизъюнктивной нормальной формы:
Найдём наборы, на которых функция принимает истинное значение: { 0, 0, 1 } { 0, 1, 0 } { 0, 1, 1 } { 1, 0, 1 } { 1, 1, 1 }
В соответствие найденным наборам поставим элементарные конъюнкции по всем переменным, причём если переменная в наборе принимает значение 0, то она будет записана с отрицанием:
K1: { 0, 0, 1 } — ¬a¬bc
K2: { 0, 1, 0 } — ¬ab¬c
K3: { 0, 1, 1 } — ¬abc
K4: { 1, 0, 1 } — a¬bc
K5: { 1, 1, 1 } — abc
Объединим конъюнкции с помощью дизъюнкции и получим совершенную дизъюнктивную нормальную форму:
K1 ∨ K2 ∨ K3 ∨ K4 ∨ K5 = ¬a¬bc ∨ ¬ab¬c ∨ ¬abc ∨ a¬bc ∨ abc
Построение совершенной конъюнктивной нормальной формы:
Найдём наборы, на которых функция принимает ложное значение: { 0, 0, 0 } { 1, 0, 0 } { 1, 1, 0 }
В соответствие найденным наборам поставим элементарные дизъюнкции по всем переменным, причём если переменная в наборе принимает значение 1, то она будет записана с отрицанием:
D1: { 0, 0, 0 } — a∨b∨c
D2: { 1, 0, 0 } — ¬a∨b∨c
D3: { 1, 1, 0 } — ¬a∨¬b∨c
Объединим дизъюнкции с помощью конъюнкции и получим совершенную конъюнктивную нормальную форму:
D1 ∧ D2 ∧ D3 = (a∨b∨c) ∧ (¬a∨b∨c) ∧ (¬a∨¬b∨c)
Построение полинома Жегалкина:
Добавим новый столбец к таблице истинности и запишем в 1, 3, 5 и 7 строки значения из тех же строк предыдущего столбца таблицы истинности, а значения в строках 2, 4, 6 и 8 сложим по модулю два со значениями из соответственно 1, 3, 5 и 7 строк:
Добавим новый столбец к таблице истинности и запишем в 1 и 2, 5 и 6 строки значения из тех же строк предыдущего столбца таблицы истинности, а значения в строках 3 и 4, 7 и 8 сложим по модулю два со значениями из соответственно 1 и 2, 5 и 6 строк:
Добавим новый столбец к таблице истинности и запишем в 1 2, 3 и 4 строки значения из тех же строк предыдущего столбца таблицы истинности, а значения в строках 5, 6, 7 и 8 сложим по модулю два со значениями из соответственно 1, 2, 3 и 4 строк:
Окончательно получим такую таблицу:
Выпишем наборы, на которых получившийся вектор принимает единичное значение и запишем вместо единиц в наборах имена переменных, соответствующие набору (для нулевого набора следует записать единицу):
{ 0, 0, 1 } — c, { 0, 1, 0 } — b, { 0, 1, 1 } — bc, { 1, 1, 0 } — ab, { 1, 1, 1 } — abc
Объединяя полученные конъюнкции с помощью операции исключающего или, получим полином Жегалкина: c⊕b⊕bc⊕ab⊕abc