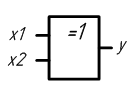Мультиплексор –
это устройство,
обеспечивающее коммутацию на выходе
одного из нескольких информационных
входных сигналов в соответствии с
заданным кодом на управляющих входах.
Такая схема
позволяет управлять переключением
информационных входов мультиплексора
при помощи двоичных кодов, подаваемых
на его управляющие входы. Количество
информационных входов в таких схемах
выбирают кратным степени числа два.
Таблица истинности
для мультиплексора с двумя управляющими
входами изображена в таблице 2.3.
Таблица 2.3 –
Таблица истинности для мультиплексора
|
D |
x2 |
x1 |
|
z |
0 |
0 |
|
z |
0 |
1 |
|
z |
1 |
0 |
|
z |
1 |
1 |
Условное графическое
обозначение одного из вариантов
мультиплексора (рис.23).
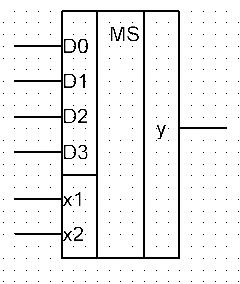
Рис. 23. Мультиплексор
D0,
D1,
D2,
D3
– информационные входы, а х1 и х2 –
управляющие.
Пример структурной
схемы мультиплексора (рис.24).
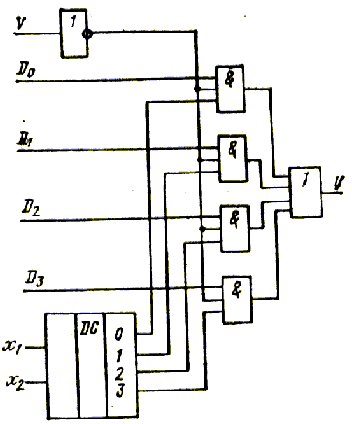
Рис. 24. Схема
мультиплексора.
Создание
принципиальной схемы
Всё делаем аналогично
методике создания схем шифратора и
дешифратора.
Создадим
новый проект, задаем название FPGA_lab2MS.
Вызываем мастер создания нового
источника New
Source Wizard,
чтобы создать новую схему Schematic,
необходимую для дальнейшей работы.
Зададим имя нового модуля, File
name
– MS.
Нарисуем
принципиальную схему мультиплексора
(рис.25). Данная схема содержит встроенную
схему дешифратора, методика создания
которого приведена выше.
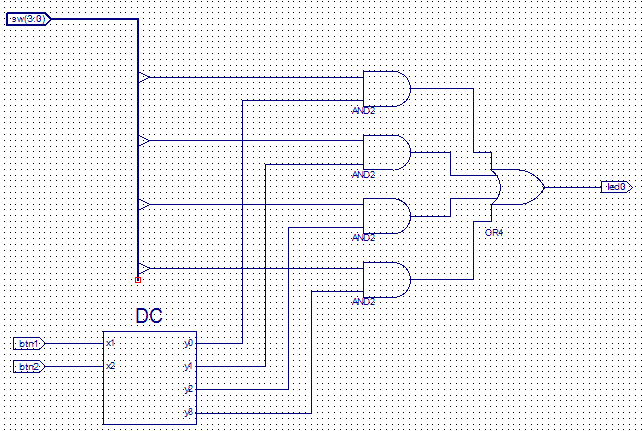
Рис. 25. Принципиальная
схема мультиплексора.
Теперь
нам необходимо представить данную схему
мультиплексора в виде отдельного
элемента, назовём его МS.
На главной панели выбираем вкладку
ToolsSymbol
WizardОткроется
окно (рис.26)
В строке Using
schematic
выберем
имя элемента – MSNextОткроется
окно (рис.27) В этом окне заданы параметры
нашего мультиплексора.
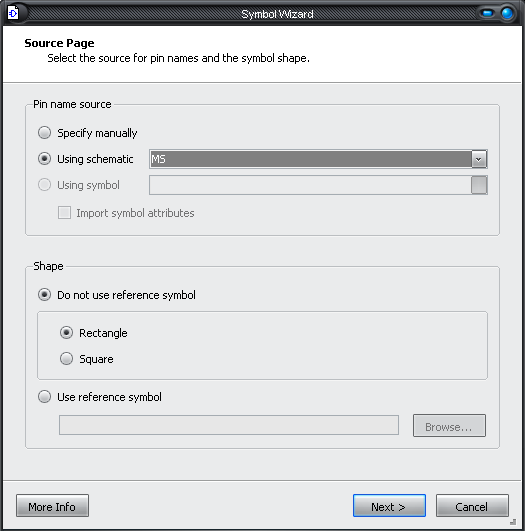
Рис. 26

Рис. 27
Далее нажимаем
NextFinish
элемент создан (рис.28). Новый элемент
добавился в библиотеку элементов и
теперь мы можем его использовать в любой
схеме.
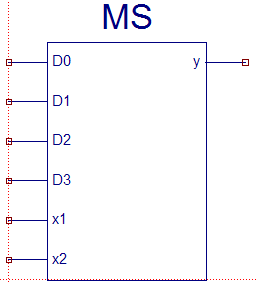
Рис. 28
Вызываем
мастер создания нового источника New
Source Wizard,
чтобы создать новую схему Schematic,
необходимую для дальнейшей работы.
Зададим имя нового модуля, File
name
–Lab2_schema.
На основе нового элемента MS
начертите
схему (рис.29).

Рис. 29
Остаётся создать
файл param
с расширением *.ucf.
В нём опишем
привязку выводов проекта к входам-выводам
кристалла. Пропишем следующие строки
(рис.30).

Рис. 30
Далее необходимо
выполнить проверку работоспособности
схемы. А так же написать программу на
VHDL,
которая будет описывать работу
мультиплексора.
2.4 Демультиплексор
Представляет
собой цифровое устройство для коммутации
информационного входного сигнала на
один из нескольких выходов в соответствии
с заданным кодом на управляющих входах,
т.е. решают задачи, обратные
мультиплексированию. Условное графическое
обозначение демультиплексора с четырьмя
информационными выходами (рис.31).
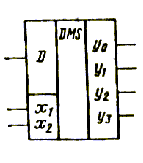
Рис. 31
Таблица истинности
для демультиплексора изображена в
таблице 2.4.
Таблица 2.4 –
Таблица истинности для демультиплексора
|
D |
x2 |
x1 |
y3 |
y2 |
y1 |
y0 |
|
z |
0 |
0 |
0 |
0 |
0 |
z |
|
z |
0 |
1 |
0 |
0 |
z |
0 |
|
z |
1 |
0 |
0 |
z |
0 |
0 |
|
z |
1 |
1 |
z |
0 |
0 |
0 |
Создание
принципиальной схемы
Всё делаем аналогично
методике создания схемы мультиплексора.
Создадим
новый проект, задаем название FPGA_lab2DMS.
Вызываем мастер создания нового
источника New
Source Wizard,
чтобы создать новую схему Schematic,
необходимую для дальнейшей работы.
Зададим имя нового модуля, File
name
– DMS.
Нарисуем
принципиальную схему демультиплексора
(рис.32). Данная схема содержит встроенную
схему дешифратора, методика создания
которого была приведена выше.
Теперь
нам необходимо представить данную схему
мультиплексора в виде отдельного
элемента, назовём его DМS.
На главной панели выбираем вкладку
ToolsSymbol
WizardОткроется
окно (рис.33)
В строке Using
schematic
выберем
имя элемента – DMSNextОткроется
окно (рис.34) В этом окне заданы параметры
нашего демультиплексора.
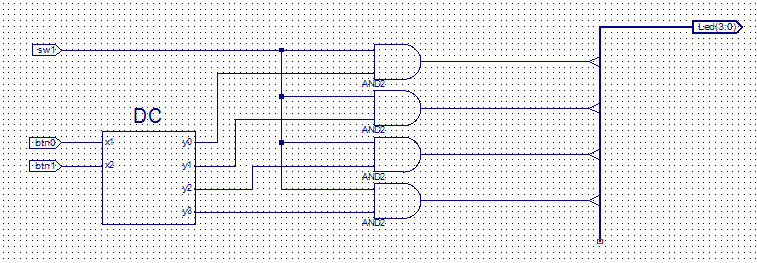
Рис. 32
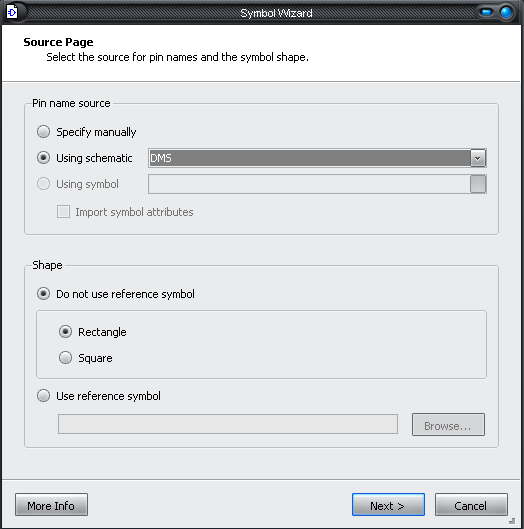
Рис.33
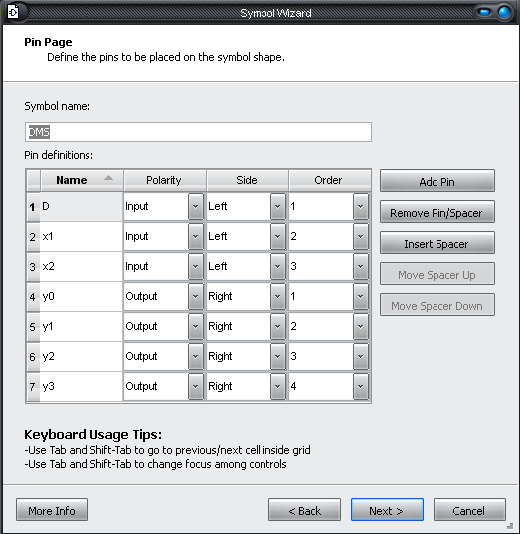
Рис. 34
Далее нажимаем
NextFinish
элемент создан (рис.35). Новый элемент
добавился в библиотеку элементов и
теперь мы можем его использовать в любой
схеме.
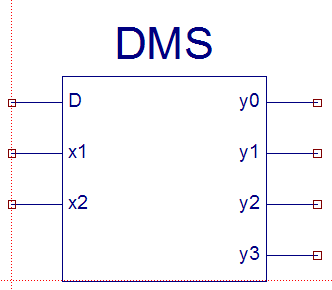
Рис. 35
Вызываем
мастер создания нового источника New
Source Wizard,
чтобы создать новую схему Schematic,
необходимую для дальнейшей работы.
Зададим имя нового модуля, File
name
–Lab2_schema.
На основе нового элемента DMS
начертите
схему (рис.36).
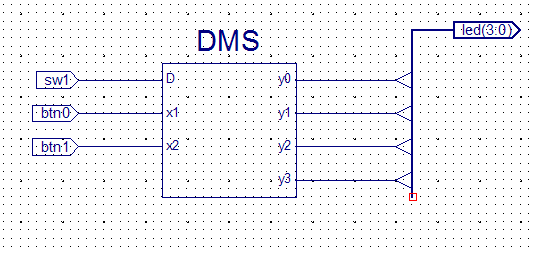
Рис. 36
Остаётся создать
файл param
с расширением *.ucf.
В нём опишем
привязку выводов проекта к входам-выводам
кристалла. Пропишем следующие строки
(рис.37).
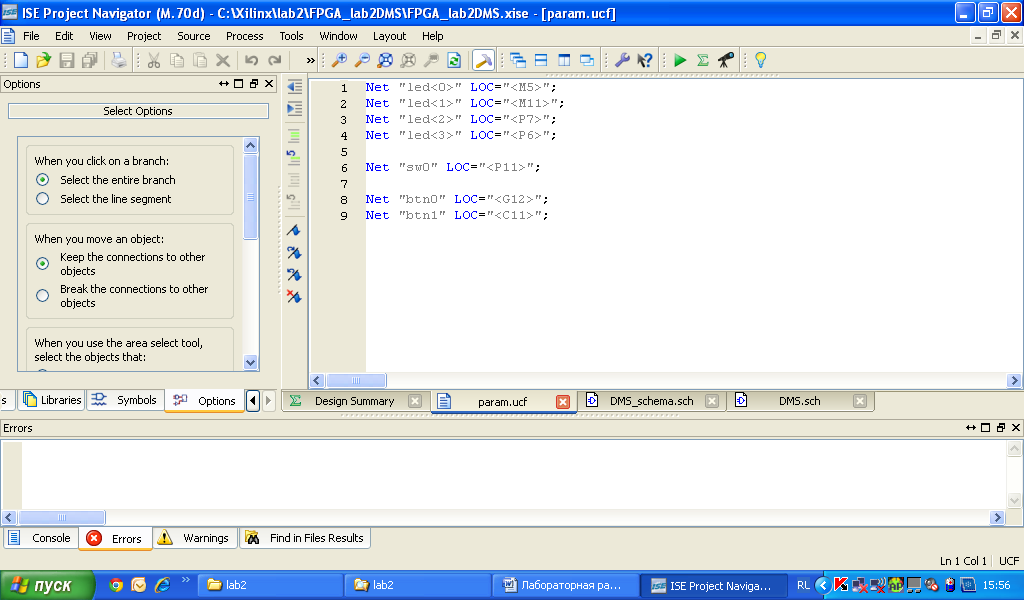
Рис. 37
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #

1 Цель работы
Целью работы является изучение принципов действия комбинационных схем: дешифратора, шифратора, преобразователя кода для семисегментного индикатора, мультиплексора, сумматора.
2 Краткие теоретические сведения
2.1 Дешифратор (декодер)
Дешифратор (декодер) служит для преобразования n-разрядного позиционного двоичного кода в единичный выходной сигнал на одном из 2n выходов. При каждой входной комбинации сигналов на одном из выходов появляется 1. Таким образом, по единичному сигналу на одном из выходов можно судить о входной кодовой комбинации. Таблица истинности для декодера с двумя входами изображена в таблице 2.1.
Таблица 2.1 – Таблица истинности двухразрядного дешифратора
| x1 | x2 | y0 | y1 | y2 | y3 |
| 0 | 0 | 1 | 0 | 0 | 0 |
| 0 | 1 | 0 | 1 | 0 | 0 |
| 1 | 0 | 0 | 0 | 1 | 0 |
| 1 | 1 | 0 | 0 | 0 | 1 |
Для построения схемы декодера по таблице истинности воспользуемся методикой, изложенной в лабораторной работе №1, выполняемой на стенде LESO2. Например, устройство должно иметь 4 выхода. Для каждого выхода записываем логическое выражение. На основе СДНФ:
y0 = x1·x2
y1 = x1·x2
y2 = x1·x2
y3 = x1·x2
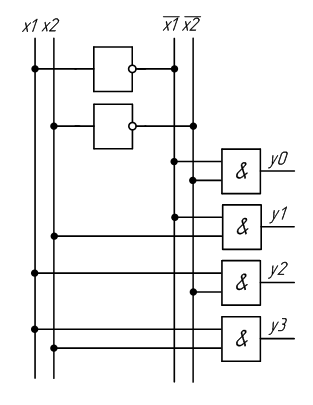
По этой системе выражений несложно построить схему требуемого дешифратора (рисунок 2.1).
Рисунок 2.1 – Схема дешифратора
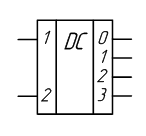
Условное графическое обозначение такого дешифратора изображено на рисунке 2.2.
Рисунок 2.2 – Условное графическое обозначение дешифратора
2.2 Шифратор (кодер)
Шифратор выполняет функцию, обратную декодеру (дешифратору), то есть преобразует непозиционный (унитарный) двоичный 2n разрядный код в n разрядный позиционный код. При подаче на один из входов единичного сигнала на выходе формируется соответствующий двоичный код. Составим таблицу истинности шифратора при n = 2.
Таблица 2.2 – Таблица истинности шифратора при n = 2
| x1 | x2 | x3 | x4 | y1 | y0 |
| 1 | 0 | 0 | 0 | 0 | 0 |
| 0 | 1 | 0 | 0 | 0 | 1 |
| 0 | 0 | 1 | 0 | 1 | 0 |
| 0 | 0 | 0 | 1 | 1 | 1 |
Синтезируем шифратор. Для этого запишем систему его собственных функций:
y1 = x1 · x2 · x3 · x4 + x1 · x2 · x3 ·x4
y0 = x1 · x2 · x3 · x4 + x1 · x2 · x3 ·x4
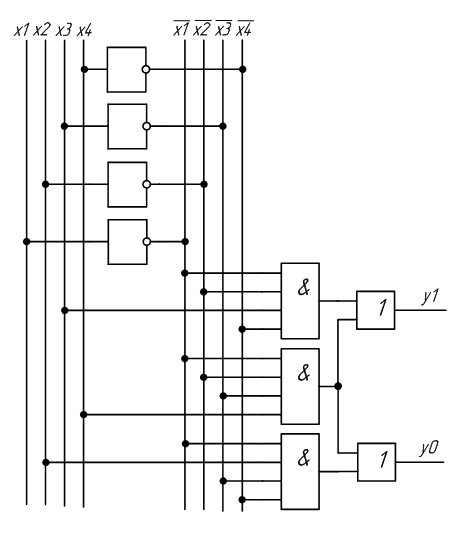
Рисунок 2.3 – Схема шифратора
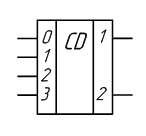
Рисунок 2.4 – Условное графическое обозначение шифратора
2.3 Преобразователь кода для семисегментного индикатора
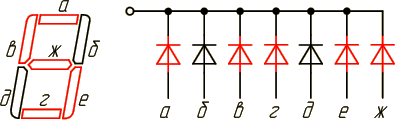
Наиболее широко преобразователи кодов известны применительно к цифровым индикаторам. Например, преобразователь 4-х разрядного позиционного двоичного кода в десятичные цифры. Имеется семи сегментный индикатор и с его помощью требуется высветить десять цифр.
Рисунок 2.5 – Семи сегментный индикатор
Очевидно, что двоичный код должен иметь не менее 4 — х разрядов (2^4 = 16, что больше 10). Составим таблицу истинности работы такого преобразователя.
Таблица 2.3 – Таблица истинности преобразователя
| Цифра | Двоичный код 8-4-2-1 | a | б | в | г | д | е | ж | |||
| 0 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 0 |
| 1 | 0 | 0 | 0 | 1 | 0 | 1 | 1 | 0 | 0 | 0 | 0 |
| 2 | 0 | 0 | 1 | 0 | 1 | 1 | 0 | 1 | 1 | 0 | 1 |
| 3 | 0 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 0 | 0 | 1 |
| 4 | 0 | 1 | 0 | 0 | 0 | 1 | 1 | 0 | 0 | 1 | 1 |
| 5 | 0 | 1 | 0 | 1 | 1 | 0 | 1 | 1 | 0 | 1 | 1 |
| 6 | 0 | 1 | 1 | 0 | 1 | 0 | 1 | 1 | 1 | 1 | 1 |
| 7 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 0 | 0 | 0 | 0 |
| 8 | 1 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
| 9 | 1 | 0 | 0 | 1 | 1 | 1 | 1 | 1 | 0 | 1 | 1 |
По ТИ несложно составить систему собственных функций для всех выходов, т.е. СДНФ, минимизировать её и составить принципиальную схему.
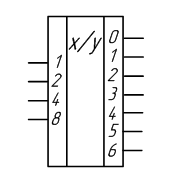
Рисунок 2.6 – Условное графическое обозначение преобразователя кода
2.4 Мультиплексор
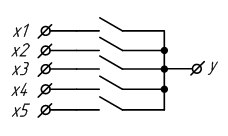
Мультиплексор – устройство, которое позволяет коммутировать один из 2^n информационных входов X на один выход Y под действием n управляющих (адресных) сигналов. На рисунке. 2.7 изображена упрощенная функциональная схема мультиплексора на идеализированных электронных ключах.
Рисунок 2.7 – Схема мультиплексора на идеализированных электронных ключах
В цифровых схемах требуется управлять ключами при помощи логических уровней. Поэтому желательно подобрать устройство, которое могло бы выполнять функции электронного ключа с управлением цифровым сигналом. Попробуем «заставить» работать в качестве электронного ключа уже знакомые нам логические элементы. Рассмотрим ТИ логического элемента «И». При этом один из входов логического элемента «И» будем рассматривать как информационный вход электронного ключа, а другой вход – как управляющий. Так как оба входа логического элемента «И» эквивалентны, то не важно какой из них будет управляющим входом. Пусть вход X будет управляющим, а Y – информационным. Для простоты рассуждений, разделим ТИ на две части в зависимости от уровня логического сигнала на управляющем входе X.
Таблица 2.4 – Таблица истинности
| y | x | Out |
| 0 0 |
0 1 |
0 0 |
| 1 1 |
0 1 |
0 1 |
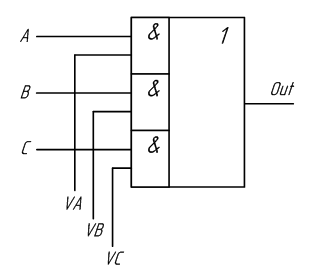
По таблице истинности отчётливо видно, что если на управляющий вход X подан нулевой логический уровень, сигнал, поданный на вход Y, на выход Out не проходит. При подаче на управляющий вход X логической единицы, сигнал, поступающий на вход Y, появляется на выходе Out. Это означает, что логический элемент «И» можно использовать в качестве электронного ключа. При этом не важно, какой из входов элемента «И» будет использоваться в качестве управляющего входа, а какой – в качестве информационного. Остается только объединить выходы элементов «И» на один общий выход. Это делается при помощи логического элемента «ИЛИ» точно так же как и при построении схемы по произвольной таблице истинности. Получившийся вариант схемы коммутатора с управлением логическими уровнями приведён на рисунке 2.8.
Рисунок 2.8 – Принципиальная схема мультиплексора, выполненная на логических элементах
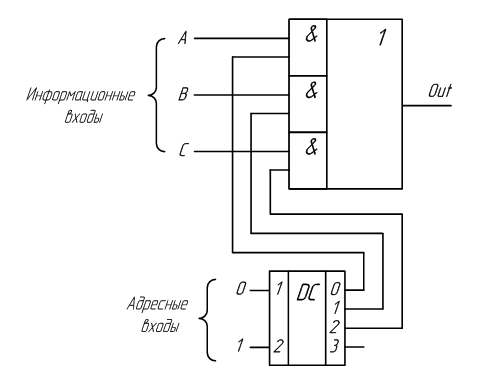
В схемах, приведенных на рисунках 2.7 и 2.8, можно одновременно включать несколько входов на один выход. Однако обычно это приводит к непредсказуемым последствиям. Кроме того, для управления таким коммутатором требуется много входов, поэтому в состав мультиплексора обычно включают двоичный дешифратор, как показано на рисунке 2.9. Такая схема позволяет управлять переключением информационных входов мультиплексора при помощи двоичных кодов, подаваемых на его управляющие входы. Количество информационных входов в таких схемах выбирают кратным степени числа два.
Рисунок 2.9 – Принципиальная схема мультиплексора, управляемого двоичным кодом
Условное графическое обозначение 4–х входового мультиплексора с управлением двоичным кодом приведено на рисунке 2.10. Входы A0 и A1 являются управляющими входами мультиплексора, определяющими адрес информационного входного сигнала, который будет соединён с выходным выводом мультиплексора Y. Информационные входные сигналы обозначены: X0, X1, X2 и X3.
Рисунок 2.10 – Условное графическое обозначение 4-х входового мультиплексора
В условном графическом обозначении названия информационных входов A, B, C и D заменены названиями X0, X1, X2 и X3, а название выхода Out заменено на название Y. Такое обозначение входов и выходов мультиплексора более распространено в отечественной литературе. Адресные входы обозначены как A0 и A1.
Об особенностях реализации мультиплесоров на языке Verilog можно почитать в статье:
Архитектура ПЛИС. Часть 2. Мультиплексор
2.5 Сумматор
Сумматор – узел компьютера, предназначенный для сложения двоичных чисел. Построение двоичных сумматоров обычно начинается с сумматора по модулю 2.
Сумматор по модулю 2
Схема сумматора по модулю 2 совпадает со схемой исключающее «ИЛИ».
Таблица 2.5 – Таблица истинности сумматора по модулю 2
| x1 | x2 | y |
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
Логическое выражение, описывающее сумматор по модулю 2:
y = x1 · x2 + x1 · x2
Рисунок 2.11 – Условное графическое обозначение сумматора по модулю 2
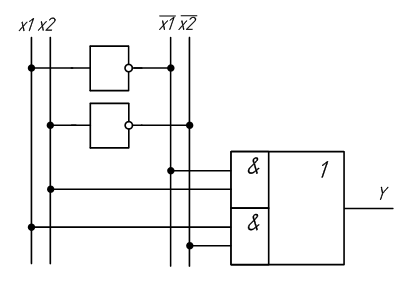
На основе логического уравнения, описывающего этот элемент можно синтезировать схему:
Рисунок 2.12 – Схема сумматора по модулю 2
Сумматор по модулю 2 выполняет суммирование без учёта переноса. В обычном двоичном сумматоре требуется учитывать перенос, поэтому требуются схемы, позволяющие формировать перенос в следующий двоичный разряд. Таблица истинности такой схемы, называемой полусумматором, приведена в таблице 2.6.
Таблица 2.6 – Таблица истинности полусумматора
| A | B | S | P0 |
| 0 | 0 | 0 | 0 |
| 0 | 1 | 1 | 0 |
| 1 | 0 | 1 | 0 |
| 1 | 1 | 0 | 1 |
Здесь A и B – слагаемые;
S – сумма;
P0 – перенос в старший разряд (выход переноса Pout).
Запишем систему собственных функций для полусумматора:
S = A · B + A · B
P0 = A · B
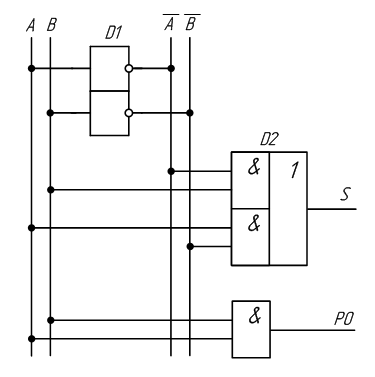
Рисунок 2.13 – Принципиальная схема, реализующая таблицу истинности полусумматора
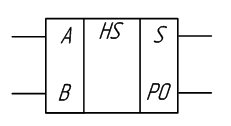
Рисунок 2.14 – Изображение полусумматора на схемах
Полный сумматор.
Схема полусумматора формирует перенос в старший разряд, но не может учитывать перенос из младшего разряда. При сложении многоразрядных двоичных чисел необходимо складывать три цифры в каждом разряде – 2 слагаемых и единицу переноса из предыдущего разряда PI.
Таблица 2.7 – Таблица истинности полного сумматора
| PI | A | B | S | PO |
| 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 1 | 0 |
| 0 | 1 | 0 | 1 | 0 |
| 0 | 1 | 1 | 0 | 1 |
| 1 | 0 | 0 | 1 | 0 |
| 1 | 0 | 1 | 0 | 1 |
| 1 | 1 | 0 | 0 | 1 |
| 1 | 1 | 1 | 1 | 1 |
PI – вход 1 переноса из предыдущего разряда,
PO – выход 1 переноса в старший разряд.
На основании таблицы истинности запишем систему собственных функций для каждого выхода:
S = A · B · PI + A · B · PI + A · B · PI + A · B · PI
PO = A · B · PI + A · B · PI + A · B · PI + A · B · PI
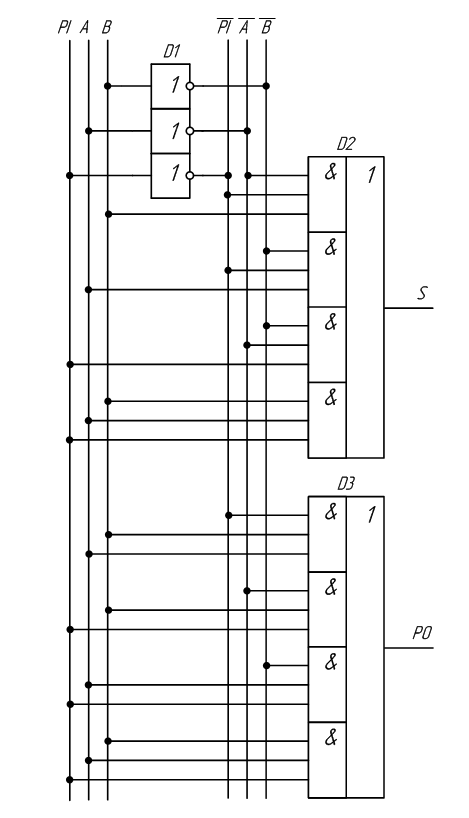
В результате получим схему полного сумматора (рисунок 2.15).
Рисунок 2.15 – Принципиальная схема, реализующая таблицу истинности полного двоичного одноразрядного сумматора
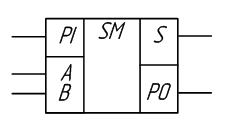
Рисунок 2.16 – Изображение полного двоичного одноразрядного сумматора на схемах
3 Задание к работе
3.1 Исследовать принцип работы дешифратора 2 x 4
Сконфигурировать ПЛИС в соответствии с рисунком 3.1. Подключить к входам X0 и X1 переключатели S7 и S8, а к выходам Y0, Y1, Y2, Y3 светодиодные индикаторы LED5, LED6, LED7, LED8. Для этого подключить входы и выходы дешифратора к соответствующим ножкам ПЛИС.
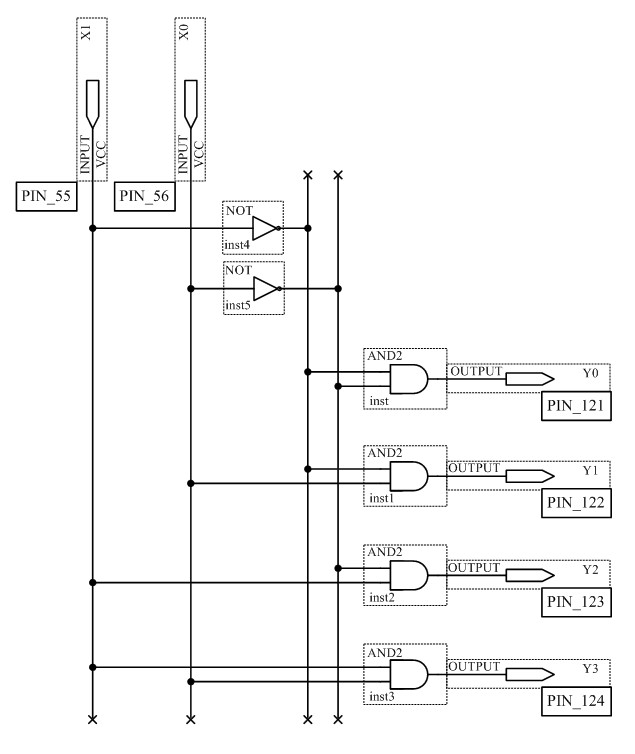
Рисунок 3.1 – Схема дешифратора
Подавая все возможные комбинации логических уровней на входы X0, X1 с помощью ключей S7, S8 и наблюдая за состояниями светодиодных индикаторов LED5, LED6, LED7, LED8, заполните таблицу истинности дешифратора.
Таблица 3.1 – Таблица дешифратора
| x1 | x2 | y0 | y1 | y2 | y3 |
| 0 | 0 | ||||
| 0 | 1 | ||||
| 1 | 0 | ||||
| 1 | 1 |
3.2 Исследовать принцип работы шифратора 4×2
Сконфигурировать ПЛИС в соответствии с рисунком 3.2.
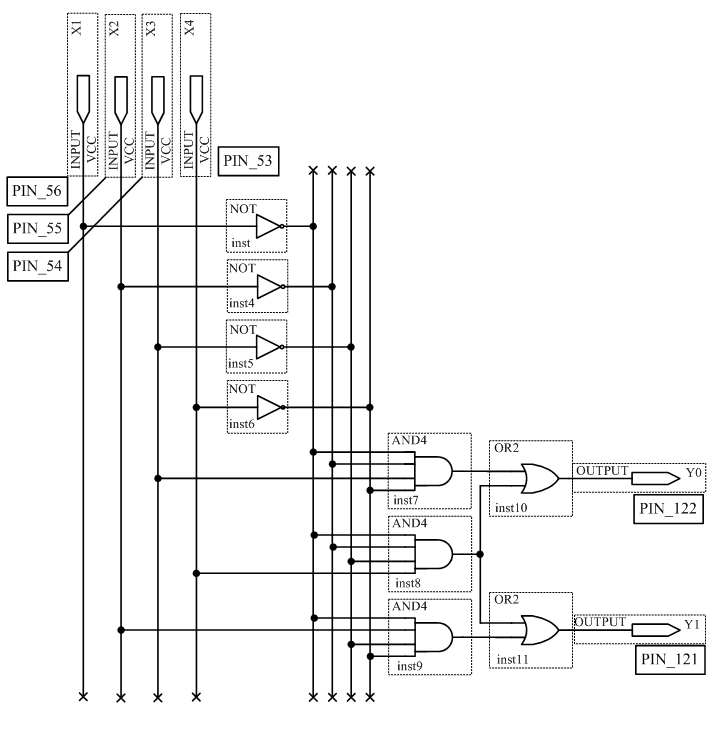
Рисунок 3.2 – Схема шифратора 4×2
Подключить к входам X1, X2, X3, X4 переключатели S8, S7, S6, S5, а к выходам Y0, Y1 светодиодные индикаторы LED8, LED7. Для этого подключить входы и выходы дешифратора к соответствующим ножкам ПЛИС. Подавая все возможные комбинации логических уровней на входы X1, X2, X3, X4 с помощью ключей S8, S7, S6, S5 и наблюдая за состояниями светодиодных индикаторов LED7, LED8, заполните таблицу истинности шифратора.
Таблица 3.2 – Таблица истинности шифратора
| x1 | x2 | x3 | x4 | y1 | y0 |
| 1 | 0 | 0 | 0 | ||
| 0 | 1 | 0 | 0 | ||
| 0 | 0 | 1 | 0 | ||
| 0 | 0 | 0 | 1 |
3.3 Исследовать работу преобразователя кода для семисегментного индикатора.
Составить таблицу истинности преобразователя кода (таблица. 3.3).
Собрать схему, изображенную на рисунке 3.3.
Таблица 3.3 – Таблица истинности преобразователя
| x3 | x2 | x1 | x0 | A | B | C | D | E | F | G |
| 0 | 0 | 0 | 0 | |||||||
| 0 | 0 | 0 | 1 | |||||||
| 0 | 0 | 1 | 0 | |||||||
| 0 | 0 | 1 | 1 | |||||||
| 0 | 1 | 0 | 0 | |||||||
| 0 | 1 | 0 | 1 | |||||||
| 0 | 1 | 1 | 0 | |||||||
| 0 | 1 | 1 | 1 | |||||||
| 1 | 0 | 0 | 0 | |||||||
| 1 | 0 | 0 | 1 |
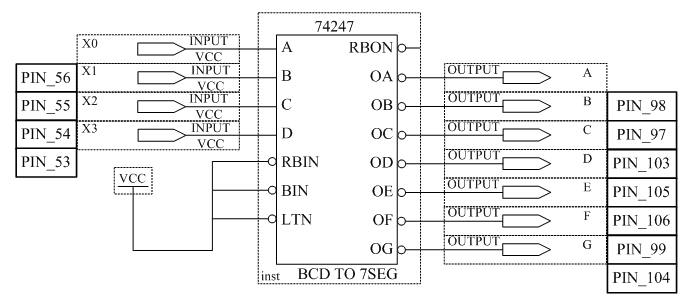
Рисунок 3.3 – Схема преобразователя кода для семисегментного индикатора
Подавая с помощью ключей S8, S7, S6, S5 различные кодовые комбинации на входы X0, X1, X2, X3 определить цифры, высвечиваемые на индикаторе. По результатам эксперимента заполнить таблицу 3.4.
Таблица 3.4 – Таблица, описывающая работу преобразователя кода для семисегментного индикатора
| x3 | x2 | x1 | x0 | Показание индикатора |
| 0 | 0 | 0 | 0 | |
| 0 | 0 | 0 | 1 | |
| 0 | 0 | 1 | 0 | |
| 0 | 0 | 1 | 1 | |
| 0 | 1 | 0 | 0 | |
| 0 | 1 | 0 | 1 | |
| 0 | 1 | 1 | 0 | |
| 0 | 1 | 1 | 1 | |
| 1 | 0 | 0 | 0 | |
| 1 | 0 | 0 | 1 |
3.4 Исследовать работу мультиплексора 4×1
Сконфигурировать ПЛИС в соответствии с рисунком 3.4.
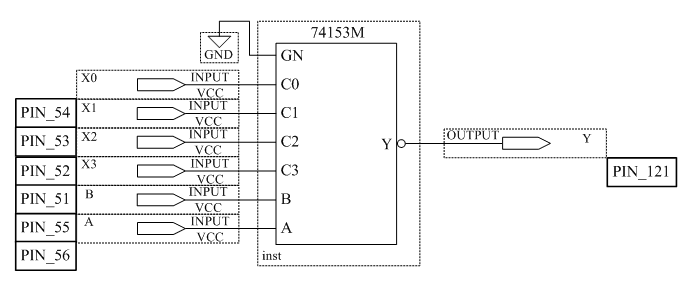
Рисунок 3.4 – Схема мультиплексора 4×1
Поочередно устанавливая все возможные кодовые комбинации на адресных входах A и B, определите номера коммутируемых каналов. Номер коммутируемого канала определяется путем поочерёдного подключения к входам X0, X2, X3, X4 уровня логической единицы и наблюдения за выходом Y. Заполните таблицу 3.5.
Таблица 3.5 – Таблица, описывающая работу мультиплексора
| B | A | Номер коммутируемого канала |
| 0 | 0 | |
| 0 | 1 | |
| 1 | 0 | |
| 1 | 1 |
3.5 Исследовать схему сумматора
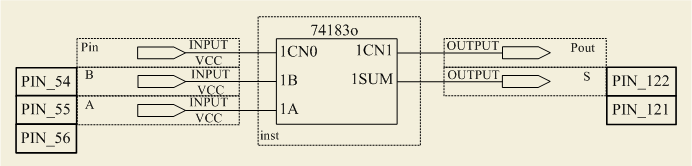
Сконфигурировать ПЛИС в соответствии с рисунком 3.5. Здесь Pin, Pout соответственно вход и выход единицы переноса, A и B – слагаемые, S – сумма.
Рисунок 3.5 – Схема сумматора
Заполнить таблицу истинности сумматора (таблица 3.6).
Таблица 2.7 – Таблица истинности полного сумматора
| Pin | B | A | Pout |
| 0 | 0 | 0 | |
| 0 | 0 | 1 | |
| 0 | 1 | 0 | |
| 0 | 1 | 1 | |
| 1 | 0 | 0 | |
| 1 | 0 | 1 | |
| 1 | 1 | 0 | |
| 1 | 1 | 1 |
4 Содержание отчета
- Цель работы.
- Схемы исследования дешифратора, шифратора, преобразователя кода для семисегментного индикатора, мультиплексора, сумматора.
- Таблицы истинности для каждой схемы.
- Выводы по каждому заданию.
5 Контрольные вопросы
- Принцип работы дешифратора?
- Как синтезировать дешифратор с произвольной разрядностью?
- Как работает шифратор?
- Изобразите таблицу истинности шифратора.
- Как работает преобразователь кода для семисегментного индикатора?
- Как устроен семи сегментный индикатор?
- Как работает мультиплексор?
- Как в лабораторной работе проводилось исследование мультиплексора?
- Как работает сумматор?
- Изобразите таблицу истинности шифратора.
- Что такое единица переноса?
Краткое описание документа:
Лабораторная работа №3
Цель работы: Построение мультиплексоров и демультиплексоров.
1. Приборы и оборудование.
Лабораторная работа выполняется на лабораторном стенде, описание которого дано в лабораторной работе №1.
2. Пояснения и порядок выполнения работы.
2.1 Построить восьмивходовой мультиплексор (8→1)
Мультиплексором называется комбинационное логическое устройство, предназначенное для передачи информации с одного из нескольких информационных входов на один выход. Выбор информационного входа осуществляется с помощью специальных входов, называемых адресными входами. Число адресных входов, определяет число информационных входов. Если n – разрядность адресных входов, то число информационных входов должно равняться N=2n.
Аннотация: Рассматривается принцип действия мультиплексоров.
Мультиплексор (селектор) — это логическая схема, производящая выбор одного из нескольких информационных входов в соответствии с выбранным адресом и коммутацию выбранного информационного входа с единственным информационным выходом.
увеличить изображение
Рис.
6.1.
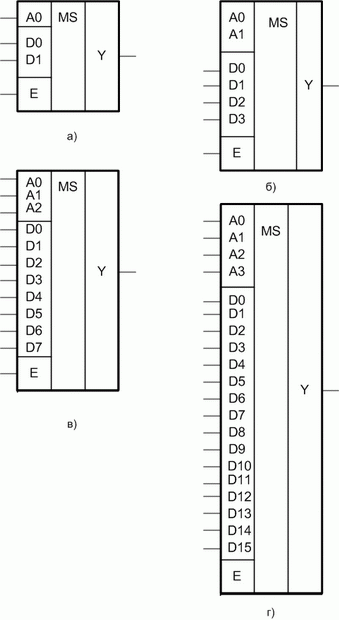
УГО мультиплексоров: а — «1 из 2»; б — «1 из 4»; в — «1 из 8»; г — «1 из 16»
На рис. 6.1 показаны УГО мультиплексоров. Здесь MS — функциональное обозначение мультиплексора, А — входные линии адреса, D — входные информационные линии, Е — разрешающий вход, Y — выходная информационная линия. Связь между количеством выбираемых входных информационных линий N и входных линий адреса n та же, что у дешифратора [1]: N=2n.
Принцип действия мультиплексора рассмотрим на примере ИМС, производящей выбор «1 из 4». УГО данного мультиплексора приведено на рис. 6.1,б, а его функциональная схема — на рис. 6.2. Здесь, А1 и А0 — входные линии адреса, D3, D2, D1 и D0 — входные информационные линии.
При наличии активного разрешающего сигнала (в нашем примере вход Е прямой, поэтому логика положительная и активный разрешающий сигнал равен 1) на адресные линии подается двоичный код адреса. При этом на выход Y будет копироваться информация с выбранного в соответствии с этим адресом информационного входа. Так, если А1А0=002=010, на выход Y подается информация с линии D0 ; если А1А0=012=110, то с линии D1, если А1А0=102=210, то с линии D2 ; а при А1А0=112=310 — с линии D3. Таким образом, таблицу истинности данного мультиплексора можно представить в виде табл. 6.1.
Как и для дешифратора, разрешающий вход Е мультиплексора может иметь активный нулевой уровень.
Рис.
6.2.
Функциональная схема мультиплексора, обеспечивающего выбор «один из четырех»
| Разрешающий сигнал | Входной код адреса | Информация на выходе | Режим работы | |
|---|---|---|---|---|
| E | А1 | А0 | Y | |
| 0 | 0 | 0 | 0 | Коммутации информационных линий нет |
| 0 | 0 | 1 | ||
| 0 | 1 | 0 | ||
| 0 | 1 | 1 | ||
| 1 | 0 | 0 | D0 | Передача с D0 на Y |
| 1 | 0 | 1 | D1 | Передача с D1 на Y |
| 1 | 1 | 0 | D2 | Передача с D2 на Y |
| 1 | 1 | 1 | D3 | Передача с D3 на Y |
Каскадное соединение мультиплексоров
Рассмотрим пример. Необходимо синтезировать схему мультиплексора, обеспечивающего выбор «1 из 16» на базе мультиплексоров «1 из 4».
Для выбора одного информационного входа из шестнадцати ( 16=24 ) необходимы 4 входные линии адреса: А3, А2, А1 и А0 (рис. 6.3). Четыре базовых мультиплексора обеспечивают выбор в зависимости от кода, поданного на А1 и А0, соответственно: первый — одного из сигналов D0, D1, D2 или D3, второй — из сигналов D4, D5, D6 или D7, третий — из сигналов D8, D9, D10 или D11, четвертый — из сигналов D12, D13, D14 или D15. Пятый мультиплексор обеспечивает выбор одного из этих ранее выбранных сигналов в зависимости от кода, подаваемого на А3 и А2. Например, при подаче А3А2А1А0=11102= 1410 на адресные входы первых
четырех мультиплексоров будет поступать двоичный код А1А0=102=210. Поэтому первая часть каскада будет выбирать входные информационные линии D2, D6, D10, D14. Они подключены соответственно ко входам D0, D1, D2 и D3 пятого мультиплексора. Поскольку на его адресные линии приходит код А3А2=112=310, на выход каскада будет передаваться информация с выхода D3 пятого выходного мультиплексора, то есть информация с входной информационной линии D14, что соответствует принципу работы мультиплексора.
Схему каскада той же разрядности можно реализовать на базе мультиплексоров с большей разрядностью, например, «1 из 8» (рис. 6.4). Для наглядности на рис. 6.4 указан тот же пример подачи информации на входы каскада: А3А2А1А0=11102= 1410.
Закономерность построения каскада мультиплексоров аналогична каскадированию дешифраторов. Но построение начинается со входной (а не выходной, как у дешифраторов) очереди каскада. На адресные линии всех мультиплексоров этой очереди подключается соответствующее разрядности базового мультиплексора количество линий адреса. Принципиальное отличие каскада мультиплексоров состоит в том, что все входящие в него мультиплексоры работают одновременно (разрешающий сигнал Е подается на все мультиплексоры сразу).
На рис. 6.3 и 6.4 показаны схемы с одной очередью. При малой разрядности базового мультиплексора количество очередей увеличивается — рис. 6.5. А на рис. 6.6 показана схема каскада мультиплексоров на 16 входов на базе «1 из 8», в которой адресные линии А1 и А2 (и, соответственно информационные линии D2-D7 ) выходного мультиплексора ( MS2.1 ) не используются в данной схеме, они остаются в резерве (на рис. 6.6 они заземлены, а в общем случае они могут быть подключены к другой схеме). В данной схеме показано состояние линий адреса и данных, соответствующее заданию: на линии адреса состояние 1110=10112, а на информационных линиях D15…D0 состояние 610= 00000000000001102. Данная схема осуществляет передачу на выход данных с
входной линии D11=0.
При синтезе каскада мультиплексоров рекомендуется придерживаться следующей последовательности действий:
- Нарисовать базовый мультиплексор.
- Определить количество мультиплексоров в первой части каскада (общее количество информационных входов схемы разделить на количество входов данных базового мультиплексора) и нарисовать входную часть каскада.
- Нарисовать входную адресную шину каскада нужной разрядности (из расчета N=2n, где N — количество информационных входов схемы, n — количество необходимых входных линий адреса).
- Соединить входные адресные линии мультиплексоров первой очереди и младшие разряды входной адресной шины.
- Определить количество мультиплексоров в следующей очереди каскада, равное количеству мультиплексоров предыдущей очереди, деленное на количество информационных линий одного мультиплексора.
- Подключить мультиплексоры следующей очереди к следующим разрядам шины адреса и т.д. до тех пор, пока на выходе каскада не останется одна информационная линия.
- Объединить разрешающие сигналы всех мультиплексоров.
Мультиплексоры. Моделирование мультиплексоров
Страницы работы
Содержание работы
Лабораторная
работа 2.5
Мультиплексоры
Основные
теоретические положения
Мультиплексор
– комбинационное цифровое устройство для управляемой передачи данных от
нескольких источников информации X в один выход F согласно
коду адреса A.
Мультиплексор
имеет n адресных шин, m = 2n – входов и один информационный выход F. Обозначение MUX(m-1).
Например, MUX(4-1): в зависимости от кода, подаваемого в адресные
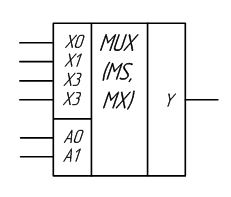
шины A0, A1
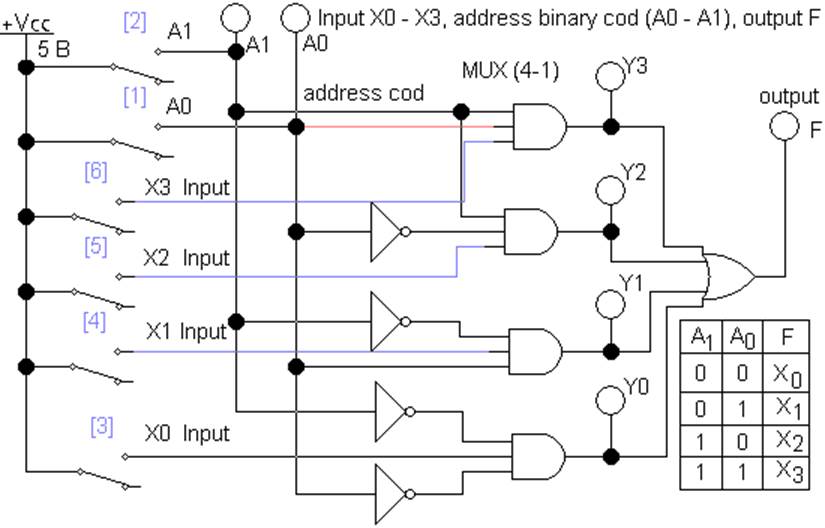
один из информационных входов X0…X3 подключается к выходному каналу F (рис.1).
Рис. 1 Мультиплексор MUX(4-1), файл L2_MUX_01.ewb
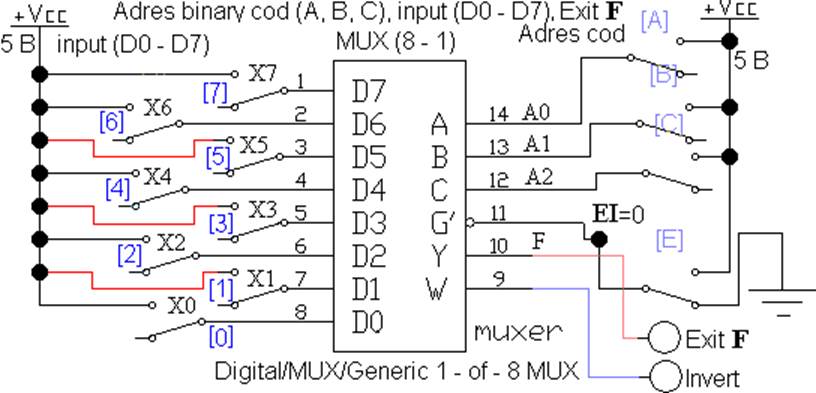
На рис. 2
представлен MUX(8-1), входы X0,
X1…X7,
адреса A0, A1,
A2, выход F.
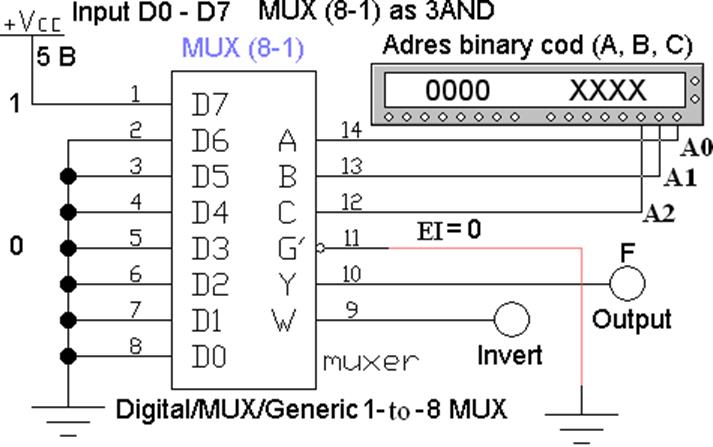
Рис. 2 Мультиплексор MUX(8-1), файл L2_MUX_02.ewb
Функция алгебры логики, описывающая работу мультиплексора (рис. 1), имеет
вид:
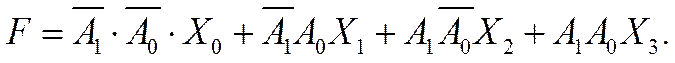 |
Файлы для моделирования
мультиплексоров расположены в папке Lab_2_5Модели.
Мультиплексоры имеют разрешающий вход EI, если на него подается логическая единица, то
происходит передача информации. На рисунке 2 этот вход инверсный.
На
мультиплексорах можно реализовать любую логическую функцию. Например, необходимо
получить логический элемент 3И (рис. 3). Для этого составляется таблица
истинности (табл. 1).
Таблица истинности
элемента «И» Таблица 1
|
№ входа X |
A2 |
A1 |
A0 |
F |
|
X0 |
0 |
0 |
0 |
0 |
|
X1 |
0 |
0 |
1 |
0 |
|
X2 |
0 |
1 |
0 |
0 |
|
X3 |
0 |
1 |
1 |
0 |
|
X4 |
1 |
0 |
0 |
0 |
|
X5 |
1 |
0 |
1 |
0 |
|
X6 |
1 |
1 |
0 |
0 |
|
X7 |
1 |
1 |
1 |
1 |
В соответствии
с адресом, выход F подключается к
соответствующему входу X. Если на эти входы
подать логические сигналы согласно столбцу F, то
получится требуемый элемент (рис. 3).
Используя табл.
1, согласно стандартным процедурам, можно записать аналитическое выражение
работы мультиплексора:
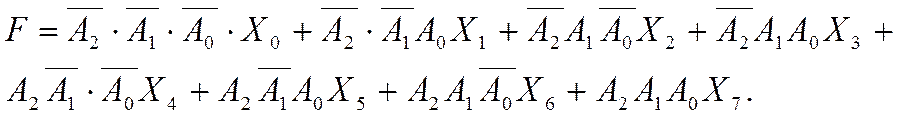 |
Рис. 3 Логический
элемент 3И на мультиплексоре MUX(8-1), файл L2_MUX_03.ewb
Пример. Реализовать
функцию F на MUX(4-1):
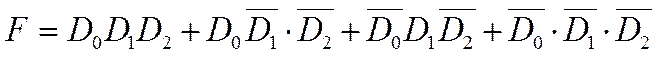 |
Последовательность операций:
Адресных входов меньше, чем переменных X.
Поскольку D0 и D1
входят во все слагаемые группы сомножителей в прямом и инверсном виде, примем: D0 = A0; D1 = A1.
Составим карту
Карно (табл. 2), используя аналитическое выражение для определения значений
функции F в клетках данной таблицы. Наборам адресов
A0; A1 соответствуют входы
мультиплексора X, которые подключаются к выходу F (таблицы 2, 3).
Из таблицы 2
следует, что на первых трех наборах адресов, функция F равна инверсному значению D2.
Для четвертого набора F = D2.
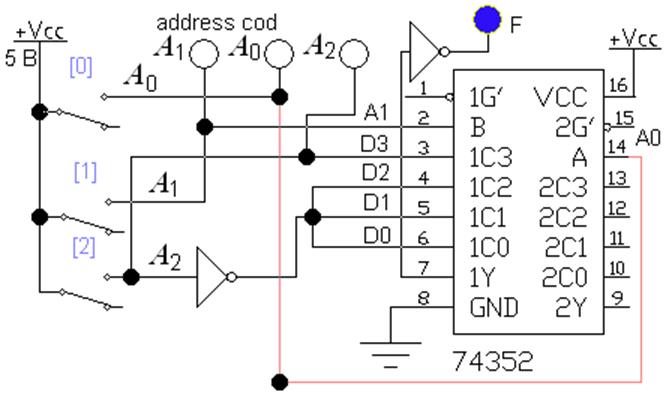
Схема устройства представлена на рис. 4. Выход микросхемы 74352 инверсный,
поэтому к нему подключен инвертор.
Карта
Карно Таблица 2 Таблица
истинности Таблица 3
|
D2D0 D1 |
00 |
01 |
11 |
10 |
№ |
D |
A1 |
A0 |
F |
|
|
0 |
1 |
1 |
0 |
1 |
1 |
D2‘ |
0 |
0 |
D0 |
|
|
1 |
0 |
0 |
1 |
0 |
2 |
D2‘ |
0 |
1 |
D1 |
|
|
Информационные |
X0 |
X1 |
X3 |
X2 |
3 |
D2‘ |
1 |
0 |
D2 |
|
|
4 |
D2 |
1 |
1 |
D3 |
X2‘ – инверсное
значение X2
Рис. 4 Реализация
логической функции на мультиплексоре MUX(4-1), файл
L2_MUX_04.ewb
Для увеличения
разрядности мультиплексора используются разрешающие
входы EI.
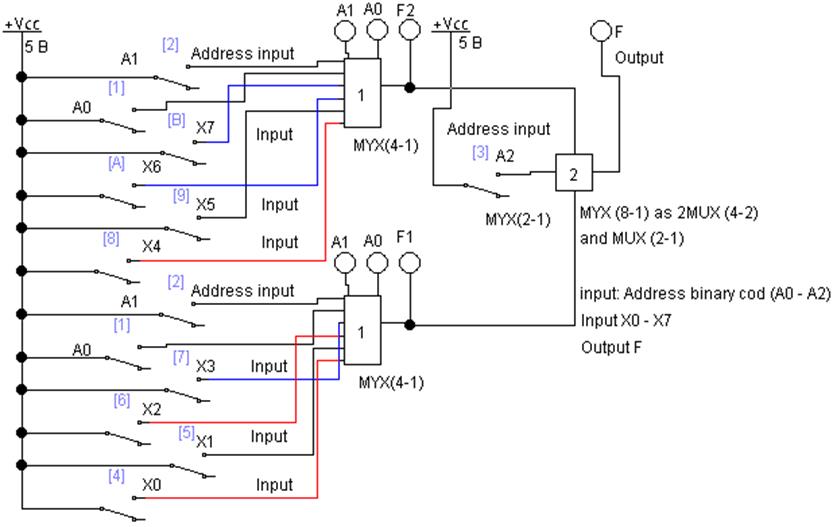
На рис. 5 представлен MUX(8-1)на двух MUX(4-1) и
одном MUX(2-1).
Мультиплексоры
расположены в модулях 1, 2, 3, которые раскрываются двойным щелчком мыши.
Переключение
между мультиплексорами (4-1) осуществляется с помощью старшего адресного
разряда A2, который управляет работой
MUX(2-1): первые четыре набора для X0…X3
считываются с MUX1, когда A2=0,
наборы X4…X7
с MUX2, при A2=1.
Рис. 5 Мультиплексор MUX(8-1) на двух MUX(4-1)
и одном MUX(2-1)
Задание 1. Задавая комбинации
входных сигналов, изучить работу мультиплексоров (рис. 1…5).
Задание 2.Составить
таблицу истинности (табл. 4) MUX(8-1), рис. 2,
файл L2_MUX_02.ewb, где A0
управляется кнопкой А, A1 – кнопкой
В, A2 – кнопкой С.
Таблица истинности MUX(8-1) Таблица 4
|
EI |
A2 |
A1 |
A0 |
Номера входов X на выходе F |
|
0 |
0 |
0 |
||
|
0 |
0 |
1 |
||
|
0 |
1 |
0 |
||
|
0 |
1 |
1 |
||
|
1 |
0 |
0 |
||
|
1 |
0 |
1 |
||
|
1 |
1 |
0 |
||
|
1 |
1 |
1 |
||
|
1 |
1 |
1 |
Задание 3. Минимизировать
и реализовать функцию F на
MUX(4-1), заполнить таблицы 5, 6, 7, дорисовать
схему (рис. 6), указать значения входных сигналов (D,
константы), подаваемых на все входы (A, X):
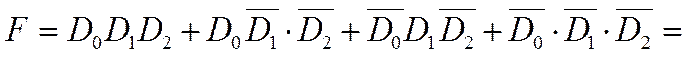
Таблица
истинности Таблица 5
|
Принять, например,: D0 Заполнить: карту Карно (табл. 3); таблицу истинности (табл. 4). |
№ |
D2 |
D1 |
D0 |
F |
|
0 |
0 |
0 |
0 |
||
|
1 |
0 |
0 |
1 |
||
|
2 |
0 |
1 |
0 |
||
|
3 |
0 |
1 |
1 |
||
|
4 |
1 |
0 |
0 |
||
|
5 |
1 |
0 |
1 |
||
|
6 |
1 |
1 |
0 |
||
|
7 |
1 |
1 |
1 |
Карта
Карно Таблица 3 Таблица
истинности Таблица 4
|
D2D0 D1 |
00 |
01 |
11 |
10 |
№ |
D |
A1 |
A0 |
F |
|
|
0 |
1 |
0 |
0 |
X0 |
||||||
|
1 |
2 |
0 |
1 |
X1 |
||||||
|
Информационные |
X0 |
X1 |
X3 |
X2 |
3 |
1 |
0 |
X2 |
||
|
4 |
1 |
1 |
X3 |
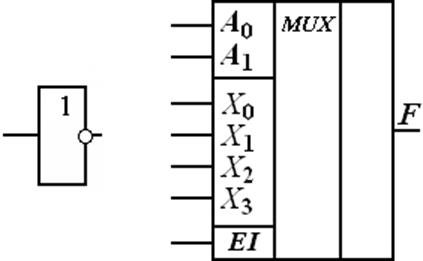
С помощью
мультиплексора можно реализовать любую логическую функцию, предварительно
преобразовав ее в совершенную дизъюнктивную нормальную форму (соответствует
таблице 2).
Количество
адресных входов (A) может быть меньше числа
переменных (D), если использовать рассмотренные
преобразования (задание 3).
Рис. 6 Реализация логической
функции На рис. 1 представлена реализация
БФ трех
переменных с помощью MUX(4 – 1)
согласно таблице 4. Если бы не преобразования, то потребовался бы MUX(8 – 1).
Задание 4. Перечислить,
где и для каких целей применяются мультиплексоры.
Похожие материалы
- Мультиплексоры. Реализация логических функций на мультиплексорах
- Однокаскадные усилители на биполярных транзисторах
- Определение характеристик триггеров. Изучение различных схем T-триггера и их функционирования
Информация о работе
Тип:
Методические указания и пособия
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание — внизу страницы.