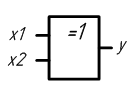Федеральное
агентство связи
Ордена
Трудового Красного Знамени федеральное
государственное бюджетное образовательное
учреждение высшего образования
«Московский
технический университет связи и
информатики»
ПРАКТИЧЕСКАЯ
РАБОТА №2
«Шифратор»
Выполнили:
студенты гр. «Сортирный Союз»
лох
чмо
чукча
Проверила: Воронкова
М.Н.
Москва
2021
Цель
работы:
ознакомление с основными характеристиками
интегральных преобразователей кодов,
получение навыков проектирования
шифраторов.
1.
По данной таблице истинности шифратора
(кодера) составить для него систему
уравнений и начертить блок-схему на
логических элементах.
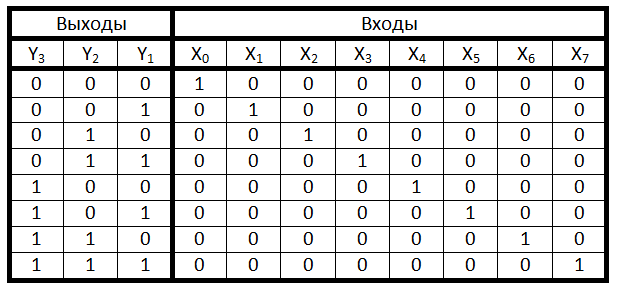
Анализ
таблицы истинности шифратора показывает,
что разряд у1 принимает значение лог.1
в том случае, когда лог.1 имеют входные
сигналы х1;x3;x5;x7:
y1=x1+x3+x5+x7
Разряд
y2
принимает значение лог.1 в том случае,
когда лог.1 имеют входные сигналы х2, х3,
х6, х7:
y2=
х2+ х3+х6+х7
И,
наконец, разряд у3 принимает значение
лог.1 в том случае, когда лог.1 имеют
входные сигналы х4, х5, х6, х7:
y3=
х4+х5+х6+х7
Из
анализа полученных выражений можно
сделать вывод, что схема шифратора 8 на
3 состоит из трех четырехвходовых ЛЭ
«ИЛИ».
Следует
отметить, что разряд х0 не участвует в
формировании выходных сигналов y3—y1,
так как при хо = 1 сигналы у3=y2
= у1= 0.
Для
обозначения шифратора служат буквы CD
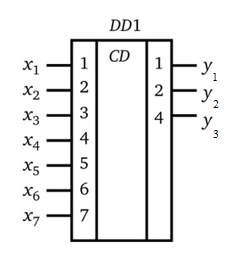
Условное
обозначение шифратора 8 на 3

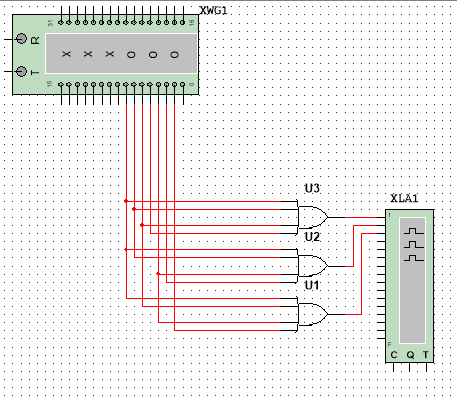
Скриншот
из Multisim
2.
По таблице истинности (согласно варианту)
шифратора (кодера) составить для него
систему уравнений и начертить блок-схему
на логических элементах.
Вариант
1
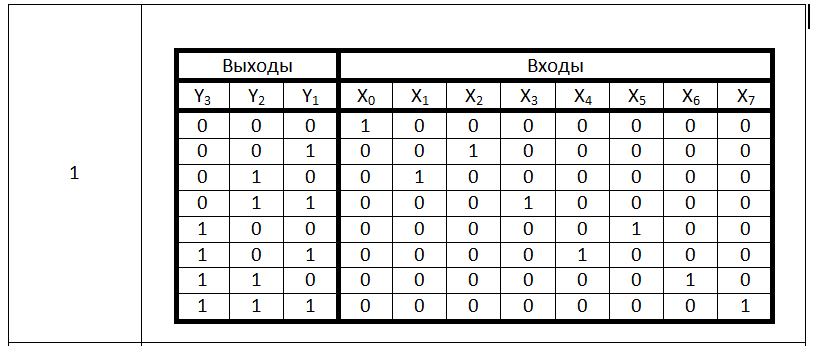
Анализ
таблицы истинности шифратора показывает,
что разряд у1 принимает значение лог.1
в том случае, когда лог.1 имеют входные
сигналы х2;x3;x4;x7:
y1=x2+x3+x4+x7
Разряд
y2
принимает значение лог.1 в том случае,
когда лог.1 имеют входные сигналы х1, х3,
х6, х7:
y2=
х1+ х3+х6+х7
И,
наконец, разряд у3 принимает значение
лог.1 в том случае, когда лог.1 имеют
входные сигналы х4, х5, х6, х7:
y3=
х4+х5+х6+х7
Из
анализа полученных выражений можно
сделать вывод, что схема шифратора 8 на
3 состоит из трех четырехвходовых ЛЭ
«ИЛИ».
Следует
отметить, что разряд х0 не участвует в
формировании выходных сигналов y3—y1,
так как при хо = 1 сигналы у3=y2
= у1= 0.
Для
обозначения шифратора служат буквы CD
Условное
обозначение шифратора 8 на 3
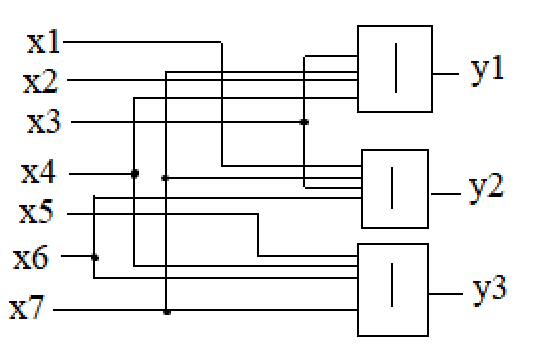
Скриншот
из Multisim
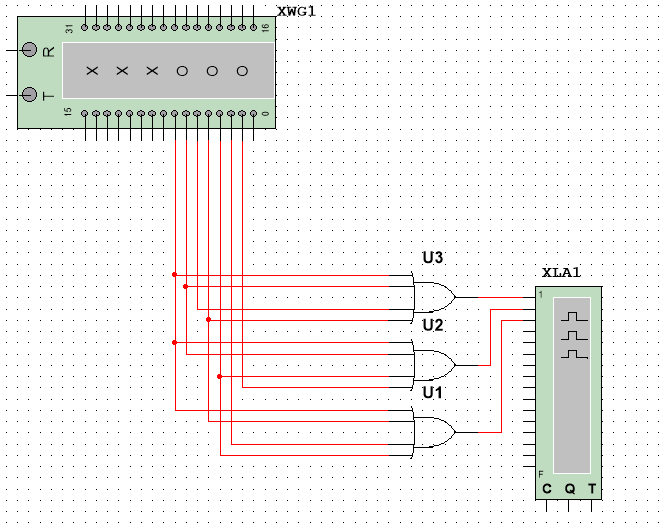
3.
Согласно заданию №1 практической работы
1 взять булеву функцию и ее таблицу
истинности, построить таблицу истинности
шифратора, составить для него систему
уравнений и начертить блок-схему на
логических элементах.

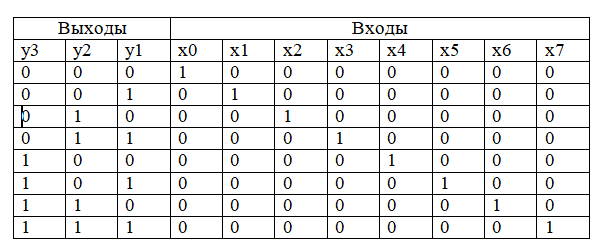
Анализ
таблицы истинности шифратора показывает,
что разряд у1 принимает значение лог.1
в том случае, когда лог.1 имеют входные
сигналы х1;x3;x5;x7:
y1=x1+x3+x5+x7
Разряд
y2
принимает значение лог.1 в том случае,
когда лог.1 имеют входные сигналы х2, х3,
х6, х7:
y2=
х2+ х3+х6+х7
И,
наконец, разряд у3 принимает значение
лог.1 в том случае, когда лог.1 имеют
входные сигналы х4, х5, х6, х7:
y3=
х4+х5+х6+х7
Из
анализа полученных выражений можно
сделать вывод, что схема шифратора 8 на
3 состоит из трех четырехвходовых ЛЭ
«ИЛИ».
Следует
отметить, что разряд х0 не участвует в
формировании выходных сигналов y3—y1,
так как при хо = 1 сигналы у3=y2
= у1= 0.
Для
обозначения шифратора служат буквы CD
Условное
обозначение шифратора 8 на 3

Скриншот
из Multisim
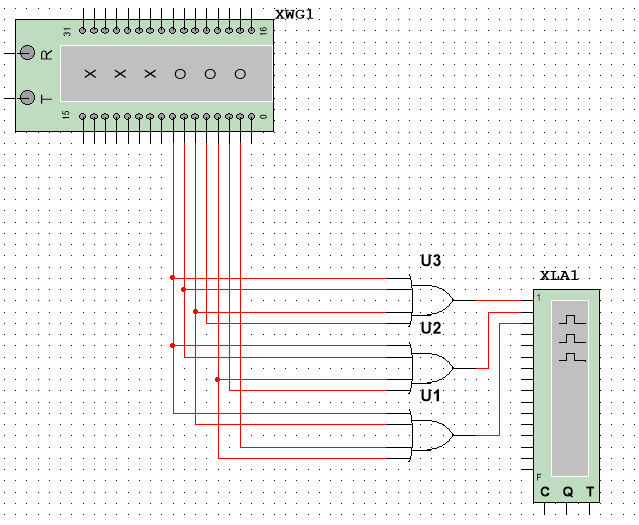
Лабораторная
работа 2.2 Шифраторы
Основные
теоретические положения
Шифраторомназывается
устройство, предназначенное для преобразования чисел, например, из десятичной
системы в двоичную систему счисления. Основное применение шифраторов – это
введение информации с клавиатуры. Обозначение CD(n—m), где n – количество входов, m – число выходов.
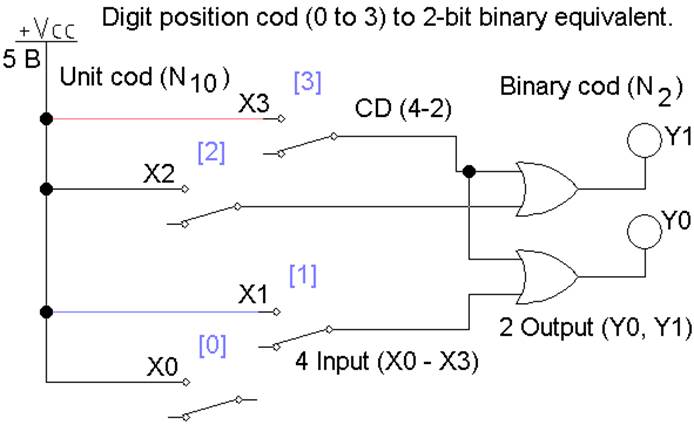
Схема и
таблица истинности CD(4 – 2) представлены на рис. 1 и в табл.
1, где X0, X1…X3 входные сигналы, номер которых представляет
десятичный код. Выходные значения Y0,
Y1 в двоичном коде, старший разряд Y1.
Файлы для
моделирования этих элементов расположены в папке Lab_2_2Модели.
Таблица истинности CD(4 – 2) Таблица 1
|
Номер входа X (N10) |
Выходной код Y (N2) |
|
|
Y1 |
Y0 |
|
|
0 |
0 |
0 |
|
1 |
0 |
1 |
|
2 |
1 |
0 |
|
3 |
1 |
1 |
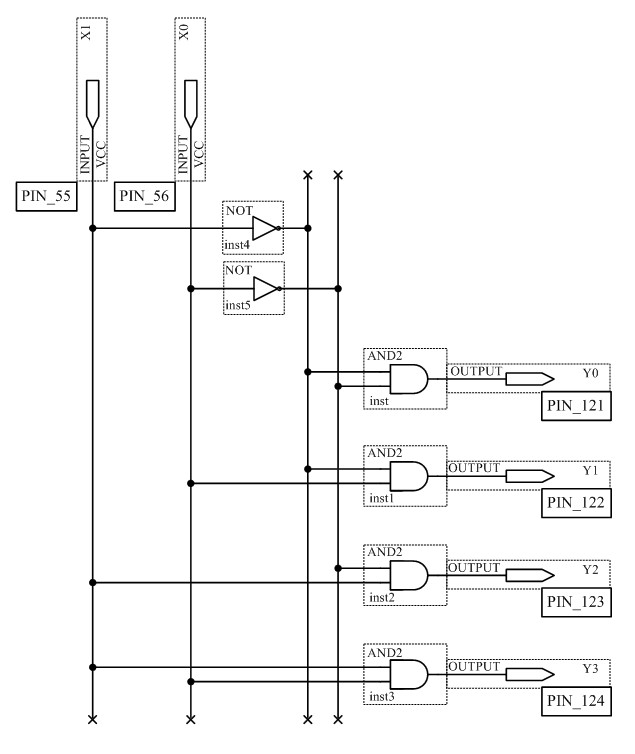
Рис. 1 Шифратор CD(4-2) на логических элементах ИЛИ
Уравнения работы шифратора CD(4-2):
Задание 1. С помощью комбинаций
входных сигналов изучить работу CD(4-2) файл
L2_CD_01.ewb, и его таблицу истинности.
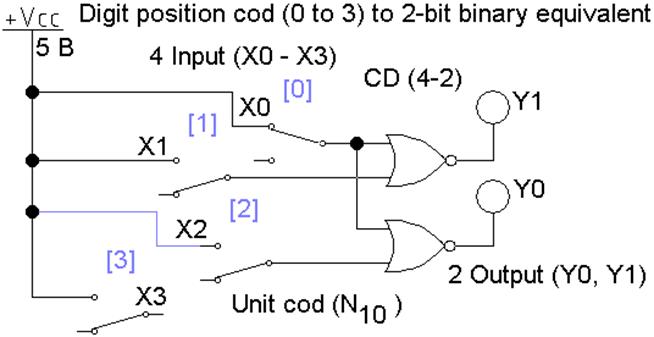
Задание 2. Составить
таблицу истинности (табл. 2) шифратора CD(4-2),
изображенного на рис. 2.
Таблица истинности CD(4 – 2) Таблица 2
|
Номер входа X (N10) |
Выходной код Y (N2) |
|
|
Y1 |
Y0 |
|
|
0 |
||
|
1 |
||
|
2 |
||
|
3 |
Рис. 2 Шифратор CD(4-2) на логических элементах ИЛИ-НЕ (файл L2_CD_04.ewb)
1
Приоритетный шифратор
Шифратор
называют приоритетным, если он формирует код, определяющий номер единицы,
стоящей в старшем разряде, из других имеющихся единиц.
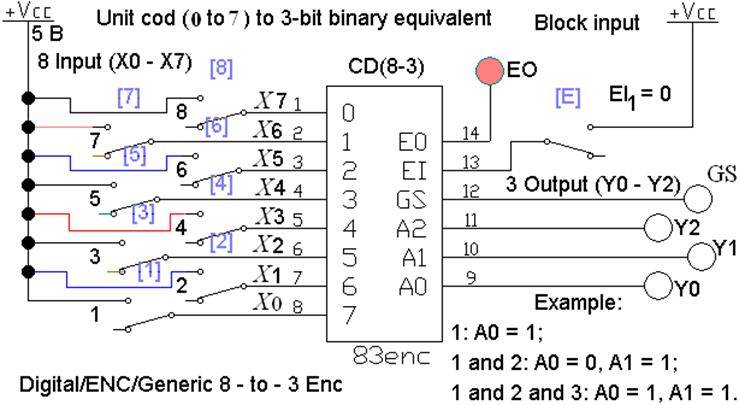
Таким
шифратором является CD(8-3) выполненный на
микросхеме (рис. 3), файл L2_CD_02.ewb.
Шифратор имеет служебные входы и выходы:
- Разрешающий вход (инверсный) EI=0 – шифратор преобразует входной код, если EI =1, то на всех информационных выходах
шифратора появляются единицы. - Выход GS в данном шифраторе указывает на использование
всех разрядов шифратора и его переполнение (все единицы). - Выход EO= 1 определяет отсутствие сигналов на всех
информационных выходах.
Особенность данной
схемы: номер старшей единицы преобразуется в код, если имеются единицы во всех
младших разрядах. Область применения – аналого-цифровые преобразователи (АЦП).
Рис. 3 Приоритетный
шифратор CD (8-3)
Задание 3. Заполнить
таблицу истинности (табл. 3) приоритетного шифратора CD(8-3)
используя модель: файл L2_CD_02.ewb.
Клетки таблицы
в разделе «Информационные входы», где может находиться 0 или 1, не оказывая
влияния на результат шифрации в разделе «Выходы», заполнить знаком «Х».
Таблица истинности CD(8 – 3) Таблица
3
|
№ |
Служебный вход |
Информационные входы |
Выходы |
||||||||||
|
EI |
X7 |
X6 |
X5 |
X4 |
X3 |
X2 |
X1 |
X0 |
EO |
Y2 |
Y1 |
Y0 |
|
|
0 |
0 |
1 |
0 |
0 |
0 |
||||||||
|
1 |
0 |
1 |
0 |
0 |
1 |
||||||||
|
2 |
0 |
1 |
0 |
1 |
0 |
||||||||
|
3 |
0 |
1 |
0 |
1 |
1 |
||||||||
|
4 |
0 |
1 |
1 |
0 |
0 |
||||||||
|
5 |
0 |
1 |
1 |
0 |
1 |
||||||||
|
6 |
0 |
1 |
1 |
1 |
0 |
||||||||
|
7 |
0 |
1 |
1 |
1 |
1 |
||||||||
|
8 |
0 |
0 |
1 |
1 |
1 |
||||||||
|
9 |
1 |
1 |
1 |
1 |
Вывод:
— Если при
достижении амплитудного значения изменяющегося во времени аналогового сигнала
уровней 1, 2…7 (столбец «№» табл. 3) будет замыкаться соответствующий ключ – на
выходе приоритетного шифратора получим цифровой код для этого значения сигнала.
Этот принцип использован в параллельных АЦП.Вход EI в таблице 3 и модели инверсный.
— Шифраторы
являются преобразователями кодов, причем результирующий код более компактен,
чем исходный.
2 Указатель
старшей единицы
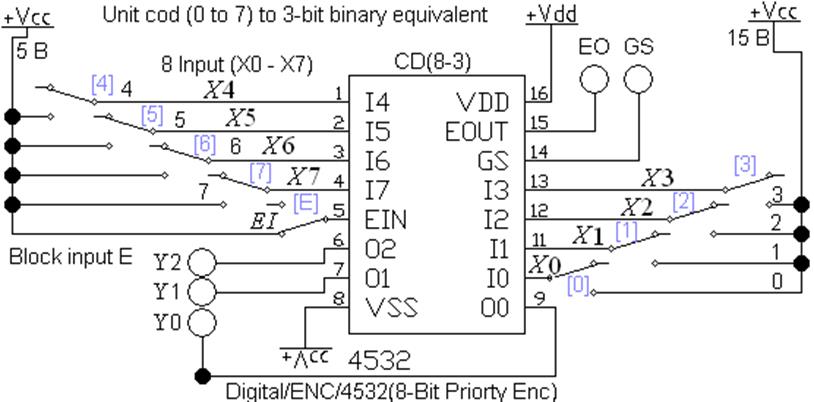
Приоритетный
шифратор CD(8-3) выполнен на микросхеме (рис. 4),
файл L2_CD_03.ewb. Шифратор
выявляет старшую (левую) единицу, в отличие от предыдущей схемы в младших разрядах, при этом, могут быть также
нули, и формирует двоичный код соответствующего единице десятичного номера.
Он называется указателем старшей единицы и исключает
ошибки, например, при одновременном нажатии двух клавиш клавиатуры, применяется
в работе светофоров и т.д.
Выход GSшифратора, указывает на наличие информационного сигнала хотя бы на
одном входе. Для разрешения работы на вход подается единица EI=1.
Рис. 4 Указатель
старшей единицы CD (8-3)
Задание 4
Заполнить
таблицу истинности (табл. 4) указателя старшей единицы CD(8-3),
используя модель: файл L2_CD_03.ewb.
Клетки таблицы
в разделе «Информационные входы», где может находиться 0 или 1, не оказывая
влияния на результат шифрации в разделе «Выходы», заполнить знаком «Х».
Таблица истинности CD(8 – 3) Таблица
4
|
№ |
Служебный вход |
Информационные входы |
Служебные выходы |
Информационные выходы |
||||||||||
|
EI |
X7 |
X6 |
X5 |
X4 |
X3 |
X2 |
X1 |
X0 |
EO |
GS |
Y2 |
Y1 |
Y0 |
|
|
0 |
1 |
0 |
0 |
0 |
||||||||||
|
1 |
1 |
0 |
0 |
0 |
||||||||||
|
2 |
1 |
0 |
0 |
1 |
||||||||||
|
3 |
1 |
0 |
1 |
0 |
||||||||||
|
4 |
1 |
0 |
1 |
1 |
||||||||||
|
5 |
1 |
1 |
0 |
0 |
||||||||||
|
6 |
1 |
1 |
0 |
1 |
||||||||||
|
7 |
1 |
1 |
1 |
0 |
||||||||||
|
8 |
1 |
1 |
1 |
1 |
||||||||||
|
9 |
0 |
Задание 5. Перечислить,
где и для каких целей применяются шифраторы.
Выводы:
Шифраторы
являются преобразователями кодов, причем результирующий код более компактен,
чем исходный.
Служебные входы и выходы шифраторов используются для
расширения их функциональных возможностей:
— вход EI(бывает прямым или инверсным) служит для определения
момента времени, когда шифратор должен преобразовать код. Это позволяет
согласовать его работу с другими устройствами, когда они готовы передавать и
считывать информацию с шифратора.
— выходы GSи EO используются с целью увеличения разрядности путем
выработки сигналов для подключения дополнительных шифраторов.
Шифраторы применяются, например, для преобразования
десятичного кода двоичный при вводе информации с клавиатуры в
компьютер (калькулятор, сотовый телефон), в аналового-цифровых преобразователях
и т.д.

1 Цель работы
Целью работы является изучение принципов действия комбинационных схем: дешифратора, шифратора, преобразователя кода для семисегментного индикатора, мультиплексора, сумматора.
2 Краткие теоретические сведения
2.1 Дешифратор (декодер)
Дешифратор (декодер) служит для преобразования n-разрядного позиционного двоичного кода в единичный выходной сигнал на одном из 2n выходов. При каждой входной комбинации сигналов на одном из выходов появляется 1. Таким образом, по единичному сигналу на одном из выходов можно судить о входной кодовой комбинации. Таблица истинности для декодера с двумя входами изображена в таблице 2.1.
Таблица 2.1 – Таблица истинности двухразрядного дешифратора
| x1 | x2 | y0 | y1 | y2 | y3 |
| 0 | 0 | 1 | 0 | 0 | 0 |
| 0 | 1 | 0 | 1 | 0 | 0 |
| 1 | 0 | 0 | 0 | 1 | 0 |
| 1 | 1 | 0 | 0 | 0 | 1 |
Для построения схемы декодера по таблице истинности воспользуемся методикой, изложенной в лабораторной работе №1, выполняемой на стенде LESO2. Например, устройство должно иметь 4 выхода. Для каждого выхода записываем логическое выражение. На основе СДНФ:
y0 = x1·x2
y1 = x1·x2
y2 = x1·x2
y3 = x1·x2
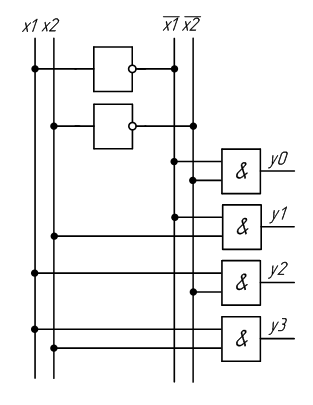
По этой системе выражений несложно построить схему требуемого дешифратора (рисунок 2.1).
Рисунок 2.1 – Схема дешифратора
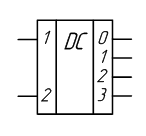
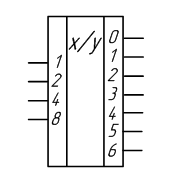
Условное графическое обозначение такого дешифратора изображено на рисунке 2.2.
Рисунок 2.2 – Условное графическое обозначение дешифратора
2.2 Шифратор (кодер)
Шифратор выполняет функцию, обратную декодеру (дешифратору), то есть преобразует непозиционный (унитарный) двоичный 2n разрядный код в n разрядный позиционный код. При подаче на один из входов единичного сигнала на выходе формируется соответствующий двоичный код. Составим таблицу истинности шифратора при n = 2.
Таблица 2.2 – Таблица истинности шифратора при n = 2
| x1 | x2 | x3 | x4 | y1 | y0 |
| 1 | 0 | 0 | 0 | 0 | 0 |
| 0 | 1 | 0 | 0 | 0 | 1 |
| 0 | 0 | 1 | 0 | 1 | 0 |
| 0 | 0 | 0 | 1 | 1 | 1 |
Синтезируем шифратор. Для этого запишем систему его собственных функций:
y1 = x1 · x2 · x3 · x4 + x1 · x2 · x3 ·x4
y0 = x1 · x2 · x3 · x4 + x1 · x2 · x3 ·x4
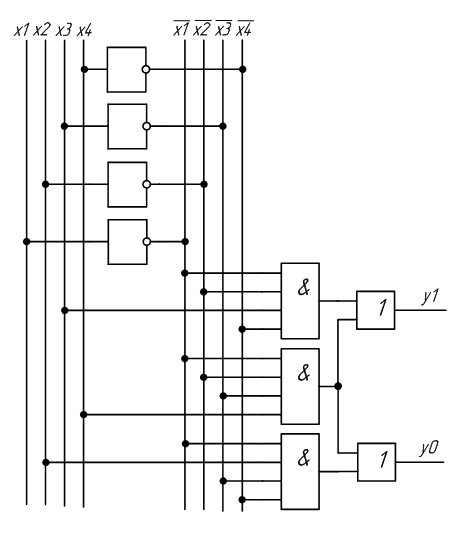
Рисунок 2.3 – Схема шифратора
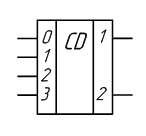
Рисунок 2.4 – Условное графическое обозначение шифратора
2.3 Преобразователь кода для семисегментного индикатора
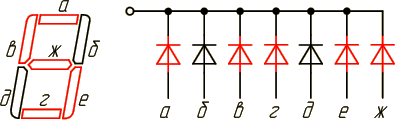
Наиболее широко преобразователи кодов известны применительно к цифровым индикаторам. Например, преобразователь 4-х разрядного позиционного двоичного кода в десятичные цифры. Имеется семи сегментный индикатор и с его помощью требуется высветить десять цифр.
Рисунок 2.5 – Семи сегментный индикатор
Очевидно, что двоичный код должен иметь не менее 4 — х разрядов (2^4 = 16, что больше 10). Составим таблицу истинности работы такого преобразователя.
Таблица 2.3 – Таблица истинности преобразователя
| Цифра | Двоичный код 8-4-2-1 | a | б | в | г | д | е | ж | |||
| 0 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 0 |
| 1 | 0 | 0 | 0 | 1 | 0 | 1 | 1 | 0 | 0 | 0 | 0 |
| 2 | 0 | 0 | 1 | 0 | 1 | 1 | 0 | 1 | 1 | 0 | 1 |
| 3 | 0 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 0 | 0 | 1 |
| 4 | 0 | 1 | 0 | 0 | 0 | 1 | 1 | 0 | 0 | 1 | 1 |
| 5 | 0 | 1 | 0 | 1 | 1 | 0 | 1 | 1 | 0 | 1 | 1 |
| 6 | 0 | 1 | 1 | 0 | 1 | 0 | 1 | 1 | 1 | 1 | 1 |
| 7 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 0 | 0 | 0 | 0 |
| 8 | 1 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
| 9 | 1 | 0 | 0 | 1 | 1 | 1 | 1 | 1 | 0 | 1 | 1 |
По ТИ несложно составить систему собственных функций для всех выходов, т.е. СДНФ, минимизировать её и составить принципиальную схему.
Рисунок 2.6 – Условное графическое обозначение преобразователя кода
2.4 Мультиплексор
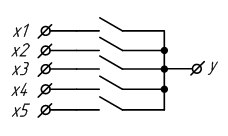
Мультиплексор – устройство, которое позволяет коммутировать один из 2^n информационных входов X на один выход Y под действием n управляющих (адресных) сигналов. На рисунке. 2.7 изображена упрощенная функциональная схема мультиплексора на идеализированных электронных ключах.
Рисунок 2.7 – Схема мультиплексора на идеализированных электронных ключах
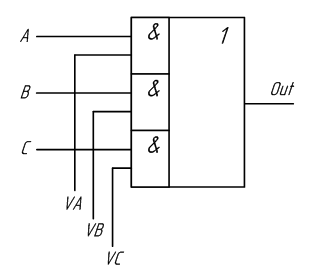
В цифровых схемах требуется управлять ключами при помощи логических уровней. Поэтому желательно подобрать устройство, которое могло бы выполнять функции электронного ключа с управлением цифровым сигналом. Попробуем «заставить» работать в качестве электронного ключа уже знакомые нам логические элементы. Рассмотрим ТИ логического элемента «И». При этом один из входов логического элемента «И» будем рассматривать как информационный вход электронного ключа, а другой вход – как управляющий. Так как оба входа логического элемента «И» эквивалентны, то не важно какой из них будет управляющим входом. Пусть вход X будет управляющим, а Y – информационным. Для простоты рассуждений, разделим ТИ на две части в зависимости от уровня логического сигнала на управляющем входе X.
Таблица 2.4 – Таблица истинности
| y | x | Out |
| 0 0 |
0 1 |
0 0 |
| 1 1 |
0 1 |
0 1 |
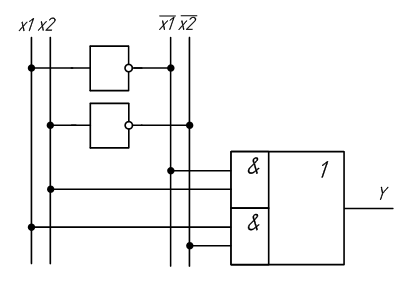
По таблице истинности отчётливо видно, что если на управляющий вход X подан нулевой логический уровень, сигнал, поданный на вход Y, на выход Out не проходит. При подаче на управляющий вход X логической единицы, сигнал, поступающий на вход Y, появляется на выходе Out. Это означает, что логический элемент «И» можно использовать в качестве электронного ключа. При этом не важно, какой из входов элемента «И» будет использоваться в качестве управляющего входа, а какой – в качестве информационного. Остается только объединить выходы элементов «И» на один общий выход. Это делается при помощи логического элемента «ИЛИ» точно так же как и при построении схемы по произвольной таблице истинности. Получившийся вариант схемы коммутатора с управлением логическими уровнями приведён на рисунке 2.8.
Рисунок 2.8 – Принципиальная схема мультиплексора, выполненная на логических элементах
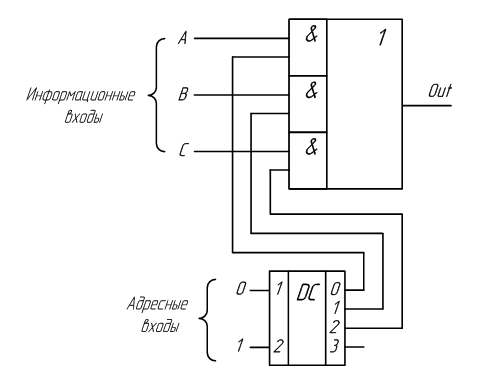
В схемах, приведенных на рисунках 2.7 и 2.8, можно одновременно включать несколько входов на один выход. Однако обычно это приводит к непредсказуемым последствиям. Кроме того, для управления таким коммутатором требуется много входов, поэтому в состав мультиплексора обычно включают двоичный дешифратор, как показано на рисунке 2.9. Такая схема позволяет управлять переключением информационных входов мультиплексора при помощи двоичных кодов, подаваемых на его управляющие входы. Количество информационных входов в таких схемах выбирают кратным степени числа два.
Рисунок 2.9 – Принципиальная схема мультиплексора, управляемого двоичным кодом
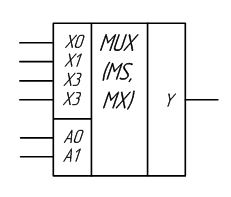
Условное графическое обозначение 4–х входового мультиплексора с управлением двоичным кодом приведено на рисунке 2.10. Входы A0 и A1 являются управляющими входами мультиплексора, определяющими адрес информационного входного сигнала, который будет соединён с выходным выводом мультиплексора Y. Информационные входные сигналы обозначены: X0, X1, X2 и X3.
Рисунок 2.10 – Условное графическое обозначение 4-х входового мультиплексора
В условном графическом обозначении названия информационных входов A, B, C и D заменены названиями X0, X1, X2 и X3, а название выхода Out заменено на название Y. Такое обозначение входов и выходов мультиплексора более распространено в отечественной литературе. Адресные входы обозначены как A0 и A1.
Об особенностях реализации мультиплесоров на языке Verilog можно почитать в статье:
Архитектура ПЛИС. Часть 2. Мультиплексор
2.5 Сумматор
Сумматор – узел компьютера, предназначенный для сложения двоичных чисел. Построение двоичных сумматоров обычно начинается с сумматора по модулю 2.
Сумматор по модулю 2
Схема сумматора по модулю 2 совпадает со схемой исключающее «ИЛИ».
Таблица 2.5 – Таблица истинности сумматора по модулю 2
| x1 | x2 | y |
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
Логическое выражение, описывающее сумматор по модулю 2:
y = x1 · x2 + x1 · x2
Рисунок 2.11 – Условное графическое обозначение сумматора по модулю 2
На основе логического уравнения, описывающего этот элемент можно синтезировать схему:
Рисунок 2.12 – Схема сумматора по модулю 2
Сумматор по модулю 2 выполняет суммирование без учёта переноса. В обычном двоичном сумматоре требуется учитывать перенос, поэтому требуются схемы, позволяющие формировать перенос в следующий двоичный разряд. Таблица истинности такой схемы, называемой полусумматором, приведена в таблице 2.6.
Таблица 2.6 – Таблица истинности полусумматора
| A | B | S | P0 |
| 0 | 0 | 0 | 0 |
| 0 | 1 | 1 | 0 |
| 1 | 0 | 1 | 0 |
| 1 | 1 | 0 | 1 |
Здесь A и B – слагаемые;
S – сумма;
P0 – перенос в старший разряд (выход переноса Pout).
Запишем систему собственных функций для полусумматора:
S = A · B + A · B
P0 = A · B
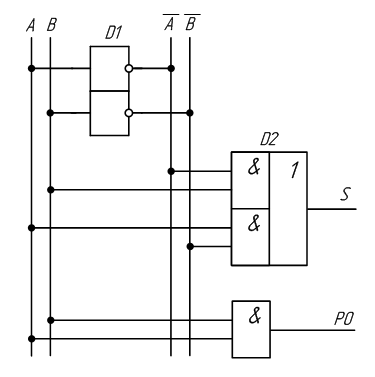
Рисунок 2.13 – Принципиальная схема, реализующая таблицу истинности полусумматора
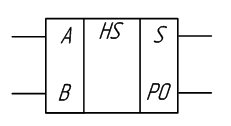
Рисунок 2.14 – Изображение полусумматора на схемах
Полный сумматор.
Схема полусумматора формирует перенос в старший разряд, но не может учитывать перенос из младшего разряда. При сложении многоразрядных двоичных чисел необходимо складывать три цифры в каждом разряде – 2 слагаемых и единицу переноса из предыдущего разряда PI.
Таблица 2.7 – Таблица истинности полного сумматора
| PI | A | B | S | PO |
| 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 1 | 0 |
| 0 | 1 | 0 | 1 | 0 |
| 0 | 1 | 1 | 0 | 1 |
| 1 | 0 | 0 | 1 | 0 |
| 1 | 0 | 1 | 0 | 1 |
| 1 | 1 | 0 | 0 | 1 |
| 1 | 1 | 1 | 1 | 1 |
PI – вход 1 переноса из предыдущего разряда,
PO – выход 1 переноса в старший разряд.
На основании таблицы истинности запишем систему собственных функций для каждого выхода:
S = A · B · PI + A · B · PI + A · B · PI + A · B · PI
PO = A · B · PI + A · B · PI + A · B · PI + A · B · PI
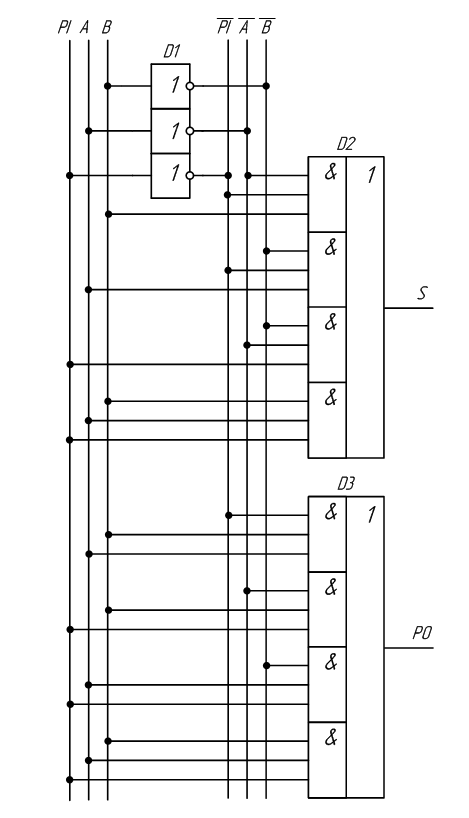
В результате получим схему полного сумматора (рисунок 2.15).
Рисунок 2.15 – Принципиальная схема, реализующая таблицу истинности полного двоичного одноразрядного сумматора
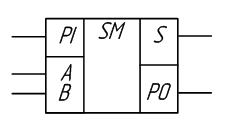
Рисунок 2.16 – Изображение полного двоичного одноразрядного сумматора на схемах
3 Задание к работе
3.1 Исследовать принцип работы дешифратора 2 x 4
Сконфигурировать ПЛИС в соответствии с рисунком 3.1. Подключить к входам X0 и X1 переключатели S7 и S8, а к выходам Y0, Y1, Y2, Y3 светодиодные индикаторы LED5, LED6, LED7, LED8. Для этого подключить входы и выходы дешифратора к соответствующим ножкам ПЛИС.
Рисунок 3.1 – Схема дешифратора
Подавая все возможные комбинации логических уровней на входы X0, X1 с помощью ключей S7, S8 и наблюдая за состояниями светодиодных индикаторов LED5, LED6, LED7, LED8, заполните таблицу истинности дешифратора.
Таблица 3.1 – Таблица дешифратора
| x1 | x2 | y0 | y1 | y2 | y3 |
| 0 | 0 | ||||
| 0 | 1 | ||||
| 1 | 0 | ||||
| 1 | 1 |
3.2 Исследовать принцип работы шифратора 4×2
Сконфигурировать ПЛИС в соответствии с рисунком 3.2.
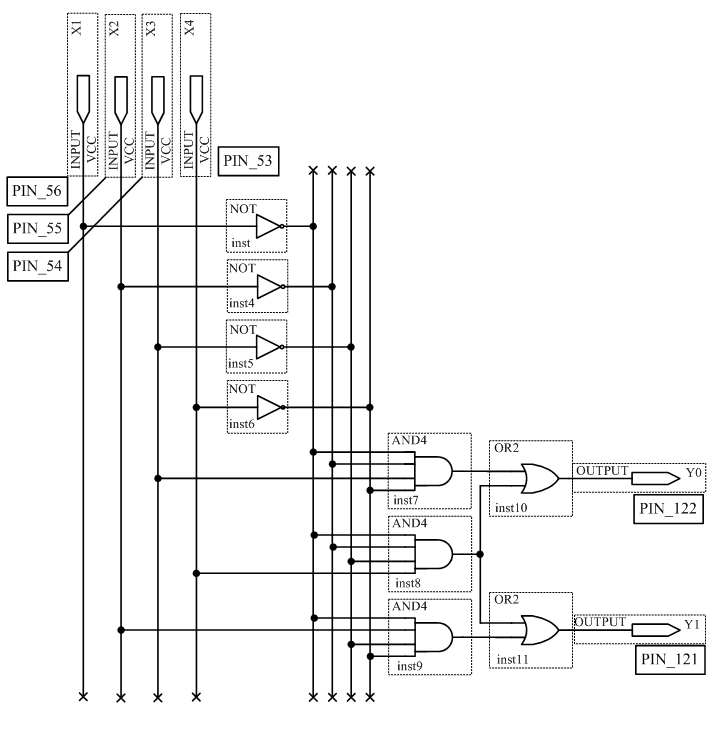
Рисунок 3.2 – Схема шифратора 4×2
Подключить к входам X1, X2, X3, X4 переключатели S8, S7, S6, S5, а к выходам Y0, Y1 светодиодные индикаторы LED8, LED7. Для этого подключить входы и выходы дешифратора к соответствующим ножкам ПЛИС. Подавая все возможные комбинации логических уровней на входы X1, X2, X3, X4 с помощью ключей S8, S7, S6, S5 и наблюдая за состояниями светодиодных индикаторов LED7, LED8, заполните таблицу истинности шифратора.
Таблица 3.2 – Таблица истинности шифратора
| x1 | x2 | x3 | x4 | y1 | y0 |
| 1 | 0 | 0 | 0 | ||
| 0 | 1 | 0 | 0 | ||
| 0 | 0 | 1 | 0 | ||
| 0 | 0 | 0 | 1 |
3.3 Исследовать работу преобразователя кода для семисегментного индикатора.
Составить таблицу истинности преобразователя кода (таблица. 3.3).
Собрать схему, изображенную на рисунке 3.3.
Таблица 3.3 – Таблица истинности преобразователя
| x3 | x2 | x1 | x0 | A | B | C | D | E | F | G |
| 0 | 0 | 0 | 0 | |||||||
| 0 | 0 | 0 | 1 | |||||||
| 0 | 0 | 1 | 0 | |||||||
| 0 | 0 | 1 | 1 | |||||||
| 0 | 1 | 0 | 0 | |||||||
| 0 | 1 | 0 | 1 | |||||||
| 0 | 1 | 1 | 0 | |||||||
| 0 | 1 | 1 | 1 | |||||||
| 1 | 0 | 0 | 0 | |||||||
| 1 | 0 | 0 | 1 |
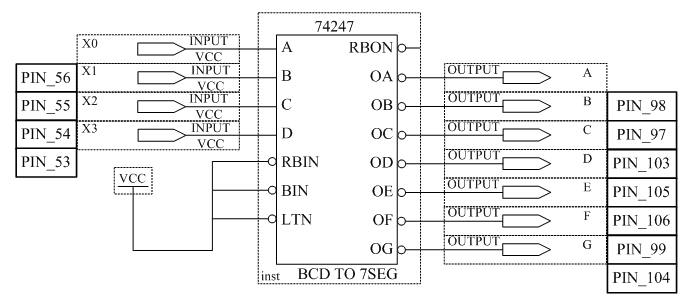
Рисунок 3.3 – Схема преобразователя кода для семисегментного индикатора
Подавая с помощью ключей S8, S7, S6, S5 различные кодовые комбинации на входы X0, X1, X2, X3 определить цифры, высвечиваемые на индикаторе. По результатам эксперимента заполнить таблицу 3.4.
Таблица 3.4 – Таблица, описывающая работу преобразователя кода для семисегментного индикатора
| x3 | x2 | x1 | x0 | Показание индикатора |
| 0 | 0 | 0 | 0 | |
| 0 | 0 | 0 | 1 | |
| 0 | 0 | 1 | 0 | |
| 0 | 0 | 1 | 1 | |
| 0 | 1 | 0 | 0 | |
| 0 | 1 | 0 | 1 | |
| 0 | 1 | 1 | 0 | |
| 0 | 1 | 1 | 1 | |
| 1 | 0 | 0 | 0 | |
| 1 | 0 | 0 | 1 |
3.4 Исследовать работу мультиплексора 4×1
Сконфигурировать ПЛИС в соответствии с рисунком 3.4.
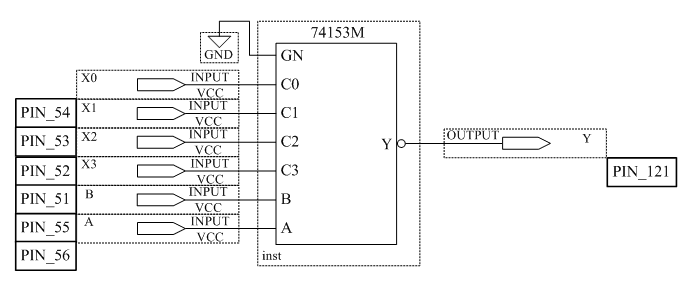
Рисунок 3.4 – Схема мультиплексора 4×1
Поочередно устанавливая все возможные кодовые комбинации на адресных входах A и B, определите номера коммутируемых каналов. Номер коммутируемого канала определяется путем поочерёдного подключения к входам X0, X2, X3, X4 уровня логической единицы и наблюдения за выходом Y. Заполните таблицу 3.5.
Таблица 3.5 – Таблица, описывающая работу мультиплексора
| B | A | Номер коммутируемого канала |
| 0 | 0 | |
| 0 | 1 | |
| 1 | 0 | |
| 1 | 1 |
3.5 Исследовать схему сумматора
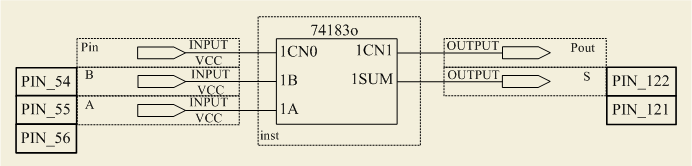
Сконфигурировать ПЛИС в соответствии с рисунком 3.5. Здесь Pin, Pout соответственно вход и выход единицы переноса, A и B – слагаемые, S – сумма.
Рисунок 3.5 – Схема сумматора
Заполнить таблицу истинности сумматора (таблица 3.6).
Таблица 2.7 – Таблица истинности полного сумматора
| Pin | B | A | Pout |
| 0 | 0 | 0 | |
| 0 | 0 | 1 | |
| 0 | 1 | 0 | |
| 0 | 1 | 1 | |
| 1 | 0 | 0 | |
| 1 | 0 | 1 | |
| 1 | 1 | 0 | |
| 1 | 1 | 1 |
4 Содержание отчета
- Цель работы.
- Схемы исследования дешифратора, шифратора, преобразователя кода для семисегментного индикатора, мультиплексора, сумматора.
- Таблицы истинности для каждой схемы.
- Выводы по каждому заданию.
5 Контрольные вопросы
- Принцип работы дешифратора?
- Как синтезировать дешифратор с произвольной разрядностью?
- Как работает шифратор?
- Изобразите таблицу истинности шифратора.
- Как работает преобразователь кода для семисегментного индикатора?
- Как устроен семи сегментный индикатор?
- Как работает мультиплексор?
- Как в лабораторной работе проводилось исследование мультиплексора?
- Как работает сумматор?
- Изобразите таблицу истинности шифратора.
- Что такое единица переноса?
Таблица истинности для шифратора
Шифратор
Рассмотрим следующее устройство – шифратор. Его назначение – преобразовать код с единицей в одной позиции в обычный позиционный код. Таблица истинности для трехразрядного шифратора приведена ниже
Таблица истинности для шифратора
| е7 | e6 | e5 | e4 | e3 | e2 | e1 | e0 | l2 | l1 | l0 |
Количество выходов определяется соотношением
m = log2n,
где m – число выходов, n – количество входов.
Схема трехразрядного шифратора показана ниже. Она непосредственно следует из таблицы истинности. Заметим, что без шины e0 в принципе можно обойтись.
Схема трехразрядного шифратора
Условное изображение трехразрядного шифратора представлено на рисунке
Условное изображение трехразрядного шифратора
Отметим, что шифратор будем называть по числу выходов, так для четырехразрядного шифратора количество входов будет 24=16 и т.п.
Мультиплексор
Мультиплексор подключает один из информационных входов к единственному выходу. Используется весьма часто в электронных устройствах и устройствах связи – когда требуется по одному каналусвязипередать информацию от нескольких источников информации. При этом возможно временное мультиплексирование, частотное мультиплексирование. Здесь мы рассмотрим и в дальнейшем промоделируем простой вариант комбинационного мультиплексора, который подключает один из 8 информационных входов к выходу устройства, причем для указания номера подключаемого сигнала служат три управляющих сигнала. При этом соблюдается приведенное ранее соотношение m = 2, но здесь m иn имеют другой смысл – соответственно это число информационных и управляющих входов мультиплексора. Так, с помощью трех управляющих сигналов можно подключить 8 информационных входов, с помощью четырех – 16 и т. д. Указанное выше соотношение показывает максимально возможное значение информационных входов при данном количестве управляющих. Однако ничего не мешает, например, при четырех управляющих сигналах подключить не 16, а 10 информационных входов, просто ряд комбинаций управляющих сигналов не будут использованы. Схема и условное обозначение мультиплексора представлены на рисунках.
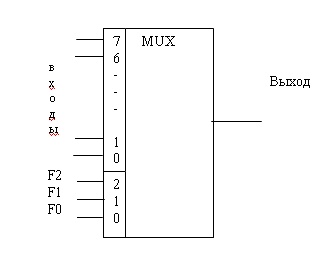
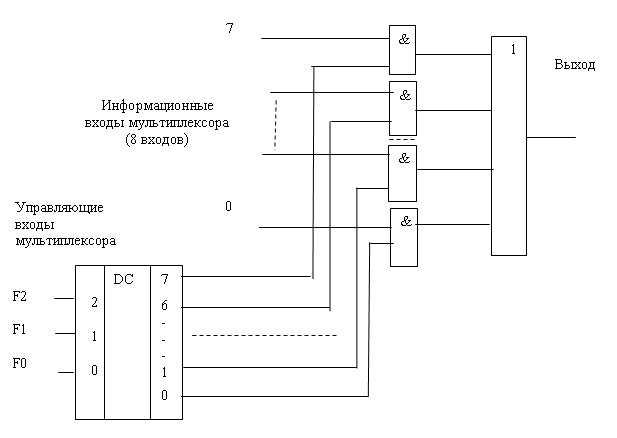
Схема мультиплексора на 8 информационных входов
Схема мультиплексора на 8 информационных входов
Условное обозначение мультиплексора на 8 информационных входов: