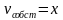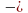Как составить таблицу к задаче с двумя неизвестными

Решение уравнений с двумя неизвестными

В математике большая часть задач ориентирована на решение стандартных уравнений, в которых представлена одна переменная. Однако, некоторые из них, помимо числовых выражений, содержат одновременно две неизвестные. Перед тем как приступить к решению такого уравнения, стоит изучить его определение.

Определение

Итак, уравнением с двумя неизвестными называют любое равенство следующего типа:

a*x + b*y =с, где a, b, c — числа, x, y — неизвестные переменные.

Ниже приведены несколько примеров:

Уравнение с двумя неизвестными точно так же, как и с одной, имеет решение. Однако такие выражения, как правило, имеют бесконечное множество разных решений, поэтому в алгебре их принято называть неопределенными.

Решение задач

Чтобы решить подобные задачи, необходимо отыскать любую пару значений x и y, которая удовлетворяла бы его, другими словами, обращала бы уравнение с неизвестными x и y в правильное числовое равенство. Найти удовлетворяющую пару чисел можно при помощи метода подбора.

Для наглядности объяснений подберем корни для выражения: y-x = 6.

При y=5 и x=-1 равенство становится верным тождеством 5- (-1) = 6. Поэтому пару чисел (-1; 5) можно считать корнями выражения y-x = 6. Ответ: (-1; 5).

Необходимо отметить, что записывать полученный ответ по правилам необходимо в скобках через точку с запятой. Первым указывается значение х, вторым — значение y.

У равенств такого вида может и не быть корней. Рассмотрим такой случай на следующем примере: x+y = x+y+9

Приведем исходное равенство к следующему виду:

В результате мы видим ошибочное равенство, следовательно, это выражение не имеет корней.

При решении уравнений можно пользоваться его свойствами. Первое их них: каждое слагаемое можно вынести в другую часть выражения. Вместе с этим обязательно нужно поменять знак на обратный. Получившееся равенство будет равнозначно исходному.

Например, из выражения 20y — 3x = 16 перенесем неизвестное y в другую его часть.

Оба равенства равносильны.

Второе свойство: допустимо умножать или делить части выражения на одинаковое число, не равное нолю. В итоге получившиеся равенства будут равнозначны.

Оба уравнения также равносильны.

Система уравнений с двумя неизвестными

Система уравнений представляет собой некоторое количество равенств, выполняющихся одновременно. В большинстве задач приходится находить решение системы, состоящей из двух равенств с двумя переменными.

Для решения системы уравнений необходимо найти пару чисел, обращающих оба уравнения системы в правильное равенство. Решением может служить одна пара чисел, несколько пар чисел или вовсе их отсутствие.

Решить подобные системы уравнений можно, применяя следующие методы.

Метод подстановки

1. Выражаем неизвестное из любого равенства через вторую переменную.
2. Подставляем получившееся выражение неизвестного во второе равенство и решаем его.
3. Делаем подстановку полученного значения неизвестного и вычисляем значение второго неизвестного.

Метод сложения

1. Приводим к равенству модули чисел при каком-либо неизвестном.
2. Производим вычисление одной из переменных, произведя сложение или вычитание полученных выражений.
3. Подставляем найденное значение в какое-либо уравнение в первоначальной системе и вычисляем вторую переменную.

Графический метод

1. Выражаем в каждом равенстве одну переменную через другую.
2. Строим графики двух имеющихся уравнений в одной координатной плоскости.
3. Определяем точку их пересечения и ее координаты. На этом шаге у вас может получиться три варианта: графики пересекаются — у системы единственно верный вариант решения; прямые параллельны друг другу — система решений не имеет; графики совпадают — у системы бесконечно много решений.
4. Делаем проверку, подставив полученные значения в исходную систему равенств.

При нахождении корней у одной системы всеми этими способами у вас обязательно должен получиться одинаковый результат, если вы, конечно, все сделали правильно.

В настоящее время есть возможность решения подобных задач с помощью встроенных средств офисной программы Excel, а также на специализированных онлайн-ресурсах и калькуляторах. С помощью них вы легко можете проверить правильность своих вычислений и результатов.

Надеемся, что наша статья помогла вам в освоении этой базовой темы школьной математики. Если же вы пока не можете справиться с решением уравнений такого вида, не расстраивайтесь. Для понимания и закрепления изученной темы рекомендуется как можно больше практиковаться, и тогда у вас без труда получится решать задачи любой сложности. Желаем вам удачи в покорении математических вершин!

Видео

Из этого видео вы узнаете, как решать уравнения с двумя неизвестными.

Решение текстовых задач. 9-й класс

Разделы: Математика

Класс: 9

1. Совершенствование навыков решения текстовых задач.
2. Продолжить формирование знаний учащихся по решению систем уравнений с двумя неизвестными.
3. Развитие математической грамотности.

1. Актуализация знаний учащихся (5 минут).

1. Найдите решение системы уравнений:

Ответы: 1) (1;3); 2) (0;3); 3) (1;2); 4) (2;1).

2. Выразите из уравнения 3х + 2у = 5 переменную х через переменную у.

1)

2)

2. Объяснение нового материала (8 минут).

Алгоритм решения задач на движение и на производительность:

1. Ввести неизвестные величины.
2. Составить краткую запись задачи в таблице (скорость, путь, время) или (производительность, работа, время).
3. Исходя из условия задачи, составить систему двух уравнений с двумя неизвестными.
4. Решить систему уравнений, исключив те корни, которые не подходят по условию задачи.
5. Записать ответ по вопросу задачи.

Расстояние между двумя пристанями 60 км. Теплоход проходит это расстояние по течению и против течения за 5,5 часов. Найдите скорость теплохода в стоячей воде и скорость течения, если одна из них больше другой на 20 км/ч.

Краткая запись: пусть скорость теплохода х км/ч, а скорость течения реки у км/ч, тогда

Скорость, км/ч	Путь, км	Время, ч
По течению	х + у	60	60/(х + у)
Против течения	х – у	60	60/(х – у)

Зная, что теплоход проходит это расстояние по течению и против течения реки за 5,5 часов и скорость катера больше скорости течения реки, составим систему двух уравнений с двумя неизвестными:

Ответ: 22 км/ч – скорость теплохода, 2 км/ч – скорость течения реки.

3. Решение задач (30 минут).

Фермер отправился на машине в город, находящийся на расстоянии 110 км от фермы. Через 20 минут из города на ферму выехал его сын, который проезжал в час на 5 км больше. Встреча произошла в 50 км от города. С какой скоростью ехал фермер?

Краткая запись: пусть скорость фермера х км/ч, а скорость сына у, тогда

Скорость, км/ч	Путь, км	Время, ч
Фермер	х	110 – 50 = 60	60/х
Сын	у	50	50/у

Зная, что встреча произошла в 50 км от города, и сын выехал на 20 минут позже, составим систему уравнений с двумя неизвестными:

Второе решение не подходит по условию задачи.

Ответ: 45 км/ч скорость фермера.

Расстояние в 360 км легковой автомобиль прошел на 2 часа быстрее, чем грузовой. Если скорость каждого автомобиля увеличить на 30 км/ч, то грузовой затратит на весь путь на 1 час больше, чем легковой. Найдите скорость каждого автомобиля.

Краткая запись: пусть скорость легкового автомобиля х км/ч, а скорость грузового у км/ч, тогда:

Скорость, км/ч	Путь, км	Время, ч
Легковой	х	360	360/х
Грузовой	у	360	360/у

Скорость, км/ч	Путь, км	Время, ч
Легковой	х + 30	360	360/(х + 30)
Грузовой	у + 30	360	360/(у + 30)

Зная, что в первом случае легковой автомобиль приезжает на 2 часа раньше, а во втором на 1 час раньше, составим систему уравнений с двумя переменными:

Ответ: 90 км/ч скорость легкового автомобиля, 60 км/ч скорость грузового автомобиля.

Бассейн наполнится. Если первую трубу открыть на 12 минут, а вторую – на 7 минут. Если же обе трубы открыть на 6 минут. То наполнится 2/3 бассейна. За сколько минут наполнится бассейн, если открыть только вторую трубу?

Краткая запись: пусть весь объем воды в бассейне равен 1, производительность 1 трубы х , а второй – у, тогда:

Производительность	Работа	Время, мин
1 труба	х	12х	12
2 труба	у	7у

Производительность	Работа	Время, мин
1 труба	х	6х	6
2 труба	у	6у	6

Зная, что в первом случае бассейн наполнится полностью, а во втором только 2/3, составим систему двух уравнений с двумя неизвестными.

Ответ: за 15 минут вторая труба заполнит весь бассейн.

Двое рабочих могут выполнить задание за 12 дней. Если сначала один из них сделает половину всей работы, а потом остальное сделает другой, то им потребуется 25 дней. За сколько дней каждый рабочий, работая один, может выполнить задание?

Краткая запись: пусть производительность 1 рабочего х, а второго у, тогда:

Производительность	Работа	Время
1 рабочий	х	1/2	1/2х
2 рабочий	у	1/2	1/2у

Зная, что вместе они сделают работу за 12 дней, а работая по очереди и выполнив по половине работы, им потребуется 25 дней, составим систему уравнений с двумя неизвестными:

Ответ: один рабочий выполнит всю работу за 30 дней, а другой за 20 дней.

4. Подведение итогов урока (2 минуты).

Домашнее задание: п. 22, №476, 479, 491.

1. Учебник «Алгебра 9», автор Макарычев Ю.Н., Миндюк Н.Г., Нешков К.И., Феоктистов И.Е.

Системы линейных уравнений

Линейные уравнения с двумя переменными

У школьника имеется 200 рублей, чтобы пообедать в школе. Пирожное стоит 25 рублей, а чашка кофе 10 рублей. Сколько пирожных и чашек кофе можно накупить на 200 рублей?

Обозначим количество пирожных через x , а количество чашек кофе через y . Тогда стоимость пирожных будет обозначаться через выражение 25x , а стоимость чашек кофе через 10y .

25x — стоимость x пирожных
10y — стоимость y чашек кофе

Итоговая сумма должна равняться 200 рублей. Тогда получится уравнение с двумя переменными x и y

Сколько корней имеет данное уравнение?

Всё зависит от аппетита школьника. Если он купит 6 пирожных и 5 чашек кофе, то корнями уравнения будут числа 6 и 5.

Говорят, что пара значений 6 и 5 являются корнями уравнения 25x + 10y = 200 . Записывается как (6; 5) , при этом первое число является значением переменной x , а второе — значением переменной y .

6 и 5 не единственные корни, которые обращают уравнение 25x + 10y = 200 в тождество. При желании на те же 200 рублей школьник может купить 4 пирожных и 10 чашек кофе:

В этом случае корнями уравнения 25x + 10y = 200 является пара значений (4; 10) .

Более того, школьник может вообще не покупать кофе, а купить пирожные на все 200 рублей. Тогда корнями уравнения 25x + 10y = 200 будут значения 8 и 0

Или наоборот, не покупать пирожные, а купить кофе на все 200 рублей. Тогда корнями уравнения 25x + 10y = 200 будут значения 0 и 20

Попробуем перечислить все возможные корни уравнения 25x + 10y = 200 . Условимся, что значения x и y принадлежат множеству целых чисел. И пусть эти значения будут бóльшими или равными нулю:

Так будет удобно и самому школьнику. Пирожные удобнее покупать целыми, чем к примеру несколько целых пирожных и половину пирожного. Кофе также удобнее брать целыми чашками, чем к примеру несколько целых чашек и половину чашки.

Заметим, что при нечетном x невозможно достичь равенства ни при каком y . Тогда значениями x будут следующие числа 0, 2, 4, 6, 8. А зная x можно без труда определить y

Таким образом, мы получили следующие пары значений (0; 20), (2; 15), (4; 10), (6; 5), (8; 0). Эти пары являются решениями или корнями уравнения 25x + 10y = 200 . Они обращают данное уравнение в тождество.

Уравнение вида ax + by = c называют линейным уравнением с двумя переменными. Решением или корнями этого уравнения называют пару значений ( x; y ), которая обращает его в тождество.

Отметим также, что если линейное уравнение с двумя переменными записано в виде ax + b y = c , то говорят, что оно записано в каноническом (нормальном) виде.

Некоторые линейные уравнения с двумя переменными могут быть приведены к каноническому виду.

Например, уравнение 2(16x + 3y − 4) = 2(12 + 8x − y) можно привести к виду ax + by = c . Раскроем скобки в обеих частях этого уравнения, получим 32x + 6y − 8 = 24 + 16x − 2y . Слагаемые, содержащие неизвестные сгруппируем в левой части уравнения, а слагаемые свободные от неизвестных — в правой. Тогда получим 32x − 16x + 6y + 2y = 24 + 8 . Приведём подобные слагаемые в обеих частях, получим уравнение 16x + 8y = 32. Это уравнение приведено к виду ax + by = c и является каноническим.

Рассмотренное ранее уравнение 25x + 10y = 200 также является линейным уравнением с двумя переменными в каноническом виде . В этом уравнении параметры a , b и c равны значениям 25, 10 и 200 соответственно.

На самом деле уравнение ax + by = c имеет бесчисленное множество решений. Решая уравнение 25x + 10y = 200, мы искали его корни только на множестве целых чисел. В результате получили несколько пар значений, которые обращали данное уравнение в тождество. Но на множестве рациональных чисел уравнение 25x + 10y = 200 будет иметь бесчисленное множество решений.

Для получения новых пар значений, нужно взять произвольное значение для x , затем выразить y . К примеру, возьмем для переменной x значение 7. Тогда получим уравнение с одной переменной 25 × 7 + 10y = 200 в котором можно выразить y

Пусть x = 15 . Тогда уравнение 25x + 10y = 200 примет вид 25 × 15 + 10y = 200. Отсюда находим, что y = −17,5

Пусть x = −3 . Тогда уравнение 25x + 10y = 200 примет вид 25 × (−3) + 10y = 200. Отсюда находим, что y = −27,5

Система двух линейных уравнений с двумя переменными

Для уравнения ax + by = c можно сколько угодно раз брать произвольные значение для x и находить значения для y . Отдельно взятое такое уравнение будет иметь бесчисленное множество решений.

Но бывает и так, что переменные x и y связаны не одним, а двумя уравнениями. В этом случае они образуют так называемую систему линейных уравнений с двумя переменными. Такая система уравнений может иметь одну пару значений (или по-другому: «одно решение»).

Может случиться и так, что система вовсе не имеет решений. Бесчисленное множество решений система линейных уравнений может иметь в редких и в исключительных случаях.

Два линейных уравнения образуют систему тогда, когда значения x и y входят в каждое из этих уравнений.

Вернемся к самому первому уравнению 25x + 10y = 200 . Одной из пар значений для этого уравнения была пара (6; 5) . Это случай, когда на 200 рублей можно можно было купить 6 пирожных и 5 чашек кофе.

Составим задачу так, чтобы пара (6; 5) стала единственным решением для уравнения 25x + 10y = 200 . Для этого составим ещё одно уравнение, которое связывало бы те же x пирожных и y чашечек кофе.

Поставим текст задачи следующим образом:

«Школьник купил на 200 рублей несколько пирожных и несколько чашек кофе. Пирожное стоит 25 рублей, а чашка кофе 10 рублей. Сколько пирожных и чашек кофе купил школьник, если известно что количество пирожных на одну единицу больше количества чашек кофе?»

Первое уравнение у нас уже есть. Это уравнение 25x + 10y = 200 . Теперь составим уравнение к условию «количество пирожных на одну единицу больше количества чашек кофе» .

Количество пирожных это x , а количество чашек кофе это y . Можно записать эту фразу с помощью уравнения x − y = 1. Это уравнение будет означать, что разница между пирожными и кофе составляет 1.

Либо второе уравнение можно записать как x = y + 1 . Это уравнение означает, что количество пирожных на единицу больше, чем количество чашек кофе. Поэтому для получения равенства, к количеству чашек кофе прибавлена единица. Это легко можно понять, если воспользоваться моделью весов, которые мы рассматривали при изучении простейших задач:

Получили два уравнения: 25x + 10y = 200 и x = y + 1. Поскольку значения x и y , а именно 6 и 5 входят в каждое из этих уравнений , то вместе они образуют систему. Запишем эту систему. Если уравнения образуют систему, то они обрамляются знаком системы. Знак системы это фигурная скобка:

Давайте решим данную систему. Это позволит увидеть, как мы придём к значениям 6 и 5. Существует много методов решения таких систем. Рассмотрим наиболее популярные из них.

Метод подстановки

Название этого метода говорит само за себя. Суть его заключается в том, чтобы одно уравнение подставить в другое, предварительно выразив одну из переменных.

В нашей системе ничего выражать не нужно. Во втором уравнении x = y + 1 переменная x уже выражена. Эта переменная равна выражению y + 1 . Тогда можно подставить это выражение в первое уравнение вместо переменной x

После подстановки выражения y + 1 в первое уравнение вместо x , получим уравнение 25(y + 1) + 10y = 200 . Это линейное уравнение с одной переменной. Такое уравнение решить довольно просто:

Мы нашли значение переменной y . Теперь подставим это значение в одно из уравнений и найдём значение x . Для этого удобно использовать второе уравнение x = y + 1 . В него и подставим значение y

Значит пара (6; 5) является решением системы уравнений, как мы и задумывали. Выполняем проверку и убеждаемся, что пара (6; 5) удовлетворяет системе:

Пример 2. Решить методом подстановки следующую систему уравнений:

Подставим первое уравнение x = 2 + y во второе уравнение 3x − 2y = 9 . В первом уравнении переменная x равна выражению 2 + y . Это выражение и подставим во второе уравнение вместо x

Теперь найдём значение x . Для этого подставим значение y в первое уравнение x = 2 + y

Значит решением системы является пара значение (5; 3)

Пример 3. Решить методом подстановки следующую систему уравнений:

Здесь в отличие от предыдущих примеров, одна из переменных не выражена явно.

Чтобы подставить одно уравнение в другое, сначала нужно выразить одну из переменных.

Выражать желательно ту переменную, которая имеет коэффициент единицу. Коэффициент единицу имеет переменная x , которая содержится в первом уравнении x + 2y = 11 . Эту переменную и выразим.

После выражения переменной x , наша система примет следующий вид:

Теперь подставим первое уравнение во второе и найдем значение y

Подставим y в первое уравнение и найдём x

Значит решением системы является пара значений (3; 4)

Конечно, выражать можно и переменную y . Корни от этого не изменятся. Но если выразить y, получится не очень-то и простое уравнение, на решение которого уйдет больше времени. Выглядеть это будет следующим образом:

Видим, что в данном примере выражать x намного удобнее, чем выражать y .

Пример 4. Решить методом подстановки следующую систему уравнений:

Выразим в первом уравнении x . Тогда система примет вид:

Подставим первое уравнение во второе и найдём y

Подставим y в первое уравнение и найдём x . Можно воспользоваться изначальным уравнением 7x + 9y = 8 , либо воспользоваться уравнением , в котором выражена переменная x . Этим уравнением и воспользуемся, поскольку это удобно:

Значит решением системы является пара значений (5; −3)

Метод сложения

Метод сложения заключается в том, чтобы почленно сложить уравнения, входящие в систему. Это сложение приводит к тому, что образуется новое уравнение с одной переменной. А решить такое уравнение довольно просто.

Решим следующую систему уравнений:

Сложим левую часть первого уравнения с левой частью второго уравнения. А правую часть первого уравнения с правой частью второго уравнения. Получим следующее равенство:

Приведем подобные слагаемые:

В результате получили простейшее уравнение 3x = 27 корень которого равен 9. Зная значение x можно найти значение y . Подставим значение x во второе уравнение x − y = 3 . Получим 9 − y = 3 . Отсюда y = 6 .

Значит решением системы является пара значений (9; 6)

Пример 2. Решить следующую систему уравнений методом сложения:

Сложим левую часть первого уравнения с левой частью второго уравнения. А правую часть первого уравнения с правой частью второго уравнения. В получившемся равенстве приведем подобные слагаемые:

В результате получили простейшее уравнение 5 x = 20, корень которого равен 4. Зная значение x можно найти значение y . Подставим значение x в первое уравнение 2 x + y = 11 . Получим 8 + y = 11 . Отсюда y = 3 .

Значит решением системы является пара значений (4;3)

Процесс сложения подробно не расписывают. Его нужно выполнять в уме. При сложении оба уравнения должны быть приведены к каноническому виду. То есть к виду ax + by = c .

Из рассмотренных примеров видно, что основная цель сложения уравнений это избавление от одной из переменных. Но не всегда удаётся сразу решить систему уравнений методом сложения. Чаще всего систему предварительно приводят к виду, при котором можно сложить уравнения, входящие в эту систему.

Например, систему можно сразу решить методом сложения. При сложении обоих уравнений, слагаемые y и −y исчезнут, поскольку их сумма равна нулю. В результате образуется простейшее уравнение 11x = 22 , корень которого равен 2. Затем можно будет определить y равный 5.

А систему уравнений методом сложения сразу решить нельзя, поскольку это не приведёт к исчезновению одной из переменных. Сложение приведет к тому, что образуется уравнение 8x + y = 28 , имеющее бесчисленное множество решений.

Если обе части уравнения умножить или разделить на одно и то же число, не равное нулю, то получится уравнение равносильное данному. Это правило справедливо и для системы линейных уравнений с двумя переменными. Одно из уравнений (или оба уравнения) можно умножить на какое-нибудь число. В результате получится равносильная система, корни которой будут совпадать с предыдущей.

Вернемся к самой первой системе , которая описывала сколько пирожных и чашек кофе купил школьник. Решением этой системы являлась пара значений (6; 5) .

Умножим оба уравнения, входящие в эту систему на какие-нибудь числа. Скажем первое уравнение умножим на 2, а второе на 3

В результате получили систему
Решением этой системы по-прежнему является пара значений (6; 5)

Это значит, что уравнения входящие в систему можно привести к виду, пригодному для применения метода сложения.

Вернемся к системе , которую мы не смогли решить методом сложения.

Умножим первое уравнение на 6, а второе на −2

Тогда получим следующую систему:

Сложим уравнения, входящие в эту систему. Сложение компонентов 12x и −12x даст в результате 0, сложение 18y и 4y даст 22y , а сложение 108 и −20 даст 88. Тогда получится уравнение 22y = 88 , отсюда y = 4 .

Если первое время тяжело складывать уравнения в уме, то можно записывать как складывается левая часть первого уравнения с левой частью второго уравнения, а правая часть первого уравнения с правой частью второго уравнения:

Зная, что значение переменной y равно 4, можно найти значение x. Подставим y в одно из уравнений, например в первое уравнение 2x + 3y = 18 . Тогда получим уравнение с одной переменной 2x + 12 = 18 . Перенесем 12 в правую часть, изменив знак, получим 2x = 6 , отсюда x = 3 .

Пример 4. Решить следующую систему уравнений методом сложения:

Умножим второе уравнение на −1. Тогда система примет следующий вид:

Сложим оба уравнения. Сложение компонентов x и −x даст в результате 0, сложение 5y и 3y даст 8y , а сложение 7 и 1 даст 8. В результате получится уравнение 8y = 8 , корень которого равен 1. Зная, что значение y равно 1, можно найти значение x .

Подставим y в первое уравнение, получим x + 5 = 7 , отсюда x = 2

Пример 5. Решить следующую систему уравнений методом сложения:

Желательно, чтобы слагаемые содержащие одинаковые переменные, располагались друг под другом. Поэтому во втором уравнении слагаемые 5y и −2x поменяем местами. В результате система примет вид:

Умножим второе уравнение на 3. Тогда система примет вид:

Теперь сложим оба уравнения. В результате сложения получим уравнение 8y = 16 , корень которого равен 2.

Подставим y в первое уравнение, получим 6x − 14 = 40 . Перенесем слагаемое −14 в правую часть, изменив знак, получим 6x = 54 . Отсюда x = 9.

Пример 6. Решить следующую систему уравнений методом сложения:

Избавимся от дробей. Умножим первое уравнение на 36, а второе на 12

В получившейся системе первое уравнение можно умножить на −5, а второе на 8

Сложим уравнения в получившейся системе. Тогда получим простейшее уравнение −13y = −156 . Отсюда y = 12 . Подставим y в первое уравнение и найдем x

Пример 7. Решить следующую систему уравнений методом сложения:

Приведем оба уравнения к нормальному виду. Здесь удобно применить правило пропорции в обоих уравнениях. Если в первом уравнении правую часть представить как , а правую часть второго уравнения как , то система примет вид:

У нас получилась пропорция. Перемножим её крайние и средние члены. Тогда система примет вид:

Первое уравнение умножим на −3, а во втором раскроем скобки:

Теперь сложим оба уравнения. В результате сложения этих уравнений, мы получим равенство, в обеих частях которого будет ноль:

Получается, что система имеет бесчисленное множество решений.

Но мы не можем просто так взять с неба произвольные значения для x и y . Мы можем указать одно из значений, а другое определится в зависимости от значения, указанного нами. Например, пусть x = 2 . Подставим это значение в систему:

В результате решения одного из уравнений, определится значение для y , которое будет удовлетворять обоим уравнениям:

Получившаяся пара значений (2; −2) будет удовлетворять системе:

Найдём еще одну пару значений. Пусть x = 4. Подставим это значение в систему:

На глаз можно определить, что значение y равно нулю. Тогда получим пару значений (4; 0), которая удовлетворяет нашей системе:

Пример 8. Решить следующую систему уравнений методом сложения:

Умножим первое уравнение на 6, а второе на 12

Перепишем то, что осталось:

Раскроем скобки в обоих уравнениях и приведём подобные слагаемые:

Первое уравнение умножим на −1. Тогда система примет вид:

Теперь сложим оба уравнения. В результате сложения образуется уравнение 6b = 48 , корень которого равен 8. Подставим b в первое уравнение и найдём a

Система линейных уравнений с тремя переменными

В линейное уравнение с тремя переменными входит три переменные с коэффициентами, а также свободный член. В каноническом виде его можно записать следующим образом:

Данное уравнение имеет бесчисленное множество решений. Придавая двум переменным различные значения, можно найти третье значение. Решением в этом случае является тройка значений (x; y; z) которая обращает уравнение в тождество.

Если переменные x, y, z связаны между собой тремя уравнениями, то образуется система трех линейных уравнений с тремя переменными. Для решения такой системы можно применять те же методы, которые применяются к линейным уравнениям с двумя переменными: метод подстановки и метод сложения.

Пример 1. Решить следующую систему уравнений методом подстановки:

Выразим в третьем уравнении x . Тогда система примет вид:

Теперь выполним подстановку. Переменная x равна выражению 3 − 2y − 2z . Подставим это выражение в первое и второе уравнение:

Раскроем скобки в обоих уравнениях и приведём подобные слагаемые:

Мы пришли к системе линейных уравнений с двумя переменными. В данном случае удобно применить метод сложения. В результате переменная y исчезнет, и мы сможем найти значение переменной z

Теперь найдём значение y . Для этого удобно воспользоваться уравнением −y + z = 4. Подставим в него значение z

Теперь найдём значение x . Для этого удобно воспользоваться уравнением x = 3 − 2y − 2z . Подставим в него значения y и z

Таким образом, тройка значений (3; −2; 2) является решением нашей системы. Проверкой убеждаемся, что эти значения удовлетворяют системе:

Пример 2. Решить систему методом сложения

Сложим первое уравнение со вторым, умноженным на −2.

Если второе уравнение умножить на −2, то оно примет вид −6x + 6y − 4z = −4 . Теперь сложим его с первым уравнением:

Видим, что в результате элементарных преобразований, определилось значение переменной x . Оно равно единице.

Вернемся к главной системе. Сложим второе уравнение с третьим, умноженным на −1. Если третье уравнение умножить на −1, то оно примет вид −4x + 5y − 2z = −1 . Теперь сложим его со вторым уравнением:

Получили уравнение x − 2y = −1 . Подставим в него значение x , которое мы находили ранее. Тогда мы сможем определить значение y

Теперь нам известны значения x и y . Это позволяет определить значение z . Воспользуемся одним из уравнений, входящим в систему:

Таким образом, тройка значений (1; 1; 1) является решением нашей системы. Проверкой убеждаемся, что эти значения удовлетворяют системе:

Задачи на составление систем линейных уравнений

Задача на составление систем уравнений решается путем ввода нескольких переменных. Далее составляются уравнения на основании условий задачи. Из составленных уравнений образуют систему и решают её. Решив систему, необходимо выполнить проверку на то, удовлетворяет ли её решение условиям задачи.

Задача 1. Из города в колхоз выехала машина «Волга». Обратно она возвращалась по другой дороге, которая была на 5 км короче первой. Всего в оба конца машина проехала 35 км. Сколько километров составляет длина каждой дороги?

Решение

Пусть x — длина первой дороги, y — длина второй. Если в оба конца машина проехала 35 км, то первое уравнение можно записать как x + y = 35. Это уравнение описывает сумму длин обеих дорог.

Сказано, что обратно машина возвращалась по дороге которая была короче первой на 5 км. Тогда второе уравнение можно записать как x − y = 5. Это уравнение показывает, что разница между длинами дорог составляет 5 км.

Либо второе уравнение можно записать как x = y + 5 . Этим уравнением и воспользуемся.

Поскольку переменные x и y в обоих уравнениях обозначают одно и то же число, то мы можем образовать из них систему:

Решим эту систему каким-нибудь из изученных ранее методов. В данном случае удобно воспользоваться методом подстановки, поскольку во втором уравнении переменная x уже выражена.

Подставим второе уравнение в первое и найдём y

Подставим найденное значение y в во второе уравнение x = y + 5 и найдём x

Длина первой дороги была обозначена через переменную x . Теперь мы нашли её значение. Переменная x равна 20. Значит длина первой дороги составляет 20 км.

А длина второй дороги была обозначена через y . Значение этой переменной равно 15. Значит длина второй дороги составляет 15 км.

Выполним проверку. Для начала убедимся, что система решена правильно:

Теперь проверим удовлетворяет ли решение (20; 15) условиям задачи.

Было сказано, что всего в оба конца машина проехала 35 км. Складываем длины обеих дорог и убеждаемся, что решение (20; 15) удовлетворяет данному условию: 20 км + 15 км = 35 км

Следующее условие: обратно машина возвращалась по другой дороге, которая была на 5 км короче первой . Видим, что решение (20; 15) удовлетворяет и этому условию, поскольку 15 км короче, чем 20 км на 5 км: 20 км − 15 км = 5 км

При составлении системы важно, чтобы переменные обозначали одни и те же числа во всех уравнениях, входящих в эту систему.

Так наша система содержит два уравнения. Эти уравнения в свою очередь содержат переменные x и y , которые обозначают одни и те же числа в обоих уравнениях, а именно длины дорог, равных 20 км и 15 км.

Задача 2. На платформу были погружены дубовые и сосновые шпалы, всего 300 шпал. Известно, что все дубовые шпалы весили на 1 т меньше, чем все сосновые. Определить, сколько было дубовых и сосновых шпал отдельно, если каждая дубовая шпала весила 46 кг, а каждая сосновая 28 кг.

Решение

Пусть x дубовых и y сосновых шпал было погружено на платформу. Если всего шпал было 300, то первое уравнение можно записать как x + y = 300 .

Все дубовые шпалы весили 46x кг, а сосновые весили 28y кг. Поскольку дубовые шпалы весили на 1 т меньше, чем сосновые, то второе уравнение можно записать, как 28y − 46x = 1000 . Это уравнение показывает, что разница масс между дубовыми и сосновыми шпалами, составляет 1000 кг.

В результате получаем два уравнения, которые образуют систему

Решим данную систему. Выразим в первом уравнении x . Тогда система примет вид:

Подставим первое уравнение во второе и найдём y

Подставим y в уравнение x = 300 − y и узнаем чему равно x

Значит на платформу было погружено 100 дубовых и 200 сосновых шпал.

Проверим удовлетворяет ли решение (100; 200) условиям задачи. Для начала убедимся, что система решена правильно:

Было сказано, что всего было 300 шпал. Складываем количество дубовых и сосновых шпал и убеждаемся, что решение (100; 200) удовлетворяет данному условию: 100 + 200 = 300.

Следующее условие: все дубовые шпалы весили на 1 т меньше, чем все сосновые . Видим, что решение (100; 200) удовлетворяет и этому условию, поскольку 46 × 100 кг дубовых шпал легче, чем 28 × 200 кг сосновых шпал: 5600 кг − 4600 кг = 1000 кг.

Задача 3. Взяли три куска сплава меди с никелем в отношениях 2 : 1 , 3 : 1 и 5 : 1 по массе. Из них сплавлен кусок массой 12 кг с отношением содержания меди и никеля 4 : 1 . Найдите массу каждого исходного куска, если масса первого из них вдвое больше массы второго.

Решение

Пусть x — масса первого куска, y — масса второго куска, z — масса третьего куска. Если из этих кусков сплавлен кусок массой 12 кг, то первое уравнение можно записать как x + y + z = 12 .

Масса первого куска вдвое больше массы второго куска. Тогда второе уравнение можно записать как x = 2y .

Полученных двух уравнений недостаточно для решения данной задачи. Если второе уравнение подставить в первое, то мы получим уравнение 2y + y + z = 12 , откуда 3y + z = 12 . Это уравнение имеет бесчисленное множество решений.

Составим ещё одно уравнение. Пусть это уравнение будет описывать количество меди, взятого с каждого сплава и сколько меди оказалось в получившемся сплаве.

Если первый сплав имеет массу x , а медь и никель находится нём в отношении 2 : 1 , то можно записать, что в новом сплаве содержится меди от первого куска.

Если второй сплав имеет массу y , а медь и никель находится в нём в отношении 3 : 1 , то можно записать, что в новом сплаве содержится меди от второго куска.

Если третий сплав имеет массу z , а медь и никель находится в отношении 5 : 1 , то можно записать, что в новом сплаве содержится меди от третьего куска.

Полученный сплав имеет имеет массу 12 кг, а медь и никель находится в нём в отношении 4 : 1 . Тогда можно записать, что в полученном сплаве содержится меди.

Сложим , , и приравняем эту сумму к 9,6. Это и будет нашим третьим уравнением:

Попробуем решить данную систему.

Для начала упростим третье уравнение. Подставим в него второе уравнение и посмотрим, что из этого выйдет:

Теперь в главной системе вместо уравнения запишем уравнение, которое мы сейчас получили, а именно уравнение 25y + 10z = 115,2

Подставим второе уравнение в первое:

Умножим первое уравнение на −10 . Тогда система примет вид:

Сложим оба уравнения. Тогда получим простейшее уравнение −5y = −4,8 откуда найдём y равный 0,96 . Значит масса второго сплава составляет 0,96 кг .

Теперь найдём x . Для этого удобно воспользоваться уравнением x = 2y. Значение y уже известно. Осталось только подставить его:

Значит масса первого сплава составляет 1,92 кг .

Теперь найдём z . Для этого удобно воспользоваться уравнением x + y + z = 12 . Значения x и y уже известны. Подставим их куда нужно:

Значит масса третьего сплава составляет 9,12 кг.

Решите с помощью системы уравнений:

1. У причала находилось 6 лодок, часть из
которых была двухместными, а часть —
трехместными. Всего в эти лодки может
поместиться 14 человек. Сколько двухместных и
сколько трехместных лодок было у причала?

2. В хозяйстве имеются куры и овцы. Сколько тех
и других, если у них вместе 19 голов и 46 ног?

Подведение итогов урока.

Домашнее задание: параграф 14 , №14.7, 14.14.

26.02.2011

Поделиться страницей:

xn--i1abbnckbmcl9fb.xn--p1ai

Решение систем уравнений с двумя неизвестными как математические модели реальных ситуаций 9 класс

Долхонова В.В. МБОУ «Еланцынская СОШ»

Урок по алгебре

Класс: 9

Тема: «Решение систем уравнений как математические модели реальных ситуаций»

Цели урока:

Обучающие:

1. Продолжать работу по формированию навыков решения задач с помощью систем уравнений второй степени.

2. Закрепить знания решения систем уравнений второй степени аналитическим способом (способ подстановки)в ходе решения задач.

3. решать задания, которые наиболее часто встречаются на «ГИА».

Развивающие:

1. использование для достижения поставленной задачи уже полученные знания;

2. умение обосновывать свои рассуждения;

Воспитательные:

1. выработка желания и потребности обобщать полученные факты;

2. воспитание настойчивости и терпения при выполнении заданий.

3. Побуждать учеников к самоконтролю, воспитывать интерес к математике.

Оборудование: проектор, ПК

Прогнозируемый результат:

1. Знать способы и методы решения систем уравнений второй степени.

2. Уметь правильно отбирать способы решения систем уравнений второй степени для решения задач с помощью систем уравнений.

Эпиграф:

1.Китайская мудрость: « Я слышу – я забываю, я вижу – запоминаю,

я делаю – я усваиваю».

2. «Если вы хотите научиться плавать, то смело входите в воду, а если хотите научиться решать задачи, то решайте их!»

Д. Пойа

План урока:

1. Организационный момент.

2. Математический диктант.

3. Объяснение материала

4. Закрепление материала

5. Подведение итога урока.

6. Домашняя работа

Ход занятия

1. Организационный момент

1. Проверка подготовленности учащихся к занятию.

2. Приветствие учителя и учащихся.

3. Постановка целей и задач занятия.

Прочитайте высказывание математика Д. Пойа. Какой совет дает ученый нам? Мудрость высказывания математика Д.Пойа объедините с предыдущей темой и сформулируйте тему урока.

Сегодня мы познакомимся с задачами, решение которых сводится к

системам уравнений. Запишем тему урока. Назовите цель урока.

Мотивация (самоопределение) к учебной деятельности.

— Работать сегодня мы будем коллективно, в парах и индивидуально.

Вспомните правила работы в парах. (Прислушиваться к мнению соседа, работать дружно, помогать друг другу). В конце урока каждый из вас оценит свою работу и работу партнёра.

2.Математический диктант

Перед вами лежат задания математического диктанта, выполните его.

1вариант.

Составьте уравнение с двумя переменными, если:

1. Сумма двух натуральных чисел равна 16.

2. Периметр прямоугольника равен 12 см.

3. Одна сторона прямоугольника на 8 см больше другой.

4. Произведение двух натуральных чисел равно 28.

5. Диагональ прямоугольника равна 5 см.

2 вариант

Составьте уравнение с двумя переменными, если:

1. Разность двух натуральных чисел равна 14.

2. Площадь прямоугольника равна 26 см².

3. Катет прямоугольного треугольника на 5 см больше другого.

4. Сумма квадратов двух натуральных чисел равна 30.

5. Гипотенуза прямоугольного треугольника равна 8 см.

На экране проецируются ответы и критерии оценивания.

Ребятам в парах предлагается проверить и оценить работу друг друга.

Объяснение материала

При решении задач с помощью системы уравнений придерживаемся следующего алгоритма: (слайд)

I. Составление математической модели:

1. Внимательно изучить условие задачи:

2. Какой процесс описывается в задаче?

3. Какими величинами характеризуется этот процесс?

4. Как связаны между собой эти величины?

5. Значения, каких величин требуется найти?

6. Обозначить буквами искомые величины;

7. Выразить искомые величины через данные;

8. Составить уравнения и из них соответствующую систему;

II. Работа с математической моделью:

Найти решение системы;

III. Ответ на вопрос задачи:

Проверить, какие из решений системы удовлетворяют условиям задачи.

Алгоритм решения задачи дать каждому ученику.

Задача 1. Прямоугольный газон обнесен изгородью, длина которого 40 м. Площадь газона 96 . Найдите длины сторон газона.

I этап:

Составим выражения по данным задачи, пусть a и b –длины сторон, тогда 2(a+b)=40 будет периметр газона, площадь газона выразим как . По данным выражениям составим систему уравнений и найдем решения данной системы.

II этап:

III этап: обе пары чисел удовлетворяют условию задачи.

Ответ: 12 м и 8м

После решения задачи необходимо ещё раз объяснить ход решения и поинтересоваться у учащихся, понятно ли им данное решение. Так же необходимо заметить, что в некоторых случаях целесообразно создавать геометрические модели для лучшего восприятия условия задачи. Чаще всего такие модели составляются к задачам на движение, которые нам еще предстоит решать.

1. Закрепление материала

Выполнение заданий на карточках:

Задача 2. Гипотенуза прямоугольного треугольника равна 13 см. Один из катетов на 7 см больше другого. Найдите катеты прямоугольного треугольника.

I этап:

Пусть катеты равны x и y, составляем 1 уравнение. По теореме Пифагора составляем 2 уравнение. Методом подстановки:

II этап:

III этап : По смыслу задачи пара чисел -5 и -12 не могут быть решением системы

Ответ: 12 см и 5 см.

Взаимопроверка решения задачи в парах. После этого решение проецируется на экран.

Задача 3. Произведение двух положительных чисел равно 96. Одно из них на 4 больше другого. Найдите эти числа.

I этап:

Пусть 1 число – x, 2 число – у.

x>0 и y>0

II этап:

III этап: По смыслу задачи исключаем числа – 8 и — 12

Ответ: 12 и 8.

Также взаимопроверка в парах.

Теперь решим задачу №7.2 коллективно.

Расстояние между двумя пунктами по реке составляет 14 км. Лодка проходит этот путь по течению за 2 часа, против течения – за 2 часа 48 минут. Найдите скорость лодки в стоячей воде и скорость течения реки.

Решение:

I этап:

Вспомним уравнение прямолинейного равномерного движения:

S – расстояние,

V – скорость,

T – время.

Переведем 2 часа 48 минут в часы, это составит 

Пусть x км/ч – скорость лодки в стоячей воде, y км/ч – скорость течения реки. Вспоминаем движение по течению и против течения реки. Составим математическую модель.

Составим таблицу:.

S, км

V, км/ч

T, ч

По течению

 14 

Против течения

14

II этап:

Решим полученную систему.

III этап:

Ответ: 6 км/ч; 1 км/ч.

Подведение итогов занятия

1.Обсуждение успешности достижения целей занятия.

2.Оценивание работы учащихся

Разъяснение дом. задания — №№ 7.6 и 7.12

infourok.ru

Решение задач составлением систем линейных уравнений с двумя неизвестными

Розробка
уроку з алгебри для 7 класу з теми:
«Розв’язування задач за допомогою систем
лінійних рівнянь з двома невідомими»
з застосуванням елементів здоров’єзберігаючих
технологій, мета уроку – формування
навичок розв’язування задач за допомогою
систем рівнянь, розвиток критичного
мислення, ділової активності та
зацікавленості учнів у збереженні
свого здоров’я.

Разработка урока алгебры для
7-го класса по теме:

«Решение
задач составлением систем линейных
уравнений»

Тема
урока. Решение задач составлением систем
линейных уравнений с двумя неизвестными.

Задачи
урока. Ознакомить учащихся с решением
задач составлением систем линейных
уравнений с двумя неизвестными;
формировать навыки решения задач
составлением систем уравнений; развивать
критическое мышление; активизировать
деятельность учащихся; развивать интерес
к своему организму и способам сохранения
здоровья, пропагандировать здоровый
образ жизни.

Оборудование.
Компьютер, проектор, плакаты с формулами.

Тип
урока. Урок усвоения новых знаний.

Эпиграф
к уроку. «Здоровье – не все,

но и
все без здоровья – ничто»

Сократ

Ход урока.

1. Организационный
   момент.

2. Разминка:

1)
Упражнение «Белая ворона» (что лишнее?)
Текст на экране:

а)
«Система, график, переменная, решение,
общение »;

б)
«Показатель, многочлен, степень, гребень
»;

в)
« Равенство, уравнение, предложение,
тождество».

г)
«Число, значение, лечение, формула,
задача»

1. «Собери формулы».
   Установите соответствие
   между выражениями. (Учащиеся объединены
   в три группы)

По команде
учителя ученики из каждой
группы по одному подходят к соответствующей
доске и составляют формулу (какая
команда быстрее…).

На трех досках в две колонки
записаны на цветных листах выражения:

(а + в)2	а3 + в3
(а + в)(а2 – а в + в2)	(а – в)2
(а + в)3	(а — в)(а2 + а в + в2)
а3— 3а2в + 3ав2 — в3	(а — в) (а + в)
а2 – 2ав +в2	(а — в)3
а3 — в3	а2 + 2ав + в2.
а2 — в2	а3 +3а2в + 3ав2 +в3

3)    
Найдите пары тождественно равных
выражений: (на экране цветные прямоугольники
с выражениями — таблица)

1) а2 + 10а + 25	5) (1 – а)2	9) 49  а2
2) (а + 7) (7– а)	6) (а 3)( 3а)	10) (а  3) (а+3)
3) а2  2а + 1	7) (5 + а)2	11) 8 – а3
4) а2  9	(2–а)(4+2а+а2 )	12) а2  6а + 9

  На уроках применяю
элементы хромотерапии.

С этой целью на уроке использую
карточки, таблицы, изображение фигур
на компьютере определенных цветов (в
зависимости от этапа урока), что влияет
на физическое и психическое состояние:

синий
цвет снимает головную боль,
(расслабляющий)
красный – повышает
работоспособность,
(стимулирующий)
желтый – улучшает настроение,
(укрепляющий)
зеленый
цвет используют для коррекции зрения
(тонизирующий)

Следующее упражнение учащиеся
выполняют стоя. (Режим динамических поз
на уроке – по необходимости ученик и
самостоятельно может, не мешая, изменит
позу…)

4)
Является ли пара чисел: (3; -2), (8; 6), (3,5;
1,5), (7; -2)

решением
системы двух уравнений

х + у = 5;

х – у = 2? (условие на
цветном экране)

(если
«да» учащиеся поднимают руки и тянутся
вверх на носочках, если «нет» — опускают
руки вниз, расслабляются)

5)
Ученик, который заботится о своем
здоровье, должен правильно питаться.

На
экране красочная таблица: «Разговор о
правильном питании» и условие следующей
задачи:

В
день можно съедать не более 1/10кг сладостей
и сахара, дневная норма потребления
хлеба составляет 1/5кг, масла (сливочного
и растительного) – 1/8кг. Сколько граммов
сладостей, хлеба, масла может съедать
в день ученик? (каждая группа отвечает
на один вопрос).

II.
Актуализация опорных знаний (этап
вызова)
1) Какие способы решения систем двух
линейных уравнений вам известны?

2)
Решить задачу: В поясничном, крестцовом
и копчиковом отделах позвоночника
позвонков поровну. В грудном отделе их
на семь больше, чем в поясничном, а шейном
отделе – на пять меньше, чем в грудном.
Сколько позвонков в каждом отделе
позвоночника, если всего их 34?

«Минутка 
здоровья»
Напомнить учащимся о правильной осанке:
“Что такое осанка? Осанка – это привычная
поза спокойно стоящего или сидящего
человека. Плохая, неправильная осанка
приносит вред здоровью: нарушает работу
внутренних органов. А как некрасиво
выглядит человек, у которого плохая
осанка. Правильная осанка не только
делает фигуру стройной, но и придает
человеку уверенность в себе, бодрость,
жизнерадостность”. Поэтому
необходимо вырабатывать правильную
осанку: опустить плечи, соединить
лопатки, поднять подбородок, втянуть
живот, и следить за своей осанкой в
течение урока. (На экране цветные плакаты
с изображением позы стоящего и сидящего
человека).

НЕПРАВИЛЬНО
ПРАВИЛЬНО

А
теперь вернемся к задаче. Учащиеся
предлагают решить задачу с помощью
составления уравнения, так как легко
все неизвестные выразить через одну
переменную, решают коллективно с записью
на доске.

III.
Мотивация учебной деятельности.

Продолжим
разговор о правильном питании. Рассмотрим
следующую задачу: Одно из чисел,
соответствующее суточной потребности
витамина В₁,
на 0,3 больше другого, соответствующего
суточной потребности – В₂.
60^º/₀

большего
числа на
0,03 больше, чем 70⁰/₀
меньшего числа. Найдите эти
числа

и
узнайте, какова суточная потребность
организма в витаминах В₁
и В₂ в
миллиграммах.

Дефицит
витамина В₁
может привести к нарушению обмена
углеводов, и как следствие к болезням.
Витамин В₂
отвечает за состояние зрения. На экране
условие задачи, цветная таблица о
витаминах и продуктах, в которых они
содержатся.

Прочитаем
еще раз условие задачи и подумаем, как
ее решить. Очевидно, что довольно трудно
решить задачу уравнением, выражая
неизвестные, через одну переменную, так
как же решить эту задачу рациональным
способом? Это вы сможете сделать, изучив
новую тему.

IV.
Сообщение темы и задач урока.

V.
Изучение нового материала. (Этап
осмысления)

1.
Работа с учебником. Прочитать п. 29 стр.
249, выделить главное. Ответьте на вопросы
(предварительно, обсудив в группах,
прием — «вертушка» учащиеся могут
переходить из одной группы в другую):

1. Приведите
   пример линейного уравнения с двумя
   переменными.

2. Что
   такое решение уравнения с двумя
   переменными?

3. Сколько
   решений может иметь система двух
   линейных уравнений с двумя переменными?

4. Сколько
   решений может иметь система двух
   уравнений первой степени с двумя
   переменными?

5. Составьте
   несколько разных моделей задачи: найдите
   два числа, если

их сумма равна 5, а разность равна
3.

2.
Решение упражнений № 1158, 1159 (устно).

3.
Решение задачи (образец записи решения)
№ 1185(коллективно).

VI.
Физкультминутка (в зависимости от номера
урока по расписанию)

VII.
Закрепление новых знаний и умений.

1.
№ 1178 (комментированное решение, образец
записи решения задачи)

2.
Вернемся теперь к задаче о витаминах и
решим ее с помощью составления системы
уравнений с записью на доске и в тетрадях.

3.
Работа в группах. Каждая группа получает
задание – решить задачу.

Для
1-й группы: Дефицит железа сказывается
на росте и устойчивости к инфекциям. От
железа зависит содержание гемоглобина
– переносчика кислорода ко всем органам.
Медь также синтезирует гемоглобин и
определяет антиоксидантный потенциал
сыворотки крови.

Задача.
Сумма двух чисел равна 11. 60⁰/₀
большего числа на 2,7 больше,
чем 70⁰/₀
меньшего числа. Найдите эти числа и
узнайте, какова суточная потребность
организма в железе и меди в миллиграммах.

Для
2-й группы:

Таблица:
«Курение – одна из вреднейших привычек»

Задача.
Сумма двух чисел равна 18. Если большее
из этих чисел

умножить
на два, а меньшее умножить на четыре, то
их сумма будет равна 48. Найдите эти
числа. Меньшее число покажет вам, сколько
минут жизни

забирает
одна сигарета.

Для
3-й группы:

Задача.
Сумма двух чисел равна 82. Если первое
число увеличить в 4,5 раза, а ко второму
прибавить 28, то их сумма будет равна
180. Найдите эти числа, и вы узнаете,
сколько лет полноценной жизни забирает
табак у курильщиков и сколько лет в
среднем живут курящие мужчины.

(Представитель
каждой группы знакомит весь класс с
условием и записывает решение задачи
на доске)

VIII.
Этап рефлексии.

Поставьте
в тетрадях буквы, соответствующие вашему
восприятию материала урока.

На
светло- синем экране:

А)
все понятно, интересно;

Б)
все понятно, но не интересно;

В)
не все понятно;

Г)
почти ничего не понятно;

Д)
ничего не понятно;

Ж)
кроме, математических знаний получил
полезную информацию;

З)
ничего полезного.

IX.
Подведение итогов. Мотивация выставления
оценок.

X.
Комментированное домашнее задание: п.
29(читать, ответить на вопросы к пункту)

I
и II
уровень №1164, 1165, 1174;

III
уровень №1184, 1187, 1189;

IV
уровень 1191, 1195, (творческое задания, по
данным на карточках составить задачу).

Карточка
№ 1. (Для первой группы) На карточке
плакат: «Никотин — яд!» — убедите в этом
своих близких, если они курят.

«Никотин
– один из самых опасных ядов растительного
происхождения. Птицы (воробьи, голуби)
погибают, если к их клюву всего, лишь
поднести стеклянную палочку, смоченную
никотином. Кролик погибает от 1/4 капли
никотина, собака – от 1/2 капли. Для
человека смертельная доза никотина
составляет от 50 до 100 мг, или 2-3 капли.
Именно такая доза поступает ежедневно
в кровь после выкуривания 20-25 сигарет
(в одной сигарете содержится примерно
6-8 мг никотина, из которых 3-4 мг попадает
в кровь). Курильщик не погибает потому,
что доза вводится постепенно, не в один
прием. К тому же, часть никотина
нейтрализует формальдегид – другой
яд, содержащийся в табаке. В течение 30
лет такой курильщик выкуривает примерно
20000 сигарет, или 160кг табака, поглощая в
среднем 800г никотина».

Карточка
№2.(Для второй группы) На карточке
плакат: «Никотин яд!» «Сломай сигарету,
пока сигарета не сломала тебя!»

«Врачи также выяснили, что рост
числа курящих параллельно увеличивает
количество опасных болезней. Начиная
с начала 1960 годов, стали публиковать в
газетах и журналах результаты научных
исследований. И люди ужаснулись!
Оказывается, если человек курит в день
от 1 до 9 сигарет, то сокращает свою жизнь
(в среднем) на 4, 6 года по сравнению с
некурящими. Если курит от 10 до 19 сигарет,
то на 5, 5 года; если выкуренных 20 до 39
сигарет – более 7 лет».

Карточка
№ 3.(Для третьей группы) На карточке
плакат: «Если человек курит…» —
статистические данные о болезнях
курильщиков.

«Длительно и много курящие в 13
раз чаще заболевают стенокардией, в 12
— инфарктом миокарда, в 10 раз — язвой
желудка и в 30 раз от тяжелейшего
заболевания легких».

gigabaza.ru

Цели урока:

• Сформулировать представление о линейных уравнениях с двумя неизвестными
  как математических моделях реальных ситуаций.
• Сформировать у учащихся представление о решении уравнения как пары чисел
  (x;y), удовлетворяющих уравнению ax + by + c = 0. Подчеркнуть, что таких
  решений бесконечно много.
• Ввести понятие графика уравнения ax + by + c = 0, пояснить, что
  геометрической моделью линейного уравнения с двумя неизвестными является
  прямая.
• Изучить алгоритм построения графика уравнения ax + by + c = 0.

Ход урока

Вступительное слово учителя. (Слайд 1.) Урок проводится при активном
участии учеников.

Подготовительная работа. Решение устных упражнений.

Объяснение нового материала.

Рассмотрим задачу^*. (Слайд 8.)

Купец в лавке купил чёрного и синего сукна за 150 рублей. Спрашивается,
сколько аршин купил он того и другого, если синее сукно стоило 5 рублей за
аршин, а чёрное – 3 рубля?

Составим таблицу по условию задачи (слайд 9). В задаче две неизвестные
величины: количество синего сукна и количество чёрного сукна. Обозначим их
соответственно через x и y.

Товар	Цена	Количество	Стоимость товара одного качества	Общая стоимость
Синее сукно	5 рублей	x аршин	5x рублей	150 рублей
Чёрное сукно	3 рубля	y аршин	3y рублей

Тогда математической моделью к этой задаче будет уравнение
5x + 3y = 150 или 5x + 3y – 150 = 0
(Слайд 10.), причём левая часть этого уравнения – многочлен первой степени
от x и y. Полученное уравнение называют линейным уравнением с двумя
неизвестными.

Как же решить такое уравнение? Решить – значит найти такие значения x и y,
при которых уравнение превратится в верное равенство. Попробуем их подобрать и
результаты занесём в таблицу.

Если купить 10 аршин чёрного сукна, то синего нужно купить 24 аршина. Если же
синего купить 18 аршин, то чёрного – 20 аршин. Заполните таблицу полностью.

x		18		6		30
y	10		30		50

Каждая пара чисел, которая превращает уравнение в верное равенство,
называется решением этого уравнения. Очевидно, что рассматриваемое уравнение
имеет бесчисленное множество решений. (Слайд 11.)
Решения можно записывать в виде:
x₁ = 24, y₁ =
10; x₂ = 12, y₂ = 30 и т.
д. Наиболее удобной является запись решений в виде упорядоченных пар:
(24;10), (12;30) и т. д. Следует заметить,
что пары (30;0) и (0;50) не могут быть решениями задачи, так как прийдя в лавку
никто не станет покупать 0 аршин сукна.

Каждой упорядоченной паре чисел можно поставить в соответствие точку на
координатной плоскости. Построим в системе координат точки (30;0), (24;10),
(18;20), (12;30), (6;40), (0;50), выбрав удобный масштаб. Все точки
расположились на прямой, которая является графиком уравнения 5x + 3y – 150 = 0.
(Слайд 12.).

Прямую можно построить, зная координаты только двух её точек: точек
пересечения с осями координат. Их легко найти, подставляя в уравнение вместо x и
y нули.

Если y = 0, то 5x – 150 =0; x = 30. Если x = 0, то 3y – 150 =0; y = 50.
Значит график пройдёт через точки (30;0) и (0;50).

Координаты любой точки прямой являются решением данного уравнения. Например
(27;5), (15;25).

Подведём итоги . (Слайд 13.)

Линейным уравнением с двумя неизвестными называется уравнение вида
ax + by + c = 0, где a, b и c – любые числа (a и b не равны нулю одновременно).
Числа a и b называются коэффициентами при неизвестных, а число c – свободным
членом уравнения.
Решить уравнение – значит найти такие значения x и y, при которых уравнение
превратится в верное равенство.
Каждая пара чисел, которая превращает уравнение в верное равенство, называется
решением этого уравнения.
Уравнение имеет бесчисленное множество решений.
Графиком линейного уравнения с двумя неизвестными является прямая.

Выполнение упражнений из задачника. (слайд 14.)

§7, № 3–№ 5 – устно; № 11(а); № 14(а); № 17(а).

Домашнее задание.

§7, № 7(а); № 8(а); № 11(б); № 14(б);№ 17(б).

________________________________________________________________________

* – выделенное красным цветом учащиеся записывают в тетради.

Решение
задач с использованием систем линейных уравнений с двумя переменными.

Переходим теперь к практическому применению систем линейных
уравнений с двумя переменными. Часто бывает, что в задачах неизвестны два, а то
и три-четыре компонента. И в этом случае обозначение какого-то одного
компонента переменной не облегчает решение задачи. Тогда нужно ввести две или
три переменные. Вот здесь нам как раз и понадобится система уравнений и способы
её решения. Приведём пример с полным описанием.

Например,
решить задачу. Лодка за 3 ч движения по течению и 4 ч против течения проходит
114 км. Найдите скорость лодки по течению и её скорость против течения, если за
6 ч движения против течения она проходит такой же путь, как за 5 ч по течению.

Решение. В задаче описывается движение
по воде. А значит, должна быть собственная скорость лодки и скорость течения
реки. Они нам и не известны, поэтому обозначим через  км/ч собственную скорость
лодки, а через  км/ч  – скорость течения
реки. Тогда скорость лодки по течению реки равна  км/ч, а скорость лодки
против течения реки —  км/ч. За 3 ч движения по
течению реки лодка пройдёт  км, а за 5 ч
—  км. За 4 ч
против течения лодка пройдёт  км, а за 6 ч —  км. По условию задачи
известно, что за 3 ч по течению и 4 ч против течения лодка пройдёт всего 114
км, значит, составляем первое уравнение:   Также по условию задачи
известно, что за 6 ч движения против течения лодка проходит такой же путь, что
и за 5 ч по течению, поэтому составляем второе уравнение:  

Для наглядности составим условие задачи в виде таблицы.

Имеем два линейных уравнения с двумя переменными, которые должны
выполняться при одних и тех же значениях переменных, значит, составляем
систему:

Раскроем
сначала скобки и приведём подобные слагаемые.

                                           

Уравнения получились достаточно простые, поэтому можно
использовать или способ подстановки, или способ сложения. Приведём оба способа
решения, чтобы показать, что выбор только за вами, сложность одинакова.

Способ подстановки	Способ сложения

Значит, собственная скорость лодки равна
 км/ч, а скорость течения
реки —  км/ч.

Тогда скорость лодки по течению реки:  км/ч.

Скорость лодки против течения реки:  км/ч.

Ответ:
18 км/ч; 15 км/ч.

Рассмотрим ещё одну задачу.

Есть две металлические отливки, одна из которых содержит 30%
меди, а вторая – 70% меди. Сколько килограммов каждой отливки надо взять, чтобы
получить 120 кг сплава, содержащего 40% меди?

Решение.
Пусть  кг – масса первой отливки,  кг – масса второй отливки.
Тогда содержание меди в первой отливке  кг, а во второй —  кг. По условию задачи
известно, что после сплава этих двух отливок, масса станет равной 120 кг,
поэтому . Кроме того известно, что
полученный сплав будет содержать 40% меди, составляем уравнение: . Запишем и решим систему
двух уравнений.

Решим
систему способом сложения. Умножим первое уравнение на  и почленно сложим два
уравнения.

                                                            

                                                            

                                
                            

Значит,
первого сплава нужно взять 90 кг, а второго – 30 кг.

Ответ: 
90 кг; 30 кг.

Задачи на стоимость.

1.          
За
7 кг апельсинов и 4 кг лимонов заплатили 1120 рублей. Сколько стоит 1 кг
апельсинов и сколько 1 кг лимонов, если 5 кг апельсинов дороже, чем 2 кг
лимонов, на 390 рублей?

2.          
За
2 стола и 6 стульев заплатили 10620 рублей. После того, как столы подешевели на
10%, а стулья – на 20%, за один стол и два стула заплатили 4135,5 рублей.
Какова была начальная цена одного стола и одного стула?

3.          
За
4 футбольных и 3 волейбольных мяча заплатили 6700 рублей. После того, как
футбольный мяч подешевел на 20%, а волейбольный подорожал на 10%, за один
футбольный и один волейбольный мячи заплатили 1830 рублей. Какова была начальная
цена каждого мяча?

4.          
За
5 ручек и 4 карандаша заплатили 300 рублей. Сколько стоит одна ручка и сколько
стоит один карандаш, если 3 ручки дороже, чем 2 карандаша, на 70 рублей?

5.          
За
7 тетрадей и 4 ручки заплатили 300 рублей. После того, как тетради подешевели
на 40%, а ручки – на 20%, одна ручка стала дороже одной тетради на 20 рублей.
Какими были первоначальные цены тетради и ручки?

6.          
Магазин
закупил конфеты двух сортов в упаковках по 240 г и 250 г, причём конфет первого
вида было куплено на 600 г больше. Сколько купили конфет каждого вида, если
упаковок с конфетами первого сорта было на 20 больше?

7.          
Таня
за 3 тетради и 2 карандаша заплатила 58 рублей, а Лена за 5 таких же тетрадей и
1 такой же карандаш заплатила 78 рублей. Сколько стоит тетрадь и сколько карандаш?

8.          
У
Толи 18 монет по 2 руб. и по 5 руб. на сумму 97 руб. Сколько монет каждого
достоинства у Толи?

9.          
Банк
продал предпринимателю г-ну Разину 8 облигаций по 2000 руб. и 3000 руб. Сколько
облигаций каждого номинала купил г-н Разин, если за все облигации было
заплачено 19 000 рублей?

10.      За 15
акций компании «Трансгаз» и 10 акций компании «Суперсталь» заплатили
35 000 руб. Сколько стоит одна акция каждой компании, если акция
«Трансгаза» на 1000 руб. дешевле акции «Суперстали»?

11.      За 4
блокнота и 3 карандаша заплатили 181 руб., а за такие же 2 блокнота и 5
карандашей заплатили 115 руб. Сколько стоит один блокнот и один карандаш?

12.      За 5 пачек
творога и 2 банки сметаны заплатили 210 руб., а за такие же 3 пачки творога и 3
банки сметаны заплатили 171 руб. Сколько стоит одна пачка творога и одна банка
сметаны?

13.      Шапка и
шарф вместе стоили 1200 руб. После того, как шапка подешевела на 20%, а шарф –
на 10%, их суммарная стоимость составила 1005 руб. Сколько стоила шапка и
сколько стоил шарф до снижения цен?

14.      Сумка и
ремень вместе стоили 2300 руб. После того как сумка подешевела на 15%, а ремень
– на 5%, их суммарная стоимость составила 2005 руб. Сколько стоила сумка и
сколько стоил ремень до снижения цен?

15.      Три
ватрушки и пять плюшек стоят 45 руб., а пять ватрушек и три плюшки стоят 43
руб. Сколько стоит ватрушка и сколько стоит плюшка?

16.      Три марки
и пять конвертов стоят 39 руб., а четыре марки и два конверта стоят 24 руб.
Сколько стоит марка и сколько стоит конверт?

17.      Пять
открыток и четыре конверта стоят 44 руб., а две открытки и три конверта стоят
26 руб. Сколько стоит открытка и сколько стоит конверт?

18.      Стоимость
50 экземпляров учебника физики для 10 класса и 25 экземпляров учебника физики
для 11 класса составляет 10 000 рублей. С учётом скидки в размере 20% на
учебники для 10 класса и 10% на учебники для 11 класса стоимость покупки
снизилась на 17%. Сколько стоит один учебник физики для 10 класса с учётом
скидки?

19.      За 1 кг
апельсинов и 1 кг яблок заплатили 120 рублей. После подорожания апельсинов на
30%, а яблок на 20% такая же покупка будет стоить 151 руб. Найдите
первоначальную стоимость 1 кг апельсинов и 1 кг яблок.

20.      За 1 кг
огурцов и 1 кг помидоров заплатили 150 руб. После того как огурцы подешевеют на
30%, а помидоры на 20%, такая же покупка будет стоить 113 руб. Найдите первоначальную
стоимость 1 кг огурцов и 1 кг помидоров.

21.      За 1
рюкзак и 1 пенал заплатили 850 руб. Если рюкзак подорожает на 10%, а пенал на
20%, такая же покупка будет стоить 950 руб. Найдите первоначальную стоимость 1
рюкзака и 1 пенала.

22.      Три
пирожка и две булки стоят 40 руб., а два пирожка и три булки стоят 45 руб.
Сколько стоит пирожок, сколько стоит булка?

Задачи на количество.

23.      В двух
ящиках лежали яблоки. Если из одного ящика переложить во второй 45 яблок, то в
обоих ящиках их станет поровну. Если же из второго ящика переложить в первый 20
яблок, то в первом станет в 3 раза больше яблок, чем во втором. Сколько яблок
было в каждом ящике?

24.      В двух
шкафах стояли книги. Если из первого шкафа переставить во второй 10 книг, то в
обоих шкафах книг станет поровну. Если же из второго шкафа переставить в первый
44 книги, то в нём останется в 4 раза меньше книг, чем в первом. Сколько книг
было в каждом шкафу?

25.      У двух
мальчиков были марки. Если один из них отдаст второму 10 марок, то у обоих
мальчиков марок станет поровну. Если же первый отдаст второму 50 марок, то у
него останется в 5 раз меньше марок, чем станет у второго. Сколько марок было у
каждого мальчика?

26.      В
туристический поход ребята взяли двухместные и трёхместные палатки. Сколько
человек разместилось в трёхместных палатках, если на 26 человек ребята взяли 10
палаток?

27.      В копилку
складывали двухрублёвые и пятирублёвые монеты. Когда копилку вскрыли, в ней
оказалось 178 рублей, причём пятирублёвых монет было на 12 штук меньше, чем
двухрублёвых. Сколько денег пятирублёвыми монетами было в копилке?

28.      В
гостинице 25 номеров. Есть четырёхместные и двухместные номера. Сколько каких
номеров, если всего в гостинице могут поместиться 70 человек?

29.      В первый
день в школьную библиотеку привезли 4 пачки учебников по геометрии и 3 пачки
учебников по алгебре: всего 96 книг. Во второй день привезли 5 пачек учебников
по геометрии и 6 пачек учебников по алгебре, причём учебников по геометрии на 3
больше, чем по алгебре. Сколько учебников по геометрии привезли в библиотеку?

30.      В магазин
привезли 3 коробки с пачками чая и 4 коробки с пачками кофе, всего 76 пачек. В
другой день привезли 6 таких же коробок чая и 5 коробок кофе, причём чая на 22
пачки больше. Сколько пачек чая привезли?

31.      В первом
отряде летнего лагеря было 25 подростков. В течение смены число девочек
увеличилось на 10%, а число мальчиков уменьшилось на 20%, в результате в отряде
стало 23 подростка. Сколько девочек и сколько мальчиков стало в первом отряде в
конце смены?

32.      На дворе
было 20 кроликов и кур, у которых 52 ноги. Сколько было кроликов и сколько было
кур на дворе?

33.      Для
кормления 5 лошадей и 25 коров ежедневно отпускают 220 кг сена, для 3 лошадей и
35 коров отпускают 272 кг сена. Найдите дневную норму сена для лошади и для
коровы.

34.      Летели
галки и сели на палки. Если на каждую палку сядет по галке, то одной галке не
хватит палки. Если на каждую палку сядут по две галки, то одна палка останется
без галок. Сколько было галок и сколько палок?

35.      Школьники
отправились в поход в составе 57 человек, при этом у них были только
трёхместные и четырёхместные палатки. Сколько трёхместных палаток и сколько
четырёхместных, если всего в поход взяли 16 палаток?

36.      83 подарка
были упакованы в большие и маленькие коробки. В большие коробки помещается по 8
подарков, а в маленькие – по 5. Всего использовали 13 коробок. Сколько было
коробок каждого вида?

37.      В
гостинице группа из 27 туристов была размещена в двухместных и трёхместных
номерах. Всего туристы заняли 10 номеров. Сколько было занято трёхместных и
сколько двухместных номеров?

38.      В классе
36 учеников. Девочек на 3 меньше, чем мальчиков. Сколько девочек и сколько
мальчиков было в классе?

39.      В магазине
продаются тетради по 96 листов и по 24 листа. Во всех тетрадях, купленных
Сашей, 528 листов. Сколько толстых и сколько тонких тетрадей купил Саша, если
все купленные им толстые тетради содержат на 48 листов больше, чем все тонкие?

40.      В
физкультурном зале 35 учеников. Мальчиков в 1,5 раза больше, чем девочек.
Сколько мальчиков и сколько девочек в физкультурном зале?

41.      В первой
рукописи на 60 страниц больше, чем во второй. Корректор, вычитывающий первую
рукопись, выполнив 60% всей работы, вычитал на 12 страниц меньше, чем
корректор, вычитывающий вторую рукопись и выполнивший 80% всей работы. Сколько
страниц в каждой рукописи?

42.      На турбазе
имеются палатки и домики, вместе их 25. В каждом домике живут 4 человека, а в
палатке – 2. Сколько на турбазе палаток и сколько домиков, если турбаза
рассчитана на 70 человек?

43.      В классе
24 человека. Чтобы девочкам выдать по три тетради, а мальчиками по две тетради,
потребуется 59 тетрадей. Сколько в классе мальчиков и сколько девочек?

44.      В классе
25 человек. Чтобы девочкам выдать по три тетради, а мальчикам по две тетради,
потребуется 62 тетради. Сколько в классе мальчиков и сколько девочек?

45.      На двух
полках стояло 210 книг. Если с первой полки убрать половину книг, а на второй
увеличить их число вдвое, то на двух полках будет 180 книг. Сколько книг стояло
на каждой полке первоначально?

46.      В двух
коробках лежало 210 карандашей. Если в первой коробке число карандашей
уменьшить вдвое, а во второй их число увеличить в 2 раза, то в двух коробках
станет 240 карандашей. Сколько карандашей было в каждой коробке первоначально?

47.      Если
раздать детям по 3 яблока, то 7 яблок останется, а чтобы раздать каждому по 5
яблок, не хватит 3 яблок. Сколько было детей?

48.      Если раздать
детям по 5 конфет, то 13 конфет останется, а чтобы раздать каждому по 8 конфет,
не хватит 5 конфет. Сколько было детей?

49.      В 5
пакетов и 4 коробки расфасовали 1 650 г печенья. В каждую коробку
уместилось на 75 г печенья больше, чем в пакет. Сколько граммов печенья
расфасовали в коробки?

50.      К
новогоднему празднику семиклассники клеили бумажные гирлянды и ёлочные игрушки.
Каждый мальчик склеил по 4 гирлянды и 3 игрушки, а каждая девочка по 3 гирлянды
и 5 игрушек. Мальчики склеили на 22 гирлянды больше, чем девочки. Игрушек всего
было сделано 118. Сколько мальчиков и девочек в этом классе?

51.      В
физкультурный зал школы привезли 5 сеток с баскетбольными мячами и 2 сетки с
волейбольными мячами, всего 23 мяча. Через неделю – 3 такие же сетки с
баскетбольными мячами и одну сетку с волейбольными мячами, причём баскетбольных
мячей на 5 больше, чем волейбольных. Сколько мячей в каждой сетке?

52.      В магазин
привезли 3 упаковки с пачками чая и 4 упаковки с пачками кофе, всего 85 пачек.
В другой день – 5 таких же упаковок с пачками чая и 4 упаковки с пачками кофе,
всего 107 пачек. Сколько пачек чая и сколько пачек кофе в каждой упаковке?

53.      Группа
туристов, в которой 21 человек, отправилась в поход на байдарках. Они взяли с
собой двухместные и трёхместные байдарки, всего 9 лодок. Сколько байдарок
каждого типа взяли с собой туристы?

54.      Десант из
130 человек был доставлен к месту назначения на 4 тяжёлых и 2 лёгких
вертолётах. Один тяжёлый и один лёгкий вертолёты вместе вмещают 36 десантников.
Сколько десантников можно перевезти в каждом вертолёте?

55.      Две
мастерские сшили в первый день 110 костюмов. Во второй день первая мастерская
увеличила выпуск костюмов на 20%, а вторая – на 10%, в результате во второй
день было сшито на 16 костюмов больше, чем в первый день. Сколько костюмов
сшила каждая мастерская во второй день?

56.      Масса
туриста с рюкзаком в 5 раз больше массы одного рюкзака. Определите массы
рюкзака и туриста в отдельности, если сумма масс двух рюкзаков и массы туриста
равна 120 кг.

57.      Шесть
метров новой верёвки имеют такую же массу, как и пять метров старой. Найдите
массу одного метра новой и старой верёвки в отдельности, если 13 м новой и 12 м
старой верёвки вместе весят 5 кг 480 г.

58.      В одном
баке было 28 л бензина, а в другом – 42 л. Если первый бак долить доверху из
второго бака, то второй бак станет наполненным наполовину. Если второй бак
дополнить доверху из первого бака, то в нём останется только четвёртая часть
объёма. Найдите объём каждого бака.

59.      У Лены 8
монет по 10 руб. и 5 руб. Сколько у неё десятирублёвых и сколько пятирублёвых
монет, если всего у неё 65 рублей?

60.      На
получение пирожка в автомате нужно 5 жетонов, а на получение булочки – 1 жетон.
Таня получила в автомате несколько пирожков и булочек, отдав за всю покупку 25
жетонов. Сколько пирожков и сколько булочек получила Таня, если за булочки она
отдала на 15 жетонов меньше, чем за пирожки?

Задачи с геометрическими фигурами.

61.      Если
ширину прямоугольника уменьшить на 2 см, а длину увеличить на 3 см, то его
площадь уменьшится на 8 см². Если же каждую сторону данного прямоугольника
увеличить на 4 см, то площадь исходного прямоугольника увеличится на 80 см².
Найдите стороны данного прямоугольника.

62.      Если длину
прямоугольника уменьшить на 2 м, а ширину увеличить на 4 м, то его площадь
увеличится на 12 м². Если же каждую его сторону уменьшить на 1 м, то
площадь исходного прямоугольника уменьшится на 13 м². Найдите
стороны данного прямоугольника.

63.      Периметр
прямоугольника равен 32 см. Если его длину увеличить на 5 см, а ширину
уменьшить на 2 см, то площадь прямоугольника увеличится на 7 см².
Найдите стороны данного прямоугольника.

64.      Одна
сторона прямоугольника на 4 см больше другой. Если меньшую сторону увеличить в
2 раза, а большую оставить без изменения, то периметр нового прямоугольника
будет равен 56 см. Найдите стороны данного прямоугольника.

65.      Периметр
прямоугольника равен 48 см. Если одну его сторону увеличить в 2 раза, а другую
уменьшить на 6 см, то периметр нового прямоугольника будет равен 64 см. Найдите
стороны данного прямоугольника.

66.      Периметр
прямоугольника равен 56 см. Найдите его стороны, если известно, что длина
прямоугольника на 14,2 см больше ширины.

67.      Периметр
прямоугольника 400 м. Длина его в 3 раза больше ширины. Найдите длину и ширину
этого прямоугольника.

68.      Периметр
равнобедренного треугольника 17 см. Основание треугольника на 2 см меньше, чем
боковая сторона. Найдите стороны этого треугольника.

69.      Боковая
сторона равнобедренного треугольника на 4 см длиннее основания. Найти стороны
треугольника, если его периметр равен 26 см.

70.      Ширина
прямоугольника на 5 см короче его длины. Найдите длину и ширину прямоугольника,
если его периметр равен 38 см.

Задачи с числами.

71.      Сумма цифр
двузначного числа равна 8. Если поменять местами его цифры, то получим число,
которое больше данного на 18. Найдите данное число.

72.      Цифра в
разряде десятков данного трёхзначного числа равна нулю, а удвоенное количество
сотен на 2 меньше, чем количество единиц. Число, записанное теми же цифрами в
обратном порядке, на 495 больше данного. Найдите данное число.

73.      Сумма
удвоенного количества десятков и количества единиц некоторого двузначного числа
равна 11. Если поменять местами цифры этого числа, то получим число, которое на
9 меньше данного. Найдите данное число.

74.    Сумма двух
чисел равна 77. Найдите эти числа, если   первого числа равны   второго числа.

75.    Разность
двух чисел равна 12. Найдите эти числа, если   первого числа равны   второго числа.

76.      Сумма цифр
двузначного числа равна 8. Если к данному числу прибавить 18, то получится
двузначное число, записанное теми же цифрами, но в обратном порядке. Найдите
данное число.

77.      Разность
между двузначным числом и числом, записанным теми же цифрами, но в обратном
порядке, равна 27. Разность между квадратами таких чисел равна 1485. Найдите
данное число.

78.      Разность
между двузначным числом и числом, записанным теми же цифрами, но в обратном
порядке, равна 45. Разность между квадратами таких чисел равна 5445. Найдите
данное число.

79.      Сумма
чисел равна 98, а из разность – 42,4. Найдите эти числа.

80.      Найдите
двузначное число, сумма цифр которого равна 15, а разность цифр равна 3.

81.      Даны два
числа. Если к первому числу прибавить половину второго, то получится 65, а если
из второго вычесть третью часть первого, то получится первое число. Найдите эти
числа.

82.      Если к
первому числу добавить четверть второго числа, получится 129, а если увеличить
второе число в 5 раз и отнять от него половину первого числа, то получится
первое число. Найдите эти числа.

83.      Разность
квадратов двух натуральных чисел равна 21, а сумма этих чисел равна 7. Найдите
эти числа.

84.      Сумма двух
чисел равна 76, а 3/4 первого числа составляют 5/6 второго числа. Найдите эти
числа.

85.      Среднее
арифметическое двух чисел равно 11. Если большее число разделить на меньшее, то
в частном получится 3, а в остатке 2. Найдите эти числа.

86.      При
сложении двузначного числа с суммой его цифр получится 50. Если от этого числа
отнять число, записанное теми же цифрами в обратном порядке, то получится 9.
Найдите это число.

87.    Если к
числителю и знаменателю несократимой дроби прибавить по 1, то получится , а если вычесть из них по 1, то получится
. Найдите эту дробь.

88.      Задумали
два числа. Если сложить 70% первого числа и 20% второго, то получится 20. Если
же первое число уменьшить на 20%, а второе увеличить на 30%, а затем сложить
полученные результаты, то получится55. Чему равно каждое из чисел?

89.      Задумали
два числа. Если сложить 30% первого числа и 40% второго, то получится 10. Если
же первое число увеличить на 10%, а второе уменьшить на 20%, а затем сложить
полученные результаты, то получится 26. Чему равно каждое из чисел?

90.      Задумали
два числа. Если сложить 40% первого числа и 20% второго, то получится 18. Если
же первое число увеличить на 20%, а второе уменьшить на 10%, а затем сложить
полученные результаты, то получится 69. Чему равно каждое из чисел?

91.      Сумма двух
чисел равна 17. Одно из чисел на 7 меньше другого. Найдите эти числа.

92.      Разность
двух чисел равна 12. Одно из них больше другого в 4 раза. Найдите эти числа.

93.      4 боксёра
тяжёлого веса и 5 боксёров лёгкого веса вместе весят 730 кг. Спортсмен тяжёлого
веса весит на 70 кг больше спортсмена лёгкого веса. Найдите вес каждого
боксёра.

94.    Среднее
арифметическое двух чисел равно 22,5; а   их разности равна  Найдите эти два числа.

95.      Одно число
на 215 больше другого; 80% большего числа на 129 больше 60% меньшего из них.
Найдите эти числа.

96.      В
трёхзначном числе сумма цифр равна 16. Цифра разряда сотен в 4 раза меньше
цифры разряда десятков и на 4 меньше цифры разряда единиц. Найдите это число.

97.      Сумма двух
чисел равна 81. а их разность равна 15. Найдите эти числа.

98.      Сумма двух
чисел равна 36. Одно из них в 2 раза больше другого. Найдите эти числа.

99.      Три яблока
и две груши весят вместе 1 кг 200 г. Яблоко легче груши на 100 г. Сколько весит
одно яблоко и сколько одна груша?

100.  Среднее
арифметическое двух чисел равно 36, а   их разности равна 0,8. Найдите эти числа.

101.  Одно число на 140
меньше другого; 60% большего числа на 64 больше 70% меньшего числа. Найдите эти
числа.

102.  В трёхзначном
числе сумма цифр равна 10. Цифра разряда сотен в 2 раза больше цифры разряда
десятков и на 5 больше цифры разряда единиц. Найдите это число.

103.  Если к числителю
дроби прибавить 1, а к знаменателю 2, то дробь не изменится. Если же к
числителю дроби прибавить 2, а из знаменателя вычесть 1, то дробь увеличится в
6 раз. Найдите эту дробь.

104.  Сумма цифр
двузначного числа равна 9. Если это число разделить на разность его цифр, то
получится 54. Найдите исходное число.

105.  Если к числителю
дроби прибавить 2, а к знаменателю дроби прибавить 3, то получится ½. Числитель
дроби в 3 раза меньше знаменателя. Найдите исходную дробь.

106.  Разность цифр
двузначного числа равна 6. Если это число разделить на сумму его цифр, то
получится 8,2. Найдите исходное число.

107.  Разность двух
чисел равна 16, а их сумма равна 26. Найдите эти числа.

108.  Сумма двух чисел
равна 47, а их разность равна 29. Найдите эти числа.

109.  Коля задумал два
числа. Удвоенное первое число в 3 раза больше второго. Если же первое из
задуманных чисел уменьшить на 49, оно станет в 3 раза меньше второго. Найдите
задуманные числа.

110.  Андрей задумал два
числа. Утроенное первое число в 2 раза больше второго. Если же первое из
задуманных чисел уменьшить на 11, оно станет в 2 раза меньше второго. Найдите
задуманные числа.

111.  Саша задумал два
числа. Утроенное первое число в 4 раза больше второго. Если же первое из
задуманных чисел уменьшить на 26, оно станет в 4 раза меньше второго. Найдите
задуманные числа.

112.  Андрей задумал два
числа. Удвоенное первое число в 5 раз больше второго. Если же первое из задуманных
чисел уменьшить на 69, оно станет в 5 раз меньше второго. Найдите задуманные
числа.

113.  Сумма двух чисел
равна 35. Если одно из них увеличить в 4 раза, а другое – на 30, то сумма
полученных чисел будет равна 125. Найдите эти числа.

Задачи на работу.

114.  На заводе
изготовили два вида деталей. Масса 8 деталей одного вида и 6 деталей другого
вида составляет вместе 29 кг. Найдите массу детали каждого вида, если масса 4
деталей второго вида на 1 кг больше, чем масса двух деталей первого вида.

115.  Саша и Витя
вскапывают грядку за 10 мин, а один Витя – за 15 мин. За сколько минут
вскапывает грядку один Саша?

116.  Игорь и Олег
вскапывают грядку за 12 мин, а один Игорь – за 20 мин. За сколько минут
вскапывает грядку один Олег?

117.  Миша вскапывает
грядку за 10 мин, Саша – за 12 мин, Олег – за 15 мин. За сколько минут они
скопают грядку втроём?

118.  Миша вскапывает
грядку за 6 мин, Саша – за 20 мин, Олег – за 30 мин. За сколько минут они
вскопают грядку втроём?

119.  Если половину
заказа выполнит мастер, а оставшуюся часть закончит ученик, то вся работы будет
сделана за 10 ч. Если мастер выполнит ¾ работы, а оставшуюся часть выполнит
ученик, то всё будет сделано за 9 ч. За какое время мог бы выполнить работу
каждый из них, работая один?

120.  Четыре одинаковых
насоса, работая вместе, наполнили нефтью первый танкер и треть второго танкера
(другого объёма) за 11 ч. Если бы три насоса наполнили первый танкер, а затем
один из насосов наполнил бы четверть второго танкера, то работа заняла бы 18 ч.
За сколько часов три насоса могут наполнить второй танкер?

121.  Три каменщика
(разной квалификации) выложили кирпичную стену, причём первый каменщик работал
6 ч, второй – 4 ч, а третий – 7 ч. Если бы первый каменщик работал 4 ч, второй
– 2 ч, а третий – 5 ч, то они выполнили бы  2/3 всей работы. За сколько часов
каменщики закончили бы кладку, если бы они работали все вместе одно и то же
время?

122.  Три бригады
вспахали два поля общей площадью 96 га. Первое поле было вспахано за 3 дня,
причём все три бригады работали вместе. Второе поле было вспахано за 6 дней
второй и третьей бригадами. Если бы все три бригады проработали на втором поле
1 день, то оставшуюся часть второго поля первая бригада могла вспахать за 8
дней. Сколько гектаров в день вспахивает первая бригада?

123.  Три одинаковых
комбайна, работая вместе, убрали первое поле, а затем два из них убрали второе
поле (другой площади). Вся работа заняла 12 ч. Если бы три комбайна выполнили
половину всей работы, а затем оставшуюся часть сделал бы один из них, то работа
заняла бы 20 ч. За какое время два комбайна могут убрать первое поле?

124.  Две бригады вместе
должны изготовить 270 изделий. К середине дня первая бригада выполнила 60%
своего задания, а вторая – 70% своего. При этом первая бригада изготовила на 6
изделий больше, чем вторая. Сколько изделий должна изготовить каждая бригада?

125.  Два токаря
изготовили 172 детали. Первый работал 3 ч, а второй – 2 ч. Если бы первый
работал 1 ч, а второй – 4 ч, то они изготовили бы 198 деталей. Сколько деталей
изготовил каждый токарь?

126.  Маша и Даша могут
вымыть окно за 1 ч, работая вместе. За сколько часов может вымыть окно Даша,
если известно, что Маша работает в 3 раза быстрее Даши?

127.  Андрей и Иван
могут покрасить забор за 2 ч, работая вместе. За сколько часов может покрасить
забор Иван, если известно, что он работает медленнее Андрея в 4 раза?

128.  Первый рабочий
работал 7 дней, а второй – 9 дней. Вместе они изготовили 174 детали. Сколько
деталей в день изготавливал каждый рабочий, если первый рабочий за 1 день
изготавливал на 8 деталей меньше, чем второй за 2 дня?

129.  Две наборщицы
подготовили к печати 171 страницу текста. Первая работала 8 ч, а вторая – 7 ч.
Сколько страниц текста готовила за 1 ч каждая наборщица, если вторая за 3 ч
работы подготовила на 29 страниц больше, чем первая за 1 ч работы?

130.  Токарь и его
ученик за 3 ч обтачивают 75 деталей. Если токарь будет работать 2 ч, а его
ученик – 4 ч, то вместе они обточат 70 деталей. Сколько деталей обтачивает
каждый из них за 1 ч?

131.  Токарь и его
ученик за 2 ч обтачивают 54 детали. Если токарь будет работать 3 ч, а его
ученик – 4 ч, то вместе они обточат 92 детали. Сколько деталей обтачивает
каждый из них за 1 ч?

132.  Мастер и его
ученик вместе могут изготовить за 1 час 17 деталей. До обеда мастер проработал
4 часа, а ученик 2 часа и изготовили вместе 54 детали. Сколько деталей
изготавливал каждый из них за 1 час?

Задачи на движение.

133.  Из двух городов,
расстояние между которыми 52 км, одновременно выехали навстречу друг другу два
велосипедиста и встретились через 2 ч. Найдите скорость каждого велосипедиста,
если известно, что второй велосипедист проезжает за 3 ч на 18 км больше, чем
первый за 2 ч.

134.  Из двух сёл
одновременно вышли навстречу друг другу два пешехода и встретились через 3 ч.
Расстояние между сёлами 30 км. Один из пешеходов прошёл до встречи на 6 км
больше, чем другой. Найдите скорость каждого пешехода.

135.  По окружности,
длина которой 100 см, движутся равномерно две точки. Они встречаются каждые 4с,
двигаясь в противоположных направлениях, и через каждые 20 с, двигаясь в одном
направлении. Найдите скорости этих точек.

136.  По окружности,
длина которой 200 см, движутся равномерно две точки. Они встречаются каждые 5
с, двигаясь  противоположных направлениях, и через каждые 20 с, двигаясь в
одном направлении. Найдите скорости этих точек.

137.  Из пункта А в
пункт В, расстояние между которыми 18 км, вышел турист. Через 1,5 ч из пункта В
ему навстречу вышел другой турист, и они встретились через 1 ч 20 мин. Если бы
они вышли одновременно, то встретились бы через 2 ч. Какова скорость каждого
туриста?

138.  Автомобиль за 3,5
ч проехал на 10 км больше, чем мотоциклист за 2,5 ч. Скорость мотоциклиста на
20 км/ч больше скорости автомобиля. Найдите скорость автомобиля и скорость
мотоциклиста.

139.  Турист прошёл 50
км за 3 дня. Во второй день он прошёл на 10 км меньше, чем в первый, и на 5 км
больше, чем в третий. Сколько километров проходил турист каждый день?

140.  Из двух пунктов А
и В, расстояние между которыми 15 км, одновременно навстречу друг другу выехали
два велосипедиста и через 30 мин встретились. Если бы они поехали в одном
направлении, то один догнал бы другого через 2 ч 30 мин. Найдите скорость
каждого велосипедиста.

141.  Два велосипедиста
выехали одновременно навстречу друг другу из двух городов, расстояние между
которыми 90 км. Через 3 ч они встретились, причём первый велосипедист проехал
на 6 км больше второго. Найдите скорость каждого велосипедиста.

142.  Пешеход сначала
шёл в горку со скоростью 3 км/ч, а затем спускался с неё со скоростью 5 км/ч.
Найдите общий путь, проделанный пешеходом, если дорога в горку на 1 км длиннее
спуска, а затраченное на весь путь время равно 3 ч.

143.  Пешеход спускался
со скоростью 4 км/ч, а затем поднимался в горку со скоростью 3 км/ч. Найдите
общий путь, проделанный пешеходом, если спуск был на 5 км длиннее подъёма, а
затраченное на весть путь время равно 3 ч.

144.  Расстояние между
домами, где живут Андрей и Борис, равно 1500 м. Школа находится между домами
мальчиков, причём от дома Андрея она на 300 м дальше, чем от дома Бориса. На
каком расстоянии от школы находится дом каждого мальчика?

145.  Поезд прошёл
первый перегон за 2 ч, а второй за 3 ч. Всего за это время он прошёл 330 км.
Найдите скорость поезда на каждом перегоне, если на втором перегоне она была на
10 км/ч больше, чем на первом.

146.  Расстояние между
Москвой и Санкт-Петербургом по шоссе 700 км. Великий Новгород находится между
этими городами, причём от Москвы на 300 км дальше, чем от Санкт-Петербурга. На
каком расстоянии от Москвы и на каком от Санкт-Петербурга находится Великий
Новгород?

147.  Туристы прошли 24
км, причём 3 ч дорога шла в гору, а 2 ч – под гору. С какой скоростью туристы
шли в гору и с какой под гору, если на первом участке они проходили в час на 2
км меньше, чем на втором?

148.  Велосипедист ехал
2 ч по лесной дороге и 1 ч по шоссе, всего он проехал 40 км. Скорость его на
шоссе была на 4 км/ч больше, чем скорость на лесной дороге. С какой скоростью
велосипедист ехал по шоссе и с какой по лесной дороге?

149.  Из посёлка на
станцию, расстояние между которыми 32 км, выехал велосипедист. Через 0,5 ч
навстречу ему со станции выехал мотоциклист и встретил велосипедиста через 0,5
ч после своего выезда. Известно, что скорость мотоциклиста на 28 км/ч больше
скорости велосипедиста. Найдите скорость каждого из них.

150.  Из пункта А в
пункт В, расстояние между которыми 17 км, вышел пешеход. Через 0,5 ч навстречу
ему из пункта В вышел второй пешеход и встретился с первым через 1,5 ч после
своего выхода. Найдите скорость каждого пешехода, если известно, что скорость
первого на 2 км/ч меньше скорости второго.

151.  Из двух городов,
расстояние между которыми по трассе равно 294 км, выехали одновременно
навстречу друг другу автомобилист и мотоциклист. Через 3 ч они встретились.
Если бы в начале движения автомобилист увеличил скорость вдвое, а мотоциклист
увеличил свою скорость на 7 км/ч, то они встретились бы через 2 ч. Найдите
скорость автомобилиста и скорость мотоциклиста.

152.  На трассе,
протянувшейся с севера на юг, расположены посёлки А и В, расстояние между
которыми 90 км. Из посёлка А, находящегося севернее посёлка В, на юг выехал
автомобилист. Одновременно с ним из посёлка В на ют выехал велосипедист. Через
1,5 ч автомобилист догнал велосипедиста. Если бы автомобилист увеличил скорость
на 26 км/ч, а велосипедист уменьшил свою скорость в 1,5 раза, то автомобилист
догнал бы велосипедиста через час после начала движения. Найдите скорость
автомобилиста и скорость велосипедиста.

153.  Сельчанин может
добраться от своего дома до города двумя способами. В первом случае ему
придётся 1 час 30 минут идти пешком и 4 часа ехать поездом, и он преодолеет в
общей сложности 206 км. Во втором случае ему придётся 2 часа идти пешком и 3
часа ехать поездом (оба поезда движутся с одинаковыми скоростями). Длина второй
дороги 158 км. С какой скоростью сельчанин ходит?

154.  В 10 часов утра
грузовой и легковой автомобили выехали навстречу друг другу из городов,
расстояние между которыми 840 км. Они встретились в 16 часов. Если бы грузовой
автомобиль выехал в 8 часов утра, а легковой автомобиль в 12 часов, то в 16
часов им оставалось бы проехать до встречи 40 км. Найдите скорость легкового
автомобиля.

155.  Туристическая
группа ехала 2 ч на электричке и шла 3 ч пешком, преодолев в общей сложности
пусть в 165 км. Скорость электрички была на 70 км/ч больше скорости движения
пешком. Какое расстояние группа прошла пешком?

156.  Туристическая
группа ехала 3 ч на автобусе и шла 4 ч пешком, преодолев в общей сложности путь
в 200 км. Скорость автобуса была на 55 км/ч больше скорости движения пешком.
Какое расстояние группа прошла пешком?

Задачи на движение по воде.

157.  Катер за 4 ч
движения по течению реки и 3 ч движения по озеру прошёл 148 км. За 5 ч движения
против течения реки он прошёл на 50 км больше, чем за 2 ч по озеру. Найдите
скорость катера в стоячей воде и скорость течения реки.

158.  Моторная лодка за
2 ч движения по течению реки и 5 ч движения против течения реки прошла 120 км.
За 7 ч движения против течения она прошла на 52 км больше, чем за 3 ч движения
по течению. Найдите скорость лодки по течению и её скорость против течения.

159.  По течению реки
лодка за 3 ч 20 мин проходит расстояние 30 км, а против течения за 4 ч –
расстояние 28 км. Какое расстояние по озеру пройдёт лодка за 5 ч?

160.  По течению реки
лодка за 3,5 ч проходит расстояние 42 км, а против течения за 4 ч – расстояние
32 км. Какое расстояние по озеру пройдёт лодка за 6 ч?

161.  Скорость теплохода
по течению реки 45,2 км/ч, а против течения – 36,2 км/ч. Найдите скорость
течения реки.

162.  Путь в 30 км катер
прошёл по течению за 2 ч, а против течения – за 3 ч. Найдите собственную
скорость катера и скорость течения.

163.  Скорость моторной
лодки по течению реки равна 14,3 км/ч, а против течения реки – 12,1 км/ч.
Найдите скорость течения реки и собственную скорость лодки.

164.  Скорость теплохода
по течению реки равна 45,2 км/ч, а против течения реки – 36,2 км/ч. Найдите
скорость течения реки и собственную скорость теплохода.

165.  Скорость моторной
лодки по течению реки равна 25,6 км/ч, а против течения реки – 16,2 км/ч.
Найдите скорость течения реки и собственную скорость лодки.

166.  Скорость моторной
лодки по течению реки равна 17,7 км/ч, а против течения реки – 14,9 км/ч.
Найдите скорость течения реки и собственную скорость лодки.

167.  Из порта
одновременно в противоположных направлениях вышли два катера. Через 3 ч
расстояние между ними составило 96 км. Найдите скорость первого катера, если
она на 10 км/ч больше скорости второго катера.

168.  Моторная лодка
прошла по течению реки 8 км, а против течения – 3 км, затратив на весь путь 45
мин. Найдите собственную скорость лодки, если скорость течения реки равна 2
км/ч.

169.  Моторная лодка
прошла по течению реки 20 км, а против течения 30 км. Найдите собственную
скорость лодки, если скорость течения реки равна 3 км/ч, а на весь путь затрачено
6 ч 40 мин.

170.  Моторная лодка
плыла по течению реки 3 ч, а на тот же путь против течения реки моторная лодка
затратила 5 ч. Найдите собственную скорость лодки, если скорость течения реки
равна 10 км/ч.

171.  Теплоход за 4 ч по
течению реки прошёл 60 км, а за 6 ч против течения прошёл 54 км. Какова была
собственная скорость теплохода и скорость течения реки?

172.  Расстояние, равное
24 км, лодка проплыла по течению за 4 ч, а против течения за 6 ч. Найдите
собственную скорость лодки и скорость течения реки.

173.  Из двух пунктов
реки одновременно навстречу друг другу вышли две моторные лодки. Через 1,2 ч
они встретились. Собственная скорость лодки, которая шла по течению реки, равна
18 км/ч, а лодки, которая шла против течения реки, 16 км/ч. До встречи одна
лодка прошла на 9,6 км больше другой. Найдите скорость течения реки.

174.  Из двух пунктов
реки одновременно навстречу друг другу движутся две моторные лодки, собственные
скорости которых равны. Скорость течения реки равна 2 км/ч. До встречи лодка,
идущая по течению, шла 0,9 ч, а другая лодка шла 1 ч. Найдите собственную
скорость лодок, если лодка, идущая по течению, прошла на 2 км больше, чем
другая лодка.

175.  По течению реки
катер прошёл за 7 ч столько же, сколько он проходит за 8 ч против течения.
Собственная скорость катера 30 км/ч. Сколько км проплывём за 4 ч спичка,
брошенная в эту реку?

176.  Моторная лодка
вышла из пункта А в пункт В и, двигаясь против течения, потратила на путь до
пункта В 4 ч, затем она повернула обратно и прибыла в пункт А ещё через 3 часа.
Собственная скорость лодки 14 км/ч. Сколько км проплывёт плот за 5 ч по этой
реке?

177.  Лодка 2 ч
двигалась по течению и 3 ч против течения, пройдя за это время 36 км. Скорость
лодки против течения составляет  2/3 скорость лодки по течению. Какое
расстояние пройдёт лодка за это время в стоячей воде, если будет двигаться с
той же собственной скоростью?

178.  За 3 ч против
течения реки лодка проплыла на 5 км больше, чем за 2 ч по течению. Скорость
лодки против течения составляет 0,75 её скорости по течению. Какое расстояние
прошла лодка за это время?

179.  Расстояние между
двумя пристанями равно 60 км. Это расстояние лодка проплывает по течению реки
за 4 ч, а против течения реки – за 5 ч. Найдите собственную скорость лодки
скорость течения реки.

180.  Расстояние между
двумя пристанями равно 80 км. Это расстояние лодка проплывает по течению реки
за 5 ч, а против течения реки – за 8 ч. Найдите собственную скорость лодки и
скорость течения реки.

181.  Моторная лодка в
первый день прошла 120 км по течению реки за 5 ч, а во второй день она прошла
72 км против течения за 6 ч. Найдите собственную скорость лодки и скорость
течения реки.

182.  Расстояние между
двумя пристанями равно 75 км. Катер прошёл это расстояние по течению реки за 3
ч, а против течения за 5 ч. Найдите собственную скорость катера и скорость
течения реки.

Задачи на смеси и сплавы.

183.  Сколько граммов
трёхпроцентного и сколько граммов восьмипроцентного растворов соли надо взять,
чтобы получить 260 г пятипроцентного раствора?

184.  Есть металлолом
двух сортов, содержащих 12% и 30% меди. Сколько килограммов лома каждого вида
надо взять, чтобы получить 180 кг сплава, содержащего 25% меди?

185.  Сколько граммов
75%-го и 15%-го растворов кислоты надо смешать, чтобы получить 72 г 50%-го
раствора кислоты?

186.  Сколько граммов
15%-го и 60%-го растворов кислоты надо смешать, чтобы получить 90 г 40%-го
раствора кислоты?

187.  В одном ведре
находится молоко жирностью 30%, а в другом – сливки жирностью 18%. Сколько
нужно взять молока и сколько сливок, чтобы получить 10 л молока жирностью 6%?

188.  В одной бочке
находится смесь спирта с водой в отношении 3:7 соответственно, а в другой –
40%-ная спиртовая смесь. Сколько следует взять спиртовой смеси из каждой бочки,
чтобы получить 16 л смеси, в которой спирт и вода были в отношении 5:11?

Задачи на возраст.

189.  Если сложить возраст
отца и возраст сына, то получится 52. Через 8 лет отношение возраста отца к
возрасту сына будет равно 3. Сколько лет отцу и сколько сыну в настоящий
момент?

190.  Если сложить
возраст отца и возраст сына, то получится 30. Через 7 лет отношение возраста отца
к возрасту сына будет равно 3. Сколько лет отцу и сколько сыну в настоящий
момент?

191.  Мальчик на вопрос
о том, сколько лет ему и его отцу, ответил так: «Вместе нам 44 года. Через 2
года отец будет старше меня в 3 раза». Сколько лет каждому из них сейчас?

192.  Мальчик на вопрос
о том, сколько лет ему и его брату, ответил так: «Вместе нам 20 лет. 4 года
назад я был в 2 раза старше своего брата». Сколько лет каждому из них сейчас?

Задачи повышенной сложности.

193.  * В корзине лежат
35 шаров, среди которых есть шары белого и чёрного цвета. Сколько шаров каждого
цвета лежит в корзине, если известно, что среди каждых 17 шаров есть хотя бы
один белый, а среди каждых 20 шаров есть хотя бы 1 чёрный?

194.  * Коля и Вася
получили за сентябрь по 64 оценки, причём Коля получил пятёрок столько же,
сколько Вася – четвёрок, четвёрок столько же, сколько Вася – троек, троек
столько же, сколько Вася – двоек и двоек столько же, сколько Вася – пятёрок.
Кроме того оказалось, что их средние баллы совпадают. Сколько и Коли двоек?

Решение задач с использованием систем линейных уравнений с двумя переменными.

Переходим теперь к практическому применению систем линейных уравнений с двумя переменными. Часто бывает, что в задачах неизвестны два, а то и три-четыре компонента. И в этом случае обозначение какого-то одного компонента переменной не облегчает решение задачи. Тогда нужно ввести две или три переменные. Вот здесь нам как раз и понадобится система уравнений и способы её решения. Приведём пример с полным описанием.

Например, решить задачу. Лодка за 3 ч движения по течению и 4 ч против течения проходит 114 км. Найдите скорость лодки по течению и её скорость против течения, если за 6 ч движения против течения она проходит такой же путь, как за 5 ч по течению.

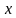
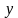
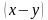
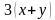
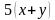
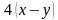
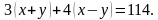
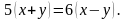
Решение. В задаче описывается движение по воде. А значит, должна быть собственная скорость лодки и скорость течения реки. Они нам и не известны, поэтому обозначим через км/ч собственную скорость лодки, а через км/ч – скорость течения реки. Тогда скорость лодки по течению реки равна км/ч, а скорость лодки против течения реки — км/ч. За 3 ч движения по течению реки лодка пройдёт км, а за 5 ч — км. За 4 ч против течения лодка пройдёт км, а за 6 ч — км. По условию задачи известно, что за 3 ч по течению и 4 ч против течения лодка пройдёт всего 114 км, значит, составляем первое уравнение: Также по условию задачи известно, что за 6 ч движения против течения лодка проходит такой же путь, что и за 5 ч по течению, поэтому составляем второе уравнение:

Для наглядности составим условие задачи в виде таблицы.

Имеем два линейных уравнения с двумя переменными, которые должны выполняться при одних и тех же значениях переменных, значит, составляем систему:

Раскроем сначала скобки и приведём подобные слагаемые.

Уравнения получились достаточно простые, поэтому можно использовать или способ подстановки, или способ сложения. Приведём оба способа решения, чтобы показать, что выбор только за вами, сложность одинакова.

Способ подстановки	Способ сложения

Значит, собственная скорость лодки равна км/ч, а скорость течения реки — км/ч.

Тогда скорость лодки по течению реки: км/ч.

Скорость лодки против течения реки: км/ч.

Ответ: 18 км/ч; 15 км/ч.

Рассмотрим ещё одну задачу.

Есть две металлические отливки, одна из которых содержит 30% меди, а вторая – 70% меди. Сколько килограммов каждой отливки надо взять, чтобы получить 120 кг сплава, содержащего 40% меди?

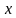
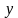
Решение. Пусть кг – масса первой отливки, кг – масса второй отливки. Тогда содержание меди в первой отливке кг, а во второй — кг. По условию задачи известно, что после сплава этих двух отливок, масса станет равной 120 кг, поэтому . Кроме того известно, что полученный сплав будет содержать 40% меди, составляем уравнение: . Запишем и решим систему двух уравнений.

Решим систему способом сложения. Умножим первое уравнение на и почленно сложим два уравнения.

Значит, первого сплава нужно взять 90 кг, а второго – 30 кг.

Ответ: 90 кг; 30 кг.

Задачи на стоимость.

1. За 7 кг апельсинов и 4 кг лимонов заплатили 1120 рублей. Сколько стоит 1 кг апельсинов и сколько 1 кг лимонов, если 5 кг апельсинов дороже, чем 2 кг лимонов, на 390 рублей?

2. За 2 стола и 6 стульев заплатили 10620 рублей. После того, как столы подешевели на 10%, а стулья – на 20%, за один стол и два стула заплатили 4135,5 рублей. Какова была начальная цена одного стола и одного стула?

3. За 4 футбольных и 3 волейбольных мяча заплатили 6700 рублей. После того, как футбольный мяч подешевел на 20%, а волейбольный подорожал на 10%, за один футбольный и один волейбольный мячи заплатили 1830 рублей. Какова была начальная цена каждого мяча?

4. За 5 ручек и 4 карандаша заплатили 300 рублей. Сколько стоит одна ручка и сколько стоит один карандаш, если 3 ручки дороже, чем 2 карандаша, на 70 рублей?

5. За 7 тетрадей и 4 ручки заплатили 300 рублей. После того, как тетради подешевели на 40%, а ручки – на 20%, одна ручка стала дороже одной тетради на 20 рублей. Какими были первоначальные цены тетради и ручки?

6. Магазин закупил конфеты двух сортов в упаковках по 240 г и 250 г, причём конфет первого вида было куплено на 600 г больше. Сколько купили конфет каждого вида, если упаковок с конфетами первого сорта было на 20 больше?

7. Таня за 3 тетради и 2 карандаша заплатила 58 рублей, а Лена за 5 таких же тетрадей и 1 такой же карандаш заплатила 78 рублей. Сколько стоит тетрадь и сколько карандаш?

8. У Толи 18 монет по 2 руб. и по 5 руб. на сумму 97 руб. Сколько монет каждого достоинства у Толи?

9. Банк продал предпринимателю г-ну Разину 8 облигаций по 2000 руб. и 3000 руб. Сколько облигаций каждого номинала купил г-н Разин, если за все облигации было заплачено 19 000 рублей?

10. За 15 акций компании «Трансгаз» и 10 акций компании «Суперсталь» заплатили 35 000 руб. Сколько стоит одна акция каждой компании, если акция «Трансгаза» на 1000 руб. дешевле акции «Суперстали»?

11. За 4 блокнота и 3 карандаша заплатили 181 руб., а за такие же 2 блокнота и 5 карандашей заплатили 115 руб. Сколько стоит один блокнот и один карандаш?

12. За 5 пачек творога и 2 банки сметаны заплатили 210 руб., а за такие же 3 пачки творога и 3 банки сметаны заплатили 171 руб. Сколько стоит одна пачка творога и одна банка сметаны?

13. Шапка и шарф вместе стоили 1200 руб. После того, как шапка подешевела на 20%, а шарф – на 10%, их суммарная стоимость составила 1005 руб. Сколько стоила шапка и сколько стоил шарф до снижения цен?

14. Сумка и ремень вместе стоили 2300 руб. После того как сумка подешевела на 15%, а ремень – на 5%, их суммарная стоимость составила 2005 руб. Сколько стоила сумка и сколько стоил ремень до снижения цен?

15. Три ватрушки и пять плюшек стоят 45 руб., а пять ватрушек и три плюшки стоят 43 руб. Сколько стоит ватрушка и сколько стоит плюшка?

16. Три марки и пять конвертов стоят 39 руб., а четыре марки и два конверта стоят 24 руб. Сколько стоит марка и сколько стоит конверт?

17. Пять открыток и четыре конверта стоят 44 руб., а две открытки и три конверта стоят 26 руб. Сколько стоит открытка и сколько стоит конверт?

18. Стоимость 50 экземпляров учебника физики для 10 класса и 25 экземпляров учебника физики для 11 класса составляет 10 000 рублей. С учётом скидки в размере 20% на учебники для 10 класса и 10% на учебники для 11 класса стоимость покупки снизилась на 17%. Сколько стоит один учебник физики для 10 класса с учётом скидки?

19. За 1 кг апельсинов и 1 кг яблок заплатили 120 рублей. После подорожания апельсинов на 30%, а яблок на 20% такая же покупка будет стоить 151 руб. Найдите первоначальную стоимость 1 кг апельсинов и 1 кг яблок.

20. За 1 кг огурцов и 1 кг помидоров заплатили 150 руб. После того как огурцы подешевеют на 30%, а помидоры на 20%, такая же покупка будет стоить 113 руб. Найдите первоначальную стоимость 1 кг огурцов и 1 кг помидоров.

21. За 1 рюкзак и 1 пенал заплатили 850 руб. Если рюкзак подорожает на 10%, а пенал на 20%, такая же покупка будет стоить 950 руб. Найдите первоначальную стоимость 1 рюкзака и 1 пенала.

22. Три пирожка и две булки стоят 40 руб., а два пирожка и три булки стоят 45 руб. Сколько стоит пирожок, сколько стоит булка?

Задачи на количество.

1. В двух ящиках лежали яблоки. Если из одного ящика переложить во второй 45 яблок, то в обоих ящиках их станет поровну. Если же из второго ящика переложить в первый 20 яблок, то в первом станет в 3 раза больше яблок, чем во втором. Сколько яблок было в каждом ящике?

2. В двух шкафах стояли книги. Если из первого шкафа переставить во второй 10 книг, то в обоих шкафах книг станет поровну. Если же из второго шкафа переставить в первый 44 книги, то в нём останется в 4 раза меньше книг, чем в первом. Сколько книг было в каждом шкафу?

3. У двух мальчиков были марки. Если один из них отдаст второму 10 марок, то у обоих мальчиков марок станет поровну. Если же первый отдаст второму 50 марок, то у него останется в 5 раз меньше марок, чем станет у второго. Сколько марок было у каждого мальчика?

4. В туристический поход ребята взяли двухместные и трёхместные палатки. Сколько человек разместилось в трёхместных палатках, если на 26 человек ребята взяли 10 палаток?

5. В копилку складывали двухрублёвые и пятирублёвые монеты. Когда копилку вскрыли, в ней оказалось 178 рублей, причём пятирублёвых монет было на 12 штук меньше, чем двухрублёвых. Сколько денег пятирублёвыми монетами было в копилке?

6. В гостинице 25 номеров. Есть четырёхместные и двухместные номера. Сколько каких номеров, если всего в гостинице могут поместиться 70 человек?

7. В первый день в школьную библиотеку привезли 4 пачки учебников по геометрии и 3 пачки учебников по алгебре: всего 96 книг. Во второй день привезли 5 пачек учебников по геометрии и 6 пачек учебников по алгебре, причём учебников по геометрии на 3 больше, чем по алгебре. Сколько учебников по геометрии привезли в библиотеку?

8. В магазин привезли 3 коробки с пачками чая и 4 коробки с пачками кофе, всего 76 пачек. В другой день привезли 6 таких же коробок чая и 5 коробок кофе, причём чая на 22 пачки больше. Сколько пачек чая привезли?

9. В первом отряде летнего лагеря было 25 подростков. В течение смены число девочек увеличилось на 10%, а число мальчиков уменьшилось на 20%, в результате в отряде стало 23 подростка. Сколько девочек и сколько мальчиков стало в первом отряде в конце смены?

10. На дворе было 20 кроликов и кур, у которых 52 ноги. Сколько было кроликов и сколько было кур на дворе?

11. Для кормления 5 лошадей и 25 коров ежедневно отпускают 220 кг сена, для 3 лошадей и 35 коров отпускают 272 кг сена. Найдите дневную норму сена для лошади и для коровы.

12. Летели галки и сели на палки. Если на каждую палку сядет по галке, то одной галке не хватит палки. Если на каждую палку сядут по две галки, то одна палка останется без галок. Сколько было галок и сколько палок?

13. Школьники отправились в поход в составе 57 человек, при этом у них были только трёхместные и четырёхместные палатки. Сколько трёхместных палаток и сколько четырёхместных, если всего в поход взяли 16 палаток?

14. 83 подарка были упакованы в большие и маленькие коробки. В большие коробки помещается по 8 подарков, а в маленькие – по 5. Всего использовали 13 коробок. Сколько было коробок каждого вида?

15. В гостинице группа из 27 туристов была размещена в двухместных и трёхместных номерах. Всего туристы заняли 10 номеров. Сколько было занято трёхместных и сколько двухместных номеров?

16. В классе 36 учеников. Девочек на 3 меньше, чем мальчиков. Сколько девочек и сколько мальчиков было в классе?

17. В магазине продаются тетради по 96 листов и по 24 листа. Во всех тетрадях, купленных Сашей, 528 листов. Сколько толстых и сколько тонких тетрадей купил Саша, если все купленные им толстые тетради содержат на 48 листов больше, чем все тонкие?

18. В физкультурном зале 35 учеников. Мальчиков в 1,5 раза больше, чем девочек. Сколько мальчиков и сколько девочек в физкультурном зале?

19. В первой рукописи на 60 страниц больше, чем во второй. Корректор, вычитывающий первую рукопись, выполнив 60% всей работы, вычитал на 12 страниц меньше, чем корректор, вычитывающий вторую рукопись и выполнивший 80% всей работы. Сколько страниц в каждой рукописи?

20. На турбазе имеются палатки и домики, вместе их 25. В каждом домике живут 4 человека, а в палатке – 2. Сколько на турбазе палаток и сколько домиков, если турбаза рассчитана на 70 человек?

21. В классе 24 человека. Чтобы девочкам выдать по три тетради, а мальчиками по две тетради, потребуется 59 тетрадей. Сколько в классе мальчиков и сколько девочек?

22. В классе 25 человек. Чтобы девочкам выдать по три тетради, а мальчикам по две тетради, потребуется 62 тетради. Сколько в классе мальчиков и сколько девочек?

23. На двух полках стояло 210 книг. Если с первой полки убрать половину книг, а на второй увеличить их число вдвое, то на двух полках будет 180 книг. Сколько книг стояло на каждой полке первоначально?

24. В двух коробках лежало 210 карандашей. Если в первой коробке число карандашей уменьшить вдвое, а во второй их число увеличить в 2 раза, то в двух коробках станет 240 карандашей. Сколько карандашей было в каждой коробке первоначально?

25. Если раздать детям по 3 яблока, то 7 яблок останется, а чтобы раздать каждому по 5 яблок, не хватит 3 яблок. Сколько было детей?

26. Если раздать детям по 5 конфет, то 13 конфет останется, а чтобы раздать каждому по 8 конфет, не хватит 5 конфет. Сколько было детей?

27. В 5 пакетов и 4 коробки расфасовали 1 650 г печенья. В каждую коробку уместилось на 75 г печенья больше, чем в пакет. Сколько граммов печенья расфасовали в коробки?

28. К новогоднему празднику семиклассники клеили бумажные гирлянды и ёлочные игрушки. Каждый мальчик склеил по 4 гирлянды и 3 игрушки, а каждая девочка по 3 гирлянды и 5 игрушек. Мальчики склеили на 22 гирлянды больше, чем девочки. Игрушек всего было сделано 118. Сколько мальчиков и девочек в этом классе?

29. В физкультурный зал школы привезли 5 сеток с баскетбольными мячами и 2 сетки с волейбольными мячами, всего 23 мяча. Через неделю – 3 такие же сетки с баскетбольными мячами и одну сетку с волейбольными мячами, причём баскетбольных мячей на 5 больше, чем волейбольных. Сколько мячей в каждой сетке?

30. В магазин привезли 3 упаковки с пачками чая и 4 упаковки с пачками кофе, всего 85 пачек. В другой день – 5 таких же упаковок с пачками чая и 4 упаковки с пачками кофе, всего 107 пачек. Сколько пачек чая и сколько пачек кофе в каждой упаковке?

31. Группа туристов, в которой 21 человек, отправилась в поход на байдарках. Они взяли с собой двухместные и трёхместные байдарки, всего 9 лодок. Сколько байдарок каждого типа взяли с собой туристы?

32. Десант из 130 человек был доставлен к месту назначения на 4 тяжёлых и 2 лёгких вертолётах. Один тяжёлый и один лёгкий вертолёты вместе вмещают 36 десантников. Сколько десантников можно перевезти в каждом вертолёте?

33. Две мастерские сшили в первый день 110 костюмов. Во второй день первая мастерская увеличила выпуск костюмов на 20%, а вторая – на 10%, в результате во второй день было сшито на 16 костюмов больше, чем в первый день. Сколько костюмов сшила каждая мастерская во второй день?

34. Масса туриста с рюкзаком в 5 раз больше массы одного рюкзака. Определите массы рюкзака и туриста в отдельности, если сумма масс двух рюкзаков и массы туриста равна 120 кг.

35. Шесть метров новой верёвки имеют такую же массу, как и пять метров старой. Найдите массу одного метра новой и старой верёвки в отдельности, если 13 м новой и 12 м старой верёвки вместе весят 5 кг 480 г.

36. В одном баке было 28 л бензина, а в другом – 42 л. Если первый бак долить доверху из второго бака, то второй бак станет наполненным наполовину. Если второй бак дополнить доверху из первого бака, то в нём останется только четвёртая часть объёма. Найдите объём каждого бака.

37. У Лены 8 монет по 10 руб. и 5 руб. Сколько у неё десятирублёвых и сколько пятирублёвых монет, если всего у неё 65 рублей?

38. На получение пирожка в автомате нужно 5 жетонов, а на получение булочки – 1 жетон. Таня получила в автомате несколько пирожков и булочек, отдав за всю покупку 25 жетонов. Сколько пирожков и сколько булочек получила Таня, если за булочки она отдала на 15 жетонов меньше, чем за пирожки?

Задачи с геометрическими фигурами.

1. Если ширину прямоугольника уменьшить на 2 см, а длину увеличить на 3 см, то его площадь уменьшится на 8 см². Если же каждую сторону данного прямоугольника увеличить на 4 см, то площадь исходного прямоугольника увеличится на 80 см². Найдите стороны данного прямоугольника.

2. Если длину прямоугольника уменьшить на 2 м, а ширину увеличить на 4 м, то его площадь увеличится на 12 м². Если же каждую его сторону уменьшить на 1 м, то площадь исходного прямоугольника уменьшится на 13 м². Найдите стороны данного прямоугольника.

3. Периметр прямоугольника равен 32 см. Если его длину увеличить на 5 см, а ширину уменьшить на 2 см, то площадь прямоугольника увеличится на 7 см². Найдите стороны данного прямоугольника.

4. Одна сторона прямоугольника на 4 см больше другой. Если меньшую сторону увеличить в 2 раза, а большую оставить без изменения, то периметр нового прямоугольника будет равен 56 см. Найдите стороны данного прямоугольника.

5. Периметр прямоугольника равен 48 см. Если одну его сторону увеличить в 2 раза, а другую уменьшить на 6 см, то периметр нового прямоугольника будет равен 64 см. Найдите стороны данного прямоугольника.

6. Периметр прямоугольника равен 56 см. Найдите его стороны, если известно, что длина прямоугольника на 14,2 см больше ширины.

7. Периметр прямоугольника 400 м. Длина его в 3 раза больше ширины. Найдите длину и ширину этого прямоугольника.

8. Периметр равнобедренного треугольника 17 см. Основание треугольника на 2 см меньше, чем боковая сторона. Найдите стороны этого треугольника.

9. Боковая сторона равнобедренного треугольника на 4 см длиннее основания. Найти стороны треугольника, если его периметр равен 26 см.

10. Ширина прямоугольника на 5 см короче его длины. Найдите длину и ширину прямоугольника, если его периметр равен 38 см.

Задачи с числами.

1. Сумма цифр двузначного числа равна 8. Если поменять местами его цифры, то получим число, которое больше данного на 18. Найдите данное число.

2. Цифра в разряде десятков данного трёхзначного числа равна нулю, а удвоенное количество сотен на 2 меньше, чем количество единиц. Число, записанное теми же цифрами в обратном порядке, на 495 больше данного. Найдите данное число.

3. Сумма удвоенного количества десятков и количества единиц некоторого двузначного числа равна 11. Если поменять местами цифры этого числа, то получим число, которое на 9 меньше данного. Найдите данное число.

4. Сумма двух чисел равна 77. Найдите эти числа, если первого числа равны второго числа.

5. Разность двух чисел равна 12. Найдите эти числа, если первого числа равны второго числа.

6. Сумма цифр двузначного числа равна 8. Если к данному числу прибавить 18, то получится двузначное число, записанное теми же цифрами, но в обратном порядке. Найдите данное число.

7. Разность между двузначным числом и числом, записанным теми же цифрами, но в обратном порядке, равна 27. Разность между квадратами таких чисел равна 1485. Найдите данное число.

8. Разность между двузначным числом и числом, записанным теми же цифрами, но в обратном порядке, равна 45. Разность между квадратами таких чисел равна 5445. Найдите данное число.

9. Сумма чисел равна 98, а из разность – 42,4. Найдите эти числа.

10. Найдите двузначное число, сумма цифр которого равна 15, а разность цифр равна 3.

11. Даны два числа. Если к первому числу прибавить половину второго, то получится 65, а если из второго вычесть третью часть первого, то получится первое число. Найдите эти числа.

12. Если к первому числу добавить четверть второго числа, получится 129, а если увеличить второе число в 5 раз и отнять от него половину первого числа, то получится первое число. Найдите эти числа.

13. Разность квадратов двух натуральных чисел равна 21, а сумма этих чисел равна 7. Найдите эти числа.

14. Сумма двух чисел равна 76, а 3/4 первого числа составляют 5/6 второго числа. Найдите эти числа.

15. Среднее арифметическое двух чисел равно 11. Если большее число разделить на меньшее, то в частном получится 3, а в остатке 2. Найдите эти числа.

16. При сложении двузначного числа с суммой его цифр получится 50. Если от этого числа отнять число, записанное теми же цифрами в обратном порядке, то получится 9. Найдите это число.

17. Если к числителю и знаменателю несократимой дроби прибавить по 1, то получится , а если вычесть из них по 1, то получится . Найдите эту дробь.

18. Задумали два числа. Если сложить 70% первого числа и 20% второго, то получится 20. Если же первое число уменьшить на 20%, а второе увеличить на 30%, а затем сложить полученные результаты, то получится55. Чему равно каждое из чисел?

19. Задумали два числа. Если сложить 30% первого числа и 40% второго, то получится 10. Если же первое число увеличить на 10%, а второе уменьшить на 20%, а затем сложить полученные результаты, то получится 26. Чему равно каждое из чисел?

20. Задумали два числа. Если сложить 40% первого числа и 20% второго, то получится 18. Если же первое число увеличить на 20%, а второе уменьшить на 10%, а затем сложить полученные результаты, то получится 69. Чему равно каждое из чисел?

21. Сумма двух чисел равна 17. Одно из чисел на 7 меньше другого. Найдите эти числа.

22. Разность двух чисел равна 12. Одно из них больше другого в 4 раза. Найдите эти числа.

23. 4 боксёра тяжёлого веса и 5 боксёров лёгкого веса вместе весят 730 кг. Спортсмен тяжёлого веса весит на 70 кг больше спортсмена лёгкого веса. Найдите вес каждого боксёра.

24. Среднее арифметическое двух чисел равно 22,5; а их разности равна Найдите эти два числа.

25. Одно число на 215 больше другого; 80% большего числа на 129 больше 60% меньшего из них. Найдите эти числа.

26. В трёхзначном числе сумма цифр равна 16. Цифра разряда сотен в 4 раза меньше цифры разряда десятков и на 4 меньше цифры разряда единиц. Найдите это число.

27. Сумма двух чисел равна 81. а их разность равна 15. Найдите эти числа.

28. Сумма двух чисел равна 36. Одно из них в 2 раза больше другого. Найдите эти числа.

29. Три яблока и две груши весят вместе 1 кг 200 г. Яблоко легче груши на 100 г. Сколько весит одно яблоко и сколько одна груша?

30. Среднее арифметическое двух чисел равно 36, а их разности равна 0,8. Найдите эти числа.

31. Одно число на 140 меньше другого; 60% большего числа на 64 больше 70% меньшего числа. Найдите эти числа.

32. В трёхзначном числе сумма цифр равна 10. Цифра разряда сотен в 2 раза больше цифры разряда десятков и на 5 больше цифры разряда единиц. Найдите это число.

33. Если к числителю дроби прибавить 1, а к знаменателю 2, то дробь не изменится. Если же к числителю дроби прибавить 2, а из знаменателя вычесть 1, то дробь увеличится в 6 раз. Найдите эту дробь.

34. Сумма цифр двузначного числа равна 9. Если это число разделить на разность его цифр, то получится 54. Найдите исходное число.

35. Если к числителю дроби прибавить 2, а к знаменателю дроби прибавить 3, то получится ½. Числитель дроби в 3 раза меньше знаменателя. Найдите исходную дробь.

36. Разность цифр двузначного числа равна 6. Если это число разделить на сумму его цифр, то получится 8,2. Найдите исходное число.

37. Разность двух чисел равна 16, а их сумма равна 26. Найдите эти числа.

38. Сумма двух чисел равна 47, а их разность равна 29. Найдите эти числа.

39. Коля задумал два числа. Удвоенное первое число в 3 раза больше второго. Если же первое из задуманных чисел уменьшить на 49, оно станет в 3 раза меньше второго. Найдите задуманные числа.

40. Андрей задумал два числа. Утроенное первое число в 2 раза больше второго. Если же первое из задуманных чисел уменьшить на 11, оно станет в 2 раза меньше второго. Найдите задуманные числа.

41. Саша задумал два числа. Утроенное первое число в 4 раза больше второго. Если же первое из задуманных чисел уменьшить на 26, оно станет в 4 раза меньше второго. Найдите задуманные числа.

42. Андрей задумал два числа. Удвоенное первое число в 5 раз больше второго. Если же первое из задуманных чисел уменьшить на 69, оно станет в 5 раз меньше второго. Найдите задуманные числа.

43. Сумма двух чисел равна 35. Если одно из них увеличить в 4 раза, а другое – на 30, то сумма полученных чисел будет равна 125. Найдите эти числа.

Задачи на работу.

1. На заводе изготовили два вида деталей. Масса 8 деталей одного вида и 6 деталей другого вида составляет вместе 29 кг. Найдите массу детали каждого вида, если масса 4 деталей второго вида на 1 кг больше, чем масса двух деталей первого вида.

2. Саша и Витя вскапывают грядку за 10 мин, а один Витя – за 15 мин. За сколько минут вскапывает грядку один Саша?

3. Игорь и Олег вскапывают грядку за 12 мин, а один Игорь – за 20 мин. За сколько минут вскапывает грядку один Олег?

4. Миша вскапывает грядку за 10 мин, Саша – за 12 мин, Олег – за 15 мин. За сколько минут они скопают грядку втроём?

5. Миша вскапывает грядку за 6 мин, Саша – за 20 мин, Олег – за 30 мин. За сколько минут они вскопают грядку втроём?

6. Если половину заказа выполнит мастер, а оставшуюся часть закончит ученик, то вся работы будет сделана за 10 ч. Если мастер выполнит ¾ работы, а оставшуюся часть выполнит ученик, то всё будет сделано за 9 ч. За какое время мог бы выполнить работу каждый из них, работая один?

7. Четыре одинаковых насоса, работая вместе, наполнили нефтью первый танкер и треть второго танкера (другого объёма) за 11 ч. Если бы три насоса наполнили первый танкер, а затем один из насосов наполнил бы четверть второго танкера, то работа заняла бы 18 ч. За сколько часов три насоса могут наполнить второй танкер?

8. Три каменщика (разной квалификации) выложили кирпичную стену, причём первый каменщик работал 6 ч, второй – 4 ч, а третий – 7 ч. Если бы первый каменщик работал 4 ч, второй – 2 ч, а третий – 5 ч, то они выполнили бы 2/3 всей работы. За сколько часов каменщики закончили бы кладку, если бы они работали все вместе одно и то же время?

9. Три бригады вспахали два поля общей площадью 96 га. Первое поле было вспахано за 3 дня, причём все три бригады работали вместе. Второе поле было вспахано за 6 дней второй и третьей бригадами. Если бы все три бригады проработали на втором поле 1 день, то оставшуюся часть второго поля первая бригада могла вспахать за 8 дней. Сколько гектаров в день вспахивает первая бригада?

10. Три одинаковых комбайна, работая вместе, убрали первое поле, а затем два из них убрали второе поле (другой площади). Вся работа заняла 12 ч. Если бы три комбайна выполнили половину всей работы, а затем оставшуюся часть сделал бы один из них, то работа заняла бы 20 ч. За какое время два комбайна могут убрать первое поле?

11. Две бригады вместе должны изготовить 270 изделий. К середине дня первая бригада выполнила 60% своего задания, а вторая – 70% своего. При этом первая бригада изготовила на 6 изделий больше, чем вторая. Сколько изделий должна изготовить каждая бригада?

12. Два токаря изготовили 172 детали. Первый работал 3 ч, а второй – 2 ч. Если бы первый работал 1 ч, а второй – 4 ч, то они изготовили бы 198 деталей. Сколько деталей изготовил каждый токарь?

13. Маша и Даша могут вымыть окно за 1 ч, работая вместе. За сколько часов может вымыть окно Даша, если известно, что Маша работает в 3 раза быстрее Даши?

14. Андрей и Иван могут покрасить забор за 2 ч, работая вместе. За сколько часов может покрасить забор Иван, если известно, что он работает медленнее Андрея в 4 раза?

15. Первый рабочий работал 7 дней, а второй – 9 дней. Вместе они изготовили 174 детали. Сколько деталей в день изготавливал каждый рабочий, если первый рабочий за 1 день изготавливал на 8 деталей меньше, чем второй за 2 дня?

16. Две наборщицы подготовили к печати 171 страницу текста. Первая работала 8 ч, а вторая – 7 ч. Сколько страниц текста готовила за 1 ч каждая наборщица, если вторая за 3 ч работы подготовила на 29 страниц больше, чем первая за 1 ч работы?

17. Токарь и его ученик за 3 ч обтачивают 75 деталей. Если токарь будет работать 2 ч, а его ученик – 4 ч, то вместе они обточат 70 деталей. Сколько деталей обтачивает каждый из них за 1 ч?

18. Токарь и его ученик за 2 ч обтачивают 54 детали. Если токарь будет работать 3 ч, а его ученик – 4 ч, то вместе они обточат 92 детали. Сколько деталей обтачивает каждый из них за 1 ч?

19. Мастер и его ученик вместе могут изготовить за 1 час 17 деталей. До обеда мастер проработал 4 часа, а ученик 2 часа и изготовили вместе 54 детали. Сколько деталей изготавливал каждый из них за 1 час?

Задачи на движение.

1. Из двух городов, расстояние между которыми 52 км, одновременно выехали навстречу друг другу два велосипедиста и встретились через 2 ч. Найдите скорость каждого велосипедиста, если известно, что второй велосипедист проезжает за 3 ч на 18 км больше, чем первый за 2 ч.

2. Из двух сёл одновременно вышли навстречу друг другу два пешехода и встретились через 3 ч. Расстояние между сёлами 30 км. Один из пешеходов прошёл до встречи на 6 км больше, чем другой. Найдите скорость каждого пешехода.

3. По окружности, длина которой 100 см, движутся равномерно две точки. Они встречаются каждые 4с, двигаясь в противоположных направлениях, и через каждые 20 с, двигаясь в одном направлении. Найдите скорости этих точек.

4. По окружности, длина которой 200 см, движутся равномерно две точки. Они встречаются каждые 5 с, двигаясь противоположных направлениях, и через каждые 20 с, двигаясь в одном направлении. Найдите скорости этих точек.

5. Из пункта А в пункт В, расстояние между которыми 18 км, вышел турист. Через 1,5 ч из пункта В ему навстречу вышел другой турист, и они встретились через 1 ч 20 мин. Если бы они вышли одновременно, то встретились бы через 2 ч. Какова скорость каждого туриста?

6. Автомобиль за 3,5 ч проехал на 10 км больше, чем мотоциклист за 2,5 ч. Скорость мотоциклиста на 20 км/ч больше скорости автомобиля. Найдите скорость автомобиля и скорость мотоциклиста.

7. Турист прошёл 50 км за 3 дня. Во второй день он прошёл на 10 км меньше, чем в первый, и на 5 км больше, чем в третий. Сколько километров проходил турист каждый день?

8. Из двух пунктов А и В, расстояние между которыми 15 км, одновременно навстречу друг другу выехали два велосипедиста и через 30 мин встретились. Если бы они поехали в одном направлении, то один догнал бы другого через 2 ч 30 мин. Найдите скорость каждого велосипедиста.

9. Два велосипедиста выехали одновременно навстречу друг другу из двух городов, расстояние между которыми 90 км. Через 3 ч они встретились, причём первый велосипедист проехал на 6 км больше второго. Найдите скорость каждого велосипедиста.

10. Пешеход сначала шёл в горку со скоростью 3 км/ч, а затем спускался с неё со скоростью 5 км/ч. Найдите общий путь, проделанный пешеходом, если дорога в горку на 1 км длиннее спуска, а затраченное на весь путь время равно 3 ч.

11. Пешеход спускался со скоростью 4 км/ч, а затем поднимался в горку со скоростью 3 км/ч. Найдите общий путь, проделанный пешеходом, если спуск был на 5 км длиннее подъёма, а затраченное на весть путь время равно 3 ч.

12. Расстояние между домами, где живут Андрей и Борис, равно 1500 м. Школа находится между домами мальчиков, причём от дома Андрея она на 300 м дальше, чем от дома Бориса. На каком расстоянии от школы находится дом каждого мальчика?

13. Поезд прошёл первый перегон за 2 ч, а второй за 3 ч. Всего за это время он прошёл 330 км. Найдите скорость поезда на каждом перегоне, если на втором перегоне она была на 10 км/ч больше, чем на первом.

14. Расстояние между Москвой и Санкт-Петербургом по шоссе 700 км. Великий Новгород находится между этими городами, причём от Москвы на 300 км дальше, чем от Санкт-Петербурга. На каком расстоянии от Москвы и на каком от Санкт-Петербурга находится Великий Новгород?

15. Туристы прошли 24 км, причём 3 ч дорога шла в гору, а 2 ч – под гору. С какой скоростью туристы шли в гору и с какой под гору, если на первом участке они проходили в час на 2 км меньше, чем на втором?

16. Велосипедист ехал 2 ч по лесной дороге и 1 ч по шоссе, всего он проехал 40 км. Скорость его на шоссе была на 4 км/ч больше, чем скорость на лесной дороге. С какой скоростью велосипедист ехал по шоссе и с какой по лесной дороге?

17. Из посёлка на станцию, расстояние между которыми 32 км, выехал велосипедист. Через 0,5 ч навстречу ему со станции выехал мотоциклист и встретил велосипедиста через 0,5 ч после своего выезда. Известно, что скорость мотоциклиста на 28 км/ч больше скорости велосипедиста. Найдите скорость каждого из них.

18. Из пункта А в пункт В, расстояние между которыми 17 км, вышел пешеход. Через 0,5 ч навстречу ему из пункта В вышел второй пешеход и встретился с первым через 1,5 ч после своего выхода. Найдите скорость каждого пешехода, если известно, что скорость первого на 2 км/ч меньше скорости второго.

19. Из двух городов, расстояние между которыми по трассе равно 294 км, выехали одновременно навстречу друг другу автомобилист и мотоциклист. Через 3 ч они встретились. Если бы в начале движения автомобилист увеличил скорость вдвое, а мотоциклист увеличил свою скорость на 7 км/ч, то они встретились бы через 2 ч. Найдите скорость автомобилиста и скорость мотоциклиста.

20. На трассе, протянувшейся с севера на юг, расположены посёлки А и В, расстояние между которыми 90 км. Из посёлка А, находящегося севернее посёлка В, на юг выехал автомобилист. Одновременно с ним из посёлка В на ют выехал велосипедист. Через 1,5 ч автомобилист догнал велосипедиста. Если бы автомобилист увеличил скорость на 26 км/ч, а велосипедист уменьшил свою скорость в 1,5 раза, то автомобилист догнал бы велосипедиста через час после начала движения. Найдите скорость автомобилиста и скорость велосипедиста.

21. Сельчанин может добраться от своего дома до города двумя способами. В первом случае ему придётся 1 час 30 минут идти пешком и 4 часа ехать поездом, и он преодолеет в общей сложности 206 км. Во втором случае ему придётся 2 часа идти пешком и 3 часа ехать поездом (оба поезда движутся с одинаковыми скоростями). Длина второй дороги 158 км. С какой скоростью сельчанин ходит?

22. В 10 часов утра грузовой и легковой автомобили выехали навстречу друг другу из городов, расстояние между которыми 840 км. Они встретились в 16 часов. Если бы грузовой автомобиль выехал в 8 часов утра, а легковой автомобиль в 12 часов, то в 16 часов им оставалось бы проехать до встречи 40 км. Найдите скорость легкового автомобиля.

23. Туристическая группа ехала 2 ч на электричке и шла 3 ч пешком, преодолев в общей сложности пусть в 165 км. Скорость электрички была на 70 км/ч больше скорости движения пешком. Какое расстояние группа прошла пешком?

24. Туристическая группа ехала 3 ч на автобусе и шла 4 ч пешком, преодолев в общей сложности путь в 200 км. Скорость автобуса была на 55 км/ч больше скорости движения пешком. Какое расстояние группа прошла пешком?

Задачи на движение по воде.

1. Катер за 4 ч движения по течению реки и 3 ч движения по озеру прошёл 148 км. За 5 ч движения против течения реки он прошёл на 50 км больше, чем за 2 ч по озеру. Найдите скорость катера в стоячей воде и скорость течения реки.

2. Моторная лодка за 2 ч движения по течению реки и 5 ч движения против течения реки прошла 120 км. За 7 ч движения против течения она прошла на 52 км больше, чем за 3 ч движения по течению. Найдите скорость лодки по течению и её скорость против течения.

3. По течению реки лодка за 3 ч 20 мин проходит расстояние 30 км, а против течения за 4 ч – расстояние 28 км. Какое расстояние по озеру пройдёт лодка за 5 ч?

4. По течению реки лодка за 3,5 ч проходит расстояние 42 км, а против течения за 4 ч – расстояние 32 км. Какое расстояние по озеру пройдёт лодка за 6 ч?

5. Скорость теплохода по течению реки 45,2 км/ч, а против течения – 36,2 км/ч. Найдите скорость течения реки.

6. Путь в 30 км катер прошёл по течению за 2 ч, а против течения – за 3 ч. Найдите собственную скорость катера и скорость течения.

7. Скорость моторной лодки по течению реки равна 14,3 км/ч, а против течения реки – 12,1 км/ч. Найдите скорость течения реки и собственную скорость лодки.

8. Скорость теплохода по течению реки равна 45,2 км/ч, а против течения реки – 36,2 км/ч. Найдите скорость течения реки и собственную скорость теплохода.

9. Скорость моторной лодки по течению реки равна 25,6 км/ч, а против течения реки – 16,2 км/ч. Найдите скорость течения реки и собственную скорость лодки.

10. Скорость моторной лодки по течению реки равна 17,7 км/ч, а против течения реки – 14,9 км/ч. Найдите скорость течения реки и собственную скорость лодки.

11. Из порта одновременно в противоположных направлениях вышли два катера. Через 3 ч расстояние между ними составило 96 км. Найдите скорость первого катера, если она на 10 км/ч больше скорости второго катера.

12. Моторная лодка прошла по течению реки 8 км, а против течения – 3 км, затратив на весь путь 45 мин. Найдите собственную скорость лодки, если скорость течения реки равна 2 км/ч.

13. Моторная лодка прошла по течению реки 20 км, а против течения 30 км. Найдите собственную скорость лодки, если скорость течения реки равна 3 км/ч, а на весь путь затрачено 6 ч 40 мин.

14. Моторная лодка плыла по течению реки 3 ч, а на тот же путь против течения реки моторная лодка затратила 5 ч. Найдите собственную скорость лодки, если скорость течения реки равна 10 км/ч.

15. Теплоход за 4 ч по течению реки прошёл 60 км, а за 6 ч против течения прошёл 54 км. Какова была собственная скорость теплохода и скорость течения реки?

16. Расстояние, равное 24 км, лодка проплыла по течению за 4 ч, а против течения за 6 ч. Найдите собственную скорость лодки и скорость течения реки.

17. Из двух пунктов реки одновременно навстречу друг другу вышли две моторные лодки. Через 1,2 ч они встретились. Собственная скорость лодки, которая шла по течению реки, равна 18 км/ч, а лодки, которая шла против течения реки, 16 км/ч. До встречи одна лодка прошла на 9,6 км больше другой. Найдите скорость течения реки.

18. Из двух пунктов реки одновременно навстречу друг другу движутся две моторные лодки, собственные скорости которых равны. Скорость течения реки равна 2 км/ч. До встречи лодка, идущая по течению, шла 0,9 ч, а другая лодка шла 1 ч. Найдите собственную скорость лодок, если лодка, идущая по течению, прошла на 2 км больше, чем другая лодка.

19. По течению реки катер прошёл за 7 ч столько же, сколько он проходит за 8 ч против течения. Собственная скорость катера 30 км/ч. Сколько км проплывём за 4 ч спичка, брошенная в эту реку?

20. Моторная лодка вышла из пункта А в пункт В и, двигаясь против течения, потратила на путь до пункта В 4 ч, затем она повернула обратно и прибыла в пункт А ещё через 3 часа. Собственная скорость лодки 14 км/ч. Сколько км проплывёт плот за 5 ч по этой реке?

21. Лодка 2 ч двигалась по течению и 3 ч против течения, пройдя за это время 36 км. Скорость лодки против течения составляет 2/3 скорость лодки по течению. Какое расстояние пройдёт лодка за это время в стоячей воде, если будет двигаться с той же собственной скоростью?

22. За 3 ч против течения реки лодка проплыла на 5 км больше, чем за 2 ч по течению. Скорость лодки против течения составляет 0,75 её скорости по течению. Какое расстояние прошла лодка за это время?

23. Расстояние между двумя пристанями равно 60 км. Это расстояние лодка проплывает по течению реки за 4 ч, а против течения реки – за 5 ч. Найдите собственную скорость лодки скорость течения реки.

24. Расстояние между двумя пристанями равно 80 км. Это расстояние лодка проплывает по течению реки за 5 ч, а против течения реки – за 8 ч. Найдите собственную скорость лодки и скорость течения реки.

25. Моторная лодка в первый день прошла 120 км по течению реки за 5 ч, а во второй день она прошла 72 км против течения за 6 ч. Найдите собственную скорость лодки и скорость течения реки.

26. Расстояние между двумя пристанями равно 75 км. Катер прошёл это расстояние по течению реки за 3 ч, а против течения за 5 ч. Найдите собственную скорость катера и скорость течения реки.

Задачи на смеси и сплавы.

1. Сколько граммов трёхпроцентного и сколько граммов восьмипроцентного растворов соли надо взять, чтобы получить 260 г пятипроцентного раствора?

2. Есть металлолом двух сортов, содержащих 12% и 30% меди. Сколько килограммов лома каждого вида надо взять, чтобы получить 180 кг сплава, содержащего 25% меди?

3. Сколько граммов 75%-го и 15%-го растворов кислоты надо смешать, чтобы получить 72 г 50%-го раствора кислоты?

4. Сколько граммов 15%-го и 60%-го растворов кислоты надо смешать, чтобы получить 90 г 40%-го раствора кислоты?

5. В одном ведре находится молоко жирностью 30%, а в другом – сливки жирностью 18%. Сколько нужно взять молока и сколько сливок, чтобы получить 10 л молока жирностью 6%?

6. В одной бочке находится смесь спирта с водой в отношении 3:7 соответственно, а в другой – 40%-ная спиртовая смесь. Сколько следует взять спиртовой смеси из каждой бочки, чтобы получить 16 л смеси, в которой спирт и вода были в отношении 5:11?

Задачи на возраст.

1. Если сложить возраст отца и возраст сына, то получится 52. Через 8 лет отношение возраста отца к возрасту сына будет равно 3. Сколько лет отцу и сколько сыну в настоящий момент?

2. Если сложить возраст отца и возраст сына, то получится 30. Через 7 лет отношение возраста отца к возрасту сына будет равно 3. Сколько лет отцу и сколько сыну в настоящий момент?

3. Мальчик на вопрос о том, сколько лет ему и его отцу, ответил так: «Вместе нам 44 года. Через 2 года отец будет старше меня в 3 раза». Сколько лет каждому из них сейчас?

4. Мальчик на вопрос о том, сколько лет ему и его брату, ответил так: «Вместе нам 20 лет. 4 года назад я был в 2 раза старше своего брата». Сколько лет каждому из них сейчас?

Задачи повышенной сложности.

1. * В корзине лежат 35 шаров, среди которых есть шары белого и чёрного цвета. Сколько шаров каждого цвета лежит в корзине, если известно, что среди каждых 17 шаров есть хотя бы один белый, а среди каждых 20 шаров есть хотя бы 1 чёрный?

2. * Коля и Вася получили за сентябрь по 64 оценки, причём Коля получил пятёрок столько же, сколько Вася – четвёрок, четвёрок столько же, сколько Вася – троек, троек столько же, сколько Вася – двоек и двоек столько же, сколько Вася – пятёрок. Кроме того оказалось, что их средние баллы совпадают. Сколько и Коли двоек?

5