Конечная группа
Таблицы умножения для конечных групп [ править ]
Таблица умножения (таблица Кэли) — таблица, которая описывает структуру конечных алгебраических систем с одной бинарной операцией. Таблица позволяет определить, является ли группа абелевой, найти ядро группы и обратные элементы по отношению к другим элементам в этой группе.
Структура [ править ]
Тогда таблица будет выглядеть следующим образом:
| * | a1 | a2 | . | an |
|---|---|---|---|---|
| a1 | a1a1 | a1a2 | . | a1an |
| a2 | a2a1 | a2a2 | . | a2an |
| . | . | . | . | . |
| an | ana1 | ana2 | . | anan |
Свойства [ править ]
Примеры таблиц умножения для конечных групп [ править ]
Ниже перечислены все группы до шестого порядка включительно:
- [math]|G| = 1[/math]
- [math]|G| = 2[/math]
Группа вычетов по модулю два относительно сложения: [math]mathbb/2mathbb[/math]
- [math]|G| = 3[/math]
Группа вычетов по модулю три относительно сложения: [math]mathbb/3mathbb[/math]
- [math]|G| = 4[/math]
Группа вычетов по модулю четыре относительно сложения: [math]mathbb/4mathbb[/math]
| + | 0 | 1 | 2 | 3 |
|---|---|---|---|---|
| 0 | 0 | 1 | 2 | 3 |
| 1 | 1 | 0 | 3 | 2 |
| 2 | 2 | 3 | 0 | 1 |
| 3 | 3 | 2 | 1 | 0 |
- [math]|G| = 5[/math]
Группа вычетов по модулю пять относительно сложения: [math]mathbb/5mathbb[/math]
- [math]|G| = 6[/math]
Группа вычетов по модулю шесть относительно сложения: [math]mathbb/6mathbb[/math]
| + | 0 | 1 | 2 | 3 | 4 | 5 |
|---|---|---|---|---|---|---|
| 0 | 0 | 1 | 2 | 3 | 4 | 5 |
| 1 | 1 | 2 | 3 | 4 | 5 | 0 |
| 2 | 2 | 3 | 4 | 5 | 0 | 1 |
| 3 | 3 | 4 | 5 | 0 | 1 | 2 |
| 4 | 4 | 5 | 0 | 1 | 2 | 3 |
| 5 | 5 | 0 | 1 | 2 | 3 | 4 |
Группа перестановок множества из трех элементов: [math]mathbb_3[/math]
| * | e | a | aa | b | c | d |
|---|---|---|---|---|---|---|
| e | e | a | aa | b | c | d |
| a | a | aa | e | c | d | b |
| aa | aa | e | a | d | b | c |
| b | b | d | c | e | aa | a |
| c | c | b | d | a | e | aa |
| d | d | c | b | aa | a | e |
Для группы [math]mathbb_3[/math] [math]a[/math] — это циклическая перестановка [math](123)rightarrow(231)[/math] , а [math]b,,c,,d[/math] — транспозиции [math](123)rightarrow(213),,(123)rightarrow(132),,(123)rightarrow(321)[/math] соответственно.
Таблица Кэли
Пусть $mathbb A_=left ,a_,…,a_right >$ — конечное множество из $n$ элементов, с заданной на нем бинарной алгебраической операцией $*$ так, что каждой паре элементов из этого множества будет поставлен в соответствие элемент из того же множества.
Тогда таблица Кэли (была введена А.Кэли в 1854) будет выглядеть следующим образом:
Таблица Кэли позволяет определить свойства операции:
- Если таблица симметрична относительно главной диагонали, то $*$ — коммутативна.
- Если $i$-ая строка повторяет верхнюю строку и $i$-ый столбец повторяет левый столбец, то $a_$ — нейтральный элемент.
- Если каждая строка и каждый столбец таблицы содержит нейтральный элемент, то для каждого элемента из $mathbb A_$ существует симметричный.
Замечание. Также существует метод проверки ассоциативности БАО по таблице Кэли, но так как он очень громоздкий приводить мы его не будем.
Пример 1
Дано множество $mathbb A=left .$ На этом множестве задана операция $*$ такая, что $ forall , a,b in mathbb A, a*b=max(a,b).$ Построить таблицу Кэли и определить свойства операции:
Построим таблицу Кэли:
$begin * & 1 & 2 & 3 & 4 & 5 & 6 & 7 & 8 \ 1 & 1 & 2 & 3 & 4 & 5 & 6 & 7 & 8 \ 2 & 2 & 2 & 3 & 4 & 5 & 6 & 7 & 8 \ 3 & 3 & 3 & 3 & 4 & 5 & 6 & 7 & 8\ 4 & 4 & 4 & 4 & 4 & 5 & 6 & 7 & 8 \ 5 & 5 & 5 & 5 & 5 & 5 & 6 & 7 & 8\ 6 & 6 & 6 & 6 & 6 & 6 & 6 & 7 & 8\ 7 & 7 & 7 & 7 & 7 & 7 & 7 & 7 & 8 \ 8 & 8 & 8 & 8 & 8 & 8 & 8 & 8 & 8 \ end$
- Таблица симметрична относительно главной диагонали, значит операция $*$ — коммутативна.
- Первая строка совпадает с верхней строкой и первый столбец совпадает с левым столбцом, значит 1 — нейтральный элемент.
- Симметричный элемент существует только для 1.
- Можем сделать вывод, что $left (mathbb A,* right )$ не является группой.
Пример 2
Дано множество преобразований правильного треугольника $mathbb B=left ,varphi _,varphi _,varphi _,varphi _,varphi _ right >,$ переводящих треугольник в самого себя.
$varphi _,varphi _,varphi _$ — повороты треугольника против часовой стрелки соответственно на углы $0, frac,frac$ вокруг точки $O.$
$varphi _,varphi _,varphi _$ — симметрия относительно осей $m, l, p$
Построить таблицу Кэли и показать, что $left (mathbb B,circ right )$ — группа:
Каждое преобразование представим в виде подстановки:
Составим таблицу Кэли:
$begin & varphi _ & varphi _ & varphi _ & varphi _ & varphi _ & varphi _ \ varphi _ & varphi _ & varphi _ & varphi _ & varphi _ & varphi _ & varphi _ \ varphi _ & varphi _ & varphi _ & varphi _ & varphi _ & varphi _ & varphi _ \ varphi _ & varphi _ & varphi _ & varphi _ & varphi _ & varphi _ & varphi _\ varphi _ & varphi _ & varphi _ & varphi _ & varphi _ & varphi _ & varphi _\ varphi _ & varphi _ & varphi _ & varphi _ & varphi _ & varphi _ & varphi _ \ varphi _ & varphi _ & varphi _ & varphi _ & varphi _ & varphi _ & varphi _ \ end$
puuuk
Бинарная операция — это, по определению, отображение множества A ╢ A в множество A, при этом образ пары (x, y) обозначим, например, x © y, где © — символ операции. Здесь A — произвольное непустое множество и A ╢ A — множество всех упорядоченных пар (x, y) — таких, что x, y Î A (то есть, декартов квадрат множества A). Непустое множество A называется основным множеством операции.
Можно составить следующую иерархию множеств с бинарной операцией (разумеется, вместо © может быть вставлена любая — +, √, *, È , Ç , Å , Ä , Ñ , ° и т.д. и т.п. — в зависимости от необходимости и вкуса автора.
Группоид, обозначаемый символом (A, © ) — множество A, на котором задана некоторая бинарная операция, обозначаемая © . Если множество группоида конечно, то есть ╫ A ╫ = card (A) = n, то таблица Кэли операции группоида есть таблица n ╢ n, в которой элемент x © y Î A находится в клетке пересечения строки x и столбца y. Конечный группоид можно считать заданным, если выписана его таблица Кэли.
Задача об авторитетах
У Саши и Даши авторитет Даша.
У Саши и Маши авторитет Саша.
У Саши авторитет Саша.
У Даши и Маши авторитет Саша.
У Даши авторитет Даша.
У Маши авторитет Петя.
У Пети и Даши авторитет Петя.
У Пети и Маши авторитет Петя.
У Пети и Саши авторитет Саша.
У Пети авторитет Саша.
ТАБЛИЦА КЭЛИ ДЛЯ ОПЕРАЦИИ «АВТОРИТЕТ»
* Затенен операционный квадрат
ТАБЛИЦА КЭЛИ, КОРЕЙСКИЙ ВАРИАНТ
Квазигруппа (от латинского слова quasi — как будто, почти и слова группа) — группоид, бинарная операция которого (например, © ) такова, что каждое из уравнений a © x = b, y © a = b имеет единственное решение для любых элементов a, b этого множества. Квазигруппа — одно из обобщений понятия группа. Особенно близки к группам квазигруппы с единицей — лупы, определение которых получается из аксиом групп отбрасыванием требования ассоциативности. Квазигруппу можно рассматривать и как унивесальную алгебру с тремя бинарными операциями (дополнительно левое и правле деление).
Гомоморфный образ квазигруппы, вообще говоря, не квазигруппа, а группоид с делением. Гомоморфизмам квазигруппы на квазигруппе соответствуют конгруэнции специального типа (т.н. нормальные конгруэнции). Значительно большую роль, чем гомоморфизмы, в теории и классификации групп играют изотопии. Изотопия — отношение эквивалентности для бинарных операций на фиксированном множестве, определяемое с помощью трех подстановок этого множества. Оказывается, что всякий группоид, изотопный квазигруппе, — сам квазигруппа, а всякая квазигруппа изотопна некоторой лупе. Для групп понятие изотопии совпадает с понятием изоморфизма.
Таблица умножения конечной квазигруппы (ее таблица Кэли) в комбинаторике известна по названием латинский квадрат. Одна из задач комбинаторной теории квазигрупп — отыскание систем взаимно ортогональных квазигрупп на заданном множестве — важна для построения конечных проективных плоскостей.
Лупа, или квазигруппа с единицей, определение которой получается из аксиом группы отбрасыванием требования ассоциативности, особенно близка к группе.
Полугруппа — множество, с определенной на нем бинарной операцией, удовлетворяющей закону ассоциативности, т.е. группоид (A, © ), в котором для каждой тройки элементов a , b и с выполняется условие a © ( b © с) =(a © b) © с). Понятие полугруппы есть обобщение понятия группы: из аксиом группы остается лишь одна; этим объясняется и термин «полугруппа».
Теория полугрупп принадлежит к числу сравнительно молодых областей алгебры. Первые исследования, посвященные полугруппам, относятся к 20-м гг. 20 в. и связаны с именем А. К. Сушкевича. Он, в частности, определил строение конечной полугруппы без собственных идеалов. К концу 50-х гг. теория полугрупп сформировалась в самостоятельную ветвь современной алгебры с богатой проблематикой, разнообразными методами и тесными связями с многими областями математики — как собственно алгебраическими (в первую очередь, с теорией групп и теорией колец), так и другими, например, с функциональным анализом, дифференциальной геометрией, алгебраической теорией автоматов.
- Примеры полугрупп чрезвычайно многочисленны. Это, например:
- различные множества чисел вместе с операцией сложения или умножения, замкнутые относительно рассматриваемой операции (т.е. содержащие вместе с любыми двумя своими элементами их сумму или, соответственно, произведение);
- Полугруппа матриц относительно умножения;
- Полугруппа функций относительно «поточечного» умножения * , задаваемого формулой (f* g) (x) = f(x) g(x);
- Полугруппа матриц относительно операции пересечения или объединения;
- Один из простейших примеров полугруппы — множество всех натуральных чисел относительно сложения; эта полугруппа является частью (подполугруппой) группы целых чисел по сложению или, как говорят, вложима в группу целых чисел.
Далеко не всякая полугруппа вложима в какую-нибудь группу: необходимыи условием такой вложимости является закон сокращения — каждое из равенств ac = bc, ca = cb влечет за собой a = b; выполнение закона сокращения не достаточно для такой вложимости, но, например, коммутативная полугруппа с законом сокращения вложима в группу.
- Если на множестве FX всех конечных последовательностей элементов произвольного множества (алфавита) X задать операцию * формулой
то FXстанет полугруппой; она называется свободной полугруппой над алфавитом X. Роль свободных полугрупп в общей теории определяется тем, что всякая полугруппа есть гомоморфный образ подходящей свободной полугруппы. Важную роль играют свободные полугруппы и в некоторых приложениях, прежде всего в теории формальных языков и кодов.
- Всякая совокупность пребразований произвольного множества M, замкнутая относительно операции композиции (последовательного выполнения), будет полугруппой относительно этой операции; такова, в частности, совокупность всех преобразований множества M, называемая симметрической полугруппой на множестве M. Многие важные совокупности преобразований оказываются полугруппами относительно композиции, причем часто они не являются группами. С другой стороны, всякая полугруппа изоморфна некоторой полугруппе преобразований. Все это определяет как роль полугрупп преобразований в общей теории полугрупп, так и роль теории полугрупп для изучения в самом общем виде преобразований с точки зрения их композиции. В большой степени через рассмотрение преобразований осуществляются связи теории полугрупп с другими областями математики.
Как и в других алгебраических теориях, одной из главных задач теории полугрупп является классификация всевозможных полугрупп, описание их строения. Это осуществляется прежде всего наложением на рассматриваемые полугруппы различых ограничений и выделение тем самым различных типов полугрупп. Среди важных типов — регулярные полугруппы, то есть полугруппы, в которых для любого элемента a существует такой элемент x, что axa = a. Регулярными являются, например, полугруппа всех матриц данного порядка над телом, симметрические полугруппы, полугруппы всех частичных преобразований множеств. Регулярные полугруппы принадлежат к числу наиболее активно изучаемых в теории полугрупп.
Заметную часть общей теории составляет теория представлений полугрупп преобразованиями и матрицами. Точка зрения теории представлений нередко проливает дополнительный свет на некоторые типы полугрупп, естественно определяемые с точки зрения аксиоматики. Внесение в полугруппы дополнительных структур, согласованных с полугрупповой операцией, выделяет особые разделы теории полугрупп, такие, как теория топологических полугрупп, теория упорядоченных полугрупп.
Моноид — это, по определению, полугруппа с единицей.
Группа (нем. Gruppe) — одно из основных понятий современной математики — есть лупа, являющаяся в то же время полугруппой.
Теория групп изучает в самой общей форме операции, наиболее часто встречающиеся в математике и ее приложениях (примеры таких операций — сложение чисел, умножение чисел, сложение векторов, последовательное выполнение преобразований и т.п.). При этом теория групп изучает не совсем произвольные операции, а лишь те, которые обладают рядом основных войств, перечисляемых в определении группы.
Формальное определение группы таково. Пусть G — произвольное непустое множество, на котором задана бинарная алгебраическая операция ° , т.е. для любых двух элементов a, b, из G определен некоторый элемент (обозначаемый, например, a ° b) также из G. Если при этом выполняются условия: 1) (a ° b) ° c = a ° (b ° c) для любых a, b и c из G; 2) в G существует такой элемент e (называемый единицей, иногда — нейтральным элементом), что a ° e = e ° a = a для любого a из G; 3) для любого a из G существует такой элемент a √1 (обратный к a элемент), что a ° a √1 = a √1 ° a = e, то множество G с заданной на нем операцией ° назовем группой.
Примеры групп. 1) множество G различных движений эвклидовой плоскости, самосовмещающих данную фигуру, операцией на котором служит композиция движений (если j , y — два движения из G, то результатом их композиции назовем движение j ° y , равносильное последовательному выполнению сначала движения j , а затем движения y ), образует т.н. группу симметрий фигуры. Единицей в этой группе будет тождественное преобразование плоскости, а обратным к j элементом — обратное к j преобразование. Группа G является характеристикой большей или меньшей симметричности фигуры: чем больше множество G, тем симметричнее фигура. Например, группа симметрий квадрата (рис., а) состоит из восьми движений
(четыре поворота вокруг центра квадрата и четыре отражения: два — относительно диагоналей и два — относительно прямых, соединяющих середины противоположных сторон). Для круга (рис. б) группа симметрий уже содержит бесконечно много элементов (например, все повороты вокруг центра), а для фигуры, нарисованной на рисунке (в) группа симмерий состоит из одного тождественного преобразования.
Если Z — множество всех целых чисел, а операция на Z — их обычное сложение + , то Z — группа. Роль e будет играть число 0, а роль обратного к z элемента — число √z. Часть H множества Z , состоящая из четных чисел, сама будет группой относительно той же операции. В таком случае говорят, что H — подгруппа группы Z . Обе групы Z и H удовлетворяют следующему дополнительному условию: 4) a + b = b + a для любых a и b из группы. Всякая группа, в которой выполняется условие 4) называется коммутативной или абелевой.
3) Множество всех подстановокn символов образует группу относительно умножения подстановок, называемую симметрической группой. При n ¨ 3 симметрическая группа неабелева. Порядок (число элементов) симметрической группы равен n!.
| Определение: |
| Группа называется конечной, если множество ее элементов конечно. Мощность множества элементов группы называют порядком группы и обозначают . |
Содержание
- 1 Таблицы умножения для конечных групп
- 1.1 Структура
- 1.2 Свойства
- 1.3 Примеры таблиц умножения для конечных групп
Таблицы умножения для конечных групп
Таблица умножения (таблица Кэли) — таблица, которая описывает структуру конечных алгебраических систем с одной бинарной операцией. Таблица позволяет определить, является ли группа абелевой, найти ядро группы и обратные элементы по отношению к другим элементам в этой группе.
Структура
Пусть — группа из элементов.
Тогда таблица будет выглядеть следующим образом:
| * | a1 | a2 | … | an |
|---|---|---|---|---|
| a1 | a1a1 | a1a2 | … | a1an |
| a2 | a2a1 | a2a2 | … | a2an |
| … | … | … | … | … |
| an | ana1 | ana2 | … | anan |
Свойства
| Утверждение: |
|
Каждая строка или столбец являются перестановкой элементов группы. |
| Пусть . Тогда и . Так как количество клеток в строке равно количеству элементов, то, по принципу Дирихле, каждый элемент группы встречается в строке один раз. |
| Утверждение: |
|
Если таблица симметрична относительно главной диагонали, то операция умножения коммутативна. |
| Таблица симметрична для любых |
| Утверждение: |
|
В конечной группе порядок каждого элемента является делителем порядка группы. |
| Рассмотрим элемент c порядком и подмножество (все различны при — в противном случае при , т.е. не является порядком элемента ). Легко проверить, что — подгруппа . По теореме Лагранжа порядок любой подгруппы делит порядок группы. Значит, и делит порядок . |
| Утверждение: |
|
Все группы простого порядка изоморфны . |
| Рассмотрим элемент c порядком и подмножество (все различны при — см. выше). Очевидно, — подгруппа , изоморфная . Но тогда делит (как порядок подгруппы) и не равняется единице(), значит . Раз порядок конечной подгруппы совпадает с порядком группы, то группа и подгруппа просто совпадают: . |
Примеры таблиц умножения для конечных групп
Ниже перечислены все группы до шестого порядка включительно:
Тривиальная группа
| * | e |
|---|---|
| e | e |
Группа вычетов по модулю два относительно сложения:
| + | 0 | 1 |
|---|---|---|
| 0 | 0 | 1 |
| 1 | 1 | 0 |
Группа вычетов по модулю три относительно сложения:
| + | 0 | 1 | 2 |
|---|---|---|---|
| 0 | 0 | 1 | 2 |
| 1 | 1 | 2 | 0 |
| 2 | 2 | 0 | 1 |
Группа вычетов по модулю четыре относительно сложения:
| + | 0 | 1 | 2 | 3 |
|---|---|---|---|---|
| 0 | 0 | 1 | 2 | 3 |
| 1 | 1 | 0 | 3 | 2 |
| 2 | 2 | 3 | 0 | 1 |
| 3 | 3 | 2 | 1 | 0 |
Группа
| + | (0,0) | (0,1) | (1,0) | (1,1) |
|---|---|---|---|---|
| (0,0) | (0,0) | (0,1) | (1,0) | (1,1) |
| (0,1) | (0,1) | (0,0) | (1,1) | (1,0) |
| (1,0) | (1,0) | (1,1) | (0,0) | (0,1) |
| (1,1) | (1,1) | (1,0) | (0,1) | (0,0) |
Группа вычетов по модулю пять относительно сложения:
| + | 0 | 1 | 2 | 3 | 4 |
|---|---|---|---|---|---|
| 0 | 0 | 1 | 2 | 3 | 4 |
| 1 | 1 | 2 | 3 | 4 | 0 |
| 2 | 2 | 3 | 4 | 0 | 1 |
| 3 | 3 | 4 | 0 | 1 | 2 |
| 4 | 4 | 0 | 1 | 2 | 3 |
Группа вычетов по модулю шесть относительно сложения:
| + | 0 | 1 | 2 | 3 | 4 | 5 |
|---|---|---|---|---|---|---|
| 0 | 0 | 1 | 2 | 3 | 4 | 5 |
| 1 | 1 | 2 | 3 | 4 | 5 | 0 |
| 2 | 2 | 3 | 4 | 5 | 0 | 1 |
| 3 | 3 | 4 | 5 | 0 | 1 | 2 |
| 4 | 4 | 5 | 0 | 1 | 2 | 3 |
| 5 | 5 | 0 | 1 | 2 | 3 | 4 |
Группа перестановок множества из трех элементов:
| * | e | a | aa | b | c | d |
|---|---|---|---|---|---|---|
| e | e | a | aa | b | c | d |
| a | a | aa | e | c | d | b |
| aa | aa | e | a | d | b | c |
| b | b | d | c | e | aa | a |
| c | c | b | d | a | e | aa |
| d | d | c | b | aa | a | e |
Для группы — это циклическая перестановка , а — транспозиции соответственно.
Пусть g – произвольный
элемент группы G. Тогда, принимая
,
мы получим минимальную подгруппу,
порожденную одним элементом.
Определение. Минимальная
подгруппа
,
порожденная одним элементом g группы
G, называетсяциклической
подгруппой
группы G.
Определение. Если
вся группа G порождена одним элементом,
т.е.
,
то она называетсяциклической
группой.
Пусть
элемент мультипликативной группы G,
тогда минимальная подгруппа, порожденная
этим элементом, состоит из элементов
вида
Рассмотрим степени
элемента
,
т.е. элементы
.
Имеются две
возможности:
1. Все
степени элемента g различны, т.е.
,
то в этом случае говорят, что элемент g
имеет бесконечный порядок.
2. Имеются
совпадения степеней, т.е.
,
но.
В этом случае
элемент g имеет конечный порядок.
Действительно,
пусть, например,
и
,
тогда,,
т.е. существуют положительные степениэлемента
,
равные единичному элементу.
Пусть d – наименьший
положительный показатель степени
элемента
,
для которого.
Тогда говорят, что элементимеет конечный порядок равный d.
Вывод. В
любой группе G конечного порядка ()
все элементы будут конечного порядка.
Пусть g элемент
мультипликативной группы G, тогда
мультипликативная подгруппа
состоит из всех различных степеней
элемента g. Следовательно, число элементов
в подгруппесовпадает с порядком элемента
т. е.
число элементов
в группе
равно порядку элемента
,
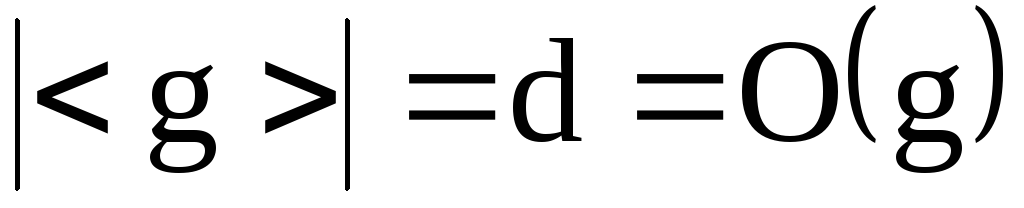
С другой стороны,
имеет место следующее утверждение.
Утверждение. Порядок
любого элемента
равен порядку минимальной подгруппы,
порожденной этим элементом.
Доказательство. 1.Если
– элемент конечного порядка
,
то
,
и
если
.
2. Если
– элемент бесконечного порядка, то
доказывать нечего.
Если элемент
имеет порядок
,
то, по определению, все элементы
различны и любая
степень
совпадает с одним из этих элементов.
Действительно,
пусть показатель степени
,
т.е.– произвольное целое число и пусть
.
Тогда числоможно представить в виде
,
где,
.
Тогда, используя свойства степени
элемента g, получаем
.
В частности, если
.
Пример. Пусть
– аддитивнаяабелева
группа
целых чисел. Группа G
совпадает с минимальной подгруппой
порожденной одним из элементов 1 или
–1:
и
,
следовательно,
– бесконечная
циклическая группа.
Циклические группы конечного порядка
В качестве примера
циклической группы конечного порядка
рассмотрим группу
вращений правильного n-угольника
относительно его центра
.
Элементами группы
являются повороты
n-угольника
против
часовой стрелки на углы
:
Элементами
группы
являются
При этом
,
а из геометрических
соображений ясно, что
и
.
Группа
содержитn
элементов, т.е.
,
а образующим элементом группыявляется
,
т.е.
.
Пусть
,
тогда (см. рис. 1)
.
Рис. 1 – Группа
– вращений правильного треугольника
АВС относительно центра О.
Алгебраическая
операция
в группе
– последовательное вращение против
часовой стрелки, на угол, кратный,
т.е.
.
Обратный элемент
– вращение по часовой стрелке на угол1,
т.е.
.
Таблица Кэли
Анализ
конечных групп наиболее наглядно
осуществлять с помощью таблицы
Кэли,
которая
является обобщением известной «таблицы
умножения».
Пусть группа
G содержит
n
элементов.
В этом случае
таблица
Кэли
представляет собой квадратную
матрицу
имеющую n
строк и n
столбцов.
Каждой строке и
каждому столбцу соответствует один и
только один элемент группы.
Элемент
таблицы Кэли,
стоящий на пересечении i-той
строки и j-того
столбца, равен результату выполнения
операции «умножения» i-го
элемента с j-тым
элементом группы.
Пример.
Пусть группа
G содержит
три
элемента{g1,g2,g3}.Операция
в группе «умножение».В
этом случае таблица Кэли имеет вид:
Замечание.
В каждой строке и каждом столбце таблицы
Кэли
находятся все элементы группы и только
они. Таблица Кэли
содержит полную информацию о группе.Что
можно сказать о свойствах этой группы?
1.
Единичным
элементом этой группы является g1.
2.Группа абелева
т.к. таблица симметрична относительно
главной диагонали.
3.Для каждого
элемента группы существуют обратные-
для
g1обратным
является элемент
g1,для
g2
элемент
g3.
Построим для групп
таблицу Кели.
Для нахождения
обратного элемента элементу, например,
,
необходимо в строке, соответствующей
элементунайти столбецj
содержащий элемент
.
Элементсоответствующий данному столбцу и
является обратным к элементу,
т.к..
Если таблица Кели
симметрична относительно главной
диагонали, то это означает, что
– т.е. операция в
рассматриваемой группе коммутативна.
Для рассматриваемого примера таблица
Кели симметрична относительно главной
диагонали это означает, что операция в
коммутативна, т.е.
,
а группа
– абелева.
Можно рассматривать
полную группу преобразований симметрий
правильного n – угольника
,
добавив к операции вращения дополнительные
операции пространственного поворота
вокруг осей симметрии.
Для треугольника,
а группа
содержит шесть элементов
,
где
это повороты (см. рис. 2) вокруг
высоты, медианы, биссектрисы имеют вид:
;
,
,
.
Рис. 2. – Группа
– преобразований симметрии
правильного
треугольника АВС.
Соседние файлы в папке ЛЕКЦИИ АиГ
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Let L be a Cayley table for a finite group G. Let a, b be two fixed elements of G and let H be a subgroup of G. The intersection of the rows bordered by elements of the left coset aH and columns bordered by elements of the right coset Hb is a latin subsquare of L of order |H|.
From: Latin Squares and their Applications (Second Edition), 2015
Elementary properties
A. Donald Keedwell, József Dénes, in Latin Squares and their Applications (Second Edition), 2015
1.2 The Cayley table of a group
Next, we take a closer look at the internal structure of the multiplication table of a group.
Theorem 1.2.1
Any Cayley table of a finite group G (with its bordering elements deleted) has the following properties:
- (1)
-
It is a latin square, in other words a square matrix ‖aik‖ in which each row and each column is a permutation of the elements of G.
- (2)
-
The quadrangle criterion holds. This means that, for any indices i, j, k, l and i′, j′, k′, l′, it follows from the equations aik = ai′k′, ail = ai′l′and ajk = aj′k′, that ajl = aj′l′.
Conversely, any matrix satisfying properties (1) and (2) can be bordered in such a way that it becomes the Cayley table of a group.
Proof
Property (1) is an immediate consequence of Theorem 1.1.1. Property (2) is implied by the group axioms, since by definition aik = aiak and hence, using the conditions given, we have
ajl=ajal=aj(akak−1)(ai−1ai)al=(ajak)(aiak)−1(aial)=ajkaik−1ail=aj′k′ai′k′−1ai′l′=(aj′ak′)(ai′ak′)−1(ai′al′)=aj′al′=aj′l′
To prove the converse, a bordering procedure has to be found which will show that the Cayley table thus obtained is, in fact, a multiplication table for a group. If we use as borders the first row and the first column of the latin square, the invertibility of the multiplication defined by the Cayley table thus obtained is easy to show and is indeed a consequence merely of property (1). For, in the first place, when the border is so chosen, the leading element of the matrix acts as an identity element, e. In the second place, since this element occurs exactly once in each row and column of the matrix, the equations arx = e and yas = e are soluble for every choice of ar and as.
Now, only the associativity has to be proved. Let us consider arbitrary elements a, b and c. If one of them is identical with e, it follows directly that (ab)c = a(bc). If, on the other hand, each of the elements a, b and c differs from e, then the submatrix determined by the rows e and a and by the columns b and bc of the multiplication table is
while the submatrix determined by the rows b and ab and by the columns e and c is
Hence, a(bc) = (ab)c because of property (2), and we have associativity. □
Corollary
If a1, a2, …, an are distinct elements of a group of order n, and if b is any fixed element of the group, then the sets of products {ba1, ba2, …, ban} and {a1b, a2b, …, anb} each comprise all of the n group elements in some order.
Property (2) was first observed by Frolov(1890a) who remarked that it is valid for any regular latin square (as defined below). Later Brandt(1927) showed that it was sufficient to postulate the quadrangle criterion to hold only for quadruples in which one of the four elements is the identity element. Textbooks on the theory of finite groups [see for example Speiser(1927)] adopted the criterion established by Brandt. Aczél(1969) and Bondesen(1969) have both published papers in which they have rediscovered the quadrangle criterion. Also, Hammel(1968) has suggested some ways in which testing the validity of the quadrangle criterion may in practice be simplified when it is required to test the multiplication tables of finite quasigroups of small orders for associativity.
Definition
We say that a latin square is group-based if the quadrangle criterion holds for it. That is, a latin square is group-based if, when appropriately bordered, it becomes a Cayley table for a finite group.
A condition quite different to the quadrangle criterion, for testing whether a latin square is group-based, was given by Suschkewitsch(1929) [see also Siu(1991)]. It is very closely related to Cayley’s classic proof that every group of order n is isomorphic to a subgroup of the symmetric group Sn and can be stated as follows:
Theorem 1.2.2
Let γ be any fixed column of a latin square L with symbol set Q of cardinality n. For i = 1, 2, …, n let σi : Q → Q be the permutation which maps γ to the i-th column of L. Then L is group-based if and only if the set ∑ = {σi : i = 1, 2, … n} is closed under the usual composition operation for permutations. If the latter is the case then ∑ forms a group isomorphic to the group on which L is based.
Proof
Without loss of generality, we can assume that the columns of L have been permuted so as to make γ the first column and that the symbols of L have been replaced by the symbols of the set {1, 2, …, n} = Q*, say, in such a way that γ has these entries in natural order. If we then border L by its own first row and first column (which is γ), we get the Cayley table of a loop (Q*, .) with identity element 1. The bth column of L is the permutation σb : x → xb(= xRb) of the first column γ. If ∑ is closed under composition of permutations then and only then, for each pair b, c ∈ Q*, we have RbRc = Rd for some d ∈ Q*. So xRbRc = xRd for all x ∈ Q*. That is, (xb)c = xd. In particular, this is true when x = 1. So bc = d and we have (xb)c = x(bc) for all x, b, c ∈ Q*. Thus, (Q*, .) is a group and L is group-based. Moreover, in this case, RbRc = Rbc for all b, c ∈ Q* and so the group formed by σ under composition of permutations is isomorphic to (Q*, .). □
To use the above theorem to test whether a latin square L is group-based it is often convenient to permute either the rows or symbols of L so that the entries in γ are in natural order (assuming the symbols of L are 1, 2, …, n). Then the elements of ∑ can be read directly from the columns of L. Of course, the same test will work if rows instead of columns are used throughout.
A third condition for a latin square to be group-based arises from a concept also due to Frolov (1890a,b), who called a reduced latin square “regular” if it has the following property: The squares obtained by raising each row in turn to the top and then re-arranging first the columns and then the remaining rows so that the square is again reduced are all the same.
We shall show (in Theorem 1.2.3 and as a corollary to Theorem 2.4.1 of the next chapter) that a latin square is regular in this sense if and only if it is group-based, though it seems that Frolov did not realize this.5
Theorem 1.2.3
A reduced latin square is group-based if and only if it is regular.
Proof
Let us border the square with its own first row and column so as to form the Cayley table of a loop with identity element 1. We show that, if and only if the square is regular, the quadrangle criterion must hold for all quadrangles which include 1 as one member. (This is sufficient, as we remarked earlier.) Let us choose arbitrarily a quadrangle which contains the element 1 in row h and column k say and suppose that the remaining cells of this quadrangle which are in row h and column k are b (in column v) and a (in row u) respectively. Then the fourth member of the quadrangle is in the cell (u, v). We move row h to row 1 and re-arrange the columns (to make the new first row coincide with the border) so that the k-th column becomes column 1 and so that the element b is in row 1 and column b. Also, the element a is now in column 1. After re-arranging the rows to make the new square reduced, a will be in row a of column 1. So the fourth member of the quadrangle will be the entry in the cell (a, b) of the reduced square. But, if and only if the square is regular, this is always the same whatever the initial choices of cells containing 1 and the selected elements a and b. □
Note. If we wish to test whether a latin square is group-based using the Suschkewitsch method, we require n2 tests since there are n2 pairs of permutations in the set ∑. If we use the method which Frolov used to test whether a latin square is regular, we need at most n tests. In fact, we shall show in the next chapter that at most n/p tests are needed, where p is the smallest prime which divides the order n of the latin square.
Parker(1959a) proposed an algorithm for deciding whether a loop is a group but that author later found an error in his paper and his method turned out to give only a necessary condition, not a sufficient one.
Wagner(1962) proved that to test whether a finite quasigroup Q of order n is a group it is sufficient to test only about 3n3/8 appropriately chosen ordered triples of elements for associativity. However, if a minimal set of generators of Q is known, then it is sufficient to test the validity of at most n2log2(2n) associative statements provided that these are appropriately selected.
Wagner also showed in the same paper that every triassociative quasigroup Q (that is, every quasigroup whose elements satisfy xy · z = x · yz whenever x, y, z are distinct) is a group, and the same result has been proved independently by D.A.Norton(1960).
These results lead us to ask the question “What is the maximum number of associative triples which a quasigroup may have and yet not be a group?”
Faragó(1953) proved that the validity of any of the following identities in a loop guarantees both its associativity and commutativity:
- (i)
-
(ab)c = a(cb),
- (ii)
-
(ab)c = b(ac),
- (iii)
-
(ab)c = b(ca),
- (iv)
-
a(bc) = b(ca),
- (v)
-
a(bc) = c(ab),
- (vi)
-
a(bc) = c(ba),
- (vii)
-
(ab)c = (ac)b,
- (viii)
-
(ab)c = (bc)a,
- (ix)
-
(ab)c = (ca)b.
In fact, as Sade(1962) has pointed out, the identities (iv) and (v) are equivalent and so also are (viii) and (ix). For example, if we permute the elements a, b, c in (v) it becomes b(ca) = a(bc), which is (iv).
More recently, it has been shown with computer aid that there are just four identities of length at most six (if we exclude mirror images and re-labellings) which force a quasigroup to be a group: namely, (A) a·bc = ab·c, (B) a·bc = ac·b, (C) a · bc = ca · b and (D) a · bc = b · ca. Moreover, all but the first of these forces the group to be abelian. See Fiala(2007) and Keedwell(2009a,b).
In fact, (i) is equivalent to (B) and (ii) to the mirror image of (B), (iii) to (C) and to its mirror image, (iv) and (v) to (D) and (viii) and (ix) to the mirror image of (D). (vi) and (vii) do not force a quasigroup to have an identity element.
Theorem 1.2.4
A finite quasigroup is commutative if and only if its multiplication table (with row and column borders taken in the same order) has the propertythat products located symmetrically with respect to the main diagonal represent the same element (i.e. the table is symmetric in the usual matrix sense).
Proof
By the commutative law, ab = ba = c for any arbitrary pair of elements a, b and so the cells in the a-th row and b-th column and in the b-th row and a-th column are both occupied by c. If this were not the case for some choice of a and b, we would have ab ≠ ba and the commutativity would be contradicted. □
A Cayley table of a group is called normal if every element of its main diagonal (from the top left-hand corner to the bottom right-hand corner) is the identity element of the group [see page 4 of Zassenhaus(1958)].
If the notation of Theorem 1.1.1 is used, it follows as a consequence of the definition that a normal multiplication table ‖aij‖ of a group has to be bordered in such a way that aij=aiaj−1 holds. Thus, if the element bordering the i-th row is ai, the element bordering the j-th column must be aj−1.
Obviously, the following further conditions are satisfied: (i) aijajk = aik (since aiaj−1ajak−1=aiak−1); and (ii) aji−1=aij (since (ajai−1)−1=aiaj−1). For example, the normal multiplication table of the cyclic group of order 6, written in additive notation, is shown in Figure 1.2.1.
Fig. 1.2.1.
As was first suggested by an example which appeared in Zassenhaus’ book on Group Theory [Zassenhaus(1958), page 168, Example 1], the normal multiplication table of a finite group has a certain amount of redundancy since every product aiaj−1 can be found n times in the table, where n is the order of the group. In fact, aiaj−1=aij=aikakj for k = 0, 1, …, n − 1. Consequently, it is relevant to seek smaller tables that give the same information. A multiplication table having this property is called a generalized normal multiplication table if it has been obtained from a normal multiplication table by the deletion of a number of columns and corresponding rows. The idea of such generalized normal multiplication tables was first mentioned by Tamari(1949), who subsequently gave some illustrative examples in Tamari(1951) but without proof. As one of his examples, he stated that the table given in Figure 1.2.2 is a generalized normal multiplication table of the cyclic group of order 6, obtained from the complete table displayed in Figure 1.2.1 by deleting the rows bordered by 3 and 5 and the columns bordered by 3−1 = 3 and 5−1 = 1.
Fig. 1.2.2.
The same idea was mentioned again by Ginzburg(1964), who gave a reduced multiplication table for the quaternion group of order 8. Later, in Ginzburg(1967), he developed the concept in much more detail and gave full proofs of his results. This paper contains, among other things, a complete list of the minimal generalized normal multiplication tables for all groups of orders up to 15 inclusive.
It will be clear to the reader that of special importance to the theory is the determination of the minimal number of rows and columns of a generalized normal multiplication table. If r denotes the minimal number of rows (or columns), then Erdős and Ginzburg(1963) proved that r < C(n2 log n)1/3 (where C is a sufficiently large absolute constant) while Ginzburg(1967) showed that, in general, r > n2/3 and that, for the cyclic group Cn of order n, r < (6n2)1/3.
For further generalizations of the concept of a generalized normal multiplication table and for discussion of some of the mathematical ideas relevant to it, the reader should consult Ginzburg(1960), Ginzburg and Tamari(1969a,b), Tamari(1960) and Specnicciati(1966).
The perceptive reader will realize that these ideas may have application in coding and cryptography.
Read full chapter
URL:
https://www.sciencedirect.com/science/article/pii/B9780444635556500015
Latin Squares
J. Dénes, A.D. Keedwell, in Annals of Discrete Mathematics, 1991
(4) Two-dimensional coding problems
The coding and transmission of pictures, one aspect of which we discussed in the previous section, may be regarded as one kind of two-dimensional coding problem in which latin squares have a role to play. Another concerns the allocation of frequencies in a mobile radio telephone system and a third arises in connection with the so-called two dimensional codes (especially cyclic codes) which have recently become a subject of attention.
In a mobile radio telephone system, each region is served by a local transmitter and it is required to allocate frequencies to these transmitters in such a way that there is no interference between neighbouring transmitters. Consequently, adjacent transmitters must be allocated different frequencies. In practice, each transmitter will require several frequencies for sending messages and further frequencies will be required for receiving back messages from the outstations. Since the total number of frequencies which are available for the system is usually limited, it is important to be able to allocate frequencies as efficiently as possible.
In a recent paper [J. Dénes and A. D. Keedwell (1988)], the present authors have suggested several ways in which the frequency allocation may be carried out. Two of these make use of latin squares and we shall now describe them.
If we suppose that the transmitters are arranged in the form of a rectangular grid, an optimal solution may be obtained as follows:
Since each transmitter is surrounded by eight others, of which no two adjacent ones may be assigned the same frequency, at least five different frequencies are necessary, one for the central transmitter of the group and at least four for the eight transmitters which surround it. We show that this minimal number of frequencies is achievable by repetition (in both horizontal and vertical directions) of a certain 5×5 latin square as many times as is required for coverage of the entire area of the mobile radio system. Our construction is illustrated in Figure 4.1. In this schema, there is at least a knight’s move separation between any two transmitters which are allocated the same frequency.
Figure 4.1.
The 5×5 latin square which we use is one which has appeared many times in the literature of Mathematics. It has the remarkable properties of being both a strict knight’s move square (as defined by P. J. Owens (1987), see also Part II of the present book) and also a totally diagonal latin square or Knut Vik design (as defined by A. Hedayat and W. T. Federer (1975)).
If a schema which provides at least a knight’s move separation between any two transmitters which are allocated the same frequency is insufficient, a considerable improvement can be obtained if a minimum of seven frequencies is available. In this case, we regard the area which lies within the range of each transmitter as being circular and the various circular regions as being close-packed so that each region is adjacent to six others. It is then possible to distribute the available seven frequencies in such a way that each transmitter is surrounded by six others all of which are transmitting on frequencies which are distinct both from that of the transmitter in their centre and also from each other. The array which has to be repeated is a skewed latin square. The required repeating pattern is shown in Figure 4.2 and it. is clear that the solution is again optimal. Transmitters which use the same frequency are an extended knight’s move apart.
Figure 4.2.
In his paper (1984), H. Imai has defined a two-dimensional binary cyclic code of area m×n as a set C of m×n matrices with symbols from GF[2] which satisfies the following conditions: (i) C is a linear code; (ii) the matrix obtained by shifting the columns of any code array in C cyclically one step to the right is also in C; and (iii) the matrix obtained by shifting the rows of any code array in C one step downwards is also in C. Imai has pointed out that one way of constructing such codes is by forming the direct product of two one-dimensional cyclic codes. As an example, he has given the code whose arrays are shown in Figure 4.3, which is the direct product of the cyclic code 0 0 0 0 1 1 1 0 1 1 1 0 of four words with itself. In general, it is not easy to find the minimum Hamming distance between the code arrays of a two-dimensional binary cyclic code.
Figure 4.3.
However, we should like to draw attention here to the fact that a two-dimensional non-binary cyclic code of constant weight and whose minimum Hamming distance is easy to state can be derived by means of latin squares. The arrays of the code comprise ail possible distinct Cayley tables of the cyclic group of order n and then, by virtue of theorem 3.2.1 of [DK], the minimum Hamming distance between any two arrays of the code is 2n. For convenience, we repeat our theorem here and we also illustrate our construction by giving in Figure 4.4 the two-dimensional non-binary cyclic code obtained when n = 3.
Figure 4.4.
Theorem 4.1
Two different Cayley tables, A and B, of a given group G of order n differ from each other in at least 2n places.
Proof. If no two corresponding rows of the two Cayley tables are the same then every row of A differs from the corresponding row of B in at least two places. Likewise, if no two corresponding columns of the two tables are the same, then every column of A differs from the corresponding column of B in at least two places. In either event, B differs from A in at least 2n places.
For the remaining part of the proof, we may suppose that at least one row and at least one column of B are the same as the corresponding row and column of A. Let us suppose that the equal rows are the u-th rows and that the equal columns are the v-th columns. Then, we have auv = buv, auj = buj and aiv = biv whence, by the quadrangle criterion, aij = bij for all pairs of indices i and j, and so A ≡ B. Consequently, this case cannot occur.
It was shown by E. N. Gilbert (1965) that the number of different Cayley tables of a given cyclic group G of order n is n! (n-1)! (n-1)!/ϕ(n), where ϕ(n) is Euler’s function. For example, when n = 3, this number is 12, as in Figure 4.4.
Another class of two-dimensional arrays which arise in coding theory and which have connections with latin squares are the so-called Costas arrays.
A Costas array of order n is an nxn array of blanks and ones with the property that the
12n(n−1) vectors which connect pairs of ones in the matrix are all distinct as vectors. (For an example of order six, see Figure 4.5). Thus, a translation of the array without rotation produces at most one pair of superimposed cells both of which contain an entry one. Such arrays are of value in determining the range and velocity of a moving object by means of radar or sonar signals. A detailed account of the history of these arrays and of their applications will be found in J. P. Costas (1984).
Figure 4.5.
A Costas array is called vertically singly-periodic (horizontally singly-Periodic) if all its vertical translates (horizontal translates), when read cyclically as if on a horizontal (vertical) cylinder, are also Costas arrays. It is known that singly-periodic Costas arrays exist for all orders p-1, where p is a prime number, and the question has been raised as to whether they exist for orders not of this form. Several attempts have been made to solve this problem with the aid of latin squares. In order to be able to show the connection, let us first remark that if we replace the blanks of a Costas array by zeros, we may regard it as a permutation matrix. If the corresponding permutation of the integers 1, 2, …, n maps i to θ(i) then the cells of the array which contain the entry one have co-ordinates [i, θ(i)] and the Costas property requires that the vectors [i+k, θ(i+k)] — [i, θ(i)] and [j+k, θ(j+k)] — [j, θ(j)] be different whenever i≠j. So θ must be a permutation of 1, 2, …, n such that θ(i+k) -θ (i) = θ(j+k)-θ(j) ⇒ i = j for all choices of k, k = 1, 2, …, n−2. We shall call this the first condition on θ.
As an example, the permutation
θ=[1 2 3 4 5 64 1 2 6 5 3] defines the Costas array given in Figure 4.5. We observe that the differences θ(i+1)-θ(i) = −3, 1, 4, −1, −2 are all different, the differences θ(i+2)-θ(i) = −2, 5, 3, −3 are all different, the differences θ(i+3)-θ(i) − 2, 4, 1 are all different and, finally, the differences θ(i+4)-θ(i) = 1, 2 are different. We can exhibit the differences compactly in the form of a triangle as in Figure 4.5.
In terms of the permutation θ, a Costas array is vertically singly-periodic if, in addition to the permutation e, each of the permutations i → θ(i+h), h = 1, 2, …, n-1, defines a Costas array. It is horizontally singly-periodic if, in addition to the permutation θ, each of the permutations i → θh(i), where θh(i) = θ(i)-h (mod n) and h = 1, 2, …, n-1, defines a Costas array. For the example of Figure 4.5, we note that i → θ(i+2) defines a Costas array (shown in Figure 4.6) but i → θ(i+1) does not. Also, i → θ1(i) = θ(i)-1 (mod 6) gives a Costas array (shown in Figure 4.7) but i → θ2(i) does not.
Figure 4.6.
Figure 4.7.
T. Etzion (1989) has shown that when and only when a Costas array is horizontally singly-periodic, the first condition on θ is replaced by the stronger condition θ(i+k)-θ(i)≡θ(j+k)-θ(j) (mod n) ⇒ i=j for all choices of k, k=1, 2, …, n−2. We shall call this the second condition on θ.
When the second condition on θ holds, the latin square whose (i, j)-th cell contains θ(j)+(i-1) is a Vatican square: that is, a Tuscan-(n-1) square which is a latin square. (For a discussion of these concepts, see Section 5 of Chapter 3.) A Vatican square which takes this particular form (in which the i-th row is obtained by adding i-1 to each of the elements of the first row) is said to be constructed by the polygonal path construction [S. W. Golomb, T. Etzion and H. Taylor (1990)] because, when the vertices of a regular n-gon are numbered 1, 2, …, n in order, the joins θ(i+1)-θ(i) form n-1 directed chords no two of which coincide when the polygon is rotated.
Thus we have the following theorems:
Theorem 4.2
A Costas array is horizontally singly-periodic if and only if its defining permutation e satisfies the second conditon above.
Proof. It is easy to see that the second condition on θ inplies that each of the mappings i → ϕh(i) = θ(i)-h(mod n) satisfies the first condition on θ.
Conversely, suppose if possible that θ defines a Costas array which is horizontally singly-periodic and that, for some set of values i, j, k, the first condition on θ holds but the second does not. We can suppose without loss of generality that θ(i+k)-θ(i) = θ(j+k)-θ(j)+n, i≠j. Then, θ(i+k)-θ(j)>0 and θ(j+k)−θ(j)< 0 since all differences lie between ±(n-1). Let m = min[θ(i), θ(j+k)]. Then ϕm(i+k) = θ(i+k)-m since θ(i+k)>θ(i)≥m, and ϕm(j) = θ(j)-m since θ(j)>θ(j+k)≥m.
If m = θ(i), we have ϕm(i) = n (since all permutation entries lie between 1 and n) and ϕm(j+k) = θ(j+k)-m. Then ϕm(i+k)-ϕm(i) = θ(i+k)-m-n = θ(i+k)-θ(i)-n = θ(j+k)-θ(j) = ϕm(j+k)-ϕm(j) which cannot occur with i≠j because i → ϕ(i) defines a Costas array.
If m = θ(j+k), we have ϕm(i) = θ(i)-m and ϕm(j+k) = n. This gives ϕm(j+k)-ϕm(j) = n-[θ(j)-m] = n+θ(j+k)-θ(j) = θ(i+k)-θ(i) = ϕm(i+k)-ϕm(i) which again cannot occur with i≠j.
From these contradictions, we conclude that the second condition on θ holds when θ defines a Costas array which is horizontally singly-periodic.
Theorem 4.3
[T. Etzion, S. W. Golomb and H. Taylor (1990)]. A Costas array of order n which is horizontally singly-periodic exists if and only if a Vatican square of order n constructed by the polygonal path construction exists.
Proof. The permutation e which defines the Costas array satisfies the second condition on e and consequently the latin square whose i-th row is θ(1)+(i-1), θ(2)+(i-1), …, θ(n)+(i-1), where arithmetic is mod n, is a Vatican square.
An illustration of Theorem 4.3 is given in Figure 4.8, where both the Costas array and the Vatican square to which it is equivalent are exhibited.
Figure 4.8.
Since the permutation i → θ (i) in Figure 4.8 defines a horizontally singly-periodic Costas array whose non-empty cells have co-ordinates [i, θ(i)], it follows that the Costas array whose non-empty cells have co-ordinates [θ(i),i] or [j, θ-1(j)] will be vertically singly-periodic. Consequently, each of the permutations j → θ-1(j+h) defines a Costas array. In particular, this means that, when the six differences θ-1(j+1)- θ(j), where j = 1, 2, 3, 4, 5, 6 and 6+1 = 1, are read cyclically, every consecutive five of them are distinct and define a proper difference triangle. Moreover, when the six differences θ-1 (j+h) θ-1 (j), h = 2, 3, 4, are read cyclically, every consecutive 6-h of them are distinct. Now, it is easy to see that if a sequence of n symbols is arranged in a circle and if every subset of
r≥1+⌊n/2⌋ consecutive symbols has all its members distinct, then the n symbols must be distinct.
Generalizing our example, we have:
Theorem 4.4
If the Costas array with defining permutation θ is vertically singly-periodic then the Costas array with defining permutation θ-1 is horizontally singly-periodic. A necessary condition that a Costas array of order n should be vertically singly-periodic is that its defining permutation e satisfies the condition θ(i+k)- θ(i) = θ(j+k)- θ(i) ⇒ i = j for all
k≥1+⌊n/2⌋, where j+k is computed modulo n.
In fact, only one systematic construction for vertically singly-periodic Costas arrays is known. This is due to L. R. Welch [see S. W. Golomb and H. Taylor (1982)] and is as follows:
Let p be a prime and α a generating integer of the multiplicative group of the Galois field GF[p]. Then a Costas array of order p-1 is obtained by defining θ(i) = αi, i = 1, 2, …, p-1.
Since θ(i+k)- θ(i) = αi (αk-1), the defining permutation of a Costas array which is constructed by the Welch method has a stronger property than that required by Theorem 4.4: namely, it satisfies the condition
θ(i+k)- θ(i) = θ(j+k)- θ(j) mod(n+1) ⇒ i = j for all values of k, 1≤k < n, where j+k is computed modulo n. We shall call this the third condition on θ.
It follows then that the (n+1)xn array whose (i, j)-th cell is θ(j) + (i-1) and where arithmetic is modulo n+1, is a circular Vatican array.
T. Etzion (198γ) has shown further that if and only if a permutation θ satisfies the above third condition then θ-1 satisfies the condition θ-1 (i+k)- θ-1 (i) θ-1 (j+k)- θ-1 (j)mod n ⇒ i = j for all values of k, 1≤k≤n, where j+k is computed modulo n+1. Consequently, the integers θ-1(1), θ-1(2), …, θ-1(n) form a polygonal path for an n × (n+1) circular Vatican array whose (i, n+1)-th entry is 0 and whose (i, j)-th entry is e-1(i)+(i-1), for 1≤ i, j≤n, where arithmetic is modulo n. It has been proved that such a circular Vatican array can only exist if n+1 is prime. [See T. Etzion, S. W. Golomb and H. Taylor (1989).] Also, we have:
Theorem 4.5
[T. Etzion (198α)] An n × (n+1) circular Vatican array exists if and only if there exists a complete set {A1, A2, …, An} of mutually orthogonal latin squares of order n+1 for which all the rows are cyclic permutations of 0, 1, 2, …, n and the top row of each square begins with 0.
Proof. For 2≤i, j≤n+1, we put k in the (i-l, j-1)-th cell of the Vatican array if and only if the (i, j)-th cell of Ak contains 0. The last column of the Vatican array consists entirely of zeros.
[Compare Theorem 5.1 of Chapter 3 and the remarks which follow it and also Theorem 7.4.1 of [DK]. The latter theorem gives a direct construction of a complete set of mutually orthogonal latin squares from an (n+1) × n circular Vatican array of the type whose existence is guaranteed by the third condition on θ.]
We provide illustrations of some of the above-mentioned results in Figures 4.9, 4.10 and 4.11. Thus, the Costas array given in Figure 4.9 is constructed by the Welch construction taking p = 7 and α = 5. It is vertically singly-periodic and its defining permutation
ψ=[1 2 3 4 5 65 4 6 2 3 1] is the inverse of that used in Figure 4.8. So the integers 5, 4, 6, 2, 3, 1 provide a polygonal path for an n × (n+1) circular Vatican array as shown in Figure 4.10 and the integers 6, 4, 5, 2, 1, 3 form a polygonal path for an (n+1) × n Vatican array as in Figure 4.11. A further observation is that a vertically (horizontally) singly-periodic Costas array of order n defines an nxn latin square with the property that all those cells which contain the same symbol represent a vertical (horizontal) translate of the Costas array defined by the cells which contain the entry one. This fact also is illustrated in Figure 4.9. We may think of it as a means of filling the plane with Costas arrays each of which is a translate of each other.
Figure 4.9.
Figure 4.10.
Figure 4.11.
Since it appears likely that singly-periodic Costas arrays only exist for orders of the form p-1, we may ask the more interesting (but more difficult) question whether the plane can be filled with Costas arrays in such a way that no one is the translate of any other. In other words, is it possible to construct a latin square of order n such that all those cells which contain the same symbol form a Costas array and no two of these n Costas arrays are translates one of another?
To construct such a latin square, we require n permutations i → θu(i), u = 1, 2, …, n, such that (i) each permutation has the difference properties required for it to define a Costas array, (ii) θu(i)≠θv(i) for u≠v, (iii) θv (i)≠θu(i+h) and θv(i)≠ θu(i)-h mod n for any fixed h; where i varies from 1 to n.
In an unpublished preprint, the present authors called the Costas arrays constructed from such a set of permutations a set of plane-filling Costas arrays. They showed that such a set exists when n = 6 (as in Figure 4.12) but were unable to find a set for n = 5. More recently, T. Etzion (198β) has obtained several general constructions for sets of plane-filling Costas arrays to which he has given the alternative name of latin Costas arrays. He has also shown the existence of plane-filling Costas arrays with a stronger property: namely that the latin square which they fill is a Vatican square. He has called such a design a Vatican Costas square. All these squares have orders of the form p-1, p prime.
Figure 4.12.
The following two constructions are claimed to give Vatican Costas squares:
- (1)
-
Let a be a primitive root modulo the prime number p. We put k in the (i, j)-th cell of a (p-1)x(p-1) square if and only of αk-i≡j (mod p), where l ≤i, j, k ≤p-1.
- (2)
-
Let p = 2r-1 be a Mersenne prime and let α and β be primitive elements of the field GF[p+1]. We put k in the (i, j)-th cell of a (p-1)×(p-1) square if and only if αi +β jk = 1, where l ≤i, j, k ≤p-1.
However, the first of these constructions does not give a set of plane-filling Costas arrays according to the above definition since each Costas array which it constructs is a vertical translate of each other and so is vertically singly-periodic. On the other hand, the second construction does appear to give a plane-filling set, although Etzion does not prove this.
The following two constructions from T. Etzion (198γ) give latin Costas arrays which partially satisfy our definition of plane-filling. (A few of the Costas arrays are translates of others, according to Etzion, private communication.)
- (3)
-
Let p be a prime of the form p = (2n, t)+1, where t is odd and n≥1, and let a be a primitive root modulo p. We put k in the (i, j)-th cell of a (p-1) × (p-1) square if and only if α(-k+j)(2kt+1) ≡ i (mod p), where l ≤i, j, k ≤p-1.
- (4)
-
Let α and β be primitive roots modulo the prime p and let us construct a (p-1) × (p-1) square by putting k in the (i, j)-th cell if (i) when k is odd, α(-k+j) ≡ i (mod p), and (ii) when k is even, β(-k+j) ≡ i (mod p).
Finally, in this Section, we draw attention to the use of a single latin square in connection with the allocation of the pixels of a two-dimensional raster-graphics display to the M memory chips which store the display in such a way that it is possible to copy or alter small rectangles of N pixels very rapidly whatever their shape. Essentially, the requirement is that the N pixels of a randomly chosen rectangle should all be allocated to distinct memory chips. In B. Chor, C. E. Leiserson and R. L. Rivest (1982), the authors have shown that this requirement can be met using only approximately √5N memory chips if the allocation of memory chips to the pixels of the complete array is described by a certain cyclic latin square with rows rearranged in a prescribed way. The prescription for rearranging the rows is described in terms of Fibonacci numbers.
Read full chapter
URL:
https://www.sciencedirect.com/science/article/pii/S0167506008709695
Special types of latin square
A. Donald Keedwell, József Dénes, in Latin Squares and their Applications (Second Edition), 2015
2.4 Group-based latin squares and nuclei of loops
In Section 1.2, we gave three ways of checking whether a given latin square L (which can be assumed to be in reduced form) is group-based: namely, the quadrangle criterion, Suschkewitsch’s test and Frolov’s regularity test. To be certain that L is group-based using the quadrangle criterion, it is necessary either to check every pair of quadrangles which agree in three corresponding places or else to border the square with its own first row and column so as to form the Cayley table of a loop and then check the subset of all such pairs of quadrangles which have the identity of the loop as top left member. [See Brandt(1927)]. Thus, the number of tests required is of order at least n3. If Suschkewitsch’s test is used, it is necessary to check every pair of row (or column) permutations. (See Theorem 1.2.2.) This requires n2 tests. If Frolov’s test for regularity is used, it follows from Theorem 1.2.3 that at most n tests are required. However,by treating L as the Cayley table of a loop and making use of the concept of loop nuclei, we show in this section that in fact at most n/2 tests are necessary and this only when the square is idempotent and of even order.
We shall require two definitions and a theorem:
Definition
The left nucleus Nl of a loop (Q, .) comprises all elements x ∈ Q such that x(bc) = (xb)c for all b, c ∈ Q. The middle nucleus Nm comprises all elements y ∈ Q such that a(yc) = (ay)c for all a, c ∈ Q and the right nucleus Nr comprises all elements z ∈ Q such that a(bz) = (ab)z for all b, c ∈ Q. The set Nl ∩ Nm ∩ Nr is called the nucleus N.
Definition
The hth row(column) of the Cayley table of a loop (Q, ·) is said to have the Frolov property if, when the columns(rows) of the latin square formed by the body of the table are re-ordered in such a way that the elements of the hth row(column) are in the same order as that of the row(column) border, each row(column) of the re-ordered square coincides with some row(column) of the body of the original Cayley table.
We note that, if every column (or row) of a latin square has the Frolov property, this is equivalent to saying that the latin square is regular. See page 5.
Theorem 2.4.1
Suppose that the cell (i, j) of the Cayley table T of the loop (Q, ·) contains the entry aibj for i, j = 0, 1,…, n − 1, a0 = b0 = e, where e is the identity element. Then a necessary and sufficient condition that the element bk belong to the middle nucleus of the loop is that the column of T indexed by bk has the Frolov property. A necessary and sufficient condition that the element ah belong to the middle nucleus of the loop is that the row of T indexed by ah has the Frolov property.
Proof
As in Theorem 1.2.2, we may suppose without loss of generality that the symbols used for the loop (Q, .) are 1, 2,…, n, that 1 is the identity element and that the Cayley table is in reduced form: that is, with the elements of the first row and column in natural order.
Let us suppose that the mapping θ permutes the rows so that the elements 1b, 2b, …, xb, …, nb of the column headed by the element b are in the order of the first column: that is, in natural order. Then, (xθ)b = x for x =1, 2, …,n. (The columns may be re-arranged if we wish so that the new square becomes reduced.)
The elements of the column headed by the element u are xu for x = 1, 2, …, n. These become (xθ)u for x =1, 2, …, n. (See Figure 2.4.1.) Suppose that this is another column of T for each u ∈ Q. Then, for each u ∈ Q, there exists an element w ∈ Q such that (xθ)u = xw for all x ∈ Q, where (xθ)b = x. Thus, xθ=xRb−1 and so (xRb−1)u=xw. Putting x = b, we get u = bw or w=uLb−1 so (xRb−1)u=x(uLb−1) for all x, u ∈ Q, or, equivalently, (xRb−1)(bw)=xw for all x, w ∈ Q. If we put x = yb, this becomes y(bw) = (yb)w for all y, w ∈ Q. Thus, b lies in the middle nucleus of the loop.
Fig. 2.4.1. Loop table T after re-arranging rows so that the symbols in column b are in natural order.
To prove the second statement, we need only remark that the loop whose rows are the columns of (Q, .) has middle nucleus the same as that of (Q, .). □
Theorem 1.2.3 is an immmediate corollary to Theorem 2.4.1 since, if and only if all rows(columns) have the Frolov property, the middle nucleus is the whole of Q and so (Q, .) is a group.
However, it is well-known that the order of each of the nuclei of a loop divides the order of the loop. [See, for example, Pflugfelder(1990a) for a proof.] So, if p is the smallest prime which divides the order |Q| of a loop (Q, .) (or reduced latin square L formed by its Cayley table) and if |Q|/p rows, excluding the first, of L have the Frolov property, this is sufficient to ensure that L is group-based since it ensures that at least 1 + (|Q|/p) elements of Q are in the middle nucleus of (Q, .) whereas the maximum size of the middle nucleus is |Q|/p if it is not the whole loop.
(Note that, in particular, for a latin square of odd order, it is sufficient that at most a third of the rows have the Frolov property to be sure that the square is group-based. For a square of prime order, just one row is sufficient. Thus, for use by hand, our third test for a latin square to be group-based is considerably more economic than its two predecessors.)
But it is also well-known [again see Pflugfelder(1990a)] that each of the nuclei is a group and so all the powers of an element of the middle nucleus and likewise the product of each pair of its elements are themselves members. By exploiting these facts, we may reduce further the number of columns (or rows) which we need to test for the Frolov property to ensure that a given latin square is group-based. (When the square is idempotent, no further reduction is possible.)
In Keedwell(2005), the reader intersted in loop theory will find analogues of Theorem 2.4.1 for testing for elements of the left and right nuclei and will also find examples of loops of small order which have such (proper) nuclei.
Read full chapter
URL:
https://www.sciencedirect.com/science/article/pii/B9780444635556500027
Latin Squares
K. Heinrich, in Annals of Discrete Mathematics, 1991
(2) Without subsquares
One should notice that the latin square constructions described in Section 1 all produce subsquares. We now wish to discuss the problem of constructing latin squares without certain subsquares. Until now only two problems of this type have been considered.
A. Kotzig, C. C. Lindner and A. Rosa (1975) asked if for all n, n ≠ 2, 4, there exists an LS(n) with no order 2 subsquares. Such squares were termed N2-latin squares and interest in them arose as they could be used to construct sets of disjoint Steiner triple systems. In fact, to construct a set of (v+1)/2 pairwise disjoint Steiner triple systems of order v, v ≡ 3 or 7 (mod 12) and v > 7, they needed an LS((v+1)/2) with at least one column no cell of which was contained in a subsquare of order 2. Clearly N2-latin squares have this property.
A second problem, posed by A. J. W. Hilton, asks if for all sufficiently large n there exists an LS(n) with no proper subsquares. Following the above notation we will call this an N∞-latin square.
We will exhibit a complete solution to the first problem and then describe constructions for N∞-latin squares giving a partial solution to the second. In both problems we use mainly a product construction.
M. McLeish (1975) has remarked that if A and B are N2-latin squares then so too is their product. As pointed out by R. H. F. Denniston (1978) this now provides a straightforward recursive construction for N2-latin squares of all orders n, ≠ 2, 4, once N2-latin squares of order 8, 16, 32, 2k+1, 2(2k+1), and 4(2k+1), where k ≥ 1, have been constructed. Historically, however, progress proceeded along the following lines.
A. Kotzig, C. C. Lindner and A. Rosa (1975) began by constructing N2-latin squares for all n ≠ 2a and then M. McLeish (1975) gave constructions based on direct and generalized direct product which included the cases n = 2a for a ≥ 6 and a ≠ 7, 8 or 13. Using prolongation (later exploited more fully in M. McLeish (1980)) she was able to produce N2-latin squares of orders 27 (and hence by direct product 213) and 28. One easily sees that every LS(2) and LS(4) has an order 2 subsquare and so only the cases n = 8, 16 and 32 remained. An N2-latin square of order 8 proved to be the most difficult to find. R. H. F. Denniston (1978) has shown (by computer search) that there are exactly three non-isomorphic N2-latin squares of order 8. However, the first N2-latin square of order 8 (as shown in Figure 2.1) was constructed by E. Regener (and appears in A. Kotzig and J. Turgeon (1976)). In that same paper A. Kotzig and J. Turgeon gave a general construction for N2-latin squares of order n provided n ≠ 0 (mod 3) and n ≠ 3 (mod 5), by a prolongation involving the projection of three transversals from the Cayley table of the cyclic group of order n − 3. This included the cases n = 16 and 32, and so the problem was solved. Since then M. McLeish (1980) has given a direct construction for N2-latin squares of all orders n ≥ 12, n ≠ 14, 20 or 30. The construction consists of a prolongation involving the projection of s transversals from the Cayley table of the cyclic group of order n-s for suitably chosen n and s.
Figure 2.1.
And now the proof.
Lemma 2.1
There exist N2-latin squares of orders 8, 16 and 32.
Proof. An N2-latin square of order 8 is shown in Figure 2.1
We will describe the Kotzig-Turgeon construction for N2-latin squares of order n+3 when n is odd, n ≢ 0(mod 3) and n ≢ 0 (mod 5). Let A be an LS(n) in which eA(i, j) ≡ i+j (mod n). In A there are transversals Ti = {(2j-3i+6, j): 1 ≤ j ≤ n}, 1 ≤ i ≤ 3. Apply prolongation using these by projecting Ti onto row and column n+i and inserting the LS(3), B, with eB(i, j) ≡ 2-(i+j)(mod 3) and e(B) = (n+1, n+2, n+3). Putting n = 13 and n = 29 yields N2-latin squares of orders 16 and 32.
Lemma 2.2
For every odd n there is an N2-latin square.
Proof. The Cayley table of the cyclic group of odd order is an N2-latin square. In fact the Cayley table of the cyclic group of prime order has no proper subsquare.
Lemma 2.3
There are N2-latin squares of orders 2(2k+1) and 4(2k+1), k ≥ 1.
Proof. The construction (due to A. Kotzig, C. C. Lindner and A. Rosa (1975)) is in each case simply a non-uniform product.
Let A, B and C be LS(2k+1) defined by eA(i, j) ≡ i-j+1(mod 2k+1) eB(i, J) ≡ i+j-1(mod 2k+1) and eC(i, j) = i+j-2(mod 2k+1). These three squares are isotopic to the Cayley table of the cyclic group of order 2k+1 and so are N2-latin squares. Define a latin square X as the non-uniform product of A, B and C with the latin square E of order 2 in which eE(i, j) ≡ i+j-1(mod 2) so that cells (1, 1) and (2, 2) are replaced by A, (1, 2) is replaced by B and (2, 1) by C. Then X is an N2-latin square of order 2(2k+1).
We similarly construct Y, an N2-latin square of order 4(2k+1), by the non-uniform product of A, B and C with F, the LS(4) shown with Y in Figure 2.2. In Y, Di denotes a copy of D on the appropriate element set. Notice that any order 2 subsquare in Y must lie in one of the four order 2(2k+1) subsquares and so Y has no order 2 subsquares.
Figure 2.2.
Theorem 2.4
There exists an N2-latin square of order n unless n = 2 or 4 and in these cases such a square does not exist.
Proof. The proof follows immediately from Lemmas 2.1, 2.2, 2.3, the remark that the direct product of two N2-latin squares produces another, and the fact that N2-latin squares of orders 2 and 4 are impossible.
We now turn to the existence of latin squares with no proper subsquares, N∞-latin squares. To date the best general result is that for all n ≠ 2a3b there exists an N∞-latin square.
One easily discovers (for example from the list of LS(4) and LS(6) given in [DK, p. 129–137]) that every latin square of order 4 or 6 has a proper subsquare, and that all three of the N2-latin squares of order 8 are in fact N∞-latin squares.
A. Rosa (and others) have noted that if there exists a perfect 1-factorization of the complete graph on 2n vertices, K2n, then there exists an N∞-latin square of order 2n-1. (A perfect 1-factorization of a graph G is a 1-factorization of G with the property that the union of any two of the 1-factors is a hamiltonian cycle.) Given a perfect 1-factorization of K2n, with vertices 1, 2, …, 2n, consisting of the 1-factors F1, F2, …, F2n-1, where edge {i, 2n} is in Fi, define the N∞-latin square A by eA(i, j) = k if i ≠ j and {i, j} ∈ Fk, and eA(i, i) = i. Observe that if A has a proper subsquare B containing no cell of the main diagonal of A, then any two elements in B can yield a cycle of length at most twice the order of B, contradicting the fact that they correspond to a hamilton cycle. Since A is symmetric, if B has an entry on the main diagonal, then B is symmetric about the main diagonal and has odd order. It is easy to see that any two elements yield a cycle of length at most one more than the order of B, again a contradiction.
Perfect 1-factorizations of K2n are known to exist when 2n ∈ {p+1, 2p: p prime}∪{16, 28, 36, 50, 244, 344, 1332, 6860}. These are described in A. Kotzig (1964), B. A. Anderson (1973), (1974), E. Seah and D. R. Stinson (1987), E. C. Ihrig, E. Seah and D. R. Stinson (1987), B. A. Anderson and D. Morse (1974), and a recent personal communication from Z. Kiyasu and M. Kobayashi respectively. Note that while perfect 1-factorizations yield N∞-latin squares the converse is not true. The smallest unresolved case for perfect 1-factorizations is K40, whereas the smallest order for N -latin squares is 16.
The first results on the existence of N∞-latin squares were obtained by K. Heinrich (1980) who showed that for distinct primes p and q, there is an N∞-latin square of order n = pq, n ≠ 6. L. D. Andersen and E. Mendelsohn (1982) generalized this construction to obtain N -latin squares of all orders n ≠ 2a3b.
We shall give the construction of L. D. Andersen and E. Mendelsohn (1982); the case n = pq being contained in it. Because of its length and detail the proof will not be given. We begin by defining three latin squares of order t each isotopic to the Cayley table of the cyclic group of order t. Recall that when t is a prime these squares have no proper subsquares.
Let A(t), B(t) and C(t) be latin squares defined by eA(t)(i, j) ≡ i+j-1(mod t), eB(t) (i, j) ≡ 4-(i+j)(mod t) and
eC(t) (i,j)≡{t if i+j≡1(mod t)2 if i+j≡3(mod t)3–(i+j)(mod t) otherwise.
Notice that in each square cells (1, 1) and (1, 2) contain the entries 1 and 2. Using these we construct N∞-latin squares of orders n = pm where p is prime and p ≥ 5.
We perform a non-uniform product of squares of order p and A(m) to produce a latin square P(p, m) of order pm. We then exchange some of the entries of P(p, m) so that the result is an N∞-latin square of order pm. Let q be the smallest prime divisor of m. Replace cell (r, s) in A(m) by a copy of C(p) if
1≤r≤mq and
m–mq+1≤s≤m by a copy of B(p) if
⌊m+12⌋+1≤r≤⌊m+12⌋+mq and
m–mq+1≤m and by a copy of A(p) in all other cases. (See Figure 2.3.)
Figure 2.3.
Because Cayley tables were used all proper subsquares of P(p, m) can be located. Having done this we look at the m × 2m subarrary S(p, m) consisting of the first two cells in the first row of each A(p), B(p) and C(p). Clearly S(p, m) is a latin rectangle in which each row contains the entries 1, 2, p+1, p+2, …, (m-1)p+1, (m-2)p+2. From P(p, m) we now construct the N∞-latin square of order pm, D(p, m), by permuting the rows of S(p, m) according to the permutation ρ = (1 2 3 … m). Clearly D(p, m) is a latin square and it is not difficult to show that all subsquares in P(p, m) have been destroyed. Unfortunately, considerable work is involved in showing that this permutation of S(p, m) does not introduce subsquares.
It still remains to construct N∞-latin squares of order n = 2a3b where n ≥ 16. An N∞-latin square of order 12 was recently found by P. Gibbons and E. Mendelsohn (personal communication) after a computer search. The square is shown in Figure 2.4.
Figure 2.4.
Read full chapter
URL:
https://www.sciencedirect.com/science/article/pii/S0167506008709646
Appendix on Number Theory and Group Theory
Maurice R. Kibler, in Galois Fields and Galois Rings Made Easy, 2017
5.2.11 Abstract group — group table
An abstract group is a group for which the nature of its elements and the group law are not explicitly given. A finite group (G, τ) can be given by its group table (called the multiplication table when τ = × or the addition table when τ = +): the set of elements aτb, for all a and b in G, can be displayed in a |G| by |G| array, the group table or Cayley table of G. The number of abstract finite groups of a given order, that are not isomorphic, is finite. As an illustration, Table 5.4 gives the number of abstract finite groups for some low order.
Table 5.4. Number of (not isomorphic) abstract finite groups of low order
| Order of the group | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Number of groups | 1 | 1 | 1 | 2 | 1 | 2 | 1 | 5 | 2 | 2 | 1 | 5 | 1 |
From Table 5.4, there is only one group table for G=2 or 3 and two group tables for G=4. This means that there is only one possibility for a group of order 2 or 3 (all groups of order 2 or 3 are isomorphic) and that there are two possibilities for a group of order 4. The corresponding group tables are given in Table 5.5 for G=2, in Table 5.6 for G=3 and in Tables 5.7 and 5.8 for G=4. All groups of order 2 or 3 are Abelian and cyclic. There are two families of groups of order 4: in one family, all the groups are Abelian and cyclic, whereas in the other family, the groups are Abelian but not cyclic. The family of Abelian but not cyclic groups correspond to the abstract group referred to as the Klein four-group V (called Vierergruppe in German). It can be checked that V is isomorphic to the direct product C2 × C2, where C2 stands for the cyclic group of order 2.
Table 5.5. Group table for the abstract group (G, τ) of order 2; the element at the intersection of the line x and the column y is xτy (the table is symmetrical with respect to the diagonal of the table since the group is commutative); the elements of G are a and e = a2 so that the group (G, τ) is cyclic (isomorphic to C2)
Table 5.6. Group table for the abstract group (G, τ) of order 3; the element at the intersection of the line x and the column y is xτy (the table is symmetrical with respect to the diagonal of the table since the group is commutative); the elements of G are a, b = a2 and e = a3 so that the group (G, τ) is cyclic (isomorphic to C3)
Table 5.7. Group table for the cyclic abstract group (G, τ) of order 4; the element at the intersection of the line x and the column y is xτy (the table is symmetrical with respect to the diagonal of the table since the group is commutative); the elements of G are a, b = a2, c = aτb = a3 and e = b2 = a4 so that the group (G, τ) is cyclic (isomorphic to C4)
| C4 | e | a | b | c |
|---|---|---|---|---|
| e | e | a | b | c |
| a | a | b | c | e |
| b | b | c | e | a |
| c | c | e | a | b |
Table 5.8. Group table for the not cyclic abstract group (G, τ) of order 4; the element at the intersection of the line x and the column y is xτy (the table is symmetrical with respect to the diagonal of the table since the group is commutative); the elements of G are a, b, c = aτb and e = a2 so that the group (G, τ) is not cyclic; the abstract group corresponding to this table is called the Klein four-group generally denoted as V
| V | e | a | b | c |
|---|---|---|---|---|
| e | e | a | b | c |
| a | a | e | c | b |
| b | b | c | e | a |
| c | c | b | a | e |
As realizations of the abstract group of order 3, let us mention the group of rotations leaving an equilateral triangle invariant (rotations around an axis perpendicular to the triangle, the group law being the composition of rotations) and the group (Z3, +) of residues modulo 3 (the law group being the addition modulo 3). Along this vein, a realization of the Klein four-group V is the group of rotations leaving a rhombus invariant and realizations of the cyclic group C4 are the group of rotations leaving a square invariant and the group (Z4, +).
Read full chapter
URL:
https://www.sciencedirect.com/science/article/pii/B9781785482359500051
Representation Analysis of Magnetic Structures
Rafik Ballou, Bachir Ouladdiaf, in Neutron Scattering from Magnetic Materials, 2006
Characters tables.
Characters are constant over conjugacy classes, that is, χ (hgh−1) = χ (g) for all g and h in G, owing to the invariance of a trace over cyclic permutation of matrices. On equipping the set of all the functions ϕ over G into C such that ϕ (hgh−1) = ϕ (g) ∀g ∈ G and ∀h ∈ G with addition and multiplication by a complex number, we get a vector space K, the dimension of which is the number of the conjugacy classes in G. The characters χ U of the irreducible matrix representations Γ U of G forms in K an orthonormal set since 〈χ V|χ U〉 = 1 if U = V and 0 if U ≠ V. We prove that it is a basis for showing that if {ϕ |χ U} = 0 ∀χ U then Σg∈Gϕ (g)χ (g) = 0 so that ϕ = 0 on choosing χ = χ reg. Thus, the number of the irreducible matrix representations Γ U of a group G is equal to the number of the conjugacy classes.
We recall that two elements g and h of a group G are conjugate and belong to the same class if and only if there exist another element t in G such that h = tgt−1. Assuming that G contains ncl classes Ce (e = 1, ncl), each containing n(Ce) elements so that Σe n(Ce) = nG (class equation) and writing χ eU the common value of χ U(g) for all the g in Ce, the orthogonality relations for characters (18) rewrite as
(25)∑e-1nc1n(Ce)χeU(χeV)*=nGδUV.
Using (25), the character table of a group G can be constructed, but the different classes must be known. These can be deduced from the multiplication table of the group, also called Cayley table of the group: let q be an element in the diagonal of the Cayley table which can be written as the square q = p2 of an element p. Whenever an element c in the same column as q and an element d in the same row as q are conjugate (∃s: d = s · c · s−1) we deduce that the elements a and b such that c = b · p and d = p · a are conjugate and hence belong to the same class, for c = b · p = s−1 · (p · a) · s then b = t ·a ·t−1 (t = s−1 p). On iterating the procedure on all the elements in the diagonal, all the classes are obtained (see Table 1).
Table 1. Schematic search of conjugate elements
| p | a | |
|---|---|---|
| ⋮ | ↑ | |
| p | q… | d =s ·c ·s−1 |
| ⋮ | ||
| b = t · a · t−1 ← | c |
The number of conjugates of an element g of a group G is equal to the number of right cosets of the centralizer CG(g) of g. CG(g) = {x ∈ G | gx = xg} is a subgroup of G, not necessarily invariant. The intersection Z(G) = ∩g CG(g) = {x ∈ G |∀g, gx = xg] of all the centralizers is the center of G. Z(G) is an invariant subgroup of G. Any element of Z(G) commutes with all the elements of G and forms a conjugacy class by its own: the cardinal of Z(G) is the number of classes Ce for which n(Ce) = 1.
We define the product of two classes Ce and Cf as the set CeCf of all the products gegf where ge ∈ Ce and gf ∈ Cf. Any product CeCf expands as
(26)CeCf∑wcefwCw.
A matrix Γ eU can be associated to each Ce by summing all the Γ U(g) for g over Ce. ΓeU commutes with all the Γ U (g) for g in G. Owing to the second Shür lemma, Γ eU = λe1(dU), which transposes in terms of the characters χ U and χ eU as n(Ce)χ eU = λeχU(ε). Using (26) we deduce, on the other hand, that Γ eUΓ fU = Σw cefw ΓwU so that λe1(dU)λ f1(dU) = Σw cefwλ w1(dU) and then
(27)n(Ce)n(Cf)χeUχfU=χU(ɛ)∑wcefwn(Cw)χwU
which forms another relation helping to build up the character table of a group G.
On summing over U in (27) and using (22), together with the fact that cef{ε } = n(Ce) if and only if Cf is the class containing the inverses of the elements of Ce and zero otherwise, an additional relation helping to build up the character table of a group G is obtained as
(28)∑UχeU(χfU)*=nGn(Ce)δef.
Read full chapter
URL:
https://www.sciencedirect.com/science/article/pii/B9780444510501500045
Latin squares with particular properties
A. Donald Keedwell, József Dénes, in Latin Squares and their Applications (Second Edition), 2015
9.2 Homogeneous latin squares
Definition
A latin square is said to be h-homogeneous if each of its cells lies in exactly h intercalates.
For example, a cyclic latin square of order 4 is 1-homogeneous whereas a latin square of order 4 based on Klein’s Viergruppe Z2 × Z2 is 3-homogeneous.
A latin square which is 0-homogeneous has also been called an N2—square. (In this notation, a latin square which has no latin subsquares of any size is an N∞—square. We discuss these in Section 9.4.) By combining the results obtained in a series of papers, it was proved in the late 1970s that N2-squares exist for all orders n except n = 2 and 4. Details of the proof are given on pages 113-116 of [DK2].
To return to h-homogeneous latin squares, it is easy to see that 1-homogeneous latin squares exist only of even orders and that (n − 2)-homogeneous latin squares of order n do not exist since any such square must in fact be (n − 1)-homogeneous. Also, (n − 1)-homogeneous latin squares exist if and only if n is a power of 2. See Heinrich and Wallis(1981). It was shown in Hobbs, Kotzig and Zacs(1982) that (n − 3)-homogeneous latin squares exist if and only if n ∈ {3, 4, 6, 8, 12, 16}. Killgrove(2001) called a 1-homogeneous latin square two-tiled and he proved:
Killgrove’s lemma
A group-based latin square is two-tiled if and only if the group has a unique element of order two.
Proof
Suppose without loss of generality that the latin square is in reduced form and is bordered by its own first row and column so as to form the Cayley table of a group.
If the square is 2-tiled, the identity element e in the cell (e, e) belongs to a unique intercalate whose remaining cells are (h, h), (e, h) and (h, e) for some element h. But then h2 = e, since the cell (h, h) must contain e. Thus, the group has an element of order two. If there were a second element k of order two, then the cells (e, e), (k, k), (e, k) and (k, e) would form an intercalate overlapping the first, which is a contradiction. Therefore, the element h of order two must be unique.
Conversely, suppose that there is a unique element h of order two. Any inner automorphism fixes h since g−1hg also has order two, so h is in the centre of the group. Consider any cell (i, j). This cell, and also the cell (ih, hj), contains the element ij. Similarly, the cells (ih, j) and (i, hj) both contain the element ihj so the three cells (ih, hj), (ih, j) and (i, hj) form an intercalate with the cell (i, j). Suppose, if possible, that the cells (r, s), (r, j) and (i, s) also form an intercalate with the cell (i, j). Then rs = ij and is = rj. Thus, r−1i = sj−1 and r−1i = js−1 whence sj−1 = js−1 or (sj−1)2 = e. That is, sj−1 = h. Therefore, s = hj and r = ih. This proves that the cell (i, j) lies in only one intercalate, so the square is 2-tiled. □
In two unpublished papers by D’Angelo and Turgeon and by Abrham and Kotzig, these authors obtained some further results; in particular, the latter authors show that 4-homogeneous latin squares do not exist if n < 8 but that they do exist of all orders n = 8k. (This leaves open the question whether and/or for which other orders such squares exist.) The former authors mention and/or prove several results: (i) There are 2-homogeneous latin squares of all orders divisible by 4 except 4 itself; (ii) If n = 4k and k ≥ 1, there is an (n − k)- or (n − k + 1)-homogeneous latin square of order n according as k is odd or even; (iii) If A is an h-homogeneous latin square of order m and B is a k-homogeneous latin square of order n, then A × B is an (hk + h + k)-homogeneous latin square of order mn (where A × B denotes the direct product of the quasigroups whose Cayley tables are defined by A and B); (iv) The Cayley table of a group G is an h-homogeneous latin square, where h is the number of elements of order 2 in G (cf. Killgrove’s lemma above). From (iv) it follows that, for each positive integer h ≥ 2, there is an h-homogeneous or (h + 1)-homogeneous latin square of order 2h according as h is odd or even. This last result makes use of the dihedral groups and had already been proved earlier in Heinrich and Wallis(1981) and in Hobbs, Kotzig and Zaks(1982).
So far as the present author is aware, the complete spectrum of integers h for which h-homogeneous latin squares exist is still an open question. But Hobbs and Kotzig(1983) contains a summary of results which were known at the time that paper was written regarding squares of orders up to 26. Another interesting question is: For which integers h do orthogonal h-homogeneous latin squares exist or, alternatively, can it be proved that they do not exist for some values of h? This question is partly answered by remark (iv) above. We notice, for example, that the three mutually orthogonal latin squares which are based on Klein’s Viergruppe are all 3-homogeneous.
Read full chapter
URL:
https://www.sciencedirect.com/science/article/pii/B978044463555650009X
Alternative versions of orthogonality
A. Donald Keedwell, József Dénes, in Latin Squares and their Applications (Second Edition), 2015
(e) Quasi-orthogonal latin squares
This concept was introduced by Bedford(1998a) and is as follows:
Definition
Two latin squares of order n defined on the same symbol set are quasi-orthogonal if, when the two squares are juxtaposed, each unordered pair (u, υ) of distinct elements occurs exactly twice and each pair (u, u) occurs exactly once.
We illustrate this definition by means of the triple of mutually quasi-orthogonal latin squares (MQOLS) of order four shown in Figure 10.1.4.
Fig. 10.1.4..
It is well-known that a group based latin square has an orthogonal mate if and only if the group possesses a complete mapping or orthomorphism. Similarly, a group based latin square has a quasi-orthogonal mate if and only if the group possesses a quasi-complete mapping (defined below).
A group which has no complete mappings may nonetheless have quasi-complete mappings. This fact also is demonstrated by the triple of mutually quasi-orthogonal latin squares of order four based on the cyclic group of order four (which has no complete mappings) and shown in Figure 10.1.4. They were first given in Bedford and Whitaker(2000b,2003). Because there exist statistical experiments for which a pair of quasi-orthogonal latin squares may serve as well as an orthogonal pair, the former concept may be practically useful. In that connection, Bedford has shown (see below) that quasi-orthogonal latin squares of order six exist, although these are not group based.
In order to introduce the concept of quasi-complete mapping, we shall need the following definition.
Definition
Let G be a finite group of order n with identity element e. A listing a1, a2, …, an of some of the elements of G (with repetitions allowed) is called a quasi-ordering of G if and only if (i) the list contains the identity element and each element of order two exactly once and, (ii) for every element g ∈ G such that g2 ≠ e, the list contains two occurrences of g and none of g−1 or one occurrence of each of g and g−1 or two occurrences of g−1 and none of g.
Hence we get:
Definition
Let G be a finite group of order n with G = {g1, g2, …, gn}. A mapping θ of G into G is a quasi-complete mapping if the mapping ϕ defined by ϕ(x) = xθ(x) is a permutation of G and θ is such that θ(g1), θ(g2), …, θ(gn) is a quasi-ordering of G. The permutation ϕ is then a quasi-orthomorphism of G.
Bedford(1998a) gave the following example of a quasi-complete mapping of the group (Z4, +) and the corresponding quasi-orthomorphism.
θ=(01230233)ϕ=(01230312)
Thus, for example, ϕ(3) = 3 + θ(3) = 3 + 3 ≡ 2 mod 4.
If ψ1 and ψ2 are permutations of a group (G, ·), where G = {g1, g2, …, gn}, such that ψ1(g1)−1ψ2(g1), ψ1(g2)−1ψ2(g2), …, ψ1(gn)−1ψ2(gn) is a quasi-ordering of G, then ψ1 and ψ2 will be called quasi-orthogonal permutations of G. (If, on the other hand, the above sequence is an ordering of G, then ψ1 and ψ2 are orthogonal permutations of G.)
Using this concept, Bedford proved the following theorem and corollary.
Theorem 10.1.1
Let L be the Cayley table of the finite group (G, ·) and let ϕ1and ϕ2be permutations of G. LetLϕ1andLϕ2be obtained from L by permuting its columns according to ϕ1and ϕ2respectively. Then, if ϕ1and ϕ2are quasi-orthogonal, Lϕ1andLϕ2are quasi-orthogonal.
Proof
Let A=(Lϕ1,lϕ2) denote the array obtained by juxtaposing Lϕ1 and Lϕ2. Then the (i, j)th cell of A contains the ordered pair [giϕ1(gj), giϕ2(gj)]. For any ordered pair (u, υ) of elements of G, let d = u−1υ denote the difference between u and υ. Then the jth column of A contains all the ordered pairs whose difference is ϕ1(gj)−1ϕ2(gj). For a particular ordered pair (u, υ) of elements of G, there are two possibilities:
- (i)
-
if d2 = e then, since ϕ1 and ϕ2 are quasi-orthogonal, there exists a unique element gk in G such that ϕ1(gk)−1ϕ2(gk) = d. So the kth column of A contains all ordered pairs whose difference is d and these include both (u, v) and (v, u) since d = d−1.
- (ii)
-
if d2 ≠ e, then there are exactly two distinct elements gk and gl of G such that ϕ1(gk)−1ϕ2(gk) and ϕ1(gl)−1ϕ2(gl) are either both equal to d, both equal to d−1 or one equal to d and the other equal to d−1.
In the first case of (ii), because u occurs once in the kth column of Lϕ1 and also once in the lth column of Lϕ1, the ordered pair (u, v) occurs both in the kth column and in the lth column of A. In the second case, because u occurs once in the kth column of Lϕ2 and also once in the lth column of Lϕ2, the ordered pair (v, u) occurs both in the kth column and in the lth column of A. From these arguments, it is easy to see that, in the third case, the ordered pairs (u, v) and (v, u) each occur just once, one in the kth column of A and the other in the lth column of A.
It follows that Lϕ1, Lϕ2 are quasi-orthogonal. Moreover, if ϕ1 and ϕ2 are orthogonal permutations, only the third possibility occurs and so Lϕ1 and Lϕ2 are orthogonal in that case. □
Corollary
If (G, ·) is a finite group which possesses a quasi-complete mapping θ with corresponding quasi-orthomorphism ϕ, then L and Lϕ are quasi-orthogonal.
Proof
We need to show that the identity permutation I on G and ϕ are quasi-orthogonal. However, this is indeed the case since I(x)−1ϕ(x) = x−1ϕ(x) = θ(x) and we know that θ(g1), θ(g2), …, θ(gn) is a quasi-ordering of G by definition of θ. □
Bedford(1998a) observed that the following two quasi-orthomorphisms of (Z4, +) are quasi-orthogonal.
ϕ1=(01230312)ϕ2=(01230231)
Hence, from the above theorem and corollary, the latin squares L, Lϕ1, Lϕ2 shown in Figure 10.1.4 are a set of MQOLS.
REMARKS.
- (i)
-
The argument of the above theorem remains valid when ϕ1 and ϕ2 are neither quasi-orthomorphisms nor orthomorphisms but, in that case, the corollary no longer applies.
- (ii)
-
When ϕ1 and ϕ2 are both orthomorphisms (rather than quasi-orthomorphisms), the latin squares Lϕ1, Lϕ2 and L are mutually orthogonal.
We illustrate these remarks by means of Figure 10.1.5. In that figure, ψ1, ψ2 are orthogonal permutations but ψ1 is neither an orthomorphism nor a quasi-orthomorphism of Z2 × Z2 = 〈a, b: a2 = b2 = (ab)2 = e〉 so L is not orthogonal or quasi-orthogonal to Lψ1. (In fact, those ordered pairs which appear when L and Lψ1 are juxtaposed all appear four times.) However, ψ2 is an orthomorphism with corresponding complete mapping θ2=(eabababeab) and ψ1, ψ2 are orthogonal permutations so each of L, Lψ2 and Lψ1, Lψ2 are orthogonal pairs of latin squares.
Fig. 10.1.5..
In Bedford and Whitaker(2000b), these authors used a computer and the connection with equidistant permutation arrays to help them find all sets of MQOLS of largest size for orders n ≤ 6. In particular, they obtained sets of three MQOLS for each of the orders 4 and 6. In the case of the latter order, the squares are not group-based. One triple of order 4 is that given in Figure 10.1.4 and one of order 6 is shown in Figure 10.1.6. This raises the question “What is the upper bound Nq(n) on the number of squares in a set of MQOLS of order n?”. It is well-known that the upper bound for a set of MOLS is n − 1 (see Theorem 5.1.2) but no similar argument can be used for MQOLS because a permutation of symbols in any one member of the set may, and often does, destroy its property of being quasi-orthogonal to the remaining members of the set. In Bedford and Whitaker(2001), the authors reported their own efforts to solve this problem and also mentioned the very weak bound Nq(n) ≤ (n−1)(n−2) obtained earlier by Wild(1997). In particular, it is not known whether, for some n, n > 6, Nq(n) > n − 1.
Fig. 10.1.6..
In a further paper, Bedford and Whitaker(2003), these authors discuss connections between quasi-orthogonal latin squres and various other combinatorial designs. In particular, they consider connections with orthogonal Steiner triple systems (see Section 2.3 and Section 5.4) and with Room squares (see Section 6.4).
First, they point out and prove that there exists a skew Room square of side n if and only if there exists a pair of quasi-orthogonal, symmetric and idempotent latin squares of order n.
Definition
A Room square in normalized form is said to be skew if, when cell (a, b) of the square is filled, cell (b, a) is empty.
In the construction of a Room square from a pair of Room quasigroups which we described in Section 6.4, the multiplication tables of the quasigroups have the properties of being symmetric and idempotent and if, when they are juxtaposed, the ordered pair a, b occurs in row u and column υ (and in row υ and column u by the symmetry), then the unordered pair u, υ occurs as the entry in the cell (a, b) of the Room square. When the juxtaposed squares are quasi-orthogonal, the ordered pair b, a cannot occur because the ordered pair a, b has already occurred twice and, consequently, when cell (a, b) of the square is filled, cell (b, a) is empty as required.
Bedford and Whitaker define two Steiner triple systems to be quasi-orthogonal if the Cayley tables of their associated Steiner quasigroups are quasi-orthogonal. O’Shaugnessy’s construction of Room squares from orthogonal Steiner triple systems is just a special case of the construction discussed above in which the Room pair of quasigroups are both Steiner quasigroups and so are totally symmetric. Consequently, when the Steiner quasigroups are quasi-orthogonal, the Room square is skew. In that case, the orthogonal Steiner triple systems, say S and S′, have the additional property that when (a, b, u) and (c, d, υ) both occur in S and (a, b, υ) and (c, d, w) occur in S′, then w ≠ u. The above authors point out that Dukes and E.Mendelsohn(1999) have introduced such pairs of Steiner triple systems independently and have called them skew-orthogonal rather than quasi-orthogonal. The latter authors have investigated for which orders such pairs of systems exist (or, equivalently, for which orders pairs of quasi-orthogonal totally symmetric idempotent latin squares exist).
Quite recently, Liang(201?) has studied standardized (defined as first row in natural order) quasi-orthogonal latin squares and has shown that some classical results of Parker, MacNeish and Sade can be modified to apply to such squares.
Since the pairs of latin squares which we have just been considering have all been perpendicular pairs, this seems a convenient point at which to discuss such squares more generally.
If a symmetric latin square is of odd order, the elements of its main diagonal are necessarily all different (see Theorem 1.5.4) and so it can be made idempotent. If a second idempotent square of the same odd order 2m + 1 is juxtaposed, the number of distinct ordered pairs then arising can be (1 + 2 + … + 2m) + (2m + 1) = (m + 1)(2m + 1) but not more. When the latter number is achieved, the squares are perpendicular. Symmetric squares of even order cannot be made idempotent so the same definition is not valid. In Gross, Mullin and Wallis(1973a,b), the maximum number ν(r) of idempotent symmetric latin squares which can occur in a pairwise perpendicular set has been investigated. The procedure used by these authors makes use of the connection with Room squares mentioned above and in Section 6.4. See also Section 4.3.
Steiner quasigroups (defined in Section 2.3) also have multiplication tables which are idempotent symmetric latin squares. Consequently, orthogonal Steiner triple systems and their associated perpendicular Steiner quasigroups provide examples of perpendicular idempotent latin squares. Perpendicular commutative quasigroups have been investigated from this point of view in O’Shaughnessy(1968), N.S.Mendelsohn(1970), Lindner and N.S.Mendelsohn(1973), Mullin and Németh (1969), Radó(1974) and Steedley(1974). (See also Section 5.4.)
Read full chapter
URL:
https://www.sciencedirect.com/science/article/pii/B9780444635556500106
Mathematical Statistical Physics
Frank Redig, in Les Houches, 2006
2.3 Group structure
Besides its relation to spanning trees, there are some more fascinating properties of the set ℛ. Consider N = 2 for the sake of (extreme) simplicity. Define the operation ⊕ on ℛ by
η⊕ζ=S(η+ζ)
where the ordinary + means point-wise addition. This gives rise to the following table
We recognize here the Cayley table of an abelian group, i.e., (ℛ, ⊕) is an abelian group with neutral element 22. Remark that we can define ⊕ on the whole of Ω, but (Ω, ⊕) is not a group.
We now introduce still another group (which is isomorphic to the preceding one, as we will see later). Let us introduce the addition operator ai : Ω → Ω
ai(η)=S(η+δi)
for i ∈ {1, …, N}. In words, aiη is the stable result of an addition at site i. Accept (or verify) for the moment that for all i, j ∈ {1, …, N},
(2.2)aiaj=ajai
Later we will prove this so-called abelian property in full detail and generality. By definition of recurrence, if a configuration η is recurrent then there exist integers ni > 0 such that
(2.3)Πi=1Naini(η)=η
The product in (2.3) is well-defined by abelianness. The fact that ni can be chosen strictly positive derives from the fact that in the course of the Markov chain one adds to every site with strictly positive probability. Call
e=∏i=1Naini and consider
A={ζ ∈ R :eζ=ζ}
By definition A is not empty (η ∈ A), and if
g=∏i=1Naimi for some integers mi ≥ 0, then we have the implication “ζ ∈ A implies gζ ∈ A”. Indeed, by abelianness, for ζ ∈ A,
e(gζ)=g(e(ζ))=g(ζ)
Therefore, A is a “trapping set” for the Markov chain, i.e., a subset of configurations such that once the Markov chains enters it, it never leaves it. As a consequence A ⊃ ℛ, because the Markov chain has only one recurrent class which contains the maximal configuration. Since by definition we have A ⊆ ℛ, A = ℛ. Therefore, acting onℛ, e is neutral. Since ni > 0, we can define
ai−1=aini−1Πj=1Najnj
and we have the relation
(2.4)ai−1ai=aiai−1=e
From (2.4) we conclude that
(2.5)G:={Πi=1Naiki,ki∈ℕ}
acting on ℛ defines an abelian group.
Of course not all the products of addition operators defining G are different. In fact, it is easily seen that the group is finite, and we will show that once again
(2.6)|G|=N+1
For that, it is sufficient to show that the group acts transitively and freely on ℛ, i.e., for all η ∈ ℛ the orbit Oη = {gη : g ∈ G} = ℛ and if gη = g′η for some g, g′ ∈ G, then g = g′, i.e., gζ = g′ζ for all ζ ∈ ℛ. For the first statement, if η ∈ ℛ and g ∈ G, then gη can be reached from η in the Markov chain, hence gη ∈ ℛ, and Oη is clearly a trapping set for the Markov chain, hence Oη ⊃ ℛ. To prove the second statement, consider for gη = g′η the set
A={ζ∈R:gζ=g′ζ}
then A = ℛ with the same kind of reasoning used in the definition of inverses. Therefore, for all η, the map
Ψη:G→R:g↦gη
is a bijection between G and ℛ.
However, there is still another way to see that |G| = N = 1. This way of reasoning will be useful because in the general case we will not so easily be able to count the recurrent configurations. The equality |G| = |ℛ| is however completely general, and that will be useful to obtain |ℛ|. Counting the number of elements of a group can become an easy task if we find a treatable isomorphic group. For this, we have to look for closure relations in G. Here is an easy one. Suppose you add two files to some commissioner. Since he has at least one file (to save his face), he will certainly get crazy and give one file to each of his neighbors (modulo the boundary conditions of course). In symbols this means
(2.7)ai2=ai−1ai+1
for i ∈ {2, … N − 1} and
a12=a2, aN2=aN−1
Using the toppling matrix Δ introduced in (2.1), this is summarized as
(2.8)aiΔii=Πj∈V,j≠iaj−Δij
for all i ∈ V. Acting on ℛ we can bring the right hand site to the left, and obtain
(2.9)Πj∈VajΔij=e
for all i ∈ V. By abelianness, we infer from (2.9) that for all n : V → ℤ
(2.10)Πi∈VΠj∈VajniΔij=e
Using Δij = Δji and the definition (Δn)i = Σj∈V Δijnj, we obtain
(2.11)Πi∈Vai(Δn)i=e
for all n : V → ℤ. We will show now that, conversely, if
Πi∈Vaimi=e
for some mi ∈ ℤ then there exists n : V → ℤ such that
mi=(Δn)i
In words, this closure relation means that the only “trivial additions” on ℛ are (integer column) multiples of the matrix Δ.
Suppose
(2.12)Πx∈Vaxmx=e
where m ∈ ℤV. Write m = m+ − m− where m+ and m− are non-negative integer valued. The relation (2.12) applied to a recurrent configuration η yields
(2.13)Πx∈Vaxmx+η=Πx∈Vaxmx−η
In words, addition of m+ or m− to η leads to the same final stable configuration, say ζ. But then there exist k+, k− non-negative integer valued functions on V such that
η+m+−Δk+=ζ=η+m−−Δk−
which gives
m=m+−m−=Δ(k+−k−)
Arrived at this point, we can invoke a well-known theorem of elementary algebra. If you have a group G and a group H and a homomorphism
Ψ:H→G
then G is isomorphic to the quotient H/Ker(Ψ) where Ker(Ψ) is the set of h ∈ H which are mapped to the neutral element of G. In our case, define
H:={n:V→ℤ}=ℤV
with group operation pointwise addition. Next
Ψ:H→G:n↦Πi∈Vaini
Then what we just discussed can be summarized in the equality
Ker(Ψ)=ΔℤV={Δn:n∈ℤV}
and hence we have the isomorphism
G≃ℤV/ΔℤV
Therefore we have
|R|=|G|=|ℤV/ΔℤV|=det(Δ)
To see the last equality, note that ℤV is the |V| dimensional hypercubic lattice, with a volume one unit cell. ΔℤV is another lattice with the columns of Δ as vectors defining the unit cell. The quotient of these two lattices can geometrically be viewed as the non-equivalent points n ∈ ℤV of the unit cell of the lattice ΔℤV. Equivalence is here defined as
n∼m
if there exists k ∈ ℤV such that
n−m=Δk
This number of non-equivalent points is precisely the volume of the unit cell of the lattice ΔℤV, which is det(Δ) (Puzzle this out in the case N = 2 to be convinced). In general, the equality |ℤV/AℤV| = det(A) (with A a symmetric matrix with integer elements and non-negative determinant) is trivial for a diagonal matrix. Indeed, in that case Aij = aiiδij and
ℤV/AℤV≃ℤ/a11ℤ⊕ℤ/a22ℤ…⊕ℤ/annℤ
an hence
|ℤV/AℤV|=∏i=1naii=det(A). Since by row and column operations (i.e., addition and subtraction of columns, or permutation of columns) one can make every integer-valued matrix diagonal, see e.g. [22], we just have to remark that such operations do not change the determinant of a matrix, and do not change (up to isomorphism) the lattice ℤV /AℤV.
Here is still another, geometrical proof. |ℤV/AℤV| is the number of non-equivalent points in the unit cell defined by A (i.e., the parallelepiped spanned by the rows of A). We can cover ℝ|V| by disjoint copies of this unit cell. Consider now a large cube Cn = [−n, n]|V|. Let Nn denote the number of integer points (i.e., points of ℤV) in the cube, let xn denote the number of unit cells (copies of A) in Cn, and let y denote the number of non-equivalent points in one unit cell. Then we have
xny=Nn
The volume of the xn unit cells in Cn is xndet(A), so we have
xndet(A)=(2n+1)d+o(nd)
Dividing these two relations and taking the limit n → ∞ gives
ydet(A)=limn→∞Nn(2n+1)d+0(nd)=1
Read full chapter
URL:
https://www.sciencedirect.com/science/article/pii/S092480990680051X
Таблица Кэли для операции
Бинарная операция — это, по определению, отображение множества A ╢ A в множество A, при этом образ пары (x, y) обозначим, например, x © y, где © — символ операции. Здесь A — произвольное непустое множество и A╢ A — множество всех упорядоченных пар (x, y) — таких, что x, y Î A (то есть, декартов квадрат множества A). Непустое множество A называется основным множеством операции.
Можно составить следующую иерархию множеств с бинарной операцией (разумеется, вместо © может быть вставлена любая — +, √, *, È , Ç , Å , Ä , Ñ , ° и т.д. и т.п. — в зависимости от необходимости и вкуса автора.
Группоид, обозначаемый символом (A, © ) — множество A, на котором задана некоторая бинарная операция, обозначаемая © . Если множество группоида конечно, то есть ╫A╫ = card (A) = n, то таблица Кэли операции группоида есть таблица n ╢ n, в которой элемент x © y Î A находится в клетке пересечения строки x и столбца y. Конечный группоид можно считать заданным, если выписана его таблица Кэли.
Задача об авторитетах
У Саши и Даши авторитет Даша.
У Саши и Маши авторитет Саша.
У Саши авторитет Саша.
У Даши и Маши авторитет Саша.
У Даши авторитет Даша.
У Маши авторитет Петя.
У Пети и Даши авторитет Петя.
У Пети и Маши авторитет Петя.
У Пети и Саши авторитет Саша.
У Пети авторитет Саша.
ТАБЛИЦА КЭЛИ ДЛЯ ОПЕРАЦИИ «АВТОРИТЕТ»
|
АВТОРИТЕТ |
Даша |
Маша |
Петя |
Саша |
|
Даша |
Даша |
Саша |
Петя |
Даша |
|
Маша |
Саша |
Петя |
Петя |
Саша |
|
Петя |
Петя |
Петя |
Саша |
Саша |
|
Саша |
Даша |
Саша |
Саша |
Саша |
* Затенен операционный квадрат
ТАБЛИЦА КЭЛИ, КОРЕЙСКИЙ ВАРИАНТ
|
АВТОРИТЕТ |
Ким |
Пак |
Чжо |
|
Ким |
Ким |
Ким |
Ким |
|
Пак |
Ким |
Ким |
Ким |
|
Чжо |
Ким |
Ким |
Ким |
Квазигруппа (от латинского слова quasi — как будто, почти и слова группа) — группоид, бинарная операция которого (например, © ) такова, что каждое из уравнений a © x = b, y © a = b имеет единственное решение для любых элементов a, b этого множества. Квазигруппа — одно из обобщений понятия группа. Особенно близки к группам квазигруппы с единицей — лупы, определение которых получается из аксиом групп отбрасыванием требования ассоциативности. Квазигруппу можно рассматривать и как унивесальную алгебру с тремя бинарными операциями (дополнительно левое и правле деление).
Гомоморфный образ квазигруппы, вообще говоря, не квазигруппа, а группоид с делением. Гомоморфизмам квазигруппы на квазигруппе соответствуют конгруэнции специального типа (т.н. нормальные конгруэнции). Значительно большую роль, чем гомоморфизмы, в теории и классификации групп играют изотопии. Изотопия — отношение эквивалентности для бинарных операций на фиксированном множестве, определяемое с помощью трех подстановок этого множества. Оказывается, что всякий группоид, изотопный квазигруппе, — сам квазигруппа, а всякая квазигруппа изотопна некоторой лупе. Для групп понятие изотопии совпадает с понятием изоморфизма.
Таблица умножения конечной квазигруппы (ее таблица Кэли) в комбинаторике известна по названием латинский квадрат. Одна из задач комбинаторной теории квазигрупп — отыскание систем взаимно ортогональных квазигрупп на заданном множестве — важна для построения конечных проективных плоскостей.
Лупа, или квазигруппа с единицей, определение которой получается из аксиом группы отбрасыванием требования ассоциативности, особенно близка к группе.
Полугруппа — множество, с определенной на нем бинарной операцией, удовлетворяющей закону ассоциативности, т.е. группоид (A, © ), в котором для каждой тройки элементов a , b и с выполняется условие a ©( b © с) =(a © b) © с). Понятие полугруппы есть обобщение понятия группы: из аксиом группы остается лишь одна; этим объясняется и термин «полугруппа».
Теория полугрупп принадлежит к числу сравнительно молодых областей алгебры. Первые исследования, посвященные полугруппам, относятся к 20-м гг. 20 в. и связаны с именем А. К. Сушкевича. Он, в частности, определил строение конечной полугруппы без собственных идеалов. К концу 50-х гг. теория полугрупп сформировалась в самостоятельную ветвь современной алгебры с богатой проблематикой, разнообразными методами и тесными связями с многими областями математики — как собственно алгебраическими (в первую очередь, с теорией групп и теорией колец), так и другими, например, с функциональным анализом, дифференциальной геометрией, алгебраической теорией автоматов.
- Примеры полугрупп чрезвычайно многочисленны. Это, например:
- различные множества чисел вместе с операцией сложения или умножения, замкнутые относительно рассматриваемой операции (т.е. содержащие вместе с любыми двумя своими элементами их сумму или, соответственно, произведение);
- Полугруппа матриц относительно умножения;
- Полугруппа функций относительно «поточечного» умножения * , задаваемого формулой (f* g) (x) = f(x) g(x);
- Полугруппа матриц относительно операции пересечения или объединения;
- Один из простейших примеров полугруппы — множество всех натуральных чисел относительно сложения; эта полугруппа является частью (подполугруппой) группы целых чисел по сложению или, как говорят, вложима в группу целых чисел.
Далеко не всякая полугруппа вложима в какую-нибудь группу: необходимыи условием такой вложимости является закон сокращения — каждое из равенств ac = bc, ca = cb влечет за собой a = b; выполнение закона сокращения не достаточно для такой вложимости, но, например, коммутативная полугруппа с законом сокращения вложима в группу.
- Если на множестве FX всех конечных последовательностей элементов произвольного множества (алфавита) X задать операцию * формулой
(x1, . . . , xm) * (y1, . . . , yn) = (x1, . . . , xm, y1, . . . , yn),
то FX станет полугруппой; она называется свободной полугруппой над алфавитом X. Роль свободных полугрупп в общей теории определяется тем, что всякая полугруппа есть гомоморфный образ подходящей свободной полугруппы. Важную роль играют свободные полугруппы и в некоторых приложениях, прежде всего в теории формальных языков и кодов.
- Всякая совокупность пребразований произвольного множества M, замкнутая относительно операции композиции (последовательного выполнения), будет полугруппой относительно этой операции; такова, в частности, совокупность всех преобразований множества M, называемая симметрической полугруппой на множестве M. Многие важные совокупности преобразований оказываются полугруппами относительно композиции, причем часто они не являются группами. С другой стороны, всякая полугруппа изоморфна некоторой полугруппе преобразований. Все это определяет как роль полугрупп преобразований в общей теории полугрупп, так и роль теории полугрупп для изучения в самом общем виде преобразований с точки зрения их композиции. В большой степени через рассмотрение преобразований осуществляются связи теории полугрупп с другими областями математики.
Как и в других алгебраических теориях, одной из главных задач теории полугрупп является классификация всевозможных полугрупп, описание их строения. Это осуществляется прежде всего наложением на рассматриваемые полугруппы различых ограничений и выделение тем самым различных типов полугрупп. Среди важных типов — регулярные полугруппы, то есть полугруппы, в которых для любого элемента a существует такой элемент x, что axa = a. Регулярными являются, например, полугруппа всех матриц данного порядка над телом, симметрические полугруппы, полугруппы всех частичных преобразований множеств. Регулярные полугруппы принадлежат к числу наиболее активно изучаемых в теории полугрупп.
Заметную часть общей теории составляет теория представлений полугрупп преобразованиями и матрицами. Точка зрения теории представлений нередко проливает дополнительный свет на некоторые типы полугрупп, естественно определяемые с точки зрения аксиоматики. Внесение в полугруппы дополнительных структур, согласованных с полугрупповой операцией, выделяет особые разделы теории полугрупп, такие, как теория топологических полугрупп, теория упорядоченных полугрупп.
Моноид — это, по определению, полугруппа с единицей.
Группа (нем. Gruppe) — одно из основных понятий современной математики — есть лупа, являющаяся в то же время полугруппой.
Теория групп изучает в самой общей форме операции, наиболее часто встречающиеся в математике и ее приложениях (примеры таких операций — сложение чисел, умножение чисел, сложение векторов, последовательное выполнение преобразований и т.п.). При этом теория групп изучает не совсем произвольные операции, а лишь те, которые обладают рядом основных войств, перечисляемых в определении группы.
Формальное определение группы таково. Пусть G — произвольное непустое множество, на котором задана бинарная алгебраическая операция ° , т.е. для любых двух элементов a, b, из G определен некоторый элемент (обозначаемый, например, a ° b) также из G. Если при этом выполняются условия: 1) (a °b) ° c = a ° (b ° c) для любых a, b и c из G; 2) в G существует такой элемент e (называемый единицей, иногда — нейтральным элементом), что a° e = e ° a = a для любого a из G; 3) для любого a из G существует такой элемент a √1 (обратный к a элемент), что a ° a √1 = a √1 ° a = e, то множество G с заданной на нем операцией ° назовем группой.
Примеры групп. 1) множество G различных движений эвклидовой плоскости, самосовмещающих данную фигуру, операцией на котором служит композиция движений (если j , y — два движения из G, то результатом их композиции назовем движение j ° y , равносильное последовательному выполнению сначала движения j , а затем движения y ), образует т.н. группу симметрий фигуры. Единицей в этой группе будет тождественное преобразование плоскости, а обратным к j элементом — обратное к j преобразование. Группа G является характеристикой большей или меньшей симметричности фигуры: чем больше множество G, тем симметричнее фигура. Например, группа симметрий квадрата (рис., а) состоит из восьми движений
(четыре поворота вокруг центра квадрата и четыре отражения: два — относительно диагоналей и два — относительно прямых, соединяющих середины противоположных сторон). Для круга (рис. б) группа симметрий уже содержит бесконечно много элементов (например, все повороты вокруг центра), а для фигуры, нарисованной на рисунке (в) группа симмерий состоит из одного тождественного преобразования.
Если Z — множество всех целых чисел, а операция на Z — их обычное сложение + , то Z — группа. Роль e будет играть число 0, а роль обратного к z элемента — число √z. Часть H множества Z , состоящая из четных чисел, сама будет группой относительно той же операции. В таком случае говорят, что H — подгруппа группы Z . Обе групы Z и H удовлетворяют следующему дополнительному условию: 4) a + b = b + a для любых a и b из группы. Всякая группа, в которой выполняется условие 4) называется коммутативной или абелевой.
3) Множество всех подстановокn символов образует группу относительно умножения подстановок, называемую симметрической группой. При n ¨ 3 симметрическая группа неабелева. Порядок (число элементов) симметрической группы равен n!.



























