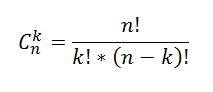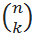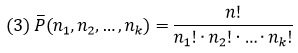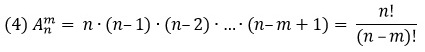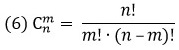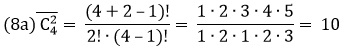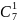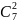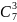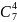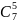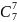Подсчитаем в MS EXCEL количество сочетаний из n элементов по k. С помощью формул выведем на лист все варианты сочетаний (английский перевод термина: Combinations without repetition).
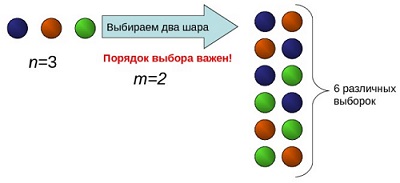
Сочетаниями из n различных элементов по k элементов называются комбинации, которые отличаются хотя бы одним элементом. Например, ниже перечислены ВСЕ 3-х элементные сочетания, взятые из множества, состоящего из 5 элементов {1; 2; 3; 4; 5}:
(1; 2; 3); (1; 2; 4); (1; 2; 5); (1; 3; 4); (1; 3; 5); (1; 4; 5); (2; 3; 4); (2; 3; 5); (2; 4; 5); (3; 4; 5)
Примечание
: Это статья о подсчете количества сочетаний с использованием MS EXCEL. Теоретические основы советуем прочитать в специализированном учебнике. Изучать сочетания по этой статье — плохая идея.
Отличие Сочетаний от Размещений
В отличие от
Размещений
следующие 3-х элементные комбинации (1; 2; 3); (1; 3; 2); (2; 1; 3); (2; 1; 3); (3; 2; 1); (3; 1; 2) считаются одинаковыми, и в набор
Сочетаний
включается только одна из этих комбинаций. Очевидно, что для тех же n и k число
Сочетаний
всегда меньше чем число
Размещений
(так как при размещениях порядок важен, а для сочетаний — нет), причем в k! раз.
Подсчет количества Сочетаний
Число всех
Сочетаний
из n элементов по k можно вычислить по формуле:
Например, количество 4-х элементных комбинаций из 6 чисел {1; 2; 3; 4; 5; 6} равно 15=6!/(4!(6-4)!)
Примечание
: Для
Сочетаний
из n элементов по k также используется и другая запись:
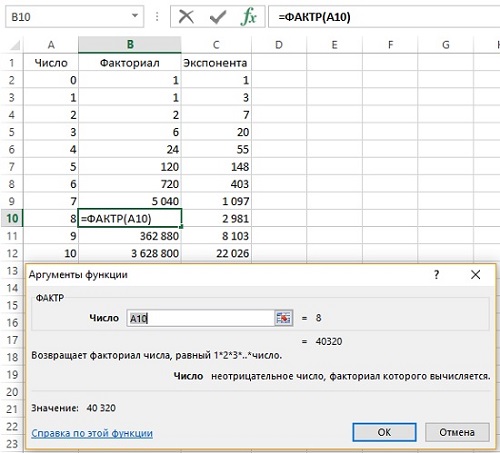
В MS EXCEL для подсчета количества комбинаций без повторов существует специальная функция ЧИСЛКОМБ() , английское название функции — COMBIN(). Для предыдущего примера формула =ЧИСЛКОМБ(6;4) , разумеется, также вернет 15. Альтернативная формула для подсчета сочетаний =ФАКТР(6)/ФАКТР(6-4)/ФАКТР(4) .
Очевидно, что k меньше или равно n, т.к. нельзя выбрать из множества элементов n больше элементов, чем в нем содержится (предполагается, что элементы после выбора обратно не возвращаются). При k=n количество сочетаний всегда равно 1.
Примечание
: О Сочетаниях с повторениями (с возвращением элементов) можно прочитать в статье
Сочетания с повторениями: Комбинаторика в MS EXCEL
Вывод всех комбинаций Сочетаний
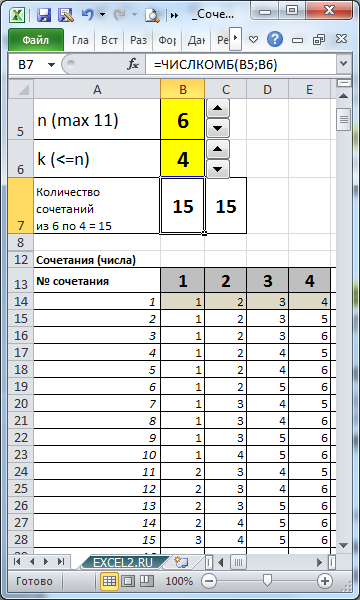
В файле примера созданы формулы для вывода всех Сочетаний для заданных n и k.
Задавая с помощью
элементов управления Счетчик
количество элементов множества (n) и количество элементов, которое мы из него выбираем (k), с помощью формул можно вывести все Сочетания.
В файле примера не забывайте увеличивать количество строк с формулами, чтобы поместились все ваши комбинации. Для этого выделите последние ячейки с формулами (сочетание №330) и скопируйте их вниз на нужно количество строк. При увеличении строк с формулами размер файла быстро растет, а скорости пересчета листа падает. Если строк 4 тысячи, то размер файла составляет около 2 Мб.
Задача
Автовоз может перевозить по 4 легковые машины. Необходимо перевезти 7 разных машин (LADA Granta, Hyundai Solaris, KIA Rio, Renault Duster, Lada Kalina, Volkswagen Polo, Lada Largus). Сколькими различными способами можно заполнить первый автовоз? Конкретное место машины в автовозе не важно.
Нам нужно определить число
Сочетаний
7 машин на 4-х местах автовоза. Т.е. n=7, а k=4. Оказывается, что таких вариантов =ЧИСЛКОМБ(7;4) равно 35.
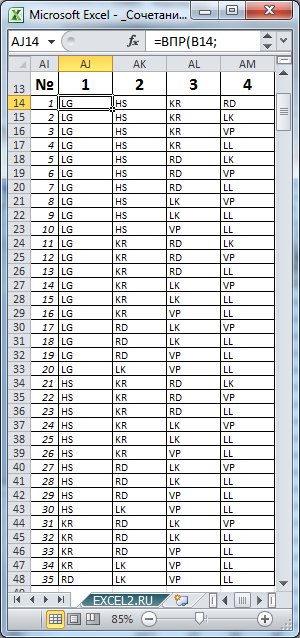
Воспользуемся файлом примера (ссылка внизу статьи) , чтобы наглядно убедиться, что мы решили задачу правильно.
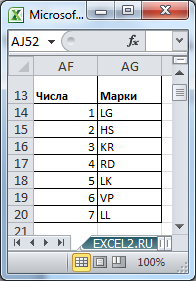
Произвольным образом сопоставим маркам машин числовые значения и сделаем сокращения названий марок: LADA Granta (LG=1), Hyundai Solaris (HS=2), …
Выставив в ячейках
В5
и
В6
значения 7 и 4 соответственно, определим все варианты размещений машин в автовозе (см. столбцы AJ:AM).
Примечание
: О Перестановках можно прочитать в статье
Перестановки без повторений: Комбинаторика в MS EXCEL
, а о Размещениях в статье
Размещения без повторений: Комбинаторика в MS EXCEL
.
Таблица вариантов для комбинаций из двух элементов
Допустим, мы бросаем два игральных кубика, и нас интересуют все комбинации, когда сумма выпавших чисел кратна 5.
Каждый из кубиков имеет 6 возможных «состояний»: 1,2,3,4,5,6.
Для того, чтобы описать все возможные комбинации двух кубиков, нужно составить таблицу вариантов:
| Второй кубик | |||||||
| 1 | 2 | 3 | 4 | 5 | 6 | ||
| Первый кубик | 1 | 11 | 12 | 13 | 14 | 15 | 16 |
| 2 | 21 | 22 | 23 | 24 | 25 | 26 | |
| 3 | 31 | 32 | 33 | 34 | 35 | 36 | |
| 4 | 41 | 42 | 43 | 44 | 45 | 46 | |
| 5 | 51 | 52 | 53 | 54 | 55 | 56 | |
| 6 | 61 | 62 | 63 | 64 | 65 | 66 |
Сумма выпавших чисел на кубиках кратна 5 в 7 случаях (ячейки таблицы закрашены). Общее количество возможных комбинаций – 36.
Правило суммы и правило произведения
Правило суммы: если элемент a можно выбрать m различными способами и независимо от него элемент b можно выбрать n различными способами, то выбрать все различные комбинации элементов «a или b» можно m + n способами.
ИЛИ $iff$ «+»
Например:
Сколькими способами можно выбрать 1 ИЛИ 2 игроков из трёх кандидатов на участие в соревновании?
Одного игрока из трёх можно выбрать $C_3^1 = 3$ разными способами.
Двух игроков из трёх можно выбрать $C_3^2 = 3$ разными способами.
По правилу суммы у нас 3+3 = 6 способов для выбора.
Правило произведения: если элемент a можно выбрать m различными способами и независимо от него элемент b можно выбрать n различными способами, то все различные комбинации элементов «a и b» можно выбрать $mcdot n$ способами.
И $iff «cdot»$
Например:
Сколько существует различных двузначных кодовых слов, состоящих из одной буквы И одной цифры, если разрешенные символы – это 5 букв «a,b,c,d,e» и 3 цифры «1,2,3»?
По правилу произведения число всех кодовых слов – всех возможных комбинаций: $m cdot n = 5 cdot 3 = 15$ слов.
Примеры
Пример 1. При составлении расписания завуч хочет на первый урок поставить алгебру или физику, а на второй – историю, географию или иностранный язык. Сколько существует вариантов расписания для первых двух уроков? Изобразите их с помощью таблицы вариантов.
Для первого урока есть m = 2 варианта.
Для второго урока n = 3 варианта.
По правилу произведения общее число вариантов для двух уроков
$mn = 2 cdot 3 = 6$ вариантов.
|
2й урок |
||||
|
История |
География |
Иностранный язык |
||
|
1й урок |
Алгебра |
Алгебра История |
Алгебра География |
Алгебра Ин. язык |
|
Физика |
Физика История |
Физика Геграфия |
Физика Ин. язык |
Ответ: 6 вариантов
Пример 2. Из коробки с 12 фломастерами разного цвета один фломастер берет Коля, а за ним – один фломастер берет Петя. Сколько существует различных вариантов такого выбора фломастеров?
Перед Колей на выбор 12 фломастеров – у него m = 12 вариантов.
Перед Петей остаётся на выбор 11 фломастеров – у него n = 11 вариантов.
По правилу произведения общее число вариантов: $ mn = 12 cdot 11 = 132$
Ответ: 132 варианта
Пример 3. Сколько различных трёхзначных чисел можно записать с помощью цифр 0,1,2,3,4,5, если а) цифры могут повторяться; б) цифры не повторяются.
а) цифры могут повторяться
В разряде сотен могут быть цифры 1,2,3,4,5, всего m=5 вариантов
В разряде десятков могут быть цифры 0,1,2,3,4,5, всего n=6 вариантов
В разряде единиц могут быть цифры 0,1,2,3,4,5, всего k=6 вариантов
По правилу произведения общее количество возможных трёхзначных чисел:
$$ mnk = 5 cdot 6 cdot 6 = 180 $$
б) цифры не повторяются
В разряде сотен могут быть цифры 1,2,3,4,5, всего m = 5 вариантов
В разряде десятков не цифра сотен, всего n = 5 вариантов
В разряде единиц не цифра десятков и не цифра сотен, всего k = 4 варианта
Всего $mnk = 5 cdot 5 cdot 4 = 100$
Ответ: а) 180; б) 100
Пример 4. Сколькими способами можно рассадить четырёх щенков по четырём углам комнаты?
У первого щенка $m_1 = 4$ варианта углов.
У второго щенка, т.к. один угол уже занят, остаётся $m_2 = 3$ варианта углов.
У третьего щенка, т.к. два угла уже заняты, остаётся $m_3 = 2$ варианта углов.
У четвертого щенка выбора нет, ему остался $m_4 = 1$ угол, без вариантов.
Общее количество способов по правилу произведения:
$$ m_1 cdot m_2 cdot m_3 cdot m_4 = 4 cdot 3 cdot 2 cdot 1 = 24 $$
Ответ: 24 способа
Пример 5. Сколько существует способов занять 1,2 и 3 места на чемпионате, в котором участвуют 10 команд?
Для того, чтобы занять 1-е место существует $m_1 = 10$ претендентов.
Если 1-е место определено, для 2-го места остаётся $m_2 = 9$ претендентов.
Если 1-е и 2-е определено, для 3-го места остаётся $m_3 = 8$ претендентов.
Итого, по правилу произведения:
$m_1 cdot m_2 cdot m_3 = 10 cdot 9 cdot 8 = 720$ вариантов распределения призовых мест.
Ответ: 720 способов
Четырёхмерные таблицы в комбинаторике — два странных способа посчитать сочетания
Время на прочтение
5 мин
Количество просмотров 4.9K
В комбинаторике сочетанием из
по
называют набор
элементов, выбранных из
элементов. В отличие от размещений, число сочетаний не учитывает последовательность размещения элементов, например: «Сколько групп из 4 человек, можно получить, если всего в классе 20 человек?». Хотя удобные способы подсчёта давно известны, на ещё два стоит взглянуть.
Обозначается сочетание из
по
так:
. В литературе они чаще обозначаются
(но мне больше нравится первый вариант, чтобы не путать с матрицами).
В комбинаторике известны несколько способов подсчёта:
Где
— эн факториал, произведение всех целых чисел от 1 до n (например:
), а
считается равным единице. Для вышесказанной задачи получается:
Или так:
Вторая формула сочетаний выводится очень просто. Есть понятие числа размещений из
по
, когда последовательность элементов имеет значение (то есть набор «первый со вторым с пятым» это не тоже самое, что «первый с пятым со вторым»), обозначается
.
Например все размещения из 3 по 2 выглядят так:
12 21
13 31
23 32
Первый элемент можно выбрать
способами, второй —
способами, последний —
способами. Поэтому число размещений из
по
равно
, всего
множителей.
Для подсчёта сочетаний получившиеся число нужно разделить на
, поскольку есть
способов разместить
элементов. В данном случае —
способа (первый со вторым и второй с первым — это одно и тоже сочетание).
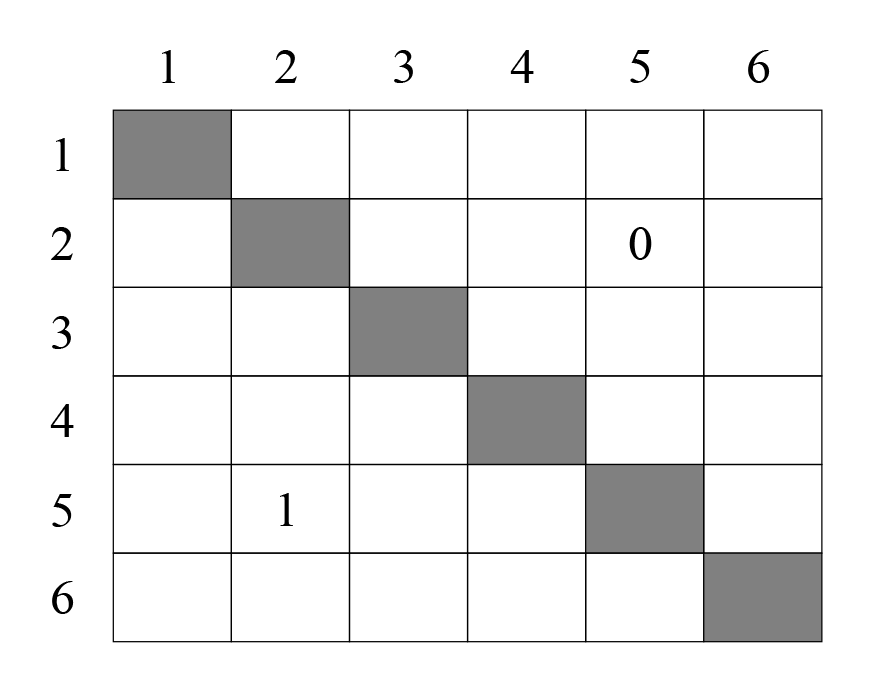
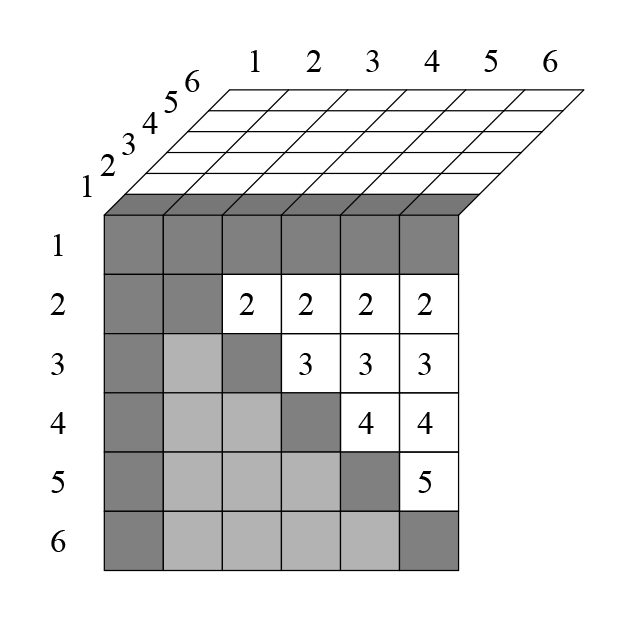
Вспомним, как идет счёт в шашках по круговой системе (когда все играют со всеми). Для этого пишут обычную таблицу:
По горизонтали и вертикали идут номера игроков. Диагональ можно закрасить — игрок не может играть сам с собой. Результат каждой партии записывают в таблицу два раза. Как сыграл второй с пятым и как сыграл пятый со вторым. Таким образом, количество партий в турнире — и есть число сочетаний по 2.
Число вычеркнутых клеток равно
, а число всех клеток — это
. Стало быть, число сочетаний по 2 можно посчитать так:
Когда я это заметил, не сразу увидел что это равно
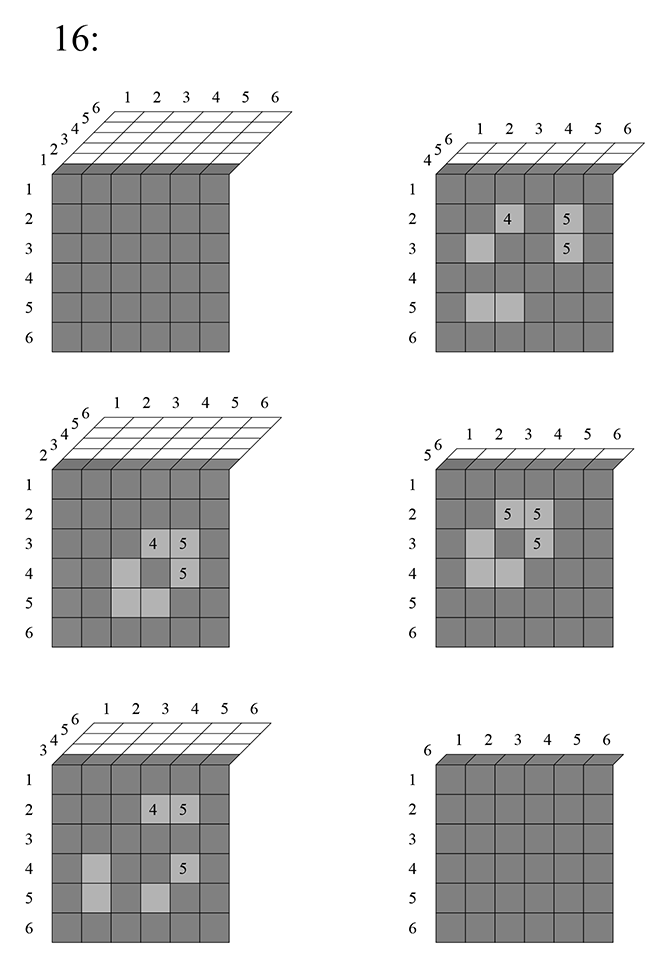
. Решил сделать также для
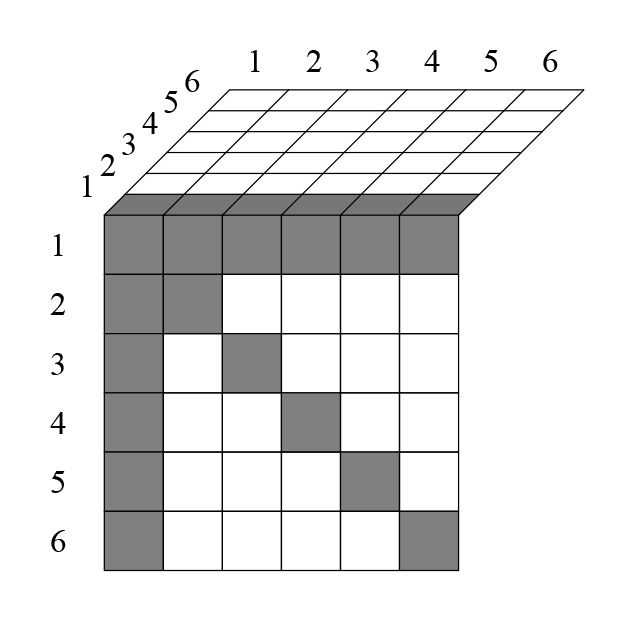
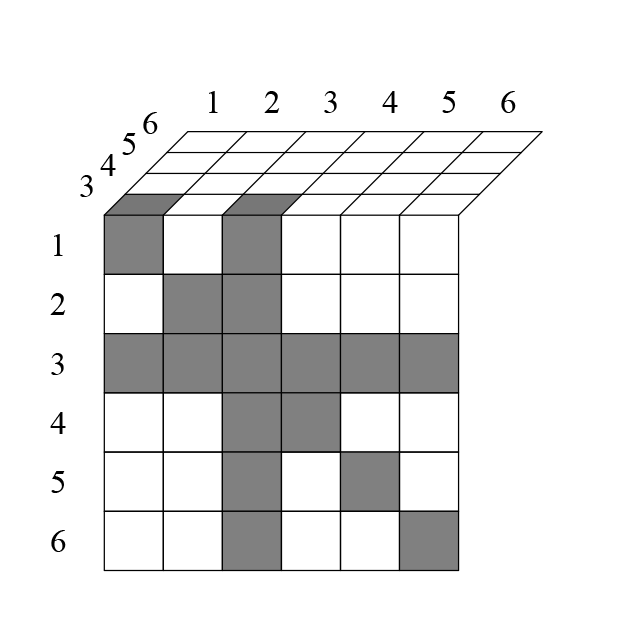
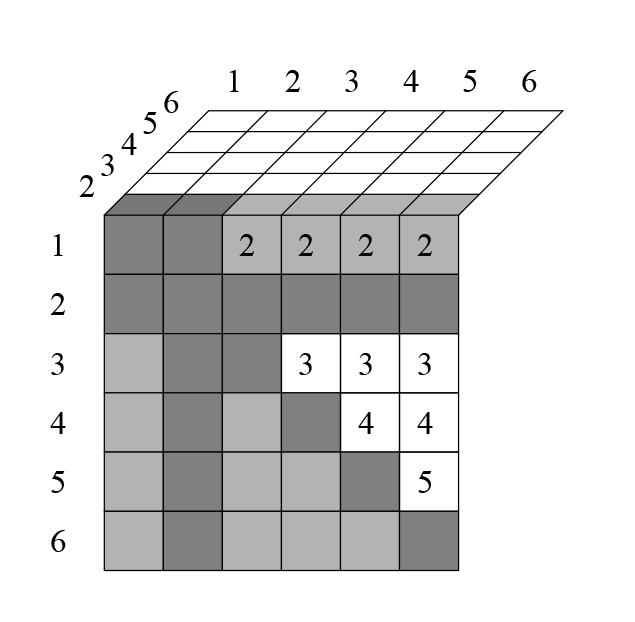
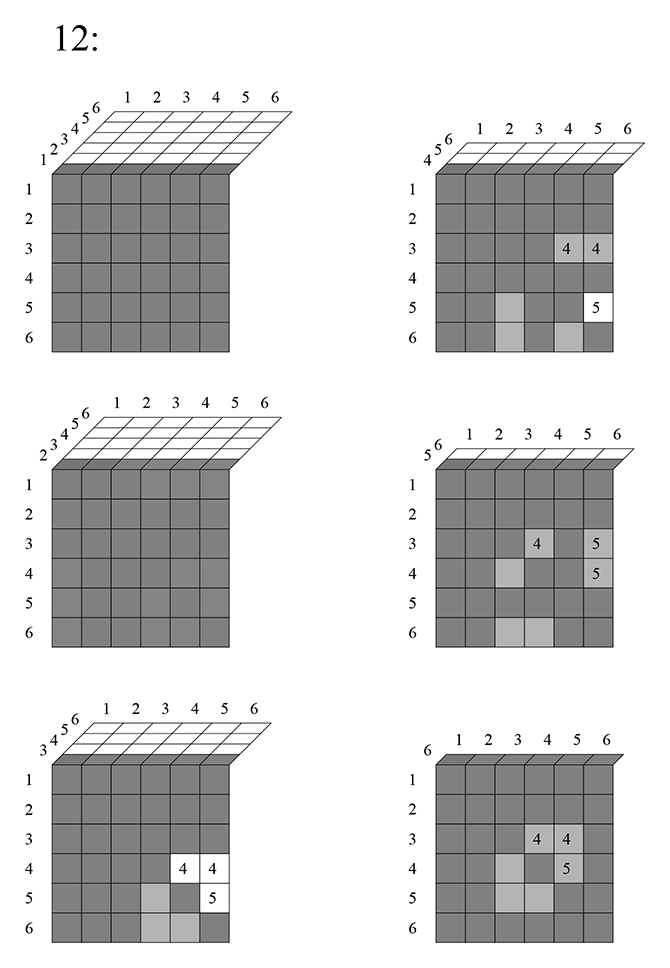
, с трёхмерной таблицей:
На каждом её слое, кроме диагонали исключаются еще клетки. Например, клетка 161 исключается, потому что единица повторилась два раза.
Всего на каждом слое исключается
клеток.
Итак, на каждом слое исключается
клетки. Всего
слоёв, поэтому общее число исключившихся ячеек:
А вся таблица —
. Значит, число сочетаний по 3 можно посчитать так:
Как уже сказано выше, это и есть общая формула, в которой просто раскрыли скобки:
И тут возник вопрос, можно ли посчитать сочетания, так же представив их через таблицы, не используя факториалы вообще? К слову, в комбинаторике уже известна рекуррентная формула для числа сочетаний:
(число сочетаний по 0 равно 1, из любого количества элементов можно получить только одну группу в которой 0 элементов). Итак, я попробовал посмотреть, какие еще клетки исключаются в трёхмерной таблице, когда мы делим число оставшихся клеток на
.
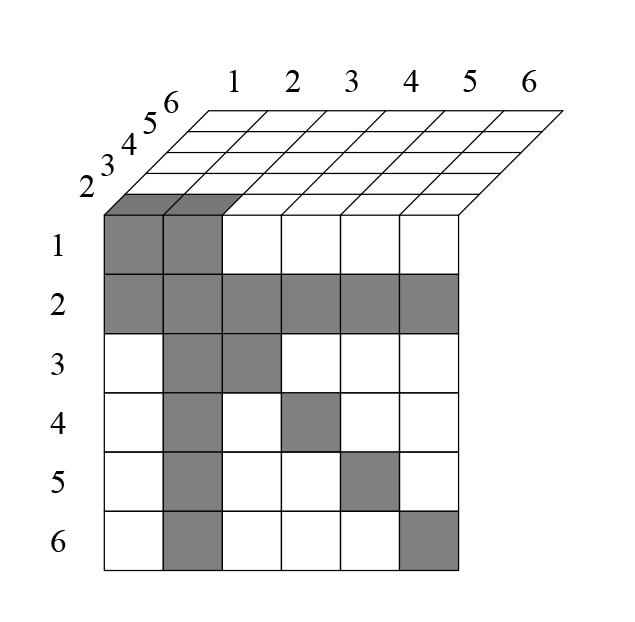
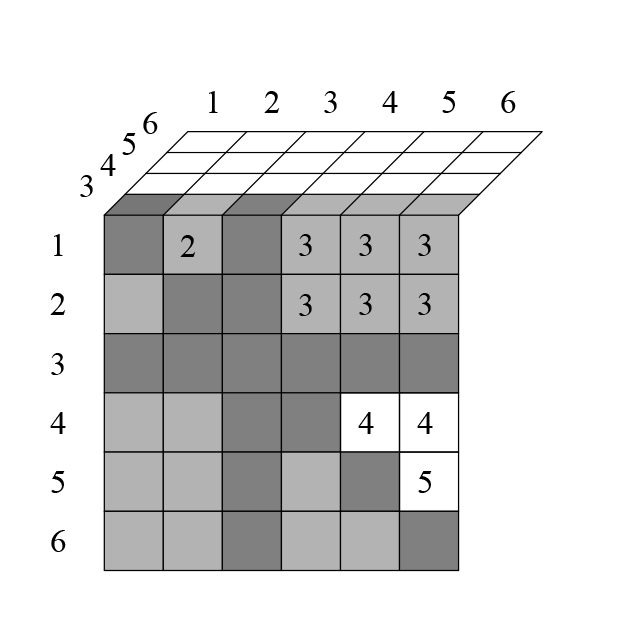
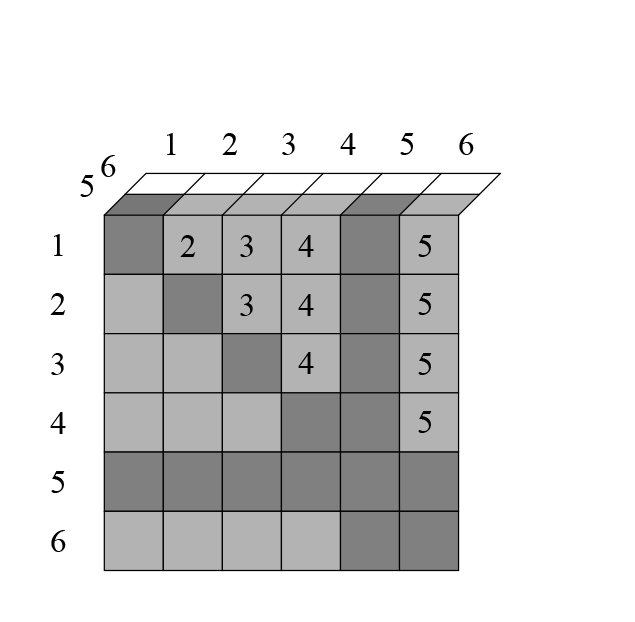
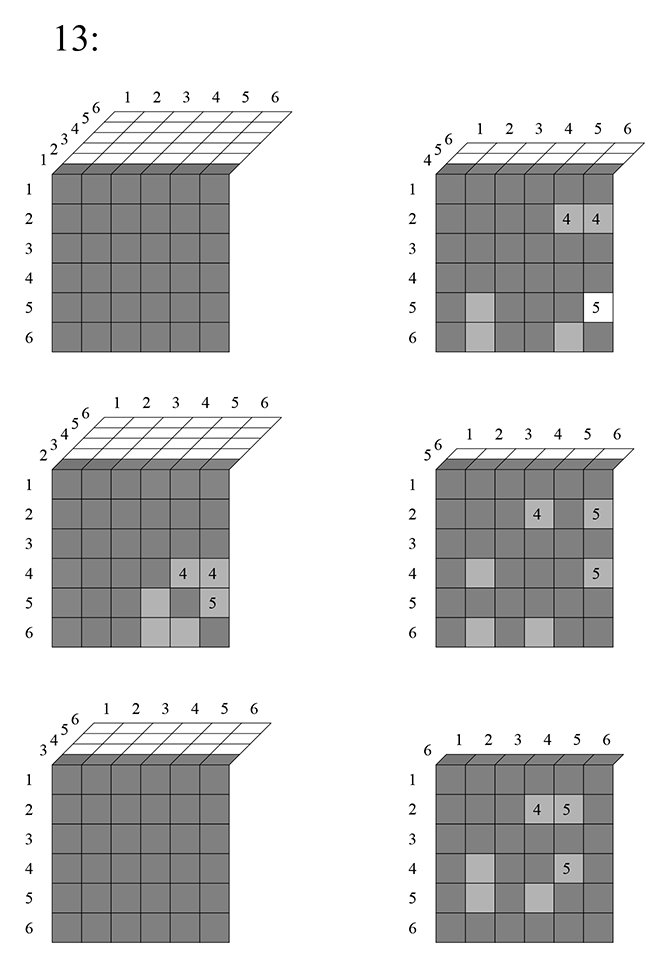
Клетки ниже диагонали дублируют клетки, которые выше диагонали — вычеркнем их (ячейка 431 — то же самое, что и 341). Для того, чтобы получить такое же количество клеток, просто поделим число размещений на 2. Цифрами в самой таблице я отметил, в какой строке встретилось данное сочетание. Например, сочетание 251 впервые встретилось здесь во второй строке, поэтому отмечено цифрой 2. Посмотрим на следующий слой:
Закрашенные клетки с цифрой означают, что данное сочетание уже встречалось. Например, комбинация 152 уже встречалась во второй строке (в виде 251), поэтому отмечена цифрой 2 в закрашенной клетке.
Итак, на втором слое исключается ещё
клетки (кроме тех, которые вычеркнуты из-за повторяющихся чисел в них, и тех, которые вычеркнуты ниже диагонали, из-за того что дублируют верхние). Перебрав так всю таблицу, я получил следующее. На третьем слое исключается ещё
клеток:
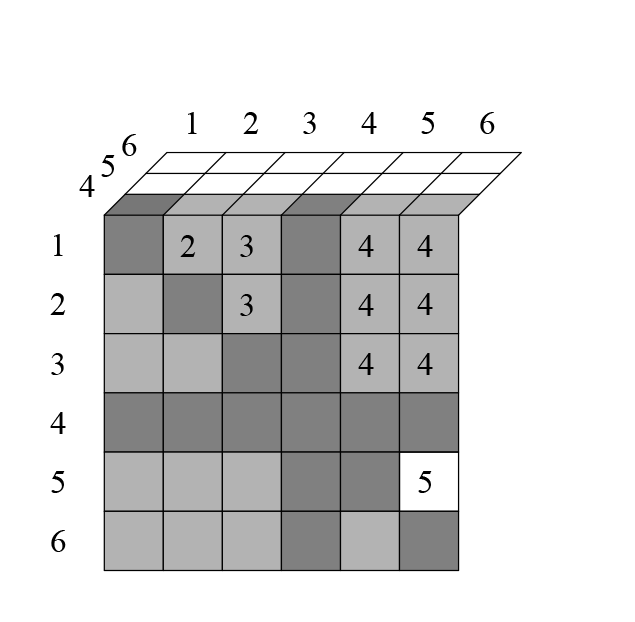
На четвертом слое вычеркивается ещё
клеток:
На пятом —
:
На шестом, по видимому,
:
Получается, что для подсчёта сочетаний по 3, из числа
нужно вычесть такую сумму:
Это можно переписать в таком виде:
Ещё можно переписать эту сумму так:
То есть:
Значит, число сочетаний по 3 можно вычислить так:
Например число сочетаний из 8 по 3:
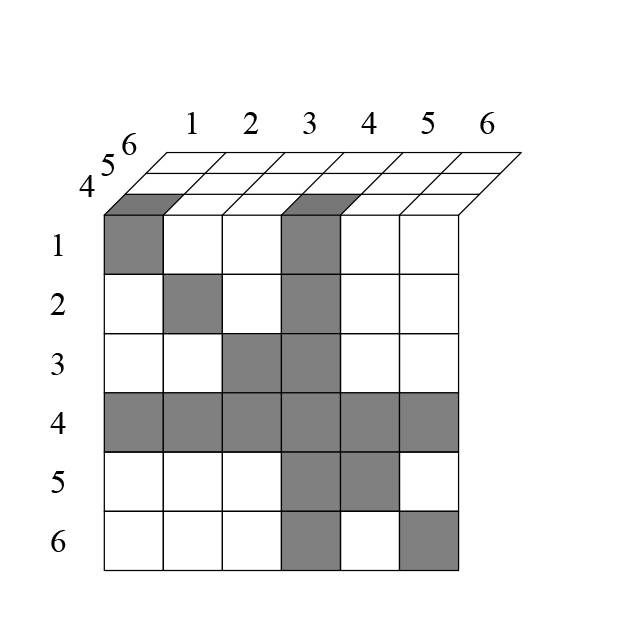
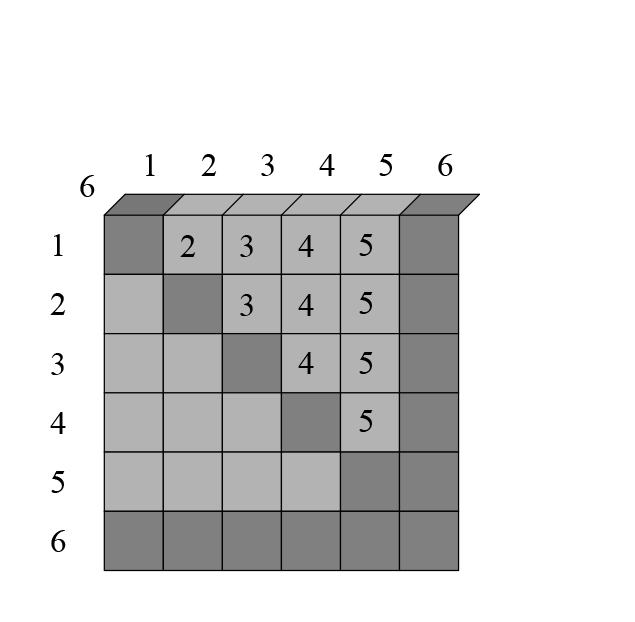
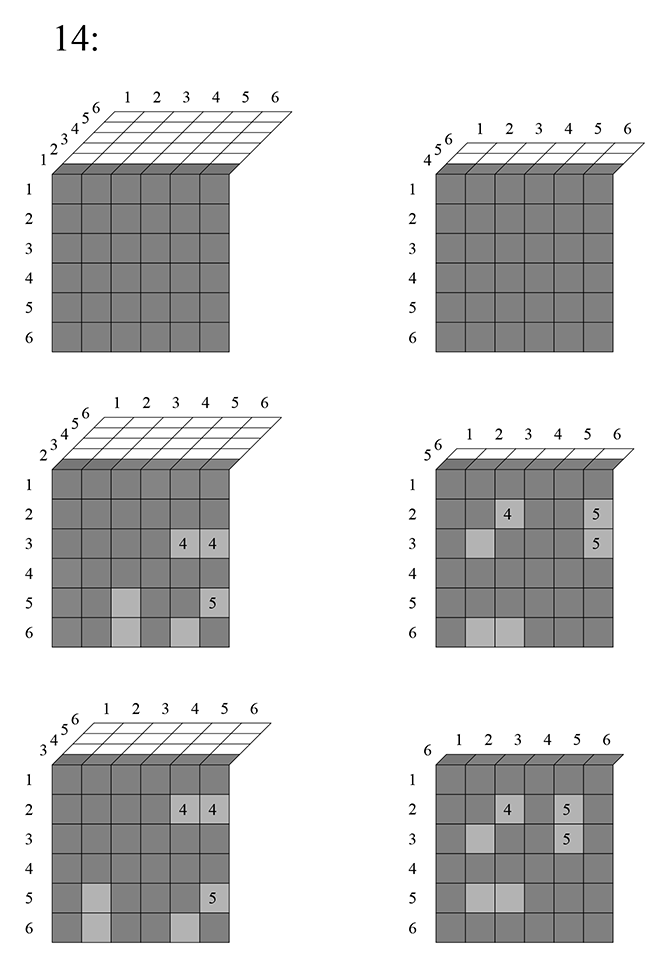
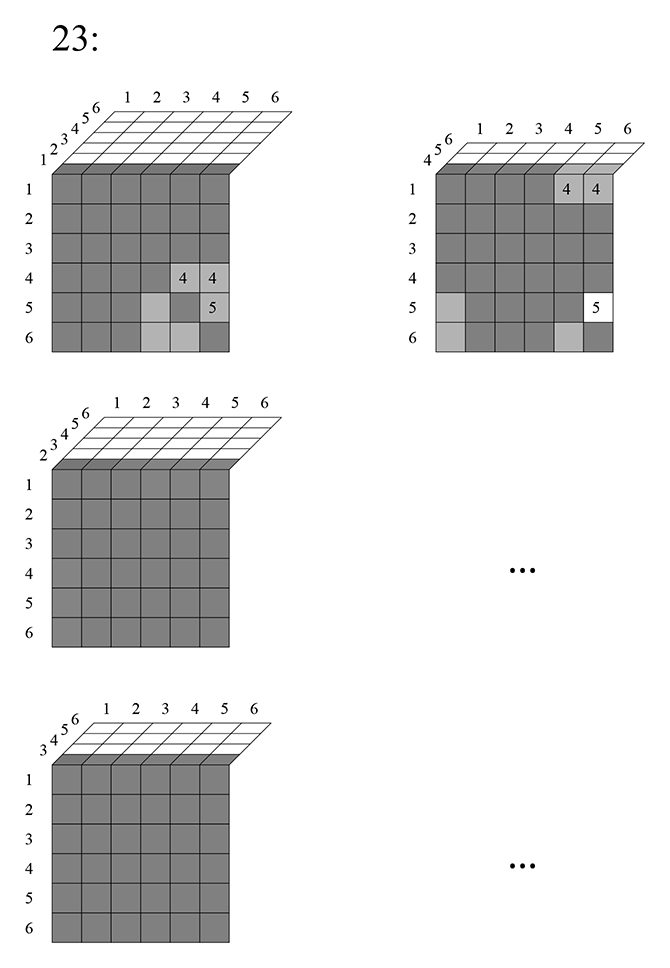
На этом этапе вряд ли видна какая-либо зависимость, посмотрим то же самое с четырёхмерной таблицей. Изобразить её можно в виде нескольких трёхмерных (у трёхмерной таблицы слои двухмерные, у четырёхмерной — трёхмерные). То есть, первый фрагмент четырёхмерной таблицы будет выглядеть так (первая ячейка будет иметь координаты 1111):
Весь первый двухмерный слой этого слоя исключается (на нем единица везде повторяется). В итоге на первом трёхмерном слое вычитается такая сумма:
Слагаемые в столбик записаны лишь для наглядности. Прочерком я отметил первый двухмерный слой, который итак исключился весь. Посмотрим следующий «слой» четырёхмерной таблицы:
Значит, на втором слое исключается такая сумма:
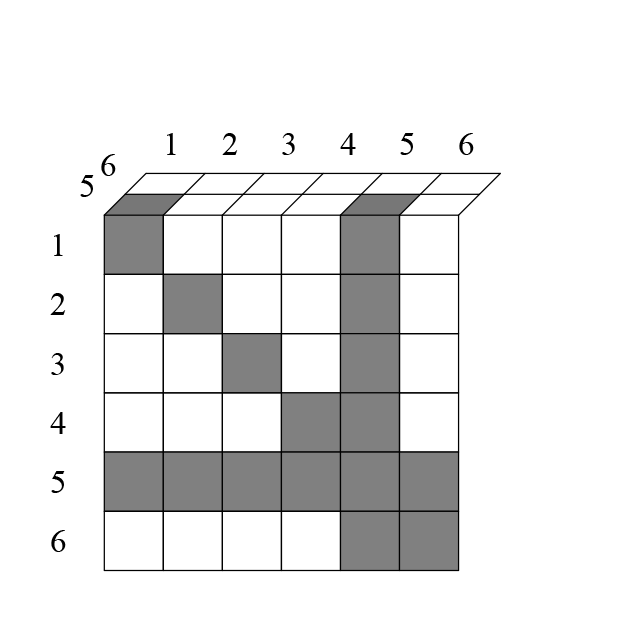
Посмотрим на третий:
На третьем исключается сумма:
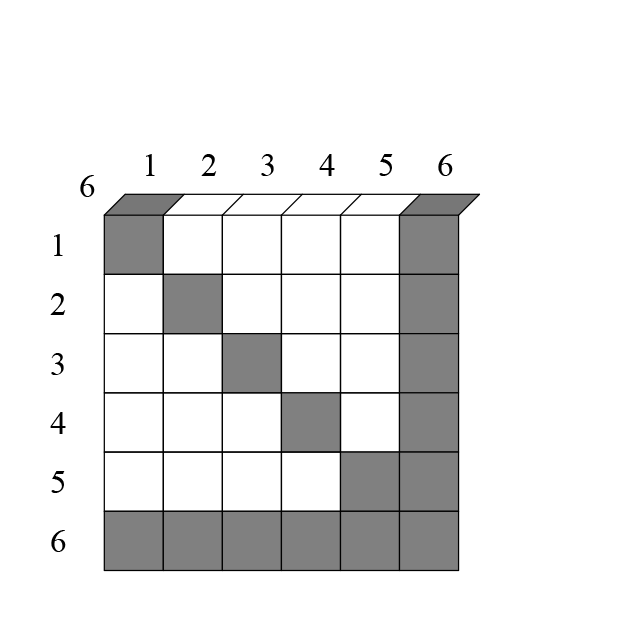
Уже здесь видно, что общая сумма, которая будет вычитаться будет такой:
её можно переписать в таком виде:
4(n-3)+3(n-4)+2(n-5)+1(n-n)+
5(n-3)+4(n-4)+3(n-5)+2(n-n)+
5(n-3)+5(n-4)+4(n-5)+3(n-n)+
5(n-3)+5(n-4)+5(n-5)+4(n-n)+
5(n-3)+5(n-4)+5(n-5)+5(n-n)+
5(n-3)+5(n-4)+5(n-5)+5(n-n)
Получаем:
Видно, что коэффициенты перед скобками уменьшаются на число, которое возрастает на единицу. Поэтому можем записать:
Однако, получившаяся формула будет работать только для
, ведь для других
коэффициенты будут другие. И, поскольку я не увидел зависимости от
и здесь, решил посмотреть тоже самое для
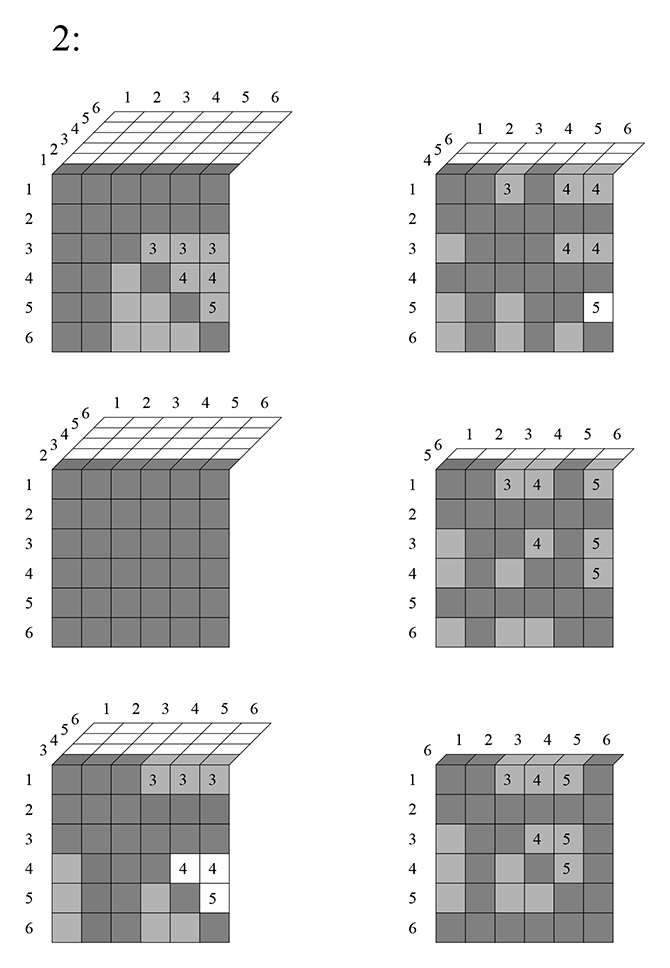
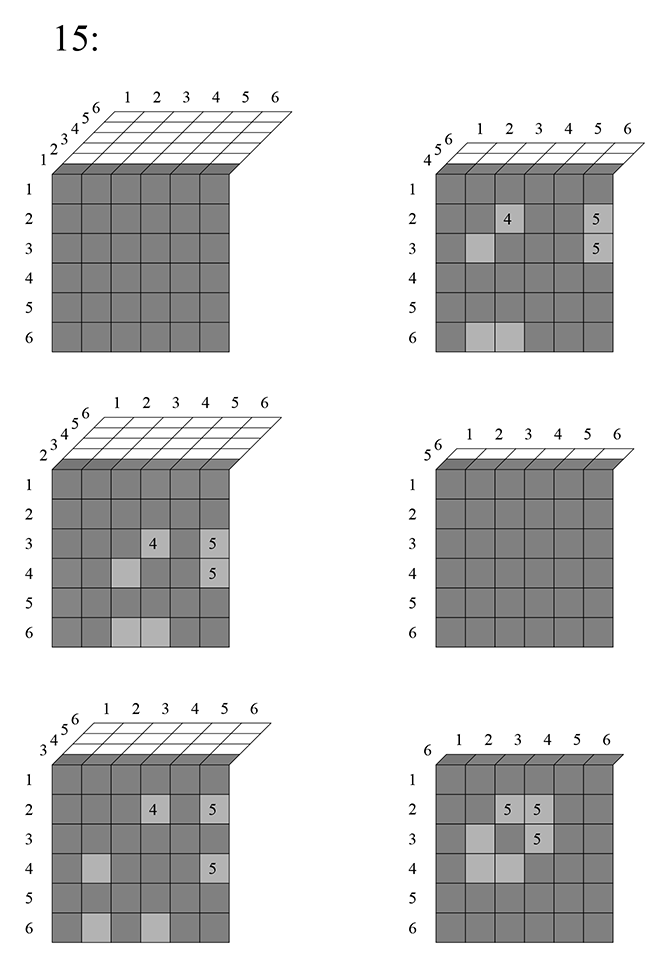
, через пятимерную таблицу, весь её первый трёхмерный «слой» исключается, поскольку единица здесь повторяется во всех ячейках:
Для наглядности запишем это так:
Смотрим дальше:
Тут, как видно, вычитается такая сумма:
Третий:
Тут вычитается:
Затем, шестой фрагмент:
На этом первый четырёхмерный слой заканчивается. Не сложно понять, что трёхмерный «слой» 21 будет дублировать слой 12, а слой 22 исключится весь, также как 11.
Перейдем к «слою» 23:
Здесь встретилось последнее сочетание из 6 по 5 — 56423 (клетки, которые встретились впервые отмечены белым, если кто забыл)). Напишем, какую в итоге надо вычесть сумму из
, чтобы получить число сочетаний из
по 5. На первом четырёхмерном слое исключилось:
На втором:
Получается что каждая сумма в скобке обозначает исключившиеся ячейки на трёхмерных слоях. Всего
четырёхмерных слоёв. Запишем это в виде суммы:
Получается, что последняя сумма суммирует исключившиеся ячейки на одномерных слоях, образуя исключения на двухмерных. Предпоследняя сумма складывает исключившиеся ячейки на двухмерных слоях, образуя исключившиеся ячейки на трёхмерных и т.д.
Индекс второй суммы берем до
, поскольку она «образует» исключения на четырёхмерных слоях, суммируя вычеркнутые ячейки на трёхмерных, как мы могли видеть выше, у пятимерной таблицы на каждом четырёхмерном слое исключается один трёхмерный, то есть для
, на каждом четырёхмерном остается пять трёхмерных слоёв,
.
Для
, шестимерную таблицу можно не смотреть, достаточно выписать индексы её последних трёх измерений:
111 121 131 141 151 161
112 122 132 142 152 162
113 123 133 143 153 163
114 124 134 144 154 164
115 125 135 145 155 165
116 126 136 146 156 166211 …
212 …
…
Опять же, вычеркнули мы те слои, где хоть одна цифра повторилась. Уже по первому пятимерному слою видно, что на пятимерных слоях для шестимерной таблицы останется на один четырёхмерный слой меньше. Количество оставшихся четырёхмерных слоёв равно
. А трёхмерных слоёв на каждом четырёхмерном остается все также
(по 4 в данном случае:
). Запись в виде сумм получилась такой:
Запись для
можно переписать так:
Для
получается:
Для
:
В общем виде запись для
получается такой (сумма, которую мы вычитаем вычисляется рекуррентно):
Второй способ
Как я уже писал выше, число сочетаний по 3 можно записать через одну сумму:
А число сочетаний из 6 по 4 можно записать так:
Оказывается, что 30 во вторых скобках, это
(логического обоснования этому я так и не смог найти).
Вторые скобки здесь представляют собой коэффициент, который умножается на
. Для
этот коэффициент просто уменьшается на 1 с каждым слагаемым первой суммы. Для
— число, на которое уменьшается этот коэффициент возрастает на 1. Затем я просто посчитал количество слагаемых
,
и
в сумме которая вычитается для
:
Число, на которое увеличивается число, на которое уменьшается коэффициент, возрастает на 1. Этот коэффициент можно записать через две суммы:
Зависимость ясна — для
эта формула будет выглядеть так:
А в общем виде (опять же, для
) получилось так:
Под конец скажу, что метод действительно получился неоптимальный, хотя мне и было интересно найти его. Фактически, деление на факториал здесь просто заменяется вычитанием, но думаю лишним не будет.
Комбинаторика в Excel
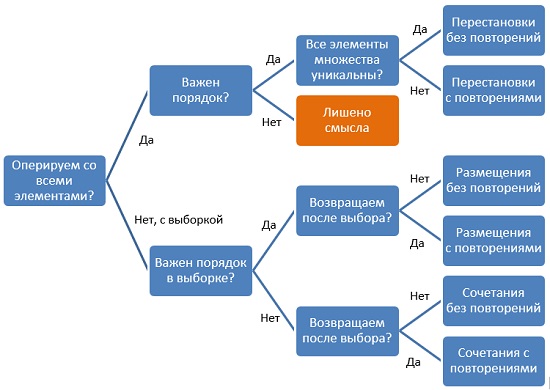
Комбинаторика — раздел математики, изучающий дискретные объекты, множества (сочетания, перестановки, размещения элементов) и отношения на них. Термин комбинаторика был введён в математический обиход Лейбницем, который в 1666 году опубликовал свой труд «Рассуждения о комбинаторном искусстве». Excel поддерживает ряд функций комбинаторики. Чтобы разобраться, какую формулу использовать, следует ответить на ряд вопросов:
- Исходное множество содержит только уникальные элементы, или некоторые из них могут повторяться?
- Операция выполняется со всеми элементами множества, или только с некоторой выборкой из них?
- Важен ли порядок элементов в выборке?
- После выбора элемента мы его возвращаем назад?
Рис. 1. Дерево решений, какую формулу комбинаторики использовать
Скачать заметку в формате Word или pdf, примеры в формате Excel
Перестановки без повторений
Возьмем несколько различных элементов (предметов) и будем переставлять их всевозможными способами, оставляя неизменным их число и меняя только их порядок (рис. 2). Каждая из получившихся таким образом комбинаций носит название перестановки. Перестановкой из n элементов называется упорядоченное множество, составленное из всех элементов множества.
Рис. 2. Перестановки (картинка взята здесь)
Если все n элементы разные, то число перестановок обозначается Pn от perturbation.
С другой стороны, произведение n первых натуральных чисел называется n-факториал и обозначается n!
Например
По определению: 1! = 1; 0! = 1.
Функция в Excel =ФАКТР(n). Факториал растет очень быстро. Существенно быстрее экспоненты (рис. 3).
Рис. 3. Расчет числа перестановок без повторений с помощью факториала
Перестановки с повторениями
Если в основном n множестве не все элементы разные, то число перестановок будет меньше n! Например, если наше множество состоит из трех яблок и одной груши, то всего возможно 4 перестановки (рис. 4). Груша может быть первой, второй, третьей или четвертой, а яблоки неразличимы).
Рис. 4. Перестановки с повторениями (картинка найдена здесь)
В общем случае, можно сказать: последовательность длины n, составленная из k разных символов, первый из которых повторяется n1 раз, второй – n2 раз, третий – n3 раз, …, k-й – nk раз (где n1 + n2 + … + nk = n) называется перестановкой с повторениями из n элементов.
Пример. Сколько различных пятибуквенных слов можно составить из букв слова «манна»?
Решение. Буквы а и н повторяются 2 раза, а буква м один раз.
Размещение без повторений
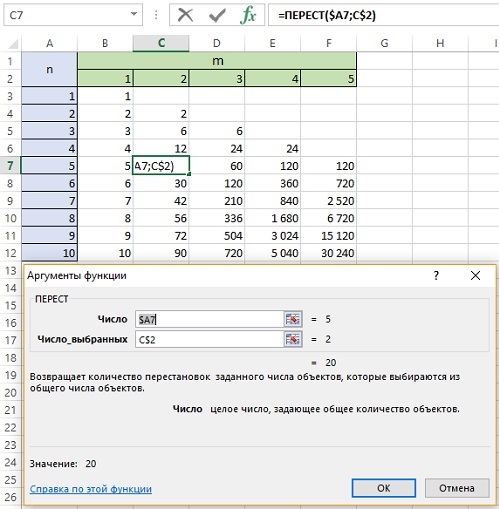
Размещением из n элементов по m называется упорядоченный набор из m различных элементов, выбранных из n-элементного множества (все элементы множества уникальны; позиции элементов в выборке важны). Число размещений обозначается от arrangement.
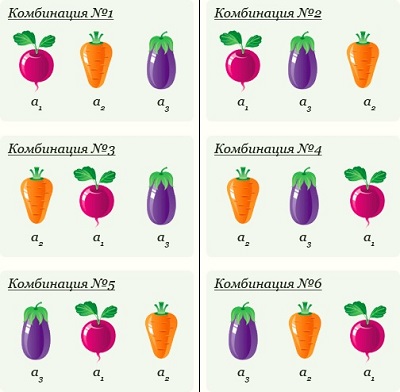
Например, два элемента из трех можно выбрать и расположить шестью способами (рис. 4):
Рис. 5. Размещение без повторений (картинка из презентации)
Если m = n количество элементов совпадает с количеством имеющихся мест для размещения. Знаменатель в формуле (4) превращается в 0! = 1. Остается только числитель n! А это – изученная выше перестановка без повторений; см. формулу (1).
Название функции в Excel несколько обескураживает. Но… что поделаешь: =ПЕРЕСТ(n;m)
Рис. 6. Размещение без повторений; обратите внимание на смешанные ссылки, которые позволяют протянуть формулу на всю таблицу
Размещение с повторениями
Размещение с повторениями по смыслу отличается от перестановок с повторением. Перестановки с повторением – это операция над множеством, которое состоит из нескольких видов элементов, так что каждый вид представлен несколькими одинаковыми элементами. Размещение с повторениями – выборки из множества с возвращением выбранного элемента назад перед каждым новым выбором.
Например, если у вас множество, включающее грушу, яблоко и лимон, и вам нужно выбрать два элемента, так что после первого выбора вы возвращаете выбранный предмет назад, то существует девять различных комбинаций (рис. 7).
Рис. 7. Размещение с повторениями
В общем случае размещение с повторениями или выборка с возвращением – это размещение «предметов» в предположении, что каждый «предмет» может участвовать в размещении несколько раз. По правилу умножения количество размещений с повторениями из n по k:
В Excel используется функция ПЕРЕСТА(n;k).
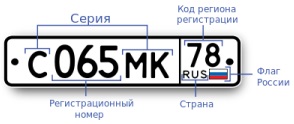
Задача. Сколько различных номеров можно составить в одном коде региона?
Подсказка. В номере используется 12 букв алфавита, также существующих и в латинском алфавите (А, В, Е, К, М, Н, О, Р, С, Т, У, Х).
Рис. 8. Номер автомобиля
Решение. Можно воспользоваться формулой для размещения с повторениями:
Каждую цифру можно выбрать 10 способами, а всего цифр 3, при этом они могут повторяться, и их порядок важен. Каждую букву можно выбрать 12 способами, при этом буквы могут повторяться, и их порядок важен.
Сочетания без повторений
Сочетаниями из n множества по m элементов называются комбинации, составленные из данных n элементов по m элементов, которые различаются хотя бы одним элементом (в сочетаниях не учитывается порядок элементов).
Например, два элемента из 4 сочетаются 6 способами (порядок следования не важен):
Рис. 9. Сочетания без повторений из 4 по 2
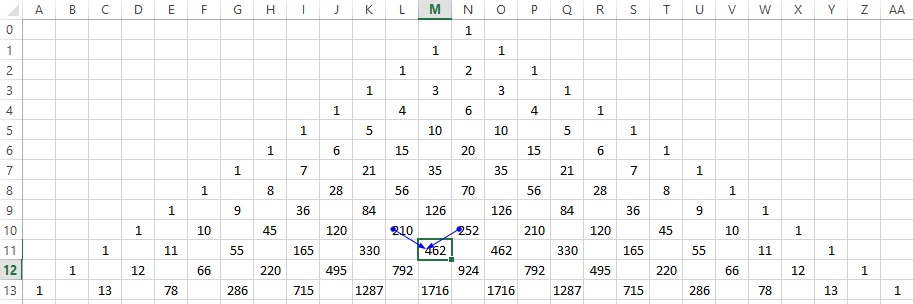
Сочетания без повторений образуют знаменитый треугольник Паскаля (рис. 10). В этом треугольнике на вершине и по бокам стоят единицы. Каждое число равно сумме двух расположенных над ним чисел. Строки треугольника симметричны относительно вертикальной оси. Числа в строках, составляющие треугольник Паскаля, являются сочетаниями
где n – номер строки, m – номер элемента в строке, начиная с нулевого. Например, в строке 7:
Рис. 10. Треугольник Паскаля; чтобы увеличить изображение кликните на нем правой кнопкой мыши и выберите Открыть картинку в новой вкладке
В Excel используется функция =ЧИСЛКОМБ(n;m).
Сочетания с повторениями
Сочетания с повторениями по смыслу похожи на размещение с повторениями – это выборки из множества с возвращением выбранного элемента назад перед каждым новым выбором. При этом порядок в выборке не важен.
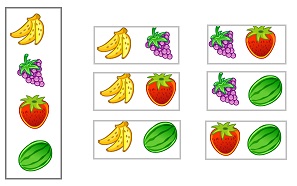
Например, два предмета из четырех можно выбрать 10 способами, если после каждого выбора предмет возвращается назад (рис. 11).
Рис. 11. Сочетания с повторениями
В общем случае, число сочетаний с повторениями:
Для нашего примера с фруктами
В Excel для подсчета числа сочетаний с повторениями используется функция =ЧИСЛКОМБА(n;m). В нашем примере =ЧИСЛКОМБА(4;2) = 10.
Добавил:
Upload
Опубликованный материал нарушает ваши авторские права? Сообщите нам.
Вуз:
Предмет:
Файл:
СДЭ.docx
Скачиваний:
0
Добавлен:
23.11.2019
Размер:
207.16 Кб
Скачать
-
Составление таблицы всех разрешенных комбинаций
Таблица разрешенных
комбинаций составляется путем сложения
двух, трех, четырех, пяти, шести и семи
строк образующей матрицы.
Код (15,7) имеет 27
= 128 разрешенных комбинаций.
Первая разрешенная комбинация
состоит из пятнадцати нулей (в таблице
она не указана).
W – вес кодовой комбинации,
указывает на количество единиц в данной
кодовой комбинации.
|
Число вариантов |
№ п/п |
№ строки |
Информационные |
Избыточные |
W |
|||||||||||||
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
15 |
||||
|
|
1 |
1 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
1 |
1 |
0 |
1 |
0 |
0 |
0 |
5 |
|
2 |
2 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
1 |
1 |
0 |
1 |
0 |
0 |
5 |
|
|
3 |
3 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
1 |
1 |
0 |
1 |
0 |
5 |
|
|
4 |
4 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
1 |
1 |
0 |
1 |
5 |
|
|
5 |
5 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
1 |
1 |
1 |
0 |
0 |
1 |
1 |
0 |
6 |
|
|
6 |
6 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
1 |
1 |
1 |
0 |
0 |
1 |
1 |
6 |
|
|
7 |
7 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
1 |
1 |
0 |
1 |
0 |
0 |
0 |
1 |
5 |
|
|
|
8 |
1+2 |
1 |
1 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
1 |
1 |
1 |
0 |
0 |
6 |
|
9 |
1+3 |
1 |
0 |
1 |
0 |
0 |
0 |
0 |
1 |
1 |
0 |
1 |
0 |
0 |
1 |
0 |
6 |
|
|
10 |
1+4 |
1 |
0 |
0 |
1 |
0 |
0 |
0 |
1 |
1 |
1 |
1 |
0 |
1 |
0 |
1 |
8 |
|
|
11 |
1+5 |
1 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
1 |
1 |
0 |
5 |
|
|
12 |
1+6 |
1 |
0 |
0 |
0 |
0 |
1 |
0 |
1 |
0 |
0 |
1 |
1 |
0 |
1 |
1 |
7 |
|
|
13 |
1+7 |
1 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
1 |
1 |
1 |
0 |
0 |
1 |
6 |
|
|
14 |
2+3 |
0 |
1 |
1 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
1 |
1 |
1 |
0 |
6 |
|
|
15 |
2+4 |
0 |
1 |
0 |
1 |
0 |
0 |
0 |
0 |
1 |
1 |
0 |
1 |
0 |
0 |
1 |
6 |
|
|
16 |
2+5 |
0 |
1 |
0 |
0 |
1 |
0 |
0 |
1 |
0 |
0 |
1 |
0 |
0 |
1 |
0 |
5 |
|
|
17 |
2+6 |
0 |
1 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
1 |
1 |
5 |
|
|
18 |
2+7 |
0 |
1 |
0 |
0 |
0 |
0 |
1 |
1 |
0 |
1 |
0 |
0 |
1 |
0 |
1 |
6 |
|
|
19 |
3+4 |
0 |
0 |
1 |
1 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
1 |
1 |
1 |
6 |
|
|
20 |
3+5 |
0 |
0 |
1 |
0 |
1 |
0 |
0 |
1 |
1 |
0 |
1 |
1 |
1 |
0 |
0 |
7 |
|
|
21 |
3+6 |
0 |
0 |
1 |
0 |
0 |
1 |
0 |
0 |
1 |
0 |
0 |
1 |
0 |
0 |
1 |
5 |
|
|
22 |
3+7 |
0 |
0 |
1 |
0 |
0 |
0 |
1 |
1 |
1 |
1 |
0 |
1 |
0 |
1 |
1 |
8 |
|
|
23 |
4+5 |
0 |
0 |
0 |
1 |
1 |
0 |
0 |
1 |
1 |
1 |
1 |
1 |
0 |
1 |
1 |
9 |
|
|
24 |
4+6 |
0 |
0 |
0 |
1 |
0 |
1 |
0 |
0 |
1 |
1 |
0 |
1 |
1 |
1 |
0 |
7 |
|
|
25 |
4+7 |
0 |
0 |
0 |
1 |
0 |
0 |
1 |
1 |
1 |
0 |
0 |
1 |
1 |
0 |
0 |
6 |
|
|
26 |
5+6 |
0 |
0 |
0 |
0 |
1 |
1 |
0 |
1 |
0 |
0 |
1 |
0 |
1 |
0 |
1 |
6 |
|
|
27 |
5+7 |
0 |
0 |
0 |
0 |
1 |
0 |
1 |
0 |
0 |
1 |
1 |
0 |
1 |
1 |
1 |
7 |
|
|
28 |
6+7 |
0 |
0 |
0 |
0 |
0 |
1 |
1 |
1 |
0 |
1 |
0 |
0 |
0 |
1 |
0 |
5 |
|
|
|
29 |
1+2+3 |
1 |
1 |
1 |
0 |
0 |
0 |
0 |
1 |
0 |
1 |
0 |
0 |
1 |
1 |
0 |
7 |
|
30 |
1+2+4 |
1 |
1 |
0 |
1 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
5 |
|
|
31 |
1+2+5 |
1 |
1 |
0 |
0 |
1 |
0 |
0 |
0 |
1 |
1 |
1 |
1 |
0 |
1 |
0 |
8 |
|
|
32 |
1+2+6 |
1 |
1 |
0 |
0 |
0 |
1 |
0 |
1 |
1 |
1 |
0 |
1 |
1 |
1 |
1 |
10 |
|
|
33 |
1+2+7 |
1 |
1 |
0 |
0 |
0 |
0 |
1 |
0 |
1 |
0 |
0 |
1 |
1 |
0 |
1 |
7 |
|
|
34 |
1+3+4 |
1 |
0 |
1 |
1 |
0 |
0 |
0 |
1 |
1 |
0 |
0 |
1 |
1 |
1 |
1 |
9 |
|
|
35 |
1+3+5 |
1 |
0 |
1 |
0 |
1 |
0 |
0 |
0 |
0 |
1 |
1 |
0 |
1 |
0 |
0 |
6 |
|
|
36 |
1+3+6 |
1 |
0 |
1 |
0 |
0 |
1 |
0 |
1 |
0 |
1 |
0 |
0 |
0 |
0 |
1 |
6 |
|
|
37 |
1+3+7 |
1 |
0 |
1 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
1 |
5 |
|
|
38 |
1+4+5 |
1 |
0 |
0 |
1 |
1 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
1 |
1 |
6 |
|
|
39 |
1+4+6 |
1 |
0 |
0 |
1 |
0 |
1 |
0 |
1 |
0 |
0 |
0 |
0 |
1 |
1 |
0 |
6 |
|
|
40 |
1+4+7 |
1 |
0 |
0 |
1 |
0 |
0 |
1 |
0 |
0 |
1 |
0 |
0 |
1 |
0 |
0 |
5 |
|
|
41 |
1+5+6 |
1 |
0 |
0 |
0 |
1 |
1 |
0 |
0 |
1 |
1 |
1 |
1 |
1 |
0 |
1 |
9 |
|
|
42 |
1+5+7 |
1 |
0 |
0 |
0 |
1 |
0 |
1 |
1 |
1 |
0 |
1 |
1 |
1 |
1 |
1 |
10 |
|
|
43 |
1+6+7 |
1 |
0 |
0 |
0 |
0 |
1 |
1 |
0 |
1 |
0 |
0 |
1 |
0 |
1 |
0 |
6 |
|
|
44 |
2+3+4 |
0 |
1 |
1 |
1 |
0 |
0 |
0 |
0 |
1 |
0 |
1 |
0 |
0 |
1 |
1 |
7 |
|
|
45 |
2+3+5 |
0 |
1 |
1 |
0 |
1 |
0 |
0 |
1 |
0 |
1 |
0 |
1 |
0 |
0 |
0 |
6 |
|
|
46 |
2+3+6 |
0 |
1 |
1 |
0 |
0 |
1 |
0 |
0 |
0 |
1 |
1 |
1 |
1 |
0 |
1 |
8 |
|
|
47 |
2+3+7 |
0 |
1 |
1 |
0 |
0 |
0 |
1 |
1 |
0 |
0 |
1 |
1 |
1 |
1 |
1 |
9 |
|
|
48 |
2+4+5 |
0 |
1 |
0 |
1 |
1 |
0 |
0 |
1 |
0 |
0 |
0 |
1 |
1 |
1 |
1 |
8 |
|
|
49 |
2+4+6 |
0 |
1 |
0 |
1 |
0 |
1 |
0 |
0 |
0 |
0 |
1 |
1 |
0 |
1 |
0 |
6 |
|
|
50 |
2+4+7 |
0 |
1 |
0 |
1 |
0 |
0 |
1 |
1 |
0 |
1 |
1 |
1 |
0 |
0 |
0 |
7 |
|
|
51 |
2+5+6 |
0 |
1 |
0 |
0 |
1 |
1 |
0 |
1 |
0 |
0 |
0 |
1 |
1 |
1 |
1 |
8 |
|
|
52 |
2+5+7 |
0 |
1 |
0 |
0 |
1 |
0 |
1 |
1 |
1 |
1 |
0 |
0 |
0 |
0 |
1 |
7 |
|
|
53 |
2+6+7 |
0 |
1 |
0 |
0 |
0 |
1 |
1 |
1 |
1 |
0 |
1 |
0 |
1 |
1 |
0 |
8 |
|
|
54 |
3+4+5 |
0 |
0 |
1 |
1 |
1 |
0 |
0 |
1 |
1 |
0 |
0 |
0 |
0 |
0 |
1 |
6 |
|
|
55 |
3+4+6 |
0 |
0 |
1 |
1 |
0 |
1 |
0 |
0 |
1 |
0 |
1 |
0 |
1 |
0 |
0 |
6 |
|
|
56 |
3+4+7 |
0 |
0 |
1 |
1 |
0 |
0 |
1 |
1 |
1 |
1 |
1 |
0 |
1 |
1 |
0 |
9 |
|
|
57 |
3+5+6 |
0 |
0 |
1 |
0 |
1 |
1 |
0 |
0 |
0 |
0 |
0 |
1 |
1 |
0 |
1 |
6 |
|
|
58 |
3+5+7 |
0 |
0 |
1 |
0 |
1 |
0 |
1 |
1 |
0 |
1 |
0 |
1 |
1 |
1 |
1 |
9 |
|
|
59 |
3+6+7 |
0 |
0 |
1 |
0 |
0 |
1 |
1 |
0 |
0 |
1 |
1 |
1 |
0 |
1 |
0 |
7 |
|
|
60 |
4+5+6 |
0 |
0 |
0 |
1 |
1 |
1 |
0 |
1 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
5 |
|
|
61 |
4+5+7 |
0 |
0 |
0 |
1 |
1 |
0 |
1 |
0 |
0 |
1 |
0 |
1 |
0 |
1 |
0 |
6 |
|
|
62 |
4+6+7 |
0 |
0 |
0 |
1 |
0 |
1 |
1 |
0 |
0 |
0 |
1 |
1 |
1 |
0 |
1 |
7 |
|
|
63 |
5+6+7 |
0 |
0 |
0 |
0 |
1 |
1 |
1 |
1 |
1 |
1 |
0 |
0 |
1 |
1 |
0 |
8 |
|
|
|
64 |
1+2+3+4 |
1 |
1 |
1 |
1 |
0 |
0 |
0 |
1 |
0 |
1 |
1 |
1 |
0 |
1 |
1 |
9 |
|
65 |
1+2+3+5 |
1 |
1 |
1 |
0 |
1 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
5 |
|
|
66 |
1+2+3+6 |
1 |
1 |
1 |
0 |
0 |
1 |
0 |
1 |
1 |
0 |
1 |
0 |
1 |
0 |
1 |
9 |
|
|
67 |
1+2+3+7 |
1 |
1 |
1 |
0 |
0 |
0 |
1 |
0 |
1 |
1 |
1 |
0 |
1 |
1 |
1 |
10 |
|
|
68 |
1+2+4+5 |
1 |
1 |
0 |
1 |
1 |
0 |
0 |
0 |
1 |
1 |
0 |
0 |
1 |
1 |
1 |
9 |
|
|
69 |
1+2+4+6 |
1 |
1 |
0 |
1 |
0 |
1 |
0 |
1 |
1 |
1 |
1 |
0 |
0 |
1 |
0 |
9 |
|
|
70 |
1+2+4+7 |
1 |
1 |
0 |
1 |
0 |
0 |
1 |
0 |
1 |
0 |
1 |
0 |
0 |
0 |
0 |
6 |
|
|
71 |
1+2+5+6 |
1 |
1 |
0 |
0 |
1 |
1 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
1 |
6 |
|
|
72 |
1+2+5+7 |
1 |
1 |
0 |
0 |
1 |
0 |
1 |
1 |
0 |
1 |
0 |
1 |
0 |
1 |
1 |
9 |
|
|
73 |
1+2+6+7 |
1 |
1 |
0 |
0 |
0 |
1 |
1 |
0 |
0 |
1 |
1 |
1 |
1 |
1 |
0 |
9 |
|
|
74 |
1+3+4+5 |
1 |
0 |
1 |
1 |
1 |
0 |
0 |
0 |
0 |
1 |
0 |
1 |
0 |
0 |
1 |
7 |
|
|
75 |
1+3+4+6 |
1 |
0 |
1 |
1 |
0 |
1 |
0 |
1 |
0 |
1 |
1 |
1 |
1 |
0 |
0 |
9 |
|
|
76 |
1+3+4+7 |
1 |
0 |
1 |
1 |
0 |
0 |
1 |
0 |
0 |
0 |
1 |
1 |
1 |
1 |
0 |
8 |
|
|
77 |
1+3+5+6 |
1 |
0 |
1 |
0 |
1 |
1 |
0 |
0 |
1 |
0 |
0 |
0 |
1 |
1 |
1 |
8 |
|
|
78 |
1+3+5+7 |
1 |
0 |
1 |
0 |
1 |
0 |
1 |
1 |
1 |
1 |
0 |
0 |
1 |
0 |
1 |
9 |
|
|
79 |
1+3+6+7 |
1 |
0 |
1 |
0 |
0 |
1 |
1 |
0 |
1 |
1 |
1 |
0 |
0 |
0 |
0 |
7 |
|
|
80 |
1+4+5+6 |
1 |
0 |
0 |
1 |
1 |
1 |
0 |
0 |
1 |
1 |
0 |
0 |
0 |
0 |
0 |
6 |
|
|
81 |
1+4+5+7 |
1 |
0 |
0 |
1 |
1 |
0 |
1 |
1 |
1 |
0 |
0 |
0 |
0 |
1 |
0 |
7 |
|
|
82 |
1+4+6+7 |
1 |
0 |
0 |
1 |
0 |
1 |
1 |
0 |
1 |
0 |
1 |
0 |
1 |
1 |
1 |
9 |
|
|
83 |
1+5+6+7 |
1 |
0 |
0 |
0 |
1 |
1 |
1 |
1 |
0 |
1 |
0 |
1 |
1 |
0 |
0 |
8 |
|
|
84 |
2+3+4+5 |
0 |
1 |
1 |
1 |
1 |
0 |
0 |
1 |
0 |
1 |
1 |
0 |
1 |
0 |
1 |
9 |
|
|
85 |
2+3+4+6 |
0 |
1 |
1 |
1 |
0 |
1 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
5 |
|
|
86 |
2+3+4+7 |
0 |
1 |
1 |
1 |
0 |
0 |
1 |
1 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
6 |
|
|
87 |
2+3+5+6 |
0 |
1 |
1 |
0 |
1 |
1 |
0 |
1 |
1 |
0 |
1 |
1 |
0 |
1 |
1 |
10 |
|
|
88 |
2+3+5+7 |
0 |
1 |
1 |
0 |
1 |
0 |
1 |
0 |
1 |
1 |
1 |
1 |
0 |
0 |
1 |
9 |
|
|
89 |
2+3+6+7 |
0 |
1 |
1 |
0 |
0 |
1 |
1 |
1 |
1 |
1 |
0 |
1 |
1 |
0 |
0 |
9 |
|
|
90 |
2+4+5+6 |
0 |
1 |
0 |
1 |
1 |
1 |
0 |
1 |
1 |
1 |
1 |
1 |
1 |
0 |
0 |
10 |
|
|
91 |
2+4+5+7 |
0 |
1 |
0 |
1 |
1 |
0 |
1 |
0 |
1 |
0 |
1 |
1 |
1 |
1 |
0 |
9 |
|
|
92 |
2+4+6+7 |
0 |
1 |
0 |
1 |
0 |
1 |
1 |
1 |
1 |
0 |
0 |
1 |
0 |
1 |
1 |
9 |
|
|
93 |
2+5+6+7 |
0 |
1 |
0 |
0 |
1 |
1 |
1 |
0 |
0 |
1 |
1 |
0 |
0 |
0 |
0 |
6 |
|
|
94 |
3+4+5+6 |
0 |
0 |
1 |
1 |
1 |
1 |
0 |
1 |
0 |
1 |
1 |
0 |
0 |
1 |
0 |
8 |
|
|
95 |
3+4+5+7 |
0 |
0 |
1 |
1 |
1 |
0 |
1 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
5 |
|
|
96 |
3+4+6+7 |
0 |
0 |
1 |
1 |
0 |
1 |
1 |
1 |
0 |
0 |
0 |
0 |
1 |
0 |
1 |
7 |
|
|
97 |
3+5+6+7 |
0 |
0 |
1 |
0 |
1 |
1 |
1 |
0 |
1 |
1 |
1 |
1 |
1 |
1 |
0 |
10 |
|
|
98 |
4+5+6+7 |
0 |
0 |
0 |
1 |
1 |
1 |
1 |
0 |
1 |
0 |
1 |
1 |
0 |
0 |
1 |
8 |
|
|
|
99 |
1+2+3+4+5 |
1 |
1 |
1 |
1 |
1 |
0 |
0 |
0 |
1 |
0 |
1 |
1 |
1 |
0 |
1 |
10 |
|
100 |
1+2+3+4+6 |
1 |
1 |
1 |
1 |
0 |
1 |
0 |
1 |
1 |
0 |
0 |
1 |
0 |
0 |
0 |
8 |
|
|
101 |
1+2+3+4+7 |
1 |
1 |
1 |
1 |
0 |
0 |
1 |
0 |
1 |
1 |
0 |
1 |
0 |
1 |
0 |
9 |
|
|
102 |
1+2+3+5+6 |
1 |
1 |
1 |
0 |
1 |
1 |
0 |
0 |
0 |
1 |
1 |
0 |
0 |
1 |
1 |
9 |
|
|
103 |
1+2+3+5+7 |
1 |
1 |
1 |
0 |
1 |
0 |
1 |
1 |
0 |
0 |
1 |
0 |
0 |
0 |
1 |
8 |
|
|
104 |
1+2+3+6+7 |
1 |
1 |
1 |
0 |
0 |
1 |
1 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
6 |
|
|
105 |
1+2+4+5+6 |
1 |
1 |
0 |
1 |
1 |
1 |
0 |
0 |
0 |
0 |
1 |
0 |
1 |
0 |
0 |
7 |
|
|
106 |
1+2+4+5+7 |
1 |
1 |
0 |
1 |
1 |
0 |
1 |
1 |
0 |
1 |
1 |
0 |
1 |
1 |
0 |
10 |
|
|
107 |
1+2+4+6+7 |
1 |
1 |
0 |
1 |
0 |
1 |
1 |
0 |
0 |
1 |
0 |
0 |
0 |
1 |
1 |
8 |
|
|
108 |
1+2+5+6+7 |
1 |
1 |
0 |
0 |
1 |
1 |
1 |
1 |
1 |
0 |
1 |
1 |
0 |
0 |
0 |
9 |
|
|
109 |
1+3+4+5+6 |
1 |
0 |
1 |
1 |
1 |
1 |
0 |
0 |
1 |
0 |
1 |
1 |
0 |
1 |
0 |
9 |
|
|
110 |
1+3+4+5+7 |
1 |
0 |
1 |
1 |
1 |
0 |
1 |
1 |
1 |
1 |
1 |
1 |
0 |
0 |
0 |
10 |
|
|
111 |
1+3+4+6+7 |
1 |
0 |
1 |
1 |
0 |
1 |
1 |
0 |
1 |
1 |
0 |
1 |
1 |
0 |
1 |
10 |
|
|
112 |
1+3+5+6+7 |
1 |
0 |
1 |
0 |
1 |
1 |
1 |
1 |
0 |
0 |
1 |
0 |
1 |
1 |
0 |
9 |
|
|
113 |
1+4+5+6+7 |
1 |
0 |
0 |
1 |
1 |
1 |
1 |
1 |
0 |
1 |
1 |
0 |
0 |
0 |
1 |
9 |
|
|
114 |
2+3+4+5+6 |
0 |
1 |
1 |
1 |
1 |
1 |
0 |
1 |
1 |
0 |
0 |
0 |
1 |
1 |
0 |
9 |
|
|
115 |
2+3+4+5+7 |
0 |
1 |
1 |
1 |
1 |
0 |
1 |
0 |
1 |
1 |
0 |
0 |
1 |
0 |
0 |
8 |
|
|
116 |
2+3+4+6+7 |
0 |
1 |
1 |
1 |
0 |
1 |
1 |
1 |
1 |
1 |
1 |
0 |
0 |
0 |
1 |
10 |
|
|
117 |
2+3+5+6+7 |
0 |
1 |
1 |
0 |
1 |
1 |
1 |
0 |
0 |
0 |
0 |
1 |
0 |
1 |
0 |
7 |
|
|
118 |
2+4+5+6+7 |
0 |
1 |
0 |
1 |
1 |
1 |
1 |
0 |
0 |
1 |
0 |
1 |
1 |
0 |
1 |
9 |
|
|
119 |
3+4+5+6+7 |
0 |
0 |
1 |
1 |
1 |
1 |
1 |
0 |
1 |
1 |
0 |
0 |
0 |
1 |
1 |
9 |
|
|
|
120 |
1+2+3+4+5+6 |
1 |
1 |
1 |
1 |
1 |
1 |
0 |
0 |
0 |
1 |
0 |
1 |
1 |
1 |
0 |
10 |
|
121 |
1+2+3+4+5+7 |
1 |
1 |
1 |
1 |
1 |
0 |
1 |
1 |
0 |
0 |
0 |
1 |
1 |
0 |
0 |
9 |
|
|
122 |
1+2+3+4+6+7 |
1 |
1 |
1 |
1 |
0 |
1 |
1 |
0 |
0 |
0 |
1 |
1 |
0 |
0 |
1 |
9 |
|
|
123 |
1+2+3+5+6+7 |
1 |
1 |
1 |
0 |
1 |
1 |
1 |
1 |
1 |
1 |
0 |
0 |
0 |
1 |
0 |
10 |
|
|
124 |
1+2+4+5+6+7 |
1 |
1 |
0 |
1 |
1 |
1 |
1 |
1 |
1 |
0 |
0 |
0 |
1 |
0 |
1 |
10 |
|
|
125 |
1+3+4+5+6+7 |
1 |
0 |
1 |
1 |
1 |
1 |
1 |
1 |
0 |
0 |
0 |
1 |
0 |
1 |
1 |
10 |
|
|
126 |
2+3+4+5+6+7 |
0 |
1 |
1 |
1 |
1 |
1 |
1 |
0 |
0 |
0 |
1 |
0 |
1 |
1 |
1 |
10 |
|
|
|
127 |
1+2+3+4+5+6+7 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
15 |
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #