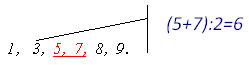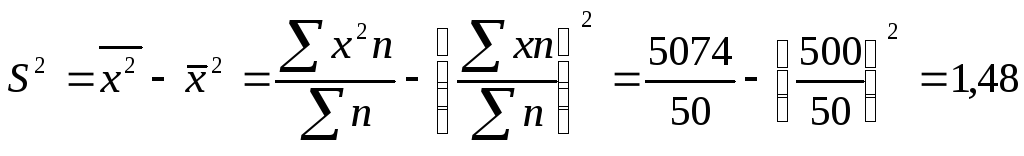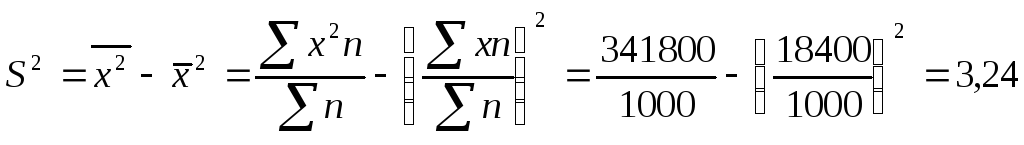Изучая математическую статистику в 7-м классе,
важно наглядно представить учащимися образец
для решения практических задач. Именно для этого
мною был разработан данный справочный материал.
1.Представление данных.
1.1. Таблицы
Смета расходов на покупку спортивного
инвентаря.
| № | Наименование | Ед. измерения | Количество | Цена (едруб) | Стоимость (руб) |
| 1 | Мяч футбольный | Шт. | 30 | 1000 | |
| 2 | Мяч волейбольный | Шт. | 15 | 800 | 12000 |
| 3 | Ракетка | Шт. | 24 | 250 | 6000 |
| 4 | Воланы | коробка | 10 | 300 | 3000 |
| ИТОГО: | 51000 |
Таблицы предназначены для упорядочивания
большого количества данных. Часто в таблицы
заносят результаты вычислений, измерений.
1.2. Диаграммы.
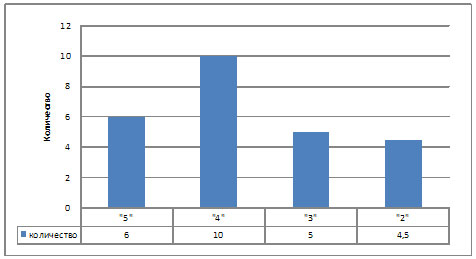
За контрольную работу по математике
школьники получили 6 оценок “отлично”, 10 оценок
“хорошо”, 5 оценок “ удовлетворительно” и 3
оценки “не удовлетворительно”.
Столбиковая диаграмма.
Построим столбиковую диаграмму по
этим данным.
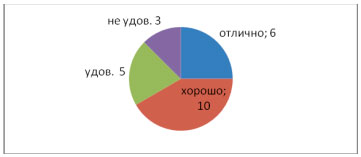
Круговая диаграмма.
Построим круговую диаграмму по этим
данным.
Для построения этой диаграммы мы:
- Разделили 360° на общее число учащихся (24)
- Затем последовательно умножаем 15° на
количество учащихся, получивших ту или иную
оценку. - Затем круг делим на полученные сектора,
подписываем данные.
360°24=15° (такому углу соответствует
оценка одного учащегося)
15°6=90° —
сектор образованный этим углом соответствует
учащимся с оценкой “5”
15°10=150°
— сектор образованный этим углом соответствует
учащимся с оценкой “4”
15°5=75° —
сектор образованный этим углом соответствует
учащимся с оценкой “3”
15°3=45° —
сектор образованный этим углом соответствует
учащимся с оценкой “2”
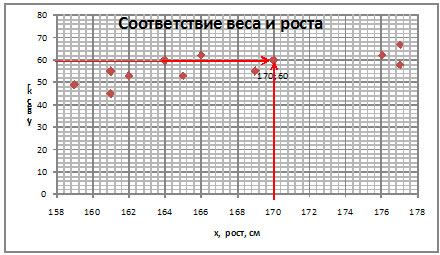
Диаграмма рассеивания.
Для выявления связи между величинами
применяются диаграммы рассеивания.
В таблице приведены данные о весе и
росте 12 девушек.
|
Рост, см |
165 |
177 |
161 |
162 |
170 |
176 |
177 |
164 |
166 |
161 |
169 |
159 |
Х |
|
Вес, кг |
53 |
67 |
45 |
53 |
60 |
62 |
58 |
60 |
62 |
55 |
55 |
49 |
У |
Для построения этой диаграммы нужно в
системе координат поставить точки, абсциссы
которых – рост, а ординаты – вес.
- Описательная статистика
2.1. Среднее значение
Определение: Средним арифметическим
нескольких чисел называется число, равное
отношение суммы этих чисел к их количеству.
Среднее арифметическое набора чисел х1,х2,х3,х4,х5
принято обозначать . Например, среднее арифметическое
пяти чисел запишется так:
Здесь в числителе дроби — сумма данных пяти
чисел, а в знаменателе – их количество – 5.
Найти среднюю оценку учащегося по
математике, если за истекший период он получил: 3,
4, 4, 5, 3, 2, 4, 3.
Запишем дробь и вычислим ее значение:
2.2. Медиана
Определение: Число, разделяющее набор
чисел на две части, равные по численности, так что
с одной стороны от этого числа все значения
больше медианы, а с другой – меньше.
Метод вычисления медианы: Чтобы найти
медиану набора чисел нужно:
- Записать числа в порядке возрастания.
- Если в полученном наборе нечетное количество
членов, то медианой служит число стоящее
посередине. - Если в полученном наборе четное количество
членов, то медианой набора – есть полусумма двух
чисел, расположенных посередине.
Найти медиану набора чисел: 9,3, 1, 5, 7.
Запишем числа в порядке возрастания.
1, 3, 5, 7, 9.
Здесь медиана набора число, стоящее
посередине – 5.
Найти медиану набора чисел: 9,3, 1, 5, 7,8
Запишем числа в порядке возрастания.
Выберем два центральных числа: 5 и 7. Найдем их
полусумму: (5+7):2=6. То есть медиана
данного набора есть число-6.
2.3. Наибольшее и наименьшее значение и размах.
Найти наибольшее, наименьшее значение и
размах для ряда чисел:
12,7,25,3,19,15.
Очевидно, что наибольшим значением данного
ряда является число 25, тогда как наименьшим число
– 3. Найдем размах данного ряда.
Определение: Разность между наибольшим и
наименьшим числом называется размахом набора
чисел.
Размах показывает насколько велико
рассеивание в числовом наборе. Итак, размах
данного набора равен разности 25 и 3, т.е. 22.
2.4. Отклонение.
Определение: Отклонением данного
значения от среднего арифметического значения
данного набора является разность между этим
числом и средним арифметическим. Соответственно
если некоторое значение меньше среднего, то его
отклонение отрицательно, если больше среднего –
его отклонение положительно. Так же необходимо
помнить, что сумма всех отклонений ряда чисел от
среднего арифметического этих чисел равна нулю.
Составить таблицу отклонений от
среднего арифметического для набора чисел:
2,4,5,7,10.
Вычислим среднее арифметическое этих чисел:
Составим таблицу отклонений.
| Число | Отклонение от среднего арифметического |
| 2 | 2-5,6= -3,6 |
| 4 | 4-5,6= -1,6 |
| 5 | 5-5,6= -0,6 |
| 7 | 7-5,6=1,4 |
| 10 | 10-5,6=4,4 |
2.5. Дисперсия.
Определение: Среднее арифметическое
квадратов отклонений от среднего значения
называется дисперсией набора чисел. Дисперсию
обозначают S2.
В таблице представлены средние
месячные температуры, в градусах. Вычислите
дисперсию температуры за приведенный период.
| Месяцы | Январь | Февраль | Март | Апрель | Май |
| Средняя температура | -12 | -7 | 0 | 9 | 16 |
Решение:
- Вычислим среднюю температуру за 5 месецев.
- .Составим таблицу отклонений и их квадратов.
- Найдем среднее арифметическое для квадратов
отклонений от среднего значения
Итак, средняя температура составила 6
градусов.
| Число (температура) | Отклонение от среднего | Квадрат отклонения |
| -12 | -12-6=-18 | (-18)2=324 |
| -7 | -13 | 169 |
| 0 | -6 | 36 |
| 9 | 3 | 9 |
| 16 | 10 | 100 |
( последний столбец таблицы)
Итак, дисперсия средних температур за 5 месяцев
составила 127,6. Ответ: S2=127,6
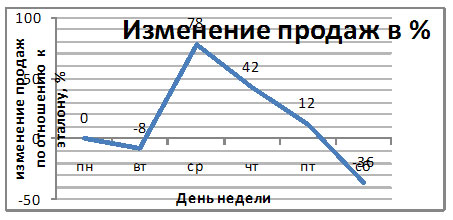
Составление таблицы изменений в процентах.
В таблице представлено количество
продаваемых за неделю шоколадок в школьном
буфете. Составьте таблицу изменения продаж по
отношению к понедельнику в процентах.
|
День недели |
понедельник |
вторник |
среда |
четверг |
пятница |
суббота |
|
Количество |
50 |
46 |
89 |
71 |
44 |
32 |
Число проданных в понедельник шоколадок
составляет 100% — эталон.
Вычислим, сколько составляет 1% эталона.
1% =50:100=0,5.
Вычислим, сколько процентов эталона составляет
количество проданных шоколадок в другие дни
недели.
Вторник – 46. Какой процент составляет 46 от 50.
46:0,5=92
Среда -89. 89 : 0,5= 178
Четверг – 71. 71 :0,5=142
Пятница – 44 44:0,5=88
Суббота -32 32 :0,5 =64
|
День недели |
понедельник |
вторник |
среда |
четверг |
пятница |
суббота |
|
Количество проданных |
50 |
46 |
89 |
71 |
44 |
32 |
|
% от эталона |
100 |
92 |
178 |
142 |
88 |
64 |
|
Изменение продаж в % |
0 |
-8 |
78 |
42 |
-12 |
-36 |
Ответ:
Для решения этой задачи нужно выполнить следующие шаги:
Вычислить среднее значение. Среднее значение вычисляется как сумма всех элементов выборки, деленная на количество элементов в выборке.
Для выборки г:
2 + 6 + 7 + 5 = 20
Среднее значение =20/4 = 5
Для выборки д:
-2 + -1 + 1 + 2 + 5 = 1
Среднее значение = 1/5 = 0.2
Для выборки е:
-1 + -3 + -2 + 3 + 3 = 0
Среднее значение = 0/5 = 0
Составить таблицу отклонений от среднего. Отклонение от среднего — это разница между значением элемента и средним значением.
Вычислить квадраты отклонений от среднего. Квадрат отклонения от среднего — это квадрат значения отклонения от среднего.
Выборка г:
Значение элемента Среднее значение Отклонение от среднего Квадрат отклонения от среднего
2 5 -3 9
6 5 1 1
7 5 2 4
5 5 0 0
Выборка д:
Значение элемента Среднее значение Отклонение от среднего Квадрат отклонения от среднего
-2 0.2 -2.2 4.84
-1 0.2 -1.2 1.44
1 0.2 0.8 0.64
2 0.2 1.8 3.24
5 0.2 4.8 23.04
Выборка е:
Значение элемента Среднее значение Отклонение от среднего Квадрат отклонения от среднего
-1 0 -1 1
-3 0 -3 9
-2 0 -2 4
3 0 3 9
3 0 3 9
Вычислить дисперсию. Дисперсия — это среднее значение квадратов отклонений от среднего. Для вычисления дисперсии нужно сначала сложить все квадраты отклонений от среднего, а затем разделить результат на количество элементов в выборке.
Дисперсия для выборки г: (9 + 1 + 4 + 0)/4 = 2.75
Дисперсия для выборки д: (4.84 + 1.44 + 0.64 + 3.24 + 23.04)/5 = 7.44
Дисперсия для выборки е: (1 + 9 + 4 + 9 + 9)/5 = 6.4
Объяснение:
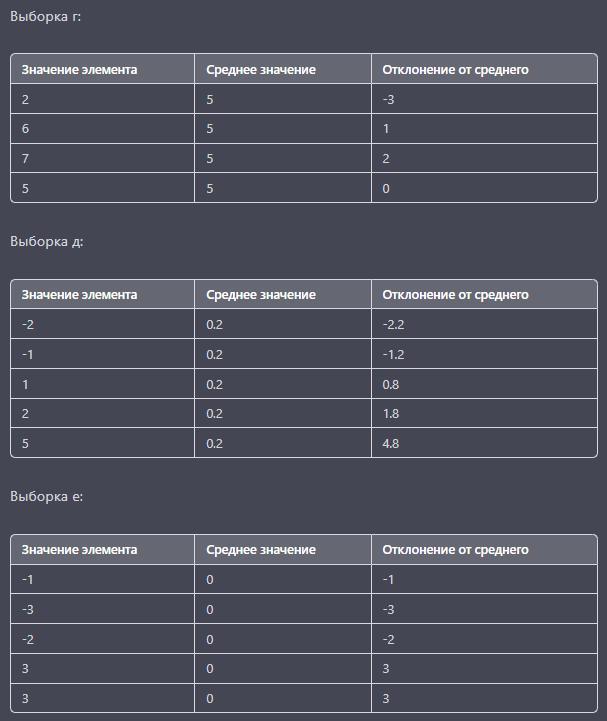
Картинка с табличками вложена. Искомые величины выделены цветом.
а)
Сначала находим среднее значение выборки:
Хс = (-1 + 0 + 4)/3 = 1
Среднее квадратичное отклонение:
sqrt{frac{(X1 — Xc)^2 +(X2 — Xc)^2 +(X3 — Xc)^2}{n}} =
sqrt{frac{(-1 — 1)^2 +(0 — 1)^2 +(4 — 1)^2}{3}} = 2,1602
Дисперсия — это средний квадрате отклонений от средней величины:
frac{(X1 — Xc)^2 +(X2 — Xc)^2 +(X3 — Xc)^2}{n} =
frac{(-1 — 1)^2 +(0 — 1)^2 +(4 — 1)^2}{3}} = 4,6667
б)
Среднее значение выборки:
Хс = (-3 + 1 + 2 + 4)/4 = 1
Среднее квадратичное отклонение:
sqrt{frac{(X1 — Xc)^2 +(X2 — Xc)^2 +(X3 — Xc)^2+(X4 — Xc)^2}{n}} =
sqrt{frac{(-3 — 1)^2 +(1 — 1)^2 +(2 — 1)^2 + (4 — 1)^2}{4}} = 2,5495
Дисперсия:
frac{(X1 — Xc)^2 +(X2 — Xc)^2 +(X3 — Xc)^2+(X4 — Xc)^2}{n} =
frac{(-3 — 1)^2 +(1 — 1)^2 +(2 — 1)^2 + (4 — 1)^2}{4}} = 6,5
в) смотри б)
г)
Среднее значение выборки:
Хс = (2 + 6 + 7 + 5)/4 = 5
Среднее квадратичное отклонение:
sqrt{frac{(X1 — Xc)^2 +(X2 — Xc)^2 +(X3 — Xc)^2+(X4 — Xc)^2}{n}} =
sqrt{frac{(2 — 5)^2 +(6 — 5)^2 +(7 — 5)^2 + (5 — 5)^2}{4}} = 1,8708
Дисперсия:
frac{(X1 — Xc)^2 +(X2 — Xc)^2 +(X3 — Xc)^2+(X4 — Xc)^2}{n} =
frac{(2 — 5)^2 +(6 — 5)^2 +(7 — 5)^2 + (5 — 5)^2}{4}} = 3,5
Расчет дисперсии и среднего квадратического отклонения по индивидуальным данным и в рядах распределения.
Основными
обобщающими показателями вариации в
статистике являются дисперсии и среднее
квадратическое отклонение.
Дисперсия
— это средняя арифметическая квадратов
отклонений каждого значения признака
от общей средней. Дисперсия обычно
называется средним квадратом отклонений
и обозначается
.
В зависимости от исходных данных
дисперсия может вычисляться по средней
арифметической простой или взвешенной:
—дисперсия
невзвешенная (простая);
—дисперсия
взвешенная.
Среднее
квадратическое отклонение представляет
собой корень квадратный из дисперсии
и обозначается S:
—среднее
квадратическое отклонение невзвешенное;
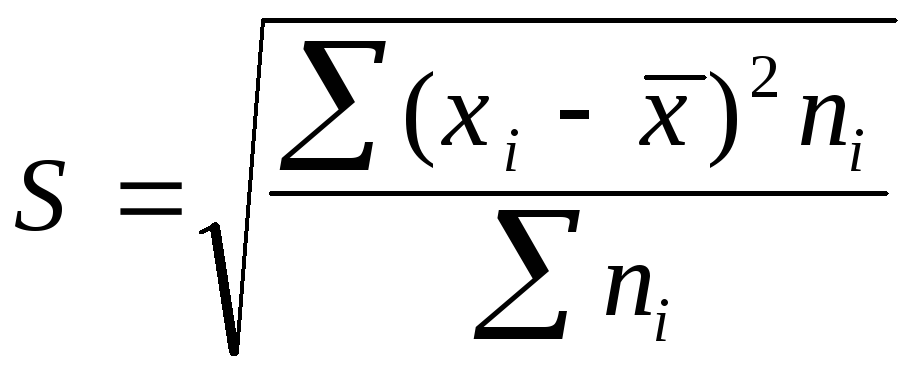
квадратическое отклонение взвешенное.
Среднее
квадратическое отклонение
— это обобщающая характеристика абсолютных
размеров вариации признака в совокупности.
Выражается оно в тех же единицах
измерения, что и признак (в метрах,
тоннах, процентах, гектарах и т.д.).
Среднее
квадратическое отклонение является
мерилом надежности средней. Чем меньше
среднее квадратическое отклонение, тем
лучше средняя арифметическая отражает
собой всю представляемую совокупность.
Вычислению
среднего квадратического отклонения
предшествует расчет дисперсии.
Порядок
расчета дисперсии взвешенную:
1)
определяют среднюю арифметическую
взвешенную
;
2)
определяются отклонения вариант от
средней
;
3)
возводят в квадрат отклонение каждой
варианты от средней
;
4)
умножают квадраты отклонений на веса
(частоты)
;
5)
суммируют полученные произведения
;
6)
Полученную сумму делят на сумму весов
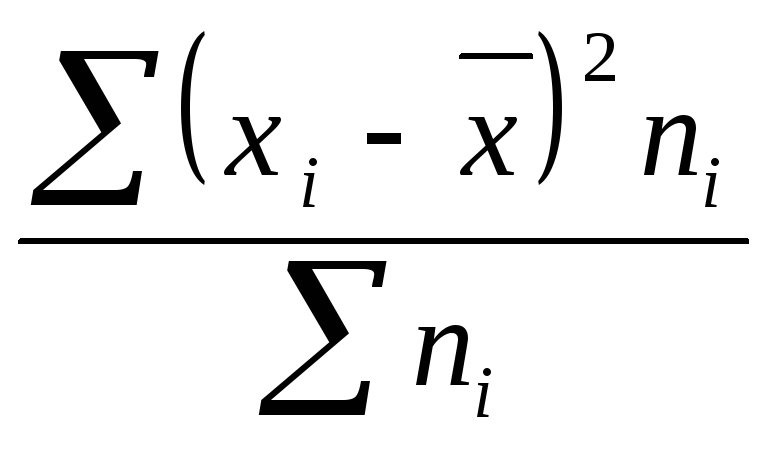
Пример
3.
Таблица
6.3.
|
Произведено ( |
Число |
|
|
|
|
|
8 |
7 |
56 |
-2 |
4 |
28 |
|
9 |
10 |
90 |
-1 |
1 |
10 |
|
10 |
15 |
150 |
0 |
0 |
0 |
|
11 |
12 |
132 |
1 |
1 |
12 |
|
12 |
6 |
72 |
2 |
4 |
24 |
|
ИТОГО |
50 |
500 |
74 |
Исчислим
среднюю арифметическую взвешенную:
шт.
Значения
отклонений от средней и их квадратов
представлены в таблице 6.3. Определим
дисперсию:
=1,48
Среднее
квадратическое отклонение будет равно:
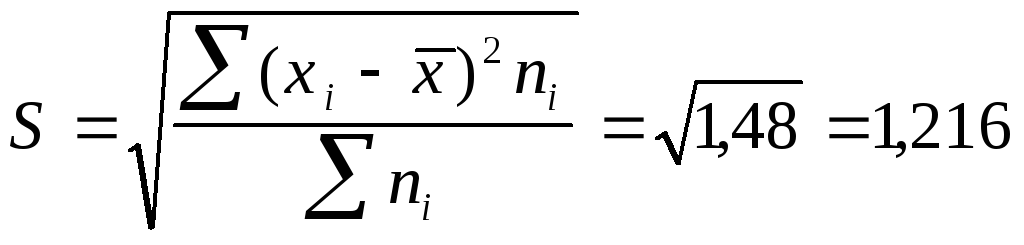
Если
исходные данные представлены в виде
интервального ряда распределения, то
сначала надо определить дискретное
значение признака, а далее применить
тот же метод, что изложен выше.
Пример
4.
Покажем
расчет дисперсии для интервального
ряда на данных о распределении посевной
площади колхоза по урожайности пшеницы:
Таблица
6.4
|
Урожайность |
Посевная |
|
|
|
|
|
|
14 |
100 |
15 |
1500 |
-3,4 |
11,56 |
1156 |
|
16 |
300 |
17 |
5100 |
-1,4 |
1,96 |
588 |
|
18 |
400 |
19 |
7600 |
0,6 |
0,36 |
144 |
|
20 |
200 |
21 |
4200 |
2,6 |
6,76 |
1352 |
|
ИТОГО |
1000 |
18400 |
3240 |
Средняя
арифметическая равна:
ц с
1га.
Исчислим
дисперсию:
Расчет дисперсии по формуле по индивидуальным данным и в рядах распределения.
Техника
вычисления дисперсии сложна, а при
больших значениях вариант и частот
может быть громоздкой. Расчеты можно
упростить, используя свойства дисперсии.
Свойства
дисперсии.
-
Уменьшение
или увеличение весов (частот) варьирующего
признака в определенное число раз
дисперсии не изменяет. -
Уменьшение
или увеличение каждого значения признака
на одну и ту же постоянную величину А
дисперсии не изменяет. -
Уменьшение
или увеличение каждого значения признака
в какое-то число раз к соответственно
уменьшает или увеличивает дисперсию
в
раз, а среднее квадратическое отклонение
— в к раз. -
Дисперсия
признака относительно произвольной
величины всегда больше дисперсии
относительно средней арифметической
на квадрат разности между средней и
произвольной величиной:
.
Если А равна нулю, то приходим к
следующему равенству:
,
т.е. дисперсия признака равна разности
между средним квадратом значений
признака и квадратом средней.
Каждое
свойство при расчете дисперсии может
быть применено самостоятельно или в
сочетании с другими.
Порядок
расчета дисперсии простой:
1)
определяют среднюю арифметическую
;
2)
возводят в квадрат среднюю арифметическую;
3)
возводят в квадрат каждую варианту ряда
;
4)
находим сумму квадратов вариант
;
5)
делят сумму квадратов вариант на их
число, т.е. определяют средний квадрат
;
6)
определяют разность между средним
квадратом признака и квадратом средней
.
Пример
5.
Имеются
следующие данные о производительности
труда рабочих:
Таблица
6.4
|
Табельный |
Произведено |
|
|
1 |
8 |
64 |
|
2 |
9 |
81 |
|
3 |
10 |
100 |
|
4 |
11 |
121 |
|
5 |
12 |
144 |
|
ИТОГО |
50 |
510 |
Произведем
следующие расчеты:
шт.
Пример
6.
Определить
дисперсию в дискретном ряду распределения,
используя табл. 6.5.
Таблица
6.5.
|
Произведено |
Число |
|
|
|
|
8 |
7 |
56 |
64 |
448 |
|
9 |
10 |
90 |
81 |
810 |
|
10 |
15 |
150 |
100 |
1500 |
|
11 |
12 |
132 |
121 |
1452 |
|
12 |
6 |
72 |
144 |
864 |
|
ИТОГО |
50 |
500 |
510 |
5074 |
Получим
тот же результат, что в табл. 6.3.
Рассмотрим
расчет дисперсии в интервальном ряду
распределения.
Порядок
расчета дисперсии взвешенной (по формуле
):
-
определяют
среднюю арифметическую
;
-
возводят
в квадрат полученную среднюю
;
-
возводят
в квадрат каждую варианту ряда
;
-
умножают
квадраты вариант на частоты
;
-
суммируют
полученные произведения
;
-
делят
полученную сумму на сумму весов и
получают средний квадрат признака
;
-
определяют
разность между средним значением
квадратов и квадратом средней
арифметической, т.е. дисперсию
.
Пример
7.
Имеются
следующие данные о распределении
посевной площади колхоза по урожайности
пшеницы:
Таблица
6.6
|
Урожайность |
Посевная |
|
|
|
|
|
14 |
100 |
15 |
1500 |
225 |
22500 |
|
16 |
300 |
17 |
5100 |
289 |
36700 |
|
18 |
400 |
19 |
7600 |
361 |
144400 |
|
20 |
200 |
21 |
4200 |
441 |
88200 |
|
ИТОГО |
1000 |
18400 |
341200 |
В
подобных примерах прежде всего
определяется дискретное значение
признака в каждом интервале, а затем
применяется метод расчета, указанный
выше:
Средняя
величина отражает тенденцию развития,
т.е. действие главных причин. Среднее
квадратическое отклонение измеряет
силу воздействия прочих факторов.
Соседние файлы в папке statistica
- #
- #
- #
- #
- #
- #
- #
- #
- #
Зимой 1841 года, оказавшись в отпуске в Петербурге, Лермонтов пытался выйти в отставку, мечтая полностью посвятить себя литературе, но не решился сделать это, так как бабушка была против, она надеялась, что её внук сможет сделать себе карьеру и не разделяла его увлечение литературой. Поэтому весной 1841 года он был вынужден возвратиться в свой полк на Кавказ.
Уезжал из Петербурга он с тяжёлыми предчувствиями — сначала в Ставрополь, где стоял тенгинский полк, потом в Пятигорск. В Пятигорске произошла его ссора с майором в отставке Мартыновым Николаем Соломоновичем.
Впервые Лермонтов познакомился с Мартыновым в Школе гвардейских подпрапорщиков, которую Мартынов закончил на год позже Лермонтова. В 1837 году Лермонтов, переведённый из гвардии в Нижегородский полк за стихи «На смерть поэта» , и Мартынов, отправляющийся на Кавказ, две недели провели в Москве, часто завтракая вместе у Яра. Лермонтов посещал московский дом родителей Мартынова. Впоследствии современники считали, что прототипом княжны Мери была Наталья Соломоновна — сестра Мартынова.
Как писал в своих «Записках декабриста» Н. И. Лорер:
Мартынов служил в кавалергардах, перешёл на Кавказ, в линейных казачий полк и только что оставил службу. Он был очень хорош собой и с блестящим светским образованием. Нося по удобству и привычке черкесский костюм, он утрировал вкусы горцев и, само собой разумеется, тем самым навлекал на себя насмешки товарищей, между которыми Лермонтов по складу ума своего был неумолимее всех. Пока шутки эти были в границах приличия, всё шло хорошо, но вода и камень точит, и, когда Лермонтов позволил себе неуместные шутки в обществе дам… , шутки эти показались обидны самолюбию Мартынова, и он скромно заметил Лермонтову всю неуместность их. Но желчный и наскучивший жизнью человек не оставлял своей жертвы, и, когда они однажды сошлись в доме Верзилиных, Лермонтов продолжал острить и насмехаться над Мартыновым, который, наконец, выведенный из терпения, сказал, что найдёт средство заставить молчать обидчика. Избалованный общим вниманием, Лермонтов не мог уступить и отвечал, что угроз ничьих не боится, а поведения своего не переменит.
Причины дуэли и смерти Лермонтова Мартынов рассказал посетившим его в эмиграции молодёжи, слова его, сказанные тогда молодому А. А. Игнатьеву, служащему в посольстве во Франции, приведены в книге Андрея Кончаловского:
В другой раз, намного позже, зашла речь о Лермонтове.
— Говорят страшный был зануда, — сказал Алексей Алексеевич.
Мне было уже пятнадцать лет и я был страшно поражён, что слышу о Лермонтове как о ком-то лично знакомом говорящему.
— Откуда вы его знаете?
— Я встречал Мартынова в Париже. Мы тогда молодые, окружили его, стали дразнить, обвинять: «Вы убили солнце русской поэзии! Вам не стыдно? » — «Господа, сказал он, — если бы вы знали, что это был за человек! Он был невыносим. Если бы я промахнулся тогда на дуэли, я бы убил его потом. Когда он появлялся в обществе, единственной его целью было испортить всем настроение. Все танцевали, веселились, а он садился где-то в уголке и начинал над кем-нибудь смеяться, посылать из своего угла записки с гнусными эпиграммами. Поднимался скандал, кто-то начинал рыдать, у всех портилось настроение. Вот тогда Лермонтов чувствовал себя в порядке»
Дуэль произошла 15 июля. Лермонтов выстрелил вверх (основная версия) , Мартынов — прямо в грудь поэту.
Похороны Лермонтова не могли быть совершены по церковному обряду, несмотря на все хлопоты друзей, официальное известие об его смерти гласило: 15-го июля, около 5 часов вечера, разразилась ужасная буря с громом и молнией; в это самое время между горами Машуком и Бештау скончался лечившийся в Пятигорске М. Ю. Лермонтов.