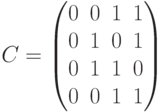Реферат Отчет 38 с., 3 главы, 22 рис., 2 табл., 16 источников, 4 прил видео стеганография, стеганография mpeg, сокрытие информации в видео, встраивание и извлечение информации, дискретное косинусное преобразование, помехоустойчивое кодирование, циклические
Построение таблицы синдромов ошибок
|
Скачать 318,6 Kb.
|
- Навигация по данной странице:
- Декодирование и исправление ошибок
Построение таблицы синдромов ошибок
Перед тем как начать декодирование, необходимо построить таблицу синдромов ошибок, с помощью которой будет происходить исправление ошибок. Для этого нужно знать количество ошибок, которое двоичный циклический 


где 

Минимальное кодовое расстояние 



Таблица 1.1
Кодовые слова двоичного циклического (7,4)-кода (
|
0000000 |
0100111 |
1000101 |
1100010 |
|
0001011 |
0101100 |
1001110 |
1101001 |
|
0010110 |
0110001 |
1010011 |
1110100 |
|
0011101 |
0111010 |
1011000 |
1111111 |
Так как двоичный циклический (7,4)-код исправляет всего одну ошибку, то общее количество многочленов ошибок равно длине кодового слова 

Таблица 1.2
Синдромы однократных ошибок двоичного циклического (7,4)-кода с порождающим многочленом 
|
Ошибка |
Синдром |
|
0000001 |
001 |
|
0000010 |
010 |
|
0000100 |
100 |
|
0001000 |
011 |
|
0010000 |
110 |
|
0100000 |
111 |
|
1000000 |
101 |
Декодирование и исправление ошибок
Декодирование двоичного циклического 

-
Вычисляется синдром ошибки с помощью алгоритма деления Евклида, описанном в 1.2.1.1.
-
Если синдром нулевой, то кодовое слово не содержит ошибок. Если синдром ненулевой, то определятся ошибочный бит с помощью таблицы синдромов и исправляется.
-
Так как кодирование систематическое, то можно просто отсечь проверочную часть длиныи получить декодированное информационное слово.
Ниже представлен пример декодирования кодового слова (0010011) с помощью двоичного циклического (7,4)-кода с порождающим многочленом 
-
Находим остаток от деления (синдром ошибки) с помощью алгоритма деления Евклида
0
0
1
0
0
1
1
=
0
0
1
0
1
1
0
=
1
0
1
=
-
Синдром не равен нулю, поэтому находим синдром в таблице синдромов (табл. 1.2) и соответствующий ему ошибочный бит (1000000).
-
Исправляем ошибочный бит и получаем правильное кодовое слово (1010011). Отсекаем проверочную часть и получаем информационное слово (1010).
-
Каталог: data -> 2014
2014 -> Программа дисциплины для направления/ специальности подготовки бакалавра/ магистра/ специалиста
2014 -> «Особенности реализации личностно-ориентированного подхода в профессиональной подготовке студентов высших учебных заведений»
2014 -> Программа «Управление образованием»
2014 -> Кадровая политика вуза
2014 -> Баврина Анна Петровна профессиональная мотивация преподавателей вуза (на примере нгма) Выпускная квалификационная работа по направлению 080200. 68 «Менеджмент» магистранта группы №12учр
2014 -> «Российское общество эпохи реформ Александра ii»
2014 -> «Корпоративная культура средств массовой информации на примере телеканала рен тв»
2014 -> Начиная с восьмидесятых годов двадцатого века тема корпоративной или организационной культуры стала одной из центральных в управленческой литературе. Все больше исследователей посвящают этому феномену свои научные труды
2014 -> Система методического сопровождения педагогов по формированию метапредметных результатов в условиях подготовки и введения Федеральных государственных образовательных стандартовСкачать 318,6 Kb.
Поделитесь с Вашими друзьями:
Помехоустойчивое кодирование. Часть 1: код Хэмминга
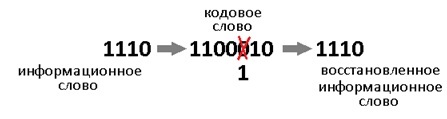
Код Хэмминга – не цель этой статьи. Я лишь хочу на его примере познакомить вас с самими принципами кодирования. Но здесь не будет строгих определений, математических формулировок и т.д. Эта просто неплохой трамплин для понимания более сложных блочных кодов.
Самый, пожалуй, известный код Хэмминга (7,4). Что значат эти цифры? Вторая – число бит информационного слова — то, что мы хотим передать в целости и сохранности. А первое – размер кодового слова: информация удобренная избыточностью. Кстати термины «информационное слово» и «кодовое слово», употребляются во всех 7-ми книгах по теории помехоустойчивого кодирования, которые мне довелось бегло пролистать.
Такой код исправляет 1 ошибку. И не важно где она возникла. Избыточность несёт в себе 3 бита информации, этого достаточно, чтобы указать на одно из 7 положений ошибки или показать, что её нет. То есть ровно 8 вариантов ответов мы ждём. А 8 = 2^3, вот как всё совпало.
Чтобы получить кодовое слово, нужно информационное слово представить в виде полинома и умножить его на порождающий полином g(x). Любое число, переведя в двоичный вид, можно представить в виде полинома. Это может показаться странным и у не подготовленного читателя сразу встаёт только один вопрос «да зачем же так усложнять?». Уверяю вас, он отпадёт сам собой, когда мы получим первые результаты.
К примеру информационное слово 1010, значение каждого его разряда это коэффициент в полиноме:
Во многих книгах пишут наоборот x+x^3. Не поддавайтесь на провокацию, это вносит только путаницу, ведь в записи числа 2-ичного, 16-ричного, младшие разряды идут справа, и сдвиги мы делаем влево/вправо ориентируясь на это. А теперь давайте умножим этот полином на порождающий полином. Порождающий полином специально для Хэмминга (7,4), встречайте: g(x)=x^3+x+1. Откуда он взялся? Ну пока считайте что он дан человечеству свыше, богами (объясню позже).
Если нужно складывать коэффициенты, то делаем по модулю 2: операция сложения заменяется на логическое исключающее или (XOR), то есть x^4+x^4=0. И в конечном итоге результат перемножения как видите из 4х членов. В двоичном виде это 1001110. Итак, получили кодовое слово, которое будем передавать на сторону по зашумлённому каналу. Замете, что перемножив информационное слово (1010) на порождающий полином (1011) как обычные числа – получим другой результат 1101110. Этого нам не надо, требуется именно «полиномиальное» перемножение. Программная реализация такого умножения очень простая. Нам потребуется 2 операции XOR и 2 сдвига влево (1й из которых на один разряд, второй на два, в соответствии с g(x)=1011):
Давайте теперь специально внесём ошибку в полученное кодовое слово. Например в 3-й разряд. Получиться повреждённое слово: 1000110.
Как расшифровать сообщение и исправить ошибку? Разумеется надо «полиномиально» разделить кодовое слово на g(x). Тут я уже не буду писать иксы. Помните что вычитание по модулю 2 — это то же самое что сложение, что в свою очередь, тоже самое что исключающее или. Поехали:
В программной реализации опять же ничего сверх сложного. Делитель (1011) сдвигаем влево до самого конца на 3 разряда. И начинаем удалять (не без помощи XOR) самые левые единицы в делимом (100110), на его младшие разряды даже не смотрим. Делимое поэтапно уменьшается 100110 -> 0011110 -> 0001000 -> 0000011, когда в 4м и левее разрядах не остаётся единиц, мы останавливаемся.
Нацело разделить не получилось, значит у нас есть ошибка (ну конечно же). Результат деления в таком случае нам без надобности. Остаток от деления является синдром, его размер равен размеру избыточности, поэтому мы дописали там ноль. В данном случае содержание синдрома нам никак не помогает найти местоположение повреждения. А жаль. Но если мы возьмём любое другое информационное слово, к примеру 1100. Точно так же перемножим его на g(x), получим 1110100, внесём ошибку в тот же самый разряд 1111100. Разделим на g(x) и получим в остатке тот же самый синдром 011. И я гарантирую вам, что к такому синдрому мы придём в обще для всех кодовых слов с ошибкой в 3-м разряде. Вывод напрашивается сам собой: можно составить таблицу синдромов для всех 7 ошибок, делая каждую из них специально и считая синдром.
В результате собираем список синдромов, и то на какую болезнь он указывает:
Теперь у нас всё есть. Нашли синдром, исправили ошибку, ещё раз поделили в данном случае 1001110 на 1011 и получили в частном наше долгожданное информационное слово 1010. В остатке после исправления уже будет 000. Таблица синдромов имеет право на жизнь в случае маленьких кодов. Но для кодов, исправляющих несколько ошибок – там список синдромов разрастается как чума. Поэтому рассмотрим метод «вылавливания ошибок» не имея на руках таблицы.
Внимательный читатель заметит, что первые 3 синдрома вполне однозначно указывают на положение ошибки. Это касается только тех синдромов, где одна единица. Кол-во единиц в синдроме называют его «весом». Опять вернёмся к злосчастной ошибке в 3м разряде. Там, как вы помните был синдром 011, его вес 2, нам не повезло. Сделаем финт ушами — циклический сдвиг кодового слова вправо. Остаток от деления 0100011 / 1011 будет равен 100, это «хороший синдром», указывает что ошибка во втором разряде. Но поскольку мы сделали один сдвиг, значит и ошибка сдвинулась на 1. Вот собственно и вся хитрость. Даже в случае жуткого невезения, когда ошибка в 6м разряде, вы, обливаясь потом, после 3 мучительных делений, но всё таки находите ошибку – это победа, лишь потому, что вы не использовали таблицу синдромов.
А как насчёт других кодов Хэмминга? Я бы сказал кодов Хэмминга бесконечное множество: (7,4), (15,11), (31,26),… (2^m-1, 2^m-1-m). Размер избыточности – m. Все они исправляют 1 ошибку, с ростом информационного слова растёт избыточность. Помехоустойчивость слабеет, но в случае слабых помех код весьма экономный. Ну ладно, а как мне найти порождающую функцию например для (15,11)? Резонный вопрос. Есть теорема, гласящая: порождающий многочлен циклического кода g(x) делит (x^n+1) без остатка. Где n – нашем случае размер кодового слова. Кроме того порождающий полином должен быть простым (делиться только на 1 и на самого себя без остатка), а его степень равна размеру избыточности. Можно показать, что для Хэмминга (7,4):
Этот код имеет целых 2 порождающих полинома. Не будет ошибкой использовать любой из них. Для остальных «хэммингов» используйте вот эту таблицу примитивных полиномов:
Соответственно для (15,11) порождающий многочлен g(x)=x^4+x+1. Ну а теперь переходим к десерту – к матрицам. С этого обычно начинают, но мы этим закончим. Для начала преобразую g(x) в матрицу, на которую можно умножить информационное слово, получив кодовое слово. Если g = 1011, то:
Называют её «порождающей матрицей». Дадим обозначение информационному слову d = 1010, а кодовое обозначим k, тогда:
Это довольно изящная формулировка. По быстродействию ещё быстрее, чем перемножение полиномов. Там нужно было делать сдвиги, а тут уже всё сдвинуто. Вектор d указывает нам: какие строки брать в расчёт. Самая нижняя строка матрицы – нулевая, строки нумеруются снизу вверх. Да, да, всё потому что младшие разряды располагаются справа и от этого никуда не деться. Так как d=1010, то я беру 1ю и 3ю строки, произвожу над ними операцию XOR и вуаля. Но это ещё не всё, приготовьтесь удивляться, существует ещё проверочная матрица H. Теперь перемножением вектора на матрицу мы можем получить синдром и никаких делений полиномов делать не надо.
Посмотрите на проверочную матрицу и на список синдромов, который получили выше. Это ответ на вопрос откуда берётся эта матрица. Здесь я как обычно подпортил кодовое слово в 3м разряде, и получил тот самый синдром. Поскольку сама матрица – это и есть список синдромов, то мы тут же находим положение ошибки. Но в кодах, исправляющие несколько ошибок, такой метод не прокатит. Придётся вылавливать ошибки по методу, описанному выше.
Чтобы лучше понять саму природу исправления ошибок, сгенерируем в обще все 16 кодовых слов, ведь информационное слово состоит всего из 4х бит:
Посмотрите внимательно на кодовые слова, все они, отличаются друг от друга хотя бы на 3 бита. К примеру возьмёте слово 1011000, измените в нём любой бит, скажем первый, получиться 1011010. Вы не найдёте более на него похожего слова, чем 1011000. Как видите для формирования кодового слова не обязательно производить вычисления, достаточно иметь эту таблицу в памяти, если она мала. Показанное различие в 3 бита — называется минимальное «хэммингово расстояние», оно является характеристикой блокового кода, по нему судят сколько ошибок можно исправить, а именно (d-1)/2. В более общем виде код Хэмминга можно записать так (7,4,3). Отмечу только, что Хэммингово расстояние не является разностью между размерами кодового и информационного слов. Код Голея (23,12,7) исправляет 3 ошибки. Код (48, 36, 5) использовался в сотовой связи с временным разделением каналов (стандарт IS-54). Для кодов Рида-Соломона применима та же запись, но это уже недвоичные коды.
Список используемой литературы:
1. М. Вернер. Основы кодирования (Мир программирования) — 2004
2. Р. Морелос-Сарагоса. Искусство помехоустойчивого кодирования (Мир связи) — 2006
3. Р. Блейхут. Теория и практика кодов, контролирующих ошибки — 1986
Вычисление синдрома и исправление ошибок в циклических кодах
Вычисление синдрома для циклических кодов является довольно простой процедурой, совершенно аналогичной процедуре кодирования. Рассмотрим ее.
Пусть и(х) и и(х) — полиномы, соответствующие переданному кодовому слову и принятой последовательности. Они могут совпадать, если передача сообщения была осуществлена безошибочно, или не совпадать в противном случае.
Разделив й(х) на порождающий полином g(x), получим
где q(х) — частное от деления; s(x) — остаток от деления.
Если й(х) является допустимым кодовым полиномом, то он делится на g(x) без остатка, т.е. s(x) = 0.
Следовательно, результат s(x) ф 0 является условием наличия ошибки в принятой последовательности, а полином s(x) имеет смысл синдрома ошибки в последовательности и(х).
Синдром s(x) имеет в общем случае вид
Поскольку синдром вычисляется как остаток от деления некоего полинома на порождающий полином, то очевидно, что схема вычисления синдрома подобна схемам кодирования, рассмотренным выше, с той лишь разницей, что в качестве входной последовательности в нее подается вектор й (см. рис. 4.8).
При наличии в принятой последовательности й хотя бы одной ошибки вектор синдрома s будет иметь по крайней мере один ненулевой элемент, при этом факт наличия ошибки легко обнаружить, объединив по элементу ИЛИ выходы всех ячеек регистра синдрома.
Покажем, что синдромный многочлен s(x) однозначно связан с многочленом ошибки е(х), а значит, с его помощью можно не только обнаруживать, но и локализовать ошибку в принятой последовательности.
Рис. 4.8. Схема получения синдрома для порождающего полинома д(х) =х 3 +х+1
Пусть е(х) — полином вектора ошибки. Тогда полином принятой последовательности
Учтем, что п(х) — допустимый кодовый полином, нацело делящийся на порождающий полином g(x), и запишем два выражения:
По определению вектора (полинома) ошибки:
То есть синдромный полином s(x) есть остаток от деления полинома ошибки е(х) на порождающий полином д(х).
Отсюда следует, что по синдрому s(x) можно однозначно определить вектор ошибки е(х), а следовательно, и исправить эту ошибку.
Декодирование линейных кодов
1. Пусть с = (ci, С2. сп) — передаваемый вектор кодового слова линейного кода С над GF(q), av = (vi, Vi. vn) — соответствующий принятый вектор. Векторы с и v могут различаться по причине возникновения ошибок в процессе передачи кодового слова. Это различие может быть записано следующим образом:
где е = (©1, ©2,еп) — вектор, символы которого принимают ненулевые значения в ошибочных разрядах и нулевые — в разрядах, переданных без ошибки.
Вектор е из соотношения (2.13) называется вектором ошибок.
Собственно, задача декодирования линейного кода состоит в том, чтобы отыскать вектор ошибок и по известному вектору ошибок восстановить исходное кодовое слово.
Далее для определения одного из алгоритмов декодирования нам понадобятся дополнительные сведения из алгебры.
2. Непустое подмножество Н группы (G, *) называется подгруппой группы (G, *), если Н является группой относительно той же групповой операции *.
Очевидно, что подгруппа как самостоятельная группа должна удовлетворять всем аксиомам группы. При этом очевидно, что ассоциативность наследуется из исходной группы G (как и коммутативность в случае, если G — абелева группа, см. параграф 1.1).
В качестве примера подгруппы можно привести множество всех четных чисел в группе % всех целых чисел относительно операции арифметического сложения.
Подгруппа, содержащая конечное число элементов, называется конечной подгруппой.
Пример 2.1.5. Пусть G = <0,1,2,3>- аддитивная абелева группа с групповой операцией, задаваемой следующей таблицей:
Легко проверить, что элементы 0 и 2 образуют множество, замкнутое относительно групповой операции группы G:
Остальные аксиомы групп также имеют место для указанных элементов. Таким образом, элементы 0 и 2 группы 6 образуют подгруппу Н = <0, 2 > относительно групповой операции исходной группы G.
Пусть Н — произвольная подгруппа произвольной группы G.
Предположим, что для любых а и b из Н а*Ь и а -1 также принадлежат Н. Тогда для Ь = а -1 элемент а*Ь = а*а -1 также принадлежит Н. Таким образом, в Н для любого элемента а найдется элемент а*а
что означает выполнение аксиомы групп о существовании единичного элемента. Выполнение аксиомы замкнутости в этом случае очевидно. Предположим теперь, что, помимо предыдущего предположения, для каждого а и b из Н а*Ь -1 также принадлежат Н. Пусть с = = а*Ь
В силу первого предположения, а -1 принадлежит Н и а _1 *а = е. Тогда а- 1 *а*Ь -1 = а _1 *с или Ь -1 = а _1 *с, что означает существование обратного элемента любого элемента Н.
Таким образом, необходимым и достаточным условием того, что непустое подмножество Н элементов группы G образует подгруппу, является выполнение для любых двух элементов а и Ь из Н следующих условий:
- — если а и Ь принадлежат Н, то а*Ь и а- 1 также принадлежат Н
- — если а и Ь принадлежат Н, то а*Ь -1 также принадлежит Н.
Кроме того, следует отметить, что единичный элемент подгруппы всегда совпадает с единичным элементом исходной группы [8].
Очевидно, что подмножество <е>любой группы G, состоящее только из единичного элемента, а также сама группа G удовлетворяют условиям образования подгруппы. Такие подгруппы называются тривиальными подгруппами.
Пусть Н — подгруппа группы G, a g — произвольный фиксированный элемент G. Множество
называется правым смежным классом группы G по подгруппе Н, порождаемым элементом g. Аналогично множество
называется левым смежным классом группы G по подгруппе Н, порождаемым элементом g.
В случае некоммутативной группы G число левых смежных классов группы G по подгруппе Н совпадает с числом правых смежных классов. При этом в общем случае никакой левый смежный класс не совпадает ни с каким правым смежным классом. Исключение составляют так называемые нормальные делители — подгруппы, для любого элемента которых H*g = g*H [10].
Очевидно, что если G — абелева группа, то ее левые смежные классы по подгруппе Н совпадают с правыми. Условимся в случае абелевой группы обозначать смежные классы группы G по подгруппе Н в форме соотношения (2.14).
Пусть Н — подгруппа некоторой конечной группы G.
Предположим, что два элемента одного и того же смежного класса группы G
по подгруппе Н равны: gi*hj = gi*hk. Тогда умножение слева на g;
1 дает равенство hj = hk. Но это противоречит определению подгруппы.
Предположим теперь, что два элемента двух смежных классов g;*H и gk*H
равны: gi*hj = gk*hs. Умножение справа на hj— 1 дает равенство g; = gk*hs*hj
Рассмотрим теперь смежный класс:
В силу замкнутости Н относительно операции *, элемент hs*hj-‘ l *h также принадлежит Н. Обозначив hs*hj-‘*h = h‘, получим:
Итак, рассматриваемые элементы g/ и g* порождают один и тот же смежный класс группы G по подгруппе Н.
Таким образом, смежные классы группы G по подгруппе Н, содержащие хотя бы один общий элемент, совпадают.
Из двух последних соотношений также следует, что число повторяющихся смежных классов группы G по подгруппе Н для каждого элемента g группы G соответствует порядку подгруппы Н.
Для получения смежного класса, совпадающего с некоторым исходным смежным классом g/c* Н и порождаемого отличным от gk элементом G, в качестве порождающего элемента можно взять любой элемент gj-g к* hj данного смежного класса g/c* Н, где е.
Иными словами, если выбрать в качестве элемента, порождающего смежный класс, любой отличный от порождающего элемент уже определенного смежного класса, то получим исходный смежный класс.
Пусть Н = hn> — подгруппа конечной группы G. Пусть g n ) как векторном пространстве GF n (q).
Таким образом, векторное подпространство GF k (q) кода С разбивает исходное векторное пространство GF n (q) на непересекающиеся смежные классы, определяемые следующим образом:
где а — элемент GF n (q), порождающий смежный класс.
Как было показано в предыдущем пункте этого подпараграфа, число элементов каждого смежного класса совпадает с числом кодовых слов кода С. Иными словами, каждый смежный класс а + С содержит q k элементов. Число всех непересекающихся смежных классов определяется соотношением (2.15) и имеет значение q n
Таким образом, векторное пространство GF n (q) можно представить как объединение множеств:
где a s ), s = 0,1. q n
k — 1 — элементы GF n (q), образующие все различные
(не пересекающиеся) смежные классы.
Будем считать, что в соотношении (2.16) а(°) = 0. Тогда смежный класс а(°) + + С совпадает с кодом С.
Как было показано в предыдущем пункте этого подпараграфа, каждый смежный класс вида (2.16) может быть порожден q k различными элементами (векторами) векторного пространства GF n (q).
Пример 2.1.7. Рассмотрим построение отличных от исходного кода смежных классов двоичного линейного (6, 3)-кода С из примера 2.1.4.
Множество всех кодовых слов в данном случае содержит восемь элементов (векторов) векторного пространства GF 6 (2), которые можно представить в виде двоичных последовательностей длиной не более шести двоичных символов:
Число элементов (векторов) каждого смежного класса соответствует числу q k = 8 кодовых слов кода С.
Пусть, например, а = 000001. Тогда смежный класс а + С будет состоять из следующих элементов (векторов):
Нетрудно проверить, что то же множество векторов может быть получено при а = 001100, 010010, 011111, 100111,101010,110100,111001. То есть при любом другом отличном от исходного порождающего элемента а значении, принадлежащем указанному смежному классу.
Согласно соотношению (2.16), число не пересекающихся смежных классов в этом случае: q n
k = 8 (в следующем примере мы укажем их все). Все остальные (отличные от самого кода С) смежные классы могут быть получены, например, при следующих значениях порождающего элемента а:
При этом каждый смежный класс может быть образован, помимо указанных, семью другими значениями вектора а из GF 6 (2), принадлежащими тому же смежному классу.
Любой элемент (вектор) каждого смежного класса, как и сам смежный класс, может быть получен восемью различными способами как а + с для восьми различных значений порождающего элемента а и всех восьми кодовых слов с кода С. Например, элемент 111001 рассмотренного выше в этом примере смежного класса, порожденного элементом а = 000001, может быть получен как а + с для значений а = 000001, 001100, 010010, 011111, 100111, 101010, 110100, 111001 и с = 111000, 110101, 101011, 100110, 011110, 010011, 001101, 000000 соответственно.
4. Пусть С — линейный (л, к)-код над GF(q) и v = с + е — вектор принятого сообщения.
Как было показано выше в этом подпараграфе, вектор v всегда принадлежит одному из q n
k не пересекающихся смежных классов вида (2.16). При отсутствии ошибок вектор v принадлежит смежному классу, совпадающему с кодом С. При ненулевом векторе ошибок вектор i/оказывается в другом смежном классе а + С (пока будем считать, что вес вектора ошибок не превосходит максимального числа t исправляемых кодом ошибок).
Принимая вектор е за порождающий элемент смежного класса е + С, по известному вектору v мы можем определить q k возможных значений вектора е. Очевидно, наиболее вероятным является значение е наименьшего веса.
Элемент (вектор) минимального веса в смежном классе а + С называется лидером смежного класса а + С.
Если в смежном классе а + С несколько векторов имеют минимальный вес, то в качестве лидера смежного класса выбирается любой из них. Таким образом, вектор ошибок принимается равным лидеру смежного класса, которому принадлежит принятый вектор v.
В этом случае аппаратная реализация декодера основана на так называемом табличном методе и требует хранения в памяти устройства всех смежных классов и их лидеров. Подобного рода декодер даже при небольшой длине кода требует значительных аппаратных затрат. Например, для рассмотренного в примерах 2.1.4 и 2.1.7 двоичного линейного (6, 3)-кода требуется хранить в памяти декодера q n
k = 8 смежных классов по q k = 8 двоичных векторов длины п = 6 символов.
Однако табличный декодер может быть несколько упрощен.
Пусть Н — проверочная матрица линейного (л, /с)-кода С. Тогда матрица-строка s(y) = у-Н т размера 1 х к называется синдромом вектора у.
Пусть у = v = с + е — вектор принятого сообщения. Тогда, в силу соотношения (2.10), s(y) = s(e) и, стало быть, равенство нулю s(v) означает принадлежность вектора v коду С. Это в свою очередь означает отсутствие ошибок вектора v. Пока будем считать, что вес вектора ошибок не превосходит максимального числа t исправляемых кодом ошибок. К этому вопросу мы еще вернемся ниже, в конце этого подпараграфа.
Пусть С — линейный (л, к)-код над GF(q), а у и z — два вектора векторного пространства GF n (q).
Очевидно, что s(y) = s(z) тогда и только тогда, когда у-Н т = z-H T или (у — z) х х Н т = 0. Это означает, что вектор у — z принадлежит С. Тогда y-z = Ck- некоторое кодовое слово кода С. Последнее равенство выполняется и в том случае,
если у = а + CiVz = а + Cj, где с,- — су = с*, а — некоторый вектор GF n (q). Равенство синдромов векторов у и z означает принадлежность обоих векторов одному смежному классу.
Таким образом, в силу равенства синдромов s(v) и s(e), вектор v принятого сообщения и вектор ошибок е всегда принадлежат одному смежному классу и по известному синдрому s(v) можно однозначно определить лидер соответствующего смежного класса.
Теперь мы можем описать один из возможных алгоритмов декодирования линейных кодов.
- 1. Определить синдром s(v) принятого сообщения v.
- 2. По известному синдрому s[v) определить соответствующий лидер смежного класса, синдром которого совпадает с s(v).
- 3. Определить исходное кодовое слово с согласно соотношению (2.13) как c-v-e.
Аппаратная реализация декодера в этом случае требует хранения q k синдромов длины п — к (/-ичных символов и q k соответствующих им лидеров смежных классов длины п q-ичных символов в памяти устройства.
Такой метод декодирования называется декодированием линейных кодов по лидерам смежных классов.
Пример 2.1.8. Рассмотрим снова двоичный линейный (6, 3)-код из примеров 2.1.4 и 2.1.7.
В таблице 2.1 показаны смежные классы, лидеры смежных классов и соответствующие им синдромы рассматриваемого кода. Во избежание громоздкости элементы смежных классов представлены соответствующими десятичными значениями. Жирным шрифтом выделены значения лидеров смежных классов.
Лидер смежного класса
< 1, 12, 18,31,39, 42, 52, 57 >
< 2, 15, 17, 28, 36,41,55, 58 >
< 4, 9, 23, 26, 34,47, 49, 60 >
- 001010
- 010100
- 100001
Нетрудно убедиться в том, что синдром любого элемента каждого смежного класса совпадает с синдромом лидера этого смежного класса.
Как видно из таблицы 2.1, в данном случае лидеры смежных классов представлены всеми возможными двоичными векторами веса 1. Эти векторы определены однозначно (в каждом смежном классе только один такой вектор). Таким образом, в случае одиночной ошибки существует единственным образом определяемый синдром, позволяющий однозначно определить вектор ошибки. Поэтому рассмотренный линейный (6,3)-код позволяет гарантированно исправлять одиночную ошибку.
Кроме того, в одном (последнем) смежном классе три лидера веса 2. Это позволяет с небольшой (1/3) вероятностью декодировать двойную ошибку (при условии, что вероятности всех векторов принимаемых сообщений с двойной ошибкой равны).
Очевидно, избыточность рассмотренного в примерах 2.1.4, 2.1.7 и 2.1.8 двоичного линейного (6, 3)-кода немного превышает накладываемые на него корректирующие свойства, так как помимо достаточных для декодирования лидеров смежных классов веса 1 в одном из смежных классов имеют место лидеры веса 2.
Если в качестве лидеров q n
k смежных классов кода удается взять векторы веса t и менее и только их, то код называется совершенным кодом. Если же в качестве лидеров q n
k смежных классов кода удается взять все необходимые для исправления не менее t ошибок векторы веса t и менее, а также несколько векторов веса t + 1, то код называется квазисовершенным кодом.
Проще говоря, у совершенных кодов избыточности «ровно столько, сколько нужно» для исправления не менее чем t ошибок кодового слова.
Возвращаясь к примеру 2.1.4, отметим, что в случае двоичного линейного
- (5,3)-кода вообще нельзя определить однозначно лидеры смежных классов веса
- 1. Пусть, например, проверочная матрица (5,3)-кода имеет вид:
Тогда порождающая матрица:
В этом случае лидер смежного класса веса 1 будет однозначно определен только в одном смежном классе, отличном от смежного класса самого кода. В двух других смежных классах будет по два лидера веса 1. В смежном классе, совпадающем с кодом, также будут два лидера веса 2. Таким образом, данный код не может исправлять одиночную ошибку кодового слова.
Этот вывод подтверждается неравенством (2.5), так как минимальное расстояние (5, 3)-кода равно двум и, следовательно, ни одно целое положительное значение t исправляемых кодом ошибок данному неравенству не удовлетворяет.
Таким образом, при длине информационного сообщения к = 3 двоичных символа и длине проверочной последовательности г=п-к = 2 символа код вообще не позволяет исправлять одиночную ошибку кодового слова, а при длине г — 3 символа уже оказывается не совершенным (хотя и квазисовершенным).
Следует отметить, что совершенные коды, равно как и квазисовершенные, для некоторых значений п и к вообще могут не существовать [10]. Далее мы рассмотрим несколько видов кодов из класса линейных кодов, конструкция которых часто позволяет получить квазисовершенный или даже совершенный код.
Выше мы считали, что вес вектора ошибок не превосходит значение t исправляемых кодом ошибок, так как восстановление исходного кодового слова возможно только в этом случае. В противном случае исходное кодовое слово и принятый вектор могут попасть в один смежный класс, и восстановление кодового слова будет невозможно. Таким образом, число ошибок, превышающее корректирующую способность кода, приводит к ошибочному декодированию.
Если же число ошибок превосходит t и принятый вектор попадает в смежный класс, отличный от смежного класса кода, то декодирование возможно лишь с некоторой (обычно небольшой) вероятностью. При этом возможны два способа декодирования:
- — декодирование любого полученного кодового слова в ближайшее кодовое слово;
- — декодирование только кодовых слов, число ошибок которых не превосходит максимально возможное для данного кода число ошибок t, если число ошибок превышает t, происходит отказ от декодирования.
В первом случае декодер называется полным декодером, а во втором — неполным декодером.
Очевидно, что по сравнению с неполным декодером полный декодер чаще декодирует неправильно. Поэтому полный декодер используется обычно только в тех случаях, когда лучше «угадывать» сообщение, чем вообще не иметь никакой оценки.
В силу указанных особенностей мы будем рассматривать только неполные декодеры.
Метод декодирования линейных кодов по лидерам смежных классов является общим для всех линейных кодов. При этом вполне очевидно, что этот метод связан с трудоемким процессом определения лидеров смежных классов.
Например, для линейного (31, 26)-кода над GF(2) требуется определить 32 смежных класса по 67108864 вектора длины 31 в каждом и найти лидеры каждого смежного класса.
Таким образом, метод декодирования линейных кодов по лидерам смежных классов в общем случае не является приемлемым.
Однако мы можем заранее определить некоторый удобный метод декодирования и на его основе построить линейный код специального вида.
http://studme.org/110002/informatika/vychislenie_sindroma_ispravlenie_oshibok_tsiklicheskih_kodah
http://studref.com/365851/tehnika/dekodirovanie_lineynyh_kodov
Добавил:
Upload
Опубликованный материал нарушает ваши авторские права? Сообщите нам.
Вуз:
Предмет:
Файл:
Скачиваний:
735
Добавлен:
19.05.2015
Размер:
3.09 Mб
Скачать

Матрица называется канонической ступенчатой, если она выглядит так:
Теорема о минимальном весе кода. Код С имеет минималь-
ный вес w тогда и только тогда, когда каждое множество из w–1 столбцов матрицы Н линейно независимы.
Из этой теоремы следует: чтобы найти (n,k)-код с минимальным расстоянием d, достаточно найти (n-k) n-матрицу Н, в которой d любых столбцов независимы.
Из данного (n,k)-кода можно получить новый код, если выбрать две позиции в кодовом слове и переставить в каждом кодовом слове символы на этих позициях. Этот новый код будет отличаться от исходного только видом кодовых слов, а все параметры кода сохранятся. Говорят, что такой код эквивалентен исходному.
Порождающие матрицы G1 и G2 эквивалентных кодов могут быть получены друг из друга с помощью элементарных операций над строками и перестановкой столбцов. Каждая порождающая матрица G эквивалентна некоторой матрице канонического ступенчатого вида. Легко показать, что если порождающие матрицы содержат линейно независимые векторы, то и в матрице канонического вида все строки будут ненулевыми.
Эквивалентную матрицу можно записать в виде:
(5.3)
где 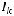
ми k k; 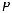
Если порождающая матрица представлена в виде (5.3), то ее называют порождающей матрицей в систематическом виде. Естественно определить проверочную матрицу в систематическом виде:
|
H |
Pò I |
n |
k |
, |
(5.4) |
|||
|
где |
– транспонированная подматрица из выражения (5.3), |
|||||||
|
– единичная подматрица с размерами (n–k) |
(n–k). |
|||||||
|
Очевидно, что если код задан с помощью матриц в система- |
||||||||
|
тическом виде, то и сам код будет систематическим. |
89
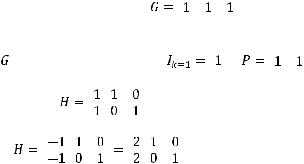
|
Пример 5.2. По заданной матрице |
кода С по- |
|
|
строить проверочную матрицу, считая, что код С а) задан над F2, |
||
|
б) задан над F3. |
||
|
Матрицу составляют подматрицы |
и |
. |
|
Тогда для двоичного случая: |
,
для случая F3:
.
Теорема о систематическом виде порождающей матрицы.
Каждый линейный код эквивалентен систематическому линейному коду.
5.3. Синдромы и смежные классы
Умножение верного кодового слова с на транспонированную проверочную матрицу дает в результате ноль:
сHт=0.
Что произойдет, если заменить верное кодовое слово с на слово, со-
держащее ошибку v=c+e, где e – вектор ошибки: s=vHт=(c+e)Hт=eHт.
Результирующий вектор s=eHт будет содержать в закодированном виде информацию об ошибках, которые повредили верное кодовое слово. Этот вектор принято называть синдромом по аналогии с медицинским термином, который позволяет определить болезнь пациента. Синдром в теории информации позволяет найти ошибку (болезнь) вектора, полученного из канала связи.
Если синдром равен нулю, то можно сделать вывод, что из канала получено верное кодовое слово, или это слово было так повреждено в канале, что превратилось в другое верное кодовое слово. В таких ситуациях декодер принимает решение о том, что получено верное кодовое слово. Если же синдром не равен нулю, то необхо-
90

димо по искаженному кодовому слову попытаться найти верное кодовое слово.
Будем говорить, что все кодовые слова сi C, поврежденные одним и тем же вектором ошибок, лежат в одном смежном классе.
Теорема о смежных классах. Все векторы из одного смежного класса имеют одинаковый синдром, присущий только этому смежному классу.
Доказательство.
Если векторы v1 и v2 (v1 v2) лежат в одном смежном классе, то для них справедливо v1=сi+e, v2=cj+e для некоторого вектора ошибок e и кодовых слов сi, сj. Для каждого кодового слова выполняется сHт=0, отсюда: s1=v1Hт= eHт, s2=v2Hт= eHт, следовательно s1=s2.
Обратное, если s1=s2, тогда (v1–v2)Hт=0, следовательно, разность (v1–v2) является кодовым словом и значит, что v1 и v2 принадлежат одному смежному классу.
Вектор минимального веса в смежном классе называют ли-
дером класса.
Пример 5.3. Рассмотрим код из примера 5.1. Для вектора ошибок, е=10000, построим смежный класс. Для этого все кодовые векторы
{00000, 00111, 01001, 01110, 10010, 10101, 11011, 11100}
просуммируем с вектором ошибок по модулю 2:
{10000, 10111, 11001, 11110, 00010, 00101, 01011, 01100}.
Легко проверить, что всем искаженным векторам соответствует один и тот же синдром s=10. Таким образом, мы построили смежный класс. Лидером этого класса будет вектор минимального веса: 10000, wt(10000)=1. Обратите внимание, что лидером класса является вектор ошибок.
Сколько же существует различных смежных классов? Ровно столько же сколько существует различных синдромов. А сколько существует синдромов? Можно посчитать. Синдром получают в результате умножения вектора на матрицу s=vHт. Исходя из размерно-
91
сти используемых величин видно, что синдром – это вектор длиной n–k. Следовательно, общее число синдромов и общее число смежных классов qn–k, где q – мощность кодового алфавита.
Итак, для кодов, заданных в матричном виде, мы можем кодировать информационные слова, умножая их на порождающую матрицу, умеем с помощью проверочной матрицы определять, является ли вектор, принятый из канала связи, верным кодовым словом. Что нужно делать дальше, чтобы декодировать всю принятую последовательность? Существуют два подхода к построению декодера. Первый – построение универсального декодера, который подходит для работы с произвольными кодами рассматриваемого класса кодов. Второй – построение специального декодера, который учитывает особенности кода и декодирует его либо быстрее универсального, либо с меньшими техническими затратами. Рассмотрим алгоритм работы универсального лидерного декодера блочных линейных кодов.
5.4. Лидерное декодирование
Рассмотрим (n,k)-код, заданный над полем F2 и определенный матрицами G и H. Создадим таблицы, необходимые для работы декодера (табл. 5.1 и 5.2).
Табл. 5.1 кодовых слов состоит из двух столбцов и 2k строк. В первом столбце запишем все информационные слова кода, а во втором – кодовые слова, соответствующие информационным словам. Для получения кодовых слов используем формулу c=iG.
Табл. 5.2 синдромов и лидеров классов содержит 2n–k строк и два столбца. В первом столбце запишем все возможные синдромы, а во втором – соответствующие им лидеры смежных классов, или (что то же самое) векторы ошибок, вызывающие появление соответствующего синдрома.
92
|
Таблица 5.1 |
|
|
Кодовые слова |
|
|
i F2k (информаци- |
c F2n, (кодовые |
|
онные слова) |
слова) |
|
i1 |
c1 |
|
i2 |
c2 |
|
… |
… |
|
i2k |
c2k |
Таблица 5.2 Синдромы и лидеры классов
|
s=vHт |
V (векторы |
|
(синдромы) |
ошибок) |
|
s1 |
v1 |
|
s2 |
v2 |
|
… |
… |
|
s2n k |
v2n k |
Алгоритм декодирования полученного из канала слова v представлен на рис. 5.1.
•Вычислить синдром s=vHт
•Если s=0, то с=v и переход на шаг 3.
•Если s 0, то найти этот синдром в столбце синдромов таблицы синдромов и лидеров классов.
•Просуммировать полученный из канала вектор v и вектор ошибок e, соответствующий синдрому (из таблицы синдромов) с=v+e.
•Считаем слово c верным кодовым словом, находим его во втором столбце таблицы кодовых слов. Соответствующее ему информационное слово (из первого столбца этой таблицы) и будет результатом декодирования.
Рис. 5.1. Алгоритм декодирования кодового слова
Рассмотрим примеры помехоустойчивого кодирования и декодирования с помощью матричного описания кодов.
Пример 5.4. Код С над полем F2 задан порождающей матри-
цей:
93
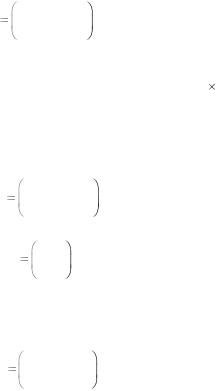
|
G |
1 |
1 |
1 |
0 . |
|
0 |
0 |
1 |
1 |
Определить основные параметры эквивалентного систематического кода и декодировать слово 0101.
Известно, что генерирующая матрица имеет размер k n, где k – число строк матрицы, а n – число столбцов. Скорость кода вычисляется как отношение k/n. Следовательно, в задании рассматривается (4,2)-код, скорость которого равна 2/4=1/2.
Преобразуем матрицу G в систематический вид Gsys=(I|P), для чего переставим второй и четвертый столбцы:
|
Gsys |
1 |
0 |
1 |
1 . |
|
0 |
1 |
1 |
0 |
Таким образом, проверочная подматрица
Отметим, что в данном случае выполняется соотношение Р=Рт. Коды, у которых выполняется такое соотношение, называются самодуальными. Согласно формуле Нsys=(–Pт|I), запишем проверочную матрицу:
|
Í sys |
1 |
1 |
1 |
0 . |
|
1 |
0 |
0 |
1 |
Для построения декодера составим матрицы кодовых слов и матрицы синдромов. Информационными словами i являются все возможные двоичные слова длиной k=2. Кодовые слова c вычислим, используя формулу c=iG. Отметим, что в зависимости от того, в систематическом или несистематическом виде использовать порождающую матрицу, одному и тому же информационному слову могут соответствовать различные кодовые слова. Но так как для декодирования мы будем использовать матрицу Н в систематическом виде, то и матрицу G нужно использовать систематическую. Для используемых матриц должно выполняться равенство GHт=0. Построим таблицу кодовых слов.
|
Информационные слова |
Кодовые слова в систематической форме |
94
|
00 |
0000 |
|
01 |
0110 |
|
10 |
1011 |
|
11 |
1101 |
Построим таблицу синдромов и лидеров классов. Для этого организуем таблицу из двух столбцов и 2n–k=24–2=22=4 строк. Найдем произвольное слово e1 F2n минимального веса Хемминга, не являющееся кодовым и не включенное в предыдущие строки таблицы. Пусть e1=1000, вычисляем синдром этого вектора по формуле:
|
1 |
1 |
||
|
s eH ò (1000) |
1 |
0 |
(11) . |
|
1 |
0 |
||
|
0 |
1 |
Запишем полученный синдром s1=11 в первый столбец таблицы, а во второй столбец запишем вектор e1=1000. Далее находим новое произвольное слово e2 F2 минимального веса Хемминга, не являющееся кодовым и не включенное в предыдущие строки таблицы синдромов. Пусть e2=0100, вычисляем синдром этого вектора:
|
1 |
1 |
||
|
s eH ò (0100) |
1 |
0 |
(10) . |
|
1 |
0 |
||
|
0 |
1 |
Запишем полученный синдром s2=10 и соответствующий ему вектор ошибок во вторую строку таблицы синдромов. Продолжим аналогично до полного заполнения всех 2n–k строк таблицы
|
Синдромы s |
Лидеры классов (векторы ошибок) e |
|
00 |
0000 |
|
11 |
1000 |
|
10 |
0100 |
|
01 |
0001 |
95
Итак, у рассматриваемого кода 4 смежных класса, лидерами которых являются: e0=0000, e1=1000, e2=0100, e3=0001.
При построении таблицы в качестве вектора ошибок не был выбран вектор e=0010. Причина этого в том, что синдром вектора е=0100 совпадает с синдромом вектора e2=0100, что, в свою очередь, происходит из-за того, что данный код является кодом с неравной защитой от ошибок, т. е. число исправляемых ошибок зависит от местоположения ошибок. Из таблицы видно, что есть векторы ошибок весом 1, которые данный код не может исправить. Заранее оценить корректирующую способность кода, можно используя значение минимального кодового расстояния.
Согласно заданию, из канала получено v=0101. Если сравнить его со списком кодовых слов, то видно, что в смысле расстояния Хемминга, полученное слово ближе всего к кодовому слову 1101, т. е. можно предположить, что информационным словом, соответствующим полученному из канала v=0101, будет i=11. Проверим это предположение по алгоритму декодирования.
Вычислим синдром s=11. В таблице синдромов этому синдрому соответствует вектор ошибок e=1000. Суммируем вектор ошибок и вектор, полученный из канала связи: v+e=0101+1000=1101. Находим вектор 1101 в таблице кодовых слов (вектор находится в последней строке таблицы). Соответствующий информационный вектор i=11 и является результатом декодирования.
Оценим теперь корректирующие способности этого кода. Для чего вычислим минимальное расстояние Хемминга для данного кода, как минимум хемминговых весов ненулевых кодовых слов кода С. Веса Хемминга кодовых слов: wth(0110)=2, wth(1011)=3, wth(1101)=2. Минимальное расстояние Хемминга: dmin=min{2, 3, 2}=2 и означает, что рассматриваемый код гарантированно обнаруживает 1 ошибку, а исправляет 0 ошибок.
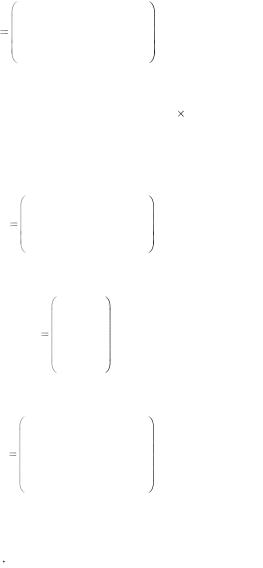
Пример 5.5. Код С над F2 задан проверочной матрицей:
96
|
1 |
1 |
1 |
0 |
1 |
0 |
0 |
|
|
H |
0 |
1 |
1 |
1 |
0 |
1 |
0 . |
|
0 |
0 |
1 |
1 |
1 |
0 |
1 |
Определить основные параметры эквивалентного систематического кода и декодировать слова 001011 и 0111111.
Проверочная матрица Н имеет размер (n–k) n. Следовательно, длина кода n=7, размерность кода k=n–(n–k)=7–3=4, скорость кода равна 4/7.
Приведем матрицу H к систематическому виду. Переставим местами столбцы 2 и 6, 3 и 7.
|
1 |
0 |
0 |
0 |
1 |
1 |
1 |
||
|
H |
sys |
0 |
1 |
0 |
1 |
0 |
1 |
1 . |
|
0 |
0 |
1 |
1 |
1 |
0 |
1 |
Правые четыре столбца матрицы Hsys представляют собой транспонированную проверочную подматрицу Р:
|
0 |
1 |
1 |
|
|
Ð |
1 |
0 |
1 . |
|
1 |
1 |
0 |
|
|
1 |
1 |
1 |
Согласно формуле Gsys=(Ik|P), запишем порождающую матрицу в систематическом виде:
|
1 |
0 |
0 |
0 |
0 |
1 |
1 |
||
|
Gsys |
0 |
1 |
0 |
0 |
1 |
0 |
1 . |
|
|
0 |
0 |
1 |
0 |
1 |
1 |
0 |
||
|
0 |
0 |
0 |
1 |
1 |
1 |
1 |
Построим таблицу кодовых слов. Число кодовых слов определяется как 2k=24=16. Информационными словами i являются все возможные двоичные слова длиной k=4. Кодовые слова c вычислим, используя формулу c=i G и используя матрицу Gsys.
|
i i |
ci |
i i |
ci |
i i |
ci |
|
0000 |
0000000 |
0110 |
0110011 |
1100 |
1100110 |
97

|
0001 |
0001111 |
0111 |
0111100 |
1101 |
1101001 |
|
0010 |
0010110 |
1000 |
1000011 |
1110 |
1110000 |
|
0011 |
0011001 |
1001 |
1001100 |
1111 |
1111111 |
|
0100 |
0100101 |
1010 |
1010101 |
– |
– |
|
0101 |
0101010 |
1011 |
1011010 |
– |
– |
Построим таблицу синдромов. Используем число различных синдромов этого кода 2n–k=27–4=8. У рассматриваемого кода 8 смежных классов, лидерами которых являются: e0=0000000, e1=0000001, e2=0000010, e3=0000100, e4=0001000, e5=0010000, e6=0100000, e7=1000000.
|
Синдромы s |
Лидеры классов |
|
(векторы ошибок) e |
|
|
000 |
0000000 |
|
111 |
0000001 |
|
110 |
0000010 |
|
101 |
0000100 |
|
011 |
0001000 |
|
001 |
0010000 |
|
010 |
0100000 |
|
100 |
1000000 |
Декодируем слово 001011. Вычислим синдром s=0. Нулевой синдром говорит о том, что кодовое слово не содержит ошибок. Найдем его в таблице кодовых слов. Результатом декодирования будет соответствующее ему информационное слово 0010.
Декодируем слово 0111111. Вычислим синдром s = 100. Этому синдрому соответствует вектор ошибок 1000000. Следовательно, верное кодовое слово с=0111111+1000000=1111111. Вектору с соответствует информационное слово 1111.
Оценим корректирующие способности этого кода. Минимальное расстояние Хемминга этого кода найдем как минимум хем-
минговых весов dmin=min{wth(0001111)=4, wth(0010110)=3, wth(0011001)=3, wth(0100101)=3, wth(0101010)=3, wth(0110011)=4, wth(0111100)=4, wth(1000011)=3, wth(1001100)=3, wth(1010101)=4,
98
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Декодирование линейного кода по синдрому
Путь 
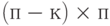

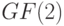

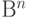
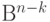
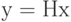
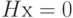
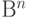
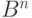
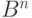

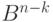
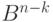
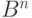
Отображение 
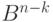


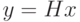
Рис.
7.8.
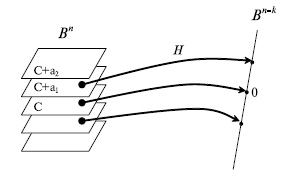
Разбиение пространства Bn на классы равнообразности
Произведение 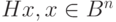
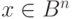
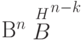
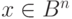
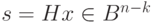
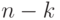
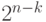
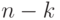


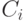
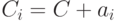


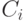

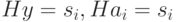
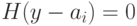

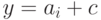
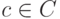





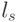
Алгоритм декодирования заключается в следующем. Если получен вектор 
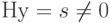
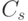
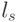
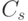
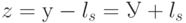
Рассмотрим пример построения кода по заданной проверочной матрице и декодирования полученного сообщения по синдрому. Пусть дана проверочная матрица 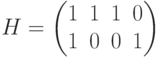



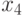


где 
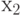
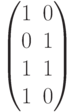
Кодовые слова, рассматриваемые как векторы-столбцы, образуют матрицу кода
Расстояние кода 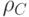
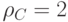
Найдем смежные классы, которые состоят из векторов пространства 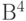
Синдромом является любое возможное значение произведения 
В данном случае имеется 4 синдрома: 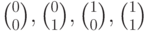

В третьем смежном классе — два потенциальных лидера с весом (нормой), равным 1. Один из них выбирается в качестве лидера произвольно.
Рассмотрим на этом примере процесс декодирования полученного вектора (слова) с использованием синдромов. Пусть передавался кодовый вектор 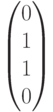
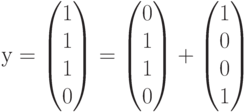
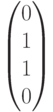
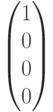

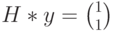

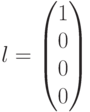
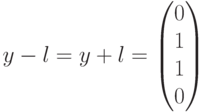


 и получить декодированное информационное слово.
и получить декодированное информационное слово.