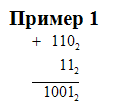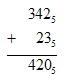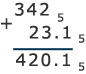Презентация по дисциплине «Основы теории информации» на тему «Пятеричная система счисления»
Презентация по дисциплине«Основы теории информации»на тему«Пятеричная система счисления»
Выполнил:
Студент гр. Кс117
Корешков Никита Николаевич
Принял:
Ситова Анна Алексеевна
Департамент образования Владимирской области
Государственное автономное професиональное образовательное учреждение Владимирской области
«Гусь-Хрустальный технологический колледж» им. Г.Ф. Чехлова
Гусь- Хрустальный, 2019
Содержание Определение Применение
Содержание
Определение
Применение
Возможности перевода
Арифметические действия
Список источников
2
Определение Пятеричная система счисления — позиционная система счисления с основанием 5
1.Определение
Пятеричная система счисления — позиционная система счисления с основанием 5. Число в пятеричной системе изображается пятью цифрами: 0, 1, 2, 3, 4. В этой системе цифра 4 — наибольшая (как 9 — в десятичной), единица высшего разряда не в 10, а в 5 раз больше единицы низшего.
При изображении числа в пятеричной системе счисления, на первом месте справа стоят простые единицы (не свыше 4), на втором — не десятки, а пятерки, на третьем — не сотни, а «25» и т.д.
3
Применение Очевидна связь пятеричной системы со строением человеческой руки
2.Применение
Очевидна связь пятеричной системы со строением человеческой руки.
По свидетельству известного исследователя Африки Стэнли, у ряда африканских племен была распространена пятеричная система счисления. Долгое время пользовались этой системой счисления и в Китае. Также пятеричная система использовалась в Древнем Риме.
4
Применение в римской сисчтеме счисления 5
Применение в римской сисчтеме счисления
5
Возможность перевода Перевод из пятеричной
3.Возможность перевода
Перевод из пятеричной СС в десятеричную СС осуществляется по формуле:
Aq = an-1*qn-1 + an-2*qn-2 + … + a0*q0 + a-1*q-1+ a-2*q-2+ … +a-m*q-m
Где ai – цифры СС
n и m число целых и дробных разрядов
Пример:
4405 перевести в десятеричную СС
4405=0*50+4*51+4*52= 0+20+100=12010
Ответ: 4405= 12010
6
Возможность перевода Перевод из десятеричной
3.Возможность перевода
Перевод из десятеричной СС в пятеричную СС производиться с помощью алгоритма перевода из десятичной системы в пятеричную:
Выполнить деление исходного числа на 5. Если результат деления больше или равен 5, продолжать делить его на 5 до тех пор, пока результат деления не станет равен 1,2,3 или 4. Выписать результат последнего деления и все остатки от деления в обратном порядке в одну строку.
Пример:
4610 переведем в пятеричную СС
46:5=9(остаток 1)
9:5=1(ост. 4)
1:5=0(ост. 1)
Ответ: 4610= 1415
7
Арифметические действия Сложение и вычитание
4.Арифметические действияСложение и вычитание
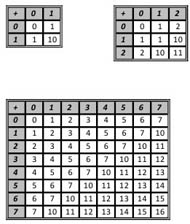
Составим таблицу сложения для пятеричных цифр (будем использовать ее при сложении и вычитании чисел в «столбик»).
|
0 |
1 |
2 |
3 |
4 |
|
1 |
2 |
3 |
4 |
10 |
|
2 |
3 |
4 |
10 |
11 |
|
3 |
4 |
10 |
11 |
12 |
|
4 |
10 |
11 |
12 |
13 |
8
Арифметические действия Пример операции сложения:
4.Арифметические действия
Пример операции сложения:
Найдем 2345 + 3125. Складываем поразрядно в «столбик», используя таблицу сложения. Важно правильно записать числа друг под другом поразрядно справа налево.
Ответ:2345+3125=11025
9
Арифметические действия Пример операции вычитания:
4.Арифметические действия
Пример операции вычитания:
Найдем 2035 – 345. Вычитать будем поразрядно в «столбик», используя таблицу сложения. Важно правильно записать числа друг под другом поразрядно справа налево.
Ответ: 2035-345=1145
10
Арифметические действия Умножение
4.Арифметические действияУмножение
Составим таблицу умножения для пятеричной системы счисления (цифру 0 не включаем, т.к. умножение на 0 всегда равно 0).
|
0 |
1 |
2 |
3 |
4 |
|
1 |
1 |
2 |
3 |
4 |
|
2 |
2 |
4 |
11 |
13 |
|
3 |
3 |
11 |
14 |
22 |
|
4 |
4 |
13 |
22 |
31 |
Пример операции умножения:
135*245 . Умножать будем в «столбик», используя таблицу умножения. Важно правильно записать числа друг под другом поразрядно справа налево.
Ответ: 135*245 =4225
11
Арифметические действия Деление
4.Арифметические действияДеление
Рассмотрим так же пример деления:
Разделим 124215 на 325
Ответ:124215: 325=2135
12
Список источников Worksbase [электронный ресурс]
5.Список источников
Worksbase [электронный ресурс]. – Режим доступа: http://worksbase.ru. – Заглавие с экрана. – (Дата обращения: 4.02.2019)
Uzluga [электронный ресурс]. – Режим доступа: http://uzluga.ru Заглавие с экрана. – (Дата обращения: 4.02.2019)
Wikipedia [электронный ресурс]. – Режим доступа: https://ru.wikipedia.org – Заглавие с экрана. – (Дата обращения: 4.02.2019)
Studfiles [электронный ресурс]. – Режим доступа: https://studfiles.net – Заглавие с экрана. – (Дата обращения: 4.02.2019)
Yaklass [электронный ресурс]. – Режим доступа: https://www.yaklass.ru – Заглавие с экрана. – (Дата обращения: 4.02.2019)
13
Арифметические
операции в рассматриваемых позиционных
системах счисления выполняются по
законам, известным из десятичной
арифметики. Двоичная система счисления
имеет основание 2, и для записи чисел
используются всего две цифры 0 и 1 в
отличие от десяти цифр десятичной
системы счисления.
Рассмотрим
сложение одноразрядных чисел: 0+0=0, 0+1=1,
1+0=0. Эти равенства справедливы как для
двоичной системы, так и для десятичной
системы. Чему же равно 1+1? В десятичной
системе это 2. Но в двоичной системе нет
цифры 2! Известно, что при десятичном
сложении 9+1 происходит перенос 1 в старший
разряд, так как старше 9 цифры нет. То
есть 9+1=10. В двоичной системе старшей
цифрой является 1. Следовательно, в
двоичной системе 1+1=10, так как при сложении
двух единиц происходит переполнение
разряда и производится перенос в старший
разряд. Переполнение разряда наступает
тогда, когда значение числа в нем
становится равным или большим основания.
Для двоичной системы это число равно 2
(102=210).
Продолжая
добавлять единицы, заметим: 102+1=112,
112+1=1002
— произошла «цепная реакция», когда
перенос единицы в один разряд вызывает
перенос в следующий разряд.
Сложение
многоразрядных
чисел происходит по этим же правилам с
учетом возможности переносов из младших
разрядов в старшие.
Вычитание
многоразрядных
двоичных чисел производится с учетом
возможных заёмов
из старших разрядов.
Действия
умножения и деления чисел в двоичной
арифметике можно выполнять по общепринятым
для позиционных систем правилам.
В
основе правил арифметики любой позиционной
системы лежат таблицы
сложения и умножения одноразрядных
чисел.
Таблицы,
аналогичные таблицам арифметических
операций в двоичной системе счисления
(см. п.1.3), составляются для любой
позиционной системы счисления. Пользуясь
такими таблицами, можно выполнять
действия над многозначными числами.
Пример
4.Выполнить
действия в пятеричной системе счисления:
3425+235;
2135.55.
Решение:
Составим
таблицы сложения и умножения для
пятеричной системы счисления:
Рассуждаем
так: два плюс три равно 10 (по таблице); 0
пишем, 1 — в уме. Четыре плюс два равно 11
(по таблице), да еще один, 12. 2 пишем, 1 — в
уме. Три да один равно 4 (по таблице).
Результат — 420.
Рассуждаем
так: трижды три — 14 (по таблице); 4 пишем,
один — в уме. Трижды один дает 3, да плюс
один, — пишем 4. Дважды три (по таблице) —
11; 1 пишем, 1 переносим влево. Окончательный
результат — 1144.
Если
числа, участвующие в выражении,
представлены в разных системах, нужно
сначала привести их к одному основанию.
Пример
5.Сложить
два числа: 178
и 1716.
Решение:
Приведем
число 1716
к основанию 8 посредством двоичной
системы (пробелами условно обозначено
деление на тетрады и триады):
1716=101112=101112=278.
Выполним
сложение в восьмеричной системе:
Таким
образом, арифметические действия в
позиционных системах счисления
выполняются по общим правилам. Необходимо
только помнить, что перенос в следующий
разряд при сложении и заем из старшего
разряда при вычитании определяются
величиной основания системы счисления.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
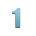
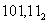
Решение: 
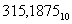
Решение: 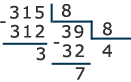
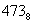
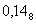
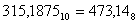
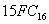
Решение: 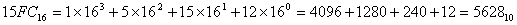
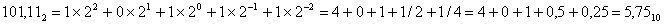

Решение: для решения необходимо каждую цифру шестнадцатеричного числа заменить на соответствующую ей четверку двоичных знаков (там, где знаков меньше четырех, слева добавить нули).
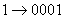
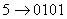
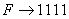
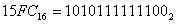

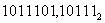
Решение: для решения необходимо разделить целую часть данного числа на группы по четыре цифры справа налево, а дробную часть числа аналогично по четыре двоичных знака от запятой слева направо (если в крайней левой или правой группе окажется меньше четырех цифр, то дополнить их нулями).
0101 1101, 1011 1000 ⇒ 5D,В816.
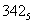
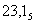
Ответ:
Решение: для того, чтобы производить арифметические операции над пятеричными числами, надо знать таблицу сложения и умножения в пятеричной системе.
Таблицы сложения и умножения в пятеричной системе счисления выглядят так:
|
Таблица сложения |
Таблица умножения |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|

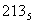
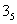
Решение: 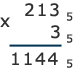
Содержание:
Что такое пятеричная система счисления
Как перевести целое десятичное число в пятеричную систему счисления
Как перевести десятичную дробь в пятеричную систему счисления
Как перевести число из пятеричной системы счисления в десятичную
Как перевести дробное пятеричное число в десятичное
Таблица значений десятичных чисел от 0 до 100 в пятеричной системе счисления
Что такое пятеричная система счисления
Пятеричная система счисления, является позиционной системой счисления, то есть имеется зависимость от позиции цифры в записи числа.
Для записи числа в пятеричной системе счисления используется пять цифр 0, 1, 2, 3 и 4.
Для определения в какой системе счисления записано число, внизу, справа от числа ставят цифру, которая называется основанием системы счисления.
Например, 13045 или 20335
Если вам необходимо перевести число любой системы счисления в другую систему счисления, воспользуйтесь
калькулятором систем счисления с подробным решением онлайн.
Как перевести целое десятичное число в пятеричную систему счисления
Для того, чтобы перевести целое десятичное число в пятеричную систему счисления нужно десятичное число делить на 5 до тех пор, пока неполное частное не будет равно нулю.
В результате будет получено число из остатков деления записанное справа налево.
Например, переведем число 7010 в пятеричную систему счисления:
70 : 5 = 14 остаток: 0
14 : 5 = 2 остаток: 4
2 : 5 = 0 остаток: 2
7010 = 2405
Как перевести десятичную дробь в пятеричную систему счисления
Для того чтобы перевести десятичную дробь в пятеричную систему счисления необходимо сначала перевести целую часть десятичной дроби в пятеричную систему счисления,
а затем дробную часть, последовательно умножать на 5, до тех пор, пока в дробной части произведения не получиться ноль (результатом произведения будет целое число)
или не будет достигнуто необходимое количество знаков после запятой. Если в результате умножения целая часть не равна нулю, тогда необходимо заменить значение целой части на ноль.
В результате будет получено число из целых частей произведений, записанное слева направо.
Например, переведем десятичное число 4.310 в пятеричную систему счисления:
Переведем целую часть
4 : 5 = 0 остаток: 4
410 = 45
Переведем дробную часть
0.3 · 5 = 1.5
0.5 · 5 = 2.5
0.5 · 5 = 2.5
0.5 · 5 = 2.5
0.5 · 5 = 2.5
0.5 · 5 = 2.5
0.5 · 5 = 2.5
0.5 · 5 = 2.5
0.5 · 5 = 2.5
0.5 · 5 = 2.5
0.310 = 0.12222222225
4.310 = 4.12222222225
Пятеричные дроби, как и десятичные могут быть как конечными, так и бесконечными. Не всегда конечная десятичная дробь может быть представлена конечной пятеричной.
В данном примере получается бесконечная периодическая пятеричная дробь, поэтому умножение на 5 можно производить бесконечное число раз и все равно дробная часть частного не будет равна нулю.
В данном случае десятичная дробь 4.3 не может быть точно представлена в пятеричной системе счисления.
К примеру, дробь 12.3610 может быть представлена в пятеричной системе счисления в виде конечной 12.3610 = 22.145.
Как перевести число из пятеричной системы счисления в десятичную
Для того, чтобы перевести число из пятеричной системы счисления в десятичную систему счисления, необходимо записать позиции каждой цифры в числе с права на лево начиная с нуля.
Каждая позиция цифры будет степенью числа 5, так как система счисления 5-ичная. Необходимо последовательно умножить каждое число на 5 в
степени соответствующей позиции числа и затем сложить с последующим произведением следующего числа в степени соответствующей его позиции.
Например, переведем число 40235 в десятичную систему счисления:
| Позиция в числе | 3 | 2 | 1 | 0 |
| Число | 4 | 0 | 2 | 3 |
40235 = 4 ⋅ 53 + 0 ⋅ 52 + 2 ⋅ 51 + 3 ⋅ 50 = 51310
Как перевести дробное пятеричное число в десятичное
Для того, чтобы перевести дробное пятеричное число в десятичное, необходимо записать дробное пятеричное число, убрав точку и затем сверху расставить индексы.
Индексы в дробной части числа начинаются от -1 и продолжаются на уменьшение вправо, индексы в целой части начинаются с 0 и ставятся с права на лево по возрастанию.
Каждая позиция цифры (индекс) будет степенью числа 5, так как система счисления 5-ичная. Необходимо последовательно умножить каждое число на
5 в степени соответствующей позиции числа и затем сложить с последующим произведением следующего числа в степени соответствующей его позиции.
Например, переведем дробное пятеричное число 21.135 в десятичное:
| Позиция в числе | 1 | 0 | -1 | -2 |
| Число | 2 | 1 | 1 | 3 |
21.135 = 2 ⋅ 51 + 1 ⋅ 50 + 1 ⋅ 5-1 + 3 ⋅ 5-2 = 11.3210
Таблица значений десятичных чисел от 0 до 100 в пятеричной системе счисления
| Значение числа в десятичной системе счисления | Значение числа в пятеричной системе счисления |
| 010 | 05 |
| 110 | 15 |
| 210 | 25 |
| 310 | 35 |
| 410 | 45 |
| 510 | 105 |
| 610 | 115 |
| 710 | 125 |
| 810 | 135 |
| 910 | 145 |
| 1010 | 205 |
| 1110 | 215 |
| 1210 | 225 |
| 1310 | 235 |
| 1410 | 245 |
| 1510 | 305 |
| 1610 | 315 |
| 1710 | 325 |
| 1810 | 335 |
| 1910 | 345 |
| 2010 | 405 |
| 2110 | 415 |
| 2210 | 425 |
| 2310 | 435 |
| 2410 | 445 |
| 2510 | 1005 |
| 2610 | 1015 |
| 2710 | 1025 |
| 2810 | 1035 |
| 2910 | 1045 |
| 3010 | 1105 |
| 3110 | 1115 |
| 3210 | 1125 |
| 3310 | 1135 |
| 3410 | 1145 |
| 3510 | 1205 |
| 3610 | 1215 |
| 3710 | 1225 |
| 3810 | 1235 |
| 3910 | 1245 |
| 4010 | 1305 |
| 4110 | 1315 |
| 4210 | 1325 |
| 4310 | 1335 |
| 4410 | 1345 |
| 4510 | 1405 |
| 4610 | 1415 |
| 4710 | 1425 |
| 4810 | 1435 |
| 4910 | 1445 |
| 5010 | 2005 |
| Значение числа в десятичной системе счисления | Значение числа в пятеричной системе счисления |
| 5110 | 2015 |
| 5210 | 2025 |
| 5310 | 2035 |
| 5410 | 2045 |
| 5510 | 2105 |
| 5610 | 2115 |
| 5710 | 2125 |
| 5810 | 2135 |
| 5910 | 2145 |
| 6010 | 2205 |
| 6110 | 2215 |
| 6210 | 2225 |
| 6310 | 2235 |
| 6410 | 2245 |
| 6510 | 2305 |
| 6610 | 2315 |
| 6710 | 2325 |
| 6810 | 2335 |
| 6910 | 2345 |
| 7010 | 2405 |
| 7110 | 2415 |
| 7210 | 2425 |
| 7310 | 2435 |
| 7410 | 2445 |
| 7510 | 3005 |
| 7610 | 3015 |
| 7710 | 3025 |
| 7810 | 3035 |
| 7910 | 3045 |
| 8010 | 3105 |
| 8110 | 3115 |
| 8210 | 3125 |
| 8310 | 3135 |
| 8410 | 3145 |
| 8510 | 3205 |
| 8610 | 3215 |
| 8710 | 3225 |
| 8810 | 3235 |
| 8910 | 3245 |
| 9010 | 3305 |
| 9110 | 3315 |
| 9210 | 3325 |
| 9310 | 3335 |
| 9410 | 3345 |
| 9510 | 3405 |
| 9610 | 3415 |
| 9710 | 3425 |
| 9810 | 3435 |
| 9910 | 3445 |
| 10010 | 4005 |
Материал по информатике «Таблицы сложения чисел в различных системах счисления»
В разработке содержатся таблицы сложения в двоичной, троичной, пятеричной, восьмеричной и шестнадцатиричной системах счисления.
Селезнева Светлана Геннадьевна
31.08.2014
Описание разработки
В разработке содержатся таблицы сложения в двоичной, троичной, пятеричной, восьмеричной и шестнадцатиричной системах счисления.
Весь материал — смотрите документ.
-80%
Курсы профессиональной переподготовке
Учитель, преподаватель информатики в начальной школе
Продолжительность 300 или 600 часов
Документ: Диплом о профессиональной переподготовке
13800 руб.
от 2760 руб.
Подробнее
Получите комплекты видеоуроков + онлайн версии
Информатика 9 класс ФГОС
Электронная тетрадь по информатике 7…
Информатика 6 класс ФГОС
Информатика и ИКТ 11 класс (к учебнику…
Информатика 10 класс ФГОС
Информатика 4 класс ФГОС
Электронная тетрадь по информатике 6…
Информатика 8 класс
Скачать разработку
Сохранить у себя:

Файлы по информатике




0
Добавить эту разработку
в избранное
Похожие файлы
-
Программа по информатике 10 — 11 класс по учебнику Фиошина
-
Мастер-класс по информатике «Моделирование поразрядных вычислений в различных системах счисления в среде электронных таблиц»
-
Табличный процессор MS Excel 2007
-
Итоговая контрольная работа по информатике (8 класс)
-
Разработка урока по информатике Виртуальные музеи вычислительной техники
Комментарии
0
Чтобы добавить комментарий зарегистрируйтесь или войдите на сайт