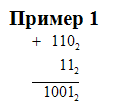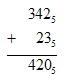Как составить таблицу умножения в позиционных системах счисления

Информатика, 10 класс. Урок № 9.

Тема урока — Арифметические операции в позиционных системах счисления

Урок посвящен теме «Арифметические операции в позиционных системах счисления»». В ходе урока школьники научатся складывать, вычитать, умножать и делить в разных позиционных системах счисления.

Ключевые слова:

— позиционные системы счисления,

— арифметические операции в системе счисления с основанием q,

— таблица сложения,

— таблица умножения.

Учебник:

— Информатика. 10 класс: учебник / Л. Л. Босова, А. Ю. Босова. — М.: БИНОМ. Лаборатория знаний, 2016. — 288 с.

— Математические основы информатики: учебное пособие / Е. В. Андреева, Л. Л Босова, И. Н. Фалина — М.: БИНОМ. Лаборатория знаний, 2008. — 328 с.

Мы продолжаем изучать позиционные системы счисления. Вы узнали, что позиционные системы счисления бывают разные: десятичная, двоичная, восьмеричная и шестнадцатеричная. Вы научились переводить числа из одной системы счисления в другую. Но зачем нам с вами это надо? Конечно для того, чтобы производить расчеты. С 1 класса нас учат производить расчеты в десятичной системе счисления. А как вы думаете, можно ли производить расчеты в произвольной позиционной системе счисления? И зачем это нужно?

Двоичная система счисления издавна была предметом пристального внимания многих ученых. Первый кто заговорил о двоичном кодировании, был Лейбниц Готфрид Вильгельм. Он написал трактат «Expication de l’Arithmetique Binary» — об использовании двоичной системы счисления в вычислительных машинах. В рукописи на латинском языке, написанной в марте 1679 года, Лейбниц разъясняет, как выполнять вычисление в двоичной системе, в частности умножение, а позже в общих чертах разрабатывает проект вычислительной машины, работающей в двоичной системе счисления. Вот что он пишет: « Вычисления такого рода можно было бы выполнять и на машине». Эти слова подчеркивают универсальность алфавита, состоящего из двух символов.

Все позиционные системы счисления “одинаковы”, а именно, во всех них выполняются арифметические операции по одним и тем же правилам:

— справедливы одни и те же законы арифметики: коммутативный (переместительный), ассоциативный (сочетательный), дистрибутивный (распределительный);

— справедливы правила сложения, вычитания, умножения и деления столбиком.

Мы узнаем на уроке:

1. как строить таблицы сложения и умножения в заданной позиционной системе счисления;
2. как выполнять сложение, умножение, вычитание и деление чисел, записанных в двоичной, восьмеричной и шестнадцатеричной системах счисления;
3. как подсчитывать количество единиц в двоичной записи числа, являющегося результатом суммирования или вычитания степеней двойки.

Арифметические операции в позиционных системах счисления с основанием q выполняются по правилам, аналогичным правилам, действующим в десятичной системе счисления.

Рассмотрим сложение.

Чтобы в системе счисления с основанием q получить сумму S двух чисел A и B, надо просуммировать образующие их цифры по разрядам i справа налево:

1. если a_i + b_i < q, то s_i = a_i + b_i,
   старший (i + 1)-й разряд не изменяется
2. если a_i + b_i ≥ q, то s_i = a_i + b_i – q,
   старший (i + 1)-й разряд увеличивается на 1

Можно составить таблицу сложения:

Давайте рассмотрим правило сложения на примере в двоичной системе счисления

Это мы рассмотрели сложение в двоичной системе счисления, а теперь сложим два числа в троичной, восьмеричной и шестнадцатеричной системе счисления.

— 1 + 2 = 3 ≥ 3
записываем 3 – 3 = 0 под 1-м разрядом,
а 2-й разряд увеличиваем на 1

— 1 + 2 = 3 ≥ 3
записываем 3 – 3 = 0 под 2-м разрядом,
а 3-й разряд увеличиваем на 1

— 1 + 1 + 2 = 4 ≥ 3
записываем 4 – 3 = 1 под 3-м разрядом,
а 4-й разряд увеличиваем на 1

— 1 + 1 = 2 < 3
записываем 2 под 4-м разрядом

Сложим в восьмеричной и шестнадцатеричной системе счисления.

Теперь разберём вычитание в системах счисления с основанием q.

Чтобы в системе счисления с основанием q получить разность R двух чисел A и B, надо вычислить разности образующих их цифр по разрядам i справа налево:

— если a_i ≥ b_i, то r_i = a_i – b_i,
старший (i + 1)-й разряд не изменяется

— если a _i < b _i , то r_i = q + a_i – b_i ,

старший (i + 1)-й разряд уменьшается на 1

Рассмотрим правило вычитания в двоичной системе счисления на примере.

Рассмотрим правило вычитания в троичной системе счисления, где q=3

1. 1 ≥ 0
   записываем 1 – 0 = 1 под 1-м разрядом
2. 0 < 1
   записываем 3 + 0 – 1 = 2 под 2-м разрядом,
   делая заем в 3-м разряде
3. 0 < 2
   записываем 3 + 0 – 2 = 1 под 3-м разрядом,
   делая заем в 4-м разряде
4. 0 = 0
   записываем 0 под 4-м разрядом
5. 0 < 1
   записываем 3 + 0 – 1 = 2 под 5-м разрядом,
   делая заем в 6-м разряде

В восьмеричной и шестнадцатеричной системе выполним вычитание.

Как же выполняется умножение чисел в системе счисления с основанием q? Если мы рассмотрим таблицы умножения в двоичной, троичной, восьмеричной и шестнадцатеричной системах счисления, то увидим, что алгоритм умножения точно такой же, как и в десятичной системе.

Чтобы в системе счисления q получить произведение M многозначного числа A и однозначного числа b, надо вычислить произведения b и цифр числа A по разрядам i:

1. если a_i · b <q, то m_i = a_i · b,
   старший (i + 1)-й разряд не изменяется
2. если a_i · b ≥ q, то m_i = a_i · b mod q,
   старший (i + 1)-й разряд увеличивается на a_i · b div q

Рассмотрим примеры:

— 2 · 2 = 4 ≥ 3
записываем 4 mod 3 = 1 под 1-м разрядом,
2-й разряд увеличиваем на 4 div 3 = 1

— 1 · 2 + 1 = 3 ≥ 3
записываем 3 mod 3 = 0 под 2-м разрядом,
3-й разряд увеличиваем на 3 div 3 = 1

— 2 · 2 + 1 = 3 ≥ 3
записываем 5 mod 3 = 2 под 3-м разрядом,
4-й разряд увеличиваем на 5 div 3 = 1

— 2 · 1 + 1 = 3 ≥ 3
записываем 3 mod 3 = 0 под 4-м разрядом
и в 5-й разряд записываем 3 div 3 = 1

По этому алгоритму выполним умножение в других системах счисления.

Умножение многозначного числа на многозначное число выполняется столбиком. При этом два множителя располагаются один под другим так, чтобы разряды чисел совпадали (находились в одном столбце). Посмотрим пример в двоичной системе счисления.

Деление нельзя свести к поразрядным операциям над цифрами, составляющими число. Деление чисел в системе счисления с произвольным основанием q выполняется так же, как и в десятичной системе счисления. А значит, нам понадобятся правила умножения и вычитания чисел в системе счисления с основанием q. Давайте разберем деление в двоичной системе.

И попробуем поделить в восьмеричной системе счисления.

В числе 233₈ поместится 2 ∙ 73₈ = 166₈

В числе 456₈ поместится 5 ∙ 73₈ = 447₈

В числе 73₈ поместится 1 ∙ 73₈ = 73₈

Теперь мы знаем, как производится арифметика в двоичной системе счисления. Используя таблицы, мы можем решить любой пример.

Давайте рассмотрим пример:

Задание 1. Найдём количество единиц в двоичной записи числа, являющегося результатом десятичного выражения

2⁴⁰⁰⁰ + 4²⁰¹⁶ + 2²⁰¹⁸ – 8⁶⁰⁰ + 6

Решение:

Представим все операнды исходного выражения в виде степеней двойки:

Исходное выражение 2⁴⁰⁰⁰ + 4²⁰¹⁶ + 2²⁰¹⁸ – 8⁶⁰⁰ + 6

примет вид 2⁴⁰⁰⁰ + 2⁴⁰³² + 2²⁰¹⁸ – 2¹⁸⁰⁰ + 2² + 2¹

Перепишем выражение в порядке убывания степеней: 2⁴⁰³² + 2⁴⁰⁰⁰ + 2²⁰¹⁸ – 2¹⁸⁰⁰ + 2² + 2¹

Для работы с десятичными числами вида 2ⁿ полезно иметь в виду следующие закономерности в их двоичной записи:

2¹ = 10 = 1 + 1; 2² = 100 = 11 + 1; 2³ = 1000 = 111 + 1; …

В общем виде

Для натуральных n и m таких, что n > m, получаем:

Эти соотношения позволят подсчитать количество «1» в выражении без вычислений. Двоичные представления чисел 2⁴⁰³² и 2⁴⁰⁰⁰ внесут в двоичное представление суммы по одной «1». Разность 2²⁰¹⁸ – 2¹⁸⁰⁰ в двоичной записи представляет собой цепочку из 218 единиц и следующих за ними 1800 нулей. Слагаемые 2² и 2¹ дают ещё 2 единицы.

Так как в задаче надо найти единицы, то получаем:

Итого: 1 + 1 + 218 + 1 + 1 = 222.

Давайте разберем еще одну задачу.

Найдём количество цифр в восьмеричной записи числа, являющегося результатом десятичного выражения: 2²⁹⁹ + 2²⁹⁸ + 2²⁹⁷ + 2²⁹⁶.

Решение:

Двоичное представление исходного числа имеет вид:

Всего в этой записи 300 двоичных символов. При переводе двоичного числа в восьмеричную систему счисления каждая триада исходного числа заменяется восьмеричной цифрой. Следовательно, восьмеричное представление исходного числа состоит из 100 цифр.

Ответ: 100 цифр

Итак, сегодня вы узнали, что арифметические операции в позиционных системах счисления с основанием q выполняются по правилам, аналогичным правилам, действующим в десятичной системе счисления. Если необходимо вычислить значение арифметического выражения, операнды которого представлены в различных системах счисления, можно:

1. все операнды представить в привычной нам десятичной системе счисления;
2. вычислить результат выражения в десятичной системе счисления;
3. перевести результат в требуемую систему счисления.

Для работы с десятичными числами вида 2ⁿ, полезно иметь ввиду следующие закономерности в их двоичной записи:

Для натуральных n и m таких, что n > m, получаем:

Тренировочный модуль.

1 задание

Выберите выражения, значения которых одинаковые.

Возьми карандаш и подчеркни результат сложения

14₅ + 32₅

22₅ 103₅ 43₅ 101₅

Реши кросснамбер

По вертикали:

1. Найди сумму и запиши в двоичной системе счисления 153₈ + F9₁₆

3. Найди произведение и запиши в двоичной системе счисления 122₃ * 11₂

6. Выполни операцию деления 10010000₂ / 1100₂

7. Реши пример, ответ запиши в десятичной системе счисления (564₈ + 234₈) * C₁₆

По горизонтали:

2. Разность двоичных чисел 11001100 — 11111

4. Найти разность 167₈ – 56₈

5. Выполнить операцию деления 41612₈ / 12₈

8. Найти разность 12E₁₆ – 79₁₆ ответ запиши в десятичной системе счисления

Проверь себя:

Рассмотрим примеры умножения в разных позиционных системах счисления.

Рис. (1). Таблица умножения в двоичной СС

Рис. (2). Таблица умножения в восьмеричной СС

Рис. (3). Таблица умножения в шестнадцатеричной СС

1. Двоичная система счисления.

Умножение в двоичной системе счисления по факту сводится к сложению.

Рис. (4). Умножение

в двоичной СС

2. Восьмеричная система счисления.

Рис. (5). Умножение

в восьмеричной СС

3. Шестнадцатеричная система счисления.

Рис. (6). Умножение

в шестнадцатеричной СС

Арифметические
операции в рассматриваемых позиционных
системах счисления выполняются по
законам, известным из десятичной
арифметики. Двоичная система счисления
имеет основание 2, и для записи чисел
используются всего две цифры 0 и 1 в
отличие от десяти цифр десятичной
системы счисления.

Рассмотрим
сложение одноразрядных чисел: 0+0=0, 0+1=1,
1+0=0. Эти равенства справедливы как для
двоичной системы, так и для десятичной
системы. Чему же равно 1+1? В десятичной
системе это 2. Но в двоичной системе нет
цифры 2! Известно, что при десятичном
сложении 9+1 происходит перенос 1 в старший
разряд, так как старше 9 цифры нет. То
есть 9+1=10. В двоичной системе старшей
цифрой является 1. Следовательно, в
двоичной системе 1+1=10, так как при сложении
двух единиц происходит переполнение
разряда и производится перенос в старший
разряд. Переполнение разряда наступает
тогда, когда значение числа в нем
становится равным или большим основания.
Для двоичной системы это число равно 2
(10₂=2₁₀).

Продолжая
добавлять единицы, заметим: 10₂+1=11₂,
11₂+1=100₂
— произошла «цепная реакция», когда
перенос единицы в один разряд вызывает
перенос в следующий разряд.

Сложение
многоразрядных
чисел происходит по этим же правилам с
учетом возможности переносов из младших
разрядов в старшие.

Вычитание
многоразрядных
двоичных чисел производится с учетом
возможных заёмов
из старших разрядов.

Действия
умножения и деления чисел в двоичной
арифметике можно выполнять по общепринятым
для позиционных систем правилам.

В
основе правил арифметики любой позиционной
системы лежат таблицы
сложения и умножения одноразрядных
чисел.

Таблицы,
аналогичные таблицам арифметических
операций в двоичной системе счисления
(см. п.1.3), составляются для любой
позиционной системы счисления. Пользуясь
такими таблицами, можно выполнять
действия над многозначными числами.

Пример
4.Выполнить
действия в пятеричной системе счисления:
342₅+23₅;
213₅^.5₅.
     Решение:
     Составим
таблицы сложения и умножения для
пятеричной системы счисления:

Рассуждаем
так: два плюс три равно 10 (по таблице); 0
пишем, 1 — в уме. Четыре плюс два равно 11
(по таблице), да еще один, 12. 2 пишем, 1 — в
уме. Три да один равно 4 (по таблице).
Результат — 420.

Рассуждаем
так: трижды три — 14 (по таблице); 4 пишем,
один — в уме. Трижды один дает 3, да плюс
один, — пишем 4. Дважды три (по таблице) —
11; 1 пишем, 1 переносим влево. Окончательный
результат — 1144.
     Если
числа, участвующие в выражении,
представлены в разных системах, нужно
сначала привести их к одному основанию.

Пример
5.Сложить
два числа: 17₈
и 17₁₆.
     Решение:
     Приведем
число 17₁₆
к основанию 8 посредством двоичной
системы (пробелами условно обозначено
деление на тетрады и триады):
17₁₆=10111₂=10111₂=27₈.
     Выполним
сложение в восьмеричной системе:

     

     Таким
образом, арифметические действия в
позиционных системах счисления
выполняются по общим правилам. Необходимо
только помнить, что перенос в следующий
разряд при сложении и заем из старшего
разряда при вычитании определяются
величиной основания системы счисления.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

Информатика. 10 класса. Босова Л.Л. Оглавление

§12. Арифметические операции в позиционных системах счисления

---

Арифметические операции в позиционных системах счисления

Арифметические операции в позиционных системах счисления с основанием q выполняются по правилам, аналогичным правилам, действующим в десятичной системе счисления.

В начальной школе для обучения детей счёту используют таблицы сложения и умножения. Подобные таблицы можно составить для любой позиционной системы счисления.

12.1. Сложение чисел в системе счисления с основанием q

Рассмотрите примеры таблиц сложения в троичной (табл. 3.2), восьмеричной (табл. 3.4) и шестнадцатеричной (табл. 3.3) системах счисления.

Таблица 3.2

Сложение в троичной системе счисления

Таблица 3.3

Сложение в шестнадцатеричной системе счисления

Таблица 3.4

Сложение в восьмеричной системе счисления

Примеры:

12.2. Вычитание чисел в системе счисления с основанием q

Примеры:

12.3. Умножение чисел в системе счисления с основанием q

Рассмотрите примеры таблиц умножения в троичной (табл. 3.5), восьмеричной (табл. 3.6) и шестнадцатеричной (табл. 3.7) системах счисления.

Таблица 3.5

Умножение в троичной системе счисления

Таблица 3.6

Умножение в восьмеричной системе счисления

Таблица 3.7

Умножение в шестнадцатеричной системе счисления

Рассмотрим алгоритм умножения многозначного числа на однозначное.

Примеры:

Умножение многозначного числа на многозначное число выполняется столбиком. При этом два множителя располагаются один под другим так, чтобы разряды чисел совпадали (находились в одном столбце).

Если один из множителей или оба множителя оканчиваются нулями, то числа записываются так, чтобы в одном столбце оказались их самые младшие разряды с цифрами, отличными от нуля. Нули переносятся в итоговое произведение, а в поле записи поэтапных произведений не заносятся.

Поэтапные (разрядные) произведения складываются по разрядам и под чертой записывается результат.

Примеры:

12.4. Деление чисел в системе счисления с основанием q

Деление нельзя свести к поразрядным операциям над цифрами, составляющими число.

Деление чисел в системе счисления с произвольным основанием q выполняется так же, как и в десятичной системе счисления.

Примеры:

12.5. Двоичная арифметика

Арифметика двоичной системы счисления основывается на использовании следующих таблиц сложения, вычитания и умножения:

Рассмотрим несколько простых, но очень важных примеров на сложение и вычитание в двоичной системе счисления.

Пример 1. Найдём количество единиц в двоичной записи числа, являющегося результатом десятичного выражения 2⁴⁰⁰⁰ + 4²⁰¹⁶ + 2²⁰¹⁸ — 8⁶⁰⁰ + 6

Представим все операнды исходного выражения в виде степеней двойки:

4²⁰¹⁶ = (2 • 2)²⁰¹⁶ = (2²)²⁰¹⁶ = 2^2•2016 = 2⁴⁰³²,

8⁶⁰⁰ = (2³)⁶⁰⁰ = 2¹⁸⁰⁰ ,

6 = 4 + 2 = 2² + 2¹.

Исходное выражение примет вид:

2⁴⁰⁰⁰ + 4²⁰¹⁶ + 2²⁰¹⁸ — 8⁶⁰⁰ + 6 = 2⁴⁰⁰⁰ + 2⁴⁰³² + 2²⁰¹⁸ — 2¹⁸⁰⁰ + 2² + 2¹

Перепишем выражение в порядке убывания степеней:

2⁴⁰³² + 2⁴⁰⁰⁰ + 2²⁰¹⁸ — 2¹⁸⁰⁰ + 2² + 2¹

В общем виде:

Для натуральных n и m таких, что n > m, получаем:

Эти соотношения позволят нам подсчитать количество единиц в нашем выражении, не прибегая к его вычислению.

Действительно, двоичные представления чисел 2⁴⁰³² и 2⁴⁰⁰⁰ внесут в двоичное представление суммы по одной единице. Разность 2²⁰¹⁸ — 2¹⁸⁰⁰ в двоичной записи представляет собой цепочку из 218 единиц и следующих за ними 1800 нулей. Слагаемые 2² и 2¹ дают ещё 2 единицы.

Итого: 1 + 1 + 218 + 1 + 1 = 222.

Пример 2. Найдём количество цифр в восьмеричной записи числа, являющегося результатом десятичного выражения 2²⁹⁹ + 2²⁹⁸ + 2²⁹⁷ + 2²⁹⁶.

Двоичное представление исходного числа имеет вид:

Всего в этой записи 300 двоичных символов. При переводе двоичного числа в восьмеричную систему счисления каждая триада исходного числа заменяется восьмеричной цифрой. Следовательно, восьмеричное представление исходного числа состоит из 100 цифр.

---

САМОЕ ГЛАВНОЕ

Арифметические операции в позиционных системах счисления с основанием q выполняются по правилам, аналогичным правилам, действующим в десятичной системе счисления.

Для работы с десятичными числами вида 2п полезно иметь в виду следующие закономерности в их двоичной записи:

Для натуральных пит таких, что n > m, получаем:

Для натуральных n и m таких, что n > m, получаем:

---

Вопросы и задания

1. Выполните арифметические операции над двоичными числами: 1) 10010011 + 101101; 2) 110010,11 + 110110,11; 3) 110101110 — 10111111; 4) 111110 • 100010; 5) 11111100101 : 101011.

2. Какое число следует за каждым из данных: 1) 223₄; 2) 677₈; 3) 2222₃; 4) 1001₂?

3. Какое число предшествует каждому из данных: 1) 222₃; 2) 1000₅; 3) 233₄; 4) 1001₂?

4. Сумму восьмеричных чисел 17 + 1700 + 170000 + 17000000 + 1700000000 перевели в шестнадцатеричную систему счисления. Найдите в шестнадцатеричной записи числа, равного этой сумме, пятую цифру слева.

5. Вычислите значение выражения: 1) (1111101₂ + AF₁₆) : 36₈; 2) 125₈ + 11101₂ • А2₁₆ — 1417₈.

6. Найдите среднее арифметическое следующих чисел: 1) 10010110₂, 1100100₂ и 110010₂; 2) 226₈, 64₁₆ и 62₈.

7. В примерах на сложение восстановите неизвестные цифры, обозначенные знаком вопроса, определив вначале, в какой системе счисления эти числа записаны.

8. Даны 4 целых числа, записанные в двоичной системе счисления: 11000000, 11000011, 11011001, 11011111.

9. Сколько единиц в двоичной записи числа 4²⁰¹⁴ + 2²⁰¹⁵ — 9?

*10. Сколько единиц в двоичной записи числа 8⁴⁰²⁴ — 4^16O5 + 2¹⁰²⁴ — 126?

11. Сколько цифр в восьмеричной записи числа 2¹⁰²⁴ + 2¹⁰²⁶?

12. Какая первая цифра в шестнадцатеричной записи числа 2¹⁰²⁴ + 2¹⁰²⁵?

---

§ 11. Перевод чисел из одной позиционной системы счисления в другую
§ 12. Арифметические операции в позиционных системах счисления
§ 13. Представление чисел в компьютере

---

Двоичная система счисления

Восьмеричная система счисления

	0	1	2	3	4	5	6	7
0	0	0	0	0	0	0	0	0
1	0	1	2	3	4	5	6	7
2	0	2	4	6	10	12	14	16
3	0	3	6	11	14	17	22	25
4	0	4	10	14	20	24	30	34
5	0	5	12	17	24	31	36	43
6	0	6	14	22	30	36	44	52
7	0	7	16	25	34	43	5	61

Шестнадцатеричная система счисления

	0	1	2	3	4	5	6	7	8	9	A (10)	B (11)	C (12)	D(13)	E (14)	F (15)
0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0
1	0	1	2	3	4	5	6	7	8	9	A	B	C	D	E	F
2	0	2	4	6	8	A	C	E	10	12	14	16	18	1A	1C	1E
3	0	3	6	9	C	F	12	15	18	1B	1E	21	24	27	2A	2D
4	0	4	8	C	10	14	18	1C	20	24	28	2C	30	34	38	3C
5	0	5	A	F	14	19	1E	23	28	2D	32	37	3C	41	46	4B
6	0	6	C	12	18	1E	24	2A	30	36	3C	42	48	4E	54	5A
7	0	7	E	15	1C	23	2A	31	38	3F	46	4D	54	5B	62	69
8	0	8	10	18	20	28	30	38	40	48	50	58	60	68	70	78
9	0	9	12	1B	24	2D	36	3F	48	51	5A	63	6C	75	7E	87
A (10)	0	A	14	1E	28	32	3C	46	50	5A	64	6E	78	82	8C	96
B (11)	0	B	16	21	2C	37	42	4D	58	63	6E	79	84	8F	9A	A5
C (12)	0	C	18	24	30	3C	48	54	60	6C	78	84	90	9C	A8	B4
D (13)	0	D	1A	27	34	41	4E	5B	68	75	82	8F	9C	A9	B6	C3
E (14)	0	E	1C	2A	38	46	54	62	70	7E	8C	9A	A8	B6	C4	D2
F (15)	0	F	1E	2D	3C	4B	5A	69	78	87	96	A5	B4	C3	D2	E1

Двоичная система счисления

Восьмеричная система счисления

	0	1	2	3	4	5	6	7
0	0	0	0	0	0	0	0	0
1	0	1	2	3	4	5	6	7
2	0	2	4	6	10	12	14
3	0	3	6		14	17	22	25
4	0	4	10	14	20		30	34
5	0	5	12	17		31	36
6	0	6	14	22	30	36	44	52
7	0	7		25	34		5	61

Шестнадцатеричная система счисления

	0	1	2	3	4	5	6	7	8	9	A (10)	B (11)	C (12)	D(13)	E (14)	F (15)
0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0
1	0	1	2	3	4	5	6	7	8	9	A	B	C	D	E	F
2	0	2	4	6	8	A	C		10	12	14	16	18		1C	1E
3	0	3	6	9		F	12	15	18	1B		21	24	27	2A	2D
4	0	4	8		10	14	18	1C	20		28	2C	30	34	38	3C
5	0	5	A	F	14		1E	23	28	2D	32	37		41	46	4B
6	0	6	C	12	18	1E	24	2A		36	3C		48	4E	54	5A
7	0	7		15	1C	23	2A	31	38	3F		4D	54	5B	62	69
8	0	8	10	18	20	28		38	40	48	50	58	60	68	70	78
9	0	9	12	1B		2D	36	3F	48	51	5A	63	6C	75		87
A (10)	0	A	14		28	32	3C		50	5A	64		78	82	8C	96
B (11)	0	B	16	21	2C	37		4D	58	63		79	84	8F	9A
C (12)	0	C	18	24	30		48	54	60	6C	78	84	90	9C	A8	B4
D (13)	0	D		27	34	41	4E	5B	68	75	82	8F	9C		B6	C3
E (14)	0	E	1C	2A	38	46	54	62	70		8C	9A	A8	B6	C4	D2
F (15)	0	F	1E	2D	3C	4B		69	78	87	96		B4	C3	D2	E1

Двоичная система счисления

Восьмеричная система счисления

	0	1	2	3	4	5	6	7
0	0	0	0	0	0	0	0	0
1	0	1	2	3	4	5	6	7
2	0	2	4	6	10	12	14
3	0	3	6		14	17	22	25
4	0	4	10	14	20		30	34
5	0	5	12	17		31	36
6	0	6	14	22	30	36	44	52
7	0	7		25	34		5	61

Шестнадцатеричная система счисления

	0	1	2	3	4	5	6	7	8	9	A (10)	B (11)	C (12)	D(13)	E (14)	F (15)
0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0
1	0	1	2	3	4	5	6	7	8	9	A	B	C	D	E	F
2	0	2	4	6	8	A	C		10	12	14	16	18		1C	1E
3	0	3	6	9		F	12	15	18	1B		21	24	27	2A	2D
4	0	4	8		10	14	18	1C	20		28	2C	30	34	38	3C
5	0	5	A	F	14		1E	23	28	2D	32	37		41	46	4B
6	0	6	C	12	18	1E	24	2A		36	3C		48	4E	54	5A
7	0	7		15	1C	23	2A	31	38	3F		4D	54	5B	62	69
8	0	8	10	18	20	28		38	40	48	50	58	60	68	70	78
9	0	9	12	1B		2D	36	3F	48	51	5A	63	6C	75		87
A (10)	0	A	14		28	32	3C		50	5A	64		78	82	8C	96
B (11)	0	B	16	21	2C	37		4D	58	63		79	84	8F	9A
C (12)	0	C	18	24	30		48	54	60	6C	78	84	90	9C	A8	B4
D (13)	0	D		27	34	41	4E	5B	68	75	82	8F	9C		B6	C3
E (14)	0	E	1C	2A	38	46	54	62	70		8C	9A	A8	B6	C4	D2
F (15)	0	F	1E	2D	3C	4B		69	78	87	96		B4	C3	D2	E1