построить график линейной функции:
a)
y=13x+1,x∈−6;3
; b)
y=13x+1,x∈−6;3
.
Составим таблицу значений функции:
| (x) | (-6) | (3) |
| (y) | (-1) | (2) |
Построим на координатной плоскости (xOy) точки ((-6;-1)) и ((3;2)) и
проведём через них прямую.
Далее выделим отрезок, соединяющий построенные точки.
Этот отрезок и есть график линейной функции
y=13x+1,x∈−6;3
.
Точки ((-6); (-1)) и ((3); (2)) на рисунке отмечены тёмными кружочками.
b) Во втором случае функция та же, только значения (x=-6) и (x=3) не рассматриваются, так как они не принадлежат интервалу ((-6;3)).
Поэтому точки ((-6); (-1)) и ((3); (2)) на рисунке отмечены светлыми кружочками.
По графику линейной функции, можно определить наибольшее и наименьшее значения линейной функции на заданном отрезке.
В случае
a)
y=13x+1,x∈−6;3
, имеем:
yнаиб
(= 2) и
yнаим
(= -1);
b)
y=13x+1,x∈−6;3
, концы отрезка не рассматриваются, поэтому наибольшего и наименьшего значений нет.
In mathematics, a function defines a relationship between an independent variable and a dependent variable. In simple words, a function is a relationship between inputs and outputs in which each input is connected to exactly one output. If every element in set A has exactly one and only one image in set B, then the relation is said to be a function. Every function has a domain and a codomain, where a domain is a set of input values and a codomain, or range, is the set of possible output values for which the function is defined. The domain and codomain of a function are non-empty sets. If there exists a function from A → B and (a, b) ∈ f, then f (a) = b, where “a” is the image of “b” under “f” and “b” is the preimage of “b” under “f” and set A is the domain of the function and set B is its co-domain.
Examples of a function
- The formula for the circumference/perimeter of a circle is P = 2πr, where r is the radius of a circle. We can say that circumference/perimeter (P) is dependent on the radius (r) of the circle. In the language of functions, we say that P is defined as a function of r.
- The area (A) of a square A is a function of its side length. The dependence of A on s is given by A = 4s2.
Table Values of a Function
The table values of a function are referred to as the list of numbers that can be used to substitute for the given variable. By using this variable within the equation or in the other function, it is simple to determine the value of the other variable or the equation’s missing integer. In the table of values of a function, there are two kinds of variables, namely an independent variable and a dependent variable. For any equation of a function, an independent variable is selected independently to determine the value of a dependent variable, which is the output of the given function. The table of values is unique for every function. A graph of the given function can be plotted easily after the determination of the values of the independent and dependent variables. There are many uses and applications for tables of values of a function. These are used in the fields of mathematics, physics, and engineering.
How to make the Table of Values of a Function?
A function is typically represented by f(x), where x is the input, and its general representation is y = f(x).
- Create the table first, then choose a range of input values.
- In the left-hand side column, substitute each input value into the given equation.
- To determine the output value, evaluate the equation in the middle column. (A middle column is optional as the table of values just contains the input (independent variable) and output (dependent variable) pair.)
- Now, note down the output values in the right-hand side column.
Let us solve an example to understand the concept better.
Example: Write the table of the value for the function y = √x.
Here, the input is x and the output is y, where y = √x.
x value
Equation
y = √x
y value
0
y = √0 = 0
0
1
y = √1 = 1
1
4
y = √4 = 2
2
9
y = √9 = 3
3
16
y = √16 = 4
4
25
y = √25 = 5
5
Sample Problems
Problem 1: Write the table of values for the function y = 3x + 5.
Solution:
Here, the input is x and the output is y, where y = 3x + 5.
x value
Equation
y = 3x +5
y value
-2
y = 3(-2) + 5 = -6 + 5 = -1
-1
-1
y = 3(-1) + 5 = -3 + 5 = 2
2
0
y = 3(0) + 5 = 0 + 5 = 5
5
1
y = 3(1) + 5 = 3 + 5 = 8
8
2
y = 3(2) + 5 = 6 + 5 = 11
11
Problem 2: Write the table of values for the function P = 4s, where P is the perimeter of a square and a is its side length.
Solution:
Here, the input is s and the output is P, where P = 4s.
s value
Equation
P = 4s
P value
1
4 × 1 = 4
4
2
4 × 2 = 8
8
3
4 × 3 = 12
12
4
4 × 4 =16
16
5
4 × 5 = 20
20
Problem 3: Write the table of values for the function y = 2x + 3x.
Solution:
Here, the input is x and the output is y, where y = 2x + 3x .
x value
Equation
y = 2x + 3x
y value
-2
y = 2-2 + 3-2 = 1/22 + 1/32 = 1/4 + 1/9 = 13/36 = 0.3611
0.3611
-1
y = 2-1 + 3-1 = 1/2 + 1/3 = 5/6 = 0.834
0.834
0
y = 20 + 30 = 1 + 1 = 2
2
1
y = 21 + 31 = 2 + 3 = 5
5
2
y = 22 + 32 = 4 + 9 = 13
13
3
y = 23 + 33 = 8 + 27 = 35
35
Problem 4: Write the table values for the function y = cos x × sin x.
Solution:
Here, the input is x and the output is y, where y = cos x × sin x.
x value
Equation
y = cos x × sin x
y value
0°
y = cos 0 sin 0 = 1 × 0 = 0
0
30°
y = cos 30 sin 30 = √3/2 × 1/2 = 3/4
√3/4
45°
y = cos 45 sin 45 = 1/√2 × 1/√2 = 1/2
1/2
60°
y = cos 60 sin 60 = 1/2 × √3/2 = 3/4
√3/4
90°
y = cos 90 sin 90 = 0 × 1 = 0
0
180°
y = cos 180 sin 180 = -1 × 0 = 0
0
Problem 5: Write the table values for the function y = x2 – 5x + 6.
Solution:
Here, the input is x and the output is y, where y = x2 – 5x + 6.
x value
Equation
y = x2 – 5x + 6
y value
-3
y = (-3)2 – 5(-3) + 6 = 9 + 15 + 6 = 30
30
-2
y = (-2)2 – 5(-2) + 6 = 4 + 10 + 6 = 20
20
-1
y = (-1)2 – 5(-1) + 6 = 1 + 5 + 6 = 12
12
0
y = 02 – 5(0) + 6 = 0 – 0 + 6 = 6
6
1
y = 12 – 5(1) + 6 = 1 – 5 + 6 = 2
2
2
y = 22 – 5(2) + 6 = 4 – 10 + 6 = 10- 10 = 0
0
3
y = 32 – 5(3) + 6 = 9 – 15 + 6 = 15 – 15 = 0
0
Last Updated :
19 Jul, 2022
Like Article
Save Article
Данная статья не содержит графических
иллюстраций. Поэтому знакомиться с ее
содержанием будет удобнее, имея под рукой лист
бумаги и карандаш.
1. Линейная функция
При изучении линейной функции на уроках алгебры в 7-м
классе учащиеся довольно успешно осваивают
способ построения прямой по двум точкам. При этом
составляется таблица, в которой задаются
значения х и вычисляются соответствующие
значения y. Однако при построении прямой
часто допускаются неточности: из-за того, что
выбранные точки очень близко расположены друг к
другу, построенная прямая “уходит в сторону”.
Построить график линейной функции можно гораздо
быстрее, если заметить определенные
закономерности. Рассмотрим примеры.
Пример 1. Построить график функции .
Решение Составим таблицу значений функции.
| Порядковый № | 1 | 2 | 3 | 4 | 5 |
| x | 0 | 1 | 2 | 3 | 4 |
| y | -3 | -1 | 1 | 3 | 5 |
Первая точка выбирается традиционно – точка
пересечения прямой с осью ординат. А дальше
обратим внимание, что разность значений функции , т.е. совпадает
со значением углового коэффициента заданной
функции. А значит, для построения точек на
координатной плоскости вся информация заложена
в коэффициентах заданной линейной функции.
Алгоритм построения точек следующий:
- строим первую точку
;
- переносим ее на 1 единицу вправо и две единицы
вверх (это вторая точка, принадлежащая прямой): - вторую точку снова перемещаем на 1 единицу
вправо и две единицы вверх и получаем третью
точку искомой прямой; - далее все повторяется любое число раз.
Пример 2. Построить график функции .
Решение Первая точка имеет координаты . Каждая
следующая получается из предыдущей смещением на
1 единицу вправо и на 3 единицы вниз.
Рассмотрим теперь случай, когда угловой
коэффициент линейной функции задается дробью.
Пример 3. Построить график функции .
Решение Составим таблицу значений функции.
Чтобы получить точки прямой с целочисленными
координатами, возьмем значения х, кратные
трем. Ну. а первая точка, по-прежнему, – точка
пересечения прямой с осью ординат.
| x | 0 | 3 | 6 | 9 | 12 |
| y | -4 | -2 | 0 | 2 | 4 |
Построим точки на координатной плоскости.
Видно, что каждая следующая точка получается из
предыдущей сдвигом на 3 единицы вправо и 2 единицы
вверх. Проводим прямую.
Пример 4. Построить график функции .
Решение Первая точка имеет координаты . Заметим, что
угловой коэффициент прямой . Значит, каждая следующая точка
прямой будет получена из предыдущей смещением на
5 единиц вправо и на 4 единицы вниз. Строим точки и
проводим прямую.
Обратите внимание, что в случае дробного
углового коэффициента линейной функции
знаменатель дроби указывает количество единиц
для перемещения точки вправо, а числитель –
количество единиц, на которые переместится точка
вверх (при )
или вниз (при k<0).
2. Квадратичная функция
2.1. С графиком квадратичной функции учащиеся
знакомятся еще в седьмом классе. При этом, для
построения параболы, как правило, записывается
таблица значений функции для , затем полученные точки строят
на координатной прямой и рисуют параболу. Более
продвинутые ученики записывают таблицу только
для , строят
полученные точки и проводят правую ветвь
параболы. Затем, воспользовавшись симметрией
графика относительно оси ординат, строят точки
параболы для
и рисуют вторую ветвь параболы.
Записи таблицы можно избежать, если заметить
одну закономерность в расположении указанных
точек. Посмотрим таблицу значений функции :
В третьей строке таблицы записана разность
двух последующих значений функции. Видно, что
полученные числа образуют последовательность
нечетных чисел (легко убедиться, что эта
закономерность выполняется и далее, например, ). Этот факт
легко запоминается. А с учетом этой
закономерности построить характеристические
точки параболы можно так:
- первая точка – начало координат;
- вторая точка получается из первой смещением на
одну единицу вправо и на одну единицу вверх; - третья получается смещением второй точки на
один вправо и три вверх; - четвертая точка получается переносом третьей
на один вправо и пять вверх; - затем строятся точки левой ветви параболы за
счет симметрии графика относительно оси ординат.
Остается провести плавную линию через
полученные точки, и парабола построена.
2.2. Перейдем теперь к квадратичной
функции вида ,
которая изучается уже в восьмом классе. Учащиеся
узнают, что коэффициент а определяет
направление ветвей параболы, а также растяжение
или сжатие графика вдоль оси ординат. А для
построения графика все равно просчитывают
координаты точек. Но без этого можно обойтись,
если знать указанную выше закономерность
построения точек параболы . И если для нее сдвиг точек вдоль
оси OY задавался последовательностью чисел , то для функции
эта
последовательность чисел будет .
Пример 5. Построить график функции .
Решение Графиком функции служит парабола,
ветви которой направлены вниз, а вершина
находится в начале координат. Для построения
других точек параболы вспомним про нечетные
числа ,
умножим их на ,
получаем последовательность чисел Знак
говорит о том , что смещение
точек будет сделано вниз. На словах алгоритм
построения звучит так: от начала координат одна
единица вправо и две вниз; от новой точки одна
единица вправо и шесть вниз; строим точки,
симметричные полученным относительно оси
ординат; проводим параболу.
Пример 6. Построить график функции .
Решение Графиком функции – парабола, ветви
которой направлены вверх. Вершина параболы
находится в начале координат. Для построения
других точек воспользуемся последовательностью При
получаем
следующий порядок перемещений вдоль оси ординат . Строим точки
на координатной плоскости: от точки 1 клетка вправо и
полклетки вверх, от полученной точки снова одна
клетка вправо и полторы клетки вверх, потом от
новой точки опять одна клетка вправо и две с
половиной клетки вверх и т.д. (ясно, что в
указанном случае за единичный отрезок на осях
координат принимается одна клеточка в тетрадном
листе). Затем строим точки левой ветви параболы
за счет симметрии графика относительно оси OY и
рисуем параболу.
2.3. В 9-м классе учащиеся изучают
квадратичную функцию . Для построения ее графика с учетом
выше сказанного можно применять следующий
алгоритм:
- найти координаты вершины параболы
;
- построить в системе координат полученную точку
и провести оси вспомогательной системы
координат (прямыеи
);
- по коэффициенту а определить направление
ветвей параболы; - построить во вспомогательной системе координат
характеристические точки функции, следуя алгоритму пункта
2.2. - провести плавную линию через указанные точки.
График готов.
Пример 7. Построить график функции .
Решение Графиком функции – парабола.
- Вычисляем координаты вершины параболы:
.
- Строим точку
и проводим пунктиром вспомогательные оси
координат (прямые проходят через указанную точку
и параллельны осям ОХ и ОY). - Коэффициент при х2 в данной функции
равен 1. Значит, для построения
характеристических точек параболы применим ряд
чисел 1,3,5,…. , т.е. строим стандартную параболу, но
во вспомогательной системе координат (пункт 2.1.). - Проводим плавную линию через полученные точки.
Парабола построена.
ПРИМЕРЫ ДЛЯ САМОСТОЯТЕЛЬНОГО РЕШЕНИЯ
Постройте графики указанных функций:
Здравствуйте уважаемые родители и обучающиеся!
Откройте ваши тетради для классных работ и запишите тему урока: «Линейная функция, ее график и свойства»
Откройте страницу учебника 163, положите учебник перед собой. Приступим к изучению материала…
Сегодня мы поговорим о конкретных видах функции. Линейных функциях. Почему они называются линейными?
Обратимся к словарю:
Конечно, нас интересует геометрический смысл этого слова.
Линейная функция потому называется линейной, потому что ее график задает линию — одну сплошную прямую…
Давайте рассмотрим практический пример линейной функции.
Пример: Представим, что едет машина легковая с постоянной скоростью 100 км/ч. а грузовая со скоростью 60 км/ч. Скорость машин не меняется, а время идет. Проходит час, два, три, четыре… Машины еще в пути…Сколько они проехали?…
Давайте изобразим траекторию ее движения…
У нас есть две величины: Расстояние (S) и t (время). Зависимость очевидна. Дольше едешь — дальше будешь! Неправда ли?
Составим таблицу значений:
Мы получили значения по времени и расстоянию в течение 5 часов для легкового и грузового автомобилей.
Теперь можем перейти к графическому изображению, то есть графику функций: S = 60t и S=100t. За ось y ( зависимые переменные) обозначаем значения расстояния, за ось x (независимые переменные) обозначим время t. И построим графики в координатной плоскости:
Что мы видим в качестве графика — прямую! А какие формулы нам дали график — прямую??? Формулы вида: S = 60t и S=100t!!!
Получается, что формулы определенного вида дают определенные функции. Да. И мы сейчас с этим разберемся!
Записываем определение:
В колонке «Функция» (см рисунок выше) вы видите что они разные, но все они задают прямую, только под разным наклоном. Давайте убедимся, построим каждую функцию:
1 функция: у=5x+3.
Рассмотрим алгоритм ( правило построения линейной функции):
1 шаг. Это линейная функция. Почему? Потому что она представляет собой формулу y=kx+b, где к=5, b=3.
2 шаг. Согласно правилу, для построения линейной функции нужны две точки. Где их взять? И как? Легко. Вам нужно составить таблицу значений из двух чисел, которые вы сами захотите, но так, чтобы легко было их высчитать для построения самого графика.
Как видите, я взял независимые переменные x=0, x=1. Почему я так сделал? Я бы мог взять x=4334, но не стал…. Мне нужно получить всего лишь две точки, чтобы их соединить прямой. Зачем мне составлять сложные координаты. Я возьму такие, которые дают хорошие удобные числа.
3 шаг. Мы готовы построить график. Для этого обращаемся к координатной плоскости. Строим точки с координатами: (0; 3) и (3;8) и соединяем прямой. Получаем график линейной функции — прямую!!! Смотрите рисунок.
Давайте потренируемся в построении линейной функции. Я взял несколько линейных функций для эксперимента.
Давайте обсудим: Что в этих функциях одинакового? Мы видим, что у нее одинаковый коэффициент k=2. Значит графики одинаково будут построены? Как вы считаете? Смотрите на рисунок, на формулу и графики…
Что делает расположение графиков именно такими при одинаковом коэффициенте k=2? Меняет дело другой коэффициент b.
Запомните: коэффициент b в функции y=кx+b отвечает за точку пересечения графика с осью y. Проверьте это утверждение, глядя на рисунок…
С коэффициентом b в функции вида y=kx+b разобрались. Посмотрите на функцию, где коэффициент b отсутствует. То есть функция изменить немного вид: y=kx. Это не означает, что она перестала быть линейной, она просто будет проходить всегда через начало координат!!! Так как b отвечает за точку пересечения с осью y, а y =о! Давайте проиллюстрируем!!!
Слева функции, справа — их исполнение! Что их объединяет? Только то, что они линейные и проходят через одну точку — через начало координат, поскольку коэффициент b у них отсутствует, как видите сами…
Запомните: Если коэффициент b в функции y=кx+b отсутствует, то функция проходит через начало координат — (0;0). Функция вида y=кx называется прямой пропорциональной зависимостью. (стр 165 читайте)!!!
В линейной функции y=кx+b , коэффициент k тоже имеет свою роль. Его называют коэффициентом наклона. Запишем правило:
Другими словами: если прямая при пересечении с осью x образует:
——тупой угол: k<0
——острый угол: k>0
Проведем опыт: Рассмотрим несколько линейных функции:
y=-2x+1;
y=5x+3;
Первая функция:
Вторая функция:
Вот мы и разобрали значение коэффициентов. Ну, а пара чисел x и y — переменные, независимая и зависимая. Это мы обсуждали с вами уже.
Если вам необходимо больше информации: жмите сюда
Давайте посмотрим видео и подытожим все, что мы сказали выше:
Видео YouTube
Решение задач на линейную функцию y=кx+b
Сегодня мы рассмотрим с вами задачи:
№ 857 Смотрим решение и пробуем работать самостоятельно:
Видео YouTube
№ 858 Смотрим решение и пробуем работать самостоятельно:
Видео YouTube
Смотрим решение и пробуем работать самостоятельно:
Видео YouTube
Ваше домашнее задание на оценку: НАЖМИ СЮДА
Спасибо за занятие! Если есть вопросы, вы пишите мне в группе, в чате в вайбере. Я постараюсь на них ответить или записать голосовое сообщение с комментарием.
Функция, заданная формулой y=kx+b, где х – переменная, k и b – некоторые числа, называется линейной функцией. Переменную х называют независимой переменной, переменную у – зависимой переменной.
Графиком линейной функции является прямая. Для построения прямой достаточно взять два значения х, чтобы получить два значения у и, соответственно, две точки, через которые проходит единственная прямая.
Число k называется угловым коэффициентом прямой.
Свойства линейной функции
- Область определения функции – множество всех действительных чисел. То есть в данную формулу мы можем подставлять любое значение х.
- Областью значений также является множество всех действительных чисел.
- Функция не имеет ни наибольших, ни наименьших значений.
- При k – положительном, угол наклона к оси х острый, другими словами – график функции возрастает.
- При k отрицательном угол наклона к оси х тупой, то есть график функции – убывает.
- При k=0 прямая параллельна оси х.
- Частный случай линейной функции: y=kx, где число b=0, эту функцию называют прямой пропорциональностью, график такой функции проходит через начало координат.
Рассмотрим на примерах расположение прямых в координатной плоскости в зависимости от значения чисел k и b.
Пример №1
Построить график функции у=2х – 1. Для того, чтобы удобнее было выполнять вычисления, построение и т.д. сделаем таблицу для значений х и у:
Для построения графика подбираем два значения х, одно из них желательно брать равное нулю, второе, например 3 (подбираем небольшие числа).
Теперь подставляем значения х в формулу и вычисляем соответствующие значения у:
у=2х – 1=2×0 – 1= –1;
у=2х – 1=2×3 – 1= 5.
Вписываем в таблицу значения у:
Теперь строим систему координат, отмечаем в ней точки с координатами А(0; –1) и В(3;5), проводим через эти две точки прямую.
Итак, по формуле мы видим, что угловой коэффициент – положительный, значит, график – возрастает, что мы и видим на нашем графике.
Пример №2.
Построить график функции у= –3х+4. Итак, делаем таблицу на два значения, например, возьмем 0 и 2.
По формуле видим, что угловой коэффициент отрицательный, значит, прямая будет убывать. Строим убывающую прямую в системе координат через две точки А(0;4) и В(2; –2).
Пример №3
Построить график функции у=4. Видим, что в данном случае число х=0, значит, прямая будет проходить через точку с координатой (0;4) параллельно оси х. На графике это выглядит следующим образом:
Построить график функции у=3х. Данная функция является частным случаем, когда прямая проходит через начало координат. Поэтому в данном случае можно взять устно одно значение х, например 2, тогда у получим равный 6. Таким образом, имеем две точки (2;6) и (0;0). Строим их в системе координат и проводим через них прямую, которая будет возрастать, так как угловой коэффициент равен 3, т.е. положительный.
Задание OM1106o
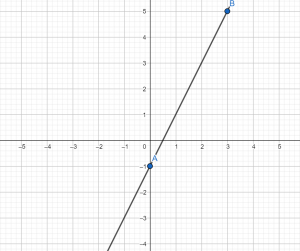
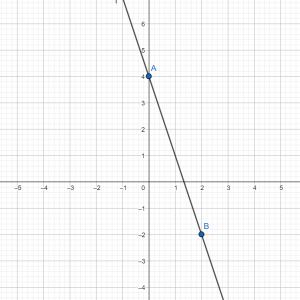
На рисунках изображены графики функций вида y=kx+b. Установите соответствие между графиками функций и знаками коэффициентов k и b.
ГРАФИКИ:
КОЭФФИЦИЕНТЫ:
1) k>0, b<0 2) k>0, b>0 3) k<0, b<0
ассмотрим коэффициенты под №3. Если k<0, значит, график имеет тупой (>900) угол с положит.направлением оси абсцисс (Ох). Если b<0, то это говорит, что график пересекает ось ординат (Оу) ниже нуля. Эти два условия реализованы на графике В. Итак, получаем для ответа пару: В–3.
У двух других пар коэффициентов (№№ 1 и 2) зафиксировано, что k>0. Это соответствует оставшимся графикам А и Б, т.к. они оба наклонены к положительно направлению оси Оx под острым углом (<900). Следовательно, выбор соответствия должен быть выполнен по коэффициенту b.
В 1-й паре коэффициентов b<0. Это означает, что соответствующий им график должен пересекать ось Оу в точке ниже начала координат. Таковым является график Б, и мы получаем пару Б–1. В паре коэффициентов №2 b>0, что соответствует графику А, который пересекает ось Оу выше начала координат. Это подтверждает, что и оставшаяся пара А–2 тоже верна.
Ответ: 213
pазбирался: Даниил Романович | обсудить разбор
Задание OM1103o
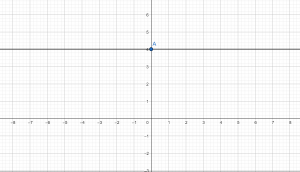
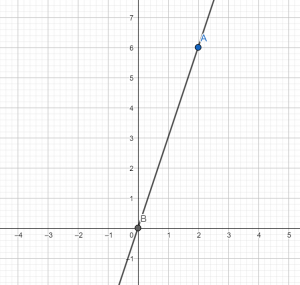
Установите соответствие между функциями и их графиками.
Функции:
A) y = 3x
Б) y = -3x
В) y = (1/3)x
Графики:
Функция представляет собой линейную зависимость, а именно уравнение первого порядка вида:
y = kx + b
График данной функции зависит от k и b.
- если k < 0, то функция убывает, то есть линия идет сверху вниз, как на третьем рисунке
- если k > 0, то функция возрастает, то есть линия идет снизу вверх, как на первых двух рисунках
- коэффициент b определяет сдвиг по оси y, если b < 0, то прямая пересекает ось y ниже 0 в точке y = b, если b > 0, то выше ноля в точке y = b
- если k >1, то прямая идет круче, чем обычная y = x (как на втором и третьем графике), если k <1 , то положе, как на примере рисунка №1
Следовательно, графику y = 3x соответствует рисунок 2, так как прямая идет снизу вверх и она более крутая, чем кривая на рисунке 1, которому соответствует функция y = (1/3)x.
Графику 3 соответствует функция y = -3x так как k = -3 < 0, и график идет сверху вниз.
Ответ:
A) 2
Б) 3
В) 1
Ответ: 231
pазбирался: Даниил Романович | обсудить разбор
Даниил Романович | Просмотров: 6.2k